Conformational Properties of Polymers at Droplet Interfaces as Model Systems for Disordered Proteins

Abstract

Polymer models serve as useful tools for studying the formation and physical properties of biomolecular condensates. In recent years, the interface dividing the dense and dilute phases of condensates has been discovered to be closely related to their functionality, but the conformational preferences of the constituent proteins remain unclear. To elucidate this, we perform molecular simulations of a droplet formed by liquid‒liquid phase separation of homopolymers, as a surrogate model for the prion-like low-complexity domains. By systematically analyzing the polymer conformations at different locations in the droplet, we find that the chains become compact at the droplet interface compared to the droplet interior. Further, segmental analysis revealed that the end sections of the chains are enriched at the interface to maximize conformational entropy, and are more expanded than the middle sections of the chains. We find that the majority of chain segments lie tangential to the droplet surface and only the chain ends tend to align perpendicular to the interface. These trends also hold for the natural proteins FUC LC and LAF-1 RGG, which exhibit more compact chain conformations at the interface compared with the droplet interior. Our findings provide important insights into the interfacial properties of biomolecular condensates and highlight the value of using simple polymer physics models to understand the underlying mechanisms.

Membraneless organelles or biomolecular condensates formed through liquid‒liquid phase separation (LLPS) have been widely reported in various cellular functions, including gene expression, signal transduction, stress response, and the assembly of macromolecular complexes^1–5. Examples of such condensates include the nucleolus, Cajal bodies, P bodies, and stress granules. Intrinsically disordered proteins (IDPs) play an important role in the formation of biomolecular condensates through LLPS^6–11. Due to the numerous similarities between IDPs and synthetic polymers, classical polymer-based models offer a powerful approach for investigating the conformations¹², dynamics¹³, and phase behavior of IDPs^14–17. In particular, such models have been extensively used to reveal the sequence-dependent conformations of IDPs in the dense and dilute phases of condensates^18–27.

In recent years, there has been increasing recognition of the important role played by the interfaces dividing the dense and dilute phases of biomolecular condensates. Folkmann et al. have reported that the IDP assemblies at the interface of PGL-3 droplets reduced the surface tension, thus preventing droplet coarsening. Kelley et al. reported that amphiphilic proteins on the surface of condensates acted like surfactants, thus regulating the size and structure of condensates²⁸. Further, the interface can affect the interactions between biomolecular condensates and other biomolecules within the cell²⁹. Böddeker et al. demonstrated that cytoskeletal filaments had a nonspecific affinity for stress granule interfaces, which explained the distinct enhancement of tubulin density around granules³⁰. Lipiński et al. reported that the condensate interface can serve as a nucleation site promoting the aggregation of amyloidogenic proteins³¹. Inspired by the critical role of interfaces in various functionalities, much research has focused on determining mesoscopic interfacial properties such as surface tension^13,32,33, surface adsorption³⁴, and electrochemical properties³⁵, which are deemed important for regulating biological functions^29,36. For example, it was shown that the condensates could form an autophagosome only if the surface tension is lower than a critical value³⁷. The film formed by protein adsorption at the air/water interface has a low interfacial elasticity at the protein’s isoelectric pH because of the compact structure³⁸.

However, the microscopic conformations of individual IDPs at interfaces remain largely unclear, even though these exposed polymers largely dictate the surface properties. . For example, surfaces grafted by a synthetic polymer such as PNIPAM have been shown to result in a four-fold difference in the Young’s modulus between the swollen and collapsed states,³⁹ and the surface wettability is stronger for polymer interfaces in stretched states than in collapsed states⁴⁰. For biomolecular condensates, the chain conformations can be important for their functions like the regulation of condensates conformation on mRNA decapping⁴¹. To shed light on this question, Farag et al. recently studied the interface conformations of biomolecular condensates using lattice-based Monte Carlo simulations^42,43.They reported that the overall dimensions of prion-like low-complexity domains and homopolymers varied within the condensates, being most expanded at the interface and preferring to be oriented perpendicular to it. These pioneering studies open up avenues for detailed characterization of the segmental-level conformational properties and their contribution to the chain-level conformational preferences at the condensate interfaces, which remain elusive.

In this letter, we report chain-level and segmental-level conformations of IDPs at the condensate interface from molecular simulations of hydrophobic homopolymers and two naturally occurring IDPs. We use an off-lattice polymer model, where each residue (“monomer”) is represented by a spherical bead in an implicit solvent (model details are provided as Supporting Information (SI)). This model is a good approximation for numerous IDPs, such as prion-like low-complexity domains⁴². Recently, we successfully used hydrophobic homopolymers as a reference to establish the biophysics of phase separation of IDPs, revealing that distributed interactions better stabilize the condensed phase than localized interactions²⁴. To understand the basic principles governing the chain conformations in the droplet, we focus here on the hydrophobic homopolymers and include the results for the natural IDPs in the SI.

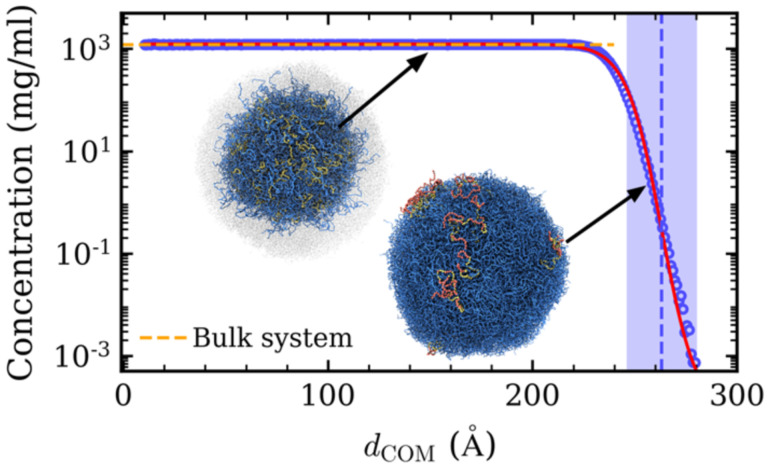
Due to the hydrophobic nature of the employed model IDP, it quickly formed a spherical condensate of radius R = 249Å, which is defined as the position where the concentration drops to half the value near the droplet center (Fig. 1). Drawing upon previous research on the liquid-vapor interface in slabs⁴⁴, the radial concentration profile is fit to a hyperbolic tangent functional form

$$lo{g}_{10}\left[c\left(d_{COM}\right)\right]=\frac{1}{2}\left[lo{g}_{10}\left(c^{\mathit{\text{dense}}}\right)+lo{g}_{10}\left(c^{\mathit{\text{dilute}}}\right)\right]-\frac{1}{2}[lo{g}_{10}\left(c^{\mathit{\text{dense}}}\right)-lo{g}_{10}\left(c^{\mathit{\text{dilute}}}\right)]\mathit{\text{tanh}}\left(\frac{2\left(d_{COM}-d_{MID}\right)}{\delta }\right),$$ (1)

where d_COM is the distance from the droplet’s center of mass, c(d_COM) is the radial monomer concentration, c^dense and c^dilute are the monomer concentrations of the dense phase and dilute phase, respectively, d_MID is the midpoint of the interface, and δ is the width of the interface. By fitting the computed radial concentration curve to (Eq. 1), the interfacial region was defined (Fig. 1). To establish a bulk reference without interface effects, we simulated a concentrated homopolymer solution in a cubic box at a constant pressure of P = 0 atm. With increasing d_COM, the concentration in the droplet interior remained constant (equal to the expected concentration in the bulk system), while it monotonically decreased at the interface. In this case, the dilute phase concentration is equal to 0 mg⁄ml, as all chains are inside the droplet.

Fig. 1.

Concentration as a function of distance from the droplet’s center of mass (d_COM). The horizontal dashed line represents the concentration in the bulk system. The red line is the fitted curve for the simulation data (symbols). The purple shaded area is the interface region. The vertical dashed line represents the middle of the interface. The inset shows simulation snapshots of the droplet interior and interface. The yellow chains in the interior snapshot are at a distance of d_COM = 150 Å. The chains colored yellow and red in the interface snapshot have their center-of-mass in the interface, with the red beads representing segments in the interface.

After determining the droplet interface, we studied the conformations of polymer chains within the interface and dense phase of the droplet. For this purpose, we computed the radius of gyration of the chains⁴⁵

$$R_g={\left(\frac{1}{N}{\sum }_{i=1}^N{r}_i^2\right)}^{\frac{1}{2}},$$ (2)

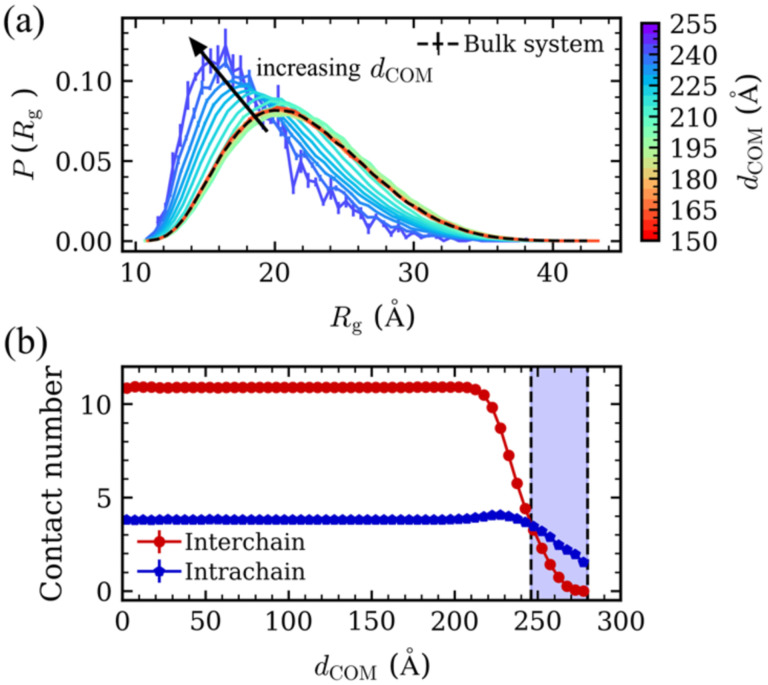
where the sum goes over the N monomers in the chain, and r_i is the distance from the i^th monomer to the chain’s center of mass (COM). We find that the corresponding R_g distribution in the bulk system (Fig. 2) was significantly broader, as compared to that of the single chain (Fig. S1), highlighting the preference of chains to expand inside the condensate, as expected from Flory’s ideality hypothesis⁴⁶. Next, we analyzed the distribution of R_g at different positions within the droplet. Based on the distance between the chain’s COM and the droplet’s COM (d_COM), we assigned the polymer chains into different positional bins (Fig. 2a). We found that when d_COM ≤ 210 Å, where the local monomer concentration is equal to the bulk system concentration (Fig. 1), the R_g distributions overlapped with the bulk distribution, indicating the consistency between the interior of the droplet and the bulk phase. With increasing d_COM, the peak of the R_g distribution shifted gradually to smaller R_g values (Fig. 2a), demonstrating a continuous transition from expanded conformations to more compact conformations when moving from the interior of the droplet towards the interface. This result is also supported by the average number of interchain and intrachain contacts for each monomer (Fig. 2 b), which decreased monotonically with increasing d_COM, because of the decreasing monomer concentration (Fig. 1). At the interface, the number of average intrachain contacts was larger than the number of interchain contacts, which means that the chains interacted primarily with themselves and thus were more compact than in the droplet interior, where interchain interactions dominated.

Fig. 2.

(a) Distribution of radius of gyration (R_g). The dashed line represents the R_g distribution in a bulk system. The color gradient from red to purple corresponds to the distribution of R_g for chains with d_COM ranging from 150 to 255 Å. (b) Average contact number per monomer as a function of d_COM for the interchain and intrachain contacts. The vertical dashed lines represent the interface boundaries.

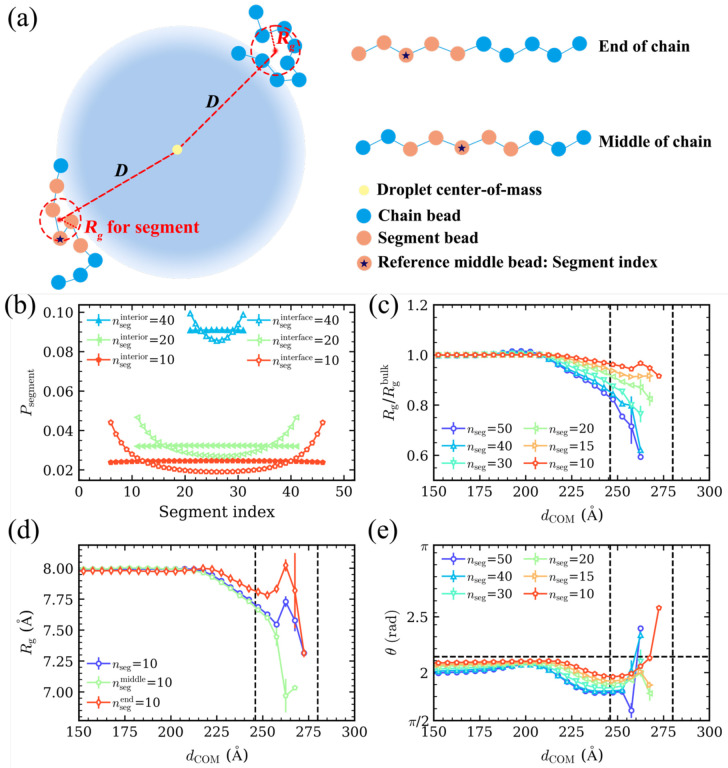
Our observation of compact chain-level conformations at the interface led us to investigate how segments within a chain contributed to its compaction, following previous calculations for the end-to-end vector of grafted polymers⁴⁷ and R_g of polymer thin films⁴⁸. We first characterized the distribution of chain segments of different length n_seg at the droplet interface (Fig. 3a,b). The middle bead of the segments for a given n_seg serves as the reference bead, the index of which we refer to as segment index. Note that a segment index closer to 1 or 50 corresponds to a segment closer to the chain termini, and the curves are symmetrical because the homopolymer chains do not have any “heads” or “tails”. We found that the highest probability always occurred at the position closest to the chain’s ends at the interface, regardless of the length of the segment, suggesting that the chain terminals were more inclined to distribute at the interface compared to the middle of the chains. This is in stark contrast to the droplet interior, where we found the same probabilities for segments at different relative positions within the chain (Fig. 3b). The enrichment of chain ends at the interface can be understood by considering the loss in conformational entropy incurred by placing a monomer at the interface, which is smaller for the end monomers compared to any other monomer.

Fig. 3.

Segmental analysis. (a) Schematic diagram of the R_g calculation method for chains and their segments. Blue beads represent the chain monomers, while orange beads represent a specific segment. (b) Probability distribution of the segments for different segment lengths (n_seg) at the interface (hollow symbols) and in the droplet interior (solid symbols). The segment index is represented by the index of middle bead of each segment (reference bead). When n_seg is even, the larger index between the two middle beads is considered as the segment index. (c) Normalized average R_g of the different length segments with respect to d_COM. The black dashed lines represent the boundaries of the interface. (d) R_g of segments consisting of 10 monomers as a function of d_COM. The purple line represents for the average R_g for all segments in the chain of that length. The green and red lines represent the segments located at the middle and end of the chains, respectively. (e) Angle (θ) of the different length segments with respect to d_COM. The horizontal dashed line represents the average angle for isotropic distribution of segments.

We next asked if the spatial preference of the chain segments at the droplet interface vs its interior had an effect on the segmental-level conformations. For this purpose, we calculated the average R_g for the segments of different lengths n_seg as a function of distance d_COM between their COM and the droplet’s COM (Fig. 3c). We found that the R_g at the interface is smaller than that in the droplet interior for all n_seg considered. For n_seg > 15, R_g monotonically decreased as the droplet interface is approached. For n_seg = 15, R_g no longer decreased in the interface region. Interestingly, for n_seg = 10, we found that R_g marginally increased in the middle of the interface region, following which it decreased again. To explain this nonmonotonic trend in R_g for the short segments at the interface, we analyzed R_g of different n_seg located only at the chain ends and compared it with that in the middle of the chain. For longer segments n_seg ≥ 20, the segmental R_g monotonically decreased from the droplet interior to the interface, regardless of the position of the segments (Fig. S2). However, for shorter segments n_seg ≤ 15 (Figs. 3d and S2), we found that the R_g of the segments located at the chain ends exhibited a nonmonotonic trend in the interface region: we observed an increase in segmental R_g for d_COM > 250 Å, attaining the maximum value in the middle of the interface region, following which it continued to decrease. Surprisingly, the R_g of shorter segments located in the middle of the chains monotonically decreased throughout the interface region. These observations indicate that the chain termini are the only contributors to the observed expansion of short segments (Fig. 3c). In summary, although the whole chain is more compact at the interface, short terminal segments are more expanded than middle segments at the interface and even slightly more expanded than the short segments in the droplet interior.

Given the stark differences in the global and local conformations of the chains in the interface region, we next investigated their chain-level and segmental-level orientations. We defined the angle θ between the segment-to-droplet COM vector and the segment end-to-end vector to characterize the orientation of the chains in the interface region (Fig. S3a). The positions of segments are again defined through d_COM. When the angle is close to π⁄2, the segment lies tangential to the droplet surface, whereas an angle close to π corresponds to an orientation perpendicular to the droplet surface. For different segment lengths (n_seg = 10, 15, 20, 30, 40) and the whole chain (n_seg = 50), the angles show an increasing trend at the interface (Fig. 3e). This increase primarily originates from the segments near the chain ends (Fig. S3b) rather than segments in the middle of the chains (Fig. S3c). This observation can be explained by considering the end-to-end distance (R_e) (Fig. S4). The smallest angle for segments (Fig. S3a) can be estimated as:

$${\theta }_{\min }=\mathit{\text{arcsin}}\left(\frac{\sqrt{R^2-{\left(\frac{R_e}{2}\right)}^2}}{R}\right),$$ (3)

where R is the distance between the terminal bead of the segment and the droplet COM, and R_e is the end-to-end distance of the segment. At the interface, R is much larger than R_e, so that θ_min becomes close to π⁄2 (i.e., tangential orientation). πIf segments are oriented randomly, the average angle should be close to π − 1 (calculation shown in SI). We found that the angles of segments located in the middle of chains were between π⁄2 and π − 1, indicating that these segments lied predominantly tangential to the surface (Fig. S3c). While the angles of end segments located in the droplet interior were between π⁄2 and π − 1, end segments near the interface exhibited a tendency to form angles larger than π − 1 (Fig. S3b). However, these segments remained closer to the angle representing isotropic segments, π − 1, than perpendicular segments, π. These results demonstrate that despite the tendency of chain ends to align perpendicular to the surface, the majority of chain segments remain primarily tangential to the droplet surface.

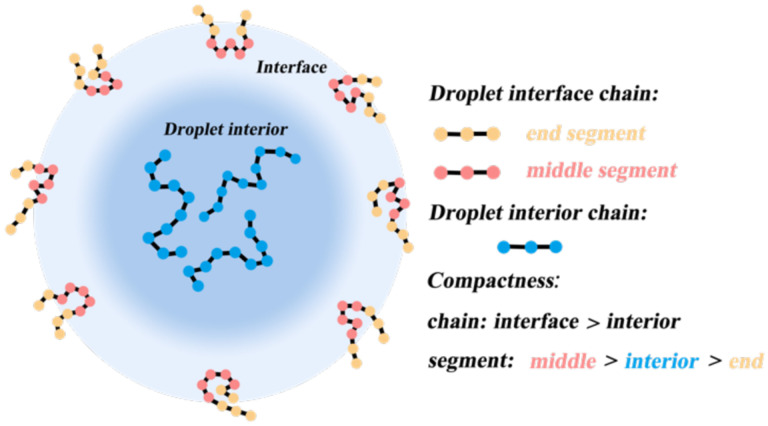
Based on our investigation of size and orientation of chain segments at different positions in the droplet, we propose a model for homopolymer conformations in condensates as depicted in Fig. 4. Compared with the droplet interior, which we found to be consistent with the bulk phase, the distribution of R_g in the interface shifted to smaller values, indicating more compact chain conformations at the droplet interface. Through our characterization of the conformational preferences of segments of different lengths at different positions, we have discovered that segments located at the chains’ ends slightly expand more in the droplet interface compared to the droplet interior, while the middle segments of the chains are more collapsed in the interface region than in the droplet interior. These end segments are enriched at the interface to minimize the entropy loss during LLPS. At the interface, the chain ends exhibit a tendency to align perpendicularly to the interface, but the majority of the chains are still parallel to the surface. We speculate that these conformational changes originate from the change in the local environment surrounding the chains: Compared to the interior of the droplet, the lower monomer concentration at the interface leads to a decrease in the (effective) solvent quality, thus resulting in chain collapse. Similar compact chain conformations at the interface have been reported previously for hydrophobic homopolymers^49–51.

Fig. 4.

Schematic of homopolymer conformations at the droplet interface. Polymer chains are more compact at the interface than in the droplet interior. Compared to the interior of the droplet, the chain ends are more expanded, while the middle segments of the chains are more collapsed at the interface. The chain ends exhibit a tendency to be perpendicular to the droplet surface, whereas the majority of chains lie predominantly tangential to the droplet surface.

Our findings illustrate the conformational preferences at the condensate interface using a homopolymer model, which can also be observed for naturally occurring IDPs. For FUS LC and LAF-1 RGG (Fig. S5), chains are more collapsed at the interface compared with the expanded conformations in the droplet interior. In future work, quantitatively describing the relationship between conformations and interfacial properties will be highly beneficial for our understanding of the biological functions of biomolecular condensates.