Summary
Neuronal wiring diagrams reconstructed by electron microscopy1–5 pose new questions about the organization of nervous systems following the time-honored tradition of cross-species comparisons 6,7. The C. elegans connectome has been conceptualized as a sensorimotor circuit that is approximately feedforward 8–11, starting from sensory neurons proceeding to interneurons and ending with motor neurons. Overrepresentation of a three-cell motif often known as the “feedforward loop” has provided further evidence for feedforwardness10,12. Here we contrast with another sensorimotor wiring diagram that was recently reconstructed from a larval zebrafish brainstem13. We show that the three-cycle, another three-cell motif, is highly overrepresented in the oculomotor module of this wiring diagram. This is a first for any neuronal wiring diagram reconstructed by electron microscopy, whether invertebrate12,14 or mammalian15–17. The three-cycle of cells is “aligned” with a three-cycle of neuronal groups in a stochastic block model18 of the oculomotor module. However, the cellular cycles exhibit more specificity than can be explained by the group cycles; recurrence to the same neuron is surprisingly common. Cyclic structure could be relevant for theories of oculomotor function that depend on recurrent connectivity. The cyclic structure coexists with the classic vestibulo-ocular reflex arc for horizontal eye movements19, and could be relevant for recurrent network models of temporal integration by the oculomotor system20,21.
eTOC Blurb:
Yang et al. analyze a wiring diagram of a larval zebrafish brainstem. Cycles of three synaptically connected cells are highly overrepresented. They are aligned with a three-cycle of neuronal groups in a stochastic block model, but exhibit more specificity. Recurrence to the same neuron is surprisingly common.
Results
The center subgraph and its degree distributions
Previously we reconstructed a neuronal wiring diagram from a larval zebrafish brainstem13. The number of presynaptic sites (“presynapses”) and postsynaptic sites (“postsynapses”) on a neuron varies greatly (Figures S1A, B). Some of this variation is biological, and some results from truncation of arbors by the borders of the EM imaged volume. To exclude reconstructed cells that are highly truncated, we define a “center subgraph” that retains only neurons with presynapse numbers and postsynapse numbers exceeding thresholds (Figures 1A; S1A, B). The center subgraph includes 419 neurons and 5,605 connections, and was used for subsequent analyses. This definition of the center subgraph is simpler than our previous spectral definition13.
Figure 1.
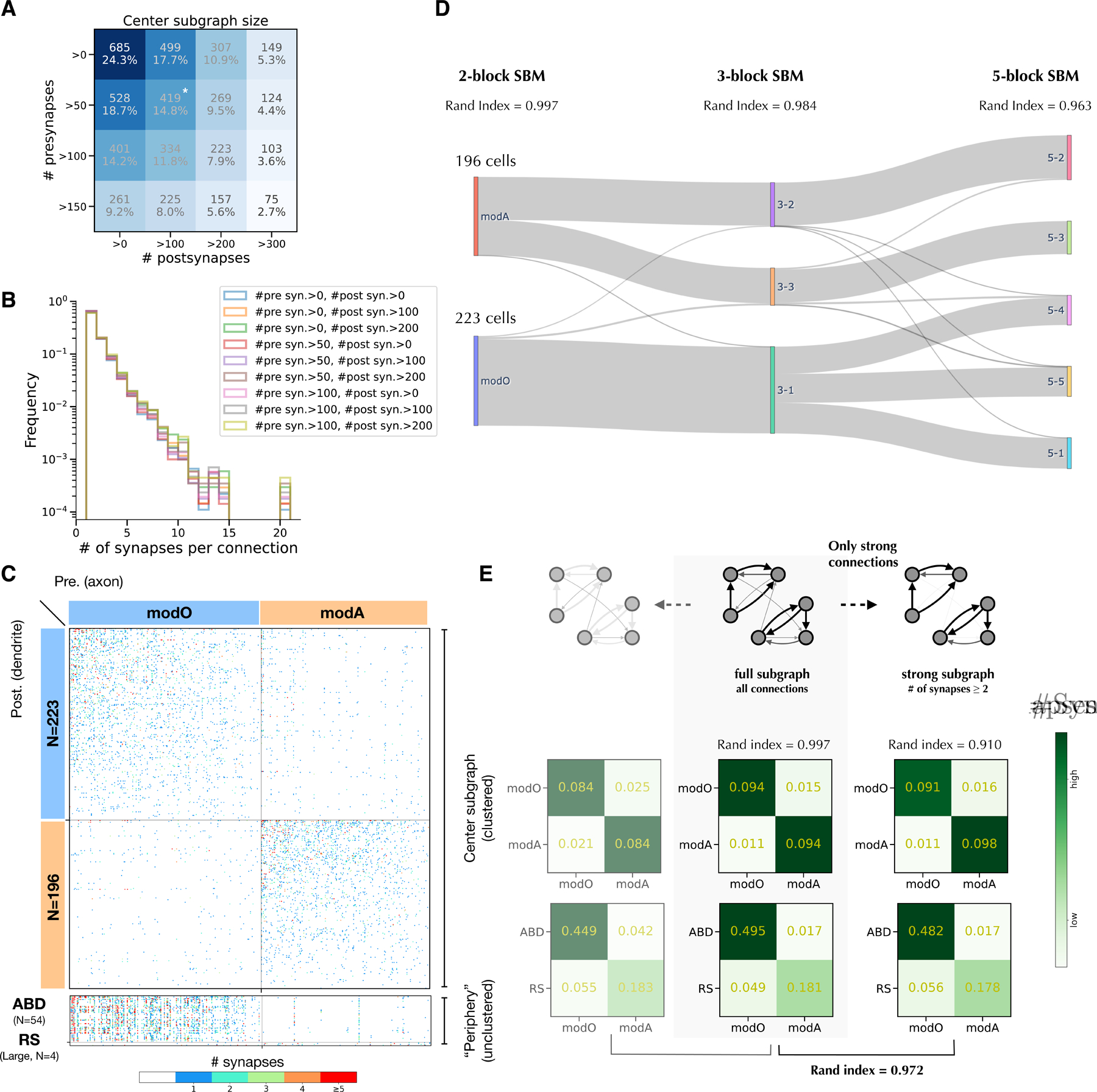
Modularity of the center subgraph.
A. Sizes of center subgraphs defined by thresholds for presynapse and postsynapse numbers. Star indicates the version of the center subgraph used in our main analysis. Results are similar for other center definitions (Figure S1G).
B. Distribution of the number of synapses per connection for different center definitions.
C. (Top) Matrix of connections in the center, with neurons grouped into two modules (modO, modA) found by the SBM. (Bottom) Matrix of connections from center to abducens (ABD) neurons and selected reticulospinal (RS) in the unclustered periphery.
D. Sankey diagram illustrating the hierarchical organization of blocks found by the SBMs as the block number increases. The thinness of gray lines indicates that few cells switch block membership
E. (middle) Modularity structures inferred by a degree-corrected SBM algorithm. Numbers indicate normalized synapse counts. Columns are presynaptic. (left and right) Modularity structures in the weak subgraph and strong subgraph are inferred by a degree-corrected SBM algorithm. The weak subgraph only contains single-synapse connections (64.3% of total connections), and the strong subgraph only contains multiple-synapse connections (35.7% of total connections).
See also Figures S1 and S2
Varying the thresholds changes the size of the center (Figure 1A), but will be shown to have little effect on subsequent analyses (Figure S1G, modularity results for other center subgraphs). We previously identified 34 secondary vestibular (Ve2) neurons in the center, which receive input from primary vestibular afferents13. Neurons excluded from the center subgraph will be referred to as the “periphery.” They include 54 abducens (ABD) neurons, and 4 large reticulospinal (RS) neurons.
The in-degree of a node was defined as the number of its presynaptic partners contained in the center subgraph (Figure S1C). The weighted in-degree of a node was defined as the total number of incoming synapses received by that node from its presynaptic partners contained in the center (Figure S1E). The maximum in-degree was 59, and the maximum weighted in-degree was 246. Similarly, we defined the out-degree (Figure S1D) and the weighted out-degree (Figure S1D) of a neuron as its number of postsynaptic partners and outgoing synapses in the center subgraph. The maximum out-degree was 101, and the maximum weighted out-degree was 271.
Division of wiring diagram into oculomotor and axial modules
We previously applied Louvain clustering to the neuronal wiring diagram to discover two modules specialized for oculomotor and axial movements13. The Louvain algorithm22 assumes that the graph is modular, i.e., intra-cluster connectivity is stronger than inter-cluster connectivity. More generally, we would like to identify clusters of nodes with similar connectivity patterns. The stochastic block model (SBM) is a way of doing this18, and can work whether or not the clusters are modules. The SBM has previously been applied to neuronal wiring diagrams23,24, and revealed nonmodular structure in the C. elegans connectome23. We will begin by applying the SBM to identify oculomotor and axial modules in our zebrafish wiring diagram, similar to our earlier work on Louvain clustering13. Later on, we will show that the SBM can identify a nonmodular, cyclic structure in our zebrafish wiring diagram. We will also make use of another feature of the SBM: it can be used to estimate the probability of connectivity motifs, since it is a probabilistic model.
We use a microcanonical degree-corrected SBM25, because the degrees of the nodes in the center subgraph are highly variable (Figure S1C, D). The model assumes that the neurons are divided into a fixed number of blocks, and the connection probability between neurons is a function of their block memberships only, after correcting for the degrees of the neurons. We applied the SBM to divide our center subgraph into two blocks. After the block memberships and connection probabilities were found by maximizing posterior probability25, the blocks ended up being roughly equal in size (Figure 1C). The blocks satisfy the definition of modules or communities in network science26; within-module connectivity is stronger than between-module connectivity (modularity Q = 0.37, p < 0.001).
Following our previous work13, we named the modules modO and modA. To biologically validate the modules, we checked their relation to neurons in the “periphery,” which were not used to construct the SBM. As in our previous work13, ABD neurons received much stronger connectivity from modO than from modA (Figure 1C), and the 4 large RS neurons in the periphery received much stronger connectivity from modA than from modO (Figure 1C). All 34 of the Ve2 neurons are members of modO; none were in modA. Of the 7 RS neurons contained in the center, all were in modA, and none were in modO. Therefore, all our structural observations imply that modO plays a role in eye movements, and modA plays a role in movements of the body axis.
To probe the robustness of the SBM, one can run the algorithm multiple times starting from random initial conditions and evaluate whether the solutions are similar every time. We generated 10 solutions in this way, and found that the Rand index was 0.997 after averaging over all pairs of solutions. This indicates that the solutions are highly similar; the Rand index is equal to one when the block structures are identical27. We also applied an SBM without degree correction, and the result was almost identical (Figure S2A). Finally, we applied a multi-graph SBM with degree correction25, and obtained almost identical results (Figure S2A).
As another test of robustness, we also applied the SBM with greater than two blocks. The 3-block and 5-block SBMs turn out to be approximate refinements of the 2-block SBM (Figure 1D). The 3-block SBM splits modA of the 2-block SBM into two sub-modules (Rand index=0.985, N=10), with one sub-module containing all center RS neurons. The 5-block SBM (Rand index = 0.963, N=10) further splits modO into 3 sub-blocks. These three sub-blocks are not modular, due to off-diagonal connectivity that will be discussed later on. The 4-block SBM (data not shown) is less robust (Rand index = 0.913, N=10), which implies that dividing the network into 4 blocks is not as “natural” as dividing it into 2, 3, or 5 blocks, so we exclude it from consideration. In summary, the 2-block, 3-block, and 5-block SBMs form an approximately nested hierarchy.
A connection from neuron A to neuron B may be mediated by more than one synapse from neuron A to neuron B. The number of synapses per connection varies from 1 to 20 (Figure 1B). About 65% of connections involve a single synapse, and we will refer to these as “weak” connections. We manually proofread these connections, and verified that they include very few false positive synapses (Methods).
Applying the SBM to the weak connections only, or to the strong connections only, yields similar modO and modA blocks (Figure 1E). When both are compared to the SBM based on the entire center subgraph, the SBM based on strong connections only is more similar (Figure 1E).
The number of synapses per connection is greater when the connection is within a module than between modules (Figure S2F). The average size of a synapse is roughly the same, whether the synapse is between modules or within a module (Figure S2G).
Bidirectional connections in modO
The analysis of network motifs relies on models of random graphs to assess statistical significance. The Erdős-Rényi (ER) and configuration (CFG) models of random graphs are widely used12,14. An ER model assumes that all connections are equally probable. A CFG model preserves in- and out- degrees of all nodes while randomizing connections (Figure 2A).
Figure 2.
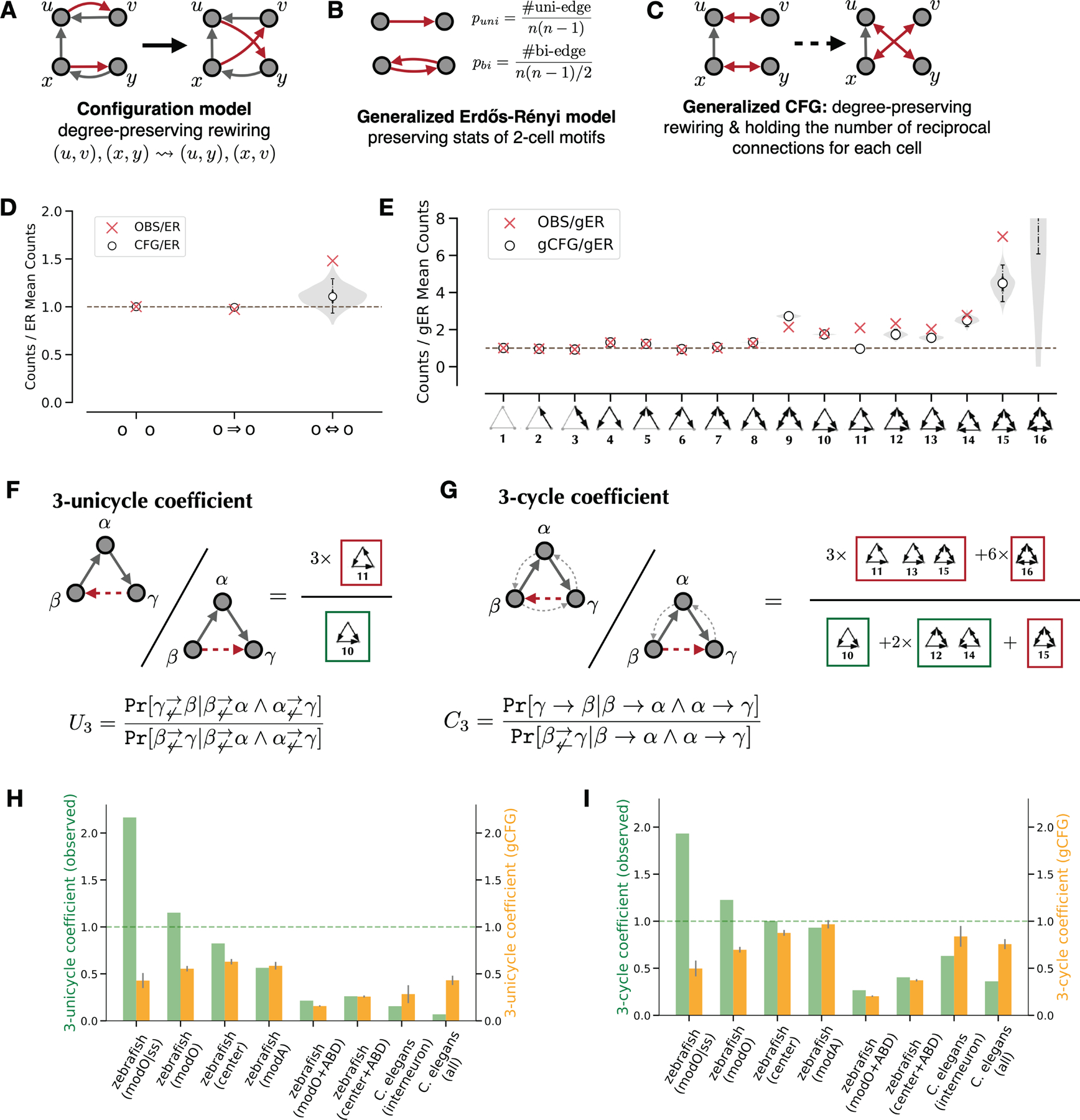
Quantification of modO recurrence.
A. Illustration of the configuration model.
B. Illustration of the generalized ER model.
C. Illustration of the generalized CFG model.
D. 2-cell motif frequencies in modO and a configuration model (CFG) relative to the ER model. The shaded region shows the smoothed distribution of motif counts sampled from the configuration model. White points indicate medians, solid vertical lines indicate quartiles, and dashed lines indicate the 95% confidence interval for 1,000 samples.
E. 3-cell motif frequencies in the modO and the configuration model relative to a generalized ER model (gER). The violin plot shows the smoothed distribution of the motif counts sampled from the generalized configuration model (gCFG). White points indicate medians, solid vertical lines indicate quartiles, and dashed lines indicate the 95% confidence interval for 1,000 samples.
F. 3-unicycle coefficient is the probability ratio of completing two consecutive unidirectional edges with a 3-cycle rather than a feedforward motif.
G. 3-cycle coefficient is the probability ratio of completing two consecutive edges with one recurrent edge rather than a feedforward edge.
H-I. Comparisons of 3-unicycle coefficients and 3-cycle coefficients, respectively. Green bars indicate the measurement of observed networks, yellow bars indicate the expected values from the configuration model, and gray error bars indicate standard deviations (N=1,000). modO|ss stands for the strong subgraph of modO. The last two columns include results for the C. elegans interneuron subnetwork (79 neurons) and the entire wiring diagram (270 neurons + 115 end-organ cells).
See also Figure S4.
We compared the frequencies of two-cell motifs with values expected from the ER and CFG models. There is an overrepresentation of bidirectional connections (Figure 2D, p = 0.001). The overrepresentation is weak relative to C. elegans, where the overrepresentation factor is much greater than one12.
We repeated the analysis for strong connections, defined as those containing at least a threshold number of synapses. The results were qualitatively similar for strong connections (Figure S4B). We also repeated the analyses for modA, and found qualitatively similar results (Figure S4E).
Global and local analyses of feedforwardness in the C. elegans connectome
For C. elegans, the graph of chemical synapses has been argued to be approximately feedforward. (Durbin 1987) was able to order the neuronal classes so that only a small fraction of synapses point in the “backward” direction8,11, and reported that almost all of the backward-pointing synapses belong to bidirectionally connected cell pairs. His work suggested that there is little violation of feedforwardness beyond this overrepresented two-cell motif. Similar orderings of all neurons have been derived11,12,13.
In addition to these global analyses involving neuron ordering or SBM, evidence for approximate feedforwardness comes from local analyses of three-cell connectivity motifs11,12. In particular, the “feedforward loop” (Figure S3A) is known to be overrepresented in the C. elegans connectome. A feedforward loop might arise, for example, because of the coexistence of two pathways from a sensory neuron to a motor neuron, one pathway that is direct and the other that is mediated by an interneuron. However, it has been reported that the feedforward loop is overrepresented even when the analysis is restricted to interneurons only12.
Building on this finding, we can regard the division of the C. elegans nervous system into three blocks–sensory neurons, interneurons, and motor neurons–as the basis of a naive SBM. The matrix of connection probabilities (Figure S3C) between blocks is asymmetric, because connections are more likely from sensory neuron to interneuron, and interneuron to motor neuron, than in the opposite direction9. A similar asymmetry is observed for the matrix of synapse counts (Figure S3B). This SBM is naive, because the blocks are manually identified. A similar demonstration of asymmetry with a larger number of manually identified blocks has also been given 11. An SBM was previously fit to the C. elegans connectome to find more than three blocks23.
In the naive SBM of Figure S3C, we find that 29% of feedforward loops are intra-block, and for only 6% do the three cells conform to sensory, inter-, and motor neuron (Figure S3D). In other words, the feedforward loop is not “aligned” with the global structure captured by the three-block SBM of Figure S3B and Figure S3C, elaborating on a previous report that the feedforward loop is overrepresented even if restricted to interneurons only11,12.
Instead of using the naive SBM, one could fit a three-block SBM, including the block assignments, to the connectivity data. For the simple graph version of the fitted SBM (Figure S3E), blocks 1, 2, and 3 end up being mostly (but not exclusively) sensory, inter-, and motor neurons, respectively. The connection probabilities are asymmetric, but there are no connections from block 1 to 3. Therefore the feedforward loop does not align at all with the fitted SBM. For the multi-graph version of the fitted SBM (Figure S3F), the connection probabilities do not display much asymmetry.
3-cycles of cells in modO
Approximate feedforwardness of the C. elegans connectome is consistent with the conception of some C. elegans behaviors as sensorimotor reflexes, mediated by reflex arcs from sensory neurons to interneurons to motor neurons28. Vertebrate oculomotor behaviors have also been conceptualized as reflexes. For example, the vestibulo-ocular reflex involves a three neuron reflex arc traveling from primary vestibular neuron to secondary vestibular neuron to motor neuron29. This reflex arc is indeed present in our zebrafish wiring diagram, and travels through modO. Therefore one might ask whether the modO has an approximately feedforward organization, similar to C. elegans.
We first address this question with a local analysis of three-neuron motifs11,12. Following previous work11,12, we use generalizations of ER (gER, Figure 2B) and CFG models (gCFG, Figure 2C) that preserve frequencies of all two neuron motifs (Figure 2D). This enables us to look for recurrent connectivity that is above and beyond bidirectional connections between pairs of cells, which are overrepresented (Figure 2D).
The frequencies of all three neuron motifs are shown in Figures 2E and S4A. The most striking finding is that the three-cycle (motif #11) is overrepresented in modO relative to gCFG (z-score=22.67, N=1,000). Its overrepresentation is both absolutely large and also has high statistical significance. Another striking finding is that the feedforward loop (motif #10) is fairly well predicted in modO by gCFG (z-score=2.52, N=1,000). There is a slight overrepresentation that is statistically significant, but its magnitude is not large.
These findings about motifs #10 and #11 should be interpreted in the context of other motifs. All highly connected motifs (#10 to #16) are overrepresented relative to gCFG (Figures 2E; S4A). However, the different motifs are correlated in the sense that they share individual ‘legs’ of the connectivity triangles. For example, both motifs 10 and 11 have directed connections from beta to alpha and alpha to gamma, and differ only in the direction of the third connection between beta and gamma. Such correlations can be normalized away by defining relative measures of recurrence that involve both motifs #10 and #11 as well as other highly connected three neuron motifs #12–16.
The “3-unicycle coefficient” (U3) estimates the probability ratio between completing a unidirectional 3-cycle (motif #11) and making a feedforward loop (motif #10) among three neurons, conditioned on two consecutive unidirectional connections (Figure 2F). A higher U3 indicates higher network recurrence. We found the increasing recurrence indicated by U3 from the whole C. elegans connectome, C. elegans interneuron subgraph, to our zebrafish center subgraph, modO, and the modO subgraph of strong connections (Figure 2H). The center subgraph and modO do not include sensory or motor neurons, so they are regarded here as analogous to the C. elegans interneuron subgraph. The 3-unicycle coefficient of modO is higher than 1, indicating that modO is even more recurrent than ER, for which U3 ≈ 1.
The preceding suggests that zebrafish networks are more recurrent than C. elegans networks in an absolute sense. Comparing with the generalized CFG model, we find that zebrafish center subgraph and the oculomotor module (modO) have a higher U3 than gCFG, while both C. elegans interneuron subnetwork (79 neurons) and the entire wiring diagram (270 neurons + 115 end-organ cells) have lower U3 scores than gCFG (Figure 2H). Therefore zebrafish remains more recurrent than C. elegans, even if we normalize U3 by its gCFG model value.
The “3-cycle coefficient” (C3) is similar to the 3-unicycle coefficient, but allows bidirectional connections (Figure 2G). Given three neurons , , and with two consecutive connections ( and ), it calculates the probability ratio of existing a feedback connection between neurons and and a unidirectional connection from to . The 3-cycle coefficient C3 shows similar trends as U3 (Figure 2I). The above analyses included all connections in modO. If we include only the strong connections in modO, then the effects are even stronger (Figures 2H,I).
We also analyzed three-cell motifs in modA. In contrast to modO, the feedforward loop (motif #10) is more overrepresented in modA relative to gCFG (z-score=+22.32, N=1,000), and the 3-cycle (motif #11) is less overrepresented (z-score=+8.04, N=1,000). Consequently, we found modA is less recurrent than modO and the center subgraph, but still much more recurrent than C. elegans networks, as indicated by U3 and C3 (Figures 2H,I). The same trend holds after normalizing U3 and C3 with their gCFG values, and the recurrence of modA is close to gCFG.
To summarize, modO exhibits a strong cyclic structure at the block and cellular levels, modA is slightly less cyclic than gCFG, and C. elegans is much less cyclic than gCFG8,10,12,30.
3-cycle of blocks in modO
We looked for a block structure in modO that could contribute to the cellular cycles noted above. When we applied a 3-block SBM to modO, we found that the blocks were not modular; intra-block connectivity was weaker than inter-block connectivity (Figure 3A). The inter-block connectivity could be approximated as cyclic (Figure 3A), with the connection probabilities from blockO1 to blockO2 to blockO3 to blockO1 higher (8✕, 3✕, 14✕) than those in the opposite direction. Similar cyclic structure also holds for normalized synapse counts between the blocks (Figure 3D).
Figure 3.
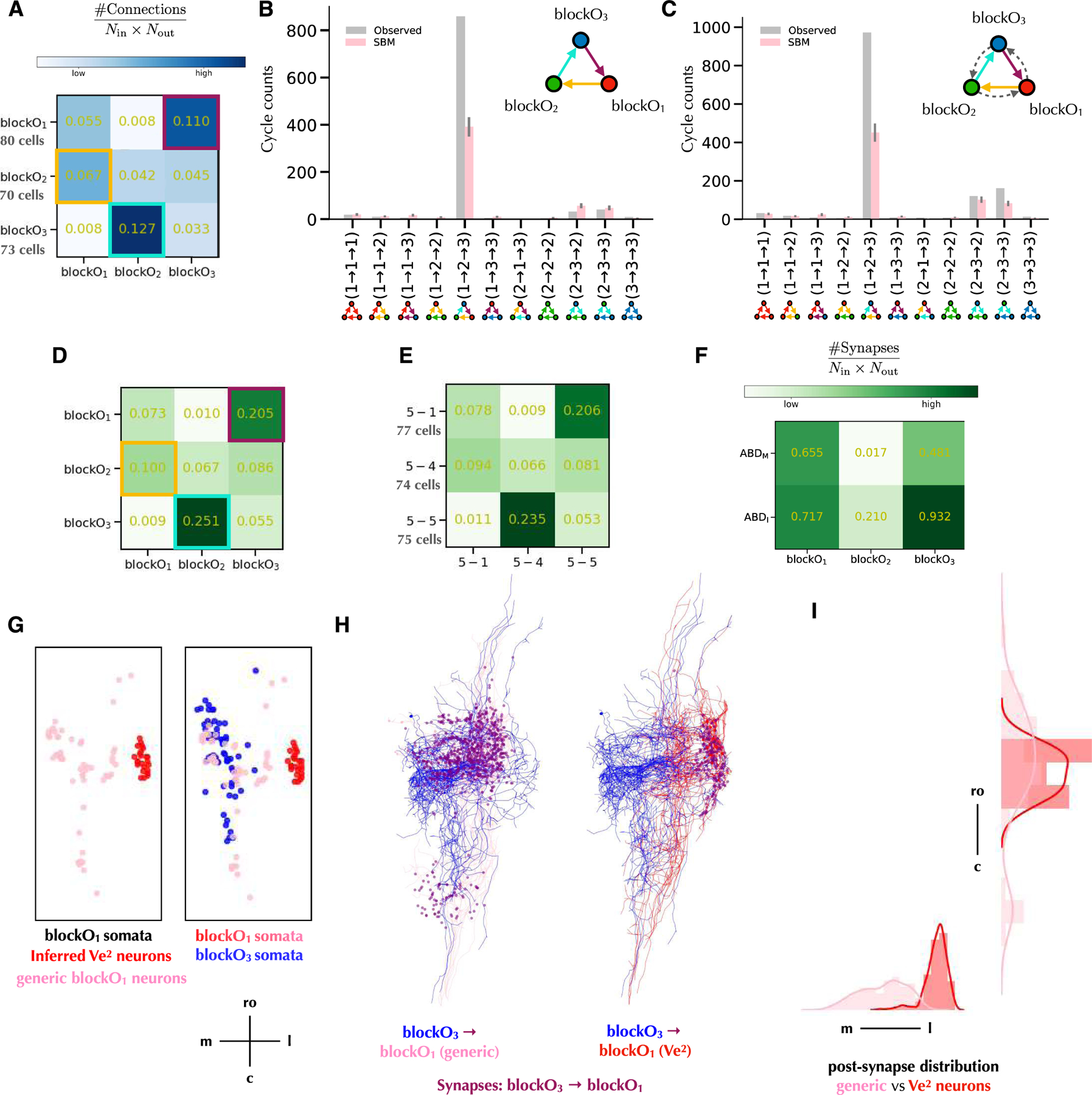
3-cycle block structure of modO.
A. Connection probability matrix of 3-cycle blocks. Blocks in columns send connections to blocks in rows. Cyclic inter-block connections are highlighted.
B. Counts of 3-unicycles from different blocks. Gray bars indicate observed 3-unicycle counts between blocks. Pink bars report the mean counts of 3-unicycles in graphs sampled from the 3-block SBM in Figure 3A, with error bars indicating the standard deviations (N=1,000).
C. Counts of motifs containing 3-cycles from different blocks. Gray bars indicate observed 3-cycle counts between blocks. Pink bars report the mean counts of 3-cycles in graphs sampled from the 3-block SBM in Figure 3A, with error bars indicating the standard deviations (N=1,000).
D. Matrix of normalized synapse counts of 3-cycle blocks. Numbers in blocks are synapse counts normalized by the numbers of input and output neurons. Blocks in columns send connections to blocks in rows.
E. Matrix of normalized synapse counts of 3 blocks (5-1, 5-4, and 5-5) in the 5-block SBM of Figure 1D that correspond best to the 3-block SBM. Numbers in blocks are synapse counts normalized by the numbers of input and output neurons.
F. Normalized output synapse counts matrix of 3-cycle blocks to abducens motor neurons (ABDM) and abducens interneuclear neurons (ABDI).
G. Soma distribution of blockO1 and blockO3. Ve2 neurons are identified by soma locations.
H. Synapse from neurons in blockO3 to neurons in blockO1. For clarity reasons, only 15 neuron skeletons are visualized for each block.
I. Post-synapse distribution of synapse from neurons in blockO3 to neurons in blockO1.
See also Figure S3.
We also found that the 3-cycles of cells identified above are related to the 3-cycle of blocks. About 87% of 3-unicycles (Figure 3B) and 72% of 3-cycles (Figure 3C) are aligned with the 3-cycle of blocks, from a blockO1 neuron, to a blockO2 neuron, then to a blockO3 neuron, and finally back to the same blockO1 neuron. There is only one 3-unicycle in the opposite direction. If we generate networks from the 3-block SBM (Figure 3A), the expected number of 3-cycles of cells is much less than the observed number (Methods, Figures 3B,C). In other words, 3-cycles are overrepresented relative to the prediction of the 3-block SBM, indicating positive correlations between inter-block connections, rather than the statistical independence assumed by the SBM.
BlockO1 contains almost all Ve2 neurons in the reconstruction. These are secondary vestibular neurons, which receive signals from primary vestibular afferents and provide input to the vestibulo-ocular reflex. Therefore, blockO1 can be seen as the start of the 3-cycle. BlockO3 neurons have a high probability of connection (>90%) to ABDI neurons (Figure 3F), and therefore can be seen as the exit of the 3-cycle. BlockO2 is the least connected to ABD neurons (Figure 3F), suggesting that blockO2 are mainly intermediating the 3-cycle to create richer dynamics.
BlockO1 contains both Ve2 neurons and other neurons (Figure 3G). We found that the number of 3-cycle motifs containing Ve2 neurons is much less than the portion of Ve2 neurons in blockO1, which means Ve2 neurons do not participate in 3-cycles as often as generic modO neurons (Figures 4D,E). Ve2 neurons receive synapses from blockO3 neurons close to its soma, while the generic modO neurons in blockO1 receive synapses at various locations (Figures 3H,I).
Figure 4.
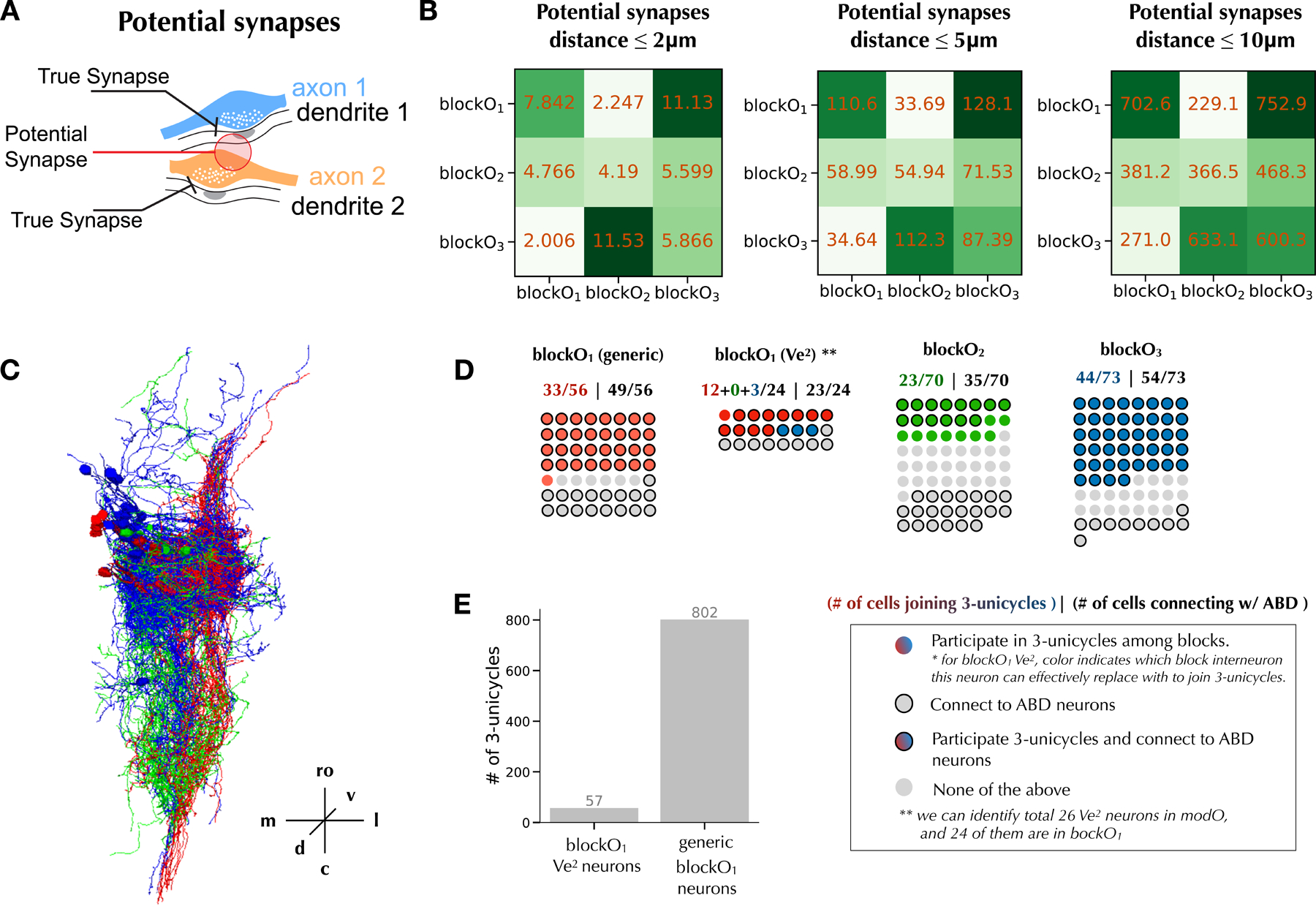
Potential synapses partially predict the 3-block structure.
A. Illustration of potential synapses defined by proximity of pre and postsynaptic sites.
B. 3-block structure of modO. Numbers in blocks are potential synapse counts normalized by the numbers of input and output neurons. Blocks in columns send connections to blocks in rows.
C. All neurons from blockO1 (red), blockO2 (green), blockO3 (blue) that participate in 3-unicycles.
D. Participation in 3-unicycles and connectivity to ABD neurons of neurons in each block.
E. Number of 3-unicycles among blocks having Ve2 neurons versus having generic blockO1 neurons.
The neuron morphology and spatial organization can at least partially explain the cyclic connections among three blocks. Figure 4C demonstrates morphological similarity between the neurons in each block that participate in 3-unicycles. This suggests that the blocks, though derived by analysis of connectivity, are similar to those that might be found by morphological analysis.
The power and limitations of morphological analysis can be seen by attempting to predict the true connectivity matrix of Figure 3A from axodendritic overlap. This is done through computing the number of potential synapses with different distance thresholds (Figure 4B), where we define potential synapses as pairs of pre- and post- synaptic sites within a distance threshold (Method, Figure 4A). When the threshold is 10μm, the normalized potential synapse counts from blockO1 to blockO2 to blockO3 to blockO1 are higher (1.66✕, 1.35✕, 2.79✕) than those in the opposite direction (Figure 4B).
This suggests that blockO2 axons are close to blockO3 dendrites, and blockO3 axons are close to blockO1 dendrites. And blockO1 sends much fewer potential synapses to blockO3 than blockO2 and itself, suggesting that blockO3 dendrites do not overlap with blockO1 axons. So potential synapses do partially predict true connectivity. However, the intra-blockO1 potential connection becomes stronger than the blockO1 to blockO2 potential connection in Figure 4B, which does not match the cyclic structure of Figure 3A. In short, axodendritic overlap can partially predict true connectivity but fails to reproduce the cyclic structure.
The 3-block SBM applied to modO is almost identical (with only 9 neurons assigned differently) to a subset of three blocks that are discovered when a 5-block SBM is applied to the entire center subgraph (Figure 3E). Such consistency confirms the robustness of the 3-cycle block structure of modO.
Discussion
One might question whether it makes sense to compare species as different as a worm and a fish, or an entire worm connectome with a small portion of a fish connectome. The comparison is motivated by the fact that both wiring diagrams can be regarded as sensorimotor circuits. Furthermore, our comparison has been at the level of general principles of organization; a cell-by-cell comparison seems impractical in species that are so different.
We discovered a strong overrepresentation of three-cell cycles in the oculomotor module (modO) of a neuronal wiring diagram reconstructed from a larval zebrafish brainstem (Figure 2E). We introduced the 3-unicycle coefficient, which compares the frequency of three-cell cycles vs. the frequency of feedforward loops (Figure 2F). This measure of recurrence is high in an absolute sense, and also high relative to a CFG model (Figure 2H). Similar results were found for the 3-cycle coefficient, another measure of recurrence that includes motifs with bidirectional connections (Figure 2G,I).
As far as we know, this is the first finding of overrepresented three-cell cycles in any neuronal wiring diagram reconstructed by electron microscopy (EM). Three-cell cycles are underrepresented in the C. elegans connectome; this is a flip side of the well-known overrepresentation of the feedforward loop motif12,14. In an EM-reconstructed cortical wiring diagram, three-cell cycles occurred with frequencies consistent with chance, but were not especially common17.
Cortical motifs were also studied in small wiring diagrams obtained via multi-neuron patch-clamp recording. Based on one dataset15, three-cell cycles were reported to be overrepresented relative to generalized ER15 and a morphology-constrained null model31. However, based on a larger dataset, three-cell cycles were not overrepresented relative to generalized ER 16. Since studies have utilized different random null models, it is helpful to compare the absolute value of the 3-unicycle coefficient across studies. For cortical wiring diagrams, the 3-unicycle coefficient varies from (3 × 4 / 9) ≈ 1.3 in (Song et al. 2005), to less than 1 in (Perin et al. 2011), to only (3 × 75 / 355) ≈ 0.64 in the EM-reconstructed wiring diagram17. The last value is much less than the 3-unicycle coefficient in our zebrafish modO.
We also applied an SBM to modO to find a three-cycle of blocks (Figure 3A). The three-cell cycles strongly aligned with the three-block cycle, indicating that the coarse-grained connectivity pattern of modO matches its highly recurrent local connectivity. However, the three-cell cycles are only partially explained by the probabilistic prediction of the SBM. The three-cell cycles return to the same cell more often than predicted by the degree-corrected SBM (Figures 3B, C). Cycles of connectivity between brain regions32,33 and cell types34 have long been known.
One might ask, by analogy, whether the feedforward loop in C. elegans is aligned with an SBM. We investigated two versions of this idea. In the naive SBM, the blocks are sensory, inter-, and motor neurons. The connection probabilities between blocks form an asymmetric matrix, which has previously been interpreted as evidence for approximate feedforwardness of the C. elegans connectome9,11,12. In the SBM fit to the simple connectivity graph, the block memberships are adjusted along with the connection probabilities to optimize the posterior probability of the model. The three blocks end up being mostly (but not exclusively) sensory, inter-, and motor neurons. It turns out that only 6% of three-cell cycles are aligned with the naive SBM, and none are aligned with the fitted SBM. Our finding elaborates on the previous report that the feedforward loop remains overrepresented even in the subgraph of the C. elegans connectome consisting of interneurons only, i.e., the subgraph that remains after excluding sensory and motor neurons12. Interestingly, the feedforward loop is overrepresented in the pharyngeal35 as well as the somatic nervous system.
In C. elegans, the strong overrepresentation of bidirectional connections has been interpreted as an outcome of spatial adjacency 8,12. If neuron A synapses onto neuron B, they must be adjacent to each other, and therefore the likelihood of a nearby reciprocal synapse from B onto A is increased. In our vertebrate wiring diagram, synapses are generally axodendritic, and a nearby reciprocal synapse is not possible. Therefore one would expect the overrepresentation of bidirectional connections to be weaker here, and indeed that is the case (Figure 2D). A quantitatively similar overrepresentation relative to the generalized CFG model has also been reported for a recent wiring diagram from mammalian cortex 17. Note that other reports of motif overrepresentation in cortex were relative to the Erdős-Rényi model 15,36.
We previously concluded that modO cells are largely excitatory, based on registration of the EM volume to gene expression patterns in the Z-Brain atlas13. The only exceptions are the secondary vestibular neurons, which are inhibitory37. The vast majority of 3-cycles do not contain secondary vestibular neurons (Figure 4E), and are hence expected to be all-excitatory loops mediating positive feedback.
Cyclic structure is reminiscent of the “closed chains” of neurons that were proposed long ago to maintain “reverberating activity”38. Cyclic structure could serve the function of mediating positive feedback, as in recurrent network models of temporal integration in the oculomotor system20,21. However, the functional role of cellular specificity is unclear; the 3-block cycle would be sufficient for positive feedback.
Star★Methods
Resource Availability
Lead Contact
Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Sebastian Seung (sseung@princeton.edu)
Materials Availability
The study did not generate new unique reagents.
Data and Code Availability
All data reported in this paper was released with Vishwanathan et al. 202113. DOIs are listed in the key resources table.
All original code has been deposited at GitHub and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Morphological segmentation | Vishwanathan et al. 2021 | https://seung-lab.github.io/zebrafish/data/ |
| Synaptic connectivity tables | Vishwanathan et al. 2021 | https://seung-lab.github.io/zebrafish/data/ |
| C. elegans wiring diagram | Cook et al. 2019 | https://www.wormwiring.org/pages/emmonslab.html |
| Cell skeletons used for analysis | Vishwanathan et al. 2021 | https://seung-lab.github.io/zebrafish/data/ |
| Analysis intermediate data | This paper | https://github.com/RunzheYang/ZfishCycles |
| Software and algorithms | ||
| Python 3 | Python.org | python.org |
| Graph-Tool | Peixoto, 2014 | https://graph-tool.skewed.de |
| Neuroglancer | https://github.com/google/neuroglancer | |
| Data analysis source code | This paper | https://github.com/RunzheYang/ZfishCycles |
Method Details
Identification of center subgraphs with less truncated neurons
To alleviate the truncation effect, we restrict our analysis to subsets of neurons that possess relatively complete axons and dendrites within the reconstructed volume. The “completeness” of a neuron is determined by the total number of presynaptic sites and postsynaptic sites in the connectome (Figures S1A,B). When the number of synaptic sites of a neuron is small, the total number of synapses of that neuron among other neurons is likely bounded by the number of synaptic sites in the connectome, which indicate a notable truncation effect to that neuron. The presynaptic sites distribution is more skewed than the distribution of the postsynaptic site (Figures S1A,B). Varying two thresholds for the numbers of pre and postsynaptic sites result in subgraphs gθpre,θpost of different sizes (Figure 1A). The nodes in the subgraph mainly contain interneurons that are far away from the boundary of volume, and the edges of the graph are synaptic connections. Specifically, we investigated two center subgraphs g50,100 and g100,100. There are 419 neurons in g50,100, of which 418 neurons are connected, and one neuron is isolated. All 334 neurons in g100,100 are connected. We manually proofread all synapses in center subgraph g50,100, and there are only 0.55% false positives. Distributions of the number of synapses per connection remain similar across different center subgraphs (Figure 1B). Our main analysis is based on g50,100, and we confirm a similar modular structure in g100,100 (Figure S1G).
Stochastic block modeling
We apply different variants of stochastic block modeling (SBM) algorithms with the graph-tool package25 to discover the block structure based on connectivity. The traditional SBM39 is composed of vertices, divided into B blocks with vertices in each block, and with the probability, , that an edge exists from block to block . Here we follow the equivalent microcanonical definition25, which uses average edge counts from the observed network to replace the probability parameters. The degree-corrected stochastic block model (DC-SBM)40 further specifies the in- and out-degree sequences of the graph as additional parameters.
To infer the best block membership bi of the vertices in the observed graph G, we can maximize the likelihood , where is the total number of different graph realizations with the same degree distribution , and edges among and within blocks of sizes , corresponding to the block membership . Therefore, maximizing likelihood is equivalent to minimizing the microcanonical entropy41, , which can be calculated as
where is the total number of edges. In practice, we also consider some noninformative priors on block sizes and degree distribution within each block, as described in [25]. Maximizing a posterior that considers all these priors induces additional terms to the entropy .
Given the number of blocks B, solving the best block membership that minimizes the above microcanonical entropy can be achieved by a Markov Chain Monte Carlo (MCMC) approach. At each step, we randomly propose a vertex moving its membership , with acceptance probability
where is the inverse temperature, is the fraction of neighbors of vertex in block , and is computed before the proposed move with a parameter ensuring ergodicity, and is computed after the move. One MCMC sweep is of time complexity , where E is the edge set of G.
To bisect the central subgraphs using DC-SBM, we apply the above algorithm to the unweighted, directed network of the identified less truncated neurons. We set B=2, , and anneal from 1 to 10 until S is no longer decreasing. We take the solution with minimal entropy from 10 independent runs. Figure 1E shows the average Rand index of the inferred block membership from 10 runs, which indicates the discovered modular structure is very stable.
We explore clustering the center subgraph with more blocks by setting B=3,4,5,6. The entropy S is monotonically increasing when we have more blocks. However, the 4-block structure and 6-block structure is less stable with average Rand indices =0.913 and 0.904, from 10 independent runs. The 3-block structure and 5-block structure are more stable with average Rand indices=0.984 and 0.963 (Figure 1D). 2-block, 3-block, and 5-block structures are nested and nearly hierarchical (Figure 1D), which validates the topological stability of the 2-block structure.
We also use the non-degree-corrected SBM and a “multi-graph” variant, where edges are weighted by the number of synapses, to obtain the structure of the center subgraph (Figure S2A). All algorithms consistently reveal the modO and modA structure, with only maximal 16 cells being assigned differently.
To further obtain the 3-block structure of modO, we apply the same DC-SBM algorithm to the unweighted, directed network of the modO neurons with B=3. We stably obtain the same 3-block structure of modO as the minimal entropy solution from 10 independent runs. The average Rand index for results from 10 runs is 0.893.
Definition of 3-unicycle coefficient (U3) and 3-cycle coefficient (C3)
The “3-unicycle coefficient” (U3) is defined to be the probability ratio between completing a unidirectional 3-cycle (motif #11) and making a feedforward loop (motif #10) among three neurons, conditioned on two consecutive unidirectional connections (Figure 2F).
The probability of completing a unidirectional 3-cycle (motif #11) conditioned on two consecutive unidirectional connections is given by (3× number of motif #11 / number of consecutive unidirectional connections), where the 3x factor accounts for the number of ways of getting two consecutive unidirectional connections in motif #11, which also insures a maximum value of unity. The probability of completing a feedforward loop (motif #10) conditioned on two consecutive unidirectional connections is given by (number of motif #10 / number of consecutive unidirectional connections). Thus, the ratio of the probability is calculated as (3× number of motif #11 / number of motif #10).
The “3-cycle coefficient” (C3) is defined similarly to the 3-unicycle coefficient, but allows bidirectional connections (Figure 2G). Given three neurons , , and with two consecutive connections ( and ), it calculates the probability ratio of there existing a feedback connection between neurons and and a unidirectional connection from to .
The probability of completing a 3-cycle (motifs #11, #13, #15, or #16) conditioned on two consecutive connections is given by ((3× number of motifs #11, #13, #15 + 6× number of motif #16) / number of consecutive connections), where the 3× and 6× factors accounts for the numbers of ways of getting two consecutive unidirectional connections in motifs #11, #13, #15 and #16, which also insures a maximum value of unity. The probability of completing with feedforward connection (motifs #10, #12, #14, or #15) conditioned on two consecutive connections is given by ((number of motif #10 + 2× number of motifs #12, #14 + number of motif #15) / number of consecutive connections). Motif #15 is counted in both cases because its unidirectional connection can be seen as feedforward or feedback, condition on the direction of two given consecutive connections. Finally, the ratio of these two probabilities is calculated as ((3× number of motifs #11, #13, #15 + 6× number of motif #16) / (number of motif #10 + 2× number of motifs #12, #14 + number of motif #15)).
Comparing connectivity motifs with random graphs
We compare the local connectivity pattern in different zebrafish subnetworks and C. elegans networks by contrasting them with random graphs.
We first use a directed Erdős-Rényi (ER) model 42, G(n,p), as a baseline for comparing 2-neuron motifs, where a directed edge between any two distinct vertices is uniformly drawn at random with a probability p. The expected number of edges of a directed ER model is m=n(n-1)p. To match the data, for example, the zebrafish modO, we set n=223, m=2725, and p=m/[n(n-1)]=0.055. We directly calculated the expected number of different two-neuron motifs in this ER model. The bidirectionally connected pairs are significantly overrepresented in all networks. Figure 2D shows the 2-neuron motif results for modO.
We also use a directed configuration model, G(n, k+,k−), which generates rewired graphs preserving the original degree distribution uniformly at random, where k+ and k− are predefined in- and out-degree sequences of the network. We sample 1,000 random networks uniformly from a set of graphs with the same degree sequences as the observed network by applying the switch-and-hold algorithm43 (Figure 2A), where we randomly select two edges in each iteration and swap their target endpoints if that does not introduce self-loops or multiple edges (switch), or otherwise keep them unchanged (hold). In the original paper, the switch step is implemented by selecting four vertices at random, while our implementation selects two edges at random because that is more efficient on a sparse network. In general, the Markov chain for our sampling procedure is reducible, so samples are drawn from only one ergodic component of the set of all simple graphs with the same degree sequence44. However, all ergodic components share the same motif frequencies, so the lack of ergodicity has no consequence for our analysis45. A more complex Markov-chain sampling procedure with true ergodicity is known46, but as mentioned above would yield the same motif frequencies. To generate one sample, we run the algorithm for 10,000 iterations from the previously sampled network.
When studying recurrence scores U3 and C3 based on 3-neuron motifs, we use generalized ER (Figure 2B) and generalized configuration models (Figure 2C) to preserve two-neuron motif statistics. We directly calculated the expected number of different three-neuron motifs in the generalized ER model. For the generalized configuration model, we modify the switch-and-hold algorithm such that the number of bidirectional edges for each neuron is preserved (gCFG, Figure 2C). Sampling from the first generalized configuration model, we constrain the switch operation to swap two bidirectional connections or two unidirectional connections. In the experiment, we sampled 1,000 random networks to estimate the mean gCFG U3 and C3 for all networks in Figures 2H,I.
We can also use a fitted degree-corrected SBM as a null model. The expected number of 3-unicycle motifs from the 3-block SBM of modO (Figure 3A) is 391.23, which is 2.20 times lower than our observation (Figure 3B, p < 0.001). Similarly, the expected number of 3-cycle motifs from 3-block SBM is 450.67, which is 2.15 times lower than our observation. In other words, 3-cycles are overrepresented relative to the prediction of the 3-block SBM (Figure 3C, p < 0.001), indicating positive correlations between inter-block connections, rather than the statistical independence assumed by the SBM.
Potential Synapse Formalism
We define a potential synapse as a (presynaptic site, postsynaptic site) pair within a certain threshold distance (Figure 4A). This definition is somewhat different from the light microscopic approach, which defines a potential synapse47,48 as an approach of an axon and dendrite within some threshold distance. Also, we use neurons reconstructed from a single animal, while the light microscopic approach aggregates neurons from multiple animals, or “clones” a single neuron many times49.
Supplementary Material
Highlights:
Larval zebrafish oculomotor module exhibits highly overrepresented three-cell cycles.
These cellular cycles are aligned with a global cycle of inferred neuronal groups.
Cellular cycles are surprisingly more precise than can be explained by group cycles.
The discovered cyclic structure is relevant for theories of oculomotor function.
Acknowledgments
We thank Jay Gager, James Hebditch, Ben Silverman, Kyle Willie, Ryan Willie, and Szi-chieh Yu for manual proofreading of connections within the center subgraph, and Alex Sood for comments on the manuscript. ERFA, MSG, AV and HSS acknowledge support from R01 NS104926, R01 EY027036. ERFA and MSG acknowledge support from R01 EY021581, Simons Foundation Global Brain Initiative. MSG acknowledges support from the NIH-NINDS Brain Initiative award 5U19NS10468-2. HSS acknowledges support from NIH/NCI UH2 CA203710 and the Mathers Foundation, as well as assistance from Google, Amazon, and Intel. HSS is grateful for support from the Intelligence Advanced Research Projects Activity (IARPA) via Department of Interior/Interior Business Center (DoI/IBC) contract number D16PC0005. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright annotation thereon.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Interests
H. S. Seung has a financial stake in Zetta AI.
References
- 1.Wanner AA, and Friedrich RW (2020). Whitening of odor representations by the wiring diagram of the olfactory bulb. Nat. Neurosci 23, 433–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Witvliet D, Mulcahy B, Mitchell JK, Meirovitch Y, Berger DR, Wu Y, Liu Y, Koh WX, Parvathala R, Holmyard D, et al. (2021). Connectomes across development reveal principles of brain maturation. Nature 596, 257–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Scheffer LK, Xu CS, Januszewski M, Lu Z, Takemura S-Y, Hayworth KJ, Huang GB, Shinomiya K, Maitlin-Shepard J, Berg S, et al. (2020). A connectome and analysis of the adult Drosophila central brain. Elife 9. 10.7554/eLife.57443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.MICrONS Consortium, Alexander Bae J, Baptiste M, Bodor AL, Brittain D, Buchanan J, Bumbarger DJ, Castro MA, Celii B, Cobos E, et al. (2021). Functional connectomics spanning multiple areas of mouse visual cortex. bioRxiv, 2021.07.28.454025. 10.1101/2021.07.28.454025. [DOI] [Google Scholar]
- 5.Shapson-Coe A, Januszewski M, Berger DR, and Pope A (2021). A connectomic study of a petascale fragment of human cerebral cortex. bioRxiv [Google Scholar]
- 6.Bullock T, and Horridge GA (1965). Structure and function in the nervous systems of invertebrates [Google Scholar]
- 7.Nieuwenhuys R, ten Donkelaar HJ, and Nicholson C (1998). The Central Nervous System of Vertebrates: With Posters (Springer Science & Business Media; ). [Google Scholar]
- 8.Durbin RM (1987). Studies on the development and organisation of the nervous system of Caenorhabditis elegans
- 9.Varshney LR, Chen BL, Paniagua E, Hall DH, and Chklovskii DB (2011). Structural properties of the Caenorhabditis elegans neuronal network. PLoS Comput. Biol 7, e1001066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jarrell TA, Wang Y, Bloniarz AE, Brittin CA, Xu M, Thomson JN, Albertson DG, Hall DH, and Emmons SW (2012). The connectome of a decision-making neural network. Science 337, 437–444. [DOI] [PubMed] [Google Scholar]
- 11.Cook SJ, Jarrell TA, Brittin CA, Wang Y, Bloniarz AE, Yakovlev MA, Nguyen KCQ, Tang LT-H, Bayer EA, Duerr JS, et al. (2019). Whole-animal connectomes of both Caenorhabditis elegans sexes. Nature 571, 63–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Reigl M, Alon U, and Chklovskii DB (2004). Search for computational modules in the C. elegans brain. BMC Biol 2, 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vishwanathan A, Ramirez AD, Wu J, Sood A, Yang R, Kemnitz N, Ih D, Turner N, Lee K, Tartavull I, et al. (2021). Predicting modular functions and neural coding of behavior from a synaptic wiring diagram. bioRxiv, 2020.10.28.359620. 10.1101/2020.10.28.359620. [DOI] [Google Scholar]
- 14.Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, and Alon U (2002). Network motifs: simple building blocks of complex networks. Science 298, 824–827. [DOI] [PubMed] [Google Scholar]
- 15.Song S, Sjöström PJ, Reigl M, Nelson S, and Chklovskii DB (2005). Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol 3, e68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Perin R, Berger TK, and Markram H (2011). A synaptic organizing principle for cortical neuronal groups. Proc. Natl. Acad. Sci. U. S. A 108, 5419–5424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Turner NL, Macrina T, Bae JA, Yang R, Wilson AM, Schneider-Mizell C, Lee K, Lu R, Wu J, Bodor AL, et al. (2022). Reconstruction of neocortex: Organelles, compartments, cells, circuits, and activity. Cell 185, 1082–1100.e24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lee C, and Wilkinson DJ (2019). A review of stochastic block models and extensions for graph clustering. Appl. Netw. Sci 10.1007/s41109-019-0232-2; [DOI] [Google Scholar]
- 19.Szentagothai J (1950). The elementary vestibulo-ocular reflex arc. J. Neurophysiol 13, 395–407. [DOI] [PubMed] [Google Scholar]
- 20.Seung HS (1996). How the brain keeps the eyes still. Proc. Natl. Acad. Sci. U. S. A 93, 13339–13344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fisher D, Olasagasti I, Tank DW, Aksay ERF, and Goldman MS (2013). A modeling framework for deriving the structural and functional architecture of a short-term memory microcircuit. Neuron 79, 987–1000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Blondel VD, Guillaume JL, and Lambiotte R (2008). Fast unfolding of communities in large networks. Journal of statistical [Google Scholar]
- 23.Pavlovic DM, Vértes PE, Bullmore ET, Schafer WR, and Nichols TE (2014). Stochastic blockmodeling of the modules and core of the Caenorhabditis elegans connectome. PLoS One 9, e97584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jonas E, and Kording K (2015). Automatic discovery of cell types and microcircuitry from neural connectomics. Elife 4, e04250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Peixoto TP (2017). Nonparametric Bayesian inference of the microcanonical stochastic block model. Phys Rev E 95, 012317. [DOI] [PubMed] [Google Scholar]
- 26.Newman M (2018). Networks (Oxford University Press; ). [Google Scholar]
- 27.Rand WM (1971). Objective Criteria for the Evaluation of Clustering Methods. J. Am. Stat. Assoc 66, 846–850. [Google Scholar]
- 28.Chalfie M, Sulston JE, White JG, Southgate E, Thomson JN, and Brenner S (1985). The neural circuit for touch sensitivity in Caenorhabditis elegans. J. Neurosci 5, 956–964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Straka H, and Baker R (2013). Vestibular blueprint in early vertebrates. Front. Neural Circuits 7, 182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Brittin CA, Cook SJ, Hall DH, Emmons SW, and Cohen N (2021). A multi-scale brain map derived from whole-brain volumetric reconstructions. Nature 591, 105–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Udvary D, Harth P, Macke JH, Hege H-C, de Kock CPJ, Sakmann B, and Oberlaender M (2022). The impact of neuron morphology on cortical network architecture. Cell Rep 39, 110677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Alexander GE, DeLong MR, and Strick PL (1986). Parallel organization of functionally segregated circuits linking basal ganglia and cortex. Annu. Rev. Neurosci 9, 357–381. [DOI] [PubMed] [Google Scholar]
- 33.Foster NN, Barry J, Korobkova L, Garcia L, Gao L, Becerra M, Sherafat Y, Peng B, Li X, Choi J-H, et al. (2021). The mouse cortico–basal ganglia–thalamic network. Nature 598, 188–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gilbert CD, and Wiesel TN (1979). Morphology and intracortical projections of functionally characterised neurones in the cat visual cortex. Nature 280, 120–125. [DOI] [PubMed] [Google Scholar]
- 35.Cook SJ, Crouse CM, Yemini E, Hall DH, Emmons SW, and Hobert O (2020). The connectome of the Caenorhabditis elegans pharynx. J. Comp. Neurol 528, 2767–2784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Markram H (1997). A network of tufted layer 5 pyramidal neurons. Cereb. Cortex 7, 523–533. [DOI] [PubMed] [Google Scholar]
- 37.Pastor AM, Calvo PM, de la Cruz RR, Baker R, and Straka H (2019). Discharge properties of morphologically identified vestibular neurons recorded during horizontal eye movements in the goldfish. J. Neurophysiol 121, 1865–1878. [DOI] [PubMed] [Google Scholar]
- 38.Lorente De Nó R (1938). Analysis of the activity of the chains of internuncial neurons. J. Neurophysiol [Google Scholar]
- 39.Holland PW, Laskey KB, and Leinhardt S (1983). Stochastic blockmodels: First steps. Soc. Networks 5, 109–137. [Google Scholar]
- 40.Karrer B, and Newman MEJ (2011). Stochastic blockmodels and community structure in networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys 83, 016107. [DOI] [PubMed] [Google Scholar]
- 41.Bianconi G (2009). Entropy of network ensembles. Phys. Rev. E Stat. Nonlin. Soft Matter Phys 79, 036114. [DOI] [PubMed] [Google Scholar]
- 42.Gilbert EN (1959). Random Graphs. The Annals of Mathematical Statistics 30, 1141–1144. 10.1214/aoms/1177706098. [DOI] [Google Scholar]
- 43.Artzy-Randrup Y, and Stone L (2005). Generating uniformly distributed random networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys 72, 056708. [DOI] [PubMed] [Google Scholar]
- 44.Carstens CJ, and Horadam KJ (2016). Switching edges to randomize networks: what goes wrong and how to fix it. J Complex Netw 5, 337–351. [Google Scholar]
- 45.Berger A, and Müller-Hannemann M (2010). Uniform Sampling of Digraphs with a Fixed Degree Sequence. Graph Theoretic Concepts in Computer Science, 220–231. 10.1007/978-3-642-16926-7_21. [DOI] [Google Scholar]
- 46.Roberts ES, and Coolen ACC (2012). Unbiased degree-preserving randomization of directed binary networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys 85, 046103. [DOI] [PubMed] [Google Scholar]
- 47.Stepanyants A, Hof PR, and Chklovskii DB (2002). Geometry and structural plasticity of synaptic connectivity. Neuron 34, 275–288. [DOI] [PubMed] [Google Scholar]
- 48.Shepherd GMG, Stepanyants A, Bureau I, Chklovskii D, and Svoboda K (2005). Geometric and functional organization of cortical circuits. Nat. Neurosci 8, 782–790. [DOI] [PubMed] [Google Scholar]
- 49.Markram H, Muller E, Ramaswamy S, Reimann MW, Abdellah M, Sanchez CA, Ailamaki A, Alonso-Nanclares L, Antille N, Arsever S, et al. (2015). Reconstruction and Simulation of Neocortical Microcircuitry. Cell 163, 456–492. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data reported in this paper was released with Vishwanathan et al. 202113. DOIs are listed in the key resources table.
All original code has been deposited at GitHub and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Morphological segmentation | Vishwanathan et al. 2021 | https://seung-lab.github.io/zebrafish/data/ |
| Synaptic connectivity tables | Vishwanathan et al. 2021 | https://seung-lab.github.io/zebrafish/data/ |
| C. elegans wiring diagram | Cook et al. 2019 | https://www.wormwiring.org/pages/emmonslab.html |
| Cell skeletons used for analysis | Vishwanathan et al. 2021 | https://seung-lab.github.io/zebrafish/data/ |
| Analysis intermediate data | This paper | https://github.com/RunzheYang/ZfishCycles |
| Software and algorithms | ||
| Python 3 | Python.org | python.org |
| Graph-Tool | Peixoto, 2014 | https://graph-tool.skewed.de |
| Neuroglancer | https://github.com/google/neuroglancer | |
| Data analysis source code | This paper | https://github.com/RunzheYang/ZfishCycles |


