Calibration and Validation of the Colorectal Cancer and Adenoma Incidence and Mortality (CRC-AIM) Microsimulation Model Using Deep Neural Networks

Abstract

Objectives

Machine learning (ML)–based emulators improve the calibration of decision-analytical models, but their performance in complex microsimulation models is yet to be determined.

Methods

We demonstrated the use of an ML-based emulator with the Colorectal Cancer (CRC)-Adenoma Incidence and Mortality (CRC-AIM) model, which includes 23 unknown natural history input parameters to replicate the CRC epidemiology in the United States. We first generated 15,000 input combinations and ran the CRC-AIM model to evaluate CRC incidence, adenoma size distribution, and the percentage of small adenoma detected by colonoscopy. We then used this data set to train several ML algorithms, including deep neural network (DNN), random forest, and several gradient boosting variants (i.e., XGBoost, LightGBM, CatBoost) and compared their performance. We evaluated 10 million potential input combinations using the selected emulator and examined input combinations that best estimated observed calibration targets. Furthermore, we cross-validated outcomes generated by the CRC-AIM model with those made by CISNET models. The calibrated CRC-AIM model was externally validated using the United Kingdom Flexible Sigmoidoscopy Screening Trial (UKFSST).

Results

The DNN with proper preprocessing outperformed other tested ML algorithms and successfully predicted all 8 outcomes for different input combinations. It took 473 s for the trained DNN to predict outcomes for 10 million inputs, which would have required 190 CPU-years without our DNN. The overall calibration process took 104 CPU-days, which included building the data set, training, selecting, and hyperparameter tuning of the ML algorithms. While 7 input combinations had acceptable fit to the targets, a combination that best fits all outcomes was selected as the best vector. Almost all of the predictions made by the best vector laid within those from the CISNET models, demonstrating CRC-AIM’s cross-model validity. Similarly, CRC-AIM accurately predicted the hazard ratios of CRC incidence and mortality as reported by UKFSST, demonstrating its external validity. Examination of the impact of calibration targets suggested that the selection of the calibration target had a substantial impact on model outcomes in terms of life-year gains with screening.

Conclusions

Emulators such as a DNN that is meticulously selected and trained can substantially reduce the computational burden of calibrating complex microsimulation models.

Highlights

• Calibrating a microsimulation model, a process to find unobservable parameters so that the model fits observed data, is computationally complex.

• We used a deep neural network model, a popular machine learning algorithm, to calibrate the Colorectal Cancer Adenoma Incidence and Mortality (CRC-AIM) model.

• We demonstrated that our approach provides an efficient and accurate method to significantly speed up calibration in microsimulation models.

• The calibration process successfully provided cross-model validation of CRC-AIM against 3 established CISNET models and also externally validated against a randomized controlled trial.

A crucial component of developing cancer microsimulation models is calibration, which involves estimating the directly unobservable natural history parameters from repeated simulation experiments. ¹ Conventional approaches to calibration require running the microsimulation model with a large number of input combinations to identify a parameter set that best fits calibration targets such as observed cancer incidence and mortality. ² There are 2 important challenges in calibration. First, running a complex simulation model with many input combinations is computationally prohibitive. Second, there is little knowledge of how different targets for calibration may affect model outcomes.

Previous efforts to improve the calibration of simulation models with heuristic or statistical engines such as simulated annealing^3–5 and Bayesian calibration^6–9 are powerful yet timely and complex. Alternatively, machine learning (ML) and statistical methods are simpler to implement, do not require optimization knowledge, and can be used to accelerate the calibration process compared with conventional calibration methods.

To address these challenges, we compared several ML algorithms and selected a deep neural network (DNN) framework as an emulator to facilitate microsimulation model calibration. Emulators or surrogate models have recently received attention for calibration of simulation models^2,10; however, previous studies either used only 1 ML algorithm or calibrated using only a few targets. Furthermore, we incorporated multiple calibration targets into our framework and showed that the heterogeneity in the estimated unknown parameters can be achieved.

We demonstrate the effectiveness and validity of our approach using the Colorectal Cancer-Adenoma Incidence and Mortality (CRC-AIM) model, which is designed to answer questions related to colorectal cancer (CRC) progression and screening. CRC is the second leading cause of cancer deaths in the United States, ¹¹ and early detection through screening reduces CRC incidence and mortality. ¹² While screening is recommended by major medical organizations including the US Preventive Services Task Force (USPSTF), ¹³ American Cancer Society (ACS), ¹⁴ and American College of Gastroenterology, ¹⁵ full consensus has not been achieved with respect to some key considerations, such as the optimal frequency, age range for screening, and so forth. In addition, as new CRC screening modalities with different accuracies are developed, comparative effectiveness must be carefully reassessed. For this purpose, microsimulation models are increasingly used by policy makers to address comparative effectiveness and other questions related to CRC screening. ¹⁶

In this study, we first show how we develop, train, and tune the hyperparameters of several ML algorithms and select the best emulator for the calibration. Then, we illustrate how our DNN-based emulator efficiently identifies multiple sets of unknown natural history–related parameters of CRC-AIM that fit well to primary calibration targets. We then demonstrate the validity of the calibrated CRC-AIM model using cross-model validation and external validation. For cross-model validation, we compare CRC-AIM’s outcomes for CRC incidence, mortality, and life-years gained (LYG) from screening to the 3 established microsimulation models of the National Cancer Institute’s (NCI’s) Cancer Intervention and Surveillance Modeling Network (CISNET), which were used to inform USPSTF and ACS CRC screening guidelines.^14,16,17 For external validation, we replicate a large randomized controlled trial on CRC screening using CRC-AIM and compare the model’s outcomes against the trial’s findings. Finally, we demonstrate how calibration targets used for CRC-AIM affect the predicted CRC mortality reduction and LYG by screening.

Methods

Overview of CRC-AIM

CRC-AIM was inspired by the ColoRectal Cancer Simulated Population Incidence and Natural history (CRC-SPIN) model, 1 of 3 CISNET CRC models, and therefore shares many of this model’s features (as obtained or derived from publicly available sources).^18,19 In this section, we provide a brief description of the CRC-AIM and include full details of the model in Supplementary Section A. We also describe the key differences between CRC-AIM and CRC-SPIN models in Supplementary Section B.

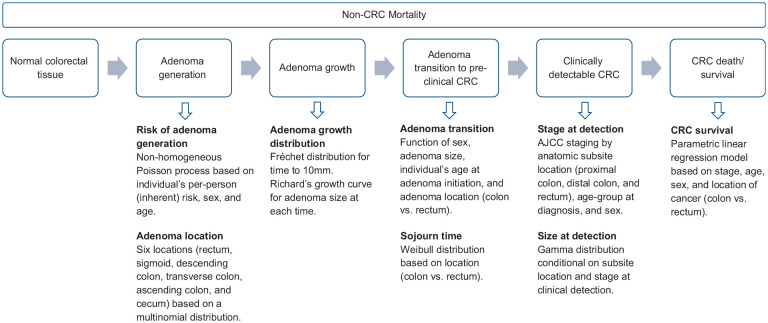
CRC-AIM simulates CRC-related events for individuals at average risk of developing CRC. The natural history of CRC is based on an adenoma-carcinoma sequence and consists of 5 subcomponents: 1) adenoma generation, 2) adenoma growth, 3) transition from adenoma to preclinical cancer, 4) transition from preclinical cancer to clinically detectable cancer (i.e., sojourn time), and 5) survival (Figure 1). CRC-AIM included stylistic probability distributions to model CRC progression. We used these probability distributions as they have been reported to accurately represent CRC natural history. ¹⁹

Figure 1.

Overview of the CRC-AIM natural history model.

AJCC,American Joint Committee on Cancer; CRC, colorectal cancer; CRC-AIM, Colorectal Cancer-Adenoma Incidence and Mortality model.

1. Adenoma generation. CRC-AIM assumes that the risk of developing an adenoma depends on an individual’s sex, age, and baseline risk, in which individuals younger than age 20 are not at risk of developing adenomas. ²⁰ After an adenoma is created, it is assigned to 1 of the 6 locations according to a multinomial distribution derived from several autopsy studies: rectum, sigmoid colon, descending colon, transverse colon, ascending colon, and cecum (Supplementary Table 1).

2. Adenoma growth. The size (i.e., diameter) of an adenoma is determined using the Richard’s growth model, ²¹ in which its growth rate is calculated by the time required to reach 10 mm in diameter, sampled from a Fréchet distribution. ²² The parameters of the adenoma growth model are differentiated by colon and rectum.

3. Transition from adenoma to preclinical cancer. CRC-AIM models the cumulative transition probability of progressing from adenoma to preclinical cancer using a log-normal cumulative distribution function that is based on sex, size, and age at initiation of adenoma.^23,24 Adenoma to preclinical cancer transitions differ between colon and rectum.

4. Transition from preclinical cancer to clinically detectable cancer (sojourn time). A Weibull distribution is used to model the time between the transition from preclinical cancer to when the preclinical cancer becomes clinically symptomatic (also known as the sojourn time) for colon cancers. A proportional hazards model is assumed between colon and rectal cancers, and consequently, the sojourn times for both locations follow the Weibull distribution.

5. Survival. Upon clinical detection of cancer, the stage at clinical detection is sampled using NCI’s Surveillance, Epidemiology, and End Results (SEER) Program 1975–1979 data ²⁵ and is found to be a function of age, sex, and location (rectum, proximal colon, and distal colon). The size at clinical detection, conditional on location and stage at clinical detection, is modeled as a gamma distribution (Supplementary Table 2) using SEER 2010–2015 data that are confined within cases diagnosed at ages 20 to 50 y (prior to eligibility for CRC screening in the United States). SEER 2010–2015 data for CRC size generation are preferred to SEER 1975–1979 data due to 1) the uncertainty regarding American Joint Committee on Cancer (AJCC) staging estimate within the older era and 2) notable differences in cancer sizes between the 2 time periods (Supplementary Figure 2). Survival from CRC is sampled from parametric models, with age at diagnosis and sex as covariates for each stage and location (colon v. rectum) fitted to cause-specific survival from SEER (see Supplementary Section A.5). We applied a 7% reduction in hazard, estimated using the 5-y cause-specific relative survival between periods 2000–2003 and 2010–2019 from SEER, for cases diagnosed after 2000 to reflect the improvement in CRC-specific survival in the recent years. ²⁶ All-cause mortality by age were based on the 2017 U.S. life table. ²⁷

List of Calibrated Natural History Parameters

CRC-AIM includes 23 directly unobservable parameters governing the natural history of CRC (Table 1), which need to be estimated using calibration. To calibrate these parameters, we first identified a plausible range for each parameter, which was informed by CRC-SPIN.^18,19 We then supplemented the initial plausible range using our calibration process.

Table 1.

Unknown Parameters of CRC-AIM Natural History Model

Unknown Parameter	Plausible Range	Best Parameter Value Selected by Calibration
Adenoma generation
Baseline log risk, ${\beta }_0$	${\beta }_0~T{N}_{[-7,-5]}(-6.3,0.4)$	−5.661
Standard deviation of baseline log-risk, ${\sigma }_0$	${\sigma }_0~T{N}_{[1,2]}(1.1,0.2)$	1.270
Sex effect, ${\beta }_1$	${\beta }_1~T{N}_{[-0.5,-0.1]}(-0.5,0.1)$	−0.384
Age effect (ages 20–<50), ${\beta }_2$	${\beta }_2~T{N}_{[0.03,0.07]}(0.045,0.007)$	0.039
Age effect (ages 50–<60), ${\beta }_3$	${\beta }_3~T{N}_{[0.01,0.05]}(0.03,0.01)$	0.023
Age effect (ages 60–<70), ${\beta }_4$	${\beta }_4~T{N}_{[-0.01,0.05]}(0.03,0.01)$	0.020
Age effect (ages ≥70), ${\beta }_5$	${\beta }_5~T{N}_{[-0.02,0.03]}(0.03,0.03)$	−0.018
Adenoma growth (time to 10 mm)
Scale (colon), $s_c$	$s_c~U(10.7,40)$	24.364
Shape (colon), ${\alpha }_c$	${\alpha }_c~U(0.5,4)$	1.388
Scale (rectum), $s_r$	$s_r~U(5,20)$	6.734
Shape (rectrum), ${\alpha }_r$	${\alpha }_r~U(2,5)$	3.601
Adenoma growth (Richard’s growth model)
Shape parameter, $p$	$p~T{N}_{[0.5,3.2]}(1.0,0.5)$	0.710
Transition from adenoma to cancer
Size (male, colon), ${\gamma }_{1\mathrm{cm}}$	${\gamma }_{1\mathrm{cm}}~U(0.02,0.06)$	0.040
Age at initiation (male, colon), ${\gamma }_{2\mathrm{cm}}$	${\gamma }_{2\mathrm{cm}}~U(0.0,0.02)$	0.016
Size (male, rectum), ${\gamma }_{1\mathrm{rm}}$	${\gamma }_{1\mathrm{rm}}~U(0.02,0.07)$	0.039
Age at initiation (male, rectum), ${\gamma }_{2\mathrm{rm}}$	${\gamma }_{2\mathrm{rm}}~U(0.0,0.02)$	0.004
Size (female, colon), ${\gamma }_{1\mathrm{cf}}$	${\gamma }_{1\mathrm{cf}}~U(0.02,0.05)$	0.043
Age at initiation (female, colon), ${\gamma }_{2\mathrm{cf}}$	${\gamma }_{2\mathrm{cf}}~U(0.0,0.02)$	0.014
Size (female, rectum), ${\gamma }_{1\mathrm{rf}}$	${\gamma }_{1\mathrm{rf}}~U(0.02,0.055)$	0.035
Age at initiation (female, rectum), ${\gamma }_{2\mathrm{rf}}$	${\gamma }_{2\mathrm{rf}}~U(0.0,0.02)$	0.010
Sojourn time
Scale (colon), ${\lambda }_c$	${\lambda }_c~U(3.0,5.0)$	4.683
Shape (colon and rectum), $k$	$k~U(2.0,5.0)$	3.620
Log-hazard ratio, $\alpha$	$\alpha ~U(-1.0,1.0)$	−0.018

$T{N}_{[a,b]}(\mu ,\sigma )$ represents a truncated normal distribution with mean µ and standard deviation σ over the domain [a,b]. U(a,b) represents a uniform distribution with domain (a,b). CRC-AIM, Colorectal Cancer-Adenoma Incidence and Mortality Model.

Calibration Targets

To estimate the natural history parameters, we used several calibration targets. Our primary targets included SEER 1975–1979 CRC incidence per 100,000, which encompass the most comprehensive population-based nationwide CRC data prior to widespread CRC screening in the United States, hence providing a crucial input for natural history model development. These data have also been used by several other CRC models focusing on the United States, including CISNET CRC models.^28–31 Because AJCC staging was not recorded in SEER data prior to 1988, stage-specific CRC incidence was not available to be used as a calibration target. To overcome this limitation, in addition to using overall CRC incidence by age as a calibration target, we also included the CRC incidence by location (colon and rectum) and gender (male and female) among our calibration targets. While SEER data include very useful data, they do not provide sufficient details such as average adenoma size, which are needed for precise natural history model development. For this purpose, we supplemented the primary calibration targets by including studies by Corley et al. ³² and Pickhardt et al., ³³ 2 high-impact studies reporting the adenoma prevalence and distribution by size based on a large sample of asymptomatic patients.^32,33

In addition, we used 3 studies as secondary calibration targets to verify preclinical cancer prevalence and size distribution.^34–36 Since preclinical cancer prevalence is highly attributed with prior screening history and removal of adenomas, these studies were unique in identifying participants without a history of screening. The chances of detecting precancerous lesions are low; thus, for each of the secondary calibration targets, we generated a tolerance interval based on confidence intervals to determine whether model predictions fall within the reported values (Supplementary Table 7b). The use of secondary targets required adapting CRC-AIM to replicate the study settings in terms of the age and sex distribution of the study population (Supplementary Table 6).

Model Calibration

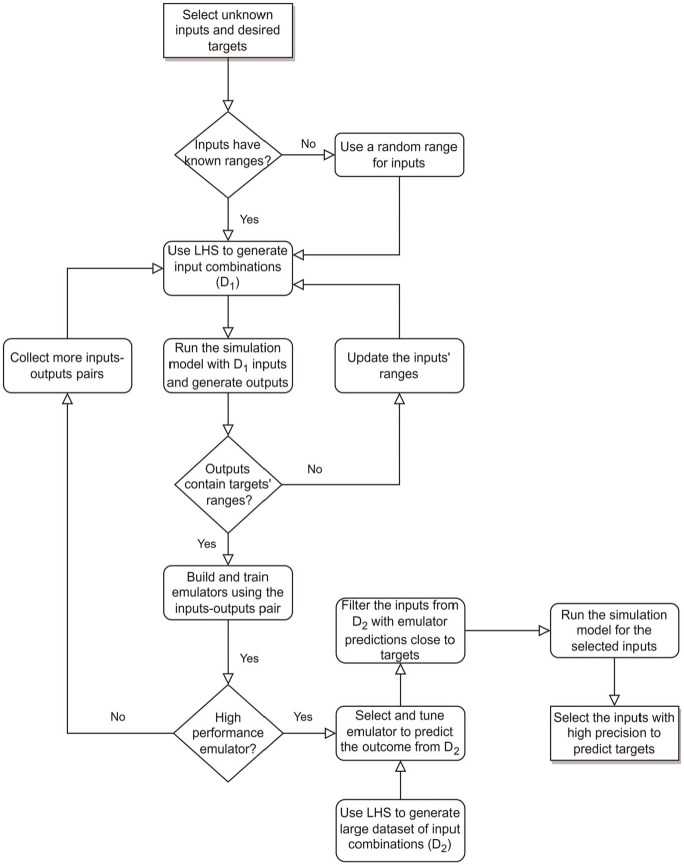
Because a single run of CRC-AIM simulation takes approximately 30 min in a standalone desktop PC with population size of 500K, it is computationally infeasible to evaluate all possible combinations of the parameters listed in Table 1 to identify the best combination. To speed up this process, we evaluated several ML algorithms as an emulator, which approximates the CRC-AIM model outcomes based on inputs and has substantially shorter computational times compared with CRC-AIM. ³⁷ Figure 2 shows a schematic flowchart of our calibration framework.

Figure 2.

Calibration framework using an emulator as a surrogate for actual microsimulation model.

LHS, Latin hypercube sampling.

Emulator Selection

We first generated 15,000 different combinations of the unknown parameters from the plausible ranges using Latin hypercube sampling (LHS) ³⁸ and ran CRC-AIM to evaluate the corresponding target values (shown as ${\mathrm{D}}_1$ in Figure 2). To select the best population size for generating outcomes, the precision of CRC-AIM in predicting CRC with different population sizes was evaluated. We found that the modeled incidence remained relatively stable when the population size was at least 500K (Supplementary Figure 4). Hence, we simulated 500K individuals in each run, and we used the following aggregated calibration targets to select ML algorithms: CRC incidence by location and gender from SEER (4 outcomes), adenoma size distribution for the age groups of 50 to 59, 60 to 69, and 70+ y based on Corley et al. ³² (3 outcomes), and the percentage of small adenoma detected by same-day virtual and optical colonoscopy from Pickhardt et al. ³³ (1 outcome). Since the confidence intervals around the mean for secondary targets were wide (Supplementary Table 7b), the additional value of adding them as outcomes to our ML algorithms was minimal; hence, they were excluded in selecting the best emulator but included in calibration validation.

Using the 15,000 input-output combination pairs, we evaluated several ML algorithms, such as DNN, ³⁹ random forest, ⁴⁰ and several gradient boosting methods including conventional gradient boosting,^41,42 eXtreme Gradient Boosting (XGBoost) with advanced L1 and L2 regularization, ⁴³ LightGBM ⁴⁴ (light gradient boosting machine), and CatBoost (categorical boosting) ⁴⁵ and compared their performance. For this purpose, we divided the simulation runs into training and testing data sets with the ratio of 3:1 and trained each ML algorithm with the training data. To preprocess the data set, we evaluated 2 scaling methods, standardization (mean of zero and standard deviation of unity) and normalization (min-max scaler). The goodness-of-fit (GOF) metrics (i.e., mean squared error [MSE], mean absolute error, mean absolute percentage error, and mean squared log error) for the training and testing data sets were calculated. To investigate and tune hyperparameters of each ML model, we used k-fold cross-validation (k = 5) and a random search with 100 hyperparameter combinations for finding the best set that maximizes GOF.

Calibration Process with the Trained Emulator

Once the best ML algorithm for the emulator was identified, we compared emulator-based predictions against CRC-AIM–generated outcomes with the testing data set and confirmed the predictive accuracy of the emulator. We then used the emulator to evaluate 10 million input vector combinations generated from LHS (denoted as ${\mathrm{D}}_2$ in Figure 2) to identify the most promising input vector combinations that are within 5% difference to targets. We used this 5% deviation from the calibration target to ensure that all potentially acceptable inputs suggested by the emulator would be further analyzed. The selected input vector combinations were simulated by CRC-AIM, and their simulated outcomes were compared with the calibration targets.

Since we had several primary and secondary calibration targets, among vectors with simulated outcomes fall within targets’ ranges, a rank-ordered hierarchical process of eliminating implausible models based on their fit to the calibration targets was employed. The list of target priorities and the scoring framework are provided in Supplementary Table 14. For the natural history modeling, our highest-rank target was CRC incidence by age, location, and sex, followed by adenoma prevalence and sojourn time. Adenoma size distribution for different age groups, dwell time, and secondary calibration targets were weighted less. The input vectors with acceptable natural history fit to primary and secondary calibration targets were further examined by cross-model validation experiments.

Cross-Model Validation

After the calibration was completed and all of the input vector combinations with high precision to primary and secondary calibration targets were selected, CRC-AIM was cross-validated against the 3 CISNET models, CRC-SPIN, MISCAN-COLON, and SimCRC, which reported extensive results as part of the 2021 USPSTF CRC screening guideline update. ⁴⁶ We compared several outcomes such as LYG with screening, CRC incidence and deaths (in the presence and absence of screening), and total number of colonoscopies conducted by screening modality. Three screening strategies (at their recommended screening intervals) for individuals aged 45 to 75 y were compared: colonoscopy every 10 y, annual fecal immunochemical test (FIT), and triennial multitarget stool DNA (mt-sDNA) test. Screening test sensitivity for CRC and adenomas (by size) and specificity are provided in Supplementary Table 10. Consistent with the USPSTF modeling approach, ⁴⁶ sensitivity for stool tests was calibrated to match the overall nonadvanced adenoma sensitivity (Supplementary Section F). Perfect adherence to screening (100%) was assumed, and an incidence rate ratio was applied to reflect the increasing underlying risk of developing CRC since 1970. ⁴⁷ Previous analysis showed that the CRC incidence for adults younger than 50 y who were not eligible to receive national screening has substantially increased for both men and women in colon and rectum. ⁴⁷ Based on prior analysis reported in USPSTF, ⁴⁶ the incidence rate ratio was set to 1.19. The incidence rate ratio was assumed to be driven by an increase in the baseline log risk, $\left({\beta }_0\right)$ in adenoma generation (the full equation is provided in Supplementary Section A.1), and is applied throughout each simulated individuals’ life span.

Similar to natural history model selection, we used a hierarchical process to rank our cross-model validation experiments since multiple outputs were compared against other models. The criteria specified that the differences of model-predicted outcomes compared with those from the 3 CISNET models should be sufficiently small. The outcomes, sorted from most important to least, included CRC incidence, LYG due to screening, CRC deaths averted with screening, total number of colonoscopies, and CRC cases and deaths without screening. We prioritized LYG due to screening since USPSTF “focused on estimated LYG (compared with no screening) as the primary measure of the benefit of screening” in their 2021 CRC screening guideline update. ⁴⁸

External Validation Using the United Kingdom Flexible Sigmoidoscopy Screening Trial (UKFSST)

External validation was performed by comparing modeled outcomes from CRC-AIM against those reported by UKFSST, a randomized controlled trial that examined CRC incidence and mortality outcomes following a 1-time flexible sigmoidoscopy.^49–51 UKFSST was conducted in a population that was not yet routinely screened for CRC; therefore, published trial results provided unique information on the preclinical duration of CRC and the screening impact on the risk of CRC. As a result, many simulation models including CSNET CRC models used UKFSST as an external validation target.^52–55

Briefly, in UKFSST, participants aged 55 to 64 y from 14 centers were randomized into a control group and a sigmoidoscopy screening group. As the UKFSST was a UK-based trial, 1996–1998 UK life tables were used to modify all-cause mortality in CRC-AIM. ⁵⁶ No other modifications to the natural history of the model were made. The trial was simulated 500 times, each time generating a cohort with size, age, and sex distributions similar to the observed data from the trial. Details regarding sensitivity and specificity of sigmoidoscopy and colonoscopy, referral to colonoscopy, and surveillance with colonoscopy are presented in Supplementary Section G. Primary outcomes included hazard ratios of CRC incidence and mortality, whereas secondary outcomes included long-term cumulative incidence and mortality over 17 y of follow-up.

For each of the input combinations that demonstrated successful fit to natural history targets and screening cross-validation, external validity against UKFSST was also examined. A vector that partially fails to meet this criterion (i.e., only 1 of incidence or mortality hazard ratio is within confidence interval range) was regarded as acceptable, since it is likely for that vector to demonstrate external validity against other trials. At the end of selecting final input vectors, we identified 1 single input vector that has the best performance in terms of calibration targets. However, we also included multiple input vectors with acceptable performance in our final model, to reflect the heterogeneity of the CRC natural history.

Impact of Calibration Targets on Outcomes

To test the importance of calibration target selection, we examined the LYG from screening for 4 input combinations that were regarded as unacceptable for 1 of the primary targets: 1 that fit SEER incidence and the calibration target from the study by Pickhardt et al. but not that from the study by Corley et al. (model U1), 1 that fit the calibration target from the studies by Corley et al. and Pickhardt et al. well but not SEER incidence (model U2), 1 that fit SEER incidence and the calibration target from the study by Corley et al. but not that from the study by Pickhardt et al. (model U3), and 1 that fit SEER incidence but not the studies by Corley et al. and Pickhardt et al. well (model U4). We also performed the external validation experiments for these models.

Results

Selection and Fine-Tuning of the Emulator

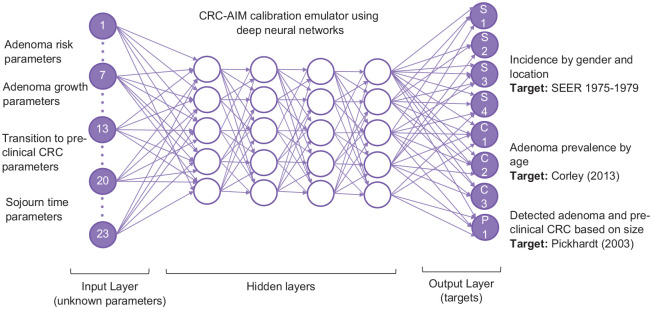
Among all ML algorithms, DNN had the best GOF when standardization was used (Supplementary Table 8). Hence, DNN was selected to build the emulator for the calibration. For the hyperparameter tuning of the DNN, we explored its performance with different GOF measures, the number of nodes in hidden layers, activation functions, optimization algorithms, learning rates, epochs, and batch sizes. We used 5-fold cross-validation and random search with 100 hyperparameter combinations that took 4.16 h to complete. We further verified several parameter combinations with trial and error, to ensure the best hyperparameters were selected. The final DNN had an input layer with 23 nodes, an output layer with 8 nodes, and 4 dense hidden layers with 128, 64, 64, and 64 nodes, respectively (Figure 3). The activation function used in the first and third layers was the sigmoid function, whereas rectified linear units were used in other layers. We selected the Adam optimization algorithm, ⁵⁷ a first-order gradient-based optimization of stochastic objective functions with a learning rate of 0.001 to train the model. Since the outputs are continuous and MSE provides a combination measurement of bias and variance of the prediction, it was used to quantify the GOF between the predicted and observed values in the test data set and as the loss function.

Figure 3.

Graphical representation of the DNN emulator for CRC-AIM. The DNN consists of 23 nodes in the input layer representing the unobservable parameters, 4 hidden layers, and an output layer with 8 nodes representing the primary calibration targets, which include CRC incidence by location and gender from SEER 1975-1979, adenoma prevalence by age, and percentage of detected adenomas ≤ 5 mm).

CRC, colorectal cancer; CRC-AIM, Colorectal Cancer-Adenoma Incidence and Mortality model; DNN, Deep neural networks; SEER, Surveillance, Epidemiology, and End Results.

Performance of DNN

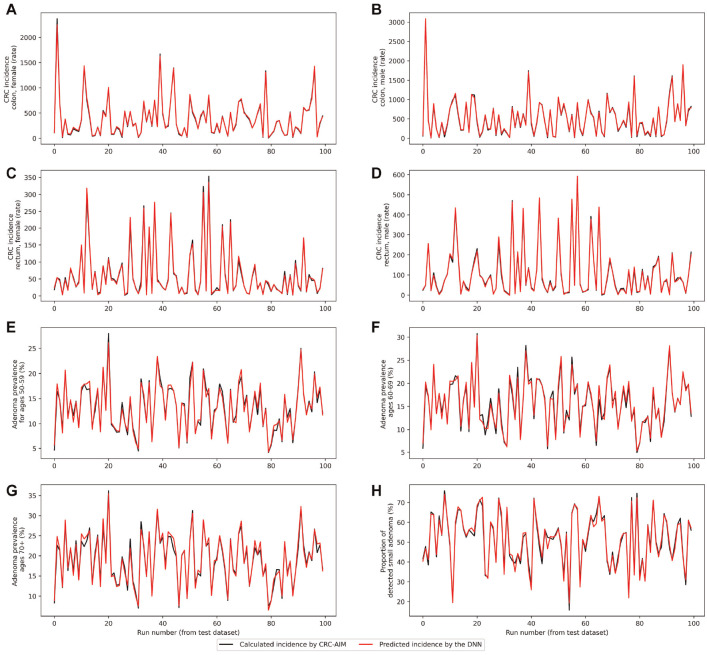
Using AWS (p3.2xlarge EC2 instance), it took 10 min to run 1 replication of CRC-AIM, whereas the DNN model was trained in 28.4 s with a training MSE of 0.014. On the test data set, predicted outcomes were comparable with actual outcomes in most cases, with an MSE less than 0.016. DNN-predicted versus CRC-AIM–predicted outcomes for the first 100 testing input combinations are shown in Figure 4. While the outcomes may substantially differ between each combination of input vector (shown in the x-axis), the DNN model was also able to predict these differences accurately (shown by the red line). For instance, the input vector used for run 20 of the testing data set (i.e., x-axis value equal to 20) led to a high adenoma prevalence and low CRC incidence, indicating a slow-growing adenoma scenario in which the proportion of small adenomas is high and they would not transition to cancer. The red and black points at x = 20 represent the DNN and CRC-AIM estimates, respectively. In most cases, red and black points associated with input vectors are very close to each other, indicating that the DNN successfully predicted the CRC incidence for each location and sex, adenoma prevalence by age, and proportion of small adenoma detected.

Figure 4.

DNN- and CRC-AIM–predicted outcomes for the first 100 testing input combinations. CRC incidence rate by sex and location is represented in panels A through D, followed by adenoma prevalence by age groups in panels E through G and percentage of small adenoma (≤5 mm) in panel H. Note that the red lines and black lines perfectly overlap for most of the instances; therefore, black lines are often invisible.

CRC, colorectal cancer; CRC-AIM, Colorectal Cancer-Adenoma Incidence and Mortality model; DNN, deep neural networks.

The trained DNN was used to predict outcomes for 10 million newly generated inputs in 473.16 s. Considering the computation times for input-output pair data generation (2,500 h), the generation, storage, and retrieving of 10 million LHS combinations for prediction (7 min), Emulator model selection (5 h), training, testing, hyperparameter tuning of selected emulator (4.5 h), and filtering the predicted outcomes (10 min), the calibration process took approximately about 104 CPU days. In contrast, conventional calibration would have required a total of 190 CPU y with CRC-AIM.

Of 10 million inputs, only 101 input combinations that were within a deviation of 5% from the point estimates of primary calibration targets and were considered well-fitting and selected for further investigation. We then used CRC-AIM to evaluate these 101 input combinations for primary and secondary calibration targets. As shown in Supplementary Table 9, the overall difference between CRC-AIM’s actual outcomes and the predicted outcomes by DNN were 4.4% (CI: 3.9%–4.7%), and the largest margin between predicted and actual outcomes was seen in CRC incidence of colon in females and rectal in males.

Selection of a Calibrated CRC-AIM

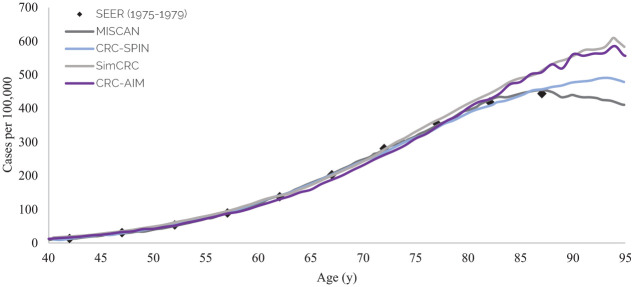
In total, 56 of 101 input vectors showed acceptable natural history outcomes and were further examined for cross-model validation. Among them, 16 of the 56 input parameters resulted in outcomes that were consistent with those reported by the CISNET models. We then used the UKFSST to test the external validity of our best input vectors. Seven input vectors with acceptable fit to the calibration targets and cross-model validity were selected as our final input vector combinations. These inputs with corresponding values, reflecting the heterogeneity of CRC natural history, are presented in Supplementary Table 12. Model predictions for all outcomes considered in cross-validation and external validation are presented in Supplementary Table 13. The score of each input vector for targets is summarized in Supplementary Table 14. One vector that best fits all outcomes was selected as the representative input vector (Table 1). The difference between predicted outcomes from DNN and actual outcomes from CRC-AIM for the representative input vector was 1.9%. The selected input vector matched age-specific CRC incidence as reported by SEER’s 1975–1979 data (Figure 5) as well as adenoma prevalence reported by the autopsy studies ⁴⁶ (Supplementary Figure 7). Distributions of adenomas by location (Supplementary Figure 8), adenoma size by age group (Supplementary Figure 9), and cancer stage at diagnosis (Supplementary Figure 11) estimated by CRC-AIM compared well against our estimates with SEER data ⁵⁸ and CISNET models. The dwell time and sojourn time estimated by CRC-AIM were 20.3 y and 4.1 y, respectively, both of which fall within the estimated values from the literature^59–61 and CISNET models (Supplementary Figure 10).

Figure 5.

CRC-AIM and CISNET predictions of colorectal cancer cases per 100,000 people by age (adapted from Knudsen et al. ⁴⁶ ).

CRC-AIM, Colorectal Cancer-Adenoma Incidence and Mortality model; CRC-SPIN, ColoRectal Cancer Simulated Population Incidence and Natural history model; MISCAN, MIcrosimulation SCreening Analysis; SEER, Surveillance, Epidemiology, and End Results; SimCRC, Simulation Model of Colorectal Cancer.

Cross-Model Validation with CISNET Models and External Validation with UKFSST

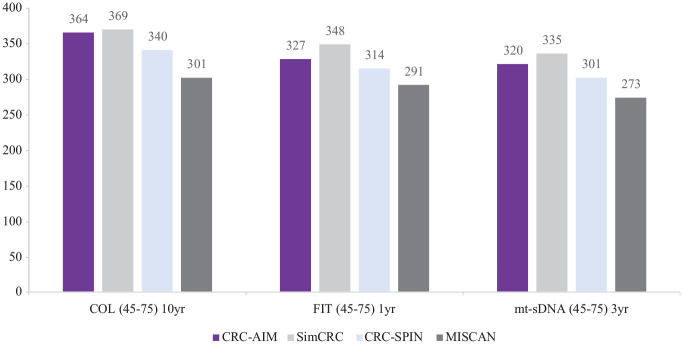
Screening-related outcomes estimated by CRC-AIM, including LYG, incidence and mortality reductions associated with colonoscopy, FIT, and mt-sDNA screening strategies (Figure 6) as well as the associated numbers of colonoscopies and stool-based tests (Supplementary Figures 12–15), were comparable with CISNET model predictions.

Figure 6.

CRC-AIM and CISNET ⁴⁶ estimates of life-years gained from screening by modality (10 y colonoscopy, annual FIT, and triennial mt-sDNA).

COL, colonoscopy; CRC-AIM, Colorectal Cancer-Adenoma Incidence and Mortality model; CRC-SPIN, ColoRectal Cancer Simulated Population Incidence and Natural history model; FIT, fecal immunochemical test; MISCAN, MIcrosimulation SCreening Analysis; mt-sDNA, multi-target stool DNA; SimCRC, Simulation Model of Colorectal Cancer; yr, year.

The hazard ratios of CRC incidence and CRC mortality at 17-y follow-up (Figure 7) and the cumulative probabilities of CRC incidence and mortality (Supplementary Figure 16) estimated by CRC-AIM were consistent with the reported outcomes from UKFSST, ⁵⁰ demonstrating the external validity of CRC-AIM.

Figure 7.

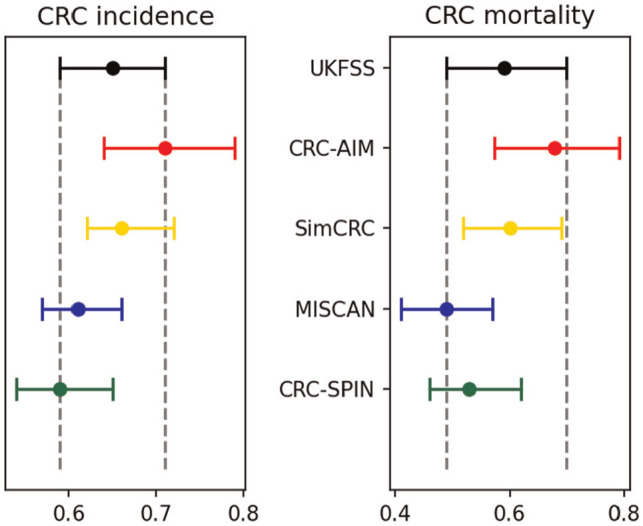
External validation with UKFSST: hazard ratios of colorectal cancer incidence and mortality between screening and control groups over the 17-y follow-up (adapted from Knudsen et al. ⁴⁶ )

CRC, colorectal cancer; CRC-AIM, Colorectal Cancer-Adenoma Incidence and Mortality model; CRC-SPIN, Colorectal Cancer Simulated Population Incidence and Natural history model; MISCAN, MIcrosimulation SCreening Analysis; SimCRC, simulation model of colorectal cancer; UKFSST, United Kingdom Flexible Sigmoidoscopy Screening Trial.

Impact of Calibration Targets on Outcomes

The LYG from screening colonoscopy for individuals aged 45 to 75 y was 338, 283, 344, and 414 per 1,000 people screened for models U1, U2, U4, and U4, respectively (Supplementary Table 13). Models U2 and U4 were unable to predict LYG within expected range, and models U2 and U3 failed external validation. Therefore, fitting to SEER incidence and calibration targets from screening studies are both critical for model validation.

Discussion

Extensive computational needs for calibration, a crucial step in the development of cancer microsimulation models, require methods to accelerate this lengthy process. In this study, we used an ML-based framework to increase the efficiency of calibration for simulation models without compromising the quality of the calibrated parameters. We demonstrated our framework’s utility using CRC-AIM, a microsimulation model representing the CRC epidemiology in the United States. We found that using a DNN as an emulator substantially reduced calibration time from 190 CPU-years to 104 CPU-days. We demonstrated the validity of calibrated parameters by comparing model-predicted outcomes such as CRC incidence, LYG, and CRC mortality reduction due to screening to those reported by the 3 established CISNET CRC models. Model-predicted LYG and CRC incidence and mortality reduction resulting from the evaluated CRC screening strategies were within CISNET models’ predictions. In addition, we showed that the calibrated CRC-AIM estimated a reduction in CRC incidence and mortality from 1-time sigmoidoscopy screening similar to that reported by the UKFSS trial, representing the external validity of the model.

There is a growing interest in improving the calibration process for microsimulation models.^62–66 Since the early 2000s, when the conventional approaches to calibration were trial and error, ⁶⁷ maximum likelihood–based methods,^68–70 and grid or random search, ⁷¹ novel methods are increasingly being introduced. Hazelbag et al. ⁶³ reviewed 84 publications that used calibration methods in simulation models. Only 40 of the models reported a search strategy that was further classified into optimization and sampling algorithms. Among optimization methods, grid search^72–74 and iterative optimization algorithms ⁷⁵ were most commonly used. Examples of iterative optimization algorithms (e.g., meta-heuristic methods) that have been extensively used for calibration are genetic algorithms, simulated annealing, and particle swarm optimization. The methods have been suggested as a way to shorten the calibration time.^1,5,76,77 However, the complexity of the proposed methods has limited their use in real-world applications. Heuristic algorithms start from an initial input vector and sequentially update the vector by exploring the neighboring solutions at each iteration. The sequential nature of these algorithms and the likelihood of converging to a local optimum are the biggest limitations of these heuristic approaches. Compared with these methods, our approach enables parallel computations, thus achieving computational feasibility and time efficiency. We note that meta-models and emulators have also been used in simulation models for purposes other than calibration, such as conducting cost-effectiveness and value-of-information analyses or developing online decision support tools.^78,79

Another class of search strategies for calibration involves statistical and sampling methods, ⁶³ which includes Bayesian calibration with several variations such as Bayesian melding, ⁸⁰ Sampling Importance Resampling, Rejection Approximate Bayesian Computation (ABC), and Incremental Mixture Importance Sampling (IMIS). ⁸¹ Volpatto et al. ⁹ and Wade et al. ⁸² used Bayesian calibration with Cascading Adaptive Transitional Metropolis in Parallel (CATMIP) ⁸³ for parallel sampling. Ryckman et al. ⁶⁴ considered 3 calibration techniques comparing random search to Bayesian calibration with the sampling-importance-resampling algorithm and IMIS to model the natural history of cholera and showed that Bayesian calibration with IMIS provided the best model fit while requiring the most computational resources.

Among Bayesian calibration methods, ABC received more attention, with Shewmaker et al. ⁷ and Niyukuri et al. ⁶ using ABC rejection sampling. ABC offers a likelihood-free method that provides an estimate from the posterior distribution by choosing parameters that closely fit the data. However, ABC can be inefficient when the number of unknown parameters for calibration is large or many calibration targets are involved. Also, these models are sensitive to the differences between prior and posterior distributions. Slipher and Carnegie ⁸⁴ explored parameter calibration in epidemic network models using 2 search strategies: LHS and ABC. They found that parameter estimation with LHS is more dispersed and better covers the entire parameter space, while approximate Bayesian inference creates a focused distribution of values and is more computationally efficient. To overcome some of the shortcomings of ABC, the Bayesian Calibration using Artificial Neural Networks (BayCANN) framework was recently proposed. ¹⁰ BayCANN estimates the posterior joint distribution of calibrated parameters using neural networks and was 5 times faster than the IMIS algorithm. ¹⁰

Compared with the present study, BayCANN included a smaller number of unknown parameters (9 inputs) while predicting a large number of outcomes (36). For a better comparison between our method and the Bayesian calibration with neural network emulators, we used the open-source code of BayCANN for our calibration experiment (Supplementary Section E.1). We observed that our method was more successful than BayCANN in matching calibration targets. Furthermore, our method generates a set of heterogeneous input vectors rather than clustered inputs, which may be more helpful when dealing with uncertainty. However, we also recognize that BayCANN was previously tested on multiple models and therefore has more promise for generalizability. Thus, while our approach appears to work well for our problem, its potential performance for other simulation models is unknown.

Recent calibration literature advocates for the use of ML algorithms and their efficiency. Chopra et al. ⁸⁵ and Anirudh et al. ⁸⁶ used neural networks to calibrate simulation models. These studies did not compare their calibration method with other ML algorithms but found neural network framework to be effective for calibration. Angione et al. ⁸⁷ compared several ML algorithms (e.g., linear regression, support vector machines, neural networks) for an agent-based model of social care provision in the United Kingdom and found ML-based meta-models can facilitate robust sensitivity analyses while reducing computational time. However, this proof-of-concept study predicted only a single outcome of interest, rather than multiple outcomes concurrently. Sai et al. ⁸⁸ and Reiker et al. ⁸⁹ used Gaussian process for calibration. Reiker and colleagues proposed an optimization framework employing Gaussian process as a ML emulator function to calibrate a complex malaria transmission simulator. ⁸⁹

Similar to our study, Cevik et al. ² demonstrated how an active learning-based algorithm could accelerate natural history calibration in microsimulation model, specifically a CISNET breast cancer model. However, that active learning algorithm required a feedback mechanism between the ML and microsimulation models, whereas our framework used the microsimulation model only to provide inputs to the ML algorithm. Therefore, unlike the study by Cevik et al., ² our framework does not require specifying a stopping condition to end the feedback mechanism between the ML and microsimulation models. Furthermore, our ML algorithm incorporated multiple calibration targets rather than a single calibration target, and such differences may have led to performance differences between the 2 studies.

We showed that the choice and number of calibration targets and the differential weights applied to them affected modeled outcomes. Because several input combinations generated outcomes close to the targets, adding cross-model targets for validation of our complex simulation model was crucial in identifying the final set of inputs. We demonstrated that if our study had relied on only 1 of the primary calibration targets sets instead of using all 3 of them, the model’s LYG predictions would have been substantially different, demonstrating the impact of calibration target selection on model predictions. In fact, even the use of SEER data, the most comprehensive population-based calibration target for cancer modeling, was by itself insufficient to identify a model that passed the cross-model validation and external validation. The findings suggest the importance of establishing cross-model and external validity to obtain a robust set of input combinations that is best supported by all available evidence. To the best of our knowledge, no previous cancer simulation study has demonstrated the impact of choosing calibration targets on long-term model outcomes such as LYG, prohibiting direct comparison to these studies. Our findings suggest that modelers and policy makers may need to conduct a sensitivity analysis on the calibration targets to assess the robustness of the conclusions drawn from modeling studies and the uncertainties in the natural history of the disease. Such structural sensitivity analyses experiments and robust decision-making approaches could be useful for model development.

Unlike many of the calibration studies in the literature, we identified a set of input vectors that have acceptable performance in terms of calibration and validation targets. The selection of multiple input vectors as opposed to a single input vector provides an opportunity to evaluate the impact of heterogeneity and uncertainty in directly unobservable natural history parameters on final model outcomes. We identified an input vector with good fit to the outcomes explored in the natural history, but the LYG outcomes did not compare well with the CISNET model predictions (model U5 in Supplementary Table 14). While this vector may be regarded as unacceptable simply due to its failure to demonstrate cross-validity, we recognize that the choice of comparing well to CISNET models may appear arbitrary and suggest that models that predicted outcomes that are out of range must not be plausible. Excluding this vector may jeopardize the goal of obtaining robust conclusions. While we plan to use the best input vector for the base-case analyses, multiple input vectors will be used to conduct a structural and parametric sensitivity analysis of the natural history parameters in future experiments.

This study has several limitations. One of the challenges in calibrating complex cancer simulation models is overidentification. To assess the level of overidentification in our study, we plotted the distribution of the model parameters corresponding to the best-fitting 500K input combinations from our emulator, as shown in Supplementary Figure 5. While some parameters are tightly clustered (e.g., the mean and standard deviation of the baseline risk for developing adenoma and the impact of adenoma size in colon and rectum on transitioning of adenoma to preclinical cancer), no clustering was observed for other parameters (e.g., the impact of person’s age at the time of adenoma initiation on transition of adenoma to preclinical cancer). The heterogeneity of our final selected sets of inputs also indicates that there might be multiple solutions for our calibration problem. Alarid-Escudero et al. ⁹⁰ and Ryckman et al. ⁶⁴ suggested using additional calibration targets, narrowing prior distribution ranges, and weighting the GOF function, as some methods to address nonidentifiability, which also applies to overidentification. Identifying and addressing the degree of overidentification solutions with meta-models is a topic of interest and recommended for future research.

While our approach has impressive empirical performance, it is not based on rigorous statistical methodology. Also, other sections of our calibration procedure such as input selection scoring system, targets’ weights and importance, and selection of additional cross-validation target were based on empirical evidence rather than on a theoretical framework, which can be further investigated with more theoretical approaches. While empirical, we showed that having a sufficiently large sample for prediction, the difference between the emulator and statistical methods such as Bayesian calibration may be minimal. Although substantial time may need to be spent to fine-tune and tailor the DNN to a specific simulation model including hyperparameter tuning, the overall calibration time can be reduced. Unlike Bayesian calibration models, our method is not capable of producing conventional posterior distribution and uncertainty bounds around the estimates. However, our method generates a set of heterogeneous input vectors rather than clustered inputs, as discussed earlier. Furthermore, identifying the correlation between inputs and calibration targets is not trivial when using a DNN emulator. While some ML algorithms such as random forests generate the correlation of inputs to outputs, such a task is computationally burdensome for other models such as DNN, with many deep layers and thousands of hidden parameters.^91–93 There are methods that approximate the importance of inputs in DNN^94,95 but are beyond the scope of this research.

While we investigated the importance of calibration target selection in our research, we did not quantify uncertainty and incompatibility of calibration targets in cancer simulation modeling. Mandrik et al. ⁶⁶ discussed methods for dealing with biased calibration targets, including adjustment of target means and standard errors to account for sampling uncertainty and data incompatibility. Further investigation is required to understand the efficiency of ML compared with Bayesian calibration when calibration data are incomplete or biased. Note that prior information about the input parameters from the CRC-SPIN model, which was used to design our model structure, may have helped us identify high-quality inputs relatively quickly. Therefore, our approach may not work efficiently on models in which there is no prior information. In terms of modeling the natural history of CRC, CRC-AIM does not consider the modeling of CRCs that occur through the sessile serrated pathway (SSP), which is a major limitation. Approximately 14% to 30%^96–98 of CRCs are estimated to arise from sessile serrated lesions and polyps, which develop mainly via the CpG island methylation pathway.^99,100 In fact, several CRC simulation models considered both adenoma-carcinoma and SSP pathways and have been extensively validated through several clinical trials.^101–103 Finally, further work is needed to demonstrate that CRC-AIM predictions approximate CISNET CRC model predictions for other screening scenarios and modalities.

In summary, this study showed that the use of powerful DNNs as an emulator could significantly speed up calibration for complex cancer microsimulation models with extensive computational requirements.