Abstract
Background and objective
The trabecular meshwork (TM) consists of extracellular matrix (ECM) with embedded collagen and elastin fibers providing its mechanical support. TM stiffness is considerably higher in glaucoma eyes. Emerging data indicates that the TM moves dynamically with transient intraocular pressure (IOP) fluctuations, implying the viscoelastic mechanical behavior of the TM. However, little is known about TM viscoelastic behavior. We calculated the viscoelastic mechanical properties of the TM in n=2 healthy and n=2 glaucoma eyes.
Methods
A quadrant of the anterior segment was submerged in a saline bath, and a cannula connected to an adjustable saline reservoir was inserted into Schlemm’s canal (SC). A spectral domain-OCT (SD-OCT) provided continuous cross-sectional B-scans of the TM/JCT/SC complex during pressure oscillation from 0 to 30mmHg at two locations. The TM/JCT/SC complex boundaries were delineated to construct a 20-μm-thick volume finite element (FE) mesh. Pre-tensioned collagen and elastin fibrils were embedded in the model using a mesh-free penalty-based cable-in-solid algorithm. SC pressure was represented by a position- and time-dependent pressure boundary; floating boundary conditions were applied to the other cut edges of the model. An FE-optimization algorithm was used to adjust the ECM/fiber mechanical properties such that the TM/JCT/SC model and SD-OCT imaging data best matched over time.
Results
Significantly larger short- and long-time ECM shear moduli (p=0.0032), and collagen (1.82x) and elastin (2.72x) fibril elastic moduli (p=0.0001), were found in the TM of glaucoma eyes compared to healthy controls.
Conclusions
These findings provide additional clarity on the mechanical property differences in healthy and glaucomatous outflow pathway under dynamic loading. Understanding the viscoelastic properties of the TM may serve as a new biomarker in early diagnosis of glaucoma.
Keywords: Glaucoma, Trabecular Meshwork, Ocular Biomechanics, Finite Element-Optimization, Collagen and Elastin Fibers
1. Introduction
Primary open angle glaucoma (POAG) is a leading cause of progressive and irreversible blindness [1–4]. High intraocular pressure (IOP) is a key risk factor in POAG patients, and is the only risk factor that is amenable to intervention [5–7]. While great strides have been made in understanding aqueous outflow [8–10], gaps in our knowledge remain. It is important to fully understand the mechanisms that maintain IOP within a normal range so glaucoma patient’s abnormalities can be diagnosed and treated. [11, 12]. The resistance to the aqueous outflow in both the conventional and unconventional pathways regulates the IOP to maintain it within a normal range of ~15 mmHg [13–15]. The aqueous in the conventional outflow pathway drains through the trabecular meshwork (TM), which consists of several layers of perforated cell-lined lamellae that form beams. Aqueous flows through the TM to reach a thin layer of loose extracellular matrix (ECM) with embedded cells that form the juxtacanalicular tissue (JCT). The flow then passes through the inner wall endothelium of Schlemm’s canal (SC) to enter the SC lumen, which is a torus-like structure in the sclera that encompasses the circumference of the eye at the limbus. Aqueous humor flows circumferentially along the SC to one of 20–30 collector channels followed by exiting to aqueous and episcleral veins [16–20].
The biomechanical properties of the outflow system play an important role in IOP regulation. It has been shown that alterations in TM stiffness result in a change in TM motion. The stiffness alteration is thought to be a hallmark of ocular hypertension that leads to glaucoma [21–23]. Therefore, TM/JCT/SC motion, resultant contributions to aqueous outflow resistance, and altered stiffness in glaucoma largely depend on the biomechanical properties of these tissues. Alterations in the ECM components and TM cellularity are known to contribute to the change in TM biomechanical properties [24–27].
The TM consists of ECM with embedded collagen [27–29] and elastin [30–33] fibers that are the main determinates of TM stiffness. Several studies have found that the TM is considerably stiffer in POAG eyes [17, 34–42] implicating the collagen and elastin fibers. Phase-sensitive optical coherence tomography (PhS-OCT) imaging data in human eyes revealed less TM motion in glaucoma eyes compared to normal controls [19–22, 43]. The reduced motion detected by OCT also implies a stiffer TM and altered collagen and elastin properties in POAG eyes.
Numerical approaches, such as the finite element method (FEM), have also suggested a higher stiffness in glaucomatous human TM. A study using FE modeling of spectral-domain OCT (SD-OCT) images suggested that TM motion determines bulk TM stiffness [44, 45]. Experimental studies have also shown that outflow facility is related to TM stiffness in both healthy and glaucomatous eyes [45]. The TM in the computational studies was treated as an isotropic hyperelastic material [44, 45], although it is known that soft biological tissues are viscoelastic and anisotropic [46–52]. Hence, simulating the TM as an isotropic elastic or hyperelastic material does not incorporate its time-dependent anisotropic mechanical behavior under dynamic loading in the aqueous outflow system.
In elastic materials, the stress is proportional to the strain and is independent of both loading rate and time. In contrast, viscoelastic materials exhibit time dependent behavior, so the stress is proportional to the time-dependent strain rate as well. The TM mechanical response, resistance, or motion with respect to the aqueous outflow varies with transient IOP fluctuation magnitude [53, 54]. IOP fluctuation [55–57] induces a dynamic mechanical environment in the outflow system, which results in both viscous and elastic behaviors in the outflow system connective tissues, especially the TM.
While the elastic (spring) connective tissue of the TM stores energy as it is being deformed by aqueous outflow, its viscous component (dashpot) dissipates energy. It is plausible to speculate that the mechanical response of the TM is load rate dependent, which could lead to dynamic flow resistance changes and fluctuations in conventional aqueous outflow. The TM lamellae experience a large portion of the OCT-measured motion capable of driving pulsatile aqueous outflow. Pulsatile flow reduces in humans with glaucoma. Mechanical properties of the TM lamellae are thus of great significance to the understanding of IOP control [20].
Trabecular meshwork finite element simulations used tetrahedral element type [45], while these elements are mathematically ‘stiffer’ due to their reduced degrees-of-freedom [58]. Prior trabecular meshwork finite element simulation studies considered the cornea and sclera as the boundary components of the TM [44, 45]; however, the mechanical properties of the cornea and sclera are eye-specific, which was not considered. We recently developed a floating displacement boundary condition approach [59]. The approach allows us to apply dynamic nodal displacement at the interface between the TM to the sclera and cornea over time. The nodal displacement is derived from continuously acquired SD-OCT images, and accounts for their biomechanical effects on the TM. Prior studies also modeled the walls of SC lumen as being exposed to a simple linear pressure profile [44, 45]. However, the pressure profile in the walls of SC lumen can be both position- and time-dependent. The additional parameters are due to unequal flow through irregularly spaced collector channels, and a dynamically fluctuating TM and SC configuration related to pressure-dependent aqueous flow oscillations and transients.
Calculating the mechanical properties of the TM with embedded collagen and elastin fibers is a challenging task that cannot be achieved with currently available imaging techniques. Assessment of these biomechanical properties in relation to dynamic outflow system mechanics can advance our understanding of IOP control mechanisms and the abnormalities in glaucoma [37].The improved understanding can provide new targets for diagnostic and therapeutic approaches to ocular hypertension and glaucoma [53]. In this study, we evaluated the viscoelastic mechanical properties of the TM in healthy and glaucoma eyes using FE-optimization of TM dynamic motion from SD-OCT imaging data. The optimized viscoelastic mechanical properties and resultant stresses in the ECM and collagen and elastin fibers are reported for normal and glaucoma eyes.
2. Materials and Methods
2.1. Human Donor Eyes and Organ Culture Prep
The healthy and glaucoma human eyes (age: 74 to 88 years) were obtained within 72 hours postmortem from the Oregon VisionGift eye bank (Portland, Oregon), and anterior segments were perfused under organ culture conditions [60]. Eye tissue procurement followed the principles of the Declaration of Helsinki.
The eye was removed from the anterior organ culture chamber and a quadrant of the anterior segment was dissected, placed interior up, and the SC cannulated as shown in Fig. 1 and fully described in our previous publication [44]. Briefly, a quadrant of the anterior segment including the cornea, limbal region with TM, SC, and ~5 mm of sclera was mounted in a petri dish with pins, with the inner TM surface facing upward. The entire quadrant was submerged in a saline bath. (Fig. 1) [44, 61]. This saline bath also helped to eliminate surface motion artifacts when dynamic TM motion occurred [44]. A cannula connected to a moveable height reservoir filled with saline was inserted into SC with the help of a dissecting microscope and a micromanipulator, while the other end remained open. The tip of the cannula made a tight contact with the interior walls of the SC lumen, and was connected to a saline reservoir such that SC lumen pressure was controlled by changing the height of the reservoir in an oscillating fashion to mimic either steady-state or transient IOP fluctuations (Fig. 1).
Fig. 1.
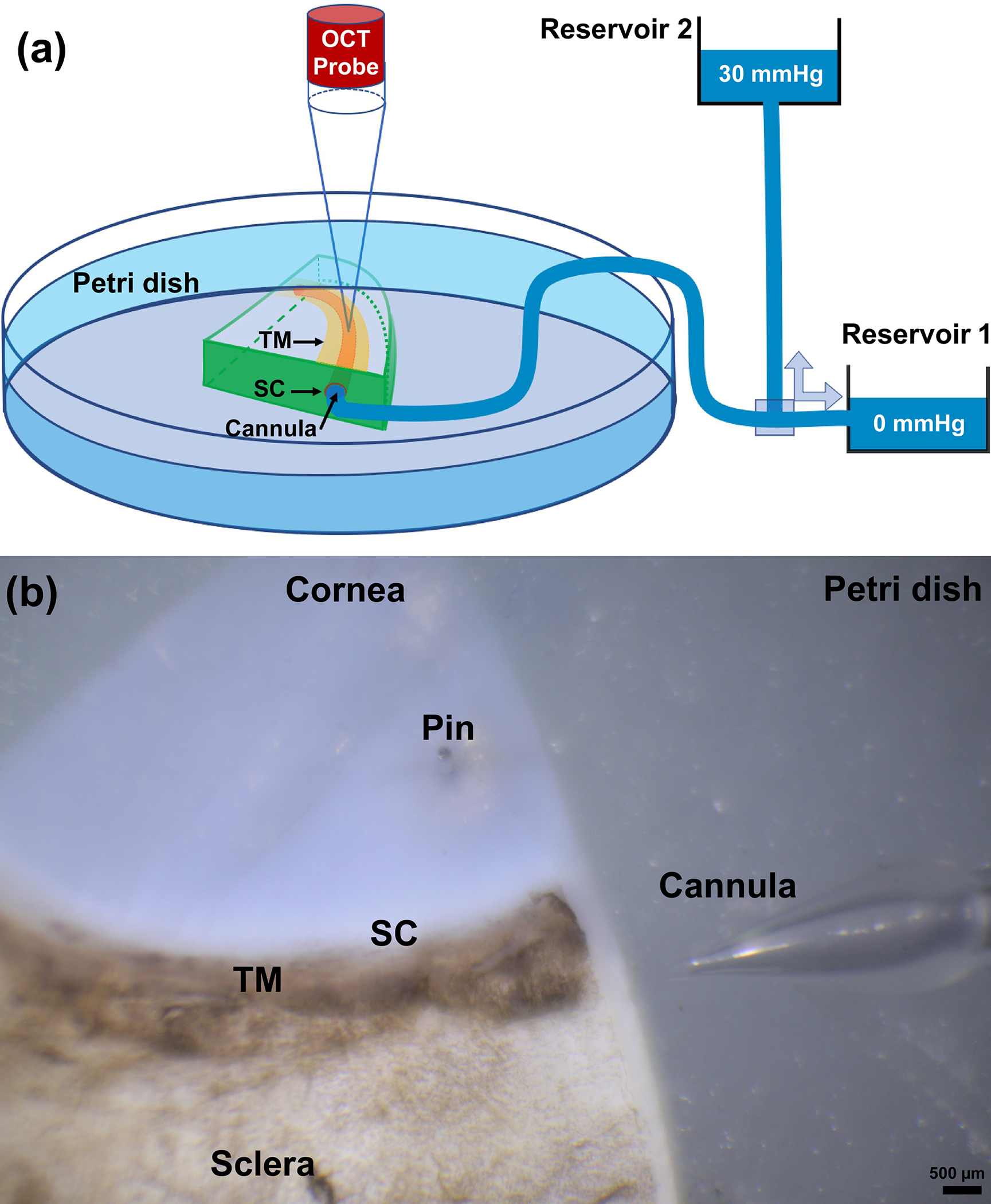
(a) Schematic overview of experimental setup, including the spectral domain optical coherence tomography (SD-OCT) system, two reservoirs used for controlling pressure in Schlemm’s canal (SC). Continuous acquisition SD-OCT B-scan images were acquired through the trabecular meshwork (TM), juxtacanalicular tissues (JCT) and SC at 30 Hz, resulting in a very high resolution images from which TM/JCT/SC motion can be determined in real time [132]. (b) A quadrant of the eye pinned in a petri dish and the structure of the cannula immediate before cannulation.
To capture high-resolution dynamic movement of TM/JCT/SC complex, the SD-OCT imaging probe was adjusted to face the TM (Fig. 1). A series of cross-sectional scans through the TM/JCT/SC complex were captured at multiple locations for SC reservoir pressures varying from 0 to 30 mmHg. The OCT system used in this study was capable of an imaging speed of 92 kHz with imaging done through air without contact to the sample. The central wavelength of the SD-OCT system was 1310 nm, and the spatial resolution in each scan was 5.0 and 5.75 μm in the axial and lateral dimensions, respectively. At this setting, a system sensitivity (dynamic range) of 105 dB was measured when the light power on the sample was 5 mW [44]. The spacing between two adjacent B-scans was ~10 μm. Two-dimensional structural scanning electron microscopy (SEM) and a comparable OCT of the SC perfused at the pressures of 0 mmHg and 30 mmHg from the limbal region are shown in Fig. 2. Structures included are the ciliary muscle (CM), TM, SC, collector channels, septa at collector channels ostia, and cylindrical attachments between SC walls (CAS) connecting the TM to the septa.
Fig. 2.
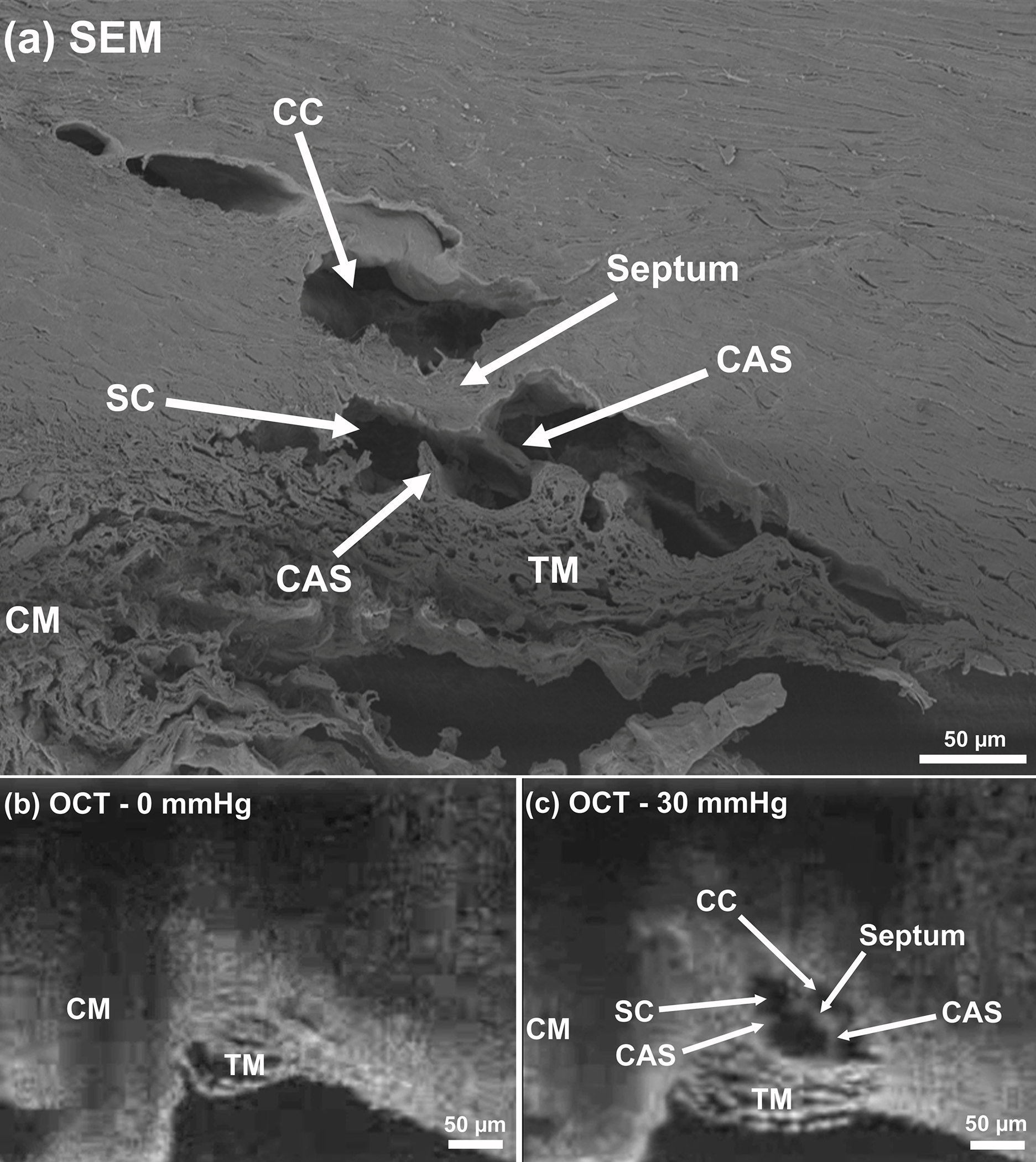
(a) Two-dimensional structural OCT and scanning electron microscopy (SEM) images from the limbal region of a human eye, including ciliary muscle (CM), trabecular meshwork (TM), Schlemm’s canal (SC), collector channel (CC), septa at the collector channel ostia, and cylindrical attachments between SC walls (CAS) septum and the trabecular meshwork. SD-OCT images captured with the cannula perfusing the SC at pressures of (b) 0 mmHg and (c) 30 mmHg.
2.2. Trabecular Meshwork Delineation and Finite Element Volume Meshing
The SD-OCT with 30 B-scans/second provided a set of dynamic images of the TM/JCT/SC complex as the pressure in the SC lumen cannula increases from 0 to 30 mmHg. The first step of the segmentation was to convert an SD-OCT video to a stack of images through a custom Matlab (Mathworks, Natick, Massachusetts, US) program. Thereafter, using our recently developed and updated semi-automatic delineation program [59] under the supervision of an expert glaucoma specialist (MJ), the boundaries of the TM/JCT/SC complex were delineated as shown in Fig. 3a. The Matlab program also provides the nodal coordinates of the TM/JCT/SC complex boundaries, so they could be used to define the floating displacement boundary condition of the FE model.
Fig. 3.
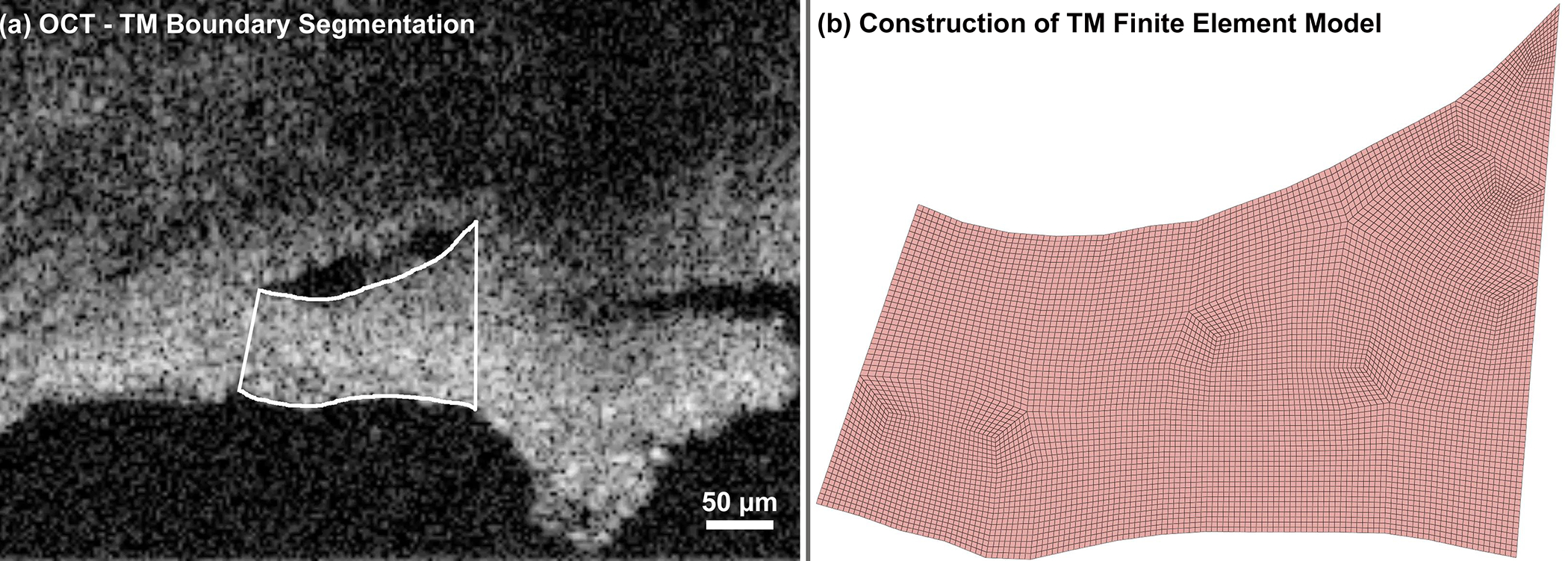
(a) The TM boundary was semi-automatically segmented in each SD-OCT B-scan using a custom Matlab program, as SC cannula pressure was increased from 0 to 30 mmHg. (b) Resulting FE volume mesh of the TM/JCT/SC complex, created by extruding the segmented boundary seen in (a) by 20 μm.
Since the upper and lower boundaries of the TM/JCT/SC complex were noisy in the images and hence form sharp vertices in the FE mesh, the boundaries were smoothed using a smoothing spline algorithm as follows [62]:
| (1) |
where the smoothing spline is constructed for the specified smoothing parameter and the specified weights . The smoothing spline minimized Eq. (1). In the above equation, , where equals to zero generates a least-square straight-line fit, while equals to one generates a cubic spline interpolation. Since we wanted to both preserve the shape of the upper and lower boundaries and have the best smoothing fit for them, the specified smoothing parameter of 0.999 was used. The first 2D SD-OCT image was delineated as described above, extruded to 20-μm thickness, and volume meshed using our image-to-mesh program [63] as illustrated in Fig. 3b.
2.3. Collagen and Elastin Fiber Distribution, Material Model, and Mesh-Free Penalty-Based Cable-in-Solid Coupling Algorithm
Our team recently developed a mesh-free penalty-based cable-in-solid coupling algorithm, which allows us to simulate the anisotropic mechanical behavior of collagenous ocular tissues [64]. The same approach was employed herein to embed the collagen and elastin fibers into the FE models of the ECM of the healthy and glaucomatous TM/JCT/SC complex. Briefly, the surface mesh of the TM/JCT/SC complex was imported to a custom Matlab program to distribute the control points throughout the FE model. The distance between the control points was set to 5 μm and 7 μm for the collagen and elastin fibers, respectively, which are restricted by the 20-μm thickness of the TM/JCT/SC complex model. To separate the external and internal regions in the TM/JCT/SC complex FE models, a line was drawn between the sclera spur and Schwalbe’s line through a custom Matlab code for both the healthy and glaucoma eyes.
The collagen and elastin fibers were distributed to form an asymmetric fan-shaped configuration parallel to the external and internal edges of the TM [20, 30, 33, 61, 65–69] using a custom Matlab program. The collagen and elastin fibers in the TM/JCT/SC complex were modeled by elastic cable elements and the surrounding ground substance matrix was modelled as a viscoelastic material using 8-noded hexahedral solid elements with an r-adaptive remeshing function based on the Galerkin element free formulation [70]. The coupling algorithm transfers the load from the collagen and elastin fibers to the ECM of the TM/JCT/SC complex and vice-versa [71] via strong coupling under both the static and dynamic loadings.
The force that is generated in the collagen and elastin fibers of the TM/JCT/SC complex under SC pressurization will be nonzero when the cables/fibers are in tension. When the TM lamellae experience large excursions in response to pressure elevation in the walls of the SC lumen, the fibers experience increasing tension. The induced forces in the collagen and elastin fibers can be calculated as [72]:
| (2) |
where is the change in the length of a cable element.
| (3) |
and the stiffness ( only) is presented as:
| (4) |
A constant force element can be achieved through:
| (5) |
Elastin and collagen form unit fibrils of 0.1–0.2 μm [68, 73] and 0.02–0.5 μm [74] thickness, respectively. In this study, we assumed the elastin and collagen fibrils have the diameter of 0.2 μm and 0.5 μm, respectively, and a bundle of 10 collagen (5 μm in diameter) and elastin (2 μm in diameter) fibrils form a bundle of collagen and elastin fibrils for the purposes of representing the collagen and elastin in the model. Collagen and elastin fibrils have elastic moduli of ~100 MPa [75–78] and 1 MPa [79, 80], respectively; since 10 fibers were bundled together in the model, the elastic moduli of 1,000 MPa and 10 MPa were chosen for the cable elements representing collagen and elastin, respectively. The ECM of the TM FE model was embedded with cable elements representing the directional stiffness imparted by collagen and elastin, with parameter ranges set such that they encompass the range of behavior seen in experimental tensile tests of TM specimens [81, 82]. With that being said, the cable elements were embedded into the ECM of the FE model to represent the “collagen” and “elastin” fibrils, so it is worth mentioning that the cable elements cannot be interpreted as collagen and elastin fibrils in the model, while they just were used to provide directional stiffness for the tissue.
The aqueous outflow pump model encompasses prestress from the ciliary muscle tension that induces pre-tension in the TM collagen and elastin fibers [20]. IOP provides a loading force on the TM, forcing it outward, favoring distention into SC. The ciliary muscle contractile force continuously counterbalances this TM distention, providing the prestress required for the ciliary muscle involvement in pump-conduit regulation of IOP [20]. To incorporate this concept into the models, the tensile force (~500 μN) in the fibers as well as the ECM was generated first through two-steps of pressurization immediately before SC lumen pressure elevation. Since the magnitude of the resultant stress in the TM and the resultant forces in the collagen and elastin fibrils are unknown, the model generated a small tensile force (~1500 μN) in the fibrils, and in turn, in the ECM of the TM/JCT/SC complex [20, 83]. To simulate the force, a custom subroutine was written to pre-tension the cable elements. An advantage of this approach is that it prevents sudden application of forces in the cable element at time zero. Without such a pre-tension, an excessively dynamic response may occur at the start of the simulation [64].
The ECM of the TM/JCT/SC complex was simulated as a viscoelastic material model, with mechanical behavior assigned through a Prony series [84–87]. A viscoelastic material model has both viscous and elastic properties [88]. The behavior of a viscoelastic material can be defined via a shear relaxation modulus as follows:
| (6) |
where and are the short-term and long-time shear moduli, respectively, and is the decay constant.
A Jaumann rate formulation is also used as follows:
| (7) |
where the prime denotes the deviatoric portion of the stress rate, , and the strain rate, .
2.4. Trabecular Meshwork Specimen Finite Element Model – Viscoelastic Material Properties Calculations
While there is a wide range of human TM elastic moduli reported in the literature (0.004 to 51.5 MPa [40]), we are not aware of any studies that have reported the viscoelastic mechanical properties of the TM. Hence, these properties were estimated before modeling the TM/JCT/SC complex. First, an FE model of an experimental TM specimen was constructed, subjected to a tensile displacement, and the resultant stresses were compared to published experimental data on the healthy [81] and glaucoma [82] human TM tested in tension. The FE model of the TM specimen of 10 mm length × 0.24 mm width × 0.136 mm thickness matches the specimen dimensions in the experimental study [81, 82] as shown in Fig. 4a. Cable elements representing the anisotropic collagen and elastin fibrils were incorporated into the TM specimen FE model as described in section 2–3 and coupled to the ECM using mesh-free penalty-based cable-in-solid algorithm [64]. Thereafter, the TM specimen FE model was subjected to a uniaxial tensile strain, where the displacement boundary condition (2% strain) was applied to the FE model to mimic the uniaxial mechanical testing protocol [81, 82]. The Fminsearch-Unconstrained nonlinear minimization optimization algorithm was coupled with the LS-DYNA solver (Ansys/LS-DYNA, PA, US) to calculate the viscoelastic parameters for the TM specimen ECM, as well as the elastic moduli of the collagen and elastin fibrils [59, 89]. Fminsearch finds the minimum of a scalar function of several parameters, starting at an initial estimation, which were chosen as (short-time shear modulus)=7.30 MPa, (long-time shear modulus)=6.20 MPa, and (decay constant)=500 1/s for both healthy and glaucoma TM specimens [90]. The upper and lower parameter boundaries were chosen as , and . Wide parameter ranges based on the scleral mechanical properties [90] were chosen to allow the FE-optimization algorithm to work within an unconstrained parameter space to ensure unbiased random selection for the material parameters. The initial guess was set to [75–78] and [79, 80] for the collagen and elastin fibrils, with the upper and lower boundaries of and . The bulk modulus () was chosen as 2,700 MPa for both the healthy and glaucoma TM specimen FE models [91]. The model was run in Matlab with the cost function of mean squared error [92] that is the sum of the squared differences between the experimental data [81, 82] and optimization value. The resultant stress-strain in the gauge at the center of the TM specimen FE model (Fig. 4a) was calculated and plotted versus the experimental data [81, 82] as displayed in Figs. 4b. The optimized viscoelastic ECM properties and the elastic moduli of the collagen and elastin fibrils in the healthy and glaucoma TM patch FE models are listed in Table 1.
Fig. 4.
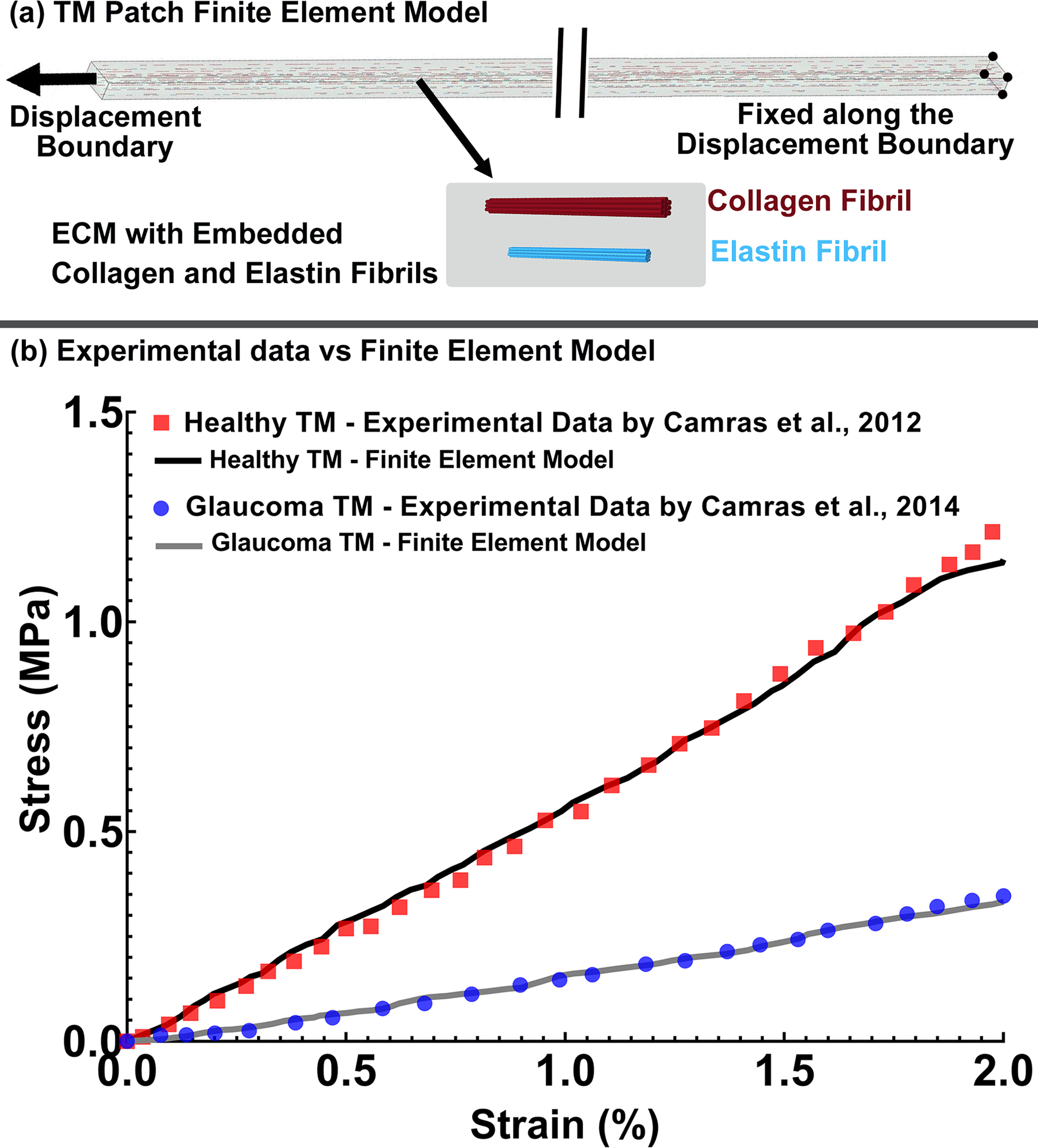
(a) FE model of the TM with axial cable elements representing collagen (10 μm length and 5 μm diameter) and elastin (4 μm length and 2 μm diameter) fibrils distributed through the TM specimen within a solid extracellular matrix (ECM). Stress-strain curves representing the average responses from the (b) previously published healthy [81] and glaucoma [82] experimental uniaxial tensile testing of human TM, compared to identical FE cable-in-solid models.
Table 1.
The optimized material properties of the TM in healthy and glaucoma eyes. The ECM was modeled as the viscoelastic material, and the collagen and elastin fibrils were simulated as elastic cable elements.
| Healthy Eyes | |||||
|---|---|---|---|---|---|
|
| |||||
| Tissues and Fibers | G0 (MPa) | G∞ (MPa) | β (1/s) | ρ (kg/m3) | |
|
| |||||
| ECM | 24.50 | 17.02 | 500 | 1243 | |
|
| |||||
| E (MPa) | ρ (kg/m3) | ||||
|
| |||||
| Collagen fibril | 2800 | 1100 | |||
| Elastin fibril | 90 | 1100 | |||
|
| |||||
| Glaucoma Eyes | |||||
|
| |||||
| Tissues and Fibers | G0 (MPa) | G∞ (MPa) | β (1/s) | ρ (kg/m3) | |
|
| |||||
| ECM | 6.90 | 4.85 | 510 | 1243 | |
|
| |||||
| E (MPa) | ρ (kg/m3) | ||||
|
| |||||
| Collagen fibril | 1100 | 1100 | |||
| Elastin fibril | 50 | 1100 | |||
FE simulations of viscoelastic materials and/or time varying loading conditions can be done at various time scales (simulation times) and step times. Although timing would not be a primary concern for a non-viscous material model, it would have a considerable influence in time-dependent viscoelastic material models. Herein, the pressure in the SC lumen elevates from 0 to its maximum value within ~1–2 seconds, but such a long timescale cannot be run efficiently as a dynamic FE simulation. As a result, we scaled the simulation time down to a range that allows for reasonable computational times, while limiting the error in TM mechanical properties to <6.5%. Herein, a set of FE simulations were performed using the same TM specimen FE model (Fig. 4a) with optimized material parameters extracted from FE-optimization simulations as described above (Table 1). The TM specimen FE model was subjected to the same loading and boundary conditions, but different simulation times to calculate the simulation time that results in minimizing the dependency of the volumetric average von Mises stresses on the shear relaxation moduli of the tissue (Table 2). Time dependency was minimized for simulations >10ms, so all the healthy and glaucoma FE models were simulated in 10 ms; SD-OCT imaging B-scan timing was also scaled to 10 ms, representing the 0 to 30 mmHg pressure ramp at the SC cannula.
Table 2.
The volumetric average von Mises stresses in the healthy and glaucoma eye TM at different simulation times.
| Time (ms) | Average von Mises Stress (MPa) | |
|---|---|---|
|
| ||
| Healthy Eyes | Glaucoma Eyes | |
|
|
||
| 1 | 1.35 | 0.41 |
| 5 | 1.26 | 0.37 |
| 10 | 1.17 | 0.33 |
| 50 | 1.17 | 0.33 |
| 100 | 1.17 | 0.33 |
| 250 | 1.16 | 0.33 |
| 500 | 1.15 | 0.33 |
| 1,000 | 1.14 | 0.32 |
| 5,000 | 1.14 | 0.32 |
| 10,000 | 1.13 | 0.32 |
| 30,000 | 1.12 | 0.32 |
| 50,000 | 1.12 | 0.32 |
| 100,000 | 1.11 | 0.32 |
| 250,000 | 1.11 | 0.31 |
| 500,000 | 1.10 | 0.31 |
| 600,000 | 1.10 | 0.31 |
2.5. Dynamic FE Optimization Algorithm, Pressure Boundary, and Floating Boundary Conditions
In the experimental prep of the wedge of TM/SC, a cannula was inserted into one end of the SC lumen and pressurized from 0 to 30 mmHg, while the other end of the SC remained open. The flow in the SC lumen can be drained through the collector channels or from the distal end of SC circumference. Although the objective in the experiments is to elevate the pressure in the walls of the SC lumen from 0 to 30 mmHg, the actual SC lumen pressure would be lower, dependent on distance from the cannula, any pressure losses from collector channels, drainage from SC’s distal end and the time-dependent input cannula pressure [89]. A fully coupled FE optimization algorithm [59, 89] was employed to optimize the unknown pressure profile in the SC lumen. The position- and time-dependent pressure profile was the optimization parameter, while the distance between the corresponding nodes in the FE model and in the SD-OCT images at the SC lumen where the pressure is applied was the cost function. Fminsearch-Unconstrained nonlinear minimization [59, 89] with the initial guess of mmHg and with the upper and lower bounds of , , and were set for the pressure profile. The initial guesses for the ECM viscoelastic properties and fibrils stiffness were defined as listed in Table 1 for the healthy and glaucoma TM/JCT/SC complex, with upper and lower bounds of , and . The TM/JCT/SC complex FE model was run in Matlab using the LS-DYNA solver. A 4th-order polynomial function was used to describe the position-dependent pressure profile and a two-variable (Mean±SD) normal distribution function was used for the time-dependent pressure profile as shown in Figs. 5a, and defined as follows:
| (8) |
| (9) |
where , and are the pressure parameters, is the vector of the distance that denotes the normal distance between the center of each element and a surface node on the TM/JCT/SC complex FE model in Eq. (8), and and are mean and standard deviation in Eq. (9), respectively. The final optimized position and time-dependent pressure profile is defined as follows:
| (10) |
Fig. 5.
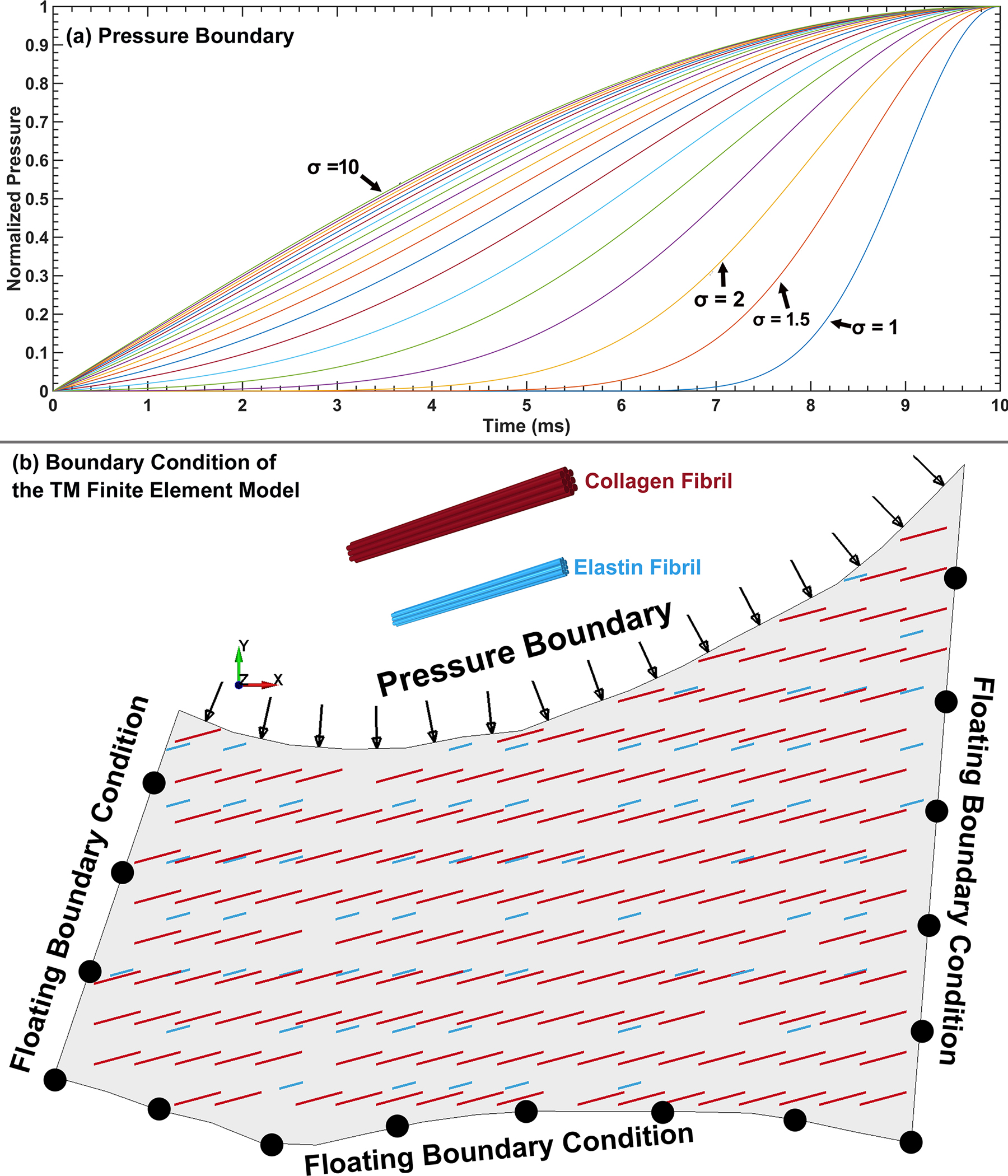
(a) Functions representing the time-dependent pressure boundary in the SC lumen that were optimized in the analysis. (b) FE model of the TM/JCT/SC complex with a position- and time-dependent pressure boundary as well as floating displacement boundary conditions at the junctions with the scleral and cornea.
The cost function was defined as:
| (11) |
where is the position vector corresponding to the node of the TM/JCT/SC complex nodes in the SC lumen, is the position matrix of all TM/JCT/SC complex nodes and is the number of TM/JCT/SC complex nodes. The converged pressure parameters for the healthy and glaucoma eyes were 27±3 (Mean±SD), 29±3, 16±3, 8±2, 2±1, and 4±0.50 for the and , respectively.
The next step was to define the boundary conditions at three free edges of the FE model (Fig. 5b). We recently developed a floating displacement boundary condition approach [59] that allows us to account for the stresses and strains of the tissues in the vicinity of the TM, namely the sclera and cornea, through selective 2D segmentation of SD-OCT imaging data of the TM/JCT/SC complex. The dynamic motion in the outer wall (nodes) of the TM/JCT/SC complex was extracted through a custom Matlab program. The dynamic motion (displacement as a function of time) was quantified and used to define the floating boundary condition [59]. A flow chart summarizing the model generation and optimization process is shown in Fig. 6.
Fig. 6.
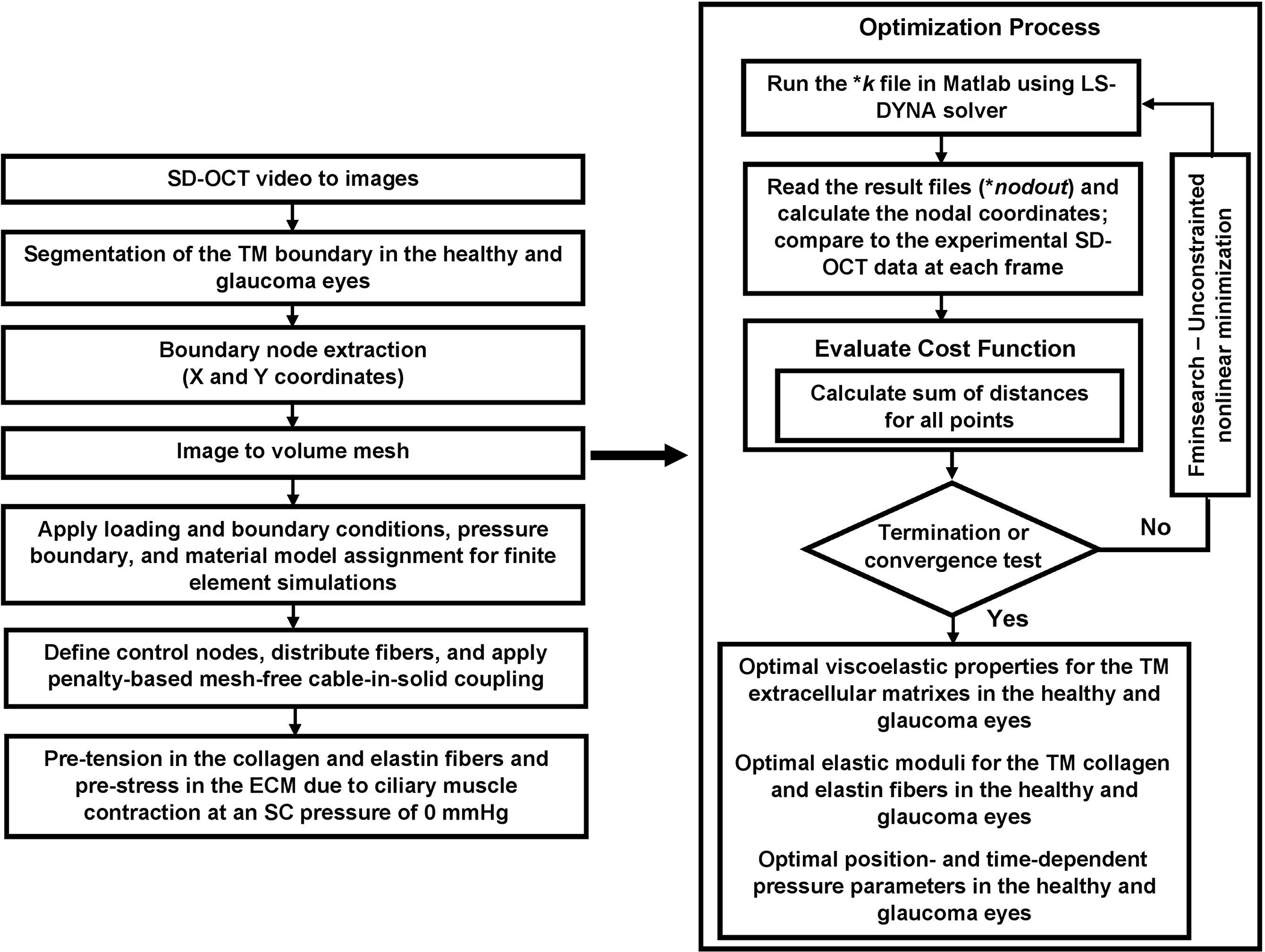
The flow chart of model construction and FE-optimization processes.
A computer with a 10-core Intel® Xeon® CPU W-2155@3.30 GHz and 256GB RAM was used to run the simulations in explicit-dynamic LS-DYNA using dynamic SC pressurization time-compressed to 10 ms, with the time step of 0.1 ms (100 time steps).
2.5.1. Fminsearch-Unconstrained Nonlinear Minimization – Parameter Uniqueness
Fminsearch-Unconstrained nonlinear minimization finds the minimum of an unconstrained multivariable function using the derivative-free method [93]. Fminsearch is a multivariate curve resolution (MCR) approach, in which uncertainty in the parameters may result in non-uniqueness of the results [94]. Although the problem of non-uniqueness is ubiquitous to all MCR methods, it can be alleviated or avoided in some cases by using the data structure intelligently and imposing appropriate parameter constraints [95, 96]. In this case, we constrained all parameters within bounds that were consistent with other published studies, and did not allow solutions sets that would be obviously non-physiologic. In addition, one of the most effective strategies to check the reliability or uniqueness of the results is to perturb the system, for instance, through selecting various initial guesses [93, 95]. To do that, typical healthy and glaucoma TM FE models were subjected to eight different sets of initial guesses, defined as 10%, 20%, 30%, and 40% greater and lesser than the optimized pressure and material parameters (Table 3). In all cases, optimization resulted in the same parameters (less than ~4.5% difference) reported in the Results below.
Table 3.
The optimized material properties of the TM/JCT/SC complex in the healthy and glaucoma eyes. The ECM was modeled as the viscoelastic material, and the collagen and elastin fibrils were simulated as elastic cable elements.
| Healthy Eyes | |||||
|---|---|---|---|---|---|
|
| |||||
| G0 (ECM) (MPa) | G∞ (ECM) (MPa) | Β (ECM) (1/s) | ECollagen fibril (MPa) | EElastin fibril (MPa) | |
|
| |||||
| 115 (sample #1) | 6.42 | 1.27 | 1000 | 2838 | 83 |
| 115 (sample #2) | 7.10 | 1.02 | 1000 | 2840 | 50 |
| 118 (sample #1) | 5.45 | 1.02 | 999 | 2837 | 75 |
| 118 (sample #2) | 6.50 | 1.02 | 998 | 2744 | 42 |
|
| |||||
| Mean±SD | 6.36±0.68 | 1.08±0.12 | 999.25±0.95 | 2814±47.18 | 62.5±19.6 |
|
| |||||
| Glaucoma Eyes | |||||
|
| |||||
| 125 (sample #1) | 37.90 | 5.85 | 822.52 | 5196 | 150 |
| 125 (sample #2) | 35.40 | 6.35 | 978.75 | 4956 | 178 |
| 126 (sample #1) | 46.90 | 4.85 | 572.50 | 5196 | 174 |
| 126 (sample #2) | 43.90 | 4.85 | 947.74 | 5144 | 178 |
|
| |||||
| Mean±SD | 41.02±5.29 | 5.47±0.75 | 830.37±184.70 | 5123±114 | 170±13.46 |
2.6. Importance of Viscoelasticity
There could be an argument that the existence of dynamic TM motion as the pressure is being changed does not, by itself, indicate that viscoelastic effects are present. Although all soft tissues are viscoelastic to some extent [46–52], but the question is how significant this effect is when it comes to the TM. To address this concern, TM/JCT/SC complex FE model of donor 118-healthy was subjected to the same loading and boundary conditions as explained in the above sections with the cable elements removed from the ECM. Two material models, including elastic and viscoelastic, were assigned to the FE model along with the pressure profile parameters to run an independent FE-optimization. There is a wide range of human TM elastic moduli reported in the literature: 0.004 MPa using atomic force microscopy [36], 0.128 MPa using an in vivo beam bending model [97], and 51.5 MPa using uniaxial tensile tests [81], however, the stiffness of 0.004 MPa seems to be the most reliable stiffness in the literature. Therefore, this stiffness was used for the TM/JCT/SC complex FE model as an initial guess with the upper and lower boundaries of 0.0001 and 1 MPa, respectively. The TM/JCT/SC FE model was assumed to be nearly incompressible with the Poisson’s ratio of ν=0.495. For the viscoelastic model, the same mechanical properties parameters as explained in the above section were used. The same optimization algorithm was employed with the distance between the corresponding nodes in the FE model and in the SD-OCT images at the SC lumen where the pressure is applied as the cost function. The results in terms of the agreement of the mechanical response of the TM with respect to the experimental SD-OCT data were presented.
2.7. Statistical Analysis
Data from the simulation of four eye-specific FE models were determined to be normally distributed. The statistical significance of the difference between sample means was evaluated using a randomized one-way analysis of variance (ANOVA). When indicated by a significant F statistic after a one-way ANOVA, post hoc comparisons with the Scheffe method [98] were used to determine the individual levels of significant differences among the material parameters for the ECM and collagen and elastin fibers, as well as the resultant stresses in the fibrils. The criterion chosen to discard the null hypothesis was p<0.05.
3. Results
The shape of the SC wall that resulted in the best possible match between the experimental SD-OCT data and the TM/JCT/SC complex FE model is shown in Fig. 7 for the healthy eye with the elastic and viscoelastic material models. The shape of the SC wall that resulted in the best possible match between the experimental SD-OCT data and the TM/JCT/SC complex FE model is shown in Fig. 8 for the healthy and glaucoma eyes. The model considers the optimal mechanical properties of the ECM with embedded collagen and elastin fibrils. The SD-OCT imaging data and FE model of the TM/JCT/SC complex exposed to an SC cannula pressure of 0, 15, and 30 mmHg for one TM/JCT/SC complex cross-section in a representative healthy and glaucoma eye are shown in Fig. 9.
Fig. 7.
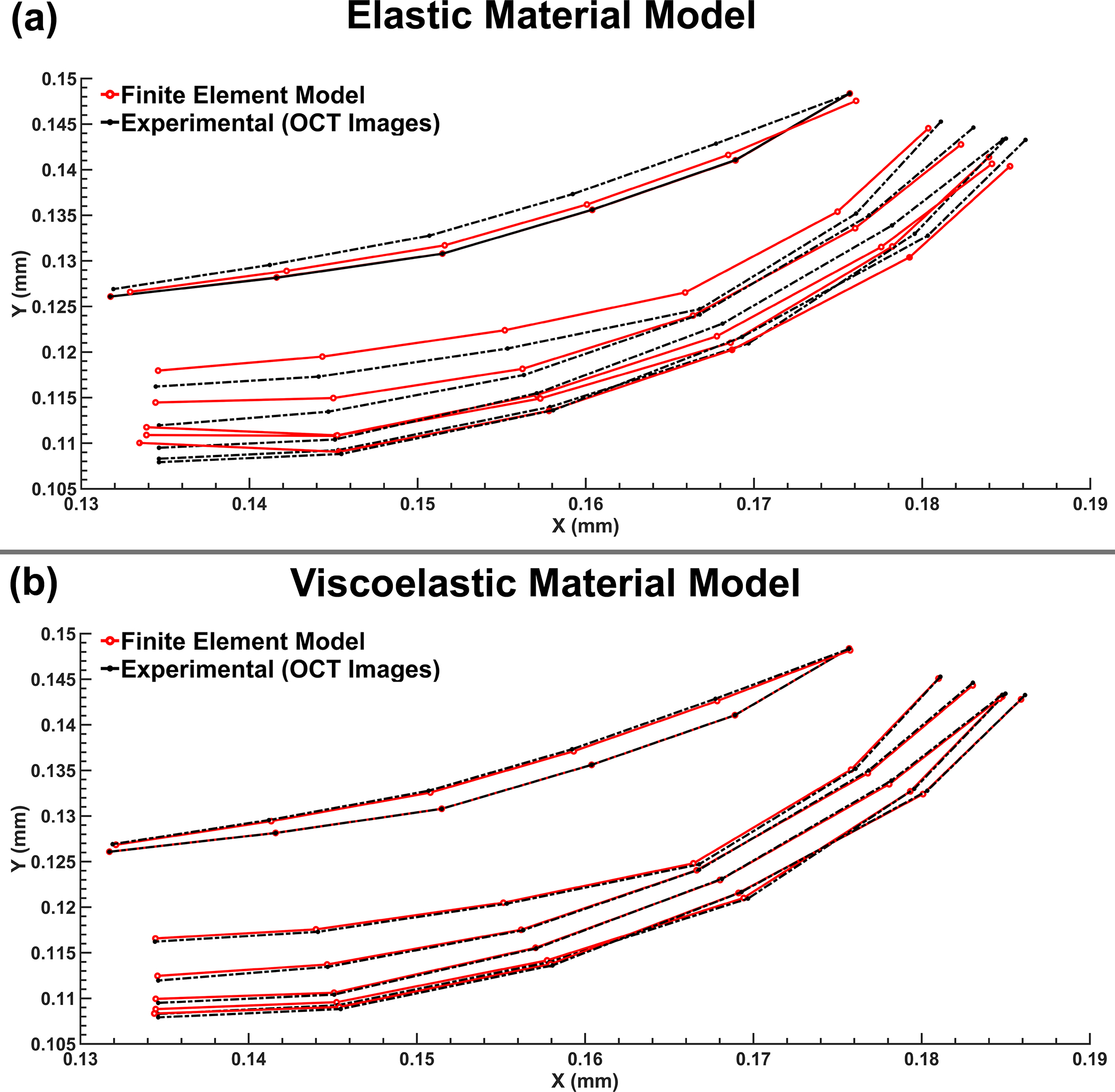
Nodal coordinates at the pressure boundary (SC wall) from the FE model and experimental SD-OCT imaging data in 118-healthy with (a) elastic and (b) viscoelastic material models.
Fig. 8.
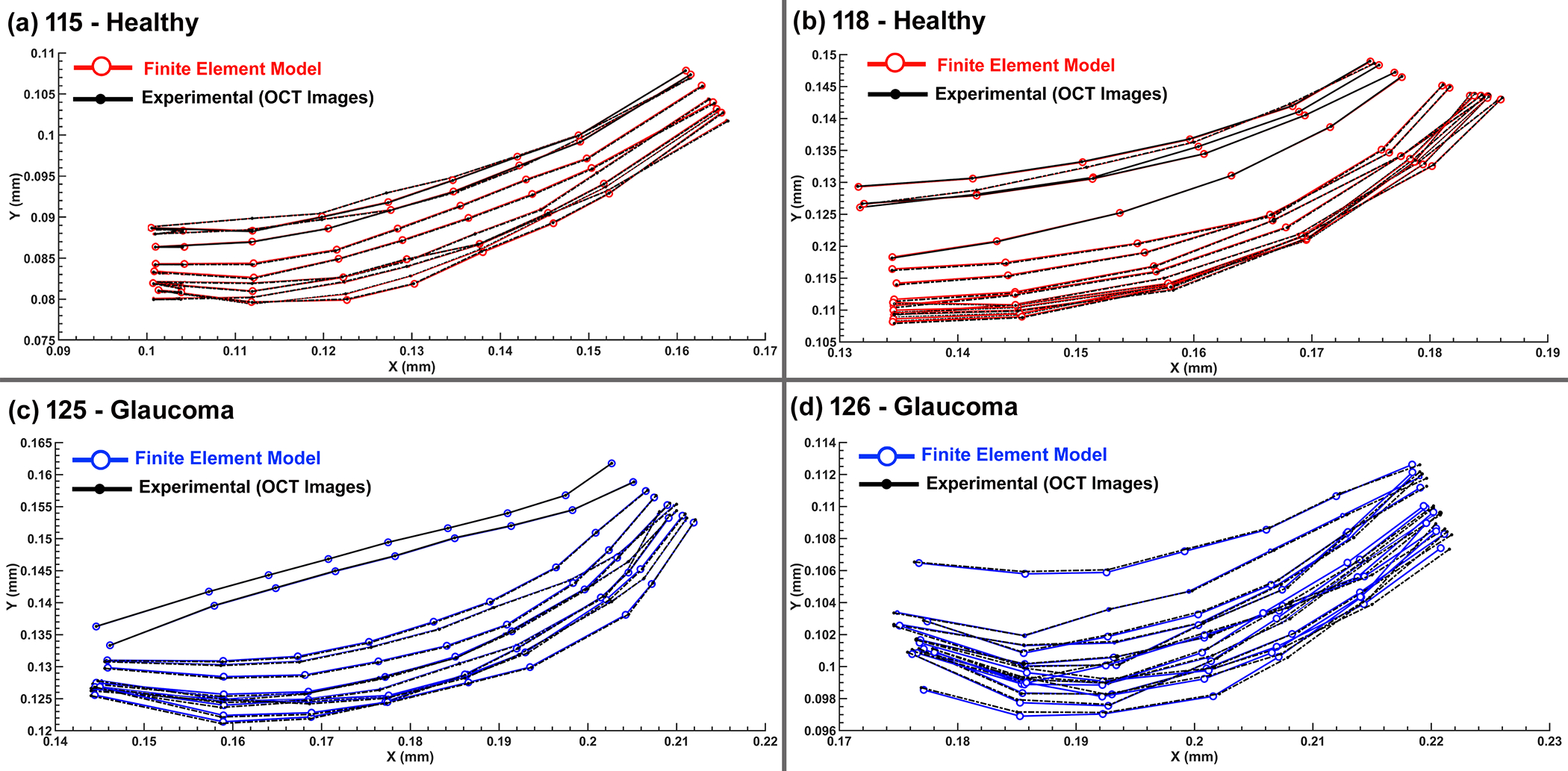
Nodal coordinates at the pressure boundary (SC wall) from the FE model and experimental SD-OCT imaging data in (a) 115-healthy, (b) 118-healthy, (c) 125-glaucoma, and (d) 126-glaucoma eyes.
Fig. 9.
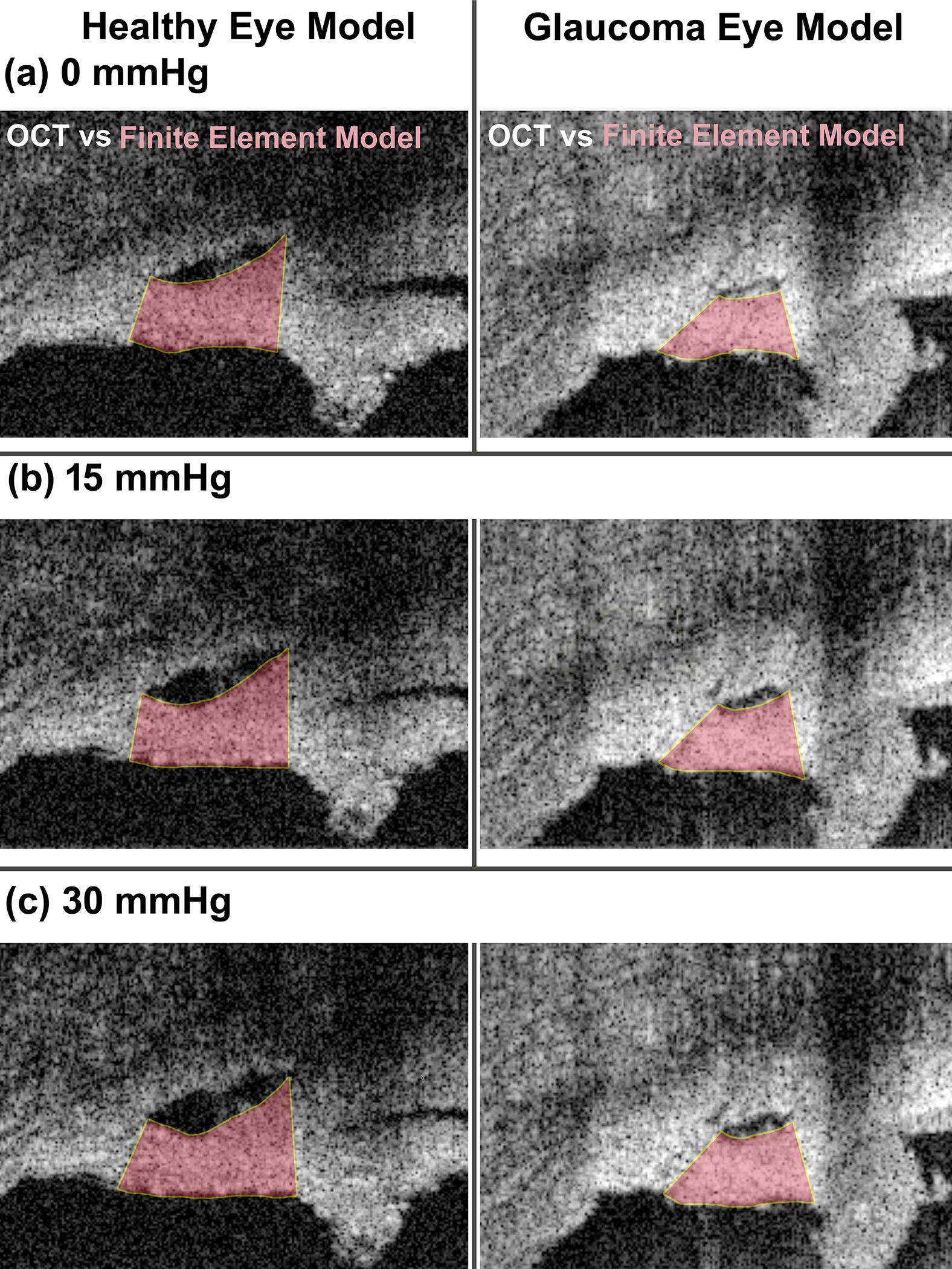
Comparison of specimen geometry of the OCT imaging data and FE simulation results in the healthy and glaucoma eyes under the pressures of (a) 0, (b) 15, and (c) 30 mmHg.
The optimized material parameters for the TM/JCT/SC complex in the healthy and glaucoma eyes at two different cross-sections are listed in Table 3. In terms of parameter uniqueness, the Fminsearch-Unconstrained nonlinear minimization algorithm yielded the same pressure and material parameters (p=0.999) even when initial guesses were very different (see Methods). Similarity of pressure and material parameters despite large initial guess differences lends confidence in the algorithm’s ability to yield unique results within the allowed bounds of the fitted parameters.
Results revealed significantly higher short-time (G0) and long-time (G∞) shear moduli in the ECM of the glaucoma eyes compared to healthy controls (p=0.0032, Table 3). In addition, the resultant elastic moduli of the collagen and elastin fibrils in the TM/JCT/SC complex of the glaucoma eyes were significantly stiffer compared to the healthy eyes (p=1e-6 for collagen and p=0.001 for elastin, Table 3). The short-time (G0) and long-time (G∞) shear moduli of the ECM, as well as the elastic moduli of the collagen and elastin fibrils, were not significantly different in the same eye at different cross-sections (p=0.999, Table 3). The two cross-sections modeled and imaged from the same eye were spaced 10 μm apart [44], but were modeled and optimized independently, so similar results imply that the optimization procedures were robust to non-unique local minima (Section 2.5.1). The FE models captured the complex mechanical behavior of the TM/JCT/SC complex throughout the course of pressure elevation in the walls of the SC lumen for both the healthy and glaucoma eyes (Fig. 9).
The TM/JCT/SC complex was divided into two different regions: the external region (proximal to the SC) and the internal region (proximal to the anterior chamber) that were defined in both the SD-OCT imaging data and the FE model as shown in Figs. 10a–b. The resultant volumetric average stresses in these two regions were calculated in the ECM (Figs. 10c) with embedded collagen and elastin (Figs. 10d–e) fibrils in the healthy and glaucoma eyes. Results showed significantly higher stresses in the ECM, collagen and elastin fibrils of the TM/JCT/SC complex in the glaucoma eyes compared to the healthy eyes (p<0.05). The resultant stresses were higher in the internal region where the tissues are more proximal to the anterior chamber.
Fig. 10.
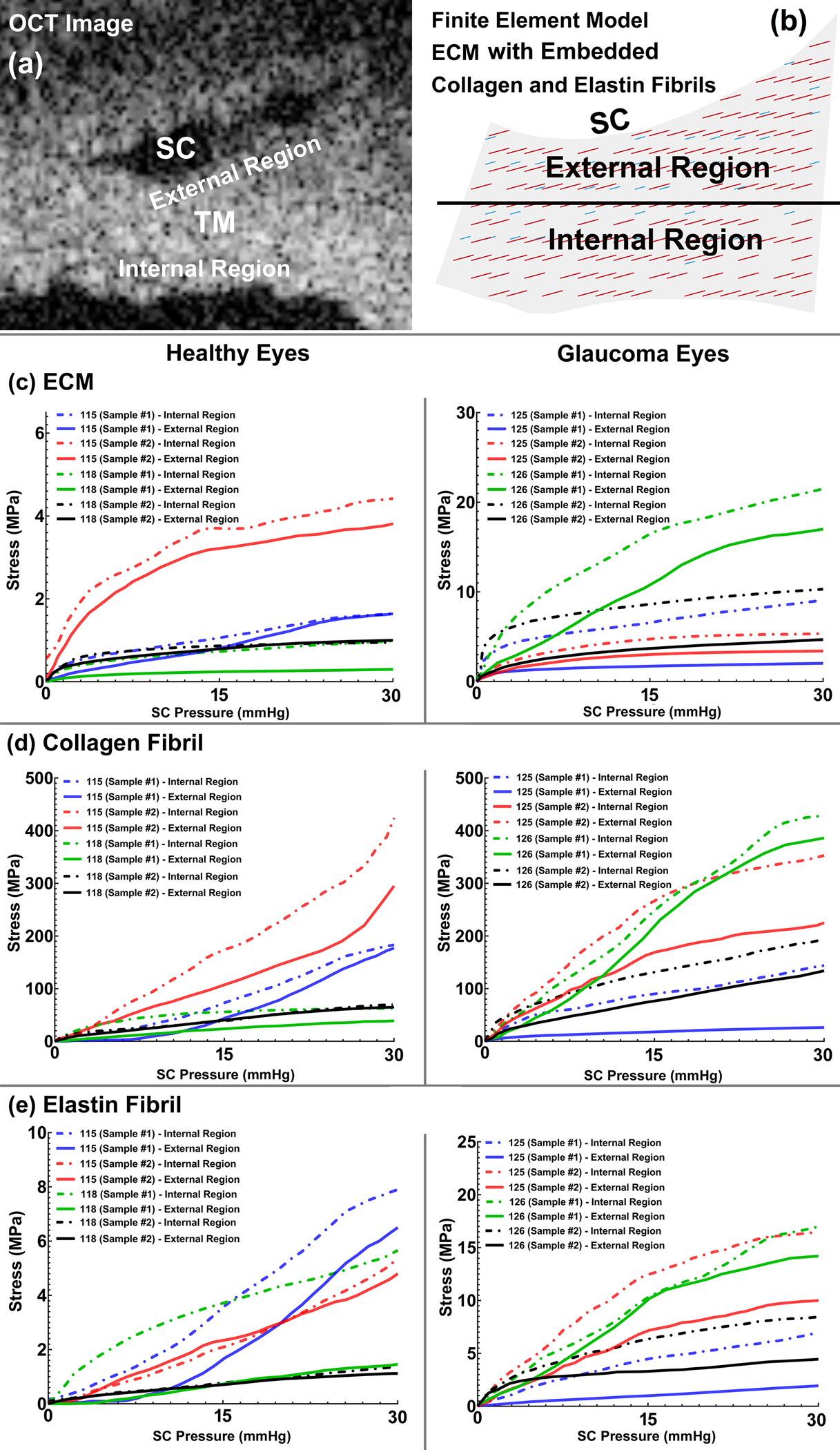
(a) OCT image of a TM/JCT/SC complex and (b) FE model of the TM/JCT/SC complex showing the boundary between the internal and external regions of the TM. The volumetric average stress-SC pressure response of the (c) ECM, the average stress-SC pressure response of the (d) collagen and (e) elastin fibrils in the healthy and glaucoma eyes.
4. Discussion
In this study, we calculated the viscoelastic mechanical properties of the TM/JCT/SC complex in two healthy and two glaucomatous cadaveric human eyes, including the embedded collagen and elastin fibrils. The optimization results in terms of the comparison between the elastic and viscoelastic material models resulted in the TM/JCT/SC elastic modulus of 0.148 MPa, which is 15% higher than that of reported by Johnson and colleagues (0.128 MPa) [97]. While Johnson and colleagues performed an in vivo mechanical characterization in living human eyes, we used ex vivo SD-OCT imaging data, which could be the cause of higher stiffness in the TM. Regarding the viscoelastic model, the initial- and long-term shear moduli of 7.08 and 1.54 MPa, respectively, were calculated with the decay constant of 995. The results revealed that the elastic material model cannot capture the dynamic mechanical response of the TM under SC pressure elevation, while both of the elastic and viscoelastic FE models were simulated under the same loading and boundary conditions (Fig. 7). While the viscoelastic material model could result in better match with the SD-OCT imaging data, it is worth mentioning that the SC pressure elevation was non-physiologic, which may affect the results. However, in general, under the exactly same loading and boundary conditions the elastic material was not able to capture the mechanical response of the TM tissue, implying the importance of considering viscoelasticity of the TM when it comes to accuracy in mechanical characterizations and simulations of the conventional aqueous outflow pathway. In addition, it should be noted that herein the pressure in the SC was elevated to ~30 mmHg with changing the height of the reservoirs. However, in living human eyes IOP fluctuates so there is an active dynamic mechanical environment in the conventional aqueous outflow pathway, so the TM understands the history of the applied load and its deformation will be affected in respect to the history of the applied load. While elastic material response is independent to the history of the load, viscoelastic material models understand it.
The optimal pressure and material parameters resulted in good agreement between the TM/JCT/SC complex FE models and the SD-OCT images (Fig. 8). It has been well documented that a stiffer TM can disrupt the normal pulsatile flow in the outflow system [18, 53, 99–102], so characterizing the time-dependent mechanical behavior of the TM/JCT/SC complex could significantly contribute to our understanding of how dynamic motion of the outflow pathway tissues are involved in aqueous outflow and IOP regulation [20].
The main challenge of modeling the quadrant of an anterior segment cannulation was the resultant pressure in the walls of the SC lumen, because the cannula in the experiments was only inserted in one end of the SC and the other end was left open. Therefore, the pressure in the SC lumen is both position- and time-dependent (Fig. 5). The FE-optimization algorithm (Fig. 6) was used to find the optimal pressures and materials parameters with the cost function of the least sum of the squared differences compared to the experimental SD-OCT imaging data (Fig. 8). The advantage of calculating an accurate time-dependent pressure profile applied to the walls of the SC lumen is that the pulsatile pressure in the SC can be used in future studies to calculate the flow in the SC lumen. Schlemm’s canal flow exposes the endothelial cells of the walls of SC to the rapidly moving fluid wave and induces shear stress in endothelial cells [17, 34]. Pulsatile outflow increases as IOP increases in normal eyes while pulsatile outflow slows or stops in glaucoma patients [101, 103], so the resultant shear stresses in the endothelial cells of the SC wall are very much dependent on the time-dependent pressure in the SC lumen.
The collagen and elastin fibrils in the TM lamellae primarily determine how far the tissues can distend into SC in response to a pressure elevation and how the tissues recover when the pressure in the SC returns to zero [104]. To date, the role of the collagen and elastin fibrils in the ECM of the TM/JCT/SC complex has been ignored. Our results revealed significantly higher time-dependent shear moduli in the ECM of the glaucoma eyes compared to the healthy eyes (p<0.01, Table 3), which is in agreement with recent findings on the TM stiffness in glaucoma eyes [17, 34–42, 44]. The short-time shear modulus reflects the near instantaneous stiffness of the tissue, while the long-time shear modulus captures the mechanical response of the TM over longer timescales (Table 3). The healthy and glaucoma eyes exhibited collagen elastic moduli of 2814±47 MPa and 5123±114 MPa (Mean±SD) and elastin fibril elastic moduli of 62.5+19.6 MPa and 170+13.5 MPa, respectively (Table 3). Collagen stiffness in the outflow pathway has been shown to play an important role in IOP elevation [105, 106].
The ECM, collagen and elastin fibrils experienced higher stresses in the internal region of the TM/JCT/SC complex, where they are more proximal to the anterior chamber (Fig. 10). This is presumably because the internal region of the TM experiences more radial expansion/strain during the SC lumen pressurization, so higher stresses can be expected there. The resultant stresses in the ECM, collagen and elastin fibrils were higher in the glaucoma eyes. Collagen and elastin fibrils in the TM are highly aligned perpendicular to the loading direction [107]; such tissue properties explain reversible deformation due to pressure-dependent tissue loading [61, 108, 109].
In general, collagenous components contribute to structural support under tension, while elastin ensures a recoverable response over a wide range of excursions [110]. Our results also revealed a significantly higher decay constant in the healthy TM/JCT/SC complex compared to glaucoma eyes (p<0.01, Table 3). The decay constant is defined as the viscosity of a linear dashpot divided by the stiffness of a linear spring in parallel [111]. The dashpot dissipates the energy while the spring part of the tissue tries to hold back the tissue to its initial structure. Glaucomatous TM exhibited a larger stiffness for the linear spring (Table 3), along with a smaller decay constant, while the healthy TM showed a smaller stiffness for the linear spring, and a larger decay constant. Hence, greater TM motion was observed in healthy eyes compared to glaucoma eyes [23, 53, 54]. Therefore, a glaucomatous TM loses its viscous effect by showing a higher stiffness under while the load is applied on the tissue. However, the healthy tissue undergoes higher deformation with showing higher viscous effect under an applied load.
The ECM of the TM is where the collagen and elastin fibrils achieve mechanical homeostasis [112, 113]. The load distributes among the fibers in a way that the elastin fibers sustain the major stresses at low strain level and reflect a linear deformation. Collagen fibers are recruited at large extension of the tissue and are responsible for the nonlinear behavior [114–118]. The ECM of the glaucomatous TM loses its resiliency and becomes stiffer [119], implying that the collagen fibrils in the glaucoma eyes are stiffer than in healthy eyes [40, 120] and that elastin fibers play a reduced role in glaucoma eyes.
Whether through aging with elastin fragmentation and replacement by collagen, or by the insult of chronic exposure to ocular hypertension, the TM becomes stiffer or fibrotic in glaucoma eyes [40, 120, 121]. When the TM goes through large deformations resulting from IOP elevation, more collagen is produced, which decreases the elastin:collagen ratio and stiffens the TM [122–124]. Our results revealed 1.82 and 2.72-fold stiffer collagen and elastin fibrils elastic moduli in the glaucoma eyes compared to the healthy control ones (Table 3), which can be interpreted as additional collagen in the TM ECM in glaucoma eyes [125].
Our results also revealed the same stress pattern in the ECM of the healthy and glaucoma eyes, but different maximum values. In Fig. 10b, it is evident that the collagen fibrils in the glaucoma eyes played a larger role in TM stress at lower SC lumen pressures when compared to normal eyes. Results also revealed that the TM in glaucoma eyes reaches a stiffer long-term equilibrium mechanical response compared to a healthy TM, also implying the increased role of collagen fibers in the glaucomatous TM ECM (Table 3). This is in good agreement with results in rats in which ocular hypertension caused collagen type I augmentation [126]. Excessive collagen type IV [36] and type VI [127] have also been reported in the glaucomatous TM.
The results reported herein provide additional clarity on the mechanical property differences in healthy and glaucomatous outflow pathway under dynamic loading. These methods and results can be leveraged in future studies of aqueous outflow dynamics and outflow pathway biomechanics.
4.1. Limitations
This study is limited by the following considerations. First, the experimental setup is not physiologic, in that SC pressure was increased in a wedge of tissue immersed in chamber at ambient pressure. Normally, TM deformation would be primarily imparted by fluctuations in IOP, so this is the reverse of the in vivo condition. It has been shown that the physiological pressure in the SC lumen is within 5.59–10.51 mmHg [128, 129]. In our experiments, the SC lumen was pressurized to 30 mmHg. That said, the approach used herein does allow for relatively high-resolution imaging of large TM/JCT/SC deformations. The large deformations permit calculation of a range of mechanical properties that would be difficult if not impossible to measure using physiologic loadings that result in much smaller deformations.
Although the organ culture prep and the high-resolution SD-OCT imaging system are the only currently available setup for SC lumen pressurization and dynamic imaging, the image resolution is still not ideal for truly accurate boundary recognition. However, dynamic imaging of a soft biological tissue is very challenging and SD-OCT is one of the best imaging approaches for the task. Also, a quadrant of an anterior segment of cadaveric eye was tested within 72 hours postmortem, which may affect the TM’s mechanical response. However, it has been shown that when using the organ culture media under conditions of these experiments, there is an insignificant change in postmortem tissue behavior [82]. Every effort was made to keep the eyes fresh before the experiments and perfuse them to reduce tissue degradation.
Second, the unknown position- and time-dependent SC lumen pressure profile was approximated and applied to the walls of the SC lumen in the scaled timing range of 10 ms. Our FE simulations of a TM tensile test matched that of previously published experimental data, and showed that the error in the resultant stresses is less than ~ 6.5% when using a compressed timescale. The true SC lumen pressure is both time- and position-dependent because of non-uniform SC morphology through the wedge specimen, irregularly spaced pressure reducing collector channels, flow from SC at the distal end of the wedge, and the oscillating nature of the input cannula pressure. We optimized the specimen-specific SC pressure profile as a function of time, as well as the pressure along the SC wall boundary of each FE model, such that the material parameters best fit the experimental OCT image data.
Third, we cannot be certain that the optimized pressure and material parameters are unique for our non-convex cost function, and there are no validated gold standard measurements of the material properties of the TM/JCT/SC complex that we can use as a reference for comparative analyses. However, we performed a series of perturbations of the optimization process that give us confidence in the parameters reported in Table 3.
Fourth, the length, diameter, stiffness, and distribution of the collagen and elastin fibrils were assumed to be uniform throughout the entire TM. It has been shown that the fibers closer to the anterior chamber are considerably thicker than those closer to the SC [65]. However, there is a lack of quantitative data on the accurate fibril diameter in these regions, and we will incorporate locally dependent fibril morphological characteristics in future studies. Also, the collagen and elastin fibrils were simulated as elastic materials while it has been shown that the mechanical properties of those fibers are time-dependent [130, 131]. We will improve our method in future studies by including viscoelastic fibrils in a viscoelastic ECM.
Fifth, one may argue that the data reported by Camras et al., [81, 82] are not the same as some other methods. Herein, these data were only used to train the trabecular meshwork finite element model. Thereafter, the calculated data was used as initial input for a second FE-optimization algorithm that optimized the viscoelastic material properties of the TM tissue according to the SD-OCT imaging data. Therefore, although the initial steps of the optimization algorithm may be affect by the initial guess, the algorithm optimized the tissue properties based on the TM motion data; so, there is a little chance the initial starting point would affect the resultant optimized material properties. Further, a wide range of initial guesses were used for the optimization purposes to ensure us the resultant material properties are independent from the input data.
Finally, we only used two samples from each of two healthy and two glaucoma eyes for the study, which is not likely to be representative of the range of glaucoma present in the population. While we did find statistically significant differences in our results, future studies will benefit from more samples to better estimate the eye-specific TM mechanical response considering the age, race, gender, and disease severity of the human donors. In addition, patients with glaucoma were likely under treatment with pressure-lowering medications, which affect both IOP and TM/JCT/SC biomechanics. In addition, we only studied samples from the temporal quadrant, and future study will be necessary to determine the mechanical properties around the entire circumference of the outflow pathway.
In conclusion, we propose and implement a new biomechanical modeling approach to calculate the time-dependent viscoelastic mechanical properties of the healthy and glaucoma TM/JCT/SC complex ECM in humans. Results revealed a significantly (p<0.05) greater time-dependent shear moduli in the ECM of the glaucoma eyes compared to the normal controls. Collagen and elastin fibrils in the glaucoma eyes also exhibited significantly stiffer mechanical response compared to the healthy eyes. The resultant stresses in the ECM, collagen and elastin fibrils in the internal region of the TM/JCT/SC complex were higher compared to the external region. Characterizing the viscoelastic mechanical properties of the outflow pathway in healthy and glaucoma eyes may provide fresh perspectives and reveal new realms of exploration pertinent to our shared quest to understand, diagnose, and treat ocular hypertension and glaucoma.
Funding
This work was supported in part by the National Institutes of Health Grants R01-EY027924, R01-EY018926, R01EY0190601, R01EY024158, R01EY028753, P30-EY003039 (Bethesda, Maryland). EyeSight Foundation of Alabama (Birmingham, Alabama); and Research to Prevent Blindness (New York, New York).
Footnotes
Declaration of Competing Interest
The authors report no competing interests for this study.
Data availability
The raw/processed data required to reproduce these findings cannot be shared at this time, as the data are part of an ongoing study.
References
- [1].Quigley HA, Number of people with glaucoma worldwide, Br J Ophthalmol 80(5) (1996) 389–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Weinreb RN, Khaw PT, Primary open-angle glaucoma, Lancet 363(9422) (2004) 1711–20. [DOI] [PubMed] [Google Scholar]
- [3].Tham YC, Li X, Wong TY, Quigley HA, Aung T, Cheng CY, Global prevalence of glaucoma and projections of glaucoma burden through 2040: a systematic review and meta-analysis, Ophthalmology 121(11) (2014) 2081–90. [DOI] [PubMed] [Google Scholar]
- [4].Weinreb RN, Leung CK, Crowston JG, Medeiros FA, Friedman DS, Wiggs JL, Martin KR, Primary open-angle glaucoma, Nat Rev Dis Primers 2(1) (2016) 1–19. [DOI] [PubMed] [Google Scholar]
- [5].Kitazawa Y, Horie T, Diurnal variation of intraocular pressure in primary open-angle glaucoma, Am J Ophthalmol 79(4) (1975) 557–566. [DOI] [PubMed] [Google Scholar]
- [6].Sommer A, Tielsch JM, Katz J, Quigley HA, Gottsch JD, Javitt J, Singh K, Relationship between intraocular pressure and primary open angle glaucoma among white and black Americans: the Baltimore Eye Survey, Arch Ophthal 109(8) (1991) 1090–1095. [DOI] [PubMed] [Google Scholar]
- [7].Kwon YH, Fingert JH, Kuehn MH, Alward WL, Primary open-angle glaucoma, N Engl J Med 360(11) (2009) 1113–1124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Johnson M, What controls aqueous humour outflow resistance?, Exp Eye Res 82(4) (2006) 545–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Overby DR, Stamer WD, Johnson M, The changing paradigm of outflow resistance generation: towards synergistic models of the JCT and inner wall endothelium, Exp Eye Res 88(4) (2009) 656–670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Vahabikashi A, Gelman A, Dong B, Gong L, Cha ED, Schimmel M, Tamm ER, Perkumas K, Stamer WD, Sun C, Increased stiffness and flow resistance of the inner wall of Schlemm’s canal in glaucomatous human eyes, PNAS 116(52) (2019) 26555–26563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Grant WM, Further studies on facility of flow through the trabecular meshwork, AMA Arch Ophthal 60(4) (1958) 523–533. [DOI] [PubMed] [Google Scholar]
- [12].GRANT WM, Experimental aqueous perfusion in enucleated human eyes, Arch Ophthal 69(6) (1963) 783–801. [DOI] [PubMed] [Google Scholar]
- [13].Ellingsen BA, Grant WM, The relationship of pressure and aqueous outflow in enucleated human eyes, Invest Ophthalmol Vis Sci 10(6) (1971) 430–437. [PubMed] [Google Scholar]
- [14].Johnson M, Kamm R, The role of Schlemm’s canal in aqueous outflow from the human eye, Invest Ophthalmol Vis Sci 24(3) (1983) 320–325. [PubMed] [Google Scholar]
- [15].Johnson DH, Johnson M, How does nonpenetrating glaucoma surgery work? Aqueous outflow resistance and glaucoma surgery, J Glaucoma 10(1) (2001) 55–67. [DOI] [PubMed] [Google Scholar]
- [16].Dvorak-Theobald G, Kirk HQ, Aqueous pathways in some cases of glaucoma, Trans Am Ophthalmol Soc 53 (1955) 301. [PMC free article] [PubMed] [Google Scholar]
- [17].Johnstone MA, The aqueous outflow system as a mechanical pump: evidence from examination of tissue and aqueous movement in human and non-human primates, J Glaucoma 13(5) (2004) 421–438. [DOI] [PubMed] [Google Scholar]
- [18].Johnstone M, Jamil A, Martin E, Aqueous veins and open angle glaucoma, The Glaucoma Book, Springer; 2010, pp. 65–78. [Google Scholar]
- [19].Johnstone MA, Intraocular pressure regulation: findings of pulse-dependent trabecular meshwork motion lead to unifying concepts of intraocular pressure homeostasis, Mary Ann Liebert, Inc. 140 Huguenot Street, 3rd Floor New Rochelle, NY 10801 USA, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Johnstone M, Xin C, Tan J, Martin E, Wen J, Wang RK, Aqueous outflow regulation–21st century concepts, Prog Retin Eye Res (2020) 100917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Li P, Reif R, Zhi Z, Shen T, Wang RK, Martin E, Johnstone M, Phase-sensitive optical coherence tomography characterization of pulse-induced trabecular meshwork displacement in ex vivo nonhuman primate eyes, J Biomed Opt 17(7) (2012) 076026. [DOI] [PubMed] [Google Scholar]
- [22].Li P, Shen TT, Johnstone M, Wang RK, Pulsatile motion of the trabecular meshwork in healthy human subjects quantified by phase-sensitive optical coherence tomography, Biomed Opt Express 4(10) (2013) 2051–2065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Xin C, Song S, Johnstone M, Wang N, Wang RK, Quantification of Pulse-Dependent Trabecular Meshwork Motion in Normal Humans Using Phase-Sensitive OCT, Invest Ophthalmol Vis Sci 59(8) (2018) 3675–3681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Filla MS, Schwinn MK, Nosie AK, Clark RW, Peters DM, Dexamethasone-associated cross-linked actin network formation in human trabecular meshwork cells involves β3 integrin signaling, Invest Ophthalmol Vis Sci 52(6) (2011) 2952–2959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Clark R, Nosie A, Walker T, Faralli JA, Filla MS, Barrett-Wilt G, Peters DM, Comparative genomic and proteomic analysis of cytoskeletal changes in dexamethasone-treated trabecular meshwork cells, Molecular Cellular Proteomics 12(1) (2013) 194–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Stamer WD, Braakman ST, Zhou EH, Ethier CR, Fredberg JJ, Overby DR, Johnson M, Biomechanics of Schlemm’s canal endothelium and intraocular pressure reduction, Prog Retin Eye Res 44 (2015) 86–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Vranka JA, Kelley MJ, Acott TS, Keller KE, Extracellular matrix in the trabecular meshwork: intraocular pressure regulation and dysregulation in glaucoma, Exp Eye Res 133 (2015) 112–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Anderson DR, The development of the trabecular meshwork and its abnormality in primary infantile glaucoma, Trans Am Ophthalmol Soc 79 (1981) 458–85. [PMC free article] [PubMed] [Google Scholar]
- [29].Rehnberg M, Ammitzböll T, Tengroth B, Collagen distribution in the lamina cribrosa and the trabecular meshwork of the human eye, Br J Ophthalmol 71(12) (1987) 886–892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Umihira J, Nagata S, Nohara M, Hanai T, Usuda N, Segawa K, Localization of elastin in the normal and glaucomatous human trabecular meshwork, Invest Ophthalmol Vis Sci 35(2) (1994) 486–494. [PubMed] [Google Scholar]
- [31].Segawa K, [Trabecular meshwork and elastin], Nippon Ganka Gakkai Zasshi 99(12) (1995) 1291–302. [PubMed] [Google Scholar]
- [32].Huang AS, Gonzalez JM, Le PV, Heur M, Tan JC, Sources of structural autofluorescence in the human trabecular meshwork, Invest Ophthalmol Vis Sci 54(7) (2013) 4813–4820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Park CY, Lee JK, Kahook MY, Schultz JS, Zhang C, Chuck RS, Revisiting ciliary muscle tendons and their connections with the trabecular meshwork by two photon excitation microscopic imaging, Invest Ophthalmol Vis Sci 57(3) (2016) 1096–1105. [DOI] [PubMed] [Google Scholar]
- [34].Johnstone MA, A new model describes an aqueous outflow pump and explores causes of pump failure in glaucoma, Glaucoma, Springer; 2006, pp. 3–34. [Google Scholar]
- [35].Keller KE, Aga M, Bradley JM, Kelley MJ, Acott TS, Extracellular matrix turnover and outflow resistance, Exp Eye Res 88(4) (2009) 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Last JA, Pan T, Ding Y, Reilly CM, Keller K, Acott TS, Fautsch MP, Murphy CJ, Russell P, Elastic modulus determination of normal and glaucomatous human trabecular meshwork, Invest Ophthalmol Vis Sci 52(5) (2011) 2147–2152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Johnstone M, Martin E, Jamil A, Pulsatile flow into the aqueous veins: manifestations in normal and glaucomatous eyes, Exp Eye Res 92(5) (2011) 318–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Russell P, Johnson M, Elastic modulus determination of normal and glaucomatous human trabecular meshwork, Invest Ophthalmol Vis Sci 53(1) (2012) 117–117. [DOI] [PubMed] [Google Scholar]
- [39].Stamer WD, Acott TS, Current understanding of conventional outflow dysfunction in glaucoma, Curr Opin Ophthalmol 23(2) (2012) 135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Wang K, Read AT, Sulchek T, Ethier CR, Trabecular meshwork stiffness in glaucoma, Exp Eye Res 158 (2017) 3–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Carreon T, van der Merwe E, Fellman RL, Johnstone M, Bhattacharya SK, Aqueous outflow-A continuum from trabecular meshwork to episcleral veins, Prog Retin Eye Res 57 (2017) 108–133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Gao K, Song S, Johnstone MA, Zhang Q, Xu J, Zhang X, Wang RK, Wen JC, Reduced Pulsatile Trabecular Meshwork Motion in Eyes With Primary Open Angle Glaucoma Using Phase-Sensitive Optical Coherence Tomography, Invest Ophthalmol Vis Sci 61(14) (2020) 21–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Gao K, Shaozhen S, Johnstone MA, Wang RK, Wen JC, Trabecular meshwork motion in normal compared with glaucoma eyes, Invest Ophthalmol Vis Sci 60(9) (2019) 4824–4824. [Google Scholar]
- [44].Wang K, Johnstone MA, Xin C, Song S, Padilla S, Vranka JA, Acott TS, Zhou K, Schwaner SA, Wang RK, Estimating human trabecular meshwork stiffness by numerical modeling and advanced OCT imaging, Invest Ophthalmol Vis Sci 58(11) (2017) 4809–4817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Li G, Lee C, Agrahari V, Wang K, Navarro I, Sherwood JM, Crews K, Farsiu S, Gonzalez P, Lin C-W, Mitra AK, Ethier CR, Stamer WD, In vivo measurement of trabecular meshwork stiffness in a corticosteroid-induced ocular hypertensive mouse model, PNAS 116(5) (2019) 1714–1722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Karimi A, Rahmati SM, Navidbakhsh M, Mechanical characterization of the rat and mice skin tissues using histostructural and uniaxial data, Bioengineered 6(3) (2015) 153–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Karimi A, Shojaei A, Razaghi R, Viscoelastic mechanical measurement of the healthy and atherosclerotic human coronary arteries using DIC technique, Artery Res 18 (2017) 14–21. [Google Scholar]
- [48].Karimi A, Rahmati SM, Razaghi R, A combination of experimental measurement, constitutive damage model, and diffusion tensor imaging to characterize the mechanical properties of the human brain, Comput Methods Biomech Biomed Engin 20(12) (2017) 1350–1363. [DOI] [PubMed] [Google Scholar]
- [49].Karimi A, Rahmati SM, Sera T, Kudo S, Navidbakhsh M, A combination of experimental and numerical methods to investigate the role of strain rate on the mechanical properties and collagen fiber orientations of the healthy and atherosclerotic human coronary arteries, Bioengineered 8(2) (2017) 154–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Karimi A, Rahmati SM, Sera T, Kudo S, Navidbakhsh M, A combination of constitutive damage model and artificial neural networks to characterize the mechanical properties of the healthy and atherosclerotic human coronary arteries, Artificial Organs 41(9) (2017) E103–E117. [DOI] [PubMed] [Google Scholar]
- [51].Maccabi A, Shin A, Namiri NK, Bajwa N, St John M, Taylor ZD, Grundfest W, Saddik GN, Quantitative characterization of viscoelastic behavior in tissue-mimicking phantoms and ex vivo animal tissues, PloS One 13(1) (2018) e0191919–e0191919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Estermann S-J, Pahr DH, Reisinger A, Material design of soft biological tissue replicas using viscoelastic micromechanical modelling, J Mech Behav Biomed Mater 125 (2022) 104875. [DOI] [PubMed] [Google Scholar]
- [53].Xin C, Wang X, Wang N, Wang R, Johnstone M, Trabecular Meshwork Motion Profile from Pulsatile Pressure Transients: A New Platform to Simulate Transitory Responses in Humans and Nonhuman Primates, Appl Sci 12(1) (2022) 11. [Google Scholar]
- [54].Turner DC, Samuels BC, Huisingh C, Girkin CA, Downs JC, The Magnitude and Time Course of IOP Change in Response to Body Position Change in Nonhuman Primates Measured Using Continuous IOP Telemetry, Invest Ophthalmol Vis Sci 58(14) (2017) 6232–6240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Turner DC, Edmiston AM, Zohner YE, Byrne KJ, Seigfreid WP, Girkin CA, Morris JS, Downs JC, Transient Intraocular Pressure Fluctuations: Source, Magnitude, Frequency, and Associated Mechanical Energy, Invest Ophthalmol Vis Sci 60(7) (2019) 2572–2582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Turner DC, Girkin CA, Downs JC, The Magnitude of IOP Elevation Associated with Eye Rubbing, Ophthalmology 126(1) (2019) 171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Karimi A, Grytz R, Rahmati SM, Girkin CA, Downs JC, Analysis of the effects of finite element type within a 3D biomechanical model of a human optic nerve head and posterior pole, Comput Methods Programs Biomed 198 (2021) 105794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Rahmati SM, Razaghi R, Karimi A, Biomechanics of the keratoconic cornea: Theory, segmentation, pressure distribution, and coupled FE-optimization algorithm, J Mech Behav Biomed Mater 113 (2021) 104155. [DOI] [PubMed] [Google Scholar]
- [59].Abdolkarimzadeh F, Ashory MR, Ghasemi-Ghalebahman A, Karimi A, Inverse dynamic finite element-optimization modeling of the brain tumor mass-effect using a variable pressure boundary, Comput Methods Programs Biomed 212 (2021) 106476. [DOI] [PubMed] [Google Scholar]
- [60].Acott T, Kingsley P, Samples J, Van Buskirk E, Human trabecular meshwork organ culture: morphology and glycosaminoglycan synthesis, Invest Ophthalmol Vis Sci 29(1) (1988) 90–100. [PubMed] [Google Scholar]
- [61].Hariri S, Johnstone M, Jiang Y, Padilla S, Zhou Z, Reif R, Wang RK, Platform to investigate aqueous outflow system structure and pressure-dependent motion using high-resolution spectral domain optical coherence tomography, J Biomed Optics 19(10) (2014) 106013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Horová I, Kolacek J, Zelinka J, Kernel Smoothing in MATLAB: theory and practice of kernel smoothing, World Scientific 2012. [Google Scholar]
- [63].Karimi A, Rahmati SM, Grytz RG, Girkin CA, Downs JC, Modeling the Biomechanics of the Lamina Cribrosa Microstructure in the Human Eye, Acta Biomater. 2021. Oct 15;134:357–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Karimi A, Rahmati SM, Razaghi R, Girkin CA, Crawford Downs J, Finite element modeling of the complex anisotropic mechanical behavior of the human sclera and pia mater, Comput Methods Programs Biomed 215(3) (2022) 106618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Flocks M, The anatomy of the trabecular meshwork as seen in tangential section, AMA Arch Ophthal 56(5) (1956) 708–718. [DOI] [PubMed] [Google Scholar]
- [66].Hogan MJ, Histology of the human eye, An atlas and textbook (1971). [Google Scholar]
- [67].Morishige N, Petroll WM, Nishida T, Kenney MC, Jester JV, Noninvasive corneal stromal collagen imaging using two-photon-generated second-harmonic signals, J Cataract Refract Surg 32(11) (2006) 1784–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Ammar DA, Lei TC, Gibson EA, Kahook MY, Two-photon imaging of the trabecular meshwork, Molecular Vision 16 (2010) 935–944. [PMC free article] [PubMed] [Google Scholar]
- [69].Johnstone MA, Hariri S, Jiang Y, Padilla S, Zhou Z, Wang RK, OCT Imaging Shows Collector Channels Rapidly Open & Close with Pressure Changes: A Mechanism Regulating Control of Distal Resistance?, Invest Ophthalmol Vis Sci 56(7) (2015) 3539–3539. [Google Scholar]
- [70].Belytschko T, Lu YY, Gu L, Element-free Galerkin methods, Int J Numer Methods Eng 37(2) (1994) 229–256. [Google Scholar]
- [71].Chen H, An introduction to* CONSTRAINED_BEAM_IN_SOLID, FEA Information (2016) 79–83. [Google Scholar]
- [72].Hallquist JO, LS-DYNA® Keyword User’s Manual Volume II Material Models, Livermore, California, USA (2013).
- [73].Ushiki T, [The three-dimensional ultrastructure of the collagen fibers, reticular fibers and elastic fibers: a review], Kaibogaku Zasshi 67(3) (1992) 186–99. [PubMed] [Google Scholar]
- [74].Siadat SM, Silverman AA, DiMarzio CA, Ruberti JW, Measuring collagen fibril diameter with differential interference contrast microscopy, J Struct Biol 213(1) (2021) 107697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Haut RC, The influence of specimen length on the tensile failure properties of tendon collagen, J Biomech 19(11) (1986) 951–955. [DOI] [PubMed] [Google Scholar]
- [76].Pollock CM, Shadwick RE, Relationship between body mass and biomechanical properties of limb tendons in adult mammals, American Journal of Physiology-Regulatory, Integrative and Comparative Physiology 266(3) (1994) R1016–R1021. [DOI] [PubMed] [Google Scholar]
- [77].Manssor NAS, Radzi Z, Yahya NA, Mohamad Yusof L, Hariri F, Khairuddin NH, Abu Kasim NH, Czernuszka JT, Characteristics and Young’s Modulus of Collagen Fibrils from Expanded Skin Using Anisotropic Controlled Rate Self-Inflating Tissue Expander, Skin Pharmacol Physiol 29(2) (2016) 55–62. [DOI] [PubMed] [Google Scholar]
- [78].Dutov P, Antipova O, Varma S, Orgel JPRO, Schieber JD, Measurement of Elastic Modulus of Collagen Type I Single Fiber, PLOS ONE 11(1) (2016) e0145711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Aaron B, Gosline J, Elastin as a random-network elastomer: A mechanical and optical analysis of single elastin fibers, Biopolymers: Original Research on Biomolecules 20(6) (1981) 1247–1260. [Google Scholar]
- [80].Gosline J, Lillie M, Carrington E, Guerette P, Ortlepp C, Savage K, Elastic proteins: biological roles and mechanical properties, Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences 357(1418) (2002) 121–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Camras LJ, Stamer WD, Epstein D, Gonzalez P, Yuan F, Differential Effects of Trabecular Meshwork Stiffness on Outflow Facility in Normal Human and Porcine Eyes, Invest Ophthalmol Vis Sci 53(9) (2012) 5242–5250. [DOI] [PubMed] [Google Scholar]
- [82].Camras LJ, Stamer WD, Epstein D, Gonzalez P, Yuan F, Circumferential Tensile Stiffness of Glaucomatous Trabecular Meshwork, Invest Ophthalmol Vis Sci 55(2) (2014) 814–823. [DOI] [PubMed] [Google Scholar]
- [83].Lepple-Wienhues A, Stahl F, Wiederholt M, Differential smooth muscle-like contractile properties of trabecular meshwork and ciliary muscle, Exp Eye Res 53(1) (1991) 33–38. [DOI] [PubMed] [Google Scholar]
- [84].Miller K, Chinzei K, Constitutive modelling of brain tissue: experiment and theory, J Biomech 30(11–12) (1997) 1115–21. [DOI] [PubMed] [Google Scholar]
- [85].Prange MT, Margulies SS, Regional, directional, and age-dependent properties of the brain undergoing large deformation, J Biomech Eng 124(2) (2002) 244–52. [DOI] [PubMed] [Google Scholar]
- [86].Rashid B, Destrade M, Gilchrist MD, Mechanical characterization of brain tissue in compression at dynamic strain rates, J Mech Behav Biomed Mater 10 (2012) 23–38. [DOI] [PubMed] [Google Scholar]
- [87].Forte AE, Gentleman SM, Dini D, On the characterization of the heterogeneous mechanical response of human brain tissue, Biomech Model Mechanobiol 16(3) (2017) 907–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [88].Herrmann L, A numerical procedure for viscoelastic stress analysis, Seventh Meeting of ICRPG Mechanical Behavior Working Group, Orlando, FL, 1968, 1968. [Google Scholar]
- [89].Abdolkarimzadeh F, Ashory MR, Ghasemi-Ghalebahman A, Karimi A, Inverse dynamic finite element-optimization modeling of the brain tumor mass-effect using a variable pressure boundary, Comput Meth Program Biomed 212 (2021) 106476. [DOI] [PubMed] [Google Scholar]
- [90].Karimi A, Razaghi R, Navidbakhsh M, Sera T, Kudo S, Mechanical properties of the human sclera under various strain rates: elastic, hyperelastic, and viscoelastic models, J Biomater Tissue Eng 7(8) (2017). [Google Scholar]
- [91].Hoang QV, Rohrbach D, Wen Q, McFadden SA, Silverman RH, Mamou J, Characterization of the Elastic Properties of Lower Field Myopia in Guinea Pig Eyes at the Micrometer Scale with Acoustic Microscopy, Invest Ophthalmol Vis Sci 57(12) (2016) 5532–5532. [Google Scholar]
- [92].Schmidt DA, Shi C, Berry RA, Honig ML, Utschick W, Minimum mean squared error interference alignment, 2009 Conference Record of the Forty-Third Asilomar Conference on Signals, Systems and Computers, IEEE, 2009, pp. 1106–1110. [Google Scholar]
- [93].Ma K, Farajzadeh R, Lopez-Salinas JL, Miller CA, Biswal SL, Hirasaki GJ, Non-uniqueness, numerical artifacts, and parameter sensitivity in simulating steady-state and transient foam flow through porous media, Transport in porous media 102(3) (2014) 325–348. [Google Scholar]
- [94].Chiandussi G, Codegone M, Ferrero S, Varesio FE, Comparison of multi-objective optimization methodologies for engineering applications, Comput Math Appl 63(5) (2012) 912–942. [Google Scholar]
- [95].Abdollahi H, Tauler R, Uniqueness and rotation ambiguities in Multivariate Curve Resolution methods, Chemometr Intell Lab Syst 108(2) (2011) 100–111. [Google Scholar]
- [96].Goffe WL, Ferrier GD, Rogers J, Global optimization of statistical functions with simulated annealing, J Econometrics 60(1) (1994) 65–99. [Google Scholar]
- [97].Johnson M, Schuman JS, Kagemann L, Trabecular Meshwork Stiffness in the Living Human Eye, Investig. Ophthalmol. Vis. Sci 56(7) (2015) 3541–3541.26030108 [Google Scholar]
- [98].Scheffe H, A method for judging all contrasts in the analysis of variance, Biometrika 40(1–2) (1953) 87–110. [Google Scholar]
- [99].Ascher K, Backflow Phenomena in aqueous veins of normal and of glaucomatous eyes, Am J Ophthalmol 27(10) (1944) 1074–1089. [Google Scholar]
- [100].Ascher K, Spurgeon W, Compression tests on aqueous veins of glaucomatous eyes: application of hydrodynamic principles to the problem of intraocular-fluid elimination, Am J Ophthalmol 32(6) (1949) 239–253. [PubMed] [Google Scholar]
- [101].Kleinert HW, The compensation maximum: a new glaucoma sign in aqueous veins, AMA Arch Ophthal 46(6) (1951) 618–624. [PubMed] [Google Scholar]
- [102].Ascher KW, Glaucoma and aqueous veins, Arch Ophthal 73(2) (1965) 302–302. [DOI] [PubMed] [Google Scholar]
- [103].STAMBAUGH JL, FUHS JC, ASCHER KW, Study of the compensation-maximum test on aqueous veins, AMA Arch Ophthal 51(1) (1954) 24–31. [DOI] [PubMed] [Google Scholar]
- [104].Xin C, Johnstone M, Wang N, Wang RK, OCT Study of Mechanical Properties Associated with Trabecular Meshwork and Collector Channel Motion in Human Eyes, PLoS One 11(9) (2016) e0162048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [105].Huang W, Fan Q, Wang W, Zhou M, Laties AM, Zhang X, Collagen: a potential factor involved in the pathogenesis of glaucoma, Med Sci Monit Basic Res 19 (2013) 237–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [106].Chang J, Huang J, Li L, Liu Z, Yuan F, Stiffness characterization of anisotropic trabecular meshwork, J Biomech 61 (2017) 144–150. [DOI] [PubMed] [Google Scholar]
- [107].Hernandez M, Gong H, Extracellular matrix of the trabecular meshwork and optic nerve head, The Glaucomas: Basic Sciences 1 (1996) 213–249. [Google Scholar]
- [108].Johnstone MA, Grant WM, Pressure-dependent changes in structures of the aqueous outflow system of human and monkey eyes, Am J Ophthalmol 75(3) (1973) 365–383. [DOI] [PubMed] [Google Scholar]
- [109].Xin C, Wang RK, Song S, Shen T, Wen J, Martin E, Jiang Y, Padilla S, Johnstone M, Aqueous outflow regulation: Optical coherence tomography implicates pressure-dependent tissue motion, Exp Eye Res 158 (2017) 171–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [110].Humphrey JD, Continuum biomechanics of soft biological tissues, Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 459(2029) (2003) 3–46. [Google Scholar]
- [111].Effinger V, Dubois P, Feucht M, Haufe A, Bischoff M, Nonlinear viscoelastic modeling of foams, 13th European LS-DYNA Forum, 2014. [Google Scholar]
- [112].Frantz C, Stewart KM, Weaver VM, The extracellular matrix at a glance, J Cell Sci 123(24) (2010) 4195–4200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [113].Humphrey JD, Dufresne ER, Schwartz MA, Mechanotransduction and extracellular matrix homeostasis, Nat Rev Mol Cell Biol 15(12) (2014) 802–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [114].Roach MR, Burton AC, The reason for the shape of the distensibility curves of arteries, Can J Biochem Physiol 35(8) (1957) 681–690. [PubMed] [Google Scholar]
- [115].Zoumi A, Lu X, Kassab GS, Tromberg BJ, Imaging coronary artery microstructure using second-harmonic and two-photon fluorescence microscopy, Biophys J 87(4) (2004) 2778–2786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [116].Mithieux SM, Weiss AS, Elastin, Adv Protein Chem 70 (2005) 437–461. [DOI] [PubMed] [Google Scholar]
- [117].Chen H, Liu Y, Slipchenko MN, Zhao X, Cheng J-X, Kassab GS, The layered structure of coronary adventitia under mechanical load, Biophy J 101(11) (2011) 2555–2562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [118].Chen H, Slipchenko MN, Liu Y, Zhao X, Cheng J-X, Lanir Y, Kassab GS, Biaxial deformation of collagen and elastin fibers in coronary adventitia, J Appl Phys 115(11) (2013) 1683–1693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [119].Schlunck G.n., Han H, Wecker T, Kampik D, Meyer-ter-Vehn T, Grehn F, Substrate Rigidity Modulates Cell–Matrix Interactions and Protein Expression in Human Trabecular Meshwork Cells, Invest Ophthalmol Vis Sci 49(1) (2008) 262–269. [DOI] [PubMed] [Google Scholar]
- [120].Coudrillier B, Pijanka JK, Jefferys JL, Goel A, Quigley HA, Boote C, Nguyen TD, Glaucoma-related Changes in the Mechanical Properties and Collagen Micro-architecture of the Human Sclera, PLOS ONE 10(7) (2015) e0131396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [121].Liu B, McNally S, Kilpatrick JI, Jarvis SP, O’Brien CJ, Aging and ocular tissue stiffness in glaucoma, Surv Ophthalmol 63(1) (2018) 56–74. [DOI] [PubMed] [Google Scholar]
- [122].Robert L, Robert A, Fülöp T, Rapid increase in human life expectancy: will it soon be limited by the aging of elastin?, Biogerontology 9(2) (2008) 119–133. [DOI] [PubMed] [Google Scholar]
- [123].Sherratt MJ, Tissue elasticity and the ageing elastic fibre, Age 31(4) (2009) 305–325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [124].Handorf AM, Zhou Y, Halanski MA, Li W-J, Tissue stiffness dictates development, homeostasis, and disease progression, Organogenesis 11(1) (2015) 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [125].Speakman J, Leeson T, Pathological findings in a case of primary congenital glaucoma compared with normal infant eyes, Br J Ophthalmol 48(4) (1964) 196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [126].Aihara M, Lindsey JD, Weinreb RN, Ocular hypertension in mice with a targeted type I collagen mutation, Invest Ophthalmol Vis Sci 44(4) (2003) 1581–1585. [DOI] [PubMed] [Google Scholar]
- [127].Tektas O-Y, Lütjen-Drecoll E, Structural changes of the trabecular meshwork in different kinds of glaucoma, Exp Eye Res 88(4) (2009) 769–775. [DOI] [PubMed] [Google Scholar]
- [128].Mäepea O, Bill A, Pressures in the juxtacanalicular tissue and Schlemm’s canal in monkeys, Exp Eye Res 54(6) (1992) 879–83. [DOI] [PubMed] [Google Scholar]
- [129].Mäepea O, Bill A, The pressures in the episcleral veins, Schlemm’s canal and the trabecular meshwork in monkeys: effects of changes in intraocular pressure, Exp Eye Res 49(4) (1989) 645–63. [DOI] [PubMed] [Google Scholar]
- [130].Silver FH, Seehra GP, Freeman JW, DeVore D, Viscoelastic properties of young and old human dermis: a proposed molecular mechanism for elastic energy storage in collagen and elastin, J Appl Polym Sci 86(8) (2002) 1978–1985. [Google Scholar]
- [131].Ryan AJ, O’Brien FJ, Insoluble elastin reduces collagen scaffold stiffness, improves viscoelastic properties, and induces a contractile phenotype in smooth muscle cells, Biomaterials 73 (2015) 296–307. [DOI] [PubMed] [Google Scholar]
- [132].Johnstone M, Xin C, Acott T, Vranka J, Wen J, Martin E, Wang RK, Valve-Like Outflow System Behavior With Motion Slowing in Glaucoma Eyes: Findings Using a Minimally Invasive Glaucoma Surgery–MIGS-Like Platform and Optical Coherence Tomography Imaging, Front Med 9 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The raw/processed data required to reproduce these findings cannot be shared at this time, as the data are part of an ongoing study.


