Abstract
The evaluation of coronary morphology provides important guidance for the treatment of coronary heart disease (CHD). A chaotic Gaussian mutation antlion optimizer algorithm (CGALO) is proposed in the paper, and it is combined with SVM to construct a classification prediction model for Fractional flow reserve (FFR). To overcome the limitations of the original antlion optimizer (ALO) algorithm, the chaotic Gaussian mutation strategy is introduced, which leads to an improvement in its convergence speed and accuracy. To evaluate the proposed algorithm's performance, comparative experiments were conducted on 23 benchmark functions alongside 12 other cutting-edge optimization algorithms. The experimental outcomes demonstrate that the proposed algorithm achieves superior convergence accuracy and speed compared to the alternative comparison algorithms. Additionally, it is combined with SVM and FS to construct a hierarchical FFR classification model, which is utilized to make effective predictions for 84 patients at the affiliated hospital of medical school, Ningbo university. The experimental results demonstrate that the proposed model achieves an average accuracy of 92%. Moreover, it concludes that smoking history, number of lesion vessels, lesion location, diffuse lesions and ST segment changes, and other factors are the most critical indicators for FFR. Therefore, the model that has been established is a new FFR intelligent classification prediction technology that can effectively assist doctors in making corresponding decisions and evaluation plans.
Keywords: Coronary heart disease, Fractional flow reserve, Ant lion optimizer, Global optimization, Support vector machine, Feature selection
1. Introduction
Coronary angiography or intravascular imaging results are the main basis for the implementation of percutaneous coronary intervention (PCI), but imaging examination can only evaluate the morphology of coronary artery, and can not reflect the degree of myocardial ischemia, which is easy to lead to inappropriate PCI. Research shows that although the number of PCI is increasing year by year [1], about 20% of PCI is not suitable [2]. Correct assessment of myocardial ischemia caused by coronary artery stenosis is helpful to avoid unnecessary PCI. The rise of functional assessment of hemodynamic significance of coronary lesions provides a new method to evaluate myocardial ischemia, and is gradually paid attention by cardiovascular interventional physicians. Fractional flow reserve (FFR) is widely recognized as the primary evaluation parameter for functional stenosis of coronary lesions. The ratio of blood flow at the distal end of the stenosis to that of normal coronary arteries under maximum coronary artery congestion calculates the FFR value.
A majority of current coronary risk assessment methods solely depend on baseline data [3]. As an illustration, a multivariate risk score can serve as a reliable means of evaluating the influence of various coronary heart disease risk factors. This method is suitable for coronary heart disease patients with a small population sample, and in the face of rare disease patients, multiple covariates cannot be modeled. In fact, most physicians tend to estimate a patient's cardiovascular risk based on baseline data and their own experience [4]. However, sometimes wrong estimates can lead to irreparable risks. Consequently, incorporating artificial intelligence technology into diagnosing coronary heart disease in patients offers a cost-effective and convenient auxiliary diagnostic approach, paving the way for novel ideas and strategies to design and develop intelligent medical diagnosis techniques. This possesses significant theoretical value alongside extensive practical application potential.
Nowadays, more and more researchers use machine learning techniques combined various indicators to assist in diagnosing patients with coronary heart disease and have harvested good benefits. Sun et al. [5] designed an SVM model to identify antioxidant proteins and extract key features, indicating that the constructed model was superior to other advanced models. Tian et al. [6] propose a novel coronary computed tomography angiography (CCTA) image division framework that combines depth learning and digital image processing algorithms, which was important for clinicians to evaluate CCTA. Sharma et al. [7] proposed an improved artificial plant optimization algorithm and combined with the machine learning algorithm to predict coronary heart disease, and effectively verified the accuracy of the model in the comparative experiment. LV et al. [8] utilized optical coherence tomography and intravascular ultrasound imaging to quantify coronary plaque cap stress, achieving a promising accuracy of 90.8%. Liang et al. [9] designed a convolivable cardiovascular image segmentation method based on convolutional neural network to accurately and effectively extract vascular related information. Guo et al. [10] designed a dynamic treatment strategy of artificial intelligence to learn coronary heart disease to help clinical decision to treat CHD patients. Infante et al. [11] leveraged artificial intelligence techniques, specifically machine learning algorithms, to discern CHD and characterize atherosclerotic lesions and myocardial abnormalities. Gruson et al. [12] explored the integration method of artificial intelligence and laboratory medicine, providing an effective tool for diagnosing cardiogathic diseases. Cui et al. [13] adopted a combination of an acoustic waveform coronary heart disease wrist diagnosis method that can effectively identify CHD stable patients. Kusuma et al. [14] introduced a new improving principal component analysis method to reduce the characteristic set of coronary heart disease, combined with recursive neural network and restricted Bolzmann machine effective classification. Monhamed [15] et al. proposed a depth neural network and Adagrad optimization algorithm based on automated depth learning to predict the risk of CHD patients. Jamthikar et al. [16] introduced the challenge of traditional cardiogathic disease prediction, which leads to artificial intelligence methods with unique advantages in card crown disease. Wang et al. [17] built six interpretable machine learning models for assessing and layered the risk of death risk caused by CHD, assisting doctors understood the impact of key features in the model. Dutta [18] designed a neural network model with a convolution layer for classification for CHD patient data, and realizes an accurate diagnosis of CHD patients. Huang et al. [19] proposed a multi-scale feature fusion depth residual division network based on attention mechanism, and realizes the accurate segmentation of CHD blood chambers. Huang et al. [20] developed a comprehensive model for diagnosing coronary heart disease, demonstrating its user-friendly nature as a valuable tool for reducing medical costs and devising optimal treatment plans. Wang et al. [21] used a deep learning method to diagnose coronary heart disease and effectively verify the comprehensive performance of the method by comparison with traditional methods. It can be seen that the tendency to assist the doctor's diagnosis of CHD patients with the machine learning method constantly grow. However, so far, there are few reports on the construction of clinical prediction model of FFR. Theoretically, it is feasible to construct FFR prediction model based on clinical data, but its accuracy still needs to be proved to be suitable for clinical application.
This paper attempts to design a novel CGALO-SVM-FS model to predict and classify the results of FFR, so as to realize the noninvasive evaluation of functional parameters of coronary heart disease. Aiming at the problems of slow convergence and low precision of ALO [22], a chaotic Gaussian mutation strategy is introduced to enhance its performance. Meantime, based on the characteristic data of 84 CHD patients, combined SVM and FS techniques were used to screen key characteristics and predict classification. The experimental results show that the features SH, NV, PL, DL and STC become the key features for classifying FFR, and the classification accuracy rate is as high as 92%. In conclusion, the proposed method is expected to be a powerful tool for the prediction and classification of FFR.
The main contributions of the paper are shown as follows:
-
1)
A novel chaos Gaussian mutation ant lion optimizer algorithm (CGALO) is designed.
-
2)
Chaos strategy and Gaussian mutation are used to enhance the convergence accuracy and speed of the basic ALO.
-
3)
The performance of CGALO is verified on 23 basic benchmark functions.
-
4)
The proposed CGALO is combined with support vector machine and feature selection (CGALO-SVM-FS) to gain the key features and predict and classify flow reserve results.
-
5)
The proposed CGALO-SVM-FS model gains the highest accuracy in various reported methods.
The core structure of the paper is as follows. Section 2 briefly introduces the ALO algorithm. Section 3 describes the proposed CGALO algorithm. Section 4 builds the CGALO-SVM-FS model. Section 5 conducts benchmark experiments on the proposed algorithm. Section 6 predicts the classification result of FFR for patients with coronary heart disease. Section 7 makes the discussion. Finally, the full paper is summarized and prospected.
2. Ant lion optimizer
In recent years, many swarm optimization algorithms has developed, such as hunger games search (HGS) [23], weighted mean of vectors (INFO) [24], Runge Kutta optimizer (RUN) [25], colony predation algorithm (CPA) [26], slime mould algorithm (SMA) [27,28], Harris hawks optimization (HHO) [29], and rime optimization algorithm (RIME) [30]. They have been applied to solve many problems such as bankruptcy prediction [31], global optimization [32,33], constrained multi-objective optimization [34], numerical optimization [[35], [36], [37]], scheduling optimization [38,39], large-scale complex optimization [40], feature selection [[41], [42], [43], [44], [45]], multi-objective optimization [46], economic emission dispatch [47], and feed-forward neural networks [48]. In addition to these, ant lion optimizer (ALO) was designed in 2015, which mainly inspired the predatory action of ant lions of nature, mainly including ants, ant lions and elite ant lions [22]. The ALO algorithm is structured as follows: Initially, ant colony and ant positions are randomly initialized using roulette and random walk methods. Each ant is evaluated using a fitness function once they have traversed their path. The ant's position is considered the current optimal solution if it proves superior to its surrounding ant lions. Additionally, if an ant is captured by an ant lion, that ant lion's position becomes the optimal solution. During each iteration, the elite antlion represents the optimal solution in the ant lion population. Comparatively, if the optimal antlion surpasses the elite antlion, the latter is updated; otherwise, it remains unchanged until the iteration concludes, ultimately outputting the elite antlion. Among them, the random walk is used to exhibit the movement of ants, and can be expressed by Eq. (1) as follows:
| (1) |
where represents the cumulative sum, and represents the random walk function of the -th iteration.
Further, Eq. (1) is further normalized as shown in Eq. (2).
| (2) |
where and represent the min and max values of the -th individual, respectively, and and respectively represent the -th iteration of the -th variable maximum value.
The random walk of ants is affected by antlion traps, which is shown in Eq. (3) and Eq. (4):
| (3) |
| (4) |
where and are the minimum and maximum values of the individual in the -th iteration, respectively, and represents the position of -th ant-lion of the -th iteration.
As shown in Eq. (5), ants walk around the antlion by roulette or random walk.
| (5) |
where and are the random walk of the roulette wheel or the random walk around the elite on the second day of the -th day, respectively, and shows the position of the -th ant at the -th iteration.
With the increase of iterations, antlion will approach the approximate optimal solution by shrinking the bounds as follows by Eq. (6) and Eq. (7):
| (6) |
| (7) |
where represents the ratio and are the minimum and maximum values of all variables at the -th iteration, respectively.
After the iteration, the ant lion will prey on the ants, and the position update formula is shown in Eq. (8):
| (8) |
where and represent the positions of the -th and -th ant-lions of the -th iteration.
3. Suggested CGALO
3.1. Chaotic strategy and Gaussian mutation
The chaotic strategy refers to using the chaotic system to gain a novel solution within the range of specified solutions when the ant-lion is searching [[49], [50], [51], [52]]. By selecting the best solution among all the new solutions and comparing it with the original optimal solution, if the former is better than the latter, then make a replacement [53].
The chaotic strategy is used in the initial stage of each iteration, and the Gaussian mutation is used after the ant lion iteration, improving the performance of algorithms [54]. Among them, Gaussian distribution probability distribution function is shown in Eq. (9):
| (9) |
The variation formula of Gaussian mutation to antlion population is shown in Eq. (10):
| (10) |
where G(α) is a uniformly distributed random number drawn from a Gaussian distribution.
3.2. Proposed CGALO
This section addresses the challenges of slow convergence and limited precision associated with the ant lion optimization algorithm by introducing a Chaotic Gaussian Mutation Ant Lion Optimizer (CGALO). The population is initialized by chaotic strategy, improving the diversity of population. Further, a Gaussian mutation strategy is adopted to get rid of the algorithm falling into local optimum. The flow chart of CGALO is exhibited in Fig. 1. The algorithm is divided into three steps, which are initialization, the main function and chaotic Gaussian mutation strategy. The initialization mainly completes the generation of antlion population and obtains the local optimal location of antlion. The main function process is to complete the iteration of the population and update the local optimal ant-lion location. Finally, after each generation of ant-lion population renewal, we adopted a chaotic Gaussian mutation strategy to avoid the ant-lion population falling into local optimal. The source code is provided at https://github.com/vqnqig/CGALO.
Algorithm 1.
CGALO.
| Input: Objective function f(x); upper limit ub; lower limit lb; population size N; dimension size dim;: max evaluation MaxFEs: Output: optimal Elite Individual x Step 1. Initialize 1). Randomly initialize ant and antlion positions; 2). Get the fitness value of ants and antlions; 3). Determining the best antlion; Step 2. Main Loop 4). while t MaxFES 5). for i = 1:N 6). Use roulette to choose antlion; 7). Update parameters and ; 8). Perform random walk and normalization operations; 9). Update ant location; Step 3. Chaotic Gaussian Mutation 10). Gain the fitness of ants; 11). Use chaotic Gaussian mutation to get the ant position; 12). Replace the ant position with the ant lion; 13). Update Elite Antlion; 14). end for 15). end while Step 4. Return to Elite Individual |
Fig. 1.
Flow chart of CGALO.
4. Proposed CGALO-SVM-FS model
Support vector machine (SVM) is a famous supervised learning algorithm in machine learning [55]. However, the accuracy of SVM is susceptible to hyperparameters. Therefore, for known datasets, how to accurately and reliably select appropriate hyperparameters is a key factor for the strong generalization ability of the model. Based on the basis of grid search and random algorithm, this section proposes a chaotic Gaussian mutation ant lion optimization support vector machine model, which is used to optimize two extremely important parameters in SVM, kernel width and regularization coefficient. As shown in Fig. 2, firstly, feature engineering was performed on the collected dataset of 114 patients, and then key features were filtered out through Feature Selection (FS) to reduce the dimension of the dataset, and then CGALO-SVM was used for the processed data. The final output is whether the patient has functional coronary stenosis or non-functional stenosis.
Fig. 2.
Schematic diagram of CGALO-SVM-FS.
Typically, the ten-fold crossover method is utilized for SVM model training to test algorithm accuracy. Firstly, the dataset is partitioned into 10 subsets, of which nine are designated as the training set and one as the test set. Furthermore, the nine data subsets are further subdivided into five sets, with four being consecutively chosen as the training data combined with CGALO to train the SVM model. Subsequently, evaluating the SVM model trained with one subset as test data enables the acquisition of the optimal SVM model. Finally, the initial reserved test data is employed to evaluate the SVM model. The experimental outcomes are analyzed and evaluated based on the accurate (ACC), sensitivity (Sens), specificity (Spec), and Matthews correlation coefficient (MCC).
5. Performance evaluation of CGALO
5.1. Mechanism combination analysis
This section delves into the incorporation of chaotic and Gaussian variation strategies into ALO to analyze their impact on the original algorithm further. This leads to the development of two improved algorithms, the Chaos Ant Lion Optimizer (CALO) and Gaussian Mutation Ant Lion Optimizer (CGALO). Table 1 illustrates the combination of the “C" for chaotic strategy and “G" for Gaussian mutation technique in the original ALO algorithm. A value of “1″ indicates a combined strategy, while “0″ denotes an uncombined strategy. For instance, CGALO refers to combining both chaotic and Gaussian mutation strategies with ALO concurrently. The experiment was conducted on a Windows 10 operating system PC with a 3.4 GHz main frequency, using MATLAB R2016a software.
Table 1.
ALO variants combining two strategies.
| Algorithm | C | G |
|---|---|---|
| CGALO | 1 | 1 |
| GALO | 0 | 1 |
| CALO | 1 | 0 |
| ALO | 0 | 0 |
For fair comparison, the experiment uses 23 benchmark function test sets [56,57] (See Table A in appendix), the dimension of the comparison algorithm is 30, and the number of iterations is 500. In addition, Friedman's test was used to examine the performance mean rank values of the algorithms involved. According to the results in Table 2, the average performance of ALO using both strategies is the best. It can be seen that under the combined action of chaotic strategy and Gaussian mutation, the comprehensive performance of ALO is greatly improved. Further, the convergence curves of CGALO, CALO, GALO and ALO on 9 benchmark test functions are shown in Fig. 3. Results exhibit CGALO has excellent performance in F1, F3, F6, F8, F11, F13, F14, F15 and F23 in ALO.
Table 2.
Average performance of the four variants.
| Algorithm | Rank | ARV |
|---|---|---|
| CGALO | 1 | 1.86232 |
| GALO | 2 | 2.225362 |
| CALO | 3 | 2.37971 |
| ALO | 4 | 3.532609 |
Fig. 3.
Convergence curves of ALO variants on F1, F3, F6, F8, F11, F13, F14, F15 and F34 corresponding to (a), (b), (c), (d), (e), (f), (g), (h) and (i).
5.2. Comparison with advanced algorithms
CGALO is compared with 12 advanced methods, which are ACLPSO [58], CLPSO [59], HCLPSO [60], GWO [61], WOA [62], DE [63], ABC [64], SMA [65], SCA [66], MFO [67], IWOA [68] and CDLOBA [69]. All contrasting algorithms have 30 individuals, 30 dimension, and 500 iterations. For the sake of fairness, all algorithms execute 30 times, and statistically corresponding experimental results. The parameter configuration of the comparison algorithm is shown in Table 3. All parameter Settings are taken from the original algorithm paper. In addition, Table 4 presents the comparative performance of CGALO and 12 other contemporary algorithms on 23 benchmark function test sets. The experiment outlines average results (Avg) and standard deviation (Std) metrics for the various algorithms on corresponding benchmark functions. Furthermore, to vividly represent algorithm performance, we conducted a comprehensive evaluation utilizing Friedman and Wilkerson tests. CGALO ranks first in the comprehensive performance of all comparison algorithms, with an average index of 3.769565. Among them, the comprehensive performance of SMA ranks second. This reflects the superior performance of CGALO in solving 23 benchmark function sets. In addition, it also shows the promotion effect of CG strategy on ALO algorithm.
Table 3.
Parameter configuration.
| Method | Parameter |
|---|---|
| CGALO | |
| ALCPSO | = 0.4; = 2; = 2; = 2 |
| CLPSO | = [0.2 0.9]; = 1.496 |
| HCLPSO | = [0.2 0.9]; = 1.496 |
| GWO | = |
| WOA | ; ; |
| DE | ; ; |
| ABC | |
| SMA | |
| SCA | |
| MFO | |
| IWOA | |
| CDLOBA |
Table 4.
Comparison results of CGALO and other 12 advanced algorithms.
| F1 |
F2 |
F3 |
||||
|---|---|---|---|---|---|---|
| Avg | Std | Avg | Std | Avg | Std | |
| CGALO | 2.25072E-25 | 7.11738E-25 | 0.00000E+00 | 0.00000E+00 | 0.00000E+00 | 0.00000E+00 |
| ALCPSO | 1.11816E-06 | 1.76199E-06 | 3.56429E-04 | 6.32931E-04 | 2.20732E+03 | 6.73459E+02 |
| CLPSO | 4.24334E+02 | 9.57023E+01 | 6.17125E+00 | 1.02888E+00 | 1.43423E+04 | 2.57935E+03 |
| HCLPSO | 1.58339E-02 | 7.00024E-03 | 2.41038E-02 | 7.76300E-03 | 7.81003E+02 | 3.54486E+02 |
| GWO | 8.27217E-31 | 1.43225E-30 | 1.57746E-18 | 1.20272E-18 | 6.64049E-07 | 7.64617E-07 |
| WOA | 6.74051E-83 | 1.27623E-82 | 2.40169E-55 | 3.32624E-55 | 3.89959E+04 | 6.41134E+03 |
| DE | 5.77940E-04 | 1.32855E-04 | 2.70095E-03 | 8.64691E-04 | 3.14339E+04 | 2.57071E+03 |
| ABC | 2.44640E-05 | 3.44638E-05 | 5.57342E-03 | 2.46882E-03 | 1.71626E+04 | 2.78670E+03 |
| SMA | 4.60559E-105 | 1.13497E-104 | 1.35998E-66 | 4.29429E-66 | 3.35632E-33 | 1.06136E-32 |
| SCA | 4.47665E+00 | 5.22579E+00 | 5.50882E-03 | 5.68930E-03 | 7.37608E+03 | 4.25488E+03 |
| MFO | 3.00223E+03 | 6.74885E+03 | 2.60918E+01 | 2.11326E+01 | 2.16095E+04 | 1.43447E+04 |
| IWOA | 7.78609E-83 | 1.39420E-82 | 1.37843E-52 | 2.67947E-52 | 2.76100E+04 | 9.96031E+03 |
| CDLOBA |
2.17010E-02 |
4.88500E-03 |
1.58240E+01 |
4.14329E+01 |
3.47723E-01 |
1.85811E-01 |
| F4 |
F5 |
F6 |
||||
| CGALO | 1.30705E-12 | 3.39621E-12 | 6.73180E-03 | 4.20622E-03 | 8.66149E-05 | 5.22036E-05 |
| ALCPSO | 1.26319E+01 | 3.45996E+00 | 1.91904E+02 | 1.79104E+02 | 3.51327E-06 | 5.75114E-06 |
| CLPSO | 3.93904E+01 | 3.12360E+00 | 1.34642E+05 | 5.57821E+04 | 4.19322E+02 | 5.15840E+01 |
| HCLPSO | 3.84479E+00 | 1.11316E+00 | 1.31496E+02 | 1.52608E+02 | 1.25347E-02 | 1.12649E-02 |
| GWO | 1.96265E-07 | 2.98585E-07 | 2.68273E+01 | 4.38713E-01 | 5.22612E-01 | 2.74381E-01 |
| WOA | 4.46669E+01 | 3.08489E+01 | 2.76915E+01 | 3.96289E-01 | 1.56577E-01 | 1.12006E-01 |
| DE | 1.25070E+01 | 8.53973E-01 | 1.88821E+02 | 5.81275E+01 | 4.04530E-04 | 1.55293E-04 |
| ABC | 4.35732E+01 | 3.66719E+00 | 3.81513E+01 | 3.49385E+01 | 1.76901E-05 | 1.45589E-05 |
| SMA | 1.63129E-01 | 1.69210E-01 | 1.54070E+00 | 2.42430E+00 | 7.71877E-02 | 9.06019E-02 |
| SCA | 2.18838E+01 | 1.10384E+01 | 3.59399E+03 | 5.37368E+03 | 6.63131E+00 | 1.94613E+00 |
| MFO | 6.27620E+01 | 1.23635E+01 | 9.47590E+03 | 2.83838E+04 | 3.98300E+03 | 9.62314E+03 |
| IWOA | 2.63515E+01 | 2.98400E+01 | 2.71952E+01 | 6.52235E-01 | 7.90039E-02 | 8.34462E-02 |
| CDLOBA |
4.45215E+01 |
6.63587E+00 |
1.34848E+02 |
1.04525E+02 |
2.36643E-02 |
8.04182E-03 |
| F7 |
F8 |
F9 |
||||
| CGALO | 1.22911E-04 | 1.19773E-04 | −1.25692E+04 | 6.97952E-01 | 0.00000E+00 | 0.00000E+00 |
| ALCPSO | 6.57642E-02 | 2.05592E-02 | −1.00368E+04 | 7.11659E+02 | 5.72213E+01 | 1.19285E+01 |
| CLPSO | 2.21351E-01 | 6.87472E-02 | −1.05143E+04 | 3.40458E+02 | 4.43052E+01 | 4.38326E+00 |
| HCLPSO | 2.21667E-02 | 8.32481E-03 | −8.75020E+03 | 5.36384E+02 | 2.37844E+01 | 5.46974E+00 |
| GWO | 1.61007E-03 | 9.11014E-04 | −6.19918E+03 | 5.20229E+02 | 2.00470E+00 | 2.46105E+00 |
| WOA | 3.18582E-03 | 3.16521E-03 | −1.09487E+04 | 1.76617E+03 | 1.13687E-14 | 3.59509E-14 |
| DE | 4.97243E-02 | 1.20536E-02 | −9.73300E+03 | 6.57542E+02 | 9.13850E+01 | 6.39406E+00 |
| ABC | 2.41818E-01 | 5.87743E-02 | −1.15951E+04 | 2.88057E+02 | 5.54723E+00 | 1.59870E+00 |
| SMA | 6.68105E-04 | 2.83616E-04 | −1.25692E+04 | 6.47840E-01 | 0.00000E+00 | 0.00000E+00 |
| SCA | 9.39056E-02 | 8.13209E-02 | −3.71151E+03 | 3.01794E+02 | 3.13686E+01 | 2.20046E+01 |
| MFO | 4.70318E+00 | 9.04260E+00 | −8.76507E+03 | 8.67805E+02 | 1.71571E+02 | 3.71464E+01 |
| IWOA | 2.35571E-03 | 2.85500E-03 | −1.07918E+04 | 1.93131E+03 | 0.00000E+00 | 0.00000E+00 |
| CDLOBA |
5.16734E+01 |
3.61681E+01 |
−7.03478E+03 |
8.36545E+02 |
2.65593E+02 |
3.41741E+01 |
| F10 |
F11 |
F12 |
||||
| CGALO | 5.37513E-09 | 1.67931E-08 | 0.00000E+00 | 0.00000E+00 | 5.20699E-06 | 5.01699E-06 |
| ALCPSO | 2.81020E-01 | 6.01361E-01 | 2.40906E-02 | 2.32274E-02 | 1.60638E-01 | 2.21350E-01 |
| CLPSO | 8.92590E+00 | 5.96026E-01 | 4.50425E+00 | 9.29237E-01 | 1.61237E+01 | 3.62803E+00 |
| HCLPSO | 1.99064E-01 | 3.34069E-01 | 2.70776E-02 | 1.22446E-02 | 4.26800E-04 | 3.86785E-04 |
| GWO | 6.05738E-14 | 7.06584E-15 | 7.27172E-03 | 9.63129E-03 | 4.84395E-02 | 2.40181E-02 |
| WOA | 4.79616E-15 | 3.11074E-15 | 0.00000E+00 | 0.00000E+00 | 1.00700E-01 | 1.74669E-01 |
| DE | 6.43396E-03 | 1.43332E-03 | 2.34270E-03 | 1.72743E-03 | 7.77783E-05 | 3.12423E-05 |
| ABC | 1.35504E-01 | 9.27041E-02 | 3.88863E-02 | 2.82115E-02 | 1.30216E-05 | 1.14871E-05 |
| SMA | 3.73035E-15 | 1.49796E-15 | 0.00000E+00 | 0.00000E+00 | 1.68779E-03 | 3.32444E-03 |
| SCA | 1.42414E+01 | 9.64622E+00 | 6.81840E-01 | 2.69682E-01 | 3.20871E+03 | 5.89224E+03 |
| MFO | 1.11256E+01 | 8.89928E+00 | 1.88952E+01 | 3.78548E+01 | 5.16881E+00 | 1.66529E+00 |
| IWOA | 3.73035E-15 | 3.26472E-15 | 0.00000E+00 | 0.00000E+00 | 9.35959E-03 | 9.03805E-03 |
| CDLOBA |
1.79540E+01 |
5.44917E+00 |
1.65714E+02 |
9.16164E+01 |
1.95474E+01 |
7.24918E+00 |
| F13 |
F14 |
F15 |
||||
| CGALO | 7.17184E-05 | 5.77107E-05 | 1.49502E+00 | 5.23898E-01 | 3.10514E-04 | 7.41128E-06 |
| ALCPSO | 6.80419E-03 | 5.80258E-03 | 9.98004E-01 | 1.04673E-16 | 2.82873E-03 | 6.17560E-03 |
| CLPSO | 2.00654E+04 | 3.06818E+04 | 1.09741E+00 | 3.14339E-01 | 6.10543E-04 | 6.96083E-05 |
| HCLPSO | 2.10613E-02 | 2.05455E-02 | 9.98004E-01 | 0.00000E+00 | 4.82186E-04 | 9.61065E-05 |
| GWO | 3.78482E-01 | 1.64122E-01 | 5.00366E+00 | 4.94637E+00 | 1.03563E-02 | 1.05484E-02 |
| WOA | 3.39359E-01 | 1.58489E-01 | 2.66641E+00 | 3.22856E+00 | 7.89045E-04 | 5.39225E-04 |
| DE | 2.98545E-04 | 8.54251E-05 | 9.98004E-01 | 0.00000E+00 | 6.91117E-04 | 6.71595E-05 |
| ABC | 1.33550E-03 | 3.45636E-03 | 9.98004E-01 | 1.81299E-16 | 1.04912E-03 | 5.01129E-04 |
| SMA | 3.05463E-03 | 2.24228E-03 | 9.98004E-01 | 2.81840E-16 | 7.21974E-04 | 2.17543E-04 |
| SCA | 1.54197E+04 | 3.29006E+04 | 1.59366E+00 | 9.58116E-01 | 9.65891E-04 | 3.44445E-04 |
| MFO | 4.10063E+07 | 1.29673E+08 | 1.69107E+00 | 1.32261E+00 | 9.29513E-04 | 3.29612E-04 |
| IWOA | 2.55226E-01 | 1.36568E-01 | 2.37134E+00 | 3.06180E+00 | 5.11733E-04 | 1.45359E-04 |
| CDLOBA |
1.81347E+01 |
1.82496E+01 |
2.28708E+00 |
1.14819E+00 |
6.77470E-03 |
9.38343E-03 |
| F16 |
F17 |
F18 |
||||
| CGALO | −1.03163E+00 | 2.60333E-13 | 3.97887E-01 | 1.26733E-14 | 3.00000E+00 | 2.42249E-13 |
| ALCPSO | −1.03163E+00 | 1.48030E-16 | 3.97887E-01 | 0.00000E+00 | 3.00000E+00 | 1.59433E-15 |
| CLPSO | −1.03163E+00 | 3.60400E-15 | 3.97887E-01 | 0.00000E+00 | 3.00000E+00 | 4.64351E-15 |
| HCLPSO | −1.03163E+00 | 1.81299E-16 | 3.97887E-01 | 0.00000E+00 | 3.00000E+00 | 1.23851E-15 |
| GWO | −1.03163E+00 | 1.33393E-08 | 3.97888E-01 | 8.70736E-07 | 3.00001E+00 | 1.10260E-05 |
| WOA | −1.03163E+00 | 7.08592E-11 | 3.97889E-01 | 2.82645E-06 | 3.00001E+00 | 1.57722E-05 |
| DE | −1.03163E+00 | 0.00000E+00 | 3.97887E-01 | 0.00000E+00 | 3.00000E+00 | 0.00000E+00 |
| ABC | −1.03163E+00 | 2.22045E-16 | 3.97887E-01 | 0.00000E+00 | 3.00078E+00 | 2.47138E-03 |
| SMA | −1.03163E+00 | 2.34056E-16 | 3.97887E-01 | 0.00000E+00 | 3.00000E+00 | 2.09346E-16 |
| SCA | −1.03160E+00 | 4.16225E-05 | 3.99202E-01 | 1.49848E-03 | 3.00005E+00 | 4.22397E-05 |
| MFO | −1.03163E+00 | 0.00000E+00 | 3.97887E-01 | 0.00000E+00 | 3.00000E+00 | 1.42755E-15 |
| IWOA | −1.03163E+00 | 1.73502E-10 | 3.97887E-01 | 1.59917E-07 | 3.00000E+00 | 4.16132E-06 |
| CDLOBA |
−1.03131E+00 |
3.44855E-04 |
3.98016E-01 |
1.53223E-04 |
3.01865E+00 |
1.86683E-02 |
| F19 |
F20 |
F21 |
||||
| CGALO | −3.86278E+00 | 1.50744E-13 | −3.26232E+00 | 6.29067E-02 | −1.01532E+01 | 2.31862E-11 |
| ALCPSO | −3.86278E+00 | 8.63154E-16 | −3.23877E+00 | 5.74308E-02 | −8.25000E+00 | 2.39336E+00 |
| CLPSO | −3.86278E+00 | 7.83300E-16 | −3.32199E+00 | 2.06058E-05 | −1.01522E+01 | 2.45176E-03 |
| HCLPSO | −3.86278E+00 | 8.63154E-16 | −3.32200E+00 | 7.32724E-12 | −1.01532E+01 | 2.93661E-06 |
| GWO | −3.86237E+00 | 1.22753E-03 | −3.23971E+00 | 7.72532E-02 | −1.01518E+01 | 8.59178E-04 |
| WOA | −3.85475E+00 | 9.52748E-03 | −3.24503E+00 | 1.01272E-01 | −9.12350E+00 | 2.14425E+00 |
| DE | −3.86278E+00 | 9.36222E-16 | −3.32198E+00 | 3.98596E-05 | −9.87762E+00 | 5.74792E-01 |
| ABC | −3.86278E+00 | 4.68111E-16 | −3.32200E+00 | 5.33729E-16 | −1.01233E+01 | 6.30522E-02 |
| SMA | −3.86278E+00 | 4.68111E-16 | −3.26255E+00 | 6.26622E-02 | −1.01532E+01 | 1.15858E-09 |
| SCA | −3.85692E+00 | 3.18981E-03 | −2.97163E+00 | 3.87692E-01 | −3.05802E+00 | 2.09893E+00 |
| MFO | −3.86278E+00 | 9.36222E-16 | −3.25600E+00 | 7.22482E-02 | −6.14934E+00 | 3.57078E+00 |
| IWOA | −3.85963E+00 | 4.06951E-03 | −3.28617E+00 | 8.02673E-02 | −9.13143E+00 | 2.14852E+00 |
| CDLOBA |
−3.84789E+00 |
7.25403E-03 |
−2.90965E+00 |
1.39352E-01 |
−6.31596E+00 |
3.51089E+00 |
| F22 |
F23 |
Overall Rank |
||||
| CGALO | −1.04029E+01 | 4.06288E-11 | −1.05364E+01 | 3.05578E-11 | 1 | 3.769565 |
| ALCPSO | −6.77470E+00 | 3.84063E+00 | −7.55744E+00 | 3.85580E+00 | 5 | 5.8 |
| CLPSO | −1.03910E+01 | 1.94816E-02 | −1.05312E+01 | 1.32507E-02 | 11 | 8.532609 |
| HCLPSO | −1.04029E+01 | 1.87244E-15 | −1.05364E+01 | 1.77636E-15 | 3 | 5.356522 |
| GWO | −1.04018E+01 | 7.54628E-04 | −1.05349E+01 | 7.37556E-04 | 8 | 7.343478 |
| WOA | −7.66314E+00 | 3.56613E+00 | −1.05241E+01 | 1.59078E-02 | 9 | 7.443478 |
| DE | −1.04026E+01 | 8.95150E-04 | −1.05364E+01 | 3.43044E-05 | 6 | 5.878261 |
| ABC | −1.04015E+01 | 4.53667E-03 | −1.05364E+01 | 1.70711E-05 | 4 | 5.723913 |
| SMA | −1.04029E+01 | 1.88744E-09 | −1.05364E+01 | 3.44267E-08 | 2 | 3.976087 |
| SCA | −4.65557E+00 | 5.92514E-01 | −5.45005E+00 | 1.97506E+00 | 12 | 10.67391 |
| MFO | −8.53569E+00 | 3.02938E+00 | −6.98627E+00 | 3.81337E+00 | 10 | 8.502174 |
| IWOA | −8.67082E+00 | 2.81084E+00 | −5.84795E+00 | 3.40094E+00 | 7 | 6.886957 |
| CDLOBA | −5.70185E+00 | 3.63325E+00 | −8.42791E+00 | 3.08793E+00 | 13 | 11.11304 |
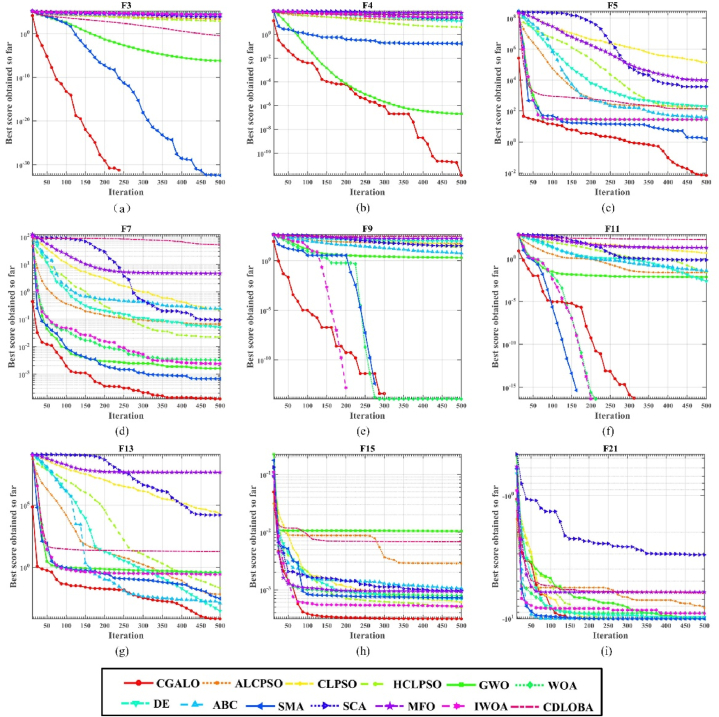
To enhance the clarity of the proposed algorithm's performance, Fig. 4 illustrates the convergence curves of CGALO and other comparative algorithms on F3, F4, F5, F7, F9, F11, F13, F15, and F21. Here, F denotes function. It is obvious that CGALO shows excellent convergence speed and convergence accuracy in the selected 9 reference functions. For unimodal function F3, F4 and F5, CGALO has certain competitiveness with SMA in convergence accuracy. For function F7, F9, F11, F13, F15 and F21, CGALO not only has superior convergence speed, but also performs very well in convergence accuracy. The experimental findings demonstrate that CGALO exhibits impressive performance across unimodal, multimodal, and fixed-dimension multimodal functions. Additionally, Table 5 presents the p-values of CGALO against the twelve other known variants, with bold data indicating p-values over 0.05. Based on this table, a majority of the data is below 0.05, highlighting the superior performance of the proposed algorithm compared to well-known variant algorithms.
Fig. 4.
Convergence curves of CGALO and other algorithms on F3, F4, F5, F7, F9, F11, F13, F15 and F21 corresponding to (a), (b), (c), (d), (e), (f), (g), (h) and (i).
Table 5.
The p-value of CGALO and other 12 advanced algorithm.
| ALCPSO | CLPSO | HCLPSO | GWO | WOA | DE | ABC | SMA | SCA | MFO | IWOA | CDLOBA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 1.88E-01 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 |
| F2 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-01 | 6.25E-02 |
| F3 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 |
| F4 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 3.13E-01 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 |
| F5 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 |
| F6 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 |
| F7 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 3.13E-01 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 |
| F8 | 4.38E-01 | 6.25E-02 | 6.25E-01 | 6.25E-02 | 4.38E-01 | 6.25E-02 | 6.25E-02 | 4.38E-01 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 |
| F9 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 |
| F10 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 3.13E-01 | 6.25E-02 |
| F11 | 1.25E-01 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 1.25E-01 | 6.25E-02 |
| F12 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 |
| F13 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 |
| F14 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 1.00E+00 | 3.13E-01 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 8.13E-01 | 6.25E-02 | 1.88E-01 | 4.38E-01 |
| F15 | 6.25E-02 | 1.00E+00 | 6.25E-02 | 6.25E-02 | 3.13E-01 | 8.13E-01 | 6.25E-01 | 4.38E-01 | 4.38E-01 | 3.13E-01 | 6.25E-02 | 6.25E-01 |
| F16 | 6.25E-02 | 6.25E-01 | 6.25E-02 | 6.25E-02 | 3.13E-01 | 8.13E-01 | 1.25E-01 | 6.25E-02 | 6.25E-01 | 3.13E-01 | 6.25E-02 | 6.25E-01 |
| F17 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 1.25E-01 | 1.88E-01 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 1.25E-01 | 6.25E-02 | 6.25E-02 | 6.25E-02 |
| F18 | 6.25E-02 | 6.25E-01 | 6.25E-02 | 3.13E-01 | 1.00E+00 | 6.25E-01 | 6.25E-01 | 6.25E-02 | 6.25E-01 | 3.13E-01 | 1.25E-01 | 6.25E-01 |
| F19 | 6.25E-02 | 6.25E-01 | 6.25E-02 | 6.25E-02 | 1.00E+00 | 6.25E-02 | 6.25E-02 | 1.25E-01 | 6.25E-01 | 6.25E-02 | 1.25E-01 | 1.88E-01 |
| F20 | 1.25E-01 | 6.25E-02 | 6.25E-02 | 1.25E-01 | 1.00E+00 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 1.25E-01 | 6.25E-02 | 6.25E-02 |
| F21 | 8.13E-01 | 6.25E-02 | 6.25E-02 | 6.25E-01 | 6.25E-01 | 4.38E-01 | 1.25E-01 | 6.25E-02 | 6.25E-02 | 6.25E-01 | 6.25E-02 | 1.25E-01 |
| F22 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 6.25E-02 | 1.00E+00 | 6.25E-02 | 4.38E-01 | 6.25E-01 | 6.25E-02 | 8.13E-01 | 6.25E-02 | 6.25E-02 |
| F23 | 1.00E+00 | 1.88E-01 | 6.25E-02 | 1.25E-01 | 4.38E-01 | 1.00E+00 | 1.88E-01 | 6.25E-02 | 1.25E-01 | 6.25E-01 | 1.00E+00 | 1.25E-01 |
6. Classification prediction of fractional flow reserve
6.1. Collection of data
This study retrospectively gathered data from patients who underwent selective coronary angiography (CAG) and invasive fractional flow reserve (FFR) examination at the Affiliated Hospital of Medical School, Ningbo University and Ningbo First Hospital between March 2015 to December 2020. Clinical data encompassing age, gender, height, weight, hypertension history, hyperlipidemia history, diabetes history, smoking history, drinking history, and serological examination was collected. The criteria for inclusion are as follows: (1) Age ≥18 years old; (2) CAD was diagnosed by CAG, and it was the main branch lesion of LAD, LCX or RCA; (3) The FFR was measured after CAG. The exclusion criteria are as follows: (1) The branch vessel disease other than LAD, LCX and RCA; (2) The history of cardiovascular surgery, such as PCI, Coronary artery bypass grafting (CABG), heart valve surgery, heart transplantation and pacemaker implantation, etc; (3) Data missing. All patients had signed informed consent for CAG and informed consent for FFR. The study has been approved by the ethics committee of the Affiliated Hospital of Medical School, Ningbo University.
All patients were assessed with invasive CAG to assess the degree of stenosis. First, the guiding catheter (5–7F) was placed in the aorta and connected to the baroreceptor to record the near end pressure (Pa). The cardiovascular interventional physician assessed the severity of coronary stenosis in the digital subtraction angiography system. Then, the invasive FFR was measured by the interventional physician of cardiovascular department. The specific steps are as follows: (1) Connect the pressure wire and the arterial physiological detector, and adjust the zero of the in vitro pressure guide wire; (2) The pressure guide wire was sent to the proximal end of the coronary artery through the guiding catheter, so that the pressure sensor with a head length of 3 cm exceeded the catheter, then EQUALIZE; (3) Continue to push the pressure guide wire, and position it at the distal 20–30 mm of the coronary artery lesion. When the reference pressure reading is stable, record the distal pressure (Pd); (4) Intravenous infusion of adenosine (140 μg/kg/min) to maintain a state of maximal coronary hyperemia, at which FFR was determined. FFR was defined as the ratio of Pd and Pa at maximal hyperemia of the coronary artery. FFR≤0.80 indicates that coronary stenosis has myocardial ischemia significance. Table 6 shows the demographic characteristics of the 84 eligible patients. Features are expressed as mean ± standard deviation or frequency and percentage. Functional coronary stenosis was detected in 39 patients (46.43%) and non-functional stenosis was detected in 45 patients (53.57%). Besides, the data is scaled to [−1,1]. -fold cross-validation (CV) was used to split the data, where was set to 10.
Table 6.
Detail of the involved dataset.
| Variable | FFR>0.80 |
FFR≤0.80 |
|---|---|---|
| (n = 45) | (n = 39) | |
| Age (A) (years, ± s) | 64.47 ± 7.79 | 65.33 ± 10.44 |
| Marriage (M) [unmarried/married/divorce, n (%) ] | 0(0.0)/45 (100.0)/0 (0.0) | 0(0.0)/39 (100.0)/0 (0.0) |
| Gender (G) [male/female, n (%)] | 27 (60.0)/18 (40.0) | 34 (87.1)/5 (12.8) |
| Weight (W) (kg, ± s) | 63.25 ± 8.88 | 69.35 ± 11.29 |
| Height (H) (cm, ± s) | 165.06 ± 6.96 | 169.30 ± 7.12 |
| Systolic blood pressure (SBP) (mmHg, ± s) | 139.58 ± 22.11 | 143.51 ± 26.80 |
| Diastolic blood pressure (DBP) (mmHg, ± s) | 79.38 ± 14.01 | 80.59 ± 12.11 |
| Heart rate (HR) (/min, ± s) | 73.62 ± 13.12 | 72.41 ± 11.01 |
| History of hypertension (HBP) [yes/no, n (%)] | 33 (73.3)/12 (26.7) | 31 (79.4)/8 (20.5) |
| History of hyperlipidemia (HPA) [yes/no, n (%)] | 10 (22.2/35 (77.8) | 14 (35.8)/25 (64.1) |
| Diabetes history (DM) [yes/no, n (%)] | 11 (24.4)/34 (75.6) | 19 (48.7)/20 (51.2) |
| Renal insufficiency (RF) [yes/no, n (%)] | 0(0.0)/45 (100.0) | 3 (7.6)/36 (92.3) |
| History of psychiatric disorders (HMI) [yes/no, n (%)] | 0 (0.0)/45 (100.0) | 0 (0.0)/39 (100.0) |
| History of vascular disease (HVD) [yes/no, n (%)] | 4 (8.9)/41 (91.1) | 4 (10.2)/35 (89.7) |
| History of pulmonary disease (HPD) [yes/no, n (%)] | 5 (11.1)/40 (88.9) | 8 (20.5)/31 (79.4) |
| Smoking history (SH) [yes/no, n (%)] | 15 (33.3)/30 (66.7) | 25 (64.1)/14 (35.8) |
| Drinking history (DH) [yes/no, n (%)] | 10 (22.2)/35 (77.8) | 18 (46.1)/21 (53.8) |
| Hemoglobin (HB) (g/L, ± s) | 134.93 ± 15.22 | 138.44 ± 14.96 |
| White blood cell count (WBC) (/L, ± s) | 6.28 ± 1.53 | 6.10 ± 1.68 |
| Platelet (Plt) (/L, ± s) | 186.60 ± 58.69 | 216.64 ± 58.47 |
| Sodium (Na) (mmol/L, ± s) | 140.74 ± 1.94 | 140.11 ± 2.46 |
| Potassium (K) (mmol/L, ± s) | 3.86 ± 0.45 | 3.98 ± 0.30 |
| Calcium (Ca) (mmol/L, ± s) | 2.30 ± 0.11 | 2.27 ± 0.11 |
| Glucose (Glu) (mmol/L, ± s) | 5.32 ± 1.65 | 5.87 ± 1.65 |
| Creatinine (Cr) (umol/L, ± s) | 74.84 ± 18.05 | 84.23 ± 34.25 |
| Estimated glomerular filtration rate (eGFR) (mL/min ± s) | 164.86 ± 19.56 | 132.00 ± 31.14 |
| Blood urea nitrogen (BUN) (mmol/L, ± s) | 5.75 ± 1.49 | 6.06 ± 2.47 |
| Cholesterol (TC) (mmol/L, ± s) | 2.42 ± 2.13 | 4.05 ± 1.61 |
| Triglyceride (TG) (mmol/L, ± s) | 3.33 ± 1.51 | 1.94 ± 1.19 |
| High density lipoprotein (HDL) (mmol/L, ± s) | 1.30 ± 0.53 | 1.17 ± 0.34 |
| Low density lipoprotein (LDL) (mmol/L, ± s) | 2.47 ± 1.12 | 2.44 ± 0.95 |
| Thyrotropin (TSH) (mmol/L, ± s) | 2.36 ± 1.38 | 1.96 ± 1.12 |
| Left ventricular ejection fraction (LVEF) (%, ± s) | 64.71 ± 5.46 | 65.10 ± 4.98 |
| Degree of vessel stenosis (DVS) (%, ± s) | 67.44 ± 10.59 | 82.31 ± 7.60 |
| Number of diseased vessels (NV) [1/2/3, n (%)] | 27(60.0)/15 (33.3)/3 (6.7) | 10(25.6)/19 (48.7)/10 (25.6) |
| Position of the lesion (PL) [proximal/mid/distal, n (%)] | 20(44.4)/25 (55.6)/0 (0.0) | 25(64.1)/12 (30.7)/2 (5.1) |
| Diffuse lesions (DL) [yes/no, n (%)] | 10 (22.2)/35 (77.8) | 35 (89.7)/4 (10.2) |
| Vascular calcification (VC) [yes/no, n (%)] | 3 (6.7)/42 (93.3) | 27 (69.2)/12 (30.7) |
| Slow coronary flow (SF) [yes/no, n (%)] | 1 (2.2)/44 (97.8) | 6 (15.3)/33 (84.6) |
| ST segment changes (STC) [yes/no, n (%)] | 0 (0.0)/45 (100.0) | 8 (20.5)/31 (79.4) |
6.2. Experimental analysis
To avoid experimental chance, each algorithm conducts ten classification tests in the same environment. Table 7 presents comprehensive simulation outcomes of CGALO-SVM-FS. The table enumerates the performance statistics of ten cross-validations, including ACC, sensitivity, MCC, F1-score, Kappa, and classification success index. Statistical analysis was conducted to assess the experimental results, with mean value and standard deviation metrics employed to evaluate the proposed model's average performance and algorithm stability, respectively. The experimental findings showcase that CGALO-SVM-FS classification yields an average (Avg) accuracy of 92%, sensitivity of 91%, specificity of 91%, MCC of 82%, F1 score of 88%, Kappa of 73%, and classification success index of 85%. The standard deviation (Std) results of each indicator of CGALO-SVM-FS are 0.073, 0.16, 0.12, 0.19, 0.22, 0.26 and 0.24 respectively, and the overall error fluctuation is relatively stable. Further, the results of other models are uniformly represented by histograms, as shown in Fig. 5. The accuracy, sensitivity, specificity and MCC are 89%, 90%, 88% and 78%, respectively. Through the feature selection operation, the accuracy of the model is effectively improved. In addition, the accuracies of ALO-SVM, kernel based extreme learning machine (KELM), random forest (RF) and artificial neural networks (ANN) models are 11%, 5%, 3% and 7% lower than CGALO-SVM-FS, respectively. It can be seen that the proposed CGALO-SVM-FS model has better classification results than existing methods. According to the analysis of the results of the above indicators, the overall accuracy of the proposed classifier and the consistency with the actual situation can be obtained. Table 8 shows the results of the two-tailed t-test for the comparison methods of CGAL-SVM-FS with other methods, including p-values, statistical t-values (t), and degrees of freedom (df). Further, the difference between CGALO-SVM-FS and CGALO-SVM is that the former uses feature selection, while the latter does not. The key features screened by FS in the experiment are shown in Fig. 6, in which the occurrence times of features SH, NV, PL, DL and STC are 8, 10, 9, 9, and 10, respectively, which can be used as a marker for classifying functional stenosis of coronary heart disease. key features.
Table 7.
Classification results of CGALO-SVM-FS about four metrics.
| Fold | ACC | Sensitivity | Specificity | MCC | F1-score | Kappa | Classification Success Index |
|---|---|---|---|---|---|---|---|
| 1 | 0.875 | 1 | 0.6667 | 0.7454 | 0.952 | 0.6206 | 0.895 |
| 2 | 0.8889 | 1 | 0.8 | 0.8 | 0.889 | 0.609 | 0.815 |
| 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 0.7778 | 0.5 | 0.8571 | 0.3571 | 0.288 | 0.219 | 0.25 |
| 5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 6 | 0.875 | 1 | 0.75 | 0.7746 | 1 | 0.625 | 1 |
| 7 | 0.8889 | 0.8571 | 1 | 0.7559 | 0.814 | 0.597 | 0.791 |
| 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 10 | 0.875 | 0.75 | 1 | 0.7746 | 0.837 | 0.676 | 0.7 |
| Avg | 0.92 | 0.91 | 0.91 | 0.82 | 0.88 | 0.73 | 0.85 |
| Std | 0.073 | 0.16 | 0.12 | 0.19 | 0.22 | 0.26 | 0.24 |
Fig. 5.
The mean value and standard deviation of compared methods.
Table 8.
The t-test results of the ACC of CGALO-SVM-FS and other methods.
| CGALO-SVM vs CGALO-SVM-FS | ALO-KELM vs CGALO-SVM-FS | KELM vs CGALO-SVM-FS | RF vs CGALO-SVM-FS | ANN vs CGALO-SVM-FS | |
|---|---|---|---|---|---|
| One or two-tailed P value | Two-tailed | Two-tailed | Two-tailed | Two-tailed | Two-tailed |
| t | 3.151 | 4.958 | 4.678 | 3.010 | 3.348 |
| df | 18 | 18 | 18 | 18 | 18 |
| P value | 0.0055 | 0.0001 | 0.0002 | 0.0075 | 0.0036 |
| Significantly different (P < 0.05) | Yes | Yes | Yes | Yes | Yes |
Fig. 6.
Feature selection results.
7. Discussion
FFR has become a consensus in the decision-making of CHD revascularization treatment. However, due to the limitations of being invasive and expensive, its clinical application is limited, and the clinical application varies greatly in different countries, with the promotion rate from less than 1% to nearly 20% [[70], [71], [72], [73]]. Taking CAG as the representative, imaging examination is still the main basis for decision-making of CHD intervention treatment in reality. Unfortunately, the severity of coronary artery stenosis and myocardial ischemia are not completely parallel. Studies have shown that 96% of patients with coronary artery stenosis more than 90% have myocardial ischemia, and only 80% of patients with coronary artery stenosis between 71% and 90% have myocardial ischemia; In 50%–70% of patients with stenosis, only 35% had myocardial ischemia [74].
In order to further improve the generalization of functional diagnosis of CHD, this study uses ML algorithm to build a FFR classification model. During variable selection, we consulted previous relevant studies on the factors affecting coronary functional stenosis. Tsukamoto et al. investigated the correlation between CHD's traditional risk factors, myocardial flow reserve (MFR), and the severity of coronary artery stenosis. The findings revealed that aside from the severity of coronary artery stenosis, smoking and diabetes exhibited a robust correlation [75]. Our study further verified the results. Smoking and diabetes may damage coronary artery endothelial cells and further affect coronary fluid dynamics. Gashi et al. explored the influence of geometric characteristics of coronary artery on the prediction of FFR, and the results showed that vascular curvature, lesion length, stenosis degree and other characteristics were correlated with FFR [76]. In our study, diffuse lesions and degree of vascular stenosis also showed a high characteristic frequency. In addition, considering that myocardial ischemia may lead to abnormal left ventricular systolic activity and further change of LVEF, we also included LVEF as a variable in the construction of the model. Our results show that LVEF has a good correlation with FFR, which is inconsistent with the results of Kobayashi et al. [77]. In addition, a meta-analysis of the effect of coronary artery calcification score on CT-FFR value carried out by Han et al. Showed that calcified lesions had a negative effect on CT-FFR [78]. In our results, coronary calcification did not show a high characteristic frequency. Theoretically, vascular wall calcification should have an impact on hemodynamics. This result may be related to the small number of samples in this study, which can be further demonstrated in the future.
This study has certain limitations, including a relatively small sample size and solely conducting internal validation. To establish the model's prediction accuracy, further research is required to expand the sample size and conduct external validation in the future. Second, this study did not include patients with FFR of coronary branches (eg, intermediate, septal, diagonal, etc.), and whether this model is applicable to such patients remains to be further demonstrated. In conclusion, the CGALO-based FFR intelligent classification model is a promising tool with potential value for coronary functional stenosis screening. This study preliminarily demonstrated that the model has good accuracy for the classification of coronary functional lesions. In the future, we can further improve the existing algorithm and explore more clinical data related to functional stenosis of CHD. With the establishment of large cardiac centers and the improvement of the CHD database, the clinical application of this study will be further evaluated. Undoubtedly, the proposed CGALO algorithm can be utilized in a broader spectrum of scenarios, such as optimization of machine learning models [79], iris or retinal vessel segmentation [80,81], service ecosystem [82], renewable energy generation [83], medical signals [84], MRI reconstruction [85], and computational experiments [86,87].
8. Conclusion and future work
This paper presents the Chaotic Gaussian Mutation Ant Lion Optimizer (CGALO) algorithm, paired with support vector machine (SVM) to develop a classification prediction model for fractional flow reserve (FFR). The incorporation of CGMALO to improve ALO algorithm convergence speed and accuracy overcomes limitations in the original ALO algorithm. To ascertain the proposed algorithm's performance, 11 additional advanced optimization algorithms were evaluated across 23 benchmark functions. Experimental outcomes reveal that the proposed algorithm outperforms the comparison algorithms concerning both convergence accuracy and speed. Furthermore, we combine the algorithm with SVM and feature selection (FS) to build a hierarchical flow reserve classification model and achieve effective prediction of 84 patients from Ningbo University. The experimental outcomes demonstrate that the proposed model attains an average accuracy of 92%. In addition, we find that smoking history, number of lesion vessels, lesion location, diffuse lesions and ST segment changes are the most critical indicators for FFR. Therefore, the established model is a new FFR intelligent classification prediction technology that can effectively assist doctors in making corresponding decisions and evaluation plans.
In future scientific investigations, the proposed CGALO algorithm can be applied to tackle more intricate problems, including but not limited to engineering optimization, image segmentation, parameter identification, and corporate bankruptcy prediction. In addition, the constructed model can also be used for classification and prediction of other diseases.
Data availability statement
The data involved in this study are all public data, which can be downloaded through public channels.
CRediT authorship contribution statement
Haoxuan Lu:Wrote the paper,Conceived and designed the experiments, Performed the experiments; Li Huang: Wrote the paper, Performed the experiments; Yanqing Xie: Wrote the paper, Analyzed and interpreted the data; Zhong Zhou: Performed the experiments; Hanbin Cui: Performed the experiments.
Sheng Jing: Contributed reagents, materials, analysis tools or data; Zhuo Yang: Analyzed and interpreted the data; Decai Zhu: Analyzed and interpreted the data; Shiqi Wang: Analyzed and interpreted the data; Donggang Bao: Analyzed and interpreted the data; Guoxi Liang: Analyzed and interpreted the data; Zhennao Cai: Analyzed and interpreted the data.
Huiling Chen: Wrote the paper,Conceived and designed the experiments, Performed the experiments, Analyzed and interpreted the data, Contributed reagents, materials, analysis tools or data; Wenming He: Wrote the paper,Conceived and designed the experiments, Performed the experiments, Analyzed and interpreted the data, Contributed reagents, materials, analysis tools or data.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This project is supported by Ningbo Natural Science Foundation (project ID No. 2021J240); General research program of Zhejiang Provincial Department of Health (project ID No. WKJZJ-2137) and Key R & D Program of Zhejiang (project ID No. 2023C04017).
Contributor Information
Guoxi Liang, Email: guoxiliang2017@gmail.com.
Huiling Chen, Email: chenhuiling.jlu@gmail.com.
Wenming He, Email: fyhewenSming@nbu.edu.cn.
Appendix.
Table A.
Description of 23 benchmark functions.
References
- 1.Chockalingam P., Natarajan V., Sekar T.J.E.H.J. 2022. A Survey-Based Comparison of Cardiovascular Health Risk Behaviours in Indian Men and Women during the Pandemic. [Google Scholar]
- 2.Jelmer W., et al. Diagnostic performance of in‐procedure angiography‐derived quantitative flow reserve compared to pressure‐derived fractional flow reserve. The FAVOR II Europe‐Japan Study. 2018;7(14) doi: 10.1161/JAHA.118.009603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Karp I., et al. Updated risk factor values and the ability of the multivariable risk score to predict coronary heart disease. Am. J. Epidemiol. 2004;160(7):707–716. doi: 10.1093/aje/kwh258. [DOI] [PubMed] [Google Scholar]
- 4.Pignone M., et al. Physicians' ability to predict the risk of coronary. Heart Dis. 2003;3(1):1–6. doi: 10.1186/1472-6963-3-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sun D., et al. ANOX: a robust computational model for predicting the antioxidant proteins based on multiple features. Anal. Biochem. 2021;631 doi: 10.1016/j.ab.2021.114257. [DOI] [PubMed] [Google Scholar]
- 6.Tian F., et al. Automatic coronary artery segmentation algorithm based on deep learning and digital image processing. Appl. Intell. 2021;51(12):8881–8895. [Google Scholar]
- 7.Sharma P., et al. Artificial plant optimization algorithm to detect heart rate & presence of heart disease using machine learning. Artif. Intell. Med. 2020;102 doi: 10.1016/j.artmed.2019.101752. [DOI] [PubMed] [Google Scholar]
- 8.Lv R., et al. Using optical coherence tomography and intravascular ultrasound imaging to quantify coronary plaque cap stress/strain and progression: a follow-up study using 3D thin-layer models. Front. Bioeng. Biotechnol. 2021;9 doi: 10.3389/fbioe.2021.713525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Liang D., et al. Coronary angiography video segmentation method for assisting cardiovascular disease interventional treatment. BMC Med. Imag. 2020;20(1):65. doi: 10.1186/s12880-020-00460-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Guo H., et al. Learning dynamic treatment strategies for coronary heart diseases by artificial intelligence: real-world data-driven study. BMC Med. Inf. Decis. Making. 2022;22(1):39. doi: 10.1186/s12911-022-01774-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Infante T., et al. Radiogenomics and artificial intelligence approaches applied to cardiac computed tomography angiography and cardiac magnetic resonance for precision medicine in coronary heart disease: a systematic review. Circ. Cardiovasc. Imag. 2021;14(12):1133–1146. doi: 10.1161/CIRCIMAGING.121.013025. [DOI] [PubMed] [Google Scholar]
- 12.Gruson D., et al. Collaborative AI and Laboratory Medicine integration in precision cardiovascular medicine. Clin. Chim. Acta. 2020;509:67–71. doi: 10.1016/j.cca.2020.06.001. [DOI] [PubMed] [Google Scholar]
- 13.Cui J., Song L. Wrist pulse diagnosis of stable coronary heart disease based on acoustics waveforms. Comput. Methods Progr. Biomed. 2022;214 doi: 10.1016/j.cmpb.2021.106550. [DOI] [PubMed] [Google Scholar]
- 14.Kusuma S., R D.-J.-K. Heart disease classification using multiple K-pca and hybrid deep. Learning Approach. 2022;41(3):1273–1289. [Google Scholar]
- 15.Mohamed A.-T., Santhoshkumar S. Deep learning based process analytics model for predicting type 2 diabetes. Mellitus. 2022;40(1):191–205. [Google Scholar]
- 16.Jamthikar A.D., et al. Artificial intelligence framework for predictive cardiovascular and stroke risk assessment models: a narrative review of integrated approaches using carotid ultrasound. Comput. Biol. Med. 2020;126 doi: 10.1016/j.compbiomed.2020.104043. [DOI] [PubMed] [Google Scholar]
- 17.Wang K., et al. Interpretable prediction of 3-year all-cause mortality in patients with heart failure caused by coronary heart disease based on machine learning and SHAP. Comput. Biol. Med. 2021;137 doi: 10.1016/j.compbiomed.2021.104813. [DOI] [PubMed] [Google Scholar]
- 18.Dutta A., et al. An efficient convolutional neural network for coronary heart disease prediction. Expert Syst. Appl. 2020;159 [Google Scholar]
- 19.Huang C., et al. A deep segmentation network of multi-scale feature fusion based on attention mechanism for IVOCT lumen contour. IEEE ACM Trans. Comput. Biol. Bioinf. 2021;18(1):62–69. doi: 10.1109/TCBB.2020.2973971. [DOI] [PubMed] [Google Scholar]
- 20.Huang H., et al. An integrated model for medical expense system optimization during diagnosis process based on artificial intelligence algorithm. J. Combin. Optim. 2021:1–18. doi: 10.1007/s10878-021-00761-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang Z., et al. Application of CT coronary flow reserve fraction based on deep learning in coronary artery diagnosis of coronary heart disease complicated with diabetes mellitus. Neural Comput. Appl. 2022;34(9):6763–6772. [Google Scholar]
- 22.Mirjalili S. The ant lion optimizer. Adv. Eng. Software. 2015;83:80–98. [Google Scholar]
- 23.Yang Y., et al. Hunger games search: visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Syst. Appl. 2021;177 [Google Scholar]
- 24.Ahmadianfar I., et al. INFO: an efficient optimization algorithm based on weighted mean of vectors. Expert Syst. Appl. 2022 [Google Scholar]
- 25.Ahmadianfar I., et al. Expert Systems with Applications; 2021. RUN beyond the Metaphor: an Efficient Optimization Algorithm Based on Runge Kutta Method. [Google Scholar]
- 26.Tu J., et al. The colony predation algorithm. JBE. 2021;18(3):674–710. [Google Scholar]
- 27.Chen H., et al. Slime mould algorithm: a comprehensive review of recent variants and applications. Int. J. Syst. Sci. 2022:1–32. [Google Scholar]
- 28.Li S., et al. Slime mould algorithm: a new method for stochastic optimization. Future Generat. Comput. Syst. 2020;111:300–323. [Google Scholar]
- 29.Heidari A.A., et al. Harris hawks optimization: algorithm and applications. Future Gener. Comp. Sys. Int. J. Esci. 2019;97:849–872. [Google Scholar]
- 30.Su H., et al. Neurocomputing; 2023. RIME: A Physics-Based Optimization. [Google Scholar]
- 31.Zhang Y., et al. Towards augmented kernel extreme learning models for bankruptcy prediction: algorithmic behavior and comprehensive analysis. Neurocomputing. 2021;430:185–212. [Google Scholar]
- 32.Deng W., et al. An enhanced MSIQDE algorithm with novel multiple strategies for global optimization problems. IEEE Transact. Sys. ManCybern.: Systems. 2022;52(3):1578–1587. [Google Scholar]
- 33.Sun G., et al. Swarm and Evolutionary Computation; 2023. Hierarchical Structure-Based Joint Operations Algorithm for Global Optimization. [Google Scholar]
- 34.Liang J., et al. Utilizing the relationship between unconstrained and constrained pareto fronts for constrained multiobjective optimization. IEEE Trans. Cybern. 2022:1–14. doi: 10.1109/TCYB.2022.3163759. [DOI] [PubMed] [Google Scholar]
- 35.Sun G., Yang G., Zhang G. Two-level parameter cooperation-based population regeneration framework for differential evolution. Swarm Evol. Comput. 2022;75 [Google Scholar]
- 36.Li C., et al. A population state evaluation-based improvement framework for differential evolution. Inf. Sci. 2023;629:15–38. [Google Scholar]
- 37.Sun G., Li C., Deng L. An adaptive regeneration framework based on search space adjustment for differential evolution. Neural Comput. Appl. 2021;33:9503–9519. [Google Scholar]
- 38.Wen X., et al. A two-stage solution method based on NSGA-II for Green Multi-Objective integrated process planning and scheduling in a battery packaging machinery workshop. Swarm Evol. Comput. 2021;61 [Google Scholar]
- 39.Wang G., et al. Mobile Information Systems; 2022. Research on Vessel Speed Heading and Collision Detection Method Based on AIS Data. [Google Scholar]
- 40.Huang C., et al. Co-evolutionary competitive swarm optimizer with three-phase for large-scale complex optimization problem. Inf. Sci. 2023;619:2–18. [Google Scholar]
- 41.Liu Y., et al. Simulated annealing-based dynamic step shuffled frog leaping algorithm: optimal performance design and feature selection. Neurocomputing. 2022;503:325–362. [Google Scholar]
- 42.Xue Y., Xue B., Zhang M. Self-adaptive particle swarm optimization for large-scale feature selection in classification. ACM Trans. Knowl. Discov. Data. 2019;13(5):1–27. [Google Scholar]
- 43.Xue Y., Cai X., Neri F. A multi-objective evolutionary algorithm with interval based initialization and self-adaptive crossover operator for large-scale feature selection in classification. Appl. Soft Comput. 2022;127 [Google Scholar]
- 44.Wang X., et al. Crisscross Harris hawks optimizer for global tasks and feature selection. JBE. 2022:1–22. doi: 10.1007/s42235-022-00298-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Shan W., et al. Multi-strategies boosted mutative crow search algorithm for global tasks: cases of continuous and discrete optimization. JBE. 2022;19(6):1830–1849. [Google Scholar]
- 46.Zhao C., Zhou Y., Lai X. An integrated framework with evolutionary algorithm for multi-scenario multi-objective optimization problems. Inf. Sci. 2022;600:342–361. [Google Scholar]
- 47.Dong R., et al. Boosted kernel search: framework, analysis and case studies on the economic emission dispatch problem. Knowl. Base Syst. 2021;233 [Google Scholar]
- 48.Xue Y., Tong Y., Neri F. An ensemble of differential evolution and Adam for training feed-forward neural networks. Inf. Sci. 2022;608:453–471. [Google Scholar]
- 49.Zhao D., et al. Chaotic random spare ant colony optimization for multi-threshold image segmentation of 2D Kapur entropy. Knowl. Base Syst. 2021;216 [Google Scholar]
- 50.Wang X., et al. Multi-population following behavior-driven fruit fly optimization: a Markov chain convergence proof and comprehensive analysis. Knowl. Base Syst. 2020;210 [Google Scholar]
- 51.Chen H., et al. Multi-population differential evolution-assisted Harris hawks optimization: framework and case studies. Future Generat. Comput. Syst. 2020;111:175–198. [Google Scholar]
- 52.Wang M., et al. Toward an optimal kernel extreme learning machine using a chaotic moth-flame optimization strategy with applications in medical diagnoses. Neurocomputing. 2017;267:69–84. [Google Scholar]
- 53.Zhang, et al. 2019. Antlion Optimizer Algorithm Based on Chaos Search and its Application. [Google Scholar]
- 54.Hadikhani P., Lai D., Ong W.H.J. 2022. A Novel Skeleton-Based Human Activity Discovery Technique Using Particle Swarm Optimization with Gaussian Mutation. [Google Scholar]
- 55.Saunders C., et al. Support Vector Machine. 2002;1(4):1–28. [Google Scholar]
- 56.Digalakis J.G., Margaritis K.G. On benchmarking functions for genetic algorithms. Int. J. Comput. Math. 2001;77(4):481–506. [Google Scholar]
- 57.Xin Y., Yong L., Guangming L. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999;3(2):82–102. [Google Scholar]
- 58.Chen W.N., et al. Particle swarm optimization with an aging leader and challengers. IEEE Trans. Evol. Comput. 2013;17(2):241–258. [Google Scholar]
- 59.Cao Y., et al. Comprehensive learning particle swarm optimization algorithm with local search for multimodal functions. IEEE Trans. Evol. Comput. 2019;23(4):718–731. [Google Scholar]
- 60.Elaziz M.A., et al. 2021. Code_identifying Integer and Fractional Order PV Models by HCLPSO. [Google Scholar]
- 61.Mirjalili S., Mirjalili S.M., Lewis A. Grey wolf optimizer. Adv. Eng. Software. 2014;69:46–61. [Google Scholar]
- 62.Mirjalili S., Mirjalili S.M., Hatamlou A. Multi-Verse Optimizer: a nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016;27(2):495–513. [Google Scholar]
- 63.Storn R., Price K. Differential evolution - a simple and efficient heuristic for global optimization over continuous spaces. J. Global Optim. 1997;11(4):341–359. [Google Scholar]
- 64.Karaboga D., J.o B.J., Basturk G.O. 2007. A Powerful And Efficient Algorithm For Numerical Function Optimization: Artificial Bee Colony (ABC) Algorithm; pp. 459–471. 39(3) [Google Scholar]
- 65.Li S., et al. 111 aliasgharheidari. com; 2020. pp. 300–323. (Slime Mould Algorithm: A New Method for Stochastic Optimization). [Google Scholar]
- 66.Mirjalili S. SCA: a Sine Cosine Algorithm for solving optimization problems. Knowl. Base Syst. 2016;96:120–133. [Google Scholar]
- 67.Mirjalili S. Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl. Base Syst. 2015;89:228–249. [Google Scholar]
- 68.Tubishat M., et al. Improved whale optimization algorithm for feature selection in Arabic sentiment analysis. Appl. Intell. 2019;49(5):1688–1707. [Google Scholar]
- 69.Yong J., et al. Proceedings of the 2018 IEEE 22nd International Conference on Computer Supported Cooperative Work in Design. CSCWD; 2018. A novel bat algorithm based on collaborative and dynamic learning of opposite population. [Google Scholar]
- 70.Härle T., et al. 2016. Real-World Use Of Fractional Flow Reserve In Germany: Results Of The Prospective ALKK Coronary Angiography And PCI Registry; pp. 1–11. 106(2) [DOI] [PubMed] [Google Scholar]
- 71.Gudnason T., et al. Comparison of interventional cardiology in two European countries. Nationwide Int. Bas. Reg. Study. 2013;168(2):1237–1242. doi: 10.1016/j.ijcard.2012.11.054. [DOI] [PubMed] [Google Scholar]
- 72.Parikh R.V., et al. Utilization and outcomes of measuring fractional flow reserve in patients with stable ischemic. Heart Dis. 2020;75(4):409–419. doi: 10.1016/j.jacc.2019.10.060. [DOI] [PubMed] [Google Scholar]
- 73.Fr?Hlich G.M., et al. 2014. Long-Term Survival In Patients Undergoing Percutaneous Interventions With Or Without Intracoronary Pressure Wire Guidance Or Intracoronary Ultrasonographic Imaging: A Large Cohort Study; pp. 1360–1366. 174(8) [DOI] [PubMed] [Google Scholar]
- 74.Pijls N.H.J., et al. 2010. Fractional Flow Reserve Versus Angiography For Guiding Percutaneous Coronary Intervention In Patients With Multivessel Coronary Artery Disease: 2-Year Follow-Up Of The FAME (Fractional Flow Reserve Versus Angiography For Multivessel Evaluation) Study; pp. 177–184. 56(3) [DOI] [PubMed] [Google Scholar]
- 75.Tsukamoto T., et al. 2006. Myocardial Flow Reserve Is Influenced By Both Coronary Artery Stenosis Severity And Coronary Risk Factors In Patients With Suspected Coronary Artery Disease; pp. 1150–1156. 33(10) [DOI] [PubMed] [Google Scholar]
- 76.Gashi K., Bosboom E., Vosse F.J.J.o.B. 2018. The Influence of Model Order Reduction on the Computed Fractional Flow Reserve Using Parameterized Coronary Geometries; p. 82. [DOI] [PubMed] [Google Scholar]
- 77.De, et al. 2016. The Impact of Left Ventricular Ejection Fraction on Fractional Flow Reserve: Insights from the FAME (Fractional Flow Reserve versus Angiography for Multivessel Evaluation) Trial. [DOI] [PubMed] [Google Scholar]
- 78.Han D., et al. Influence of coronary artery calcium score on the diagnostic performance of computed tomography angiography derived fractional flow reserve. A Meta-analysis. 2020;14(3) doi: 10.1016/j.jcmg.2020.09.022. [DOI] [PubMed] [Google Scholar]
- 79.Zhao C., et al. JAMSNet: a remote pulse extraction network based on joint attention and multi-scale fusion. IEEE Trans. Circ. Syst. Video Technol. 2022:1. [Google Scholar]
- 80.Chen Y., et al. Accurate iris segmentation and recognition using an end-to-end unified framework based on MADNet and DSANet. Neurocomputing. 2023;517:264–278. [Google Scholar]
- 81.Li Y., et al. Dual encoder-based dynamic-channel graph convolutional network with edge enhancement for retinal vessel segmentation. IEEE Trans. Med. Imag. 2022;41(8):1975–1989. doi: 10.1109/TMI.2022.3151666. [DOI] [PubMed] [Google Scholar]
- 82.Xue X., et al. Research roadmap of service ecosystems: a crowd intelligence perspective. Int. J. Crowd Sci. 2022;6(4):195–222. [Google Scholar]
- 83.Sun X., et al. Multistage dynamic planning of integrated hydrogen-electrical microgrids under multiscale uncertainties. IEEE Trans. Smart Grid. 2022:1. [Google Scholar]
- 84.Dai Y., et al. MSEva: a musculoskeletal rehabilitation evaluation system based on EMG signals. ACM Trans. Sens. Netw. 2022;19(1):1–23. [Google Scholar]
- 85.Lv J., et al. Transfer learning enhanced generative adversarial networks for multi-channel MRI reconstruction. Comput. Biol. Med. 2021;134 doi: 10.1016/j.compbiomed.2021.104504. [DOI] [PubMed] [Google Scholar]
- 86.Xue X., et al. Computational experiments: past, present and future. arXiv preprint arXiv. 2022;2202 [Google Scholar]
- 87.Xue X., et al. Computational experiments for complex social systems—Part III: the docking of domain models. IEEE Trans. Comput. Soci. Sys. 2023:1–15. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data involved in this study are all public data, which can be downloaded through public channels.