Experimental design and power calculation in omics circadian rhythmicity detection using the cosinor model

Summary

Circadian clocks are 24-hour endogenous oscillators in physiological and behavioral processes. Though recent transcriptomic studies have been successful in revealing the circadian rhythmicity in gene expression, the power calculation for omics circadian analysis have not been fully explored. In this paper, we develop a statistical method, namely CircaPower, to perform power calculation for circadian pattern detection. Our theoretical framework is determined by three key factors in circadian gene detection: sample size, intrinsic effect size and sampling design. Via simulations, we systematically investigate the impact of these key factors on circadian power calculation. We not only demonstrate that CircaPower is fast and accurate, but also show its underlying cosinor model is robust against variety of violations of model assumptions. In real applications, we demonstrate the performance of CircaPower using mouse pan-tissue data and human post-mortem brain data, and illustrate how to perform circadian power calculation using mouse skeleton muscle RNA-Seq pilot as case study. Our method CircaPower has been implemented in an R package, which is made publicly available on GitHub (https://github.com/circaPower/circaPower).

1 |. INTRODUCTION

Circadian rhythms are endogenous ~24 hour oscillations of behavior, physiology, and homeostasis in adaption to the diurnal cycle caused by the earth’s daily rotation. The circadian clock is found in virtually all cells throughout the body and controls oscillations in a wide variety of physiological processes, including sleep-wake cycles, body temperature, and melatonin secretion^1,2,3,4. From the literature, the mechanism that drives circadian rhythms is a transcriptionial-translational feedback loop encoded by a set of core clock genes 5, including CLOCK, BMAL1 as the transcriptional activators; and period family (PER1, PER2, PER3) and cryptochrome family (CRY1, CRY2) as the major inhibitors. In addition to core clock genes, genome-wide transcriptomic studies have revealed additional circadian genes in post-mortem brain^6,7, skeletal muscle⁸, liver⁹, and blood¹⁰. Transcriptomic circadian analyses in human¹¹, mouse¹², and baboon¹³ have shown that the circadian pattern in gene expression could be tissue-specific. Beyond transcriptomic data, circadian rhythmicity was also discovered in other types of omics data including DNA methylation¹⁴, ChIP-Seq (chromatin immunoprecipitation assays with sequencing)¹⁵, proteomics¹⁶, and metabolomics¹⁷. From epidemiology and animal studies, the disruption in clock and circadian gene expression was found to be linked to diseases including type 2 diabetes¹⁸, cancer^19,20, sleep¹⁰, major depression disorder²¹, aging⁶, schizophrenia⁷, and Alzheimer’s disease²².

As the circadian omics studies have become increasingly popular over the years (Figure. 1), the experimental design of such circadian omics studies has come into focus^23,24, where the design refers to the distribution of the collected Zeitgeber time (ZT; standardized diurnal time with ZT0/ZT24 for the beginning of day and ZT12 for the beginning of night). In this paper, we consider two types of sampling design: passive and active sampling design. In passive design, investigators have no control of the collected ZT. Such a passive design is commonly seen in studies with human tissues that are difficult to obtain (e.g., post-mortem brain tissues^6,7,21) and the irregular sampling distribution should be considered in power calculation. In contrast, investigators have full control of the sample collection time in an active sampling design. Such an active design is commonly seen in animal studies 12 or human blood studies 10. In the literature, 6 time points (every 4 hours) per cycle across one or multiple full cycles have been widely adopted in many actively designed studies^25,26,27. Hughes et al.²⁸ recommended evenly sampling at least 12 time points per cycle (i.e., every 2 hours) across 2 full cycles. For the ease of discussion, we refer to this type of design as the “evenly-spaced sampling design”. Though these empirical practices and guidelines were presented and well-received, limited quantitative benchmarks are available. To address this, Ness-Cohn et al.²⁹ developed a user-friendly website, TimeTrial, which allows researchers to explore the effects of experimental design on cycling detection. Although multiple circadian detection methods are allowed, the results are benchmarked through simulation using classification error rate and area under the curve of a ROC curve. However, a statistical method that enables exact power calculation is still lacking. Previous studies have reported the lack of overlapping circadian genes because of smaller number of samples^9,30, indicating statistical power, i.e., the probability of successfully detecting the underlying circadian pattern, is not fully considered/justified. Thus, an analytical method that allows exact power calculation under different experimental designs is urgently needed. In addition, all these prior works on circadian study design were discussed within the scope of active design, where investigators have control of sample collection time. In the scope for passive design, there are no guidelines in the literature. It is unclear whether and how the irregular ZT distribution will impact the circadian power calculation.

Figure 1.

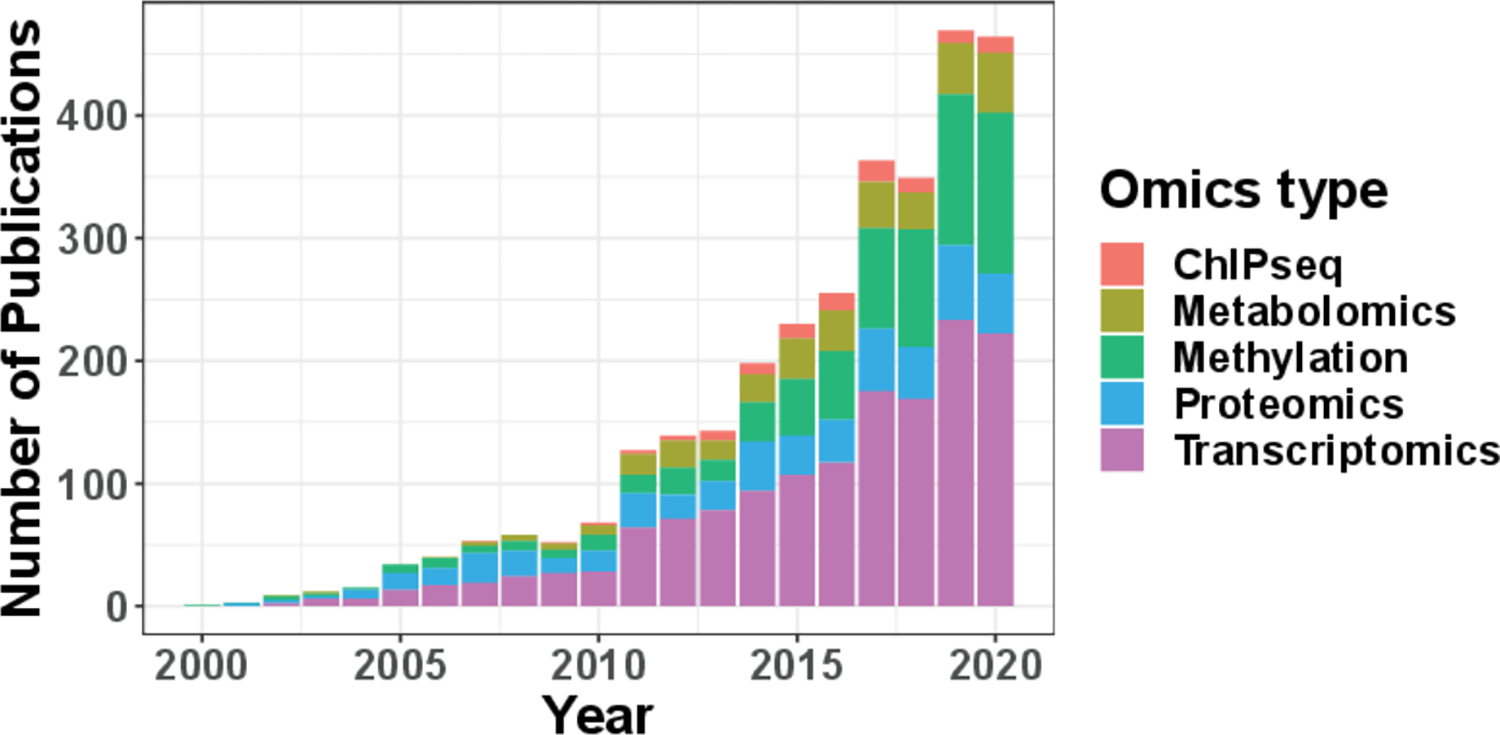
Annual number of publications on PubMed that contain the keywords “circadian/clock” and one of the following omics type: “ChIPseq”, “Metabolomics”, “Methylation”, “Proteomics”, “Transcriptomics”.

To fill in these research gaps, we propose a model-based approach to accurately calculate the circadian power (namely CircaPower), based on the cosinor model^31,32. It assumes the expression level of a gene is a sinusoidal function of the circadian time 31. The biological rationale for using a cosinor model is that the circadian rhythm is amenable to adapt the cycles in the environment⁵, including the day-light cycle, the tides, the phases of the moon, the seasons, etc³³. Since the day-light cycle is the leading environmental factor that governs circadian rhythms, a cosinor wave model is widely used to mimic the cosinor cycle of the day-light intensity and many previous literatures^6,7,34 have used this model to identify biological meaningful findings. In the literature, there are several other algorithms developed for circadian rhythm detection. Lomb-Scargle periodograms ³⁵ and COSOPT³⁶ are more complicated parametric models. By assuming mixture of multiple cosinor curves with distinct periods, these methods facilitate the detection of oscillating transcripts with irregular shape. ARSER³⁷, RAIN³⁸ and JTK CYCLE³⁹ are non-parametric methods, which are free of modeling assumption and more powerful to capture irregular curve shapes. Both parametric and non-parametric algorithms were widely applied in transcriptomic studies, and comparisons of these algorithms have been conducted in several review studies^28,24,40,41. Although the complex methods have advantages to detect irregular curves beyond cosinor models, the power calculation using these methods are not always feasible since the effect size and data variability are not explicitly defined in these models. In addition, concerns about the accuracy of the statistical inference for these complex methods have been raised41. To be specific, the p-values generated by many of these methods may not be correct (i.e., do not follow a uniform distribution (0, 1) under the null), implying a potential inflated or deflated type I error rate. Therefore, we propose the power calculation framework based on the cosinor model, because of its flexibility in deriving closed-form test statistics and accurate statistical inference. We acknowledge that other complex parameters models and non-parametric approaches are also popular with their own unique merit, and exploring circadian power calculation using these complex methods is one of our future directions.

To the best of our knowledge, this is the first theoretical methodology developed for circadian power calculation in omics data. The unique contribution of this paper includes: (i) identifying factors related to the statistical power of circadian rhythmicity detection, including sample size, intrinsic effect size and sampling design; (ii) developing CircaPower, an analytical solution based on a closed-form formula, for fast and accurate circadian power calculation; (iii) demonstrating via simulations that the evenly-spaced sampling design is superior because of its phase-invariant property, which is also corroborated by theoretical proofs; (iv) illustrating how to calculate statistical power and to design a circadian experiment with pilot data via a case study; (v) collecting, calculating, and summarizing the intrinsic effect sizes of existing human and animal studies, which serves as a useful reference resource when no pilot data is available; and (vi) providing an open-source R package.

The superior performance of our method is demonstrated in comprehensive simulation studies, as well as multiple transcriptomic applications in human and mouse. We demonstrate the performance of CircaPower using continuous gene expression data throughout this manuscript, but our method is also applicable in single biomarker data or other types of continuous omics data, including but not restricted to ChIP-Seq, DNA methylation, proteomics, and metabolomics.

2 |. METHODS

The CircaPower framework assumes the relationship of the expression level (continuous data type) of a gene and the Zeitgeber time (ZT) fits a sinusoidal wave curve, and is based on the $F$ statistics of a cosinor model³¹. Below we introduce the model notations, the construction of the $F$ statistics, the null and alternative distribution of the $F$ statistics, the closed-form formula for circadian power calculation, and factors affecting the power calculation of circadian rhythmicity detection.

2.1 |. Notations and basic model

As illustrated in Figure. 2a denote $y$ as a cosine function of $t$ (i.e., $y_i=A\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega \left(t_i-\varphi \right)\right)+M)$; $t$ as the ZT; $M$ as the MESOR (Midline Estimating Statistic Of Rhythm, a rhythm-adjusted mean); $A$ as the amplitude. $\omega$ is the frequency of the sinusoidal wave, where $\omega =\frac{2\pi }{Period}$. Without loss of generality, we set period $Period=24$ hours to mimic the diurnal period. $\varphi$ is the phase shift of the sinusoidal wave curve. Whenever there is no ambiguity, we will omit the unit “hours” in period, phase, and other related quantities. Due to the periodicity of a sinusoidal wave, $\left({\varphi }_1,{\varphi }_2\right)$ are not identifiable when ${\varphi }_1={\varphi }_2+24$. Therefore, we will restrict $\varphi \in [0,24)$. Under the current cosine formula, $\varphi$ also denotes the peak time $t_P$.

Figure 2.

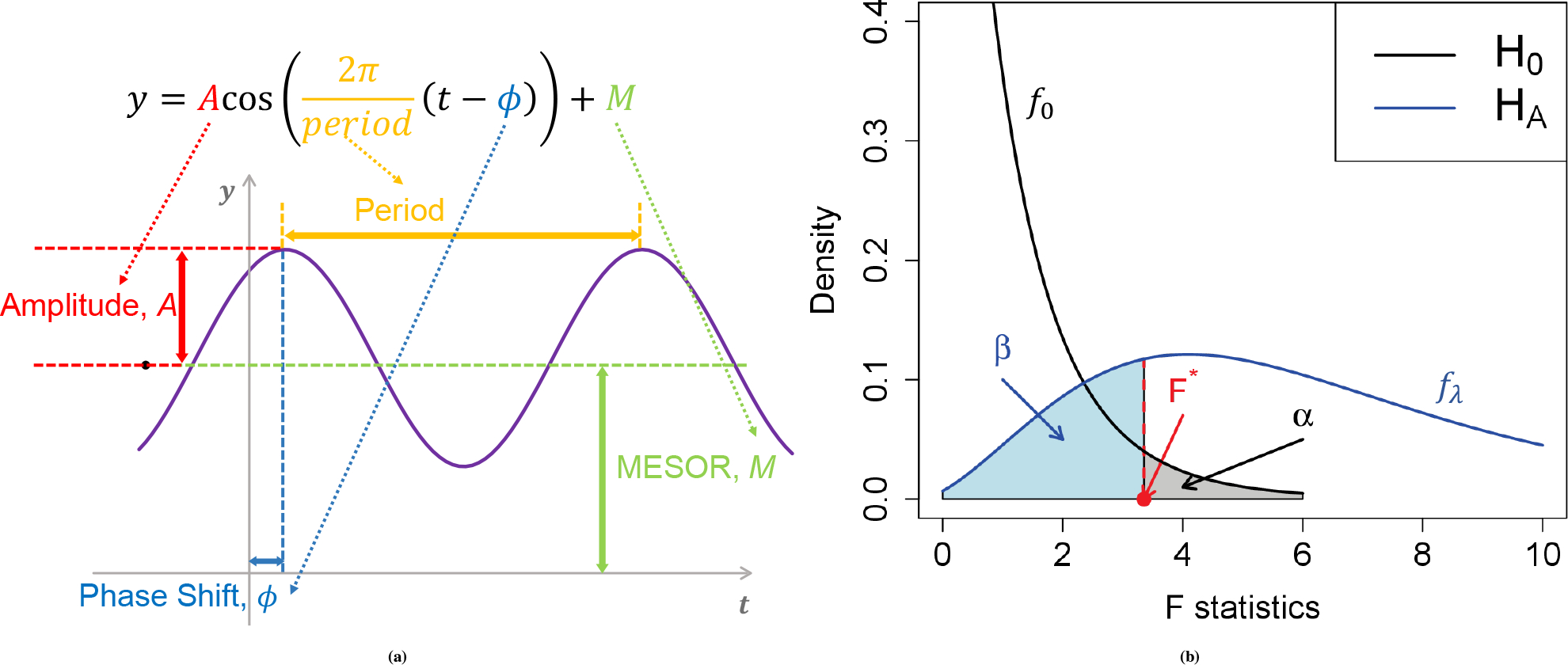
Basic sinusoidal model and the power/type I error discriminatory curve. (a) shows a sinusoidal wave curve underlying circadian rhythmicity power calculation framework. (b) shows the relationship between power and type I control in detecting circadian rhythmicity. The black curve represents the density function $f_0(\cdot \mid 2,n-3)$ of the $F$ statistics under the null distribution (no circadian pattern) whose expectation is $\frac{n-3}{n-5}$; the blue curve represents the density function $f_{\lambda }(\cdot \mid 2,n-3)$ of the $F$ statistics under the alternative distribution whose expectation is $\frac{(\lambda +2)(n-3)}{2(n-5)}$. The difference in expectation between $f_{\lambda }(\cdot \mid 2,n-3)$ and $f_0(\cdot \mid 2,n-3)$ is $\frac{\lambda (n-3)}{2(n-5)}$. The red dashed line represents the decision boundary (i.e., $F^{\mathrm{*}}$) such that the type I error rate is controlled at $\alpha$ (shaded gray). The corresponding type II error $\beta$ is the area with lightblue color and the detection power is $1-\beta$.

For a given sample $i(1\le i\le n$, $n$ is the total number of samples), denote by $y_i$ the expression value of a gene and $t_i$ the observed ZT. We assume the following sinusoidal wave function:

$$y_i=A\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega \left(t_i-\varphi \right)\right)+M+{\epsilon }_i,$$ (1)

where ${\epsilon }_i$ is the error term for sample $i$; we assume ${\epsilon }_i$ ‘s are identically and independently distributed (i.i.d.) from ${\epsilon }_i~N\left(0,{\sigma }^2\right)$, where $\sigma$ is the noise level. To benchmark the goodness of sinusoidal wave fitting, we define the coefficient of determination

$$R^2=1-\frac{RSS}{TSS}$$

where $RSS={\sum }_{i=1}^n {\left(y_i-{\hat{y}}_i\right)}^2$, $TSS={\sum }_{i=1}^n {\left(y_i-\bar{y}\right)}^2$, ${\hat{y}}_i=\hat{A}\mathrm{s}\mathrm{i}\mathrm{n}(\omega (t_i+\hat{\varphi }))+\hat{M}$, $\bar{y}={\sum }_i y_i/n$, with $\hat{A}$, $\hat{\varphi }$, and $\hat{M}$ being the fitted value for $A$, $\varphi$, and $M$ in Equation 1 under least squares loss. $R^2$ ranges from 0 to 1, with 1 indicating perfect sinusoidal wave fitting, and 0 indicating no fitting at all. Denote $H_1=A\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega \varphi \right)$, $H_2=A\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega \varphi \right)$. Equivalently, we could re-write Equation 1 as

$$y_i=H_1\sin \left(\omega t_i\right)+H_2\cos \left(\omega t_i\right)+M+{\epsilon }_i,$$ (2)

where $H_1=A\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega \varphi \right)$, and $H_2=A\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega \varphi \right)$, which turns into a linear regression problem.

According to the linear model theory, the $F$ statistics $\left(F^{stat}\right.)$ for the circadian model in Equation 1 can be derived as

$$F^{stat}=\frac{\frac{TSS-RSS}{r-1}}{\frac{RSS}{n-r}},$$ (3)

where $n$ is number of independent samples, $r=3$ is number of parameters (i.e., $A,\varphi$, and $M$ in Equation 1.

2.2 |. Power calculation

2.2.1 |. Analytical power calculation

Under the null hypothesis of no circadian fitting (i.e., $H_1=H_2=0$ in Equation 1), from the linear model theory, $F^{stat}~f_0\left(\cdot \mid 2,n-3\right.)$, where $f_0\left(\cdot \mid d{f}_1,d{f}_2\right)$ denotes a regular $\mathrm{F}$ distribution with degrees of freedom $d{f}_1$ and $d{f}_2$ (see Appendix A.1 for details). Under the alternative hypothesis (i.e., $H_1\ne 0$ or $H_2\ne 0$ in Equation 11), $F^{stat}~f_{\lambda }(\cdot \mid 2,n-3)$, where $f_{\lambda }\left(\cdot \mid d{f}_1,d{f}_2\right)$ denotes a non-central F distribution with with noncentrality parameter $\lambda =\frac{A^2}{{\sigma }^2}{\sum }_i {\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(w\left(t_i-\varphi \right)\right)$ (see Appendix A.2 for details). Figure. 2b shows the relationship between the null and alternative distributions of the $F$ statistics for the circadian model. By assuming the type I error rate at the rejection boundary $F^{\mathrm{*}}$ is $\alpha$, the relationship between $\alpha$ and the power $1-\beta$ is

$$F_{\lambda }^{-1}(\beta \mid 2,n-3)=F_0^{-1}(1-\alpha \mid 2,n-3),$$

where $F_{\lambda }\left(x\mid d{f}_1,d{f}_2\right)$ represents cumulative density function of $f_{\lambda }\left(\cdot \mid d{f}_1,d{f}_2\right)$ evaluated at $x$, and $F_0\left(x\mid d{f}_1,d{f}_2\right)$ represents cumulative density function of $f_0\left(\cdot \mid d{f}_1,d{f}_2\right.)$ evaluated at $x$ (see Appendix A for details).

As shown in the caption of Figure. 2b the non-centrality parameter $\lambda$ controls the degree of separation of the null distribution $f_0$ and the alternative distribution $f_{\lambda }$. The larger the $\lambda$ is, the more likely the alternative distribution will be away from the null distribution, and the higher power a gene will achieve. We thus define $\lambda$ as the total effect size for the circadian power calculation. By inspecting the total effect size $\lambda =\frac{A^2}{{\sigma }^2}\times n\times \frac{1}{n}{\sum }_{i=1}^n {\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(w\left(t_i-\varphi \right)\right)$, this non-centrality parameter can be decomposed into three parts: (i) sample size $n$, (ii) intrinsic effect size $r=A/\sigma$ (closely relate to the goodness of fit statistics $R^2$), and (iii) sampling design effect $d=\frac{1}{n}{\sum }_{i=1}^n {\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(w\left(t_i-\varphi \right)\right)$. We then discuss the impact of each of these components on the circadian rhythmicity power calculation:

1. Sample size: As expected, given fixed $d$ and $r$, a larger sample size $n$ will result in a larger total effect size $\lambda$, and achieve a higher statistical power.

2. Intrinsic effect size: Intuitively, a larger circadian amplitude $A$ with smaller residual variability $\sigma$ will lead to a better sinusoidal curve fitting (i.e. larger $R^2$). Our formula suggests that circadian fitting parameters $A$ and $\sigma$ work together as an intrinsic effect size $r=A/\sigma$ and has a quadratic effect on the total effect size $\lambda$.

3. Sampling design effect: The sampling design effect $d=\frac{1}{n}{\sum }_{i=1}^n {\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(w\left(t_i-\varphi \right)\right)$ is more complicated, because it involves both observed $t_i$ and the unknown parameter phase shift $\varphi$. It should be noted that the values of $t_i$ can either be unique, meaning that each sample $i$ has a distinct circadian time, or replicated, indicating that several replicates are taken at each time point. In general, given an arbitrary circadian sampling design, we need to estimate $\varphi$ before performing power calculation. Fortunately, the power calculation for the evenly-spaced sampling design is independent of the phase value (i.e., phase-invariant). For example, Hughes et al.²⁸ recommended a collection of 12 time points (every 2 hours) per cycle across 2 full cycles, which belongs to the evenly-spaced sampling design. Such active design is commonly seen in animal studies or human blood studies, where researchers can control the exact time to sacrifice the animal or to collect blood. The following theorem (phase-invariant property) shows that the sampling design effect $d$ is a constant under the one-period one-sample evenly-spaced design, i.e., $t_i^{\prime }s$ are evenly spread within one period with only one sample per time point.

Theorem 1

(Phase-invariant property - one-period one-sample). Assuming there is a total of $n$ ZT points $t_i(1\le i\le n)$ within a circadian period $2\pi /\omega$, which are ordered such that $t_i<t_{i+1}$ for all $1\le i\le n-1$. If $n\ge 3$, and $t_i$ is evenly-spaced over the period (i.e., $t_{i+1}-t_i=C$ for all $1\le i\le n-1$, $C>0$ is a fixed time interval, $\left(t_1+2\pi /\omega \right)-t_n=C)$, then regardless of the value for $\varphi$, we have

$$\frac{1}{n}\sum _{i=1}^n {\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(w\left(t_i-\varphi \right)\right)=\frac{1}{2}$$

The proof is given in Appendix B It can immediately be extended to the following corollary.

Corollary 1

(Phase-invariant property - multi-period multi-sample). For multi-period (two or more cycles) multi-sample evenly-spaced design, the sampling design effect is phase-invariant.

$$\frac{1}{n}\sum _{i=1}^n {\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(w\left(t_i-\varphi \right)\right)=\frac{1}{2}$$

This is because the multi-period multi-sample evenly-spaced design just replicates the one-period one-sample evenly-spaced design, therefore the average of them remains to be 1/2.

Remark 1.

The even spread/space design invariance property is a mathematical derivation resulting from the equation $\frac{1}{n}{\sum }_{i=1}^n {\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(w\left(t_i-\varphi \right)\right)=\frac{1}{2}$, which holds true regardless of the phase. The intuition behind this is based on the cosinor function’s curvatures, which dictate that the sample’s contribution to power is more significant when $t_i$ is at a peak or trough, resulting in ${\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(w\left(t_i-\varphi \right)=1\right.$, and less significant when $t_i$ is at MESOR, resulting in ${\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(w\left(t_i-\varphi \right)=0\right.$. If the samples are evenly distributed across the period, their effects will be even out when averaged over, and the final sampling design effect $d=\frac{1}{2}$.

2.2.2 |. Assumptions underlying the circadian modeling framework

The proposed circadian modeling framework has two underlying assumptions: (i) the relationship between the expression level of a gene and the ZT follows a sinusoidal wave curve; (ii) the error terms of each sample on top of the sinusoidal wave curve follows independent and identical Gaussian distribution. We discuss the implication of sinusoidal assumption on sampling design in Section 3.2 and demonstrate that the $F$ statistics is robust against various types of violation of model assumptions in Appendix C and Figure. C1.

3 |. SIMULATIONS

Throughout simulation and real application, we control type I error $\alpha =0.001$ for circadian power calculations to account for potential multiple comparisons.

3.1 |. Comparison between CircaPower and Monte-Carlo simulation

Without the proposed analytical method CircaPower, a conventional method for circadian detection power calculation is by Monte-Carlo simulation (MC), which assumes known $A$, $\varphi$, $M$, $\sigma$ and $t_i$, $1\le i\le n$.

We compare CircaPower with the MC algorithm described in Appendix D. For both methods, the ZT points are simulated from one-period one-sample evenly-spaced design for the ease of discussion, which enjoys the phase-invariant property ($d=1/2$, Theorem 1). Since phase shift $\varphi$ and MESOR $M$ have no impact on circadian detection power calculation in this case, we fix $\varphi =0$ and $M=10$. We evaluate their power derived at a grid of $A=(0.4,0.8,1,1.2)$ and $\sigma =(1,2,3,4)$. Note that for CircaPower, we only need the underlying parameters $A∕\sigma$, $t_i$, and $\varphi$ to perform power calculation, which does not rely on the simulated dataset. We simulate the data for the purpose of evaluating the MC algorithm.

Figure. D2a shows that the power calculated from CircaPower is almost identical to the MC algorithm, corroborating the correctness of the closed-form solution in CircaPower. In addition, the power increases with respect to (i) larger $n$, (ii) larger $A$, and (iii) smaller $\sigma$, which are consistent with our theoretical formula of the total effect size $\lambda$.

As discussed in Section 2.2.1 the two curve fitting parameters $A$ and $\sigma$ work together as the intrinsic effect size $r=A/\sigma$ and therefore can be reduced to one parameter in MC approach. We further validate this observation by co-varying $A$ and $\sigma$ simultaneously (i.e., $=\sigma =1,2,3$) while keeping their ratio as a constant (i.e., $r=1$). Figure. D2b shows that the power trajectories remain the same, indicating the proposed intrinsic effect size is sufficient to capture the goodness-of-fit of the model for the power calculation.

In terms of computing time, to generate all the results in Figure. D2a, it takes 1.84 seconds for the CircaPower using 1 CPU thread on a regular PC (8th Gen Intel Core i5–8250U Quad-Core processor, 1.60 GHz), while it requires 8 hours for the MC algorithm using the same computing resource. With parallel computing, the computing time reduces to 0.13 seconds for CircaPower using 40 CPU threads on a Linux server (Intel Xeon Gold 6130, 2.10GHz), while it still needs 24 minutes for the MC algorithm.

3.2 |. Impact of sampling design on CircaPower

Since the sample collection scheme for active design and passive design are quite different, we will discuss them separately. For active designs, we vary the intrinsic effect $r=0.8,1,1.5,2$ and $n=12,24,36,48$. For passive designs, we vary the intrinsic effect $r=0.4,0.8,1,1.2$ and $n=12,24,...,180$. The maximal sample size we use for the active design is smaller than that of the passive design, because the estimated intrinsic effect is usually higher in animal studies compared with human studies (see Table 1). Due to the fact that not all designs have the phase-invariant property, we also vary the phase shift $\varphi =0,3,6$.

Table 1.

Intrinsic effect sizes for public available transcriptomic circadian data, including 3 passively designed human post-mortem brain studies and 14 actively designed mouse studies from 20 types of tissues. These data are processed using the cosinor method³¹. Two types intrinsic effect sizes are used: (i) median $r$ of the 7 core circadian genes; (ii) minimum $r$ of the top 100 significant circadian genes. These intrinsic effect sizes can be used as a reference resource when investigators need to perform power calculation without any pilot data.

Organism	Study	Data Availability	Tissue	Sample Size	Median r of the 7 core circadian genes	Minimum r of the top 100 circadian genes
Homo sapiens	Chen6	GSE71620	Pre-frontal cortex (BA11)	147	0.91	0.46
			Pre-frontal cortex (BA47)	147	0.77	0.44
	Ketchesin34	GSE160521*	Striatum (NAc)	59	0.71	1.06
			Striatum (caudate)	59	1.04	0.82
			Striatum (putamen)	59	0.83	1.02
	Seney7	Common Mind Consortium*	Pre-frontal cortex	104	0.79	0.55
Mus musculus	Aguilar-Arnal42	GSE49638	Fibroblast	18	2.38	2.94
	Bray43	GSE10045	Atrium	32	3.43	1.46
			Ventricle	32	0.96	1.09
	Cho44	GSE34018	Liver	12	2.84	4.11
	Gerstner45	GSE78215	Cerebral cortex	34	2.46	2.18
	Hoogerwerf46	GSE10644	Colon	18	1.86	1.56
	Hughes9	GSE11922	Fibroblast	48	1.27	1.02
		GSE11923	Liver	48	2.00	2.77
	Mari47	GSE52333	Liver	18	4.11	3.39
	Masri48	GSE73222	Liver	18	3.83	2.47
	Masri49	GSE57830	Liver	36	2.69	2.20
	Na50	GSE11516	Liver	36	3.65	3.69
	Nikolaeva51	GSE27366	Kidney	12	2.39	2.61
	Paschos52	GSE35026	Adipose	12	2.48	2.58
	Solanas53	GSE84580	Satellite	24	3.64	2.30
			Epidermal	20	5.03	2.62
	Zhang12	GSE54650	Adrenal gland	24	5.17	2.27
			Aorta	24	5.55	2.29
			Brainstem	24	3.90	2.07
			Brown fat	24	5.05	2.72
			Cerebellum	24	3.52	2.01
			Heart	24	4.47	2.82
			Hypothalamus	24	2.67	1.74
			Kidney	24	6.33	3.65
			Liver	24	3.51	3.67
			Lung	24	5.78	3.47
			Muscle	24	3.58	2.23
			White fat	24	5.35	2.28
		GSE54651*	Adrenal gland	8	5.29	5.40
			Aorta	8	3.97	5.23
			Brainstem	8	2.21	4.16
			Brown fat	8	4.15	5.94
			Cerebellum	8	4.06	4.86
			Heart	8	4.73	6.23
			Hypothalamus	8	2.19	4.19
			Kidney	8	5.11	6.44
			Liver	8	4.40	6.16
			Lung	8	4.57	5.41
			Muscle	8	5.26	5.24
			White fat	8	3.71	3.87

^*denotes RNA-Seq data and others are microarray data.

For a typical active design, researchers usually need to control the number of (i) ZT points per cycle; (ii) replicates at each time point within a cycle; and (iii) cycles. Because of the periodicity property of the sinusoidal curve in the cosinor model, (ii) and (iii) are statistically equivalent. Therefore, for the ease of discussion, we summarize the following two key parameters for an active design: (i) number of ZT points per cycle $N_T$; (ii) total number of samples $n$. The number of replicated samples (at the same ZT across all cycles) could be calculated as $n/N_T$.

We denote the active design scheme with $N_T$ points per cycle as FixTime $N_T$ and the one-period one-sample evenly-spaced design (i.e., FixTime-n) as the EvenSpace. For $N_T=3,4,6,n$, Figure. 3a shows that (i) the power curves are the same regardless of phi, confirming the phase-invariant property; (ii) the power trajectories for different $N_T^{\prime }s$ are also identical, which implies that under evenly-spaced sampling design with $N_T\ge 3$, the detection power only depends on the total number of samples $n$ but not the $N_T$. Note that these arguments are purely based on the statistical power given sinusoidal wave assumption. In the perspective of curve fitting, smaller number of time points may not necessarily guarantee the goodness-of-fit for a sinusoidal curve, resulting in potentially false positive findings. To explore the impact of number of $N_T$ on the goodness-of-fit, we then simulate expression data from the sinusoidal model and perform non-parametric curve fitting (see Appendix E and Figure. E3. E4 for details). Considering both circadian power calculation and smooth curve fitting, our results suggest $N_T=6$ (i.e., every 4 hours for 24h period design) to be the minimum number of ZT points to fully capture the circadian rhythmicity pattern, which is commonly adopted in the literature.

Figure 3.

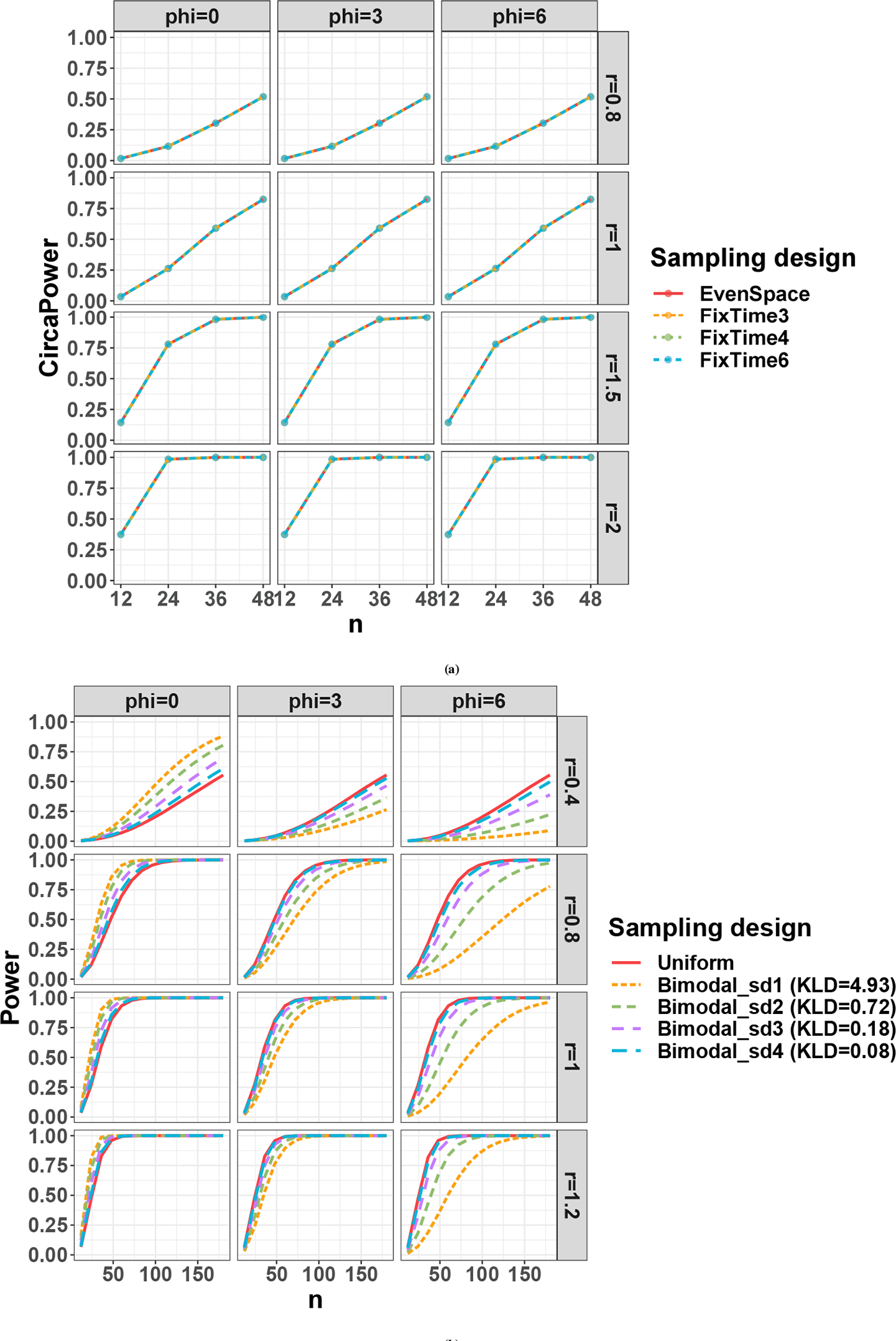
Sampling design effect on circadian power calculation. (a) shows the sampling design effect for active design; (b) shows the sampling design effect for passive design.

For passive designs, the collection of the ZT cannot be controlled. We therefore simulate $t_i^{\prime }s$ from (i) uniform distribution (uniform design): $t_i\stackrel{iid}{~}\mathrm{U}\mathrm{N}\mathrm{I}\mathrm{F}(0,24)$; and (ii) bimodal Gaussian distributions (bimodal designs): $t_i~p_{i}N(7,sd)+\left(1-p_i\right)N(17,sd)$; $p_i~\mathrm{B}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{i}\left(0.5\right)$. We allow $sd=1,2,3,4$ and calculate their corresponding Kullback-Leibler divergence (KLD) against the uniform distribution as a relative measurement to benchmark their divergence from the uniform. Figure. 3b shows that for the uniform design, the power trajectory is close to phase-invariant. This is expected since the uniform distribution is a random realization of the evenly-spaced sampling design, and the impact of phase on the individual $t_i$ will average out. The bimodal designs show phase-dependent circadian power trajectories and the impact of phase influence increases as the distribution deviates more from uniform (i.e., larger KLD). Specifically, the power loss of bimodal designs when $\varphi =3,6$ is significant when KLD is 0.72 or greater (green and yellow curve) while negligible when KLD is only 0.18 or smaller (purple and blue curve). In fact, since the phase shift impacts the sampling design through $d=\frac{1}{n}{\sum }_{i=1}^n {\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(w\left(t_i-\varphi \right)\right)$, it achieves higher power if the mode of the ZT distribution occurs at the underlying peak/trough time. In real omics applications, circadian genes usually have different phase shift values over the day. If the collected ZT distribution is far away from the uniform distribution, the detection power of each circadian gene would be affected differently across the genome as a result of its unique phase shift.

4 |. REAL APPLICATIONS

4.1 |. CircaPower for human studies with passive design

We investigate the power trajectories of human studies using three human post-mortem brain transcriptomic studies (Chen⁶, Seney⁷ and Ketchesin³⁴) with different time of death distributions. Detailed descriptions of each dataset can be found in the original papers. Briefly, Chen⁶ and Seney⁷ performed gene expression circadian analysis using microarray $(n=147)$ and RNA-seq $(n=104)$ respectively using pre-frontal cortex tissues; and Ketchesin³⁴ performed RNA-seq gene expression circadian analysis with $n=59$ participants using dorsal and ventral striatum tissues.

To estimate the intrinsic effect sizes from the three brain studies, we apply the cosinor method³¹ to identify genes with rhythmic patterns and obtain estimates for their amplitude $\hat{A}$ and noise level $\hat{\sigma }$. We estimate the intrinsic effect sizes $\hat{r}=\hat{A}/\hat{\sigma }$ using the 7 core circadian genes, or the top 100 significant rhythmic genes (ranked by p-values from the cosinor method). The 7 core circadian genes include Arntl, Dbp, Nrld1, Nrld2, Perl, Per2, and Per3, which showed persistent circadian pattern across 12 mouse tissues¹². The Homo sapiens section of Table 1 shows the estimated intrinsic effect sizes for: (i) median $r$ of the 7 core circadian genes; (ii) minimum $r$ of the 100 most significant circadian genes. The estimated intrinsic effect sizes for these three human studies range between 0.44 and 1.06 (see Table 1).

To demonstrate the power trajectories in real data, we vary intrinsic effect sizes $r=0.4,0.6,0.8,1$, which roughly cover the estimated range of $r$ in the post-mortem brain studies. The ZT points are sampled 1000 times from the kernel density estimated from the observed time-of-death distributions in these three studies (see top panels of Figure. 4). Since investigators in these human post-mortem brain studies have no control of sample collection time (i.e., time of death) and can only accept passive sampling design, the detection power curves are not phase-invariant. We vary phase shift $\varphi =-6,-5,\dots ,0,\dots ,5,6$ and use a confidence band to represent the range of power achieved across phase shifts (see bottom panels of Figure. 4). For each scenario (i.e., fixed $r$, $n$ and $\varphi$), the mean power among the 1000 times repetitions is reported. The power trajectory from an evenly-spaced design is also calculated as a comparison.

Figure 4.

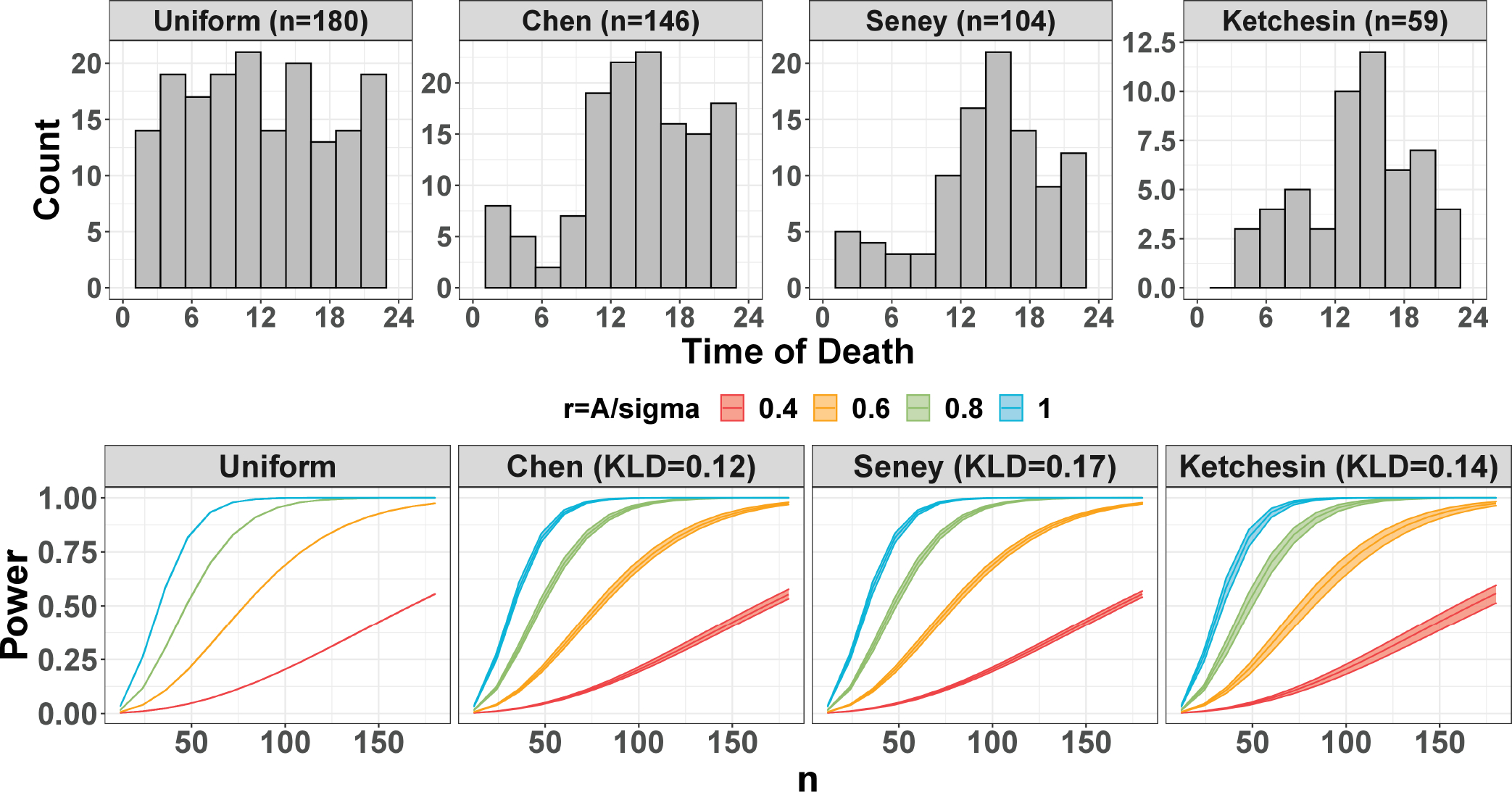
The circadian power calculation using publicly available human datasets. The top panel shows the time of death distribution for Chen, Seney, and Ketchesin. The bottom panel shows the mean power trajectories of different study designs over 1000 repetitions with different intrinsic effect sizes $r=(0.4,0.6,0.8,1)$. The confidence bands represent the range of power achieved across phase values at $\varphi =-6,-5,\dots ,0,\dots ,5,6$ for each scenario.

As expected, larger sample size $n$ and larger intrinsic effect size $r$ lead to a larger circadian power. In addition, the power trajectory is phase-invariant for the evenly-spaced sampling design with 0 band width, but not for the passive designs from the three human studies. As discussed in Section 3.2, the power will depend on the relationship between the mode of the ZT distribution and the underlying peak/trough time. To further demonstrate the impact of phase on the irregular ZT distribution, we fix $n=120$, $r=0.6$, while varying $\varphi =-6,-5,\dots ,0,\dots ,5,6$. As shown in Figure. E5. the power trajectories fluctuate across different ${\varphi }^{\prime }s$ when samples are drawn from irregular distributions in the three post-mortem studies, while the trajectory stays the same for evenly-spaced ZT. However, since the KLDs of the kernel densities estimated from the Chen, Seney and Ketchesin are relatively low (i.e., 0.12, 0.17, 0.14) compared with the bimodal designs in Section 3.2 the variation of power as a result of phase shift is small, with 3.8%, 4.4%, and 9.9% maximum drop, respectively.

4.2 |. CircaPower for animal studies with with active design

We next examine the power trajectories of actively designed mouse studies using 14 mouse gene expression circadian data^{42,43,44,45,46,9,47,48,49,50,51,52,53,12} from 20 types of tissues.Sample sizes of each study tissue are shown in Table 1. To estimate the intrinsic effect sizes of these tissues, we apply the cosinor method³¹ similarly to identify genes with rhythmic patterns and obtained estimates for their amplitude $\hat{A}$ and noise level $\hat{\sigma }$. The estimated intrinsic effect sizes for the median $r$ of the 7 core circadian genes and the minimum $r$ of the top 100 significant circadian genes are shown in the Mus musculus section of Table 1, ranging from 0.96 to 6.33, a much larger magnitude than previous human studies. This is reasonable since human studies are usually more heterogeneous in terms of genetics and environmental background. We thus fix the intrinsic effect sizes to be $r=1,2,3,4$ in our subsequent power calculation. Since these experiments employ an evenly-spaced active sampling design, the sampling design factor is a constant (i.e., $d=1/2$, Corollary 1) regardless of the phase value.. As a result, we employ the one-sample one-period evenly-spaced design (see left panel of Figure. 5) for the purpose of power calculation. By further assuming the alpha levels to be $\alpha =0.05,0.01,0.001$, the power trajectories with respect to sample size $n$ is shown in Figure. 5 (right panel).

Figure 5.

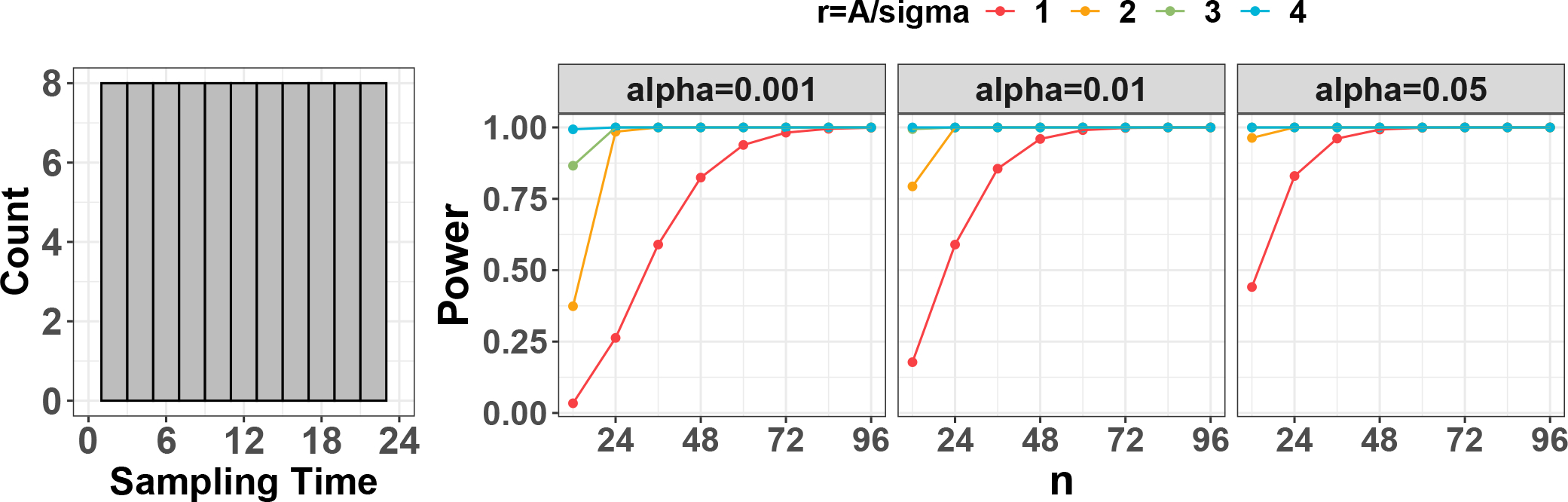
Circadian power calculation using publicly available mouse datasets. The left panel shows the distribution of one-sample one-period evenly-spaced design. The right panel shows the power trajectories for each of the type I error control $\alpha =(0.001,0.01,0.05)$ assuming intrinsic effect sizes $r=(1,2,3,4)$.

4.3 |. Case study: circadian power calculation using mouse pilot dataset

To demonstrate how to perform circadian power calculation using pilot dataset from scratch, we utilize a circadian gene expression data in mouse with skeletal muscle, which is part of the mouse pan-tissue gene expression circadian microarray data¹². Detailed description of this dataset has been described previously⁸. Briefly, 24 mouse muscle samples were collected (every 2 hours) across 2 full cycles. With this pilot data, we perform genome-wide circadian rhythmicity detection using the cosinor method³¹. Under $p<0.001$, we identify 716 significant genes showing circadian pattern. We similarly estimate the intrinsic effect sizes for: (i) median $r$ of the 7 core circadian genes; (ii) minimum $r$ of the top 100 significant circadian genes. The resulting intrinsic effect sizes are 3.58 and 2.23 respectively. By assuming different $\alpha$ to be 0.05, 0.01, 0.001, the power curves with respect to sample size are shown in Figure. 6. We observe that $n=12$ can achieve 97.1% and 50.5% detection power for the two intrinsic effect sizes at $\alpha =0.001$.

Figure 6.

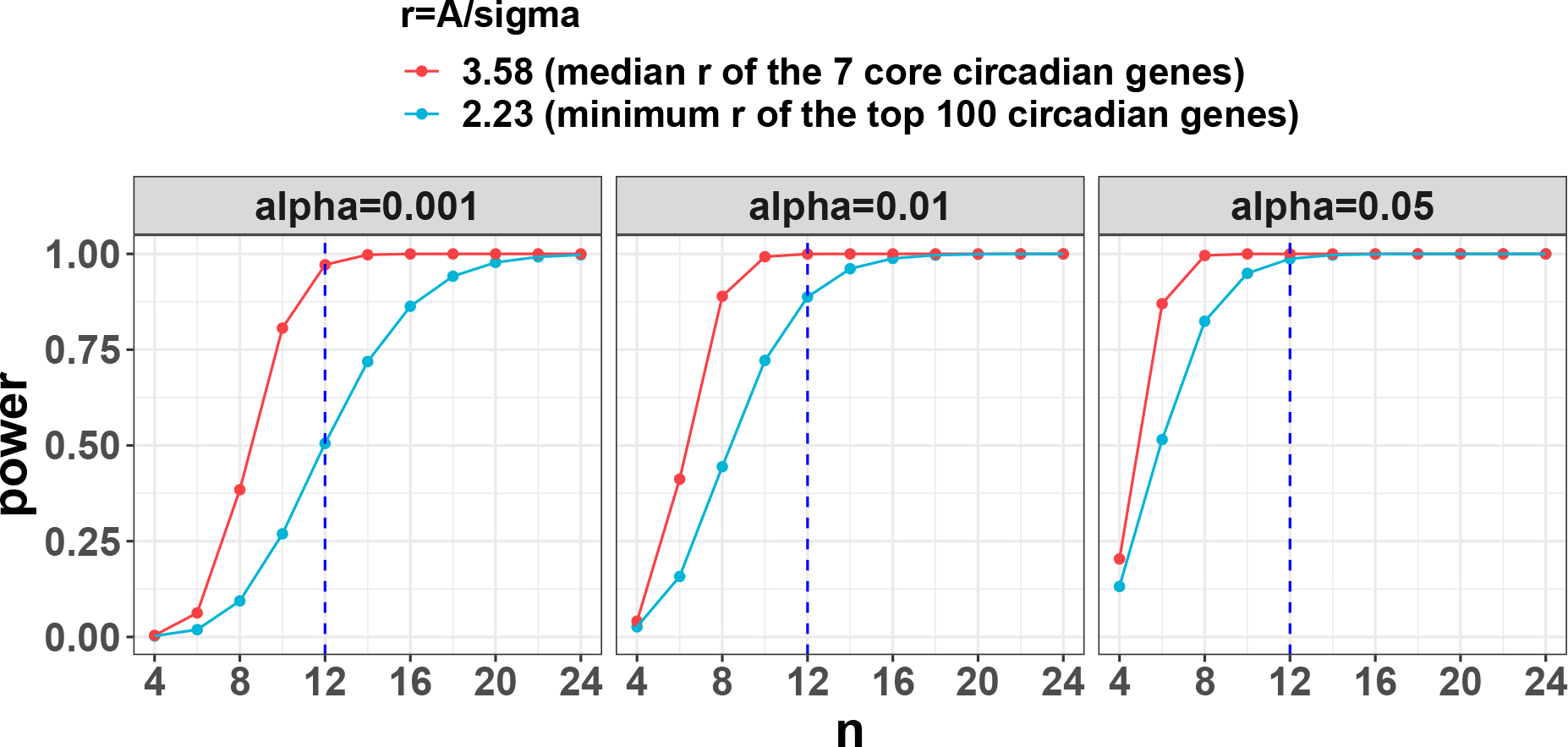
Case study: power trajectories using mouse muscle gene expression circadian data as the pilot data. The pilot data contains 24 mouse muscle samples collected every 2 hours across 2 full cycles. CircaPower is used to calculate the power. The intrinsic effect sizes were used as (i) median $r$ of the 7 core circadian genes; (ii) minimum $r$ of the top 100 significant circadian genes. By assuming different $\alpha$ to be 0.05, 0.01, 0.001, the power trajectories with respect to sample size is shown in this figure. The blue dashed lines indicate the detection power when $n=12$ per cycle which is statistically equivalent to sampling every two hours across two full cycles.

5 |. DISCUSSION

In this paper, we propose an analytical framework, CircaPower, to calculate the statistical power for circadian gene detection. To the best of our knowledge, this is the first analytical method to perform circadian power analysis. In simulations, we not only demonstrate the CircaPower is fast and accurate, but also show that its underlying cosinor model is robust against violations of model assumptions. In real applications, we show the performance of the CircaPower in mouse studies and postmortem human studies. In addition, we obtain the estimated intrinsic effect sizes from publicly available human and mouse transcriptomic circadian data. These summarized intrinsic effect sizes can be used as a reference resource to facilitate investigators without pilot data to perform circadain power calculation. In case study, we also demonstrate circadian power calculation step-by-step given a pilot dataset.

Our method has several advantages. To begin with, the theoretical framework suggests that the power calculation is related to a total effect size, which can be decomposed into sample size, intrinsic effect size (representing goodness-of-fit of circadian curve), and sampling design factor. Moreover, the sampling design factor brings about the concept of active design and passive design when samples are collected. This is an important concept in circadian experiment design, since the ZT collection for human (passive design) and animal (active design) could be quite different. After that, we demonstrate the phase-invariant property of the evenly-spaced sampling design, which provides theoretical foundation for the design of many published circadian studies. In addition, the closed-form formula in CircaPower allows unique inverse calculation of sample size given desired power at fast computing speed compared with the conventional MC algorithm. In this paper, we also systematically examine the intrinsic effect sizes of published mouse or human gene expression circadian data, which could provide guidance for future researchers to design their transcriptomic circadian experiment when pilot data are not available. Although we present our work using transcriptomic data, CircaPower is applicable to other omics data, such as DNA methylation, ChIP-Seq proteomics, metabolomics, and clinical data (e.g., body temperature).

Our work has the following limitations and future work. Firstly, the CircaPower assumes a pre-fixed alpha level. We intentionally select a more stringent alpha (e.g., $\alpha =0.001$) to account for multiple comparison when thousands of genes are tested simultaneously. Additional modeling is needed to extend for calculating genome-wide power calculation while controlling false discovery rate. Secondly, in addition to detecting genes with rhythmic pattern, another important research question is to identify differential circadian pattern^32,54,55,56 (i.e., the circadian pattern is disrupted because of the treatment or condition), which will be another future direction. Thirdly, the Gaussian assumptions are widely assumed in biomedical research, and we have demonstrated that the cosinor model is robust against violations of Gaussian assumptions. If an investigator still worries about these assumptions, we would recommend data transformations (e.g. Box–Cox transformation) before applying our method. Our previous work³² has shown that the Box-Cox transformation can rescue the normality assumption for circadian rhythmicity detection using cosinor models. Similar justifications have been adopted in the literature. For example, though the student T test also assumes Gaussian assumptions, but it is still widely used in the literature, as long as there are methods to rescue the violation (i.e., data transformation). Lastly, as discussed in the introduction, both parametric and non-parametric models are popular and widely used in the literature. In the proposal, we only focus on the cosinor model for its simplicity and accurate statistical inference³². Further extending the current framework to a more flexible family of circadian pattern is of biological interests to the general circadian research field.

APPENDIX

A. PROOF OF $\mathit{F}$ STATISTICS DISTRIBUTION UNDER THE ALTERNATIVE

A.1. Derivation of $F$ statistics distribution under the null

Lemma 1.

Under the null distribution in the linear model framework, $F^{stat}~f_0(\cdot \mid r-1,n-r)$, where $f_0(\cdot \mid r-1,n-r)$ denotes a regular F distribution with degrees of freedom $r-1$ and $n-r$.

Proof.

The proof is given in⁵⁷.

Therefore, under the null hypothesis that there is no circadian rhythmicity. i.e., $A=0$ in Equation 1, or equivalently, $H_1=H_2=0$ in Equation 2,

$$F^{stat}~f_0(\cdot \mid 2,n-3),$$

where 2 and $n-3$ are the degrees of freedom of the $F$ distribution, and $f_0$ denotes a regular $F$ distribution with non-centrality parameter 0

A.2. Derivation of $F$ statistics distribution under the alternative

Lemma 2.

If $X~N_p(\mu ,\mathrm{\Sigma })$ and $\mathrm{\Sigma }$ is positive definite variance-covariance matrix for the $p$ dimensional multivariate normal distribution, then

$$X^{\mathrm{\top }}{\mathrm{\Sigma }}^{-1}X~{\chi }_p^2\left(\lambda \right),$$

where $\lambda ={\mu }^{\mathrm{\top }}{\mathrm{\Sigma }}^{-1}\mu$ is the non-centrality parameter for the ${\chi }_p^2$ distribution with degree of freedom $p$.

Proof.

The proof is given in⁵⁷.

Lemma 3.

In a linear model framework, if the design matrix $X\in {\mathbb{R}}^{n\times p}$, the regression coefficient $\beta \in {\mathbb{R}}^p$, there are $q$ hypotheses to be tested $A^{\mathrm{\top }}\beta =b$, where $A\in {\mathbb{R}}^{p\times q}$, $b\in {\mathbb{R}}^q$ represents the true parameters $b=A^{\mathrm{\top }}{\beta }^{\mathrm{*}}$.

We have the following results:

$$F^{stat}=\frac{{(A^{\mathrm{\top }}\hat{\beta })}^{\mathrm{\top }}{B}^{-1}(A^{\mathrm{\top }}\hat{\beta })}{RSS}={\chi }_q^2(\lambda )/{\chi }_{n-r}^2~f_{\lambda }(\cdot \mid q,n-r),$$

where $f_{\lambda }(\cdot \mid q,n-r)$ denotes a non-central F distribution with non-centrality parameter $\lambda ={\left(A^{\mathrm{\top }}\beta \right)}^{\mathrm{\top }}{B}^{-1}\left(A^{\mathrm{\top }}\beta \right)$ and degrees of freedom $q$ and $n-r;B=A^{\mathrm{\top }}{\left(X^{\mathrm{\top }}X\right)}^{g}A$.

Proof.

$$A^{\mathrm{\top }}\hat{\beta }=A^{\mathrm{\top }}{\left(X^{\mathrm{\top }}X\right)}^g{X}^{\mathrm{\top }}Y$$

$$A^{\mathrm{\top }}\hat{\beta }~N_q(\left(A^{\mathrm{\top }}\beta \right),{\sigma }^2{A}^{\mathrm{\top }}{\left(X^{\mathrm{\top }}X\right)}^{g}A)$$

If we denote $B=A^{\mathrm{\top }}{\left(X^{\mathrm{\top }}X\right)}^{g}A$, and base on Lemma 2 we have:

$$\frac{{(A^{\mathrm{\top }}\hat{\beta })}^{\mathrm{\top }}{B}^{-1}(A^{\mathrm{\top }}\hat{\beta })}{{\sigma }^2}~{\chi }_q^2(\lambda )$$

where $\lambda ={\left(A^{\mathrm{\top }}\beta \right)}^{\mathrm{\top }}{B}^{-1}\left(A^{\mathrm{\top }}\beta \right)$. In addition, since

$$\frac{RSS}{{\sigma }^2}=\frac{Y^{\mathrm{\top }}(I-P)Y}{{\sigma }^2}~{\chi }_{n-r}^2,$$

therefore we could derive the following relationship⁵⁸.

$$F^{stat}=\frac{{(A^{\mathrm{\top }}\hat{\beta })}^{\mathrm{\top }}{B}^{-1}(A^{\mathrm{\top }}\hat{\beta })}{RSS}={\chi }_q^2(\lambda )/{\chi }_{n-r}^2~f_{\lambda }(\cdot \mid q,n-r)$$

Theorem 2.

Under the sinusoidal model assumption (Equation 2), under the alternative hypothesis (there is a circadian fitting, i.e., $H_1\ne 0$ or $H_2\ne 0$), we have

$$F^{stat}~f_{\lambda }(\cdot \mid 2,n-3),$$

where $\lambda =\frac{A^2}{{\sigma }^2}{\sum }_i {\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(w\left(t_i-\varphi \right)\right)$.

Proof.

Fitting the sinusoidal model Equation 2 into the linear model framework, the design matrix is

$$X=\left(\begin{array}{cc}\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t_1\right)& \mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t_1\right)\\ \cdots & \cdots \\ \mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t_n\right)& \mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t_n\right)\end{array}\right)$$

And

$$X^{\mathrm{\top }}X=\left(\begin{array}{cc}\sum _i{\mathrm{s}\mathrm{i}\mathrm{n}}^2\left(\omega t_i\right)& \sum _i\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t_i\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t_i\right)\\ \sum _i\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t_i\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t_i\right)& \sum _i{\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(\omega t_i\right)\end{array}\right)$$

The regression coefficient is

$$\beta =\left(\begin{array}{l}{H}_1\\ H_2\end{array}\right)$$

The joint hypotheses are $H_1=0$ and $H_2=0$, which is equivalent to the following:

$$\left(\begin{array}{ll}1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{l}{H}_1\\ H_2\end{array}\right)=\left(\begin{array}{l}0\\ 0\end{array}\right)$$

By denoting $A=I_2$, the hypothesis is equivalent to $A\beta =0$. According to Lemma 3 we have

$$F^{stat}~f_{\lambda }(\cdot \mid 2,n-3)$$

$$\begin{gathered} \lambda =\frac{{\beta }^{\top }{X}^{\top }X\beta }{{\sigma }^2} \\ =\frac{A^2}{{\sigma }^2}\sum _i{\cos }^2\left(w\left(t_i-\varphi \right)\right) \end{gathered}$$

B. PROOF OF THE PHASE-INVARIANT PROPERTY IN THE ONE-SAMPLE ONE-PERIOD EVENLY-SPACED DESIGN

Lemma 4.

For $n\in {\mathbb{N}}^{+}$, $a\in \mathbb{R}$, $d\in \mathbb{R}$, define $R=\frac{\mathrm{s}\mathrm{i}\mathrm{n}(Nd/2)}{\mathrm{s}\mathrm{i}\mathrm{n}(d/2)}$.

$$\sum _{i=0}^{N-1} \mathrm{c}\mathrm{o}\mathrm{s}(a+id)=\left\{\begin{array}{ll}n\mathrm{c}\mathrm{o}\mathrm{s}\left(a\right)& \text{if}\mathrm{s}\mathrm{i}\mathrm{n}(d/2)=0\\ R\mathrm{c}\mathrm{o}\mathrm{s}\left(a+\frac{1}{2}(n-1)d\right)& \text{otherwise}\end{array}\right.$$

Proof.

See ⁵⁹.

Corollary 2.

When $n\ge 3$, $\varphi \in \mathbb{R}$;

$$\frac{1}{n}\sum _{i=0}^{n-1} \mathrm{c}\mathrm{o}\mathrm{s}(\frac{4\pi i}{n}-\varphi )=0$$

With that being said, the evenly spaced design with $n\ge 3$ time points will achieve the same design effect, regardless of phase $\varphi$

Proof.

Following Lemma 4, set $N=n$, where $n\ge 3$, $d=4\pi /n$, then $\mathrm{s}\mathrm{i}\mathrm{n}(d/2)=\mathrm{s}\mathrm{i}\mathrm{n}(2\pi /n)\ne 0$, $R=0$.

$$\begin{gathered} \frac{1}{n}\sum _{i=0}^{n-1}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{4\pi i}{n}-\varphi ) =R\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{1}{2}(N-1)d-a\right) \\ =0 \end{gathered}$$

Theorem 3

(Phase-invariant property - one-period one-sample). Assuming there is a total of $n$ ZT points within a circadian period $2\pi /\omega$, the ZT $t_i^{\prime }s$ are ordered such that $t_i<t_{i+1}$ for all $1\le i\le n-1$. If $n\ge 3$, and $t_i$ is evenly-spaced over the period (i.e., $t_{i+1}-t_i=C$ for all $1\le i\le n-1$, $C>0$ is a fixed time interval, $\left(t_1+2\pi /\omega \right)-t_n=C)$, then regardless of the value for $\varphi$,

$$\frac{1}{n}\sum _{i=1}^n{\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(w\left(t_i-\varphi \right)\right)=\frac{1}{2}$$

Proof.

$$\begin{gathered} \frac{1}{n}\sum _{i=0}^{n-1}{\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(w\left(t_i-\varphi \right)\right)=\frac{1}{2n}\sum _{i=0}^{n-1} \left(1+\mathrm{c}\mathrm{o}\mathrm{s}\left(2w\left(t_i-\varphi \right)\right)\right) \\ =\frac{1}{2}-\frac{1}{2n}\sum _{i=0}^{n-1} \mathrm{c}\mathrm{o}\mathrm{s}(2\omega (\frac{2i\pi }{\omega n}-\varphi ))) \\ =\frac{1}{2}-\frac{1}{2n}\sum _{i=0}^{n-1} \mathrm{c}\mathrm{o}\mathrm{s}(\frac{4i\pi }{n}-\varphi ))) \\ =\frac{1}{2} \end{gathered}$$

C. ROBUSTNESS ANALYSIS OF $\mathit{F}$ STATISTICS

To examine the robustness of our method when the iid Gaussian assumption is violated, we investigate the type I error control of $F$ statistics in the following scenarios: (i) heavy tail error distribution (i.e., student T distribution); (ii) existence of outliers; (iii) non-independent Gaussian errors. For all these simulations, $G=10,000$ noisy genes are simulated with error term ${\epsilon }_{gi}$ ‘s specified above. By declaring circadian rhythmicity at 5% nominal $\alpha$ level, we will evaluate the actual type I error rate of the $F$ test from the cosinor model. Since CircaPower is built on the $F$ statistics for rhythmicity detection it will be benchmarked as robust if the actual type I error rate is close to the nominal $\alpha$ level. The detailed simulateion setting is provided below:

1. Heavy tail error distribution. Instead of sampling the error term ${\epsilon }_{gi}\stackrel{iid}{~}N\left(0,{\sigma }^2\right)$, $1\le g\le G$ and $1\le i\le n$, we sample ${\epsilon }_{gi}\stackrel{iid}{~}t(df)$, where $t\left(df\right)$ is the student T distribution with degree of freedom $df$. In general, the smaller the $df$ is, the heavier tail the error distribution is. When $df=1$, the error distribution becomes the Cauchy distribution, and when $df\to \mathrm{\infty }$, the error distribution converges to standard Gaussian distribution (i.e., $N\left(0,{\sigma }^2\right)$). To evaluate the impact of heavy tail error distribution on CircaPower, we simulate a grid of $df=(2.5,3,5,\mathrm{\infty })$. Figure. C1a shows that when there is no or mild violation of the Gaussian assumption (i.e., $df=\mathrm{\infty }$ or $df=5$), the cosinor method achieves accurate type I error control (i.e., 5%). When there is moderate to severe violation of the Gaussian assumption (i.e., $df=3$ or $df=2.5$), type I error rate is only slightly conservative (i.e., below the nominal $\alpha =0.05$). Putting together, the type I error rate of the cosinor method can be correctly controlled against the heavy tail error distribution.

2. Existence of outliers To evaluate the impact of outliers on type I error control, we replace $q\mathrm{\%}$ of the expression values with outliers, where $q=(5,10,20)$. To be specific, for a gene $g$, there is $q\mathrm{\%}$ chance that the expression level is simulated from $y_{gi}\stackrel{iid}{~}\mathrm{U}\mathrm{N}\mathrm{I}\mathrm{F}(M-A,M+A)$; and $1-q\mathrm{\%}$ chance that the expression level is simulated independently based on Equation 1 under $H_0:A=0$ (i.e., $y_{gi}=M+{\epsilon }_{gi},{\epsilon }_{gi}\stackrel{iid}{~}N\left(0,{\sigma }^2\right)$). Figure. C1b shows that the cosinor method achieves accurate nominal type I error rate control (i.e., 5%), showing robustness to outliers.

3. Correlated gene structure Instead of assuming all genes are independent, we simulate every 50 genes as a gene module with correlation coefficient $\rho$. The error term for each gene module ${\mathit{\epsilon }}_{50}~N\left(\mathbf{0},{\mathbf{\Sigma }}_{50}\right)$ where ${\mathbf{\Sigma }}_{50}$ is a symmetric matrix with diagonal elements being ${\sigma }^2$ and off-diagonal elements being ${\sigma }^2\rho$. We simulate a grid of $\rho =(0,0.25,0.5,0.75)$. Figure. C1c shows that when genes are correlated, the cosinor method maintains accurate nominal type I error rate control (i.e., 5%).

Since our goal is to evaluate the type I error rate control, which does not involve any multiple testing issue, we directly use 5% nominal $\alpha$ level. Figure. C1 shows that the cosinor model only has slightly conservative type I error from cosinor model when error terms are drawn from very heavy tail $\mathrm{t}$ distribution $(\mathrm{d}\mathrm{f}=2.5\mathrm{o}\mathrm{r}3)$ while maintains accurate type I error rate in all other scenarios suggesting the robustness against the three types of violation in general.

Figure C1.

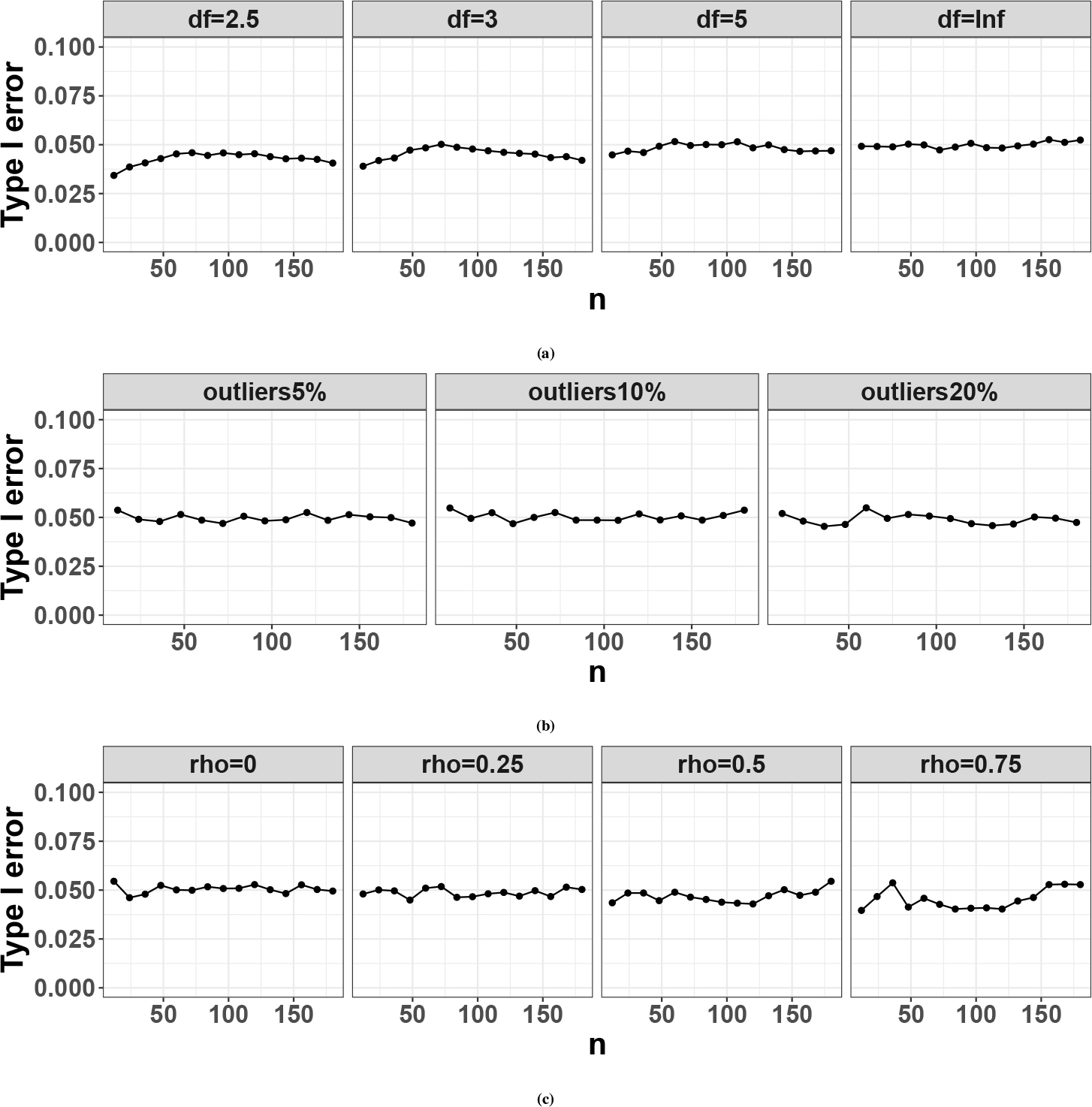
Actual type I error rate for the cosiner method in detecting circadian rhythmicity pattern at 5% nominal $\alpha$ level when there exist violation of model assumptions (i.e., independent Gaussian errors.) (a) shows the case when the error term comes from a heavy tail $t$ distribution (i.e., ${ϵ}_i~t\left(df\right)$, $df$ is the degree of freedom of the $t$ distribution); (b) shows the case when there exists outliers; (c) shows the case when the errors of multiple genes are correlated (i.e., $\left({ϵ}_1,\dots ,{ϵ}_m\right)~\mathrm{M}\mathrm{V}\mathrm{N}(0,\mathrm{\Sigma })$, $m$ is number of correlated genes, and $\mathrm{\Sigma }$ is the variance-covariance matrix for the multivariate normal distribution).

D. ALTERNATIVE POWER CALCULATION METHOD BY MONTE-CARLO SIMULATION

Without the proposed analytical method CircaPower, a conventional method for circadian detection power calculation is by Monte-Carlo simulation (MC), which assumes known $A$, $\varphi$, $M$, $\sigma$ and $t_i$, $1\le i\le n$ in Equation 1. The detailed algorithm for MC is described as following:

1. Given the ZT $t_i^{\prime }s$ for $n$ samples $(1\le i\le n)$ and key parameters ($A$, $\varphi$, $M$, and $\sigma$), we simulate gene expression $y_{gi}$ based on Equation 11 where $1\le g\le G$ is the gene index and $G$ is the total number of genes. $G=10,100$ genes is used in the simulation comparison between CircaPower and MC algorithm in Section 3.1 in the main text.

2. We apply the cosinor method³¹ to derive the rhythmic p-value $p_g$ for each gene $g(1\le g\le G)$. Given a pre-specified alpha level $\alpha$, the power of MC algorithm is calculated as $\frac{{\sum }_g I\left(p_g\le \alpha \right)}{G}$.

Although both the CircaPower and the MC algorithm rely on the $F$ statistics for rhythmicity detection (see Figure. D2), the CircaPower has several obvious advantages over the MC algorithm. First of all, the explicit representation of total effect size in CircaPower provides insights on the three determining factors $(n,r,d)$ in circadian detection power calculation while it is hard for MC algorithm to determine selections and trends on the many parameters ($A$, $\varphi$, $M$, $\sigma$, and $t_i$, $1\le i\le n$). In addition, our simulation shows the closed-form solution by CircaPower is at least 10,000 folds faster than the MC algorithm (see Section 3.1 in the main text). More importantly, even though both approaches can calculate power given sample size, only CircaPower can directly solve the inverse problem of deriving the smallest sample size meeting the desired detection power, while MC algorithm needs repeated interpolation to obtain an answer.

Figure D2.

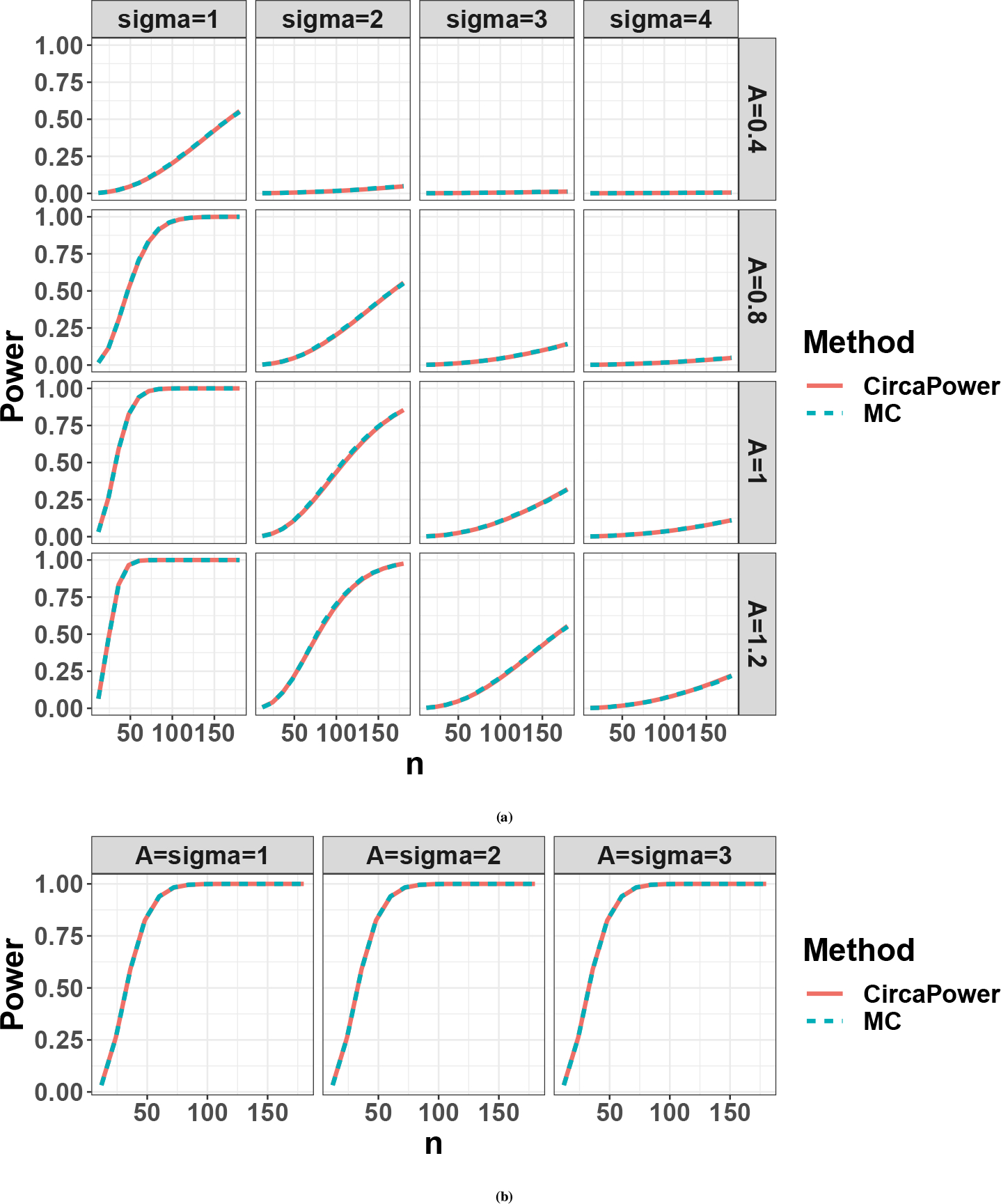
Compare power trajectories from the CircaPower with the Monte-Carlo (MC) algorithm. The red color curve denotes the CircaPower method, and the cyan color curve denotes the MC approach. (a) We vary the amplitude $A=0.4,0.8,1,1.2$ and $\sigma =1,2,3,4$. (b) We co-vary $A$ and $\sigma$ simultaneously (i.e., $A=1,2,3,\sigma =1,2,3$) while keeping their ratio as a constant (i.e., $r=A/\sigma =1)$.

E. NON-PARAMETERIC CURVE FITTING SIMULATION SETTING

From the perspective of circadian power calculation, Figure. 3a implies that the evenly-spaced sampling design is phase-invariant as long as $N_T\ge 3$, which is further corroborated by Corollary 1. However, in the perspective of curve fitting, smaller number of time points may not necessarily guarantee the goodness-of-fit for a sinusoidal curve, resulting in potentially false positive findings.

To explore the impact of number of $N_T$ on the goodness-of-fit for a sinusoidal wave, we simulate expression data from the sinusoidal model and perform non-parametric curve fitting to identify the minimum $N_T$ necessary to capture the sinusoidal wave curve. To be specific, we first choose the ZT points within a cycle to be $N_T=3,4,6,8,12$, where $N_T$ starts from 3 as at least 3 sampling times are needed to characterize the three parameters in sine (or cosine) model. Then for each $N_T$, we simulate $n=48$ samples, and evenly allocated them at $2N_T$ time points across 2 full cycles (every $24/N_T$ hours, from - 12h to 36h), resulting in $24/N_T$ samples at each time point. The expression values of samples at each time point $t_j$ are simulated independently from Equation 1] where we set $=1$, $M=0$, and $\sigma =1$. The LOESS regression is then used to fit a smooth curve through the data points. The LOESS regression is a nonparametric method using locally-weighted regression to fit a smooth curve over a scatter plot⁶⁰. Such LOESS regression represents the smooth curve fitting without the sinusoidal assumption, which could reflect the minimum of $N_T$ that is necessary to capture the sinusoidal wave curve. The rationale for 2 full cycles is to improve the boundary behavior of the curve fitting within one cycle. In addition, to evaluate the effect of the phase shift, we set $\varphi =0,-1,\dots ,-\mathrm{m}\mathrm{i}\mathrm{n}\left(24/N_T-1,6\right)$. By comparing the fitted non-parametric curves with the underlying sinusoidal wave, we can observe the minimum of NT that is necessary to capture the sinusoidal wave curve.

The data points and fitted smooth curves in one circadian cycle [0, 24] are shown in Figure. E3 When $N_T\le 4$, it is uncertain whether the underlying curve fitting is a sinusoidal wave. Only when $N_T$ increases to 6 or more, the curve fitting is stable and almost identical to the underlying sinusoidal wave. To further justify this choice, we calculate the root mean square distance between the fitted non-parametric curve and the underlying sinusoidal curve at evenly spaced 1000 points between [0, 24] and plot against $N_T$. The elbow plot (Figure. E4) suggests that $N_T=6$ is an inflection point after which the change of distance between the fitted curve and the underlying curve becomes stably small. Therefore, considering both circadian power calculation and smooth curve fitting, our results suggest $N_T=6$ to be the minimum number of ZT points to fully capture the circadian rhythmicity pattern, which is commonly adopted in the literature.

Figure E3.

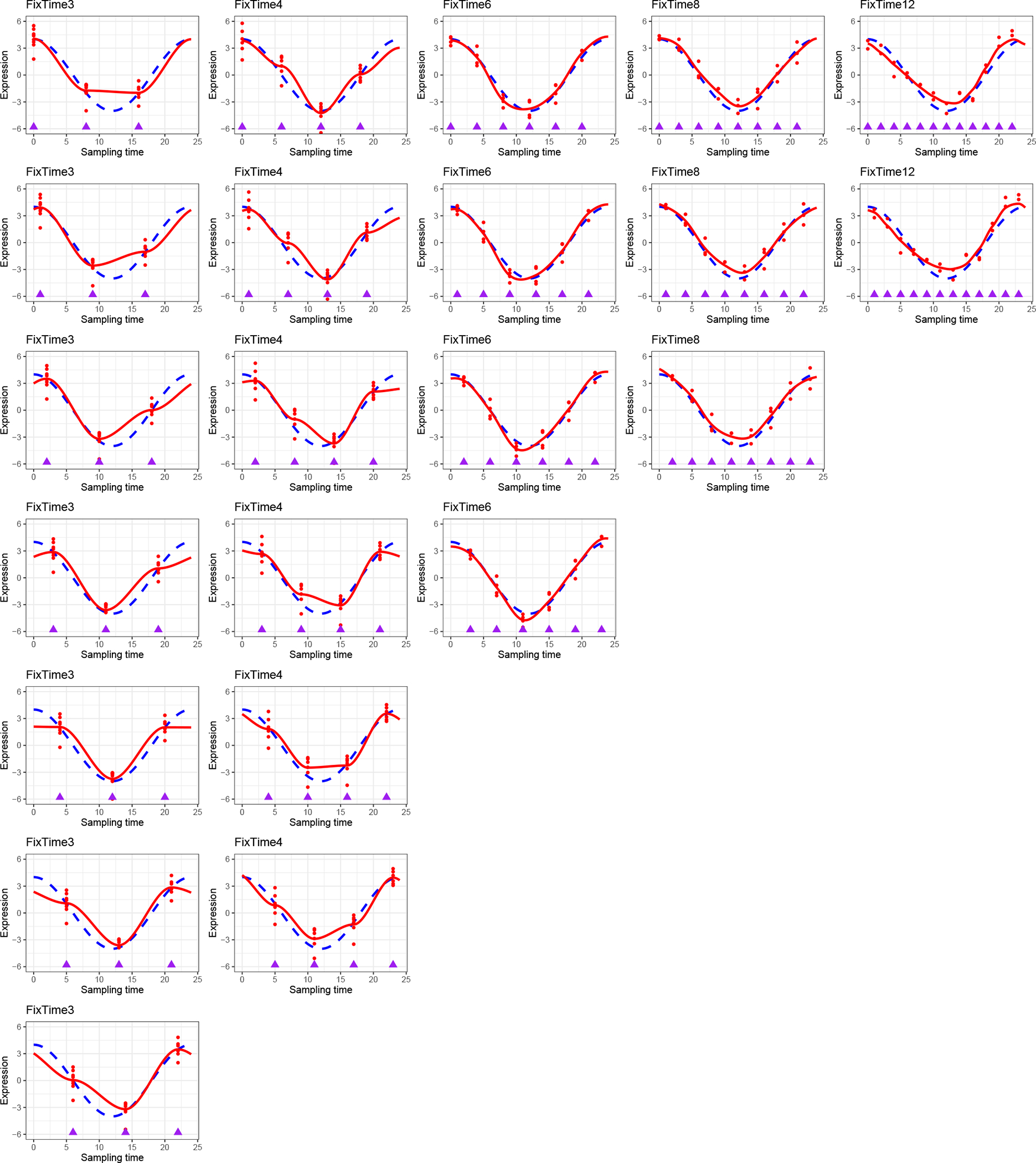
Non-parametric curve fitting to explore the impact of number of ZT points per cycle (i.e., $N_T$) on the goodness of fit for a sinusoidal wave. We choose the ZT points within a cycle to be $N_T=3,4,6,8,12$ (on columns). Then for each $N_T$, we simulate $n=48$ samples evenly allocated at $2N_T$-time points across 2 full cycles (every $24/N_T$ hours, from −12h to 36h), resulting in $24/N_T$ samples at each time point. The rationale for 2 full cycles is to improve the boundary behaviour of the curve fitting within one cycle. The purple rectangles indicate sampling time points. The expression values of samples at each time point $t_j$ are simulated independently from Equation 1 with $=1$, $M=0$, and $\sigma =1$. The LOESS regression is used to fit a smooth curve through the all data points. To evaluate the effect of the phase shift, we set $\varphi =0,-1,\dots ,-\mathrm{m}\mathrm{i}\mathrm{n}\left(24/N_T-1,6\right)$ (on rows). The data points and fitted smooth curve in one circadian cycle [0, 24] are shown in this figure, which represents the smooth curve fitting without the sinusoidal assumption.

Figure E4.

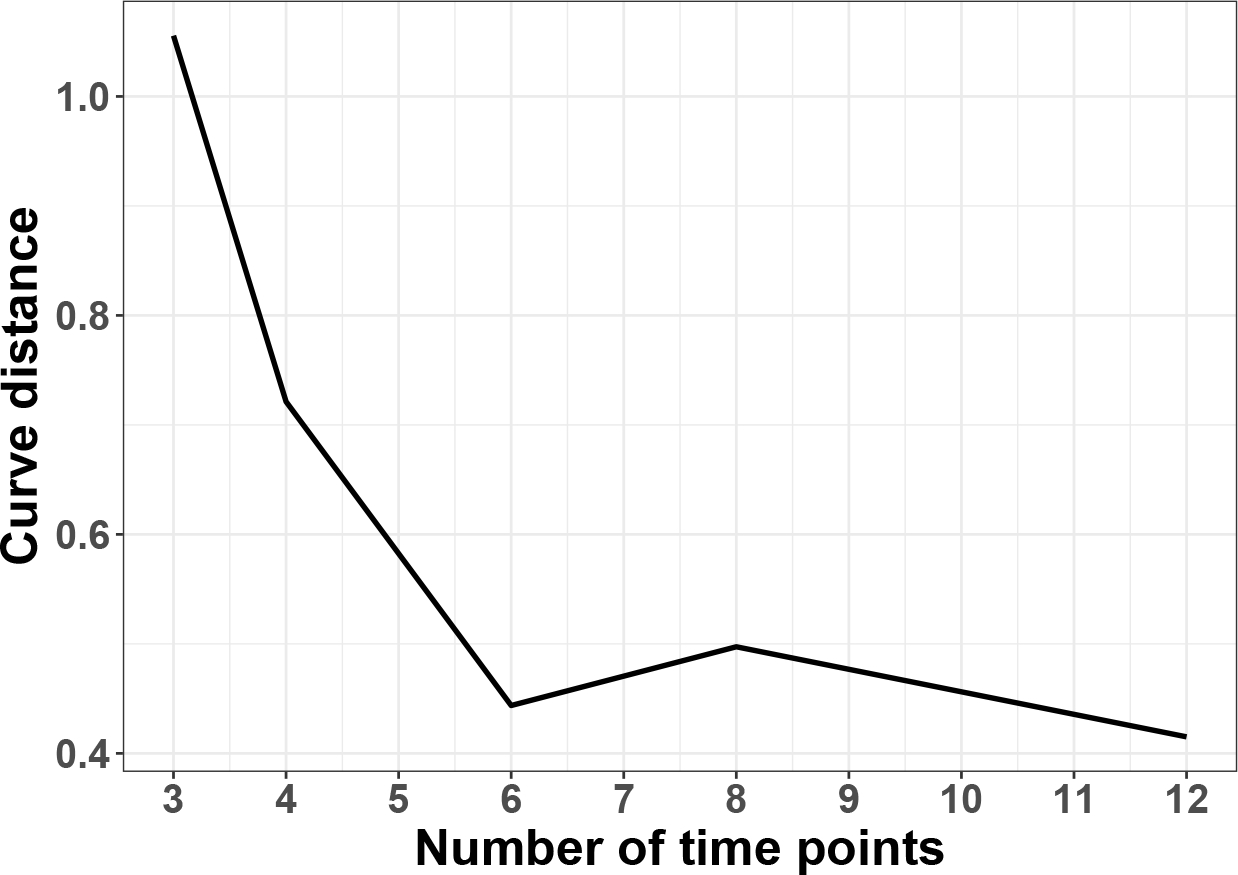
Elbow plot to evaluate the effect of number of ZT points per cycle (i.e., $N_T$) on the goodness of fit for a sinusoidal wave. The curve distance is calculated as $\sqrt{\frac{{\sum }_x (f(x)-\hat{f}(x){)}^2}{1000}}$ where $x$ are 1000 points evenly spaced between 0 and 24, $f\left(x\right)$ is the underlying sinusoidal curve evaluated at $x$ and $\hat{f}(x)$ is the fitted non-parametric curve evaluated at $x$. To avoid randomness, for each $N_T$, the non-parametric fitting is repeated 100 times and the mean curve distance is plot against the $N_T$.

Figure E5.

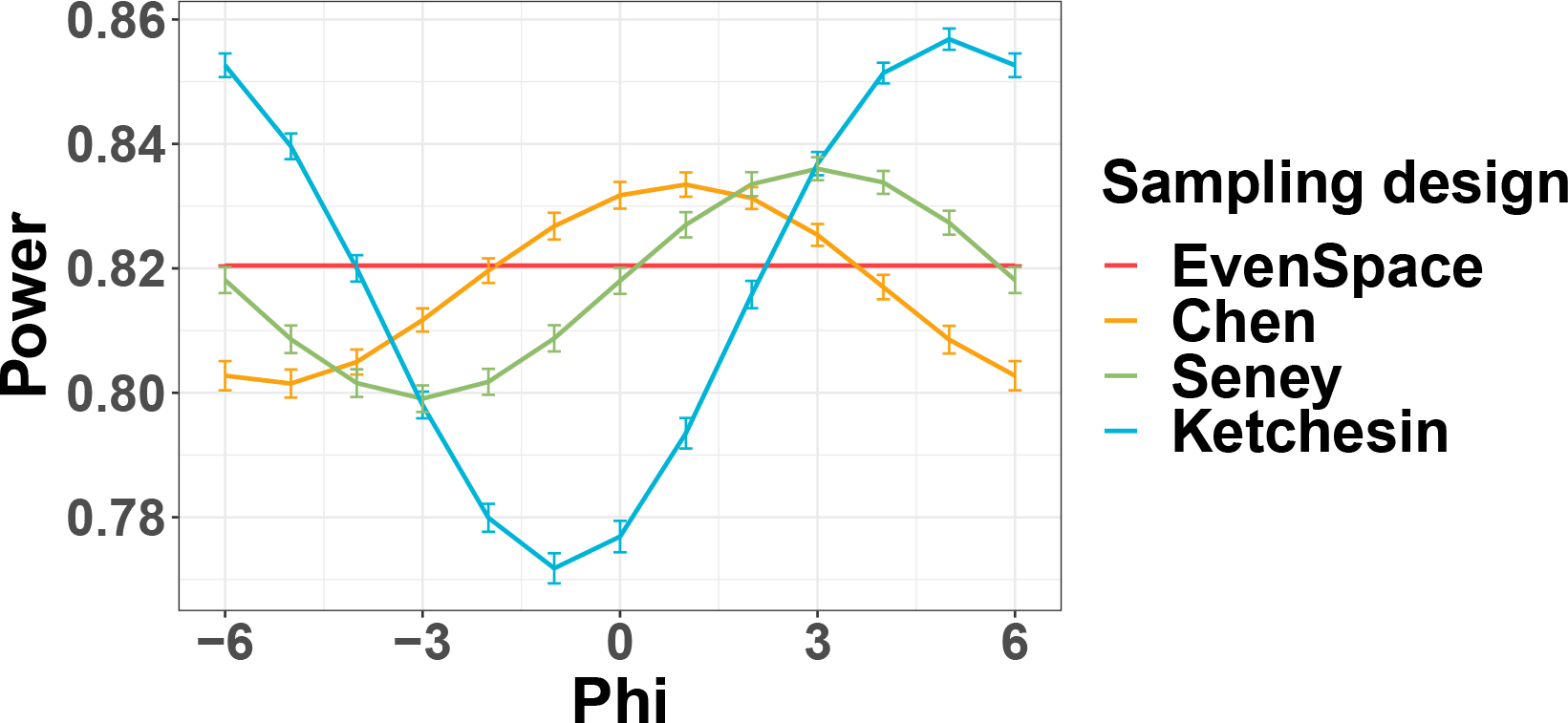
The mean power trajectories across different $\varphi$ when $n=120$ and $r=0.6$. For each $\varphi$ and sampling distribution, we draw sampling times 1000 times and calculate corresponding power. Vertical bars indicate the 95% confidence interval of power estimates calculated form $\bar{x}\pm 1.96s/\sqrt{1000}$ where $\bar{x}$ and $s$ are mean and standard deviation of power estimates respectively. Maximum power drop $\frac{{max}_{\varphi }\left(mean\text{\_}Power\right)-{min}_{\varphi }\left(mean\text{\_}Power\right)}{{max}_{\varphi }\left(mean\text{\_}Power\right)}$) is 3.8%, 4.4%, and 9.9% respectively.

DATA AVAILABILITY STATEMENT

To allow easy application by other researchers, our methods have been implemented in the R package CircaPower, which is publicly available in github (https://github.com/circaPower/CircaPower). Seneyl⁷ dataset is available in the Common Mind Consortium at https://www.nimhgenetics.org/available_data/commonmind/ through an approval process. All other datasets are publicly available on the NCBI GEO database with accession numbers shown in Table 1.