Skip to main content
NCBI home page
RSC Advances logoLink to RSC Advances
. 2023 Aug 15;13(35):24491–24498. doi: 10.1039/d3ra04509a

Heavy alloy based on tungsten and bismuth: fabrication, crystal structure, morphology, and shielding efficiency against gamma-radiation

Daria I Tishkevich a, Anastasia A Rotkovich a,✉, Stepan A German a,b, Aliaksandr L Zhaludkevich a, Tatiana N Vershinina c,d, Anastasia A Bondaruk a, Ihar U Razanau a, Mengge Dong e,f, M I Sayyed g,h, Sergey V Leonchik a, Tatiana Zubar a, Maxim V Silibin i, Sergei V Trukhanov a,j, Alex V Trukhanov a,j,k
PMCID: PMC10426328  PMID: 37588974

Abstract

W–Bi2O3 composites were fabricated using the hot isostatic pressing technique for the first time. The duration of the samples sintering was 3 minutes under conditions of high pressure and temperature. The study of microstructural features and chemical composition of sintered samples was carried out using scanning electron microscopy and energy-dispersive X-ray spectroscopy, respectively. The effect of temperature on the quality of the obtained W–Bi2O3 composites is determined. The densest samples were obtained at a pressure of 5 GPa and temperatures of 25 °C and 500 °C, the densities of which were 18.10 and 17.85 g cm−3, respectively. It is presented that high temperature exposure during sintering adversely affects both the composite density and microstructure due to the redox reaction accompanied by the reduction of Bi and the oxidation of W. The results of the W–Bi2O3 structure study using X-ray diffraction analysis showed that all samples included the main bulk-centered cubic W phase. The presence of the WO2 phase is noted only when the sintering temperature is increased up to 850 °C, which is confirmed by the appearance of diffraction peaks that correspond to 111 and 22−2 crystallographic planes. The shielding efficiency of the W–Bi2O3 composite against gamma radiation using the Phy-X/PSD software was evaluated. A Co60 isotope with an energy of 0.826–2.506 MeV was used as a source of gamma radiation. The calculation results were compared with those for Pb and Bi. Key shielding parameters such as the linear attenuation coefficient, half-value layer, tenth-value layer, mean free path, and effective atomic number are determined. The calculation results revealed that the W–Bi2O3 composite surpasses Pb and Bi in its shielding properties, which makes it promising for use as a prospective material for radiation shielding applications.

For the first time shields based on W–Bi2O3 composites against gamma-rays were sintered via the hot isostatic pressing. The calculation results showed that the composites better than Pb and Bi, which makes them promising for shielding application.graphic file with name d3ra04509a-ga.jpg

Introduction

Currently, microelectronic products are widely used in many industries (electronic, nuclear, medicine, space, etc.), and the application of ionizing radiation in various fields of scientific activity is strongly increasing.1 Modern technologies make it possible to obtain microelectronic devices with a high degree of miniaturization and performance, due to which their reliability strongly depends on environmental conditions.2 Ionizing radiation (IR) is any radiation whose interaction with the environment leads to its ionization (gamma-, X-rays, electrons, protons, etc.).3,4 For example, the interaction of gamma radiation with matter leads to the following: photoeffect, Compton effect, and formation of electron–positron pairs.5–7

Nowadays, there are methods for protecting electronic devices from IR.8 An effective method of protection from IR is local protection, based on the use of heavy element-based materials. The most widely used material in this area is lead.9 The physical and mechanical properties of lead make it a promising material for radiation protection. Lead is inexpensive and easy to process, but its toxicity can cause serious harm to the human body and the environment.9–12 In this regard, there is a need to develop alternative materials that will perform their function as shielding materials and be more eco-friendly.13

The authors of ref. 9 made a comparison between lead, tungsten, and WC–Co composites obtained by hot pressing. WC–Co and lead showed almost identical results in terms of linear attenuation coefficient values of Cs137 (1.06 and 1.05 cm−1, respectively) and Co60 (0.64 and 0.62 cm−1, respectively) gamma-radiation isotopes, while W showed more outstanding results: 1.7 cm−1 for Cs137 and 1.02 cm−1 for Co60. At the same time, pure W had the lowest value of the half-value layer (0.407 cm for Cs137 and 0.676 cm for Co60). For WC–Co, these values were 0.652 cm and 1.07 cm, respectively, compared to 0.66 cm and 1.1 cm for Pb. In ref. 10, the properties of WC and Pb with thicknesses of 0.1, 0.5, and 1 cm were discussed and analyzed. The results of this work showed that WC in the gamma radiation energy range of 0.160–0.662 MeV has practically equivalent linear and mass attenuation coefficients. The authors of works11,12,14–16 synthesized light composites such as high-density polyethylene and tellurite glasses with the addition of barium oxide in various ratios and revealed that their properties as radiation protection materials are worse than lead (lead density 11.34 g cm−3, tellurite glasses density 5.29–5.34 g cm−3 depending on composition), but the safety of such materials puts them one step above lead protection. In works,17–19 various lead-free composites (Sb/Bi, Ba/Bi, Sb/W, etc.) and single-component materials (Bi, W, Sb, Ba, Cs, etc.) were considered, and their comparison with Pb was performed. These materials demonstrated shielding properties almost equivalent to those of lead. Various cement compositions20 and tungsten-based compositions21–24 were also reviewed and studied in detail. And composites with tungsten (W–C, W–Cu) showed the best results of all the above materials. Thus, in ref. 21, a composite material of WC and ethylene vinyl acetate (WC–EVA) in different ratios (50% EVA and 50% WC; 40% EVA and 60% WC; 30% EVA and 70% WC) was synthesized, and the shielding efficiency of the samples was compared with that of Pb of 1 and 2 mm thickness. The Cs137 isotopes acted as the radiation source. The shielding efficiencies of the WC–EVA compositions under consideration were equivalent to each other and exceeded the shielding efficiencies of lead by 5% for 1 mm thickness and by 9–10% for 2 mm thickness. Whereas, for the I131 source, these values were 1.5 times the effectiveness of lead shielding.

The most important parameter defining radiation shielding materials is their density. An excellent alternative to lead is tungsten, which has a high density and melting point and is inexpensive.17,18,21–23 However, due to the refractoriness of tungsten, modern methods of powder metallurgy in the production of radiation shields from it are expensive, and the production process is very long.25 To solve this problem, it is possible to use fusible materials as binders (matrix). In most composites (with the exception of layered composites), components can be divided into a matrix with reinforcing elements included in it.26 For such purposes, carbon materials, copper, cobalt, bismuth, etc. are used as binder components in tungsten-based composites.21–30

There are many methods of manufacturing composites based on refractory materials: magnetron sputtering, gas sputtering, centrifugal sputtering, spark plasma sintering, 3D printing technologies, selective laser melting, extrusion, inkjet printing, hot stamping, etc.25,31–37 However, the high duration of the processes suggests the need to use other synthesis methods, the duration of which is shorter and the final result matches the requirements for the material.

The purpose of this work is for the first time to obtain W–Bi2O3 composite via hot isostatic pressing, to analyze the effect of high pressure and temperature on the samples sintering process, to determine the dependence of microstructural and structural parameters, chemical composition, and density on sintering conditions, and to determine the shielding efficiency against gamma radiation.

Experimental

All chemicals used were commercial reagents with analytical purity (Sigma-Aldrich, USA). The initial material was a mixture of powders obtained by grinding and mixing separately taken powders W (99 wt%) and binding material Bi2O3 (1 wt%) using a planetary Fritsch Pulverisette ball mill (FRITSCH Laboratory Instruments, Idar-Oberstein, Germany). The duration of homogenization was 3 hours at a rotational speed of 300 rpm. The obtained powder mixture was molded into samples in the form of 2.3 ± 0.1 cm tablets by cold solid-phase pressing.

Then, samples of W–Bi2O3 composite material were obtained by the hot isostatic pressing method for further studies. The main point of the hot isostatic pressing method is the simultaneous thermobaric action on the closed volume. Each of the samples was placed in a container that included a low-resistance graphite mixture, which provides a rapid set of high temperature values. High temperature values help to achieve plasticity in the grains, as a consequence of which it is possible to obtain materials with a density value close to the theoretical one.31 The high value of pressure applied to all samples (5 GPa) contributes to the increase in the reaction area due to the good compaction of the powder grains.

The main feature of this method is the high speed of the process, which is ensured by the fact that the heating and cooling of the produced samples occur under the constant action of high pressure. In our experiments, the duration of the samples sintering was 3 minutes, as described in detail in ref. 23. The samples were 2 × 2 cm2 plates with a thickness of 2 mm. Using this method, six samples of the same shape were received. For each of the samples, there were different synthesis conditions, as presented in Table 1.

Features of synthesis of composite materials based on the W–Bi2O3 system.

Sample No. Sintering temperature, °C Pressure, GPa
1 2000 5
2 1500
3 1000
4 850
5 500
6 25
Open in a new tab

The morphology and chemical composition of the composite samples were studied using a Carl Zeiss EVO10 scanning electron microscope (SEM) (Carl Ziess, Oberkochen, Germany) in combination with an Oxford energy dispersive X-ray spectroscopy (EDX) detector (Oxford Instruments NanoAnalysis, Wiesbaden, Germany). A statistical analysis of tungsten powder grain size was performed using SmartSEM and Gwyddion software. Initial data for the analysis was collected from at least three SEM images.

The calculation of the effective densities of the samples was carried out using the method of hydrostatic weighing.38 The main idea of this method is to measure sample mass, which occurs in two stages: first in air and then in liquid with known exact values of density. In our example, the liquid was distilled water. The values of densities were obtained by calculation, using the reference values of densities of separate components of the composite and the results of hydrostatic weighing. The formula for calculating the theoretical density (ρtheor) of the composite is presented below.

graphic file with name d3ra04509a-t1.jpg 1
graphic file with name d3ra04509a-t2.jpg 2

where V is the composite volume, cm3; x is the percentage content of the composite component; ρ is the density of the composite component, g cm−3.

The effective densities (ρef) of each sample were compared with the theoretical density using the expression:

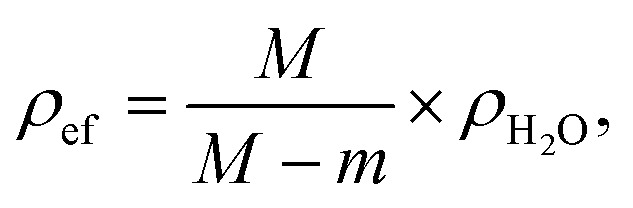graphic file with name d3ra04509a-t3.jpg 3
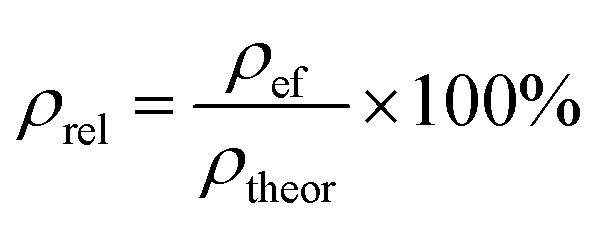graphic file with name d3ra04509a-t4.jpg 4

where ρrel is relative density, %; M is mass of composite in air, g; m is mass of composite in liquid, g; ρH2O is liquid density, g cm−3.

Expression (3) shows how close the values of the effective density of samples are to the theoretical one for W–Bi2O3 composition in percentage terms.

The relative porosity (Prel) of the samples was calculated by the following formula:

Prel = 100% − ρrel 5

The phase composition and lattice parameters were investigated by X-ray diffraction (XRD) analysis using a PANalytical EMPYREAN powder diffractometer (Malvern Panalytical Ltd, Malvern, UK) with Cu-Kα radiation. Diffraction lines were recorded for 2Θ = 20–106° in 0.02° increments. Evaluation of the volume fractions of individual phases was performed using the PowderCell 2.4 program.

The shielding efficiency of gamma radiation was evaluated by simulation using the Phy-X/PSD software package.39 The source of gamma rays was Co60 with energies of 0.826–2.506 MeV. This software was used to calculate the following parameters: linear attenuation coefficient (LAC), half-value layer (HVL), tenth-value layer (TVL), mean free path (MFP), and effective atomic number (Zeff). The estimated parameters were compared with Pb and Bi, the results for which were also obtained using Phy-X/PSD.

graphic file with name d3ra04509a-t5.jpg 6
graphic file with name d3ra04509a-t6.jpg 7
graphic file with name d3ra04509a-t7.jpg 8
graphic file with name d3ra04509a-t8.jpg 9

where ρ is the density of the material; x is the material thickness; N0 is the intensity of the incident gamma radiation on the shield; N is the intensity of the gamma radiation that has passed through the shield.

It should be explained that the HVL is the thickness of the shield material, after which the intensity of directional ionizing radiation will decrease by a factor of two. TVL also characterizes the thickness of the material, but to attenuate radiation by a factor of ten. These values serves as a characteristic of the material's protective properties against the effects of IR. The effective atomic number (Zeff) of a material is equivalent to the atomic number, and the higher it is, the more effective the shielding of gamma radiation. MFP is the average distance a gamma ray can pass without collision, after which its direction or energy changes.

Results and discussion

The results of the density and porosity evaluation of the W–Bi2O3 composite are shown in Table 2. It can be seen that the highest density value of 18.10 g cm−3 corresponds to the sample sintered at 25 °C (sample No. 6). The sample with the lowest density value of 16.98 g cm−3 was sample No. 1, obtained at 2000 °C. Relative density analysis presented that it is sufficiently high for all samples and is 89.13–95.01%. At the same time, the relative porosity decreases with the sintering temperature decreasing from 10.87 to 4.99%, which indicates a small deviation from the theoretical values and corresponds to a high degree of sample compaction.

Results of effective, relative density and porosity parameter of W–Bi2O3 composites.

Sample No. ρ ef, g cm−3 ρ rel, % P rel, %
1 16.98 89.13 10.87
2 17.29 90.76 9.24
3 17.45 91.06 8.94
4 17.36 91.11 8.89
5 17.85 93.70 6.30
6 18.10 95.01 4.99
Open in a new tab

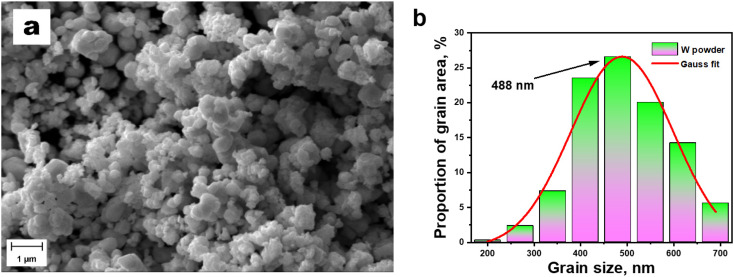
Fig. 1 depicts the SEM image of the surface of the initial tungsten powder (a) and the grain size distribution (b). It is seen that tungsten grains smaller than 480 nm occupy about 26% of the entire area. Based on the results of the Gaussian function approximation, a grain size distribution diagram was plotted. The most probable grain size of the W powder is 488 nm.

Fig. 1. SEM image of the initial W powder (a) and grain size distribution diagram (b).

Fig. 1

Open in a new tab

The analysis of SEM images (Fig. 2) revealed that with the sintering temperature increasing for the W–Bi2O3 composite, defects on its surface and in the volume arise. Microstructure defects are especially noted for sample No. 1 (Fig. 2a), which was obtained at the highest temperature.

Fig. 2. Results of SEM investigation of W–Bi2O3 composites: No. 1 (a), No. 3 (b), No. 5 (c), No. 6 (d). Insets: enlarged SEM images.

Fig. 2

Open in a new tab

Whereas, sample No. 3 (Fig. 2b) has smaller defects, and their quantity decreases with the reduction of the sintering temperature to 1000 °C. Samples No. 5 (Fig. 2c) and No. 6 (Fig. 2d), obtained at 500 °C and 25 °C, respectively, whose density is the highest, have significantly fewer defects compared to samples obtained at higher temperatures.

The results of the chemical composition analysis (Fig. 3) showed that the content of the oxygen phase increased with the rise in sintering temperature.

Fig. 3. Distribution map of the chemical elements of the W–Bi2O3 composites: No. 1 (a), No. 3 (b), No. 5 (c), No. 6 (d).

Fig. 3

Open in a new tab

Samples synthesized in the temperature range from 25 °C to 500 °C have a higher tungsten content, indicating a denser structure (samples No. 5 and No. 6). The increase in oxygen content in samples No. 1 and No. 3 (temperatures of 2000 °C and 1000 °C, respectively) may be due to the course of the redox reaction (RR) with the rising sintering temperature. Obviously, the structure defects of samples No. 1 and No. 3 are directly related to the increased oxygen content (Fig. 3a and b). In this case, bismuth oxide is reduced to metallic bismuth while tungsten is oxidized and becomes WO2, which is confirmed by the results of XRD analysis (Fig. 4). Probably, the occurrence of RR can be called the main cause of defects appearance.

Fig. 4. XRD results of the W–Bi2O3 composites.

Fig. 4

Open in a new tab

XRD results revealed that all samples include bulk-centered cubic W phase, and the presence of the WO2 phase is noted when the synthesis temperature is increased up to 850 °C, which is confirmed by the appearance of diffraction peaks which correspond to 111 and 22−2 crystallographic planes. The volume fraction of bismuth oxide in the sintered material is 1 wt% and it cannot be fixed on the diffractograms, since this amount of phase corresponds to the detection limit of the method. The presence peaks corresponding to the WO2 phase can be associated with the oxidation temperature of tungsten, the value of which under normal conditions is in the range of 400–490 °C. However, under high pressure and limited volume conditions this value can increase. It explains the absence of the oxide phase in the sample obtained at 500 °C and the appearance of the same phase in the sample obtained at 850 °C.

Fig. 5a presents the dependence of the pure W and tungsten oxide WO2 phases content in the W–Bi2O3 composite materials on the sintering temperature.

Fig. 5. Dependence of the phase content (a) and of the tungsten lattice parameter (b) on the sintering temperature of the W–Bi2O3 composite.

Fig. 5

Open in a new tab

It can be seen that the increase in the volume fraction of WO2 occurs with the rise of the samples sintering temperature. So, in sample No. 6 sintered at 5 GPa and 25 °C, there is no WO2 phase, as well as in sample No. 5 obtained at 5 GPa and 500 °C. However, as the sintering temperature increases from 1000 to 2000 °C (samples No. 4 and No. 1, respectively), the WO2 phase appears and the W content decreases from ∼91% to ∼83% (sample No. 1 obtained at 2000 °C).

Fig. 5b depicts the dependence of the W lattice parameter on the sintering temperature. It shows that when the temperature increases up to 1500 °C, the W lattice parameter rises, and then, when the temperature increases up to 2000 °C, the lattice parameter remains unchanged. In this regard, we can assume that bismuth is insignificantly soluble in tungsten.

The shielding efficiency against gamma radiation was obtained from the W–Bi2O3 sample with the highest density (sample No. 6, density 18.10 g cm−3) and compared with those for Pb and Bi to demonstrate the advantages of the composite material compared to other high-Z materials. Fig. 6 presents the dependence of parameters characterizing the shielding efficiency against gamma radiation in the energy range of 0.826–2.506 MeV.

Fig. 6. Dependences of parameters characterizing the shielding efficiency against gamma radiation in the energy range of 0.340–2.506 MeV: LAC (a), HVL (b), TVL (c), MFP (d), Zeff (e).

Fig. 6

Open in a new tab

Fig. 6a suggests that the W–Bi2O3 composite material has a higher LAC value, which indicates its efficiency with respect to the compared materials. In this energy range, the main mechanism of interaction of gamma rays with high atomic number materials, such as W, Pb, and Bi, is Compton scattering, which depends on Z and density.40,41 Thus, when reaching an energy of 0.826 MeV, the LAC value for the W–Bi2O3 composite is 1.19 cm−1, whereas for Pb and Bi, it is 0.97 and 0.85 cm−1, respectively.

The results of the calculation of the half-value layer thickness (Fig. 6b) showed that W–Bi2O3 has the lowest HVL values compared to Pb and Bi. Thus, at an energy of 2.506 MeV, the HVL for Pb is 1.4 cm, whereas it is 1.6 cm for Bi and 0.91 cm for the W–Bi2O3 composite. The same can equally be reported for the TVL calculating results. The values correlate perfectly with the HVL values. It is shown that the W–Bi2O3 composite material also has the lowest TVL values, which are 3.04 cm at a radiation energy of 2.506 MeV. These results demonstrate that W–Bi2O3 composite has the best mass-dimension parameters of all the investigated materials. Therefore, it is recommended to make shields of 2 mm thick and more for effective protection from gamma radiation in the energy range of 0.826–2.506 MeV.

The results of mean free path calculations presented in Fig. 6d showed that for the energy of 2.506 MeV, the MFP value for W–Bi2O3 composite is 1.3 cm, for Pb it is 2.02 cm, and for Bi it is 2.3 cm, which also indicates the superiority of the composite material over the compared materials.

Fig. 6e shows a graph of the dependence of the Zeff on the gamma-ray energy. Calculating of Zeff values is presented only for the W–Bi2O3 composite, since for pure Pb and Bi these values are constants. The Zeff characterizes the interaction of gamma-quants with the medium of a certain composition. The value of the parameter demonstrates that the shielding efficiency of a given composite material will be no worse than shielding by a material with the corresponding atomic number. The graph illustrates that the change of Zeff for the considered composite material in the range of 0.826–2.506 MeV is insignificant. Depending on the energy of gamma rays, the value of the Zeff decreases within hundredths of a fraction (Zeff = 73.52 at energy 0.826 MeV and Zeff = 73.49 at energy 2.506 MeV), but the reduction of this parameter cannot greatly affect the properties of the composite as a radiation shield, because the reduced parameter is too small.

Conclusions

W–Bi2O3 composite samples were synthesized using hot isostatic pressing. The study of the effect of high pressure and temperature conditions on the microstructure and density showed that at a pressure of 5 GPa with increasing temperature from 25 to 2000 °C the number of defects in the W–Bi2O3 composites rose, and the density values decreased from 18.10 to 16.98 g cm−3, while the calculated values of porosity increased from 4.99 to 10.87%, respectively.

The results of structure studies of the W–Bi2O3 composite show that all samples have bulk-centered cubic W phase, and the presence of the WO2 phase is observed when the sintering temperature rises up to 850 °C, which is confirmed by the appearance of diffraction peaks which correspond to 111 and 22−2 crystallographic planes. An increase in the WO2 phase content with the rising sintering temperature was noted. When the temperature changes to 1500 °C, the W lattice parameter growth is observed, and then, when the temperature increases to 2000 °C, the lattice parameter remains unchanged. In this regard, it can be assumed that bismuth has insignificant solubility in tungsten.

The shielding effectiveness of the W–Bi2O3 composites against gamma radiation using the calculation method in the PhyX-PSD software has been evaluated. Co60 isotopes with energies of 0.826 to 2.506 MeV were used as gamma radiation sources. For comparative analysis, simulations were performed for such materials as Pb and Bi. Calculations showed that W–Bi2O3 composites are the most promising among the materials considered for use as radiation shields. W–Bi2O3 composite is most effective in the region of lowest energies (0.826–1.173 MeV), whereas when exposed to gamma radiation with energies from 1.173 to 2.506 MeV, it is necessary to produce shields with higher mass-dimensional parameters, namely, with a thickness in the range from 1.5 to 2 mm.

Conflicts of interest

The authors declare that they have no conflict of interest.

Supplementary Material

Acknowledgments

This research was funded by the scientific and technical program of the Common State “Complex-SG” (contract No. 42-2023 from 27.03.2023). M. S. acknowledge the Academic leadership program Priority 2030 proposed by Federal State Autonomous Educational Institution of Higher Education I.M. Sechenov First Moscow State Medical University of the Ministry of Health of the Russian Federation (Sechenov University).

References

  1. Thibeault S. Kang J. Sauti G. Park C. Fay C. King G. MRS Bull. 2015;40:836–841. [Google Scholar]
  2. Shultis J. K. Faw R. E. Health Phys. 2005;88(4):297–322. [PubMed] [Google Scholar]
  3. Zinkle S. Wiffen F. AIP Conf. Proc. 2004;699:733–740. [Google Scholar]
  4. Abbas M. I. Alzahrani J. S. Sayyed M. I. Tishkevich D. I. Alabsy M. T. El-Khatib A. M. Elsafi M. Materials. 2021;14:5051. doi: 10.3390/ma14175051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Li R. Gu Y. Yang Z. Li M. Hou Y. Zhang Z. Mater. Des. 2017;124:121–130. [Google Scholar]
  6. Vorobjova A. I. Shimanovich D. L. Sycheva O. A. Ezovitova T. I. Tishkevich D. I. Trykhanov A.V. Russ. Microelectron. 2019;48:107–118. [Google Scholar]
  7. Pavlenko V. I. Cherkashina N. I. Noskov A. V. Yastrebinskii R. N. Sokolenko I. V. Russ. Phys. J. 2016;59(8):1192–1197. [Google Scholar]
  8. Li C.-P. Kang C.-Y. Huang S.-L. Lee P.-T. Kuo H.-C. Hsu F.-C. Mater. Lett. 2019;260:126961. [Google Scholar]
  9. Buyuk B. Tugrul A. B. Acta Phys. Pol. 2014;125:423–425. [Google Scholar]
  10. Jamal AbuAlRoos N. Azman M. N. Baharul Amin N. A. Zainon R. Phys. Med. 2020;78:48–57. doi: 10.1016/j.ejmp.2020.08.017. [DOI] [PubMed] [Google Scholar]
  11. Almurayshid M. Alsagabi S. Alssalim Y. Alotaibi Z. Almsalam R. Radiat. Phys. Chem. 2021;183:7. [Google Scholar]
  12. Boonin K. Yasaka P. Limkitjaroenporn P. Rajaramakrishna R. Askin A. Sayyed M. I. Kothan S. Kaewkhao J. J. Non-Cryst. Solids. 2020;550:8. [Google Scholar]
  13. Dong M. Zhou S. Xue X. Feng X. Yang H. Sayyed M. I. Tishkevich D. Trukhanov A. Almousa N. J. Cleaner Prod. 2022;355:131817. [Google Scholar]
  14. Tishkevich D. I. Vorobjova A. I. Trukhanov A.V. Solid State Phenom. 2020;299:281–286. [Google Scholar]
  15. Kurtulus R. Sayyed M. I. Kavas T. Mahmoud K. A. Tashlykov O. L. Khandaker M. U. Bradley D. A. Radiat. Phys. Chem. 2021;186:8. [Google Scholar]
  16. Kozlovskiy A. L. Kenzhina I. E. Zdorovets M. V. Saiymova M. Tishkevich D. I. Trukhanov S. V. Trukhanov A. V. Ceram. Interfaces. 2019;45:17236–17242. [Google Scholar]
  17. McCaffrey J. P. Shen H. Downton B. Mainegra-Hing E. Med. Phys. 2007;34:530–537. doi: 10.1118/1.2426404. [DOI] [PubMed] [Google Scholar]
  18. McCaffrey J. P. Mainegra-Hing E. Shen H. Med. Phys. 2009;36:5586–5594. doi: 10.1118/1.3260839. [DOI] [PubMed] [Google Scholar]
  19. Tishkevich D. I. Grabchikov S. S. Lastovskii S. B. Trukhanov S. V. Zubar T. I. Vasin D. S. Trukhanov A. V. J. Alloys Compd. 2018;749:1036–1042. [Google Scholar]
  20. Waly E.-S. A. Bourham M. A. Ann. Nucl. Energy. 2015;85:306–310. [Google Scholar]
  21. Soylu H. M. Lambrecht F. Y. Ersöz O. A. J. Radioanal. Nucl. Chem. 2015;305:529–534. [Google Scholar]
  22. Vorobjova A. Tishkevich D. Shimanovich D. Zubar T. Astapovich K. Kozlovskiy A. Zdorovets M. Zhaludkevich A. Lyakhov D. Michels D. Vinnik D. Fedosyuk V. Trukhanov A. RSC Adv. 2021;11:3952. doi: 10.1039/d0ra07529a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Tishkevich D. I. Zubar T. I. Zhaludkevich A. L. Razanau I. U. Vershinina T. N. Bondaruk A. A. Zheleznova E. K. Dong M. Hanfi M. Y. Sayyed M. I. Silibin M. V. Trukhanov S. V. Trukhanov A. V. Nanomater. 2022;12:1642. doi: 10.3390/nano12101642. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Dong M. G. Tishkevich D. I. Hanfi M. Y. Semenishchev V. S. Sayyed M. I. Zhou S. Y. Grabchikov S. S. Khandaker M. U. Xue X. X. Zhaludkevich A. L. Razanau I. U. Vinnik D. A. Trukhanov S. V. Zubar T. I. Trukhanov A. V. Radiat. Phys. Chem. 2022;200:110175. [Google Scholar]
  25. Tishkevich D. I. Grabchikov S. S. Lastovskii S. B. Trukhanov S. V. Vasin D. S. Zubar T. I. Kozlovskiy A. L. Zdorovets M. V. Sivakov V. A. Muradyan T. R. Trukhanov A. V. J. Alloys Compd. 2019;771:238–245. [Google Scholar]
  26. Jadhav S. D. Dhekne P. P. Brodu E. Hooreweder B. V. Dadbakhsh S. Kruth J.-P. Humbeeck J. V. Vanmeensel K. Mater. Des. 2021;198:16. [Google Scholar]
  27. AbuAlRoos N. J. Amin N. A. B. Zainon R. Radiat. Phys. Chem. 2019;165:7. [Google Scholar]
  28. Sazali M. A. Md Rashid N. K. A. Hamzah K. IOP Conf. Ser.: Mater. Sci. Eng. 2019;555:012008. [Google Scholar]
  29. Xie T. Fu L. Gao B. Zhu J. Yang W. Li D. Zhou L. Thin Solid Films. 2019;690:8. [Google Scholar]
  30. Kelly J. P. Elmer J. W. Ryerson F. J. Lee J. R. I. Haslam J. J. Addit. Manuf. 2021;39:12. [Google Scholar]
  31. Li H. Yang W. Ma L. Liu G. Yu Y. Cao J. Wei Q. J. Chem. Eng. 2021;426:131479. [Google Scholar]
  32. Günay G. Zienert T. Endler D. Aneziris C. G. Biermann H. Weidner A. Adv. Eng. Mater. 2022;24(8):2200292. [Google Scholar]
  33. Vinnik D. A. Kokovkin V. V. Volchek V. V. Zhivulin V. E. Abramov P. A. Cherkasova N. A. Sun Z. Sayyed M. I. Tishkevich D. I. Trukhanov A. V. Mater. Chem. Phys. 2021;270:124818. [Google Scholar]
  34. Fedotov A. Shendyukov V. Tsybulskaya L. Perevoznikov S. Dong M. Xue X. Feng X. Sayyed M. I. Zubar T. Trukhanov A. Tishkevich D. J. Alloys Compd. 2021;887:10. [Google Scholar]
  35. Zhu X. Cheng J. Chen P. Wei B. Gao Y. Gao D. J. Alloys Compd. 2019;793:352–359. [Google Scholar]
  36. Li Y. Luo G. Sun Y. Zhang J. Shen Q. Zhang L. Appl. Surf. Sci. 2020;516:9. [Google Scholar]
  37. Trukhanov A. V. Kozlovskiy A. L. Ryskulov A. E. Uglov V. V. Kislitsin S. B. Zdorovets M. V. Trukhanov S. V. Zubar T. I. Astapovich K. A. Tishkevich D. I. Ceram. Int. 2019;45:15412–15416. [Google Scholar]
  38. Crawley A. F. Int. Mater. Rev. 1974;19(1):32–48. [Google Scholar]
  39. Şakara E. Özpolatb Ö. F. Alımc B. Sayyed M. I. Kurudireka M. Radiat. Phys. Chem. 2020;166:12. [Google Scholar]
  40. Chen S. Bourham M. Rabiei A. Radiat. Phys. Chem. 2015;117:12–22. [Google Scholar]
  41. Tishkevich D. I. Vorobjova A. I. Vinnik D. A. Mater. Sci. Forum. 2019;946:235–241. [Google Scholar]

Articles from RSC Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES