Abstract
We investigate main-chain liquid crystal elastomers (LCEs) formed by photoresponsive azobenzene units with different populations of trans and cis conformers (from fully trans to fully cis). We study their macroscopic properties as well as their molecular organization using extensive Monte Carlo simulations of a simple coarse-grained model where the trans and cis conformers are represented by soft-core biaxial Gay–Berne particles with size and interaction energy parameters obtained by fitting a bare bone azobenzene moiety represented at atomistic level. We find that increasing the fraction of cis conformers, as could be obtained by near-UV irradiation, shifts the nematic–isotropic transition to a lower temperature, consistently with experiment, while generating internal stress in a clamped sample. An analysis of pair distributions shows that the immediate surroundings of a bent cis molecule are slightly less dense and more orientationally disordered in comparison with that of a trans conformer. Comparing nematic and smectic LCEs, actuation in the smectic phase proved less effective, disrupting the smectic layers to some extent but preserving orientational order of the azobenzene moieties.
Keywords: liquid crystal elastomers, azobenzene, actuation, Gay−Berne potential, Monte Carlo simulations
Introduction
Stimuli-responsive materials are an important class of smart materials capable of responding to an externally applied trigger through an observable property change. These triggers can include temperature variation, application of an external electric or magnetic field, and irradiation with light, of interest here.1 The latter applies, for example, to photoresponsive polymers2,3 containing azobenzene moieties whose molecular shape anisotropy changes significantly upon irradiation with near-ultraviolet (UV) light causing a trans to cis isomerization.4,5 If these moieties are themselves mesogenic and exhibit nematic or smectic phases,6,7 it is found that their orientational, liquid-crystalline ordering can be decreased or destroyed upon irradiation with light even at constant temperature (with an effect similar to that of increasing temperature).8−14 Somewhat amazingly the conformational changes take place even in very viscous glassy materials, possibly through photofluidization,15 although the issue is still debated.16 Photoresponsive liquid crystal elastomers (LCEs), characterized by a pronounced strain-alignment coupling, can be obtained when azobenzenes are covalently linked to a cross-linked polymeric network1,17−19 or even just dissolved as guest in the LCE matrix.20 Such materials can exhibit significant elastic deformations upon phase transitions between the orientationally ordered liquid crystalline state and the disordered isotropic phase and can thus act as photoactuators converting light energy into mechanical work.20−23 In view of this, photoresponsive LCEs are promising candidates for a variety of applications,24 including sensors and actuators,1,25−27 photomechanical devices,19 morphing surfaces,22 soft robotics,28,29 and more, also thanks to advances in chemical synthesis.30
The photophysics process of switching between the trans and cis states (see Figure 1) of an individual azobenzene molecule has been modeled in many studies in vacuum4,5 or, at the atomistic level, for azobenzene in isotropic solvents,31,32 but simulations performed at this level of detail can be considered only for systems with a small number of molecules. Atomistic and multiscale modeling has also been performed for the low molar mass azobenzene mesogen 4,4′-dioctyloxyazobenzene (8AB8) to investigate its phase changes.33 7AB (p,p′-diheptylazobenzene) in 8CB (4-octyl-4′-cyanobiphenyl) has also been studied, in particular to examine the preferred location of trans- and cis-7AB in the smectic A phase of 8CB and finding that while the trans form is hosted inside the smectic layers, the cis tends to reside between the layers.34 Recently, atomistic simulations of azobenzenes in molecular- and polymer-network glasses have been carried out to study their behavior during and after photoactivation in a rigid matrix environment.35,36
Figure 1.

(a) Sketch of the typical main-chain LCE network topology. The dashed circle indicates one of the trans or cis azobenzene units whose united-atom representation is shown together with their coarse-grained GB ellipsoids in (b), trans, and (c), cis. The grey and blue spheres represent the −CH– groups and the nitrogen atoms, respectively. The conformational change at the double bond between the nitrogen atoms results in a significant modification of the fitted coarse-grained molecular shape depicted by the transparent ellipsoids. Insets: locations of bond site positions at the GB ellipsoid surface and easy bond directions for the main-chain bonding (red) and for the optional cross-linking via the equatorial site (blue), as used in simulation. For the trans isomer, the head and tail bonding sites are assumed to impose an easy direction along the molecular long axis, while the optional site on the equator is taken to impose an easy direction along the second-longest molecular axis. In the cis isomer, the linking directions of the head/tail sites are tilted to make an angle of ≈46° with the long molecular axis.
As far as liquid crystal polymers are concerned, apart from theoretical efforts37 aimed at understanding azobenzene-based polymers, a few particle-based computer simulation studies have also been performed at the coarse-grained level,38,39 particularly with the purpose of studying the photoselective azobenzene excitation followed by effective reorientation of the director under linearly polarized UV light excitation.14
It is worth noting that, although very interesting in themselves, the details of the trans–cis conversion are not of central interest in terms of properties of the material exposed to isotropically distributed unpolarized UV light, if only for a time-scale argument. Indeed, the photoinduced trans-to-cis conversion is a very fast one that can even be performed in a few femtoseconds with a sufficiently powerful light source, while the rate of the spontaneous thermal cis-to-trans back conversion depends greatly on the specific compound40 and, unless pumped back by irradiation in the visible, where the typical cis absorption peak occurs, is typically slow to very slow (even well over a day41). We can then imagine that a system, initially with all azobenzenes in the trans state, could be suitably irradiated to yield a system with a certain controlled fraction of cis and that this system will be sufficiently long-lived to establish different molecular organizations according to the achieved fraction. Accordingly, our aim here is to investigate how the presence of this mixture of conformers will affect LCE phase transitions, sample deformation, and the differences of local structure around the two types of conformers. As far as we know, these aspects have not been dealt with before.
In the next sections, we describe our coarse-grained model for azobenzene LCEs and the range of Monte Carlo (MC) simulations performed on LCEs with various percentages of trans and cis conformers, monitoring ordering and structure as a function of temperature. Stress–strain curves at selected temperatures and trans and cis conformer ratio will also be provided. Conclusions will be collected in the last section.
Model and Simulations
We choose a generic particle model where only the essentials of an azobenzene-based LCE are retained. This type of approach is probably unavoidable, considering that the actuation in LCE is a collective phenomenon involving a large number of particles. Moreover, reliable microscopic modeling of any cross-linked LCE system should involve samples whose size well exceeds the characteristic distance between the cross-links (that, in turn, significantly exceeds the size of a single molecule) to exclude the effects related to local irregularities in the LCE polymer network. Currently, sufficiently large sample sizes can only be achieved at the coarse-grained simulation level. Ideally, one would want to connect the benefits of the atomistic and coarse-grained treatment in a suitable multiscale approach. For this reason, in this study, we start from an atomistic-level optimization of the molecular structure for both azobenzene conformers, trans and cis, and use them to estimate the corresponding interaction parameters of the soft-core Gay–Berne (GB) attractive–repulsive potential acting between biaxial ellipsoidal particles representing the molecules42,43 that is commonly used in large-scale simulations of liquid-crystalline systems.7 With the thus obtained GB molecular building blocks, we assemble suitable LCE networks, following the methodologies developed in refs (44–46) and perform large-scale MC simulations. From the results, we determine the shift of the nematic–isotropic (NI) transition temperature upon increasing the cis particles content, together with the magnitude of the internal stress generated upon irradiation of the sample with UV light. Moreover, we examine the positional and orientational intermolecular correlations in the vicinity of both trans and cis particles.
We have previously modeled and simulated LCEs using soft GB units47 linked together by finitely extendable nonlinear elastic (FENE)48,49 spring-like bonds.44−46 The soft-core modification of the original GB (Appendix A)42,50 reduces its harsh repulsion, making entangling of the chains more manageable, and turns out to be essential for a proper equilibration of cross-linked GB polymer networks. In addition, a soft biaxial version of the GB potential (SBGB) has also been developed.43 It is thus natural to extend this approach to photosensitive LCEs by replacing some or all of monomer units with SBGBs modeling either trans or cis azobenzene moieties (see Figure 1a).
It is worth noting that an atomistic model, apart from being hardly feasible in terms of resources, as already mentioned, could even be not ideal, since it has to pay the appealing feature of being chemically realistic with the specificity of being applicable only to a certain chemical formulation. Since the actuation phenomenon we aim to better understand takes place for a variety of molecular structures, which have in common only the presence of the photoresponsive azobenzene moiety, it is desirable to develop a minimal model where only the trans–cis conversion is accounted for and other chemical details abandoned.
In practice, we study, using MC simulations, the effect of replacing a certain fraction of trans azobenzenes with cis conformers in the LCE. We shall go from full trans to full cis, considering fractions of ciswc = 0, 0.2, 0.4, 0.6, 0.8, and 1.0 fixed during the simulation at various temperatures. In order to maximize the order-disruption effect and, consequently, the actuation, here all GB ellipsoids, both those of the polymer strands and the cross-linkers, are taken to be switchable azobenzenes as, for example, in ref (21). The coarse-graining step from the atomistic to coarse-grained description of a model azobenzene molecule is sketched in Figure 1b,c. As we can see, our minimal molecular model of an azobenzene photoresponsive unit consists of two aromatic rings connected via a N=N double bond whose loosening under the effect of UV light gives rise to the trans–cis isomerism5,51 that is responsible for the difference in the effective molecular shape. At the coarse-grained level, both isomers are represented by biaxial ellipsoids (since no molecule is perfectly uniaxial), whose interaction parameters need to be determined from an atomistic representation. Since we now have various types of units, interactions between dissimilar biaxial GB particles have to be considered.52
The main input parameters of the soft-core GB potential describing the two isomers are particle dimensions expressed through ellipsoidal axes (σx, σy, and σz) and the energy parameters (ϵx, ϵy, and ϵz) related to the attractive potential well depths for corresponding homogeneous particle alignments.50 Their values are reported in Table 1 and have been obtained from atomistic representations at united atom (UA), rather than at all-atom level. Note that not only the molecular aspect ratio and the relative characteristic potential well depths can be derived from the fitting but also their absolute values that eventually translate into macroscopically observable quantities. More details can be found in Appendix A and Appendix B.
Table 1. Soft-Core GB Potential Parameters (Ellipsoidal Axes in Units of σ0 = 0.35 nm and Energy Parameters in Units of ϵ0 = 1.3 × 10–21 J) for the Two Azo Isomers, as Obtained From the UA Fitting (Appendix B).
| conformer | σx | σy | σz | ϵx | ϵy | ϵz |
|---|---|---|---|---|---|---|
| trans | 1.00 | 1.21 | 4.00 | 1.00 | 0.25 | 0.08 |
| cis | 0.86 | 1.36 | 3.14 | 1.21 | 0.81 | 0.26 |
We consider a main-chain system where the elongated mesogenic moieties belong to the polymer backbone. In order to build an elastomer network, the fitted SBGB particles are bonded with other ellipsoids to build the main chains, as well as connected to other chains via cross-linking particles. In our minimal model, we neglect, apart from the change of shape, any realistic chemical details and just assume that each trans particle is decorated with a “head” and “tail” bonding site, that will be displaced at an angle in the cis molecule, following the conformational change. We also arbitrarily assume (ignoring at this idealistic model level any chemical difficulty) that the cross-linking particles have an additional bonding site on the equator. The positions of the bonding sites and the easy (preferred) directions of the resulting bonds, as assumed in the GB simulation, are indicated in the insets of Figure 1b,c.
The bonds themselves are modeled using the FENE potential48 applied both to bond stretching and bending,44 see Appendix A. The FENE potential, which is often used in modeling polymer chains, has the important feature of being stiffer for large deformations than its Hookean counterpart, imposing a maximum stretching and bending range.
All samples considered in this study contain N = 64,000 GB particles. Like in our previous work,44−46 we consider LCE swollen with a liquid-crystalline solvent (in practice a monomeric excess), which are characterized by a greater mobility of polymeric chains and have been experimentally studied.53−55 Thus, only one-half of the mesogens is used to build the elastomeric polymer network itself, while the rest represents the nonbonded swelling monomers introduced to facilitate the relaxation of polymer chains in simulation, while conveying nematicity at the same time.44 Periodic boundary conditions56,57 are applied in each sample preparation and in simulations to mimic a larger bulk sample. The polymer network is assembled following the steps similar to those presented in ref (46) to build polydomain LCE samples. Here, however, again to maximize actuation, we consider monodomain samples where the average molecular orientation, the nematic director, is the same throughout the sample and is imprinted parallel to, say, the laboratory z-axis. This is accomplished by growing, at low density, straight individual chains of particles, polydisperse and on average ∼12 monomers long, each starting from a random position within a cubic simulation box, directed at a random angle smaller than arccos(0.6) ≈ 53°, measured from the z-axis. Then, the active heads and tails of each chain are connected laterally to a nearest equatorial site on another, neighboring chain. A schematic representation of the typical resulting elastomer architecture is shown in Figure 1a. Finally, the system is soaked with swelling monomers and isotropically compressed almost to close-packing, increasing the density more than 20 times, to yield a cubic sample that we consider as a “reference” one. In principle, one should consider several of these reference samples to obtain a collection of LCE networks grown under the same conditions, but this is practically unfeasible in view of the computer time required. We have thus considered a single reference, also because, based on our previous experience,44−46 one replica for each cis particle concentration is sufficiently representative for a sample size as large as our one (N = 64,000) where the simulation box side significantly exceeds the average distance between the network cross-links.
Note that in our simulations,
the reduced number densities  , where V is the sample
volume and σ0 is the shortest axis of the trans ellipsoid, depend on the cis particle
fraction wc. This is because the fitted
coarse-grained molecular volume (proportional to σxσyσz) is somewhat smaller for the cis isomer than for the trans one (see Table 1), and it is necessary to avoid
shifts of the NI transition due to a mere dilution effect. Consequently,
the final sample densities increase with increasing wc. In a simplified approach, we determine these densities,
summarized in Table 2, by keeping the molecular packing fraction unchanged for all wc. Note that the ρ* values employed are
taken to be relaxed equilibrium values that are assumed constant during
a simulation run. At variance with this, experiments22 have shown a reduction in sample density upon sample irradiation,
which, however, is a transient phenomenon beyond the scope of the
present study.
, where V is the sample
volume and σ0 is the shortest axis of the trans ellipsoid, depend on the cis particle
fraction wc. This is because the fitted
coarse-grained molecular volume (proportional to σxσyσz) is somewhat smaller for the cis isomer than for the trans one (see Table 1), and it is necessary to avoid
shifts of the NI transition due to a mere dilution effect. Consequently,
the final sample densities increase with increasing wc. In a simplified approach, we determine these densities,
summarized in Table 2, by keeping the molecular packing fraction unchanged for all wc. Note that the ρ* values employed are
taken to be relaxed equilibrium values that are assumed constant during
a simulation run. At variance with this, experiments22 have shown a reduction in sample density upon sample irradiation,
which, however, is a transient phenomenon beyond the scope of the
present study.
Table 2. Reduced Sample Densities ρ* as a Function of cis Particle Fraction wc.
| wc | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
|---|---|---|---|---|---|---|
| ρ* | 0.176 | 0.185 | 0.195 | 0.206 | 0.218 | 0.232 |
To find equilibrium configurations at a given wc and temperature T, we performed MC simulations following the standard Metropolis algorithm.7,58 In each MC cycle (a cycle being a set of N attempted MC moves), particles are selected one by one in random order and undergo an individual trial move that is accepted if the associated interaction energy change ΔU is negative, or with a probability of exp(−ΔU/kBT) otherwise, where kB denotes the Boltzmann constant. For a full definition of the interaction energy U, see Appendix A.
In each MC cycle, different trial move types are attempted separately: translational moves, rotational moves,59 and bonded pair rotations.44 In addition, every 5 MC cycles, a collective resize move is performed, where the cuboidal simulation box itself is randomly and affinely deformed at a constant volume, and subjected to the same Metropolis acceptance criterion as above (more details can be found in refs (44−46)). The trial move amplitudes are adjusted on the fly to maintain a trial move acceptance ratio of around 50% while ensuring that the system is evolving in terms of particle positions and orientations. In the calculations of interaction energies, the computational effort is reduced by setting up particle neighbor lists60 with interaction and list cutoffs at 6σ0 and 7σ0, respectively. Moreover, neighbor list updates are facilitated by means of cell-linked lists,56 and further parallelization schemes are employed to provide additional simulation speedup.
As a result, several 107 MC cycles have typically been performed for sample equilibration and ∼106 cycles for production. Typical averages of interest include (i) the reduced sample length λz along the z-axis, the nematic director of the monodomain, to monitor actuation, (ii) the standard nematic order parameter P2 to follow the underlying changes in orientational order, and (iii) the specific heat of the sample to facilitate the detection of the associated phase transitions. (i) Here, λz is conveniently defined as the average simulation box length along the z-axis, divided by the side of a reference sample containing trans particles only. (ii) The nematic order parameter calculation is performed calculating, for a certain MC cycle, the nematic ordering matrix
| 1 |
where ui stands for the long molecular axis of the ith molecule and I is a 3 × 3 identity matrix, and diagonalizing Q to identify its largest eigenvalue, which is then averaged over MC cycles to yield the order parameter indicated here as P2.7 (iii) Further, the reduced specific heat (per particle and in units of kB) is calculated as c* = d⟨U*⟩/dT*, where the reduced internal energy and temperature are introduced as U* = U/Nϵ0 and T* = kBT/ϵ0, respectively, and ⟨···⟩ stands for averaging over MC cycles. (Here, ϵ0 is the energy parameter related to the attractive GB potential well depth for a pair of perfectly aligned biaxial trans particles approaching along their shortest axes.50,52)
Finally, to identify layered smectic phases, the structure factor S(q) can be calculated as61
| 2 |
where q denotes the scattering
vector and rj stands for
the center-of-mass position of the jth anisotropic
bead. Then, to assess the degree of smectic ordering, we define and
calculate a smectic-like positional order parameter as  , where q1 is parallel
to the nematic director and corresponds to the first-order peak of S(q) resulting from smectic layering, similarly
as in ref (62).
, where q1 is parallel
to the nematic director and corresponds to the first-order peak of S(q) resulting from smectic layering, similarly
as in ref (62).
Results and Discussion
In an aligned nematic containing trans azobenzene moieties either as part of the mesogens or as solutes, the presence of cis conformers represents a source of disruption in the alignment of their environment. This destabilizes the nematic phase and decreases the NI transition temperature, as observed experimentally.8−14 Therefore, we first explore the phase diagram of the LCE samples we have generated, as a function of reduced temperature T* and cis particle content, wc, even for very large values of the latter.
Simulation
runs at all temperatures have been launched from the
corresponding “reference” samples, except for a few
cases at low temperatures (T* ≤ 3.0) where
the runs were started from a pre-equilibrated configuration at a nematic
temperature to facilitate MC equilibration. In an all-trans sample (wc = 0), plots of the sample
dimension λz and of the nematic
order parameter P2 against temperature
(Figure 2) reveal an
isotropic-to-nematic phase transition at 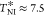 . (Taking ϵ0 ≈ 1.3
× 10–21 J, as obtained from the UA fitting,
this yields a NI transition at ∼430 °C.) Below this temperature,
the sample acquires an elongation along the z-axis,
as imprinted upon sample preparation, that coincides with the nematic
director, and a nonzero degree of nematic order (Figure 2b,c). The transition itself
is also accompanied by a peak in the temperature dependence of the
reduced specific heat, c* (Figure 2a). For this all-trans sample,
there is also an additional peak in c* below T* ≈ 1.5 corresponding to the phase transition from
the aligned nematic into the aligned and layered smectic phase—characterized
by a nonzero smectic order parameter τ, Figure 2d—suffering from extremely slow MC
relaxation.
. (Taking ϵ0 ≈ 1.3
× 10–21 J, as obtained from the UA fitting,
this yields a NI transition at ∼430 °C.) Below this temperature,
the sample acquires an elongation along the z-axis,
as imprinted upon sample preparation, that coincides with the nematic
director, and a nonzero degree of nematic order (Figure 2b,c). The transition itself
is also accompanied by a peak in the temperature dependence of the
reduced specific heat, c* (Figure 2a). For this all-trans sample,
there is also an additional peak in c* below T* ≈ 1.5 corresponding to the phase transition from
the aligned nematic into the aligned and layered smectic phase—characterized
by a nonzero smectic order parameter τ, Figure 2d—suffering from extremely slow MC
relaxation.
Figure 2.
(a) Reduced constant volume specific heat per particle (c*), (b) sample length along the z-axis (λz), as well as the (c) nematic and (d) smectic order parameters (P2 and τ, respectively), plotted as a function of reduced temperature for samples with different cis particle contents wc. The corresponding cis fractions are wc = 0.0 (×), 0.2 (circles), 0.4 (triangles), 0.6 (squares), 0.8 (diamonds), and 1.0 (+). Additional data points, obtained for the same wc but choosing a different set of cis particles, are also plotted for comparison (open symbols).
As the cis particle content is increased, parallel
nematic alignment is destabilized and the NI transition shifts toward
lower temperatures as 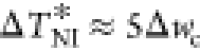 . (Taking again ϵ0 ∼
1.3 × 10–21 J, the NI temperature is estimated
to drop by ∼4.7 K for every additional % of sample particles
excited into the cis state. Note, however, that a
comparison with experiments is not straightforward here since both
the NI transition temperature and its shift depend not only on the
precise chemical nature of the mesogen but also on other features
of the elastomer network and are thus quite system-dependent.) In
a simulation, it is also possible to investigate the all-cis limit (wc = 1.0), which may be rather
far from reach with photoirradiation experiments, and from a nonzero P2 value (see Figure 2c), one can deduce that an aligned phase
with orientational ordering is established even in this case. (Our
simulations suggest that this happens for T* <
3.5 also in a nonbonded liquid-crystalline system consisting of monomers
alone. In an LCE sample, such order is further enhanced by the mechanical
aligning field18 imprinted along the z-axis upon sample preparation.)
. (Taking again ϵ0 ∼
1.3 × 10–21 J, the NI temperature is estimated
to drop by ∼4.7 K for every additional % of sample particles
excited into the cis state. Note, however, that a
comparison with experiments is not straightforward here since both
the NI transition temperature and its shift depend not only on the
precise chemical nature of the mesogen but also on other features
of the elastomer network and are thus quite system-dependent.) In
a simulation, it is also possible to investigate the all-cis limit (wc = 1.0), which may be rather
far from reach with photoirradiation experiments, and from a nonzero P2 value (see Figure 2c), one can deduce that an aligned phase
with orientational ordering is established even in this case. (Our
simulations suggest that this happens for T* <
3.5 also in a nonbonded liquid-crystalline system consisting of monomers
alone. In an LCE sample, such order is further enhanced by the mechanical
aligning field18 imprinted along the z-axis upon sample preparation.)
We note that while
working with a certain fraction wc of cis-azobenzenes, the specific selection
of cis particles is chosen (randomly) before the
simulation and then left fixed. Ideally, one could consider many sample
replicas with different cis–trans particle sets and perform an average over simulations of these isomeric
replicas. In practice, each simulation for our sample size takes too
long to make this feasible. However, to check the robustness of our
results, typically obtained from a single isomeric replica, we have
repeated the temperature-scan experiment on a second alternative sample
with a different cis-particle distribution (and the
same wc) and the results for the two replicas
considered (especially the  values) turn out to be in very
good agreement
(see Figure 2 and compare
full and empty symbols).
values) turn out to be in very
good agreement
(see Figure 2 and compare
full and empty symbols).
The presence of shorter cis particles locally disrupts the nematic orientational order established by the more anisotropic trans particles. To gain more insight into how this happens, it is instructive to study the surroundings of each isomer type separately by calculating their radial distribution functions g(rij) and orientational order correlation functions G2(rij), for example, from a single molecular snapshot. g(rij) is calculated by identifying and counting all particle pairs where the first particle belongs to the selected azo-species and then creating a corresponding histogram with respect to the interparticle distance rij. The histograms are normalized with respect to an uncorrelated uniform fluid and then averaged over all possible selections of the first particle of the given species. As such, g(rij) is then proportional to the local density of all particles surrounding a particle of a given azo-species. A similar analysis can be performed by averaging P2(ui·uj) over eligible pairs of particles i and j (instead of just counting the pairs), where ui and uj denote the particle long axes and P2(x) = (3x2 – 1)/2 is the second Legendre polynomial, giving the second-rank orientational pair correlation7
| 3 |
The correlation properties in a sample with 20% cis-content are summarized in Figure 3a. The radial distribution functions gc(rij) and gt(rij) for the surroundings of cis and trans isomers (top plate), respectively, show no major qualitative differences at a nematic temperature of T* = 3.0, but the details are compatible with the somewhat different particle shapes (see Table 1). The difference of average local particle densities in the vicinity of cis and trans particles, given by Δg(rij)ρ*, where Δg(rij) = gc(rij) – gt(rij) and ρ* is the average sample density, is shown as inset in Figure 3a at different T* in the aligned nematic phase. At smallest distances, gc(rij) > gt(rij) due to the smaller σx for the cis isomer, which is followed by a pronounced gc(rij) < gt(rij) region. As a result, within a small sphere ∼4σ0 in diameter surrounding a cis particle, there are slightly less molecules than in an equal-sized sphere surrounding a trans particle. This appears to be consistent with observations and hypotheses by Liu.63 Recall that here wc = 0.2, so that the vast majority of isomers are in trans state. A cis particle thus represents a slight ordering disruption and is somewhat less efficiently embedded into its predominantly trans-environment, than any trans particle itself. From the inset of Figure 3a, it also follows that these effects are more pronounced at lower temperatures.
Figure 3.
Pair correlation properties. (a) Top: radial distribution functions gc(rij) (+) and gt(rij) (×) at T* = 3.0 and wc = 0.2, plotted separately for the surroundings of cis and trans particles, respectively. Bottom: same as above but showing the corresponding orientational correlation functions G2(rij). Inset: the difference of the local densities surrounding the two particle types (see text) at T* = 2.0 (squares), 3.0 (circles), and 4.0 (triangles), for wc = 0.2. (b) G2(rij) correlation functions at T* = 3.0 for the surroundings of cis and trans particles (open and closed symbols, respectively) for wc = 0.2 (squares), wc = 0.4 (circles), wc = 0.6 (triangles up), and wc = 0.8 (triangles down). The interparticle distances rij are plotted in units of σ0.
Further, the orientational correlation functions G2(rij) are shown for wc = 0.2 in the bottom plate of Figure 3a separately for both isomers. At small rij, they show a similar structure as their g(rij) counterparts, while for large rij where the short-range correlations are already lost, they are expected to relax to a value equal to the product of the nematic order parameters of the central (cis or trans) and a far-away (any type) azobenzene particle. (This follows from the addition theorem for second-order spherical harmonics in the absence of biaxial molecular ordering.) From the lower G2(rij → ∞) value for a cis particle at the center in comparison with the corresponding value for a central trans particle, one can conclude that the degree of orientational order of cis particles themselves (in a trans-rich wc = 0.2 sample) is lower than that of the trans particles. Similar behavior is also systematically observed at larger wc values (see Figure 3b): the longer trans particles are always more orientationally ordered than the shorter cis ones, which results in a higher G2(rij → ∞) value in case of a central trans particle, compared with that of a central cis particle. At the same time, the G2(rij → ∞) values, at given temperature, for both particle types decrease with increasing wc due to a general weakening of the nematic ordering (Figure 2c).
Studying photoresponsive LCE, it is also interesting to look at sample behavior when increasing the wc fraction at fixed temperature. Figure 4a shows a series of molecular snapshots in such a situation at T* = 4.0 where the actuative effect upon changing wc is largest (as can be deduced from Figure 2). At this temperature, an all-trans (wc = 0) sample is nematically ordered and the sample strongly elongated along the z-axis. The increase of cis-content, wc, results in a gradual destruction of orientational order, as well as in the loss of sample elongation. This behavior could be exploited in actuation to extract useful mechanical work from the system. The simulation box side λz vs wc is shown as inset, Figure 4b, for different temperatures. All dependences decrease monotonically, whereby lower temperatures generally result in a higher value of λz.
Figure 4.
(a) Molecular snapshots depicting a gradual irradiation of an LCE sample at T* = 4.0, with corresponding cis particle fractions wc displayed. Trans particles are colored blue, and cis particles orange. Upon cis fraction increasing, nematic orientational order is lost and the sample contracts along the director, z axis. (b) Reduced sample length along the z-axis, λz, plotted against wc for different temperatures: T* = 1.0 (closed squares), 2.0 (open squares), 3.0 (closed circles), 4.0 (open circles), 5.0 (closed triangles up), 6.0 (open triangles up), 7.0 (closed triangles down), and 8.0 (open triangles down).
At low enough temperatures, the simulated LCE samples are in the smectic phase. Given that in an LCE system, the ellipsoidal molecules are bonded in a rather complex cross-linked network, the smectic layers are well-defined but present plenty of defects. The molecular snapshot close-ups depicting actuation as wc increases in a simulated smectic LCE at T* = 1.0 are shown in Figure 5a. The increasing presence of the short cis particles additionally perturbs the smectic layers initially consisting of longer trans particles, but the orientational order, together with sample elongation, persists even in an all-cis sample at wc = 1.0. In addition to molecular organization snapshots (Figure 5a), the presence of positional smectic ordering is further evidenced by the structure factor patterns depicted in Figure 5b where a series of peaks along the z-axis (parallel to the smectic layer normal and the nematic director) is clearly visible. (The less pronounced arcs in the direction perpendicular to z are a signature of interlayer molecular ordering.) Figure 5c further shows the evolution of the smectic order parameter τ with increasing cis-content: at first, τ decreases due to the somewhat disrupted layering. However, approaching the all-cis sample, τ increases again, which can be attributed to the absence of the perturbing longer trans particles in a cis-rich environment. Note also that with increasing wc, the structure factor peaks move to a slightly higher wavevector value |q1|, compatibly with the shorter long axis of cis particles.
Figure 5.
(a) Close-up snapshots for wc = 0 (all-trans), wc = 0.4, and wc = 1.0 (all-cis) in the smectic phase (T* = 1.0), together with the corresponding structure factor patterns (b). Same molecular color coding as in Figure 4a is used. The two dashed horizontal hairlines in plots (b) indicate the position of the first maximum associated with smectic layering in the all-trans and all-cis samples. (c) Smectic order parameter τ as a function of wc. Smectic layering is partially disrupted as the cis-particle content increases, but the orientational ordering and sample elongation are preserved even for wc = 1.0. In an all-cis sample, the smectic ordering is to some extent restored.
Above we have seen that
upon light-induced actuation, an initially
elongated sample contracts along the nematic director, z-axis. Such behavior applies to a free (unclamped) sample. Alternatively,
one could also consider an irradiation experiment with a clamped sample
whose length λz is fixed. A trans–cis photoisomerization under such conditions
is inevitably accompanied by a generation of internal stress resulting
from an increase of molecular disorder that is, in turn, balanced
by the external stress of the clamps. To estimate the magnitude of
stress thus generated at a given temperature, we consider a contracted
sample with wc ≠ 0 and apply external
stress to stretch the sample along the z-axis to
its initial length λz measured at wc = 0. Each stretching experiment is performed
through an isostress MC run57 where, apart
from temperature, engineering stress Σzz along the z-axis (here calculated with respect
to the surface area corresponding to a face of the all-trans reference sample) is fixed. Having fixed an additional extensive
thermodynamic variable, the Metropolis acceptance criterion has to
be modified: the internal energy change ΔU is
replaced by the change of enthalpy ΔH,57,64 where the interaction enthalpy H is given by U – ΣzzVλz; V here denotes the corresponding sample volume. The reduced external
engineering stress is conveniently defined as 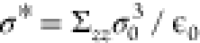 .
.
It is quite impossible to guess the correct value of stress σ* necessary to stretch an irradiated sample far enough to exactly match its initial length. For this reason, we simulate full stress–strain curves λz(σ*) and perform the necessary extrapolation between the data points thus obtained to find σ*. Each of the necessary simulation runs was started from a sample previously equilibrated at the required conditions (T*, wc) and zero stress. In Figure 6, stress–strain curves for two values of wc (0.2 and 0.4) and two temperatures (4.0 and 6.0) are plotted. In the low-stress region, σ* < 0.03, the dependence is close to linear and, as a byproduct, the corresponding isothermal Young elastic moduli can be estimated from the λz(σ*) slopes determined by appropriate fitting. Taking ϵ0 ∼ 1.3 × 10–21 J and σ0 ∼ 0.35 nm from the UA fitting, the resulting values at T* = 4.0 are ∼3.3 and ∼2.6 MPa for wc = 0.2 and wc = 0.4, respectively. At a higher temperature of T* = 6.0, ∼1.0 and ∼0.2 MPa are estimated for wc = 0.2 and wc = 0.4, respectively. The modulus decreases with increasing cis particle content and decreases with temperature; its values are relatively high but compatible with our previous results for simulated LCE in the nematic phase.
Figure 6.
Stress–strain curves used for the estimation of the internal stress generated upon sample irradiation with light. The open symbols correspond to wc = 0.2, the closed ones to wc = 0.4; the squares correspond to T* = 4.0, the circles to T* = 6.0. Dotted lines represent the linear fits in the low-stress region (σ* < 0.03).
Turning now to the values of internal stress σ* in a clamped sample, at T* = 4.0, we obtain 0.010 and 0.017 for wc = 0.2 and wc = 0.4, respectively. At T* = 6.0, the corresponding values are 0.009 and 0.021. (Assuming the same values for ϵ0 and σ0 as above, the given σ* values are to be multiplied by ∼30 MPa to obtain the engineering stress Σzz.) At a given temperature, internal stress in a clamped sample thus increases with irradiation (leading to higher cis-content wc) since a larger sample contraction has to be compensated for by the clamps. For the same reason, at a given wc, one would expect internal stress to increase also with increasing temperature, but this is not always the case since at higher temperature our samples also become softer, which reflects in a reduction of the Young’s elastic modulus. Finally, the typical magnitude of the generated internal stress is estimated to be of the order of several hundred kPa.
Conclusions
We have performed a computational study of the effects that different percentages of trans and cis azobenzene monomeric units can have on the properties of a model LCE. More specifically, a large number of coarse-grained MC computer simulations (over 80) have been employed to study shape changes in monodomain main-chain LCEs formed by azobenzene moieties with various fractions of trans and cis conformers. The photoresponsive moieties were represented by soft-core GB biaxial ellipsoids whose interaction parameters were obtained from a fit of the UA-level interaction energy for selected pair configurations. Our results reveal a decrease of the NI transition temperature upon increasing cis population (e.g., by increased sample irradiation). In samples with prevailing trans-particle presence, the immediate neighborhood of cis particles is slightly less dense than that of the trans ones that are more compatible with their average environment. Simulations of light-induced actuation at fixed temperature reveal a significant contraction of the sample along the monodomain director, which could be exploited to perform useful mechanical work. This effect is most pronounced when actuating at temperatures not too far below the NI transition. Finally, from the simulated stress–strain curves, we conclude that in a clamped sample, internal mechanical stress of the order of several hundred kPa can be generated upon irradiation with light and that this stress increases with the content of cis-isomers, but not necessarily with temperature.
Acknowledgments
The support from the Slovenian Research Agency (program P1-0099 and project J1-9147) and the European Union (NAMASTE and Space-SI Centers of Excellence) is acknowledged. The coarse-grained molecular snapshots have been plotted using Ovito software.71
Appendix A
Coarse-Grained Pair Potentials
As mentioned in the text, the coarse-grained pair potentials considered in our study are the soft-core biaxial GB (SBGB) for the nonbonded interactions and the finitely extensible nonlinear potential (FENE) for the bonded ones.
The biaxial soft-core GB potential43 acting between dissimilar ellipsoidal particles i and j is defined as47
| 4 |
where 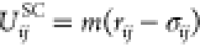 is the linear repulsive soft-core potential
and
is the linear repulsive soft-core potential
and 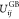 is the biaxial GB potential.50,52 The sigmoidal logistic
function
is the biaxial GB potential.50,52 The sigmoidal logistic
function 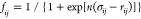 switches smoothly between the
soft-core
repulsion at small interparticle distances rij and the attractive potential well of the
GB potential at larger rij. Above, m and n are parameters
(we use m = −70ϵ0/σ0 and n = −100/σ044−46), and σij is the anisotropic distance
function for the two particles given by
switches smoothly between the
soft-core
repulsion at small interparticle distances rij and the attractive potential well of the
GB potential at larger rij. Above, m and n are parameters
(we use m = −70ϵ0/σ0 and n = −100/σ044−46), and σij is the anisotropic distance
function for the two particles given by  . Here
. Here 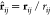 , where rij is the interparticle
vector and rij = |rij|. The distance function σij also
depends on the relative particle orientation, which is encoded into
the Aij overlap matrix defined
by
, where rij is the interparticle
vector and rij = |rij|. The distance function σij also
depends on the relative particle orientation, which is encoded into
the Aij overlap matrix defined
by  , where Mi is the rotation matrix that brings any vector from
the laboratory
reference frame to that of molecule i.65 Moreover, Si are range matrices describing the molecular shape, with the
corresponding σx, σy, and σz ellipsoidal
axes on the diagonal and zeros elsewhere.
, where Mi is the rotation matrix that brings any vector from
the laboratory
reference frame to that of molecule i.65 Moreover, Si are range matrices describing the molecular shape, with the
corresponding σx, σy, and σz ellipsoidal
axes on the diagonal and zeros elsewhere.
The biaxial GB potential is now given by
 |
5 |
where σij and rij were defined above and σc denotes the minimum interparticle
contact distance. (In the case of dissimilar particles, an arithmetic
average of the shortest axes of the particles is taken.52) Further,  , where ϵ0 sets
the energy
scale and μ and ν are empirical constants. (We consider
μ = 1 and ν = 3 for compatibility with previous work.)
Moreover, here
, where ϵ0 sets
the energy
scale and μ and ν are empirical constants. (We consider
μ = 1 and ν = 3 for compatibility with previous work.)
Moreover, here 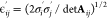 , with
, with  . Finally, the attractive
potential well
anisotropy is incorporated into
. Finally, the attractive
potential well
anisotropy is incorporated into 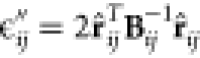 , where
, where 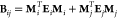 , and Ei are diagonal matrices
with elements
, and Ei are diagonal matrices
with elements 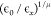 ,
,  , and
, and  , where ϵx, ϵy, and ϵz are related
to the well depths for the homogeneous interactions
in characteristic orthogonal molecular configurations (see refs (50) and (52)).
, where ϵx, ϵy, and ϵz are related
to the well depths for the homogeneous interactions
in characteristic orthogonal molecular configurations (see refs (50) and (52)).
We employ the FENE potential48 for interparticle bonds to describe both their stretching and bending. Consider a bond connecting two neighboring ellipsoids i and j, with a length of sij. Then, the deviation from its equilibrium value se equals δsij = |sij – se|, and let us assume that δsij < δsm. (There is a limitation on stretching.) Similarly, the bond angle θij is defined as the angle between the preferred bond directions imposed by each of the particles.66 The deviation from its equilibrium value θe is δθij = |θij – θe|, with a requirement that δθij < δθm. (There is a limitation on bending, too.) Now, the FENE bond energy is given by66,67
| 6 |
the first contribution referring to bond stretching
and the second one to bond bending. The values of the potential parameters
introduced above are se = 0.15σ0, δsm = 0.25σ0, and  for
stretching, and θe = 0°, δθm = 150°, and kθ = 3.8
× 10–4ϵ0/deg2 ≈
1.72 × 10–21 J/rad2 for bending.44−46,66,67
for
stretching, and θe = 0°, δθm = 150°, and kθ = 3.8
× 10–4ϵ0/deg2 ≈
1.72 × 10–21 J/rad2 for bending.44−46,66,67
The total interaction energy U for a system
of N particles is obtained by summing up all nonbonded
and
bonded intermolecular pairwise contributions,  , where wij = 1 if the monomers i and j are bonded, and wij = 0 otherwise.
, where wij = 1 if the monomers i and j are bonded, and wij = 0 otherwise.
Appendix B
United-Atom Fitting of Azobenzene Conformers
We performed a simple energy minimization of atomistic structures of the two isomers of azobenzene with “Argus Lab”68 choosing the semiempirical Quantum Chemistry (QC) method AM1 (Austin model 1) and the Restricted Hartree–Fock self-consistent field method (for closed shells).69 We recall that we are only interested in getting the basic shape change upon trans–cis photoisomerization of the bare bone azobenzene unit in Figure 1, thus using more sophisticated QC methods is unnecessary, if not inappropriate. Using the force field published in ref (31), we have obtained molecular ellipsoids overdimensioned with respect to the atomistic structures. Hence, we have applied a UA approach, maintaining the same nomenclature of the force field but including into the carbon atom of the benzene ring the hydrogen attached to it.7 Atomic masses and charges have been modified accordingly to take into account the collapsed hydrogens. The dimensions of the biaxial molecular ellipsoid are computed using the “shape tensor” Ts, a modified version of the inertia matrix in which the masses are substituted with the van der Waals radii70 to consider steric hindrance of the atomic centers, as reported below
 |
7 |
Here, ri is the van der Waals radius of the ith atom and the total sum of radii is denoted by rT = ∑iri. The eigenvalues λxx, λyy, and λzz of Ts are related to the dimensions of the ellipsoid and can be used to define its axes as follows
| 8 |
| 9 |
| 10 |
When the molecule is flat (as in the trans isomer), the length of the shortest axis approaches zero. Therefore, the standard distance of π–π stacking, 0.35 nm, has been used instead.
The energy parameters ϵx, ϵy, and ϵz related to the potential well depths are computed using the atomistic structure and the UA force field described above. Two identical molecules have been placed at different distances, and their interaction energy within the chosen force field has been computed. The interaction energy has been obtained as a function of intermolecular distance for the three most significant pair configurations: side-by-side, face-to-face, and end-to-end. These profiles have then been fitted with the soft-core GB potential, using the ellipsoid dimensions obtained from the shape tensor.
The parameters summing up fitting results for the cis and trans UA azobenzene conformers represented as prolate GB ellipsoids are reported in the text (Table 1).
The authors declare no competing financial interest.
References
- Zhao Y.; Ikeda T.. Smart Light-Responsive Materials. Azobenzene Containing Polymers and Liquid Crystals; Wiley: Hoboken, NJ, 2009. [Google Scholar]
- Ravve A.Light-Associated Reactions of Synthetic Polymers; Springer: New York, 2006, p 246. [Google Scholar]
- Bertrand O.; Gohy J.-F. Photo-responsive polymers: synthesis and applications. Polym. Chem. 2017, 8, 52–73. 10.1039/c6py01082b. [DOI] [Google Scholar]
- Cembran A.; Bernardi F.; Garavelli M.; Gagliardi L.; Orlandi G. On the mechanism of the cis-trans isomerization in the lowest electronic states of azobenzene: S0, S1, and T1. J. Amer. Chem. Soc. 2004, 126, 3234–3243. 10.1021/ja038327y. [DOI] [PubMed] [Google Scholar]
- Aleotti F.; Soprani L.; Nenov A.; Berardi R.; Arcioni A.; Zannoni C.; Garavelli M. Multidimensional potential energy surfaces resolved at the RASPT2 Level for accurate photoinduced isomerization dynamics of azobenzene. J. Chem. Theory Comput. 2019, 15, 6813–6823. 10.1021/acs.jctc.9b00561. [DOI] [PubMed] [Google Scholar]
- de Gennes P. G.; Prost J.. The Physics of Liquid Crystals; Oxford University Press: Oxford, 1993. [Google Scholar]
- Zannoni C.Liquid Crystals and Their Computer Simulations; Cambridge University Press: Cambridge, 2022. [Google Scholar]
- Kurihara S.; Ikeda T.; Tazuke S. Photochemically induced isothermal phase transition in liquid crystals. Effect of interaction of photoresponsive molecules with matrix mesogens. Mol. Cryst. Liq. Cryst. 1990, 178, 117–132. 10.1080/00268949008042713. [DOI] [Google Scholar]
- Ikeda T.; Horiuchi S.; Karanjit D. B.; Kurihara S.; Tazuke S. Photochemically induced isothermal phase-transition in polymer liquid crystals with mesogenic phenyl benzoate side-chains. 1. Calorimetric studies and order parameters. Macromolecules 1990, 23, 36–42. 10.1021/ma00203a008. [DOI] [Google Scholar]
- Ikeda T.; Horiuchi S.; Karanjit D. B.; Kurihara S.; Tazuke S. Photochemically induced isothermal phase-transition in polymer liquid crystals with mesogenic phenyl benzoate side-chains. 2. Photochemically induced isothermal phase-transition behaviors. Macromolecules 1990, 23, 42–48. 10.1021/ma00203a009. [DOI] [Google Scholar]
- Ikeda T.; Kurihara S.; Karanjit D. B.; Tazuke S. Photochemically induced isothermal phase-transition in polymer liquid crystals with mesogenic cyanobiphenyl side-chains. Macromolecules 1990, 23, 3938–3943. 10.1021/ma00219a012. [DOI] [Google Scholar]
- Tsutsumi O.; Shiono T.; Ikeda T.; Galli G. Photochemical phase transition behavior of nematic liquid crystals with azobenzene moieties as both mesogens and photosensitive chromophores. J. Phys. Chem. B 1997, 101, 1332–1337. 10.1021/jp961565d. [DOI] [Google Scholar]
- Vecchi I.; Arcioni A.; Bacchiocchi C.; Tiberio G.; Zanirato P.; Zannoni C. Expected and unexpected behavior of the orientational order and dynamics induced by azobenzene solutes in a nematic. J. Phys. Chem. B 2007, 111, 3355–3362. 10.1021/jp0651788. [DOI] [PubMed] [Google Scholar]
- Ichimura K. Photoalignment of liquid crystal systems. Chem. Rev. 2000, 100, 1847–1874. 10.1021/cr980079e. [DOI] [PubMed] [Google Scholar]
- Fang G. J.; Maclennan J. E.; Yi Y.; Glaser M. A.; Farrow M.; Korblova E.; Walba D. M.; Furtak T. E.; Clark N. A. Athermal photofluidization of glasses. Nat. Commun. 2013, 4, 1521. 10.1038/ncomms2483. [DOI] [PubMed] [Google Scholar]
- Yadav B.; Domurath J.; Kim K.; Lee S.; Saphiannikova M. Orientation approach to directional photodeformations in glassy side-chain azopolymers. J. Phys. Chem. B 2019, 123, 3337–3347. 10.1021/acs.jpcb.9b00614. [DOI] [PubMed] [Google Scholar]
- Warner M.; Terentjev E. M.. Liquid Crystal Elastomers; Oxford University Press: Oxford, 2003. [Google Scholar]
- de Gennes P. G. Réflexions sur un type de polymères nématiques (Some reflections about a type of nematic liquid crystal polymers). C. R. Acad. Sc. Paris 1975, 281, 101–103. [Google Scholar]
- White T. J. Photomechanical effects in liquid crystalline polymer networks and elastomers. J. Polym. Sci. B 2018, 56, 695–705. 10.1002/polb.24576. [DOI] [Google Scholar]
- Camacho-Lopez M.; Finkelmann H.; Palffy-Muhoray P.; Shelley M. Fast liquid-crystal elastomer swims into the dark. Nat. Mater. 2004, 3, 307–310. 10.1038/nmat1118. [DOI] [PubMed] [Google Scholar]
- Yu Y. L.; Nakano M.; Ikeda T. Directed bending of a polymer film by light - Miniaturizing a simple photomechanical system could expand its range of applications. Nature 2003, 425, 145. 10.1038/425145a. [DOI] [PubMed] [Google Scholar]
- Liu D. Q.; Broer D. J. New insights into photoactivated volume generation boost surface morphing in liquid crystal coatings. Nat. Commun. 2015, 6, 8334. 10.1038/ncomms9334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White T. J.Photomechanical Materials, Composites, and systems: Wireless Transduction of Light Into Work, 1st ed.; White T. J., Ed.; Wiley: Hoboken, NJ, 2017; pp 153–178. [Google Scholar]
- Photomechanical Materials, Composites, and Systems: Wireless Transduction of Light into Work; White T. J., Ed.; Wiley: Hoboken, 2017. [Google Scholar]
- Zheng X. X.; Jia Y. N.; Chen A. H. Azobenzene-containing liquid crystalline composites for robust ultraviolet detectors based on conversion of illuminance-mechanical stress-electric signals. Nat. Commun. 2021, 12, 4875. 10.1038/s41467-021-25178-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ceamanos L.; Kahveci Z.; López-Valdeolivas M.; Liu D. L.; Broer D. J.; Sánchez-Somolinos C. Four-Dimensional Printed Liquid Crystalline Elastomer Actuators with Fast Photoinduced Mechanical Response toward Light-Driven Robotic Functions. ACS Appl. Mater. Interfaces 2020, 12, 44195–44204. 10.1021/acsami.0c13341. [DOI] [PubMed] [Google Scholar]
- Shimamura A.; Priimägi A.; Mamiya J.-i.; Ikeda T.; Yu Y.; Barrett C. J.; Shishido A. Simultaneous Analysis of Optical and Mechanical Properties of Cross-Linked Azobenzene-Containing Liquid-Crystalline Polymer Films. ACS Appl. Mater. Interfaces 2011, 3, 4190–4196. 10.1021/am200621j. [DOI] [PubMed] [Google Scholar]
- Zeng H.; Wasylczyk P.; Wiersma D. S.; Priimägi A. Microrobotics: Light Robots: Bridging the Gap between Microrobotics and Photomechanics in Soft Materials. Advanced Materials 2018, 30, 1870174. 10.1002/adma.201870174. [DOI] [PubMed] [Google Scholar]
- Kotikian A.; McMahan C.; Davidson E. C.; Muhammad J. M.; Weeks R. D.; Daraio C.; Lewis J. A. Untethered soft robotic matter with passive control of shape morphing and propulsion. Sci. Robot. 2019, 4, eaax7044 10.1126/scirobotics.aax7044. [DOI] [PubMed] [Google Scholar]
- Herbert K. M.; Fowler H. E.; McCracken J. M.; Schlafmann K. R.; Koch J. A.; White T. J. Synthesis and alignment of liquid crystalline elastomers. Nat. Rev. Mater. 2021, 7, 23–38. 10.1038/s41578-021-00359-z. [DOI] [Google Scholar]
- Tiberio G.; Muccioli L.; Berardi R.; Zannoni C. How does the trans–cis photoisomerization of azobenzene take place in organic solvents?. ChemPhysChem 2010, 11, 1018–1028. 10.1002/cphc.200900652. [DOI] [PubMed] [Google Scholar]
- Cantatore V.; Granucci G.; Persico M. Simulation of the π → π* photodynamics of azobenzene: Decoherence and solvent effects. Comput. Theor. Chem. 2014, 1040–1041, 126–135. 10.1016/j.comptc.2014.02.011. [DOI] [Google Scholar]
- Böckmann M.; Marx D.; Peter C.; Delle Site L.; Kremer K.; Doltsinis N. L. Multiscale modelling of mesoscopic phenomena triggered by quantum events: light-driven azo-materials and beyond. Phys. Chem. Chem. Phys. 2011, 13, 7604–7621. 10.1039/c0cp01661f. [DOI] [PubMed] [Google Scholar]
- Lansac Y.; Glaser M. A.; Clark N. A.; Lavrentovich O. D. Photocontrolled nanophase segregation in a liquid-crystal solvent. Nature 1999, 398, 54–57. 10.1038/17995. [DOI] [Google Scholar]
- Salerno K. M.; Lenhart J. L.; de Pablo J. J.; Sirk T. W. Vapor-deposited glasses highlight the role of density in photostability. J. Phys. Chem. B 2020, 124, 6112–6120. 10.1021/acs.jpcb.0c03579. [DOI] [PubMed] [Google Scholar]
- Salerno K. M.; Lenhart J. L.; de Pablo J. J.; Sirk T. W. Photoisomerization and local stability in molecular and polymer-network glasses. Mol. Syst. Des. Eng. 2023, 8, 105–114. 10.1039/D2ME00092J. [DOI] [Google Scholar]
- Toshchevikov V.; Saphiannikova M. Theory of light-induced deformation of azobenzene elastomers: Effects of the liquid crystalline interactions and biaxiality. J. Phys. Chem. B 2014, 118, 12297–12309. 10.1021/jp5063226. [DOI] [PubMed] [Google Scholar]
- Ilnytskyi J. M.; Saphiannikova M. Reorientation dynamics of chromophores in photosensitive polymers by means of coarse-grained modeling. ChemPhysChem 2015, 16, 3180–3189. 10.1002/cphc.201500500. [DOI] [PubMed] [Google Scholar]
- Ilnytskyi J. M.; Toshchevikov V.; Saphiannikova M. Modeling of the photo-induced stress in azobenzene polymers by combining theory and computer simulations. Soft Matter 2019, 15, 9894–9908. 10.1039/c9sm01853k. [DOI] [PubMed] [Google Scholar]
- García-Amorós J.; Velasco D. Recent advances towards azobenzene-based light-driven real-time information-transmitting materials. Beilstein J. Org. Chem. 2012, 8, 1003–1017. 10.3762/bjoc.8.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou L.; Chen L.; Ren G.; Zhu Z.; Zhao H.; Wang H.; Zhang W.; Han J. Monitoring cis-to-trans isomerization of azobenzene using terahertz time-domain spectroscopy. Phys. Chem. Chem. Phys. 2018, 20, 27205–27213. 10.1039/C8CP04570D. [DOI] [PubMed] [Google Scholar]
- Gay J. G.; Berne B. J. Modification of the overlap potential to mimic a linear site-site potential. J. Chem. Phys. 1981, 74, 3316–3319. 10.1063/1.441483. [DOI] [Google Scholar]
- Berardi R.; Lintuvuori J. S.; Wilson M. R.; Zannoni C. Phase diagram of the uniaxial and biaxial soft–core Gay–Berne model. J. Chem. Phys. 2011, 135, 134119. 10.1063/1.3646310. [DOI] [PubMed] [Google Scholar]
- Skačej G.; Zannoni C. Main-chain swollen liquid crystal elastomers: a molecular simulation study. Soft Matter 2011, 7, 9983–9991. 10.1039/c1sm05709j. [DOI] [Google Scholar]
- Skačej G.; Zannoni C. Molecular simulations elucidate electric field actuation in swollen liquid crystal elastomer. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 10193–10198. 10.1073/pnas.1121235109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skačej G.; Zannoni C. Molecular simulations shed light on supersoft elasticity in polydomain liquid crystal elastomers. Macromolecules 2014, 47, 8824–8832. 10.1021/ma501836j. [DOI] [Google Scholar]
- Berardi R.; Zannoni C.; Lintuvuori J. S.; Wilson M. R. A soft-core Gay-Berne model for the simulation of liquid crystals by Hamiltonian replica exchange. J. Chem. Phys. 2009, 131, 174107. 10.1063/1.3254019. [DOI] [PubMed] [Google Scholar]
- Bird R. B.; Curtiss C. F.; Armstrong R. C.; Hassager D.. Dynamics of polymeric liquids; John Wiley & Sons: New York, 1987; Vol. 2, p 21. [Google Scholar]
- Khare R. S.; de Pablo J. J.; Yethiraj A. Rheology of confined polymer melts. Macromolecules 1996, 29, 7910–7918. 10.1021/ma960083x. [DOI] [Google Scholar]
- Berardi R.; Fava C.; Zannoni C. A generalized Gay-Berne intermolecular potential for biaxial particles. Chem. Phys. Lett. 1995, 236, 462–468. 10.1016/0009-2614(95)00212-m. [DOI] [Google Scholar]
- Persico M.; Granucci G.. Photochemistry: A Modern Theoretical Perspective; Springer: Cham, 2018, pp 23–128. [Google Scholar]
- Berardi R.; Fava C.; Zannoni C. A Gay-Berne potential for dissimilar biaxial particles. Chem. Phys. Lett. 1998, 297, 8–14. 10.1016/s0009-2614(98)01090-2. [DOI] [Google Scholar]
- Urayama K.; Honda S.; Takigawa T. Electrooptical effects with anisotropic deformation in nematic gels. Macromolecules 2005, 38, 3574–3576. 10.1021/ma0503054. [DOI] [Google Scholar]
- Fukunaga A.; Urayama K.; Koelsch P.; Takigawa T. Electrically driven director-rotation of swollen nematic elastomers as revealed by polarized Fourier transform infrared spectroscopy. Phys. Rev. E 2009, 79, 051702. 10.1103/PhysRevE.79.051702. [DOI] [PubMed] [Google Scholar]
- Urayama K.; Takigawa T.. Cross-Linked Liquid Crystalline Systems: from Rigid Polymer Networks to Elastomers; Broer D., Crawford G. P., Žumer S., Eds.; CRC Press, Taylor & Francis: Boca Raton, 2011; pp 473–486. [Google Scholar]
- Allen M. P.; Tildesley D.. Computer Simulations of Liquids, 2nd ed.; Clarendon Press: Oxford, 2017; pp 35–195. [Google Scholar]
- Frenkel D.; Smit B.. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: San Diego, 1996; pp 28–112. [Google Scholar]
- Metropolis N.; Rosenbluth A. W.; Rosenbluth M. N.; Teller A. H.; Teller E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. 10.1063/1.1699114. [DOI] [Google Scholar]
- Barker J. A.; Watts R. O. Structure of water; A Monte Carlo calculation. Chem. Phys. Lett. 1969, 3, 144–145. 10.1016/0009-2614(69)80119-3. [DOI] [Google Scholar]
- Verlet L. Computer ”experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 1967, 159, 98–103. 10.1103/physrev.159.98. [DOI] [Google Scholar]
- Chaikin P. M.; Lubensky T. C.. Principles of Condensed Matter Physics; Cambridge University Press: Cambridge, 1995, p 33. [Google Scholar]
- Polson J. M.; Frenkel D. First-order nematic-smectic phase transition for hard spherocylinders in the limit of infinite aspect ratio. Phys. Rev. E 1997, 56, R6260–R6263. 10.1103/PhysRevE.56.R6260. [DOI] [Google Scholar]
- Liu D. Q. Volume generation towards dynamic surface morphing in liquid crystal polymer networks. Liq. Cryst. 2016, 43, 2136–2143. 10.1080/02678292.2016.1195898. [DOI] [Google Scholar]
- Callen H. B.Thermodynamics and an Introduction to Thermostatistics; John Wiley & Sons: New York, 1985, p 147. [Google Scholar]
- Rose M. E.Elementary Theory of Angular Momentum; Wiley: New York, 1957, p 48. [Google Scholar]
- Berardi R.; Micheletti D.; Muccioli L.; Ricci M.; Zannoni C. A computer simulation study of the influence of a liquid crystal medium on polymerization. J. Chem. Phys. 2004, 121, 9123–9130. 10.1063/1.1790453. [DOI] [PubMed] [Google Scholar]
- Micheletti D.; Muccioli L.; Berardi R.; Ricci M.; Zannoni C. Effect of nano-confinement on liquid crystal polymer chains. J. Chem. Phys. 2005, 123, 224705. 10.1063/1.2125707. [DOI] [PubMed] [Google Scholar]
- Thompson M. A.Molecular Docking Using ArgusLab, an Efficient Shape-Based Search Algorithm and the AScore Scoring Function; ACS Meeting: Philadelphia, 2004. [Google Scholar]
- Cramer C. J.Essentials of Computational Chemistry. Theories and Models; Wiley: New York, 2004, pp 126–145. [Google Scholar]
- Bondi A. Van der Waals volumes and radii. J. Phys. Chem. 1964, 68, 441–451. 10.1021/j100785a001. [DOI] [Google Scholar]
- Stukowski A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Modell. Simul. Mater. Sci. Eng. 2010, 18, 015012. 10.1088/0965-0393/18/1/015012. [DOI] [Google Scholar]








