Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Jul 26;127(31):15630–15640. doi: 10.1021/acs.jpcc.3c03512

Band-Gap Energy and Electronic d–d Transitions of NiWO4 Studied under High-Pressure Conditions

Daniel Errandonea †,*, Fernando Rodriguez ‡, Rosario Vilaplana §, David Vie ∥, Siddhi Garg ⊥, Bishnupriya Nayak ⊥, Nandini Garg ⊥,#, Jaspreet Singh ∇, Venkatakrishnan Kanchana ∇, Ganapathy Vaitheeswaran ○,*
PMCID: PMC10426340  PMID: 37588813

Abstract

graphic file with name jp3c03512_0010.jpg

We report an extensive study of the optical and structural properties of NiWO4 combining experiments and density functional theory calculations. We have obtained accurate information on the pressure effect on the crystal structure determining the equation of state and compressibility tensor. We have also determined the pressure dependence of the band gap finding that it decreases under compression because of the contribution of Ni 3d states to the top of the valence band. We report on the sub-band-gap optical spectrum of NiWO4 showing that the five bands observed at 0.95, 1.48, 1.70, 2.40, and 2.70 eV correspond to crystal-field transitions within the 3d8 (t2g6eg2) configuration of Ni2+. Their assignment, which remained controversial until now, has been resolved mainly by their pressure shifts. In addition to the transition energies, their pressure derivatives are different in each band, allowing a clear band assignment. To conclude, we report resistivity and Hall-effect measurements showing that NiWO4 is a p-type semiconductor with a resistivity that decreases as pressure increases.

1. Introduction

Because of global warming the development of renewable energy sources and environmentally friendly energy storage is a hot topic. Photocatalytic water splitting and supercapacitors are two of the most promising technologies. Nickel tungstate (NiWO4) has been studied as an efficient material for both technologies.1,2 This and other tungstates are also extraordinary scintillator materials for high-energy physics.3 The accurate understanding of the properties of NiWO4 is fundamental for the above-mentioned technological applications. NiWO4 crystallizes in a monoclinic structure described by space group P2/c.4 It is isomorphic to the mineral wolframite - (Fe,Mn)WO4 –5 sharing the structure with several tungstates, including CoWO4, CdWO4, MgWO4, MnWO4, and ZnWO4.6 High-pressure studies have contributed to the understanding of the structural and electronic properties of wolframites.7−10 High pressure (HP) can substantially modify the structural and electronic properties of materials favoring a deep understanding of them.11 NiWO4 is one of the wolframites that has been less studied under compression, there being only one article recently published.10 In this work, a phase transition was reported around 20 GPa, which is in consistent with results previously reported for other wolframites.6 In addition, the pressure dependence of the band-gap energy (Egap) and two Ni2+d–d intra-band transitions were reported. However, there are several issues regarding the electronic properties of NiWO4, and their HP behavior that still needs to be clarified. For instance, the assignment of Ni2+d–d transitions made by Ye et al.10 from measurements carried out in the 1.45–3.5 eV region is at odds with the assignment made by Ejima et al.12 and by de Oliveira et al.13 from experiments performed in the 0.82–6.0 eV region and in the 1.3–6.5 eV region, respectively. On the other hand, for the band-gap energy, a value of 2.87 eV has been reported in the most recent work.10 However, a large dispersion of band-gap energies can be found in the literature for NiWO4. For instance, Egap = 3.4 eV was reported in ref (12), Egap = 3.7 eV in ref (13), Egap = 2.73–2.93 in ref (14), Egap = 2.1 eV in ref (15), Egap = 2.2–2.6 eV in ref (16), Egap = 2.77 eV in ref (17), and Egap = 2.28 eV in ref (18). These results clearly show that it is timely to perform additional studies on NiWO4. Photocatalytic water splitting and photocatalytic wastewater treatment require semiconductors with the band-gap energy in the visible part of the solar spectrum, in particular with values from 2.0 to 2.6 eV.19 The accurate knowledge of the band-gap energy is therefore crucial for the use of NiWO4 for these applications.

In this work, we report a HP study of NiWO4 up to 20 GPa. Our study includes HP synchrotron X-ray diffraction (XRD) experiments and optical-absorption experiments in the 0.82–3.6 eV region up to 20 GPa, resistivity and Hall-effect measurements up to 10 GPa, and density-functional theory (DFT) calculations up to 20 GPa. The combination of all the methods allows us to accurately determine the electronic properties of NiWO4 and the effect of pressure on them up to 20 GPa. We show that changes in the fundamental band gap and Ni2+ internal d–d absorption bands are intimately related to structural changes. The assignment of Ni2+d–d transitions is discussed, clarifying previous discrepancies in the literature.

2. Methods

Polycrystalline NiWO4 has been synthesized from a stoichiometric mixture of nickel(II) acetate hexahydrate Ni(CH3CO2)2· 6H2O (Fluka, 98%) and ammonium metatungstate (NH4)W12O39 (Aldrich, 99.0%). The starting Ni- or W-containing solutions were prepared by dissolving their respective salts in distilled water. Then they were combined to obtain Ni-W source solutions having a total cationic concentration of 0.3 M and a total volume of 21.7 mL. The masses of the different reagents were adjusted to obtain 1 g of the final product. Droplets of the solution were flash-frozen by projection onto liquid nitrogen and then freeze-dried at a pressure of 1–10 Pa in a Telstar Cryodos freeze-dryer. In this way, a dried solid precursor was obtained as amorphous loose powder. Thermal evolution of the precursor was monitored by means of thermogravimetric experiments under an oxygen atmosphere (heating rate 10 K min–1, flow rate 60 cm3 min–1), carried out using a TA Instruments TG550 thermogravimetric analyzer. The final NiWO4 polycrystalline product was obtained by decomposing the precursor in an oven at 800 °C for 1 h. The purity and crystal structure of the synthesized NiWO4 was confirmed by powder XRD using a Bruker D8 Advance A25 system and Cu Kα radiation. We have not detected any impurity in the XRD experiments. The unit-cell parameters at ambient conditions are a = 4.599(3) Å, b = 5.664(5) Å, c = 4.910(5) Å, β = 90.06(7)°. These values agree with those determined from single-crystal neutron diffraction experiments.20

HP synchrotron powder XRD measurements were carried out at the Extreme Conditions XRD beamline (BL-11)21 in the Indus-2 synchrotron using monochromatic X-rays (λ = 0.731 Å) and a diamond-anvil cell (DAC). We used diamond anvils with a culet size of 400 μm and a tungsten gasket with a thickness of 50 μm with a centered hole of 200 μm in diameter. The pressure medium was a 16:3:1 methanol–ethanol–water mixture (MEW)22 and copper was used as a pressure marker.23 Diffraction images were collected in a MAR345 imaging-plate detector. Their integration into intensity vs 2θ patterns was made using Dioptas.24 The XRD results patterns were analyzed using the graphical interface of GSAS.25

Optical-absorption measurements were carried out in a DAC using a 3-μm-thin platelet of NiWO4 obtained by compacting NiWO4 powder between diamond anvils. The characteristics of the DAC were the same as in XRD measurements. The pressure medium was also the same, and the gasket had similar dimensions but was made of Inconel. Pressure was determined using the ruby fluorescence method.26 Measurements in the 0.82–3.6 eV range were performed in an optical setup, which consisted of a tungsten lamp, fluorite lenses, reflecting optics objectives, and several Ocean Optics spectrometers.27

Hall-effect and resistivity measurements were performed with a hydraulic press and steel-belted Bridgman tungsten-carbide anvils28 using annealed pyrophyllite gaskets and boron nitride as pressure medium and to electrically isolate the sample from the anvils. Samples were compact pellets made from the NiWO4 powder. Electrical contacts were made with silver wires and soldered with indium to the sample in a Van der Pauw configuration. The pressure was calibrated against the transition pressures of Bi, Yb, CdTe, and InSe.29

The Vienna Ab-initio Simulation Package (VASP) code,30,31 which is based on plane waves, was used to study the electronic and structural characteristics of NiWO4 at HP. The exchange correlation functionals were computed using the Perdew–Burke–Ernzerhof (PBE) potentials within the Generalized-Gradient Approximation (GGA),32 and Projector augmented wave (PAW)33 potentials were used to approximate the ion-electron interactions. In calculations we treated Ni 3d8 4s2, W 6s2 5d4, and O 2s2 2p4 explicitly as valence electrons and the rest of electrons as core electrons. To ensure accuracy and high precision in the calculations, we used a plane-wave energy cutoff of 600 eV. The energy convergence criteria have been chosen to be 10–6 eV. The geometry optimization calculations have been performed at 0 K by doubling the unit-cell along the a-axis to consider magnetic configurations and using a 4 × 6 × 8 k-mesh in accordance with the Monkhorst–Pack method.34 According to the various investigations of transition metal compounds, the GGA frequently produces the wrong findings in case of highly correlated systems. In this case, the inclusion of Hubbard parameter (U) has been found to have some impact on transition metal compounds.35 The significant correlation effects of nickel d states were treated by using a Hubbard (U) parameter (GGA + U) of 6.5 eV.36 Because NiWO4 presents a magnetic moment, we considered non-magnetic, ferromagnetic, and different antiferromagnetic configurations.37 We found that the configuration with the lowest energy is an antiferromagnetic order with a magnetic unit cell (2a, b, c) which doubles the crystallographic one along the a-axis. The spins at nickel atoms are arranged collinearly making a linear chain running nearly along the crystallographic [0,1̅,1] direction, but are antiparallel to the spins in adjacent chains. This configuration agrees with the magnetic configuration determined below 67 K from neutron diffraction experiments.38 After optimizing the crystal structure at different pressure, band structures, and electronic densities of states have been calculated. We have also determined the complex dielectric function which has been used to calculate the absorption coefficient by means of the Kramers–Kronig relationship.39

3. Results and Discussions

3.1. XRD Experiments

In Figure 1a, we present a selection of XRD patterns measured at different pressures. In agreement with ref (10), we have found that NiWO4 does not undergo any phase transition in the pressure range covered by our studies, i.e., the crystal structure can be described as isomorphic to wolframite up to 20 GPa. This is supported by the results of Rietveld refinements shown in Figure 1a at 1.5 and 18.7 GPa. The goodness-of-fit parameters are Rp = 3.46% and Rwp = 5.38% at 1.5 GPa (Rp = 7.42% and Rwp = 10.53% at 18.7 GPa). The broadening of peaks observed at 18.7 GPa is a consequence of the solidification of the pressure medium at 10 GPa and the consequent increase of pressure gradients across the pressure chamber.22 The observed peak broadening is typical in experiments performed using 16:3:1 MEW as pressure-medium and has also been observed in ref (10).

Figure 1.

Figure 1

Open in a new tab

(a) XRD patterns measured at different pressures which are indicted in the figure. In the top and bottom traces, we show experiments (black dots), refinements (red lines), residuals (black lines), and positions of reflections (vertical ticks). The green asterisks identify the peak of Cu used to determine pressure. (b) Pressure dependence of the lattice parameters a, b, and c. (c) Pressure dependence of the β angle. (d) Pressure dependence of the unit-cell volume. Blue symbols are from our experiment performed outside the DAC. Red symbols are from our HP experiments, and black symbols are from ref (10). The black lines are from our DFT calculations, and the red line represents the 3rd order Birch–Murnaghan EOS determined from our experiments.

From the structural refinements, we have obtained the pressure dependence of unit-cell parameters. The results are shown in Figure 1b–d. In the figures, we compare the results of our experiments with the previous experiments10 and our DFT calculations. All results show a similar pressure dependence with the calculations slightly overestimating the value of the β angle. Interestingly the previous experiments10 show an abrupt decrease of the volume compressibility around 7 GPa. This phenomenon is not observed in our experiments and calculations. The change of compressibility could not be related to non-hydrostatic effects because the present and the previous experiment were performed using the same pressure medium, which is quasi-hydrostatic up to 10 GPa. We think the change of compressibility might be related to sample bridging between diamonds, which could strongly affect the compressibility of the sample.40

We have used a third-order Birch–Murnaghan equation of state41 to fit the pressure dependence of the volume obtained from our experiments. The zero-pressure volume (V0), bulk modulus (K0), and its pressure derivative (K0′) we have determined are V0 = 128.0(3) Å3, K0 = 137(17) GPa, and K0′ = 5.5(2.3). From our calculations we have obtained V0 = 129.12(1) Å3, K0 = 147.4(6) GPa, and K0′ = 5.38(8). The values of K0 and K0′ obtained from our experiments and calculations agree within uncertainties, which shows that calculations accurately describe the changes induced by pressure in the crystal structure. In the previous study,10 it was reported that according to experiments, V0 = 129.12(1) Å3, K0 = 146.05(2) GPa, and K0′ = 14.40(1). We consider that the overestimation of the pressure derivative of the bulk modulus is an artifact caused by the abrupt change of compressibility that occurs in previous experiments at 7 GPa.10 From previous calculations, it was reported that V0 = 133.16(8) Å3, K0 = 162.91(2) GPa, and K0′ = 3.64(2). The bulk modulus is larger than in our present results, but the pressure derivative is smaller. Thus, since both parameters are correlated,42 it is not obvious to compare results from previous calculations and the previous study. To do it, we have refitted the results of previous calculations, but fixing K0′ = 5.38, the values obtained from our calculations. This way we have obtained V0 = 133.39(8) Å3 and K0 = 147.3(1.5) GPa in excellent agreement with our results. Therefore, we are confident that the bulk modulus of NiWO4 is 137–147 GPa, and its pressure derivative is 5.4–5.5.

From Figure 1b, it can be seen that the compressibility of NiWO4 is slightly anisotropic. Since the crystal structure is monoclinic, the analysis of compressibility is not straightforward and requires the use of the compressibility tensor, which has four elements different than zero,43 and the determination of its eigenvalues and eigenvectors. We have obtained them using PASCal.44 We have found that the main axes of compressibility are (010), (8̅09), and (806). The corresponding linear compressibilities are 2.6(1) × 10–3 GPa, 2.0(2) × 10–3 GPa, and 1.3(1) × 10–3 GPa, respectively. As in other wolframites, the most compressible axis is the b-axis. The other two axes have similar compressibilities. They are in the plane perpendicular to the b-axis making an angle of 86° between them.

3.2. Optical-Absorption Experiments

In Figure 2a, we show the results of our optical-absorption measurements at different pressures. At 0 GPa, there is a sharp absorption at high-energy that corresponds to the fundamental band gap and five absorption bands that correspond to sub-gap Ni2+d–d internal transitions which are identified as Ei (i = 1–5). As pressure increases, the band gap red-shifts (see Figure 2a) and four of the Ni2+d–d bands blue-shift, while the fifth one does not move with pressure. Consequently, the Ni2+d–d band which is at 2.7 eV at 0 GPa moves into the fundamental band gap. To determine the band-gap energy, we have used a Tauc plot45 assuming an indirect band gap (as supported by our DFT calculations which are reported at the end of this subsection). In this method, the band-gap energy is determined from the extrapolation to the abscissa of the linear region of (Eα)1/2 versus energy (see Figure 2a). Readers should be aware that this energy should be considered as a lower bound for the band-gap energy.46 As it can be seen in the inset of Figure 2a, the band-gap energy at 0 GPa is estimated to be 3.00(5) eV. Comparing with previous experiments,10,12−18 our band-gap energy best agrees with the result reported by Ye et al.9 From our experiments, we have determined the pressure dependence of the band-gap energy (Egap) which is shown in Figure 2b. The pressure dependence of Egap can be well described by a linear function as shown with a red solid line in Figure 2b. The pressure coefficient of this function, dEgap/dP, is −13(1) meV/GPa, which is in excellent agreement with previous results.10 The pressure dependence obtained from experiments also agrees with that obtained from our calculations (see Figure 2b).

Figure 2.

Figure 2

Open in a new tab

(a) Absorbance (α) of NiWO4 at different pressures. The spectra have been offset vertically to make their identification easier. The assignment for the sub-gap bands is provided at 0 GPa. The dashed lines follow the sub-gap bands with pressure increase. The inset shows the Tauc plot at 0 GPa with the solid line used to determine the band-gap energy, Egap = 3.0 eV. (b) Egap determined from experiments (symbols), present calculations (dotted line), and from ref (10) (dashed line). The red solid line is a linear fit to experiments.

From the experiments, we could also follow the pressure dependence of Ni2+d–d transitions (see dashed lines in Figure 2a). The results are shown in Figure 3a. We have determined the pressure dependence for the five Ni2+d–d bands. In ref (10), only the pressure dependence of bands here labeled as E3 and E5 was reported. For these two bands, we observed the same linear increase of the energy with pressure. In our case, we obtained dE5/dP = 14.8 meV/GPa and dE3/dP = 11.8 meV/GPa, while the values reported for the pressure coefficients in ref (10) are 14.8 and 7.4 meV/GPa, respectively. In Figure 3a, it can be also seen than E1 and E4 increase under compression, whereas E2 is not affected by pressure. A detailed behavior of the pressure dependence of Ni2+d–d transitions will be discussed in the next section.

Figure 3.

Figure 3

Open in a new tab

(a) Pressure dependence of the energy of Ni2+d–d transitions. Symbols are from the present experiment. The solid lines are from present pressure fits collected in Table 1. The pressure shift of each band is given right side in meV/GPa units. (b) Tanabe–Sugano (TS) diagram used for the interpretation of experiments showing the variation of the crystal-field transition energies, E/B, as a function of Δ/B within the d8 configuration of Ni2+. Circles are experimental data obtained at different pressures. In both figures, dark blue and cyan curves represent results for the spin-allowed transitions and for transition with spin change, respectively.

Interestingly, in NiWO4, the band gap closes under compression as observed in isomorphic MnWO4,6 CoWO4,7 and CuWO4.8 On the other hand, this behavior is the opposite to what happens in wolframite-type CdWO4, ZnWO4, and MgWO46 in which the band gap opens under compression. This latter behavior is a result of the increase of the crystal field (CF) which enhances the splitting between the top of the valence band and the bottom of the conduction band which are dominated by O 2p states and W 5d states. As in MnWO4, CoWO4, and CuWO4, it is possible that the closing under pressure of the band gap in NiWO4 could be related to the contribution of Ni 3d states to the top of the valence band or the bottom of the conduction band. This hypothesis is supported by our DFT calculations as we will show next.

In Figure 4, we show the calculated band structure (4a and 4b) and electron density of states (4c and 4d) at 0 and 20 GPa. Previous calculations gave a band-gap energy of 2.1 eV10 and 3.91 eV47 at 0 GPa. Our calculations give a band-gap energy of 2.7 eV, which is much closer to the experimental value. Calculations by Ye et al.10 might have underestimated the band gap because they consider a non-magnetic configuration and/or used a Hubbard parameter U = 3.2 eV for Ni. We carried out simulations for the magnetic stable configuration using the same Hubbard parameter and obtained a band-gap energy of 2.07 eV showing that the problem of previous calculations was mainly the choice of the Hubbard parameter. On the other hand, Rosal et al.47 performed calculations using the Becke 3-paramters Lee–Yang–Parr (B3LYP) hybrid functional48 assuming a non-magnetic configuration and ignoring the Hubbard term. In the Supplementary Material of their work, it can be seen that this approach does not describe as accurately as our calculations the crystal structure of NiWO4 at 0 GPa. Thus, it is not surprising that their DFT approach leads to an overestimated band-gap energy.

Figure 4.

Figure 4

Open in a new tab

(a) Band structure at 0 GPa. (b) Band structure at 20 GPa. (c) Electron density of states at 0 GPa. (d) Electron density of states at 20 GPa.

The band structure at 0 and 20 GPa is represented in Figure 4a,b. The electron density of states at 0 and 20 GPa is represented in Figure 4c,d. We have also calculated the absorption coefficient which is shown in Figure 5. Figure 4 shows that NiWO4 is an indirect band gap semiconductor and that the top of the valence is dominated by O 2p states with a minor contribution from Ni 3d states. Contrastingly, the bottom of the conduction band is dominated by W 5d states. A schematic representation of the electronic density of states around the Fermi energy is shown in Figure 6. As expected for a compound with a conduction band with d character, the conduction is not very dispersive, and its energy minimum is not in the zone center being at the Y2 point of the Brillouin zone (see Figure 4a). On the other hand, the top of the valence band is at a point near the A point in the Brillouin zone. Regarding the absorption-coefficient, calculations show that NiWO4 has an abrupt absorption starting at 2.7 eV (see Figure 5), which agrees with the sharp absorption edge found in the experiments performed by Ejima et al. at 3.0 eV. Indeed, the shape of measured and calculated absorption is qualitatively similar. However, calculations do not predict the sub-bandgap Ni2+d–d transitions because they are not accounted by the electric dipole approximation. In order to accurately calculate d–d transitions occurring below the band gap, it may be necessary to employ alternative methodologies that go beyond the electric dipole approximation. For example, methods such as time-dependent DFT or more advanced approaches like many-body perturbation theory (MBPT) can be utilized. These methods are capable of considering higher-order effects and providing a more precise description of the d–d transitions occurring below the bandgap.49,50 Such calculations are beyond the scope of the present work.

Figure 5.

Figure 5

Open in a new tab

Calculated absorbance spectrum at 0 GPa for different polarizations.

Figure 6.

Figure 6

Open in a new tab

Schematic representation of the electronic density of states of NiWO4 around the Fermi level.

Regarding pressure effects on the band structure, Figure 4b shows that at 20 GPa, the topology of the band structure has not changed significantly from 0 GPa (Figure 4a). However, though the bottom of the conduction band goes down with pressure, the top of the valence band remains at the same energy due to the increase of the contribution of Ni 3d states to it. This is translated into the band-gap energy decrease we have observed in experiments. This behavior in NiWO4 is qualitatively like those previously reported MnWO46 and CoWO47 as the contribution to band-gap energy in these compounds is also due to the contribution of 3d states of Mn and Co near the Fermi level.

3.3. Ni2+d–d Transitions

The origin of the sub-band-gap absorption features in NiWO4 has been controversial and still deserves clarification.10,12,13,49 So far, all papers dealing with the optical properties of NiWO4 have reported different origins or misinterpretations of the sub-band-gap bands as Ni2+ CF transitions, defect related absorption, or excitonic components of the gap. Lima et al.51 as well as Ye et al.10 assigned bands at 1.68 and 2.73 eV to spin forbidden CF transitions from 3A2g to 1Eg and 1T2g, respectively. In contrast, Ejima et al.,12 who reported energies similar to ours, assigned these bands to spin-allowed CF transitions with 3T1 symmetry after comparison with the assignment given for [Ni(H2O)6]2+ and NiO.52 Ye et al.10 attributed the band at 2.74 eV to an exciton associated with the band gap and the band at 1.48 eV, which does not move with pressure, to “the presence of Frenkel defects with the dislocation of Ni2+ from the octahedron to the tetrahedron site.” On the other hand, de Oliveira et al.13 assigned a shoulder at ∼2.7 eV as probably due to the presence of a midgap defect state. In all cases, the pressure experiments associated with the sub-band-gap spectra lack absorption bands, or they are poorly resolved by reflectometry measurements on NiWO4 powders, making a proper band assignment difficult. In this context, HP measurements are important because the associated pressure shifts provide critical information for a proper band assignment. In this work, we have used a NiWO4 sample sintered at HP using a DAC. This method provides a transparent parallelepipedal sample to perform suitable optical-absorption measurements at ambient conditions and as a function of pressure, which was crucial to achieve this goal.

The room-temperature optical absorption sub-gap spectrum of NiWO4 shows five absorption bands, named Ei, at 0.95, 1.48, 1.70, 2.40, and 2.70 eV from i = 1 to 5, respectively. These five bands are also observed as main absorption features in the CF spectra of Ni2+ in oxides, fluorides, and chlorides,52−57 as well as in NiWO4.12 The proposed band assignment to electronic CF transitions within the 3d8 configuration of Ni2+ is given in Figure 3b. Peak labels have been assigned according to the sixfold Oh symmetry of the NiO6 local environment of Ni2+. Although the actual local symmetry around Ni2+ is slightly distorted with respect to Oh, the CF transition energies as well as their pressure dependence are well described on the basis of the TS diagram for d8(58,59) (See Figure 3b). The energy of the five measured bands and their different pressure shifts were crucial for a correct band assignment. The Supplemental Material collects the measured transition energies at each pressure and the corresponding calculated energies as a function of the Racah parameters B and C and the CF energy Δ (=10Dq) of the 3d-orbitals split into eg + t2g. The assignment and CF parameters are similar to those originally given elsewhere53−57 (See Figure S1). Therefore, the sub-gap bands correspond to intra-configurational CF transitions within the 3d8 configuration from the 3A2g(F) [t2g6eg2] ground state to the excited states 3T2g(F), 3T1g,a(F), 1Eg(D), 1T2g(D), and 3T1g,a(P), in order of increasing energy, in the low CF limit (Δ/B < 10). However, the 3T1g,a(F) state energy exceeds the 1Eg(D) energy for (Δ/B > 10). Their transition energy as a function of B and C and Δ (see Figure 3b) is given by58,59

3.3.
3.3.
3.3. 1

for the spin-allowed transitions, and by

3.3.
3.3. 2

for transitions with spin change.

In particular, the energy of the 3A2g(F) → 1Eg(D), E2, is practically independent of Δ for Δ/B > 5. The TS for Ni2+ as a plot of E/B vs Δ/B can be obtained directly from eqs 1 and 2 for a given C/B ratio. The energy of the 3A2g(F) → 1Eg(D) transition, which corresponds to a spin-flip transition within the t2g6eg2 configuration, runs parallel to the Δ/B abscissa axis in the TS diagram for about Δ/B > 5 (Figure 3b). The parameters B and Δ at ambient pressure were obtained by least-squares fitting of the experimental energies E1, E3, and E5, whose energies depend on B and Δ but not on C, to eq 1. On the other hand, the spin-flip transition energies E2 and E4, which both depend on B, C, and Δ, were used to determine the parameter C from eq 2. The TS diagram of Figure 3b shows the experimental CF transition energies of the NiWO4 absorption spectrum and the calculated ones using B = 0.088 eV, Δ = 1.01 eV; C/B = 4.5 (Δ/B = 11.5). Comparisons between measured and calculated energies at ambient pressure and as a function of pressure are collected in Table S1 at SI. It should be noted that the values obtained for B, C, and Δ at ambient pressure are somewhat unusual compared to other oxides and fluorides.53−57 For example, the spectrum of NiWO4 looks similar to the Ni2+ in MgO (bunsenite) or NiO (periclase) where energies of the spin-allowed transitions appear at 1.07 eV (3T2g(F)), 1.67 eV (3T1g(F)), and 3.05 eV (3T1g(P)); and 1.09, 1.75 and 2.99 eV, respectively;53,54 or 0.91, 1.55, and 2.95 eV in KNiF3.55 It must be noted that the separation between the experimental 4T1g energies, E = E(3T1g(P))- E(3T1g(F)) = E5 – E3, which has values of 1.38 eV for MgO, 1.24 eV for NiO, and 1.40 eV for KNiF3, is only of 1.0 eV for NiWO4 having a similar Δ value. This relatively smaller energy difference between E5 and E3 reflects the lower value of the measured CF splitting Δ = 0.95 eV as compared to that obtained by fitting Δ = 1.01 eV (about 6%). The opposite trend is observed for E3 (see Table S1 in Supplementary Material).

An examination of the optical absorption of NiWO4 at ambient pressure suggests that the second band E2 could initially be assigned to 3T1g(F) and the third band E3 to 1Eg(D). In fact, such an assignment is in better agreement with the transition energies of other Ni2+ compounds with CF splitting lower than 1.0 eV (E1 < 1.0 eV) such as KNiF354 than with Ni2+ oxides with CF values of about 1.2 eV (E1 > 1.0 eV) obtained in NiO and other oxides.53−55 In addition, the assignment of E3 to 1Eg(D) would be supported by the fact that its intensity is lower than E2 as it would be expected for a spin-flip transition such as 1Eg(D) as opposed to a spin-allowed transition such as 3T1g(F). The assignment given elsewhere10,51 is consistent with this interpretation. However, the fact that we are close to the crossover of the 3T1g(F)-1Eg(D) states around Δ/B = 10 makes the band assignment more complicated. Under such circumstances, the Fano resonance induced by the spin-orbit coupling interaction at the crossover point can equal their respective absorption coefficient, as occurs at the 4T2g – 2Eg crossover point in Cr3+.60 Furthermore, the electric-dipole exchange-induced mechanism, which is very active in exchange-coupled Ni2+ pairs or concentrated materials,56,57 can modify the absorption intensities of spin-flip transitions.

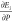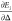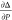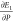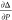Pressure measurements definitely clarify the band assignment based on the pressure shifts. Besides the transition energies Ei, the pressure derivatives Inline graphic are very different for E2 and E3 as it is shown in the TS diagram of Figure 3b. Furthermore, we can directly compare the measured pressure shifts Inline graphic and the calculated CF-derivatives of Ei, Inline graphic, as derived from eqs 1 and 2. These two derivatives are related by the pressure derivative of the CF, Inline graphic, which for Ni2+ coincides with the pressure derivative of the first band: Inline graphic = Inline graphic.

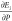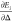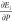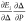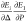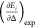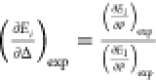Therefore, Inline graphic and Inline graphic are related by the expression: Inline graphic = Inline graphic = Inline graphic. So that, the experimental variation Inline graphic can be obtained from the pressure shifts through the expression: Inline graphic.

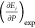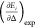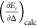The variations Ei(P) are shown in Figure 3a together with their respective pressure derivative Inline graphic. Table 1 compares the experimental pressure derivatives Inline graphic with the calculated ones Inline graphic from eqs 1 and 2 for Δ/B = 11.5. It turns out that, as in most oxides, the energy of the CF-independent spin-flip transition 1Eg(D) corresponds to E2, while 3T1g(F) to E3. The assignment of E1, E4, and E5 to 3T2g(F), 1T2g(D) and 3T1g(P), respectively, is consistent with both their energy and CF-derivative, thus clarifying the origin of the present sub-gap bands in NiWO4. Figure 3b shows the TS diagram and the measured energies with respect to the B parameter. The agreement between the measured and calculated energies with Δ/B is fully consistent with the proposed band assignment.

Table 1. Transition Energies and Corresponding Pressure Shifts of the Five Sub-Gap Bands Ei (i = 1–5) of NiWO4 at Ambient Pressurea.

transition energy E1 E2 E3 E4 E5
band assignment 3A2g(F)→ 3T2g(F) 1Eg(D) 3T1g(F) 1T2g(D) 3T1g(P)
experimental Ei (P = 0; eV) 0.95 1.48 1.70 2.40 2.70
experimental 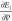Inline graphic (meV GPa–1) 8.9 0.7 11.8 7.4 14.1
experimental 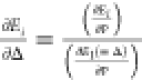Inline graphic 1.0 0.08 1.33 0.83 1.62
calculated from TS 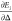Inline graphic 1.0 0.04 1.40 1.07 1.60
Open in a new tab
a

The proposed band assignment to crystal-field transitions within the 3d8 configuration of Ni2+ is included. The comparison between experimental and calculated crystal-field derivatives of the transition energies are shown in last two rows. The crystal-field derivatives were calculated from eqs 1 and 2 for Δ/B = 11.5.

The present work also provides the dependence of the CF splitting Δ with the crystal volume through V(P) and B(P). Figure 7 shows the variation of the CF splitting with V and the inset is the variation B(P) in the studied pressure range. An important conclusion is that, within the accuracy of the data, parameter B can be considered as B = 0.088 eV in the range 0–20 GPa. In fact, B changes only 0.8 meV (from 0.0882 to 0.0890 eV) in this pressure range. In contrast, the variation Δ(P) as 8.9 meVGPa–1 is plotted as a function of the volume and gives an exponent in the variation 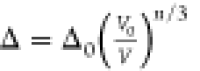Inline graphicas n = 3.8(4). This value is smaller than the CF estimates n = 5 for an Oh symmetry and what has been found for other divalent transition-metal ions in oxides61 and even fluorides.55,62 The low local symmetry of Ni2+ in NiWO4 can probably account for the different n exponent compared to compounds containing the transition-metal ions in Oh sites.

Figure 7.

Figure 7

Open in a new tab

Variation of the CF splitting Δ(P) with the crystal volume V using the V(P) data of Figure 1b. The Δ(V) data have been fitted to the equation 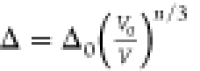Inline graphicwith fit parameters of n = 3.8(4), Δ0= 0.946(2) eV, and V0= 129.1(2) Å3. The inset is the variation B(P) in the explored pressure range. Within the data accuracy, B = 0.088 eV as it changes from 0.0882 to 0.0890 eV in the 0–20 GPa range. We obtain that C/B = 4.5 in this pressure range.

To close this subsection, we would like to comment on finding that a sub-band-gap transition energy (E5) at the highest pressure of this study becomes the same energy as the fundamental band-gap energy. This fact can be related to the closing of the band gap with pressure in NiWO4, which as we discussed before is a typical feature of MWO4 orthotungstates when the divalent cation M is a 3d element as opposed to the opening of the gap when M is a closed-shell element.7

3.4. Resistivity and Hall-Effect Experiments

To conclude, we will present results we obtained for electrical transport properties. Our Hall-effect measurements indicate that NiWO4 behaves as a p-type semiconductor. This could be related with the presence of acceptor levels associated with the presence of Ni vacancies.63Figure 8 shows the pressure dependence of the resistivity (ρ), carrier concentration (p), and mobility (μ) up to 10 GPa. The resistivity at 0 GPa is comparable with that reported by Bharati et al.64 from experiments performed in single crystals. In the past, it was proposed that electrical conductivity can be related to the transfer of d-electrons between neighboring metal ions and by exciting electrons from the valence bands to the conduction bands. However, the carrier concentration we measured is more consistent with an extrinsic semiconductor in which related acceptor levels can be caused by a small concentration of Ni vacancies as recently reported in nickel oxide.63 Under compression, we found that the resistivity decreases. This is a consequence of both the increase of the carrier concentration and mobility. The increase of the carrier mobility could be related to a decrease of the effective mass of holes, which is consistent with the increase of the convexity of the valence band around the maximum as pressure increases (see Figure 4a,b). On the other hand, assuming the semiconductor is extrinsic, from the pressure dependence of the carrier concentration, we can obtain how the activation energy of donors changes with pressure. From our results, we obtain the activation energy decreases with pressure at a rate of −3.6(3) meV/GPa. Such pressure dependence is comparable to that reported for shallow acceptors in other p-type semiconductors.65,66 Thus, the presence of acceptors associated with nickel vacancies in NiWO4 provides a reasonable hypothesis to explain our transport measurements at ambient and high pressure.

Figure 8.

Figure 8

Open in a new tab

(a) Resistivity, (b) carrier concentration, and (c) carrier mobility of NiWO4 versus pressure.

4. Conclusions

From powder XRD experiments, we determined the changes induced by pressure in the crystal structure of NiWO4. We confirmed that it does not undergo any phase transition up to 20 GPa and determined its bulk modulus, main axes of compressibility, and linear compressibility of these axes. We also determined that NiWO4 has a band-gap energy of 3.0 eV which decreases with a pressure coefficient of −13(1) meV/GPa. Both conclusions are supported by DFT calculations which provide a rationale for the changes induced by pressure in the band-gap energy. In particular, calculations show that Ni 3d electrons play a crucial role in the closing of the band gap. We also demonstrated that the five sub-gap bands of NiWO4 correspond to crystal-field transitions within the 3d8 (t2g6eg2) configuration of Ni2+ and clarified their assignment based on their respective energy and pressure shifts. In particular, the different pressure shifts of bands E2 (0.7 meVGPa–1) and E3 (11.8 meVGPa–1) allowed us to unravel their origin as CF transitions to the 1Eg(D) and 3T1g(F) states, respectively, thus resolving a controversial issue in NiWO4. Both the energy and pressure dependence were well described on the basis of the semiempirical CF theory using the Tanabe–Sugano method. Finally, resistivity and Hall-effect measurements showed that NiWO4 is a p-type semiconductor in which the resistivity decreases under compression due to the increase of both the carrier concentration and mobility. This implies that thin films of NiWO4 under compressive stress can prove to be better electrode materials for supercapacitors.

Acknowledgments

D.E. acknowledges the financial support from the Generalitat Valenciana under grant nos. PROMETEO CIPROM/2021/075-GREENMAT and MFA/2022/007 and Spanish Ministerio de Ciencia e Innovación and Agencia Estatal de Investigación (MCIN/AEI/10.13039/501100011033) and the European Union under grant nos. PID2019-106383GB-41/42 and RED2018-102612-T (MALTA Consolider-Team network). This study forms part of the Advanced Materials program and is supported by MCIN with funding from European Union Next Generation EU (PRTR-C17.I1) and by the Generalitat Valenciana. F.R. acknowledges financial support from Projects PID2021-127656NB-I00 and MALTA-Consolider Team (RED2018-102612-T) from the State Research Agency of Spain, Ministry of Science and Innovation. The authors J.S. and V.K. would like to acknowledge IIT Hyderabad for computational facility. V.K. would like to acknowledge DST-FIST (SR/FST/PSI-215/2016) for the financial support. J.S. would like to acknowledge CSIR for the fellowship. G.V. would like to acknowledge Institute of Eminence, University of Hyderabad (UoH-IoE-RC3-21-046) for funding and CMSD University of Hyderabad for providing the computational facility. We thank Dr. Velaga Srihari and Smt. Vasanthi for helping with the data acquisition at BL11 beamline at INDUS2.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.3c03512.

  • Comparisons between measured and calculated energies at ambient pressure and as a function of pressure (PDF)

Author Contributions

D.E. conceived the project. R.V. and D.V. synthesized and characterized the sample. S.G., B.N., and N.G. performed powder XRD experiments. D.E. performed optical and transport experiments, D.E., F.R., and R.V. performed data analysis. J.S., V.K., and G.V. performed density-functional theory calculations. D.E., F.R., N.G., and G.V. contributed to discussions. All authors participated in writing and editing of the manuscript. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

jp3c03512_si_001.pdf (134.2KB, pdf)

References

  1. Shaheen N.; Aadil M.; Zulfiqar S.; Sabeeh H.; Agboola P. O.; Warsi M. F.; Aboud M. F. A.; Shakir I. Fabrication of different conductive matrix supported binary metal oxides for supercapacitors applications. Ceram. Int. 2021, 47, 5273–5285. 10.1016/j.ceramint.2020.10.108. [DOI] [Google Scholar]
  2. Ji Y.; Yang L.; Ren X.; Cui G.; Xiong X.; Sun X. Full Water Splitting Electrocatalyzed by NiWO4 Nanowire Array. ACS Sustainable Chem. Eng. 2018, 6, 9555–9559. 10.1021/acssuschemeng.8b01841. [DOI] [Google Scholar]
  3. Mikhailik V. B.; Kraus H. Performance of Scintillation Materials at Cryogenic Temperatures. Phys. Status Solidi B 2010, 247, 1583–1599. 10.1002/pssb.200945500. [DOI] [Google Scholar]
  4. Keeling R.O. Jr. The structure of NiWO4. Acta Crystallogr. 1957, 10, 209–213. 10.1107/S0365110X57000651. [DOI] [Google Scholar]
  5. Cornelis K.; Hurlbut C.S. Jr.. Manual of Mineralogy, 20th ed.; Wiley, 1985; pp 355–356. [Google Scholar]
  6. Errandonea D.; Ruiz-Fuertes J. A Brief Review of the Effects of Pressure on Wolframite-Type Oxides. Crystals 2018, 8, 71. 10.3390/cryst8020071. [DOI] [Google Scholar]
  7. Ruiz-Fuertes J.; López-Moreno S.; López-Solano J.; Errandonea D.; Segura A.; Lacomba-Perales R.; Mũnoz A.; Radescu S.; Rodríguez-Hernández P.; Gospodinov M.; Nagornaya L. L.; Tu C. Y. Pressure Effects on the Electronic and Optical Properties of AWO4 Wolframites (A = Cd, Mg, Mn, and Zn): The Distinctive Behavior of Multiferroic MnWO4. Phys. Rev. B 2012, 86, 125202 10.1103/PhysRevB.86.125202. [DOI] [Google Scholar]
  8. Bandiello E.; Rodríguez-Hernández P.; Muñoz A.; Buenestado M. B.; Popescu C.; Errandonea D. Electronic Properties and High-Pressure Behavior of Wolframite-Type CoWO4. Mater. Adv. 2021, 2, 5955–5966. 10.1039/D1MA00510C. [DOI] [Google Scholar]
  9. Ruiz-Fuertes J.; Segura A.; Rodríguez F.; Errandonea D.; Sanz-Ortiz M. N. Anomalous High-Pressure Jahn-Teller Behavior in CuWO4. Phys. Rev. Lett. 2012, 108, 166402 10.1103/PhysRevLett.108.166402. [DOI] [PubMed] [Google Scholar]
  10. Ye M.; Zhou Y.; Shao T.; Liu H.; Tao Q.; Wang X.; Tang R.; Yue H.; Li Y.; Zhu P. Effects of High Pressure on the Bandgap and the d–d Crystal Field Transitions in Wolframite NiWO4. J. Phys. Chem. C 2023, 127, 6543–6551. 10.1021/acs.jpcc.2c09036. [DOI] [Google Scholar]
  11. Liang A.; Turnbull R.; Errandonea D. A review on the advancements in the characterization of the high-pressure properties of iodates. Prog. Mater. Sci. 2023, 136, 101092 10.1016/j.pmatsci.2023.101092. [DOI] [Google Scholar]
  12. Ejima T.; Banse T.; Takatsuka H.; Kondo Y.; Ishino M.; Kimura N.; Watanabe M.; Matsubar I. Microscopic optical and photoelectron measurements of MWO4 (M= Mn, Fe, and Ni). J. Lumin. 2006, 119–120, 59–63. 10.1016/j.jlumin.2005.12.012. [DOI] [Google Scholar]
  13. de Oliveira A. L. M.; Ferreira J. M.; Silva M. R. S.; de Souza S. C.; Vieira F. T. G.; Longo E.; Souza A. G.; Santos M. G. Influence of the thermal treatment in the crystallization of NiWO4 and ZnWO4. J. Therm. Anal. Calorim. 2009, 97, 167–172. 10.1007/s10973-009-0244-8. [DOI] [Google Scholar]
  14. Oliveira Y. L.; Costa M. J. S.; Juca A. C. S.; Silva L. K. R.; Longo E.; Arul N. S.; Cavalcante L. S. Structural characterization, morphology, optical and colorimetric properties of NiWO4 crystals synthesized by the co-precipitation and polymeric precursor methods. J. Mol. Struct. 2020, 1221, 128774 10.1016/j.molstruc.2020.128774. [DOI] [Google Scholar]
  15. Bhattacharya A. K.; Biswas R. G.; Hartridge A. Environment sensitive impedance spectroscopy and dc conductivity measurements on NiWO4. J. Mater. Sci. 1997, 32, 353–356. 10.1023/A:1018545131216. [DOI] [Google Scholar]
  16. Ahmed M. I.; Adam A.; Khan A.; Siddiqui M. N.; Yamani Z. H.; Qamar M. Q. Synthesis of mesoporous NiWO4 nanocrystals for enhanced photo electrochemical water oxidation. Mater. Lett. 2016, 177, 135–138. 10.1016/j.matlet.2016.04.143. [DOI] [Google Scholar]
  17. Dridi R.; Dridi D.; Hammami S.; Dimassi W.; Chtourou R.; Amlouk M. Growth and physical investigations on NiWO4 thin films as a potential for NO2 sensing. Optik 2023, 273, 170330 10.1016/j.ijleo.2022.170330. [DOI] [Google Scholar]
  18. Pandey P. K.; Bhave N. S.; Kharat R. B. Structural, optical, electrical and photovoltaic electrochemical characterization of spray deposited NiWO4 thin films. Electrochim. Acta 2006, 51, 4659–4664. 10.1016/j.electacta.2005.12.042. [DOI] [Google Scholar]
  19. AlShehri S. M.; Ahmed J.; Alzahrani A. M.; Ahamad T. Synthesis, characterization, and enhanced photocatalytic properties of NiWO4 nanobricks. New J. Chem. 2017, 41, 8178–8186. 10.1039/C7NJ02085F. [DOI] [Google Scholar]
  20. Weitzel H. Kristallstrukturverfeinerung von Wolframiten und Columbiten. Z. Kristallogr. - Cryst. Mater. 1976, 144, 238–258. 10.1524/zkri.1976.144.1-6.238. [DOI] [Google Scholar]
  21. Pandey K. K.; Poswal H. K.; Mishra A. K.; Dwivedi A.; Vasanthi R.; Garg N.; Sharma S. M. Energy-dispersive X-ray diffraction beamline at Indus-2 synchrotron source. Pramana 2013, 80, 607–619. 10.1007/s12043-012-0493-0. [DOI] [Google Scholar]
  22. Klotz S.; Chervin J. C.; Munsch P.; Le Marchand G. Hydrostatic limits of 11 pressure transmitting media. J. Phys. D: Appl. Phys. 2009, 42, 075413 10.1088/0022-3727/42/7/075413. [DOI] [Google Scholar]
  23. Dewaele A.; Loubeyre P.; Mezouar M. Equations of state of six metals above 94 GPa. Phys. Rev. B 2004, 70, 094112 10.1103/PhysRevB.70.094112. [DOI] [Google Scholar]
  24. Prescher C.; Prakapenka V. B. DIOPTAS: a program for reduction of two-dimensional X-ray diffraction data and data exploration. High Pressure Res. 2015, 35, 223–230. 10.1080/08957959.2015.1059835. [DOI] [Google Scholar]
  25. Toby B. H. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 2001, 34, 210–213. 10.1107/S0021889801002242. [DOI] [Google Scholar]
  26. Mao H. K.; Xu J.; Bell P. M. Calibration of the Ruby Pressure Gauge to 800 Kbar under Quasi-Hydrostatic Conditions. J. Geophys. Res. 1986, 91, 4673–4676. 10.1029/JB091iB05p04673. [DOI] [Google Scholar]
  27. Errandonea D.; Bandiello E.; Segura A.; Hamlin J. J.; Maple M. B.; Rodriguez-Hernandez P.; Muñoz A. Tuning the band gap of PbCrO4 through high-pressure: Evidence of wide-to-narrow semiconductor transitions. J. Alloys Compd. 2014, 587, 14–20. 10.1016/j.jallcom.2013.10.179. [DOI] [Google Scholar]
  28. Errandonea D.; Segura A.; Martínez-García D.; Muñoz-San Jose V. Hall-effect and resistivity measurements in CdTe and ZnTe at high pressure: Electronic structure of impurities in the zinc-blende phase and the semimetallic or metallic character of the high-pressure phases. Phys. Rev. B 2009, 79, 125203 10.1103/PhysRevB.79.125203. [DOI] [Google Scholar]
  29. Errandonea D.; Martinez-Garcia D.; Segura A.; Ruiz-Fuertes J.; Lacomba-Perales R.; Fages V.; Chevy A.; Roa L.; Muñoz V. High-pressure electrical transport measurements on p-type GaSe and InSe. High Pressure Res. 2006, 26, 513–516. 10.1080/08957950601101787. [DOI] [Google Scholar]
  30. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  31. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  32. Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  33. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  34. Monkhorst H. J.; Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
  35. Dudarev S. L.; Botton G. A.; Savrasov S. Y.; Humphreys C. J.; Sutton A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+ U study. Phys. Rev. B 1998, 57, 1505–1509. 10.1103/PhysRevB.57.1505. [DOI] [Google Scholar]
  36. Tran F.; Blaha P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 2009, 102, 226401 10.1103/PhysRevLett.102.226401. [DOI] [PubMed] [Google Scholar]
  37. Kuzmin A.; Kalinko A.; Evarestov R. A. First-principles LCAO study of phonons in NiWO4. Cent. Eur. J. Phys. 2011, 9, 502–509. 10.2478/s11534-010-0091-z. [DOI] [Google Scholar]
  38. Weitzel H. Magnetische struktur von CoWO4, NiWO4 und CuWO4. Solid State Commun. 1970, 8, 2071–2072. 10.1016/0038-1098(70)90221-8. [DOI] [Google Scholar]
  39. Jiao Z. J.; Ma S. H.; Yang J. F. A comparison of the electronic and optical properties of zinc-blende, rocksalt and wurtzite AlN: A DFT study. Solid State Sci. 2011, 13, 331–336. 10.1016/j.solidstatesciences.2010.11.030. [DOI] [Google Scholar]
  40. Errandonea D.; Muñoz A.; Gonzalez-Platas J. Comment on “High-pressure x-ray diffraction study of YBO3/Eu3+, GdBO3, and EuBO3: Pressure-induced amorphization in GdBO3” [J. Appl. Phys. 115, 043507 (2014)]. J. Appl. Phys. 2014, 115, 216101. 10.1063/1.4881057. [DOI] [Google Scholar]
  41. Birch F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. 10.1103/PhysRev.71.809. [DOI] [Google Scholar]
  42. Anzellini S.; Burakovsky L.; Turnbull R.; Bandiello E.; Errandonea D. P–V–T Equation of State of Iridium up to 80 GPa and 3100 K. Crystals 2021, 11, 452. 10.3390/cryst11040452. [DOI] [Google Scholar]
  43. Errandonea D.; Popescu C.; Achary S.-N. A. K.; Tyagi A. K.; Bettinelli M. In situ high-pressure synchrotron X-ray diffraction study of the structural stability in NdVO4 and LaVO4. Mater. Res. Bull. 2014, 50, 279–284. 10.1016/j.materresbull.2013.10.047. [DOI] [Google Scholar]
  44. Cliffe M. J.; Goodwin A. L. PASCal: a principal axis strain calculatorfor thermal expansion and compressibility determination. J. Appl. Crystallogr. 2012, 45, 1321–1329. 10.1107/S0021889812043026. [DOI] [Google Scholar]
  45. Tauc J. Optical properties and electronic structure of amorphous Ge and Si. Mater. Res. Bull. 1968, 3, 37–46. 10.1016/0025-5408(68)90023-8. [DOI] [Google Scholar]
  46. Garg A. B.; Vie D.; Rodriguez-Hernandez P.; Muñoz A.; Segura A.; Errandonea D. Accurate Determination of the Bandgap Energy of the Rare-Earth Niobate Series. J. Phys. Chem. Lett. 2023, 14, 1762–1768. 10.1021/acs.jpclett.3c00020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Rosal F. J. O.; Gouveia A. F.; Sczancoski J. C.; Lemos P. S.; Longo E.; Zhang B.; Cavalcante L. S. Electronic structure, growth mechanism, and sonophotocatalytic properties of sphere-like self-assembled NiWO4 nanocrystals. Inorg. Chem. Commun. 2018, 98, 34–40. 10.1016/j.inoche.2018.10.001. [DOI] [Google Scholar]
  48. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  49. List N. H.; Kauczor J.; Saue T.; Jensen H. J.; Norman P. Beyond the electric-dipole approximation: A formulation and implementation of molecular response theory for the description of absorption of electromagnetic field radiation. J. Chem. Phys. 2015, 142, 244111. 10.1063/1.4922697. [DOI] [PubMed] [Google Scholar]
  50. Begum V.; Gruner M. E.; Vorwerk C.; Draxl C.; Pentcheva R. Theoretical description of optical and x-ray absorption spectra of MgO including many-body effects. Phys. Rev. B 2021, 103, 195128 10.1103/PhysRevB.103.195128. [DOI] [Google Scholar]
  51. Lima N. A.; Alencar L. D.; Siu-Li M.; Feitosa C. A.; Mesquita A.; M’peko J. C.; Bernardi M. I. NiWO4 powders prepared via polymeric precursor method for application as ceramic luminescent pigments. J. Adv. Ceram. 2020, 9, 55–63. 10.1007/s40145-019-0347-z. [DOI] [Google Scholar]
  52. Fujimori A.; Minami F. Valence-band photoemission and optical absorption in nickel compounds. Phys. Rev. B 1984, 30, 957–971. 10.1103/PhysRevB.30.957. [DOI] [Google Scholar]
  53. Burns R. G.Mineralogical applications of crystal field theory, Cambridge Topics in Mineral Physics and Chemistry; Cambridge University Press, 1993, Vol. 5; pp 1 −551, 10.1017/CBO9780511524899. [DOI] [Google Scholar]
  54. Hush N. S.; Hobbs R. J. M.. Absorption Spectra of Crystals Containing Transition Metal Ions. Prog. Inorg. Chem.1968, Vol. 10; pp 259 −486. [Google Scholar]
  55. Barreda-Argüeso J. A.; Rodríguez F. Pressure dependence of the crystal-field spectrum of KNiF3: Single and double excitations. Phys. Rev. B 2021, 103, 085115 10.1103/PhysRevB.103.085115. [DOI] [Google Scholar]
  56. Knox K.; Shulman R. G.; Sugano S. Covalency Effects in KNiF3. II. Optical Studies. Phys. Rev. B 1963, 130, 512–516. 10.1103/PhysRev.130.512. [DOI] [Google Scholar]
  57. Ferguson J.; Guggenheim H. J. Electronic Absorption Spectrum of Ni (II) in Cubic Perovskite Fluorides. II. Concentration and Exchange Effects. J. Chem. Phys. 1966, 44, 1095–1102. 10.1063/1.1726793. [DOI] [Google Scholar]
  58. Sugano S.; Tanabe Y.; Kamimura H.. Multiplets of Transition-Metal Ions in Crystals; Acad Press.: New York, 1970; pp 1–348. ISBN: 9780323154796. [Google Scholar]
  59. Griffith J.S.The theory of transition-metal ions Cambridge University Press, 1964. [Google Scholar]
  60. Hernandez I.; Rodriguez F.; Tressaud A. Optical Properties of the (CrF6)3– Complex in A2BMF6: Cr3+ Elpasolite Crystals: Variation with M– F Bond Distance and Hydrostatic Pressure. Inorg. Chem. 2008, 47, 10288–10298. 10.1021/ic800606h. [DOI] [PubMed] [Google Scholar]
  61. Gavriliuk A. G.; Trojan I. A.; Struzhkin V. V. Insulator-metal transition in highly compressed NiO. Phys. Rev. Lett. 2012, 109, 086402 10.1103/PhysRevLett.109.086402. [DOI] [PubMed] [Google Scholar]
  62. Barreda-Argüeso J. A.; Aguado F.; González J. A.; Valiente R.; Nataf L.; Sanz-Ortiz M. N.; Rodríguez F. Crystal-Field Theory Validity Through Local (and Bulk) Compressibilities in CoF2 and KCoF3. J. Phys. Chem. C 2016, 120, 18788–18793. 10.1021/acs.jpcc.6b06132. [DOI] [Google Scholar]
  63. Karsthof R.; Anton A. M.; Kremer F.; Grundmann M. Nickel vacancy acceptor in nickel oxide: Doping beyond thermodynamic equilibrium. Phys. Rev. Mater. 2020, 4, 034601 10.1103/PhysRevMaterials.4.034601. [DOI] [Google Scholar]
  64. Bharati R.; Singh R. A.; Wanklyn B. M. Electrical conductivity, thermoelectric power and dielectric constant of NiWO4. J. Mater. Sci. 1980, 15, 1293–1296. 10.1007/BF00551819. [DOI] [Google Scholar]
  65. Gonzalez J.; Calderon E.; Capet F.; Baert F. Pressure dependence of shallow acceptors in CuGa(SxSe1–x)2 alloys. Phys. Rev. B 1998, 58, 13654–13659. 10.1103/PhysRevB.58.13654. [DOI] [Google Scholar]
  66. Karaouzène L. I.; Ouahrani T.; Morales-García A.; Errandonea D. Theoretical calculations of the effect of nitrogen substitution on the structural, vibrational, and electronic properties of wolframite-type ScTaO4 at ambient conditions. Dalton Trans. 2022, 51, 3642–3651. 10.1039/D1DT04369B. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp3c03512_si_001.pdf (134.2KB, pdf)

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES