Modeling Likert scale outcomes with trend-proportional odds with and without cluster data

Abstract

Likert scales are commonly used in epidemiological studies employing surveys. In this tutorial we demonstrate how the proportional odds model and the trend odds model can be applied simultaneously to data measured in Likert scales, allowing for random cluster effects. We use two datasets as examples: an epidemiological study on aging and cognition among community-dwelling Black persons, and a clustered large survey data from 28,882 students in 81 middle schools. The first example models the Likert outcome from the question: “People act as if they think you are dishonest”. The trend-proportional odds model indicates that Black men have higher odds than Black women of reporting being perceived dishonest. The second example models the Likert outcome from the question: “How often have you been beaten up at school?”. The trend-proportional odds model indicates that children with disability have a higher odds of severe violence than other children. For both examples, the cumulative odds ratio increases by more than 60% at the higher Likert levels.

Introduction

Likert scales are commonly used in epidemiological studies. Individual Likert items are discrete and ordinal by definition, commonly with three to seven possible levels depending on the design. Likert questions are useful when relying on the participant’s report of experiences or symptoms (Huang et al., 2010). These questions provide a closed ordinal array of response options (Likert, 1932). It is relatively common practice to have multiple Likert questions of interest. Often, the main outcome is obtained by summing individual Likert scores. These scores are adopted values, for example they can go from 0 to 3 in a four-level Likert. This paper does not focus on such composite Likert scores but on individual Likert outcomes based on a single Likert item. Studies that employ a single Likert item may also be motivated by secondary hypothesis or by the need to generate preliminary data for future research.

Analysis of Likert outcomes should involve methods designed for ordinal data. However, these scales are often dichotomized for analyses, resulting in loss of information and reduction of power (Capuano, Dawson, & Gray, 2007). Another practice is to use models based on normal distribution. This approach is commonly criticized (Agresti, 2002; Clason & Dormody, 1994) given the discrete nature of the Likert (e.g. flooring, ceiling and no halves) and the fact that data are often skewed. A better alternative is, therefore, to use methods designed for this type of data, such as ordinal logistic regressions. Constrained cumulative ordinal models are a popular parsimonious method of analyzing ordinal outcomes. These include the proportional odds model (Aitchison & Silvey, 1957; McCullagh, 1980; Snell, 1964) and the trend odds model (Capuano & Dawson, 2013). These models are an extension of the binary logistic regression for ordinal outcomes with more than two levels.

In this paper, we first discuss the detailed formulas for the proportional odds model, the trend odds model, and a hybrid model known as the proportional-trend odds model. We then give a tutorial on how to fit these models. These models are also extended to clustered data, which, to our knowledge, has not been demonstrated in the literature for the case of trend odds models. Simple and complex examples with different 4-level Likert outcomes are used to illustrate the basic multivariate model and the extension. To illustrate the basic application, we model the Likert outcome from the question: “People act as if they think you are dishonest”. To illustrate the application to clustered data we model the Likert outcome from the question: “How often have you been beaten up at school?”. Sample SAS and R code are provided in the appendices.

The Proportional Odds Model

Consider a Likert outcome Y with k+1 categories. The “cumulative odds” are the odds of Y being at least equal to k. The cumulative odds can also be related to a predictor variable X₁ through a linear function based on the inverse log. We can express this function as

$$\mathit{\text{log}}\left(\frac{\text{Pr}\left(\mathit{Y}\ge \mathit{k}\mid {\mathit{X}}_1\right)}{\text{Pr}\left(\mathit{Y}<\mathit{k}\mid {\mathit{X}}_1\right)}\right)={\mathit{\alpha }}_{\mathit{k}}+{\mathit{\beta }}_{\mathit{k},1}{\mathit{X}}_1,$$ (1)

where ${\beta }_{k,1}$ is the parameter associated with the log odds ratio at each level of the outcome Y for predictor variable X₁.

In the unconstrained cumulative ordinal model, all ${\beta }_{k,x}$ are different and unrelated. That is ${\beta }_{1,x}\ne {\beta }_{2,x}\ne {\beta }_{3,x}\ne {\beta }_{4,x}$. In other words, there are no constraints imposed on the cumulative log odds ratio, ${\beta }_{k,x}$ (Agresti, 2002; McCullagh, 1980; Peterson, Harrell, & Brant, 1992; Peterson & Harrell, 1990). That there are multiple unrelated cumulative odds ratios makes interpretation of this model more challenging in practice. The number of parameters ${\beta }_{k,x}$ increases with the number of levels in the outcome. For example, a complex 7-level-Likert will have six cumulative odds ratios associated with each predictor, resulting in less parsimony and possible model fitting problems. The constrained cumulative ordinal models are a family of models that try to identify a relationship between the cumulative odds ratios. These models are theoretically justified by the underlying logistic distribution. The proportional odds model and the trend odds models belong to the constrained cumulative ordinal family of models.

The proportional odds model was initially discussed by Aitchison and Silvey in 1957 and Snell in 1964, but popularized and named by McCullagh in 1982. The development of the method is based on an underlying (unobserved or latent) continuous variable that follows a logistic distribution. It is possible to calculate log odds ratios by assuming cut-points in the distribution (i.e. probability above or below any value in the distribution). When there are shifts in the location of the distribution with changes in a predictor (i.e. males may have lower mean than females), it has been proved that proportional log odds ratios are observed. Note that this latent variable is not directly modeled.

The proportional odds model works on the assumption that all ${\beta }_{k,x}$ are represented by a common ${\beta }_{•,x}$, that is ${\beta }_{•,x}={\beta }_{1,x}={\beta }_{2,x}={\beta }_{3,x}$ (McCullagh, 1980). That leads to the proportional odds assumption that the odds of being above any given level are the same. In other words, instead of having several different odds ratio for a given independent variable, a single odds ratio is calculated. In this model, the cumulative odds is related to an independent variable X₁ through a linear function based on the inverse log. We can express this function as

$$\mathit{\text{log}}\left(\frac{\text{Pr}\left(Y\ge k\mid X_1\right)}{\text{Pr}\left(Y<k\mid X_1\right)}\right)={\alpha }_k+{\beta }_{•,1}{X}_1.$$ (2)

Because the proportional odds model summarizes data more succinctly, results are easier to interpret and it is the preferred model if the proportional odds assumption is met. The proportional odds assumption can be tested using a score test for proportional odds when the sample is not too large (Scott, Goldberg, & Mayo, 1997; Stokes, Davis, & Koch, 2012). When the sample is large, graphical displays of observed odds and estimates from binary logistic regression can be used (Scott et al., 1997).

The Trend Odds Model

The trend odds model was developed by Capuano and Dawson in 2012 as an attempt to provide a parsimonious alternative to the proportional odds model. The development of the method is also based on an underlying continuous variable that follows a logistic distribution. When there are shifts in the scale of the distribution with changes in a predictor (i.e. males have more variability than females), it has been proved that trend log odds ratios are observed. The theoretical shifts in location and scale are of practical interest because they yield an increasing risk or protective effect that is represented respectively by all log odds below zero or all log odds above zero. As in the case for the proportional odds model, the latent variable is not directly modeled.

The trend odds models works on the assumption that all ${\beta }_{\text{k},\text{x}}$ have a monotonic relationship. That is ${\beta }_{1,\text{x}}<{\beta }_{2,\text{x}}<{\beta }_{3,\text{x}}$ or ${\beta }_{1,\text{x}}>{\beta }_{2,\text{x}}>{\beta }_{3,\text{x}}$ (Capuano & Dawson, 2013). That means that the cumulative odds have a trend, increasing or decreasing monotonically with the increase of outcome level k. In this model, the cumulative odds is also related to an independent variable through a linear function based on the inverse log. For an independent variable X₂, the trend odds model can be expressed as

$$\mathit{\text{log}}\left(\frac{\text{Pr}\left(Y\ge k\mid X_2\right)}{\text{Pr}\left(Y<k\mid X_2\right)}\right)={\alpha }_k+{\beta }_{1,2}{X}_2+{\gamma }_2{t}_k{X}_2,t_k<t_{k+1}.$$ (3)

The scalar values t_k are assumed to be equal to k-1 when no a priori information is available, for example, from previous studies.

The Proportional-Trend Odds Model

The above models have being previously used with different types of ordinal data such as classification groups, levels of antibody titers and temperament scales (Capuano et al., 2007; Singh, Bard, & Jackson, 2014; Zerwas et al., 2012). Models often include multiple covariates (multivariate models). The proportional odds assumption may not hold for all the covariates in the model. Although some researchers are careful in examining the assumption, violations are sometimes ignored (Singh et al., 2014). Peterson and Harrell discussed the relief of the proportional odds assumption for some but not all covariates. This strategy has being used by some researchers so that some covariates have one beta (proportional odds) and others have multiple betas (unconstrained odds) (Zerwas et al., 2012). Alternatively, we can use a combination of the proportional odds and the trend odds, here called the proportional-trend odds model. This strategy implies that some predictors assume proportional odds and some assume trend odds.

Consider again a Likert outcome Y with k+1 categories. There may be two covariates of cumulative log odds of Y given X₂ be an increasing or decreasing trend. The proportional-trend odds model can be expressed as

$$\mathit{\text{log}}\left(\frac{\text{Pr}\left(Y\ge k\mid X_1,X_2\right)}{\text{Pr}\left(Y<k\mid X_1,X_2\right)}\right)={\alpha }_k+{\beta }_{•,1}{X}_1+{\beta }_{1,2}{X}_2+{\gamma }_2{t}_k{X}_2,t_k<t_{k+1}$$ (4)

In certain designs, randomization of data occurs at a cluster level. For example several participants may be recruited from a specific location, leading to within-location correlation. Random effects models are commonly used because they can handle unbalanced clusters as discussed by Hedeker and others (Hedeker, Gibbons, & Flay, 1994). Consider t11hat k is a nested observation within cluster j. Equation (4) can be expanded to a random cluster effect with the trend-proportional odds expressed as

$$\mathit{\text{log}}\left(\frac{\text{Pr}\left(Y\ge k\mid X_{1,j},X_{2,j}\right)}{\text{Pr}\left(Y<k\mid X_{1,j},X_{2,j}\right)}\right)={\alpha }_k+{\beta }_{•,1}{X}_{1,j}+{\beta }_{1,2}{X}_{2,j}+{\gamma }_2{t}_k{X}_{2,j}+{\phi }_j,t_k<t_{k+1}$$ (5)

The random cluster effect ${\phi }_j$ is assumed to follow a normal distribution with mean equal to zero and variance equal to $\sigma$.

The proportional-trend odds model assumes that the log odds are either proportional or have a specific patterns of increasing or decreasing trends. The proportional odds and the trend odds are theoretically justified by an underlying logistic distribution that has shifts in location and scale, respectively. Less parsimonious parameterizations can be used for some covariates (i.e. unconstrained) for exploration analyses of covariates that violate both proportional and trend odds assumptions.

Tutorial

Analytical Strategy

To fit the proportional-trend odds model the researcher can follow some steps detailed in this section⁹. Preliminary analyses of the data should include an examination of the frequency distribution. If data are too sparse, ordinal modeling may not be possible (i.e. only two of the Likert levels have frequencies greater than 5), or it may be necessary to combine the last or first Likert level with the closest level. Assuming that there are enough observations per ordinal level, analyses can follow four steps.

Step 1 - Bivariable Analyses - Binary Logistic Regression

The objective of this step is to obtain cumulative odds for each possible cut-point in the initial inspection of the data. For example a 4-level Likert has three cut-points and three cumulative odds ratios: ${\theta }_1,{\theta }_2$, and ${\theta }_3$. Cumulative odds ratios for each possible cut-point can be obtained by fitting separate logistic regressions per cut-point (i.e. a Likert 0123 have three indicator variables with values: 0111, 0011, and 0001). Modeling can be performed using the Glm procedure in R (with family specified as binomial), or the Proc Logistic procedure in SAS. Alternatively one can fit the unconstrained model that will generate several parameters, one per cut-point. That can be accomplished by using the Proc Nlmixed procedure in SAS or the Vglm procedure in R (with family specified as cumulative and parallel specified as false). In contrast to SAS Proc Nlmixed, R Vglm does not require the user to select initial values and it is easier to use, especially for the less sophisticated user. Graphical displays of the log odds such as in Figures 1 and 2 can be used to investigate the proportional odds assumption and the trend odds assumption.

Figure 1.

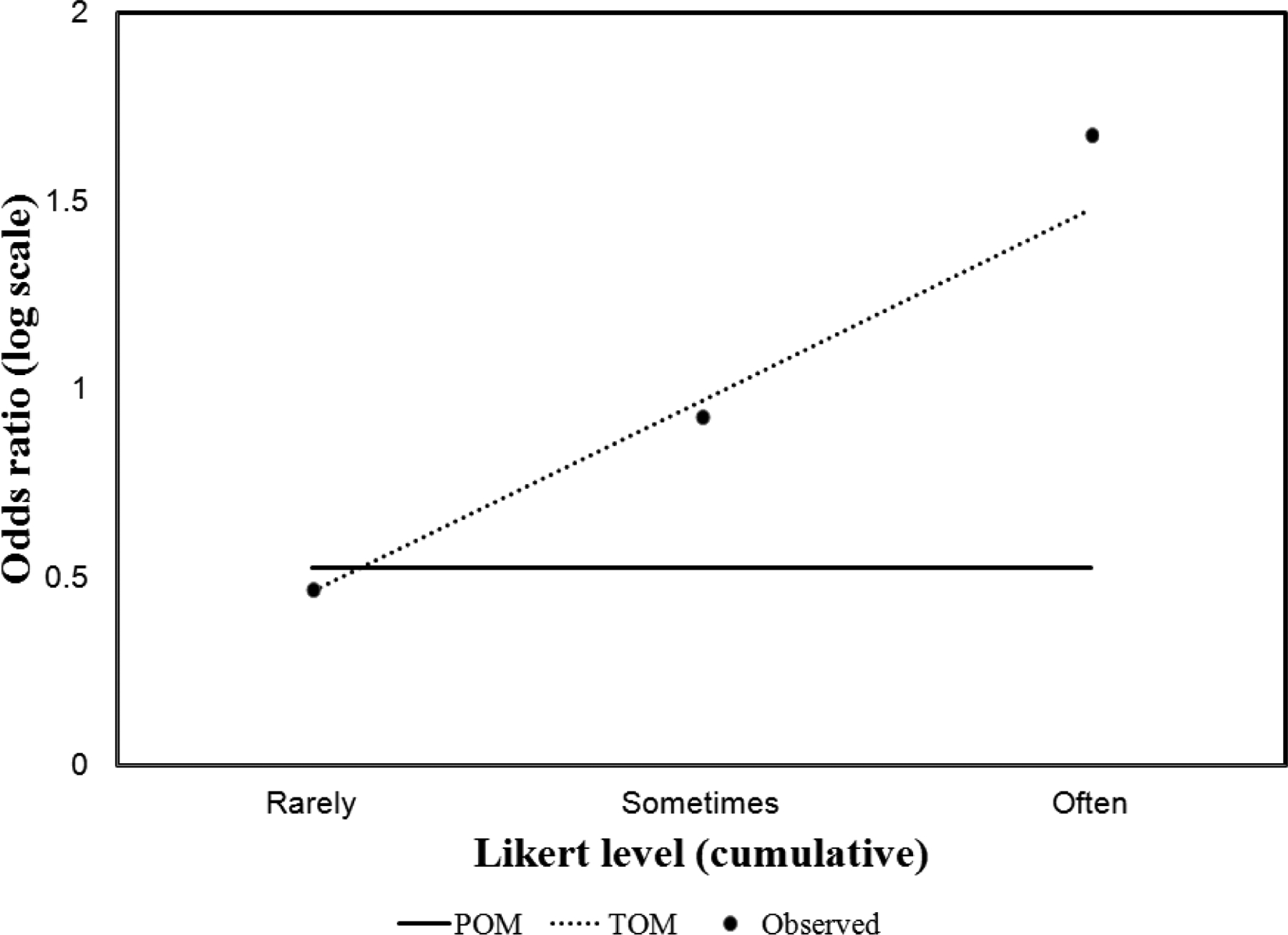
Unadjusted cumulative log odds ratio of dishonesty perception for Black men compared to Black women.

Figure 2.

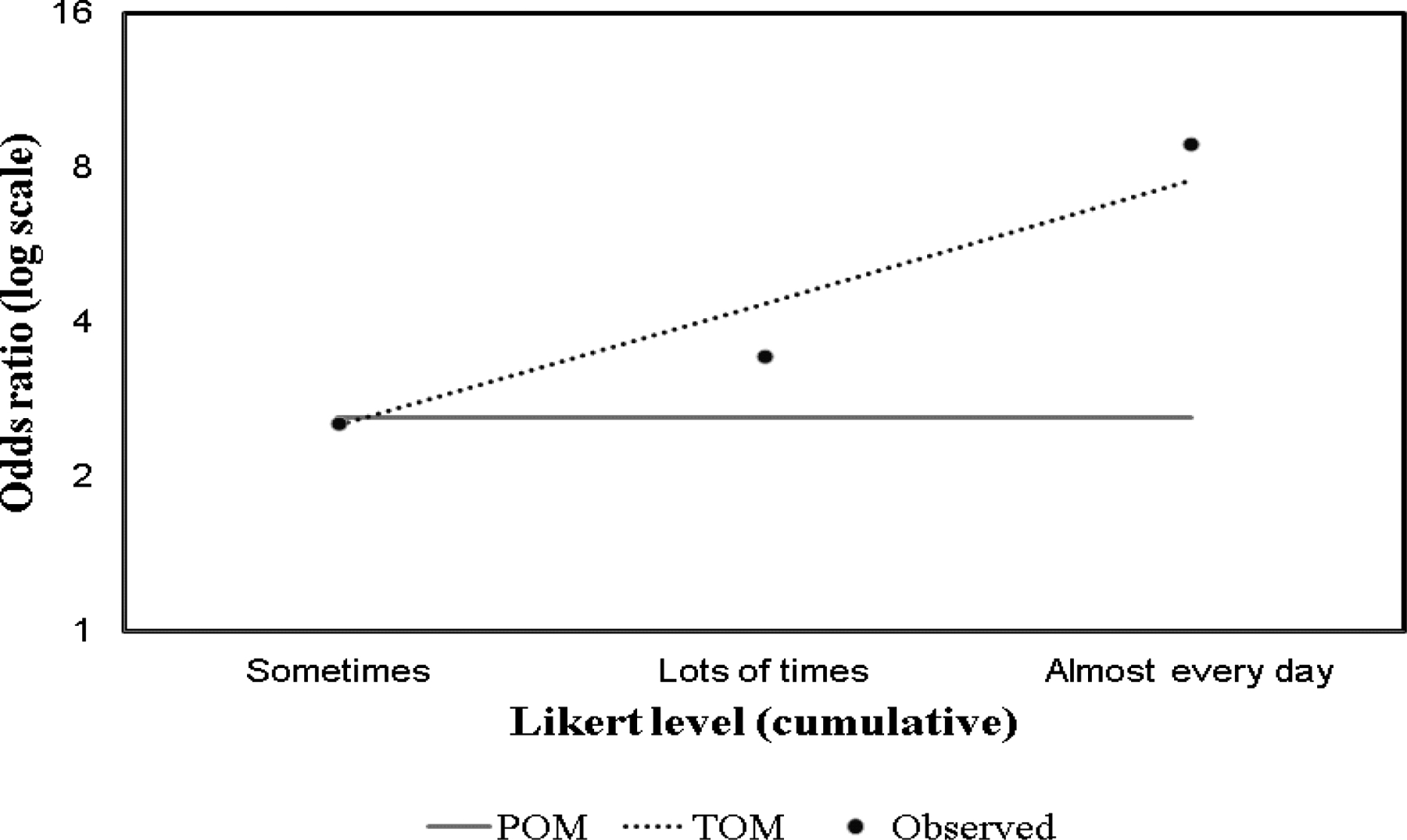
Unadjusted cumulative log odds ratio of severe violence for children with disability compared to others.

Step 2 - Bivariable Analyses - Proportional Odds Model

The objective of this step is to inspect the significance of the independent variables when entered individually in the proportional odds model and to assess the proportional odds assumption. The proportional odds model can be fit with the Proc Logistic procedure in SAS or the Glm procedure in R (with family specified as cumulative and parallel specified as true). The score test for proportional odds assumption is obtained from the SAS procedure logistic. In R the proportional odds assumption can be tested using likelihood ratio tests calculated from the difference in the deviance of proportional odds model and the deviance of the unconstrained model.

The proportional odds model provides a common odds ratio. That is the odds ratio of being above any level compared to the odds ratio of being below the level are the same $\left(\theta ={\theta }_1={\theta }_2={\theta }_3\right)$. A significant or borderline score test provides partial support for rejecting the proportional odds assumption because large samples have sufficient power to detect very small deviations of proportionality of odds. A non-significant score test for proportional odd or likelihood ratio test results in failure to reject the proportional odds assumption. For example, a $p$ value above .2 provides strong evidence that the proportional odds model is adequate. In this case, step 3 is particularly important to verify if the proportional odds assumption is being rejected due to a trend in odds.

In SAS, parameters estimates from the proportional odds model with independent variables that present a trend can be stored to be used as initial values for modeling in step 3.

Step 3 - Bivariable Analyses - Trend Odds Model

The objective of this step is to inspect the significance of the independent variables when entered individually in the trend odds model and respective trend parameter $\gamma$. The trend odds model can be fit in SAS with the Proc Nlmixed procedure, and approximate calculation can be performed in R using parameters obtained from the Vglm procedure. The initials required for modeling with Proc Nlmixed are: (a) obtained from the proportional odds model, or (b) entered as zero. For example, estimated values for the three intercepts and beta from the proportional odds model of 4-level Likert can serve as initials for the three intercepts and beta of the trend odds model. Gamma can have zero as the initial value.

A significant or borderline score test for proportional odds ascertained in step 2 and a significant trend parameter $\gamma$ obtained in this step together provide sufficient evidence to reject the proportional odds assumption and accept the trend odds assumption. A trend odds model provides the baseline odds and a multiplicative trend effect. In a 4-level Likert the scalars ${\text{t}}_1=0,{\text{t}}_2=1,{\text{t}}_3=2$ would yield the cumulative odd ratios: ${\theta }_1={\text{e}}^{\beta },{\theta }_2={\text{e}}^{\beta }{\text{e}}^{\gamma },{\theta }_3={\text{e}}^{\beta }{\text{e}}^{\gamma }{\text{e}}^{\gamma }$. Note that there is a monotonic multiplicative effect on cumulative odds ratios $\left({\theta }_1={\text{e}}^{\beta },{\theta }_2={\theta }_1{\text{e}}^{\gamma },{\theta }_3={\theta }_2{\text{e}}^{\gamma }\right)$. The multiplicative trend effect is used to calculate the consecutive odds ratio when multiplying it to previous odds ratio. A multiplicative trend effect above one indicates that the odds ratios are increasing with each level of the Likert outcome (a positive trend, ${\theta }_3>{\theta }_2>{\theta }_1$). Similarly, a multiplicative trend effect below one indicates that the odds ratios are decreasing with each level of the Likert outcome (a negative trend, ${\theta }_3<{\theta }_2<{\theta }_1$). Again we can use graphical displays such as figures 1 and 2 to compare the observed odds to the odds calculated with the proportional odds model and odds calculated with the trend odds model.

Step 4 - Multivariable Proportional-Trend Analyses

The objective of this step is to identify the trend parameter and to build the final multivariate model. First, a proportional odds model including all the independent variables can be fit in SAS using Proc Logistic or in R using the Vglm procedure. In SAS, parameters estimates can be stored to be used as initials values of the proportional-trend model.

In SAS, the proportional-trend odds model can be fit with the Proc Nlmixed procedure. Similar to step 3 the seeds required for modeling with Proc Nlmixed are: (a) obtained from the multivariable proportional odds model using Proc Logistic, or (b) entered as zero. Multivariable modeling can start with a saturate trend odds model including all the independent variables and respective baseline and trend parameters. Using a backward elimination, the non-significant parameters can be gradually removed from the model. In R, an approximate calculation can be performed using parameters obtained from the Vglm procedure. The Vglm procedure can be used with family specified as cumulative and parallel specified as false only for the independent variable that has a trend. The gamma related to the several parameters for the independent variable that was unconstrained can be approximated by assuming a scalar set such as 0, 1 and 2. Appendix A and B include the SAS and R code described in this section.

Example I - Data on perceived discrimination reported in the Minority Aging Research Study

Our first example uses data on perceived discrimination from the Minority Aging Research Study (MARS), an epidemiologic cohort study of aging and Alzheimer’s disease in older African Americans. Participants were recruited from various community-based organizations, churches, and senior subsidized housing facilities in and around the Chicago metropolitan area. The Everyday Discrimination Scale (Williams, Yan, Jackson, & Anderson, 1997) is a 9-item questionnaire that measures chronic but minor forms of unfair treatment in everyday life. The scale, along with other psychosocial measures was given at baseline. A total of 603 participants without dementia at baseline are included in this analysis. The sample population is 24% men, and participants had a mean age of 73.6 years at baseline (range from 60.2 to 97.6). All participants self-reported their race as African American using the race classification question from the U.S. Census. For this illustrative example we focus on one question from the Everyday Discrimination Scale: “People act as if they think you are dishonest”.

Dishonesty perception is based on a 4-level Likert: never, rarely, sometimes, and often. The first cumulative odds (baseline odds, ${\theta }_1$) are the probability of experiencing a perception of dishonesty at least rarely over the probability of experience it less than rarely. The second cumulative odds $\left({\theta }_2\right)$ are the probability of experiencing a dishonesty perception at least sometimes over the probability of experiencing it less than sometimes. The third cumulative odds $\left({\theta }_3\right)$ are the probability of experiencing a dishonesty perception often over the probability of experiencing it less than often.

For the first step of the analysis, dishonesty perception is examined as the independent variable in the binary logistic regression, fitting three separate models:

$$\mathit{\text{log}}\left(\frac{\text{Pr}\left(Y\ge \mathit{\text{ rarely}}\mid \mathit{\text{gender }}\right)}{\text{Pr}(Y<\mathit{\text{ rarely}}\mid \mathit{\text{gender }})}\right)={\alpha }_{\mathit{\text{rarely }}}+{\beta }_{\mathit{\text{rarely}},\text{sex}}\text{ sex,}$$

$$\mathit{\text{log}}\left(\frac{\text{Pr}\left(Y\ge \mathit{\text{ sometimes}}\mid \mathit{\text{gender }}\right)}{\text{Pr}(Y<\mathit{\text{ sometimes}}\mid \mathit{\text{gender }})}\right)={\alpha }_{\mathit{\text{sometimes }}}+{\beta }_{\mathit{\text{sometimes}},\text{sex }}\text{ sex,}$$

and

$$\mathit{\text{log}}\left(\frac{\text{Pr}(Y\ge \mathit{\text{often}}\mid \mathit{\text{gender }})}{\text{Pr}(Y<\mathit{\text{ often}}\mid \mathit{\text{gender }})}\right)={\alpha }_{\mathit{\text{often }}}+{\beta }_{\mathit{\text{often}},\text{sex }}\text{ sex.}$$

Sex is a dichotomous indicator for Black men. In the example above, the term ${\beta }_{\text{rarely,sex}}$ is interpreted as the log odds ratio of dishonesty perception at least rarely versus less than rarely for back men compared to Black women. The term ${\beta }_{\text{sometimes,sex}}$ is interpreted as the log odds ratio of experiencing dishonesty perception at least sometimes versus less than sometimes for Black men compared to Black women. The term ${\beta }_{\text{often,sex}}$ is interpreted as the log odds ratio of experiencing dishonesty perception often versus less than often for Black men compared to Black women.

For the second step of the analysis, we fit a separate proportional odds model for each covariate:

$$\mathit{\text{log}}\left(\frac{\mathrm{Pr}\left(Y\ge k∣\mathit{\text{gender }}\right)}{\text{Pr}\left(Y<k∣\mathit{\text{gender }}\right)}\right)={\alpha }_k+{\beta }_{•,\text{ sex }}\text{sex}.$$

For the third step of the analysis, we fit a separate trend odds model for each covariate:

$$\mathit{\text{log}}\left(\frac{\text{Pr}(Y\ge k\mid \mathit{\text{gender }})}{\text{Pr}(Y<k\mid \mathit{\text{gender }})}\right)={\alpha }_k+\left({\beta }_{\mathit{\text{rarely}},\text{sex }}+{\gamma }_{\text{sex }}{t}_k\right)\text{ sex}.$$

Models under step 1 to 3 are repeated replacing age at baseline. Sex is a dichotomous indicator of men. The term ${\gamma }_{\text{sex}}$ is interpreted as the trend in log odds ratios with frequencies of dishonesty perception for Black men compared to Black women. We use graphical displays to investigate the proportional odds assumption and the trend odds assumption. For example, figure 1 shows observed and estimated log odds by cut-points of the outcome. We can see that the log odds cannot be summarized by a flat line and that estimates from the trend odds model are less biased.

For the fourth step of the analysis, we use the effects obtained from previous steps as starting values. The initial trend odds model includes all the independent variables with parameters for baseline and trend:

$$\mathit{\text{log}}\left(\frac{\text{Pr}(Y\ge k\mid \mathit{\text{ sex, age}})}{\text{Pr}(Y<k\mid \mathit{\text{ sex, age }})}\right)={\alpha }_k+\left({\beta }_{\mathit{\text{rarely}},\text{sex }}+{\gamma }_{\text{sex }}{\text{t}}_{\text{k}}\right)\text{sex}+\left({\beta }_{\mathit{\text{rarely}},\text{age }}+{\gamma }_{\text{age }}{\text{t}}_{\text{k}}\right)\text{ age}$$

Using a backward elimination, parameters are gradually removed from the model. The final model is reduced to:

$$\mathit{\text{log}}\left(\frac{\text{Pr}(Y\ge k\mid \mathit{\text{gender, age }})}{\text{Pr}(Y<k\mid \mathit{\text{gender, age }})}\right)={\alpha }_k+\left({\beta }_{\mathit{\text{rarely}},\text{sex }}+{\gamma }_{\text{sex}}{\text{t}}_{\text{k}}\right)\text{sex}+{\beta }_{•,\text{ age }}\text{ age}$$

Results from these analysis show that sex and age are associated with dishonesty perception. There was a trend in the observed unadjusted cumulative odds ratios odds of reporting being perceived as dishonest at least rarely, at least sometimes and often that increased from 1.59 to 2.52 to 5.34.

The unadjusted proportional odds model estimated that the cumulative odds of increased frequency of dishonesty perception was 69% higher for Black men compared to Black women.

The unadjusted trend odds model estimated a trend multiplicative effect of about 1.66 ($p=.047)$, although a score test for proportional odds assumptions provided weak evidence of deviation from proportionality (chi-square = 4.21, $p=.12$). That represents a series of odds ratios 1.59 (${\theta }_1$, odds of dishonesty perception at least rarely versus less than rarely), 2.63 (${\theta }_2$, odds of dishonesty perception at least sometimes versus less than sometimes), and 4.37 (${\theta }_3$, odds of dishonesty perception often versus less than often). This series of odds ratios was obtained by multiplying the multiplicative trend effect by the previous odds ratio (i.e. ${\theta }_2={\theta }_1\cdot 1.66=2.63$ and $\left.{\theta }_3={\theta }_2\cdot 1.66=4.37\right)$.

The proportional-trend odds model included sex and age as covariates. Trend odds was assumed for sex and proportional odds was assumed for age. In the final model in Table 1, men had 61% higher odds of dishonesty perception at least rarely versus less than rarely compared with women. The final multivariate model shows a significant trend effect of about 1.67. That is the cumulative odds increased by 67% with each increase in Likert frequency. That represents a series of adjusted cumulative odds ratios of 1.61 (${\theta }_1$, odds of dishonesty perception at least rarely versus less than rarely), 2.67 (${\theta }_2$, odds of dishonesty perception at least sometimes versus less than sometimes), and 4.46 (${\theta }_3$, odds of dishonesty perception often versus less than often).

Table 1.

Example I, multivariable analyses of frequencies of perceived dishonesty with Proportional-Trend Odds model

Variable	Multivariable Proportional-Trend Odds model
	β	Odds Ratio (eβ)	p value for β	γ	Trend Multiplicative Effect (eγ)	p value for γ
Sex
Male	0.47	1.61	.029	0.51	1.66	.047
Female	Ref.	Ref.	Ref.	Ref.	Ref.	Ref.
Age at baseline	−0.06	0.94	.001	---	---	---

Notes. LRT=0.2, p = .90, compared to unconstrained model for sex.

Example II - Clustered data on severe violence victimization at school

In certain designs, randomization of data occurs at a cluster level. To illustrate, we use clustered data on school violence from 81 middle schools from a large multicultural urban school district. The schools were surveyed in the spring of 2004 and represent a total of 103 middle school programs (i.e. magnet, special education, and regular education) (Ramirez et al., 2012). The survey uses a questionnaire composed of items on exposure to violence. Respondents were asked if violence was experienced at specific locations such as school, neighborhood, and others. A total of 28,882 students completed self-administered paper-pencil scantron surveys at school, which were administered by school staff at each school site. The sample included 49% males. The racial/ethnic distribution was 68% Latinos, 11% Blacks/African Americans, 10% Whites, 4% Asians and 7% others. A total of 196 children (0.7%) were in special education. Variables on past violence exposure were combined into two distinct subscales: witnessed (Mdn = 3.0, $M=3.10,SD=2.63)$ and victimized $(\text{Mdn}=1.0,M=1.32,SD=1.65)$. Past violence subscales, as well as disability, ethnicity and sex were considered potential risk factors in analyses (independent variables). In this example, we investigate risk factors for self-reported victimization to severe physical violence at school (dependent variable), based on the question “How often have you been beaten up at school?”.

Severe violence victimization was based on a 4-level Likert: never, sometimes, lots of times, and almost every day. The first cumulative odds (baseline odds, ${\theta }_1$) are the probability of experiencing severe violence at least sometimes over the probability of experience it less than sometimes. The second cumulative odds $\left({\theta }_2\right)$ are the probability of experiencing severe violence at least lots of times over the probability of experience it less than lots of times. The third cumulative odds $\left({\theta }_3\right)$ are the probability of experiencing severe violence almost every day over the probability of experiencing it less than almost every day.

For the first step of the analysis, disability was examined as the independent variable in the binary logistic regression, fitting three separate models:

$$\mathit{\text{log}}\left(\frac{\text{Pr}\left(Y\ge \mathit{\text{ sometimes }}\mid \mathit{\text{ disability }}\right)}{\text{Pr}(Y<\mathit{\text{ sometimes }}\mid \mathit{\text{ disability }})}\right)={\alpha }_{\mathit{\text{sometimes }}}+{\beta }_{\mathit{\text{sometimes,disability }}}\mathit{\text{ disability }}+{\phi }_j$$

$$\mathit{\text{log}}\left(\frac{\text{Pr}\left(Y\ge \mathit{\text{lots of times}}\mid \mathit{\text{disability }}\right)}{\text{Pr}(Y<\mathit{\text{lots of times}}\mid \mathit{\text{ disability }})}\right)={\alpha }_{\mathit{\text{lots of times}}}+{\beta }_{\mathit{\text{lots of times,disability }}}\mathit{\text{ disability }}+{\phi }_j$$

and

$$\mathit{\text{log}}\left(\frac{\text{Pr}\left(Y\ge \mathit{\text{ every day }}\mid \mathit{\text{ disability }}\right)}{\text{Pr}(Y<\mathit{\text{ every day }}\mid \mathit{\text{ disability }})}\right)={\alpha }_{\mathit{\text{every day }}}+{\beta }_{\mathit{\text{every day,disability }}}\mathit{\text{ disability }}+{\phi }_j,$$

Disability is a dichotomous indicator for children in special education. Hence, in the example above, the term ${\beta }_{\text{sometimes,disability,}}$ is interpreted as the log odds ratio of experiencing severe violence at least sometimes versus less than sometimes for children in special education compared to others. The term ${\beta }_{\text{lots\_of\_times,disability,}}$ is interpreted as the log odds ratio of experiencing severe violence at least lots of times versus less than lots of times for children in special education compared to others. The term ${\beta }_{\text{almost\_every\_day,disability, }}$ is interpreted as the log odds ratio of experiencing severe violence almost every day versus less than almost every day for children in special education compared to others. The term ${\gamma }_{\text{disability}}$ is interpreted as the trend in log odds ratios with frequencies of severe violence victimization for children in special education compared to others. Figure 2 shows that there is a trend in observed log odds ratios and that the trend odds will provide an estimate that is less biased.

For the second step of the analysis, we fit a separate proportional odds model for each covariate:

$$\mathit{\text{log}}\left(\frac{\text{Pr}\left(Y\ge k∣\mathit{\text{disability }}\right)}{\text{Pr}\left(Y<k∣\mathit{\text{ disability }}\right)}\right)={\alpha }_k+{\beta }_{•,\mathit{\text{ disability}}}\mathit{\text{ disability }}+{\phi }_j,$$

For the third step of the analysis, we fit a separate trend odds model for each covariate:

$$\mathit{\text{log}}\left(\frac{\text{Pr}(Y\ge k\mid \mathit{\text{ disability }})}{\text{Pr}(Y<k\mid \mathit{\text{ disability }})}\right)={\alpha }_k+\left({\beta }_{\mathit{\text{sometimes,disability }}}+{\gamma }_{\mathit{\text{disability}}}{\text{t}}_{\text{k}}\right)\mathit{\text{ disability }}+{\phi }_{j.}$$

Models under step 1 to 3 were repeated replacing disability by sex, ethnicity, past violence victimization and past violence witnessed. Sex is a dichotomous indicator of males. Ethnicity is multinomial and was parameterized as 0/1 for each type of ethnicity, with Black representing a reference group. Past violence subscales were considered as continuous variables.

For the fourth step of the analysis, we use the effects obtained from previous steps as starting values. The initial trend odds model included all the independent variables with parameters for respective baseline and trend:

$$\begin{gathered} \mathit{\text{log}}\left(\frac{\text{Pr}\left(Y\ge k\mid \mathit{\text{ disability }}\right)}{\text{Pr}(Y<k\mid \mathit{\text{ disability }})}\right) ={\alpha }_k+\left({\beta }_{\mathit{\text{sometimes, disability }}}+{\gamma }_{\mathit{\text{disability }}}{\text{t}}_{\text{k}}\right)\mathit{\text{ disability}} \\ +\left({\beta }_{\mathit{\text{sometimes,sex }}}+{\gamma }_{\mathit{\text{sex }}}{\text{t}}_{\text{k}}\right)\mathit{\text{ sex}} \\ +\left({\beta }_{\mathit{\text{sometimes,white }}}+{\gamma }_{\mathit{\text{white }}}{\text{t}}_{\text{k}}\right)\mathit{\text{ white }} \\ +\left({\beta }_{\mathit{\text{sometimes,asian }}}+{\gamma }_{\mathit{\text{asian }}}{\text{t}}_{\text{k}}\right)\mathit{\text{ asian}} \\ +\left({\beta }_{\mathit{\text{sometimes,latino }}}+{\gamma }_{\mathit{\text{latino }}}{\text{t}}_{\text{k}}\right)\mathit{\text{ latino }} \\ +\left({\beta }_{\mathit{\text{sometimes,others }}}+{\gamma }_{\mathit{\text{others }}}{\text{t}}_{\text{k}}\right)\mathit{\text{ others }} \\ +\left({\beta }_{\mathit{\text{sometimes}},\text{ witnessed }}+{\gamma }_{\text{witnessed }}{\text{t}}_{\text{k}}\right)\text{ witnessed } \\ +\left({\beta }_{\mathit{\text{sometimes}},\text{ victimized }}+{\gamma }_{\text{victimized}}{\text{t}}_{\text{k}}\right)\text{ victimized }+{\phi }_j. \end{gathered}$$

Using a backward elimination, parameters were gradually removed from the model. The final model was reduced to:

$$\begin{gathered} \mathit{\text{log}}\left(\frac{\text{Pr}\left(Y\ge k\mid \mathit{\text{ disability }}\right)}{\text{Pr}(Y<k\mid \mathit{\text{ disability }})}\right)={\alpha }_k+\left({\beta }_{\mathit{\text{sometimes,disability }}}+{\gamma }_{\mathit{\text{disability }}}{\text{t}}_{\text{k}}\right)\mathit{\text{ disability}} \\ +{\beta }_{\mathit{\text{sometimes,sex }}}\mathit{\text{ Sex }}+{\beta }_{\mathit{\text{sometimes,white }}}\mathit{\text{ white }} \\ +{\beta }_{\mathit{\text{sometimes,asian }}}\mathit{\text{ asian }}+{\beta }_{\mathit{\text{sometimes,latino }}}\mathit{\text{latino }} \\ +{\beta }_{\mathit{\text{sometimes,others }}}\mathit{\text{ others }}+{\beta }_{\mathit{\text{sometimes}},\text{ witnessed }}\text{ witnessed} \\ +{\beta }_{\mathit{\text{sometimes}},\text{ victimized }}\text{ victimized }+{\phi }_j. \end{gathered}$$

Results from these analysis show that disability is the strongest risk factor for victimization to severe physical violence in these data. There is a significant random effect for schools. In the final model in Table 2, children in special education had 3.18 times higher odds of being the victim of severe violence at least sometimes versus less than sometimes compared to children in regular education. The final multivariate model showed a significant trend effect of about 1.68. That indicates a cumulative odd increase of 68% with each increase in Likert frequency, representing a series of adjusted cumulative odds ratios of 3.18 (${\theta }_1$, odds of experiencing severe violence at least sometimes versus less than sometimes), 5.34 (${\theta }_2$, odds of experiencing severe violence at least lots of times versus less than lots of times), and 8.98 (${\theta }_3$, odds of experiencing severe violence almost every day versus less than almost every day).

Table 2.

Example II, multivariable analyses of level of severe violence victimization (victim beat school) with Proportional and Trend Odds model, accounting for school random effect

Variable	Multivariable Proportional-Trend Odds model
	β	Odds Ratio (eβ)	p value for β	γ	Trend Multiplicative Effect (eγ)	p value for γ
Sex
Male	1.03	2.81	<.0001	---	---	---
Female	Ref.	Ref.	Ref.	---	---	---
Student Ethnicity
All others	0.46	1.58	<.01	---	---	---
Asian	0.45	1.57	<.01	---	---	---
Black/African-American	Ref.	Ref.	Ref.	---	---	---
Latino	0.46	1.58	<.0001	---	---	---
White	0.35	1.42	<.01	---	---	---
Disability
Not in special education	Ref.	Ref.	Ref.	Ref.	Ref.	Ref.
In special education	1.16	3.18	<.0001	0.52	1.68	.056
Past Violence exposure subscales
Victimized	0.65	1.91	<.0001	---	---	---
Witnessed	−0.02	0.98	.05	---	---	---

Notes. School random effect = 2.3947 (SE=0.544, p <.0001). LRT=2, p= .37, compared to unconstrained model disability.

For this tutorial, we repeated the models removing the random school effect to compare results. In the final model in Table 3, children in special education had 2.56 times higher odds of experiencing severe violence at least sometimes versus less than sometimes compared to children in regular education. The final multivariate model showed a significant trend effect of about 1.66, indicating a cumulative odd increase of 66% with each increase in Likert frequency. That represented a series of adjusted cumulative odds ratios of 2.56 $\left({\theta }_1\right.$, odds of experiencing severe violence at least sometimes versus less than sometimes), 4.26 (${\theta }_2$, odds of experiencing severe violence at least lots of times versus less than lots of times), and 7.07 (${\theta }_3$, odds of experiencing severe violence almost every day versus less than almost every day).

Table 3.

Example II, multivariable analyses of level of severe violence victimization (victim beat school) with Proportional and Trend Odds model, without a random effect for school.

Variable	Multivariable Proportional-Trend Odds model
	β	Odds Ratio (eβ)	p value for β	γ	Trend Multiplicative Effect (eγ)	p value for γ
Sex
Male	0.85	2.34	<.0001	---	---	---
Female	Ref.	Ref.	Ref.	---	---	---
Student Ethnicity
All others	0.39	1.48	<.01	---	---	---
Asian	0.45	1.57	<.01	---	---	---
Black/African-American	Ref.	Ref.	Ref.	---	---	---
Latino	0.40	1.49	<.0001	---	---	---
White	0.32	1.38	<.01	---	---	---
Disability
Not in special education	Ref.	Ref.	Ref.	Ref.	Ref.	Ref.
In special education	0.94	2.56	<.0001	0.51	1.66	.03
Past Violence exposure subscales
Victimized	0.48	1.61	<.0001	0.06	1.06	<.0001
Witnessed	---	---	---	---	---	---

Notes. LRT = 16, p<0.01, compared to unconstrained model for disability and past violence victimized.

Final Remarks

In this paper, we detailed use of the proportional—trend odds model and its particular application to modeling of individual Likert outcomes. This tutorial is based on previous research by McCullagh (McCullagh, 1980), Capuano and Dawson (Capuano & Dawson, 2013), Peterson and Harrel (Peterson & Harrell, 1990), and others (Aitchison & Silvey, 1957; Hedeker et al., 1994; Snell, 1964). We provide instructions on how to fit the model and provide two didactic examples from real datasets. The scalar set 0,1,2 and 3 was used for both examples. As discussed previously, it is recommended to use this type of scalar when no a priori information is available. It is possible, however, to optimize the scalar set as a priori information becomes available.

Motivated by the situations commonly found in surveys, we extended the method to clustered data. This is an important addition to the literature as clustered data are common. This was the case of our second example where data were collected at multiple schools and resulted in within school correlation. Here we performed the analysis with and without a random effect for school. We detected a significant trend in disability with both approaches but odds were different. In addition, there was a differential effect of the previous violence subscales. It is possible that these differences are generated by the way the data were collected or, in other words, an artifact of the variability between schools.

This article outlines how to build a proportional-trend model. Such models provide interpretable measures of association. The proportional-trend model can provide additional insights into the extent of the risk factor. Both the proportional odds model and the trend odds model have a theoretical justification in underlying latent variables, making of them more than just a parameterization. The ability to flexibly use them in a single model can streamline analyses.

This paper demonstrates how to fit models for ordinal data in SAS and R; however, we recognize that there are a number of limitations to our work. First of all, the models make some specific assumptions, which can be challenging to prove or disprove. Second, sometimes the software may fail to converge to a specific answer if there are no reasonably accurate initial estimates for the parameters.

Appendix A-. A sample if analyses in SAS

Appendix B. A sample analyses in R