Tracking Epidemics With Google Flu Trends Data and a State-Space SEIR Model

Abstract

In this article, we use Google Flu Trends data together with a sequential surveillance model based on state-space methodology to track the evolution of an epidemic process over time. We embed a classical mathematical epidemiology model [a susceptible-exposed-infected-recovered (SEIR) model] within the state-space framework, thereby extending the SEIR dynamics to allow changes through time. The implementation of this model is based on a particle filtering algorithm, which learns about the epidemic process sequentially through time and provides updated estimated odds of a pandemic with each new surveillance data point. We show how our approach, in combination with sequential Bayes factors, can serve as an online diagnostic tool for influenza pandemic. We take a close look at the Google Flu Trends data describing the spread of flu in the United States during 2003–2009 and in nine separate U.S. states chosen to represent a wide range of health care and emergency system strengths and weaknesses. This article has online supplementary materials.

1. INTRODUCTION

The 2009 H1N1 strain was met with little immunity in humans and was able to infect almost 300,000 people worldwide by mid-September of 2009, according to the World Health Organization (WHO). Unlike H5N1 (the avian influenza), which is slowspreading but a more deadly strain, the fast-spreading H1N1 influenza was quickly declared a pandemic. A pandemic toll far exceeds that of a regular seasonal influenza, which usually severely sickens 3 to 6 million people, and results in between a quarter and a half million deaths worldwide each year (Vaillant et al. 2009).

Infectious disease surveillance has traditionally played a sentinel role in public health preparedness of a pandemic. In the United States, the Centers for Disease Control and Prevention (CDC) serve as the main agency in charge of surveillance of “reportable” infectious diseases, such as SARS, influenza, or West Nile virus. Similarly, WHO tracks infectious diseases throughout the world, including endemic diseases in the developing countries. Public health officials rely on surveillance data to estimate disease activity levels and prepare intervention strategies. To this end, epidemic models have become an important part of public health response planning and early warning systems (Kaplan, Craft, and Wein 2002; Webby and Webster 2003; Eubank et al. 2004; Elderd, Dukic, and Dwyer 2006).

1.1. Mathematical Models for Epidemics

Modern mathematical epidemiology models date back to the early twentieth century, most notably to the work by Kermack and McKendrick (1927) whose susceptible-infectious-recovered (SIR) model was used for modeling the plague (London 1665–1666, Bombay 1906) and cholera (London 1865) epidemics. The basic SIR model assumes that at any given time, a fixed population can be split into three compartments (fractions): susceptible people (those naive to the disease), infectious people (those with disease that are able to infect others), and recovered people (those who had the disease and are now immune). The total number of people in all three compartments, $N$, is assumed constant through time, with no births and no deaths from causes other than the disease itself. These models assume homogeneous mixing, where each individual is equally likely to come in contact with any other.

The SIR model is an example of models commonly referred to as “compartmental models,” as they describe the flow (transition) of people through different compartments (which represent the stages of disease) over time. When considering influenza, however, an immediate extension of the original SIR model is to introduce a fourth compartment corresponding to the incubation (disease latency) stage—when a person is infected with influenza but still not infectious enough to be able to transmit it. This extension is called the “susceptible-exposed-infected-recovered” (SEIR) model (Anderson and May 1991; Hethcote 2000) and describes the epidemic over time as follows:

$$\begin{gathered} {\dot{S}}_t=-\beta S_t{I}_t/N \\ {\dot{E}}_t=\beta S_t{I}_t/N-\alpha E_t \\ {\dot{I}}_t=\alpha E_t-\gamma I_t \\ {\dot{R}}_t=\gamma I_t. \end{gathered}$$ (1)

Here, the dot denotes a time derivative, and the parameters $\theta =(\beta ,\alpha ,\gamma )$ are related to the transition rates from one disease stage to the next. The first equation describes disease transmission resulting from contacts between susceptible and infectious people—each infectious individual transmits the pathogen to $\beta$ individuals per unit time, but the new disease cases only arise if the contact is with a susceptible person (i.e., with probability $S_t/N$). Thus, at time $t$, the individuals in the class $S$ move to the “exposed but not yet infectious” class $E$ at the rate $\beta I_t/N$. The exposed but not yet infectious individuals move to the infectious class at the rate $\alpha$ per unit time, while $\gamma$ is the rate (per unit time) at which infectious individuals $I$ cease to be infectious because of recovery (or, in some cases, death). In the contact process terminology, $\alpha$ and $\gamma$ correspond to the inverse of the average of an exponentially distributed time to onset of infectiousness and to recovery, respectively.

The model (1) is completed with the specification of initial values, $S_0,E_0,I_0$, and $R_0$ : often, epidemics are modeled with an introduction of a single infectious person into a society where everyone else is susceptible, meaning that $I_0=1,S_0=(N-1)$, $E_0=0$, and $R_0=0$. It is also possible to consider $I_0=k$, where $k$ is an unknown number of initially infected people, to be estimated from the data. As in the classic SIR model, the SEIR model in this form assumes constant population size: $S_t+E_t+I_t+R_t=N$, for all $t$. Though extensions of the SIR-type models exist where the population size is allowed to vary (e.g., via birth, death, and migration processes), for many fast evolving outbreaks in large populations $N$ can be considered approximately constant and estimated from the census statistics.

Mathematically, one can prove that the epidemic will not be able to take off if $\dot{E}+\dot{I}<0$ for all times, or equivalently, $\beta S_0/N\gamma <1$. If $S_0\approx N$, the quantity $\beta /\gamma$ is commonly of interest instead, and is referred to as the basic reproductive ratio, or $R_0$. That quantity can be interpreted as the number of secondary infections a single infected person would cause during his or her infectious stage in an entirely susceptible population. Higher values of $R_0$ are associated with faster spreading infections. When $\gamma =1$, that is, when there is on average 1 recovery per unit time, the value of $R_0$ equals the value of transmission parameter $\beta$.

Solving the system of equations (1) is done numerically, using a solver such as the one implemented in the lsoda function in the statistical software R, based on the method originally developed by Petzold (1983) and Hindmarsh (1983). An example of the solution to the deterministic SEIR system of equations (1), for a specific value of $\theta$, is shown in Figure 1. The solution describes $S_t,E_t,I_t$, and $R_t$ trajectories over time, thus allowing the fraction of susceptible, latent, infectious, and recovered people to be determined at any point in time $t$. Compartmental models with various modifications (including birth and death rates for example, or migration) have proven useful in analyzing epidemics and particularly for modeling the spread of moderately to highly infectious diseases in a larger and well-mixed society (Anderson and May 1991; Gani and Leach 2001; Ferguson et al. 2003; Elderd, Dukic, and Dwyer 2006; Cauchemez and Ferguson 2008).

Figure 1.

An example solution to an SEIR system specified in Equation (1), in a population of size 100.

1.2. State-Space Models for Epidemics

The main appeal of compartmental models lies in their simplicity, well-understood behavior, and intuitive interpretation of the model parameters. Their simplicity is, however, also a limiting factor when it comes to capturing changes in the epidemic course, such as those induced by a public health intervention or a media event, variations in behavior, contact, and vaccination patterns. Casting the traditional compartmental models in a state-space framework is one way to allow the models to capture changes in the dynamics over time in a flexible way. In this article, we provide a state-space extension of the SEIR model, specifically designed to track epidemic behavior based on surveillance data.

In addition, epidemic outbreaks are almost always observed with error, making it necessary to estimate the solution of the system in (1) in the presence of statistical noise. In such situations, the true solution (the true susceptible, latent, infected, and recovered fractions) is referred to as the hidden state of the system. In many state-space models, estimation of the trajectory of the hidden state over time is the primary objective.

In our state-space SEIR model, one objective will be to estimate the trajectory of the hidden state vector $x_t=\left(S_t,E_t,I_t,R_t\right)$, based on a noisy time series of epidemic surveillance data $y_t$ (e.g., counts of the newly infected people or some function thereof). However, along with the hidden state, we will also want to estimate the parameter vector driving the SEIR system, $\theta =(\beta ,\alpha ,\gamma )$, which contains the transmission, latency, and recovery parameters, and quantify the uncertainty in those parameters. Joint inference for states and parameters has been a topic of interest in the recent state-space modeling literature (Liu and West 2001; Fearnhead 2002; Storvik 2002; Fearnhead 2008; Doucet and Johansen 2009; Kantas et al. 2009; Lopes, Carvalho, Johannes, and Polson 2011).

2. INFLUENZA DATA

In the United States, flu surveillance starts with the sentinel network of health care establishments, including individual health care professionals, clinics, diagnostic test laboratories, and public health departments, called the U.S. Outpatient Influenza-like Illness Surveillance Network (ILINet). Some 2400 sites in over 122 cities and 50 states are responsible for monitoring and reporting observed influenza-like cases to the CDC, which then analyzes and publishes consolidated reports on estimated flu activity in nine major U.S. regions. ILINet tracks several indicators of flu activity throughout the United States (hospitalizations, mortality, and outpatient visits due to “influenza-like illness” (ILI)) on a weekly basis during the regular flu season from October through mid-May. According to the CDC guidelines, ILI is defined as fever of 100°F (or higher) and a cough and/or sore throat in the absence of a known cause other than influenza.

According to the CDC estimates, the average number of U.S. ILI-related patient visits is about 16 million per year. The reported fraction of ILI-visits among all patient visits is weighted based on the population of each state and averaged to form the overall U.S. ILI activity, as well as the activity for 10 major U.S. regions. Estimates for the finer geographic resolution are not provided due to unevenly distributed locations and catchment areas of the ILINet members, and consequently, lower precision for ILI estimates. As with many traditional surveillance systems, the CDC reports are published with a delay of approximately 2 weeks, and all past postings are subject to a retroactive adjustment reflecting receipt of corrected reports from the ILINet members. More information about the CDC surveillance program and the definition of the 10 regions can be found on the CDC website (http://www.cdc.gov/flu).

2.1. Google Flu Trends

Due to a remarkable increase in the online community and search engine activity over the last decade, several alternative surveillance systems have been proposed. Some are based on search engines, such as Google or Bing, and some on tracking micro-blogging content, such as Twitter. Following an extensive variable selection process in collaboration with CDC, Ginsberg et al. (2009) were first to identify a set of search words, termed “ILI-related queries,” that were most highly predictive of the CDC’s ILI counts.

The Flu Trends algorithm that Google uses for prediction of ILI cases is based on a regression model that links the logit-transformed fraction of ILI visits to the logit-transformed fractions of the top search terms. The algorithm was found to track the ILI percentages well (see Figure 2) and now consistently predicts the ILI activity 1–2 weeks ahead of CDC publication. The results are archived every week as a part of the Google Flu Trends project (http://www.google.org/flutrends/). Unlike the CDC surveillance, these reports are made available daily and are not in general subject to future revisions. Flu Trends provides localized predictions, based on the IP address of the computer from which a search was done. IP addresses are usually tied to a specific metropolitan area, allowing for “IP surveillance” at the level of individual states as well as cities.

Figure 2.

Google Flu Trends estimated ILI percentages (dashed line) and CDC ILI surveillance percentages (solid line) for the United States, from June 2003 until September 2009. Separate plots correspond to separate influenza years, with each new influenza season starting in autumn and ending in spring. Note that CDC did not post ILI reports in summers prior to 2009, and thus no solid line appears during summer months prior to 2009.

The “National Report Card on the State of Emergency Medicine” (American College of Emergency Physicians 2009) has found that the overall U.S. emergency care system has been under a severe strain. However, as with other health-care aspects, states vary in their quality of emergency care. As a result, they vary in their pandemic preparedness, in addition to varying in their density of population and contact networks. For this reason, we will also examine individual results for nine states spanning a wide range of quality of care. We focus on two dimensions of the emergency medicine report, “public health” and “disaster preparedness,” as they are directly relevant to the management of influenza epidemics. For example, one of the fields of the “public health” category is the percentage of adults 65 years of age or older who have received an influenza vaccine in the past 12 months. Similarly, “disease preparedness” measures characteristics such as the fraction of nurses and physicians registered in a state-based emergency system, presence of rapid notification systems, and regular drills for medical and emergency personnel. Perhaps not surprisingly, states that are largely rural and face challenges, such as workforce shortages, lack of large medical facilities, and large uninsured populations, are found to have the most difficulty with this category and might be particularly vulnerable during a pandemic outbreak. According to the report, states that are among the best prepared are Maryland, Massachusetts, and Pennsylvania, while those that did not rank highly in the areas of “disaster preparedness” and “public health” include South Carolina, Oklahoma, Mississippi, South Dakota, Tennessee, and Arkansas. Google Flu Trends estimates for these nine states are shown in Figure 3.

Figure 3.

Google Flu Trends ILI surveillance in nine representative states, 2003–2009. The states were chosen to span a range of health care preparedness criteria based on the results published in the American College of Emergency Physicians 2009 Report. The states that are ranked among the best in quality of health care are Maryland, Massachusetts, and Pennsylvania. The states that ranked low in the areas of “disaster preparedness,” “emergency care access,” and “public health” include South Carolina, Oklahoma, Mississippi, South Dakota, Tennessee, and Arkansas. Note some states’ search term counts were too low to procure the Flu Trends surveillance data early on, from 2003 through 2005.

In addition to individual U.S. states and cities, Google Flu Trends has recently expanded to other countries including most of Europe, Russia, Japan, Australia, New Zealand, Canada, and Mexico. We also employ our method to study the influenza epidemic in New Zealand, a southern hemisphere and a relatively rural and well-off country with a good health care system, and two separated islands. We chose New Zealand, as it may provide insight into the subsequent influenza season in the United States, since the southern hemisphere flu epidemics generally precede the northern hemisphere ones. The New Zealand analysis is basically similar to the United States one, and the full discussion and results can be found in the online supplementary material.

2.2. Influenza Epidemics and Pandemics in the Past

Pandemics are relatively rare, with only a handful of influenza pandemics occurring in the last hundred years. The most infamous one was the H1N1 pandemic in 1918/1919, also known as the “Spanish Flu,” estimated to have caused 20–50 million deaths—more deaths than any pandemic since the bubonic plague (the Black Death) of the fourteenth century. The estimates of its basic reproductive number $R_0$ range from 1.8 to 3.5 in different communities (Mills, Robins, and Lipsitch 2004; Chowell et al. 2006, Chowell, Nishiura, and Bettencourt 2007; Nishiura 2007). The other notable influenza pandemics were the Asian Influenza (H2N2) of 1957–1958 with 70,000 estimated deaths in the United States, and the Hong Kong Flu of 1968–1969 (H3N2) with 34,000 estimated deaths in the United States. Both had basic reproductive numbers in the range of 1.5–2.2 (Longini et al. 2004; Gani et al. 2005; Vynnycky and Edmunds 2008). A pandemic is considered mild if its reproductive rate is below 1.5, moderate if between 1.5 and 1.8, and severe if above 1.9 (Yang et al. 2009). On the other hand, seasonal influenza’s basic reproductive number is lower and historically estimated to range up to 1.35 (Cintrón-Arias et al. 2009).

In the most recent H1N1 epidemic in 2009, the virus’ potential for a pandemic was deemed nonnegligible (Fraser et al. 2009). Its overall basic reproductive rate was estimated between 1.3 and 1.7 based on the first few months of data, but in some instances it was found to be as high as 2.9 based on data from several city initial outbreaks (Yang et al. 2009). In terms of the other influenza parameters, namely the latency $\left(\alpha \right)$ and recovery rate $\left(\gamma \right)$, most estimates seem to point to the average incubation time being between 3 and 4 days, while the average infectious time is 7–8 days (Tuite et al. 2010). People infected with the recent H1N1 virus are thought to be infectious longer however, as continued viral shedding was observed for over 10 days post infection, with nearly half of the people continuing to shed the virus on and after the 7th day of illness (Center for Infectious Disease Research & Policy 2009). Under the best fit exponential distribution, these preliminary studies would imply the mean recovery time of about 10 days.

3. STATE-SPACE SEIR MODELS

State-space modeling [often termed dynamic modeling, West and Harrison (1997)] usually relies on sequential Bayes inference that facilitates sequential learning by incorporating additional information with every new surveillance data point. It can be designed to sequentially learn about the epidemic parameters, to produce near real-time estimates of the epidemic states while accounting for uncertainty in the epidemic parameters, and to provide the posterior odds of a pandemic at any point in time. In this section, we describe a state-space extension of the classic SEIR-type model for influenza dynamics and introduce a sequential learning algorithm to update the posterior distributions of the hidden (dynamic) states $x_t={\left(S_t,E_t,I_t,R_t\right)}^{\prime }$ (the vector of susceptible, latent, infectious, and recovered fractions in the population) at any time $t$, and the parameters guiding the disease evolution $\theta =(\beta ,\alpha ,\gamma )$. We also show how the algorithm can be used to provide online pandemic alerts based on sequential Bayes factors.

3.1. Notation

The dynamics of influenza are described by the evolution of hidden (unobserved) states of the SEIR-type epidemics, $x_t={\left(S_t,E_t,I_t,R_t\right)}^{\prime }$, which depends on the unknown three-dimensional vector of epidemic parameters $\theta =(\beta ,\alpha ,\gamma )$ as in Equation (1). A discretized version of the influenza dynamics in (1), assuming a discretization time-step of 1 week, can be expressed as follows:

$$\begin{gathered} S_t=S_{t-1}-\beta S_{t-1}{I}_{t-1}/N \\ {E}_t=\left(1-\alpha \right)E_{t-1}+\beta S_{t-1}{I}_{t-1}/N \\ {I}_t=\left(1-\gamma \right)I_{t-1}+\alpha E_{t-1} \\ {R}_t=R_{t-1}+\gamma I_{t-1}, \end{gathered}$$ (2)

where $N$ is the total population size. The discretization replaces ${\dot{S}}_t$ in Equation (1) by the weekly change in the susceptible fraction, $S_t-S_{t-1}$, and does so analogously for ${\dot{E}}_t,{\dot{I}}_t$, and ${\dot{R}}_t$.

Due to the nature of ILI surveillance data, our observations will consist only of noisily observed weekly counts of ILI visits, ${\tilde{I}}_t$, which can be thought of as a proxy to the true fraction of infected population, $I_t$, in each week-long time period $(t-1,t]$. Instead of working directly with ${\tilde{I}}_t$ however, we will model the observed growth rate of the infectious population, $y_t=\left({\tilde{I}}_t-\right.\left.{\tilde{I}}_{t-1}\right)/{\tilde{I}}_{t-1}$. This leads to the following state-space model for the growth rate:

$$y_t=g_t+{\epsilon }_t^y{\epsilon }_t^y~N\left(0,{\sigma }_y^2\right)$$ (3)

$$g_t=-\gamma +\alpha \frac{E_{t-1}}{I_{t-1}}+{\epsilon }_t^g{\epsilon }_t^g~N\left(0,{\sigma }_g^2\right).$$ (4)

We will refer to Equation (3) as the “observation equation” and Equation (4) as the “evolution equation” for the growth rate. The mean component of Equation (4) is derived from the deterministic evolution of $I_{t-1}$ based on the discretized SEIR model (2) above, with the true number of infections $I_t$ related to $g_t$ via $I_t=\left(1+g_t\right)I_{t-1}$. With the infectious state $I_t$ modeled directly in the growth rate evolution Equation (4), the state-space SEIR model is then completed with the evolution of the rest of the state components:

$$\left(\begin{array}{c}{S}_t\\ E_t\\ R_t\end{array}\right)=\left(\begin{array}{c}{S}_{t-1}\\ E_{t-1}\\ R_{t-1}\end{array}\right)+\left(\begin{array}{cc}-\beta S_{t-1}/N& 0\\ \beta S_{t-1}/N& -\alpha \\ \gamma & 0\end{array}\right)\left(\begin{array}{c}{I}_{t-1}\\ E_{t-1}\end{array}\right).$$ (5)

Given that we are now working with the growth rate that can be both positive and negative, it may be computationally convenient to assume that ${\epsilon }_t^y$ and ${\epsilon }_t^g$ are normally distributed, with means 0 and variances ${\sigma }_y^2$ (observation variance) and ${\sigma }_g^2$ (evolution variance), respectively. Before doing so, we recommend a normality check for the growth rates. In the Google dataset, normality seems to be a reasonable assumption (see Figure 4 for the U.S. growth rates). However, if normality had not seemed appropriate, a transformation of the growth rate (e.g., a log transformation) could have been employed to help achieve approximate normality.

Figure 4.

Normality assumption checks: the left column shows the box plots of growth rates and the right column shows the empirical (unfilled circles) and normal cumulative distribution functions (CDFs) (filled circles). The top row shows the 2003/2004 season and the bottom row shows the 2008/2009 season.

The classical SEIR formulation assumes that ${\sigma }_g^2=0$. In fact, the magnitude of ${\sigma }_g^2$ can in essence be viewed as a measure of the underlying deterministic SEIR model fit, while the relative magnitudes of the two variances, ${\sigma }_y^2$ and ${\sigma }_g^2$, can be viewed as confidence in observations (data) and the underlying autonomous SEIR model, respectively.

While it is tempting to translate concepts and intuition from the classical compartmental models directly to their state-space counterparts, it is important to note that there are substantial differences between the two. For example, while the classical mathematical biology models produce smooth solutions for the entire disease trajectory over time, the state-space models will only yield a set of pointwise state estimates. The latter only gives an illusion of the trajectory. Also, in general, largestep discretizations and addition of weekly error pulses would not be recommended in pure nonlinear compartmental models (Atkinson 1978; Cauchemez and Ferguson 2008; King et al. 2008; He, Ionides, and King 2009); however, the state-space models are, in principle, able to compensate for the consequences of such errors via their evolution variances.

3.2. Sequential Learning Algorithm

Recently, particle filtering methods have been proposed for surveillance and early detection of epidemics (Rodeiro and Lawson 2006; Jagat et al. 2008), though not within the context of state-space compartmental models. While powerful for rapid online estimation, particle filter methods can suffer from the “particle impoverishment” problem and loss of inferential capability as the process evolves (Storvik 2002; Fearnhead 2008). Motivated by the desire for a fast online surveillance method, we implement a sequential learning algorithm based on a particle filter that is a hybrid of the Liu-West (2001) filter and the particle learning filter (Carvalho et al. 2010), relying on the use of sufficient statistics to help alleviate particle impoverishment and information loss over time (Fearnhead 2002; Kantas et al. 2009; Lopes, Carvalho, Johannes, and Polson 2011).

The proposed sequential learning algorithm proceeds as follows. For notational convenience, we introduce $Z_t$, the “essential state vector” containing the hidden state vector $x_t={\left(I_t,E_t,I_t,R_t\right)}^{\prime }$, the vector of unknown static disease parameters $\theta =(\alpha ,\beta ,\gamma )$, the observation and evolution variances ${\sigma }_y^2$ and ${\sigma }_g^2$, and all (partial) sufficient statistics $s_t$. The sufficient statistics $s_t$ govern sequential parameter learning via $p\left(\theta \mid s_t\right)$. (We will talk more about sufficient statistics in Section 3.3.) The goal of the algorithm is to track the distribution of the essential state vector at each point in time $t$ via sequential Monte Carlo (SMC)—that is, sets of $M$ particles, $Z_t^{\left(1\right)},\dots ,Z_t^{\left(M\right)}$ (denoted hereafter by $\left.{\left\{Z_t^{\left(i\right)}\right\}}_{i=1}^M\right)$. The set of particles at time $t$ will thus need to be sampled from the posterior distribution of the essential state vector $Z_t$, given the observed infection growth rates up to time $t,y^t=\left\{y_1,y_2,\dots ,y_t\right\}$. Formally, ${\left\{Z_t^{\left(i\right)}\right\}}_{i=1}^M$ will need to be iid draws from $p\left(Z_t\mid y^t\right)$.

The algorithm for sampling ${\left\{Z_t^{\left(i\right)}\right\}}_{i=1}^M$ from $p\left(Z_t\mid y^t\right)$ is based on the following decomposition of the posterior distribution:

$$p\left(Z_{t+1}\mid y^{t+1}\right)\propto \int p\left(Z_{t+1}\mid Z_t,y_{t+1}\right)p\left(y_{t+1}\mid Z_t\right)\text{dP}\left(Z_t\mid y^t\right),$$ (6)

which is a consequence of the following:

$$p\left(Z_t\mid y^{t+1}\right) \propto p\left(y_{t+1}\mid Z_t\right)p\left(Z_t\mid y^t\right)$$ (7)

$$p\left(Z_{t+1}\mid y^{t+1}\right) =\int p\left(Z_{t+1}\mid Z_t,y_{t+1}\right)\text{dP}\left(Z_t\mid y^{t+1}\right).$$ (8)

Here, and throughout this section, $p(\cdot )$ refers to the appropriate continuous/discrete measure and

$$p\left(y_{t+1}\mid Z_t\right)=\int p\left(y_{t+1}\mid Z_{t+1}\right)p\left(Z_{t+1}\mid Z_t\right)d{Z}_{t+1}$$ (9)

plays the role of the predictive density of $y_{t+1}$.

Expressions (6)–(9) suggest a two-step algorithm for sampling ${\left\{Z_{t+1}^{\left(i\right)}\right\}}_{i=1}^M$ from the posterior $p\left(Z_{t+1}\mid y^{t+1}\right)$ at time $t+1$, given that we have stored the set of particles from the previous time $t,{\left\{Z_t^{\left(i\right)}\right\}}_{i=1}^M$. The first step would be to resample the old particles ${\left\{Z_t^{\left(i\right)}\right\}}_{i=1}^M$ with weights proportional to $p\left(y_{t+1}\mid Z_t^{\left(i\right)}\right)$ and generate $M$ resampled particles ${\left\{Z_t^{(*)}\right\}}_{i=1}^M$. These resampled particles can be viewed as a sample from $p\left(Z_t\mid y^{t+1}\right)$ in (7). Once we have the resampled particles ${\left\{Z_t^{(*)}\right\}}_{i=1}^M$, we will sample a new set of particles ${\left\{Z_{t+1}^{\left(i\right)}\right\}}_{i=1}^M$ from the mixture of densities $p\left(Z_{t+1}\mid Z_t^{(*)},y_{t+1}\right)$, an approximation to the integral in Equation (8). In short, the sequential learning algorithm comprises repeating the following steps for $i=1,\dots ,M$, at each time point:

• Step 1 (Resample): Sample, with replacement, integers $k^i$ from the set $\{1,\dots ,M\}$, such that $\text{Pr}\left(k^i=j\right)\propto p\left(y_{t+1}\mid Z_t^{\left(j\right)}\right)$, for each $j=1,\dots ,M$.

• Step 2 (Sample): Sample $Z_{t+1}^{\left(i\right)}$ from $p\left(Z_{t+1}\mid Z_t^{\left(k^i\right)},y_{t+1}\right)$.

The key ingredients in the two-step algorithm are thus the posterior predictive density $p\left(y_{t+1}\mid Z_t\right)$ and the posterior updating rule $p\left(Z_{t+1}\mid Z_t,y_{t+1}\right)$.

The sequential learning algorithm above can be used to produce out-of-sample forecasts and to provide estimates of sequential predictive densities and Bayes factors. This comes from the fact that the predictive density for $h$ periods ahead, $p\left(y_{t+h}\mid y^t\right)$, can be approximated by

$$p^M\left(y_{t+h}\mid y^t\right)=\frac{1}{M}\sum _{i=1}^{M}p\left(y_{t+h}\mid Z_t^{\left(i\right)}\right),$$ (10)

where ${\left(Z_t\right)}^{\left(i\right)}$ come from the current set of particles ${\left\{Z_t^{\left(i\right)}\right\}}_{i=1}^M$, acting as an approximation to $p\left(Z_t\mid y^t\right)$.

A natural further application of the above approximations is to sequential Bayes factors, which can be used to sequentially test a set of hypotheses. For example, we could sequentially compare the evidence for a seasonal epidemic $\left({ℳ}_1\right)$ with the evidence for a pandemic $\left({ℳ}_2\right)$, given all the observed data up to the week $t$. The approximate sequential Bayes factor is computed via the following equation:

$${\text{BF}}_t^M\left({ℳ}_1,{ℳ}_2\right)=\frac{p^M\left(y^t\mid {ℳ}_1\right)}{p^M\left(y^t\mid {ℳ}_2\right)},$$

where

$$p^M\left(y^t\mid {ℳ}_m\right)=\prod _{k=1}^t{p}^M\left(y_k\mid y^{k-1},{ℳ}_m\right).$$

Here, $p^M\left(y_t\mid y^{t-1},{ℳ}_m\right)$ are the one-step-ahead approximate predictive densities [based on Equation (10)], for $m=\mathrm{1,2}$.

The two-step sequential learning algorithm presented above produces a sequence of particle sets, ${\left\{Z_0^{\left(i\right)}\right\}}_{i=1}^M,\dots ,{\left\{Z_t^{\left(i\right)}\right\}}_{i=1}^M$, which can also be used to perform online parameter learning for the static parameters ($\theta ,{\sigma }_y^2,\text{ and }{\sigma }_g^2$). Given the current set of particles ${\left\{Z_t^{\left(i\right)}\right\}}_{i=1}^M$, one can simply draw, using the Metropolis–Hastings algorithm for example, a new set of ${\left\{{\theta }^{(*i)}\right\}}_{i=1}^M~p\left(\theta \mid s_t^{\left(i\right)},y^t\right)$, which will in fact be a sample from the marginal density $p\left(\theta \mid y^t\right)$ (recall that sufficient statistics are a part of ${\left\{Z_t^{\left(i\right)}\right\}}_{i=1}^M$). Similar learning can be done for the two variance parameters, ${\sigma }_y^2$ and ${\sigma }_g^2$. These additional sampling (“learning”) steps are, of course, unnecessary for posterior inference at time $t$, which can be performed via Rao-Blackwellization, but they are important to further replenish the particles and alleviate particle impoverishment (Lopes, Carvalho, Johannes, and Polson 2011).

The “look ahead” step in Equation (7) also provides extra protection against particle degeneration in the algorithm (see Kong, Liu, and Wong 1994; Pitt and Shephard 1999) and reduces the propagation of the Monte Carlo error (Lopes, Carvalho, Johannes, and Polson 2011). To alleviate particle degeneration even further, a Liu and West (2001) kernel-shrinkage approximation can be used to reweigh and propagate (“jitter”) the static parameters and can be added to the Sample step. Indeed, we do so in the implementation of the sequential surveillance algorithm described in Section 3.3.

Although we use only one sequential learning approach, it is important to note that there are multiple other filtering variations that could be used instead, as long as they take steps to alleviate and assess particle degeneration and information loss. For recent reviews of SMC methods and alternative filtering approaches, as well as issues with particle degeneration, see, among others, Arulampalam et al. (2002), Storvik (2002), Ristic, Arulampalam, and Gordon (2004), Cappé, Godsill, and Moulines (2007), Fearnhead (2008), Doucet and Johansen (2009), Kantas et al. (2009), and Lopes and Tsay (2011). They highlight some of the recent developments over the last decade, including efficient particle smoothers, particle filters for highly dimensional dynamical systems, parameter learning, and the interconnections between Markov chain Monte Carlo (MCMC) and SMC methods.

3.2.1. Example of the Sequential Learning Algorithm for AR(1) Model.

We give now an example of the sequential learning algorithm implemented for a simple AR(1) state-space model. We choose this model in part as an illustration, before moving to the full implementation of the sequential learning algorithm for the state-space SEIR model in the next subsection. The AR(1) model is also a simpler alternative that could be used to model the observed growth rate of infection, $y_t$, instead of the more complex SEIR model. As such, we will also treat the AR(1) state-space model as a simple benchmark model and compare it with the state-space SEIR model performance in the Results section.

In the AR(1) plus noise model, the observed growth rate of infection, $y_t$, is modeled via the standard first order dynamic linear model of West and Harrison (1997), with the hidden state $g_t$ (the growth rate at time $t$) evolving according to an autoregressive process of order one, that is,

$$\begin{gathered} y_t\mid g_t,\xi ~N\left(g_t,V\right) \\ {g}_t\mid g_{t-1},\xi ~N\left(\mu +\varphi g_{t-1},W\right), \end{gathered}$$

where $\xi =(V,\mu ,\varphi ,W)$ and $g_0$ comes from an initial distribution $N\left(m_0,C_0\right)$ with fixed values of $m_0$ and $C_0$.

When the joint prior distribution, $p\left(\xi \right)=p\left(V\right)p(\mu ,\varphi ,W)$ with $V~IG\left(a_0,b_0\right),W~IG\left(c_0,d_0\right),$ and $(\mu ,\varphi \mid W)~N\left(q_0,W{Q}_0\right)$, then the joint posterior distribution $p\left(\xi \mid y^t,g^t\right)\equiv p\left(\xi \mid s_t\right)$ is given as $p\left(V\mid s_t\right)p\left(\mu ,\varphi ,W\mid s_t\right)$. Here, $s_t$ is again the vector of conditional sufficient statistics for $\xi$ given the data up to time $t$. More specifically, for $g^t=\left(g_1,\dots ,g_t\right),x_t={\left(1,g_{t-1}\right)}^{\prime }$, and $X^t={\left(x_1,\dots ,x_t\right)}^{\prime }$, we have $\left(\mu ,\varphi \mid W,g^t,X^t\right)~N\left(q_t,W{Q}_t\right)$ and $\left(W\mid g^t,X^t\right)~IG\left(c_t,d_t\right)$, where $c_t=c_{t-1}+1/2,Q_t^{-1}=Q_{t-1}^{-1}+x_t{x}_t^{\prime },Q_t^{-1}{q}_t=Q_{t-1}^{-1}{b}_{t-1}+g_t{x}_t$, and $d_t=d_{t-1}+\left(g_t-q_t^{\prime }{x}_t\right)y_t/2+\left(q_{t-1}-\right.{\left.q_t\right)}^{\prime }{Q}_{t-1}^{-1}{q}_{t-1}/2$. Additionally, $\left(V\mid y^t,g^t\right)~IG\left(a_t,b_t\right)$, where $a_t=a_{t-1}+1/2$ and $b_t=b_{t-1}+{\left(y_t-g_t\right)}^2/2$. Therefore, $s_t=\left(a_t,b_t,c_t,d_t,q_t,Q_t\right)$.

Furthermore, $p\left(g_t\mid y^t,\xi \right)\equiv p\left(g_t\mid s_t^k,\xi \right)~N\left(m_t,C_t\right)$, where $s_t^k=\left(m_t\left(\xi \right),C_t\left(\xi \right)\right)$ are the standard Kalman filter moments at time $t$. In this state-space model, the key ingredients in the sequential learning algorithm are thus all available: $p\left(y_t\mid s_{t-1}^k,\xi \right)=p_M\left(y_t;\mu +\varphi m_{t-1},V+W+\right.\left.{\varphi }^2{C}_{t-1}\right),p\left(s_t^k\mid s_{t-1}^k,\xi \right)$ (a deterministic mapping) and $p\left(\xi \mid s_t\right)$ (above updates). In this example, the essential state vector is $Z_t=\left(s_t,s_t^x,\xi )\right.$ and Step 2 (sampling) of the sequential learning algorithm translates into deterministic updates for $s_t$ given $\left(s_{t-1},y_t,g_t\right)$ and for $s_t^k$ given $\left(s_{t-1}^k,\xi ,y_t\right)$.

3.3. Sequential Learning Algorithm Implementation for Flu Trends Data

This subsection describes the specifics of the sequential learning algorithm implemented for Google Flu Trends surveillance. The algorithm consists of three modules: predictive density, posterior updating rule, and parameter learning. Below we describe the details of each of the three modules. We refer the reader to the algorithm box for the detailed implementation steps for the Flu Trends data.

3.3.1. Predictive Density.

This is Step 1 (Resample) of the sequential learning algorithm of Section 3.2. The tracking and learning algorithm presented in the previous section depends crucially on the predictive density $p\left(y_{t+1}\mid Z_t\right)$. To find this density, observe that $y_{t+1}\mid g_{t+1},\theta ,{\sigma }_y^2~N\left(g_{t+1},{\sigma }_y^2\right)$, which follows from Equation (3) and the fact that ${\epsilon }_t^y~N\left(0,{\sigma }_y^2\right)$. Similarly, $g_{t+1}\mid Z_t~N\left(-\gamma +\alpha E_t/I_t,{\sigma }_g^2\right)$, based on Equation (4) and the fact that ${\epsilon }_t^g~N\left(0,{\sigma }_g^2\right)$. Combining these two densities, and integrating $g_{t+1}$ out, leads to the predictive density for next growth rate observation, that is, $\left(y_{t+1}\mid Z_t\right)~N\left(-\gamma +\alpha E_t/I_t,{\sigma }_y^2+{\sigma }_g^2\right)$. Note that this computation can be done for any step size, including those smaller than the intervals at which the observations are collected, by solving the SEIR equations numerically forward, and using the final values at the previous time-step as the initial values for the next.

3.3.2. Posterior Updating Rule.

This is Step 2 (Sample) of the sequential learning algorithm of Section 3.2. After resampling the particles with weights proportional to the predictive distribution above, the next step is to “propagate” these particles and obtain a sample from the updated posterior at time $t+1$. The update for the hidden growth rate of infection, $g_t$, follows from the conditional linear state-space model, and can be done by the standard Kalman-type recursions (West and Harrison 1997). More precisely, let the initial (time = 0) growth rate of infection be modeled as $g_0~N\left(m_0,C_0\right)$. Then, for any time $t+1$, it follows that $\left(g_{t+1}\mid Z_t,y^{t+1}\right)~N\left(m_{t+1},C_{t+1}\right)$ with moments

$$m_{t+1}=C_{t+1}\left({\sigma }_y^{-2}{y}_{t+1}+{\sigma }_g^{-2}\left(-\gamma +\alpha E_t/I_t\right)\right)\text{ and }{C}_{t+1}^{-1}={\sigma }_y^{-2}+{\sigma }_g^{-2}.$$

Then, $I_{t+1}=\left(1+g_{t+1}\right)I_t$, and the other states of the SEIR model, $\left(S_{t+1},E_{t+1},R_{t+1}\right)$ are deterministically updated via Equation (5). The particle set ${\left\{{\left(S_{t+1},E_{t+1},I_{t+1},R_{t+1}\right)}^{\left(i\right)}\right\}}_{i=1}^M$ serves as an approximation to $p\left(S_{t+1},E_{t+1},I_{t+1},R_{t+1}\mid y^{t+1}\right)$.

3.3.3. Parameter Learning.

To carry out parameter learning, we also need to identify a set of conditional sufficient statistics for the next time $t+1$, which we denote by $s_{t+1}$. These conditional sufficient statistics are a part of $Z_{t+1}$ and allow us to easily obtain new parameter samples from $p\left(\theta ,{\sigma }_y^2,{\sigma }_g^2\mid Z_{t+1}\right)$. Note, we have implicitly assumed that given the complete state history up to time $t+1,x^{t+1}=\left(x_1,\dots ,x_{t+1}\right)$, the parameters admit conditional sufficient statistics, so that $p\left(\theta ,{\sigma }_y^2,{\sigma }_g^2\mid x^{t+1},y^{t+1}\right)=p\left(\theta ,{\sigma }_y^2,{\sigma }_g^2\mid s_{t+1}\right)$, with $s_{t+1}$ being recursively and deterministically obtained from $\left(s_t,x_{t+1},y_{t+1}\right)$, as follows.

Assuming an inverse gamma prior distribution for the observational variance ${\sigma }_y^2$ in Equation (3), that is, ${\sigma }_y^2~IG\left(a_0,b_0\right)$, it follows ${\sigma }_y^2\mid y^{t+1},g^{t+1}~IG\left(a_{t+1},b_{t+1}\right)$, where $a_{t+1}=a_t+1/2$ and $b_{t+1}=b_t+{\left(y_{t+1}-g_{t+1}\right)}^2$. Then, $s_{t+1}$ is a deterministic function of $s_t,y_{t+1}^2,g_{t+1}^2$ and $g_{t+1}{y}_{t+1}$. Similarly, a bivariate normal-inverse gamma prior for $\left(\gamma ,\alpha ,{\sigma }_g^2\right)$ leads to a bivariate normal-inverse gamma posterior with sufficient statistics, $E_t/I_t,E_t^2/I_t^2$, and $g_{t+1}{E}_t/I_t$, included in $s_{t+1}$. The transmission parameter $\beta$ appears nonlinearly via $E_t$ and $I_t$ in the evolution equation and is sampled via the Liu and West (2001) filter, together with $\alpha$ and $\gamma$. For that reason, particle replenishing (via particle learning) is only performed for the two variances, ${\sigma }_y^2$ and ${\sigma }_g^2$.

3.3.4. Sequential Bayes Factors.

In situations where rapid decisions are needed, an estimate of the odds of pandemic might be the only quantity desired. In that case, we will be testing ${\beta }_{\text{pan}}$ versus ${\beta }_{\text{epi}}$, with ${\beta }_{\text{epi}}$ corresponding to a regular (seasonal) epidemic and ${\beta }_{\text{pan}}$ to a pandemic regime. Sequential computation of the Bayes factor describing the odds of a pandemic through time is then straightforward following the details in Section 3.2.

Hence, for an online detection of a pandemic, we can append the sequential learning algorithm with the sequential Bayes factor computation, comparing the cases where the parameter $\beta$ takes one of two levels. Evidence for the high-level $\beta$ indicates that the epidemic is about to become a pandemic, and evidence for the low-level $\beta$ indicates a regular seasonal epidemics where the disease spreads to a relatively small fraction of the population (CDC estimates 5%−20%) and dies out in a few months in a typical yearly cycle. Note that in the Bayes factor computation, different prior odds of a pandemic can be used: for example, they could be 1:20 (roughly corresponding to the historical frequency of flu pandemics in the past) or 1:1, which could be viewed as corresponding to a “pandemic vigilance” prior.

Sequential Learning Algorithm for state-space SEIR.

Definitions:

• $M$ = the number of particles used at each iteration ($M$ used in the paper is 1,000,000)

• $\alpha$ is the latency parameter, $\beta$ transmission parameter, and $\gamma$ recovery parameter in SEIR

• $\psi =(\text{log }\alpha ,\text{log }\beta ,\text{log }\gamma )$ is the log-transformation of the SEIR parameters

• $m_{\psi }$ and $V_{\psi }$ are the sample mean and variance of the ${\psi }^{\left(i\right)}$ draws $(i=1,\dots ,M)$, at each time point $t,t=1,\dots ,T$

• $\eta$ is the Liu-West shrinkage factor ($\eta$ used in the paper was 0.99)

• ${\sigma }_g^2$ is the evolution variance, and ${\sigma }_y^2$ is the observation variance

• ${\text{ILI}}_t$ is the observed (Google Flu Trends) ILI percentage for week $t$

The algorithm:

1. Draw the initial particle set ${\left\{{\left(\beta ,\alpha ,\gamma ,{\sigma }_g^2,{\sigma }_y^2\right)}^{\left(i\right)}\right\}}_{i=1}^M$ from the priors: $\beta ~N\left(1.5,{0.5}^2\right)I_{\beta >0},\alpha ~N\left(2,{0.5}^2\right)I_{\alpha >0},\gamma ~N\left(1,{0.5}^2\right)I_{\gamma >0},{\sigma }_g^2~\text{IG}\left(\mathrm{1.1,0.005}\right),{\sigma }_y^2~IG\left(\mathrm{1.1,0.05}\right)$ (see Section 4 of the article)

2. Initialize the particle set for states $(S,E,I,R{)}^{\left(i\right)}=(1-\left.{\text{ILI}}_1,0,{\text{ILI}}_1,0\right)$, for $i=1,\dots ,M$

Repeat the following steps for $t=1,\dots ,T$:

1. Compute $m_{\psi },V_{\psi }$

2. Compute ${\tilde{\psi }}^{\left(i\right)}=\eta {\psi }^{\left(i\right)}+(1-\eta )m_{\psi }$

3. Obtain ${\tilde{\alpha }}^{\left(i\right)}=\text{exp}\left\{{\tilde{\psi }}_1^{\left(i\right)}\right\},{\tilde{\beta }}^{\left(i\right)}=\text{exp}\left\{{\tilde{\psi }}_2^{\left(i\right)}\right\}$, and ${\tilde{\gamma }}^{\left(i\right)}=\text{exp}\left\{{\tilde{\psi }}_3^{\left(i\right)}\right\}$

4. Compute ${\mu }_g^{\left(i\right)}=-{\tilde{\gamma }}^{\left(i\right)}+{\tilde{\alpha }}^{\left(i\right)}{E}_{t-1}^{\left(i\right)}/I_{t-1}^{\left(i\right)}$

5. Compute weights ${\omega }_t^{\left(i\right)}\propto p\left(y_t\mid {\mu }_g^{\left(i\right)},{\sigma }_g^{2\left(i\right)}+{\sigma }_y^{2\left(i\right)}\right)$

6. Resample $\left(\tilde{\psi },{\sigma }_g^2,{\sigma }_y^2,S_{t-1},E_{t-1},I_{t-1},R_{t-1}\right)$ with weights ${\omega }_t^{\left(i\right)}$

7. Draw ${\psi }^{\left(i\right)}$ from $N\left({\tilde{\psi }}^{\left(i\right)},(1-\eta {)}^2{V}_{\psi }\right)$

8. Obtain $\left({\alpha }^{\left(i\right)},{\beta }^{\left(i\right)},{\gamma }^{\left(i\right)}\right)$ as in line 3 above

9. Obtain ${\tilde{\mu }}_g^{\left(i\right)}=-{\gamma }^{\left(i\right)}+{\alpha }^{\left(i\right)}{E}_{t-1}^{\left(i\right)}/I_{t-1}^{\left(i\right)}$

10. Sample $g_t^{\left(i\right)}~N(b,B)$, where $b=B\left(y_t/{\sigma }_y^{2\left(i\right)}+\right.\left.{\tilde{\mu }}_g^{\left(i\right)}/{\sigma }_g^{2\left(i\right)}\right)$ and $B=1/\left(1/{\sigma }_g^{2\left(i\right)}+1/{\sigma }_y^{2\left(i\right)}\right)$

11. Obtain

    1. $I_t^{\left(i\right)}=I_{t-1}^{\left(i\right)}\left(1+g_t^{\left(i\right)}\right)$
    2. $E_t^{\left(i\right)}={\beta }^{\left(i\right)}{I}_{t-1}^{\left(i\right)}{S}_{t-1}^{\left(i\right)}+\left(1-{\alpha }^{\left(i\right)}\right)E_{t-1}^{\left(i\right)}$
    3. $R_t^{\left(i\right)}=R_{t-1}^{\left(i\right)}+{\gamma }^{\left(i\right)}{I}_{t-1}^{\left(i\right)}$
    4. $S_t^{\left(i\right)}=1-I_t^{\left(i\right)}-R_t^{\left(i\right)}-E_t^{\left(i\right)}$

12. Compute weights ${\pi }_t^{\left(i\right)}\propto p\left(y_t\mid {\tilde{\mu }}_g^{\left(i\right)},{\sigma }_g^{2\left(i\right)}+{\sigma }_y^{2\left(i\right)}\right)/{\omega }_t^{\left(i\right)}$

13. Resample $\left(\psi ,{\sigma }_g^2,{\sigma }_y^2,S_t,E_t,I_t,R_t\right)$ with weights ${\pi }_t^{\left(i\right)}$

14. Sample ${\sigma }_g^2$ and ${\sigma }_y^2$ based on updated conditional sufficient statistics (according to the parameter learning paragraph in Section 3.3)

4. RESULTS

In this section, we present the results for influenza tracking, based on the U.S. Google Flu Trends. Individual years will be analyzed separately, with each year having a different set of epidemic parameters (latency, transmission, and recovery parameters, as well as the evolution and observation variances). The population sizes in all years are assumed known, with yearly estimates provided by the Census Bureau (U.S. Census Bureau 2009). We assume that in each season, the epidemics were started by an unknown number of infected individuals, estimated separately from the data.

We use the season-specific SEIR model within the state-space framework to track the epidemics. As a result, season-specific issues like cross-immunity from previous years will be partly accounted for; for example, the estimated transmission rate is expected to be lower in the years with residual immunity. While any compartmental influenza model—for example, a model with nonconstant population size (e.g., migration) or more detailed contact patterns—could be embedded into a state-space model, our goal here is not to build a more complex SEIR model, but to show how a simple SEIR model within a state-space framework can be successfully used to track the epidemic.

Given the abundance of prior information available for influenza, the hyper-parameters used were derived largely from the information based on historical epidemics and pandemics (see Section 2.2) and are as follows:

$$\text{Transmission parameter:}\beta ~N\left(1.5,{0.5}^2\right)I_{\beta >0}$$

$$\text{Latency parameter}:\alpha ~N\left(2,{0.5}^2\right)I_{\alpha >0}$$

$$\text{Recovery parameter}:\gamma ~N\left(1,{0.5}^2\right)I_{\gamma >0}$$

$$\text{Evolution variance}:{\sigma }_g^2~IG\left(1.1,0.005\right)$$

$$\text{Observation variance}:{\sigma }_y^2~IG\left(1.1,0.05\right).$$

Here, $I_{x>0}$ is an indicator function indicating that $x$ is positive. The 95% ranges of the prior distributions were constructed so that they encapsulate most of the parameter estimates reported in published work. Though these priors are still somewhat informative, their influence is expected to diminish with time as more surveillance data points are incorporated into the analysis.

We show the results for two flu seasons in the United States: the first season, 2003/2004, and the last season, 2008/2009. The epidemics in these two seasons had moderately more complex trajectories than those in the other four seasons. The first season, 2003/2004, shown in the first plot in Figure 2, was characterized by a notable epidemic peak in January 2004, when the number of Google-derived ILI cases increased to around 8%. The sharpness of the peak of that epidemic is somewhat at odds with the slowness of its spread early in the season. In such situations, the classic SEIR model with a time-invariant transmission rate $\beta$ and no evolution variance would likely have difficulties describing the disease activity adequately. The state-space formulation of the SEIR model however should be able to capture this sharp peak.

The 2008/2009 influenza season (the last plot in Figure 2) is the season with the most complexity in the epidemic trajectory. This season had multiple epidemic waves and multiple influenza strains merging together. The joint epidemic wave, widened by the late spring/summer H1N1 activity and the early second-wave onset of H1N1, would have presented an even greater challenge for the simple SEIR model without the state-space framework.

Although the state-space implementation is sensitive to the choice of variance parameters initially, the tracking algorithm is able to track the time progression of the 2003/2004 (see Figure 5) and 2008/2009 (see Figure 6) epidemics rather well. The uncertainty at each point in time is notable and can be assessed by examining the bottom, middle, and upper curves in all plots, which correspond to the lower 2.5th, median, and the upper 2.5th percentile of the posterior distribution for the hidden states and parameters as we learn more about them over time. For the 2003/2004 season, we see in Figure 5 that the transmission parameter decays over time as the epidemic subsides, while the latency and recovery parameters seem to stabilize: the latency parameter settled down around 1.45 (implying an average latency time of 4.8 days and median latency time of 3.2 days), while the recovery parameter settled down between 0.3 and 0.4 (implying an average recovery time between 2.5 and 3 weeks—with the median recovery time between 1.6 and 2 weeks). The 95% posterior ranges at the end of the epidemic were 0.15–0.9 for the transmission parameter, 1–2 for the latency parameter, and 0.1–0.6 for the recovery parameter. The estimate of $R_0=\beta /\gamma$ starts off between 1.5 and 2 but gradually settles down to around 1.1–1.3. This was in fact true for all seasons and regions we analyzed. The last panel in Figure 5 shows that even under 1:1 prior odds of pandemic, the Bayes factor steadily increases in favor of the regular epidemic as time progresses during the 2003/2004 season.

Figure 5.

Flu tracking results in the United States for the 2003/2004 influenza season. In the $I$ plot (second plot in the top row), the points represent weekly Google Flu Trends values, while the lines correspond to the lower 2.5 th percentile, median, and the upper 2.5 th percentile of the infectious state $\left(I_t\right)$ posterior distribution as time progresses. In the other plots, the two lines present the lower and upper 2.5 th percentiles, while the points present the weekly posterior medians. The results for Bayes factors for the two competing basic reproductive ratios (1.25 vs. 2.2), under 1:1 prior odds, are presented in the last panel, with higher log-Bayes factor meaning stronger evidence in favor of seasonal epidemics.

Figure 6.

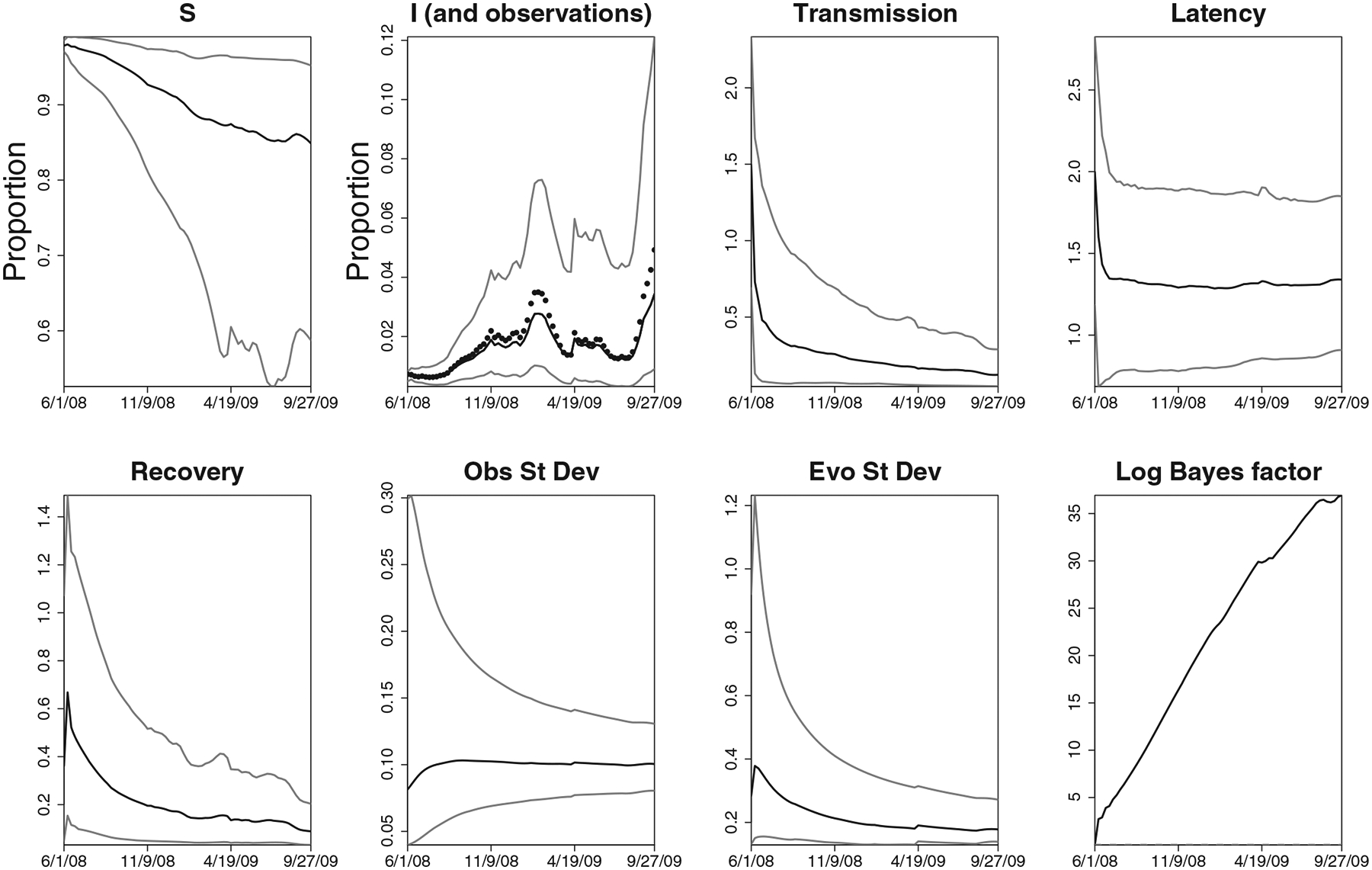
Flu tracking results in the United States for the 2008/2009 influenza season. In the $I$ plot, the points represent weekly Google Flu Trends values, while the lines correspond to the lower 2.5th percentile, median, and the upper 2.5th percentile of the infectious state $\left(I_t\right)$ posterior distribution as time progresses. In the other plots, the two lines present the lower and upper 2.5th percentiles, while the points present the weekly posterior medians. The results for Bayes factors for the two competing basic reproductive ratios (1.25 vs 2.2), under 1:1 prior odds, are presented in the last panel, with higher log-Bayes factor meaning stronger evidence for seasonal epidemics.

For the 2008/2009 season, we see in Figure 6 a similar set of findings as in the 2003/2004 season. The transmission rate of H1N1 seems slightly lower than the one for the 2003/2004 flu, while the latency parameter is approximately the same as in 2003/2004. The recovery parameter however settled down around 0.25, implying the median recovery time of 3 weeks. This is consistent with the findings that the most recent H1N1 recovery may be longer on average than the recovery from the other recent flu strains (Center for Infectious Disease Research & Policy 2009). The 95% posterior ranges at the end of the epidemic were 0.1–0.4 for the transmission parameter, 0.75−2 for the latency parameter, and 0.1–0.35 for the recovery parameter. Again, the last panel in Figure 6 shows that even under 1:1 prior odds of pandemic, the Bayes factor steadily increased in favor of the regular epidemic as time progressed during the 2008/2009 season.

All results show that while the state-space SEIR can track the epidemic processes reasonably well, there does seem to be a fair amount of uncertainty in sequential state and parameter estimates. This is also reflected in the estimated variances, with evolution variance consistently higher than the observation variance. Note that this does not imply that the state-space SEIR model does not fit well—on the contrary, the state-space model tracks the observed data fairly well. However, the large evolution variance can be taken to indicate that the underlying autonomous SEIR model would likely not describe the epidemics trajectory adequately on its own without the state-space framework.

A notable consequence of using the state-space framework is that the updated information can result in estimates of hidden states without the classic monotonicity constraints. In particular, the number of susceptibles can be updated to a higher level than in the previous time period. The shown hidden states are not actual trajectories over time, as the classic SEIR forward simulation would produce, but rather a sequence of point-wise estimates of hidden states over time—as a result, they need not be monotone.

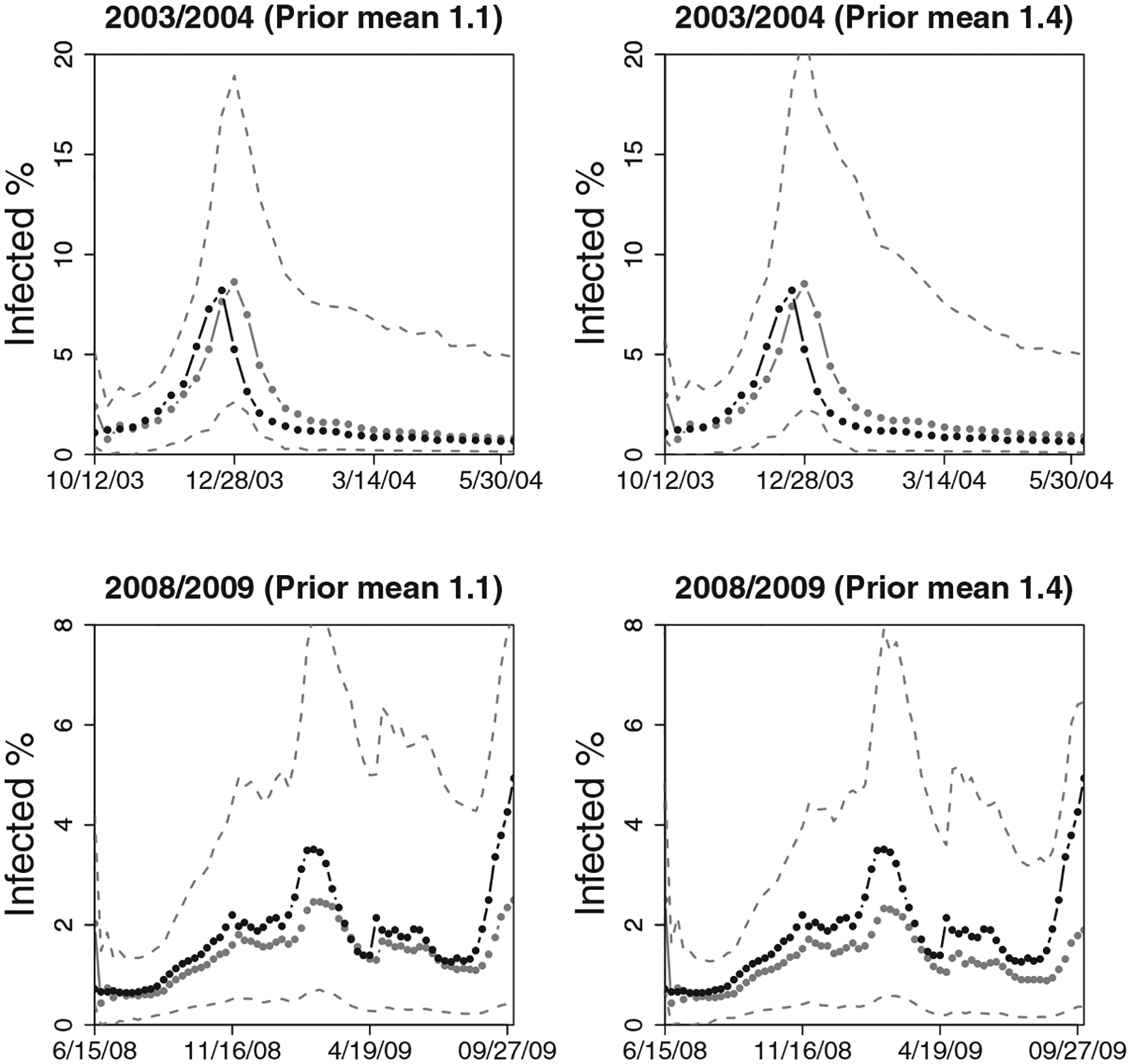
Figure 7 shows the prior sensitivity analysis under two additional priors on the transmission rate: the prior with mean of 1.4 and a slightly more “optimistic” prior with the mean of 1.1. As can be seen in both 2003/2004 and 2008/2009 seasons, the posterior means of the transmission parameter are similar under these two priors to the results under the prior mean of 1.5 shown in Figures 5 and 6. The similarity is increasing, albeit slowly, with additional data, as expected. The two Bayes factors (under 1:1 prior odds of pandemic) show slight differences under the two priors but are qualitatively the same: all still favor a regular epidemic over a pandemic.

Figure 7.

Sensitivity analysis under two additional priors on transmission rate: the gray lines correspond to a prior with the mean of 1.4 and the black lines correspond to an “optimistic” prior with the prior $\beta$ mean of 1.1. The three black and gray line sets in the left column plots correspond to the upper 97.5th percentile, posterior mean, and the 2.5 th percentile of the sequentially simulated marginal posteriors of the transmission parameter. The right column shows the log-Bayes factors, under 1:1 prior odds, with higher log Bayes factors indicating support for a regular epidemic. The top row shows the 2003/2004 season and the bottom row shows the 2008/2009 season.

In addition, Figure 8 shows the sensitivity analysis for the 1-week-ahead prediction (posterior mean and 95% credible interval) for the ILI counts in the 2003/2004 season (top row) and the 2008/2009 season (bottom row). The analysis was done under two different priors on transmission rate: the right column corresponds to the prior mean of 1.4 and the left column to the prior mean of 1.1. As we can see, 1-week-ahead prediction shows little sensitivity to the priors.

Figure 8.

Sensitivity analysis for the 1-week-ahead prediction under two different priors on transmission rate: the right column corresponds to a prior with the mean of 1.4 and the left column to an optimistic prior (with the prior $\beta$ mean of 1.1). The three gray lines correspond to the upper 97.5th percentile, posterior mean, and the 2.5 th percentile of the sequentially simulated predictive distributions, while the black line with points corresponds to the observed data. The top row shows the 2003/2004 season and the bottom row shows the 2008/2009 season. One-week-ahead prediction shows little sensitivity to the priors.

We also compared the performance of the state-space SEIR model with the simpler state-space AR(1) benchmark model. We only present a few of the interesting comparisons: Figure 9 shows the sequential posterior densities of the growth rate $p\left(g_t\mid y^t\right)$ and the infected fraction $p\left(I_t\mid y^t\right)$ for both state-space SEIR and AR(1) model for the 2003/2004 flu season in the United States. It is immediately apparent that the AR(1) model has difficulty capturing changes in the epidemic behavior and fails to track the epidemic trajectory closely after its peak. Similarly, Figure 10 shows the one-step-ahead prediction of AR(1) and SEIR state-space models in the 2003/2004 and 2008/2009 flu seasons. The state-space SEIR model’s 1-week-ahead predictions seem to be closer to the actual observations, while the state-space AR(1) model’s predictions are not as accurate after the peak, reflecting the inability of this simple model to capture the structure of the epidemic process well. The relative mean squared error of the AR(1) model versus the state-space SEIR model is 5.09 for the 2003/2004 season and 2.34 for the 2008/2009 season.

Figure 9.

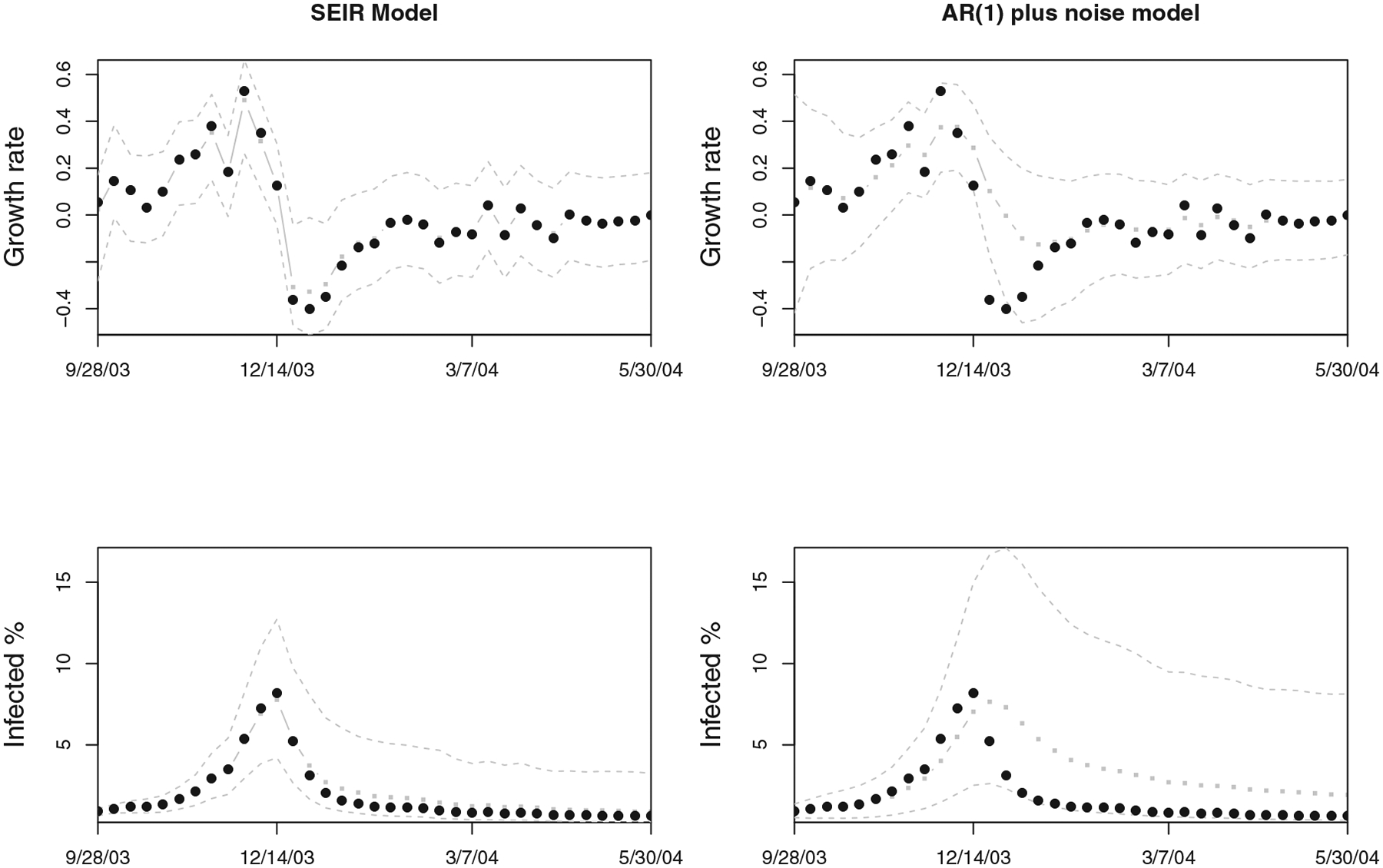
Sequential posterior distributions for the state-space SEIR model (left column) and the simple AR(1) benchmark model (right column) presented in Section 3, for the 2003/2004 flu season. The top row presents results for the growth rate of the infected population and the bottom row for the infected population fraction. The black circles correspond to the observations, gray squares (with gray line) are the fitted weekly values, and gray dashed lines are the 95% pointwise credible intervals. The AR(1) model is unable to capture the structure of the process as well as the state-space SEIR model.

Figure 10.

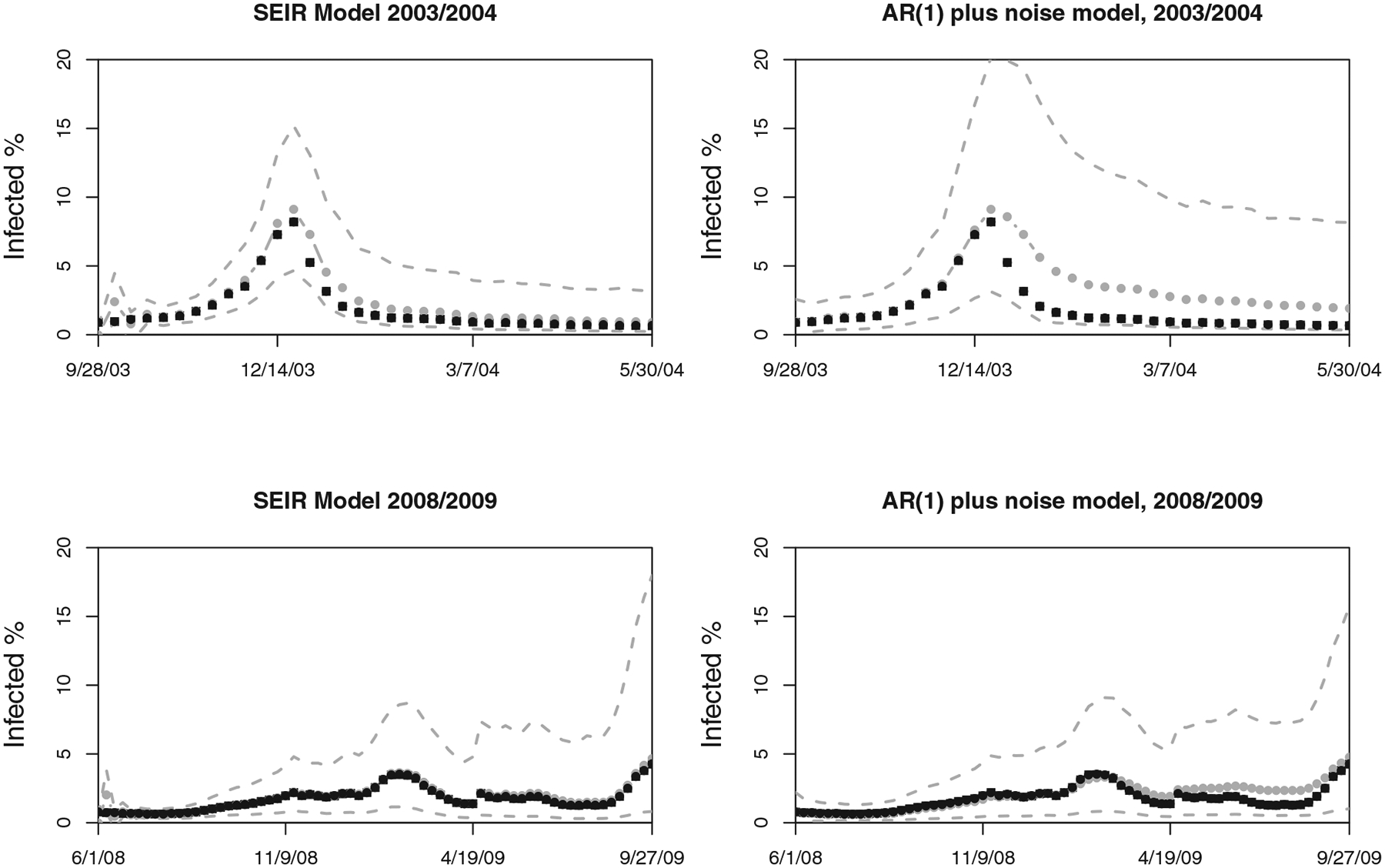
Comparison of the one-step ahead forecasts produced by the state-space SEIR model (left column) and the simple AR(1) benchmark model (right column) presented in Section 3. The top row presents results for the 2003/2004 flu season and the bottom row for the 2008/2009 flu season. The black squares correspond to the observations, gray circles (with gray line) are the predicted values (using data up to the previous week only), and gray dashed lines are the 95% pointwise credible intervals for the predictions. The AR(1) model predictions are not very accurate and reflect the inability of this simple model to capture the structure of the epidemic process well. The relative mean squared error of the AR(1) model versus the state-space SEIR model is 5.09 for the 2003/2004 season and 2.34 for the 2008/2009 season.

The other flu seasons for the entire United States showed no evidence of strong epidemics, and we do not present them for that reason. The nine individual states chosen as widely representative of the emergency health care systems present largely a similar story to the overall U.S. results. Consequently, we single out only two of the more severe epidemic states, Oklahoma and South Dakota, and present the tracking algorithm results for the 2008/2009 influenza season in those two states in Figure 11.

Figure 11.

Flu tracking results in South Dakota (top row) and Oklahoma (bottom row) for the 2008/2009 influenza season. In the $I$ plots (first plots in each row), the points represent weekly Google Flu Trends values, while the lines correspond to the lower 2.5 th percentile, median, and the upper 2.5th percentile of the posterior distribution of $I_t$ as time progresses. In the other plots, the two lines present the lower and upper 2.5th percentiles, while the points present the weekly posterior medians. The log-Bayes factor results for the two competing basic reproductive ratios, a mild one (1.25) and severe one (2.2), under 1:1 prior odds, are presented in the last panel. There seems to be little evidence for a pandemic.

The Bayes factor results are shown in the last panel of all result figures, under the 1:1 prior odds of a pandemic. A higher log-Bayes factor represents the stronger evidence for a seasonal epidemic. In all our analyses, the evidence for a regular epidemic seems to be increasing steadily over the course of the epidemic, starting to level off toward the end. None of the Bayes factors supported evidence for a pandemic in the United States and New Zealand. The full analysis of the New Zealand data is provided in the online supplementary material.

4.1. Comparison With MCMC

Pure compartmental models (without the state-space extension) have traditionally been fitted off-line, using nonlinear least-squares estimation procedures, or (as of recently) Bayesian estimation and MCMC techniques (O’Neill and Roberts 1999; Meligkotsidou and Fearnhead 2004; Neal and Roberts 2004; Elderd, Dukic, and Dwyer 2006; Leman, Chen, and Lavine 2009; Jewel et al. 2009). However, the lack of explicit likelihoods for these models generally results in slow estimation and lengthy MCMC runs. There is a large body of recent work on MCMC algorithms for dynamic models (Gilks and Berzuini 2001; Fearnhead 2002, 2008; Polson, Stroud and Muller 2008), discussing some of the computational issues with MCMC in dynamic models.

However, comparing a particle-filtering based algorithm with MCMC is useful to assess whether particle collapse might have been a problem. The sequential learning algorithm proposed in this article should perform well for dynamic models when there is a high level of conditional sufficiency for parameters of interest, which is not necessarily the case in real-life epidemics. For that reason, we take a closer look at the posterior distribution of the epidemic parameters $(\alpha ,\beta ,\gamma )$ and the two variances, and assess how the posteriors estimated via MCMC compared with those estimated via the sequential learning algorithm. The results are shown in Figure 12, at the end of the 2003/2004 U.S. flu season. There seems to be little difference between the marginal posterior densities of the three epidemic parameters and two variances. However, there was a notable difference in the length of time MCMC and sequential learning algorithm required to run: the sequential learning algorithm with 1,000,000 particles took on average less than 2 min on a 3.1GHz i5 processor for this season, while the MCMC with 1,000,000 iterations took approximately 15hr on the same processor. While this does not make MCMC infeasible for online surveillance, the time savings with sequential learning are notable.

Figure 12.

Comparison of posterior distributions between the sequential learning algorithm and MCMC, at the end of the 2003/2004 U.S. flu season. Gray histograms correspond to the marginal posterior distributions obtained via MCMC (based on 1500 samples), while the white histograms correspond to those obtained via the sequential learning algorithm (“SLA”) proposed in this article based on 1,000,000 particles

5. CONCLUSIONS

This article presents a state-space SEIR analysis of an IP influenza surveillance dataset, the Google Flu Trends. The U.S. Flu Trends surveillance has been found to closely track the CDC reports and is able to precede it by 1–2 weeks, holding potential for developing real-time surveillance mechanisms. As a result, flexible epidemic models and fast tracking algorithms capable of near real-time estimation and prediction, as new data become available, are particularly important. We present one approach to near real-time disease tracking based on the state-space methodology, compartmental modeling, and sequential Bayesian learning.

Classical compartmental models of mathematical epidemiology have been the staple of epidemic modeling for over a century. However, the unchanging dynamical structure, present in most classical models, is often not appropriate for real-life epidemics, due to seasonality (Cauchemez and Ferguson 2008), behavior changes, vaccination, quarantine, migration, or a myriad of other reasons that affect how people interact with and react to a disease. The state-space approach is one of the most flexible and yet simple ways to incorporate changes in the disease dynamics through time, as it relaxes the determinism of the compartmental models through the presence of the evolution variance. Yet, compartmental models also provide simple but powerful insight into the process of disease dynamics that can be readily tied to intervention (e.g., reducing contact intensity through school closures and hygiene, shortening recovery period through antiviral drugs, etc.). The simple state-space extension of the classic SEIR model presented in this article combines the familiar mathematical epidemiology theory with computational speed and statistical flexibility.

Although information loss and particle collapse can be a problem in our sequential learning algorithm as well as in all other particle filtering approaches, in modest-scale applications, for problems where parameters and states vary smoothly and slowly over time, any reasonable SMC scheme should perform well (Kitagawa 1998). However, when sharp changes in the dynamics are present, as may happen during real-life epidemics due to media activity or public health interventions, tracking might prove challenging. As computational power increases, taking advantage of GPU (graphics processing unit) and cloud computing, the serious information loss issues might be somewhat lessened through increased number of particles used in these algorithms.

The Bayesian framework used in the article is able to easily provide uncertainty estimates. As a result, the method such as the one presented here can be used to guide dynamic allocation of resources (Ludkovski and Niemi 2010) and to facilitate comparisons of different intervention strategies. Such comparisons can be done based on the predictive distribution of outcomes rather than just their expectations, allowing the full propagation of uncertainty in the nonlinear decision problems.

Although this article uses IP surveillance data, it is important to note that CDC surveillance plays a crucial role in the U.S. surveillance and threat preparedness and that the approach we present here is only one way among several designed to aid CDC in continuing their mission. Combining our approach with the CDC’s scan statistic methodology would be a valuable contribution, which we hope to pursue in the future as we extend our algorithm to account for spatial structure across the United States.

Finally, although CDC has done an extensive validation on Google Flu Trends, the Flu Trends algorithm has still not been validated specifically for most states and cities. There are many ways in which states and localities differ, and search terms may be correlated within state (or even within subregions of states and individual metropolitan areas). For example, the search terms found likely to be indicative of ILI for Rhode Island could differ from those used in California, especially when one allows the use of other languages. If more localized online surveillance is to be put in place, Google Trends algorithms will likely need further refinement, in collaboration with local public health authorities and CDC, to capture some of these region-specific differences. Expert opinion on geographical variations and relations among search terms might be able to shed light onto this issue.