Abstract
Calculating cardiac strains through speckle tracking echocardiography (STE) has shown promise as prognostic markers linked to functional indices and disease outcomes. However, the presence of acoustic shadowing often challenges the accuracy of STE in small animals such as rodents. The shadowing arises due to the complex anatomy of rodents, with operator dexterity playing a significant role in image quality. The effects of the semi-transparent shadows are further exacerbated in right ventricular (RV) imaging due to the thinness and rapid motion of the RV free wall (RVFW). The movement of the RVFW across the shadows distorts speckle tracking and produces unnatural and non-physical strains. The objective of this study was to minimize the effects of shadowing on STE by distinguishing “out-of-shadow” motion and identifying speckles in and out of shadow. Parasternal 2D echocardiography was performed, and short-axis B-mode (SA) images of the RVFW were acquired for a rodent model of pulmonary hypertension (n = 1). Following image acquisition, a denoising algorithm using edge-enhancing anisotropic diffusion (EED) was implemented, and the ensuing effects on strain analysis were visualized using a custom STE pipeline. Speckles in the shadowed regions were identified through a correlation between the filtered image and the original acquisition. Thus, pixel movement across the boundary was identified by enhancing the distinction between the shadows and the cardiac wall, and non-physical strains were suppressed. The strains obtained through STE showed expected patterns with enhanced circumferential contractions in the central region of the RVFW in contrast to smaller and nearly uniform strains derived from the unprocessed images.
Keywords: 2D echocardiography, speckle tracking, small animals, denoising, diffusion filtering, strain estimation
1. INTRODUCTION
Clinical diagnosis of cardiovascular diseases (CVDs), by and large, has relied on the evaluation of organ-level functional markers such as ejection fraction and end-systolic pressure.1, 2 The inclusion of medical imaging data in delineating cardiac motion has been a vital addition to standard clinical practice. In addition to the conventional diagnostic markers, the development of tissue-level measures of contractility through cardiac strain estimation has advanced the in-vivo assessment of CDVs3-5 Speckle tracking echocardiography (STE) is a widely studied method for quantifying myocardial deformation and remains the most available modality to calculate cardiac strains in clinical settings.6, 7 While two-dimensional echocardiography (2D-echo) proves to be a great asset in the global characterization of myocardial deformation, regional characteristics are often hindered by poor spatial resolution and the presence of artifacts.8 These shortcomings are more prominent in STE for small animal models, wherein ultrasound scanlines are often hindered by the rib cage and large regions of acoustic shadowing are produced.9 These artifacts have a pronounced influence on right ventricular free wall (RVFW) imaging. The slenderness of the RVFW, combined with its rapid motion, results in the random propagation of the speckles in and out of the shadows, thus distorting motion computation. Despite its clinical potential as a cost-effective tool, the inadequacies of 2D-echo in strain calculation restrict its reliability.
Multiple strategies for improving overall image quality and reducing artifacts at different stages of the acquisition process have been previously explored.10, 11 Among others, high frame-rate techniques such as myocardial elastography have been known to improve the spatial definition of the myocardial tissue,11 especially in the context of cardiac strain estimation.11, 12 However, artifacts due to reverberations (clutters) are a common sight. Indeed, the rapidness of the cardiac motion poses a great challenge in the spatiotemporal maintenance of tissue definition. Alternatively, post-processing measures such as filtering have improved the tissue contrast-to-noise ratio in brightness-mode (B-mode) images. However, the usage of these speckle reduction measures remains limited to the improvement of diagnostic accuracy10, 13 as the regularization of image intensities often results in significant blurring. This unintended consequence often leads to the underestimation of strains and undermines reproducibility. We hypothesize that cardiac strain reliability can be improved by enhancing the definition of the RVFW borders through the denoising of the “out-of-shadow” speckle motion.
In this study, we have implemented an STE framework that leverages anisotropic diffusion and speckle reduction to improve strain calculations. B-mode short-axis (SA) and four-chamber (4-CH) images of the RVFW were acquired for a Sugen-hypoxia rodent model of pulmonary hypertension.2, 14 Subsequently, acoustic shadows were observed, and the images were subjected to the edge-enhancing anisotropic diffusion (EED) filter. Cardiac strains were then evaluated using both the unprocessed and filtered images.
2. MATERIALS AND METHODS
2.1. Speckle tracking
An STE framework was implemented to evaluate cardiac strains at end systole (ES) with respect to end-diastole (ED). The framework extends upon the work of Perrot et al.,15 wherein a normalized cross-correlation algorithm was used to track pixel movement between two consecutive interrogation windows, and in the Fourier space and the inverse Fourier transform was applied to derive the Cartesian displacements as:
| (1) |
where is the displacement vector in the Cartesian space, the overline denotes the complex conjugate, and and are the Fourier transforms of and , respectively. Interrogation windows of 64 x 64 pixels were set up initially, and the resulting displacements were linearly interpolated onto a grid space of 10 x 10 pixels. A spline smoothing function was used to reduce outliers and noise. The Cartesian displacements were then used to derive the Green-Lagrange strain tensor (). Strains were estimated using the displacements () with respect to the reference frame () through the deformation gradient tensor () as:
| (2) |
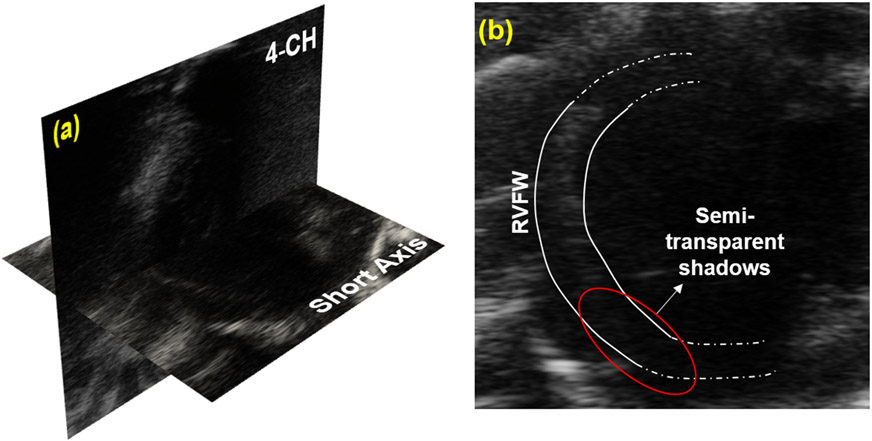
where () is the identity tensor, and denotes the strains transformed to the anatomical axes (radial, circumferential, longitudinal) through a polar transformation tensor . SA images were used to calculate circumferential strains, and the 4-CH view was used to calculate strains in the longitudinal direction. The images used for speckle tracking were obtained from 2D parasternal echocardiography in a male Sprague-Dawley Sugen-hypoxi rat (n = 1) at the third-week timepoint post Sugen5416 injection.2 SA and 4-CH images were acquired in one session (Fig. 1a). Imaging was performed using a VisualSonics Vevo 2100 small animal ultrasound machine with a center transmit transducer frequency = 21 MHz.
Figure 1.
(a) 2D echocardiographic short axis (SA) and four-chamber (4-CH) images of the right ventricular free wall (RVFW). (b) The SA image with the semi-transparent shadows across the inferior RVFW.
2.2. Edge enhancing anisotropic diffusion filter
A denoising methodology was developed using the edge-enhancing anisotropic diffusion (EED) filter to identify pixels in regions with an overwhelming presence of acoustic shadows. The EED filter was introduced in the context of image processing by Weickert et al.16 and has found applications in data compression.17 EED is a modification of the non-linear diffusion equation and is characterized by the presence of anisotropic image gradients described by:
| (3) |
where is the image intensity and is the diffusion tensor that is commonly assumed to be a null matrix in the case of linear diffusion. In this study, the diffusion tensor is defined as a function of the structure tensor derived from Gaussian smoothed gradients of each pixel such that:
| (4) |
where represents the smoothed image in which * defines a convolution between and the Gaussian kernel (). Further, denotes the standard deviation of the Gaussian kernel, and the superscript denotes the transpose. The eigenvalues of the diffusion tensor , denoted by and , are determined as
| (5) |
where and are the smallest and largest eigenvalues of the structure tensor, respectively, and and are the Weickert diffusivity coefficients (). These coefficients were chosen following their reported success in enhancing edge definition in magnetic resonance imaging and computed tomography scans of the brain.17 The partial differential equation (3) was solved using an additive operator splitting scheme,18 and the filter was applied over a period of 100 steps (total time = 10 s, step size = 0.01). Each interrogation window of the image was individually filtered. Subsequently, speckles were tracked between the unprocessed and filtered images using the cross-correlation algorithm. A threshold correlation factor was used to distinguish the spurious speckles moving into the shadows. A normalized frame-frame correlation of 0.1 was fixed to identify and suppress the tracking of the speckles in the STE framework. Structural similarity (SSIM) and mean squared error (MSE) analyses were performed between the filtered and unprocessed images across the five windows comprising the RVFW (Figs. 2a,d) to evaluate the boundary definition. Strains were calculated along the RVFW using both the unprocessed and filtered images.
Figure 2.
SA images at end-systole (ES). (a) Unprocessed image, (b) edge-enhancing anisotropic diffusion filtering, (c) denoised image due to the correlation between the filtered and unprocessed image. (1-5) Windows encompassing the RVFW.  Interrogation grid.
Interrogation grid.  Shadowed windows. RVFW: right ventricular free wall.
Shadowed windows. RVFW: right ventricular free wall.
3. RESULTS
3.1. Performance of the EED filter
The shadows over the myocardial tissue were localized to the RV inferior region (Fig. 1b), and minimal artifact presence was observed in 4-CH images. All results are presented for the SA images across the 64 x 64 interrogation windows (Fig. 2). Initial applications of the EED filter showed speckle reduction in the image sequences, and more importantly, the boundaries of the RVFW (endocardium and epicardium) remained intact (Fig 2b,c). The SSIM analysis was used to spatiotemporally quantify the edge definition of the RVFW (Figs. 2a,c), and an average SSIM of 0.8781 ± 0.1047 was achieved across the five windows at ES. Although SSIM values dropped after 100 steps, the semi-transparent speckles were entirely denoised (Fig. 2b). The MSE error of 0.0482±0.0531 confirmed image despeckling. The resulting image-matching process allowed for the isolation of the windows used for speckle tracking and strain analysis.
3.2. Strain analysis
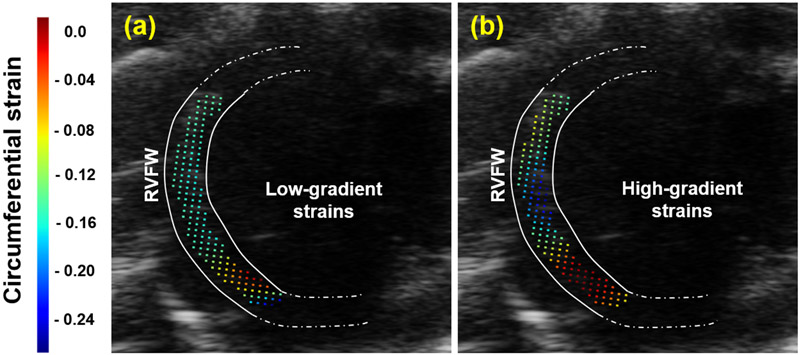
Strain calculations corroborated the above observations with expected patterns of more significant circumferential contractions in the central RV wall (Fig. 3b) improving over the low-gradient strain in the unprocessed image (Fig. 3a). These patterns arise from the contraction of the RV wall along the circumferential and longitudinal directions at ES. Strains up to −25% were observed along the anterior region of the central RVFW. Larger contractile strains in the central RVFW, away from RV-septal insertion points, can be explained by expected larger passive stretches in the central region and potential spatial variation in systolic pressure in the RV chamber. An MSE error of 0.08512 was calculated between the unprocessed and filtered strains, indicating a significant difference in the evaluated RVFW motion. However, these motion estimates require further investigations under a larger cohort to validate the performance of EED in improving strain calculations.
Figure 3.
Circumferential strain analysis at ES for (a) unprocessed image, (b) filtered image. RVFW: right ventricular free wall.
4. DISCUSSION
Filtering 2D echocardiographic images has been primarily implemented in denoising to improve image reconstruction. Pre-processing ultrasound images using Gaussian, median, or even the coherence edge enhancing diffusion (cEED) filter have been shown to improve the contrast-to-noise ratio,10 but this improvement in image quality is usually accompanied by blurring at sharp edge interfaces, specifically at the blood-tissue barrier. In this study, the effects of the EED filter on speckle reduction and its ensuing influence on strain calculations were investigated. In the SA images used here, speckles were interspersed in regions with significant shadowing along the inferior region of the RVFW. Our objective was to suppress unrealistic strain estimation by distinguishing these spurious entities from valid RVFW speckles to enhance motion calculations.
Through the application of window-specific structure tensors in the EED filter, we were able to identify noisy speckles amongst the large areas of shadowing. The inclusion of the directional variations of all neighboring gradients on an individual pixel made the EED filter ideal for our experiments. Upon application, we observed the preservation of the endocardial edges and the elimination of the majority of speckles moving in and out of the shadows. We attribute the former and latter observations to the increased presence of high-intensity speckles and low-intensity pixels, respectively. By eliminating these spurious speckles from motion quantification, the contributors to unrealistic strains (large displacements) were systematically removed from tracking (Eq. 1). We limited the application of the EED filter to 100 steps to avoid speckle loss over the tissue and optimally capture the myocardial motion. A subsequent strain analysis confirmed our initial observations with the denoised images yielding strain patterns that supported the expected behavior of the RVFW contraction during systole. Our experiments yielded drastic changes in the spatiotemporal distribution of contraction patterns. However, results are yet to be validated against regional strain calculations through other imaging modalities such as cine cardiac magnetic resonance imaging.12, 19, 20 The validation of such regional strain calculations is an active area of research,21 with a standardized cross-modality benchmark yet to be established. A potential limitation in this study is the absence of a comparative assessment of the EED filter against other commonly used measures, such as the cEED, minimum total variation, and other diffusion filters. Also, artifact detection was based on a manually set threshold, which leaves room for improvement as machine learning-based artifact detectors are growing in prevalence.22 Despite these shortcomings, the calculation pipelines provided a streamlined methodology for estimating cardiac strains with improvements in the calculated values. Our next steps will include experiments to evaluate this performance measure of the EED filter against existing studies and implement an artifact detection algorithm that relies on a completely automated approach in integrating denoising in the STE pipeline.
5. CONCLUSION
The implementation of the denoising algorithm led to a semi-automated artifact-aware strain calculation pipeline customized for RV echocardiography in small animals that offers rigorous quantification of RV motion. Drastic changes were observed in the strain gradients and values. Our study serves as an essential step towards standardizing 2D-echo-based RVFW motion estimation. The evaluation of RVFW deformation shows promise for improved assessment of RV remodeling events in pulmonary hypertension.23-25 The assessment of regional cardiac strain distribution offers significant potential in developing a complete structure-function relationship of the RV to complement and enhance standard diagnostic protocol.
REFERENCES
- [1].Wehner GJ, Jing L, Haggerty CM, Suever JD, Leader JB, Hartzel DN, Kirchner HL, Manus JNA, James N, Ayar Z, Gladding P, Good CW, Cleland JGF, and Fornwalt BK, “Routinely reported ejection fraction and mortality in clinical practice: where does the nadir of risk lie?,” European Heart Journal 41(12), 1249–1257 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Mendiola EA, da Silva Gonçalves Bos D, Leichter DM, Vang A, Zhang P, Leary OP, Gilbert RJ, Avazmohammadi R, and Choudhary G, “Right ventricular architectural remodeling and functional adaptation in pulmonary hypertension,” Circulation: Heart Failure (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Marwick TH, “Ejection fraction pros and cons,” Journal of the American College of Cardiology 72(19), 2360–2379 (2018). [DOI] [PubMed] [Google Scholar]
- [4].Karlsen S, Dahlslett T, Grenne B, Sjøli B, Smiseth O, Edvardsen T, and Brunvand H, “Global longitudinal strain is a more reproducible measure of left ventricular function than ejection fraction regardless of echocardiographic training,” Cardiovascular Ultrasound 17(1) (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Delgado V and Ajmone Marsan N, “Global and regional longitudinal strain assessment in hypertrophic cardiomyopathy,” Circulation: Cardiovascular Imaging 12(8) (2019). [DOI] [PubMed] [Google Scholar]
- [6].Marwick TH, “Measurement of strain and strain rate by echocardiography: ready for prime time?,” J Am Coll Cardiol 47(7), 1313–27 (2006). [DOI] [PubMed] [Google Scholar]
- [7].Collier P, Phelan D, and Klein A, “A test in context: Myocardial strain measured by speckle-tracking echocardiography,” Journal of the American College of Cardiology 69(8), 1043–1056 (2017). [DOI] [PubMed] [Google Scholar]
- [8].Bertrand PB, Levine RA, Isselbacher EM, and Vandervoort PM, “Fact or artifact in two-dimensional echocardiography: Avoiding misdiagnosis and missed diagnosis,” Journal of the American Society of Echocardiography 29(5), 381–391 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Tee N, Gu Y, Murni, and Shim W, “Comparative myocardial deformation in 3 myocardial layers in mice by speckle tracking echocardiography,” BioMed Research International 2015, 1–8 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Guan F, Ton P, Ge S, and Zhao L, “Anisotropic diffusion filtering for ultrasound speckle reduction,” Science China Technological Sciences 57(3), 607–614 (2014). [Google Scholar]
- [11].Konofagou EE, D’hooge J, and Ophir J, “Myocardial elastography—a feasibility study in vivo,” Ultrasound in Medicine Biology 28(4), 475–482 (2002). [DOI] [PubMed] [Google Scholar]
- [12].Wei-Ning L, Ingrassia CM, Fung-Kee-Fung SD, Costa KD, Holmes JW, and Konofagou EE, “Theoretical quality assessment of myocardial elastography with in vivo validation,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control 54(11), 2233–2245 (2007). [DOI] [PubMed] [Google Scholar]
- [13].Mei K, Hu B, Fei B, and Qin B, “Phase asymmetry ultrasound despeckling with fractional anisotropic diffusion and total variation,” IEEE Transactions on Image Processing 29, 2845–2859 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Neelakantan S, Vang A, Nicely P, Choudhary G, and Avazmohammdi R, “Mechanical remodeling of the rv and pa in ph,” in [C54. HAIGHT-ASHBURY: THE TWO VENTRICLES], A4422–A4422, American Thoracic Society; (2022). [Google Scholar]
- [15].Perrot V and Garcia D, “Back to basics in ultrasound velocimetry: tracking speckles by using a standard piv algorithm,” 2018 Ieee International Ultrasonics Symposium (Ius) (2018). [Google Scholar]
- [16].Weickert J, “Anisotropic diffusion filters for image-processing based quality-control,” Proceedings of the Seventh European Conference on Mathematics in Industry 9, 355–362 (1994). [Google Scholar]
- [17].Schmaltz C, Peter P, Mainberger M, Ebel F, Weickert J, and Bruhn A, “Understanding, optimising, and extending data compression with anisotropic diffusion,” International Journal of Computer Vision 108(3), 222–240 (2014). [Google Scholar]
- [18].Fehrenbach J and Mirebeau JM, “Sparse non-negative stencils for anisotropic diffusion,” Journal of Mathematical Imaging and Vision 49(1), 123–147 (2014). [Google Scholar]
- [19].Keshavarzian M, Fugate E, Chavan S, Chu V, Arif M, Lindquist D, Sadayappan S, and Avazmohammadi R, [An Image Registration Framework to Estimate 3D Myocardial Strains from Cine Cardiac MRI in Mice], book section Chapter 27, 273–284, Lecture Notes in Computer Science; (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Qu Y-Y, Li H, Rottbauer W, Ma G-S, Buckert D, and Rasche V, “Right ventricular free wall longitudinal strain and strain rate quantification with cardiovascular magnetic resonance based tissue tracking,” The International Journal of Cardiovascular Imaging 36(10), 1985–1996 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Tobon-Gomez C, De Craene M, McLeod K, Tautz L, Shi W, Hennemuth A, Prakosa A, Wang H, Carr-White G, Kapetanakis S, Lutz A, Rasche V, Schaeffter T, Butakoff C, Friman O, Mansi T, Sermesant M, Zhuang X, Ourselin S, Peitgen HO, Pennec X, Razavi R, Rueckert D, Frangi AF, and Rhode KS, “Benchmarking framework for myocardial tracking and deformation algorithms: An open access database,” Medical Image Analysis 17(6), 632–648 (2013). [DOI] [PubMed] [Google Scholar]
- [22].Hu R, Singla R, Deeba F, and Rohling RN, “Acoustic shadow detection: Study and statistics of b-mode and radiofrequency data,” Ultrasound in Medicine Biology 45(8), 2248–2257 (2019). [DOI] [PubMed] [Google Scholar]
- [23].Avazmohammadi R, Mendiola EA, Soares JS, Li DS, Chen Z, Merchant S, Hsu EW, Vanderslice P, Dixon RAF, and Sacks MS, “A computational cardiac model for the adaptation to pulmonary arterial hypertension in the rat,” Annals of Biomedical Engineering 47(1), 138–153 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Avazmohammadi R, Hill M, Simon M, and Sacks M, “Transmural remodeling of right ventricular myocardium in response to pulmonary arterial hypertension,” APL Bioengineering 1(1) (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Avazmohammadi R, Mendiola EA, Li DS, Vanderslice P, Dixon RAF, and Sacks MS, “Interactions between structural remodeling and hypertrophy in the right ventricle in response to pulmonary arterial hypertension,” Journal of Biomechanical Engineering 141(9) (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]