Genotype error due to low-coverage sequencing induces uncertainty in polygenic scoring

Summary

Polygenic scores (PGSs) have emerged as a standard approach to predict phenotypes from genotype data in a wide array of applications from socio-genomics to personalized medicine. Traditional PGSs assume genotype data to be error-free, ignoring possible errors and uncertainties introduced from genotyping, sequencing, and/or imputation. In this work, we investigate the effects of genotyping error due to low coverage sequencing on PGS estimation. We leverage SNP array and low-coverage whole-genome sequencing data (lcWGS, median coverage 0.04×) of 802 individuals from the Dana-Farber PROFILE cohort to show that PGS error correlates with sequencing depth (p = 1.2 × 10⁻⁷). We develop a probabilistic approach that incorporates genotype error in PGS estimation to produce well-calibrated PGS credible intervals and show that the probabilistic approach increases classification accuracy by up to 6% as compared to traditional PGSs that ignore genotyping error. Finally, we use simulations to explore the combined effect of genotyping and effect size errors and their implication on PGS-based risk-stratification. Our results illustrate the importance of considering genotyping error as a source of PGS error especially for cohorts with varying genotyping technologies and/or low-coverage sequencing.

Graphical abstract

Petter et al. investigate the impact of genotyping error on the accuracy of polygenic scores (PGSs). The study takes a probabilistic approach to create individual PGS credible intervals accounting for the genotype errors and explores the use of such credible intervals for enhanced PGS-based risk stratification.

Introduction

Polygenic scores (PGSs) carry potential for predicting disease risk from an individual’s genomic profile and are a promising tool for a wide array of applications from socio-genomic studies to personalized medicine.^1,2,3,4 For example, integration of PGSs with clinical data and personal history may enable prevention or early diagnosis of disease.^5,6,7 PGSs are estimated by a linear combination of the allele counts of the individual of interest weighted by their effect sizes. Both the effect size and the allele count components of the PGSs are unknown and are estimated with some level of error that is then propagated to the PGS estimate itself. The error in effect size occurs when non-causal SNPs are assigned non-zero effect sizes or when the wrong magnitude of effect size is assigned to a causal variant. Error in the estimated allele count (i.e., genotype), also referred to as genotyping error, occurs when an individual’s genotype is estimated incorrectly leading to a wrong value at a genomic site of interest. Unfortunately, traditional applications of PGSs usually assume the genotype data (in the form of allele counts at each site) to be error free, while genotype error still exists and may impact application and downstream analysis based on PGS if ignored. The extent of genotype-based PGS error depends on the genotyping assay in use and the different genotype-calling algorithm used, both reflecting different choices regarding the tradeoff between quality, noise, and cost.^8,9 In whole-genome sequencing (WGS), sequencing reads are sampled from the target genome, followed by assembly and variant calling generating the reported genotype. Higher coverage allows for improved genotyping accuracy with the tradeoff of greater cost; the expected accuracy of WGS (with coverage higher than 0.5×) is above 90%¹⁰ with heterozygous concordance between arrays and sequencing genotypes reaching 99% at a coverage of ∼18×.¹¹ Balancing cost with accuracy, low-coverage whole-genome sequencing (lcWGS) has been proposed as a useful approach to balance sample size with accuracy for improved statistical power.^10,12,13 lcWGS uses lower coverage for each site and thus increases the level of uncertainty in genotype calling at the benefit of sequencing more individuals within the same budget. Overall, the choice between high-coverage sequencing, low-coverage sequencing, or array genotyping is dependent on the application and the desired balance between cost and expected accuracy, with limited investigation and consideration of the impact of errors from low-coverage sequencing on PGS estimation. Recent work by our group focused on the propagation of error from effect size estimation to the error of the final PGS and calculated individual PGS uncertainty as the standard deviation of the individual’s PGS estimate.¹⁴ In this work, we focus on the propagation of error from the genotype estimation into individual PGS and show that both sources of error—effect-size error and genotype error—contribute jointly to the overall uncertainty of the PGS.

We investigate the impact of genotype error arising from low-coverage WGS on PGS error. We leverage real data from 802 individuals from the Dana-Farber PROFILE cohort^15,16 with both lcWGS (median genome wide coverage 0.036×) as well as array genotypes at 1M common SNPs across the genome. We find a strong correlation between the sequencing depth and individual PGS error, thus confirming that lcWGS introduces genotyping errors that propagate to PGS uncertainty. Next, we explore the impact of genotype error in PGS-based risk stratification and show that approaches that take uncertainty into account outperform traditional approaches; for example, increasing the percentage of high-risk individuals in a sample selected based on PGS. Finally, using simulated effect sizes and real lcWGS data, we show that ignoring genotype errors leads to miscalibrated 90% confidence intervals for the PGS predictions based on effect-size error alone. Taken together, our results showcase that genotyping errors need to be accounted for in PGS applications for datasets where lcWGS is the primary approach for obtaining genotypes.

Subjects and methods

Ethics approval and consent to participate

Dana-Farber Cancer Institute PROFILE^15,16 samples were selected and sequenced from patients who were consented under institutional review board (IRB)-approved protocol 11-104 and 17-000 from the Dana-Farber/Partners Cancer Care Office for the Protection of Research Subjects. Written informed consent was obtained from participants prior to inclusion in this study. Secondary analyses of previously collected data were performed with approval from the Dana-Farber IRB (DFCI IRB protocol 19-033 and 19-025; waiver of HIPAA authorization approved for both protocols). The research conformed to the principles of the Helsinki Declaration.

Dataset

In this work, we used a subset of data from the Dana-Farber Cancer Institute PROFILE cohort. The cohort includes ∼25K samples that were obtained as part of patients’ routine cancer care and were sequenced on the OncoPanel¹⁷ platform targeting exons of 275–447 cancer genes, selected based on their involvement in cancer-related signaling pathways and their labeling as oncogenes or tumor-suppressor genes.¹⁶ The mean on-target coverage obtained was 152×, the mean off-target coverage was 0.01×, and the mean genome-wide coverage was 0.036×. Low coverage imputation was performed using STITCH¹⁸ with the 1000 Genomes Phase 3¹⁹ as a reference panel, using variants with >1% frequency in the European population. We focused on a subset of the PROFILE cohort containing 802 European ancestry individuals who also had their whole blood samples genotyped on the Illumina Multi-Ethnic Genotyping Array (MEGA) platform²⁰ and imputed using the Haplotype Reference Consortium (HRC) reference panel.²¹ Both sequencing and genotyping data were restricted after imputation to ∼1.1 million SNPs in HapMap3 that usually exhibit high imputation accuracy and capture common SNP variation. lcWGS accuracy was measured using the Pearson correlation between array and tumor imputed genotypes, reported to be mean 0.79 (SE 0.001) across all 1.1 million SNPs.¹⁵

PGS point estimation: Array-PGS vs. dosage-PGS

We distinguish between two types of PGS point estimation, each using a different method for genotype calling. As we initially focus on the effects of only the genotype uncertainty on the variance of $\widetilde{PG{S}_{\mathrm{i}}}$, we consider the effect sizes $\beta$ to be estimated and fixed to a certain value, W. Array-PGS is defined as ${X_a}^{t}W$ where X_a is the array genotype of an individual. Dosage-PGS is defined as ${X_d}^{t}W$ where X_d is the dosage of the genotype, defined as the expected number of non-reference alleles an individual carries. More specifically, dosage can be calculated as $0·p_0+1·p_1+2·p_2\text{.}$ The probabilities p₀, p₁, and p₂ of SNP j are the posterior probabilities of a genotype matching 0, 1, or 2, respectively, as obtained from a method for genotype imputation.

Obtaining PGS distribution accounting for genotype error

The input for calculating the individual PGS distribution is lcWGS allele count posterior probabilities. Instead of fixing the genotype to a single value for each variant (dosage), we draw S = 1,000 different genotypes for SNP j of individual i set to be 0, 1, or 2 according to a multinomial distribution with the probabilities (p₀, p₁, p₂) described previously. Repeating independently for all M SNPs, an individual i is assigned S different M sized genotypes, ${\tilde{X}}_{i,1,}{\tilde{X}}_{i,2,}...{\tilde{X}}_{i,S,}\text{.}$ By combining $\tilde{X}\text{,}$ the different genotype samples of individual i, with W, the effect sizes weights we can obtain a distribution of PGS values for individual i, $\widetilde{PG{S}_{\mathrm{i},1}}$, $\widetilde{PG{S}_{\mathrm{i},2}}$… $\widetilde{PG{S}_{\mathrm{i},S}}$. This distribution is a sample of size S from the distribution of $PG{S}_i$, from which we can learn about the PGS estimate’s variance and credible interval. It should be noted that the expected value of $\widetilde{PG{S}_{\mathrm{i}}}$ is exactly the value of the dosage-PGS. The PGS CIs are obtained by calculating the empirical quantiles of $\widetilde{PG{S}_{\mathrm{i}}}$ for the desired confidence level, $\rho$.

Simulations

To confirm the calibration of the PGS CI, we simulated effect sizes and combined them with real genotypes from the PROFILE lcWGS data. We ran this experiment several times for different genetic architectures, while changing the values of the proportion of causal SNPs ($P_{causal})$ and the variance parameter ($\widetilde{h^2})\text{.}$ In each experiment we ran ten iterations of selecting $M·P_{causal}$ SNPs (out of a total of M SNPs), for which the effect sizes are drawn from $W\sim N\left(0,\frac{\widetilde{h^2}}{M·P_{causal}}\right)$ independently across SNPs, and independent of SNP minor allele frequency. Our simulations covered a wide array of genetic architectures, with $\widetilde{h^2}\in \left\{0.1,0.25,0.5\right\}$ and $P_{causal}\in \left\{0.001,0.01,0.1\right\}$. We note that as the genotypes are not standardized, the variance explained is not equal to $\widetilde{h^2}$. This is because the contribution of the genotype variance needs to be accounted for, resulting in average h² levels of 0.03, 0.08, and 0.16, respectively, for the $\widetilde{h^2}$ values above. For the empirical coverage calculations, we used the sets of simulated effect sizes with the same parameters and ran ten iterations of the following procedure: (1) calculate $\widetilde{PG{S}_{\mathrm{i}}}$ and obtain the individual PGS credible intervals for all confidence levels, as described above; (2) calculate the matching array-PGS values for all individuals; (3) calculate the percentage of individuals whose array-PGS value falls within the CI calculated.

We repeated the same procedure for $h^2\in \left\{0.1,0.25,0.5\right\}$ and $P_{causal}\in \left\{0.001,0.01,0.1\right\}$ under an effect size distribution with variance inversely proportional to the SNP minor allele frequency: $W_{scaled,m}\sim N\left(0,\frac{h^2}{M·P_{causal·}2{\theta }_m\left(1-{\theta }_m\right)}\right)$, where ${\theta }_m$ represents the minor allele frequency of SNP m. Under this model, the expected SNP heritability is equal for all sites, and the total variance explained will be h².

We tested calibration for different LD settings by selecting two sets of simulated effect sizes. The first set included 1,000 SNPs with strong LD selected by obtaining variant pairs with a HapMap r² above 0.7 and maximizing the set so it included the most SNPs with strong LD. The second set was similarly optimized to include SNPs with low LD (HapMap r² < 0.05). We set $\widetilde{h^2}=0.1$ and drew the effect sizes from the distribution described above.

To explore differences in coverage, we used simulated lcWGS genotypes as follows. First, we simulate reads followed by calculating genotype probabilities, as would be obtained from imputation algorithms. We sample reads at the desired coverage level (for example, for 10× we sample 10 reads for each site) based on the genotyping array of each individual—if the array genotype is 0 or 2, we sample all reads to match it. If the genotype is 1, we sample 1 or 0 alleles with a probability of 0.5. To allow for some level of sequencing error, we flip the read alleles at a rate of 1%. The second step is to use the obtained reads and calculate the likelihoods of observing the reads assuming the individual carries a genotype of 0, 1, or 2. The likelihood is calculated as follows:

$$\mathcal{L}\left(R|G\right)=\left(\begin{array}{c}{R}_t\\ R_{alt}\end{array}\right){\left[\left(1-e\right)p+e\left(1-p\right)\right]}^{R_{alt}}·{\left[\left(1-e\right)\left(1-p\right)+ep\right]}^{R_t-R_{alt}}$$

where R_t represents the total number of reads, R_alt represents the number of reads matching the alternate allele, e is the error rate (fixed to 0.01 in our simulations), and $p$ is the probability that the true value of the allele sampled (out of the two alleles in each site) is 1: $p=0,\mathrm{0.5,1}$ for a genotype $G=\mathrm{0,1,2}$ respectively. As we wish to obtain genotype posterior probabilities similarly to those obtained from imputation algorithms, we use a flat prior and calculate the posterior probability for each genotype possibility based on the likelihoods. The procedure yields a new set of 10× and 5× genotype probabilities for each individual in our original dataset.

Empirical data PGS calculation and risk stratification

For evaluating the effects of genotype-based PGS uncertainty on PGS robustness and risk stratification, we used a set of seven different PGSs²²—asthma, diabetes, pulmonary heart disease, height, thyroid cancer, breast cancer, and skin cancer—as published in the PGS Catalog²³ (partial R scores: 0.2284, 0.0824, 0.0397, 0.6133, 0.0295, 0.1132, and 0.1242, respectively). All of the scores were trained using 391,124 individuals from the UKBB²⁴ with Northern European ancestry. The PGSs were built for sites included in HapMap3 and that were in the LD reference used and estimated using LDPred2-auto.²⁵ All models included the following covariates: sex, age, birth date, deprivation index, and 16 PCs.

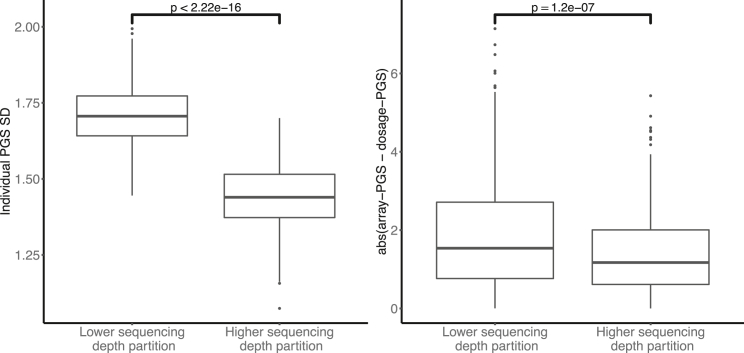
For the analysis presented in Figure 3, we split all the individuals into two equal-sized groups based on their off-target sequencing depth. We then used the effect sizes for the height PGS to obtain the dosage PGS, array PGS, and PGS distribution following the procedure described previously. For each individual in the cohort, we calculated the standard deviation of the PGS distribution obtained as well as the absolute value distance between the estimates of array PGS and dosage PGS. We compared these values across the two sequencing depth groups using a t test. We repeated the same analysis while restricting both array PGS and dosage PGS to be calculated using only the set of SNPs for which the lcWGS imputation score was above 0.4 or 0.7. Since changing the SNPs included in the PGS alters the population PGS distribution, the differences in error and standard deviation are not directly comparable. For this purpose we scaled the error and standard deviation by the matching array-PGS standard error, as marked on the y axis label.

Figure 3.

Sequencing depth impacts PGS distribution variability and PGS error

Individuals are split into two groups based on their individual sequencing depth. For each individual we obtain the PGS distribution standard deviation as well as the absolute value difference between the array PGS and dosage PGS values. The difference in sequencing depth translates into significant differences (t test p values marked) in the variability of the individual PGS distribution (left) and in the discrepancy between array PGS values and dosage PGS values (right).

For the calculation of the standard deviation of the PGS distribution for array imputation, we use the set of imputation probabilities obtained from the HRC imputation of the array results. We perform the same procedure as for the lcWGS PGS distribution while changing the imputation probabilities from which we draw the set of S = 1,000 genotypes.

We assessed the use of a probabilistic approach for PGS stratification as follows. Using the 90% dosage PGS value of the population as a threshold, we label all individuals with a higher dosage PGS as “above the threshold.” We then look to see whether that classification holds when also considering the PGS credible intervals. If the CI overlaps with the threshold, we label the individual as “uncertain above threshold,” while those who have their CI entirely above the 90% threshold are labeled “certain above threshold.” For each trait we calculate how many of the individuals initially labeled as “above the threshold” belong in each uncertainty group. We repeat the same process for individuals below the 90% threshold. We used the same procedure for the simulated set of effect sizes with different genetic architectures. For each combination of $P_{causal}$ and variance parameters, we calculated the percentage of individuals with high dosage PGS values reclassified as “uncertain above threshold.” We then performed a t test between the values obtained for different variance levels (not separated by $P_{causal}$) and separately for $P_{causal}$ (without separating by the variance level).

Finally, we investigated the impact of differential sequencing depth across individuals using a synthetic dataset as follows. We estimate the dosage PGS for all individuals across three sequencing depth levels: simulated 5× and 10× and the real unmodified lcWGS, as described previously. In each cohort, we separately set the mean dosage PGS to zero and adjust the distributions $\widetilde{PG{S}_{\mathrm{i}}}$ accordingly to avoid any biases caused by our simulation pipeline. In order to produce a mixed sequencing depth cohort, we randomly divided the individuals into three groups, so that each third has a different sequencing depth. We set t to be the 0.8 quantile of the dosage PGS values in the mixed cohort and calculated the individual probability $Pr\left(\stackrel{\sim }{PG{S}_i}>t\right)$ as the proportion of values in the distribution $\widetilde{PG{S}_{\mathrm{i}}}$ that exceed it. As a last step, for n values varying between 0 and 160 (20% of the cohort), we selected the top n ranking individuals according to $Pr\left(\stackrel{\sim }{PG{S}_i}>t\right)$ and separately according to their dosage PGS. We then calculated the percentage of individuals in each group having their array PGS in the top two deciles of the population array PGSs. We repeat the experiment 20 times, randomly changing the assignment of individual to sequencing depth levels and report the mean percentage of true high risk based on their array PGS and its standard error. When there was a tie in scores, we select all individuals who have equal scores and calculate the proportion of the entire group with a high array-PGS value, reflecting the expected accuracy we would obtain if we selected exactly n individuals out of this group. For Figure S7, for each value of n between 0 and 160, we also obtain the sequencing depth of all individuals selected as part of the top n ranking individuals in the thyroid cancer experiment. We further record the randomly assigned sequencing depth of all individuals with an array PGS in the top deciles and their $Pr\left(\stackrel{\sim }{PG{S}_i}>t\right)$ values.

Simulations investigating combined effect size uncertainty and genotype uncertainty

In the following set of simulations, we first randomly sampled genotypes to a set of causal SNPs of size M_c. We then simulated casual effect values for these M_c SNPs according to the prior ${\beta }_m\sim N\left(0,\frac{h^2}{M_c·2{\theta }_m\left(1-{\theta }_m\right)}\right)$, where ${\theta }_m$ is minor allele frequency of SNP m, with h² = 0.1. This prior matches the previous set of simulations with average equal SNP heritability. Following previous work^14,26 and the derivation provided in the supplemental methods, the GWAS marginal effects are distributed as ${\hat{\beta }}_m|{\beta }_m\sim N\left(\beta ,\frac{1-\frac{h^2}{M_c}}{N_{GWAS}·2{\theta }_m\left(1-{\theta }_m\right)}\right)$ where N_GWAS is the GWAS sample size, and the posterior distribution of ${\beta }_m$ is ${\beta }_m|{\hat{\beta }}_m\sim N\left(\frac{{{\sigma }_p}^2}{{{\sigma }_p}^2+{{\sigma }_l}^2}·\hat{\beta },\frac{{{\sigma }_p}^2{{\sigma }_l}^2}{{{\sigma }_p}^2+{{\sigma }_l}^2}\right)$, where ${{\sigma }_p}^2=\frac{h^2}{M_c·2{\theta }_m\left(1-{\theta }_m\right)}$ and ${{\sigma }_l}^2=\frac{1-\frac{h^2}{M_c}}{N_{GWAS}·2{\theta }_m\left(1-{\theta }_m\right)}$. We set M_c = 1,000 and N_GWAS = 200,000, and draw N = 1,000 samples from $\beta |\hat{\beta }$ marked as $\tilde{\beta }$. We also obtained N samples from the genotype distribution: $\tilde{x}$. We then calculate three different sets of N PGS values, to get three different $\widetilde{PG{S}_{\mathrm{i}}}$ types:

• (1)$\tilde{x}\hat{\beta }$, accounting only for the uncertainty in the genotype
• (2)$\hat{x}\tilde{\beta }$, with $\hat{x}$ standing for the lcWGS dosage values, accounting only for the uncertainty in effect sizes
• (3)$\tilde{x}\tilde{\beta }$, accounting for both uncertainty types

After obtaining the three distributions of PGSs, we calculated the credible intervals and the empirical coverage for each of the distributions, following the procedure described previously. We repeated the same procedure for different N_GWAS values ranging between 100,000 and 500,000.

For estimating the effects of the different uncertainty sources onto PGS risk stratification, we split individuals into four risk groups based on their dosage PGS and the overlap between their PGS CI and the risk threshold (90% of the population’s dosage PGS). Individuals who have their dosage PGS above the threshold were labeled as “certainly above” or “uncertainly above” the threshold, if their CI didn't or did overlap with the threshold (respectively). The same classification was done for “certainly below” and “uncertainly below” the threshold. We created a confusion matrix demonstrating the change in classification when adding the genotype-based uncertainty into PGS CI calculated based on effect-size uncertainty only.

Results

Overview

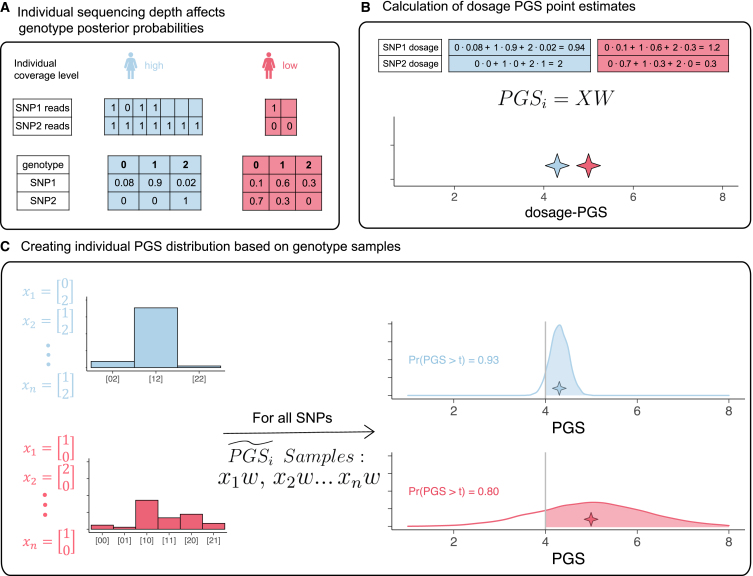
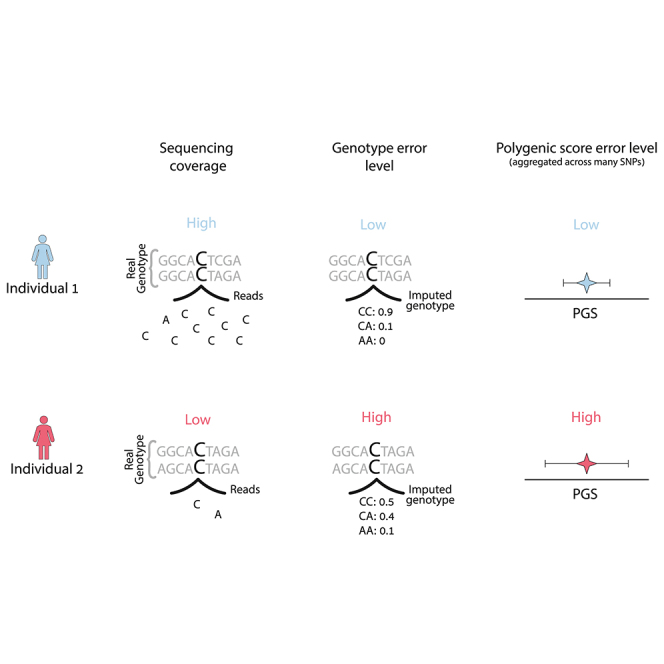
PGS can be viewed as an estimate of the individual genetic value GV_i = $X_i^t\beta$, where X_i is the vector of the true genotype values of individual i and $\beta$ is the vector of causal effect sizes. Thus, a PGS can be described as $PG{S}_i={\widehat{GV}}_i=\widehat{X_i^t\beta }$. For most of this work, we focus on uncertainty in PGSs conditional on a fixed set of PGS weights (W) and focus on errors in $\hat{X}$ and how they impact PGS estimation and downstream analyses. $\hat{X}$ is estimated either from array genotyping plus imputation or from sequencing data with or without imputation. Errors in genotyping calls are affected by many factors such as sequencing depth and/or minor allele frequencies (Figure 1A) and can vary across individuals and across experiments. We evaluate the consistency between PGSs calculated based on the expected allele count (dosage PGS) and PGSs calculated based on array genotypes (array PGS) and its connection to the sequencing depth by which the genotypes are obtained (see subjects and methods). As a motivating example, consider a situation where PGSs are used to identify high-risk individuals if their PGS is above the population’s 90% PGS value. The standard approach ignores genotyping error and uses the PGS point estimate for classification. Consider the situation of two individuals, 1 and 2 (colored red and blue, respectively, in Figure 1), where the PGS point estimate of 1 is much higher than 2. Also consider that individual 2 is sequenced at high coverage and thus has a low rate of genotyping error whereas individual 1 is sequenced at low coverage and thus has a higher level of genotyping errors. Differential coverage induces differential confidence in the PGS estimate, leading to higher uncertainty (error) for the PGS of individual 1 versus 2 (Figure 1). However, this larger uncertainty in the PGS of individual 1 can also imply that the probability of the true PGS of individual 1 to be over the risk threshold is actually smaller than for individual 2 (since the probability depends both on the point PGS and its uncertainty, see Figure 1C). This exemplifies the need for considering both the PGS point estimate as well as its uncertainty for PGS-based classifications, particularly in situations when variability in genotyping error across individuals is present in the data.

Figure 1.

Differential WGS coverage induces differential uncertainty in PGS estimation

(A) High-coverage sequencing includes more reads for each SNP, yielding a genotype distribution that is more certain compared to that of low-coverage sequencing, when only a few if any reads are available.

(B) Calculating dosage PGS point estimates based on the expected genotype of each individual, combined with PGS weights, W. Individual 1 (red) has a higher dosage PGS compared to individual 2 (blue).

(C) Illustration of the method to create individual PGS distributions; the possible genotypes are sampled, and we obtain a distribution of PGSs instead of one estimate for each individual. When considering the individual PGS distribution, it is revealed that individual 1 has a lower probability to have a PGS exceeding the threshold of interest.

Method calibration

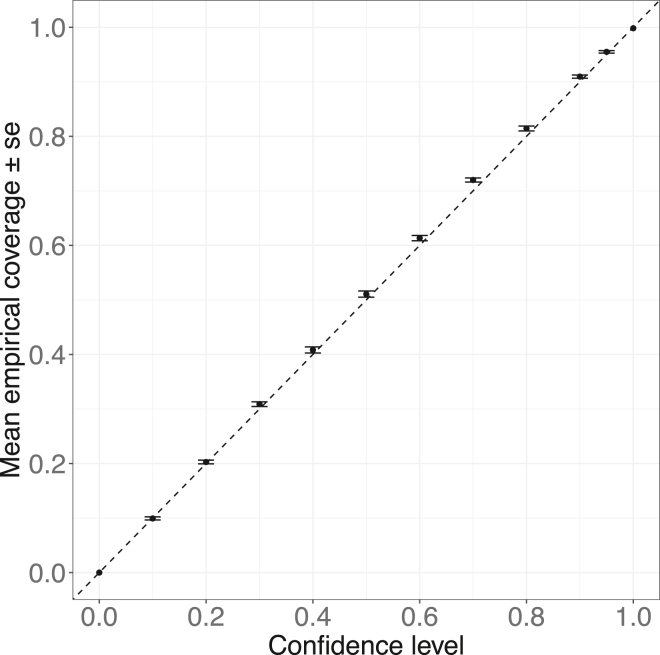
We propose a probabilistic sampling technique to generate the distribution of individual PGS values, $\widetilde{PG{S}_{\mathrm{i}}}$, build individual PGS credible intervals (CIs), and quantify the level of variance in PGS_i due to genotyping uncertainty (Figure 1, see subjects and methods). It is critical to calibrate any probabilistic approach to estimate PGS_i credible intervals. A method is calibrated when the probability of the individual’s estimated value (in this case, the genetic value, GV) to fall within the ranges of their CI matches the nominal credible value of the CI. We build CI for $\widetilde{PG{S}_{\mathrm{i}}}$ by combining real genotype data from the PROFILE cohort with simulated effect sizes under varying levels of variance parameters $\left(\widetilde{h^2}\right)$ and proportion of causal SNPs (P_causal, see subjects and methods). Next, using the matching array PGS values, we calculate the empirical coverage—the proportion of individuals whose array PGS falls within the credible intervals (substituting array PGS as the closest approximation for GV). We found that for different credibility levels and genetic parameters, the expected empirical coverage is calibrated with the observed empirical coverage (Figure S1). For example, at $\widetilde{h^2}=0.25$ and P_causal = 0.01 (Figure 2), at a credible level of 90%, the mean empirical coverage was 0.91 with a standard error of 0.003. Similarly, for a credible level of 95%, we observed an average empirical coverage of 0.95 with a standard error of 0.002. We further validated that under a model where the effect sizes are drawn dependent on the SNP minor allele frequency, the calibration remains intact (Figure S2, see subjects and methods). It is important to note that as the method samples variants independently, the presence of strong LD between variants in the PGS may create overly dispersed PGS posterior distribution, leading to an over calibration (Figure S3).

Figure 2.

Individual PGS distributions and CIs obtained from real lcWGS data are well calibrated with respect to their matching array PGS values

Individual PGS distribution and credible intervals are well calibrated with array PGS, when using real lcWGS and simulated PGS. The empirical coverage for a certain confidence level is calculated as the proportion of individuals having their array PGS within the boundaries of their PGS credible interval matching the credibility level of interest. The error bars represent one standard error of the mean empirical coverage calculated across 10 simulations. The results in this plot match an effect size configuration of $\widetilde{h^2}=0.25$ and P_causal = 0.01.

Sequencing depth impacts PGS uncertainty

Next, we investigated the effect of sequencing depth on the uncertainty of $\widetilde{PG{S}_{\mathrm{i}}}$ as measured by the standard deviation of the distribution of the individual PGS values. We split individuals into two equal-sized groups stratified by their sequencing depth levels (subjects and methods). Using height as an example trait, we calculated the values of array PGS and dosage PGS for each individual, as well as their $\widetilde{PG{S}_{\mathrm{i}}}$ distribution. We compared the $\widetilde{PG{S}_{\mathrm{i}}}$ distribution between the two sequencing depth groups. We found that higher levels of sequencing depth result in lower individual standard deviation in $\widetilde{PG{S}_{\mathrm{i}}}$ (Figure 3); the low sequencing depth group had a mean PGS standard deviation of 1.7 compared with 1.4 for the high sequencing depth group (t test p value < 2.5 × 10⁻¹⁶). For comparison, we also calculated the standard deviation of a PGS distribution built following the same procedure, using the array imputation probabilities (see subjects and methods). Matching our expectation about lower genotype uncertainties in array-based genotyping information, we found the mean standard deviation for height to be 0.3.

We further explored the relationship between individual sequencing depth levels and the error in dosage PGS estimation compared to the array PGS result. We found the discrepancy between array PGS and dosage-PGS increases with decreasing sequencing depth. The higher sequencing depth group had an average absolute value difference between array PGS and dosage PGS of 1.4, compared to an average difference of 1.89 in the lower sequencing depth group (t test p value = 1.2 × 10⁻⁷, Figure 3). These results demonstrate that the sequencing depth is an important variable even for small-scale coverage differences; even in data originating from similar pipelines and with very similar coverage levels, there is enough variability in sequencing quality to cause biases and differences in the levels of PGS uncertainty.

Finally, we wanted to investigate whether these trends remain when restricting to high-quality imputed SNPs. For this purpose, we assessed height PGS restricting to SNPs with INFO scores above 0.4 and 0.7. Both the individual PGS standard deviation and the error in dosage PGS compared to array PGS were found to be significantly different between the two sequencing depth levels (Figure S4). This demonstrates that restricting to higher-quality SNPs does not fully alleviate differences in variability occurring by individual differences in coverage.

Individual PGS uncertainty affecting risk stratification in real traits

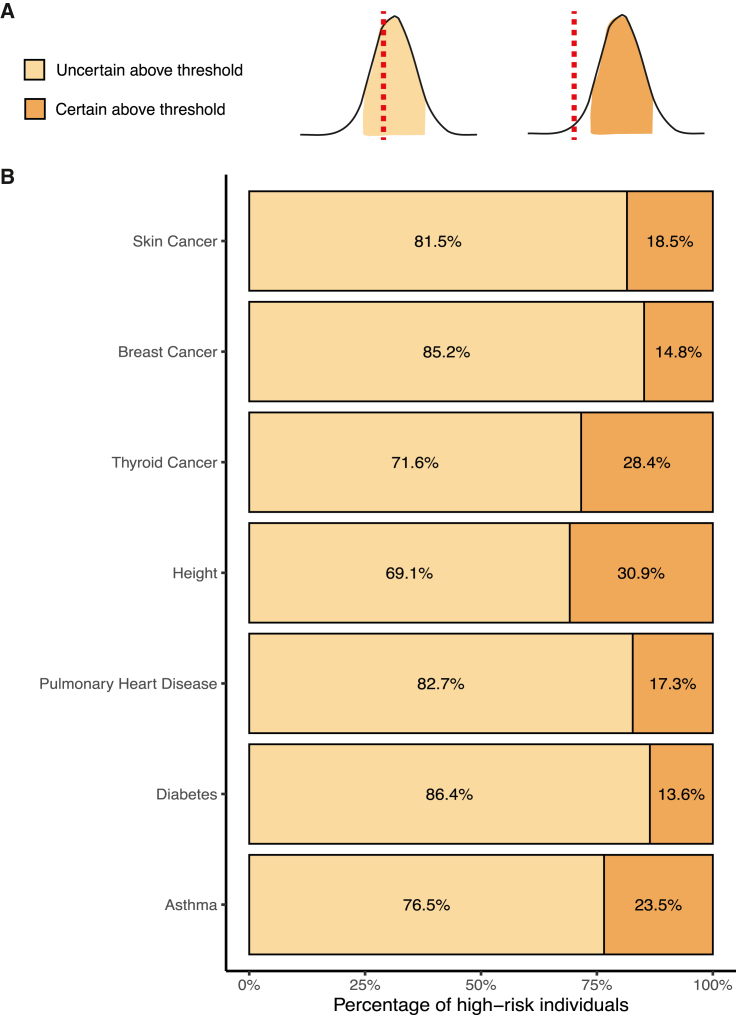
Next we investigate the effect of genotype-based PGS uncertainty on PGS-based stratification using real PGSs and traits (asthma, diabetes, pulmonary heart disease, height, thyroid cancer, breast cancer, and skin cancer; see subjects and methods).²³ All the PGSs were estimated with LDPred2-auto, using ∼390K European samples.^22,25 We stratified individuals into high-risk and low-risk groups assigned depending on whether their dosage PGS was above or below a threshold of the 90% quantile of the cohort’s dosage PGS distribution. Next, we calculated the PGS distribution for each individual and asked whether their 90% CI overlaps with the 90% threshold of the population. Individuals who had their dosage PGS above the 90% threshold and their CI did not cover it were classified as “certain above threshold.” Those who had their CI overlap with the threshold were classified as “uncertain above threshold.” We found that on average, only 20.4% (SD 6.9) of the individuals classified as “above threshold” were also classified as “certain above threshold” (Figures 4B and S5). The percentage of individuals in the “certain above threshold” category varies across traits. For example, in height, almost 31% of the individuals classified as high risk were defined as “certain above threshold” versus 14% in diabetes.

Figure 4.

lcWGS genotype uncertainty influences PGS-based risk stratification in real data

Individuals are defined as high risk for seven real PGSs if their dosage PGS value is in the top decile of the cohort’s dosage PGS values. All high-risk individuals are further classified into risk groups based on their PGS CI. Individuals who have their PGS CI overlap with the dosage PGS 90% threshold are labeled as “uncertain above threshold” (light orange), in contrast to individuals whose entire PGS CI is above the threshold, labeled as “certain above threshold” (dark orange). On average only 20% of individuals classified as high risk are also classified as “certain above threshold.”

Due to these differences, we investigated how the re-classification of high-risk individuals changes between different genetic architectures. For this purpose, we utilized the set of simulated effect sizes previously used for validation of the method’s calibration (see subjects and methods). We found that in our simulations, phenotypes with a higher variance parameter ($\widetilde{h^2}$ = 0.5) have a higher percentage of individuals reclassified as “uncertain above threshold” compared to those with lower variance parameters ($\widetilde{h^2}$ = 0.1 or 0.25). We did not detect any significant changes between simulations with different proportions of causal SNPs (Figure S6). It is important to note that a few different factors have a combined effect on the proportion of individuals classified as “uncertain above threshold.” For example, in the edge case where the genotype uncertainty of the causal SNPs is negligible, even if the heritability is high, the PGS CIs are expected to be narrow and the proportion of “uncertain above threshold” individuals is expected to be low. This demonstrates how there is no one genetic architecture factor that drives these differences alone. Ultimately, the extent of genotype error at the exact PGS sites, combined with the magnitude of their effect sizes, will determine how much genotype uncertainty will be propagated to PGS error and its impact on risk stratification.

Probability based risk stratification can improve precision in the presence of high variability in sequencing depth

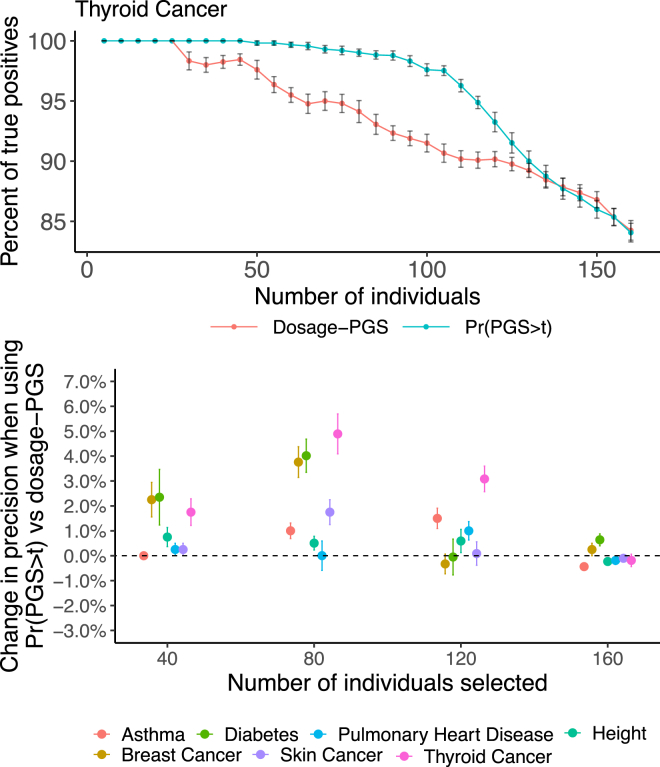
Next, we hypothesized that incorporating PGS uncertainty in stratification could improve classification accuracy in cohorts combining individuals with varying levels of sequencing depth. We split the individuals into three groups: the first group kept their original, unaltered sequencing and coverage. The second and third groups were assigned imputation probabilities representing genotypes under sequencing depths of 5× and 10× (simulated based on their matching array genotypes, see subjects and methods). Using a PGS for the seven example traits used previously, we applied our method to create the individual PGS distributions, $\widetilde{PG{S}_{\mathrm{i}}}$, for all cohort individuals. We perform risk stratification using $Pr\left(\stackrel{\sim }{PG{S}_i}>t\right)$, the area under the individual PGS distribution curve that lies above a set population risk threshold, t (see subjects and methods). We ranked all individuals by two methods: first, based on their dosage PGS and second by their $Pr\left(\stackrel{\sim }{PG{S}_i}>t\right)$, with t set to be equal to the 80% quantile of dosage PGS scores. Using the two approaches, we obtained two sets of the n highest ranking individuals and confirmed how many of them had their matching array PGS value in the top two deciles of the population array PGS values. We find differential improvements across traits, with highest boost in performance being observed for thyroid cancer, where there is a 5.8% improvement in precision when choosing the 100 individuals with highest risk (Figure 5). Importantly, for no traits do we observe a decrease in performance when using $Pr\left(\stackrel{\sim }{PG{S}_i}>t\right)$ versus the traditional approach that uses PGS point estimates.

Figure 5.

Using $Pr\left(\stackrel{\sim }{PG{S}_i}>t\right)$ for risk stratification can improve the rates of high array PGS individuals in a simulated mixed sequencing depth cohort

Risk stratification based on $Pr\left(\stackrel{\mathit{\sim }}{\mathit{P}\mathit{G}{\mathit{S}}_{\mathit{i}}}\mathit{>}\mathit{t}\right)$ yields a higher rate of high array PGS individuals compared with risk stratification based on dosage PGS. In this experiment, we take individuals with the highest scores by $Pr\left(\stackrel{\sim }{PG{S}_i}>t\right)$ and by dosage PGS and calculate the proportion of individuals with an array PGS value in the top two deciles. We changed the number of individuals inspected from 0 to 160 (20% of the entire cohort) and found we select slightly more individuals with high array PGS by using the $Pr\left(\stackrel{\sim }{PG{S}_i}>t\right)$ metric. Error bars represend one standard error of the mean percent of true positives and change in precision.

It is interesting to note that in this simulation setting, when selecting the top-ranking individuals by $Pr\left(\stackrel{\sim }{PG{S}_i}>t\right)$, individuals with higher sequencing depths tend to be prioritized over those with low sequencing depths (Figure S7). To further examine this, we calculated the average values of $Pr\left(\stackrel{\sim }{PG{S}_i}>t\right)$ of all individuals in the top two deciles by array PGS values and stratified by their sequencing depth levels. It is important to note we randomize the split of individuals into sequencing depths in each iteration, so the high-array PGS individuals are split equally between the three sequencing depth groups. We found that for the higher sequencing depth groups, the $Pr\left(\stackrel{\sim }{PG{S}_i}>t\right)$ values are significantly higher. This demonstrates two effects of sequencing depth discussed previously. First, higher sequencing depth reduces the error between dosage PGS and array PGS values. Second, higher sequencing depth reduces the PGS standard deviation, allowing individuals to score higher $Pr\left(\stackrel{\sim }{PG{S}_i}>t\right)$ values.

Finally, we examined probabilistic vs. dosage PRS stratification using the real data that is more homogeneous at low coverage. In contrast to the results of improved performance of the probabilistic method in the mixed sequencing depth cohort, we observed no difference between the method’s performance in the real homogeneous data (Figure S8). We believe this is due to the fact that the difference between the PGS standard deviation of the individuals is not strong enough to create differential rankings between the two methods. To further clarify this, we evaluated the extent of variance in PGS standard deviation across individuals in the real data and in the mixed sequencing depths cohort. In the real data, the variance of PGS standard deviation was 0.027, compared with 0.204 (SE 0.0012 across 10 iterations) for the mixed sequencing depths cohort. These results demonstrate that differential ranking based on the probabilistic method is likely to occur only in a cohort where individuals carry strong differences in genotype accuracies.

Combining effect size uncertainty with genotype uncertainty in simulations

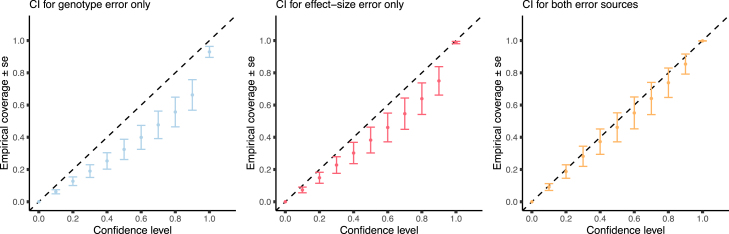
Thus far we focused on genotyping error conditional on fixed sets of PGS weights. Next, we investigated the joint impact of genotype and effect size based uncertainty. Using simulations (see subjects and methods) we find that integrating only genotype uncertainty or effect size uncertainty fails to generate calibrated credible intervals when data contain both types of uncertainty (Figure 6). For example, the observed empirical coverage for a 90% credible level of integrating genotype uncertainty only is 0.66 (SE 0.094) and that of integrating effect size uncertainty only is 0.749 (SE 0.088). In contrast, the 90% credible interval of integrating the uncertainty from both sources is well calibrated (0.854 SE 0.06). This demonstrates that when using lcWGS data, it is not sufficient to build CIs based on effect size uncertainty on its own. The extent of calibration obtained by CIs built on one type of error depends on the magnitude of error they contribute to the overall error. For example, using lower sequencing depth will increase the genotype error, making the version controlling for effect size only less calibrated. By contrast, lower GWAS sample size will increase the effect size error, making the version controlling for genotype error only less calibrated. In order to further explore this, we repeated the experiment for different magnitudes of effect size error as controlled by the simulated GWAS sample size. We found that when the effect size error is lower, the CI for genotype error only performs relatively well and the CI for effect size only performs worse (Figure S9).

Figure 6.

Combining different sources of uncertainty affects PGS CI calibration

We relax the assumption about PGS effect sizes being fixed and allow for error in effect size estimates. We evaluate the empirical coverage of PGS distributions calculated in three different manners: (left) including genotype uncertainty but not effect-size uncertainty, (middle) including only effect-size uncertainty while using dosages without accounting for genotype uncertainty, and (right) based on the posterior distribution of both effect size and genotypes. All plots show one standard error of the mean empirical coverage across 10 independent simulations. We find that when effect sizes are not fixed, both components must be accounted for in order to achieve proper calibration and estimation of accurate individual PGS CI.

Finally, we investigated the extent to which risk stratification is changed by accounting for different types of uncertainty. For this matter, we followed the procedure described previously to classify the individuals into four different risk groups compared to the threshold matching the 90% PGS value of the population—certainly below, uncertainly below, uncertainly above, and certainly above the threshold. We performed this classification using CI from two different sets of $\widetilde{PG{S}_{\mathrm{i}}}$ distributions—first accounting only for effect size uncertainty and the second including both effect size and genotype uncertainty. We repeated this procedure for 10 different simulation sets of effect sizes and obtained the mean and standard error of the number of individuals in each classification category (Table S1). We found that 69% of the classifications to the “certain above” category in the effect-size uncertainty only setting were re-classified as “uncertain above” when also incorporating the genotype uncertainty. Similarly, 39.5% of those classifications to the “certain below” threshold by the effect-size uncertainty CI were reclassified as “uncertain below” when also including the genotype uncertainty. These results further demonstrate that the procedure for accounting for PGS uncertainty in lcWGS data is incomplete without accounting for genotype error.

Discussion

In this work, we investigate the effect of sequencing error on PGS estimation. We propose a method to quantify the individual level of genotype-based uncertainty in PGSs calculated on low coverage WGS data, and to build individual PGS distributions and credible intervals. We further explore the connection between sequencing depth and the individual levels of PGS uncertainty and PGS error. We find that individuals with lower sequencing depth have higher PGS uncertainty/error, thus highlighting the importance of integrating genotype error in PGS-based risk stratification. We propose a probabilistic approach to risk stratification and show that it improves classification accuracy in simulations and real data. We find that due to differences in genotyping error levels, the comparison of PGSs across individuals may be problematic when not corrected by using individual PGS CIs.

The main limitation of the proposed method is the fact it does not account for LD between PGS variants. In case of strong LD between the variants of the PGS, there may be an over-calibration. We note however, that the LD simulation presents an extremely strong structure that is unlikely to represent true PGSs, which are commonly even intentionally pruned to remove correlated SNPs. It is of note that when combining both sources of error—genotype and effect size—we observe an over calibration in small GWAS sample sizes and a slight under calibration for large sample sizes. This could be due to the miscalibration introduced by unaccounted LD being amplified by varying levels of effect size uncertainty observed for different GWAS sample sizes. A possible direction to improve this would be to sample genotypes in haplotype groups, and we leave this as a direction for future research. We did not fully explore the impact of different genetic architectures on the individual PGS uncertainty. In our study, we assume the heritability is equal for all SNPs, leading to larger effect sizes and errors for rare variants. As the rare variants are also likely to have higher genotype error, this assumption amplifies the contribution of rare variants to the total individual PGS uncertainty. We leave the investigation of alternative genetic architectures, assuming a different relationship between allele frequency and effect sizes, such as LDAK,²⁷ for future work.

We note that we were unable to validate our framework for probabilistic PGS risk stratification in real data, due to lack of proper case/control data and the fact that all our individuals are sequenced in similar sequencing depths. We conclude with several caveats and directions for future research. First, we use the array PGS instead of the true genetic value for calibration and benchmarking which can yield extra uncertainties due to unaccounted error and biases existing in array PGSs. While we found the extent of PGS genotype uncertainty in array imputed data to be low, we note that as GWAS sample sizes increase, more rare variants are introduced into PGSs, possibly resulting in increased uncertainty even in imputed array data. Second, we focus on assessing PGS uncertainty due to genotype error conditional on a fixed set of PGS weights; we do that to match most practical uses of PGS where weights are pre-determined from a reference catalog. In practice, errors in the PGS weights also propagate into PGS uncertainties, thus further increasing the credible intervals of PGS predictions. Third, our simulation pipeline for different coverage levels is based on a simplistic likelihood imputation process, without accounting for either minor allele frequencies or LD structures. While the trends match real data, we leave a thorough investigation of uncertainty of imputation-based genotype calling from WGS data for future work.

Published: July 24, 2023

Data availability

The PGS used in the paper are available in the PGS catalog: https://www.pgscatalog.org/. The individual-level sequencing and imputation data cannot be made publicly available because the research participant consent does not include authorization to share identifiable data.