Temporal control by cofactors prevents kinetic trapping in retroviral Gag lattice assembly

Abstract

For retroviruses like HIV to proliferate, they must form virions shaped by the self-assembly of Gag polyproteins into a rigid lattice. This immature Gag lattice has been structurally characterized and reconstituted in vitro, revealing the sensitivity of lattice assembly to multiple cofactors. Due to this sensitivity, the energetic criterion for forming stable lattices is unknown, as are their corresponding rates. Here, we use a reaction-diffusion model designed from the cryo-ET structure of the immature Gag lattice to map a phase diagram of assembly outcomes controlled by experimentally constrained rates and free energies, over experimentally relevant timescales. We find that productive assembly of complete lattices in bulk solution is extraordinarily difficult due to the large size of this ∼3700 monomer complex. Multiple Gag lattices nucleate before growth can complete, resulting in loss of free monomers and frequent kinetic trapping. We therefore derive a time-dependent protocol to titrate or “activate” the Gag monomers slowly within the solution volume, mimicking the biological roles of cofactors. This general strategy works remarkably well, yielding productive growth of self-assembled lattices for multiple interaction strengths and binding rates. By comparing to the in vitro assembly kinetics, we can estimate bounds on rates of Gag binding to Gag and the cellular cofactor IP6. Our results show that Gag binding to IP6 can provide the additional time delay necessary to support smooth growth of the immature lattice with relatively fast assembly kinetics, mostly avoiding kinetic traps. Our work provides a foundation for predicting and disrupting formation of the immature Gag lattice via targeting specific protein-protein binding interactions.

Significance

Self-assembly of the HIV virion within cells is controlled by interactions of the viral Gag protein with cofactors such as RNA. The kinetics of this assembly must be tuned to prevent formation of incomplete and unproductive Gag lattices. Our work here combines theory, simulations, and experimental kinetic data to build a predictive model of how activation of the Gag proteins by interactions with cofactors can ensure robust, productive assembly. We provide theoretical guidelines that can be used to both extract key kinetic parameters from bulk experimental studies, and to design experimentally testable conditions to enhance or inhibit self-assembly. These results thus provide a quantitative model for characterizing how cofactor binding can control the kinetics of viral assembly.

Introduction

All retroviruses, including HIV, must form new virions that can bud out of the plasma membrane of the infected host cell (1). These virions are comprised of the retroviral polyprotein Gag, genomic RNA, and additional cofactors (1). Gag is the primary structural component of the virions, initially assembling an immature lattice that is bound to the membrane and forms a trihexagonal organization as revealed by cryoelectron tomography (cryo-ET) (2,3). Once the virion has budded, the Gag polyprotein is cleaved by its attached proteases (4) and reassembles into the mature viral capsid (5). The stability of the immature Gag lattice appears tuned to ensure successful assembly while also ensuring the remodeling necessary to transform from the immature lattice to the infectious mature capsid (6,7). Indeed, maturation inhibitors are a promising strategy for antiviral drugs that function by overstabilizing the immature lattice (7,8,9). Assembly of the immature lattice can be reconstituted in vitro (10,11), but because the immature lattice does not assemble from the Gag monomers alone (10), it is not known how the energetics and cooperativity of Gag-Gag contacts, Gag contacts with cofactors, or their timescales of binding drive stable lattice formation. Here, we develop a coarse-grained model of Gag assembly to quantify assembly pathways as a function of Gag-Gag binding rates and stability, ultimately designing time-dependent protocols that allow us to robustly assemble immature lattices with varying kinetics. These models on their own and with comparison to in vitro kinetics (11) predict how time-dependent control of cofactor binding can induce (or disrupt) stable assembly of the immature Gag lattice.

A primary challenge in understanding and predicting the assembly of the immature Gag lattice is its dependence and sensitivity to a range of cofactors. The minimal conditions to assemble the virus-like lattice in solution in vitro requires Gag along with at least one negatively charged molecule such as RNA or the cellular small molecule inositol hexakisphosphate (IP6) (12,13,14). Gag does form stable dimers on its own, which are further strengthened with cofactors present (15). Thus, it is the formation of the higher-order contacts in the immature lattice that must be distinctly “switched on” by interactions with cofactors, at least in part by inducing conformational changes into the Gag proteins (10). Combining RNA and IP6 together works synergistically to promote and accelerate immature Gag lattice assembly, indicating that they have somewhat complementary roles in stabilizing the lattice (11). With just RNA or just IP6, assembly takes ∼1–2 h at 50 μM Gag, whereas with both, it can proceed in seconds (11). Indeed, IP6 promotes formation of infectious Gag virions in vivo by stabilizing the immature lattice (6). IP6 coordinates with the hexamer contacts in the Gag lattice in a 1:6 stoichiometry, stabilizing Gag into an assembly-competent form for the immature Gag lattice (15). The immature Gag lattice also contains another set of interfaces that form a trimeric cycle that can provide additional stability when brought together via the dimer and hexamer assembly, although it is likely that these smaller interfaces are relatively weak (16). Through our computational models, we can reach the seconds to minutes timescales of cofactor-mediated assembly, where we observe robust growth and a high yield of virions forms if large enough concentrations of RNA and IP6 are present (11). We can thus directly test how the relative strengths and speeds of the different Gag-Gag interactions control lattice assembly.

Another challenge with the immature Gag lattice is its size; a completed spherical lattice contains ∼4000 monomers, which is an order of magnitude higher than most computational models of self-assembly. There are two major issues that arise with this larger size. The first is simply that the models become more computationally expensive to characterize across varying parameters compared with completed assemblies that contain 12 (17,18), 60, or even 100s of subunits (19,20). For smaller systems, systems of rate equations can be constructed to efficiently characterize phase diagrams and assembly pathways as thermodynamic and kinetic parameters are varied (18). Spatial simulations using Brownian dynamics simulations can also be relatively efficient for characterizing assembly pathways in systems with ∼100s of subunits (19,21), but 1000s of subunits are rare (22). Nonspatial simulations of large HIV-like assemblies must limit the types of assembly pathways followed (23). The second major issue, however, is that with more subunits required to complete the assembly the rate of nucleating new lattice structures must be correspondingly slowed to allow elongation of existing nuclei to completion, where a “nuclei” can in principle be as small as a dimer (24). Otherwise, assemblies become kinetically trapped in intermediates that cannot readily combine to form larger structures as monomers are fully depleted or starved (25). The parameter regimes that can support assembly will be significantly compressed relative to assemblies with fewer subunits. Hence, the Gag lattice is intrinsically primed to be prone to kinetic traps due to its size.

Kinetic trapping, which can dramatically slow the formation of productive and complete equilibrium assemblies, sometimes beyond experimentally relevant timescales, is a consequence of the nonequilibrium nature of the self-assembly process. The initial conditions of unbound subunits can follow pathways to long-lived metastable intermediates despite the existence of a thermodynamically favorable steady state of complete structures. Thus, unlike the quasi-equilibrium classical nucleation theory (26), these intermediates can fail (at least temporarily) to complete stable growth after formation of a critical nucleus (a free energy maxima). We note here we do not extract a precise size of a critical nucleus given that we study multiple interaction free energies (which would have different critical nuclei), or demarcate a specific “nucleation” and “growth” phase that would exhibit distinct kinetics (27), but we do define a consistent practical cutoff of 18 monomers in nucleated structures for analysis (materials and methods).

For such a large lattice, how does HIV avoid kinetic traps? In vivo, we identify two main strategies that can help avoid kinetic traps and productively assemble virions by effectively controlling initial conditions. First, subunits do not appear in bulk in the cytoplasm but are produced at a rate that slowly increases their concentration in time and space (28). Second, as detailed above, cofactors can “activate” the Gag monomers such that lattices only nucleate and thus grow when they have bound RNA. Both these mechanisms introduce additional timescales that can reduce multiple nucleations and instead promote growth of nascent viruses. Theory and modeling have shown how, although kinetic traps for smaller assemblies can be reduced by optimizing energetic parameters to moderately weak strengths (19,25), similar strategies to those used by the cell that introduce new timescales can significantly improve yield. Cooperativity during growth that disfavors formation of nascent structures by modulating binding sites helps avoid traps (29), as can variable addition of monomers (30) and allosteric activation (31). In vitro studies of HIV-1 immature lattice assembly in solution showed how the stoichiometry of the cofactors relative to the Gag monomers tune the kinetics of lattice assembly, indicating that cofactor binding can act as a rate-limiting timescale in assembly (11). In our work here, we therefore use the theory of diffusion-influenced reactions (32,33,34) to derive a timescale that could effectively represent these same biologically relevant processes used to suppress trapping, by directly controlling the concentrations of monomers with time. Our simulation results illustrate how even this single additional timescale can effectively eliminate the trapped intermediates to promote successful assembly.

A key advantage of the structure-resolved reaction-diffusion modeling approach we use here is that the timescales and assembly yield are controlled by biochemically measurable rates and free energies, and thus the predicted timescales we define compare directly with experiments. Recently, coarse-grained models of the immature HIV lattice have shown how IP6 stabilizes lattice assembly and speeds up binding with more molecular details, in ways that may promote defects in the structures (35). These coarse-grained models built on earlier work characterizing the specificity of Gag contacts needed for proper assembly (36), and the role of RNA and membrane binding in stabilizing Gag assembly (37). These models successfully captured morphological variations in assembled structures and explicit cofactor interactions but are not able to map the kinetics of binding and assembly directly to experimental timescales, and the strength of protein-protein interactions can be similarly difficult to map to experimental K_D values. Our model is thus complementary, producing assembled structures that are similarly derived from experiment and built from the monomeric building blocks, while providing direct observations of tunable assembly kinetics over longer (minutes) timescales. We are thus able to estimate rates for Gag binding to the cofactor IP6 by comparison with the in vitro kinetic data (11), and set bounds on the rates of Gag-Gag binding interactions.

In this paper, we first describe the construction of our computational model of Gag self-assembly from cryo-ET structures and validate the kinetics and equilibrium of our simulations with comparisons to theory. We test a range of binding free energies and rate constants for the distinct Gag-Gag binding interactions of dimer, hexamer, and trimer contacts. We identify regimes where assembly could be eliminated, where a two-phase equilibrium of dilute monomers and partial assemblies formed, and where kinetic trapping onset. Kinetic trapping was predominant, with our structural analysis quantifying the frequent irregularity of the ensuing lattice growth. To mimic the time-dependent activation of Gag by cofactors, we used a titration rate to slowly increase the Gag concentration, finding that, when the rate was slow enough, we produced robust and regular lattice growth. We therefore derived a titration rate dependent on the underlying Gag assembly kinetics, showing that it is remarkably successful in promoting productive lattice assembly. Finally, we connected our model to in vitro light-scattering kinetics of Gag assembly driven by cofactors RNA and IP6. We were able to estimate bounds on binding rates between Gag and IP6 and Gag-Gag using relatively simple theoretical arguments and our derived titration rate. We conclude by discussing the future extensions and applications of this integrative modeling approach.

Materials and methods

Model construction

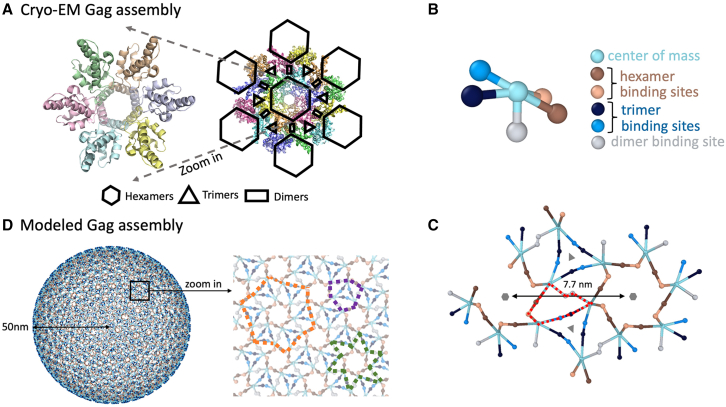
Our model consists of coarse-grained representations of Gag protein monomers derived from the cryo-ET structure (16) of the immature Gag lattice (Fig. 1 A). Each Gag is a rigid body with a center of mass point and five distinct binding sites (Fig. 1 B). The center-to-center distance between two hexamer substructures is 7.7 nm, the final sphere radius R = 50 nm, and the complete lattice contains ∼3700 Gag proteins. There are three types of binding interactions: the homo-dimer interaction, the hexamer interaction mediated by the two distinct hexamer sites, and the trimer interaction mediated by the two distinct trimer sites. All three contacts were identified and characterized in the experimental structural study (16), and here we identify the interfaces for each of these interactions using a 3.5 A cutoff between atoms in contact between two monomers (supporting methods). When two molecules bind via these specific interaction sites, they adopt a predefined orientation that ensures assembly into the experimental cryo-ET structure. To derive our model of Gag-Gag interactions from the cryo-ET structure, we must correct for the small variations of the 18 monomer positions within the lattice. Without corrections, our monomers would assemble spherical fragments with distinct curvatures and thus significant defects due to slight changes of orientations between hexamer, trimer, and dimer contacts. Thus, we symmetrized the Gag lattice to ensure a single curvature across all contacts. See supporting material for mathematical details.

Figure 1.

Coarse-grained model of Gag monomers and their binding interactions. (A) The cryo-ET immature Gag lattice from PDB: 5L93. On the left, six distinct Gag monomers form a hexameric ring with each Gag contacting its two neighbors. The right image includes 18 monomers demonstrating how the larger lattice assembles from hexagons through dimer contacts, with trimer contacts adding additional stabilizing interfaces. (B) Each coarse-grained Gag monomer has a center of mass site and five distinct interfaces that mediate the three types of interactions (materials and methods and supporting material). The hexamer and trimer interactions both involve a front-to-back contact (like actin polymerization) between distinct interfaces. (C) Geometry of the coarse-grained Gag monomers assembled into the lattice, showing all three types of interactions between 13 monomers. In addition to the stabilizing cycles of the hexamer and trimer, cycles are also formed involving all three types of interactions (red dashed lines). (D) The spherical Gag lattice was assembled from a population of monomers, requiring ∼3700 Gags to close. Some defects in the lattice are unavoidable as a rigid hexagonal lattice cannot perfectly tile a spherical surface. From the zoomed-in structure, extra cycles formed through any two interactions can be observed. The purple line follows dimer and hexamer interactions, the orange one trimer and hexamer interactions, the green one dimer and trimer interactions. To see this figure in color, go online.

A trihexagonal lattice cannot perfectly tile a spherical surface; a sphere requires pentagonal inclusions as well. However, since the hexagons are small relative to the size of the sphere, the defects that emerge due to some imperfectly aligned contacts are minimal. We allow imperfectly aligned proteins to still form bonds if they are within a cutoff distance $10\%$ longer than the binding radius $\sigma$. In this way, these contacts still contribute to stabilizing the lattice, which also mimics the inherent flexibility of molecules themselves that is not captured by the rigid orientations imposed here.

Reaction-diffusion simulations

All simulations are performed using the NERDSS (nonequilibrium reaction diffusion self-assembly simulator) software. NERDSS solves a particle-based and structure resolved reaction-diffusion model using the free-propagator reweighting algorithm (38). The method is derived from Smoluchowski’s model for reactive collisions between diffusing particles and has been rigorously tested to produce accurate binding kinetics and equilibria in 3D solution (39) and with the addition of rotational motion and assembly (40). The software and executable models are available open source at github.com/mjohn218/NERDSS, and all analysis described below is available as Python code at github.com/mjohn218/ioNERDSS.

We briefly outline here how the simulations work. Step 1 Initialization. Copies of molecules are placed randomly inside a rectangular box, followed by a steric overlap check for all reactive binding site pairs to ensure they are not at a distance less than the binding radius $\sigma$ for the reaction. Molecules that are titrated into the system (zeroth-order reaction) are also placed randomly within the box without steric overlap. Step 2 Reactions. Reaction and diffusion are treated separately, and one molecule can only participate in one of them within each time step. We evaluate reactions first by calculating the reaction probability of zeroth- (creation), first- (dissociation), and second-order (bimolecular) reactions. Dissociation reactions are modeled as Poisson processes, occurring with probability $p_{dissoc}\left(\Delta t\right)=1-\exp \left(-k_{\mathrm{b}}\Delta t\right)$, with intrinsic off-rate $k_{\mathrm{b}}$. All bimolecular reactions are reversible unless explicitly stated. The probability of bimolecular association events $p_{assoc}\left(\Delta t|r_0\right)$ within timestep $\Delta t$ depends on the initial separation $r_0$ of reactant sites A and B, microscopic association rate k_a, the total diffusion coefficient of reactants D_tot = D_A + D_B, and binding radius $\sigma$. The exact value is calculated from the Green’s function solution of Smoluchowski’s model, with reweighting applied due to the simple Brownian updates used for particle displacements (39). The binding probability is independent of the orientation of the two sites, it depends on only the separation. If an association reaction is accepted via comparison of the reaction probability with a uniform random number, the two molecules will be translated and rotated into the user-specified binding orientation. We reject association events between multiprotein complexes that result in steric overlap between protein monomers. We also reject association events that produce unphysically large rotational reorientations of complexes to “snap” them into the proper binding orientation. This is controlled by a scalar (scaleMaxDisplace) that multiplies the expected displacement due to translational and rotational diffusion to define a cutoff (see Table 1). Step 3 Propagation. If the molecules within a complex do not undergo a reaction, the rigid complex diffuses both translationally and rotationally along three orthogonal axes $x$, $y$, and $z$. Translational diffusion along any axis is simply a Brownian motion $x\left(t+\Delta t\right)=x\left(t\right)+\Delta x$, where the displacement $\Delta x$ follows a Gaussian distribution with mean zero and standard deviation $\sqrt{2D_t\Delta t}$. $D_t$ is the translational diffusion constant. Similarly, rotational diffusion characterizes molecular rotation around a specific global axis, $\theta \left(t+\Delta t\right)=\theta \left(t\right)+\Delta \theta$, where $\Delta \theta$ follows Gaussian distribution with mean zero and standard deviation $\sqrt{2D_r\Delta t}$. $D_r$ is the rotational diffusion constant. We define the diffusion coefficients of Gag monomers (Table 1) using the Einstein-Stokes equations, with $D_t$ = 10 nm²/μs and $D_r$ = 0.02 rad²/μs, which is true for a hydrodynamic radius of 20 nm at water viscosity. We also tested faster values implying a more compact radius at the same viscosity, or a monomer $D_t=$ 10 also mimics the smaller radius with the ∼3× decrease in viscosity occurring in the cytoplasm. Crowding in the cytoplasm can affect rate constants, but the effect is small when rates are not diffusion controlled, as is the case here (41). The diffusion coefficients of complexes slow as their size increases, consistent with the assumption that the hydrodynamic radius is additive (40).

Table 1.

Simulation, energetic and kinetic parameters for Gag interactions

	Parameter name	Description	Value
Simulation parameter	$\Delta t$	time step	$0.1,0.5\mu \mathrm{s}$
	box size	the size of the simulation system	${405}^3,{510}^3\mathrm{n}{\mathrm{m}}^3$
Diffusion coefficients	$D_t$	molecule’s translational diffusion constant	$10,50{\mu \mathrm{m}}^2/\mathrm{s}$
	$D_r$	molecule’s rotational diffusion constant	$0.01,0.02,0.05\mathrm{r}\mathrm{a}{\mathrm{d}}^2/\mu \mathrm{s}$
Binding parameters	dimeric $k_{\mathrm{a},\dim }$	3D microscopic association rate	$0.06,0.6,6{\mu \mathrm{M}}^{-1}{\mathrm{s}}^{-1}$
	hexameric $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}$		$0.006,0.06,0.6,6,12,60\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$
	trimeric $k_{\mathrm{a},\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}$		${0,6.02\times 10}^{-5}{\mu \mathrm{M}}^{-1}{\mathrm{s}}^{-1}$
	dimeric $k_{\mathrm{b},\dim }$	microscopic dissociation rate	$1{\mathrm{s}}^{-1}$
	hexameric $k_{\mathrm{b},\mathrm{h}\mathrm{e}\mathrm{x}}$		${10,20,100,10}^3{,{10}^4\mathrm{s}}^{-1}$
	trimeric $k_{\mathrm{b},\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}$		${1,1000\mathrm{s}}^{-1}$
	dimeric $\Delta G_{\dim }$	Gibbs free energy $\Delta G$	−11.0, −13.3, −15.6 $k_{\mathrm{B}}T$
	hexameric $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}$		−1.8, −4.1, −6.4, −8.7, −11.0, −13.3, −15.6 $k_{\mathrm{B}}T$
	trimeric $\Delta G_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}$		0, −4.1 $k_{\mathrm{B}}T$
	scaleMaxDisplace	association events that result in shifts of binding sites on either component larger than scaleMaxDisplace $\times \sqrt{6D_{tot}\Delta t}$ are rejecteda	$30$
Titration rate	$k_{\mathrm{c}}$	molecule creation (titration) rate	$0.06,0.3,1,60\mu \mathrm{M}/\mathrm{s}$

^a$D_{\mathrm{t}\mathrm{o}\mathrm{t}}$ captures effective diffusion coefficient due to translational and rotational diffusion.

Simulation conditions

We perform simulations in a rectangular volume with reflective boundary conditions at the walls. Our simulations all reach a final concentration of 50 μM of Gag monomers, consistent with experiments on immature Gag lattice assembly in solution (11). We use a box with volume ${405}^3\mathrm{n}{\mathrm{m}}^3$ that contains ∼2000 Gag proteins maximally, because it is computationally more efficient and still reports on the kinetic challenges to assembling large lattices. In mimicking activation by cofactors can ensure slow nucleation and fast growth of a single lattice we also use a larger volume of ${510}^3\mathrm{n}{\mathrm{m}}^3$ that contains ∼3700 Gag proteins and thus allows the formation of a complete spherical lattice. In addition to “bulk” simulations with all Gag monomers present at time zero, we also perform titration simulations where initially 10 monomers are present, and remaining proteins stochastically enter the system with rate $k_{\mathrm{c}}$ (see Table 1).

Energetic and kinetic parameters

All parameters used in simulations are listed in Table 1. The stability of the Gag dimerization contact is constrained by experiment (15), which found $\Delta G$ of −12 $k_{\mathrm{B}}T$ but additional stabilization occurred after cofactor interaction. However, other energetic and kinetic parameters are not known. We thus choose a biologically realistic range of rate (∼10⁻³–10² ${\mu \mathrm{M}}^{-1}{\mathrm{s}}^{-1}$) and free energy values, keeping the trimer contact weakest as indicated by previous work (16). The rates do not change throughout the simulations, meaning there is no explicit cooperativity or size dependence of binding (27). The stability or free energy $\Delta G$ of each pairwise interaction is determined by the binding ($k_{\mathrm{a}})$ and unbinding ($k_{\mathrm{b}})$ rates using standard relationships, $K_{\mathrm{D}}=\frac{k_{\mathrm{o}\mathrm{f}\mathrm{f}}}{k_{\mathrm{o}\mathrm{n}}}=\frac{k_{\mathrm{b}}}{k_{\mathrm{a}}}=c_0\exp \left(\frac{\Delta G}{k_{\mathrm{B}}T}\right)$ , where $c_0$ is the standard state 1 M, $\Delta G=G_{\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}}-G_{\mathrm{u}\mathrm{n}\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}}$ , and $k_{\mathrm{o}\mathrm{n}}$ is the corresponding macroscopic rate defined in 3D by

$$k_{\mathrm{o}\mathrm{n}}={\left(\frac{1}{k_a}+\frac{1}{4\pi \sigma D}\right)}^{-1}$$ (1)

(see, e.g., (39)). NERDSS allows for a free energy strain penalty upon formation of closed cycles, but here we apply no penalty. This means when two bonds form to close a cycle, the stability is the sum over the bond free energies.

Fitting of association kinetics to analytical theory

To quantify how the formation of higher-order contacts impacts the assembly kinetics, we analyzed the kinetics of pairwise bond formation of both dimers and hexamers. If the bonds formed independent of any lattice, their kinetics would match up with theory from rate equations, given that our components are initially well mixed and in 3D, which minimizes any spatial effects. These analytical solutions are known, and for completeness the kinetics of the monomer species $A\left(t\right)$ undergoing the reversible reaction A + A ⇌ C with rates $k_{\mathrm{o}\mathrm{n}}$ and $k_{\mathrm{o}\mathrm{f}\mathrm{f}}$ is given by:

$$\begin{array}{r}A\left(t\right)=\frac{1}{q_2}\left(\frac{{\lambda r}_1{e}^{r_{1}t}-r_2{e}^{r_{2}t}}{e^{r_{2}t}-\lambda e^{r_{1}t}}\right)\end{array}$$ (2)

where $r_{1/2}=\frac{q_1+/-\sqrt{q_1^2-4q_0{q}_2}}{2}$ , $\lambda =\frac{r_2+{A_{0}q}_2}{r_1+A_0{q}_2}$, $q_0=k_{\mathrm{o}\mathrm{f}\mathrm{f}}{A}_0$, $q_1=-k_{\mathrm{o}\mathrm{f}\mathrm{f}}$, $q_2={-2k}_{\mathrm{o}\mathrm{n}}$, and initially $A\left(t=0\right)=A_0$, $C\left(t=0\right)=0$. For distinct reactants, $q_1$ and $q_2$ change slightly (see, e.g., (42)).

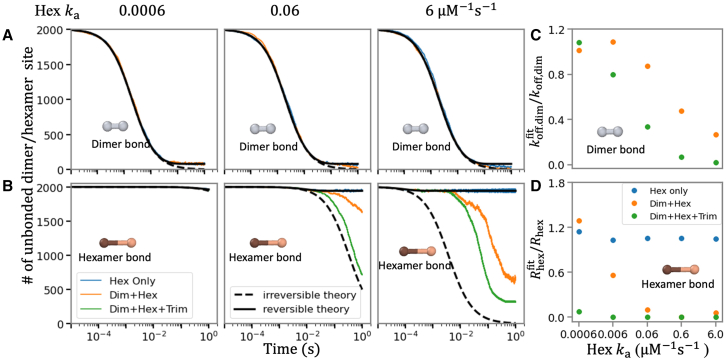
The effect of diffusion is captured in the macroscopic rate constant using Eq. 1. Given this equation, we can then fit our simulated data on bond formation (Fig. 2), where in the case of dimer association we treat only dissociation as a fit parameter, $k_{\mathrm{o}\mathrm{f}\mathrm{f},\dim }^{\mathrm{f}\mathrm{i}\mathrm{t}}$. For slow hexamer interactions, we recover $k_{\mathrm{o}\mathrm{f}\mathrm{f},\dim }^{\mathrm{f}\mathrm{i}\mathrm{t}}=k_{\mathrm{o}\mathrm{f}\mathrm{f},\dim }$, validating that the kinetics is correct as designed and dimer bonds form fully independently at short enough times. As hexamers start to form more quickly, or as trimers start to form, we see slowed dissociation of dimers, such that $k_{\mathrm{o}\mathrm{f}\mathrm{f},\dim }^{\mathrm{f}\mathrm{i}\mathrm{t}}<k_{\mathrm{o}\mathrm{f}\mathrm{f},\dim }$. We perform the same procedure for hexamer bond-forming kinetics, except that the sites are distinct (A + B ⇌ C). For the hexamers, both the association and dissociation kinetics are influenced by dimer contacts, and thus we must treat both $k_{\mathrm{o}\mathrm{f}\mathrm{f},\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{f}\mathrm{i}\mathrm{t}}$ and $k_{\mathrm{o}\mathrm{n},\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{f}\mathrm{i}\mathrm{t}}$ as fit parameters. We therefore then compare the ratio of these rates to their pairwise values, ${R_{\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{f}\mathrm{i}\mathrm{t}}=k}_{\mathrm{o}\mathrm{f}\mathrm{f},\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{f}\mathrm{i}\mathrm{t}}/k_{\mathrm{o}\mathrm{n},\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{f}\mathrm{i}\mathrm{t}}$ vs. $R_{\mathrm{h}\mathrm{e}\mathrm{x}}={\mathrm{K}}_{\mathrm{D},\mathrm{h}\mathrm{e}\mathrm{x}}\text{.}$ Without the dimer and trimer interactions turned on, $R_{\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{f}\mathrm{i}\mathrm{t}}=R_{\mathrm{h}\mathrm{e}\mathrm{x}}$ as expected, but as they are turned on, $R_{\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{f}\mathrm{i}\mathrm{t}}<R_{\mathrm{h}\mathrm{e}\mathrm{x}}$, due to both faster association and slower dissociation.

Figure 2.

Short-term kinetics of dimer and hexamer bond formation demonstrates when higher-order assembly causes deviations from theory of bimolecular association. (A) Short-time kinetics of dimer bond formation is not sensitive to formation of hexamer and trimer interactions. The theoretical kinetics of simple irreversible (A + A→B black dashed lines) and reversible (A + A ⇌ B solid black lines) association agrees with the simulations (orange and green lines), where $k_{\mathrm{a},\dim }=6.02\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathrm{b},\dim }=1{\mathrm{s}}^{-1}$. From left to right the hexamer rate is increasing, and the rightmost plot has the same association rate for both hexamers and dimers, but the hexamer bonds are very short-lived compared with the dimer bonds as $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4k_{\mathrm{B}}T$ and $\Delta G_{\dim }=-15.6k_{\mathrm{B}}T$. (B) The short-time kinetics of hexamer bond formation is dramatically shifted by the existence of dimer (orange) and dimer + trimer bonds (green) due to their stabilizing effect. With just hexamers forming (blue), the results match the reversible theory as expected. (C) Comparing the dimer dissociation rate $k_{\dim ,\mathrm{o}\mathrm{f}\mathrm{f}}$ with an effective rate that fits simulation data to theory, $k_{\dim ,\mathrm{o}\mathrm{f}\mathrm{f}}^{\mathrm{f}\mathrm{i}\mathrm{t}}$ (see materials and methods), quantifies how this ratio ($k_{\dim ,\mathrm{o}\mathrm{f}\mathrm{f}}^{\mathrm{f}\mathrm{i}\mathrm{t}}/k_{\dim ,\mathrm{o}\mathrm{f}\mathrm{f}}$ ) drops below 1 as the hexamer bonds start to form more quickly, slowing dimer dissociation. $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4k_{\mathrm{B}}T$ is constant for all simulations. (D) Comparing the pairwise hexamer stability with effective on and off rates fit to the data (see materials and methods) quantifies how $R_{\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{f}\mathrm{i}\mathrm{t}}/R_{\mathrm{h}\mathrm{e}\mathrm{x}}$ drops below 1 as dimer and trimer interactions stabilize growth $R_{\mathrm{h}\mathrm{e}\mathrm{x}}=\frac{k_{\mathrm{o}\mathrm{f}\mathrm{f},\mathrm{h}\mathrm{e}\mathrm{x}}}{k_{\mathrm{o}\mathrm{n},\mathrm{h}\mathrm{e}\mathrm{x}}}$. As expected, the ratio is 1 when only hexamer interactions are present (blue dots). With faster hexamer association rates, the ratio drops as dimer contacts form (orange dots) due to faster effective association and slower effective dissociation, with trimer contacts further helping (green dots) despite their relative weakness: $k_{\mathrm{a},\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}=6.02\times {10}^{-5}\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathrm{b},\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}=1{\mathrm{s}}^{-1}$, $\Delta G_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}=-4.1k_{\mathrm{B}}T\text{.}$ All simulations have $D_{\mathrm{t}}=10{\mu \mathrm{m}}^2{\mathrm{s}}^{-1},D_{\mathrm{r}\mathrm{o}\mathrm{t}}=0.01{\mathrm{r}\mathrm{a}\mathrm{d}}^2{\mathrm{s}}^{-1},\Delta t=0.1\mu \mathrm{s}$, boxlength = $405\mathrm{n}\mathrm{m}$. To see this figure in color, go online.

Analysis of structural regularity of assembled lattices via the regularization index

NERDSS records the sizes of complexes and the positions of molecules within them. To quantify how uniform and compact the growth of the Gag lattices were, we defined a regularization index (RI). The RI compares the surface coverage of an assembled Gag complex relative to the most compact version that contains the same number of monomers and thus has the same surface area. The most compact version is defined as growth of a spherical cap with the same radius, R = 50 nm. Thus, an ideal lattice that contains N_gag with SA_gag = 8.5 nm² covers a spherical cap defined by a polar angle ${\theta }_{\mathrm{c}\mathrm{a}\mathrm{p}}={\cos }^{-1}\left(1-\frac{N_{\mathrm{g}\mathrm{a}\mathrm{g}}{SA}_{\mathrm{g}\mathrm{a}\mathrm{g}}}{2\pi R^2}\right)$. To calculate the RI, we orient our Gag lattices to be centered relative to a polar angle of zero (centered according to their center of mass) and count what fraction of the Gag monomers are enclosed within the cap defined by the deflection angle ${\theta }_{\mathrm{c}\mathrm{a}\mathrm{p}}$.

$$\mathrm{R}\mathrm{I}=\frac{n_{\mathrm{g}\mathrm{a}\mathrm{g}}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{p}\mathrm{d}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{d}\mathrm{b}\mathrm{y}{\theta }_{\mathrm{c}\mathrm{a}\mathrm{p}}}{N_{\mathrm{g}\mathrm{a}\mathrm{g}}}$$ (3)

An RI of 1 thus has $n_{\mathrm{g}\mathrm{a}\mathrm{g}}=N_{\mathrm{g}\mathrm{a}\mathrm{g}}$ and refers to ideal, compact growth. Lower values indicate more extended, fractal-like structures. See supporting material for further details.

Derivation of an optimal titration rate that avoids kinetic traps

To avoid kinetic traps, one approach is to suppress the formation of multiple competing nucleated structures while still allowing efficient growth. We design a strategy here to achieve this by keeping the concentration of Gag monomers low via a titration rate $k_{\mathrm{c}}$, which therefore slows nucleation. We seek to derive the expression for a rate $k_{\mathrm{c}}\le \frac{1}{\tau V}$, given that $\tau$ is the timescale for a protein to bind to a nucleated structure in a volume $V$. To quantify $\tau$, consider a particle diffusing at $D_{\mathrm{t}}$ within a volume defined by the sphere of radius $R$, where the particle is initialized uniformly at any position within the volume (34). The average time for the particle to bind to a reactive sphere of radius $a$ centered in that volume, given an adsorption rate of $\kappa$ (units of length/time), is given by (34):

$$\tau =\frac{R^2}{D_{\mathrm{t}}}\left[\frac{{\left(1-x\right)}^2\left(5+6x+3x^2+x^3\right)}{15x\left(1+x+x^2\right)}+\frac{D_t\left(1-x^3\right)}{3\kappa R{x}^2}\right]$$ (4)

where $x=\frac{a}{R}$. We must therefore define how our model determines the size $a$ of the nucleated structure and its adsorption rate $\kappa$. The adsorption rate can be defined by the density of binding sites on the reactive surface, ${\rho }_0\text{,}$ multiplied by the association rate to bind those sites, or

$$\kappa ={\rho }_0{k}_a$$ (5)

where $k_{\mathrm{a}}$ is the 3D association rate. For $k_{\mathrm{a}}$, we have three different interaction types, but because the trimer interaction is weak and does not stabilize growth, we instead can compare $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}$ and $k_{\mathrm{a},\mathrm{d}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{r}}$. The hexamer interactions are more numerous than dimer contacts (two per monomer), and they are more rate limiting in essentially all our models, thus we consider those binding interactions to be the time-limiting step in growth and set $k_{\mathrm{a}}=k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}$. We note that, if the ${k_{\mathrm{a},\mathrm{d}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{r}}\ll k}_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}$, then we should use this rate instead and adjust the stoichiometry on the reactive sphere. The timescale $\tau$ scales as ${\sim \mathrm{R}}^3$ and thus the titration rate is most sensitive to R as shown in Fig. S1, whereas it grows linearly with $k_{\mathrm{a}}$.

To determine the density ${\rho }_0$ and size $a$ of the nucleus, we must choose the number of monomers N in the initial nucleus and approximate this nucleus as a reactive sphere. By model construction, the length and width of each Gag monomer are approximately 4 and 2 nm, so the surface area taken by each Gag on the sphere is of $S_{\mathrm{G}\mathrm{a}\mathrm{g}}\approx 8{\mathrm{n}\mathrm{m}}^2$. If N is small enough, the curvature of the nucleus is minimal, and it can be represented as a disk with sticky sites on the rim, with radius $r_{\mathrm{n}\mathrm{u}\mathrm{c}}=\sqrt{\frac{{NS}_{\mathrm{G}\mathrm{a}\mathrm{g}}}{\pi }}$. The number of binding sites on this disk is the number of free interfaces along the incomplete edge. From our model, we can estimate that the outer Gags are connected via dimer sites and that there remain free ∼0.54 sites/nm. Thus, the number of sites $N_{\mathrm{r}\mathrm{i}\mathrm{m}}\approx 2\pi r_{\mathrm{n}\mathrm{u}\mathrm{c}}\ast 0.5/\mathrm{n}\mathrm{m}$, and we assert that the reactive sphere has radius $a=$ $r_{\mathrm{n}\mathrm{u}\mathrm{c}}$ and binding site density ${\rho }_0=\frac{N_{\mathrm{r}\mathrm{i}\mathrm{m}}}{\pi {r_{\mathrm{n}\mathrm{u}\mathrm{c}}}^2}$. Finally, we choose a nucleus size $N=18$, since 18 monomers are the smallest number of Gag that can assemble into a lattice containing all types of higher-order structures, i.e., the structure will contain all cycles indicated in Fig. 1 D. We thus use $a=$ 6.77 nm and ${\rho }_0=0.16{\mathrm{n}\mathrm{m}}^{-2}$, and $R=\frac{405}{2}\mathrm{n}\mathrm{m}$, or half of the cubic boxlength defining the simulation volume, and $D_{\mathrm{t}}=10{\mu \mathrm{m}}^2/\mathrm{s}$. When $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}=6.0\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, we find $k_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}\le 3.3\times {10}^{-7}\mathrm{M}/\mathrm{s}$ and when $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}=0.6\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$ , $k_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}\le 6\times {10}^{-8}\mathrm{M}/\mathrm{s}\text{.}$ Despite some approximations used to estimate these reaction parameters, they provide a well-defined estimator for the rate-limiting timescale of binding to a single nucleation site within a volume, and we see below that they correctly predict a single nucleation and growth event. Our derivation assumes that $a$ and ${\rho }_0$ do not change as the nucleus grows. Topologically a fragment of a Gag lattice is not a reactive sphere, as monomers attach at the edge, and it is not a volume-excluding sphere as it grows, but we consider it a reasonable approximation to use fixed estimates, particularly as $a\ll R$. We also assume that the binding events are irreversible. For stable enough contacts, the unbinding rate is slow compared with growth, but we do see for the weakest contacts $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4k_{\mathrm{B}}T$; ultimately the growth speed lags behind unbinding as the lattice becomes large, and additional nuclei can form.

Analysis of light-scattering experimental data

To compare our simulation results quantitatively against experiment, we analyzed time-dependent light-scattering data kindly provided from recently published work (11). We estimated a conversion from the absorbance/intensity units to concentration based on the published quantification that >95% of Gag monomers, or nearly 50 μM, were assembled into lattices at the end of experiments. This corresponded to 0.45 absorbance units, au. To determine the initial growth rates of Gag assembly as a function of IP6 concentration, we identified the short-time regimes where growth was approximately linear following a lag time. We extract concentrations of IP6 given that they are initially present only in the “seed” volume, whereas Gag is in both the “bulk” and seed volume, with a bulk to seed solution ratio of 65:15. For IP6 = 1.56 μM (seed stoichiometry is Gag/RNA/IP6 = 6:2:1), we linear fit over 3–15 min, measuring a slope of 0.0053 au/min, using MATLAB (The MathWorks, Natick, MA). For IP6 = 9.375 μM (Gag/RNA/IP6 = 6:2:6), we linear fit over 1–10 min, giving a slope of 0.015 au/min, and for IP6 = 93.75 μM (Gag/RNA/IP6 = 6:2:60) we linear fit over 0.5–2.25 min, giving a slope of 0.0656 au/min. Using the conversion above, we thus extract titration rates of 0.0098, 0.028, and 0.12 μM/s with increasing IP6. Although the stoichiometry we assume will be 6Gag/1IP6, the binding event generates six activated Gag so for the rate estimation the factors cancel. We predict binding rates k_IP-Gag of 126, 60, and 26 M⁻¹ s⁻¹ with increasing IP6, using Eq. 6 defined below. If the binding to IP6 was rate limiting in all cases, we would expect the exact same rate even as the concentration increases here by 60×. The slowdown in the rate (by ∼4×) instead indicates that the growth rate of Gag assembly is being limited by both the IP6 binding and the Gag-Gag assembly kinetics. When we estimate the production of activated Gag we use the fastest rate of k_IP-Gag = 126 M⁻¹ s⁻¹, solving the set of ordinary differential equations for bulk Gag $\frac{d\left[G\left(t\right)\right]}{dt}={-k}_{\mathrm{I}\mathrm{P}-\mathrm{G}\mathrm{a}\mathrm{g}}\left[IP6\left(t\right)\right]\left[G\left(t\right)\right]$ and IP6 $\frac{d\left[IP6\left(t\right)\right]}{dt}=-k_{\mathrm{I}\mathrm{P}-\mathrm{G}\mathrm{a}\mathrm{g}}\left[IP6\left(t\right)\right]\left[G\left(t\right)\right]$. So we still assume second-order binding (not sixth order), but with $\left[G\left(0\right)\right]=\frac{50}{6}\mu \mathrm{M}$, and then $\left[G_{act}\left(t\right)\right]=50\mu \mathrm{M}-6\left[G\left(t\right)\right]$.

Finally, given these same titration rates, we estimate the rate of binding between Gag once activated, or $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{I}\mathrm{P}6}$. To extract this rate, we invert Eq. 8 defined below with the parameters derived from our model, solving for $k_a$ given $k_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}\text{.}$ We show below that these model parameters work effectively in ensuring robust lattice assembly.

Results

The coarse-grained Gag model can assemble a completed spherical lattice consistent with cryo-ET structures

To simulate assembly of the immature Gag lattice consistent with the cryo-ET structure (16), we derived a coarse-grained model of Gag monomers that form three distinct types of interactions (Fig. 1). As shown in Fig. 1, the hexamer and trimer interactions involve two distinct interfaces that thus allow cycles to form in a front-to-back arrangement. Homodimer interactions link together hexamers or trimers, and ultimately only two types of interactions are necessary to assemble a complete lattice. Below we test assembly both with and without trimer interactions “turned on.” We note that additional stabilizing cycles can form within the Gag lattice beyond just hexamers and trimers, due to the variety of intermolecular contacts between Gag, including a cycle stabilized by a trimer, hexamer, and dimer bond (red dashed lines in Fig. 1 C). Further, at larger length scales, additional stabilizing cycles form via a combination of any two interactions (Fig. 1 D). To assemble the sphere in Fig. 1 D from initially unbound monomers, we promoted nucleation of a single lattice by combining slow titration of monomers into a small volume with fast and irreversible binding rates. Below we characterize assembly kinetics and yield for reversible binding interactions.

Kinetics of fast dimer bond formation agrees with simple theory despite higher-order assembly

By tracking the formation of dimer bonds versus time in our lattice assembly simulations (Fig. 2), we find that the short-time kinetics of dimer association is in close agreement with the analytical theory of populations that can only form dimers (A + A ⇌ C), even when the hexamer association rate is as fast as the dimer rate (Fig. 2 A). This is because the dimer is much more stable than the short-lived hexamer bond; if we make the hexamer contacts more stable, the bonds will start to assemble more synchronously. Thus, as long as dimerization is faster and/or more stable than hexamer contacts, the formation of higher-order contacts does not significantly impact the faster kinetics of monomers forming dimers. Only at times approaching ∼1 s do we see that the lattice system forms more dimers than expected for the simple bimolecular theory, showing that the formation of hexamers helps to stabilize dimer bonds against disassembly and slow the dissociation process. The comparison between the true dimer dissociation rate ($k_{\dim ,\mathrm{o}\mathrm{f}\mathrm{f}}$), and an effective one ($k_{\mathrm{o}\mathrm{f}\mathrm{f},\dim }^{\mathrm{f}\mathrm{i}\mathrm{t}}$), which is fit to the simulation data (see materials and methods), shows how this stabilization effect is stronger with faster hexamer association rate over the first second of assembly (Fig. 2 C). If the trimer bonds can also form, the dimers are stabilized further against dissociation over these short times, even with a slow trimerization rate of $k_{\mathrm{a},\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}=6.02\times {10}^{-5}\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$ (Fig. 2 C). This is due to the additional cycles that are stabilized in the lattice when even weak trimer contacts can form (Fig. 1). Overall, the smallest assembly unit in most of our simulations is effectively the dimer, and the kinetics proceeds as theoretically expected for the rates we have specified. The dimer contact is known from experiments to form stably under all conditions (15) and these results are consistent with the expected higher-order lattice assembly from dimer building blocks (3).

The kinetics of hexamer bond formation is accelerated by higher-order lattice assembly

Unlike the kinetics of dimer bond formation, we find that even the short-time kinetics of hexamer bond formation deviates significantly from the simple theory for independent sites (A + B ⇌ C). This is perhaps not surprising, as the hexamer bonds allow the assembly of higher-order structures that can become stabilized against disassembly. Even for the weak binding free energy of $\Delta G=-6.4k_{\mathrm{B}}T$, or $K_{\mathrm{D}}$ = $1661\mu \mathrm{M}$ (weak relative to [C]₀ = $50\mu \mathrm{M}$), we see that dissociation of the hexamer bonds slows relative to the pairwise expectations (Fig. 2 B). In contrast, if only hexamer bonds form (we turn off dimer and trimer interactions), the model exactly reproduces theory as expected (Fig. 2). We quantified how the stabilization due to the cycles enabled by dimer and trimer interactions (see Fig. 1) can effectively accelerate hexamer association and slow hexamer dissociation. We defined an effective hexamer dissociation constant, $R_{\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{f}\mathrm{i}\mathrm{t}}=\frac{k_{\mathrm{o}\mathrm{f}\mathrm{f},\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{f}\mathrm{i}\mathrm{t}}}{k_{\mathrm{o}\mathrm{n},\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{f}\mathrm{i}\mathrm{t}}}$, with rates defined by fitting our simulated data to the functional form of the simple theory (see materials and methods). As we increase the hexamer on- and off-rates while keeping the $\Delta G$ fixed, we see that the dissociation slows systematically, allowing faster assembly of effectively more stable hexameric contacts (Fig. 2 D).

These simulations also illustrate the role that the additional trimer contacts play in stabilizing the structures against disassembly. Although we add in trimer interactions at only a weak $\Delta G_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}$ = −4.1 $k_{\mathrm{B}}T$ ($K_D$ of $16.6\mathrm{m}\mathrm{M}$), they nonetheless quantitatively shift the kinetics of hexamer bond formation, helping to accelerate bond formation by further slowing dissociation (Fig. 2 D). The impact of the trimer contacts is diminished if the strength of the hexamer bond formation is increased, as we quantify further below. This is also not surprising, as stronger hexamer bonds will not need “help” from other contacts to stabilize bonds. Finally, we confirm that, despite the faster formation of hexamer contacts, the equilibrium bonds formed after ∼100 s are the same under constant $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}$ (Fig. S2). Adding in the trimer interaction along with the dimer ensures ∼15% more hexamer bonds form for these energies (Fig. S2).

Kinetic trapping emerges even for relatively weak $\Delta G$ due to the lattice size

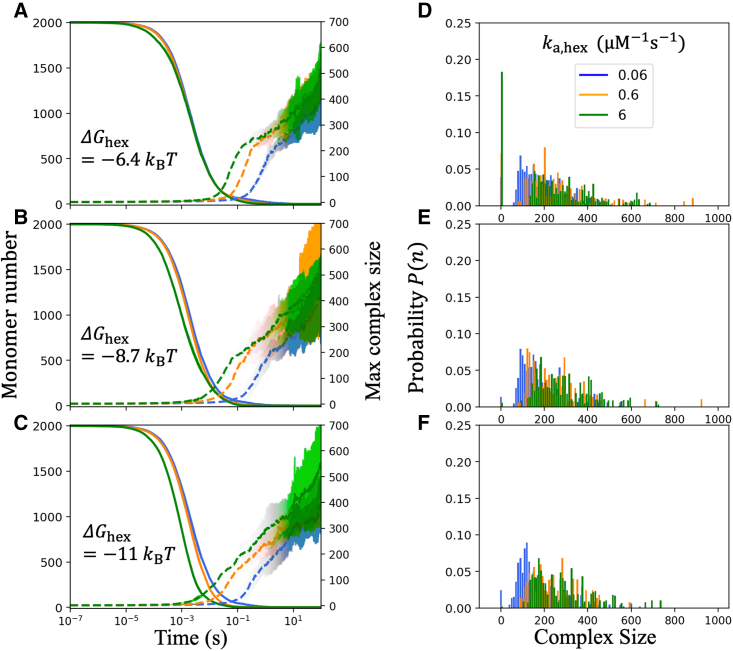
By comparing systems with the same energetics but distinct hexamer binding kinetics, our systems will eventually reach the same equilibrium distribution of assemblies, but the assembly pathways they follow will be distinct. However, even for a relatively weak set of interactions ($\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4k_{\mathrm{B}}T)$, we already see that our system is kinetically trapped. Specifically, for all systems, by ∼10 s monomers and dimers have been depleted, leaving essentially no simple building blocks to complete the growth of intermediate-sized structures (Fig. 3, A–C and Video S1). The size distribution of these assembly intermediates shifts slightly larger with faster hexamer rates over 100 s, although for the two fastest rates the distributions show a more similar steady state (Fig. 3, D–F). To grow largely complete lattices, these stalled (Fig. S3) and monomer-starved systems now must either wait for dissociation of larger complexes or wait for the rare annealing of two intermediate-sized complexes. Given enough time, our systems will eventually reach an equilibrium steady state, where the distribution of complexes is independent of the rate constants, and below we show how these same systems can be guided around these trapped intermediates to form large single complexes over much shorter timescales. A major factor driving trapping is the total number of monomers required to complete a lattice. Although our systems can assemble hundreds of Gag monomers into a single structure (Fig. 3), the complete lattice requires 3700 monomers. For high-yield assembly, the rate of nucleating new structures should be slower than the elongation rate to complete the lattice, but adding thousands of monomers onto one structure takes significantly longer than forming a capsid that contains 10 or 100 times fewer components.

Figure 3.

Kinetic traps emerge when all three interactions are turned on even with relatively weak $\mathrm{\Delta }G$. On the left column (A–C), we show the kinetics of monomer depletion (solid lines) and simultaneous formation of the largest assembled complex in the system (dashed lines). The hexamer rate $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}$ increases from $6.02\times {10}^{-2}$ (blue), $0.602$ (orange), $6.02\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$ (green), with $k_{\mathrm{b},\mathrm{h}\mathrm{e}\mathrm{x}}$ increasing to keep $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}$ constant. Then, from top (A) to bottom (C) the stability of the hexamer interaction $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}$ increases, by slowing $k_{\mathrm{b},\mathrm{h}\mathrm{e}\mathrm{x}}$. As the small building blocks are depleted by ∼10 s, growth stalls and the systems become trapped in incomplete intermediates (also see Video S1). The probability distributions on the right (D–F) show corresponding complex sizes of intermediates present after 100 s of simulation for the same simulations to their left. All systems exhibit multiple nucleated structures, rather than a single growing structure. With faster hexamer kinetics (green and orange), the distribution of complex sizes shifts to larger values compared with blue data (also see Fig. S3). Even for $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4k_{\mathrm{B}}T$, only a few monomers remain free in solution, leaving no room for additional growth without dissociation. All results are averaged over 16 trajectories, and standard deviation is shown around the plotted sample mean versus time. We set $k_{\mathrm{a},\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}=6.02\times {10}^{-5}\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathrm{b},\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}=1{\mathrm{s}}^{-1}$, $\Delta G_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}=-4.1k_{\mathrm{B}}T{;k}_{\mathrm{a},\dim }=6.02\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathrm{b},\dim }=1{\mathrm{s}}^{-1}$, $\Delta G_{\dim }=-15.6k_{\mathrm{B}}T\text{;}$ and $D_{\mathrm{t}}=10{\mu \mathrm{m}}^2{\mathrm{s}}^{-1},D_{\mathrm{r}\mathrm{o}\mathrm{t}}=0.01{\mathrm{r}\mathrm{a}\mathrm{d}}^2{\mathrm{s}}^{-1},\Delta t=0.5\mu \mathrm{s}$, boxlength = $405\mathrm{n}\mathrm{m}$. To see this figure in color, go online.

Video S1. Assembly kinetics with 50 μM bulk Gag shows kinetic trapping

$\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-11.0k_{B}T{k}_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}=6$$\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$.

As for the assembly pathways, faster binding kinetics (both on and off rates) leads to slightly fewer and thus larger intermediates on average (Figs. S3 and S4). This is consistent with the results of Fig. 2, where faster hexamer kinetics combined with dimer and trimer contacts will stabilize early growth and thus allow faster elongation of the nucleated structures before the building blocks are used up. For slower rates, in contrast, more nuclei form while the concentration is relatively high, and growth is slow. This trend was preserved for the weak and stronger free energies tested ($\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4,-8.7$, and −11.4 $k_{\mathrm{B}}T$) and with the trimer turned on and off (Fig. S4). By speeding up both the dimer and hexamer rates, we can accelerate growth, such that only 4–6 nuclei form instead of 8–10. This reduction in the number of intermediates nucleated is more sensitive to the hexamer association rate than to dimer and trimer rates, as we see a clear increase in the sizes of complexes formed with faster hexamerization (Fig. S4). We note that, while we did not establish a formal size of a critical nucleus (in terms of a free-energy maxima following critical nucleation theory), we did consistently define a nucleus as having at least 18 Gag monomers since that size structure would contain multiple stabilizing cycles that would significantly slow dissociation (materials and methods and Fig. 1).

Rapidly assembled intermediates have less uniform growth

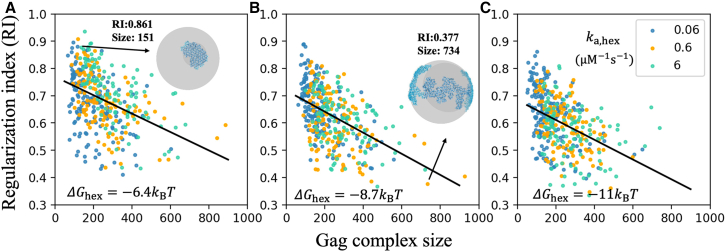
To compare the topology of our assembled structures, we defined a RI that measures how much a lattice deviates from a compact, ideal spherical growth (shaded with dark gray in Fig. 4). Ideally, compact structures have RI = 1, while a more extended fractal-like growth has increasingly lower RI. Compact structures have the shortest edge length, and thus they maximize the number of stabilizing cycles formed. Analyzing the same systems as in Fig. 3, we find that smaller complexes of ∼100 Gag monomers have a higher RI on average and that the RI systematically decreases as the sizes of the complexes increases (Fig. 4). This trend occurs for each $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}$ (Video S1), but with less stable free energy there is a shift toward higher RI. This indicates that faster dissociation allows structures to grow more uniformly and compactly by correcting contacts that extend the growth and fail to satisfy as many bonds.

Figure 4.

In kinetically trapped systems, growth of larger intermediates is less compact and regular. The regularization index (RI) of assembled complexes with N_gag >100 at steady state is on average higher for smaller assemblies. The sphere in (A) illustrates a high RI showing a significant overlap of the simulated lattice in blue with the ideal spherical cap in dark gray. The one in (B) shows a low RI. Data in (A) ${\Delta G}_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4$k_BT, (B) ${\Delta G}_{\mathrm{h}\mathrm{e}\mathrm{x}}$ = −8.7, (C) ${\Delta G}_{\mathrm{h}\mathrm{e}\mathrm{x}}$ = −11 k_BT. Black lines are from linear regression analysis, showing a clear negative correlation between RI and Gag complex size for all panels. Pearson correlation tests further substantiate this correlation, which yields Pearson correlation coefficients of −0.42, −0.5, and −0.44 from (A) to (C). The p values are all extremely small ($<{10}^{-19}$). Blue, orange, and green dots represent lattices formed in systems with association rate of 0.06, 0.6, and 6 $\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$. While there is no significant trend of the RI with changing rates, there is a significant trend of higher RI values with weaker ${\Delta G}_{\mathrm{h}\mathrm{e}\mathrm{x}}$. The best-fit lines have similar slopes from (A) to (C), but the y-intercept decreases from 0.77 to 0.72 to 0.68, respectively. Same simulation data and parameters as Fig. 3. To see this figure in color, go online.

We further quantified growth pathways, showing that they proceed primarily through addition of monomers, dimers, and small oligomers of <18 Gags, although some rare annealing events between large structures do occur (Fig. S5). These annealing events are unlikely because they require that the two complexes have compatible edge geometries and, when such annealing does happen, highly irregular structures can form (Fig. 4 B). They are also rare because the structures must be aligned properly to avoid large-scale reorientation upon binding. Our algorithms will reject moves that cause any component of the assembly to move significantly more than expected due to translational and rotational diffusion as specified by a threshold (see materials and methods).

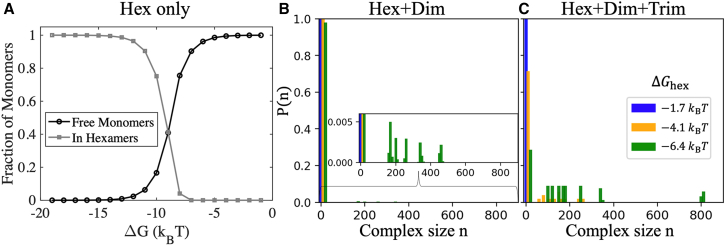
A two-phase equilibrium emerges with significantly weakened $\mathrm{\Delta }{G}_{\mathrm{h}\mathrm{e}\mathrm{x}}$

Eliminating higher-order assembly requires dropping the interaction strength significantly lower than would be required for one type of interaction (Fig. 5). A strong dimer interaction only reduces the total components from 50 $\mu \mathrm{M}$ of monomers to 25 $\mu \mathrm{M}$ of dimers, so we focus first on the hexamer strength, comparing ${\Delta G}_{\mathrm{h}\mathrm{e}\mathrm{x}}=-1.7,-4.1$, and $-6.4k_{\mathrm{B}}T$. As a baseline, we consider a system that can form up to hexamers but no higher-order lattices, meaning we turn off the homodimer and trimer contacts. At ${\Delta G}_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4k_{\mathrm{B}}T$, only 0.001% of these Gag monomers will form hexamers (Fig. 5 A). As we turn on the other interactions and increase the number of cycles possible in the lattice, the transition window from no assembly to robust assembly will shrink and shift with small changes to ${\Delta G}_{\mathrm{h}\mathrm{e}\mathrm{x}}$. With homodimer contacts added, a larger assembly will form at ${\Delta G}_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4k_{\mathrm{B}}T$, although >90% of components present in solution are Gag monomers, whereas at $-4.1k_{\mathrm{B}}T$ we see no assemblies formed (Fig. 5 B). Finally, with all three interactions present, at ${\Delta G}_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4k_{\mathrm{B}}T$, the system consumes nearly all monomers/dimers. Large assemblies form even with ${\Delta G}_{\mathrm{h}\mathrm{e}\mathrm{x}}=-4.1k_{\mathrm{B}}T$, along with a dilute phase of monomers (Fig. 5 C). For this model, we return to a fully monomeric system when ${\Delta G}_{\mathrm{h}\mathrm{e}\mathrm{x}}$ is $-1.7k_{\mathrm{B}}T$.

Figure 5.

Multivalent assembly supports lattice formation with weak hexamer contacts. (A) For reference, we numerically calculated the equilibrium for Gag monomers (50 μM) that only had hexamer contacts enabled using MATLAB. The transition to <50% fraction as free monomers occurs at $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-8.74k_{\mathrm{B}}T$. (B) For Gags that assemble the full lattice via dimer and hexamer contacts, we start to see formation of large assemblies when $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4k_{\mathrm{B}}T\left(greenbars\right)$, with no assembly for $-1.7k_{\mathrm{B}}T$ (blue bars) and $-4.1k_{\mathrm{B}}T$ (orange bars). (C) Same as (B) but now the trimer interaction is turned on at $\Delta G_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}=-4.1k_{\mathrm{B}}T$, triggering assembly at all but the lowest hexamer strength. Both (B) and (C) report distribution over a 5 s time window following steady state. We note that, due to the slow on-rates, some nucleation of lattices could still occur at longer times beyond those simulated here (100 s). The distributions are normalized over the number of distinct types of complexes, meaning that if 10 different sized complexes are present, and one is a monomer, than the probability of the monomer state is 0.1, even though only 1 in 2000 Gags are in the monomer form. Data collected from one trajectory. $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}=6.02\times {10}^{-4},6.02\times {10}^{-3},6.02\times {10}^{-2}\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathrm{b},\mathrm{h}\mathrm{e}\mathrm{x}}=1{00\mathrm{s}}^{-1},\Delta t=0.5\mu \mathrm{s}$, and $D_{\mathrm{t}}=10{\mu \mathrm{m}}^2{\mathrm{s}}^{-1},D_{\mathrm{r}\mathrm{o}\mathrm{t}}=0.01{\mathrm{r}\mathrm{a}\mathrm{d}}^2{\mathrm{s}}^{-1}\text{,}$ boxlength = $405\mathrm{n}\mathrm{m}$, $k_{\mathrm{c}}=60\mu \mathrm{M}/\mathrm{s}$. For (B) and (C) $k_{\mathrm{a},\dim }=0.602\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $\Delta G_{\dim }=-13.3k_{\mathrm{B}}T$. For (C)${,k}_{\mathrm{a},\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}=6.02\times {10}^{-5}\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $\Delta G_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}=-4.1k_{\mathrm{B}}T$. To see this figure in color, go online.

A two-phase equilibrium with a dilute phase of monomers and dimers alongside a collection of partial assemblies is thus difficult to achieve unless only two interactions are stabilizing the lattice (Fig. S6, E–G). The stable dimer interaction combined with either hexameric interactions or trimer interactions at $\Delta G$ = $-6.4k_{\mathrm{B}}T$ nucleate partial assemblies, but growth ultimately stalls as the monomer concentration dilutes (Fig. S6, A and B). These two lattices reach the same equilibrium despite the trimer being fundamentally more stabilized against disassembly, as the higher-order cycles between dimer and trimer require more bonds than dimer and hexamer (Fig. 1).

Mimicking activation by cofactors can ensure slow nucleation and fast growth of a single lattice

Our simulations above demonstrate that, to prevent kinetic trapping in bulk simulations (where all monomers are present at time zero) for the large HIV lattice, we would need to identify the very small range of $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}$ values that can complete growth of the lattice before multiple nuclei form. Without the trimer, this would require slightly more stability than −6.4 $k_{\mathrm{B}}T$ (Fig. 5), but weaker than −8.7 $k_{\mathrm{B}}T$ (Fig. S6), and with faster association rates (at 50 μM). With the trimer, values would shift to between −4.1 and −6.4 $k_{\mathrm{B}}T$. However, assembling from bulk monomers is not a problem the HIV lattice has evolved to solve. Both in vitro and in vivo, the Gag lattice assembly is only productive with cofactors, and therefore an alternate strategy for our model is to mimic the behavior of cofactors. Binding to cofactors effectively changes the concentration of “active” or assembly-competent Gag monomers in a time-dependent fashion. In the bulk simulations above (Figs. 3, 4, and 5), the activation was therefore instantaneous, implying a high concentration of cofactors and efficient binding.

Instead of considering the dependence of activation on both the concentration and binding rate of cofactors to the Gag monomers, we simplify our approach and use a titration rate $k_{\mathrm{c}}$. From mass action kinetics, the rate of activated Gag production is then $\frac{d{[G}^{act}\left(t\right)]}{dt}=k_{\mathrm{c}}$. For the explicit bimolecular process, we have $\frac{d{[G}^{\mathrm{a}\mathrm{c}\mathrm{t}}\left(t\right)]}{dt}=k_f\left[R\left(t\right)\right]\left[G\left(t\right)\right]$, where $k_f$ is the binding rate between Gag and cofactor, $\left[R\left(t\right)\right]$ the concentration of cofactor, and $\left[G\left(t\right)\right]$ the concentration of bulk Gag before activation, with initial concentrations $\left[R_0\right]$ and ${[G}_0]$, respectively, and ${[G}^{\mathrm{a}\mathrm{c}\mathrm{t}}\left(0\right)]=0$. By comparing these two we can map our titration rate to the effect of cofactor binding,

$$k_{\mathrm{c}}/\left[G_0\right]\approx k_f\left[R_0\right]$$ (6)

which is an accurate approximation at earlier times where the concentrations are close to their initial values. This comparison to a titration process will not directly match the time dependence of the bimolecular association process as concentrations become limited and thus deplete with time, in which case the bimolecular process slows relative to titration. Nonetheless, it establishes useful bounds on the timescales of binding as they relate to a single titration rate: if slow titration is necessary, this would require either a lower concentration of cofactor or slower binding of cofactor to Gag. In Fig. 6 we test how introducing a titration process to “activate” the Gag monomers can reduce the number of nuclei and thus improve the formation of more complete lattices. If the titration is too fast relative to the binding between the Gag monomers, however, improvement is minimal, indicating how this rate must be calibrated relative to the Gag assembly kinetics (Fig. 6).

Figure 6.

Titrating in Gag monomers can reduce nucleation events and improve lattice growth. (A and B) The largest lattice formed as a function of time is normalized by the number of Gag monomers, so 1 is 100% of Gag in a single complex. The figure shows bulk simulations (yellow) and titration with 60 μM/s (green) and 1 μM/s (orange). Titration was stopped when the final concentration of 50 μM was reached, which occurred after 0.83 s (green) or after 50 s (orange). (A) Has slower binding interactions, $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}=0.06$$\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$ and $k_{\mathrm{a},\dim }=0.006\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$$k_{\mathrm{b},\mathrm{h}\mathrm{e}\mathrm{x}}$ = 1 ${\mathrm{s}}^{-1}$. (B) Has faster binding, $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}=12$$\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$ and $k_{\mathrm{a},\dim }=0.6\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$$k_{\mathrm{b},\mathrm{h}\mathrm{e}\mathrm{x}}$ = 20 ${\mathrm{s}}^{-1}\text{.}$ For both (A) and (B) $k_{\mathrm{b},\dim }=1{\mathrm{s}}^{-1}$, $k_{\mathrm{a},\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}=6.02\times {10}^{-5}\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathrm{b},\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}=1{\mathrm{s}}^{-1}$. For the slowest titration rate (orange) in (B), a single nuclei was grown during most of the simulation. Results from one trajectory each. In (C) and (D), we show a representative snapshot from the end of the corresponding simulations. In (B) and (D), the slowest-titration simulation uses a larger (510 nm)³ box to allow a lattice to complete, which it nearly does in this single trajectory (bottom right) before a few small nuclei form. To see this figure in color, go online.

We note that the growth of our lattices does show some dependence on the diffusional search of the monomer. Simulations in larger boxes (510 vs. 405 nm boxlength) reach the same concentrations in time, but the larger box allows the complete ∼3700 monomer lattice to form. That means that forming a single nucleus in the larger box requires the monomers to travel larger distances before “finding” the nucleus. This increased travel time slows growth of the nucleated lattice and results in higher likelihood of a new lattice forming. Thus, the titration rate should reflect the volume needed to complete a lattice. We also found that decreasing the diffusion coefficients of the monomers could shift the distribution of complexes to slightly more nucleated structures (Fig. S7). This result could not be primarily attributed to just a slower search, as a similar trend occurred when we changed the time step. Instead, we found that our criteria for rejecting association events that involve large rotational motion by larger complexes was more permissive with faster diffusion (D_t = 50 μm²/s, D_r = 0.05 rad²/μs vs. 10 μm²/s and 0.01 rad²/μs). Practically, this indicates that some of the early growth of the complexes is occurring due to moderately sized oligomers combining to maintain fewer nucleated structures. However, this also means that the formula controlling the probability of accepting annealing events between large complexes shows a small dependence on the time step and diffusion constant. A more rigorous definition of this formula is needed to ensure that this acceptance criteria is fully invariant under changes to diffusion or time step. Importantly, however, we verified that the number of bonds formed is conserved (<3% error) regardless of spatial extent, diffusion constant, or time step. Because the effect of this annealing parameter on the distribution of assemblies is small, we do not see changes to our observed trends with rates or free energies, and in future work this unexpected coupling between rare annealing events and diffusion will be corrected.

The titration rate can be derived to promote nucleation of complete lattices

From Fig. 6 we clearly see that slowly titrating in or “activating” Gag monomers can improve nucleation and growth of larger lattices by keeping the concentration low. Here, we derive an optimal titration rate to ensure the growth of completed lattices. The idea is to limit the rate that a new protein appears in the simulation volume to below the rate that a protein will bind to a single nucleated structure in the volume. In this way, each new protein will contribute to growth of the single nuclei rather than formation of a distinct one. Hence, we seek to derive an expression:

$$k_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}\le \frac{1}{\tau V}$$ (7)

where $\tau$ is the timescale for a protein to bind to a nucleated structure in a volume $V$. We define the timescale $\tau$ by mapping to a well-defined problem in the theory of diffusion-influenced reactions for binding to a reactant in a fixed volume (34). We ignore the dissociation of proteins, or assume binding to the nuclei is irreversible, and, of the two main stabilizing reactions (dimer and hexamer), we quantify binding times using the slowest rate, which in this case is the hexamer rate. Our predicted rate is then:

$$k_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}=\frac{3{\ast 15a^{2}D}_{\mathrm{t}}}{4\pi R^6}{\left[\frac{{a\left(a-R\right)}^2\left(a^3+3a^{2}R+6a{R}^2+{5R}^3\right)}{R^3\left(a^2+aR+R^2\right)}+\frac{{5D}_t\left(1-a^3/R^3\right)}{k_a{\rho }_0}\right]}^{-1}$$ (8)

where $D_{\mathrm{t}}$ is the monomer diffusion constant, $a\approx$ 7 nm is the radius of an initially nucleated structure, $k_{\mathrm{a}}=k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}$ and ${\rho }_0\approx$ 0.16 nm⁻² is an approximate density of binding sites on a Gag lattice (see materials and methods for details). Finally, what is the appropriate value for V in a real system, or the length scale R that confines our assembly process? Both $\tau$ and $V$ scale with R³, hence the sensitivity of $k_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}$ to R (Fig. S1). The volume must be physically large enough that a complete lattice can form (with R_lattice = 50 nm) and contain enough monomers for the complete lattice given the concentration of Gag in solution. Thus, we have that

$$V=N/\left[G_0\right]$$ (9)

where $N$ is the total monomers needed to complete a lattice (∼3700 for a 50 nm sphere), and $\left[G_0\right]$ is the concentration of Gag monomers in solution. Hence, a smaller volume is needed with a higher concentration of Gag. The smaller R we choose, the faster the titration rate we can use, so ultimately, the rate of titration or “activation” must be calibrated to the concentration of Gag in solution to form completed lattices. This length scale will also ultimately control the concentration of lattices in solution, [L], as assuming all monomers add to a complete lattice, $\left[L\right]=k_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}{t}_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}/N$ where $t_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}$ is the length of time over which the monomers are titrated to reach the target Gag concentration. We used a value of R = 202 nm for our derivation, comparable with our simulation box size. The corresponding simulations (Fig. 7) then reached the same Gag concentrations as our previous ones, with 50 $\mu \mathrm{M}$ of Gag. We note that this volume does not contain the copies necessary for a complete lattice, which would instead be R = 308 nm. For the larger volume, a slower titration rate is predicted, although we see below that the assembly process can partly tolerate increases in the simulation volume.

Figure 7.

Derived titration method ensures productive nucleation and growth. (A) A single complex forms as we titrate in monomers using our derived rate $k_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}$ = 0.06 μM/s. All data are an average over 48 independent trajectories per model. $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}$ = 0.6 μM⁻¹ s⁻¹ for each curve, but $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}$ increases from −6.4 k_BT (light gray) −8.7 k_BT (gray) −11 k_BT (black) (Video S2). The total number of Gags is shown as the dashed red line. The inset shows the initial lag time which extends with faster dissociation (light gray). (B) Here, the hexamer association rate was accelerated, $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}$ = 6 μM⁻¹ s⁻¹ and thus we used a faster $k_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}$ = 0.33 μM/s. $k_{\mathrm{a},\dim }$ = 0.6 μM⁻¹ s⁻¹, $k_{\mathrm{b},\dim }$ = 1 s⁻¹, $k_{\mathrm{a},\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}=6.02\times {10}^{-5}$μM⁻¹ s⁻¹, $k_{\mathrm{b},\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{m}}$ = 1 s⁻¹. To see this figure in color, go online.

In Fig. 7 we show that this method provided excellent control to ensure the growth of a single nucleated lattice. We tested two hexamer association rates ($k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}=6$ and 0.6 $\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$) and three hexamer stabilities ($\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4,-11.0,-13.3k_{\mathrm{B}}T$). The systems remain free of kinetic traps as they nucleate and grow, forming a single large assembly in our volume (Video S2). The one exception is the weakest lattice ($\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4k_{\mathrm{B}}T)$, which after reaching a size containing ∼1200 monomers does start to nucleate additional structure in a fraction of the trajectories. The reason is that the association is counterbalanced by more frequent dissociation reactions for this weak interaction. Our simulations indicate that growth is therefore slowing somewhat as the lattice is getting larger, which would explain why ultimately new nuclei are able to form before the titrated monomers are added onto the existing structure, but they do not do so earlier in the trajectories. This further suggests that the growth of this lattice, with $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4k_{\mathrm{B}}T$, is not strongly stabilized against the competing disassembly, and thus assembly is less robust, requiring more tight temporal control to complete lattice formation.

Video S2. Assembly kinetics with k_titr = 0.33 μM/s allows for slower Gag activation and robust and compact assembly

$\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-11.0k_{B}T$$k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}=6$$\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$.

Our simulations also show how the nucleation of the initial structures is dependent on both the on- and off-rates (Fig. 7). The lag time before reaching the linear growth phase is longer when off-rates are faster, consistent with more time needed to stabilize the nucleation site. For all parameter regimes these simulations produce much more compact and ideal-like growth of our structures compared with earlier simulations (Fig. 3), with average values of the regularization index now ∼0.85–0.95 that are quite close to 1 at all times (ideal growth). Our derivation of $k_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}$ above is approximate, as it assumed a fixed size and reactivity for the nucleation site, whereas in reality the nucleus grows larger and the reactive sites remain always along the edge of the lattice. Nonetheless, we find that this method keeps a low enough concentration of Gag monomers that we can now reproduce smooth and productive growth, even for highly stable lattices ($\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-11k_{B}T$) that would otherwise rapidly become trapped into intermediates under bulk conditions (compare with Fig. 5).

Comparison with in vitro assembly kinetics reveals how slow binding of Gag to IP6 can support robust Gag assembly

The cofactor IP6 binds to Gag and activates it for assembly into the immature lattice (11,15,43). We therefore analyzed a recently collected set of in vitro experiments that tracked (via light scattering) the formation of Gag lattices versus time as a function of IP6 concentration (11) (Fig. 8). Light scattering can be analyzed to quantify assembly parameters (44), but cofactors will alter the observed kinetics. Based on our theoretical arguments above, if activation of the Gag monomers by IP6 binding was slow enough, then we would see a linear increase in Gag complex size, following a lag time. Furthermore, the Gag assembly kinetics should also accelerate with higher IP6 concentration if this activation is more rate limiting than the Gag-Gag assembly kinetics. We do observe both this linear early increase in Gag complex size and the acceleration of this growth rate with higher IP6 concentration (Fig. 8 A), indicating faster activation of Gag into its assembly-competent form. Therefore, we proceed to use our theoretical arguments to extract the effective titration rates. With titration rates, we can then estimate bounds on the binding rate of IP6 to Gag, k_IP6-Gag, and the binding rate of Gag to Gag, $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{I}\mathrm{P}6}$.

Figure 8.

Analysis of in vitro Gag assembly kinetics indicates that IP6 can activate Gag slowly enough to support assembly with limited trapping. (A) Light scattering intensity versus time is replotted here from recent experiments measuring in vitro Gag assembly (11). Gag and RNA concentration is the same for all curves, with 50 μM Gag and 3.125 μM RNA (159 nt each) in solution. Concentration of IP6 increases from 1.56 μM (purple) to 9.37 (blue) and 93.7 (red), clearly driving faster Gag lattice assembly. A regime of relatively linear growth following a lag time for each system gives a rate estimate for IP6 “activating” Gag (black lines). (B) Same experimental data, but we convert to assembly completion fraction using 0.45 absorbance units to 100% complete (completion = 1) (see materials and methods). We subtract 0.22 or 0.24 to re-zero the y axis. Using our estimated rate of Gag binding to IP6 (125 M⁻¹ s⁻¹), we predict the production of the IP6-activated Gag ([G_act(t)]) in dashed lines following a model of bimolecular association, normalized by the total Gag concentration of 50 μM (materials and methods). This activated Gag we infer as now competent to bind other Gag much more quickly, thus allowing the Gag assembly observed experimentally (solid colors). For low IP6 (purple data), it is apparent that not all Gag needs to be “activated” by IP6 to assemble, with a slower timescale of assembly occurring after the initial rapid assembly. This is known from experiment: even without IP6 (but with RNA), Gag assembly eventually occurs following a long lag time (orange data). (C) Our simulation data (solid blue lines, same as Fig. 6B) can also report a completion fraction given the average size of Gag complexes in time normalized by the maximal complex size (e.g., N_cmplxMAX = 3700 monomers). Here, the Gag is explicitly activated in time via titration, so the red dashed lines report [G_act(t)] due to titration, normalized by the total target concentration of 50 μM. In (C₁) we activate the Gag too quickly compared with its assembly, and thus the assemblies become trapped. In (C₂), we activate slowly enough that we see robust assembly growth over these shorter times. We infer that the experimental results in (B) at higher IP6 (9.37 and 93.7 μM) are a bit too fast in activating Gag, leading to assembly that results in some kinetic trapping, or a plateau that does not reach >95% yield. To see this figure in color, go online.

To extract the ${\mathrm{k}}_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}$, we simply linear fit this short-time growth rate in the experimental kinetics (see materials and methods). We thus measure three titration rates, and then we can use Eq. 6 to estimate the binding rate of IP6 to Gag, k_IP6-Gag. We predict a rate k_IP6-Gag for each titration rate, and we expect them to be identical if the growth of Gag assembly is fully rate limited by Gag-IP6 binding. The rates are indeed similar, but not identical, showing a modest slowdown in this predicted rate at higher IP6 concentrations (materials and methods). A simple interpretation is that the Gag is now being activated by IP6 a bit faster than the assembly process can keep up, so Gag activation is not fully rate limiting. We therefore use the value at the lowest concentration of IP6 as the upper bound, k_IP6-Gag ∼126 M⁻¹s⁻¹. Also, because the IP6 is initially seeded with 18% of the Gag before the full mixing and measurement (11), the IP6 binding could actually be slower than this rate, so we can interpret it as an upper bound.

In Fig. 8 B we illustrate how the full-time evolution of the experimental Gag assembly can be interpreted via these binding rates. Light scattering reports on the average molecular weight of solute, so it is most directly mapped to the average mass of complexes in simulation (Fig. 8 C), where we normalize by total Gag in a complete complex to report a completion fraction. We predict the concentration of IP6-activated Gag in Fig. 8 B using our value of k_IP6-Gag, where activated Gag can then assemble complexes. At the high IP6 concentrations (9.37 and 93.7 μM), the activation is a bit faster than assembly kinetics, which leads to initially fast growth followed by some kinetic trapping, as the growth plateaus at ∼80% completion rather than 100% (Fig. 8 B). This is similar to our simulation results in Fig. 8 C₁ except with much higher completion fraction. However, in the lowest IP6 concentration, for short times the growth is more like Fig. 8 C₂, indicating smooth growth following activation. At the lowest IP6 concentration, we can maximally activate only 9.37 μM Gag, or ∼20% of the total. However, assembly still proceeds beyond these times, albeit much more slowly, meaning that not all Gag need to be bound to IP6 to promote assembly. Although we did not include this possibility in our model, this is consistent with the known assembly dynamics of the immature Gag lattice absent of IP6 (but still with RNA), which has a very long delay but eventually a cooperative assembly into largely complete lattices (Fig. 8 B, orange curve). This comparison indicates that IP6 significantly accelerates assembly, but it can also bias away from a very slow but highly cooperative growth that occurs only due to RNA-driven activation.

Finally, we can use our fit values of $k_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}$ that we extracted from the experimental data to estimate the limiting rate of Gag-Gag assembly when IP6 activates, or $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{I}\mathrm{P}6}$ via Eq. 8. To justify estimates on $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{I}\mathrm{P}6}$, if the titration rate (IP6-driven activation rate) is too fast compared with Gag assembly then we expect a more bulk-like condition that will promote kinetic trapping (Fig. 8 C₁). If the titration rate is slow enough, the assembly kinetics will be limited by the speed of activation. Then we can estimate what the slowest assembly rate could be to ensure smooth growth, although the actual rate could also be faster; thus, we can only put a lower bound on the binding rate (Fig. 8 C₂). Using the titration rate for IP6 = 1.56 μM over short times estimated as $k_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}\sim$ 0.0098 μM/s, we have a lower bound on $k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{I}\mathrm{P}6}$ of either 7.7 × 10⁴ M⁻¹ s⁻¹ using R = 202 nm, or 1 × 10⁶ M⁻¹ s⁻¹ using R = 308 nm. An upper bound from the kinetics at IP6 = 9.73 μM where $k_{\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{r}}\sim$0.028 μM/s is then 2 × 10⁵ M⁻¹ s⁻¹ using R = 202 nm or 3.8 × 10⁶ M⁻¹ s⁻¹ using R = 308 nm. Hence, our estimates put it between 7.7 × 10⁴ M⁻¹ s⁻¹ $<k_{\mathrm{a},\mathrm{h}\mathrm{e}\mathrm{x}}^{\mathrm{I}\mathrm{P}6}<$ 3.8 × 10⁶ M⁻¹ s⁻¹. This indicates that the Gag-Gag assembly kinetics once activated by IP6 is significantly faster than IP6 binding to Gag (k_IP6-Gag ∼125 M⁻¹ s⁻¹), and thus IP6 can be effective in relatively slowly activating Gag for efficient assembly even when its concentrations are higher. It is also clear that Gag assembly kinetics slows when Gag must assemble lattices without all monomers benefiting from IP6 activation (Fig. 8 B).

Discussion

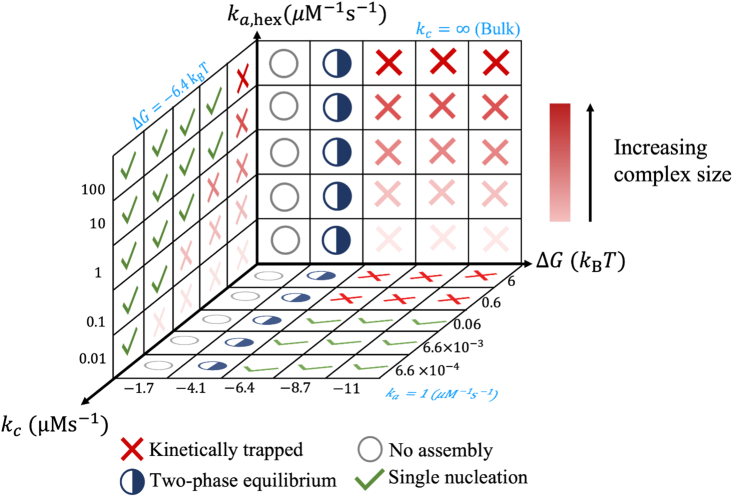
By developing a model of the immature Gag lattice from the cryo-ET structure, we quantified here how the strength and kinetics of the multiple Gag-Gag contacts within the lattice could support productive self-assembly from free monomers. A key component of this reaction-diffusion model is the energetic and kinetic parameters compare directly to free energies and biochemical rate constants and can thus inform pairwise interactions that are experimentally testable. A primary finding is that the Gag lattice is simply too large to assemble robustly from bulk conditions, requiring thousands of monomers to complete lattices built from monomer and dimer building blocks. Across a range of free energies and interaction rates, we showed that it is remarkably difficult to complete growth of any lattice before nucleation of competing lattices, leaving the systems starved of monomers and kinetically trapped. We further show that, at 50 μM of Gag monomers, suppressing assembly entirely requires very weak interactions, with K_D,Hex weaker than 1.6 mM (−6.4 $k_{B}T$), or weaker than 16 mM (−4.1 $k_{B}T$) if trimer contacts help stabilize growth (Fig. 9). The immature Gag lattice has not evolved to assemble from bulk components, and thus we mimicked the biological roles of cofactors RNA and IP6 to define time-dependent protocols that slowly “activate” Gag monomers into assembly-competent states. Our derived titration rate is quite general, applicable to a variety of self-assembling systems. This titration rate serves two general purposes: 1) designing experiments that control subunit concentration either via titrated release or via concentration of activating cofactors and 2) inverting experimental kinetics to extract protein-protein binding rates. We show that, with this additional timescale, we can keep concentrations low and dramatically improve assembly yield for a range of Gag-Gag free energies and rates, illustrating the power of cofactors in defining both assembly kinetics and yield (Fig. 9).

Figure 9.

Phase diagram summarizes how self-assembled complexes will depend on free energies, association rates, and titration rates. From our simulations, we probed regimes with no assembly (open circles), a phase separated equilibrium (half circles), kinetically trapped systems (red X′), and completed assemblies (green checks). With no assembly possible at weak $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}$, the stabilization of these subunit contacts moves from phase separated (a dilute monomer phase and a distribution of lattice sizes) to kinetically trapped, bracketing the narrow (and here unaccessed) region of $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}$ where optimal high-yield assembly is achieved (facing grid). Increasing the on and off-rates (z axis) produces larger intermediates on average when kinetic trapping stalls growth (facing grid, k_c = ∞, bulk). By titrating in components with a slow rate k_c, kinetically trapped intermediates can be circumvented to achieve complete assemblies (axis out of the page). Titration does not affect equilibrium states (no assembly, phase-separated equilibrium), as we reach the same concentrations here. The bottom grid has a fixed association rate k_a = 1 μM⁻¹ s⁻¹ (blue text). Faster titration rates can still circumvent traps if the association rates for subunit binding are fast (left grid, with $\Delta G_{\mathrm{h}\mathrm{e}\mathrm{x}}=-6.4k_{\mathrm{B}}T$). To see this figure in color, go online.

By providing theoretical justifications for our time-dependent titration protocol, we were able to analyze Gag assembly kinetics measured in vitro and provide here the first estimates of bounds on Gag-IP6 and Gag-Gag binding rates. Light-scattering experiments showed clearly that higher concentrations of IP6 lead to faster Gag assembly kinetics (11); this observation agrees with a model of IP6 activating Gag for fast assembly. We could thus interpret the early growth rates in terms of the k_IP6-Gag, estimating a relatively slow binding rate of ∼125 M⁻¹ s⁻¹. By also connecting to our microscopic model of titration-limited Gag assembly, we then estimated the Gag hexamer binding constant in a range of 8 × 10⁴ to 4 × 10⁶ M⁻¹ s⁻¹. Thus, once Gag is activated, it can assemble relatively rapidly into the immature lattice. Although the effect of cofactors in our model is reflected in our choice of Gag-Gag binding parameters, cofactors are not explicitly modeled. Thus, we do not capture how one IP6 can stabilize formation of a 6-Gag hexamer. We simplified this stabilization as a bimolecular event with 6:1 stoichiometry in our theoretical analysis, but it most likely builds through stepwise and cooperative molecular interactions. Including cooperativity adds more parameters that lack experimentally determined values, but our simulations are relatively efficient and can be further informed by molecular simulation. Recent coarse-grained MD simulations support that IP6 can accelerate Gag-Gag interactions, capturing coordination of one IP6 to a hexamer (35). These simulations similarly found evidence of kinetic trapping with IP6 (35), consistent with our finding above that fast activation of Gag by high concentrations of IP6 results in assembly that shows signs of kinetic trapping. While it will be important in future work to explicitly capture IP6 binding and its conditional influence on Gag interactions, our results here already suggest parameters for the interactions with and without IP6 present.

For assembly of HIV immature lattices in cells, both RNA (45) and the plasma membrane (37,46) provide additional means to temporally and conformationally control Gag activation. These are natural future extensions of our model. RNA can stimulate slower activation by introducing yet another timescale of RNA-Gag binding, which we could not quantify here because, in the in vitro experiments, the kinetic assays start after Gag and RNA were seeded together (11). RNA-driven activation could be important for productive assembly, as cellular IP6 concentrations are high, and we showed above that if Gag is activated too quickly then it can easily become kinetically trapped. RNA can also act to tether together components, effectively localizing and concentrating components (47), with the viral genomic RNA outcompeting cellular RNA in promoting assembly (48). Membrane binding not only helps conformationally prime Gag for immature assembly (46), it also protects Gag from degradation, with >85% of the Gag produced in the cytoplasm degraded before adsorbing to the surface (28). Restriction to the plasma membrane will fundamentally concentrate components via dimensional reduction to promote assembly (49), and the localization process introduces additional timescales that can be theoretically predicted (42) to similarly “titrate” the concentration. For the immature Gag lattice, the multiple sources of temporal and localized control most likely provide the robustness of assembly that is needed for such a large structure, protecting it against kinetic trapping and irregular growth.

Overall, our model simultaneously provides structural and kinetic details on the pathways of assembly as controlled by distinct Gag binding sites, further providing a means of quantifying in vitro kinetic measurements of Gag lattice assembly as stimulated by cofactors. Similar modeling studies of clathrin lattice nucleation and growth on membranes (50) and the immature Gag lattice dynamics following budding from the membrane using the same model here (51) demonstrate how this approach can be extended and provide quantitative connections to experimental kinetics. With this same model of the immature Gag lattice, we recently predicted (51) via comparison with experimental data in budded virions that activated Gag hexamer contacts would be in a range of −8 to −10 $k_{B}T$, with rates above 10⁴ M⁻¹ s⁻¹, or −10 to −12 $k_{B}T$ with rates above 10⁵ M⁻¹ s⁻¹, which is fully consistent with our model findings here. These advantages allow us to examine assembly kinetics here across the lifespan of immature Gag, significantly exceeding the timescales of previous computational studies of immature Gag lattices. Ultimately, simulations of self-assembly, whether using rate-based approaches (52) like here or coarse-grained energy functions (53,54), are critical to understand the dynamics of this nonequilibrium process that must proceed from unbound populations to functional assemblies, whether of viral capsids (18,19,20,54,55), nanoparticle assemblies (56), immature HIV lattices (35,36,37,51), or mature HIV capsids (57,58). Simulations can be used to construct simplified kinetic networks through diverse intermediates (59,60), allowing for design of specific pathways to reach target structures (56). Coupling to cellular factors in simulations has in several cases illustrated increased robustness to assembly (31,37,50), with modeling approaches thus offering both general and system-specific guides to interpret and integrate with further quantitative experiments.

Author contributions

M.E.J. designed the research. Y.Q., B.M., and D.E. performed simulations. Y.Q., D.E., B.M., and Y.F. developed the model. Y.Q., D.E., Y.F., S.G., and Z.H.L. developed analysis tools. Y.Q. and D.E. generated figures. Y.Q., D.E., and M.E.J. wrote the manuscript. All authors reviewed the manuscript.

Editor: Margaret Shun Cheung.