Clustering molecular dynamics conformations of the CC’-loop of the PD-1 immuno-checkpoint receptor

Abstract

Molecular mechanisms within the checkpoint receptor PD-1 are essential for its activation by PD-L1 as well as for blocking such an activation via checkpoint inhibitors. We use molecular dynamics to scrutinize patterns of atomic motion in PD-1 without a ligand. Molecular dynamics is performed for the whole extracellular domain of PD-1, and the analysis focuses on its CC’-loop and some adjacent C_α-atoms. We extend previous work by applying common nearest neighbor clustering (Cnn) and compare the performance of this method with Daura clustering as well as UMAP dimension reduction and subsequent agglomerative linkage clustering. As compared to Daura clustering, we found Cnn less sensitive to cutoff selection and better able to return representative clusters for sets of different 3D atomic conformations. Interestingly, Cnn yields results quite similar to UMAP plus linkage clustering.

Graphical Abstract

1. Introduction

1.1. Biomedical background

Tumor cells contain proteins, which are aberrant due to mutations in their genome. The release of those aberrant proteins results in cancer antigen presentation and priming in the lymph node, triggered by various molecules like IL-1, TNF-α or IL-12. Cytotoxic T cells reach the cancer cells via blood vessels and migration into the tumor, recognize the cancer cell via T cell receptor and kill the cells predominantly by use of IFN-γ and T cell granulate [1]. Whatsoever, cancer cells may escape the immune system.

Each killer cell bears a PD-1 receptor on its surface (see Fig. 1), able to act as molecular switch: If ligand PD-L1 binds to PD-1, this receptor triggers a programmed cell death (apoptosis) of its ‘own’ leucocyte, hence the name ‘Programmed Death receptor-1’. This mechanism avoids attacks of regular cells due to discrimination errors, which would otherwise cause autoimmune diseases. Cells prone to be erroneously attacked, may guard themselves by presenting PD-L1 [2], [3].

Fig. 1.

Molecular structure and ligands of immune checkpoint molecule PD-1. Cartoon representations were prepared using VMD version 1.9.3 [21]. Structure of PD-1 (cyan) is shown A: in complex with PD-L1, B: in complex with nivolumab. Dashed circles indicate the CC’-loop, seen in contact with the nivolumab antibody in B. C: PD-1 structure details: The β sheets GFCC’ (colored yellow, orange, red, magenta) and ABED (colored violet, blue, cyan, green) form a two-layer β sandwich with loops connecting the respective β strands (colored silver). The right part of panel C shows the molecule rotated. (Images partly taken from [8] and [5] with permission).

However, this useful mechanism may be exploited by cancer cells. Although they are truly aberrant and should be killed, they can present PD-L1 and thus evade destruction. PD-1 receptors are left silent, although they should act. This mechanism can also be blocked by modern drugs, immune-checkpoint-inhibitors, such as Pembrolizumab or Nivolumab. In previous work we have investigated their molecular action in detail [4], [5], [6], [7], [8]. Checkpoint-inhibitors are pharmacologically designed to bind to PD-1 without activating it. Once bound, they block any further binding of PD-L1 and thus prevent the PD-1 receptor from being activated to kill the leucocyte. As a result, the appropriate immune reaction functions correctly, and cancerous cells are killed as they should be.

1.2. Computational aspects

In the present work we investigate molecular movements of the CC’-loop of the PD-1 checkpoint receptor. PD-1 features several molecular loops, protruding out of the large molecule and moving rather freely in space. These loops are contacted by the ligand, PD-L1, and deformed [5]. It is assumed that such deformations may importantly influence PD-1 function [9], which is mediated via intracellular domains, such as ITIM and ITSM [2], [3], and cooperative effects within the immune synapse. If protruding loops of PD-1 cause any change in these processes, they are of key interest for drug design.

Using molecular dynamics (MD), movements and spatial configurations within biomolecules are simulated in detail and over time [10], [11]. Key parts of a molecule, such as a loop, may deform only slightly around some mean state for a long time, i.e. through many steps of a MD simulation. In this case, such a geometrical state (its 3D coordinates) represents a ‘conformation’ corresponding to a metastable state in the phase space of the molecule [12]. Small distances (root mean square deviations, RMSD, in terms of coordinates) between single simulation frames and a common mean value characterize a metastable state. Note that the ‘mean frame’ never actually exists as a real physical conformation but is rather a (very useful) computational result characterizing a specific shape of a part of a molecule. Many computational frames in vicinity give rise to a cluster and thereby indicate that the molecule has exhibited this shape for a substantial amount of time. Hence, such conformations are often addressed as ‘metastable’ states.

As the MD simulation proceeds, the molecule might suddenly skip to another conformation - different from all previous ones – and remain within the new ‘neighborhood’ for quite a long time.

Each such state may give rise to particular functions within the molecule and represent therefore a target of research. In this work we focus on the C_α-atoms of the CC’-loop of PD-1 and some neighboring C_α-atoms. The CC’-loop itself comprises C_α-Ser71 to C_α-Gln75 between the two beta strands, C and C′, see Fig. 1. We included the N-terminal vicinity C_α-Arg69 - C_α-Met70 and the C-terminal neighbor C_α-Thr76 in our computations (RMSD and clustering). Just for display (see 3D figures in the results section), we additionally show C_α-Tyr 68 as well as C_α-Thr 76, C_α-Asp 77 and C_α-Lys 78.

To computationally isolate important conformational states, a plethora of clustering algorithms have been proposed and their performance analyzed [13]. In the present work we focus on comparing (1) Daura-Clustering [14], (2) common nearest neighbor clustering [12], which is an extension of the previous Daura-Clustering, and (3) a combination of UMAP dimension reduction [15], [16], [17] followed by agglomerative clustering, as tested in our preceding paper [18]. Although Daura-clustering has been specifically designed for locating highly frequented areas in phase space of large molecules, there has been substantial criticism of this method [19]. Its main parameter, the cutoff, must be small enough to ensure that only configurations really close to each other enter the same cluster. Small cutoffs, however, may lose important conformations if the real cluster is fairly wide (large standard deviation within the cluster). The main weakness of original Daura-clustering is the fact that the cutoff is chosen beforehand rather than being adapted to features of the data being clustered. In our previous work [18] we have shown that, due to this weakness, small cutoffs may even generate several clusters out of the same ‘heap’ of conformations – and these clusters then fail to represent substantially different conformations. This is not surprising, as no statistical mechanism has been built into classical Daura-clustering to adapt the procedure to optimum cluster separation.

For the above reasons, an improved version of Daura-clustering, common-nearest-neighbor clustering (Cnn) has been proposed by the same group [12]. It takes two parameters, a distance cutoff, r_Cnn, and a number-of-neighbors cutoff, n_Cnn.

In this work, we test different choices of r_Cnn and compare results and typical features of performance with other algorithms. We evaluate cluster quality statistically and display conformations in 3D coordinates. We depict the distribution of MD-frames in configuration space via UMAP dimension reduction to 2D. In addition, the 2D output from UMAP was subjected to agglomerative clustering, and the result compared to the other two methods.

Different clustering methods are likely to offer different capabilities in detecting changes in conformation which have direct implications for molecular function. These issues could in future be tackled by analyzing MD-runs including PD-1 ligands, be it the natural PD-L1 or therapeutic antibodies, such as Nivolumab and Pembrolizumab. Comparing the features of different cluster analyses, as discussed here, are considered a helpful basis for these coming studies.

2. Methods

2.1. Preparing the molecular structures

The structure of PD-1 without ligand, 3RRQ, is not complete in the protein data bank (PDB; https://www.rcsb.org/ [20]) and therefore had to be manually curated. We added the C′D-loop (residues 65–92) from the PD-1-part of 5GGS and the N-loop (residues 25–34) from 5WT9, by copying and pasting the data into the PDB-file of 3RRQ after aligning the respective structures with VMD [21], [22], [23]. As a result, our PD-1 included the residues 25–149, representing the complete extracellular domain. We used VMD to display the molecular structure, see Fig. 1.

The protonation states at pH 7.0 were determined using the H++ Server (http://biophysics.cs.vt.edu/) [24]. Strands, sheets, and loops were assigned according to the classification of the Protein Feature View applet available within the 4ZQK record of the PDB.

PD-1 consists of several beta strands with loops in-between. The CC’-loop, consisting of residues 71–75, interacts with the natural ligand PD-L1 [9] and is the focus of this work. Previous work on this interaction has been done experimentally [25] and also by molecular dynamics [5], [6], [26].

2.2. All-atom molecular dynamics

We performed an all-atom MD simulation using GROMACS 2021.2 [27], the Amber99sb-ildn force field [28] and an explicit water model, as described previously [29]. A rhombic dodecahedron was chosen as simulation box, with a minimum distance of 2 nm between the respective molecules and the box boundaries. PD-1 was solvated in TIP3P water [30] and solute molecules were replaced by sodium and chloride ions to reach a physiological salt concentration of 0.15 mol/L.

Energy minimization was performed by steepest descent and systems were then equilibrated at NVT and NPT for 100 ps (time step 2 fs) each. NVT equilibration was carried out at 310 K, using a Berendsen-thermostat [31] with a time constant of 0.1 ps and position restraint MD. NPT equilibration was controlled by a Berendsen-barostat [31] set to 1 bar and a time constant of 1.0 ps.

The production run was carried out for a total simulation time of 600 ns with a time step of 2 fs using the LINCS algorithm [32] for constraining bonds to hydrogen atoms. Van der Waals interactions were cut off at 1.47 nm. Likewise, a cut-off distance of 1.4 nm was applied for the short-range neighbor list in the Verlet scheme [33]. Electrostatic interactions were accounted for by the particle-mesh Ewald (PME) algorithm [34], with a cut-off of 1.4 nm. Temperature coupling was implemented via the velocity-rescaling algorithm [35] at a temperature of 310 K, and pressure coupling at 1 bar was accomplished by the Parrinello Rahman algorithm [36] with a time constant of 2 ps. 30000 MD-frames were obtained by saving coordinates, velocities, forces, and energies every 20 ps to a trajectory file.

2.3. Preprocessing

In the following, we use ‘frame’ for reasons of conciseness to describe a set of 3D coordinates of all atoms at one given point in time.

The first 100 ns of the 600 ns MD trajectory were discarded, leaving 500 ns with 25.000 frames for evaluation, out of which we considered every tenth frame (stride = 10), yielding 2500 frames. Each frame at time t_i was fitted to the first frame (at t₁) of the trajectory, according to minimum root mean square deviation, RMSD_r:

$${RMSD}_{\mathrm{r}}\left(t_i\right)={\left[\frac{1}{N_{\mathrm{r}}}\sum _{n=1}^{N_{\mathrm{r}}}{\Vert {\mathbf{x}}_n\left(t_i\right)-{\mathbf{x}}_n\left(t_1\right)\Vert }^2\right]}^{1/2}\to Min$$ (1)

with x_n(t_i) denoting the position of atom n at time t_i and the summation running only over a ‘rigid part’ of the molecule, i.e. N_r C_α-atoms of the backbone (β-strands and α-helices) of PD-1.

To investigate the dynamics of a region of interest (ROI) of the molecule, e.g. the CC’-loop, after performing above fit, only the atoms within the ROI are further considered. Daura clustering as well as Cnn-clustering are based on relative distances between pairs of MD frames, i and j:

$${RMSD}_{\mathrm{ROI}}(t_i,t_j)={\left[\frac{1}{N_{\mathrm{ROI}}}\sum _{n\in \mathrm{ROI}}{\Vert {\mathbf{x}}_n\left(t_i\right)-{\mathbf{x}}_n\left(t_j\right)\Vert }^2\right]}^{1/2}$$ (2)

where the summation runs over all N_ROI atoms within the region of interest ($n\in \mathrm{ROI}$), in our case 8 C_α-atoms (C_α-69 to C_α-76) of the PD-1. RMSD_ROI is evaluated, following an optimum relative positioning (fitting) of frames i and j, with respect to the rigid parts of the molecule, see equ. (1). This fit needs to be performed for each pair of frames i, j, which is extremely time consuming and was accomplished by parallel processing. Values of pairwise RMSDs are distributed as shown in the curves ‘overall’ in Fig. 2 and Figure A 1.

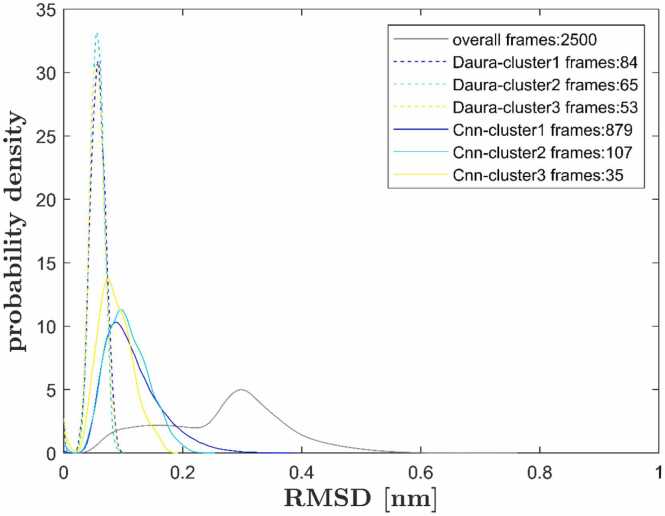
Fig. 2.

Probability distribution of pairwise RMSD for the CC’-loop as ROI. Distribution of all 2500 frames shown in black. Equal distance cutoffs for Daura and Cnn-clustering (r_c = r_Cnn = 0.05 nm), common neighbor number cutoff n_Cnn = 1. Clusters 1–3 considered, see the legend. Probability distributions were obtained from kernel density estimates [45], [46].

2.4. Daura clustering

Daura-clustering has been invented to group molecular conformations based on their similarity in terms of RMSD [14]. We have described and used it in previous work [5], [6]. It takes only one parameter, the cutoff radius, r_c. To generate the first cluster, the RMSDs between all pairs of frames of an MD trajectory are scanned to find frame i_max which has the maximum number of neigbours j within the cutoff distance

$$RMS{D}_{\mathrm{ROI}}(t_{i_{\max }},t_j)\le r_c$$ (3)

These neighbors together with frame i_max comprise the cluster, and frame i_max plays the role of a seed. All frames of the cluster are taken out of the RMSD-matrix and the procedure is repeated to generate subsequent clusters, until no frames are left. The sizes of Daura clusters thus greatly increase with r_c, and they result in descending sizes, one after the other. In our previous work [18] we have elaborated on this and its implications.

2.5. Common nearest neighbor clustering (Cnn)

Each cluster starts like in Daura clustering, with a preset cutoff, r_Cnn. According to the inventors’ notation, r_Cnn ≙ nndc, which stands for ‘nearest neighbor distance cutoff’. After the ‘initial’ building of the cluster, all frames outside this ‘initial cluster’ are inspected, if they have at least n_Cnn common nearest neighbors with one of the frames already belonging to the cluster. Again, in terms of the inventors, n_Cnn ≙ nnnc, which stands for ‘nearest neighbor number cutoff’. If common neighbors exist, such a frame is added to the cluster. This procedure is repeated until no frame outside the current cluster can be found sharing (at least n_Cnn) common neighbors with some frame inside the current cluster. Once the cluster is thus completed, all its frames are removed from the RMSD matrix and within the remaining frames, the build of the next cluster is initiated.

The Cnn mechanism reacts well on the local density of conformations (frames) in phase space (i.e. on a feature of the data to be clustered) and lets clusters grow until all configurations within the neighborhood have been captured. This is considered the major advantage compared to Daura. Of course, for large n_Cnn, Cnn converges to conventional Daura clustering.

2.6. UMAP plus linkage clustering

Daura clustering as well as Cnn are straight forward and their practical usability widely accepted. However, doubts have repeatedly been raised, based on theoretical arguments: Both draw on pairwise RMSD-distances, computed in high dimensional space, see Fig. 2 for its distribution. With the CC’-loop as ROI, we have 8 × 3 = 24 cartesian coordinates (of 8 C_α atoms) entering equ. (2). Theoreticians argue that, in higher dimensions, ‘almost every point lies on the surface’ and RMSD distance-based clustering is bound to fail. First, dimensionality should be reduced. Then, as a second step, distance based clustering in low (say 2) dimensions – seems appropriate. To scrutinize this issue, we performed UMAP (short for Uniform Manifold Approximation and Projection) dimension reduction [15], [16], [37], [38] from 24 C_α-coordinates towards 2 components. We used the defaults provided by the MATLAB procedure ‘run_umap’ [37].

The two components (Comp₁, Comp₂) resulting from UMAP for each conformational frame may be plotted conveniently, see Fig. 3.

Fig. 3.

UMAP dimension reduction 24 dim → 2 dim. 24 Cartesian coordinates of 8 C_α-atoms comprising the CC’-loop are dimensionally reduced and plotted in 2D (Comp 1, Comp 2). Dots represent MD-frames.

Although in Fig. 3 presumable clusters are fairly obvious to the naked eye, this may be very different with other data. To establish a method more generally applicable, we subjected the components (Comp₁, Comp₂) to linkage clustering using the method ‘WARD’. Agglomerative clustering starts from grouping individuals and proceeds upwards to the top of the tree. By itself, agglomeration does not yield clusters, but the tree may be pruned at an appropriate cutoff (level) to yield clusters. We pruned the tree at series of different cutoffs, each yielding a certain number of clusters. For each choice, clustering quality was evaluated via the Davies-Bouldin [39] and the Silhouette [40], [41] indices, and the optimum number of clusters (k_opt) determined by the MATLAB procedure ‘evalclusters’. Of note, Davies-Bouldin and the Silhouette criteria yielded the same results.

Summing up, we compared Daura and Cnn with the UMAP-output (Comp₁, Comp2₂), clustered according to linkage and then pruned into k_opt clusters (labelled ‘UMAPLnk’ in the results section).

3. Results

3.1. Daura and Cnn for a small cutoff

Cnn’s improvement on Daura lies in the frames added to Daura clusters, based on neighborhood relations. The ab initio Daura cutoff yields an initial guess, designating an area of high density around a seed. However, if the cutoff is chosen too small for the data investigated, the Daura criterion will not absorb all frames that ‘actually’ should belong to that cluster. Fig. 4 shows MD frames located in 2D according to UMAP, but colored according to Daura with r_c = 0.05 nm. None of the first 3 Daura clusters leaves the left heap, which, according to UMAP, should represent closely related frames (‘should be a cluster’).

Fig. 4.

Daura clustering shown on pattern generated by UMAP dimension reduction. Points, corresponding to 2500 MD frames of atomic conformations, are located in 2D according to UMAP-results (Comp 1, Comp 2) and colored according to Daura clustering with r_c = 0.05.

Cnn behaves differently, as demonstrated in Fig. 5 for the same cutoff, r_Cnn = 0.05 nm. The initial Daura-guess is shown as solid red dots (legend: Cnn-ini-cluster 1), comprising 84 frames. Due to the adding mechanism, Cnn 1 receives 795 additional frames, for a total of 879 frames constituting the completed Cnn 1. Cnn 1 extends over the whole heap and thus confirms the intuitive visual guess following from the 2D arrangement of frames via UMAP (we call these arrangements ‘UMAP-patterns’ for brevity in the following). As a result, only 10% of frames in Cnn 1 stem from the ‘initial guess’ (Daura with hard cutoff) and 90% from adding (if at least one common neighbor exists). Concomitantly, the RMSD distribution within Cnn 1 broadens, cf. the dashed blue curve (Daura) versus the solid blue curve (Cnn) in Fig. 2.

Fig. 5.

Common nearest neighbor clustering with r_Cnn = 0.05, and n_Cnn = 1, shown on UMAP dimension reduction. Points, corresponding to 2500 MD frames of atomic configurations, are located in 2D according to UMAP-results (Comp 1, Comp 2) and colored according to Cnn clustering. Solid dots represent frames of initial clusters, open circles show added frames.

When initiating the second cluster, Cnn starts from a completely different situation compared to Daura. While Daura 1 had only 84 frames taken out of further clustering, Cnn 1 has precluded 879 frames from further clustering. As a consequence, initiating Cnn 2 finds only 9 frames left fulfilling the hard cutoff criterion, shown as green solid dots in Fig. 5. For comparison, 65 frames were still available for Daura 2. But Cnn 2 then receives 98 on top of the initial guess to end up with 107 frames in total. This growth due to neighborhood is about ten-times the initial size, fairly similar to the relative growth of Cnn 1. Notably, Cnn 2 is significantly smaller than Cnn 1 (only 12% of its size). Note that the second cluster, Cnn 2, already penetrates into another heap of the UMAP-pattern.

RMSD distributions of the second clusters show differences between Daura and Cnn similar to those seen for the first clusters, see Fig. 2: Cnn 2 exhibits a broader RMSD distribution than Daura 2 (cyan curves).

With the 3rd clusters, differences between Daura and Cnn become even more apparent: While Daura 3 still finds 53 frames (about half the size of Daura 1), Cnn 3 initiates with only 8 frames (blue solid dots, in Fig. 5) and adds no more than 27 frames (blue open circles), arriving at just 35 frames altogether.

Since clusters with very few frames would not represent a significant portion of phase space, Cnn clusters with fewer frames were not considered. Table 1 gives an overview of cluster sizes.

Table 1.

Frames in first 10 clusters from Daura and Cnn, and 2 clusters from UmapLnk. For each clustering method we report the number of frames, first per cluster (column ‘total’) and then cumulative (column ‘cum’). For Cnn, we additionally display the number of initial frames and added frames. UMAPLnk covers all 2500 frames in 2 clusters (due to splitting the whole tree). For Cnn with r_Cnn = 0.1 nm, 2 clusters already represented 2488 frames, i.e. 99.5% of frames, whereas for Daura it takes as many as 10 clusters to represent not more than 65% of frames (see numbers in bold). For the small cutoff, both, Daura and Cnn are unsatisfactory, harvesting only 414 and 1224 frames, respectively.

	rc= rCnn = 0.05 nm						rc= rCnn = 0.10 nm
Cluster nr	Daura		Cnn				Daura		Cnn				UMAPLnk
	total	cum	initial	added	total	cum	total	cum	initial	added	total	cum	total	cum
1	84	84	84	795	879	879	645	645	645	297	942	942	943	943
2	65	149	9	98	107	986	213	885	213	1333	1546	2488	1557	2500
3	53	202	8	27	35	1021	131	989	3	0	3	2491	-	-
4	41	243	7	22	29	1050	122	1111	1	0	1	2492	-	-
5	34	277	6	5	11	1061	113	1224	1	0	1	2493	-	-
6	33	310	6	21	27	1088	111	1335	1	0	1	2494	-	-
7	33	343	5	6	11	1099	84	1419	1	0	1	2495	-	-
8	26	369	5	1	6	1105	73	1492	1	0	1	2496	-	-
9	25	394	7	6	13	1118	72	1564	1	0	1	2497	-	-
10	20	414	5	1	6	1224	70	1634	1	0	1	2498	-	-

3.2. UMAP plus linkage agglomerative clustering

As opposed to Daura and Cnn, UMAP plus linkage agglomeration (UMAPLnk) does not take a cutoff as input, neither for RMSD-distance nor for the number of common neighbors. The only choice required is the level where to cut the tree or, in other words, how many clusters should result. As explained above, we delegated this choice to statistics, in particular the Davies-Bouldin index. For our simulation data, 2 clusters was the optimum cut, as shown in Fig. 6. By the way, the Silhouette criterion yielded equal results. Note that this formal outcome almost perfectly underpins what one would guess intuitively. Of course, the cluster UMAPLnk 2 (shown in green) does not appear totally compact. One might visually perceive at least two sub-areas (upper and lower) within the green heap.

Fig. 6.

UMAP followed by agglomerative linkage clustering (UMAPLnk). Note that no cutoff needs to be selected for this clustering method. The legend gives number of frames within each cluster (summing up to 2550).

3.3. 3D molecular structures

While UMAP-patterns are 2-dimensional projections of RMSD, the C_α-atoms of the CC’-loop may also be displayed in 3D. As could be expected, mean frames (i.e. coordinates of each C_α-atom averaged over all frames within the respective cluster) are very similar for Daura 1 to Daura 3, see Fig. 7. This finding underpins in terms of atomic coordinates that the first few Daura clusters remain within the same area of phase space.

Fig. 7.

Daura clusters for r_c = 0.05 nm. C_α-atoms are shown for the region of interest (Arg 69 to Thr 76) and some adjacent backbone (N-terminal side: Tyr 68, C-terminal side: Asp 77, Lys 78, Leu 79), to provide a glimpse into the neighborhood. These adjacent C_α-atoms were only plotted here but did not enter RMSD and clustering calculation. For each C_α-atom, atomic coordinates (x,y,z) were averaged over the frames within each Daura cluster and displayed as heavy dots, see the legend. Additionally, one single frame is shown for each cluster (thin lines).

The result of Cnn clustering is totally different, see Fig. 8. Even for the small cutoff r_Cnn = 0.05 nm, the mean frame of Cnn 2 represents a 3D shape significantly different from Cnn 1, obviously characteristic for (part of) the second heap in the UMAP-mapping.

Fig. 8.

Mean frames of the first two Cnn clusters for r_Cnn = 0.05 nm and n_Cnn = 1.

Finally, average frames of UMAPLnk clusters were obtained, see Fig. 9. As explained above, UMAPLnk does not involve selection of a cutoff, and the agglomeration tree was cut (based on statistical criteria) to yield two clusters. Between these, differences are clearly visible. However, deviations seem much smaller than those seen with Cnn.

Fig. 9.

Mean frames of the two UMAPLnk clusters.

For an explanation, one must bear in mind that cutting an agglomerative tree at any level, always generates exhaustive clusters: Each of the 2500 frames must belong to one of the clusters and no frames remain un-clustered, irrespective of the level where the cut is placed. In consequence, the sharpness of low-order UMAPLnk clusters decreases as compared to those methods which exclude (i.e. do not cluster) frames if they fail to fit close enough.

In summary, for Daura and Cnn, one needs to preset cutoffs (r_c, r_Cnn and n_Cnn), which influences the building and contents of clusters. Additionally, one selects how many (of the generated) clusters to consider. This in fact means disregarding frames, that did not fit into these first few clusters under considereation. This approach accommodates the notion that some frames might not qualify for clustering at all, since they represent extravagant configurations (‘singles’) in phase space – not many others come close. No cluster can (and should) be formed there, and if such frames are forced into some existing cluster, they – of course – broaden its internal distribution and may even deteriorate its characteristics. Hence, leaving out certain frames from clustering may be desirable. As opposed to this, UMAPLnk requires one to select the desired number of clusters, which is achieved by choosing a corresponding cut of the tree. Note that the whole agglomerative tree is generated before being cut.

3.4. Increasing the cutoff

From Fig. 4, Fig. 7 and Fig. 8 it is evident that r_c = 0.05 is far too small to generate Daura clusters representative for the whole phase space of the simulation. Not even the first three clusters taken together, completely absorb the left heap in the UMAP-pattern, and following clusters are even smaller, as was already displayed in our previous work [18] and is likewise evident in Table 1. Cnn performs better, but also fails to yield a satisfactory set of clusters for r_Cnn = 0.05 nm, see Table 1 and Fig. 5. Cnn 1 indeed covers the first heap in the UMAP-pattern, and Cnn 2 touches configurations within the second heap, but fails to exhaust them. The following clusters (Cnn 3, etc.) rapidly shrink in size and – even if taken together - fail to cover a reasonable portion of 2500 frames. Note that frames not contained in any of the clusters considered are shown as grey dots. In fact, beyond Cnn 2, Cnn ends up similar to Daura - with many very small clusters. Considering more of them would turn grey dots in Fig. 5 step by step into new cluster colors and let the right heap appear as a multicolored, dotted area.

Needless to say, larger cutoffs need to be considered, and we continue with r_c = r_Cnn = 0.1 nm.

Fig. 10 displays Daura clusters for r_c = 0.1 nm. For this cutoff, the Daura 1 is significantly larger (645 frames) than for r_c = 0.05 nm, and covers a reasonable portion of the left heap in the UMAP-pattern. However, Daura 1 still does not exhaust it. Surprisingly however, the second Daura cluster does not take what has been left over but rather starts in a more distant area (right heap) and assembles 213 frames there. It takes Daura 3 to restart clustering within the left heap (131 frames), see the light green arrow in Fig. 10. Also, some frames of Daura 2 expatriate/move to an area that later becomes the realm of Daura 4. Implications of these findings will be discussed later.

Fig. 10.

Daura clustering for r_c = 0.1 nm. Points, corresponding to 2500 MD frames of atomic configurations, are located in 2D according to UMAP-dimension reduction (Comp 1, Comp 2) and colored according to Daura clustering. Arrow in light green: unexpected frames of Daura 3 in the realm of Daura 1. Arrow in beige: unexpected frames of Daura 2 in the realm of Daura 4.

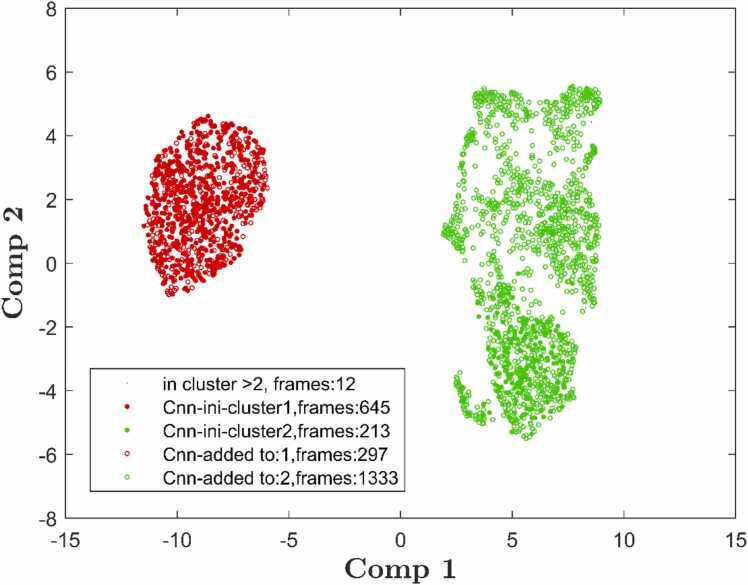
Fig. 11 again elucidates the Cnn process: The initial form of Cnn 1 covers 645 frames, see the solid dots. Note that the initial set of Cnn equals the corresponding Daura 1 only for the first cluster. The neighborhood mechanism of Cnn adds 297 frames (open red circles), out of the same heap. Thus, the Cnn mechanism covers UMAP’s results well. Then Cnn 2 continues within the right heap with 213 initial frames, and adds 1333 more, due to neighborhood. Remarkably, even though the right heap is not entirely compact, the neighboring mechanism of Cnn succeeds in bridging these gaps: Cnn works as designed.

Fig. 11.

Common nearest neighbor clustering with r_Cnn = 0.1 nm and n_Cnn = 1 shown on UMAP-pattern after dimension reduction. Solid dots represent frames of initial clusters, open circles show added frames.

Cnn 3 allocates only 3 frames, and Cnn 4 to Cnn 8 just one frame each, see those few grey points ‘lost’ within Cnn 1 and Cnn 2. Again, it calls for some consideration why these frames were not included in the clusters already existing (Cnn 1 or Cnn 2).

As indicated by mapping onto the UMAP pattern (Figure 10), for r_c = 0.1 nm Daura 2 enters a different realm of configurations, clearly seen in 3D display, see Fig. 12. Daura 3, however, slips back into the realm of Daura 1, as consistently shown by 2D and 3D display. This effect will be adressed in the discussion.

Fig. 12.

Mean frames of Daura clustering with r_c = 0.1 nm.

Cnn clustering with r_Cnn = 0.1 and n_Cnn = 1 performs stable and yields 2 sound clusters, leaving only 12 frames behind (942 + 1546 = 2488), see Fig. 13 and also Table 1. This almost equals the UMAPLnk result, shown in Fig. 6 and Fig. 9.

Fig. 13.

Mean frames of the first two Cnn clusters for r_Cnn = 0.1 nm.

Summing up, r_Cnn = 1 nm provides satisfactory performance of Cnn, and a further increase seems undesirable. On the contrary, conventional Daura clusters based on r_c = 0.1 nm still lack coverage of a representative portion of frames. Further increases of r_c to 1.5 nm and 2.0 nm were tested, and Daura clusters conquered additional areas step by step, as already described in our previous paper [18].

3.5. Comparing corresponding clusters obtained by different clustering methods

Up to now we have compared clustering methods on the whole, e.g. regarding the sizes of clusters generated. Now we evaluate differences between corresponding clusters, e.g. the difference of cluster 1 when obtained by Daura, Cnn or UMAPLnk. We recall that UMAPLnk requires to preselect the number of clusters. Since 2 Cnn clusters were found optimum, we investigate the first two clusters also for Daura and Cnn. For Daura and Cnn, selecting different cutoffs (r_Cnn = r_c) changes results drastically. Fig. 14 displays average frames of clusters: panels A and B show the differences between all three methods for a small cutoff r_Cnn = r_c = 0.05 nm. Evidently, Daura clustering does not generate its second cluster significantly different from the first one. As long as the Daura mechanism has not exhausted all frames in the vicinity, it generates more and more clusters with very similar structures (and mean frames). A very small cutoff prevents frames to enter a cluster even if they are not that far apart according to RMSD. As a consequence, Daura stops to aggregate into cluster 1 as early as after 84 frames. Cnn, being an improvement of Daura developed by the same group, additionally considers neighborhood and, even when operating with an equally small cutoff as Daura, harvests many ‘added’ frames (795) within cluster 1, see Table 1 and Fig. 14, Panel A. Cnn ends up with almost the same number of frames for cluster 1 as UMAPLnk.

Fig. 14.

Differences in Clusters 1 and 2, as obtained by Daura, Cnn and UMAPLnk. Note that UMAPLnk-clusters are unaffected by the cutoff selected for Daura and Cnn. Quantitative estimates of cluster difference are given in Table 2.

Regarding the most interesting outcome of clustering, i.e. mean frames, all three methods yield almost equal results for cluster 1, see both left panels of Fig. 14.

Turning to cluster 2, differences between methods become spectacular: While both Cnn and UMAPLnk yield clusters 2 very different from clusters 1, Daura stays close to its cluster 1, see the mean frames in Fig. 14, panel B. Clearly, Daura still samples from conformations fairly similar to those in cluster 1 – yielding a very similar mean frame.

For a larger cutoff, r_Cnn = r_c = 0.1 nm, differences in results between the three methods vanish: Not only the mean frames of clusters 1 come out similar with all three methods but also clusters 2 exhibit fairly similar mean frames, see Fig. 14, panels C and D, respectively.

The results displayed in Fig. 14 may also be underpinned numerically, by drawing on the concept of the Davies-Bouldin index [39] for cluster separation. A specific pair of clusters, C_k and C_l, is evaluated regarding separation as follows: The distance (in our case: multidimensional distance), d_k,l, between mean frames is computed via

$${\mathit{d}}_{\mathit{kl}}=\sqrt{\frac{\mathbf{1}}{{\mathit{N}}_{\text{ROI}}}\sum _{\mathit{n}\in \text{ROI}}{‖{〈{\mathit{x}}_{\mathit{n}}〉}_{{\mathit{C}}_{\mathit{k}}}-{〈{\mathit{x}}_{\mathit{n}}〉}_{{\mathit{C}}_{\mathit{l}}}‖}^{\mathbf{2}}}$$ (4)

where ${〈〉}_{C_k}$ means the average over all frames of cluster C_k. Next, the distance dSF(t_i) of each single frame in a cluster from the respective mean frame is computed

$$\mathit{dSF}\left({\mathit{t}}_{\mathit{i}}\right)=\sqrt{\frac{\mathbf{1}}{{\mathit{N}}_{\text{ROI}}}\sum _{\mathit{n}\in \text{ROI}}{‖{\mathit{x}}_{\mathit{n}}\left({\mathit{t}}_{\mathit{i}}\right)-〈{\mathit{x}}_{\mathit{n}}〉‖}^{\mathbf{2}}}$$ (5)

and its standard deviation S_k over all frames in the cluster. S_k is obtained for each of the clusters considered. Next, for each pair of clusters (in a given set of clusters) we compute the ratio

$${\mathit{dbi}}_{\mathit{kl}}=\frac{{\mathit{S}}_{\mathit{k}}+{\mathit{S}}_{\mathit{l}}}{{\mathit{d}}_{\mathit{kl}}}$$ (6)

Clearly, smaller values of dbi_kl indicate better separation of clusters. In a final step, the worst separation (i.e. the largest value of dbi_kl) is picked for each cluster, k, and these values are averaged over all clusters to obtain the Davies-Bouldin index DBI for the whole set of clusters.

As mentioned above, different numbers of clusters can be considered as a set, each set yielding a different DBI. The smallest DBI obtained, indicates the optimum number of clusters to include. We performed this analysis for all clustering methods described in this work.

Besides the quality of a whole set of clusters obtained by one given method, it is also interesting to evaluate the difference between corresponding clusters obtained by different methods, e.g. C_k ≙ Daura 1 and C_l ≙ Cnn 1. We note that the ratios dbi_kl, built to compute the Davies-Bouldin index, are closely related to ordinary two-sample t-statistics. The t-statistics considers the inverse ratio and uses weighted standard deviation rather than the plain sum (as the Davies-Bouldin index does). The weighted standard deviation, S_kl, is obtained from [42], [43]

$${\mathit{S}}_{\mathit{kl}}=\sqrt{\frac{{\mathit{S}}_{\mathit{k}}^{\mathbf{2}}\left({\mathit{N}}_{\mathit{k}}-\mathbf{1}\right)+{\mathit{S}}_{\mathit{l}}^{\mathbf{2}}\left({\mathit{N}}_{\mathit{l}}-\mathbf{1}\right)}{{\mathit{N}}_{\mathit{k}}+{\mathit{N}}_{\mathit{l}}-\mathbf{2}}}$$ (7)

with N_k and N_l being the number of frames in each cluster.

Finally, as a measure of mean-frame equality, a quantity similar to a generalized t-statistics may be constructed as

$${\mathit{t}}_{\mathit{kl}}=\frac{{\mathit{d}}_{\mathit{kl}}}{{\mathit{S}}_{\mathit{kl}}\sqrt{\frac{\mathbf{1}}{{\mathit{N}}_{\mathit{k}}}+\frac{\mathbf{1}}{{\mathit{N}}_{\mathit{l}}}}}$$ (8)

t_kl quantifies the concordance of clustering results (i.e. mean frames), in the light of single frames’ variabilities, see Table 2.

Table 2.

Differences between corresponding clusters when obtained by Daura, Cnn and UMAPLnk. Values represent dbi_kl evaluated via Eq.(6) and t_kl (in parenthesis) obtained via Eq.(8). Results reflect what is visually evident from Fig. 14. Larger values of dbi_kl and likewise smaller values of t_kl indicate better agreement between methods. Note that UMAPLnk produced not more than 2 clusters, and hence only the first two clusters of each method were included in the comparison.

dbikl(tkl)		cluster 1		cluster 2
		Cnn	UMAPLnk	Cnn	UMAPLnk
cutoff = 0.05 nm	Daura	1.78 (288)	1.83 (273)	0.17 (896)	0.33 (1182)
	Cnn	0	24.68 (73)	0	1.05 (563)
cutoff = 0.1 nm	Daura	9.06 (170)	8.99 (171)	0.83 (1095)	0.83 (1099)
	Cnn	0	217 (8.66)	0	149 (20.8)

4. Discussion

The main focus of the paper is the difference in performance of three clustering algorithms, analyzed in the context of PD-1, as an example. Naturally, explicit physiological conclusions cannot be drawn from this work. However, the performance characteristics of methods evaluated here will guide coming studies aiming to pinpoint differences in molecular dynamics induced by different ligands of PD-1.

4.1. Differences between Daura and Cnn

Common nearest neighbor clustering was invented to overcome known weaknesses of Daura clustering. It was designed to draw on local density rather than absolute distances in terms of RMSD, and thereby let the algorithm adapt to features of the actual data investigated. As we could demonstrate, Cnn works as designed and yields results far better than conventional Daura. In particular, sizes of clusters increase massively, even for the same cutoff (r_Cnn = r_c).

Considering the difference in mechanisms, the following explanation is at hand: Due to adding, Cnn 1 is able to absorb the majority of ‘should be’ members and yields a more comprehensive cluster 1. Cnn leaves behind only those that really are too different to be joined. Conversely with Daura: With a small cutoff, cluster Daura 1 absorbs only very close frames and excludes all others. As a result, these frames turn up in the second Daura cluster, which is therefore typically not much smaller than the first one.

The Cnn mechanism absorbs more frames in the first clusters, and the sizes of following clusters decrease rapidly, i.e. much faster than with Daura. After the first few clusters, only a few frames remain, unable to qualify as seeds for further clusters of reasonable size, see Table 1. Thus, Cnn terminates itself quite markedly. It renders unnecessary to deliberately choose a maximum number of clusters for consideration, as is necessary with Daura, which ‘keeps going’, with cluster size decreasing only gradually.

The above effects mean that Daura (and to some extent also Cnn) leaves certain frames un-clustered (or relegates them into mini-clusters of 1 frame each). This may mirror the fact that - in a trajectory - certain portions might represent an ongoing molecular deformation rather than a metastable state. Only the latter would be worth of giving rise to a cluster of its own. In this sense, Daura and Cnn may be considered ‘realistic’. On the other hand, agglomerative clustering (UMAPLnk) forces all frames into clusters: This is easy to handle for a researcher, since only the number of clusters needs to be selected, which can be based on statistical criteria.

Finally, 3D display confirmed possible negative features of Daura clustering, even for a moderate cutoff, r_c = 0.1 nm. Already the mapping onto the UMAP-pattern (Fig. 10) revealed that Daura 3 (light green dots) is harvested from virtually the same area (left heap) as Daura 1 (red dots). The 3D display (Fig. 12) confirms this misleading allocation, showing almost identical mean frames of Daura 1 and Daura 3. While Daura 2 clearly represents a new cluster of conformations, Daura 3 slips back into the realm of Daura 1.

4.2. RMSD-based clustering versus dimension reduction based clustering

It was not a coincidence that we chose UMAP-patterns to map clusters for display. Theoretical arguments have been put forward [44] that RMSD, although widely used, might be an unsuitable measure to deal with multi-atom coordinates. In fact, performing the method of agglomerative clustering after dimension reduction of coordinates offered a fairly promising approach, in particular since it does not require input parameters (such as r_c or r_Cnn) to be chosen. After all, choosing suitable parameters may be quite tedious and, more importantly, add deliberation to an evaluation.

Beside this advantage of UMAPLnk there are some interesting differences in performance. Unexpectedly, we found frames located in the midst of UMAP heaps that remained un-clustered by Cnn, see the grey dots near Cnn-colored frames in Fig. 5. Cnn was performed with r_Cnn = 0.05 nm, n_Cnn = 1, and terminated after Cnn 3. Some of these un-clustered frames seem much closer to clustered frames than clustered frames among themselves. How can it happen that frames much more distant are included in the same Cnn cluster (share neighbors), and other frames - seemingly much closer - are left out?

To scrutinize this effect, we have selected a few such examples and re-evaluated RMSDs by hand. It turned out that RMSDs of such seemingly close pairs were indeed beyond r_Cnn, and the implementation of Cnn had worked as designed. In consequence, points may be located very closely within a UMAP-pattern, although their distance in terms of RMSD is significant.

In terms of 3D atomic coordinates, this is an interesting finding. We must bear in mind, that $RMS{D}_{\mathrm{ROI}}(t_i,t_j)$ consists of (squared) distances, summed over the ROI, in our case 8 C_α-atoms of the CC’-loop, see Eq. (2). A large RMSD may come about either by a moderate deviation of all C_α-atoms, or else, by a large deviation of only one (or a few) C_α-atoms. For molecular function, it might make a decisive difference if the loop as a whole is deformed slightly or if a single C_α-atom widely protrudes out of an otherwise stable loop. Since RMSD is a sum of squares, single but larger protrusions will receive more weight – even if the protrusion averaged over the loop might be the same. UMAP is also a non-linear procedure, and we do not yet know precisely how it deals with atomic coordinate data as compared to RMSD. A more detailed analysis would be necessary for an answer.

Funding

No funding used.

CRediT authorship contribution statement

Wolfgang Schreiner: Conceptualization, Methodology, Software, Formal analysis, Investigation, Writing – review & editing, Visualization, Supervision. Rudolf Karch: Methodology, Investigation, Software, Writing – review & editing. Michael Cibena: Software, Writing – review & editing, Visualization. Lisa Tomasiak: Software. Michael Kenn: Conceptualization. Georg Pfeiler: Conceptualization.

Declaration of Competing Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix

See Fig. A 1.

Fig. A 1.

Probability distribution of pairwise RMSD for the CC’-loop as ROI. Distribution of all 2500 frames shown in black (equal to Fig. 3). Equal distance cutoffs for Daura and Cnn-clustering (r_c = r_Cnn = 0.1 nm), common neighbor number cutoff n_Cnn = 1. Clusters 1–3 considered, see the legend. Probability distributions were obtained from kernel density estimates [45].