Abstract

Analytical models are very important to understand physical, chemical, and biological phenomena. In many cases, obtaining an analytical model is a complex, even an impossible task. In this work, an analytical model for thermal lens spectroscopy has been developed. The model considers light absorbing liquids, a laser pulsed beam as the heat source, timescale thermal regime, and small phase change produced by heating. A simplification for low-absorption samples is obtained. A complete theoretical study of their utilization is shown. Measurements of the thermal diffusivity of water–ethanol sample mixtures in the liquid phase are analyzed. These values for pure substances are in good agreement with those reported in the literature. Our methodology could be very useful in the analysis of the optical and thermal properties of liquids.
Introduction
When a semitransparent material is illuminated with a coherent light source, the light is partially absorbed along the beam path, producing a temperature gradient with the maximum value at the center of the beam cross-section. This gradient induces a change in the thermal refraction index, and a similar effect to a lens appears. The monitoring of this lens-like behavior allows the determining of the local increase of the temperature and is the basis for what is known as thermal lens (TL) spectroscopy.1−5 This technique has become one of the most successful methodologies for the optical and thermal characterization of semitransparent liquid6 and solid materials, holography,7 and in the monitoring of a large variety of processes. The success of this methodology is based on its high sensitivity and versatility, which allows being used in combination with other techniques. The theoretical foundations of the technique were developed several decades ago. The analytical approach developed by Shen et al. is the most successful in the interpretation of the TL phenomena induced by a continuous laser beam.8 In this kind of experiment, when the excitation laser is turned-on, the change in the thermally induced lens allows monitoring the local temperature evolution. This modality has become the most useful in the characterization of a large variety of materials and systems.
TL can also be induced using a pulsed light source. It has been shown that this option allows to perform fast measurements.9,10 The pulsed option can also be used to improve the detection limit of the TL technique.11,12 However, a simple analytical approach for analyzing the evolution of the temperature profile for the pulsed TL is necessary in the current literature. In this paper, a novel analytical approach, using the basic ideas previously reported by Shen et al.,8 is used to address the TL pulsed option. Shen et al.8 obtained an analytical equation that describes the intensity at the far field, produced by the TL effect, for the mode-mismatched configuration. In this case, two laser beams are used, one to probe and the other to excite the sample. It is called mode-mismatched because the waist of the two laser beams is in different positions. To evaluate if this is a viable possibility, it is necessary to compare with the complete (numerical) model, by observing the time evolution of the pulsed TL signal. This paper aims to obtain a simple analytical approach for the pulsed beam methodology based on Fresnel diffraction.7 The limit of validity of our approach on the interpretation of experimental TL data is also investigated.
Theory
Figure 1 shows the parameters involved in a TL mode-mismatched configuration. Two laser beams are used, one as the probe laser beam (red) and the other as the excitation laser beam (green). The waist of the excitation laser beam is at the sample position, located at the distance z1 from the probe beam waist. Due to the radial symmetry of the laser beams, a cylindrical coordinate system is used. The temperature evolution profile is given by the heat diffusion equation13
| 1 |
where ΔT(r, z, t) is the temperature variation induced by the heat source. D = k/(ρc) is the thermal diffusivity of the sample, in which k, ρ, and c are the thermal conductivity, density, and specific heat of the sample, respectively. The heat source, for a pulsed laser beam, Q(r, z, t) can be represented by the following equation:
| 2 |
Q0 = 2EeAe/(cρπω0e2), in which Ee is the energy of the pulse of the excitation laser beam, Ae is the optical absorption coefficient of the sample at the wavelength of the excitation laser beam, and ω0e is the excitation laser beam waist. δ is the Dirac delta function. The time dependence of the source is well approximated by the Dirac delta function for transients at a timescale bigger than the acoustic timescale. For transients at nanosecond order, acoustic waves may give rise to pressure effects, and a local pressure gradient is created, also contributing to the TL signal.14 This pressure gradient launches acoustic waves propagating away from the heated region before the thermal diffusion starts, being possible to neglect this acoustic effect for transients on millisecond scale.
Figure 1.

Schematic representation of the parameters involved in the dual-beam mode-mismatched TL spectroscopy configuration.
Using the integral transform methods, in the Laplace and Hankel space, the heat diffusion equation is written as follows:
| 3 |
where
| 4 |
The general solution for (eq 3) is as follows:
 |
5 |
Considering the approximation of null flux
at the fluid–cuvette interface, 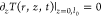 , the constants C1 and C2 are given by
, the constants C1 and C2 are given by
 |
6 |
and
 |
7 |
The null heat flux assumption is a good approximation for thick samples and short-time transients. The above solution (eq 5) does not have an analytical expression for the inverse Laplace transform. However, for TL signal, we only need the induced phase shift. The phase shift (for fluids) produced by ΔT is given as follows:8
| 8 |
where l0 is the sample thickness, dn/dT is the change in the refractive index produced by ΔT, and λp is the wavelength of the probe beam. Performing first the integration along the optical path (0 ≤ z ≤ l0), and then the inverse Laplace and the Hankel transforms, the phase change reduces to
| 9 |
where tc = ω0e2/(4D) and
| 10 |
being leff = [1 – exp(−Ael0)]/Ae. Alternatively, assuming semi-infinite space, with null heat flux in the interface z = 0, the solution of (eq 1) is as follows:15
 |
11 |
with
| 12 |
This solution is a good approximation for the temperature profile, leading only to a small difference in the second face of the cuvette. In the low absorption limit, (eq 11) reduces to15,16
| 13 |
The normalized intensity at the center of the probe beam at the detector plane is given as follows:17
 |
14 |
where  , in which ω1p is the probe
laser beam radius at the sample and
, in which ω1p is the probe
laser beam radius at the sample and 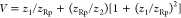 . In Figure 1, it can be observed that z1 and z2 are the distance from the probe
beam waist to the sample and from the sample to the photodetector
plane, respectively. The Rayleigh distance is given by zRp = πω0p2/λp in which ω0p is the waist of the probe laser beam.
. In Figure 1, it can be observed that z1 and z2 are the distance from the probe
beam waist to the sample and from the sample to the photodetector
plane, respectively. The Rayleigh distance is given by zRp = πω0p2/λp in which ω0p is the waist of the probe laser beam.
Considering small phase shifts, the approximation exp(−iΦ) ≈ 1 – iΦ can be used, similar to the one performed by Shen et al.8 In this approximation, a simple analytical expression for a pulsed laser TL spectroscopy is given as follows:
| 15 |
The limit of validity of this expression to describe the time evolution of the pulsed TL signal will be analyzed below. Note that for low absorption limit leff(Ae → 0) = l0, the (eq 15) becomes similar to the expression found by Marcano et al.18,19
The corresponding equation for a cw laser beam was reported by Shen et al.8
| 16 |
where
| 17 |
and
| 18 |
Results and Discussion
In Figure 2, the increment of the temperature (eq 11), as a function of the radial position r for the pulsed light beam is presented for a sample with a low absorption coefficient (Ae = 1 m–1). Note that at t = 0, the temperature reaches the maximum value close to the center of the beam, and afterward, the temperature becomes flatter along r, in such a way that for t = 100tc, the temperature is uniform along r. Parameters and physical properties of water that have been used for calculations are listed in Table 1.
Figure 2.

Radial temperature difference (eq 11), at different times for a depth of 5 mm. The optical absorption coefficient has been set at 1 m–1. Parameters for Q0 are given in Table 1.
Table 1. Parameters Used in Numerical Calculations20a.
| parameter | value | units |
|---|---|---|
| D | 1.43 × 10–7 | m2 s–1 |
| ω0e | 70 | μm |
| Ee | 100 | μJ |
| k | 0.595 | W m–1 K–1 |
| V | 3.72 | |
| ω1p | 316 | μm |
| ρ | 997 | kg m–3 |
Figure 3 shows the radial temperature difference for different absorption coefficients. Circles and continuous lines represent temperature fields calculated by using (eq 11) and its approximation for low absorption samples by using (eq 13), respectively. Calculations were made at 5 mm in depth (z). Parameters are shown in Table 1. It can be observed that the temperature shows the strongest differences for the highest absorption coefficients. Note that for optical absorptions of 10 m–1 and smaller ones, the difference between the approximated and exact temperature is almost negligible.
Figure 3.

Radial temperature profile as a function of the absorption coefficient. Circles and continuous lines were generated by using (eq 11) and (eq 13), respectively. Parameters used for calculations are given in Table 1.
Figure 4 shows numerical calculations for the temperature difference in the sample center as a function of depth normalized to the sample thickness z/l0. It is observed that when the low absorption approximation is used (red continuous lines), ΔT is constant because this quantity is independent of z (eq 13). For the case of (eq 11), a decrement as a function of z is observed in agreement with the dependence on the optical absorption coefficient appearing in the Beer–Lambert law. Note that the optical absorption coefficient increases, from (a) to (c), as ΔT is bigger at the surface where the heat source impinges. Also, for (b) and (c), it is observed a decrement as z increases.
Figure 4.
Temperature difference as a function of depth at the center of the heat source, r = 0, and for (a) Ae = 1 m–1, (b) Ae = 25 m–1, and (c) Ae = 50 m–1. Blue empty circles and red continuous-lines were generated using (eq 11) and (eq 13), respectively. A sample thickness of 1 cm has been used. Parameters involved in calculations of ΔT are given in Table 1.
Figure 5 shows the temperature distribution as a function of radius, depth, and absorption coefficient. Note that the color scale is different for each value of Ae. This is aimed to represent the fact that the temperature difference increases for higher light absorption. Absorption coefficients are (a) 1 m–1, (b) 25 m–1, (c) 50 m–1, and (d) 200 m–1, giving an approximated maximum of 3, 80, 150, and 600 mK, respectively. Usually, an excitation laser beam at the visible spectrum is used; therefore, Figure 5a shows the temperature field in transparent samples like pure liquids as water,8,22 hydrocarbons,24 among others. Note that the shape of the field maintains throughout the sample. Sometimes, the power of laser beams is not enough to provide a reasonable TL signal. In this case, it is a good idea to dye those pure liquids25 to improve the detection, see (eq 10). In Figure 5b,c the attenuation of the excitation laser beam along the sample is presented. Samples with high absorption coefficients can be understood by observing Figure 5d, which corresponds to Ael0 = 2. This case was studied by Koushki et al.,26 which reported z-scan analyses of Erioglaucine (C37H34N2O9S3Na2) with Ael0 = 1.5.
Figure 5.
Radial temperature field as a function of the normalized laser beam radius (r/ω0e) and depth z/l0 for different value of the optical absorption coefficient: (a) Ae = 1 m–1, (b) Ae = 25 m–1, (c) Ae = 50 m–1, and (d) Ae = 200 m–1. The other parameters used in our calculations are given in Table 1.
Figure 6 shows the behavior of the signal when a pulsed (a) (eq 15), and a continuous (b) (eq 16), laser beam are used as heat sources. Intensities are normalized from 0 to 1 by using Inorm = (I(t) – min(I(t)/I(0)))/(1 – min(I(t)/I(0))). In the case of a pulsed laser beam, the signal decreases almost instantaneously when thermal transport is the dominant contribution.27 After that, the signal increases until reaching the initial value due to the cooling down of the sample. In contrast, for a continuous beam, the signal decreases while the heat source is applied.
Figure 6.

Signals normalized from 0 to 1, Inorm, for: (a) pulsed laser beam: blue empty circles and continuous line are the signal and heat source, respectively; and (b) cw laser beam: red empty squares and continuous line are the signal and heat source, respectively.
Figure 7 shows a comparison between the TL signal obtained by the use of phase shift from the semi-infinite model (eq 11), in (eq 8), and the finite sample model (eq 9). For parameters used in this work (see Table 1) both approximations behave similarly. For this setup configuration, note that when θth is big enough, the minimum in the signal does not appear at the beginning of the transient, as is indicated by arrows. For the amplitude bigger than 30%, this behavior becomes significant. The signal at the center of the probe beam at the photo-detector plane is a result of the convolution of the full wavefront after the sample, which for large values m could present a maximum for t > 0. The small phase shift approximation does not capture this initial behavior since it is more significant for large values of θth, in which this approximation cannot be applied.
Figure 7.

Normalized signals generated by considering the semi-infinite and finite model for the temperature profile. Parameters used are given in Table 1.
To obtain the range of validity of the small phase shift approximation, a set of transients for typical thermal properties of water was generated from numerical integration of (eq 14) by using Φ(r, z, t) given in (eq 9). These transients were fitted to the small shift approximation model (eq 15), as shown in Figure 8. The values for θth and D obtained from fits are compared with the ones used to generate the transients. Although visual fits seem to agree, the error obtained for θth and D increases with the increasing of the TL amplitude, as shown in Figure 9. Results show that the analytical model given by (eq 15) can be used successfully for min(I(t)/I(0)) bigger than 0.7 to obtain an error smaller than 5%. Outside the blue zone indicates deviations larger than 5% for calculations of D and θth. To be inside the experimental error range, it is recommended to use the analytical approximation inside the blue area and with min(I(t)/I(0)) > 0.7. Also, care must be taken into account if the minimum of the TL signal is at t > 0.
Figure 8.

Open circles show the data generated with (eq 14) for a constant thermal diffusivity D and varying the parameter θth = θnom. Parameters for calculations are given in Table 1. Continuous lines represent the fit by the small phase shift approximation given by (eq 15).
Figure 9.

Deviations calculated for D (black-circles) and θth (red-triangles) by fitting with (eq 15). Data were generated with (eq 14) by using the parameters given in Table 1. Results indicate that in the blue zone, the analytical approximations can be adequately used with an error of the order of the experimental error.
With the purpose to explore the behavior of our approach when the thermal properties change, mixtures of water–ethanol were considered. Experimental data are shown in Figure 10. Black continuous-lines correspond to the fitting obtained using (eq 15). Figure 11 shows the thermal diffusivity (black symbols) and θth/Ee (blue symbols) values of water–ethanol mixtures for different concentrations. Experimental data were taken from the paper of Capeloto et al.20 Thermal diffusivity values obtained from fitting the analytical [numerical (eq 14), with (eq 9)] model are 1.43 × 10–7 (1.42 × 10–7) m2 s–1 and 0.91 × 10–7 (0.96 × 10–7) m2 s–1 for water22 and ethanol,19,28,29 respectively, being our results in good agreement with the literature values. The theoretical restrictions, discussed before, have been taken into account. Note that in Figure 10 the minimum value of min(I(t)/I(0)) is approximately 0.7, which agrees with the limit discussed before (see Figure 9). However, a little difference between the analytical and numerical model is observed for the highest concentrations of ethanol, because the measurements have been done very close to the limit of the approximation used to obtain the analytical model, which implies small phase shifts. Therefore, for thermal characterization, it is crucial to take into account the value of min(I(t)/I(0)). It is important to observe the deviation of the linearity as the ethanol concentration increases.30,31 This behavior could be explained due to molecular interactions.20 On the other hand, θth/Ee parameter (triangles), which is proportional to dn/dT, has similar behavior to that found in the literature.20,32 Note that for θth/Ee, numerical and analytical fits give similar results.
Figure 10.

TL signals as a function of time for different mixtures of water–ethanol. Concentration in volume of ethanol used are 0, 7, 40, 60, 80, and 100%. Circles are experimental data and black continuous-lines are the fittings obtained using (eq 15).
Figure 11.

Thermal diffusivity for water–ethanol mixtures at different concentrations obtained from the fit with (eq 14) and (eq 15) for filled and empty symbols, respectively. Also, θth/Ee parameter is shown that is linearly dependent on dn/dT, see (eq 10). Standard deviations, for which maximum percentage error value is 0.06%, are shown.
Conclusions
A novel analytical approach for the analysis of experimental data, obtained by pulsed TL spectroscopy, considering the Beer–Lambert absorption law and a small phase approximation, has been presented. The reach of our results for the TL signal was evaluated by comparing with the corresponding exact numerical TL signal. These analyses allowed determining that as soon as the minimal intensity of the signal does not surpass 70% of the initial signal, our analytical approximation provides good results. In addition, it has been shown that the approximation for low absorption liquids is only valid for absorption coefficients smaller than 30 m–1 approximately. In summary, the analytical approach presented in this work can be very useful in optimizing the experimental conditions and data analyses when performing the study of materials using pulsed laser methodologies.
Acknowledgments
Michel A. Isidro-Ojeda thanks for the Postdoctoral grant, Estancias Posdoctorales por México, provided by CONACYT. The authors also thank Luis C. Malacarne, from the Universidade Estadual de Maringá in Brazil, for his helpful comments.
The authors declare no competing financial interest.
References
- Long M. E.; Swofford R. L.; Albrecht A. C. Thermal lens technique: a new method of absorption spectroscopy. Science 1976, 191, 183–185. 10.1126/science.1246605. [DOI] [PubMed] [Google Scholar]
- Proskurnin M. A.; Volkov D. S.; Gor’kova T. A.; Bendrysheva S. N.; Smirnova A. P.; Nedosekin D. A. Advances in thermal lens spectrometry. J. Anal. Chem. 2015, 70, 249–276. 10.1134/s1061934815030168. [DOI] [Google Scholar]
- Liu M.; Franko M. Thermal Lens Spectrometry: Still a Technique on the Horizon?. Int. J. Thermophys. 2016, 37, 67. 10.1007/s10765-016-2072-y. [DOI] [Google Scholar]
- Bialkowski S. E.; Astrath N. G. C.; Proskurnin M. A.. Photothermal Spectroscopy Methods; John Wiley Sons, Ltd, 2019; Chapter 5, pp 219–284. [Google Scholar]
- Dobek K. Thermal lensing: outside of the lasing medium. Appl. Phys. B 2022, 128, 18. 10.1007/s00340-021-07718-2. [DOI] [Google Scholar]
- Bindhu C. V.; Harilal S. S.; Nampoori V. P. N.; Vallabhan C. P. G. Thermal diffusivity measurements in organic liquids using transient thermal lens calorimetry. Opt. Eng. 1998, 37, 2791–2794. 10.1117/1.601825. [DOI] [Google Scholar]
- Goodman J. W.Introduction to Fourier Optics, 3rd ed.; Roberts & Company: Englewood, Colorado, 2005. [Google Scholar]
- Shen J.; Lowe R. D.; Snook R. D. A model for cw laser induced mode-mismatched dual-beam thermal lens spectrometry. Chem. Phys. 1992, 165, 385–396. 10.1016/0301-0104(92)87053-c. [DOI] [Google Scholar]
- Brennetot R.; Georges J. Pulsed-laser mode-mismatched dual-beam thermal lens spectrometry: comparison of the time-dependent and maximum signals with theoretical predictions. Spectrochim. Acta, Part A 1998, 54, 111–122. 10.1016/s1386-1425(97)00201-1. [DOI] [Google Scholar]
- Kumar P.; Dinda S.; Chakraborty A.; Goswami D. Unusual behavior of thermal lens in alcohols. Phys. Chem. Chem. Phys. 2014, 16, 12291–12298. 10.1039/c4cp00895b. [DOI] [PubMed] [Google Scholar]
- Mori K.; Imasaka T.; Ishibashi N. Thermal lens spectrophotometry based on pulsed laser excitation. Anal. Chem. 1982, 54, 2034–2038. 10.1021/ac00249a029. [DOI] [Google Scholar]
- Hiki S.; Mawatari K.; Hibara A.; Tokeshi M.; Kitamori T. UV Excitation Thermal Lens Microscope for Sensitive and Nonlabeled Detection of Nonfluorescent Molecules. Anal. Chem. 2006, 78, 2859–2863. 10.1021/ac051967u. [DOI] [PubMed] [Google Scholar]
- Carslaw H.; Jaeger J.; Jaeger J.. Conduction of Heat in Solids; Oxford science publications; Clarendon Press, 1959. [Google Scholar]
- Capeloto O. A.; Zanuto V. S.; Camargo V. G.; Flizikowski G. A. S.; Lukasievicz G. V. B.; Herculano L. S.; Belançon M. P.; Astrath N. G. C.; Malacarne L. C. Nanosecond pressure transient detection of laser-induced thermal lens. Appl. Opt. 2020, 59, 3682–3685. 10.1364/ao.389545. [DOI] [PubMed] [Google Scholar]
- Sato F.; Malacarne L. C.; Pedreira P. R. B.; Belancon M. P.; Mendes R. S.; Baesso M. L.; Astrath N. G. C.; Shen J. Time-resolved thermal mirror method: A theoretical study. J. Appl. Phys. 2008, 104, 053520. 10.1063/1.2975997. [DOI] [Google Scholar]
- Bialkowski S. E.; Chartier A. Diffraction effects in single- and two-laser photothermal lens spectroscopy. Appl. Opt. 1997, 36, 6711–6721. 10.1364/ao.36.006711. [DOI] [PubMed] [Google Scholar]
- Malacarne L. C.; Astrath N. G. C.; Baesso M. L. Unified theoretical model for calculating laser-induced wavefront distortion in optical materials. J. Opt. Soc. Am. B 2012, 29, 1772–1777. 10.1364/josab.29.001772. [DOI] [Google Scholar]
- Marcano O. A.; Rodriguez L.; Alvarado Y. Mode-mismatched thermal lens experiment in the pulse regime. J. Opt. A: Pure Appl. Opt. 2003, 5, S256–S261. 10.1088/1464-4258/5/5/375. [DOI] [Google Scholar]
- Benítez M.; Marcano A.; Melikechi N. Thermal diffusivity measurement using the mode-mismatched photothermal lens method. Opt. Eng. 2009, 48, 043604. 10.1117/1.3119306. [DOI] [Google Scholar]
- Capeloto O. A.; Zanuto V. S.; Camargo V. G.; Flizikowski G. A. S.; Morais F. A. P.; Lukasievicz G. V. B.; Herculano L. S.; Belançon M. P.; Astrath N. G. C.; Malacarne L. C. Induction and detection of pressure waves by pulsed thermal lens technique in water–ethanol mixtures. Appl. Opt. 2021, 60, 4029–4033. 10.1364/ao.420275. [DOI] [PubMed] [Google Scholar]
- Gupta M. C.; Hong S.; Gupta A.; Moacanin J. Thermal diffusivity measurements using a pulsed dual-beam thermal lens technique. Appl. Phys. Lett. 1980, 37, 505–507. 10.1063/1.91991. [DOI] [Google Scholar]
- Marcano A.; Cabrera H.; Guerra M.; Cruz R. A.; Jacinto C.; Catunda T. Optimizing and calibrating a mode-mismatched thermal lens experiment for low absorption measurement. J. Opt. Soc. Am. B 2006, 23, 1408–1413. 10.1364/josab.23.001408. [DOI] [Google Scholar]
- English N. J.; MacElroy J. M. D. Molecular dynamics simulations of microwave heating of water. J. Chem. Phys. 2003, 118, 1589–1592. 10.1063/1.1538595. [DOI] [Google Scholar]
- Isidro-Ojeda M.; Calderón A.; Marín E. Thermal diffusivity of heptane-isooctane mixtures. Thermochim. Acta 2020, 689, 178616. 10.1016/j.tca.2020.178616. [DOI] [Google Scholar]
- Isidro-Ojeda M. A.; Marín E. Comparison between low optical absorption models for pump-probe transient thermal lens spectroscopy: a theoretical and experimental study. Laser Phys. 2020, 30, 125701. 10.1088/1555-6611/abc32c. [DOI] [Google Scholar]
- Koushki E.; Farzaneh A.; Mousavi S. H. Closed aperture z-scan technique using the Fresnel–Kirchhoff diffraction theory for materials with high nonlinear refractions. Appl. Phys. B 2010, 99, 565–570. 10.1007/s00340-010-3913-1. [DOI] [Google Scholar]
- Lukasievicz G. V. B.; Astrath N. G. C.; Malacarne L. C.; Herculano L. S.; Zanuto V. S.; Baesso M. L.; Bialkowski S. E. Pulsed-Laser Time-Resolved Thermal Mirror Technique in Low-Absorbance Homogeneous Linear Elastic Materials. Appl. Spectrosc. 2013, 67, 1111–1116. 10.1366/13-07068. [DOI] [PubMed] [Google Scholar]
- Chen J.; Xing H.; Zhan T.; Chen L.; He M.; Zhang Y. Measurement of thermal diffusivity of ethanol from (293 to 564) K and up to 10 MPa in vicinity of the critical point. Fluid Phase Equilib. 2022, 552, 113276. 10.1016/j.fluid.2021.113276. [DOI] [Google Scholar]
- Cabrera; Marcano; Castellanos Absorption coefficient of nearly transparent liquids measured using thermal lens spectrometry. Condens. Matter Phys. 2006, 9, 385. 10.5488/cmp.9.2.385. [DOI] [Google Scholar]
- Neamtu C.; Dadarlat D.; Chirtoc M.; Sahraoui A. H.; Longuemart S.; Bicanic D. Evidencing Molecular Associations in Binary Liquid Mixtures via Photothermal Measurements of Thermophysical Parameters. Instrum. Sci. Technol. 2006, 34, 225–234. 10.1080/10739140500374088. [DOI] [Google Scholar]
- Matvienko A.; Mandelis A. Ultrahigh-resolution pyroelectric thermal-wave technique for the measurement of thermal diffusivity of low-concentration water-alcohol mixtures. Rev. Sci. Instrum. 2005, 76, 104901. 10.1063/1.2074627. [DOI] [Google Scholar]
- Arnaud N.; Georges J. Investigation of the thermal lens effect in water–ethanol mixtures: composition dependence of the refractive index gradient, the enhancement factor and the Soret effect. Spectrochim. Acta, Part A 2001, 57, 1295–1301. 10.1016/s1386-1425(00)00465-0. [DOI] [PubMed] [Google Scholar]




