An Optimal Scheme to Achieve Energy Conservation in Induced Dipole Models

Abstract

Induced dipole models have proven to be effective tools for simulating electronic polarization effects in biochemical processes, yet their potential has been constrained by issues of energy conservation, particularly when historical data is utilized for dipole prediction. This study identifies error outliers as the primary factor causing this failure of energy conservation and proposes a comprehensive scheme to overcome this limitation. Leveraging maximum relative errors as a convergence metric, our data demonstrates that energy conservation can be upheld even when using historical information for dipole predictions. Our study introduces the Multi-Order Extrapolation (MOE) method to quicken induction iteration and optimize the use of historical data, while also developing the Preconditioned Conjugate Gradient with Local Iterations (LIPCG) to refine the iteration process and effectively remove error outliers. This scheme further incorporates a “peek” step via Jacobi Under-Relaxation (JUR) for optimal performance. Simulation evidence suggests that our proposed scheme can achieve energy convergence akin to that of point-charge models within a limited number of iterations, thus promising significant improvements in efficiency and accuracy.

Graphical Abstract

Introduction

Computer simulations are increasingly vital for elucidating molecular mechanisms at the microscopic level. To achieve dependable molecular dynamics (MD) simulations, force fields of high precision and consistent atomistic interaction descriptions are paramount. Polarizable force fields, encapsulating interactions between charges and induced higher moments like dipoles and quadrupoles, have shown superiority in depicting atomistic interactions over previous fixed-charge additive force field models, per comparisons with high-level quantum mechanical calculations. Strategies for polarizable force field development are varied, involving Drude oscillators^{1, 2}, fluctuating charges³, induced dipoles^4–6, and continuum dielectrics^{7, 8}. Recently, the polarizable Gaussian Multipole (pGM) model^9–14 has emerged as a promising alternative approach, employing Gaussian-shaped multipoles and dipoles to consistently treat intra- and intermolecular electrostatic interactions and circumvent “polarization catastrophe.”^{15, 16}

The pGM model has been made available to the molecular modeling community through a series of recent papers. Specifically, a set of isotropic atomic polarizabilities and radii for the pGM model has been optimized at the B3LYP/aug-cc-pVTZ level of theory.⁹ A local reference frame with unit vectors defined along covalent or virtual bonds has been suggested, enabling closed-form analytical expressions to be obtained for atomic forces.¹⁰ For molecular simulations under the periodic boundary condition, the pGM model’s electrostatic terms have been interfaced with the particle mesh Ewald (PME) approach.^{10, 17–20} The pGM internal stress tensor expression for constant pressure MD simulations of both flexible and rigid body molecular systems has also been derived.¹¹ Additionally, a python-based PyRESP program has been implemented, which enables parameterizations for various induced dipole polarizable models by reproducing the quantum mechanical (QM) electrostatic potential (ESP) around molecules.¹² Finally, the pGM model has been shown to perform with high accuracy in predicting many-body interactions in peptide oligomers and to exhibit good transferability in predicting ESPs of molecules and oligomers.^{13, 14}

In comparison to traditional point-charge models, MD simulations with polarizable induced-dipole models bring considerably higher computational costs due to the need for computing induced dipoles and electric fields. This study explores strategies for efficient induction calculations within the pGM model framework, with findings applicable to other induced dipole polarizable force fields.

A key step in the polarizable induced-dipole simulations is to compute the induced dipoles to describe the electrostatic induction. Like in other induced dipole models, induced dipoles in pGM can be obtained by solving the following equations as

$$p_i={\alpha }_i\left(E_i^{}-{\sum }_{j\ne i}^N{T}_{ij}\cdot p_j\right)$$ (1)

were ${\mathit{p}}_i$ is the induced dipole vector, ${\alpha }_i$ is the polarizability, and ${\mathit{E}}_i^{}$ is the electric field due to permanent multipoles on the ith atom. $\mathbf{T}$ is the dipole-dipole interaction tensor with elements in pGM model as¹⁰

$$T_{ij}={\partial }_i^{\alpha }{\partial }_j^{\beta }\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}.$$ (2)

Here superscripts $\alpha ,\beta =1,2,3$ refer to x, y, z directions, respectively, and ${\beta }_{ij}=\frac{{\beta }_i{\beta }_j}{\sqrt{{{\beta }_i}^2+{{\beta }_j}^2}}$ where ${\beta }_i$ and ${\beta }_j$ are the Gaussian parameters for atoms i and j. The Gaussian multipole is considered to have a radius $1/{\beta }_{ij}$ while the pGM model can be reduced to point dipole model by setting ${\beta }_{ij}$ to infinity. Additional details can be found elsewhere.¹⁰ In the matrix-vector format, it can be written as

$$P=\alpha \left(E-TP\right)$$ (3)

where $\mathit{P}$ represents the induced dipoles and $\mathit{E}$ is the electric fields due to permanent moments (including charges) on all atoms. Further transformation to the familiar $\mathbf{A}\mathit{x}=\mathit{b}$ format leads to

$$\widehat{\text{T}}P=E$$ (4)

where $\widehat{\mathbf{T}}={\mathbf{\alpha }}^{-1}+\mathbf{T}$ is a 3N-by-3N matrix for a system of N particles, which can be denoted as

$$\widehat{T}=\left[\begin{array}{cccc}{\alpha }_1^{-1}& T_{12}& \cdots & T_{1N}\\ T_{21}& {\alpha }_2^{-1}& & ⋮\\ ⋮& ⋮& & ⋮\\ T_{N1}& \cdots & \cdots & {\alpha }_N^{-1}\end{array}\right].$$ (5)

The tensor comprises two parts: inversed atomic polarizabilities as the diagonal elements $\left({\alpha }_i^{-1}\right)$ and dipole-dipole interaction terms as the off-diagonal elements $\left(T_{ij}\right)$. This general formulation is the same as other polarizable models with induced dipoles. For further discussion purposes, the matrix can also be written as the sum of diagonal terms, upper right $\left(R\right)$ and lower left $\left(L\right)$ triangular terms: $\widehat{\mathbf{T}}={\mathbf{\alpha }}^{-1}+\mathbf{L}+\mathbf{R}$.

Although Eq. (4) is a linear system, its time complexity of matrix inversion is O(N³).^{21, 22} Therefore solution of Eq (4) by direct inversion is impractical for complex molecular systems such as solvated biomolecules. In practice, iterative numerical methods are often adopted to solve the equation using some preset tolerance controlling convergence. An iterative scheme requires that the current solution can be represented as a function of the previous solution during iteration, i.e., ${\mathit{P}}_{i+1}=\mathbf{\Phi }\left({\mathit{P}}_i\right)$. To achieve this, an auxiliary matrix $\mathbf{W}$ is introduced, such that

$$WP+\left(\widehat{T}-W\right)P=E$$ (6)

$$W{P}_{i+1}+\left(\widehat{T}-W\right)P_i=E$$ (7)

By solving for ${\mathit{P}}_{i+1}$, a general iterative method can be formulated as^{21, 22}

$$P_{i+1}=P_i-W^{-1}\left(\widehat{T}{P}_i-E\right).$$ (8)

Given residue ${\mathit{r}}_i=\mathit{E}-\widehat{\mathbf{T}}{\mathit{P}}_i$, Eq. (8) can be simplified as ${\mathit{P}}_{i+1}={\mathit{P}}_i+{\mathbf{W}}^{-1}{\mathit{r}}_i$. The auxiliary matrix $\mathbf{W}$ is often referred to as a preconditioning matrix, and choice for the preconditioning matrix influences the optimality and speed of convergence. In the Jacobi method, the diagonal terms are chosen as the preconditioner $\left(W={\alpha }^{-1}\right)$ so the iteration is a highly vectorizable expression ${\mathit{P}}_{i+1}={\mathit{P}}_i+\mathbf{\alpha }{\mathit{r}}_i.$ A Jacobi under-relaxation (JUR) method can be developed to minimize the effect of overshooting by introducing a relaxation factor $\left(\omega <1\right)$, with the revised iteration as ${\mathit{P}}_{i+1}={\mathit{P}}_i+\omega \mathbf{\alpha }{\mathit{r}}_i.$²³

Iterative methods in principle converge towards the true solution by reducing the residue, which can be viewed as minimization of a residual function $f\left(\mathit{P}\right)=\frac{1}{2}{\mathit{P}}^T\widehat{\mathbf{T}}\mathit{P}-{\mathit{P}}^T\mathit{E}$.²¹ When residue $\mathit{E}-\widehat{\mathbf{T}}\mathit{P}=0$, the residue function reaches minimum. One of the primary approaches to minimize the function value is the gradient descent algorithm. At each iteration, the optimal direction and the amount of move are found. We denote the search direction to be ${\mathit{e}}^{\left(i\right)}$ for the i^th iteration and ${\alpha }_{\left(i\right)}$ to be the amount of move along the search direction. The new iterative solution is then a linear combination of all previous search directions. ${\mathit{P}}_{i+1}={\alpha }_{\left(0\right)}{\mathit{e}}^{\left(0\right)}+{\alpha }_{\left(1\right)}{\mathit{e}}^{\left(1\right)}+{\alpha }_{\left(2\right)}{\mathit{e}}^{\left(2\right)}+\dots$.^{21, 22}

The conjugate gradient (CG) method is instrumental in reducing search iterations by utilizing search directions of the initial gradient and vectors conjugate to that gradient.^{21, 22} In most cases, a preconditioner matrix that mirrors the original matrix yet is easy to invert can expedite the iteration. This method is widely employed in biomolecular applications of Poisson-Boltzmann solvent models^24–27 and is also used in induction iteration, as reviewed by Wang and Skeel, Lipparini et al, and Aviat et al.^{23, 28, 29} In this work, we introduce a local iteration-based preconditioner instead of the preconditioner presented by Wang and Skeel. This preconditioner more effectively captures the optimal search direction for updating induced dipoles as it is a better approximation to the inversed matrix.

Moreover, another efficiency-improving technique can be applied in the CG method: an extra step—known as the “peek” step—in the form of a JUR iteration can be used to accelerate convergence.²⁸ This strategy involves an additional attempted movement along the current residual direction (available during convergence evaluation). If this movement converges with the existing iteration solution, the peek step saves computation time by eliminating the need to calculate a new CG search direction. If it does not converge, the process proceeds to the next CG iteration.²⁸ In this work, we explored an alternate strategy of applying a peek step after convergence, which, as demonstrated by Aviat et al., can effectively enhance the quality of induced dipoles.²³

Aside from efficient iterative algorithms, the quality of the initial guess substantially impacts the convergence steps required. Toukmaji et al proposed using the external electric field due to permanent moments and atomic polarizability $\left(\alpha E_{\mathit{\text{perm}}}\right)$ instead of zero as the initial guess.³⁰ In the context of MD simulations, which represent continuous system time evolution, induced dipoles from prior steps present viable initial guesses. A more contemporary proposal by Wang and Skeel involves an extrapolation scheme utilizing induced dipoles from numerous previous steps, thereby enhancing convergence efficiency. However, it has been observed that NVE simulations using prior steps’ induced dipoles as initial guesses were found to lead to subpar energy conservation compared to simulations utilizing $\alpha E_{\mathit{\text{perm}}}$ as initial guesses, even when employing the same convergence criterion. This phenomenon, while well-known, remains unexplained.²⁸ Given that energy conservation is a crucial validation step for any force field development for MD simulations, addressing this issue is essential. In this context, Aviat et al. put forth a truncated conjugate gradient method involving a fixed number of iterations to achieve an approximated solution, established at a user-defined accuracy level.²³ This approximated solution is treated as the “correct” solution, ensuring consistency in energy and forces with the approximation, thereby ostensibly achieving energy conservation in NVE simulations.²³ In this study, we delve deeper into understanding this energy drift and propose an enhanced multi-order extrapolation method.

One last point worth mentioning is the convergence check in iterative solutions of linear systems. As solutions of all linear systems in the form of $\mathbf{A}\mathit{x}=\mathit{b}$ would lead to residues $\left(r=b-Ax\right)$ approaching zero as close as possible, a standard practice is to claim convergence once the relative norm is less than a preset error tolerance $\left(\tau \right)$, i.e. $‖\mathit{r}‖/‖\mathit{b}‖\le \tau$.^{21, 22} Another way is to check whether the difference between two consecutive solutions is smaller than the tolerance. Either average unsigned difference or root mean squared difference can be used.²⁸ A risk is that the iterative procedure may be stuck somewhere leading to very little change in the solution, resulting in a false convergence claim. This occurs often in solutions of the Poisson-Boltzmann equation.^24–27

In this study, we strive to enhance the induction calculation efficiency of the pGM model, balancing optimal efficiency and energy conservation in molecular dynamics. We delve into the reasons behind poor energy conservation behavior when using history in initial guesses and propose the multi-order extrapolation (MOE) scheme to maximize the use of previous steps’ induced dipoles in initial guesses. We also developed the preconditioned conjugate gradient method with a local-iteration-based preconditioner (LIPCG), enhancing convergence rates. Finally, we optimize the “peek” step in the form of Jacobi under-relaxation (JUR) to better the convergence quality and efficiency.

Method

1. Residue Norm is a Poor Measure in Convergence Check

In the development of polarizable models, it is common to use induced dipoles from previous steps to initialize the induced dipoles in the current step, as this can speed up convergence. However, it has been observed that using history in the initial guesses can make it more difficult to achieve energy conservation, compared to simulations without history unless a more stringent convergence criterion is used.^{23, 28} In the end the time saving would be reduced in induction calculation. This issue also exists in pGM simulations, as we show in the Results and Discussion. We believe that this problem arises because the system does not truly reach the intended convergence quality whether history is used or not, when convergence is determined by residue norm.

To understand this issue, let us first consider the case when no history is used for initial guesses. In this case, all induced dipoles start in a similar situation with respect to convergence. As the induction iteration progresses, all induced dipoles converge in a similar manner, with individual dipole errors being reduced similarly. Thus, the residue norm can be used to check convergence reasonably well.

However, when history is used, the induced dipoles start in different situations. On one hand, many initial guesses are so good that they converge quickly with few iterations. On the other hand, there are dipoles that are far from convergence and require many iterations to converge. Due to the larger range of initial errors, the overall residue norm is not an appropriate measure for checking convergence because the ratio, named residue error: $\epsilon =‖\mathit{r}‖/‖\mathit{b}‖$ would mask the large errors, which accumulate and cause significant energy drifts.

Therefore, it is better to use the maximum relative error in convergence checking whether history is used or not. (In the following, errors are all relative by default, so we drop “relative” for presentation clarity). This approach makes it possible to identify the slowest-converging induced dipole and ensure that convergence is achieved for all induced dipoles in the system. By using this approach, energy conservation can finally be achieved as we shown in Results and Discussion.

2. Multi-Order Extrapolation (MOE) Scheme for Initial Guesses

Given the maximum error as the measure for checking convergence, the energy drift problem would not be an issue as shown in Results and Discussion. Thus, we can safely use history in initial guesses to accelerate the induction calculation.

Since in molecular simulations atoms do not move much at each step, we can assume that induced dipoles change in a linear fashion for a few simulation steps. In general, the following linear extrapolation can be used to approximate the induced dipoles,²⁸

$$P_n\approx {\sum }_{i=1}^k{P}_{n-i}\cdot {\lambda }_i$$ (9)

where ${\mathit{P}}_n$ is a 3N-dimensional vector representing all induced dipoles of the system at the current step n. ${\lambda }_i$ is the extrapolation coefficient, and k is the number of previous steps that are used. Obviously, the above equations are over-determined and can be solved by a least square fitting approach,

$$P_{n-j}^T\cdot P_n={\sum }_{i=1}^k{P}_{n-j}^T\cdot P_{n-i}\cdot {\lambda }_i$$ (10)

where j takes values from 1 through k.

However, since ${\mathit{P}}_n$ is not known until the induction calculation is finished, the above extrapolation scheme is not feasible. One way to address this problem, as described in Ref²⁸, is to solve the above equation for ${\mathit{P}}_{n-1}$ and reuse those obtained $\lambda$ values to predict ${\mathit{P}}_n$.

Here, we introduce an alternative method, which is to solve the least square fitting equation with ${\mathit{E}}_n$, the permanent electric field (due to permanent multipoles) instead of ${\mathit{P}}_n$ at the current step n.

$$E_{n-j}^T\cdot E_n={\sum }_{i=1}^k{E}_{n-j}^T\cdot E_{n-i}\cdot {\lambda }_i$$ (11)

Next the $\lambda \prime s$ are used to extrapolate ${\mathit{P}}_n$. The advantage of the scheme is that we are using the most up-to-date information from the current step to obtain the coefficients.

Our extrapolation scheme is based on the assumption that ${\widehat{\mathbf{T}}}^{-1}={\left({\mathbf{\alpha }}^{-1}+\mathbf{T}\right)}^{-1}$ varies very little during simulations as noted before.²⁸ Thus, we have

$$P_n={\left({\alpha }^{-1}+T_n\right)}^{-1}{E}_n\approx {\left({\alpha }^{-1}+T\right)}^{-1}{E}_n\approx {\left({\alpha }^{-1}+T\right)}^{-1}{\sum }_{i=1}^k{E}_{n-i}\cdot {\lambda }_i\approx {\sum }_{i=1}^k{\left({\alpha }^{-1}+T_{n-i}\right)}^{-1}{E}_{n-i}\cdot {\lambda }_i\approx {\sum }_{i=1}^k{P}_{n-i}\cdot {\lambda }_i$$ (12)

In addition, the scheme can be extended to the second-order extrapolation since the difference between the true and extrapolated ${\mathit{P}}_n$ values also satisfy the same relation,

$$P_n^{\mathit{\text{real}}}-P_n^{\mathit{\text{extrapolated}}}\approx {\sum }_{i=1}^k\left(P_{n-1}^{\mathit{\text{real}}}-P_{n-1}^{\mathit{\text{extrapolated}}}\right)\cdot {\lambda }_i$$ (13)

Similarly, the third-order extrapolation can also be applied to extrapolate the “difference of the difference”.

Thus, this scheme is termed the multi-order extrapolation (MOE) scheme.

3. Local Iterations for Accelerating Maximum Error Convergence

In order to accelerate the convergence of induced dipoles with poor initial guesses, which significantly impact the overall convergence rate, additional methods are required even when using the maximum error as the convergence measure and an aggressive MOE scheme to take advantage of history as much as possible.

Our approach is to use “local” iterations after each “global” iteration, which can be demonstrated most clearly with a stationary point method. Eq. (3) shows that a stationary point method can be used to solve the linear system. However, if this method is used to conduct iterations to solve the system, dipoles with very poor initial guesses will converge much more slowly than most other dipoles. If the maximum error is used to verify convergence, the majority of the iterations will be wasted attempting to improve the dipoles with the poorest initial guesses. To address the limitation of the general iterations, we rewrite Eq. (3) as

$$P=\alpha \left[E-\left(T+T_{\mathit{\text{local}}}-T_{\mathit{\text{local}}}\right)\cdot \mathit{P}\right]$$ (14)

Here

$${\left(T_{ij}\right)}_{\mathit{\text{local}}}={\partial }_i^{\alpha }{\partial }_j^{\beta }\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}},if{R}_{ij}\le d;and{\left(T_{ij}\right)}_{\mathit{\text{local}}}=0,if{R}_{ij}>d.$$ (15)

Cutoff distance “d” can be chosen for optimal efficiency of the overall convergence, usually 3~4 Å. Eq. (15) above can be rewritten as:

$$\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)P=E-\left(T-T_{\mathit{\text{local}}}\right)\cdot \mathit{P}$$ (16)

Thus, we have

$$P={\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)}^{-1}\left[E-\left(T-T_{\mathit{\text{local}}}\right)\cdot P\right]$$ (17)

Since the local iterations only consider very short-range dipole-dipole interactions, it is a highly efficient way to account for the fast-changing local interactions that cause the poor initial guesses.

Eq. (17) leads to a different stationary point method, which requires two different matrix-vector operations at each iteration to solve the system, i.e.

$$P_{n+1}={\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)}^{-1}\left[E-\left(T-T_{\mathit{\text{local}}}\right)\cdot P_n\right]$$ (18)

The first one is $\left(\mathbf{T}-{\mathbf{T}}_{\mathit{\text{local}}}\right)\bullet {\mathit{P}}_n$, similar to any stationary point method. Because this iteration requires the calculation of $\mathbf{T}\bullet {\mathbf{P}}_n$, which represents interactions between all pairs of induced dipoles in the system, this step can be called the global iteration. The second one involves the inversion of ${\mathbf{\alpha }}^{-1}+{\mathbf{T}}_{\mathit{\text{local}}}$. This can be done iteratively by solving the following equation,

$$\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)\cdot P_{n+1}=b$$ (19)

where $\mathit{b}=\mathit{E}-\left(\mathbf{T}-{\mathbf{T}}_{\mathit{\text{local}}}\right)\bullet {\mathit{P}}_n$. Because this iteration does not require the calculation of $\mathbf{T}\bullet {\mathit{P}}_{n+1}$ but only a local truncated ${\mathbf{T}}_{\mathit{\text{local}}}\bullet {\mathit{P}}_{n+1}$, this step is called the local iteration. Using Eq. (17) instead of Eq. (3) adds a local iteration on top of a global iteration, which further relaxes the system in a more efficient manner.

It is worth noting that solution of Eq. (19) can be achieved by a preconditioned CG algorithm, where the diagonal term of the polarization tensor $\left(\mathbf{\alpha }\right)$ can be used to speed up convergence of the local iteration.

$$\begin{array}{l}{r}_0=b-\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)\cdot x_0\hfill \\ z_0=\alpha r_0\hfill \\ p_0=z_0\hfill \\ do\hfill \\ {\alpha }_k=\frac{r_k^T\cdot z_{\mathit{k}}}{p_k^T\cdot \left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)\cdot p_k}\hfill \\ x_{k+1}=x_k+{\alpha }_k{p}_k\hfill \\ r_{k+1}=r_{\mathit{k}}-{\alpha }_k\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)\cdot p_k\hfill \\ z_{k+1}=\alpha r_{k+1}\hfill \\ if\Vert r_{k+1}\Vert /\parallel b\parallel \le \tau \text{,\hspace{0.17em}\hspace{0.17em}}\mathrm{break}\hfill \\ {\beta }_k=\frac{r_{k+1}^T\cdot z_{k+1}}{r_k^T\cdot z_k}\hfill \\ p_{k+1}=r_{k+1}+{\beta }_k{p}_k\hfill \\ enddo\hfill \end{array}$$

4. Implementation of Local Iterations as Preconditioner for Conjugate Gradient (LIPCG)

As mentioned in Introduction, conjugate gradient (CG) methods fall into another category of linear system solvers, e.g., the Krylov method.²¹ It is often believed and practically true that CG methods are much faster than stationary point methods for induction iterations.^{23, 28} In this section, local iterations will be incorporated into the CG algorithm within the preconditioning framework.

As reviewed in the introduction, the preconditioned conjugate gradient (PCG) method leverages a preconditioner to accelerate convergence. For simpler cases, the preconditioner is often selected as the diagonal elements of matrix $\mathbf{A}$. However, for larger and more complex systems, the preconditioner can be an approximation of $\mathbf{A}$. One such example of a preconditioner was proposed by Wang and Skeel, who used a first-order approximation: ${\widehat{\mathbf{T}}}^{-1}\approx {\left({\mathbf{\alpha }}^{-1}+{\mathbf{T}}_{\mathit{l}\mathit{o}\mathit{c}\mathit{a}\mathit{l}}\right)}^{-1}\approx \mathbf{\alpha }-{\mathbf{\alpha }}^{\mathit{T}}{\mathbf{T}}_{\mathit{l}\mathit{o}\mathit{c}\mathit{a}\mathit{l}}\mathbf{\alpha }$.²⁸ The implementation of this preconditioned conjugate gradient method provides a robust and swift path to convergence. The standard operational scheme of a PCG method with a preconditioning matrix $\left(M\right)$ is detailed below.

$$\begin{array}{l}{r}_0=b-A\cdot x_0\hfill \\ z_0=M^{-1}{r}_0\hfill \\ p_0=z_0\hfill \\ do\hfill \\ {\alpha }_k=\frac{r_k^T\cdot z_k}{p_k^T\cdot A\cdot p_k}\hfill \\ x_{k+1}=x_k+{\alpha }_k{p}_k\hfill \\ r_{k+1}=r_k-{\alpha }_{k}A\cdot p_k\hfill \\ z_{k+1}=M^{-1}{r}_{k+1}\hfill \\ if\Vert r_{k+1}\Vert /\parallel b\parallel \le \tau ,\mathrm{break}\hfill \\ {\beta }_k=\frac{r_{k+1}^T\cdot \alpha r_{k+1}}{r_k^T\cdot r_k}\hfill \\ p_{k+1}=r_{k+1}+{\beta }_k{p}_k\hfill \\ enddo\hfill \end{array}$$

In this work, we extended the potential utility of preconditioners. We not only investigated the first-order approximation of ${\widehat{\mathbf{T}}}^{-1}$ by Wang and Skeel,²⁸ but also utilized the local iterations previously mentioned to enhance the approximation of ${\widehat{\mathbf{T}}}^{-1}$. To understand how to corporate this in CG, we introduce a quantity, pseudo-solution ${\mathit{x}}_k^{\prime }$. For each “real” solution, ${\mathit{x}}_k$,

$$x_k^{\prime }={\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)}^{-1}\left[b-\left(T-T_{\mathit{\text{local}}}\right)\cdot x_k\right]$$ (20)

From the Eq. (17) of the last section, we know that this is, in fact, the result of a local iteration.

Thus, instead of generating ${\mathit{r}}_k$ as $\mathit{b}-\left({\mathbf{\alpha }}^{-1}+\mathbf{T}\right)\bullet {\mathit{x}}_k$, we use ${\mathit{x}}_k^{\prime }-{\mathit{x}}_k$ as the new residue, ${\mathit{r}}_k^{\prime }$,

$$\begin{gathered} r_k^{\prime }=x_k^{\prime }-x_k={\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)}^{-1}\left[b-\left(T-T_{\mathit{\text{local}}}\right)\cdot x_k\right]-x_k \\ ={\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)}^{-1}\left[b-\left(T-T_{\mathit{\text{local}}}\right)\cdot x_k\right]-{\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)}^{-1}\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)\cdot x_k \\ ={\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)}^{-1}\left[b-\left({\alpha }^{-1}+T\right)\cdot x_k\right]={\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)}^{-1}{r}_k \end{gathered}$$ (21)

Therefore, the new residue is the standard CG residue with a constant transformation ${\left({\mathbf{\alpha }}^{-1}+{\mathbf{T}}_{\mathit{\text{local}}}\right)}^{-1}$. In another word, this extra step of local iteration effectively plays the role of a preconditioner, $\mathbf{M}$, i.e.

$$M^{-1}={\left({\alpha }^{-1}+T_{\mathit{\text{local}}}\right)}^{-1}$$ (22)

In summary, we intend to compute ${\mathit{z}}_0={\mathbf{M}}^{-1}{\mathit{r}}_0$ by calling the local-iteration CG as shown at the end of last section. Of course, this process can be expensive if we insist for high accuracy. However, this is not necessary as we do not rely on the precise search direction derived from the preconditioning step. In our testing, a few steps of iterations (2 to 3) were found to be sufficient for the local-iteration PCG method to improve convergence and reduce the overall CPU time notably.

$$\begin{array}{l}{r}_0=b-A\cdot x_0\hfill \\ z_0=\text{local}\_\text{iter}\left(r_0\right)\hfill \\ p_0=\alpha z_0\hfill \\ do\hfill \\ {\alpha }_k=\frac{r_k^T\cdot z_k}{p_k^T\cdot A\cdot p_k}\hfill \\ x_{k+1}=x_k+{\alpha }_k{p}_k\hfill \\ r_{k+1}=r_k-{\alpha }_{k}A\cdot p_k\hfill \\ z_{k+1}=local\_iter\left(r_{k+1}\right)\hfill \\ if\Vert r_{k+1}\Vert /\parallel b\parallel \le \tau ,\text{break}\hfill \\ {\beta }_k=\frac{r_{k+1}^T\cdot \alpha r_{k+1}}{r_k^T\cdot r_k}\hfill \\ p_{k+1}=r_{k+1}+{\beta }_k{p}_k\hfill \\ enddo\hfill \end{array}$$

5. Molecular dynamics simulation for performance tests

In all conducted tests, we employed a cubic box containing 512 water molecules, identical to the one used in our prior research.¹⁰ The box dimensions were (33 Å)³, and all simulations were performed under the NVE conditions. To meet the high precision necessary for energy computations, we utilized the following parameters for the PME setup: a β₀ = 0.4 Å⁻¹ setting for the Ewald coefficient, a B-spline interpolation order of 8, a Fast Fourier Transform (FFT) grid spacing size of 0.66 Å, and a direct space cutoff distance of 9.0 Å. These parameters yield a PME accuracy level of 10⁻⁶, which ensures that PME is not the primary contributor to energy drift. The timestep of 1 femtosecond was used to guarantee a good quality of energy conservation. The Jacobi-under relaxation scheme is applied for iterative approach as mentioned in the appendix. The maximum number of PCG iterations was limited to 50, and the under-relaxation parameter was set to 0.65. For local iterations, a cutoff distance of 4.0 Å and three iterations were established. The other parameters followed the default values provided in the Amber simulation package.³¹

Results and Discussion

1. Detailed Error Analysis of Induction Iteration

A vital aspect of implementing a new force field in a molecular dynamics program is validation of energy conservation. As depicted in Table 1, energy drifts are generally more substantial when using the previous step’s induced dipoles as the initial guess $\left({\mu }_{n-1}\right)$. In all examined instances, energy drifts were less than half when history was disregarded $\left(\alpha E_{\mathit{\text{perm}}}\right)$ as compared to when history was considered $\left({\mu }_{n-1}\right)$. This discrepancy between the two methods suggests a difference in convergence quality, with the scheme disregarding history achieving better convergence despite both methods employing the same tolerance. This observation aligns with Wang and Skeels’ experiments, where employing history information increased the likelihood of energy conservation failure.²⁸ This detrimental effect is likely to be more significant in pure water due to its high flexibility. However, since water molecules predominantly mimic the biomolecular environment in biomolecular simulations, addressing this issue is essential for molecular dynamics applications. This observation led us to hypothesize that the use of history information might result in more unconverged induced dipoles, as we elaborated in the Methods section. As delineated in Table S1, the average iteration count and CPU time for a simulation comprising 1000 steps are documented. It is discernible from the table that, when maintaining identical convergence criteria, the employment of historical data facilitates a reduction of approximately two iterations before convergence is achieved, thereby yielding substantial time savings. If we consider the time component, an equal number of iterations correlates with a similar time duration. This implies that utilizing historical data at certain convergence criteria will result in a simulation time comparable to a scenario where historical data is not utilized, but with looser convergence criteria. Furthermore, this observation underscores that the utilization of the standard norm as a convergence check is not unassailable.

Table 1:

Comparative Analysis of Energy Drift (expressed in kcal/(mol·ps)) and Convergence Tolerance $\left(\tau \right)$ Utilizing Residue Norm as a Convergence Measure. The number of degrees of freedom in the system is 3069. The table exhibits that energy drifts in simulations where the initial values stem from the last step $\left({\mu }_{n-1}\right)$ consistently exceed those where the initial values are drawn from the permanent field $\left(\alpha E_{\mathit{\text{perm}}}\right)$. Refer to Figures S1, S2, and S3 for more detailed energy plots pertaining to these simulations. A comprehensive timing analysis for these simulations can be found in Table S1.

$\tau$	10−4	10−5	10−6	10−7
${\mu }_{n-1}$	−8.25 × 10−2	−1.76 × 10−3	−1.11 × 10−4	6.59 × 10−4
$\alpha E_{\mathit{\text{perm}}}$	1.92 × 10−3	−5.33 × 10−4	−3.47 × 10−5	1.98 × 10−5
TIP3P energy drift	−5.56 × 10−4

In this section, we first discuss why history information forms a valuable component of the initial guess. Figure 1 illustrates the error distribution of induced dipoles on 512 water molecules before iteration, with and without history information. As depicted in the figure, employing the permanent field as an initial guess delivers relatively larger errors. Using the previous step as an initial guess, however, can expedite convergence by providing a more accurate starting point. Interestingly, despite smaller initial errors when using history, the quality of convergence tends to be worse compared to when history is not used. This conclusion is supported by Figure 2, where the error distribution post-convergence is depicted. Tests incorporating history information yielded larger errors than those disregarding history, signifying that the use of history leads to relatively poor convergence quality. As mentioned in the Methods section, when history information is employed, some large errors converge more slowly compared to quickly converging errors, potentially contributing to energy drift in induced dipole models.

Figure 1:

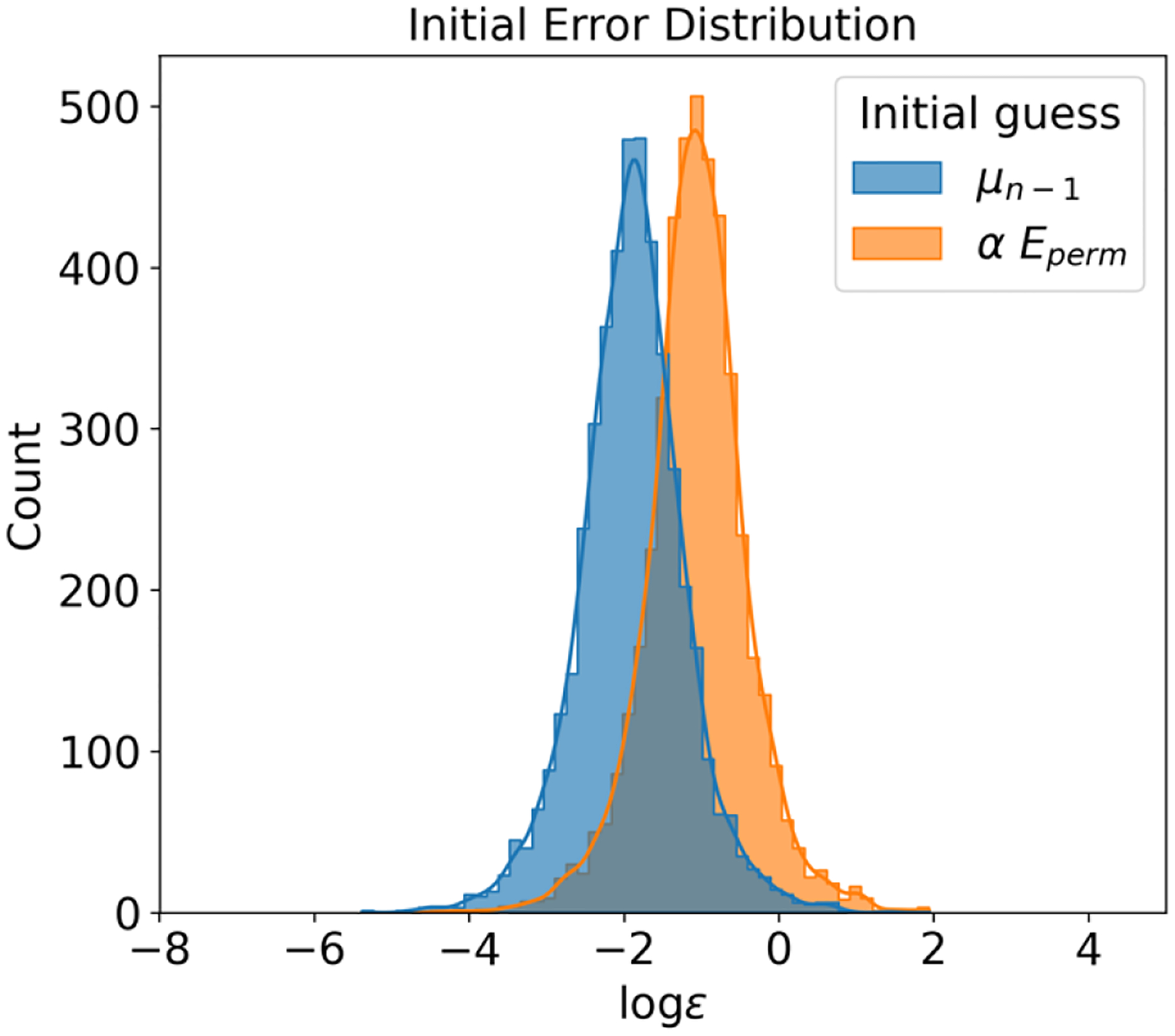
Initial Error Distribution Comparison for ${\mu }_{n-1}$ and $\alpha E_{\mathit{\text{perm}}}$ as Initial Guesses. This figure showcases the difference in initial error distribution when using either the last step $\left({\mu }_{n-1}\right)$ or the permanent field $\left(\alpha E_{\mathit{\text{perm}}}\right)$ as the initial guess. It clearly indicates that using historical data $\left({\mu }_{n-1}\right)$ as an initial guess proves to be a significantly better option than not utilizing historical data. The convergence tolerance for this comparison is set at 10⁻⁴.

Figure 2:

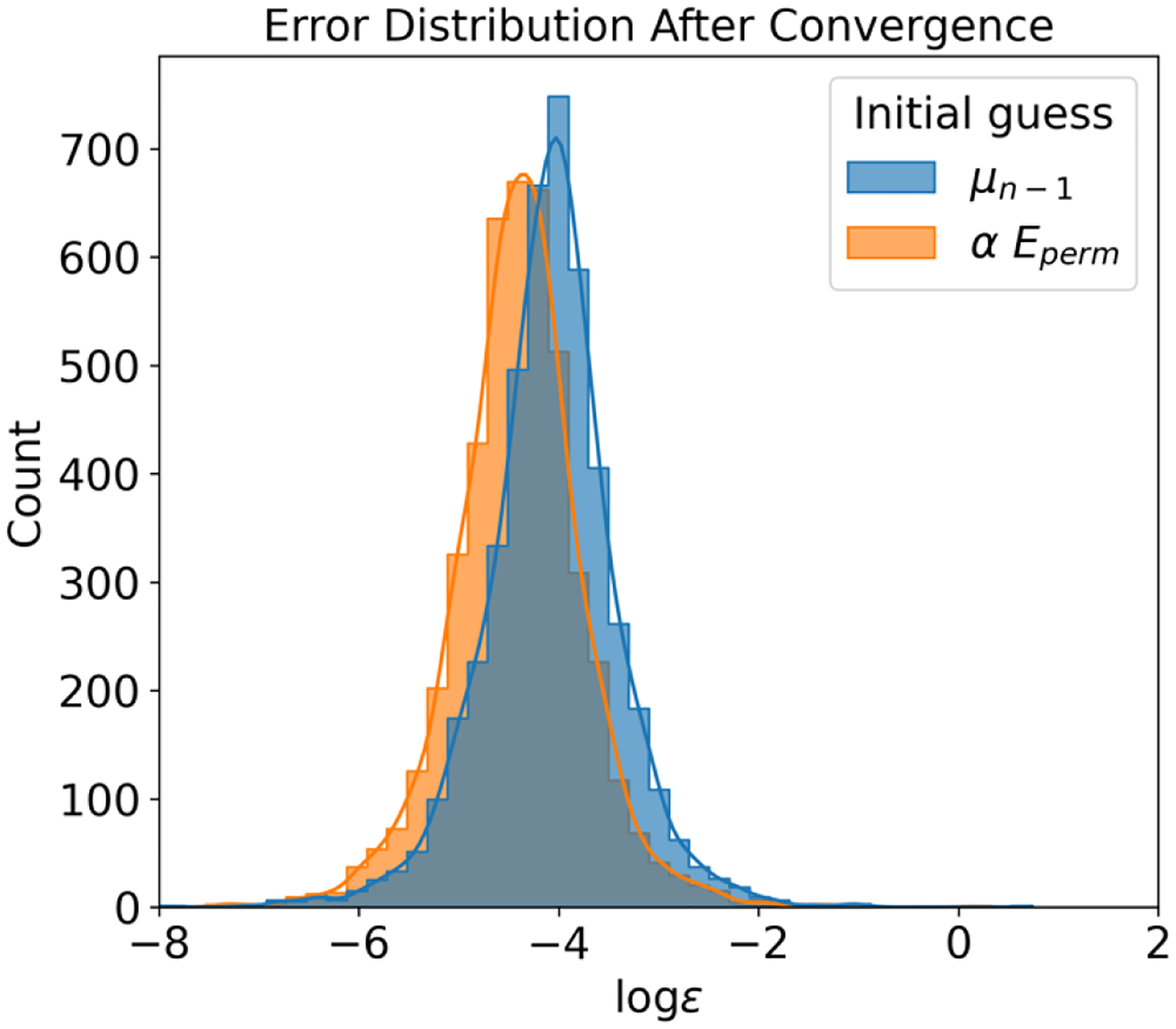
Post-convergence Error Distribution Comparison with and without the Use of Historical Data. This figure presents the error distribution after achieving convergence when employing historical data compared to not using it. It illustrates that the use of historical data results in larger errors compared to using the permanent field $\left(\alpha E_{\mathit{\text{perm}}}\right)$ as the initial guess. The convergence tolerance for this analysis is set at 10⁻⁴.

We also aim to shed light on the impact of error outliers on the issue of energy conservation failure. A detailed analysis of the error outliers’ distribution is presented in Figure 3. Here, we define the outliers when the error exceeds 1000 times the current tolerance $\tau$. As indicated in the figure, the use of history information consistently resulted in a higher number of error outliers compared to those with $\alpha E_{\mathit{\text{perm}}}$. Moreover, a stricter convergence tolerance diminishes the difference between error distributions, suggesting that energy drift should be similar for ${\mu }_{n-1}$ and $\alpha E_{\mathit{\text{perm}}}$ given a sufficiently stringent convergence tolerance. To achieve convergence with high tolerance, we propose the maximum error as a potential candidate for convergence checking.

Figure 3:

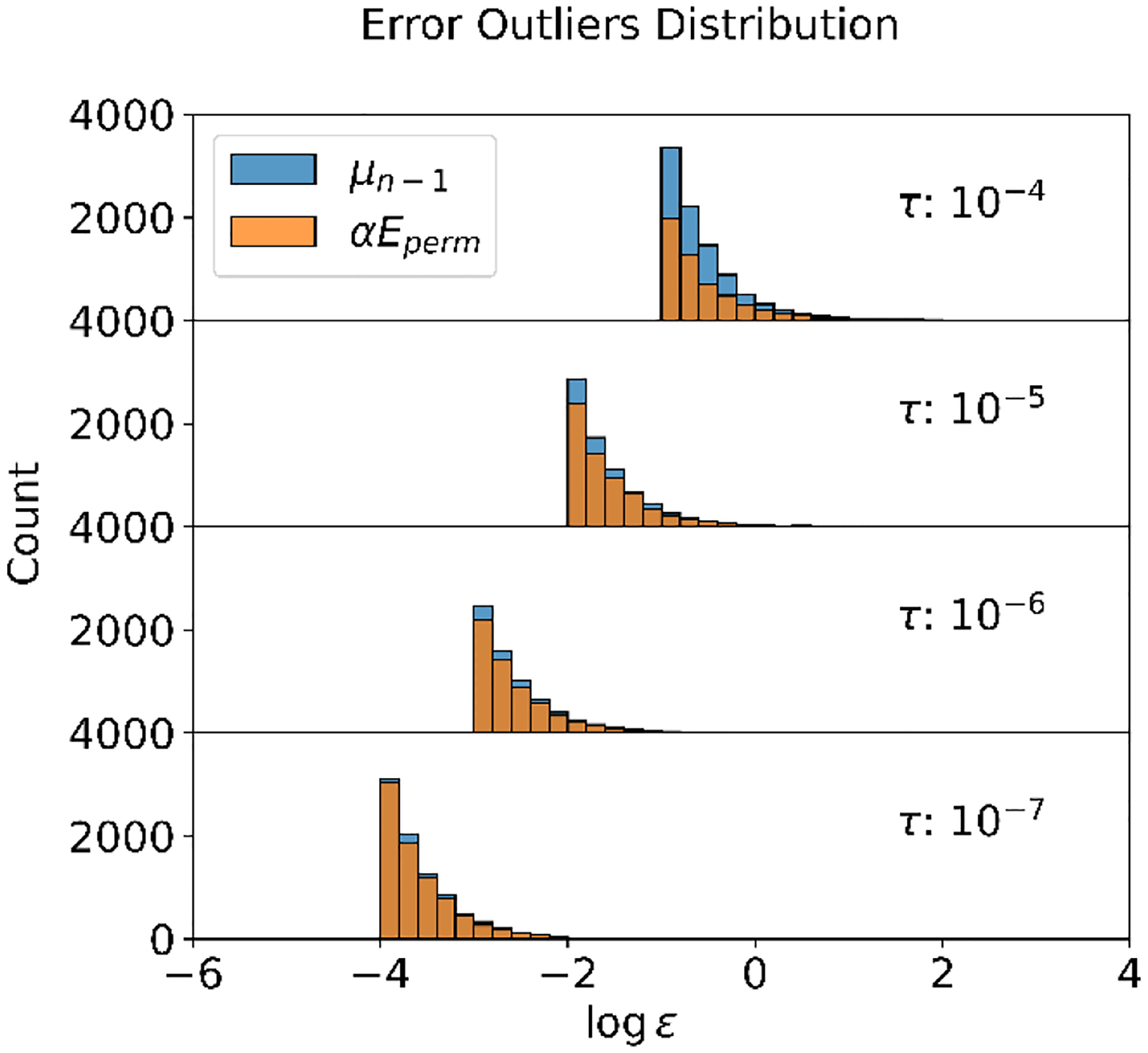
Distribution of Error Outliers Versus Convergence Tolerance $\left(\tau \right)$ in 100ps NVE Simulations Employing Residue Norm as a Convergence Measure. An error outlier is defined when the error is 1000 times larger than the convergence tolerance $\tau$, with individual relative errors analyzed. The error axes are presented on a logarithmic scale. Each plot within the figure illustrates error distributions from simulations utilizing two different initial guesses for induced dipoles (${\mu }_{n-1}$ and $\alpha E_{\mathit{\text{perm}}}$). It is evident that simulations adopting ${\mu }_{n-1}$ as the initial guess introduce more errors compared to those employing $\alpha E_{\mathit{\text{perm}}}$. However, these differences diminish as tighter convergence criteria are applied.

2. Maximum Error Is a Better Choice for Convergence Check

In our investigation, we strived to rectify the limitations of employing residue norm in convergence evaluation, thereby considering the maximum error as a possible candidate. The outcomes of our experiments demonstrated that the energy drifts in the majority of simulations, both those using and not using the history for the initial dipole assignment, were largely akin to those observed in TIP3P water (Table 2). This corresponded to an energy drift of $-5.56\times {10}^{-4}kcal/\left(mol\bullet ps\right)$ (Refer to Table 1). The only deviations from this pattern were observed with the most lenient convergence tolerance of 10⁻¹. Consequently, it was noted that an implementation of a maximum error of 10⁻² led to sufficiently low energy drift for both initial dipole assignments. Interestingly, tightening the convergence tolerance further (from 10⁻² to 10⁻⁴) did not yield any significant improvements in energy drifts. This observation suggests that induction error is no longer the primary determinant of the overall system energy drift when the maximum error in induction iteration is set to less than 10⁻².

Table 2:

Energy Drift (expressed in kcal/(mol·ps)), Energy RMSD (in kcal/mol), and Average Iteration Count for NVE Simulations Utilizing Maximum Error for Convergence Checking. This table outlines the outcomes of NVE simulations, detailing metrics such as energy drift, energy Root Mean Square Deviation (RMSD), and the average number of iterations, with the simulations specifically employing the maximum error as the criterion for convergence checking.

$\tau$		10−1	10−2	10−3	10−4
Energy drift	${\mu }_{n-1}$	−5.78 × 10−2	2.55 × 10−5	2.39 × 10−4	8.00 × 10−5
	$\alpha E_{\mathit{\text{perm}}}$	2.11 × 10−3	−7.33 × 10−4	−2.61 × 10−4	−5.63 × 10−4
Energy RMSD	${\mu }_{n-1}$	16.69	1.23 × 10−1	1.40 × 10−1	1.68 × 10−1
	$\alpha E_{\mathit{\text{perm}}}$	6.64 × 10−1	2.43 × 10−1	1.45 × 10−1	2.03 × 10−1
Average number of iterations	${\mu }_{n-1}$	7.29	9.62	11.82	14.11
	$\alpha E_{\mathit{\text{perm}}}$	10.06	12.31	14.60	16.84

It is essential to underscore that when choosing the maximum error as the convergence criterion, the quality of convergence must be high, devoid of extreme errors. This aspect becomes particularly critical when employing historical data as an initial estimate since improved convergence quality paves the way for a more accurate initial estimate.

To extend our analysis on the energy conservation properties of the tested systems, we also evaluated total energy fluctuations, as illustrated in Table 2. The table demonstrates that energy fluctuations at 10⁻², 10⁻³ and 10⁻⁴ convergence criteria were all in the order of 10⁻¹ kcal/mol, both for tests conducted with and without history. This data corroborates the energy drift analysis presented earlier. Detailed energy plots are available in Figure S4 and S5. Lastly, Table 2 also encapsulates the average number of iteration steps, indicating that the utilization of history could still lessen the iteration by 2 to 3 steps. This observation reinforces the adoption of history for a more efficient induction iteration, provided the maximum error is employed as the convergence measure.

3. Optimization of Initial Guess using MOE Scheme

To enhance the initial estimate for induced dipoles, we employed Multiple Order Extrapolation (MOE) schemes, capitalizing on historical information in an effective manner. Our investigative data implies that while the MOE scheme theoretically possesses the capacity for unlimited expansion, its potential for productivity improvement becomes marginal beyond the third order.

A rigorous investigation was conducted to assess the performance timing across diverse extrapolation orders and varying counts of preceding steps included for extrapolation. Specifically, we evaluated extrapolations of the first, second, and third orders in coordination with two to six preceding steps. A comprehensive encapsulation of the mean iteration number and cumulative CPU time per 1000 molecular dynamics (MD) steps under all test conditions is found in Table 3. Our inquiry identified several settings – five preceding steps in conjunction with first-order extrapolation, four preceding steps paired with second-order extrapolation and two preceding steps paired with third-order extrapolation – as consistently delivering the minimal iteration count and the shortest aggregate CPU duration. Moreover, in scenarios with a looser convergence tolerance, specifically around 10⁻², the second-order extrapolation proves to be a more advisable choice. Conversely, under the conditions of a tighter tolerance, in the realm of 10⁻³ and 10⁻⁴, the third-order extrapolation emerges as the recommended alternative. It is also pertinent to mention that the overall performance of our MOE could be further enhanced through the integration of a more efficient solver (as will be mentioned in later section), thereby generating richer and more valuable historical data for the MOE’s optimal application. Not surprisingly, the ideal number of historical steps for the first-order MOE converges with the results of Wang and Skeel’s study,²⁸ which is also a first-order extrapolation scheme. Consequently, aggressive utilization of historical data culminates in expected reductions in convergence duration and iteration count.

Table 3:

Performance Evaluation of the MOE (Muti-order Extrapolation) Scheme and Number of Preceding Steps Employed in the Least Square Method under Different Convergence Criteria. The table presents a detailed analysis of the performance of the MOE scheme in relation to the number of previous steps incorporated in the least square method, subject to various convergence criteria. The left column enumerates the average iteration count per MD step necessary to achieve convergence, while the right column depicts the average CPU time required to complete 1000 MD steps. Data pertaining to the WSE (Wang and Skeel’s extrapolation) scheme is included as a reference point.

Convergence Criterion: 10−2
Number of previous steps	Order 1	Order 2	Order 3
Last 2	429.43(9.98)	324.83(4.94)	344.88(6.13)
Last 3	368.03(6.89)	345.73(6.17)	405.18(9.24)
Last 4	384.98(7.59)	325.62(5.09)	364.00(7.07)
Last 5	330.77(5.14)	354.69(6.59)	412.23(9.44)
Last 6	344.73(5.95)	339.86(5.97)	398.04(8.47)
WSE	331.02(5.18)
Convergence Criterion: 10−3
	Order 1	Order 2	Order 3
Last 2	493.56(13.26)	398.00(8.04)	352.96(6.62)
Last 3	428.71(9.96)	355.74(6.64)	423.45(9.64)
Last 4	445.86(10.89)	343.77(6.17)	373.76(7.64)
Last 5	395.01(8.39)	370.13(7.11)	426.52(9.96)
Last 6	408.13(9.06)	365.97(7.00)	414.91(9.54)
WSE	396.31(8.43)
Convergence Criterion: 10−4
	Order 1	Order 2	Order 3
Last 2	552.78(16.48)	455.05(11.23)	419.93(8.86)
Last 3	496.20(13.25)	414.70(8.91)	481.73(11.61)
Last 4	505.79(14.01)	427.31(9.12)	430.84(9.74)
Last 5	457.68(11.69)	427.64(9.14)	493.01(11.98)
Last 6	470.49(12.35)	431.08(9.69)	490.83(11.81)
WSE	458.19(11.83)

The distribution of initial errors utilizing different initial guesses is exhibited in Figure 4. It is apparent from the figure that a solitary historical step only mildly decreases error, while Wang and Skeel’s extrapolation (WSE) effectuates a more substantial reduction. Our MOE, with optimal parameters, performs marginally better than WSE and subsequently reduces simulation time, though the performance improvements are higher for the tighter tolerance conditions.

Figure 4.

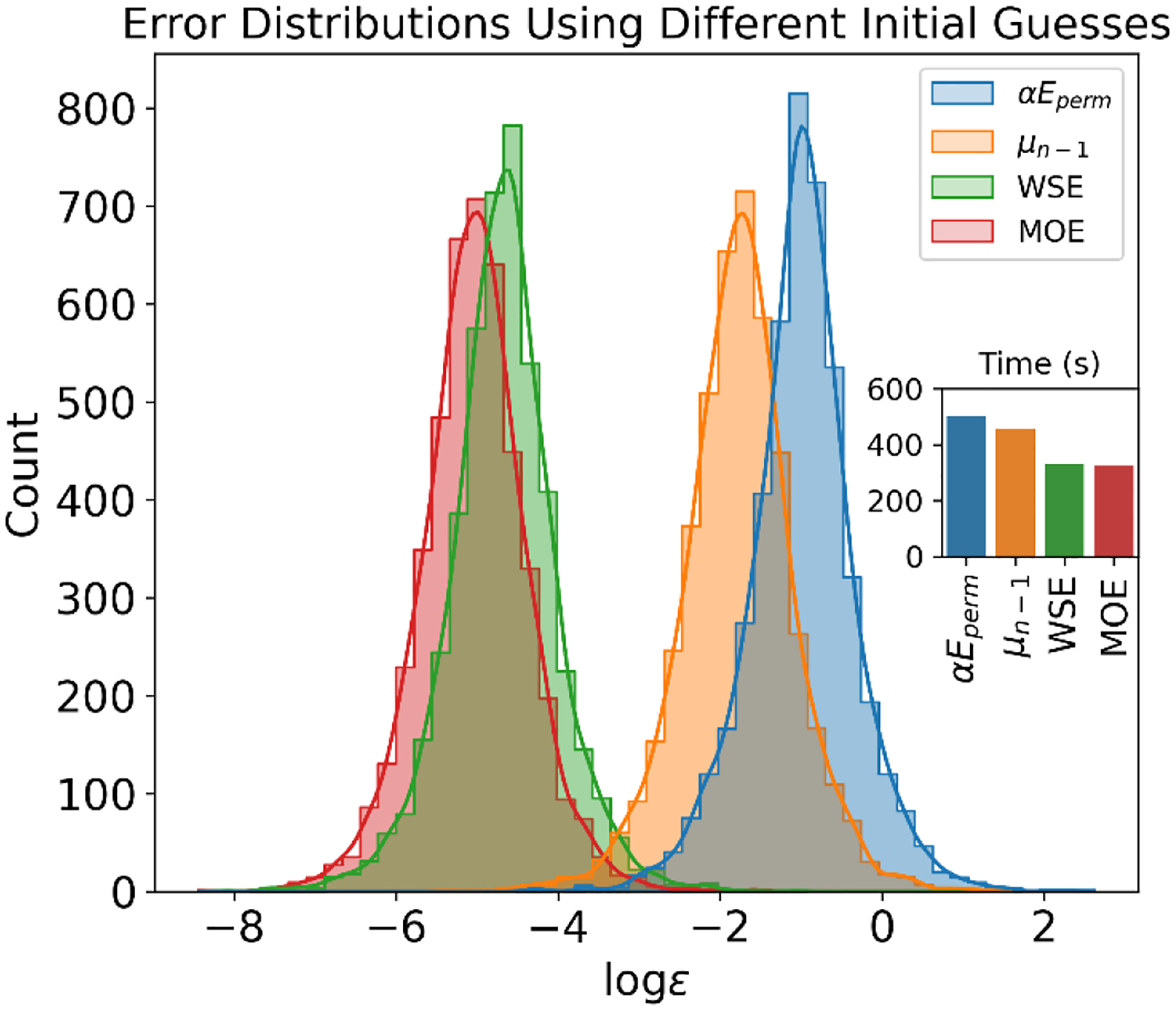
Distribution of Initial Errors with Varying Initial Guesses and their Associated CPU Time for 1000 MD Steps. The figure illustrates the initial error distribution for different initial guesses, with a convergence tolerance set at a maximum error of 10⁻². The simulation is performed using a standard Conjugate Gradient (CG). The initial guesses include: $\alpha E_{\mathit{\text{perm}}}$ (Permanent Field); ${\mu }_{n-1}$ (last step); WSE (Wang and Skeel’s extrapolation, which employs 5 preceding steps); and MOE (Multi-Order Extrapolation, which employs a third-order extrapolation using 2 previous steps). The inset demonstrates the average CPU time consumed for 1000 MD steps. The illustration suggests that the application of MOE results in the smallest error distribution and quickest overall performance.

Lastly, Table S2 portrays the energy drift values associated with varying extrapolation combinations across 1 ns NVE simulations. Contrary to observations by Wang and Skeel,²⁸ the energy drift values demonstrate remarkable consistency and similarly align with those documented in Table 2 (where $\tau \le {10}^{-2}$). This offers further substantiation for the reliability of utilizing maximum error in the convergence check as a means of ensuring energy conservation.

4. Use of Local Iterations to Speed up Convergence

In the light of the maximum error employed for induction convergence checking and the optimized initial induced dipole guess, we ventured into further diminishing induction costs via the Preconditioned Conjugate Gradient (PCG) method. The concept of deploying local iterations to refine induced dipoles possessing suboptimal initial guesses was detailed in the Methods section. Initially, we aim to demonstrate the potency of the local iteration method. Figure 5 reveals the error distribution following one iteration of computation. It is evident from the figure that while traditional CG minimally reduces error, the application of a preconditioner (as per Wang and Skeel)²⁸ significantly curtails the error in just one iteration. Further, substituting our local iteration for the preconditioner leads to even greater error reduction.

Figure 5:

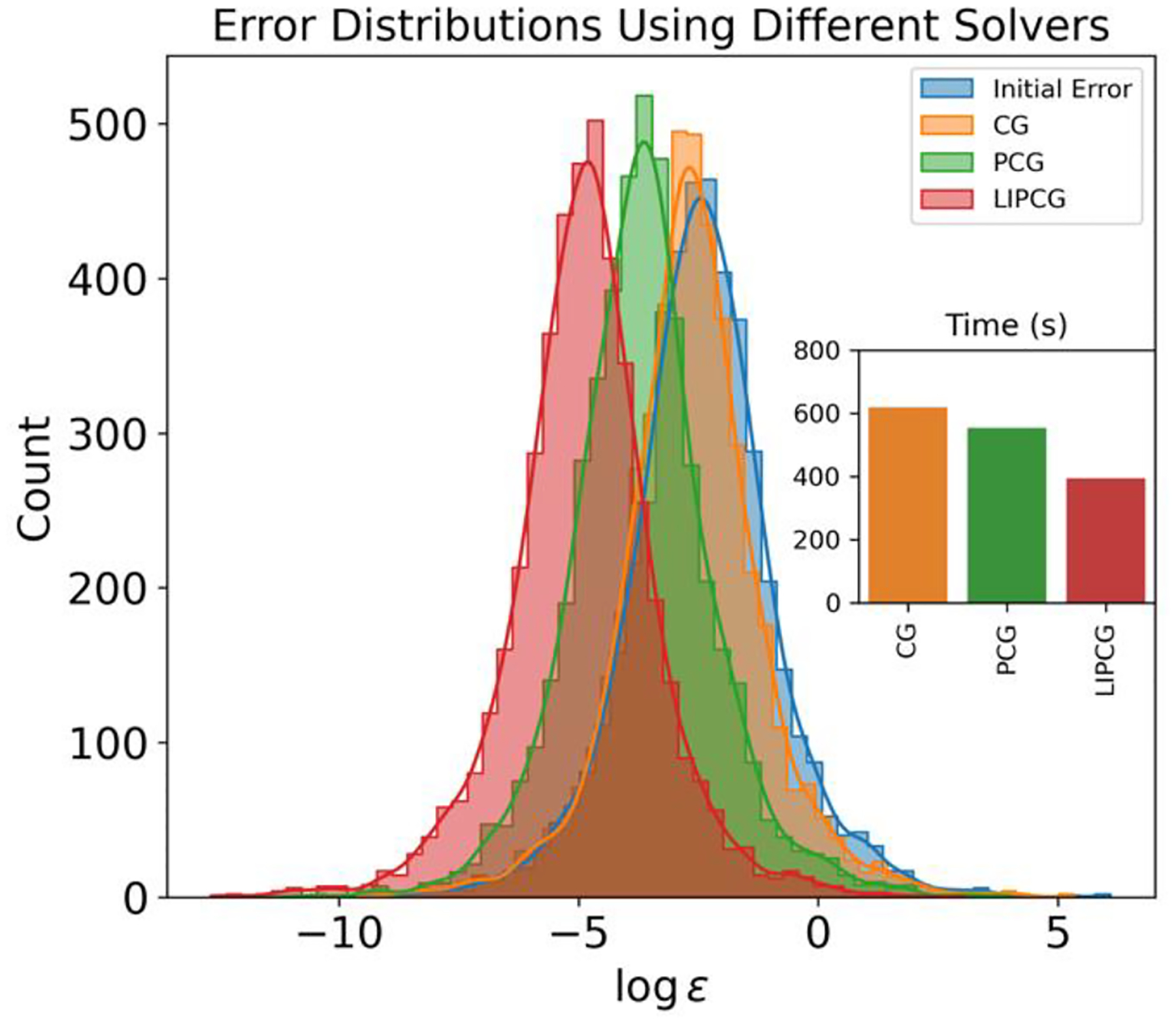
Error Distribution Following a Single Step of Iterative Method Implementation. The convergence tolerance for this analysis is set at a maximum error of 10⁻². The inset figure displays the CPU timing necessary for executing 1000 steps of Molecular Dynamics (MD). As demonstrated in the figure, the LIPCG method results in the smallest overall error distribution and is also associated with the least CPU time, thus indicating its superior efficiency in this context.

The efficacy of local iterations is inherently tied to the cut-off distance employed. An extended cut-off invariably enhances the convergence rate, albeit at a higher computational cost. Building upon the optimal initial guess identified in the previous subsection, we scrutinized different cut-off distances, the results of which are presented in Table 4. The data indicate that larger cut-off distances correlate with a decrease in iterations, which aligns with expectations, but these also increase the CPU time per MD step. Thus, it is vital to evaluate the total CPU time consumed, as portrayed in Table 4. It demonstrates that a cut-off distance of 4 Å demands the least amount of total CPU time.

Table 4:

Optimal Cutoff Distance Determination for the Local Preconditioner using Best Parameters Derived from Table 3. This table employs the optimal parameters ascertained from Table 3 to ascertain the most suitable cutoff distance for the local preconditioner. The data reveals that the optimal cutoff is 4 Å. The left column represents the average iteration count per MD step necessary to achieve convergence, while the right column indicates the average CPU time required to execute 1000 MD steps.

Convergence Criterion: 10−2
Cut-off distance	Order1	Order2	Order3
3Å	267.17(2.60)	270.80(2.82)	271.04(2.83)
4Å	260.40(2.34)	264.67(2.61)	260.93(2.60)
5Å	264.16(2.11)	275.21(2.50)	272.84(2.47)
6Å	264.23(1.96)	287.25(2.41)	280.19(2.36)
Convergence Criterion: 10−3
	Order1	Order2	Order3
3Å	305.44(4.02)	284.40(3.11)	280.23(3.09)
4Å	294.54(3.57)	272.36(2.84)	268.99(2.81)
5Å	307.48(3.38)	286.32(2.69)	284.64(2.67)
6Å	314.29(3.17)	294.79(2.57)	295.20(2.58)
Convergence Criterion: 10−4
	Order1	Order2	Order3
3Å	332.88(5.52)	298.14(4.20)	295.26(4.15)
4Å	330.32(5.05)	296.37(3.80)	292.37(3.74)
5Å	334.50(4.71)	302.83(3.56)	301.60(3.48)
6Å	341.90(4.43)	314.29(3.32)	312.98(3.25)

5. Use of Peek Step to Further Improve Performance

Striving to reduce the computational iterations and enhance overall system performance, we incorporated an additional ‘peek’ step — constructed as a single Jacobi under-relaxation iteration — into the LIPCG protocol. The optimization strategy for this procedural element is elaborated upon in the appended section. As represented in Table 5, this novel peek step hastens the convergence process when the convergence criteria are set to either 10⁻² or 10⁻³, culminating in an average reduction of approximately half an iteration step. Figure 6 visually illustrates the effects of the peek step, showing that the norm of residuals is halved, and maximum errors are significantly diminished post the peek step implementation.

Table 5:

Comparative Analysis of Average Iteration Counts for Tests Conducted Without and With Peek Steps. This table provides a contrastive evaluation of the average number of iterations required in tests conducted both without and with the inclusion of peek steps. The left column represents the average iteration count per MD step needed to achieve convergence, while the right column denotes the average time necessary to complete 1000 MD steps.

Convergence Criterion: 10−2
	Order1	Order2	Order3
Without Peek	260.40(2.34)	264.67(2.61)	260.93(2.60)
With Peek	258.26(2.23)	251.52(2.11)	245.99(2.10)
Convergence Criterion: 10−3
	Order1	Order2	Order3
Without Peek	294.54(3.57)	272.36(2.84)	268.99(2.81)
With Peek	292.74(3.54)	262.32(2.58)	257.71(2.53)
Convergence Criterion: 10−4
	Order1	Order2	Order3
Without Peek	330.32(5.05)	296.37(3.80)	292.37(3.74)
With Peek	328.98(5.03)	290.94(3.73)	285.44(3.69)

Figure 6:

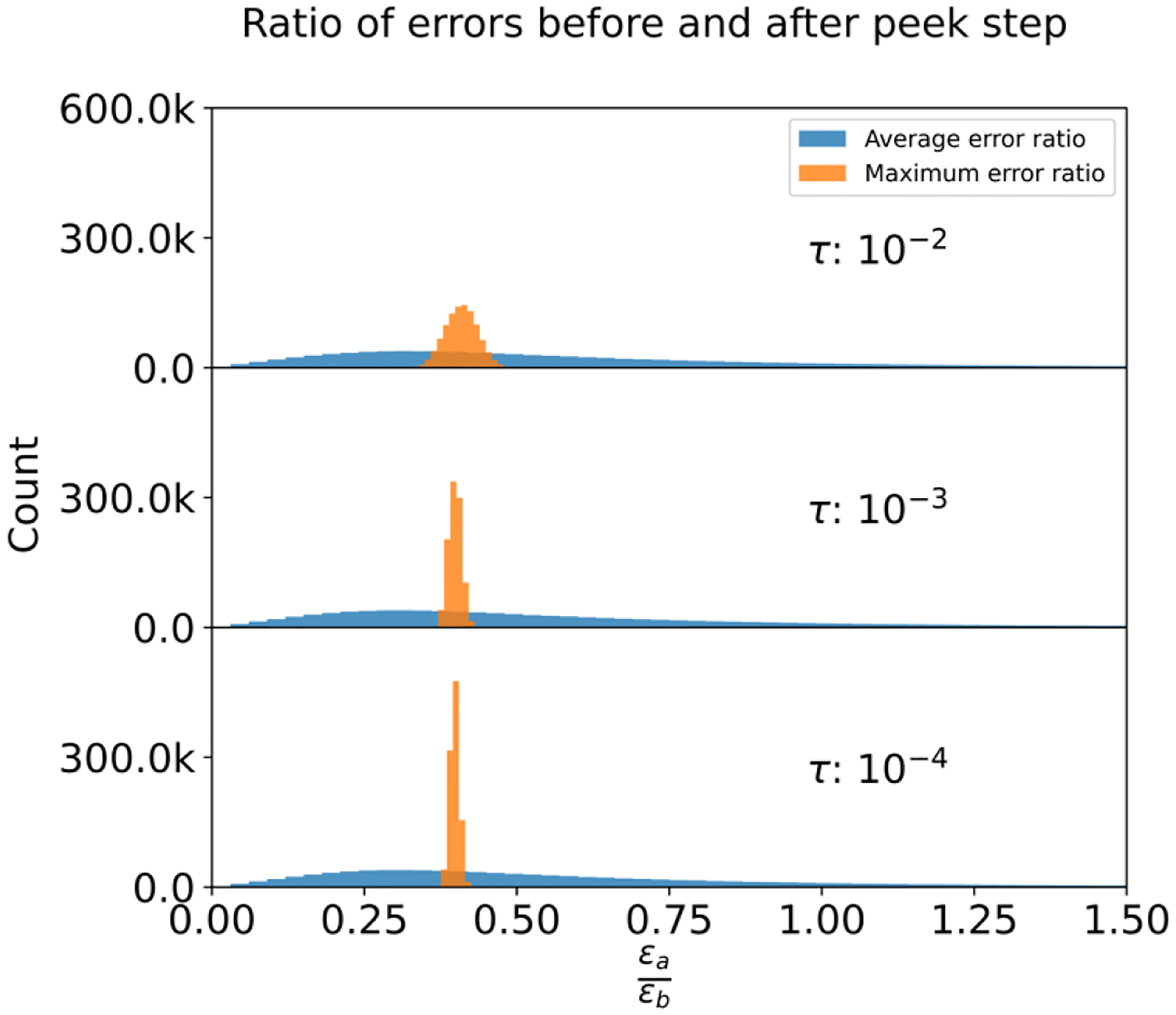
Distributions of Ratios Between Maximum/Average Errors Post-Peek Step and Pre-Peek Step. This figure illustrates the distributions of the ratios derived from the maximum and average errors after the peek step in relation to those prior to the peek step. A smaller ratio is desirable as it indicates a reduction in error.

6. Final Performance Using Optimal Strategy

With the implementation of our optimal strategy which includes local-iteration preconditioning, multi-order extrapolation, and a more proper selection of the convergence criterion, the overall performance of the induced dipole model has been significantly optimized. Our comparison of Wang and Skeel’s approach with our optimal strategy, as illustrated in Table 6, highlights this performance improvement. As the table shows, our optimal strategy managed to achieve the same convergence quality with less time. Moreover, the degree of improvement was particularly pronounced under conditions requiring tighter convergence criteria. To further emphasize this point, let us consider a comparison with the CG method which utilizes only the last step’s history information (as per Table S1). If we insist on a similar energy conservation quality which can be achieved at the convergence tolerance of 10⁻⁶, we have managed to decrease the CPU time taken from 533.14s to 245.99s; this translates to an efficiency/speed gain over 210%. The results clearly illustrate the effectiveness of our proposed enhancements to the induced dipole model.

Table 6:

Performance Comparison Between the Optimal Strategy Developed in This Study and the Approach Proposed by Wang and Skeel. This table presents a comparative evaluation of the performance between the optimal strategy derived in this research and the methodology proposed by Wang and Skeel. In all simulations, the maximum error was employed as the convergence check to ensure energy conservation.

$\tau$	10−2	10−3	10−4
This work	245.99	257.71	285.44
Wang and Skeel	259.23	294.20	329.03

Conclusion

Polarizable force fields, which account for interactions between charges and higher moments like dipoles and quadrupoles, have proven more accurate in describing atomistic interactions compared to high-level quantum mechanical calculations. Despite this, polarizable models such as the pGM model have grappled with energy conservation issues in NVE simulations unless a stringent convergence criterion is employed. Large energy drifts are indicative of inadequate convergence of induced dipoles. Tests performed using the pGM model have revealed that energy drifts are more significant when historical data is leveraged, irrespective of the tolerance used, aligning with observations made with other polarizable force fields. In all test scenarios, energy drifts when history is not incorporated are less than half of those where history is used. This discrepancy implies differences in the quality of induction convergence, even when using the same tolerance level.

Our detailed error analysis shows that the convergence quality and outlier errors are two reasons that prevents energy conservation. In general, using history will lead to a poorer convergence quality with more outlier errors compared to not using history at the same convergence criterion. As a consequence, using the residue norm in convergence check fails to safeguard the convergence of the poorly converged dipoles, leading to unacceptable energy conservation properties unless an unusually tight convergence criterion is used. We therefore explored using the maximum error in the convergence check. Our tests show that energy drifts are qualitatively the same in NVE simulations with or without history when the maximum error is set to be less than 10⁻². Additionally, history can still improve the convergence rate in these tests; the iteration steps are reduced by 2 to 3 for the tested systems.

Based on our observations, we explored a scheme to improve induction convergence by utilizing more prudent initial guesses based on previous steps’ induced dipoles. The MOE scheme was developed to produce better initial guesses. Our tests show that the third-order interpolation with two previous steps is consistently the most effective, reducing the iteration steps by another 2 to 5 for all tested conditions without impacting the energy conservation of the simulations.

Furthermore, we studied the effect of local iterations as a preconditioner to improve the convergence of error outliers when maximum errors are used in convergence check. The error analysis for the tests with and without history shows that the LIPCG scheme leads to smaller and more uniform errors than the standard CG and PCG. These analyses indicate that local iterations can be used to improve the convergence rate of the PCG method. We explored the optimal cutoff distance to be 4 Å for the local iteration and under such condition, iteration steps are reduced by another 3 to 5, and overall simulation time is also reduced, despite the extra cost of local iterations.

Finally, we studied the effect of the “peek step” on the convergence quality. Overall, the residue norms are reduced to half, and the maximum errors are mostly reduced after the peek step. Interestingly, the peek step further improves the convergence rate when the criterion is set as 10⁻² or 10⁻³, with average iteration steps reduced by as much as a half step, likely due to better initial guesses when the convergence quality is better.

In summary, the development documented here shows that it is possible to achieve reasonable energy convergence with just a few iterations when both MOE and LIPCG schemes are used along with the peek step, if the maximum error is used to check the convergence quality. Apparently, the development and optimization documented here will need to be further tested in heterogeneous systems such as ions, proteins, nucleic acids in water. We will certainly revisit the issue in our future development when pGM force fields for ions, proteins, and nucleic acids become available. In addition, our current focus has been on the quality of energy conservation, so we have focused on NVE simulations with the 1fs time step. Clearly larger time steps are often used for NVT and NPT simulations and will lead to worse initial guesses of induced dipoles. Nevertheless, the timing with 2fs is still more efficient than that with 1fs due to the use of fewer PME calls as Wang and Skeel have pointed out. Nevertheless, this indicates further optimization is still feasible when the pGM model is applied to NVT and NPT simulations.

Appendix

Jacobi under-relaxation (JUR) is utilized as the peek step in our overall optimized induction iteration. The use of JUR instead of the standard Jacobi is to minimize the effect of overshooting by introducing a relaxation factor $\left(\omega \right)$ to the Jacobi method as reviewed in the Introduction. To fully take advantage its benefit as the peek step, we have optimized $\omega$ for the pGM model as shown in Figure S6, which is similar to that identified for the amoeba induced dipole model.²³