Generalizing the information content for stepped wedge designs: A marginal modeling approach

Abstract

Stepped wedge trials are increasingly adopted because practical constraints necessitate staggered roll-out. While a complete design requires clusters to collect data in all periods, resource and patient-centered considerations may call for an incomplete stepped wedge design to minimize data collection burden. To study incomplete designs, we expand the metric of information content to discrete outcomes. We operate under a marginal model with general link and variance functions, and derive information content expressions when data elements (cells, sequences, periods) are omitted. We show that the centrosymmetric patterns of information content can hold for discrete outcomes with the variance-stabilizing link function. We perform numerical studies under the canonical link function, and find that while the patterns of information content for cells are approximately centrosymmetric for all examined underlying secular trends, the patterns of information content for sequences or periods are more sensitive to the secular trend, and may be far from centrosymmetric.

1 |. INTRODUCTION

The stepped wedge design is a unidirectional crossover design where all clusters start out in the control condition and switch to active treatment at randomly assigned time points. This design has become popular in pragmatic cluster randomized trials to evaluate health care interventions, because practical constraints necessitate staggered roll-out, or there is a need to eventually implement the intervention in all clusters (Hemming & Taljaard, 2020; Li & Wang, 2022; Ouyang et al., 2022). While a complete stepped wedge design requires all clusters to collect outcome data in all periods, resource and patient-centered considerations may call for an incomplete stepped wedge design (Hemming et al., 2015). Incomplete designs may be chosen when resource constraints place a cap on the total number of cluster-periods and study participants, or when logistical considerations dictate deviations from all clusters commencing simultaneously. This leaves many potential incomplete design variants for consideration. For example, the AFFIRM trial (Heazell et al., 2017) is a stepped wedge cluster randomized trial implementing a new package of care to increase women’s awareness of the need for prompt reporting of reduced fetal movements and standardized management to identify fetal compromise and reduce the rate of stillbirth. The study considered a design akin to Figure 1a where a transition period to allow implementation of the intervention is incorporated when clusters transition from the control to the intervention condition. No data is collected during the transition/implementation period. Alternatively, the staggered enrollment of clusters may also give rise to an incomplete stepped wedge design similar to Figure 1b. This is similar to a pregnancy trial described by Kenyon et al. (2017), where outcome data were only collected near the treatment switch (and which, in practice, had an additional implementation phase to fully roll out the intervention). Due to these emerging incomplete stepped wedge designs, there has been an increasing amount of interest in identifying cluster-period cells, treatment sequences and periods that contribute the least information to the estimation of the treatment effect and that could be preferentially omitted with minimal loss of power. To this end, methods are needed to better understand the trade-offs involved when using incomplete stepped wedge designs.

FIGURE 1.

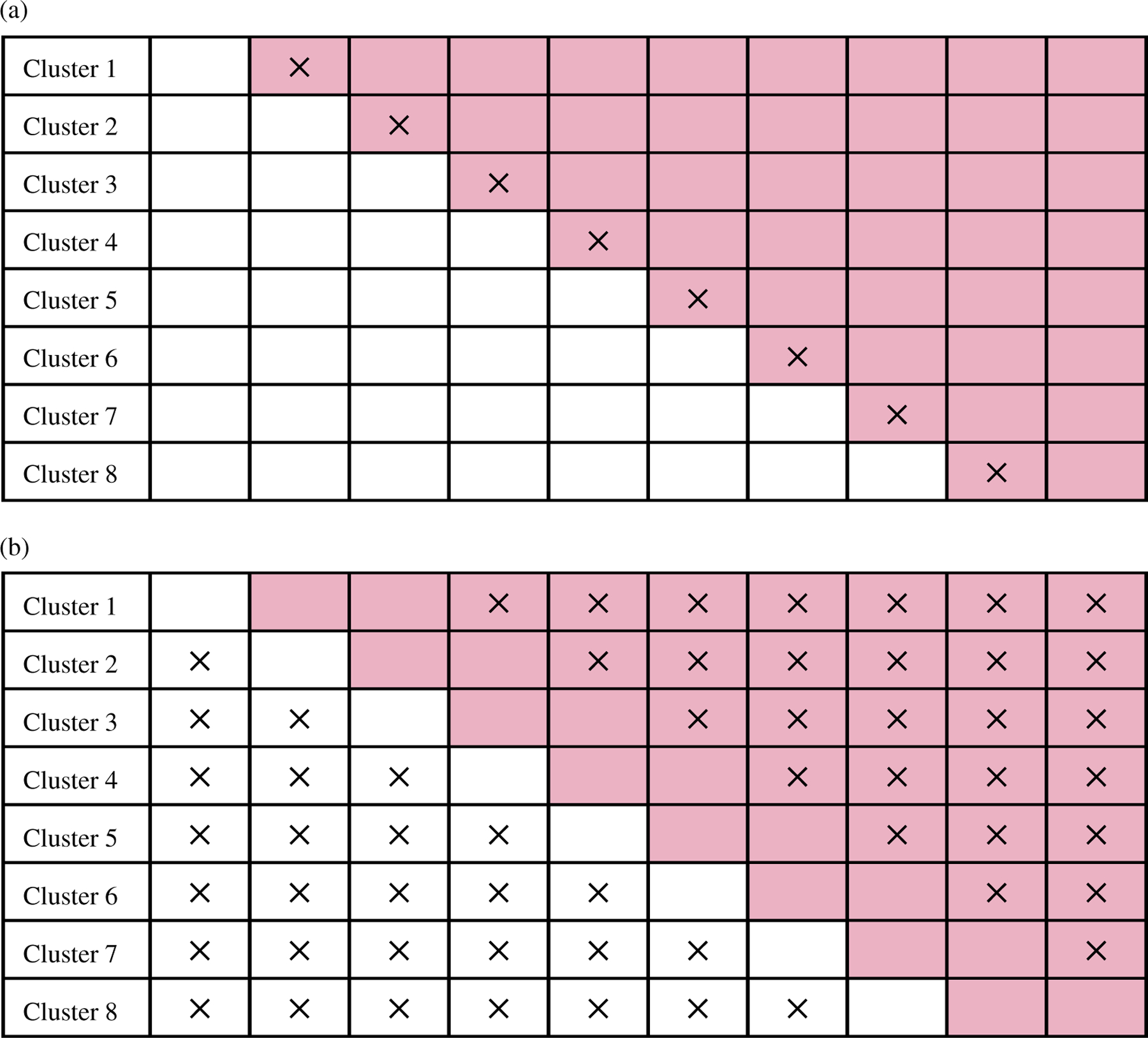
Two examples of incomplete stepped wedge CRTs with I = 8 clusters and J = 10 calendar periods. A white cell indicates a cluster-period under usual care and outcome data collection, a colored cell indicates a cluster-period under treatment and outcome data collection, a cell with ‘×’ indicates a cluster-period without any outcome data collection. (a) A schematic of a incomplete stepped wedge design with I = 8 clusters and J = 10 calendar periods and one transition period. (b) A schematic of a incomplete stepped wedge design with I = 8 clusters and J = 10 calendar periods, one before and two after measurements [Colour figure can be viewed at wileyonlinelibrary.com]

Assuming a Gaussian linear mixed model with a continuous outcome, Kasza and Forbes (2019b) defined the metric of information content of cluster-period cells, entire treatment sequences and entire periods as the relative variance inflation of the treatment effect estimator, when the corresponding data elements are omitted. They found that cells closest to the treatment switch points are most information-rich for estimating the treatment effect. Under a class of centrosymmetric intraclass correlation structures, it has been shown that the information content of cells, treatment sequences and periods also exhibits a centrosymmetric structure. Here, a centrosymmetric intraclass correlation structure is one such that the matrix element is symmetric about its center and hence one that is invariant to joint row and column reverse operation, and the information content of a stepped wedge design is centrosymmetric when the information content values are symmetric about the center of the design diagram. More precise mathematical definitions are provided in Section 3.1. Furthermore, if the three-parameter block exchangeable correlation structure for closed cohort designs (Li et al., 2020) is considered, certain cells have null information content and can be preferentially omitted with no variance inflation (Kasza & Forbes, 2019b). This result also applies to special cases including the simple exchangeable (Hussey & Hughes, 2007) and two-parameter nested correlation structure (Li et al., 2018b) for cross-sectional designs, both of which were referred to as “block exchangeable” in Kasza and Forbes (2019b). Based on the linear mixed model, Kasza et al. (2019b) further studied the information content in the presence of implementation periods as well as treatment effect heterogeneity across clusters. While the cells closest to treatment switch points remain information-rich, the presence of implementation periods elevates the information content of cells around the treatment switch points, due to fewer periods permitting direct within-cluster comparisons. On the other hand, including treatment effect heterogeneity in the outcome model reduces the differences between the information content of treatment sequences. These findings provide important insights to guide the design of incomplete stepped wedge trials with continuous outcomes, where some cluster-period cells are intentionally omitted to minimize data collection burden.

Thus far, the work to derive the information content has been limited to the linear mixed model with Gaussian random effects and error structures. However, binary and count outcomes are also common in stepped wedge designs (Barker et al., 2016; Scott et al., 2017), and it remains unknown whether the patterns of information content with Gaussian linear mixed models hold for a larger class of outcome types and models. In this article, we generalize the metric of information content to outcomes with an arbitrary mean–variance relationship and link functions. Rather than using a conditional framework with a mixed model, we operate under a marginal modeling framework with specified link and variance functions, and derive analytical expressions of the information content when certain data elements, including cluster-period cells, treatment sequences and periods, are omitted. The marginal models separately specify the mean and intraclass correlation structures, and have a population-averaged interpretation of the intervention effect (Li et al., 2018b; Li et al., 2019; Preisser et al., 2003). When the marginal variance function is independent of the marginal mean or the variance-stabilizing link function (Bartlett, 1947) is specified according to the marginal variance function, we show that the patterns of information content in Kasza and Forbes (2019b) hold beyond the linear mixed model setup. While existing information content results do not hold exactly under other link functions, we discuss approximate conditions when the information content profiles remain approximately centrosymmetric, and numerically explore cells that contribute negligible information for estimating the intervention effect. Our findings expand previous investigations to a broader class of outcomes and models, and serve to strengthen the theoretical underpinnings for incomplete stepped wedge designs.

2 |. INFORMATION CONTENT BASED ON MARGINAL MODELS

2.1 |. Marginal model and variance of the treatment effect estimator

We first consider a complete stepped wedge design with I clusters and T periods, where each cluster corresponds to a unique treatment sequence, or equivalently T = I + 1. Although we focus on this basic design, our results still apply when a constant (≥ 2) number of clusters are assigned to each sequence once we redefine the information content for the entire sequence or the sequence-period cells. Let Y_ijl be the outcome for participant l = 1,…, N from cluster i = 1,…, I in period j = 1,…, T. We assume the following marginal mean model with a known link function g

$$g\left({\mu }_{ij}\right)={\beta }_j+X_{ij}\delta ,$$ (1)

where μ_ij is the marginal mean outcome in each cluster-period, β_j refers to the categorical secular trend in the absence of intervention, X_ij is the treatment indicator (e.g., X_ij = 0 or 1 depending on whether cluster i receives the intervention at period j), and δ is the treatment effect parameter of interest on the link function scale. We write θ = (β₁,…, β_T, δ)′, denote h(μ_ij) as the variance function, and ϕ as the common dispersion parameter; thus the marginal variance of Y_ijl is ϕh(μ_ij).

Depending on the nature of the intervention and outcome variable, stepped wedge trials may employ a cross-sectional design, where different sets of participants are recruited during each period, or a closed-cohort design, where the same set of participants are followed up longitudinally over time (Copas et al., 2015). These two different designs require different assumptions on the intraclass correlation structure for the outcomes. Define ${\mathbf{Y}}_{ij}={\left(Y_{ij1},\dots ,Y_{ijN}\right)}^{\prime }$ and ${\mathbf{Y}}_i={\left({\mathbf{Y}}_{i1}^{\prime },\dots ,{\mathbf{Y}}_{iT}^{\prime }\right)}^{\prime }$ as the collection of outcomes in cluster i. Typical intraclass correlation structures considered in stepped wedge designs are special cases of a symmetric block structure (also see Appendix A of Data S1 for more explicit matrix representations)

$${\mathbf{R}}_i=corr\left({\mathbf{\text{Y}}}_i\right)=\left({\mathbf{\text{B}}}_{i1}-{\mathbf{\text{B}}}_{i2}\right)\otimes {\mathbf{\text{I}}}_N+{\mathbf{\text{B}}}_{i2} \otimes \hspace{0.17em}{\mathbf{\text{J}}}_N,$$ (2)

where I_N is the N × N identity matrix, J_N is the N × N matrix of ones, and the symmetric but otherwise unstructured T × T basis matrices are

$${\mathbf{\text{B}}}_{i1}=\left(\begin{array}{cccc}1& r_{i12}^{*}& \dots & r_{i1T}^{*}\\ r_{i12}^{*}& 1& \dots & r_{i2T}^{*}\\ ⋮& ⋮& \ddots & ⋮\\ r_{i1T}^{*}& r_{i2T}^{*}& \dots & 1\end{array}\right),\hspace{1em}{\mathbf{\text{B}}}_{i2}=\left(\begin{array}{cccc}{r}_{i11}& r_{i12}& \dots & r_{i1T}\\ r_{i12}& r_{i22}& \dots & r_{i2T}\\ ⋮& ⋮& \ddots & ⋮\\ r_{i1T}& r_{i2T}& \dots & r_{iTT}\end{array}\right).$$

For two different participants in cluster i, r_ijj is the correlation between their responses if they are both measured in the jth period, and r_ijt is the correlation if one response is measured in period j and the other is measured in period t. For repeated responses on the same participant (applicable in a closed-cohort design), $r_{ijt}^{*}$ is the correlation between responses in periods j and t, (and $r_{ijj}^{*}=1$ by definition). If r_ijj = α₀ for all j, t, and $r_{ijt}^{*}={\alpha }_0$ for |j − t| ≥ 1, R_i = (1 – α₀)I_TN + α₀ J_TN is the simple exchangeable correlation structure as implied from the linear random intercept model in Hussey and Hughes (2007). Setting r_ijj = α₀ for all j, and $r_{ijt}=r_{ijt}^{*}={\alpha }_1$ for all |j − t| ≥ 1 induces the nested exchangeable correlation structure as implied by the random cluster-by-time interaction model in Hooper et al. (2016) and Girling and Hemming (2016). The exponential decay correlation structure is implied by setting r_ijj = α₀ for all j and $r_{ijt}=r_{ijt}^{*}={\alpha }_0{\rho }^{|j-t|}$ for all |j – t| ≥ 1 (Kasza, Hemming, et al., 2019; Li et al., 2021). While the above three examples are mainly applicable to cross-sectional designs, R_i also accommodates correlation structures under closed-cohort designs. For example, the three-parameter block exchangeable correlation structure is obtained with r_ijj = α₀ for all j, r_ijt = α₁ and $r_{ijt}^{*}={\alpha }_2$ for all |j − t| ≥ 1 (Li et al., 2018a; Li et al., 2018b); the proportional decay structure (Li, 2020) is obtained with j, r_ijj = α₀ for all $r_{ijt}={\alpha }_0{\rho }^{|j-t|}$ and $r_{ijt}^{*}={\rho }^{|j-t|}$ for all |j − t| ≥ 1. Further elaborations of R_i are provided in Appendix A of Data S1.

With a suitable working correlation model, estimation of treatment effect δ can proceed with paired generalized estimating equations (GEEs) as in Preisser et al. (2008) and Li et al. (2018b). Assuming that the working correlation structure is correctly specified, the variance of the GEE treatment effect estimator, var($\widehat{\delta }$), in a complete design can be obtained as the (T + 1,T + 1)th element of the model-based variance for θ. Specifically, define the design matrix for cluster i as ${\mathbf{\text{Z}}}_i\otimes \hspace{0.17em}\hspace{0.17em}{\mathbf{\text{1}}}_N$, where Z_i = (I_T, X_i), and X_i = (X_i1,…, X_iT)′ is the vector of treatment indicators common across participants in cluster i. Defining ${\mathbf{\text{D}}}_i=\mathrm{diag}\left\{\partial g\left({\mu }_{i1}\right)/\partial {\mu }_{i1},\dots ,\partial g\left({\mu }_{iT}\right)/\partial {\mu }_{iT}\right\}$ and ${\mathit{\mu }}_i={\left({\mu }_{i1},\dots ,{\mu }_{iT}\right)}^{\prime }$, the estimation of θ can be operationalized by iteratively reweighted least squares through regression of the working outcome vector ${\mathbf{\text{Y}}}_i^{*}=\left({\mathbf{\text{Z}}}_i\otimes \hspace{0.17em}\hspace{0.17em}{\mathbf{\text{1}}}_N\right)\widehat{\mathit{\theta }}+{\mathbf{\text{D}}}_i\left({\mathbf{\text{Y}}}_i-{\widehat{\mathit{\mu }}}_i\otimes \hspace{0.17em}\hspace{0.17em}{\mathbf{\text{1}}}_N\right)\text{ on }{\mathbf{\text{Z}}}_i\otimes \hspace{0.17em}\hspace{0.17em}{\mathbf{\text{1}}}_N$ with a cluster-specific precision matrix ${\mathbf{\text{V}}}_i^{-1}$, where

$${\mathbf{\text{V}}}_i=\left\{{\mathbf{\text{D}}}_i{\mathbf{\text{A}}}_i\left({\mathbf{\text{B}}}_{i1}-{\mathbf{\text{B}}}_{i2}\right){\mathbf{\text{A}}}_i{\mathbf{\text{D}}}_i\right\}\hspace{0.17em}\otimes \hspace{0.17em}{\mathbf{\text{I}}}_N+\left({\mathbf{\text{D}}}_i{\mathbf{\text{A}}}_i{\mathbf{\text{B}}}_{i2}{\mathbf{\text{A}}}_i{\mathbf{\text{D}}}_i\right)\otimes {\mathbf{\text{J}}}_N,$$ (3)

is the variance of the working outcome, and ${\mathbf{\text{A}}}_i=\sqrt{\varphi }\mathrm{diag}\left(\sqrt{h_{i1}},\dots ,\sqrt{h_{iT}}\right)$ (Preisser & Qaqish, 1996). By this formulation, the asymptotic variance of the GEE treatment effect estimator can be obtained as

$$\mathrm{var}(\widehat{\delta })={\left\{\sum _{i=1}^I{\mathbf{\text{H}}}_i^{\prime }{\mathbf{\text{V}}}_i^{-1}{\mathbf{\text{H}}}_i-\left(\sum _{i=1}^I{\mathbf{\text{H}}}_i^{\prime }{\mathbf{\text{V}}}_i^{-1}\right)\mathbf{\text{E}}{\left(\sum _{i=1}^I{\mathbf{\text{E}}}^{\prime }{\mathbf{\text{V}}}_i^{-1}\mathbf{\text{E}}\right)}^{-1}{\mathbf{\text{E}}}^{\prime }\left(\sum _{i=1}^I{\mathbf{\text{V}}}_i^{-1}{\mathbf{\text{H}}}_i\right)\right\}}^{-1},$$

with ${\mathbf{\text{H}}}_i={\mathbf{\text{X}}}_i\otimes {\mathbf{\text{1}}}_N$ and $\mathbf{E}={\mathbf{I}}_T\otimes \hspace{0.17em}{\mathbf{\text{1}}}_N$. With an identity link function and the Gaussian variance function h_ij = 1, var($\widehat{\delta }$) can be further simplified to a scalar expression under the simple exchangeable (Hussey & Hughes, 2007), block exchangeable (Li et al., 2018b) and the proportional decay (Li, 2020) correlation structures. On the other hand, when the link function is nonidentity or the marginal variance function depends on the marginal mean, var($\widehat{\delta }$) generally does not have a simple analytical expression, even when the correlation matrix R_i has a simple closed-form inverse. To proceed, the following Lemma provides a simpler expression of var($\widehat{\delta }$) by collapsing the working outcomes by each cluster-period.

Lemma 1. The asymptotic variance of the GEE treatment effect estimator is

$$\mathrm{var}(\widehat{\delta })={\left\{\sum _{i=1}^I{\mathbf{\text{X}}}_i^{\prime }{\overline{\mathbf{\text{V}}}}_i^{-1}{\mathbf{\text{X}}}_i-\left(\sum _{i=1}^I{\mathbf{\text{X}}}_i^{\prime }{\overline{\mathbf{\text{V}}}}_i^{-1}\right){\left(\sum _{i=1}^I{\overline{\mathbf{\text{V}}}}_i^{-1}\right)}^{-1}\left(\sum _{i=1}^I{\overline{\mathbf{\text{V}}}}_i^{-1}{\mathbf{\text{X}}}_i\right)\right\}}^{-1},$$

where Xi is the treatment sequence indicator of cluster i and ${\overline{\mathbf{\text{V}}}}_i=N^{-1}\left\{{\mathbf{\text{D}}}_i{\mathbf{\text{A}}}_i\left({\mathbf{\text{B}}}_{i1}-{\mathbf{\text{B}}}_{i2}\right){\mathbf{\text{A}}}_i{\mathbf{\text{D}}}_i\right\} + {\mathbf{\text{D}}}_i{\mathbf{\text{A}}}_i{\mathbf{\text{B}}}_{i2}{\mathbf{\text{A}}}_i{\mathbf{\text{D}}}_i$ is the variance matrix for the cluster-period means of the working outcome vector, defined as ${\left({\mathbf{\text{I}}}_T\otimes \hspace{0.17em}{\mathbf{\text{1}}}_N\right)}^{\prime }{\mathbf{\text{Y}}}_i^{*}$.

The proof of Lemma 1 boils down to a key identity, ${\mathbf{\text{E}}}^{\prime }{\mathbf{\text{V}}}_i^{-1}\mathbf{\text{E}}={\left(N^{-2}{\mathbf{\text{E}}}^{\prime }{\mathbf{\text{V}}}_i\mathbf{\text{E}}\right)}^{-1}={\overline{\mathbf{\text{V}}}}_i^{-1}$ for each cluster i, which we show in Appendix B of Data S1 by block matrix inversion. Under a constant variance, h_ij = 1, and identity link such that D_i = I_T, Lemma 1 is similar to the result in Grantham et al. (2019) based on a linear mixed model, but does not require the full Gaussian distributional assumption. Lemma 1 also extends the result of Li et al. (2021) to a broader class of correlation models with the incorporation of the auto-correlation parameters $r_{ijl}^{*}\text{'s}$, albeit under the assumption of equal cluster-period sizes. In addition, Lemma 1 expands the result of Davis-Plourde et al. (2021) developed for generalized linear mixed models to GEE. Intuitively, Lemma 1 implies that the GEE treatment effect estimator with participant-level data has the same asymptotic variance as that with cluster-period means in stepped wedge designs. This intermediate step allows us to conveniently represent the information content of each cluster-period.

2.2 |. Variance of the treatment effect estimator when omitting one cell

Following Kasza and Forbes (2019b), we use $\mathrm{var}{(\widehat{\delta })}_{[ij]}$ to denote the variance of the GEE estimator when the observations in the design cell corresponding to cluster i and period j are omitted. As we operate under the basic stepped wedge design with T = I + 1 periods, each design cell in fact corresponds to a sequence-period, which is identical to a cluster-period with one cluster per sequence. Without ambiguity, below we will use a cluster-period and a sequence-period interchangeably (a cluster therefore also corresponds to a treatment sequence). Specifically, the information content of each cluster-period is defined as

$$\text{IC}(i,j)=\mathrm{var}{(\widehat{\delta })}_{[ij]}/\mathrm{var}(\widehat{\delta }),$$

which measures the relative asymptotic variance inflation when design cell (i, j) is omitted, and var($\widehat{\delta }$)is given in Lemma 1. To obtain an expression for $\mathrm{var}{(\widehat{\delta })}_{[ij]}$, we first rearrange the IT × 1 cell means of the working outcome, ${\overline{\mathbf{\text{Y}}}}^{*}={\left({\overline{\mathbf{\text{Y}}}}_1^{*\prime },\dots ,{\overline{\mathbf{\text{Y}}}}_I^{*\prime }\right)}^{\prime }$ such that the summary statistic corresponding to the omitted cell is the first element, followed by the remaining observations from the same cluster, and then the observations from other clusters; the rows and columns of cov(${\overline{\mathbf{\text{Y}}}}^{*}$) are also correspondingly rearranged such that variance of the summary statistic of the omitted cell is the upper left element. We write the IT × IT covariance matrix of the rearranged cluster-period means as

$$\overline{\mathbf{\text{V}}}=\left(\begin{array}{cc}{\overline{\nu }}_{ij}& {\overline{\mathit{\nu }}}_{ij}^{\prime }\\ {\overline{\mathit{\nu }}}_{ij}& {\mathbf{\text{V}}}_{[ij]}\end{array}\right),$$

where ${\overline{v}}_{ij}=\mathrm{var}\left({\overline{Y}}_{ij}^{*}\right)$ is the variance of the jth element of ${\overline{\mathbf{\text{Y}}}}_1^{*}$, and ${\overline{\mathit{v}}}_{ij}$ is the (IT − 1) × 1 column vector with (k,t)th element given by cov(${\overline{Y}}_{ij}^{*},{\overline{Y}}_{kt}^{*}$), with (k, t) ≠ (i, j). Due to independence of observations between clusters, we can write ${\overline{\mathit{v}}}_{ij}={\left({\overline{\mathit{v}}}_{ij}^{{(1:T-1)}^{\prime }},{\mathbf{\text{0}}}_{(I-1)T}^{\prime }\right)}^{\prime }$, where 0_s is the s-vector of zeros. Furthermore, ${\overline{\mathbf{\text{V}}}}_{[ij]}$ is a (IT − 1) × (IT − 1) block diagonal structure, with the first block given by the (T − 1) × (T − 1) matrix ${\overline{\mathbf{\text{V}}}}_{i[j]}$, the covariance matrix of cluster-period mean working outcomes in cluster i with the jth row and column removed, and the remaining blocks given by cov(${\overline{\mathbf{\text{Y}}}}_k^{*}$) for k ≠ i. We further define e_j as the T-vector with its jth element as 1 and 0 elsewhere. By deriving the expression of $\mathrm{var}{(\widehat{\delta })}_{[ij]}$, the following Theorem provides an analytical expression of the information content for the GEE treatment effect estimator when the (i,j)th cell is excluded. The detailed proof can be found in Appendix C in Data S1.

Theorem 1. The information content of design cell (i, j) is

$$IC(i,j)=\frac{{\tilde{e}}_j^{\prime }\left\{{\overline{\mathbf{\text{V}}}}_i-{\left(\sum _{k=1}^I{\overline{\mathbf{\text{V}}}}_k^{-1}\right)}^{-1}\right\}{\widetilde{\mathbf{\text{e}}}}_j}{{\tilde{e}}_j^{\prime }\left\{{\overline{\mathbf{\text{V}}}}_i-{\left(\sum _{k=1}^I{\overline{\mathbf{\text{V}}}}_k^{-1}\right)}^{-1}\right\}{\widetilde{\mathbf{\text{e}}}}_j-var(\widehat{\delta }){\left\{{\stackrel{\sim }{X}}_{ij}-\left(\sum _{k=1}^I{\mathbf{\text{X}}}_k^{\prime }{\overline{\mathbf{\text{V}}}}_k^{-1}\right){\left(\sum _{k=1}^I{\overline{\mathbf{\text{V}}}}_k^{-1}\right)}^{-1}{\widetilde{\mathbf{\text{e}}}}_j\right\}}^2}$$

where ${\widetilde{\mathbf{\text{e}}}}_j={\mathbf{\text{e}}}_j-{\mathbf{\text{I}}}_{[j]}^{\prime }{\overline{\mathbf{\text{V}}}}_{i[j]}^{-1}{\overline{v}}_{ij}^{(1:T-1)},{\mathbf{\text{I}}}_{[j]}$, is the (T − 1) × T matrix obtained by removing the jth row from I_T, and ${\tilde{X}}_{ij}=X_{ij}-{\mathbf{\text{X}}}_{i[j]}^{\prime }{\overline{\mathbf{\text{V}}}}_{i[j]}^{-1}{\overline{v}}_{ij}^{(1:T-1)}$, X_i[j] is obtained by omitting X_ij from X_i.

Several remarks are in order based on Theorem 1. First, as we show in Appendix C in Data S1, the information content of each cluster-period is at least 1, namely IC(i, j) ≥ 1 for all i, j. Second, when $h\left({\mu }_{ij}\right)\propto 1$, such as when Y_ijl follows a Gaussian or Laplace distribution, the marginal variance of the outcome is invariant to its marginal mean. Assuming R_i is identical across clusters (e.g., when treatment has no effect on the intraclass correlation structures), our information content expression simplifies to the expression obtained in Kasza and Forbes (2019b) based on a linear mixed model. Our expression, however, is more general as we allow h(μ_ij) ≥ 0 to be an arbitrary function of the mean, and accommodate scenarios even when the intraclass correlation structure R_i differs across clusters. Finally, because the information content expression is derived without restrictions on the treatment indicator X_ij, Theorem 1 is actually more general than for stepped wedge designs and holds for any complete longitudinal cluster randomized design. For example, to obtain IC(i, j) for a parallel-arm longitudinal cluster randomized trial with baseline randomization, one can consider X_i = 1_T for half of the clusters and X_i = 0_T for the remaining half. As a second example, if X_ij represents the number of periods elapsed since treatment initiation, model (1) is referred as the linear time-on-treatment effect model (Hughes et al., 2015), and Theorem 1 can be used to explore the information patterns with increasing or decreasing treatment effect over time in stepped wedge trials.

2.3 |. Information content when omitting a sequence or period

Following a similar strategy, we can define $\mathrm{var}{(\widehat{\delta })}_{[i,•]}$ as the asymptotic variance of the treatment effect estimator when an entire treatment sequence i is omitted, and $\mathrm{var}{(\widehat{\delta })}_{[•,j]}$ as the asymptotic variance of the treatment effect estimator when an entire period j is omitted. We then similarly define the relevant information content to understand which treatment sequence or period contributes the most information for estimating δ, and therefore can potentially inform the decision to randomize in earlier or later sequences for maximizing power, or the decision to omit data collection in earlier or later time periods. In Appendix D in Data S1, we establish the following information content expressions for the GEE estimator.

Theorem 2. Define $\mathbf{\text{C}}=\sum _{i=1}^I{\overline{\mathbf{\text{V}}}}_i^{-1},\mathbf{\text{d}}=\sum _{i=1}^I{\overline{\mathbf{\text{V}}}}_i^{-1}{\mathbf{\text{X}}}_i$ and ${\mathbf{\text{M}}}_i={\mathbf{\text{C}}}^{-1}\mathbf{\text{d}}-{\mathbf{\text{X}}}_i$. Then the information content for each treatment sequence i is given by

$$IC(i,•)=\frac{\mathrm{var}{(\widehat{\delta })}_{[i,•]}}{\mathrm{var}(\widehat{\delta })}=\frac{1}{1-\mathrm{var}(\widehat{\delta }){\mathbf{\text{M}}}_i^{\prime }{\left\{{\overline{\mathbf{\text{V}}}}_i-{\left(\sum _{k=1}^I{\overline{\mathbf{\text{V}}}}_k^{-1}\right)}^{-1}\right\}}^{-1}{\mathbf{\text{M}}}_i}.$$ (4)

Denote the cell means from period j across all clusters as ${\overline{\mathbf{\text{Y}}}}_j^{*}$ and then re-arrange the collection of all cell means such that ${\overline{\mathbf{\text{Y}}}}^{*}={\left({\overline{\mathbf{\text{Y}}}}_j^{{*}^{\prime }},{\overline{\mathbf{\text{Y}}}}_{[j]}^{{*}^{\prime }}\right)}^{\prime }$. Define ${\overline{\mathbf{\text{V}}}}_j=\mathrm{cov}\left({\overline{\mathbf{\text{Y}}}}_j^{*}\right)$, ${\mathbf{\text{G}}}_j^{\prime }=\mathrm{cov}\left({\overline{\mathbf{\text{Y}}}}_j^{*},{\overline{\mathbf{\text{Y}}}}_{[j]}^{*}\right)$, ${\overline{\mathbf{\text{V}}}}_{[j]}=\mathrm{cov}\left({\overline{\mathbf{\text{Y}}}}_{[j]}^{*}\right)$ and ${\mathbf{\text{W}}}_j={\overline{\mathbf{\text{V}}}}_j-{\mathbf{\text{G}}}_j^{\prime }{\overline{\mathbf{\text{V}}}}_{[j]}^{-1}{\mathbf{\text{G}}}_j$. Further define ${\mathbf{\text{Z}}}_j=\left({\mathbf{\text{1}}}_I\otimes {\mathbf{\text{e}}}_j^{\prime },{\left(X_{1j},\dots ,X_{Ij}\right)}^{\prime }\right)$, and ${\widetilde{\mathbf{\text{Z}}}}_j=\left({\widetilde{\mathbf{\text{E}}}}_j,{\widetilde{\mathbf{\text{X}}}}_j\right)={\mathbf{\text{Z}}}_j-\hspace{0.17em}{\mathbf{\text{G}}}_j^{\prime }{\overline{\mathbf{\text{V}}}}_{[j]}^{-1}{\mathbf{\text{Z}}}_{[j]}$, where Z_[j] is Z_j with jth row omitted. Then the information content for each time period j is given by

$$IC(•,j)=\frac{{\mathrm{var}(\widehat{\delta })}_{[•\cdot j]}}{\mathrm{var}(\widehat{\delta })}=\frac{1}{1-\mathrm{var}(\widehat{\delta }){\left({\widetilde{\mathbf{\text{X}}}}_j-{\widetilde{\mathbf{\text{E}}}}_j{\mathbf{\text{C}}}^{-1}\mathbf{\text{d}}\right)}^{\prime }{\widetilde{\mathbf{\text{W}}}}_j^{+}\left({\widetilde{\mathbf{\text{X}}}}_j-{\widetilde{\mathbf{\text{E}}}}_j{\mathbf{\text{C}}}^{-1}\mathbf{\text{d}}\right)},$$ (5)

where ${\widetilde{\mathbf{\text{W}}}}_j={\mathbf{\text{W}}}_j-{\widetilde{\mathbf{\text{E}}}}_j{\mathbf{\text{C}}}^{-1}{\widetilde{\mathbf{\text{E}}}}_j^{\prime }$, and “+” denotes the Moore-Penrose generalized inverse.

Importantly, when an entire period j is omitted, the period effect β_j becomes unestimable, and therefore we use the Moore–Penrose generalized inverse to represent the asymptotic variance of the GEE estimator $\widehat{\theta }$, so that we can connect $\mathrm{var}{(\widehat{\delta })}_{[•,j]}$ with var($\widehat{\delta }$) through a modified Woodbury matrix identity for rank-deficient matrices (Deng, 2011). Additional variance expressions when an arbitrary set of cluster-periods are omitted are more complicated and are pursued in Appendix D in Data S1. Finally, while we assume a standard design with one cluster per sequence for brevity of exposition, when multiple clusters of the same size are assigned to the same treatment sequence, we naturally have IC(i, •) = IC(k, •) for clusters i and k receiving the same sequence. This implies that our general formulas should directly apply for an equal number of clusters in each sequence.

3 |. PROPERTIES AND EXAMPLES OF INFORMATION CONTENT IN STEPPED WEDGE DESIGNS

3.1 |. Information content with variance-stabilizing link functions

The information content expressions derived in Theorems 1 and 3 are fairly general with an arbitrary link function and variance function. To get some further insights on these expressions, we first discuss one special case where the results can be further simplified. For a given variance function, h(μ_ij), we first tailor the choice of link function in model (1) to simplify the information content expressions. Even when the intraclass correlation model (2) is common across all clusters, both variance expressions V_i and ${\overline{\mathbf{\text{V}}}}_i$ can be cluster-dependent through matrices D_i and A_i. In the special case of an identity link, g(μ_ij) = μ_ij, and constant variance function $h\left({\mu }_{ij}\right)\propto 1$, it is apparent that ${\mathbf{\text{A}}}_i\propto {\mathbf{\text{D}}}_i={\mathbf{\text{I}}}_T$, in which case ${\overline{\mathbf{\text{V}}}}_i=\overline{\mathbf{\text{V}}}$ is common to all clusters, therefore allowing the results in Kasza and Forbes (2019b) to apply. When the variance function explicitly depends on the marginal mean, such as for binary or count outcomes, one can still ensure a common variance ${\overline{\mathbf{\text{V}}}}_i=\overline{\mathbf{\text{V}}}$, as long as the link function g(μ_ij) in model (1) is chosen from the class of variance-stabilizing link functions, whose definition is given below.

Definition 1. If $g(x)=a\int \{h(x){\}}^{-1/2}dx+b$ for constants a ≠ 0 and $b\in ℝ$, then g(x) defines a class of variance-stabilizing link functions.

The concept of a variance-stabilizing link is closely connected with the variance-stabilizing transformation techniques to achieve approximately constant variance for nonnormal data (Anscombe, 1948; Bartlett, 1947). However, the motivation here is to ensure the variance of the working outcome vector (3) is no longer cluster-dependent, which requires ${\mathbf{\text{D}}}_i\propto {\mathbf{\text{A}}}_i^{-1}$ and the link function to satisfy the following ordinary differential equation for any i and j:

$$\frac{\partial g\left({\mu }_{ij}\right)}{\partial {\mu }_{ij}}\propto \frac{1}{\sqrt{h\left({\mu }_{ij}\right)}}.$$ (6)

It is then evident that the class of link functions in Definition 1 satisfies condition (6) and stablilizes the variance of the working outcome vector such that ${\overline{\mathbf{\text{V}}}}_i=\overline{\mathbf{\text{V}}}$. Table 1 provides explicit examples of variance-stabilizing link functions (up to an affine transformation) for common data types. For example, the angular link function, arcsin ($\sqrt{{\mu }_{ij}}$) can be used for binary outcomes, while the square-root link function, $\sqrt{{\mu }_{ij}}$ can be used for Poisson count outcomes, among others. Except for the Gaussian variance function, the variance-stabilizing link functions generally do not coincide with the canonical link functions. With the use of variance-stabilizing link functions, we have $\sum _{k=1}^I{\overline{\mathbf{\text{V}}}}_k^{-1}=I{\overline{\mathbf{\text{V}}}}^{-1}$ and $\sum _{k=1}^I{\mathbf{\text{X}}}_k^{\prime }{\overline{\mathbf{\text{V}}}}_k^{-1}=\left(\sum _{k=1}^I{\mathbf{\text{X}}}_k^{\prime }\right){\overline{\mathbf{\text{V}}}}^{-1}$, the information content expression in

TABLE 1.

Common data types, canonical link, and typical variance-stabilizing link functions (up to an affine transformation) for each marginal variance function

Family	Mean-variance	Canonical link	Variance-stabilizing link
Gaussian	$h(x)\propto 1$	$g(x)=x$	$g(x)=x$
Binomial	$h(x)\propto x(1-x)$	$g(x)=\log \{x/(1-x)\}$	$g(x)=\arcsin (\sqrt{x})$
Negative binomial	$h(x)\propto x(1+x)$	$g(x)=x/(1+x)$	$g(x)=\log \left\{x+\sqrt{1+x^2}\right\}$
Poisson	$h(x)\propto \hspace{0.17em}x$	$g(x)=\log (x)$	$g(x)=\sqrt{x}$
Gamma	$h(x)\propto \hspace{0.17em}{x}^2$	$g(x)=1/x$	$g(x)=\log (x)$
Inverse Gaussian	$h(x)\propto \hspace{0.17em}{x}^3$	$g(x)=1/x^2$	$g(x)=1/\sqrt{x}$

Theorem 1 thus simplifies to

$$\mathrm{IC}(i,j)=\frac{(I-1)S_{ij}}{(I-1)S_{ij}-var(\widehat{\delta }){\left\{{\tilde{X}}_{ij}-I^{-1}\left(\sum _{k=1}^I{\mathbf{\text{X}}}_k^{\prime }\right){\widetilde{\mathbf{\text{e}}}}_j\right\}}^2},$$ (7)

with $s_{ij}={\overline{v}}_{ij}-{\overline{\mathit{v}}}_{ij}^{{(1:T-1)}^{\prime }}{\overline{\mathbf{\text{V}}}}_{i[j]}^{-1}{\overline{\mathit{v}}}_{ij}^{(1:T-1)}$, which coincides with that obtained in Kasza and Forbes (2019b) but now applies more generally to discrete outcomes.

The variance-stabilizing link function also allows us to simplify expressions of IC(i, •) and IC(•, j) (for the information content for sequences and periods, respectively), without assuming variance function $h\left({\mu }_{ij}\right)\propto 1$. These simplified expressions coincide with those derived in Kasza and Forbes (2019b) under the linear mixed model assumption, and lead to the following analytical results. To state the results, we follow Kasza and Forbes (2019b) and Bowden et al. (2021) to define a variance matrix $\mathbf{\text{Σ}}$ to be centrosymmetric as long as the permutation matrix ${\mathbf{\text{P}}}^{*}$ that reverses the order of the rows of $\mathbf{\text{Σ}}$ satisfies ${\mathbf{\text{P}}}^{*}\mathbf{\text{ΣP}}*\prime =\mathbf{\text{Σ}}$. For example, the variance matrix $\overline{V}$ obtained under the block exchangeable correlation structure and the proportional decay structure along with other special cases in Section 2.1 are all centrosymmetric (assuming a variance-stabilizing link function); for these structures, the information content profiles are also centrosymmetric.

Theorem 3. Assuming g is chosen as a variance-stabilizing link function, when all clusters have a common variance structure R_i = R that leads to a centrosymmetric variance $\overline{V}$, in a standard stepped wedge design, the information content profiles are also centrosymmetric, namely, IC(i, j) = IC(I + 1 − i, T + 1 − j), IC(i, •) = IC(I + 1 − i, •) and IC(•, j) = IC(•, T + 1 − j),

Under a variance-stabilizing link function, the expressions for IC(i, j), IC(i, •) and IC(•, j) are identical to those in Kasza and Forbes (2019b), and therefore the same arguments can be used to establish Theorem 3. However, with the application of a suitable variance-stabilizing link function, Theorem 3 extends the findings for linear mixed models to a larger class of outcome types. Intuitively, Theorem 3 suggests that omitting data from cluster-period (i, j) leads to the same variance inflation as omitting its centrosymmetric counterpart, cluster-period (I + 1 − i, T + 1 − j). Further, omitting treatment sequence i or period j can lead to the same variance inflation as omitting treatment sequence I + 1 − i or period T + 1 − j, respectively. In addition to the centrosymmetry results in Theorem 3, certain information content may be expressed more explicitly when the variance $\overline{\mathbf{V}}$ admits a closed-form inverse. This is the case when R_i = R exhibits a block exchangeable (Li et al., 2018b) and proportional decay (Li, 2020) structure, which we elaborate as two specific examples below, with details of their correlation structure components in Appendix A in Data S1.

Example 1 (Block exchangeable correlation structure). When the correlation structure (2) is block exchangeable such that r_ijj = α₀ for all i, j, r_ijt = α₁ and $r_{ijt}^{*}={\alpha }_2$ for all i and |j − t| ≥ 1, we have ${\mathbf{\text{R}}}_i=\mathbf{\text{R}}=\left({\mathbf{\text{B}}}_1-{\mathbf{\text{B}}}_2\right)\otimes {\mathbf{\text{I}}}_N+{\mathbf{\text{B}}}_2\otimes \hspace{0.17em}{\mathbf{\text{J}}}_N$, with basis matrices

$${\mathbf{\text{B}}}_1=\left(1-{\alpha }_2\right){\mathbf{\text{I}}}_T+{\alpha }_0{\mathbf{\text{J}}}_T,\hspace{1em}{\mathbf{\text{B}}}_2=\left({\lambda }_3-{\lambda }_1\right){\mathbf{\text{I}}}_T/N+\left({\lambda }_4-{\lambda }_3-{\lambda }_2+{\lambda }_1\right){\mathbf{\text{J}}}_T/(TN),$$

where λ₁ = 1 − α₀ + α₁ − α₂, λ₂ = 1 − α₀ − (T − 1)(α₁ − α₂), λ₃ = 1 + (N − 1)(α₀ − α₁) − α₂ and λ₄ = 1 + (N − 1)α₀ + (T − 1)(N − 1)α₁ + (T − 1)α₂ are four distinct eigenvalues of R_i (Li et al., 2018b). This correlation structure includes the nested exchangeable and simple exchangeable correlation structures as two special cases by equating, α₁ = α₂, and α₀ = α₁ = α₂, respectively. Under the block exchangeable correlation structure, the variance matrix of the cluster-period means, $\overline{\mathbf{V}}$, is not only centrosymmetric, but also order-invariant. Specifically, an order-invariant matrix $\mathbf{\text{Σ}}$ satisfies $\mathbf{\text{PΣ}}{\mathbf{\text{P}}}^{\prime }=\mathbf{\text{Σ}}$ for any permutation matrix P. In this case, when the variance-stabilizing link function is used, the analytical insights established with the linear mixed model can be generalized to binary and count outcomes such that IC(J/2, 1) = IC(J/2, J) = 1 (Matthews & Forbes, 2017). That is, in a standard stepped wedge design with an even number of periods and hence an odd number of sequences, observations from the first and last period in the cluster receiving the same number of treatment and control periods (namely the middle cluster in a cluster-by-period diagram) contain no information for estimating the treatment effect. Omitting these cells thus yields no increase in the asymptotic variance of the GEE treatment effect estimator.

Because a closed-form inverse is available for the block exchangeable correlation structure, we can provide a more explicit information content expression for each sequence defined in (4). Assuming the variance-stabilizing link function, we show in Appendix E in Data S1 that

$$\mathrm{IC}(i,•)=\frac{I(I-1)T\varphi /N}{I(I-1)T\varphi /N-\mathrm{var}(\widehat{\delta })\left\{\left(TW-U^2+i(i-T)I\right)/{\lambda }_3+\left(U^2+i(i-T)I^2\right)/{\lambda }_4\right\}},$$

where $W=\sum _{j=1}^T{\left(\sum _{i=1}^I{X}_{ij}\right)}^2=I(I+1)(2I+1)/6$ and $U=\sum _{i=1}^I\sum _{j=1}^T{X}_{ij}=I(I+1)/2$ are design constants in a standard stepped wedge design. Evidently, IC(i, •) is an increasing function in the quadratic term i(i − T), and will be maximized when i(i − T) is maximized. That is, the outer sequences closer to the edges of the design have larger information content and contain more information for estimating δ, which echoes the optimal allocation of sequences derived in Lawrie et al. (2015); Li et al. (2018a) and Matthews (2020).

Example 2 (Proportional decay correlation structure). A second example where R_i has a closed-form inverse is the proportional decay structure introduced in Li et al. (2020). In this model, the within-period correlation r_ijj = α₀ for all i, j, and the between-period correlations are allowed to decay exponentially with the same rate ρ over time, namely, $r_{ijt}={\alpha }_0{\rho }^{|j-t|}$ and $r_{ijt}^{*}={\rho }^{|j-t|}$ for all i and |j – t| ≥ 1. The correlation matrix is given by ${\mathbf{\text{R}}}_i=\mathbf{\text{R}}=\left({\mathbf{\text{B}}}_1-{\mathbf{\text{B}}}_2\right)\otimes \hspace{0.17em}{\mathbf{\text{I}}}_N+{\mathbf{\text{B}}}_2\otimes \hspace{0.17em}{\mathbf{\text{J}}}_N$, with ${\mathbf{\text{B}}}_2={\alpha }_0{\mathbf{\text{B}}}_1={\alpha }_0{\mathbf{\text{F}}}_T$, and ${\mathbf{\text{F}}}_T$ is the T × T first-order autoregressive correlation matrix. It is straight-forward to verify that $\overline{\mathbf{V}}$ is centrosymmetric but, as expected, not order-invariant. Under this structure, while the information content profiles are also centrosymmetric as in Theorem 3, different from the block exchangeable correlation structure, there does not exist a cluster-period cell that contributes no information to the treatment effect estimator, that is, has null information content such that IC(i, j) = 1. Furthermore, assuming a variance-stabilizing link function, we show in Appendix E in Data S1 that Equation (4) for the information content of sequence i has a more explicit expression

$$\mathrm{IC}(i,•)=\frac{I(I-1){\xi }_2\left(1-{\rho }^2\right)\varphi /N}{I(I-1){\xi }_2\left(1-{\rho }^2\right)\varphi /N-\mathrm{var}(\widehat{\delta })\left\{\rho I(I-1)+\left(1-{\rho }^2\right)W+{(1-\rho )}^{2}i(i-T)I\right\}},$$

where ${\xi }_2=1+(N-1){\alpha }_0$. Similar to Example 1, IC(i, •) obtained under the proportional decay structure is also an increasing function in i(i − T), and will be maximized when the quadratic term i(i − T) is maximized. That is, the outer sequences closer to the edges of the design still contain more information for estimating δ.

3.2 |. Information content with general link functions

If g is no longer a variance-stabilizing link function, the information content is generally not centrosymmetric under a nonconstant mean–variance relationship, except for the trivial case of null secular trend and treatment effect. Specifically, when β_j = 0 for all j ≥ 2 and δ = 0, the marginal mean and hence the variance function is no longer cluster-dependent, allowing for the results in Section 3.1 to apply. Alternatively, when there is minimal secular trend and a small treatment effect on the link function scale, the marginal variance function will have negligible differences across clusters and periods, and we can expect the information content profiles to be approximately centrosymmetric. Beyond these simple cases, we can still regard the results in Section 3.1 as a benchmark, and consider the difference between the specified link function and variance-stabilizing link function within the common parameter space (for cluster-period means) to quantify the lack of centrosymmetry. Intuitively, if we write g_vs(x) and g(x) as the variance-stabilizing link function and the specified link function, then the degree of lack of centrosymmetry can depend on any discrepancy measure between g_vs(x) and g(x) evaluated at the outcome trajectories. For example, one possible discrepancy measure is given by the set of differences $\mathcal{D}(g)=\left\{\left|g_{\mathbf{\text{vs}}}(x)-g(x)\right|;x\in \left\{{\mu }_{ij};i=1\dots ,I;j=1,\dots ,T\right\}\right\}$, for anticipated nonnull secular trend and treatment effect (by definition $\mathcal{D}\left(g_{\mathbf{\text{vs}}}\right)=0$ and corresponds to centrosymmetric patterns). Because the exact patterns under this general case are challenging to quantify analytically, in Section 4 we explore the patterns of information content numerically under the canonical link functions for binary and count outcomes, both which are common in stepped wedge trials.

4 |. NUMERICAL STUDIES OF INFORMATION CONTENT

To numerically illustrate the patterns of information content of design cells, sequences and periods under canonical link functions with binary and count outcomes, we consider one particular stepped wedge design with I = 9 clusters and T = 10 periods, with cluster-period size N = 100. We focus on the simple exchangeable correlation model with a common correlation $r_{ijt}=r_{ijt}^{*}=\hspace{0.17em}{\alpha }_0\hspace{0.17em}=\hspace{0.17em}0.05$, as well as the exponential decay correlation model with r_ijj = α₀ = 0.05 and a 5% decay per period (or equivalently ρ = 0.95). With a binary outcome and a logistic link function, we consider $e^{{\beta }_1}/\left(1+e^{{\beta }_1}\right)\in \{0.2,0.5,0.8\}$, corresponding to low, medium, and high levels of baseline prevalence. For each baseline prevalence, we consider the null secular trend (${\beta }_j-{\beta }_{j-1}=0\hspace{0.17em}\forall \hspace{0.17em}j$), the increasing secular trend ($e^{{\beta }_T}/\left(1+e^{{\beta }_T}\right)-e^{{\beta }_1}/\left(1+e^{{\beta }_1}\right)=0.15$ and ${\beta }_{j+1}-{\beta }_j={\beta }_j-{\beta }_{j-1}\forall \hspace{0.17em}j$), and the decreasing secular trend ($e^{{\beta }_T}/\left(1+e^{{\beta }_T}\right)-e^{{\beta }_1}/\left(1+e^{{\beta }_1}\right)=-0.15$ and ${\beta }_{j+1}-{\beta }_j={\beta }_j-{\beta }_{j-1}\forall \hspace{0.17em}j$). We assume the true treatment effect in log odds ratio as δ = log(1.5), and omit the results for δ = −log(1.5) due to symmetry. The compatibility of marginal mean and correlation parameters is ensured by verifying natural constraints (Qaqish, 2003).

For a count outcome with a log link, we fix the baseline event rate as $e^{{\beta }_1}=1.5$, and similarly consider the null secular trend (${\beta }_j-{\beta }_{j-1}=0\hspace{0.17em}\forall \hspace{0.17em}j$), increasing secular trend ($e^{{\beta }_T}=2.5$ and ${\beta }_{j+1}-{\beta }_j={\beta }_j-{\beta }_{j-1}\forall \hspace{0.17em}j$), and decreasing secular trend ($e^{{\beta }_T}=0.5$ and ${\beta }_{j+1}-{\beta }_j={\beta }_j-{\beta }_{j-1}\forall \hspace{0.17em}j$). We also vary the treatment effect in log rate ratio as $\delta \in \{\log (2),\log (1/2)\}$. We assume the Poisson variance function such that the marginal variance equals the marginal mean. Although we have focused on the above set of parameter choices, results under alternative parameter choices can be investigated in our R Shiny App at https://information-content-binary-count.shinyapps.io/code_for_paper/. In addition, Figure S1 presents the information content patterns under each correlation model assuming a variance-stabilizing link function. As expected from Theorem 3, the information content patterns are centrosymmetric regardless of the outcome type and the underlying secular trend. Such results serve as a benchmark for our evaluation under the canonical link functions.

4.1 |. Binary outcome with a logistic link

Figures 2, S2 and S3 present the information content of cells for three values of baseline prevalence. Within each figure, results under two correlation models and three secular trends are presented. Overall, the information content of cells under the logistic link function remains approximately centrosymmetric and does not appear to be substantially different than the benchmark patterns in Figure S1, especially when the overall prevalence is around 50%. The prevalence and secular trend only have mild effect on the information content of cells. For example, when the baseline prevalence is low (high) and the secular trend is decreasing (increasing), the information content of cells on the lower-right corner contains slightly less information than those on the upper-left corner, possibly due to implications of event rate close to zero or one. In general, the cells near treatment switch points still carry the most information in estimating the treatment odds ratio under both correlation models, similar to the benchmark results.

FIGURE 2.

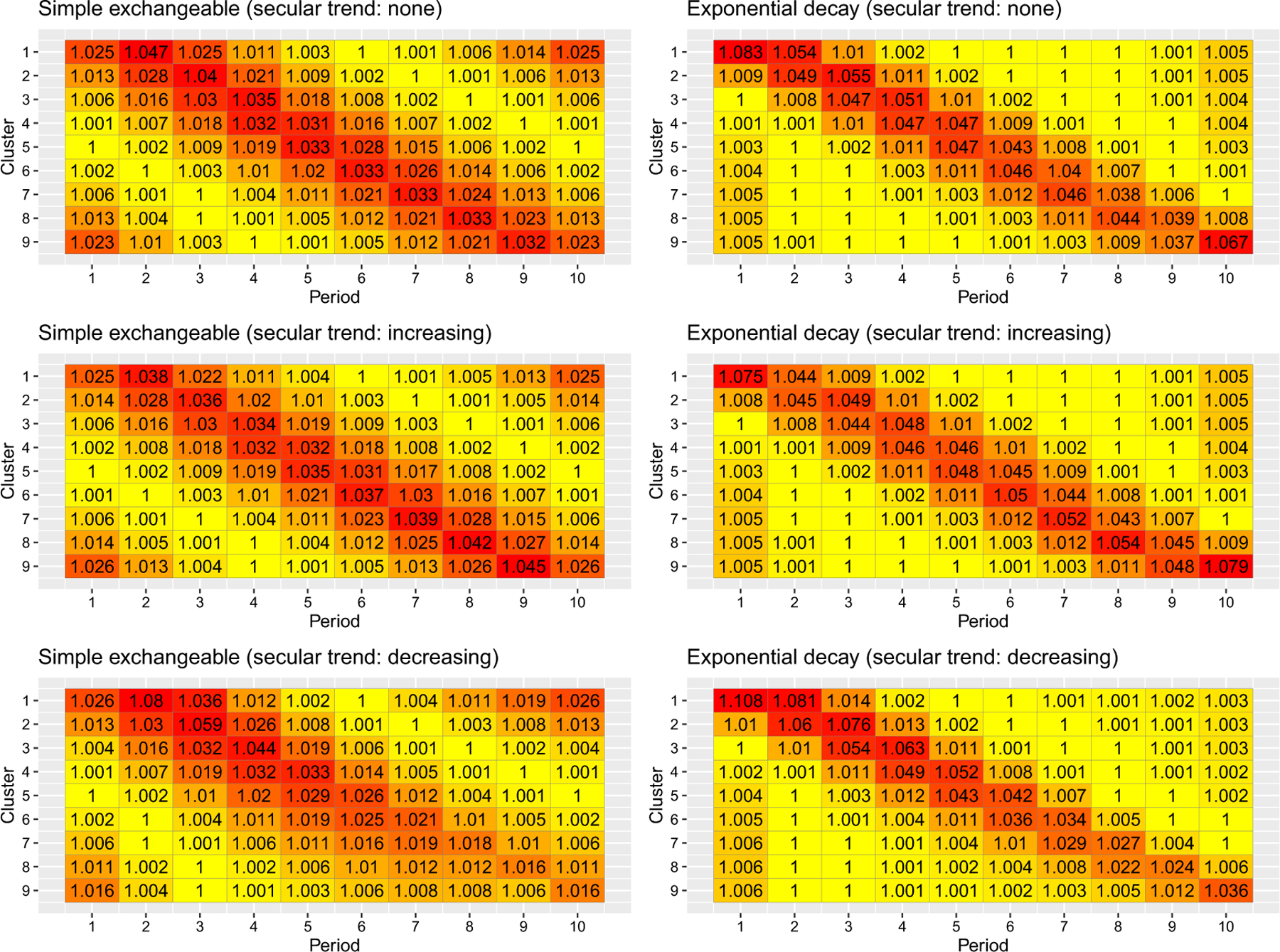
Information content of cells under two correlation models and three secular trends with a binary outcome and logistic link. The baseline prevalence is $e^{{\beta }_1}/\left(1+e^{{\beta }_1}\right)=20\%$. [Colour figure can be viewed at wileyonlinelibrary.com]

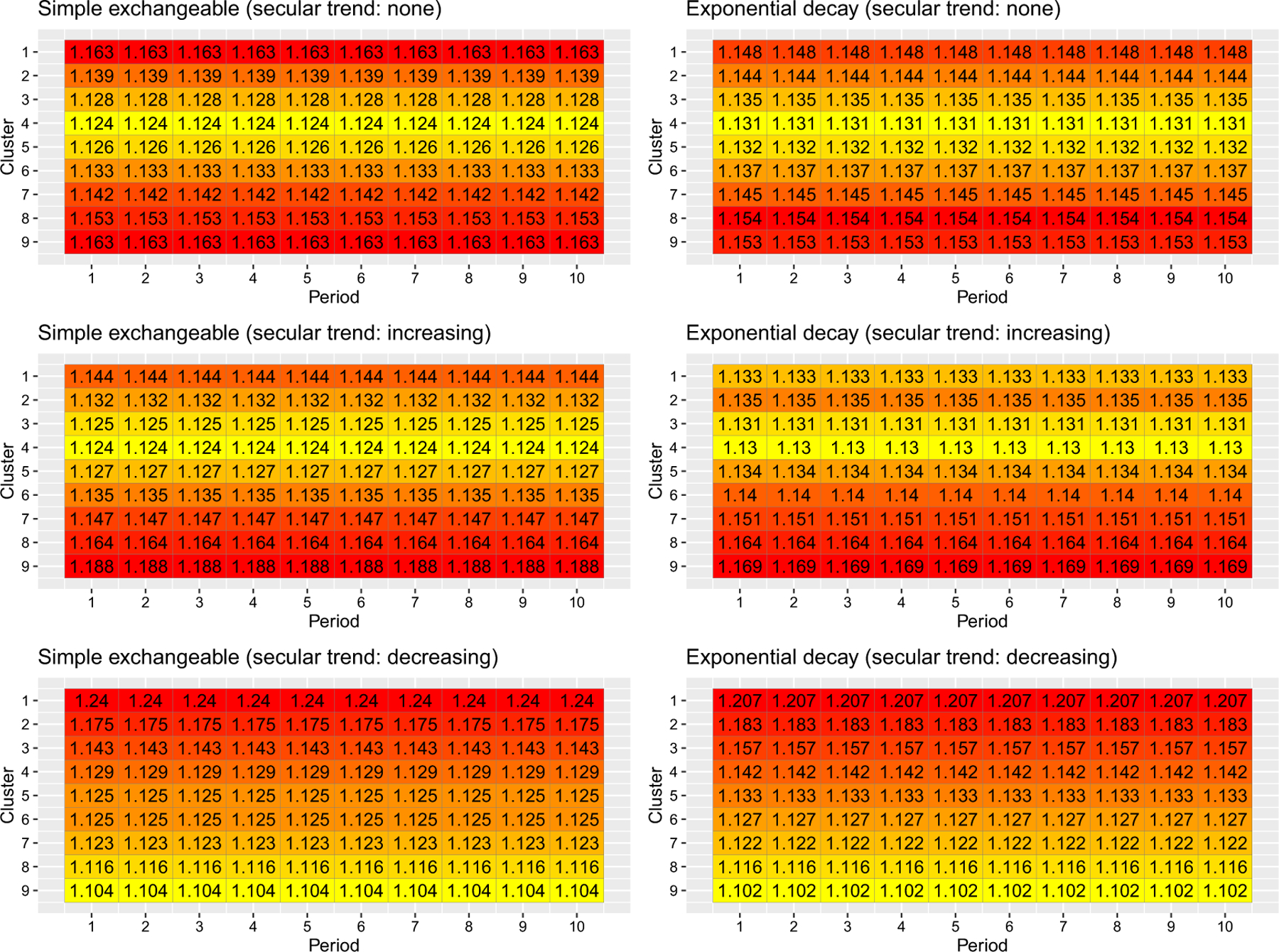
However, when considering the information content of entire sequences and periods for binary outcomes with a logistic link function, the lack of centrosymmetry is more apparent. When the baseline prevalence is low (Figure 3), the earlier sequences (sequences where clusters start implementing the intervention earlier in time) are substantially more information-rich than the later sequences under both correlation models when the secular trend is decreasing, whereas the reverse holds when the secular trend is increasing. This information content pattern might be due to the low probability of event occurrence in certain sequences, which limit the information contribution to the estimation of the overall treatment odds ratio. Likewise, Figure 4 indicates that the earlier periods contribute substantially more information to estimate the treatment odds ratio than the later periods when the baseline prevalence is low and the secular trend is decreasing, as the cluster-period prevalence moves towards zero over time. The findings for high baseline prevalence is largely symmetric to those for low baseline prevalence (Figures S6 and S7). Overall, the information content patterns of sequences and periods are closest to centrosymmetric when the baseline prevalence is 50% and the secular trend is null (Figures S4 and S6). This is likely because the logistic link function is approximately linear in a small interval around 50% and the variance function is relatively stable in that region, and therefore the results are closer to the benchmark results obtained under the variance-stabilizing link function.

FIGURE 3.

Information content of sequences under two correlation models and three secular trends with a binary outcome and logistic link. The baseline prevalence is $e^{{\beta }_1}/\left(1+e^{{\beta }_1}\right)=20\%$. [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 4.

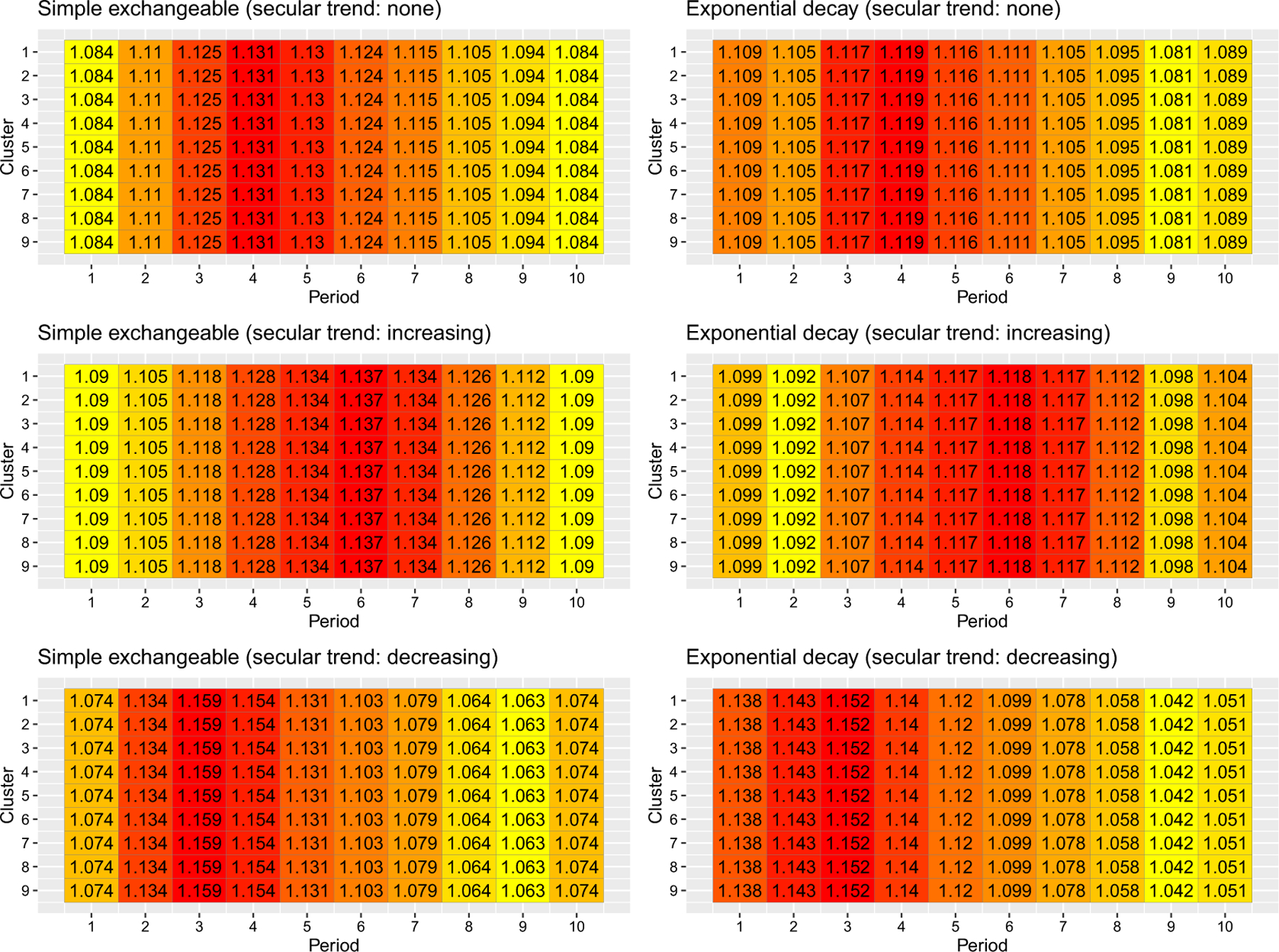
Information content of periods under two correlation models and three secular trends with a binary outcome and logistic link. The baseline prevalence is $e^{{\beta }_1}/\left(1+e^{{\beta }_1}\right)=20\%$. [Colour figure can be viewed at wileyonlinelibrary.com]

4.2 |. Count outcome with a log link

With a count outcome and a log link, the information content of design cells exhibits an approximately centrosymmetric pattern, demonstrating that deviation from the variance-stabilizing link function has limited impact on the contribution from each cell (Figures S8 and S9). However, similar to the results with a binary outcome, the secular trend plays an important role in determining the information content of sequences and periods. For example, with a decreasing secular trend, earlier sequences and earlier periods have consistently larger information content than later sequences and later periods, regardless of the two correlation models and the direction of the treatment rate ratio (Figures S10–S13). With a null or increasing secular trend, the patterns of the information content of sequences and periods can depend on the direction of the treatment rate ratio and are generally not centrosymmetric in the designs we considered.

5 |. DATA EXAMPLE: THE WASHINGTON STATE EPT TRIAL

The Washington State Expedited Partner Therapy (EPT) trial is a stepped wedge trial rolling out a partner therapy intervention in I = 24 local health jurisdictions over T = 5 periods. Figure S14 presents a cluster-by-period diagram of the study. The primary outcome of the study is the binary chlamydia infection status, collected from women attending sentinel clinics in each 6-month time period (Golden et al., 2015). While this trial was originally a complete design, we use it as an illustrative example here and investigate the relative information contribution from each cluster-period, each entire cluster and each entire period with a binary outcome. Notice that we have six clusters receiving each of the four sequences, and therefore IC(i, j) = IC(k, j) and IC(i, •) = IC(k, •) for clusters i and k receiving the same sequence. Our focus in this data example is on the removal of each individual cell, each entire cluster or period, rather than the removal of arbitrary sets of cells, clusters, or periods. Therefore, the interpretation of findings pertain to each individual data element only rather than a set of data elements. We assume N = 305 women (estimated mean cluster-period size from the actual trial data) will contribute outcome observations during each period in each cluster. Furthermore, we assume the secular trend parameter as (β₁, β₂, β₃, β₄, β₅)′ = (−2.443, −2.454, −2.535, −2.609, −2.537)′, corresponding to outcome prevalence of around 7.5% with minor period-to-period fluctuation, as well as the treatment effect δ = −0.141, corresponding to an odds ratio of 0.87; these parameters are based on previous GEE analysis of the EPT trial (Li et al., 2021). We consider both the simple exchangeable and exponential decay correlation structures, with α₀ = 0.01 for both structures and a between-period decay rate ρ = 0.7 for the latter. Figures S15 and S17 present the information content patterns. As expected from our earlier numerical results, the information content of cluster-periods has an approximately centrosymmetric pattern, with the information-rich cluster-periods near treatment switch points, under both correlation models. In particular, each cluster-period within the set {(1, 4), (2, 4), (3, 4), (4, 4), (5, 4)} (all clusters receiving the first sequence) and the set {(16, 2), (17, 2), (18, 2), (19, 2), (20, 2)} (all clusters receiving the last sequence) has IC(i, j) ≈ 1 and contributes minimal information to the treatment effect estimate. Therefore, omitting the data collection from each one of these cluster-period cells individually would have resulted in negligible loss of study power compared to the original complete design. However, we have not investigated the successive removal of cells with low values of information content. Additional work is ongoing to investigate the impact of iterative removal of such cluster-period cells and the impacts of the removal of such cells on the information content of other cells within a design. Finally, the information content of entire clusters and entire periods exhibit slight lack of centrosymmetry, possibly as a result of low outcome prevalence. Under both correlation models, clusters randomized to receive treatment earlier in time tend to have larger information content than those to receive treatment later in time. Similarly, earlier periods tend to have slightly larger information content than the later periods.

6 |. CONCLUDING REMARKS

In this article, we provide several theoretical results on the information content of cluster-period cells, treatment sequences and periods when the outcome is discrete and the analysis proceeds by the GEEs with assumed correlation structures. These results provide means to formally quantify trade-offs involved when logistical, resource and patient-centered considerations are balanced against methodological implications in cluster randomized trials employing incomplete stepped wedge designs with an arbitrary link function and variance function. Additionally, we show that the application of the variance-stabilizing link function allows the insights of Kasza and Forbes (2019b) to apply to more general outcome types. While the centrosymmetric patterns of the information content do not hold exactly under the canonical link functions, our numerical explorations suggest that the information content of cells still remain approximately centrosymmetric, but the information content patterns of sequences and periods can be subject to other design parameters including the baseline event rate, the underlying secular trend and the underlying treatment effect. To facilitate the exploration of information content, we derive analytical results for obtaining the information content of design cells, sequences, and periods, and apply these results to the Washington State EPT trial. Because incomplete stepped wedge designs are becoming increasingly common and there is a rising interest in identifying which data elements may be omitted with a minimal loss of information about the treatment effect with binary and count outcomes, our results serve to refine our understanding and theoretical underpinnings of incomplete designs when the endpoint is discrete. Of note, in our theoretical development and numerical studies, we have emphasized removal of a single data element (cluster-period cell, sequence or period) instead of multiple data elements. When the scientific interest lies in hunting for an optimal but highly incomplete design (Hooper et al., 2020), it may be useful to investigate the information content of k (k ≥ 2) cluster-periods (i.e., based on removal of k design cells) for which we currently only provide generic expressions in Appendix D in Data S1. The application of information content to inform incomplete designs through the iterative removal of cells with low information content is a current area of investigation.

Our numerical studies of the information content under the canonical link functions emphasize the importance of event rate and secular trend in planning stepped wedge trials with discrete outcomes. This is largely borne out from the information content patterns for each treatment sequence, as we vary the baseline prevalence and secular trend with a binary outcome. For example, when the baseline prevalence is one half and the secular trend is minimum, the first and last treatment sequence becomes equally information-rich about the treatment odds ratio, a result that has also been theoretically proved in Lawrie et al. (2015); Li et al. (2018a) and Matthews (2020) assuming linear mixed models with a Gaussian outcome. However, we observe that the information content of earlier sequences is consistently larger than that of the later sequences when the baseline prevalence deviates from one half and the secular trend continues to push the prevalence away from one half. In this case, it is possible that a more efficient stepped wedge design corresponds to the one that allocates more clusters to the first sequence while allocating fewer clusters to the last sequence, as opposed to uniform allocation. A more formal future investigation is needed to provide a definitive answer to the question of optimal allocation of treatment sequences in stepped wedge designs with binary outcomes.

There are several potential limitations of the study. First, we have investigated the information content in stepped wedge trials when the assumed correlation model is correctly specified. This is consistent with the prior investigations based on linear mixed models and represents a typical practice for study design calculations (Kasza & Forbes, 2019b). When the correlation model is expected to deviate from the underlying true correlation model, the information content should be derived based on the robust sandwich variance and is a function of both the assumed correlation structure and the underlying true correlation structure. For example, the GEEs assuming working independence correspond to a computationally efficient estimator for analyzing stepped wedge designs with marginal models, albeit with a potential loss in statistical efficiency due to not capitalising on within-cluster correlations. It would be interesting to explore the patterns of information content based on such an estimator with continuous and discrete outcomes. The results will be reported in a separate study. More generally, when the assumed working correlation structure is not the identity matrix but deviates from the underlying true correlation structure, evaluation of information content requires identification of the probability limits of the misspecified working correlation estimators, which are challenging to quantify analytically. Of note, the results for misspecified linear mixed models derived in Kasza and Forbes (2019a) may shed light on this evaluation for continuous outcomes. For binary outcomes, simulation-based evaluation may be a useful and practical approach to address this more complex question. Second, our analytical results are based on the equal cluster-period size assumption. A recent study indicates that the efficiency loss due to unequal cluster-period sizes is not dramatic when the correlation model is correctly specified in stepped wedge trials (Tian et al., 2022). Nevertheless, it remains of interest to extend our derivation to allow for unequal cluster-period sizes, such as along the lines of Kasza et al. (2021) with a linear mixed model. Finally, our information content results are based on marginal models with a population-averaged interpretation, and may or may not be directly applicable to generalized linear mixed models with a cluster-specific interpretation. Future work is needed to develop the theory for incomplete stepped wedge designs under the class of generalized linear mixed models.