Generative modeling of single-cell gene expression for dose-dependent chemical perturbations

Summary

Single-cell sequencing reveals the heterogeneity of cellular response to chemical perturbations. However, testing all relevant combinations of cell types, chemicals, and doses is a daunting task. A deep generative learning formalism called variational autoencoders (VAEs) has been effective in predicting single-cell gene expression perturbations for single doses. Here, we introduce single-cell variational inference of dose-response (scVIDR), a VAE-based model that predicts both single-dose and multiple-dose cellular responses better than existing models. We show that scVIDR can predict dose-dependent gene expression across mouse hepatocytes, human blood cells, and cancer cell lines. We biologically interpret the latent space of scVIDR using a regression model and use scVIDR to order individual cells based on their sensitivity to chemical perturbation by assigning each cell a “pseudo-dose” value. We envision that scVIDR can help reduce the need for repeated animal testing across tissues, chemicals, and doses.

Highlights

• •Predicts chemical perturbations in gene expression across cell types
• •Predicts response to multiple doses of a chemical
• •Enables biological interpretation of model predictions
• •“Pseudo-dose” metric evaluates cell-specific chemical sensitivity

The bigger picture

Cellular response to chemical perturbation is highly heterogeneous and dose dependent. It would be impossible to experimentally characterize the risks of chemical or drug exposure across all relevant combinations of cell types, chemicals, and doses. We introduce scVIDR, a computational method that utilizes recent advances in generative deep learning to address this challenge. Across a range of chemical exposure scenarios, we show that after training on available single-cell gene expression data, scVIDR can predict perturbations across untested cell types and doses. We envision that scVIDR will help reduce the need for repeated animal testing across tissues, chemicals, and doses.

Variational autoencoders can predict chemical perturbations across cell types using vector arithmetic. However, vector arithmetic alone cannot predict perturbations in single-cell gene expression accurately in animal studies across multiple doses. We utilize a regression-based method to improve on in vivo predictions by accounting for cell-type-specific differences in gene expression response. We then extend this model to predict the response to multiple doses of a chemical and derive a metric to characterize chemical sensitivity in individual cells.

Introduction

In 2010, Sydney Brenner suggested that it is possible to deduce the physiology of biological systems by understanding the interactions and behaviors of their constituent units.¹ The appropriate unit, in his opinion, was the cell. Single-cell sequencing (scSeq) has revolutionized the study of cell biology. With the ability to capture the transcriptomic state of thousands of cells at once, a fine-grained picture of the organization of cell physiology has begun to emerge.² Much of the effort in scSeq has been made in the realm of cell-type/-state discovery,^3,4 cellular development,^5,6,7,8 and disease progression.^9,10 These represent natural applications of scSeq, especially regarding the spatial and temporal dynamics of cellular systems and their interactions. However, relatively little attention has been given to how cells respond to environmental signals like chemical exposures, which in addition to being spatial and temporal are also chemical and dose dependent.

Broadly, cells exhibit the ability to recognize and respond to external stimuli. This process is mediated by a coordinated set of extracellular and intracellular interactions that transduce resulting signals into cellular responses.¹¹ These responses, as a function of dose, define dose-response curves.¹² The dose-response curve is heavily dependent on the type of cell and its internal state.^13,14 Thus, even cells of the same type can respond to the same exposure in a heterogeneous manner.¹⁵ scSeq provides a comprehensive measure of the transcriptome of a cell and captures the inherent variation among cells of the same type. This makes scSeq a useful tool in the study of chemical perturbations of biological systems.

However, a comprehensive cell atlas of chemical perturbations is impossible to assemble given the vast number of combinations of dose, exposure duration, and cell types.¹⁶ Recently developed resources like scPerturb¹⁷ and the multiplexed interrogation of gene expression through single-cell RNA sequencing (MIX-seq) protocol¹⁸ cover a meaningful but relatively small portion of this space. Algorithms that generalize chemical perturbations across cell state and dose can provide better estimates of the cartography of the chemical perturbation space. In this work, we use deep generative modeling to computationally predict cellular response across dose and cell types. We use a class of deep neural networks for dimensionality reduction called autoencoders. Specifically, we use a variational autoencoder¹⁹ (VAE), which relies on Bayesian priors to encode single-cell data into a latent distribution. VAEs have been used to model several technical aspects unique to single-cell data, including statistical confounders such as library size and batch effects²⁰ and zero inflation.²¹

In perturbational single-cell biology, autoencoder models such as scGen22 have been able to predict the response of interferon $\beta$ (IFN-$\beta$)-treated peripheral blood mononuclear cells (PBMCs). However, for considering more complicated in vivo perturbations, existing models do not consider cell-type-specific effects in predicting the mean expression of differentially expressed genes (DEGs). Advances in other autoencoder frameworks such as the compositional perturbational autoencoder (CPA)¹⁶ aim to deal with these issues by trying to infer basal state from the data by modeling covariates with different autoencoders and then iteratively composing them when performing predictions for a particular set of conditions. While promising, CPA can only work with vary large data samples (relative to other perturbational autoencoders), as the model needs to learn a latent space for each covariate. Thus, for confident prediction, CPA will need datasets that already have a great deal of the perturbational space mapped. Additionally, most perturbational autoencoder frameworks are uninterpretable in terms of the quantitative relationship between latent space and expression prediction. Thus, it is difficult to ascertain which specific genes the model uses to predict differential gene expression after treatment. Thus, there is a need for simpler models that better account for the complexity of in vivo experiments, that predict high doses from less data, and that provide more informative interpretations at the level of individual genes.

Here, we propose single-cell variational inference of dose-response (scVIDR), which builds on latent space vector arithmetic when using VAEs to study single-cell perturbations (Figure 1). scVIDR predicts cell-type-specific DEG expression and approximates high-dose experiments better than other state-of-the-art algorithms. We also use scVIDR to interpret the latent space using linear models to assess the pathways involved in the single-cell dose-response. We accomplish this across several datasets including the dose-response of liver cells to 2,3,7,8 tetrachlorodibenzo-p-dioxin (TCDD) in vivo,^22,23 PBMCs treated with IFN-$\beta$,²⁴ and a multiplexed dataset of 188 different drug combinations applied to three prominent cancer cell lines (sci-Plex²⁵).

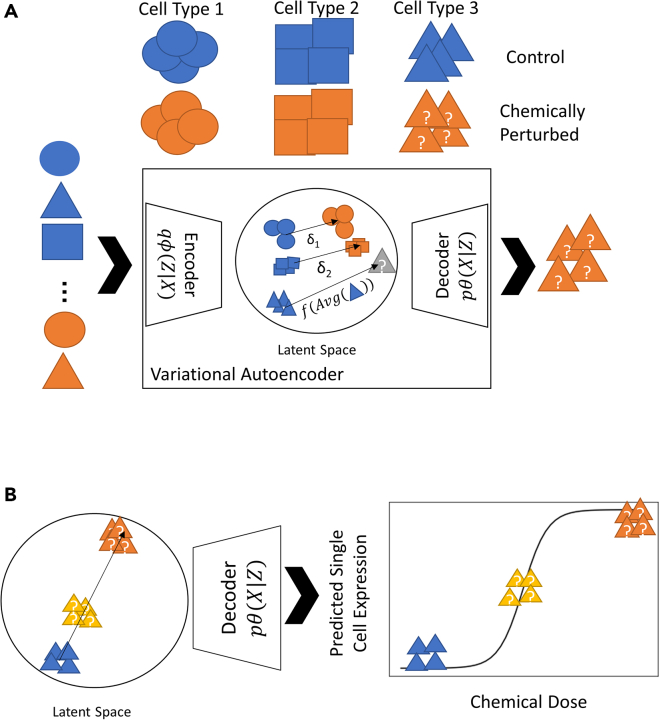
Figure 1.

Schematic of scVIDR for prediction of response to single and multiple doses for some unknown cell type

(A) Outline of the scVIDR model for expression prediction for unknown single-dose response in cell type 3. Training is done using cell types 1 and 2 as input to a variational autoencoder model. The difference between the centroids of latent representations of the control and treated groups, ${\delta }_1$ and ${\delta }_2$, are used as input into a linear regression model. The linear regression model is then used to predict the ${\delta }_3$ of the test cell type 3. We then use the decoder portion of the model to convert the latent space predictions back into gene expression space.

(B) Use of scVIDR for prediction of the unknown response of multiple doses for cell type 3. Log-linear interpolation on ${\delta }_3$ is used to predict dose-dependent changes in gene expression in the latent space. The latent space representations are then projected back into gene expression space using the decoder.

We use data from a single-nucleus dose-response experiment in livers from mice gavaged with TCDD as a case study for in vivo dose-response prediction.^22,23 Hepatic responses to TCDD represent an interesting case study, as its canonical receptor, the aryl hydrocarbon receptor (AhR), is unevenly expressed along the hepatic lobule, the functional unit of the liver. AhR is more highly expressed in the centrilobular region compared with the portal region (Figure S1).²⁶ Thus, not only does response to TCDD vary across different cell types in the liver, but it also varies within cell types (such as hepatocytes) along the portal to the central axis of the liver lobule.^22,27 To model response variation between cell types, the latent space of the VAE is used to order hepatocytes with respect to their transcriptomic response to TCDD and thus align all hepatocytes along a “pseudo-dose” axis.

Results

scVIDR predicts single-dose, single-cell perturbation expression better than other state-of-the-art algorithms

According to the manifold hypothesis, high-dimensional data often lay on a lower-dimensional, latent manifold.²⁸ For single-cell data, this is a reasonable assumption given that the expression of one gene is often highly dependent on the expression of other genes encoding transcription factors and is functionally constrained by the process of evolution.²⁹ Further evidence of this can be seen in the extensive use and success of dimensionality reduction algorithms in the analysis of scSeq data.³⁰ Lower-dimensional representations of single-cell data are at the heart of many single-cell gene expression analysis methods such as trajectory inference.³¹ One method of interest is modeling of the latent manifold using neural networks. These latent manifolds have been shown to simplify complex relationships in single-cell gene expression data.^32,33,34 Specifically, simple vector arithmetic on such spaces can predict in vitro chemical perturbations with high accuracy.^16,35 However, the accuracy of such models when predicting in vivo dose-responses is inconsistent.

We begin by considering a single-cell gene expression dataset $X={\left\{x_i\right\}}_{i=1}^N$ consisting of $N$ cells, where $x_i$ represents the expression profile of cell $i$. We assume that gene expression is generated by some continuous random process involving a lower-dimensional random variable $z$. The generative process that describes the mapping from $z$ to $X$ is given by the probability distribution, $p_{\theta }\left(X|z\right)$. Thus, given that we know $X$ and not $z$, we would like to approximate the probability distribution that maps $X$ to $z$, $p_{\theta }\left(z|X\right)$. Since calculating $p_{\theta }\left(z|X\right)$ is usually intractable, we use a neural network, the encoder, to approximate it using a different Gaussian distribution, $q_{\phi }\left(z|X\right)$. To map values back from $z$ to $X$, we use a second neural network, the decoder, to approximate $p_{\theta }\left(X|z\right)$. In practice, both the encoder and decoder are trained together to minimize the reconstruction error of the decoder and the difference between the prior distribution and the encoder distribution.

We initially developed models for a single-dose chemical perturbation where we characterize whether a cell has been treated with a set concentration of the chemical of interest with the indicator variable $t$ (Figure 1A). We set $t=1$ for cells that have been treated with the chemical (treatment) and $t=0$ for cells that have not been treated (control). Our dataset contains $c$ cell types within both the $t=0$ and $t=1$ groups. Each time a model is evaluated, one treated cell type is withheld from training and used in evaluation. In standard VAE vector arithmetic (scGen), the latent space representation of the perturbation of some cell type $A$ is approximated by ${\hat{z}}_{i,A,t=1}=z_{i,A,t=0}+\delta$. $z_{i,A,t}$ is the latent gene expression representations of cell type $A$,³⁵ and $\delta$ is the difference between the centroids of the treated and control training groups in the latent space. When we compare the difference of centroids between the treated and control groups, ${\delta }_c$, of individual cell types with $\delta$, we see that cell-type-specific differences vary greatly in a principal-component analysis (PCA) projection (Figure S2A). Examination of the magnitudes (Figure S2B) and the directions of each cell’s ${\delta }_c$ (Figure S2C) in high-dimensional space show that ${\delta }_c$ diverges greatly from $\delta$. Hence, we calculate ${\hat{\delta }}_{c=A}$, a function of the mean latent representation of the control group of cell type $A$. We approximate this function by training a linear regression model with the other cell types on the latent space (experimental procedures) and show that ${\hat{\delta }}_{c=A}$ better matches the ground truth ${\delta }_{c=A}$ (Figure S2). It should be noted that when there is only one cell type available for training, for all practical purposes, scVIDR is equivalent to scGen (Figure S7).

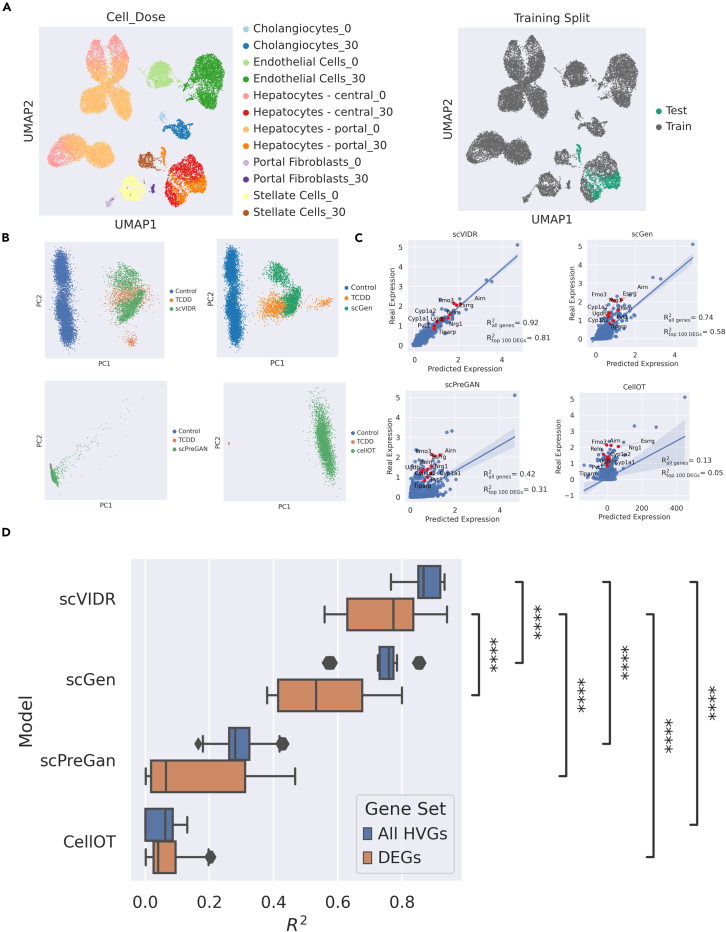
We applied this model to the case of a single dose of TCDD administered to mice. Gene expression was measured with single-nucleus RNA-seq (snRNA-seq) originating from the mouse liver. We set $t=0$ for unperturbed gene expression and $t=1$ for gene expression perturbed by 30 $\mu$g/kg TCDD. The dataset covered 6 different liver cell types: cholangiocytes, endothelial cells, stellate cells, central hepatocytes, portal hepatocytes, and portal fibroblasts (Figure 2). Our training set (Figure 2A) consisted of all control and TCDD-treated cell types except for TCDD-treated portal hepatocytes, which were used for model evaluation. We compared the performance of scGen, scPreGAN,³⁶ CellOT,³⁷ and scVIDR (our method) on the top 5,000 highly variable genes (HVGs) and the top 100 DEGs. When predicting the gene expression of portal hepatocytes, each method generated a set of virtual portal hepatocytes (Figure 2B). We then computed the average expression of each gene across all cells and compared the average gene expression in predicted cells versus cells derived from snRNA-seq experiments. Across HVGs, the scVIDR model yielded an average $R^2$ of 0.92 (Figure 2C). Across DEGs, scVIDR produced an average $R^2$ of 0.81 (Figure 2C). Continuing the evaluation across all cell types (Figure 2D), leaving out one cell-type perturbation at a time as described above for portal hepatocytes, our model outperformed all other models (with p < 0.001, one sided Mann-Whitney U test) when evaluated on both HVGs and DEGs.

Figure 2.

Prediction of in vivo single-cell gene expression of portal hepatocytes from mice treated with 30 $\mu$g/kg TCDD

(A) Uniform manifold approximation and projection (UMAP) of the latent space representation of control and treated single-cell gene expression. Each cell type and dose in $\mu$g/kg combination and by the train-test split for model training is represented by different colors. In the example in the figure, TCDD-treated portal hepatocytes were used as a test set.

(B) PCA plots of predicted portal hepatocyte responses following treatment with 30 μg/kg TCDD using scGen, scVIDR, scPreGAN, and CellOT.

(C) Regression plots of each model. Each point represents the mean expression of a particular gene. Red points represent the top ten differentially expressed genes. Shaded region around regression line represents the 95% confidence interval.

(D) Boxplot of $R^2$ values for predictions across all liver cell types treated with 30 μg/kg TCDD. Calculation of the mean $R^2$ across all highly variable genes (blue). Calculation of the mean $R^2$ across the top 100 differentially expressed highly variable genes (orange). Prediction performance distributions were compared using a one-sided Mann-Whitney U test. ∗∗∗∗p ≤ 0.0001.

We had similar results for IFN-$\beta$-treated PBMCs (Figure S3).²⁴ Here, $t=1$ for PBMCs treated with IFN-$\beta$, and $t=0$ for untreated PBMCs (Figure S3A). Across HVGs, the models yielded $R^2$ values of 0.97, 0.92, 0.77, and 0.66, and across DEGs, they yielded $R^2$s of 0.96, 0.86, 0.80, and 0.84 for scVIDR, scGen, scPreGAN, and CellOT, respectively (Figure S3C). When accuracy was assessed for all cell types, scVIDR significantly outperformed all other models (Figure S3D).

To test if scVIDR can perform out-of-distribution predictions robust to experimental batch effects and diverse genetic backgrounds, we test scVIDR on two additional experiments. In the first experiment, we recapitulate results from Lotfollahi et al.,³⁵ in which we predict perturbations across studies (in this case, we look at IFN-$\beta$ perturbation of PBMCs from Kang et al.²⁴ and try to predict it in PBMCs from Zheng et al.³⁸). We show that scVIDR can predict biologically plausible perturbations across studies (Figure S8). In the second experiment, we show that scVIDR can better predict LPS6 perturbation in rats ($R^2=0.92$ for HVGs) using perturbations from other species (pig, rabbit, and mouse)³⁹ than scGen ($R^2=0.91$ for HVGs), scPreGAN ($R^2=0.63$ for HVGs), and CellOT ($R^2=0.23$ for HVGs) (Figure S9). In both experiments, we show that scVIDR can be used to predict perturbations not only across cell types but also across multiple perturbation studies and models.

scVIDR accurately predicts the transcriptomic response for multiple doses across cell types

Next, we predicted the response for multiple doses of TCDD (Figure 1B). Here, $p$ is equal to the magnitude of the perturbation, which in our case is equivalent to the dose. Thus, $p=0$ represents expression at dose 0, and $p=30$ represents expression at dose 30, where the dose is in units of $\mu$g/kg in Figure 3 and of nM in Figure S4. As with the single-dose case, we train the model on the dose-response data for all cell types except one, for which only the $p=0$ condition is kept. We calculate the ${\hat{\delta }}_c$ (experimental procedures; Figure 3A), which is the estimated difference of means between the highest dose and the untreated groups. For scVIDR, intermediate doses are then calculated on the latent space by interpolating log linearly on the ${\hat{\delta }}_c$. For scGen, we log linearly interpolate on $\delta$ (experimental procedures). Finally, those latent space representations are decoded back into gene expression space using the decoder portion of each of the models.

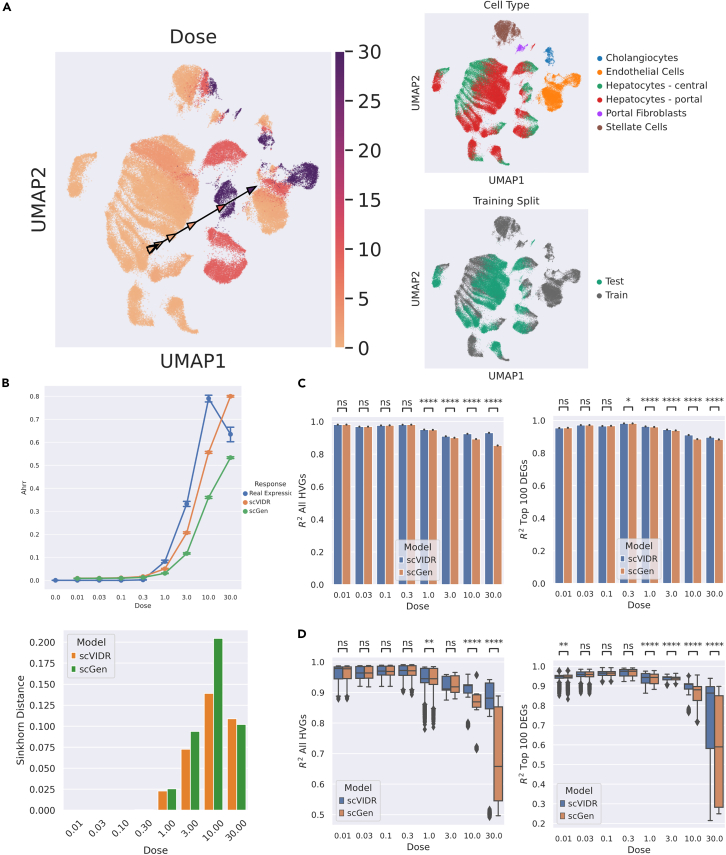
Figure 3.

Prediction of in vivo single-cell TCDD dose-response across cell types from mouse liver

(A) UMAP of the latent space representation of single-cell gene expression across TCDD dose-response. Cells are colored by dose $(\mu$g/kg), cell type, and test-training split. Arrows on UMAP represent a $\delta$ calculated on UMAP space, with each arrowhead representing a specific dose denoted by its color.

(B) Dose-response prediction for the Ahrr gene using scVIDR and scGen. The differences between the predicted and true distributions of Ahrr at each dose are measured via the Sinkhorn distance. Bars represent standard error of expression.

(C) Bar plots of the $R^2$ scores of the gene expression means in portal hepatocytes for all highly variable genes and the top 100 differentially expressed genes. Significance was determined by the one-sided Mann-Whitney U test. ∗p between 0.05 and 0.01; ∗∗∗∗p ≤ 0.0001.

(D) Boxplot of the distribution of $R^2$ scores across all cell types in liver tissue. ∗∗p between 0.01 and 0.001.

We analyzed a mouse liver snRNA-seq dataset that included 8 doses (p = [0.01, 0.03, 0.1, 0.3, 1.0, 3.0, 10, 30]) of TCDD and a control (p = 0) in $\mu$g/kg (Figure 3). scVIDR outperforms scGen in approximating expression across the dose-response of TCDD in mouse liver. We used the mean $R^2$ score across all evaluated genes as our performance metric (Figure 3B). scVIDR significantly outperformed scGen at predicting HVGs and DEGs for doses >0.3 $\mu$g/kg (Mann-Whitney one-sided U test p < 0.001). scVIDR predicts the important TCDD receptor repressor gene, Ahrr, at doses 1, 3, and 10 $\mu$g/kg in portal hepatocytes better than scGen (Figure 3C). When predicting all other cell types (cholangiocytes, endothelial cells, stellate cells, central hepatocytes, portal hepatocytes, and portal fibroblasts), scVIDR significantly outperformed scGen only at the highest doses of 10 and 30 $\mu$g/kg on prediction of all HVGs (Figure 3D). When predicting on just the DEGs, scVIDR significantly outperformed scGen for doses >0.3 $\mu$g/kg (Figure 3E).

We used scVIDR to predict the effects of a test set of 37 drugs out of 188 treatments in the sci-Plex dose-response data²⁵ at 24 h for A549 cells (Figure S4A). scVIDR was trained on all data (all drugs and doses) in K562 and MCF7 cells. The model was also trained on the remaining 151 drugs in A549 cells not used in validation, as well as the vehicle data for the 37 drugs in the test set (Figure S4A). The dose-response for the 37 drugs was predicted as above by first calculating the ${\hat{\delta }}_{A549}$ between the control and the highest dose for a particular drug and log linearly interpolating along the ${\hat{\delta }}_{A549}$ in order to predict the intermediate doses. We evaluated predictions made by scVIDR at the gene, drug, and drug pathway levels. For the drug belinostat, a histone deacetylase inhibitor, scVIDR improves on predictions of DEGs such as MALAT1 relative to scGen (Figure S4B). When predicting gene expression of the DEGs in belinostat-treated A549 cells, scVIDR also significantly outperformed scGen on all doses (Figure S4C). On predicting the DEGs of all drugs with the same mode of action as belinostat (epigenetics), scVIDR similarly outperformed scGen on all doses (Figure S4D). Finally, when looking across all 37 drugs in the test dataset, we were able to predict the expression of DEGs significantly better than scGen on average for the 3 highest doses of 100, 1,000, and 10,000 nM (Figure S4E).

Regression on the latent space infers the relationship between predicted gene expression and ${\hat{\delta }}_c$

Insight into model decisions can provide information regarding proper model usage and pitfalls. It would be useful to identify which genes and pathways are associated with scVIDR’s prediction; however, standard VAEs do not have a linear map from the latent space to the gene expression and thus are hard to interpret. To interpret the predictions of scVIDR, we approximate the function of the decoder with linear regression (experimental procedures). We take inspiration from the use of PCA in scSeq⁴⁰ and the development of linearly decoded VAEs (LDVAEs).⁴¹ PCA is a linear transformation that projects the data onto a lower-dimensional (latent) space while retaining as much variance as possible. This transformation is represented by a linear weight matrix, $W_{pca}$, with dimensions $m\times g$ where $m$ is the number of latent variables and $g$ is the number of genes. We can understand each principal component as a linear combination of genes. This allows us to assess the relationship between genes and a direction in latent space.

In a VAE, the mapping from the latent space to the gene space is done by the decoder that, unlike the inverse of PCA, is non-linear. In LDVAEs, however, the decoder portion of the VAE is a linear regression layer, and thus the weight matrix of this layer, $W_{ldvae}$, describes a linear relationship between direction in the latent space and gene prediction.⁴¹

However, interpretability comes at the expense of model accuracy. LDVAEs have higher reconstruction error than standard VAEs on single-cell data.⁴¹ Similarly, using PCA and vector arithmetic to predict scSeq perturbations performed poorly compared to scGen.³⁵ As a result, one would like to try to interpret the latent space of a standard VAE. We present an approach to interpret the VAE’s latent space using sparse regression.

We take an alternative approach to LDVAEs in which we instead approximate the non-linear function of the decoder in a standard VAE using sparse linear regression (Figure 4A). Sparse regression methods like local interpretable model-agnostic explanations (LIME) have been used to interpret complex models.⁴² We specifically use sparse linear ridge regression, given that each gene has a non-zero contribution to each latent variable and that gene weights are distributed parsimoniously. This gives us a linear transformation matrix, ${\hat{W}}_{vae}$, that approximates the function of the decoder.

Figure 4.

Interrogation of VAE using ridge regression in portal hepatocyte response prediction

(A) Schematic of calculation of latent dimension weights using ridge regression.

(B) Bar plot of top 20 genes with the highest scVIDR genes scores.

(C) Enrichr analysis of the top 100 genes with respect to the scVIDR gene scores. Bar plot of adjusted p values from statistically significant (adjusted p value < 0.05) enriched pathways from the WikiPathways 2019 Mouse Database.

(D) PCA projection of single-cell expression data colored by log dose and fatty acid oxidation pathway score.

(E) Logistic fit of median pathway score for each dose value. MAE, mean absolute error.

We use this weight matrix to interrogate the relationship between predicted gene expression and ${\hat{\delta }}_c$. The span of ${\hat{\delta }}_c$ is simply a direction in scVIDR’s latent space. The importance of ${\hat{\delta }}_c$ to each gene’s predicted expression is the sum of the latent dimensional components of ${\hat{\delta }}_c$ multiplied by the gene’s corresponding latent dimensional weight from ${\hat{W}}_{vae}$. In matrix form,

$$\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{s}={\hat{\delta }}_c^T{\hat{W}}_{vae}\text{.}$$

In practice, we found that normalizing the weight matrix by its L2 norm gives better insights when interpreting the model (experimental procedures). Gene scores represent how significant changes in latent space dimensions will impact the decoded transcriptomic response when we interpolate on the span of ${\hat{\delta }}_c$ on the latent space. Thus, genes with higher scores will be predicted to have bigger changes when we increase the dose of our prediction by scVIDR.

We utilize a trained scVIDR model where portal hepatocytes were left out of training and the ${\hat{\delta }}_{c=\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{h}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{c}\mathrm{y}\mathrm{t}\mathrm{e}\mathrm{s}}$ was approximated (Figures 4B–4D). Gene scores for ${\hat{\delta }}_{c=\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{h}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{c}\mathrm{y}\mathrm{t}\mathrm{e}\mathrm{s}}$ were calculated as described above. The genes with the top 20 highest-magnitude genes scores included well-established markers of TCDD-induced hepatotoxicity such as genes from the cytochrome P450 family (Figure 4B).²⁶ To see whether this relationship extended to pathways involved in TCDD-induced hepatotoxicity, we performed Enrichr analysis³⁸ using the 2019 WikiPathways database⁴³ on genes with the top 100 gene scores (Figure 4C). Among the top enriched terms, we found the hallmarks of hepatic response to TCDD in mice, such as oxidation by cytochrome P450,⁴⁴ fatty acid omega oxidation,⁴⁵ and tryptophan metabolism.⁴⁶ To derive the relationship between the actual doses and the gene pathways, the genes with the top 100 gene scores that were in “fatty acid oxidation” from WikiPathways were used in calculating enrichment scores for each cell using Scanpy.⁴⁷ A sigmoid function was fit to the median enrichment score in each dose (experimental procedures). We observed a small mean absolute error in our model and thus concluded that there was a sigmoidal dose-response relationship for the gene set generated by Enrichr (Figures 4D and 4E).

Pseudo-dose captures zonation in TCDD hepatocyte response

In single-cell analysis of developmental trajectories, it is useful to order cells with respect to a latent time course, termed “pseudo-time.” This is because cells develop at different rates due to natural variations among themselves and their environment. This ordering is usually done using algorithms such as Slingshot⁴⁸ and Monocle.⁴⁹ In pharmacology and toxicology, we experience a similar problem, as cells of the same type have variable sensitivities to the same toxicant. Hence, we propose to order cells in terms of a latent dose. We call this ordering of cells a “pseudo-dose.”

Working off the assumption that ${\delta }_c$ (experimental procedures) is the axis of perturbation in latent space, we orthogonally project the latent representation of each cell to the $span\left({\delta }_c\right)$ to obtain a scalar coefficient for each cell along ${\delta }_c$ (Figures 5A and 5B). We use this scalar coefficient as the pseudo-dose value for each cell.

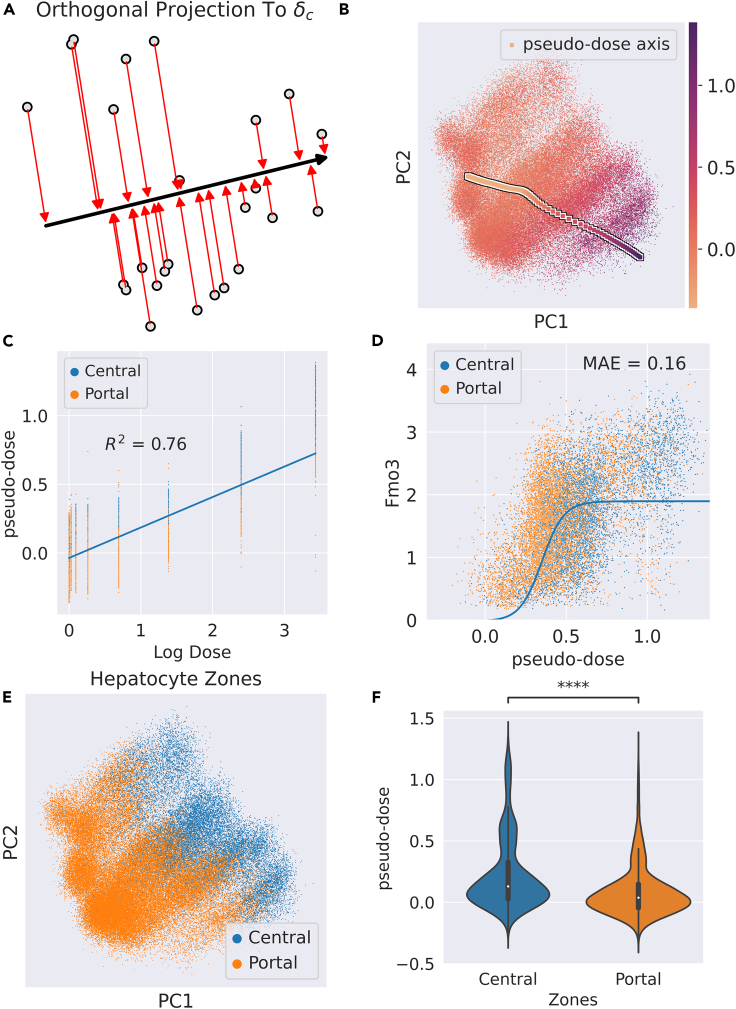
Figure 5.

Pseudo-dose ordering of hepatocytes across TCDD dose-response

(A) Schematic diagram of assigning pseudo-dose values to hepatocytes by orthogonally projecting each cell in latent space to the span of the ${\delta }_c$.

(B) PCA projection of hepatocytes colored by assigned pseudo-dose values. The arrow markers represent the pseudo-dose axis calculated by the ${\delta }_c$.

(C) Regression plot of pseudo-dose versus log transformed real dose.

(D) Plot of pseudo-dose versus Fmo3 expression. Associated logistic fit (solid blue line) and associated mean absolute error annotated as “MAE.”

(E) PCA projection of hepatocytes colored by assigned hepatocyte zone in the liver lobule.

(F) Violin plot of the distribution of pseudo-dose values in the central and portal zones of the liver lobule. Central hepatocytes exhibit a higher pseudo-dose on average than portal hepatocytes Significance was determined by the Mann-Whitney single-sided U test. ∗∗∗∗p < 0.0001.

To test whether these pseudo-dose values capture the latent response across cell types, we distinguished between the portal and central regions of the liver lobule. Zonation of the lobule not only defines differences in hepatocyte gene expression along the portal to the central axis but also defines their metabolic characteristics.⁵⁰ Thus, we expect that the two zones will exhibit different sensitivities to TCDD. The pseudo-dose correlated well with the actual dose administered to the hepatocytes with an $R^2=0.76$ (Figure 5C). We also found that the pseudo-dose displayed a sigmoidal relationship (experimental procedures) between the expression of DEGs such as Fmo3 (Figure 5D). Finally, we found the pseudo-dose to be statistically higher on average in the central hepatocytes versus the portal hepatocytes (Figures 5E and 5F). This is consistent with liver biology, given that central hepatocytes respond more strongly to treatment due to TCDD sequestration⁵¹ and higher AhR expression levels in the centrilobular zone.²⁶

Discussion

Mapping the combinatorial space of single-cell perturbation is important to toxicology and pharmacology to facilitate the generalization of drug or toxicant effects across several domains. Computational modeling allows researchers to use current large-scale databases to predict new perturbations to scSeq data. We have demonstrated an improvement to such modeling using VAEs with regression. These improvements include highly correlated prediction of cell-type-specific effects in mouse liver, PBMCs, and A549 cells. We also modeled a latent response for mouse hepatocytes using pseudo-dose and interrogated the VAE to predict dose-dependent perturbations in portal hepatocyte pathways. We show that deep generative modeling can be used to model complex perturbations in single-cell gene expression data from several different datasets.

Model limitations

When evaluating the model in the mouse liver, scVIDR performed better on the cell types most sensitive to TCDD, e.g., hepatocytes and endothelial cells (Figures S5A, S5C, and S5D). For cell types less sensitive to TCDD, the model often underestimated the expression of DEGs (Figure S5E). This is likely a result of a combination of factors including the similarity of the treatment to the control data (Figure S5A), the smaller control cell populations (Figure S5B), and the overall low expression of HVGs (Figure S5E). Thus, we believe that the VAE has less information to predict differential gene expression for these cell types. Our model improves on this problem with respect to scGen for most cell types in the liver (except for stellate cells and cholangiocytes at higher doses). Results from sci-Plex imply that incorporating scSeq data from livers treated with other compounds could improve these predictions, as the model would have more information on different liver responses.

In the sci-Plex dataset, prediction of certain drugs with epigenetic mode of actions produced the poorest prediction scores (Figure S6). This is because scSeq data provide no information regarding epigenetic modifications (e.g., chromatin accessibility, histone marks, and DNA-binding proteins). Integration with epigenetic data such as single-cell assay for transposase-accessible chromatin with sequencing (scATAC-seq) could help to predict such responses with higher accuracy.

While scVIDR and its pseudo-dose metric work on standard dose-response scenarios, it remains untested for use with more complex cellular trajectories such as those found in development and circadian rhythms.⁵² Such trajectories include branching and cycling, which involve non-linear dynamics, and may require more sophisticated models to properly capture their topology. Algorithms such as CellOT³⁷ can represent complex distributional shifts along latent dimensions; however, they are still only developed for single-perturbation measurements and extrapolate poorly to larger perturbations.

Future directions

When looking to the future of generative modeling in chemical-induced perturbation of gene expression, a problem domain of interest is time-dependent drug effects. Chemical exposures are not only a function of concentration but also of time.⁵³ Dose-time-response analysis is central to risk assessment in clinical settings.⁵⁴ Predicting the response not only as a function of amount of drug but also as a function of the time the drug is within a patient’s system and the time of day at which the drug was administered would allow for more effective and safer dosing regimens.^54,55

Developmental state can also be impacted by chemical perturbation. An example of this is the inhibition of B cell lymphopoiesis by TCDD.⁵⁶ The latent space could be useful for analyzing a simplified model of the dynamics of developmental systems and how they change with chemical perturbation. PCA for dimensionality reduction has been used in this area for successful cellular fate prediction during hematopoiesis.⁵⁷

Conclusions

Taken together, our tool facilitates dose-response predictions for a particular drug in a specific cell type using the response of other cell types. Dose-response modeling is important in the realm of drug development and toxicity testing, as the physiological response of chemical perturbation is dose dependent. We envision the use of scVIDR in optimizing dose-response studies during drug discovery and development. scVIDR enables prediction of chemical response in a wide array of cell types and doses using only the control and the highest doses of previous experiments. As more data become available on single-cell chemical perturbations, generative modeling can yield insights into the underlying manifold of gene expression and how different classes of chemicals act on that manifold. Discovery of the properties of the manifold will allow for generalizations to be made about the physiology of tissues and understudied chemical perturbations.

Experimental procedures

Resource availability

Lead contact

The lead contact for this work is Sudin Bhattacharya (sbhattac@msu.edu).

Materials availability

The study did not generate new unique materials or reagents.

Single-cell expression datasets and preprocessing

Nault et al.²³ performed all TCDD liver dose-response experiments, which were deposited in the Gene Expression Omnibus (GEO)⁵⁹ under the accession number GSE184506. Kang et al.²⁴ performed all IFN-$\beta$ PBMC experiments, which were deposited in GEO under the accession number GSE96583. Zheng et al.³⁸ performed all experiments relating to study B, which were deposited in the Sequence Read Archive⁶⁰ under accession number SRP073767. Hagai et al.³⁹ performed all LPS6 species experiments, which were deposited in BioSciences under accession number E-MTAB-5919.⁶¹

The sci-Plex dataset²⁵ and the TCDD dose-response dataset²³ were collected and processed uniformly from raw count expression matrices. The cell expression vectors are normalized to the median total expression counts for each cell. The cell counts are then log transformed with a pseudo-count of 1. Finally, we select the top 5,000 most HVGs on which to do our analysis. The preprocessing was carried out using the scanpy.pp package using the normalize_total, log1p, and highly_variable functions.⁴⁷

The TCDD dose-response dataset comprised of snRNA-seq of C57BL6 of flash frozen mouse livers. Mice in this dataset were administered, subchronically, a specified dose of TCDD via oral gavage every 4 days for 28 days. In our analysis, all immune cell types were left out, as immune cells are known to migrate from the lymph to the liver during TCDD administration.²² Thus, there is a small size for the immune cell populations in the low-dose datasets versus the higher doses. PBMC data from Kang et al.,²⁴ study B data from Zheng et al.,³⁸ and species data from Hagai et al.³⁹ were accessed as a processed dataset from Lotfollahi et al.³⁵

When training scGen and scVIDR, batch effects are accounted for with the scvi.data package using the setup_anndata function. Differential abundances of cells in different groups are accounted for by random sampling with replacement of the same number of cells for each dose and random sampling without replacement of the same number of cells for each cell type.

Implementation and training of models

All code in this manuscript is implemented in the Python programming language. The scVIDR model is built on the python package, scGen v.2.0.0,³⁵ which in turn is built on the python package scVI v.0.13.0.²⁰ Here, we modify the model to accommodate predictions of the dose-response, linear regression on the latent space, pseudo-dose calculations, and approximations of the gene importance in chemical perturbations

Hyperparameters for the model and training are the default values selected by scGen v.2.0.0. Table 1 outlines the model hyperparameters used in deploying scVIDR and scGen. Table 2 outlines the training hyperparameters when deploying scVIDR and scGen.

Table 1.

Hyperparameters for scVIDR’s and scGen’s variational autoencoder model

Hyperparameter	Value
Latent dimension	100
Number of layers	2
Layer width	800
Dropout rate	0.2
Kullback-Leibler weight	$5\mathrm{e}-5$

Table 2.

Hyperparameters for scVIDR’s and scGen’s variational autoencoder training

Hyperparameter	Value
Training epochs	100
Learning rate	0.001
Learning rate decay	$1\mathrm{e}-6$
Optimizer	Adam
Optimizer epsilon	0.01
Early stopping	true
Early stopping patience	25

Our implementation of CellOT³⁷ and scPreGAN³⁶ uses default parameters from both of their respective publications.

Calculation of the ${\delta }_c$ for single- and multiple-dose predictions

The $\delta$, as defined by Lotfollahi et al.,³⁵ is the difference between the mean latent representations of the treated (t = 1) and untreated (t = 0) conditions:

$$\delta ={\overline{z}}_{t=1}-{\overline{z}}_{t=0}\text{,}$$

where ${\overline{z}}_t$ is the mean latent representation for treatment $t$ in the dataset.

We can calculate a cell-type-specific ${\delta }_{c=A}$ for some cell type, $A$, by taking the difference between the mean latent representations of the treated and control groups, or

$${\delta }_c={\overline{z}}_{c=A,t=1}-{\overline{z}}_{c=A,t=0}\text{.}$$

If we want to estimate a ${\delta }_c$ for some type of cell type $B$ based on ${\overline{z}}_{c=B,p=0}$ and where ${\overline{z}}_{c=B,p=1}$ is unknown, we can approximate a function based on ${\overline{z}}_{c=B,p=0}$, or

$${\hat{\delta }}_{c=B}=f\left({\overline{z}}_{c=B,p=0}\right)\text{,}$$

where we approximate the above function using all other existing cell types in the dataset as input to ordinary least-squares regression as implemented by the LinearRegression function in the sklearn.linear_model package.⁶²

Predictions of dose-response in the latent space in scVIDR and scGen

To predict the latent representation for a response at some dose, $d$, we interpolate log linearly on ${\hat{\delta }}_{c=B}$ such that for each latent cell in our prediction, $z_{i,c,p=d}$:

$${\hat{z}}_{i,c,p=d}=z_{i,c,p=0}+{\hat{\delta }}_c\ast \frac{\mathit{log}\left(d+1\right)}{\log \left(\mathrm{m}ax\left(d)+1\right)\right)}\text{,}$$

where $\max \left(d\right)$ is the highest dose in the dataset. To calculate the dose-response values for scGen, we simply replace ${\hat{\delta }}_c$ with $\delta$ calculated by scGen.

Evaluating model performance

Performance of the model on the prediction task is the same as that in Lotfollahi et al.³⁵ We quantified performance using the $R^2$ value for mean gene expression for each gene across all cells. The $R^2$ was calculated using the linregress function from the scipy.stats package.⁶³ We compared the DEGs that are selected using the rank_gene_groups from the Scanpy package and taking the top 100. Models were compared on the same prediction in which we resample 80% of the cells in the cell type we are predicting 100 times. Resampling is done using the choice function from the numpy.random package.⁶⁴

Statistical significance was determined by the one-sided Mann-Whitney U test as it is implemented by the mannwhitneyu function from the scipy.stats package. We considered p values less than 0.001 as statistically significant.

Distances were used to establish relationships between distributions and vectors. Cosine distance was calculated using the cosine function in the scipy.spatial.distance package. The Sinkhorn distance was calculated using the SampleLoss class in the geomloss package.⁶⁵

Inferring feature-level contributions to perturbation prediction

In PCA, we perform an orthogonal linear transformation on the data such that our projected data preserve as much variance as possible. It is known that the solution to this maximization problem is to project the data onto the eigenvectors of the covariance matrix, or

$$Z_m=X{W}_m\text{,}$$

where $X$ is the mean-centered scRNA-seq expression matrix, $W_m$ is the eigenvectors corresponding to the $m$ highest eigenvalues of the covariance matrix of $X$, and $Z_m$ represents the $m$-dimensional projection of the data onto its principal components. We can see from this formula that $Z_m$ is calculated as a linear combination of weights and gene expression, and thus there is a linear relationship between the genes and the principal components. We can exploit this fact and calculate a loading for each gene with each corresponding eigenvector by taking the product of the eigenvector and the square root of the corresponding eigenvalue, or

$$loadin{g}_{ij}=W_{ij}\ast \sqrt{{\lambda }_i}\text{,}$$

where $W_{ij}$ is the $j^{th}$ value (corresponding to gene j) of the $i^{th}$ eigenvector and ${\lambda }_i$ is the eigenvalue for the $i^{th}$ eigenvector. These loadings represent a normalized score of the relationship between a gene’s expression and a particular principal component. These loadings are also directly proportional to the actual correlation between the gene’s expression and the principal component of interest.

It can be shown that PCA and autoencoders with a single hidden layer (with a size less than the observations) and a strictly linear map are nearly equivalent.⁶⁶ We can project principal components back into expression space using the following function:

$$\hat{X}=Z_m{W}_m^T={XW}_m{W}_m^T\text{.}$$

Additionally, we note that PCA is a solution to the minimization of the reconstruction error:

$${\Vert X-\hat{X}\Vert }_2^2\text{.}$$

We find similarly that the loss function that we try to optimize in the autoencoder we described above is

$${\Vert X-{XW}_1{W}_2^T\Vert }_2^2\text{,}$$

where $W_1$ is the weights of the hidden layer and $W_2$ is the weights of the final layer of the autoencoder. In effect, we can see that the autoencoder described above can approximate the loadings of a PCA using $W_2$.

The reconstruction error for a standard VAE with the assumption that the observations are a multivariate Gaussian is

$$\frac{1}{N}{\Vert X-Dec\left(Z\right)\Vert }^2\text{,}$$

where $N$ is the number of samples, $Dec\left(Z\right)$ is the function of the decoder neural network, and $Z$ is the transformation by the encoder of the observations onto the latent space. In an LDVAE, the $Dec\left(Z\right)$ is replaced with a single layer with linear transfer operators such that the reconstruction error is the following:

$$\frac{1}{N}{\Vert X-{ZW}_{Dec}^T\Vert }^2\text{,}$$

in which $W_{Dec}$ is the linear weights of the decoder. These weights give us an approximation of the contributions of individual genes to the dimensions of the latent space. We can interpret $W_{Dec}$ as a loadings matrix by which we can interpret the latent dimensions of the LDVAE.

To approximate feature contributions to predicting the perturbation in scVIDR, we train a ridge regression model. We then take the decoder portion of our model and sample 100,000 points from the latent space and generate their corresponding expression vectors. This will be our training dataset for a ridge regression. We then train the ridge regression using the Ridge class from the sklearn.linear_model package. We can describe the loss of our ridge regression as

$${\Vert Dec\left(Z\right)-Z{W}^T\Vert }^2+\lambda {\Vert W\Vert }^2\text{,}$$

where $Z$ are the sampled points from the latent space, $Z{W}^T$ is the approximation of the predicted gene expression vectors, and $W$ is an m × n matrix where m is the number of genes and n is the number of latent dimensions. We divide $W$ using the ${\left|\left|W\right|\right|}_2$ to normalize for the effect of overexpressed genes. We then calculate the gene scores by taking the dot product of normalized $W$ and ${\delta }_c$, or

$$\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{s}=\frac{W}{{\left|\left|W\right|\right|}_2}{·\delta }_c\text{.}$$

We use these gene scores to order genes for Enrichr⁶⁷ pathway analysis with the gseapy package.⁶⁸ Scores for each pathway were calculated using the score_genes function from the scanpy.tl package with the genes sets derived from the Enrichr results.

Calculating the pseudo-dose values

We can order each cell, $x_i$, with respect to the variable response of $x_i$ to the chemical by taking the latent representation, $z_i$, and orthogonally projecting it onto $L=span\left({\delta }_c\right)$:

$$pro{j}_L=\frac{{\delta }_c·z_i}{{\delta }_c·{\delta }_c}{\delta }_c=p{\delta }_c\text{.}$$

The scalar multiple of $\delta$, $p$, is the pseudo-dose value for $x_i$.

Regression of sigmoid function for evaluating dose-response relationships

To establish whether a standard dose-response relationship existed between the top pathways inferred by Enrichr and the pseudo-dose and gene expression, a logistic function of the form

$$f\left(d\right)=\frac{L}{1+e^{-k\left(d-d_0\right)}}+b\text{,}$$

was used, where d is the dose or pseudo-dose. The parameters of the function above were fit to the output variables (median enrichment score and Fmo3 normalized expression) using the Levenberg-Marquardt algorithm implementation in the curve_fit function in the scipy.optimize package. The regression was evaluated using the mean absolute error metric implementation in the mean_absolute_error function in the sklearn.metrics package.

Published: August 11, 2023

Data and code availability

All data used in the manuscript are publicly available and are referenced in the manuscript. The code for the software and for reproducing the figures is available at https://github.com/BhattacharyaLab/scVIDR. Long-term archive of code repository is made available via Zenodo at http://doi.org/10.5281/zenodo.8025235.⁵⁸