To predict the risk of chronic kidney disease (CKD) using Generalized Additive² Models (GA²M)

Abstract

Objective

To train and test a model predicting chronic kidney disease (CKD) using the Generalized Additive² Model (GA²M), and compare it with other models being obtained with traditional or machine learning approaches.

Materials

We adopted the Health Search Database (HSD) which is a representative longitudinal database containing electronic healthcare records of approximately 2 million adults.

Methods

We selected all patients aged 15 years or older being active in HSD between January 1, 2018 and December 31, 2020 with no prior diagnosis of CKD. The following models were trained and tested using 20 candidate determinants for incident CKD: logistic regression, Random Forest, Gradient Boosting Machines (GBMs), GAM, and GA²M. Their prediction performances were compared by calculating Area Under Curve (AUC) and Average Precision (AP).

Results

Comparing the predictive performances of the 7 models, the AUC and AP for GBM and GA²M showed the highest values which were equal to 88.9%, 88.8% and 21.8%, 21.1%, respectively. These 2 models outperformed the others including logistic regression. In contrast to GBMs, GA²M kept the interpretability of variable combinations, including interactions and nonlinearities assessment.

Discussion

Although GA²M is slightly less performant than light GBM, it is not “black-box” algorithm, so being simply interpretable using shape and heatmap functions. This evidence supports the fact machine learning techniques should be adopted in case of complex algorithms such as those predicting the risk of CKD.

Conclusion

The GA²M was reliably performant in predicting CKD in primary care. A related decision support system might be therefore implemented.

BACKGROUND

Chronic kidney disease (CKD) is a global public health issue leading to several adverse events such as kidney failure, cerebro/cardiovascular disease, and death. In the last decades, the burden of CKD showed an increase moving from 3% to 18% in the general population globally. In 2030, CKD is expected to become the fifth leading cause of death worldwide.^1,2 In Italy, the prevalence of CKD has been estimated of about 7%, with 8.1% and 7.8% in men and women, respectively.^1–3

Nonetheless, CKD is still largely underrecognized across Western countries, especially in the primary care setting. In this respect, there is a well-documented “awareness gap” among GPs to recognize CKD in several countries including Italy.³ Along this line, it was recently reported that 77% of patients with proven Stage G3 CKD were undiagnosed by their GPs in Italy.⁴

The fact that CKD is underdiagnosed depends on several reasons: first, CKD is asymptomatic in the first stage as well as coexistent with other major conditions, mainly cardiovascular diseases, which capture greater attention. As such, a consensus emerged on “Early Identification and Intervention in CKD” in which the need for implementation of effective screening coupled with risk stratification, and appropriate treatment, was underlined for primary or community care settings.^5,6

To tackle this issue a lot of country-specific models predicting the risk of CKD have been provided.⁷ They comprise algorithms gathered through several techniques, such as traditional score development and validation^7–9 as well as supervised machine learning approaches.^10–12 For the latter, Random Forest (RF), J48 algorithm, gradient boost, support vector machine, and neural network and others have been proposed for CKD prediction, but they were developed using small and/or local datasets, and suffer from poor quality reporting and high risk of bias.¹³ Furthermore, some authors demonstrated that, with moderate sample size, limited numbers of CKD events and predictors, machine learning do not improve the predictive accuracy of traditional models, such as logistic regression.^14,15

CKD is a complex clinical entity featured by multifaceted aspects. That being said, a model predicting the risk of CKD is not easily developable for several reasons. First, some determinants do not necessarily show a linear relationship with the occurrence of CKD (eg, serum creatinine, age); second, several interaction terms (eg, age×some co-morbidities) need to be systematically evaluated; third, every determinant-outcome association should be interpretable and not “black-boxed” as those typically found using machine learning methods; fourth, the contribute of each determinant should be simply quantified to be translated into a patient-specific decision support system (DSS).

In this respect, the Generalized Additive² Model (GA²M), a further extension of GAM being implemented in the Explainable Boosting Machines (EBM),^16–18 could represent an adequate response for CKD prediction, given their feasibility in learning several complex associations among several determinants through combinations of interpretable functions. As such, GA²M might systematically uncover interactions and nonlinearities among covariates to improve the predictive performance. Thus, we trained and tested a prediction model for CKD using GA²M and compared it with other algorithms stemming from traditional and machine learning approaches.

MATERIALS AND METHODS

Data source

The Health Search Database (HSD) is a representative longitudinal database containing electronic medical records of approximately 2 million adults. Demographic and clinical data are available in the HSD, and they are linked through a unique encrypted code which also tracks drug prescriptions, lifestyle-related features, clinical investigations, hospitalizations, and deaths. Diagnoses and prescribed medications are coded according to the International Classification of Diseases, 9th Revision, Clinical Modification (ICD-9-CM) and Anatomical Therapeutic Chemical (ATC) systems, respectively. The other variables are registered according to regional coding systems. Currently, a total of 1220 GPs serving 2 331 524 patients met the standard quality criteria and were included in this study. The HSD has been adopted for various research topics, including prediction models.^19–22

Study design

We adopted a cohort study design by selecting all patients aged 15 years or older being active in HSD between January 1, 2018 and December 31, 2020. We defined patients as eligible whenever they were aged 95 years or younger, those with no diagnosis of CKD (ie, using the same operational definition adopted for the outcome) before the entry date, and at least 1 year of look-back period. The date of the first contact (ie, any reason) with GP occurred in the eligibility period was the study entry date. From this date, patients were followed up until the occurrence of these events whichever came first: diagnosis of CKD (ie, event date), death, end of registration data registration with their GP, end of the study period (ie, December 31, 2020). Those with less than 6-month follow-up were excluded. Then, the cohort was randomly divided into 2 samples in a 4:1 ratio; these subcohorts are henceforth referred to as “training” and “testing” dataset, respectively.

Outcome definition

Every diagnosis of CKD being captured during follow-up was operationally defined via ICD9CM/free-text, and/or the presence of Glomerular Filtration Rate (GFR) of less than 60 mL/min per 1.73 m² as reported in Supplementary Appendix S1. The free-text search was conducted by means of keywords searching to increase the sensitivity of the outcome definition, in particular for most severe cases of CKD which could be poorly coded by GPs given that these patients are mainly treated in hospital. Each record identified via free-text was manually inspected and validated by an expert clinician.

This outcome definition was successfully adopted in several previous investigations.^23–25

Candidate determinants

All candidate determinants for CKD were selected according to our previous work,^23,25 current medical literature^7,10,26 and clinical rationale. They were operationally defined in the period preceding or on the index date. Namely, besides age and sex, we included presence of hypertension, diabetes, cardio/cerebrovascular diseases, family history for CKD, glomerulonephritis, presence of albuminuria/proteinuria, urinary tract infections, calculosis, single kidney, autoimmune disorders, other urinary disorders, use of medications with known renal adverse effects (ie, NSAIDs and other antirheumatic medications), smoking, and alcohol abuse as dichotomous covariates. Levels of creatinine (mg/dL), body mass index (BMI) values (kg/m²), systolic, and diastolic blood pressure (mmHg) were included as continuous covariates as well.

Data analysis

All the analyses were carried out according to Transparent Reporting of Multivariable Prediction Model for Individual Prognosis and Diagnosis (TRIPOD).^27,28

Descriptive statistics were reported as means with standard deviations (SDs) and proportions (%) for continuous and categorical variables, respectively. Given the reduced numbers of cases led to imbalanced datasets, the machine learning algorithms might be biased in favor of the main class. To address this issue, cases of CKD were weighted²⁹ according to noncases (=0)/cases (=1) ratio in the training dataset. Namely, 1 misclassified case was weighted as equal to 31.5 misclassified noncases.

The following models were therefore trained and tested in the respective datasets: logistic regression, Random Forest (RF), Gradient Boosting Machines (GBMs), GAM, and GA²M. The latter have been implemented in the EBMs which model each candidate determinant and their related interactions according to a series of iterative decision trees.¹⁷ The parameters used to train each model are detailed in Supplementary Appendix S2.

Missing values being registered for BMI, creatinine, and blood pressure were imputed according to Multiple Imputation by Chained Equation (MICE) methodology,³⁰ which accounts for the Missing At Random (MAR) assumption on missing values.³¹ Along this line, given the expected unbalanced distributions of the covariates between CKD cases and noncases, we adopted an analytical strategy based on K-fold Stratified Cross-Validation³² with 5 replications. The results were therefore summarized according to Rubin’s rule.³³ By doing so, we were able to compare the different models. Indeed, only GBM, GAM, and GA²M supported the training and testing procedures using the incomplete dataset, in which the covariates were codified including categories of missing values.

The predictive performances of the models were evaluated by calculating the respective Area Under the Curve (AUC^34,35 with 95% CI), and Average Precision (AP).³⁶ After examining the Precision-Recall curve for the GA²M, a Recall point was selected as threshold to identify the highest number of CKD cases. This selection was based on the calculation of the slope of Receiving Operating Characteristics (ROC) curve which accounts for the observed prevalence of CKD in the study population and Harm/Benefit (H/B) assessment, namely the maximum number of false positives acceptable by the decision maker to avoid a false negative (ie, 1/Odds(prevalence)×H/B).^37,38 Along this line, a consistent threshold was selected for the other models in order to calculate Accuracy, Specificity, Precision, F₁ Score, and Youden’s J index³⁹ for all models.

For what concerns the interpretation of nonlinearities and interaction terms, it was evaluated by inspecting the related shape and heatmap functions, respectively. The contribute of each term forming the final GA²M was calculated as SD from the overall prediction of CKD gathered in the training dataset and proportionally reported to all terms.

The predicted risk of CKD being cumulated during follow-up was gathered using the sigmoid function⁴⁰ so accounting for the application of case/noncase weighting to train the models. In essence, the sigmoid function was trained to recalibrate the GA²M on the ideal prediction between observed and predicted risk of CKD.

We conducted 2 sensitivity analyses to test the robustness of the results. First, GBM, GAM, and GA²M models, which supported the analysis including missing data, were retrained and tested using the incomplete (ie, with missing categories) datasets as well. Second, the GA²M-based algorithm was evaluated according to other risk thresholds: Accuracy, Specificity, Precision, F₁ Score, and Youden’s J index were recalculated by varying the H\B ratio.

RESULTS

As a whole, within a cohort of 997 864 patients who fulfilled the eligibility criteria (53% females, mean age: 53 [SD: 19] years), 30 705 (1.2 cases per 100 person-years; 3.1% cumulated cases) patients were newly diagnosed with CKD during follow-up. In Tables 1 and 2 are reported the patients’ features among CKD cases and noncases.

Table 1.

Characteristics (categorical variable, n (%)) of patients with or without CKD

Determinant	Total n (%)	Cases n (%)	Noncases n (%)
Sex (male)*	467 853 (46.9%)	13 064 (42.5%)	454 789 (47.0%)
Hypertension*	297 007 (29.8%)	21 023 (68.5%)	275 984 (28.5%)
Diabetes mellitus*	83 129 (8.3%)	8 564 (27.9%)	74 565 (7.7%)
Cardiovascular disease*	22 730 (2.3%)	3 106 (10.1%)	19 624 (2.0%)
Family history of CKD	103 (0.0%)	3 (0.0%)	100 (0.0%)
Glomerulonephritis	461 (0.0%)	17 (0.1%)	444 (0.0%)
Autoimmune disorders	261 (0.0%)	13 (0.0%)	248 (0.0%)
Urinary tract infections*	71 307 (7.1%)	3 733 (12.2%)	67 574 (7.0%)
Calculosis*	44 193 (4.4%)	2 322 (7.6%)	41 871 (4.3%)
Other urinary disorders*	3 541 (0.4%)	243 (0.8%)	3 298 (0.3%)
Nephrotoxic medications*	682 402 (68.4%)	25 369 (82.6%)	657 033 (67.9%)
Smoking*	171 068 (17.1%)	4 650 (15.1%)	166 418 (17.2%)
Alcohol abuse*	14 693 (1.5%)	728 (2.4%)	13 965 (1.4%)
Single kidney*	131 (0.0%)	12 (0.0%)	119 (0.0%)
Proteinuria*	6 624 (0.7%)	624 (2.0%)	6 000 (0.6%)

CKD: chronic kidney disease.

^* P < .001 describing cases versus noncases (chi-square test).

Table 2.

Characteristics (continuous variable, n (%)) of patients with or without CKD

Determinant	Total			Cases			Noncases
	Mean	SD	Missing value	Mean	SD	Missing value	Mean	SD	Missing value
Age (years)	52.6	18.9	0.0%	75.0	11.2	0.0%	51.9	18.7	0.0%
Creatinine (mg/dL)	0.846	0.197	38.7%	1.03	0.255	14.4%	0.838	0.189	39.5%
BMI (kg/m2)	26.0	5.19	46.6%	27.9	5.09	29.6%	25.9	5.18	47.2%
Diastolic blood pressure (mmHg)	78.2	9.63	35.9%	78.0	9.31	13.8%	78.3	9.64	36.6%
Systolic blood pressure (mmHg)	128	17.1	35.9%	135	16.8	13.8%	128	17.0	36.6%

BMI: body mass index; CKD: chronic kidney disease; SD: standard deviation.

P < .001 for all variables describing cases versus noncases (t test).

As expected, CKD cases reported a 2- to 5-fold higher burden of co-morbidities than noncases. For instance, the presence of hypertension, diabetes, and cardiovascular diseases were sensibly higher in cases than noncases (69% vs 29%, 28% vs 8%, 10.1% vs 2.0%, respectively). Other covariates, although with a slighter difference, still reported higher proportions in cases than noncases. Only smoking showed a little higher proportional value in noncases than cases (17.2% vs 15.1%).

When we compared the predictive performances of the 7 models, the AUC for the light GBM showed the highest value which was equal to 88.9% and AP 21.8%, followed by GA²M, with 88.8% and 21.1%, for AUC and AP, respectively. GAM and Logistic regression reported similar values for AUC and AP (88.0, 19.6% and 87.8, 18.9%, respectively). RF reported the lowest value to AUC (85.1%) and AP (17.0%) (Table 3).

Table 3.

Prediction performances across models to assess the risk of CKD

Model	AUC (95% CI)	Average precision (95% CI)
Light GBM	88.9% (88.9, 88.9)	21.8% (21.8, 21.8)
GA2M (EBM)	88.8% (88.8, 88.8)	21.1% (21.1, 21.2)
XGBoost GBM	88.6% (88.5, 88.6)	21.5% (21.5, 21.6)
CatBoost GBM	88.2% (88.2, 88.2)	21.6% (21.5, 21.6)
GAM	88.0% (87.9, 88.0)	19.6% (19.6, 19.7)
Logistic regression	87.8% (87.7, 87.8)	18.9% (18.8, 18.9)
Random forest	85.1% (85.1, 85.2)	17.0% (17.0, 17.0)

AUC: area under the curve; CKD: chronic kidney disease; CI: confidence interval; EBM: explainable boosting machines; GAM: generalized additive model; GBM: gradient boosting machines.

After inspecting the Precision-Recall curve, we opted to compare the prediction models according to a sensitivity threshold equal to 80%, which was able to identify most of the patients (ie, true positives) with a “high” risk of incurring in CKD. The selection of this sensitivity threshold was based on 3 aspects: first, the fact that this sensitivity value corresponds to a slope of the ROC curve with H/B of 15%; the choice of this value was based on the fact that GPs can prescribe a further evaluation of creatinine value to ascertain the suspect of CKD. This is a noninvasive and/or unexpensive examination; second, the size of patients, with no prior diagnosis of CKD, who would constitute the GP’s potential workload in evaluating them whether alerted by DSS; third, the proximity of this sensitivity value to the highest Youden’s J (Supplementary Figure S1). For the investigated models, accuracy and specificity were higher than 82%, and precision, F1 score and Youden’s J exceeded 12%, 21%, and 62%, respectively (Table 4). When we recalculated the sensitivity threshold according to the H/B ratio equals to 10% or 5%, Accuracy, Specificity, Precision, F₁ Score, and Youden’s J index were lower than those obtained for the primary analysis (Supplementary Table S1).

Table 4.

Prediction performances across models to assess the risk of CKD with a sensitivity threshold equal to 80%

Model	Accuracy (95% CI)	Specificity (95% CI)	Precision (95% CI)	F1 score (95% CI)	Youden’s J (95% CI)
Light GBM	82.5% (82.5, 82.5)	82.6% (82.6, 82.6)	12.7% (12.7, 12.8)	22.0% (22.0, 22.0)	62.6% (62.6, 62.6)
GA2M (EBM)	82.3% (82.3, 82.4)	82.4% (82.4, 82.4)	12.6% (12.6, 12.6)	21.8% (21.8, 21.8)	62.4% (62.4, 62.4)
XGBoost GBM	81.9% (81.8, 81.9)	81.9% (81.9, 82.0)	12.3% (12.3, 12.4)	21.4% (21.3, 21.4)	61.9% (61.9, 62.0)
CatBoost GBM	81.5% (81.4, 81.5)	81.5% (81.5, 81.6)	12.1% (12.1, 12.1)	21.0% (21.0, 21.0)	61.5% (61.5, 61.6)
GAM	80.6% (80.7, 80.7)	80.7% (80.7, 80.7)	11.6% (11.6, 11.6)	20.3% (20.3, 20.3)	60.7% (60.7, 60.7)
Logistic regression	81.0% (80.8, 81.0)	81.0% (80.9, 81.0)	11.8% (11.7, 11.8)	20.6% (20.4, 20.6)	61.0% (60.9, 61.0)
Random forest	77.4% (77.3,77.4)	77.2% (77.2, 77.3)	10.2% (10.1, 10.2)	18.0% (18.0, 18.1)	58.2% (58.1, 58.4)

AUC: area under the curve; CKD: chronic kidney disease; CI: confidence interval; EBM: explainable boosting machines; GAM: generalized additive model; GBM: gradient boosting machines.

When the analysis with GBM, GAM, and GA²M were conducted using incomplete datasets, the results were largely consistent with those after MICE (Supplementary Table S2). For this reason, the subsequent findings have been gathered using GA²M in incomplete dataset, in which categories of missing values were part of training and testing datasets.

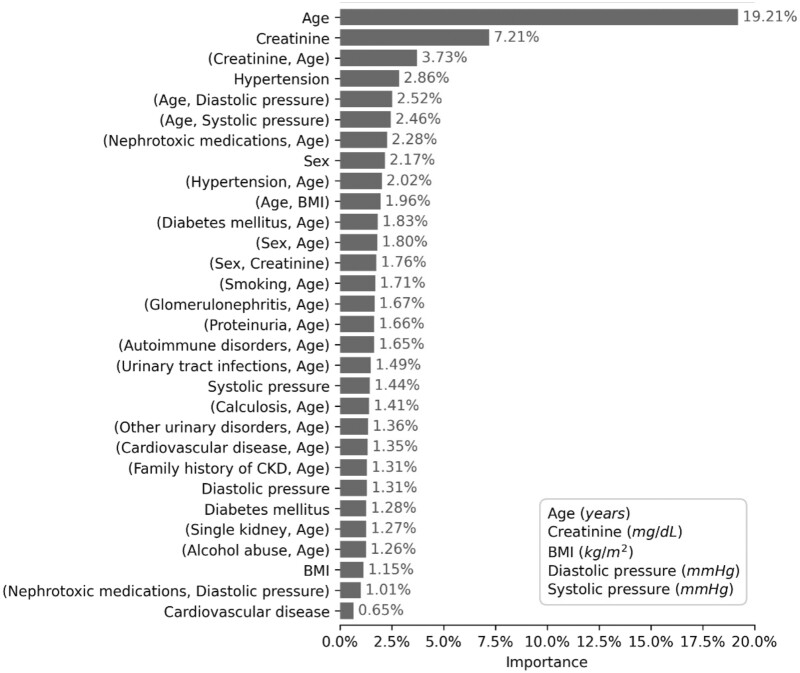
Through the iterative evaluation of 20 candidate determinants and their related combinations, GA²M selected 30 main terms explaining 75% of the model importance in predicting CKD. The other 180 terms were each able to explain the 0.6% of importance or less. In specific, age, creatinine value, interaction term between age and creatinine had a relative importance of 19.21%, 7.21%, and 3.73%, respectively. The other determinants reported an importance lower than 3%. Most of the interaction terms included age (Figure 1).

Figure 1.

Relative importance of the first 30 features forming the GA²M predicting CKD. CKD: chronic kidney disease; GA²M: Generalized Additive² Model.

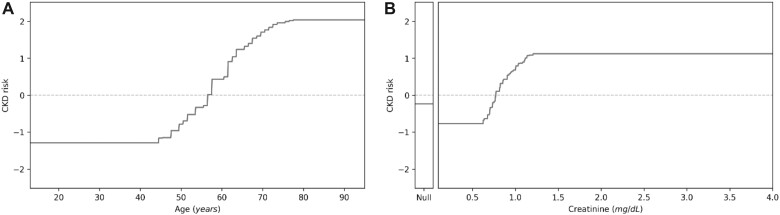
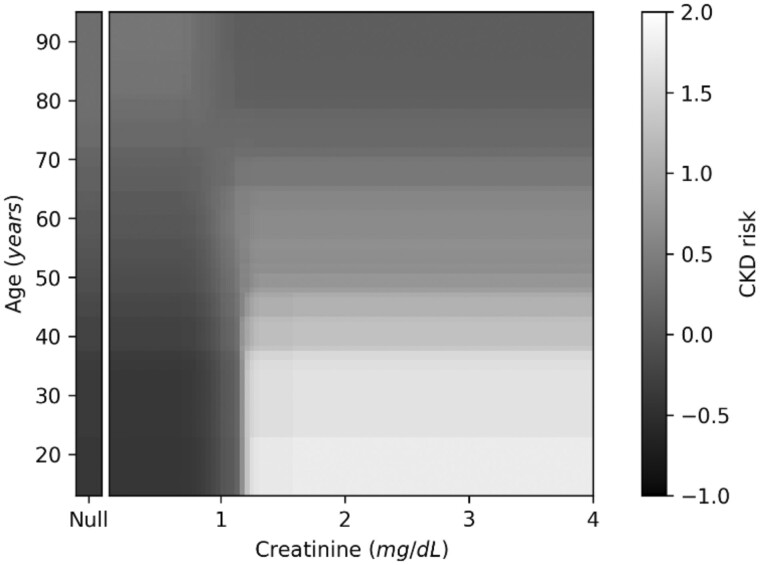
In contrast with GBM, GA²M allowed a straightforward interpretation for both individual features and interaction terms. In this respect, Figure 2 depicts the example of data interpretability which were assessed through the shape functions by plotting age and creatinine values towards the occurrence of CKD. By doing so, we can visualize the contribute of each determinant to the overall risk of CKD. Along this line, heatmaps allow to visualize the contribute of interaction terms as shown in the example for age and creatinine. Basically, for a patient aged 20 years, the risk of presenting CKD is clearly modified by creatinine value a little higher than 1 mg/dL; on the other hand, for those older than 50ies, age is an increasing factor per se (Figure 3; see Supplementary Appendix S3 for other interaction terms).

Figure 2.

Shape function for age (A) and creatinine (B) against the occurrence of CKD. CKD: chronic kidney disease.

Figure 3.

Heatmap functions for age×creatinine interaction and occurrence of CKD. CKD: chronic kidney disease.

As a whole, the predicted risk of CKD being cumulated during follow-up was equal to 3.2%. With 80% sensitivity (assuming an H/B equal to 0.15), the GA²M threshold distinguishing high versus low risk of CKD was equal to 4.43% according to sigmoid function.

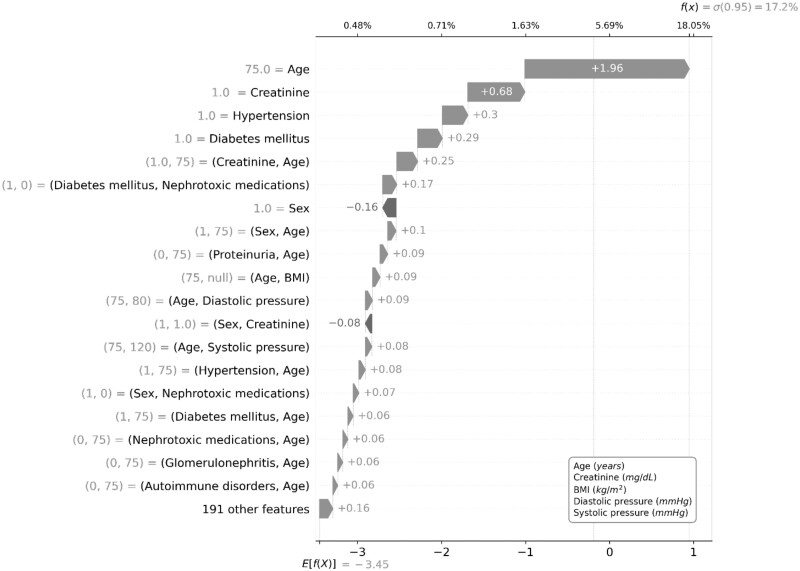
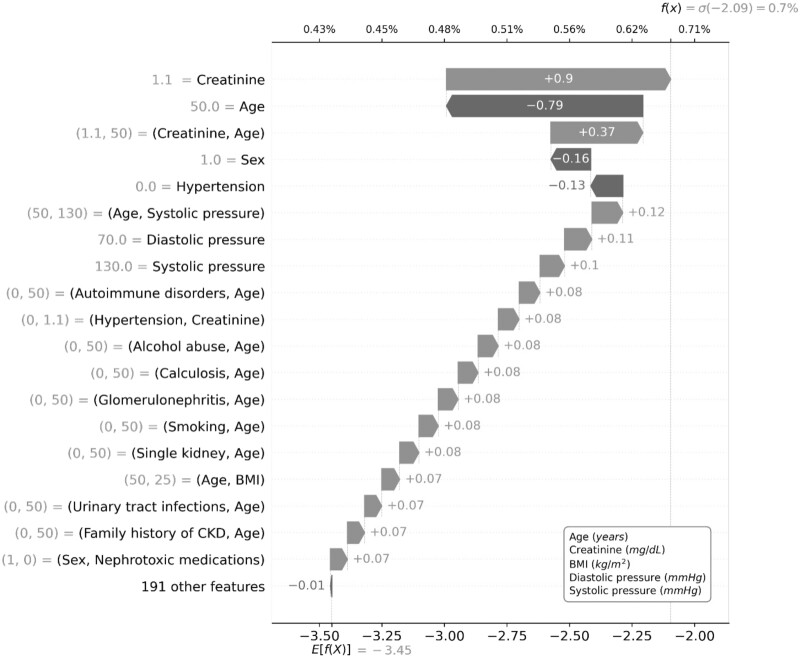
By applying the sigmoid function to the sum of individual contributes for all terms composing the GA²M, we were able to visualize the prediction of CKD for 2 hypothetical patients with high and low risk according to an algorithm threshold of 4.43% (80% sensitivity). Namely, the hypothetical patient with a GA²M-based high (17.2%) risk of CKD, age of 75 years, creatinine equal to 1 mg/dL, presence of diabetes and hypertension are the most contributing factors to the quantification of risk (Figure 4); while the hypothetical patient with a GA²M-based low (0.7%) risk, creatinine equal to 1.1 mg/dL, and the interaction between creatinine and age were the most contributing factors for the quantification of risk (Figure 5).

Figure 4.

GA²M predicting CKD for a hypothetical patient with high risk (higher than 4.43%). CKD: chronic kidney disease; GA²M: Generalized Additive² Model.

Figure 5.

GA²M predicting CKD for a hypothetical patient with low risk (equal or lower than 4.43%). CKD: chronic kidney disease; GA²M: Generalized Additive² Model.

DISCUSSION

To our knowledge, this is the first study which provides evidence on prediction performance of CKD occurrence when its determinants were modeled through GA²M. This model was the most performant over 4 machine learning algorithms and logistic regression. Among the 30 terms composing the models which provided the highest contribute to explain the risk of CKD, age, creatinine, and their respective interactions had the most relevant importance. Even if GA²M are slightly less performant than light GBM, they are not “black-box” algorithms, so being simply interpretable and applicable using shape and heatmaps functions.

In this context, prior models have been developed for CKD prediction but they were focused on small, local, and selected populations, including some Italian cohort (ie, 1249 patients with diabetes),⁷ and/or suffered from certain limitations. Indeed, the absence of prediction tools in the large primary care settings in Italy cannot allow the adoption of foreign algorithms which may not fit the Italian context well. In this respect, a systematic review of studies by Collins and coworkers¹³ on 14 risk prediction models for CKD and ESKD has highlighted methodological issues and a general poor level of reporting, along with inappropriate handling of missing data. In specific, 3 studies adopted prevalent instead of incident cases of CKD as response variables; most of them were conducted in specific settings (ie, renal or cardiovascular-based cohorts) in decades preceding 2010, so selecting patients who likely differ from those generally and/or more recently cared by GPs; only 2 studies were carried out in community-based settings similar to ours. Namely, Chien and coworkers⁹ adopted a small Chinese cohort including 5168 patients, 190 cases of CKD, and 9 covariates. This model reported a fair/modest discrimination value of 67%. Hippsley-Cox and coworkers⁸ developed and validated an algorithm for CKD prediction using 2 UK primary care databases (ie, QRESEARCH and THIN). Such a model was able to well predict moderate-severe CKD, with an explained variance of 56.4% and 57.5%, in women and men, respectively. The AUC statistic was 0.875 for women and 0.876 for men. In the light the similarities between NHS for Italy and the United Kingdom, this model could be reliably translated in the Italian context after recalibration. Nevertheless, the traditional approach using Cox regressions was not able to iteratively assess all potential interaction terms and nonlinearities which peculiarly characterized the prediction of CKD. As stated in the background, prior clinical knowledge of CKD is not likely enough to assess the profile of patients at risk of developing this multifaceted condition.

Some machine learning algorithms have been proposed for the early identification of CKD as well. In general, algorithms such as J48 and GBM,^10,26 showed a better accuracy than RF as confirmed in our analysis. Nonetheless, the traditional logistic regression demonstrated a better accuracy for CKD prediction,^14,15 reporting an AUC equal to 91%, when compared with RF, SVM, NN, K-NN, and GBM.¹⁵ In addition, the authors used GAM to assess the role of nonlinearities (ie, using spline regression) and interactions (ie, using decision trees) in predicting CKD, but did not find a relevant contribution of these terms when entered the models. These findings were likely due to the reduced sample size, number events and/or candidate determinants. In any case, the authors tested different chronic diseases as outcomes, and only for CKD there was a growing improvement reaching AUC around 0.91 with interaction depth equal to 2 when GBM were used. This result, in line with ours, was substantially related to interaction between age and GFR value, which was not significant in logistic regression.¹⁵ It confirms that decision-tree-based algorithms might be more sensitive to interactions than the traditional regression model. This evidence supports the fact that machine learning techniques should be adopted in case of highly complex algorithms with several determinants such as those that predict the risk of CKD, especially when large and heterogeneous data sources are used.

None of the previous work adopted GA²M to develop an algorithm predicting CKD. Given the relevant size of our cohort (ie, the eligible individuals were equal to 997 864 with 30 705 cases of CKD), we were able to inspect several interaction terms and nonlinearities for model specification so demonstrating the greater predictive ability of GA²M versus the other models, including logistic regression. From epidemiological and analytical perspectives, GA²M has the advantage to be interpretable by means of shape and heatmap functions. This aspect is particularly useful given the multifaceted aspects of CKD, for which the iterative investigation of predicting interactions is complex, and its implementation into a DSS would result poorly applicable. We found that GA²M allowed us to assess the relative importance of each feature and interaction terms. As expected, age had a relevant contribution along with creatinine value.

The importance of each determinant can be quantified for an individual patient according to his/her specific risk factors, so simplifying its implementation in GP’s software of DSS for early recognition of CKD. Given the relevance of CKD prevalence (ie, up to 18%)¹ and underdiagnosis (ie, up to 77%),^3,4 the 3% or greater increase of AUC obtained with GA²M and other models versus RF, might sensibly improve the model performance in terms of number of new CKD cases being potentially captured.

Through the GA²M, the values of interpolations stemming from shape and heatmap functions reveal the importance of each determinant in predicting CKD; according to the GA²M, the sum of these values provides the overall patient-specific risk of CKD. In Italy, a GP with 1500 patients (ie, the highest allowed number for most of the local health authorities), would have in charge 5.3% (n = 80) CKD patients expectedly. As such, there are 1420 patients at “high” or “low” risk of developing CKD, and they could be categorized by their GP as shown in Supplementary Figure S2. According to a population-based approach, GPs could therefore generate a list of “high-risk” patients with which to plan screening strategies. This approach is clearly complemented by patient-specific DSS embedding a GA²M-based algorithm. Yearly, the algorithm should provide a reminder to investigate kidney function (ie, evaluate or re-evaluate creatinine/GFR) in 258 (out of 1420: 18.2%) patients once they have one risk factor for CKD at least. On average, for an Italian GP, there are 10.3 encounters per patient/year; most them were due to older adults, who can reach 20 or more encounters per patient/year for those aged 85+ years.⁴¹ Given the relevance of underrecognition of CKD in primary care, this workload should be therefore acceptable for GPs and cost-effective for the NHS.

The present study suffers from limitations as well. First, in GAM and GA²M patients’ features cannot be modeled according to a time-related fashion. Nevertheless, the presence of duration (years) of follow-up in the model is not easily interpretable, and the shape functions were intrinsically able to identify the best fit for each determinant-CKD association. In this respect, the fact that we obtained similar values for observed and predicted risk (3.1% vs 3.2%) of CKD being cumulated during follow-up was reassuring. Second, the relevant presence of missing values observed for certain covariates might have partly biased the results. However, the results gathered with incomplete datasets for GBM, GAM, and GA²M were largely consistent with those obtained after MICE. Third, there were no covariates defining socioeconomic determinants in HSD. Nevertheless, GA²M allowed the analysis of a relevant the number of variable combinations (>=200) which should likely contain the risk variation due to unmeasured variables. Fourth, we did not conduct an external validation for the final model. Nevertheless, HSD is a large national primary care database which should overcome the limitations seen in small datasets in case of absent external validity. Along this line, the issue of overfitting should be minimized as well.⁴²

In conclusion, GA²M was reliable to accurately predict CKD in primary care. Such a model should therefore constitute the base for further analytic approaches to investigate the risk of renal diseases and related conditions as well as to implement new prediction algorithms for GPs’ informatic tool.

FUNDING

This work was supported by AstraZeneca Italy.

AUTHOR CONTRIBUTIONS

FL and EM—study design, data collection, data analysis, data interpretation, writing, and critical revision; IC, GM, and GP—data collection, data interpretation, writing, and critical revision; LN and MF—data collection, data analysis, and data interpretation; MG and MP—critical revision; CC—study design, data interpretation, writing, and critical revision.

SUPPLEMENTARY MATERIAL

Supplementary material is available at Journal of the American Medical Informatics Association online.

CONFLICT OF INTEREST STATEMENT

FL, EM, and IC provided consultations in protocol preparation for epidemiological studies and data analyses for AstraZeneca, Mundipharma, and MSD. IC and LN are employees at Genomedics. GM, GP, and CC provided clinical consultations for AstraZeneca, Mundipharma, and MSD. MG and MP are employees at AstraZeneca. MF is an employee at Data Life.

DATA AVAILABILITY

The data underlying this article cannot be shared publicly because it includes proprietary and private electronic medical record data.