Abstract
Crystal field (CF) control of rare-earth (RE) ions has been employed to minimize decoherence in qubits and to enhance the effective barrier of single-molecule magnets. The CF approach has been focused on the effects of symmetry on dynamic magnetic properties. Herein, the magnitude of the CF is increased via control of the RE oxidation state. The enhanced 4f metal–ligand covalency in Pr4+ gives rise to CF energy scales that compete with the spin–orbit coupling of Pr4+ and thereby shifts the paradigm from the ionic ζSOC ≫ VCF limit, used to describe trivalent RE-ion, to an intermediate coupling (IC) regime. We examine Pr4+-doped perovskite oxide lattices (BaSnO3 and BaZrO3). These systems are defined by IC which quenches orbital angular momentum. Therefore, the single-ion spin–orbit coupled states in Pr4+ can be chemically tuned. We demonstrate a relatively large hyperfine interaction of Aiso = 1800 MHz for Pr4+, coherent manipulation of the spin with QM = 2ΩRTm, reaching up to ∼400 for 0.1Pr:BSO at T = 5 K, and significant improvement of the temperature at which Tm is limited by T1 (T* = 60 K) compared to other RE ion qubits.
Introduction
In the field of quantum information science (QIS), the fundamental unit of a quantum computer is the quantum bit or qubit, which can be placed into an arbitrary superposition of two states.1 Several candidates have been proposed to exhibit a two-state quantum system that can be coherently manipulated, including superconducting circuits,2 trapped ions,3 topological states in condensed matter,4 and electron and nuclear spins in solids.5−7 Interfacing between different components of a computer by using hybrid quantum systems composed of an ensemble of electron spins has been proposed as a promising route for quantum memories operating in the microwave regime.8 Such memories are possible by exploiting the ability to coherently manipulate the electron spins, usually implemented using various magnetic impurities, as evidenced by nitrogen-vacancy centers in diamonds, phosphorous defects in silicon,7 and double-vacancy sites in silicon carbide.5,6 Building on top of these approaches, an attractive design is to incorporate nuclear spins interacting with the electron spins via hyperfine interactions, which can offer an extra resource for storage by transfer of polarization between electron and nuclear spins and the ability to have low error rates.9 Furthermore, the incorporation of nuclear spins also offers the ability to scale the number of qubits by utilizing the multitude of transitions that results from the hyperfine interaction.10 Within this framework, rare-earth (RE) ions have been extensively studied because of their excellent coherence properties and wealth of naturally abundant nuclear spins.11
Paramagnetic RE ions exhibit unquenched orbital angular momentum from the atomic-like 4f states possessing electron and nuclear spins and accessible optical transitions. These properties make them attractive materials to generate a versatile quantum interface by bringing together optical and microwave addressability. As a result, a hybrid quantum system can be achieved to develop efficient and faithful microwave-optical conversion, entanglement storage, and light–matter teleportation in the telecom wavelength. In the trivalent oxidation state (RE3+), the core-like 4f orbitals of the RE ions are only weakly perturbed by the crystal field (CF) and minimally split the otherwise 2J + 1 fold-degenerate free-ion ground-state (GS) 2S+1LJ. This electronic structure results in rich physics and has been used to design new quantum materials with emergent phenomena.12−14 Therefore, in RE ions, the CF states can act as qubit states.11 Among the RE ions, Pr3+,15 Nd3+,16 Er3+,11 and Yb3+17,18 have been of primary interest. Recently, synthetic chemistry has been proposed to offer tunability of quantum states by engineering the ligand field experienced by the electron spin in the form of molecular qubits.19−21 Besides tuning the ligand field, synthetic chemistry also offers the ability to engineer the electronic structure of the RE ion by providing control over the formal oxidation state of the metal center, as evidenced in recently explored reduced RE molecular complexes of La2+ and Lu2+. In these systems, a single unpaired electron resides in an orbital with a mixed 5d/6s character rather than the 4f orbital, giving rise to a clock transition and enhanced coherence.22,23
While 3+ is the most stable oxidation state for RE ions, synthetic chemistry has pushed the boundaries of RE ions by accessing the unusually high 4+ oxidation state in Ce, Pr, and Tb.24−28 Recently, we showed that Pr4+ ions exhibit an unusually large CF energy scale, almost an order of magnitude greater than its 3+ counterparts, and established that the traditional ionic paradigm, used to describe Ln3+ ions, breaks down for Pr4+ due to hybridization of the Pr-4f electrons with the ligand valence electrons (analogous to transition metals as shown in Figure 1a).29 Following this observation, it is enticing to use high-valent RE ions like Pr4+ as an alternative or compliment to Ln3+ systems to build novel quantum architectures with long-lived quantum memories.
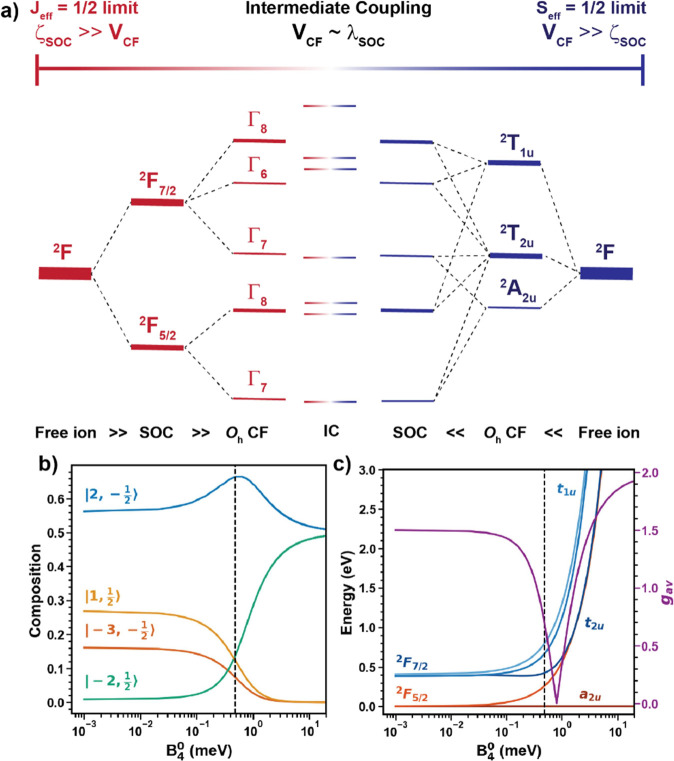
Figure 1.
(a) Energy splitting diagram of a 4f1 ion from ζSOC ≫ VCF limit (left) and ζSOC ≪ VCF limit (right) with the IC regime in the middle. (b) Composition of the GS wavefunction in Pr4+ as a function of B40. (c) Evolution of the eigen energies of the CF states and gav in Pr4+ as the paradigm shifts from ζSOC ≫ VCF limit to the ζSOC ≪ VCF limit. The black line in (b) and (c) shows the position of BaPrO3 based on our CF calculations.
A key ingredient in determining the coherence time of an electron spin is the spin–lattice relaxation time, T1, that is strongly temperature-dependent.30 The relaxation dynamics of T1 arises from the interplay of direct, Raman, and Orbach processes, which enable the exchange of energy between the spin system and lattice bath when the electronic energy levels (CF states for RE ions) are modulated.31 Suppressing the efficacy of the Raman and Orbach processes driven by acoustic and optical phonons, respectively, is key to establishing long coherence times. The intuitive approach to minimize spin–phonon coupling is engineering of lattice vibrational modes and can be achieved by judicious choice of the host lattice/ligand architecture.32−34 However, the chemical properties that drive T1 remain an open question and demonstrate that there is a rich chemical space still to be explored for QIS applications.
Alternative strategies for RE ions include CF control usually achieved by careful choice and control of symmetry and use of ions with an S-like electronic GS, where the vanishing orbital angular momentum (μorb/μspin ≈ 0) suppresses spin–phonon coupling. Within this framework, Pr4+ ions are advantageous, given that the first CF excited state is at ∼2000 cm–1 compared to a few hundreds of cm–1 observed for other Ln3+ ions.35 Furthermore, the large CF energy scale competes with spin–orbit coupling (SOC), which mixes the excited-state SOC multiplet into the GS and thereby minimizes the orbital momentum (as observed from X-ray magnetic circular dichroism measurements: μorb/μspin ≈ 1.8 for Pr4+ compared to μorb/μspin ≈ 8 for Ce3+).35 Pr4+ also has a very small g value (gav < 0.8), one of the smallest among the RE ions, which offers the ability to suppress decoherence from spectral diffusion (SD) due to magnetic dipolar interactions. As a bonus, Pr has a very large nuclear spin, 141Pr (100% natural abundance with I = 5/2), which can further be used for coherent manipulation via hyperfine interactions.
In this work, we use the anomalously large CF splitting of Pr4+ to avoid electronic excitations overlapping with the vibrational density of states. This electronic manifold is achieved by using chemical design principles to stabilize Pr in its unusually high 4+ oxidation state by a judicious choice of oxide host lattices.28 The evolution of single-ion GS wavefunction and properties of Pr4+ as the paradigm shifts from ζSOC ≫ VCF to ζSOC ≪ VCF is considered using a toy model to evaluate the unique ability to tune the spin–orbit coupled single-ion states in Pr4+-based systems. We demonstrate the single-ion electronic structure of Pr4+ in a six-coordinate perovskite lattice, BaPrO3, by using a combination of thermo-magnetic measurements and CF theory. Coherence studies on Pr4+ doped in BaZrO3 and BaSnO3 host lattices using a combination of continuous-wave (CW) and pulsed X-band EPR measurements lends credibility to our design strategy and establishes Pr4+ as a potential candidate for QIS applications.
Results and Discussion
Crystalline powder samples of BaPrO3, Pr:BaSnO3 (2% doping: 2Pr:BSO; 0.1% doping: 0.1Pr:BSO), and Pr:BaZrO3 (2% doping: 2Pr:BZO; 0.1% doping: 0.1Pr:BZO) were synthesized using traditional solid-state reactions (see Supporting Information), and phase purity was confirmed using powder X-ray diffraction (Figure S1). The parent compound, BaPrO3, crystallizes in an orthorhombic Pnma space group36,37 different from the host materials (BaMO3; M = Sn, Zr) which crystallize in a cubic, ideal perovskite Pm3̅m structure, as shown in Figure 2.38 The orthorhombic distortion in BaPrO3 is due to cooperative buckling of the corner sharing octahedra with respect to each other, resulting in reduction of local symmetry at the B site from m3̅m (Oh) in the host materials to 1̅ in the parent compound. However, the PrO6 octahedra in BaPrO3 are very close to a perfect Oh with only small changes in the nearest-neighbor oxygen coordination. Therefore, BaPrO3 is an ideal model compound to study the single-ion electronic structure of Pr4+ in the PrO6 moiety and to understand the microscopic origins of coherent spin dynamics of 141Pr4+ ions in BaMO3 (M = Zr, Sn) host lattices. It should be noted here that BaMO3 host lattices were chosen to provide stabilization of the 4+ oxidation state and to obtain phase pure compounds. Experiments to design host lattices with minimal nuclear spins in the surrounding bath (in materials such as La2M2O7 (M = Sn, Zr)) were not fruitful as phase segregation was observed.
Figure 2.
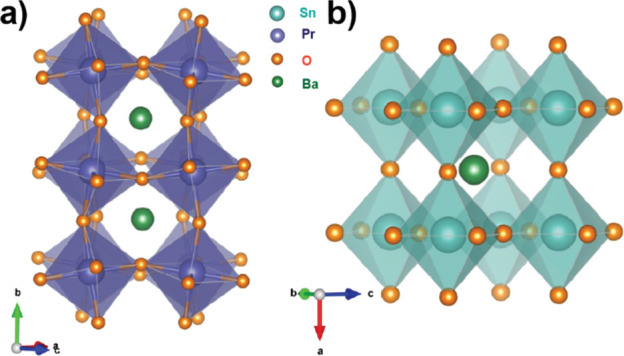
(a) Crystal structure representation of BaPrO3. (b) Crystal structure representation of the host lattice BaSnO3.
As reported by our group and others,35,39 Pr4+ exhibits an unusually large CF splitting which competes
with the SOC, yielding drastically different single-ion properties
than expected in the ζSOC ≫ VCF limit as shown in Figure 1a, and requires an intermediate coupling
(IC) scheme to describe the GS properties.35,39,40 Pr4+ is a Kramers ion with a
4f1 electron configuration and couples the electron spin, S = 1/2, and orbital angular momentum, L = 3, to give rise to a J = 5/2 GS (2F5/2) and a J = 7/2 excited state (2F7/2) in the |j, mj⟩ basis. The GS Kramers doublet
(KD) is given by 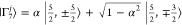 , where α2 ∼ 1/6.
In this framework, the CF Hamiltonian (ĤCF) is diagonalized only within the 2F5/2 SOC manifold as is the case for traditional trivalent Ce3+ systems.
, where α2 ∼ 1/6.
In this framework, the CF Hamiltonian (ĤCF) is diagonalized only within the 2F5/2 SOC manifold as is the case for traditional trivalent Ce3+ systems.
Since j is not
a good quantum
number in the IC
regime, the |ml, ms⟩ basis can be used
to describe the electronic structure of Pr4+. In the |ml, ms⟩ basis,
the Oh CF splits the seven 4f orbitals
to GS a2u and excited triply degenerate t1u and
t2u states. In the presence of SOC, the seven 4f orbitals
mix, yielding seven KD. In the |ml, ms⟩ basis, the nature of the GS KD is
given as 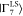
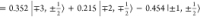
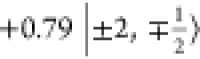 . The first two
components of Γ7LS KD (ml = −3, −2)
are derived from
. The first two
components of Γ7LS KD (ml = −3, −2)
are derived from 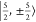 ,
, 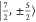 , states in the |j, mj⟩ basis, while the last components
(ml = 1, 2) are derived from
, states in the |j, mj⟩ basis, while the last components
(ml = 1, 2) are derived from 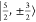 ,
, 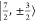 states. Within this framework of IC, the ĤCF is diagonalized using the entire set
of 14 |ml, ms⟩ states.
states. Within this framework of IC, the ĤCF is diagonalized using the entire set
of 14 |ml, ms⟩ states.
To understand the implications of the IC scheme, the evolution of the single-ion properties of Pr4+ is studied in the model Hamiltonian:
| 1 |
where Bnm are the fourth- and sixth-order terms and Ôn are the corresponding Stevens operator equivalents,41 constrained by the Oh symmetry of an isolated PrO6 unit. The eigen energies, GS wavefunction composition, and gav as a function of B40 for fixed values of B6 are calculated as shown in Figure 1b,c (see also Supporting Information). With B60 = −0.004, for small values of B4, the system can be considered as a traditional trivalent lanthanide where the ζSOC ≫ VCF limit still applies. The eigen states split as expected for the Oh CF (Figure 1c). As B40 increases, the paradigm shifts from ζSOC ≫ VCF limit to ζSOC ≪ VCF. For nonphysically large values of B4, the eigen states relax to three sets of 4f orbitals a2u, t2u, and t1u as expected in the ζSOC ≪ VCF limit. Looking at the composition of the wavefunction (Figure 1b), it is evident that with an increase in CF energy scale, ml = +1, −3 states begin to decrease from the original Γ7 KD as the system relaxes to ml = ±2 states corresponding to the a2u GS. The shift in paradigm between the two limits significantly impacts the single-ion electronic structure, evident from the consistent change in gav of the system. Within this framework, among the RE ions, Pr4+ offers the unique ability to tune the spin–orbit coupled wavefunction for a given symmetry by its ability to access the IC regime. It is important to note that the quenching of the orbital angular momentum is a product of the IC regime (Figure 1a–c). In either the CF or SOC limits, the orbital angular momentum is partially or completely recovered.
BaPrO3 exhibits a magnetic transition at TN ∼ 11 K observed in χ(T), as shown
in Figure 3a.37 Curie–Weiss analysis in the
10 < T < 40 K range yields θCW ∼ −35 K and μeffCW = 0.75(2) μB, which is significantly
lower than the expected value for a free f1 ion (2.54 μB). All CF excitations for Pr4+ in BaPrO3 (measured using optical spectroscopy) have
been reported previously with E1 = 0, E2 ≈ 249.5, E3 ≈ 252, E4 ≈ 389, E5 ≈ 655, E6 ≈ 657, and E7 ≈ 818 meV.47 As expected, Pr4+ exhibits an unusually
large VCF energy scale comparable to the
ζSOC ≈ 112 meV,48 and therefore, the single-ion properties must be modeled in the
IC regime as described earlier. The single-ion CF Hamiltonian for
Pr4+ can be written in a truncated symmetry basis, as shown
in eq 1. The CF Hamiltonian, ĤCF, is then fit to the observed eigen energies from optical
measurements, their corresponding degeneracies, and magnetic susceptibility
data at μoH = 0.1 T above 40 K (T > 40 K was chosen to avoid short-range correlations)
as
shown in Figure 3a
with a fixed value of ζSOC ≈ 112 meV. This
analysis yields a set of new KD’s with the GS wavefunction
expressed as 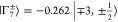
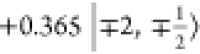
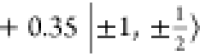
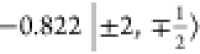 with gavCF = 0.68 comparable to the value
extracted from the CW fits. The resulting model reproduces magnetization
at T = 50 K, as shown in Figure 3b. This analysis clearly shows that the GS
of Pr4+ deviates significantly from the expected VCF ≪ ζSOC.
with gavCF = 0.68 comparable to the value
extracted from the CW fits. The resulting model reproduces magnetization
at T = 50 K, as shown in Figure 3b. This analysis clearly shows that the GS
of Pr4+ deviates significantly from the expected VCF ≪ ζSOC.
Figure 3.

(a) Magnetic susceptibility (χ(T)) and inverse susceptibility (χ(T)−1) data of BaPrO3 measured under μ0H = 0.1 T plotted together with the CF model and a Curie–Weiss analysis in the temperature range 10 < T < 40 K. (b) Isothermal magnetization M(H) at T = 50 K for BaPrO3 plotted together with the CF model. T = 50 K was chosen so that BaPrO3 is well above the ordering temperature and free from short-range correlations.
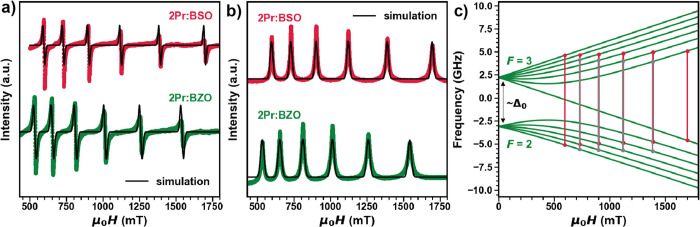
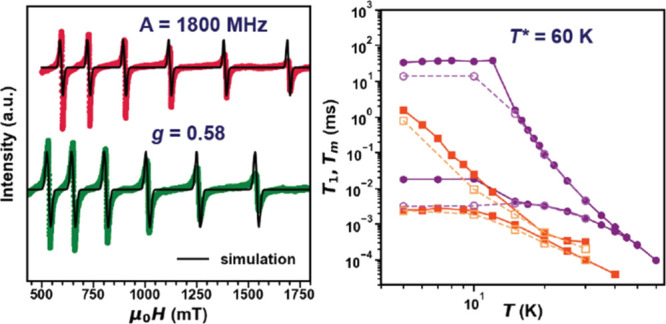
Having established the single-ion electronic structure of Pr4+ in a perovskite ABO3 lattice, the relaxation and coherent spin dynamics of electron and nuclear spins of 141Pr4+:BaMO3 (M = Zr, Sn) were investigated using CW and pulsed EPR at the X-band (f = 9.4 GHz and B0 < 1.8 T). Figure 4a shows the CW-EPR spectra for 2Pr:BSO and 2Pr:BZO measured at T = 5 K, revealing a six-line pattern due to the unpaired electron and its hyperfine coupling with the I = 5/2 141Pr isotope. The EPR spectrum was analyzed using an effective spin Hamiltonian of eq 2 describing a lone S = 1/2 electron coupled to an I = 5/2 nuclear spin:
| 2 |
where the first two terms
denote electron and nuclear Zeeman interactions, g̃ is the g-tensor, the third term represents the
electron–nuclear hyperfine interaction, and à is the hyperfine coupling tensor. The X-band EPR simulations (using
the MATLAB toolbox EasySpin)49 also shown
in Figure 4a yield
a gisoEPR ≈ 0.57 comparable to giso and a large
hyperfine interaction of Aiso ≈
1771 MHz. At zero field, where the hyperfine interaction is the strongest,
the nuclear spin and electron spin couple, yielding two states with
total angular momentum F = I ± S = 5/2 ± 1/2 = 2 and 3 separated by 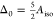 , as shown in Figure 4c. Figure 4c also
shows the six allowed EPR transitions (red lines)
expected for 141Pr4+ and the corresponding forbidden
transitions (gray lines) calculated with the parameters extracted
for 2Pr:BSO. 2Pr:BZO yields very similar
results with gisoEPR≈ 0.63 and Aiso ≈ 1789 MHz as shown in Figure 4a and are tabulated in Table S6.
, as shown in Figure 4c. Figure 4c also
shows the six allowed EPR transitions (red lines)
expected for 141Pr4+ and the corresponding forbidden
transitions (gray lines) calculated with the parameters extracted
for 2Pr:BSO. 2Pr:BZO yields very similar
results with gisoEPR≈ 0.63 and Aiso ≈ 1789 MHz as shown in Figure 4a and are tabulated in Table S6.
Figure 4.
(a) CW X-band EPR of 2Pr:BSO measured at T = 5 K and the corresponding simulation. (b) echo-detected field-swept (EDFS) spectra of 2Pr:BSO and 2Pr:BZO measured at T = 5 K and the corresponding simulation. (c) Simulated energy diagrams of Pr4+ for the B0∥Z orientations of the applied magnetic field calculated with parameters extracted from 2Pr:BSO. Given that only isotropic values were used for calculations, there was no orientation dependence for the energy diagrams.
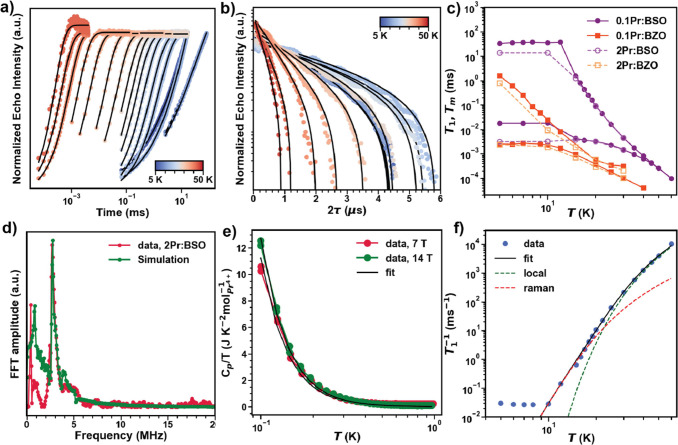
Probing the spin dynamics of 141Pr4+ with pulsed EPR methods, the echo-detected field-swept (EDFS) spectrum of 2Pr:BSO was recorded by monitoring the integrated spin echo intensity as a function of applied dc field using the two-pulse echo sequence (π/2 – τ – π – τ – echo) with τ = 120 ns and is shown in Figure 4b. The spectrum reveals six broad transitions consistent with CW-EPR. Modeling the spectrum with the parameters extracted from CW-EPR yields good agreement with the experimental data (Figure 4b). 2Pr:BZO yields very similar results in good agreement with CW data as shown in Figure 4b and are tabulated in Table S6. Electron spin relaxation, characterized by the spin–lattice relaxation time constant, T1, is commonly caused by spin–phonon coupling and, in most cases, limits the coherence times of the electron spin. Furthermore, T1 also affects decoherence indirectly, where the spin flips of neighboring electron spins lead to SD of the central spin.18 Therefore, the T1 of 141Pr4+ ions in the temperature range 5–60 K was studied using the inversion-recovery method (π – τr – π/2 – τe – π – τe – echo), where τr is swept, as shown in Figure 5a. These experiments, at an applied field of B0 = 592.7 mT (2Pr:BSO) and 530.8 mT (2Pr:BZO), focus on the field of the largest intensity echo. The resulting saturation recovery traces were fit with a standard stretched mono-exponential function (see Supporting Information), and the extracted T1 values are plotted in Figure 5c as a function of temperature. At low temperatures (<12 K), T12 Pr:BSO shows weak temperature dependence, reaching a maximum of ∼13 ms at 5 K, while T1 shows a strong temperature dependence, reaching a maximum of ∼0.7 ms at 5 K, comparable to other oxide host lattices.17,18 In either case, the electron spin–lattice relaxation rate in the low-temperature regime is inversely proportional to temperature which can be attributed to a direct one-phonon process.18 At high temperatures (>12 K), T1 begins to precipitously decrease, reaching a value of T12 Pr:BSO = 4.65 μs and T1 = 0.31 μs at T = 30 K. In order to understand the effects of dipolar magnetic interactions, further diluted samples with a Pr4+ concentration of ∼0.1% were analyzed. Dilution to ∼0.1% improves T1, reaching a maximum of T10.1 Pr:BSO ≈ 33 and T1 ≈ 16 ms for the BSO and BZO host lattices at T = 5 K, respectively. 0.1% dilution improved T1 only for T < 12 K, as shown in Figure 5c, consistent with direct processes from spin–spin-based dipolar interactions being the dominant decoherence mechanism. For T > 12 K, T1 for 0.1% dilutions overlaps with 2% dilutions for both host lattices, indicating that decoherence is not limited by dipolar interactions with additional decoherence mechanisms coming in to play.
Figure 5.
(a) Inversion recovery traces and the corresponding fits used to extract T1 for 0.1Pr:BSO measured at different temperatures. (b) Echo decays and the corresponding fits used to extract Tm for 0.1Pr:BSO measured at different temperatures. (c) T1 and Tm as a function of temperature for different Pr4+ systems studied. (d) Frequency domain data of 3P ESEEM on 2Pr:BSO measured at T = 5 K and μ0H = 597.2 mT and the corresponding simulation showing the Lamour frequency of 135Ba at the field measured. (e) Specific heat data measured for 2Pr:BSO at T < 1 K and μ0H = 7 and 14 T showing the Schottky anomaly corresponding to hyperfine interaction in Pr4+ and the corresponding fits. (f) Spin–lattice relaxation rate of 0.1Pr:BSO as a function of temperature and the fits corresponding Raman and local mode-based decoherence mechanisms.
In this higher temperature regime, two-phonon processes characterized via a combination of resonant (Orbach), nonresonant (Raman), and local modes dominate.50 The Orbach process dominates when the temperature is sufficient to excite phonons that resonate with an excited state (in this case CF states). Given the first CF excited state is ∼2000 cm–1, Orbach processes should have little effect on the relaxation. Therefore, the temperature dependence of T10.1 Pr:BSO for T > 10 K was fit to a combination of Raman and local modes based on a general description of the two-phonon process which takes into account the maximum phonon energy kbθD, where θD is the characteristic Debye temperature (Figure 5f and further details in Supporting Information). The data suggests a θD = 180 K consistent with the IR-phonon spectra of BaSnO3 which identifies the lowest optical phonon mode at 135 cm–1 (195 K).51
Having now established the bounds on spin coherence lifetimes from spin–lattice relaxation, the lifetimes of the coherent superposition state of the qubit, parameterized by phase memory time Tm, were measured through two-pulse Hahn echo measurements. The echo intensity was measured as a function of 2τ as shown in Figure 5b and clearly shows an exponentially decaying signal. Tm was extracted by fitting the data to a standard mono-exponential function, yielding Tm2 Pr:BSO = 3.1 and Tm = 2.3 μs at T = 5 K. Tm2 Pr:BSO follows T1 with weak temperature dependence, while Tm2 Pr:BZO shows weaker temperature dependence compared to T1 in the temperature range T < 12 K. Similar to T1, Tm improved on dilution to 0.1%, reaching a maximum of Tm0.1 Pr:BSO = 18 and Tm = 2.5 μs at T = 5 K for both host lattices and begins to decrease at higher temperatures, reaching Tm0.1 Pr:BSO = 0.26 and Tm = 0.1 μs at T = 60 K with minimal effects of dilution for T ≳ 12. Tm is bound by T1 above T* = 40 and 60 K for 0.1Pr:BZO and 0.1Pr:BSO, respectively. Note that at low temperatures, the echo decay curves show strong electron spin-echo envelope modulation (ESEEM) from Ba nuclear spins (vide infra). The maximum Tm value extracted for 141Pr4+ is one of the largest among the RE ions (Table 1). Furthermore, coherent spin dynamics are detectable up to T* = 60 K in 0.1Pr:BSO, which is greater than all RE ions except Gd3+. This phenomenon is attributed to the high-energy first electronic state in both Pr4+ and Gd3+. However, in Gd3+ the excited state is a SOC multiplet, whereas in Pr4+, the excited state is purely CF derived (Table 1). We note here that relaxation measurements at other hyperfine transitions also yield very similar results (see Table S5 and Figures S4 S5).
Table 1. Comparison of Parameters Extracted for Pr4+ from This Work with Other 4f-Based RE Ionsa.
| RE ion | host lattice | excited state (cm–1) | AJ (MHz) | gav | T (K) | T1 (ms) | Tm (μs) | T* (K) | ref |
|---|---|---|---|---|---|---|---|---|---|
| Pr4+ | BaSnO3 | ∼2000 | ∼1800 | ∼0.58 | 5 | ∼33 | ∼18 | ∼60 | this work |
| Ce3+ | CaWO4 | 53–135 | N/A | ∼1.4 | 5 | ∼24.7 | ∼14.2 | ∼18 | (42) |
| Nd3+ | Y2SiO5 | ∼77 | ∼530 | ∼2.6 | 5 | ∼30 | ∼106 | ∼7 | (16) |
| Gd3+ | CaWO4 | ∼33,000d | ∼15 | ∼2 | 6 | ∼8 | ∼5.4 | ∼70 | (43) |
| Gd3+ | trensalb | ∼33,000d | ∼2 | 5 | ∼0.03 | ∼12 | >30 | (44) | |
| Gd3+ | sTPATCN | ∼33,000d | ∼2 | 7 | ∼0.36 | ∼18.3 | >50 | (45) | |
| Er3+ | CaWO4 | ∼19 | ∼125 | ∼5 | 3.5 | ∼7 (50)e | (11) | ||
| Yb3+c | Y2SiO5 | ∼115 | ∼500 | ∼4 | 5 | ∼7 | ∼10 (73)e | ∼9 | (18) |
| Yb3+c | trensalb | ∼500 | ∼600 | ∼3.8 | 5 | ∼0.4 | ∼0.5 | 20 | (46) |
T* corresponds to the temperature at which Tm is limited by T1 given by Tm/T1 = 1.
Molecular complex.
Value reported for 171Yb.
For Gd3+, the excited state corresponds to the SOC multiplet and not a CF excited state. Given the 8S7/2 GS, the CF splitting is usually very small. This minimizes mixing from the excited 6P7/2 and 6D7/2 SOC multiplets and has been proposed to suppress decoherence due to the vanishing orbital angular momentum.
The values in the parenthesis correspond to the maximum value reported but measured at a lower temperature of 2–3 K. For a more direct comparison, the table is constructed with values reported at the base temperature of this study at T = 5 K.
While the two host lattices BZO and BSO are isostructural, they exhibit very different T1 relaxation rates—particularly in the T < 12 K regime, indicating that an additional decoherence mechanism besides the SD from neighboring spin-flips is active. In order to understand the decoherence mechanism, a three-pulse stimulated echo technique (π/2 – τ – π/2 – TW – π/2 – τ – echo) and T = 5 K is used. Fitting the echo decay to a combination of SD linewidth (ΓSD) and relaxation time, a T1SD = 0.7 and 1.8 ms are obtained for 2Pr:BSO and 2Pr:BZO, respectively. The extracted T1 values are half of those obtained from the inversion recovery measurements. This difference indicates that besides the spin-flip process, spin-flip flops from neighboring nuclear spins are active as well. The fast Fourier transform (FFT) of the time domain data of 2Pr:BSO measured with τ = 120 ns clearly shows a peak ≈2.8 MHz, corresponding to the Larmour frequency of 135Ba (I = 3/2) in the field measured (Figure 5d). The data is well simulated by coupling between an S = 1/2 electron and the 135Ba nuclei, yielding a hyperfine coupling of Aiso135Ba = 0.8 MHz, as shown in Figure 5d.
Additionally, Hyperfine Sublevel Correlations (HYSCORE) spectroscopy further resolves the coupling to the surrounding Ba nuclei. Both host lattices show two sets of two sharp peaks, which can be simulated by coupling to both 135Ba and 137Ba (I = 3/2) nuclei, yielding A∥Ba = 0.8 MHz and A⊥ = 1.8 MHz for both nuclei and quadrupolar contributions of QBa = 3.5 for both nuclei as shown in Figure 6a,b. The key difference between the host lattices is the presence of nuclear spin bearing 117,119Sn nuclei (I = 1/2) in BSO and 91Zr nuclei (I = 5/2) in BZO in the surrounding bath of 141Pr4+. It is possible that the large nuclear spin of 91Zr explains the faster T1 relaxation rate for BZO compared to that for BSO, leading to a faster decoherence.
Figure 6.
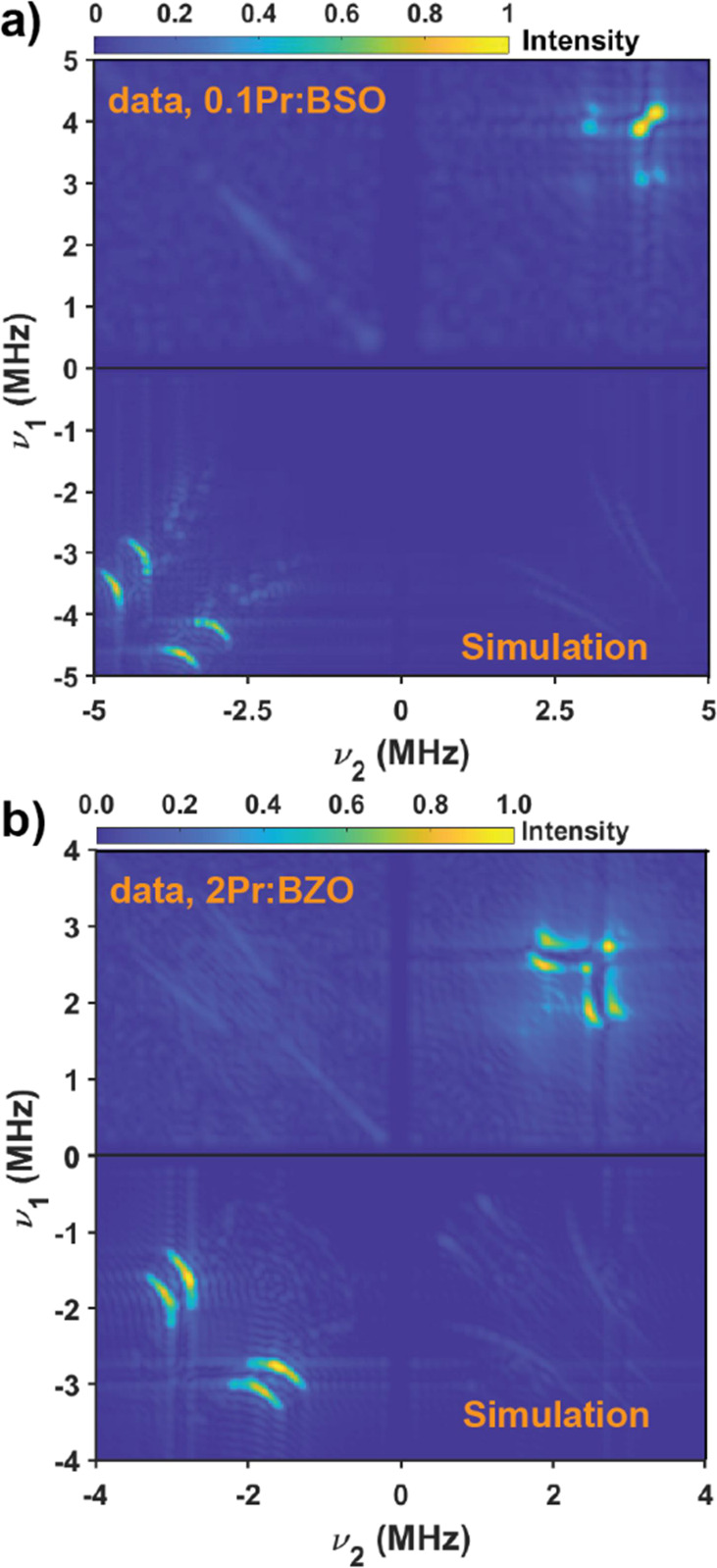
(a) HYSCORE data (top) and simulation (bottom) for 0.1Pr:BSO measured at μ0H = 901 mT (b) HYSCORE data (top) and simulation (bottom) for 2Pr:BZO measured at μ0H = 530.8 mT. All data was measured at T = 5 K.
One of the key properties of 141Pr4+ is the unusually large hyperfine interaction of ∼2000 MHz. Among the RE elements, holmium metal exhibits the largest hyperfine interaction with AJHo = 6500 MHz, followed by praseodymium metal with AJ = 4500 MHz.52 Such large hyperfine coupling interactions have been attributed to the polarization of conduction electrons by s–d mixing minimizing SOC.52 A similar argument has been invoked for a very large hyperfine interaction of AisoLu2+ ≈ 3500 MHz observed in Lu2+ molecular complexes where the spin bearing d orbitals undergoes symmetry-allowed mixing with s orbitals minimizing SOC.22 However, in the solid-state, RE ions, when doped in wide band-gap host lattices, exhibit a significantly reduced hyperfine interaction, as evidenced for Ho3+:LiYF4 with Aiso ≈ 800 MHz53 or in molecules like Ho3+ polyoxometalates with Aiso ≈ 700 MHz.54,55 This large reduction of the hyperfine interaction necessitates the need to understand the origin of the very large hyperfine coupling in 141Pr4+ and a comparison of the hyperfine interaction of 4f1 141Pr4+ with 4f2 141Pr3+.
However, since Pr3+ is a non-Kramers ion, it is often EPR silent, at least in the X-band. Therefore, specific-heat measurements were employed. The heat-capacity CN arising from a discrete set of 2I + 1 hyperfine energy levels Wm (m = I, ..., –I) occurs as a Schottky anomaly with a peak or maximum at a temperature T ≃ ⟨ΔW⟩av/k, where ⟨ΔW⟩av is the mean spacing of the energy levels and k is the Boltzmann constant. The Hamiltonian for the hyperfine Schottky contribution can be written as56
| 3 |
where A is the hyperfine interaction constant, Iz is the expectation values of I, μeff is the saturated magnetic moment, gJ is the landau g-factor, and P is the quadrupolar contribution. P for 141Pr is usually three to four orders of magnitude smaller than A and therefore can be neglected. Simply, eq 3 can be written as a function of A and μeff. By fitting the observed Schottky anomaly in the specific heat data arising from thermal depopulation of the hyperfine spin levels, experimental values of A can be extracted.
Heat-capacity measurements on Pr3+:LnCl3 yield APr3+ : LnCl3 ≃ 1089 MHz, significantly less than the Pr metal as expected.57 Following a similar approach, the heat capacity of 2Pr:BSO at μ0H = 7 and 14 T was measured (Figure 5e). Below 1 K, an upturn in specific heat is observed, which is attributed to nuclear Schottky contribution. By fitting the data to eq 3, an APr4+ ≃ 1800 MHz and a moment of ∼ 0.6 μB are extracted, which are consistent with X-band EPR (see Supporting Information for full fitting details). The APr4+ value obtained is almost twofold greater than the value reported for Pr3+ : LnCl3 or other oxide host lattices like Pr3+:Y2O315(APr3+ : Y2O3 ≃ 800 MHz, measured using spectra hall burning). On increasing the oxidation state from Pr3+ to Pr4+, two antagonistic effects compete to drive the observed hyperfine interaction with the increased nuclear charge, leading to a larger value which is diminished by the enhanced 4f metal–ligand covalency. In this system, the increase in nuclear charge appears to dominate and lead to the significant enhancement in hyperfine interaction.58
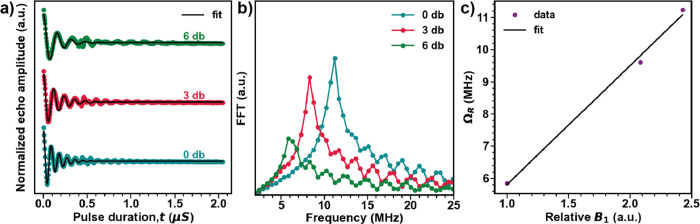
Given the relatively long Tm, coherent spin manipulations can be performed, as demonstrated by the observation of Rabi oscillations for 0.1Pr:BSO in transient nutation experiments (Figure 7a). The damping oscillations were fit with the “on-resonance” transient nutation following
| 4 |
where τR is the damping time and ΩR is the Rabi frequency. The corresponding fits are shown in Figure 7a, yielding τR ≈ 0.2 μs at 0 dB microwave power (which is significantly less than the phase memory time Tm0.1 Pr:BSO due to homogeneous and inhomogeneous broadening mechanisms). The FFT of the time domain data yields ΩR, consistent with the values obtained by fitting to eq 4 (Figure 7b). The linear relationship between ΩR and relative amplitude B1 as shown in Figure 7c establishes with certainty the provenance of the observed nutations as Rabi oscillations opposed to coherence transfer from the central spin to the dense bath of nuclear spins in the surroundings. The number of Rabi oscillations given by Nc = τR(c)ΩR with Nc ≈ 15 compares well with the value reported for 167Er3+ doped in CaWO4. The qubit figure of merit given by QM = 2ΩRTm reaches up to ∼400 for 0.1Pr:BSO at T = 5 K, the same order of magnitude as other RE qubits except for Er3+ which is in the order of 104.
Figure 7.
(a) Rabi oscillations
for 0.1Pr:BSO measured at T = 5 K at
different microwave attenuation. The black lines
correspond to fits to the data as described in the text. (b) Frequency
domain data for the nutation experiment. (c) B1 dependence of the Rabi frequency, ΩR. The
solid line is a linear fit, emphasizing the relationship B1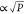 , where P is the microwave
power.
, where P is the microwave
power.
Conclusions
In conclusion, we show that Pr4+ offers the ability to chemically tune the spin–orbit coupled single-ion states as the paradigm shifts from ζSOC ≫ VCF limit to ζSOC ≪ VCF limit. CW X-band EPR measurements of Pr:BSO and Pr:BZO and CF analysis of the parent material establish the unique single-ion electronic structure of Pr4+ with a very small gav ≈ 0.6 and a large hyperfine interaction of Aiso ≈ 1800 MHz. Building on these results, pulsed X-band measurements show the possibility for coherent manipulation of the Pr4+ ion with coherence times, reaching a maximum of T1 = 33 ms and Tm = 18 μs, with spin dynamics detectable up to T* = 60 K. Therefore, in this tetravalent RE qubit, we have demonstrated long phase memory times exceeding most trivalent RE qubit systems via an alternative approach by employing the large CF energy scale of Pr4+ with a vanishing orbital angular momentum via control of the metal oxidation state. Additionally, our work establishes the IC regime as a potential avenue for designing new RE, actinide, heavy (4d and 5d) transition-metal, and main-group59,60-based quantum materials, both in solid-state and molecular systems.
Acknowledgments
The work of A.R. and H.S.L. at Georgia Tech was supported by the Beckman Foundation as part of a Beckman Young Investigator Award to H.S.L. The work of A.R. with M.M. was supported by the Georgia Tech Quantum Alliance. Some of this work was performed in part at the Materials Characterization Facility at Georgia Tech which is jointly supported by the GT Institute for Materials and the Institute for Electronics and Nanotechnology, which is a member of the National Nanotechnology Coordinated Infrastructure supported by the National Science Foundation under Grant No. ECCS-2025462. EPR studies performed by E.D.W. were supported by a grant to PNNL from the U.S. Department of Energy Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences and Biosciences, Heavy Element Chemistry program, FWP 73200.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.3c02820.
Complete experimental details and further analysis of the data (PDF)
CW data for BSO (TXT)
CW data for BZO (TXT)
EDFS data for BSO (TXT)
EDFS data for BZO (TXT)
MvH data for BaPrO3 (TXT)
MvH calculated for BaPrO3 (TXT)
MvT fit for BaPrO3 (TXT)
MvT ZFC data for BaPrO3 (TXT)
MvT FC data for BaPrO3 (TXT)
Nutation 0 db (TXT)
Nutation 3 db (TXT)
Nutation 6 db (TXT)
Nutation FFT 0 db (TXT)
Nutation FFT 3 db (TXT)
Nutation FFT 6 db (TXT)
The authors declare no competing financial interest.
Supplementary Material
References
- DiVincenzo D. P. The physical implementation of quantum computation. Fortschr. Phys.: Prog. Phys. 2000, 48, 771–783. . [DOI] [Google Scholar]
- Devoret M. H.; Schoelkopf R. J. Superconducting circuits for quantum information: an outlook. Science 2013, 339, 1169–1174. 10.1126/science.1231930. [DOI] [PubMed] [Google Scholar]
- Wright K.; Beck K. M.; Debnath S.; Amini J.; Nam Y.; Grzesiak N.; Chen J.-S.; Pisenti N.; Chmielewski M.; Collins C.; Hudek K. M.; Mizrahi J.; Wong-Campos J. D.; Allen S.; Apisdorf J.; Solomon P.; Williams M.; Ducore A. M.; Blinov A.; Kreikemeier S. M.; Chaplin V.; Keesan M.; Monroe C.; Kim J. Benchmarking an 11-qubit quantum computer. Nat. Commun. 2019, 10, 5464. 10.1038/s41467-019-13534-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarma S. D.; Freedman M.; Nayak C. Majorana zero modes and topological quantum computation. npj Quantum Inf. 2015, 1, 15001. 10.1038/npjqi.2015.1. [DOI] [Google Scholar]
- Widmann M.; Lee S.-Y.; Rendler T.; Son N. T.; Fedder H.; Paik S.; Yang L.-P.; Zhao N.; Yang S.; Booker I.; Denisenko A.; Jamali M.; Momenzadeh S. A.; Gerhardt I.; Ohshima T.; Gali A.; Janzén E.; Wrachtrup J. Coherent control of single spins in silicon carbide at room temperature. Nat. Mater. 2015, 14, 164–168. 10.1038/nmat4145. [DOI] [PubMed] [Google Scholar]
- Koehl W. F.; Buckley B. B.; Heremans F. J.; Calusine G.; Awschalom D. D. Room temperature coherent control of defect spin qubits in silicon carbide. Nature 2011, 479, 84–87. 10.1038/nature10562. [DOI] [PubMed] [Google Scholar]
- Pla J. J.; Tan K. Y.; Dehollain J. P.; Lim W. H.; Morton J. J.; Jamieson D. N.; Dzurak A. S.; Morello A. A single-atom electron spin qubit in silicon. Nature 2012, 489, 541–545. 10.1038/nature11449. [DOI] [PubMed] [Google Scholar]
- Julsgaard B.; Grezes C.; Bertet P.; Mølmer K. Quantum memory for microwave photons in an inhomogeneously broadened spin ensemble. Phys. Rev. Lett. 2013, 110, 250503 10.1103/PhysRevLett.110.250503. [DOI] [PubMed] [Google Scholar]
- Kane B. E. A silicon-based nuclear spin quantum computer. Nature 1998, 393, 133–137. 10.1038/30156. [DOI] [Google Scholar]
- Zadrozny J. M.; Niklas J.; Poluektov O. G.; Freedman D. E. Multiple quantum coherences from hyperfine transitions in a vanadium (IV) complex. J. Am. Chem. Soc. 2014, 136, 15841–15844. 10.1021/ja507846k. [DOI] [PubMed] [Google Scholar]
- Bertaina S.; Gambarelli S.; Tkachuk A.; Kurkin I.; Malkin B.; Stepanov A.; Barbara B. Rare-earth solid-state qubits. Nat. Nanotechnol. 2007, 2, 39–42. 10.1038/nnano.2006.174. [DOI] [PubMed] [Google Scholar]
- Newman D. J. Theory of lanthanide crystal fields. Adv. Phys. 1971, 20, 197–256. 10.1080/00018737100101241. [DOI] [Google Scholar]
- Paddison J. A.; Daum M.; Dun Z.; Ehlers G.; Liu Y.; Stone M. B.; Zhou H.; Mourigal M. Continuous excitations of the triangular-lattice quantum spin liquid YbMgGaO4. Nat. Phys. 2017, 13, 117–122. 10.1038/nphys3971. [DOI] [Google Scholar]
- Bordelon M. M.; Kenney E.; Liu C.; Hogan T.; Posthuma L.; Kavand M.; Lyu Y.; Sherwin M.; Butch N. P.; Brown C.; Graf M. J.; Balents L.; Wilson S. D. Field-tunable quantum disordered ground state in the triangular-lattice antiferromagnet NaYbO2. Nat. Phys. 2019, 15, 1058–1064. 10.1038/s41567-019-0594-5. [DOI] [Google Scholar]
- Serrano D.; Deshmukh C.; Liu S.; Tallaire A.; Ferrier A.; de Riedmatten H.; Goldner P. Coherent optical and spin spectroscopy of nanoscale Pr3+: Y2O3. Phys. Rev. B: Condens. Matter 2019, 100, 144304 10.1103/PhysRevB.100.144304. [DOI] [Google Scholar]
- Wolfowicz G.; Maier-Flaig H.; Marino R.; Ferrier A.; Vezin H.; Morton J. J.; Goldner P. Coherent storage of microwave excitations in rare-earth nuclear spins. Phys. Rev. Lett. 2015, 114, 170503 10.1103/PhysRevLett.114.170503. [DOI] [PubMed] [Google Scholar]
- Rakhmatullin R.; Kurkin I.; Mamin G.; Orlinskii S.; Gafurov M.; Baibekov E.; Malkin B.; Gambarelli S.; Bertaina S.; Barbara B. Coherent spin manipulations in Yb3+: CaWO4 at X-and W-band EPR frequencies. Phys. Rev. B: Condens. Matter 2009, 79, 172408 10.1103/PhysRevB.79.172408. [DOI] [Google Scholar]
- Lim H.-J.; Welinski S.; Ferrier A.; Goldner P.; Morton J. Coherent spin dynamics of ytterbium ions in yttrium orthosilicate. Phys. Rev. B: Condens. Matter 2018, 97, 064409 10.1103/PhysRevB.97.064409. [DOI] [Google Scholar]
- von Kugelgen S.; Freedman D. E. A chemical path to quantum information. Science 2019, 366, 1070–1071. 10.1126/science.aaz4044. [DOI] [PubMed] [Google Scholar]
- Atzori M.; Sessoli R. The second quantum revolution: role and challenges of molecular chemistry. J. Am. Chem. Soc. 2019, 141, 11339–11352. 10.1021/jacs.9b00984. [DOI] [PubMed] [Google Scholar]
- Leuenberger M. N.; Loss D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. 10.1038/35071024. [DOI] [PubMed] [Google Scholar]
- Kundu K.; White J. R.; Moehring S. A.; Yu J. M.; Ziller J. W.; Furche F.; Evans W. J.; Hill S. A 9.2-GHz clock transition in a Lu(II) molecular spin qubit arising from a 3,467-MHz hyperfine interaction. Nat. Chem. 2022, 14, 392–397. 10.1038/s41557-022-00894-4. [DOI] [PubMed] [Google Scholar]
- Ariciu A.-M.; Woen D. H.; Huh D. N.; Nodaraki L. E.; Kostopoulos A. K.; Goodwin C. A.; Chilton N. F.; McInnes E. J.; Winpenny R. E.; Evans W. J.; Tuna F. Engineering electronic structure to prolong relaxation times in molecular qubits by minimising orbital angular momentum. Nat. Commun. 2019, 10, 3330. 10.1038/s41467-019-11309-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice N. T.; Popov I. A.; Russo D. R.; Bacsa J.; Batista E. R.; Yang P.; Telser J.; La Pierre H. S. Design, isolation, and spectroscopic analysis of a tetravalent terbium complex. J. Am. Chem. Soc. 2019, 141, 13222–13233. 10.1021/jacs.9b06622. [DOI] [PubMed] [Google Scholar]
- Rice N. T.; Popov I. A.; Carlson R. K.; Greer S. M.; Boggiano A. C.; Stein B. W.; Bacsa J.; Batista E. R.; Yang P.; La Pierre H. S. Spectroscopic and electrochemical characterization of a Pr4+ imidophosphorane complex and the redox chemistry of Nd3+ and Dy3+ complexes. Dalton Trans. 2022, 51, 6696–6706. 10.1039/D2DT00758D. [DOI] [PubMed] [Google Scholar]
- Willauer A. l. R.; Palumbo C. T.; Fadaei-Tirani F.; Zivkovic I.; Douair I.; Maron L.; Mazzanti M. Accessing the+ IV oxidation state in molecular complexes of praseodymium. J. Am. Chem. Soc. 2020, 142, 5538–5542. 10.1021/jacs.0c01204. [DOI] [PubMed] [Google Scholar]
- Palumbo C. T.; Zivkovic I.; Scopelliti R.; Mazzanti M. Molecular complex of Tb in the+ 4 oxidation state. J. Am. Chem. Soc. 2019, 141, 9827–9831. 10.1021/jacs.9b05337. [DOI] [PubMed] [Google Scholar]
- Gompa T. P.; Ramanathan A.; Rice N. T.; La Pierre H. S. The chemical and physical properties of tetravalent lanthanides: Pr, Nd, Tb, and Dy. Dalton Trans. 2020, 49, 15945–15987. 10.1039/D0DT01400A. [DOI] [PubMed] [Google Scholar]
- Ramanathan A.; Kaplan J.; Sergentu D.-C.; Branson J. A.; Ozerov M.; Kolesnikov A. I.; Minasian S. G.; Autschbach J.; Freeland J. W.; Jiang Z.; Mourigal M.; La Pierre H. S. Chemical design of electronic and magnetic energy scales of tetravalent praseodymium materials. Nat. Commun. 2023, 14, 3134. 10.1038/s41467-023-38431-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlosshauer M. A.Decoherence: and the quantum-to-classical transition; Springer Science & Business Media, 2007. [Google Scholar]
- Chiesa A.; Cugini F.; Hussain R.; Macaluso E.; Allodi G.; Garlatti E.; Giansiracusa M.; Goodwin C.; Ortu F.; Reta D.; Skelton J. M.; Guidi T.; Santini P.; Solzi M.; de Renzi R.; Mills D. P.; Chilton N. F.; Carretta S. Understanding magnetic relaxation in single-ion magnets with high blocking temperature. Phys. Rev. B: Condens. Matter 2020, 101, 174402 10.1103/PhysRevB.101.174402. [DOI] [Google Scholar]
- Sinha M.; Pearson T. J.; Reeder T. R.; Vivanco H. K.; Freedman D. E.; Phelan W. A.; McQueen T. M. Introduction of spin centers in single crystals of Ba2CaWO6−δ. Phys. Rev. Mater. 2019, 3, 125002 10.1103/PhysRevMaterials.3.125002. [DOI] [Google Scholar]
- Stevenson P.; Phenicie C. M.; Gray I.; Horvath S. P.; Welinski S.; Ferrenti A. M.; Ferrier A.; Goldner P.; Das S.; Ramesh R.; Cava R. J.; de Leon N. P.; Thompson J. D. Erbium-implanted materials for quantum communication applications. Phys. Rev. B: Condens. Matter 2022, 105, 224106 10.1103/PhysRevB.105.224106. [DOI] [Google Scholar]
- Bayliss S.; Deb P.; Laorenza D.; Onizhuk M.; Galli G.; Freedman D.; Awschalom D. Enhancing Spin Coherence in Optically Addressable Molecular Qubits through Host-Matrix Control. Phys. Rev. X 2022, 12, 031028 10.1103/PhysRevX.12.031028. [DOI] [Google Scholar]
- Ramanathan A.; Kaplan J.; Sergentu D.-C.; Branson J. A.; Ozerov M.; Kolesnikov A. I.; Minasian S. G.; Autschbach J.; Freeland J. W.; Jiang Z., Chemical Design of Electronic and Magnetic Energy Scales in Tetravalent Praseodymium. 2022, arXiv preprint arXiv:2212.10401. [DOI] [PMC free article] [PubMed]
- Hinatsu Y. Magnetic studies on BaUO3, BaPrO3 and BaTbO3. J. Alloys Compd. 1993, 193, 113–115. 10.1016/0925-8388(93)90325-H. [DOI] [Google Scholar]
- Bickel M.; Goodman G.; Soderholm L.; Kanellakopulos B. The magnetic susceptibility of Pr4+ in BaPrO3: Evidence of long-range magnetic order. J. Solid State Chem. 1988, 76, 178–185. 10.1016/0022-4596(88)90205-8. [DOI] [Google Scholar]
- Maekawa T.; Kurosaki K.; Yamanaka S. Thermal and mechanical properties of polycrystalline BaSnO3. J. Alloys Compd. 2006, 416, 214–217. 10.1016/j.jallcom.2005.08.032. [DOI] [Google Scholar]
- Boothroyd A.; Gardiner C.; Lister S.; Santini P.; Rainford B.; Noailles L.; Currie D.; Eccleston R.; Bewley R. Localized 4f States and Dynamic Jahn-Teller Effect in PrO2. Phys. Rev. Lett. 2001, 86, 2082. 10.1103/PhysRevLett.86.2082. [DOI] [PubMed] [Google Scholar]
- Daum M. J.; Ramanathan A.; Kolesnikov A. I.; Calder S.; Mourigal M.; La Pierre H. S. Collective excitations in the tetravalent lanthanide honeycomb antiferromagnet Na2PrO3. Phys. Rev. B: Condens. Matter 2021, 103, L121109 10.1103/PhysRevB.103.L121109. [DOI] [Google Scholar]
- Stevens K. Matrix elements and operator equivalents connected with the magnetic properties of rare earth ions. Proc. Phys. Soci., Sect. A 1952, 65, 209. 10.1088/0370-1298/65/3/308. [DOI] [Google Scholar]
- Gafurov M.; Kurkin I.; Baibekov E. Coherence times of Ce3+ spin states in CaWO4 crystal. Magnet. Reson. Solids 2019, 21, 1. 10.26907/mrsej-19501. [DOI] [PubMed] [Google Scholar]
- Baibekov E.; Gafurov M.; Zverev D.; Kurkin I.; Rodionov A.; Malkin B.; Barbara B. Coherent spin dynamics in a gadolinium-doped CaWO4 crystal. Phys. Rev. B: Condens. Matter 2017, 95, 064427 10.1103/PhysRevB.95.064427. [DOI] [Google Scholar]
- Buch C. D.; Kundu K.; Marbey J. J.; van Tol J.; Weihe H.; Hill S.; Piligkos S. Spin–Lattice Relaxation Decoherence Suppression in Vanishing Orbital Angular Momentum Qubits. J. Am. Chem. Soc. 2022, 144, 17597–17603. 10.1021/jacs.2c07057. [DOI] [PubMed] [Google Scholar]
- Shah A.; Roux A.; Starck M.; Mosely J. A.; Stevens M.; Norman D. G.; Hunter R. I.; El Mkami H.; Smith G. M.; Parker D. A gadolinium spin label with both a narrow central transition and short tether for use in double electron electron resonance distance measurements. Inorg. Chem. 2019, 58, 3015–3025. 10.1021/acs.inorgchem.8b02892. [DOI] [PubMed] [Google Scholar]
- Pedersen K. S.; Ariciu A.-M.; McAdams S.; Weihe H.; Bendix J.; Tuna F.; Piligkos S. Toward molecular 4f single-ion magnet qubits. J. Am. Chem. Soc. 2016, 138, 5801–5804. 10.1021/jacs.6b02702. [DOI] [PubMed] [Google Scholar]
- Popova M.; Klimin S.; Malkin B.; Kasatkina L.; Cao G.; Crow J. Crystal field and spectrum of Pr4+ in BaPrO3. Phys. Lett. A 1996, 223, 308–312. 10.1016/S0375-9601(96)00734-7. [DOI] [Google Scholar]
- Runciman W.; Wybourne B. Spectra of Trivalent Praseodymium and Thulium Ions. J. Chem. Phys. 1959, 31, 1149–1150. 10.1063/1.1730539. [DOI] [Google Scholar]
- Stoll S.; Schweiger A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. 10.1016/j.jmr.2005.08.013. [DOI] [PubMed] [Google Scholar]
- Orbach R. Spin-lattice relaxation in rare-earth salts. Proc. R. Soc. London, Ser. A 1961, 264, 458–484. 10.1098/rspa.1961.0211. [DOI] [Google Scholar]
- Stanislavchuk T.; Sirenko A.; Litvinchuk A.; Luo X.; Cheong S.-W. Electronic band structure and optical phonons of BaSnO3 and Ba0. 97La0. 03SnO3 single crystals: Theory and experiment. J. Appl. Phys. 2012, 112, 044108 10.1063/1.4748309. [DOI] [Google Scholar]
- Bleaney B. Hyperfine Interactions in Rare-Earth Metals. J. Appl. Phys. 1963, 34, 1024–1031. 10.1063/1.1729355. [DOI] [Google Scholar]
- Popova M.; Boldyrev K. High-resolution spectra of LiYF4: Ho3+ in a magnetic field. Opt. Mater. 2017, 63, 101–104. 10.1016/j.optmat.2016.06.003. [DOI] [Google Scholar]
- Shiddiq M.; Komijani D.; Duan Y.; Gaita-Ariño A.; Coronado E.; Hill S. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 2016, 531, 348–351. 10.1038/nature16984. [DOI] [PubMed] [Google Scholar]
- Ghosh S.; Datta S.; Friend L.; Cardona-Serra S.; Gaita-Ariño A.; Coronado E.; Hill S. Multi-frequency EPR studies of a mononuclear holmium single-molecule magnet based on the polyoxometalate [HoIII(W5O18)2]9–. Dalton Trans. 2012, 41, 13697–13704. 10.1039/c2dt31674a. [DOI] [PubMed] [Google Scholar]
- Gregers-Hansen P.; Krusius M.; Pickett G. Magnetic Properties of Praseodymium in Magnetic Fields Determined from the Nuclear Heat Capacity and Applied to Nuclear Cooling. Phys. Rev. Lett. 1972, 29, 420. 10.1103/PhysRevLett.29.420. [DOI] [Google Scholar]
- Hutchison C. A. Jr.; Wong E. Paramagnetic resonance in rare earth trichlorides. J. Chem. Phys. 1958, 29, 754–760. 10.1063/1.1744587. [DOI] [Google Scholar]
- Gompa T. P.; Greer S. M.; Rice N. T.; Jiang N.; Telser J.; Ozarowski A.; Stein B. W.; La Pierre H. S. High-Frequency and-Field Electron Paramagnetic Resonance Spectroscopic Analysis of Metal–Ligand Covalency in a 4f7 Valence Series (Eu2+, Gd3+, and Tb4+). Inorg. Chem. 2021, 60, 9064–9073. 10.1021/acs.inorgchem.1c01062. [DOI] [PubMed] [Google Scholar]
- Mansikkamäki A. Theoretical study of phenylbismuth anion as a blueprint for main-group single-molecule magnets. Chem. Commun. 2023, 59, 1837–1840. 10.1039/D3CC00042G. [DOI] [PubMed] [Google Scholar]
- Pang Y.; Nöthling N.; Leutzsch M.; Kang L.; Bill E.; van Gastel M.; Reijerse E.; Goddard R.; Wagner L.; SantaLucia D.. A “non-magnetic” triplet bismuthinidene enabled by relativity. 2022, ChemRxiv. 10.26434/chemrxiv-2022-d3jl7 (accessed February 2023). [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.