The liquid-to-solid transition of FUS is promoted by the condensate surface

Significance

Cellular proteins can undergo liquid–liquid phase separation forming protein-rich functional condensates. This process enables a range of concentration-dependent reactions, promotes protein–protein interactions, but also increases the risk of dysfunctional aggregation, leading to disease-associated aberrant structures which no longer exhibit rapid reversibility of functional condensates. It is therefore crucial to monitor condensate dynamics, as they directly affect pathological states. Here, we developed two optical techniques to probe the local condensates dynamics at high resolution and revealed that condensates convert to a solid gel with inhomogeneous structures in both temporal and spatial dimensions. Importantly, we demonstrated that this transition initiated at the condensates interface, providing the basis for strategies to influence this process when it occurs in disease.

Abstract

A wide range of macromolecules can undergo phase separation, forming biomolecular condensates in living cells. These membraneless organelles are typically highly dynamic, formed reversibly, and carry out essential functions in biological systems. Crucially, however, a further liquid-to-solid transition of the condensates can lead to irreversible pathological aggregation and cellular dysfunction associated with the onset and development of neurodegenerative diseases. Despite the importance of this liquid-to-solid transition of proteins, the mechanism by which it is initiated in normally functional condensates is unknown. Here we show, by measuring the changes in structure, dynamics, and mechanics in time and space, that single-component FUS condensates do not uniformly convert to a solid gel, but rather that liquid and gel phases coexist simultaneously within the same condensate, resulting in highly inhomogeneous structures. Furthermore, our results show that this transition originates at the interface between the condensate and the dilute continuous phase, and once initiated, the gelation process propagates toward the center of the condensate. To probe such spatially inhomogeneous rheology during condensate aging, we use a combination of established micropipette aspiration experiments together with two optical techniques, spatial dynamic mapping and reflective confocal dynamic speckle microscopy. These results reveal the importance of the spatiotemporal dimension of the liquid-to-solid transition and highlight the interface of biomolecular condensates as a critical element in driving pathological protein aggregation.

Macromolecular density transitions, of which liquid–liquid phase separation (LLPS) is a prototypical example, result from the spontaneous decomposition of a uniform solution into two aqueous phases: a dense phase rich in molecules and a dilute one depleted in molecules. While phase separation phenomena have been observed for many polymer systems, their central role in functional biology was first recognized in germline P granules (1). Subsequently, many other such condensates have been identified, many of which contribute to essential biological processes, such as driving the DNA damage response (2), controlling nuclear trafficking (3), and signal transduction (4). The dynamic nature of these membraneless organelles is a key characteristic required for favoring chemical reactions within the granules and molecular exchange with the dilute phase outside. However, the high local concentration within the protein-rich phase of condensates has the potential also to enhance aberrant protein–protein interactions and therefore increases the propensity of aggregation that can lead to the formation of irreversible pathological structures (5–7). Such irreversible aggregation, initiated from initially reversible biomolecular condensates, plays a crucial role in neurodegeneration; for instance, α-synuclein aggregates, linked to Parkinson’s disease pathogenesis, have been found to nucleate through from a condensate precursor in vivo (8). Furthermore, tau, a protein associated with Alzheimer’s disease, forms irreversible intracellular deposits in disease which originate from initially reversible condensate states (9, 10). Similarly, Transactive response DNA-binding protein of 43 kDa (TDP-43) and the fused in sarcoma (FUS) proteins, connected to amyotrophic lateral sclerosis and frontotemporal lobar degeneration (ALS/FTLD), also form fibrillar aggregates in disease, which stem from originally reversible and functional condensates (5, 11–13). It is, therefore of crucial importance to understand the determinants of the liquid-to-solid transition (LST) of condensates, as they have direct implications for the emergence of pathological states through incorrectly assembled proteins. To date, the spatiotemporal dimension of LST has not been explored in detail and condensates, especially the ones formed with one protein, are generally considered as homogenous droplets rich in molecules (1, 12, 14–16) that undergo gelation. Only few recent works attempt to quantify the mechanical properties of aged condensates, for example FUS (17) and α-synuclein (18), in which an increase in intermolecular β-sheet and fibrils formation over time is also observed. Here, by deploying advanced characterization approaches, we show that single-component condensates do not uniformly convert to a solid gel, but rather liquid and gel phases coexist simultaneously within the same condensate, resulting in highly inhomogeneous structures. Importantly, our results also suggest that there is a propensity of the LST to initiate from the interface and propagate toward the center of the condensates. It has been shown that protein aggregation from dilute solutions can be driven by interfacial energy (19). When proteins form biomolecular condensates, this gives rise to a new interface between the dilute and dense phases with a surface tension which can be as high as 1 mN/m (20). The results in this paper show that this interfacial energy can drive the liquid-to-solid phase transition to form core-shell structure in condensates. These findings of the intricate role of spatiotemporal dynamics further highlight the complexity of the patterns associated with the LST and reveal the interface of the condensates as a crucial element in this process.

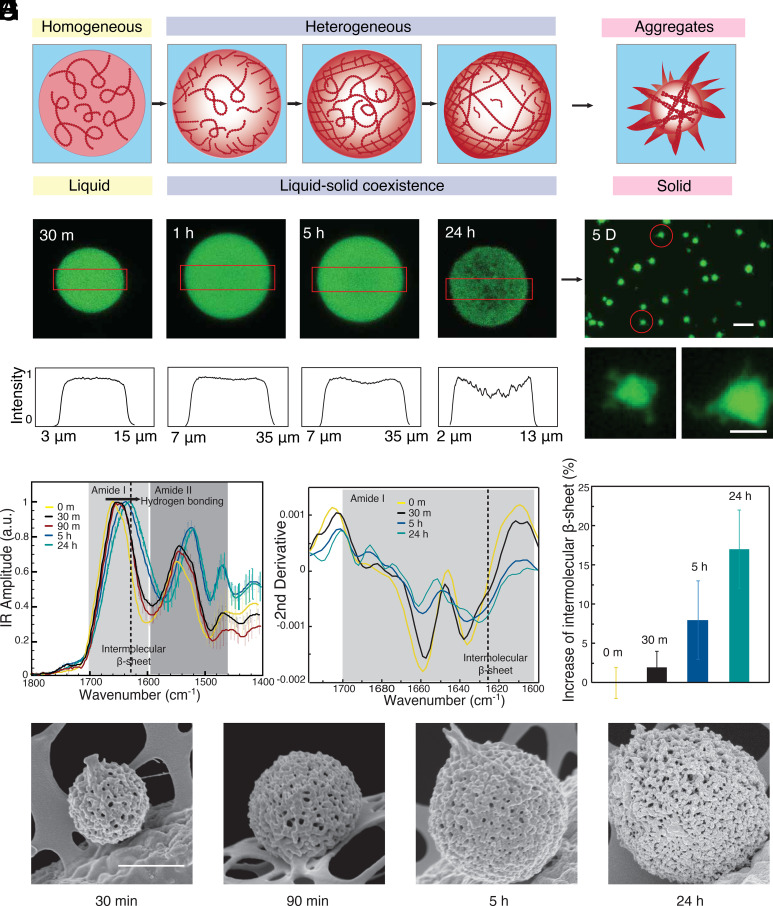
We focus our study on a key protein implicated in neurodegenerative diseases, FUS. For imaging purpose and consistency within the experiments, we use GFP-labeled FUS throughout the study. By using confocal imaging, we observe the phase transitions of condensates, from liquid droplets to liquid–solid coexisting gel to fibrillar solid (Fig. 1A). By focusing on the density from the distribution of the fluorescence intensity, we can detect changes early in the spatial distribution of molecules as a function of aging of the condensate (Fig. 1B). During the first 30 min, the protein molecules are uniformly distributed in the condensates. However, signs of spatial inhomogeneities can be detected after 5 h. After 24 h of incubation, the condensates become less homogeneous and in some cases present a weak core-shell structure (Fig. 1 B and C). Moreover, through confocal 3D scanning, the condensates show a loosely packed network (Movie S1). After further aging for 5 d, clearly defined filamentous structures form around the condensates (Fig. 1D), characteristics of the irreversible aggregation, representing the solid end state of the transition, consistent with previous studies (5).

Fig. 1.

Spatially inhomogeneities during the aging of FUS condensates. (A) The FUS protein undergoes liquid–liquid phase separation in response to changes in ionic strength. During subsequent maturation, the density within the condensates changes from homogenous to locally heterogeneous (B) Confocal images of the density distribution within a condensate during maturation at 30 min, 1 h, 5 h, and 24 h. (C) The fluorescence intensity profile from confocal microscopy at the center plane of the condensates (red boxes indicate the evaluated area in B). (D) Fluorescence images of fibrillar aggregates formed at the final stages of the liquid-to-solid transition after maturation for 5 d. (Scale bars are 20 and 5 μm in Top and Bottom.) (E) Bulk IR absorption spectra and (F) their second derivatives of condensates with different aging times. (G) Relative increase in intermolecular β-sheet with aging time, error bar: CI deriving from the integration algorithm of the second derivative. (H) SEM images of condensate with different maturation times. (Scale bar, 1 μm.)

We next perform bulk infrared spectroscopy (FTIR) on the liquid–liquid phase separated samples to characterize the molecular level changes related to the liquid-to-solid transition. The spectra show a net shift of both amide band I and amide band II toward lower wavenumbers as a function of the incubation time from 30 min to 24 h, thus demonstrating the formation of hydrogen bonding associated with intermolecular β-sheet (21–23) (Fig. 1E and SI Appendix, Fig. S1). To further evaluate the secondary and quaternary structural changes that the LLPS droplets undergo as a function of the incubation time, we perform a second derivative analysis of the amide band I (24, 25). The second derivative spectra show a continuous decrease in a-helix and random coil structure (1,660 to 1,640 cm⁻¹) versus an increase in intermolecular β-sheet structure (1,630 to 1,620 cm⁻¹) as a function of the incubation time (Fig. 1F). The relative increase in the intermolecular b-sheets with aging time compared to the native droplets is evaluated by direct integration of the area of the structural contributions in the second derivative spectra and is summarized in Fig. 1G. The increase in intermolecular β-sheet and the continuous shift at lower wavenumbers demonstrate the formation of longer intermolecular β-sheets and a denser network of hydrogen bonds, underlying the mechanism of the LST (21, 22). We next observe these condensates under SEM after flash freezing and drying. We find well-defined fibrillar networks covered all over the condensates (Fig. 1H). Thus, these results show a liquid-to-solid transition of the condensates, contributed by the intermolecular β-sheet formation with a fibrillar network.

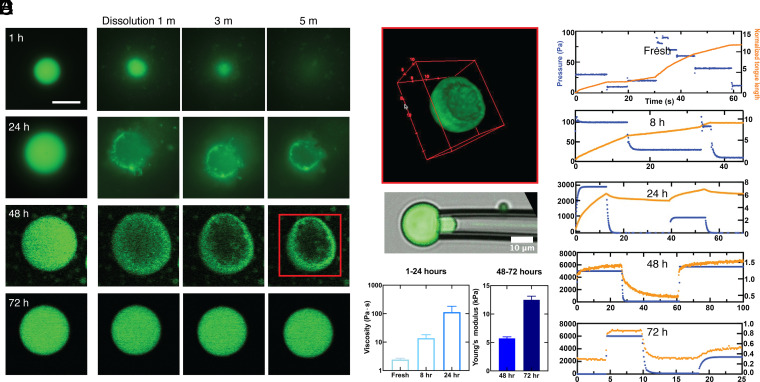
After having characterized the overall liquid-to-solid transition, we focus on probing the spatiotemporal dynamics associated with this process. First, we probe for heterogeneity developing within the condensates during aging by conducting a set of dissolution experiments on condensates (Fig. 2 A and B). To probe for the formation of any irreversible interactions between protein molecules in the condensate, we add a solution with a high-concentration KCl solution to the condensates at different points during the aging process (Fig. 2A). Freshly formed condensates aged for 1 h rapidly dissolve upon the addition of 1M KCl solution (Fig. 2 B, Top row), as predicted by the phase diagram for the LLPS of FUS measured in previous studies (26). By contrast, when 1M KCl solution is added to condensates aged for 72 h, no overall dissolution is observed (Fig. 2 B, Bottom row), indicating that this system is no longer described by the phase diagram characteristic of liquid FUS condensates and that formation of stronger irreversible intermolecular interactions has taken place. To investigate the intermediate stages of this transition, we repeat the dissolution experiment with samples aged for 24 h and 48 h (Fig. 2 B, Middle rows). Surprisingly, when 1M KCl is added to the 24-h condensates, only the center of the condensate dissolves, leaving behind a thin shell of gelled material. When the condensates aged for 48 h are subjected to high concentration KCl, the center dissolves as seen in the 24-h sample. However, again a thicker shell is left behind (Fig. 2B at 5 min). From confocal 3D reconstructed images, a clear shell structure is observed (Fig. 2C). Many condensates (>80%) show the core-shell structure after the dissolution (SI Appendix, Fig. S2). Taken together, these results strongly suggest that the gelation of the condensates initially happens at the interface and propagates inward with time.

Fig. 2.

Dissolution and micromechanics of condensates. (A) Condensates incubated at 25 °C for 1 h, 24 h, 48 h, and 72 h. (B) Dissolution of condensates monitored after addition of a solution 1M KCl in volume ratio 1:10 for 1, 3, and 5 min. (C) 3D reconstructed image of a condensate incubated for 48 h after KCl partial dissolution from KCl treatment as in B. (D) Micropipette aspiration of a condensate. (E) The relationship between tongue length and the elapsed time under different pressure during the maturation of the condensates from fresh to 72 h. (F) The increase in viscosity of condensates from fresh to 24 h (Left) and the increase in elasticity of condensates incubated for 48 h and 72 h are evaluated from the data in E.

We use micropipette aspiration experiments to connect these changing spatial patterns to variations in the mechanical properties of the condensates during aging (20). The condensates are aspirated using a glass micropipette with an inner diameter of 4 to 10 μm. Several negative pressure steps are applied using a vacuum controller, and the length of the condensate drawn into the glass pipette is measured. This approach determines both the strain and the stress associated with the deformation and therefore probes the rheological response of individual condensates. Under constant-pressure aspiration, a liquid-like condensate flows into the glass pipette with a constant velocity, resulting in a linear increase in the length of the “tongue” as a function of elapsed time. The resultant strain rate is proportional to the applied pressure and viscosity of the liquid-like condensate. By contrast, a solid-like condensate deforms rapidly when the pressure changes but then reaches a constant value. In this case, the strain, determined by the tongue length, is proportional to the stress, determined by the applied pressure, providing a measure of the elastic modulus of the condensate. By using this method, the condensates are probed at different aging stages.

Upon formation, the fresh FUS condensate is a liquid with a viscosity of the order of 1 Pa⋅s. In the following 8 h, the condensates remain liquid-like with gradually increasing viscosity. After 24 h, we measure an increase in the viscosity to about 50 times its initial value, and the elastic component remains too small to be measured precisely. After 48 h, the condensates exhibit an elasticity-dominant mechanical response with a viscoelastic creep behavior. The elastic modulus is ~5 kPa. After 72 h, the elastic modulus increases to ~12 kPa. We attribute the dramatic change in the mechanical properties of FUS condensates to the formation of a solid gel network within them.

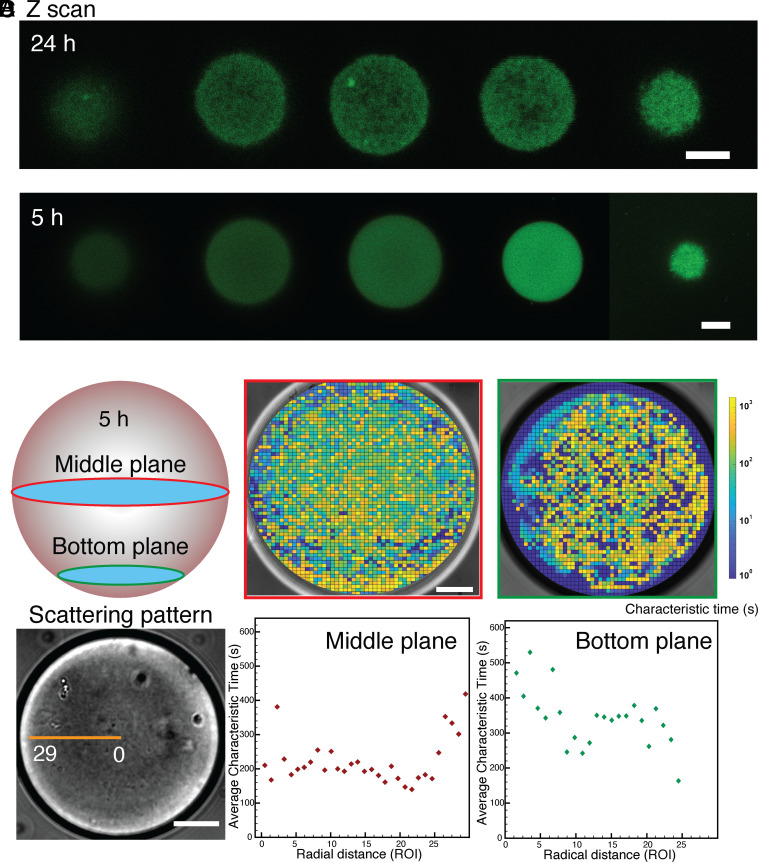
From confocal 3D scanning, it is observed that there is commonly a heterogeneous organization inside the condensates after 24-h incubation, where a weak gel network structure has developed (Fig. 3A). However, this structure can be less readily apparent for the condensates aged for less time (Fig. 3B). To unveil and quantify internal heterogeneities of the condensates we develop and apply a bespoke optical technique, spatial dynamic mapping (SDM). The condensates exhibit refractive index fluctuations due to thermal fluctuations that can be observed when the numerical aperture of the condenser lens is reduced. Thus, light traveling through a condensate forms patterns that vary over time, which can be analyzed to extract information regarding their internal dynamics and, potentially, their internal structure. We divide the condensates into small regions of interest (ROIs) and evaluate the spatial variance, ${\sigma }^2\left(\mathrm{\Delta }t\right)$ , in real space from each ROI within each frame. This is a key characteristic that differentiate our technique from other established approaches such as differential dynamic microscopy (DDM) (27, 28) and that allow us to reduce the size of the ROIs while still being able to extract meaningful dynamics information thus enhancing the spatial resolution critical for this study. We use a fast camera to record long bright field sequences of images at a high frame rate. This allows us to explore simultaneously fast (acquiring at high frame rates) and slow dynamics (by acquiring for a long time). Thus, we can extrapolate the characteristic decay time from the exponential behavior of ${\sigma }^2\left(\mathrm{\Delta }t\right)$ for each ROI, and we use this to create spatial maps such as the one in Fig. 3C. From these maps, it is possible to identify the coexistence of areas within the condensate that exhibit a liquid-like (characterized by a short decay time) and solid-like (longer decay time) behavior (detailed calculation and calibration can be found in SI Appendix, Fig. S3). In this study, SDM can reliably discriminate between characteristic decays spanning three orders of magnitude, ranging between one and a thousand seconds, within the same FUS condensate. We further perform SDM in the middle plane and at the bottom plane of a condensate exploiting the ability of SDM to extract the local dynamics of a thin slice of the condensate and thus reconstructing 3D information and find that the bottom plane (closer to the interface and therefore representative of the outer shell of the condensate) shows slower dynamics with higher heterogeneity. The condensates present a very high contact angle (about 160°, see SI Appendix, Fig. S4) on the glass slide and this allows us to extract information from the bottom plane of the condensate without being affected by wetting. We then plot the radial distribution of the characteristic decay time as a function of the distance from the center for both the middle and bottom planes. The middle plane demonstrates faster dynamics (i.e., shorter characteristic time) at the center and slower dynamics (i.e., longer characteristic time) close to the interface of the condensate (Fig. 3D). On the other hand, the bottom plane shows a slow dynamics whose characteristic time is closer in value to the decay measured at the interface of the condensate in the middle plane. These results confirm the core-shell structure of the condensates and, thus, our hypothesis of the initiation of the liquid-to-solid transition from the interface.

Fig. 3.

Confocal z-scan of condensates incubated for (A) 24 h (Scale bar, 5 µm) and (B) 5 h (Scale bar, 10 µm). (C) Spatial dynamic mapping of the characteristic correlation time of the condensate at Middle and Bottom planes respectively with aging time 5 h (Scale bar, 20 µm). (D) Radial distribution of the characteristic time from the center of the condensate to the edge within a condensate aged for 5 h.

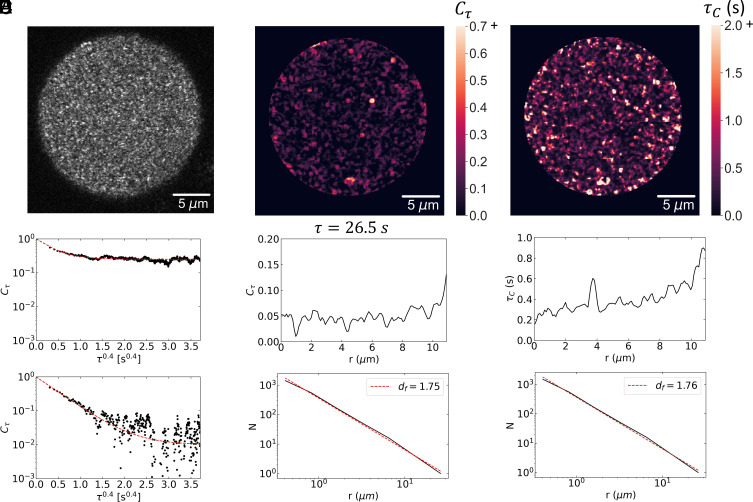
To achieve a more sensitive measure of the fluctuations of the structure in the condensate, we develop a second optical technique, reflective confocal dynamic speckle microscopy. We use a laser scanning confocal microscope to image the backscattered light from a plane near the center of the condensate. Surprisingly, when the confocal pinhole is adjusted to match the airy disk of the image, a speckle pattern is observed, as shown for a condensate after 24 h in Fig. 4A. This pattern fluctuates in time as successive images are collected at a rate of 20 Hz. We calculate the temporal correlation of each pixel and average over an area corresponding to the speckle size, which is determined from a spatial correlation of the image. These temporal correlation functions exhibit a decay to a constant value. Since we are imaging a speckle pattern, the predominant origin of the fluctuations is the relative motion of scatterers within the diffraction-limited volume detected with the confocal in a direction parallel to the scattering vector. We can, therefore, determine the local dynamics with high spatial resolution within the condensate. The correlation functions are well described as a stretched exponential decay to a constant plateau value. This behavior is consistent with scattering from a solid, gel-like network: the stretched exponential decay reflects the relaxation of the imaged volume due to fluctuations of all length scales that contribute to the relaxation (29, 30).

Fig. 4.

Confocal backscattering speckle fluctuation analysis: (A) Image of speckles from a 24-h condensate. (B) Temporal correlation function of two speckles showing stretched exponential decay to a plateau. The upper correlation function decays to a plateau, indicating a solid, while the plateau of the lower correlation function is at the noise level of the measurement. (C) Spatial map of the plateau region of the temporal correlation functions (D) Radial distribution of the value of ${\mathrm{C}}_{\tau }\left(\tau \right)$ at τ = 26.5 s, well into the plateau region (Top) and box counting analysis of the fractal dimension of the plateau regions using a threshold of ${\mathrm{C}}_{\tau }=0.10$ . The structure is fractal with ${\mathrm{d}}_{\mathrm{f}}\approx 1.75$ . The corresponding fractal dimension for the three-dimensional condensate is ${\mathrm{d}}_{\mathrm{f}}\approx 2.75$ . (E) Spatial map of decay times of the stretched-exponential correlation functions. (F) Radial distribution of decay times exhibiting pronounced increase at the outer edge (Top) and box counting analysis of decay times greater than 0.5 s (Bottom). The structure is fractal with ${\mathrm{d}}_{\mathrm{f}}\approx 1.76$ . The corresponding fractal dimension for the three-dimensional condensate is ${\mathrm{d}}_{\mathrm{f}}\approx 2.76$.

The spatial dependence of these correlation functions provides important insight into the structure and dynamics of the condensate. The plateau in the correlation functions is a direct measure of solid-like behavior, and crucially it does not exhibit a uniform value throughout the condensate. Instead, there are regions that are solid-like and regions that are liquid-like, suggesting that there is a further spatial phase separation of the solid portion with respect to the remaining liquid phase. To investigate the structure of this solid-like region, we plot the value of $C_{\tau }\left(\tau \right)$ at a lag time of τ = 26.5 s in Fig. 4C. A radial average of the plateau values shows a distinct increase at the outer edge of the condensate, supporting the view that the liquid–solid transition begins at the outer edge, as shown in the upper plot in Fig. 4D. Perhaps even more interesting is that the structure within the condensate is not homogeneous, but instead is quite heterogeneous. To quantify the spatial distribution of solid-like regions, we set a threshold of $C_{\tau }\left(\tau \right)=0.10$ and use box-counting to determine the spatial structure. It is well described as a fractal as shown by the power-law dependence plotted in Fig. 4D. The fractal dimension of the image is $d_f\approx 1.75$ as shown by the dashed line in Fig. 4D; however, since this is a two-dimensional slice through a three-dimensional image, the fractal dimension of the condensate is $d_f\approx 2.75$ . A similar heterogenous structure is found in the spatial distribution of the decay times as shown in Fig. 4E. The radial average of τ_c exhibits a pronounced peak at the outer edge of the condensate, as shown in the upper plot in Fig. 4F. Setting a threshold at τ_c = 0.5 s and performing a box-counting analysis again shows a fractal structure with essentially the same value of d_f , as shown in the lower plot in Fig. 4F. These results are strong evidence of a heterogeneous structure within the condensate, reflecting a solid, gel-like network in a more liquid-like background. We can estimate the elastic modulus of this network from the plateau value of the correlation functions. The dimension of each fluctuation element contributing to the speckle is ~q^–1, where q is the scattering vector. We take the value of the plateau as $C_{\tau }=e^{-q^2{\mathrm{\Delta }r}^2}\approx 0.10$ . This gives an elastic modulus of $G^{\prime }\sim q^3{k}_{B}T/2.3$ , where $k_{B}T$ is the thermal energy. From this, we obtain $G^{\prime }\sim 120$ Pa. Thus, the analysis of the backscattered speckles supports the view that the condensates are highly heterogenous, reflecting a second spatial phase transition, leading to the formation of a very weak solid gel-like network.

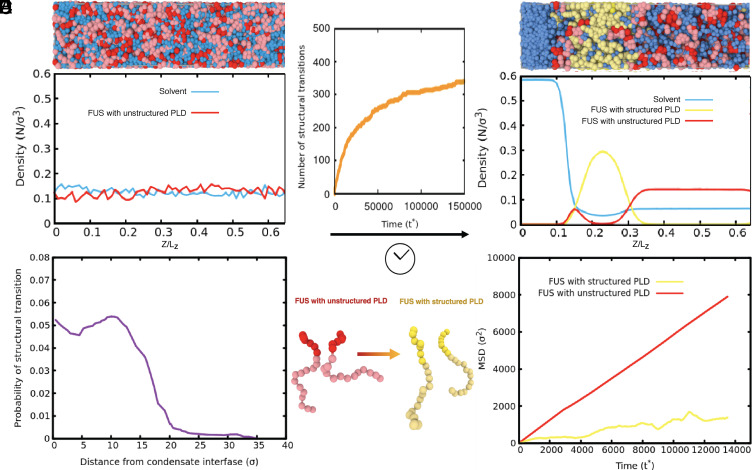
To explore the connection between molecular level interactions and the observed liquid/solid coexistence during the liquid-to-solid transition of condensates, we conduct molecular simulations with a dynamical algorithm coupled to a coarse-grained model for FUS proteins in explicit solvent, which we developed recently using a multiscale approach (31). Our dynamical algorithm describes the nonequilibrium process of condensate aging by introducing dissipation via nonconservative interprotein interactions. Specifically, we first perform direct coexistence simulations, starting from a well-mixed solution of FUS molecules at subcritical conditions (Fig. 5B), to obtain an equilibrium condensate in coexistence with a protein-poor liquid phase. We then turn on the dynamical algorithm. As time progresses, our dynamical algorithm triggers disorder-to-order transitions (i.e., from disordered to interprotein β-sheets) within the prion-like domain (PLD) of individual FUS molecules (Fig. 5A). Protein structural transitions are recapitulated by modulating the interaction strength of PLD–PLD interactions—according to the atomistic potential of mean force simulations (31)—and implemented only when high local fluctuations of protein densities emerge within the condensate. As a result, during our aging simulations, FUS condensates exhibit a gradual accumulation of strongly binding and locally rigid interprotein β-sheets (Fig. 5C). As seen in Fig. 5C, the number of structural transitions rapidly increases over time, and then plateaus as the lower density core of the condensate consolidates (Fig. 5D), showing that the transitions are disfavored at lower protein concentrations but favored at the condensate–solvent interface (Fig. 5E). The simulations recapitulate the coexistence of liquid and solid phases within a single condensate during the gelation process.

Fig. 5.

Molecular simulations with a dynamical algorithm describe the emergence of spatially inhomogeneous gel phase coexisting with a liquid phase during aging. (A) Minimal coarse-grained models for FUS with fully disordered PLDs (Red) and with structured PLDs (i.e., with interprotein β-sheet elements in the PLDs) (yellow). (B, Top) Snapshot of the initial state in our direct coexistence simulations depicting a well-mixed solution of FUS proteins with fully unstructured PLDs (Red) and explicit solvent (Blue). (B, Bottom) Density profile (in reduced units) showing an initial homogeneous distribution of FUS species and explicit solvent across the long side of the simulation box. (C) Number of structural transitions in FUS-PLD domains as a function of simulation time (t∗). (D, Top) Fraction of a snapshot focusing on the interface between the condensate and the solvent. The snapshot was drawn from a direct coexistence simulation using the dynamical algorithm at a steady state after structural transitions have saturated. (D, Bottom) Density profile (in reduced units) of FUS species and explicit solvent across the long side of the simulation box (starting near the condensate interface) estimated over the coarse-grained steady state. (E) Probability of the emergence of a structural transition inside the FUS condensates during aging as a function of the distance from the interface. (F) Mean squared displacement of FUS proteins with structured PLDs versus FUS proteins with fully disordered PLDs inside a gel-core/liquid-shell condensate.

Moreover, consistent with our experiments, at the molecular scale of the interface of the condensate we observe that interprotein β-sheets form preferentially at the interface because it is there where larger fluctuations in local FUS-PLD density occur (Fig. 5E) – such density fluctuations are precisely the ones that seed the structural transitions. These larger high-density fluctuations are likely favored by the protein PLDs presenting more extended conformations near the interfaces than at the condensate’s core (32), and the most hydrophilic parts of the protein (i.e., the non-PLD regions) being preferentially exposed to the interface to minimize the droplet surface tension. Additionally, extended protein conformations increase the molecular connectivity of the condensed liquid with respect to more compact states (33). Finally, Fig. 5F shows that the mean-square displacement of proteins with structured PLDs is much smaller than those with unstructured PLDs in a condensate. Combining with Fig. 5E, the results indicate that the outer shell of the condensate, where the proteins have undergone the transitions, is more akin of forming a gel than a liquid (yellow curve), and the inner core remains liquid (red curve).

In summary, LLPS is increasingly well understood as an essential process with crucial biological functions. By contrast, the mechanisms of liquid-to-solid transition of condensates, underlying the formation of pathological protein aggregates, have remained more challenging to elucidate. In this study, we develop and deploy a set of advanced imaging techniques to probe the onset and development of a solid phase within liquid single-component FUS condensates at multiple times and length scales. We find that there are multiple dynamics within a single condensate at all levels of maturation, indicating the coexistence of liquid and gel network within a condensate. We further unveil that the material properties of the condensates transition from liquid-like to solid-like from the interface to the core as a function of the maturation time. At first, a weak network forms within the condensate and a coexistence of this solid network with the liquid phase can be observed. As the aging progresses, the network at the interface thickens and start to form a core-shell structure that over time moves toward the center of the condensate. A core-shell structure starts to form after 24 h of incubation time and the growth of the solid shell propagate toward the center until the whole condensate becomes gel. Our findings unveil the spatiotemporal dimension of the LST of condensates and may suggest interventions to mitigate this transition when it occurs in driving such systems from physiological to pathological.

Supplementary Material

Appendix 01 (PDF)

Movie S1.

Confocal Z-scan of a 24h-incubated FUS protein condensate.

Data, Materials, and Software Availability

All study data are included in the article and/or supporting information.