Single-sequence protein structure prediction using language models and deep learning

Abstract

AlphaFold2 and related computational systems predict protein structure using deep learning and co-evolutionary relationships encoded in multiple sequence alignments (MSAs). Despite dramatic increases in prediction accuracy achieved by these systems, challenges remain in: (i) prediction of orphan and rapidly evolving proteins for which an MSA cannot be generated, (ii) rapid exploration of designed structures, and (iii) understanding the rules governing spontaneous polypeptide folding in solution. Here we report development of an end-to-end differentiable recurrent geometric network (RGN) that uses a protein language model (AminoBERT) to learn latent structural information from unaligned proteins. A linked geometric module compactly represents C_α backbone geometry. On average RGN2 outperforms AlphaFold2 and RoseTTAFold on orphan proteins and classes of designed proteins while achieving up to a 10⁶-fold reduction in compute time. These findings demonstrate the practical and theoretical strengths of protein language models relative to MSAs in structure prediction.

INTRODUCTION

Predicting 3D protein structure from amino acid sequence is a grand challenge in biophysics of practical and theoretical importance. Progress has long relied on physics-based methods that estimate energy landscapes and dynamically fold proteins within these landscapes^1–4. A decade ago, the focus shifted to extracting residue-residue contacts from co-evolutionary relationships embedded in multiple sequence alignments (MSAs)⁵ (Supplementary Figure 1). Algorithms such as the first AlphaFold⁶ and trRosetta⁷ use deep neural networks to generate distograms able to guide classic physics-based folding engines. These algorithms perform substantially better than algorithms based on physical energy models alone. More recently, the superior performance of AlphaFold2⁸ in folding a wide range of protein targets that were part of the recent CASP14 prediction challenge shows that when MSAs are available, machine learning (ML)-based methods can predict protein structure with sufficient accuracy to complement X-ray crystallography, cryoEM, and NMR as a practical means to determine structures of interest.

Predicting the structures of single sequences using ML nonetheless remains a challenge: the requirement in AlphaFold2 for co-evolutionary information from MSAs makes it less performative with proteins that lack sequence homologs, currently estimated at ~20% of all metagenomic protein sequences⁹ and ~11% of eukaryotic and viral proteins¹⁰. Protein design and studies quantifying the effects of sequence variation on function¹¹ or immunogenicity¹² also require single-sequence structure prediction. More fundamentally, the physical process of polypeptide folding in solution is driven solely by the chemical properties of that chain and its interaction with solvent (excluding, for the moment, proteins that require folding co-factors). An algorithm that predicts structure directly from a single sequence is—like energy-based folding engines^1–4—closer to the real physical process than an algorithm that uses MSAs. We speculate that ML algorithms able to fold proteins from single sequences will ultimately provide new understanding of protein biophysics.

Structure prediction algorithms that are fast and low-cost are of great practical value because they make efficient exploration of sequence space possible, particularly in design applications¹³. State of the art MSA-based predictions for large numbers of long proteins can incur substantial costs when performed on the cloud. Reducing this cost would enable many practical applications in enzymology, therapeutics and chemical engineering including designing new functions^14–16, raising thermostability¹⁷, altering pH sensitivity¹⁸, and increasing compatibility with organic solvents¹⁹. Efficient and accurate structure prediction is also valuable in the case of orphan proteins, many of which are thought to play a role in taxonomically restricted and lineage-specific adaptations. OSP24, for example, is an orphan virulence factor for the wheat pathogen F. graminearum that controls host immunity by regulating proteasomal degradation of a conserved signal transduction kinase²⁰. It is one of many orphan genes found in fungi, plants insects and other organisms²¹ for which MSAs are not available.

We have previously described an end-to-end differentiable, ML-based recurrent geometric network (hereafter RGN1)²² that predicts protein structure from position-specific scoring matrices (PSSMs) derived from MSAs; related end-to-end approaches have since been reported^23–25. RGN1 PSSM-structure relationships are parameterized as torsion angles between adjacent residues making it possible to sequentially position the protein backbone in 3D space (backbone geometry comprises the arrangement of $N,C_{\alpha }$, and $C^{\text{'}}$ atoms for each amino acid). All RGN1 components are differentiable and the system can therefore be optimized from end to end to minimize prediction error (as measured by distance-based root mean squared deviation; dRMSD). While RGN1 does not rely on the co-evolutionary information used to generate MSAs, a requirement for PSSMs necessitates that multiple homologous sequences be available.

Here, we describe a new end-to-end differentiable system, RGN2 (Figure 1), that predicts protein structure from single protein sequences by using a protein language model (AminoBERT). Language models were first developed as a means to extract semantic information from a sequence of words (a key requirement for natural language processing; NLP) ²⁶. In the context of proteins, AminoBERT aims to capture the latent information in a string of amino acids that implicitly specifies protein structure. RGN2 also makes use of a natural way of describing polypeptide geometry that is rotationally- and translationally-invariant at the level of the polypeptide as a whole. This involves using the Frenet-Serret formulas to embed a reference frame at each C_α carbon; the backbone is then easily constructed by a series of transformations. In this paper we describe the implementation and training of AminoBERT, the use of Frenet-Serret formulas in RGN2, and a performance assessment for natural and designed proteins with no significant sequence homologs. We find that on average the GDT_TS achieved by RGN2 is higher than AlphaFold2 (AF2)⁸ and RoseTTAFold (RF)²⁷ even though AF2/RF can achieve higher absolute GDT_TS scores than RGN2 on naturally occurring orphan proteins without known homologs and de novo designed proteins. While RGN2 is not as performant as MSA-based methods for proteins that permit use of MSAs, RGN2 is up to six orders of magnitude faster, enabling efficient exploration of sequence and structure landscapes.

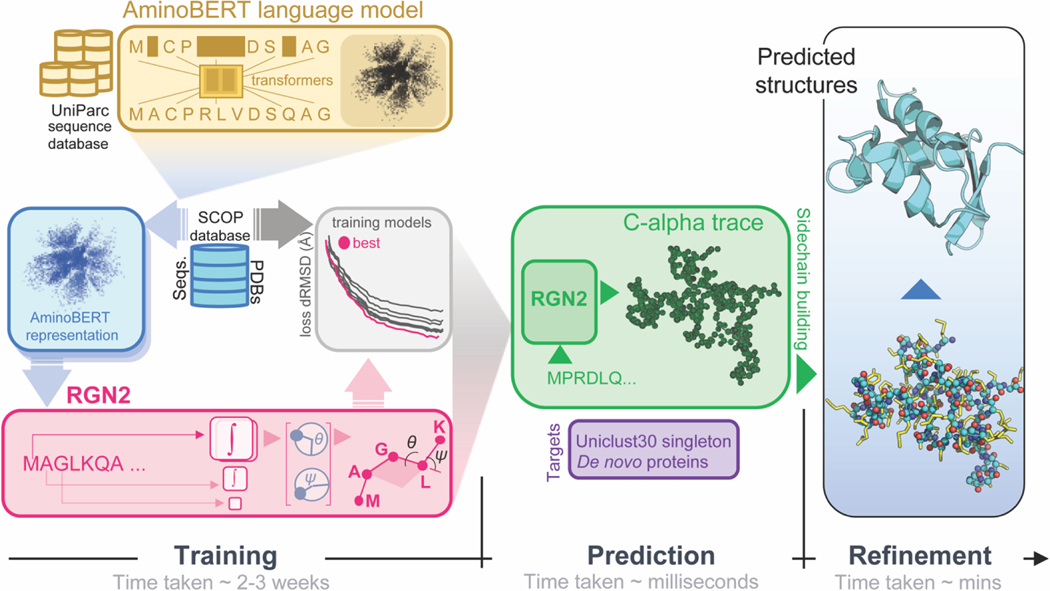
Figure 1. Organization and application of RGN2.

RGN2 combines a Transformer-based protein language model (AminoBERT; yellow) with a recurrent geometric network that utilizes Frenet-Serret frames to generate the backbone structure of a protein (green). Placement of side chain atoms and refinement of hydrogen-bonded networks are subsequently performed using the Rosetta energy function (blue).

RESULTS

RGN2 and AminoBERT models

RGN2 involves two primary innovations relative to RGN1 and other ML-based structure prediction approaches. First, it uses amino acid sequence itself as the primary input as opposed to a PSSM, making it possible to predict structure from a single sequence. In the absence of a PSSM or MSA, latent information on the relationship between protein sequence (as a whole) and 3D structure is captured using a protein language model we term AminoBERT. Second, rather than describe the geometry of protein backbones as a sequence of torsion angles, RGN2 uses a simpler and more powerful approach based on the Frenet-Serret formulas; these formulas describe motion along a curve using the reference frame of the curve itself. This approach to protein geometry is inherently translationally- and rotationally-invariant, a key property of polypeptides in solution. We refined structures predicted by RGN2 using a Rosetta-based protocol²⁸ that imputes the backbone and side-chain atoms. Refinement is first performed in torsion space to optimize side-chain conformations and eliminate clashes and then in Cartesian space using quasi-Newton-based energy minimization. These refinement steps are non-differentiable but improve the quality of predicted structures.

Language models were originally developed for natural language processing and operate on a simple but powerful principle: they acquire linguistic understanding by learning to fill in missing words in a sentence, akin to a sentence completion task in standardized tests. By performing this task across large text corpora, language models develop powerful reasoning capabilities. The Bidirectional Encoder Representations from Transformers (BERT) model²⁹ instantiated this principle using Transformers, a class of neural networks in which attention is the primary component of the learning system³⁰. In a Transformer, each token in the input sentence can “attend” to all other tokens through the exchange of activation patterns corresponding to the intermediate outputs of neurons in the neural network. In AminoBERT we utilize the same approach, substituting protein sequences for sentences and using amino acid residues as tokens.

To generate the AminoBERT language model we trained a 12-layer Transformer using ~250 million natural protein sequences obtained from the UniParc sequence database³¹. To enhance the capture of information in full protein sequences we introduced two training objectives not part of BERT or previously reported protein language models^26,32–36. First, 2–8 contiguous residues were masked simultaneously in each sequence (similar to the ProtTrans³⁷ language model) making the reconstruction task harder and emphasizing learning from global rather than local context. Second, chunk permutation was used to swap contiguous protein segments; chunk permutations preserve local sequence information but disrupt global coherence. Training AminoBERT to identify these permutations is another way of encouraging the Transformer to discover information from the protein sequence as whole. The AminoBERT module of RGN2 is trained independently of the geometry module in a self-supervised manner without fine-tuning (see Methods for details).

In RGN2 we parameterized backbone geometry using the discrete version of the Frenet-Serret formulas for one-dimensional curves³⁸. In this parameterization, each residue is represented by its $C_{\alpha }$ atom and an oriented reference frame centered on that atom. Local residue geometry was described by a single rotation matrix relating the preceding frame to the current one, which is the geometrical object that RGN2 predicts at each residue position. This rotationally- and translationally-invariant parameterization has two advantages over our previous use of torsion angles in RGN1. First, it ensured that specifying a single biophysical parameter, namely the sequential $C_{\alpha }-C_{\alpha }$ distance of ~3.8Å (which corresponds to a trans conformation) results in only physically-realizable local geometries. This overcomes a limitation of RGN1, which yielded chemically unrealistic values for some torsion angles. Second, it reduced by ~10-fold the computational cost of chain extension calculations, which often dominates RGN training and inference times (see Methods).

RGN2 training was performed using both the ProteinNet12 dataset³⁹ and a smaller dataset comprised solely of single protein domains derived from the ASTRAL SCOPe dataset (v1.75)⁴⁰. Since we observed no detectable difference between the two, all results in this paper derive from the smaller dataset as it required less training time.

Predicting structures of proteins with no homologs

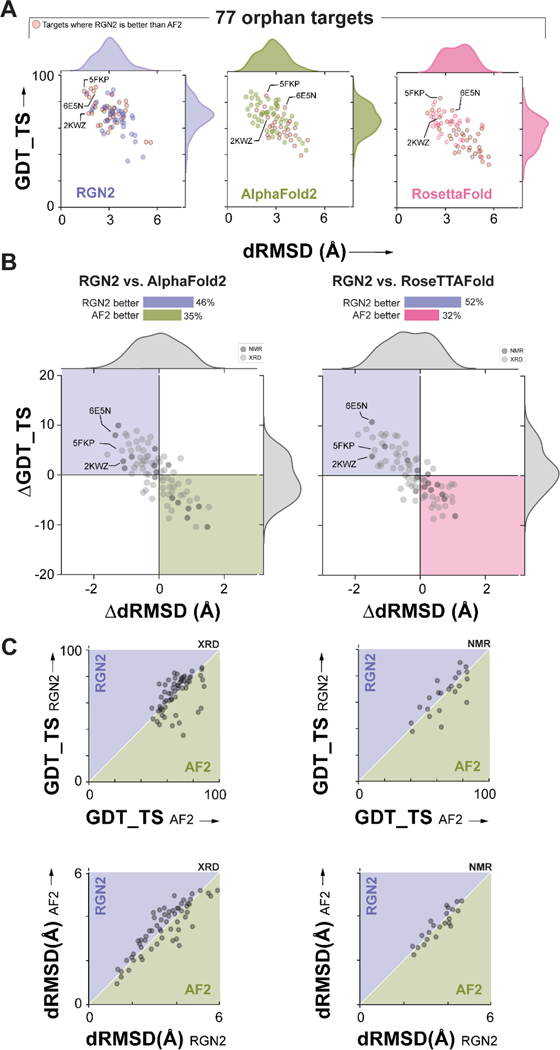
To assess how well RGN2 predicts the structures of orphan proteins having no known sequence homologs (Supplementary Figures 2 and 3), we compared it to AlphaFold2 (AF2)⁸, and RoseTTAFold (RF)²⁷, currently the best publicly available methods. In addition to UniRef30, we used two other complementary databases (PDB70 and MGnify) to prepare a list of 77 proteins with the following properties: (i) they are at least 20 residues long (ii) they are orphans (i.e., MSA depth = 1) across all three datasets simultaneously and (iii) they have solved structures in the Protein Databank (PDB)⁴¹ (see Methods for orphan test set construction details). We note that more than 85% of these sequences are included in the training sets for AF2 and RF, which may result in an overestimate of the accuracy of these methods. We predicted the structures of orphan proteins using all methods and assessed accuracy with respect to experimentally-determined structures (Figure 2A) using dRMSD and GDT_TS (the global distance test, which roughly captures the fraction of the structure that is correctly predicted). We found that RGN2 outperformed AF2 and RF on both metrics in 46% and 52% of cases, respectively (these correspond to the top-left quadrant in Figure 2B). In 35% and 32% of cases, AF2 and RF outperformed RGN2 on both metrics, respectively; split results were obtained in the remaining cases. When we computed differences in error metrics obtained for different prediction methods, we found that RGN2 outperformed AF2 and RF by an average ΔdRMSD of 0.83Å and 1.16Å and ΔGDT_TS of 4.75 and 4.91 units, respectively. When the same analysis was applied only to structures that had been determined by X-ray crystallography (i.e., 80% of the targets shown in light gray in Figure 2B) RGN2 exhibited a similar improvement over AF2 and RF: an average ΔdRMSD of 0.81Å and 1.07Å and ΔGDT_TS of 4.32 and 4.79 units, respectively.

Figure 2. Prediction performance on orphan proteins.

(A) Absolute performance metrics for RGN2 (purple), AF2 (green), and RF (pink) across 77 orphan proteins lacking known homologs. (B) Differences in prediction accuracy between RGN2 and AF2 / RF are shown for the 77 orphan proteins, using dRMSD and GDT_TS as metrics. Points in top-left quadrant correspond to targets with negative ΔdRMSD and positive ΔGDT_TS, i.e., where RGN2 outperforms the competing method on both metrics, and vice-versa for the bottom-right quadrant. The other two quadrant (white) indicate targets where there is no clear winner as the two metrics disagree. The structures of 20% of the targets were determined experimentally using NMR and are denoted with dark gray markers while the remaining 80% of targets were determined using X-ray crystallography (XRD). (C) Head-to-head comparisons of absolute GDT_TS and dRMSD scores for RGN2 and AF2 are shown broken down by experimental method (NMR and XRD). RGN2 outperforms AF2 for proteins in the upper purple triangle while AF2 outperforms RGN2 for targets in the lower green triangle.

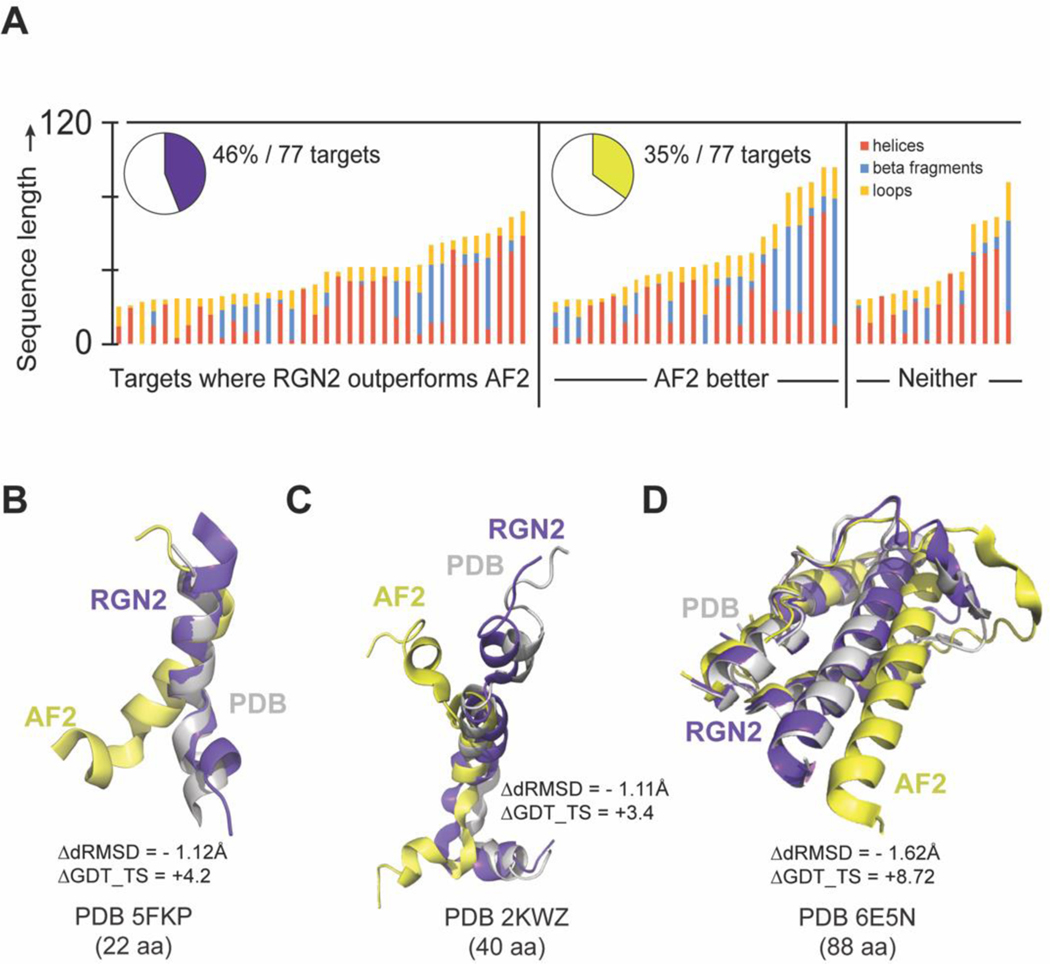
To investigate the structural basis for these differences in performance we applied the DSSP algorithm⁴² to determine the fraction of each secondary structure element (helical – alpha, 5 and 3/10, beta-strand, and bridge, and unstructured loops, bends, and hydrogen bonded turns) in PDB structures for the orphan protein test set (Figure 3A). We found that RGN2 outperformed all other methods on proteins rich in single helices and bends or hydrogen-bonded turns interspersed with helices, while other methods—AF2 in particular—better predicted targets with high fractions of beta-strand and beta-bridges (such as hairpins). Performance on the remaining ~19% targets was split between RGN2 and competing methods (Figure 2B). We also examined performance as a function of protein length and found that RGN2 generally outperformed AF2 on longer helical proteins. One possible explanation for these findings is that the Frenet-Serret geometry used by RGN2 is based on two local parameters (curvature and torsion) and these parameters have fixed values for helices. Thus, RGN2 has an intrinsic ability to learn helical patterns.

Figure 3. Comparing RGN2 and AF2 structure predictions for orphan proteins.

(A) Stacked bar charts show the relative fractions of secondary structure elements in orphan proteins broken down by these categories: RGN2 outperforms AF2, AF2 outperforms RGN2, and no clear winner. Bar height indicates protein length. (B-D) Alpha helical targets of different lengths (5FKP, 2KWZ, and 6E5N) which contain bends or hydrogen-bonded turns between helical domains tend to be better predicted by RGN2 than AF2.

In Figure 3B–D we show examples of structures for which RGN2 outperformed AF2. For example, PDB structures 5FKP and 2KWZ (97% and 73% alpha helical, respectively) have a polypeptide bend (Figure 3B) and a short alpha helix (Figure 3C) held in place by hydrogen-bonded turns, respectively. RGN2 correctly predicts the challenging, less-structured bends and turns in these proteins, yielding 4.2 and 3.4-point gains in GDT_TS and ΔdRMSD > 1.1Å over AF2, respectively. A longer protein 6E5N have an alpha-helical bundle connected by bends (Figure 3D). AF2 accurately predicted the majority of helical domains in 6E5N, but had dihedral errors in the hydrogen-bonded turns and bends; in contrast, RGN2 correctly predicted these unstructured polypeptide stretches between helices. This contributed to an 8.7-point increase in GDT_TS and 1.62Å decrease in dRMSD, respectively.

Predicting the structures of de novo (designed) proteins

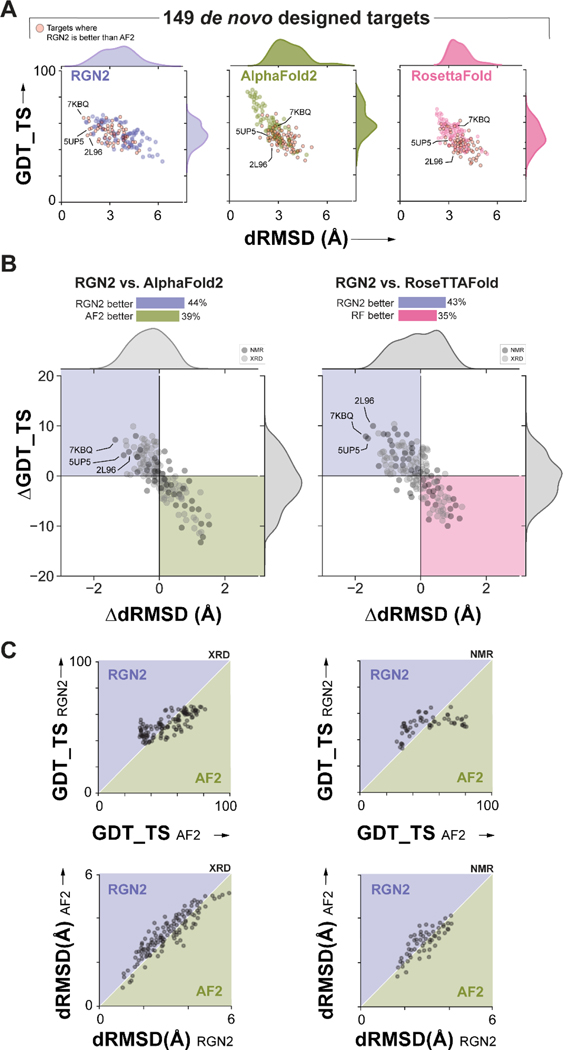
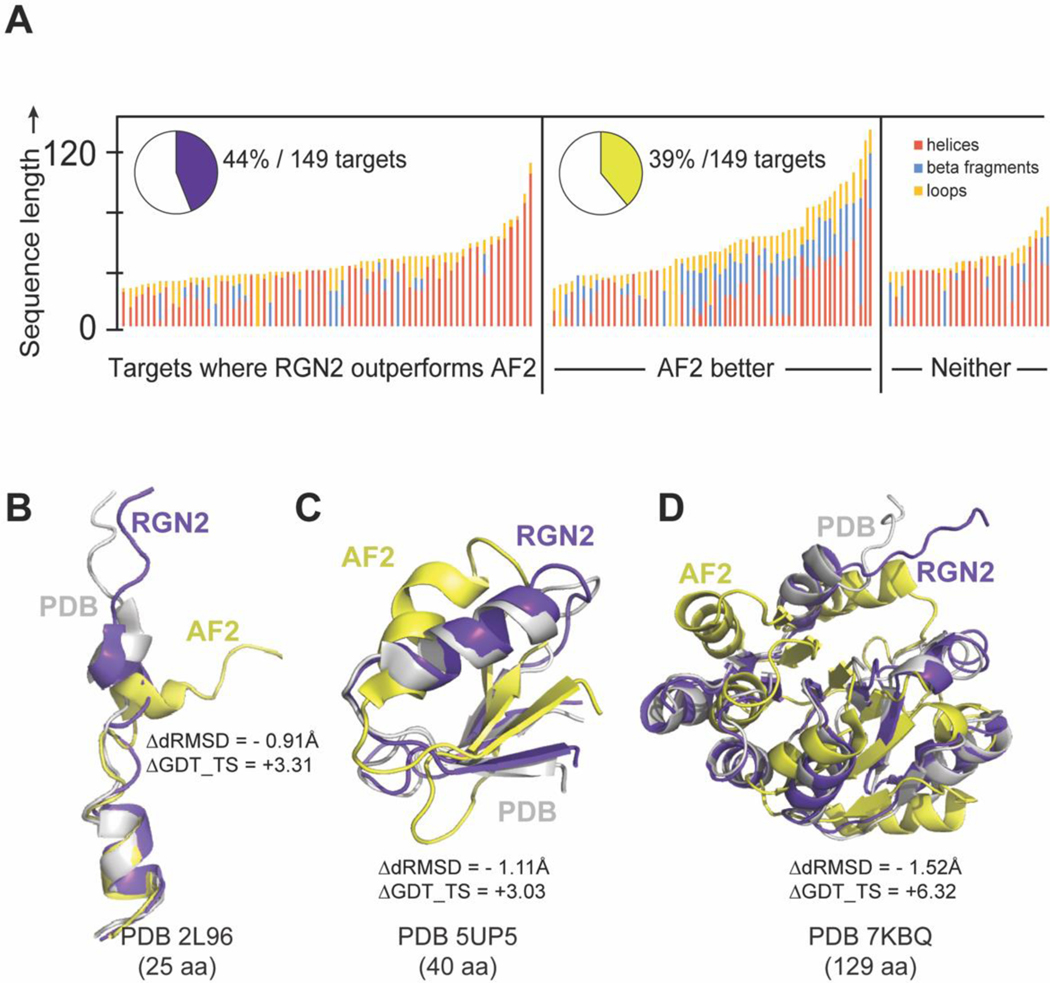
We evaluated the accuracy of RGN2 on a test set of 149 synthetic proteins that were originally designed de novo using computationally parametrized energy functions such as Rosetta and Amber; these proteins are expected to be well-suited to prediction by RosettaFold (RF). Many of these proteins are intended to have applications in therapeutic development such as novel antimicrobial peptides. This test set comprises all known designed proteins that are not part of the AF2 training set, as ascertained by PDB deposition date and filtered to have an organism annotation of synthetic construct. This filter helps to eliminate ambiguous de novo protein entries (e.g., 7NBI) which are synthesized single point mutants of known proteins. As before, we assessed prediction accuracy using dRMSD and GDT_TS. We found that RGN2 outperformed AF2 and RF on both metrics in 44% and 43% of cases, respectively (Figure 4). On average, RGN2 outperformed AF2 and RF on these targets with dRMSD and GDT_TS gains of 0.46Å and 3.62, and of 0.71Å and 4.14, respectively (Figure 4). The same analysis applied only to structures determined by X-ray crystallography (i.e., 66% of the targets shown in light gray in Figure 4B) yield similar improvements in RGN2 relative to AF2 and RF: an average ΔdRMSD of 0.42Å and 0.65Å and ΔGDT_TS of 3.58 and 4.07 units, respectively. We conclude that RGN2 can better predict sequence-structure relationships for helical regions of de novo protein space than all competing methods (Figure 5) but that beta sheet prediction from single sequences remains a challenge.

Figure 4. Prediction performance on Designed Proteins.

(A) Absolute performance metrics for RGN2 (purple), AF2 (green), and RosettaFold (pink) across 149 de novo designed proteins. (B) Differences in prediction accuracy between RGN2 and AF2 are shown for these 149 proteins using dRMSD and GDT_TS as metrics. Points in top-left quadrant correspond to targets with negative ΔdRMSD and positive ΔGDT_TS, i.e., where RGN2 outperforms the competing method on both metrics, and vice-versa for the bottom-right quadrant. The other two quadrant (white) indicate targets where there is no clear winner as the two metrics disagree. The structures of 34% of the targets were determined experimentally using NMR and are denoted with dark gray markers while the remaining 64% of targets were determined using X-ray crystallography. (XRD). (C) Head-to-head comparisons of absolute GDT_TS and dRMSD scores for RGN2 and AF2 are shown broken down by experimental method (NMR and XRD). RGN2 outperforms AF2 for proteins in the upper purple triangle while AF2 outperforms RGN2 for targets in the lower green triangle.

Figure 5. Comparing RGN2 and AF2 structure predictions for designed proteins.

(A) Stacked bar chart shows 149 de novo designed proteins. Bar height indicates protein length. (B) Overlaid ribbon diagrams of PDB entries (with increasing protein length) 2L96, 5UP5, and 7KBQ (white) and RGN2 (purple) and AF2 (yellow) predicted structures are visually depicted to show how RGN2 outperforms AF2 for each of these cases.

As an illustration of how RGN2 improves on and complements AF2 predictions, we show in Figure 5B the structure of an antimicrobial peptide (PDB Accession Code: 2L96). This is a largely helical protein comprising two short helices connected by a hydrogen-bonded turn and an N-terminal loop. Similar to orphans with similar secondary structural composition, RGN2 predicts this target more accurately than AF2 (ΔdRMSD = –0.90Å and GDT_TS = +3.31 ΔGDT_TS). In Figure 5C and 5D we show predicted structures of two different alpha-beta targets, both connected by hydrogen-bonded turns (PDB Accession Codes: 5UP5 and 7KBQ). For these targets both RGN2 and AF2 are equally accurate in capturing the ordered secondary structured elements (TM-Scores with PDB > 0.7). RGN2 is only marginally more accurate than AF2 on a global level (ΔdRMSD < −1.5Å), but hydrogen-bonded turns are better recapitulated by RGN2 and consequently result in a higher ΔGDT_TS score. Similar observations suggest that future hybrid methods using both a language model and MSAs may outperform either method alone.

Contact prediction precision

We performed a comparative contact prediction analysis between RGN2 and ESM-1b first on our newly revised set of 124 de novo protein targets (i.e., those > 20 aa long with no homolog across PDB70, MGnify, and UniRef90 datasets; Table 1a)) and our set of designed proteins (Table 1b). These tables show the percentage precision of top L/2, L/5, and L/10 contacts. We note that ESM-1b outperforms RGN2 on the beta-rich contacts, but for alpha rich contacts, RGN2 remains marginally ahead. We note that gains in contact prediction accuracy do not necessarily translate to improved tertiary structure prediction⁴³.

Table 1.

A quantitative comparison of average TM-Scores and precision of top L/2, L/5, and L/10 contacts and contacts within α-helical and β-type folds across 77 orphan proteins, and 149 de novo proteins, using ESM-1b and RGN2.

Targets	Method	Top L/x			Structural Classes
		L/2	L/5	L/10	α-helix	β-type
77 orphans	RGN2	29.3	52.3	64.4	86.5	20.3
	ESM-1b	30.1	51.8	69.6	84.1	49.5
149 de novo	RGN2	35.6	55.1	61.8	87.9	23.3
	ESM-1b	29.3	54.5	68.4	84.1	39.2

RGN2 prediction speed

Rapid prediction of protein structure is essential for tasks such as protein design and analysis of allelic variation or disease mutations. By virtue of being end-to-end differentiable, RGN2 predicts unrefined structures using fast neural network operations and does not require physics-based conformational sampling to assemble a folded chain. Because it operates directly on single sequences, RGN2 also avoids expensive MSA calculations. To quantify these benefits, we compared the speed of RGN2 and other methods on orphan and de novo proteins datasets of varying lengths (breaking down computation time by prediction stage; Table 2). In MSA-based methods, MSA generation scaled linearly with MSA depth (i.e., the number of homologous sequences used) whereas distogram prediction (by trRosetta) scaled quadratically with protein length. AF2 predictions scale cubically with protein length. In contrast, RGN2 scales linearly with protein length and both template-free and MSA-free implementations of AF2 and RF were >10⁵ fold slower than RGN2. In the absence of post-prediction refinement, RGN2 is up to 10⁶-fold faster, even for relatively short proteins. Adding physics-based refinement increased compute cost for all methods, but even so RGN2 remains the fastest available method. Of interest, even when MSA generation is discounted, neural network-based inference for AF2 and RF remains much slower than RGN2, inclusive of post-prediction refinement. This gap will only widen for design tasks involving longer proteins, whose chemical synthesis is increasingly becoming feasible⁴⁴. Thus, fast prediction is an important benefit of using a protein language model such as AminoBERT.

Table 2.

Comparison of prediction times between RGN2 and AF2, RF, and trRosetta across 330 targets spanning our orphan and de novo protein datasets. RGN2 predictions were performed in batches with maximum permissible batch size set to 128 targets. The trRosetta MSA generation step was not used since none of the targets had known homologous proteins.

Protein length (L) bins (# residues)	Total targets	Mean protein length (# residues)	Mean trRosetta prediction time per structure (s)		Mean AF2 prediction time (s)	Mean RF prediction time (s)	Mean RGN2 prediction time (ms)	Mean RGN2 prediction + refinement time (s)
			Distogram	3D-Structure
$0<L\le 100$	184	37.5	1768	1004	831.5	412.6	2.7	145.2
$100<L\le 200$	93	148.7	2791	1927	851.6	408.3	2.2	177.4
$200<L\le 300$	28	258.3	2877	1752	828.4	492.7	3.1	182.3
$300<L\le 400$	17	333.4	3647	2140	825.6	501.6	5.7	200.5
$400>L$	8	460.5	4012	3011	841.6	498.6	5.9	229.2

DISCUSSION

RGN2 represents one of the first attempts to use ML to predict protein structure from a single sequence. This is computationally efficient and has many advantages in the case of orphan and designed proteins for which generation of multiple sequence alignment is often not possible. RGN2 accomplishes this by fusing a protein language model (AminoBERT) with a simple and intuitive approach to parameterizing C_α backbone geometry based on the Frenet-Serret formulas. Whereas most recent advances in ML-based structure prediction have relied on MSAs⁵ to learn latent information about folding, AminoBERT learns this information from proteins without alignment. Training in this case involves sequences with masked residues and block permutations. We speculate that the latent space of the language model also captures recurrent evolutionary relationships⁴⁵. The use of Frenet-Serret formulas in RGN2 addresses the requirement that proteins exhibit translational and rotational invariance. From a practical standpoint, the speed and accuracy of RGN2 shows that language models are effective at learning structural information from primary sequence while having the ability to extrapolate beyond known proteins, thereby enabling effective prediction of orphan and designed proteins. Nonetheless, methods that utilize MSA information (when it is available) often outperform RGN2, most notably AlphaFold2 when assessed on proteins in the “Free Modeling” category of CASP14 (Supplementary Figure 4). Thus, language models are not a substitute for MSAs but rather a complementary way to get at the latent rules governing protein folding. We speculate that folding systems that use both language models and MSAs will be more performative than systems using one approach alone.

Transformers and their embodiment of local and distant attention is a key feature of language models such as AminoBERT. Very large Transformer-based models trained on hundreds of millions and potentially billions of protein sequences are increasingly available^26,35,36 and the scaling previously observed in natural language applications⁴⁶ makes it likely that the performance of RGN2 and similar methods will continue to improve and become broadly performative over intrinsically disordered proteins and cyclic peptides as well (Supplementary Figure 5). AlphaFold2 also exploits attention mechanisms based on Transformers to capture the latent information in MSAs. Similarly, the self-supervised MSA Transformer⁴⁷ uses a related attention strategy that attends to both positions and sequences in an MSA, and achieves state-of-the-art contact prediction accuracy. Architectures merging language models and MSAs are also likely to benefit from augmentation from high-confidence structures found in the newly reported AlphaFold Database.⁸. Finally, training on experimental data is almost certain to be invaluable in selected applications requiring high accuracy within members of multi-protein families, such as predicting structural variation within kinases or G protein-coupled receptors.

We consider RGN2 to be a first step in the development of methods able to compute sequence-to-structure maps without a requirement for explicit evolutionary information. One limitation of the current RGN2 implementation to be addressed by future systems is that the immediate output of the recurrent geometric network only constrains local dependencies between C_α atoms (curvature and torsion angles) resulting in sequential reconstruction of backbone geometry. Allowing the network to reason directly on arbitrary pairwise dependencies throughout the structure, and using a better inductive prior than immediate contact may further improve the quality of model predictions. A second limitation is that refinement in RGN2 is not part of an end-to-end implementation; refinement via a 3D rotationally- and translationally-equivariant neural network would be more efficient and likely yield better quality structures. Currently, Rosetta-based refinements results in 28% higher GDT_TS and 16% lower dRMSD values, on average, relative to predictions from RGN2 alone, as evaluated using all 213 orphan and de novo targets described in this study (Supplementary Figure 6).

It has been known since Anfinsen’s refolding experiments that single polypeptide chains contain the information needed to specify fold⁴⁸. The demonstration that a language model can learn information on structure directly from protein sequences and then guide accurate prediction of an unaligned protein suggests that RGN2 behaves in a manner that is more similar to the physical process of protein folding than MSA-based methods. Transformers can learn structural encodings present in both local and distant features of a sequence, which is reflective of the role played by local residues in the molten globule stage and distant residues in the 3D protein fold. Moreover, language models learned by deep neural networks are readily formulated in a maximum entropy framework.⁴⁹ The physical process of protein folding is also entropically driven, potentially suggesting a means to compare the two. A fusion of biophysical and learning-based perspectives may ultimately prove the key to direct sequence-to-structure prediction from single polypeptides at experimental accuracy and for understanding folding energetics and dynamics.

METHODS

AminoBERT summary

AminoBERT is a 12-layer Transformer where each layer is composed of 12 attention heads. It is trained to distill protein sequence semantics from ~260 million natural protein sequences obtained from the UniParc sequence database³¹ (downloaded May 19, 2019).

During training each sequence is fed to AminoBERT according to the following algorithm:

1. With probability 0.3 select sequence for chunk permutation, and with probability 0.7 select sequence for masked language modeling.

2. If sequence was selected for chunk permutation, then:

   With probability 0.35 chunk permute, else (with probability 0.65) leave the sequence unmodified.

3. Else if the sequence was selected for masked language modeling, then:

With probability 0.3 introduce 0.15 $\times$ sequence_length masks into the sequence with clumping, else (with probability 0.7) introduce the same number of masks into the sequence randomly across the length of the sequence (standard masked language modeling).

The loss for an individual sequence (seq) is given by:

$$Loss\left(seq\right)=I\left[seqischunkpermuted\right]\times chunk\_permutation\_loss\left(seq\right)+(1-I[seqisgloballyperturbed]\times masked\_lm\_loss(seq)$$

where I[x] is the indicator of the event x, and returns 1 if x is true, and 0 if x is false. Chunk_permutation_loss(seq) is a standard cross entropy loss reflecting the classification accuracy of predicting whether seq has been chunk permuted. Finally, masked_lm_loss(seq) is the standard masked language modeling loss as previously described in Devlin et al.²⁹. Note, that mask clumping does not affect how the loss is calculated.

Chunk permutation is performed by first sampling an integer x uniformly between 2 and 10, inclusively. The sequence is then randomly split into x equal-sized fragments, which are subsequently shuffled and rejoined.

Mask clumping is performed as follows:

1. Sample an integer clump_size ~ Poisson (2.5) + 1

2. Let n_mask = 0.15 $\times$ sequence_length. Randomly select n_mask/clump_size positions in the sequence around which to introduce a set of clump_size contiguous masks

AminoBERT architecture

Each multi-headed attention layer in AminoBERT contains 12 attention heads, each with hidden size 768. The output dimension of the feed-forward unit at the end of each attention layer is 3072. As done in BERT²⁹, we prepend a [CLS] token at the beginning of each sequence, for which an encoding is maintained through all layers of the AminoBERT Transformer. Each sequence was padded or otherwise clipped to length 1024 (including the [CLS] token).

For chunk permutation classification, the final hidden vector of the [CLS] token is fed through another feed forward layer of output dimension 768, followed by a final feed forward layer of output dimension 2, which are the logits corresponding to whether the sequence is chunk permuted or not. Masked language modeling loss calculations are set up as described in Devlin et al. ²⁹.

AminoBERT training procedure

AminoBERT was trained with batch size 3072 for 1,100,000 steps, which is approximately 13 epochs over the 260 million sequence corpus. For our optimizer we used Adam with a learning rate of 1e-4, β1 = 0.9, β2 = 0.999, epsilon=1e-6, L2 weight decay of 0.01, learning rate warmup over the first 20,000 steps, and linear decay of the learning rate. We used a dropout probability of 0.1 on all layers, and used GELU activations as done for BERT. Training was performed on a 512 core TPU pod for approximately one week.

Geometry module

The geometry of the protein backbone as summarized by the $C_{\alpha }$ trace can be thought of as a one-dimensional discrete open curve, characterized by a bond and torsion angle at each residue. Following Niemi et al.³⁸, the starting point for describing such discrete curves is to assign a frame, a triplet of orthonormal vectors, to each $C_{\alpha }$ atom. If we denote by $r_i$ the vector characterizing the position of a $C_{\alpha }$ atom at the $i$-th vertex, we could then define a unit tangent vector along an edge connecting two consecutives $C_{\alpha }$ atoms

$$t_i=\frac{r_{i+1}-r_i}{\left|r_{i+1}-r_i\right|}$$

For assigning frames to each $i$-th $C_{\alpha }$ atom, we need two extra vectors, the binormal and normal vectors defined as follows:

$$b_i=\frac{t_{i-1}\times t_i}{\left|t_{i-1}\times t_i\right|}$$

$$n_i=b_i\times t_i$$

While for a protein (in a given orientation) the tangent vector is uniquely defined, the normal and binormal vectors are arbitrary. Indeed, when assigning frames to each residue we could take any arbitrary orthogonal basis on the normal plane to the tangent vector. Such arbitrariness does not affect our strategy of predicting 3D structures starting from bond and torsion angles.

To derive the equivalent of the Frenet-Serret formulas—which describe the geometry of continuous and differentiable one-dimensional curves—for the discrete case, we need to relate two consecutive frames along the protein backbone in terms of rotation matrices

$$\left(\begin{array}{c}{n}_{i+1}\\ b_{i+1}\\ t_{i+1}\end{array}\right)={\mathcal{R}}_{i+1,i}\left(\begin{array}{c}{n}_i\\ b_i\\ t_i\end{array}\right)$$

In three-dimensions, rotation matrices are in general parametrized in term of three Euler angles. However, in our case the rotation matrices relating two consecutive frames are fully characterized by only two angles, a bond angle $\psi$ and a torsion angle $\theta$, as the third Euler angle vanishes, reflecting the following condition $b_{i+1}.t_i=0$. We can now write the equivalent of the Frenet-Serret formulas for the discrete case

$$\left(\begin{array}{c}{n}_{i+1}\\ b_{i+1}\\ t_{i+1}\end{array}\right)=\left(\begin{array}{ccc}\cos \psi \cos \theta & \cos \psi \sin \theta & -\sin \psi \\ -\sin \theta & \cos \theta & 0\\ \sin \psi \cos \theta & \sin \psi \sin \theta & \cos \psi \end{array}\right)\left(\begin{array}{c}{n}_i\\ b_i\\ t_i\end{array}\right)$$

The bond and torsion angles are defined by the following relations

$$\cos {\psi }_{i+1,i}=t_{i+1}.t_i$$

$$\cos {\theta }_{i+1,i}=b_{i+1}.b_i$$

We now turn to backbone reconstruction starting from bond and torsion angles. First, using tangent vectors along the backbone edges, we can reconstruct all $C_{\alpha }$ atom positions, and thus the full protein backbone in the $C_{\alpha }$ trace, by using the following relation:

$$r_k={\sum }_{i=0}^{k-1}\left|r_{i+1}-r_i\right|.t_i$$

where $\left|r_{i+1}-r_i\right|$ is the length of the virtual bonds connecting two consecutive $C_{\alpha }$ atoms. In most cases, the average virtual bond length is $\sim$3$.$8 Å, which corresponds to trans conformations. In terms of the familiar torsion angles $\varphi ,\psi ,$ and $\omega ,$ those conformations are achieved for $\omega \sim \pi$. For cis conformations, mainly involving proline residues, the virtual bond length is $\sim 3.0\mathrm{\AA }$ (and it corresponds to $\omega \sim 0).$ In RGN2, for backbone reconstruction, we impose the condition that the virtual bond length is strictly equal to 3$.$8 Å, and for reconstructing the backbone we use the following relation:

$$r_k={\sum }_{i=0}^{k-1}3.8\times t_i$$

The intuition behind the previous equation is the idea of a moving observer along the protein backbone. We could think of the tangent vector $t_i$ as the velocity of the observer along a given edge, and the constant virtual bond length as the effective time spent for travelling along the edge. The only freedom allowed for such observer is to abruptly change the direction of the velocity vector at each vertex.

The model outputs bond and torsion angles. By centering the first $C_{\alpha }$ atom of the protein backbone at the origin of our coordinate system, we sequentially reconstruct all the $C_{\alpha }$ atom coordinates using the following relation:

$$\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}{n}_{i+1}\\ b_{i+1}\end{array}\\ t_{i+1}\end{array}\\ r_{i+1}\end{array}\right)=\left(\begin{array}{cc}{\mathcal{R}}_{i+1,i}& \begin{array}{c}0\\ 0\\ 0\end{array}\\ \begin{array}{ccc}0& 0& \end{array}3.8& 1\end{array}\right)\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}{n}_i\\ b_i\end{array}\\ t_i\end{array}\\ r_i\end{array}\right)$$

Data preparation for comparison with trRosetta

Performance of RGN2 was compared against trRosetta across two sets of non-homologous proteins: (i) 129 orphans from the Uniclust30 database⁵⁰, and (ii) 35 de novo proteins by Xu et al.⁵¹. Both sets were filtered to ensure no overlap with the training sets of RGN2 and trRosetta. While RGN2 is trained on the ASTRAL SCOPe (v1.75) dataset⁴⁰, trRosetta was trained on a set of 15,051 single chain proteins (released before May 1, 2018).

Structure prediction with trRosetta, AF2, and RF

Conventional trRosetta-based structure prediction involves first feeding the input sequence through a deep MSA generation step. For orphans and de novo proteins without any sequence homologs, the MSA only includes the original query sequence. Next, the MSA is used by the trRosetta neural network to predict a distogram (and orientogram) that captures inter-residue (C_𝛼-C_𝛼 and C_β-C_β) distances and orientations. This information is subsequently utilized by a final Rosetta-based refinement module. This module first threads a naïve sequence of polyalanines of length equaling the target protein that maximally obeys the distance and orientation constraints. After side-chain imputation that reflects the original sequence, multiple steps including clash elimination, rotamer repacking, and energy minimization are performed to identify the lowest energy structure.

AF2 and RF predictions did not require MSAs since our target proteins don’t have homologs and so we made our predictions using their respective official Google Colab notebooks.

Structure refinement in RGN2

Raw predictions from RGN2 contain a single C_𝛼 trace of the target protein. After performing a local internal coordinate building step to generate the backbone and side-chain atoms corresponding to the target sequence, we use Rosetta-based refinement to finetune the structure. This refinement comprises hybrid optimization of side chains using five invocations of energy minimization in torsional space followed by a single step of quasi-Newton all-atom minimization in Cartesian space (using the FastRelax protocol of RosettaScripts⁵²). An optional CartesianSampler⁵² mover step can be added to further correct local strain density in the predicted model. The six-step FastRelax protocol is repeated for 300 cycles for each target. Finally, 100 cycles of coarse-grained, fast minimization using MinMover⁵² is applied to obtain the predicted structure.

RGN2 is available freely as a standalone tool from https://drive.google.com/file/d/1FIU6UZrhmc44YVCMLAzCHXWMHkSpoCkt/view?usp=sharing. Users can make structure predictions using a Python-based web user interface by uploading the protein sequence in fasta format.