Theory for Cavity-Modified Ground-State Reactivities via Electron–Photon Interactions

Abstract

We provide a simple and intuitive theory to explain how coupling a molecule to an optical cavity can modify ground-state chemical reactivity by exploiting intrinsic quantum behaviors of light–matter interactions. Using the recently developed polarized Fock states representation, we demonstrate that the change of the ground-state potential is achieved due to the scaling of diabatic electronic couplings with the overlap of the polarized Fock states. Our theory predicts that for a proton-transfer model system, the ground-state barrier height can be modified through light–matter interactions when the cavity frequency is in the electronic excitation range. Our simple theory explains several recent computational investigations that discovered the same effect. We further demonstrate that under the deep strong coupling limit of the light and matter, the polaritonic ground and first excited eigenstates become the Mulliken–Hush diabatic states, which are the eigenstates of the dipole operator. This work provides a simple but powerful theoretical framework to understand how strong coupling between the molecule and the cavity can modify ground-state reactivities.

Introduction

Coupling molecules to a quantized radiation field inside an optical cavity creates a set of photon-matter hybrid states, so-called polaritons. These polariton states hybridize the curvatures from both the ground and the excited electronic states and have shown great promise to alter the photochemistry of molecules.¹⁻⁴ Unlike traditional photochemistry, which uses light as an energy source, polariton chemistry uses quantized photons as active chemical catalysts to significantly change the shape of the potential energy surface (PES) in molecular systems and thus open up new possibilities to tune and control chemical reactions.⁵⁻⁸

Theoretical investigations play a vital role in understanding the fundamental limits and the basic principle of new chemical reactivities achieved by polariton chemistry.⁷⁻¹⁰ In particular, the molecule–cavity interactions have often been described as the following dipole gauge Hamiltonian

1

where 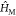is the molecular Hamiltonian, Ĥ_ph is the photon field Hamiltonian, â^† and â are the raising and lowering operators of the cavity field, and μ^ is the dipole operator of the molecule. Further, χ = χê, where χ describes the coupling strength and ê indicates the cavity field polarization direction. This Hamiltonian predicts that there will be couplings between the photon-dressed states, for example, |g,1⟩ ≡ |g⟩⊗|1⟩ (the ground electronic state with 1 photon) and |e,0⟩ ≡ |e⟩⊗|0⟩ (the excited electronic state with 0 photons), through ⟨g,1| μ^(â^†+ â)|e, 0⟩= μ_ge⟨1|(â^†+ â)|0⟩. When the energy of these two states is very close, the |g,1⟩ and |e,0⟩ states hybridize, leading to the formation of polariton states. Using such a simple Hamiltonian, it has been shown that the presence of the cavity can suppress¹¹ or enhance^8,12 photo-isomerizations,¹¹⁻¹³ increase charge transfer rates by orders of magnitude,¹⁴⁻¹⁶ modify potential energy landscapes even with no photon in the cavity,^8,11,17−19 enhance electron-phonon coupling strength,²⁰ accelerate singlet fission kinetics,²¹ remotely control chemical reactions,²² enhance excitation energy transfer processes,^16,23,24 and create new polariton induced conical intersections.^8,18,25,26 All of these emerging features of polariton chemistry demonstrate a great promise to control and tune chemical reactivities, as the cavity quantum electrodynamics (QED) processes take advantage of the quantum nature of light and its interaction with the molecular system.

Recently, several theoretical works have demonstrated that the ground state of a molecular system can be significantly modified by coupling to a cavity photon mode with a photon frequency in the electronic excitation range.²⁷⁻³⁴ In particular, ref (35) demonstrates that the aminopropenal proton-transfer reaction barrier can be modified by coupling the system with the cavity. Note that the cavity frequency in these studies is chosen to be in the range of electronic excitation (in terms of energy, a couple of eV), thus different than the recently explored vibrational strong coupling (VSC) regime^36,37 (in terms of energy, on the order of 100 meV). These modifications are caused by indirect couplings between different photon-dressed states due to the presence of both transition and permanent dipoles.³⁸ For example, the |g,0⟩ state couples with |g,1⟩ through ⟨g,1|μ^(â^† + â)|g, 1⟩ = μ_gg⟨1|(â^† + â)|0⟩ and |g,1⟩ couples to the |e,0⟩ through μ_ge⟨1|(â^† + â)|0⟩. As such, the |g,0⟩ and the |e,0⟩ states are indirectly coupled to each other (through the light–matter interactions), and the ground-state properties can also be significantly influenced under the strong light–matter interaction coupling strength. Further, the dipole self-energy (DSE) term (see eq 1, the last term) could also significantly influence the ground-state properties and reactivities, as demonstrated in ref (35). This is because the DSE operator can be expressed as 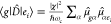where |α⟩∈{|g⟩,|e₁⟩···|e_i⟩···}. One can clearly see that the DSE term is able to connect electronic adiabatic states far away in energy. However, an intuitive and simple understanding of cavity modification of the molecular ground state is still missing. As such, the cavity-modified chemical reactivity in the ground state is an interesting new direction but not well understood due to those indirect effects as we mentioned above. We note that the existence of the DSE in the light–matter Hamiltonian has been a subject of debate in recent works with conflicting formulations of the light–matter Hamiltonian.^13,39−46 It has been argued in ref (39) that even for pure electrostatic interactions in plasmonic cavities, the Hamiltonian should have a dipole self-energy (DSE) like a quadratic term. As such, we explicitly include the DSE term in this work.

In this paper, we provide a new theory and mechanism to explain how the ground-state chemical reactivity for a molecular system can be modified by coupling to the cavity with electronic excitation frequency. Our theory is based on the recently developed polarized Fock states (PFS) representation, which uses shifted cavity Fock states associated with each specific electronic state, similar to the widely used polaron transformation,⁴⁷ Merryfield transformation,^48,49 or Lang–Fersov transformation.^50,51 These PFSs are nonorthogonal to each other but provide a compact description of the photonic Hilbert space. Using this polarized Fock states representation, we demonstrate that the change of the ground-state potential is achieved due to the scaling of diabatic electronic couplings with the overlap of the polarized Fock states. As the light–matter coupling increases, the diabatic electronic coupling is effectively reduced, resulting in a ground polaritonic potential energy surface that resembles the diabatic potential (associated with the dipole operator’s eigenstate).

Our theory predicts that for a proton-coupled electron transfer model system (Shin–Metiu model⁵²), the ground-state barrier height can be modified through light–matter interactions when the cavity frequency is in the electronic excitation range. This novel change in the ground-state chemical reactivity is achieved through strong electronic coupling as opposed to the more common use of vibrational strong coupling for modifying the ground state.^{36,37,53−55} Our simple theory explains several recent computational investigations that discovered the same effect for proton-transfer systems^35,56,57 and has the potential to add valuable insights into many more ground-state polariton studies.^{21,27−33,58−69} We further demonstrate that under the deep strong coupling limit of the light and matter, the polaritonic ground and first excited eigenstates become the Mulliken–Hush (MH) diabatic states, which are the eigenstates of the dipole operator. This work provides a simple but powerful theoretical framework to understand how strong coupling between molecule and cavity can modify ground-state reactivities.

Theoretical Framework

Theory of Polarized Fock States

We start by introducing the Pauli–Fierz (PF) nonrelativistic QED Hamiltonian⁷⁰⁻⁷² to describe the light–matter interaction. The PF Hamiltonian can bederived^15,71,73 by applying the Power–Zienau–Woolley (PZW) Gauge transformation^74,75 and a unitary phase transformation⁷³ on the minimal-coupling Hamiltonian in the Coulomb gauge (i.e., the “p·A” Hamiltonian) under the long-wavelength limit. A derivation is provided in the Appendix. For a molecule coupled to a single-photon mode inside an optical cavity, the PF Hamiltonian is

2

which is eq 1 in the Introduction section. In the last line of eq 2, Ĥ_M represents the molecular Hamiltonian, the second term 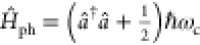represents the Hamiltonian of the vacuum photon field inside the cavity with the frequency ω_c, and the third term describes the light–matter interaction in the electric-dipole “d·E” form,⁷⁵ with characterizing the light–matter coupling vector (or alternatively the electric field vector) oriented in the direction of polarization unit vector ê, as the quantization volume for the photon field, and ε₀ as the permittivity inside the cavity. Note that the parameters used in this work correspond to quantization volumes ranging from ≈13 to 530 nm³, which while challenging to achieve experimentally is well within the theoretically estimated limits as discussed in ref (76) and is much larger than the volumes used (≈0.2 nm³) in recent theoretical works.^35,69,77 Further, â^† and â are the photon creation and annihilation operator, and are the photonic coordinate and momentum operator, respectively.

The total dipole operator of the entire molecule is

3

where z_k is the charge for the k_th charged particle. Throughout this study, we assume that ê aligns with the direction of μ^. The last term is the dipole self-energy (DSE), which describes how the polarization of the matter acts back on the photon field.⁹ The PF Hamiltonian Ĥ_PF (eq 2) is what we expressed in eq 1 of the Introduction.

The matter Hamiltonian is expressed as follows

4

where j is the index of the j_th charged particle (including all electrons and nuclei), with the corresponding mass, m_j, and canonical momentum, p̂_j = −iℏ∇_j. We denote electronic coordinate with r̂, and nuclear coordinate with R̂, and use x̂_j ∈ {r̂_j, R̂_j} to represent either the electron or nucleus, with x̂ being the coordinate operator for all charged particles. Further, T̂ = T̂_R + T̂_r is the kinetic energy operator for all charged particles, where T̂_R and T̂_r represent the kinetic energy operators for nuclei and electrons, respectively. Further, V̂(x̂) is the potential operator that describes the Coulombic interactions among the electrons and nuclei. The electronic Hamiltonian is often defined as

5

which includes the kinetic energy of electrons, electron-electron interactions, electron-nuclear interactions, and nuclear–nuclear interactions. The essential task of the electronic structure community is focused on solving the eigenstates of Ĥ_el at a particular nuclear configuration R as follows

6

where E_α(R) is commonly referred to as the α_th potential energy surface (PES) or adiabatic energy, and |Φ_α(R)⟩ is commonly referred to as the α_th adiabatic electronic state. The matrix elements of the total dipole operators can be obtained using the adiabatic states as

7

For α ≠ β, μ_αβ(R) is referred to as the transition dipole between state |Φ_α⟩ and |Φ_β⟩, while μ_αα(R) is commonly referred to as the permanent dipole for state |Φ_α⟩.

In a similar sense of defining the electronic Hamiltonian and corresponding eigenvalue equation for the matter, one can define the polaritonic Hamiltonian^9,30,62 as Ĥ_pl ≡ Ĥ_PF – T̂_R, which includes all operators of molecules and cavity, except for the nuclear kinetic energy operator T̂_R. As such, the polariton state is defined as the eigenstate of Ĥ_pl through the following eigenvalue problem

8

where Ĥ_pl ≡ Ĥ_PF – T̂_R is the polariton Hamiltonian, |Ψ_J(R)⟩ is the polariton eigenstate, and is the polariton potential energy surface. As can be seen clearly, both |Ψ_J(R)⟩ and parametrically depend on the nuclear configuration R. We denote |Ψ₀(R)⟩ as the ground state of Ĥ_pl.

Next, we briefly introduce the idea of the Polarized Fock states, whereas the details for this theoretical development can be found in ref (38). In particular, we use the Mulliken–Hush (MH) diabatic representation to express the molecular Hamiltonian and the PF QED Hamiltonian. These Mulliken–Hush diabatic states {|μ_i⟩} are the dipole operator’s eigenstates, such that

9

where μ_i is an eigen-dipole value associated with state |μ_i⟩. These |μ_i⟩ states can be obtained from the direct diagonalization of the μ^ matrix in the adiabatic representation (with the matrix element expressed in eq 7). A good example of μ_i could be the ionic and covalent dipole for a diatomic molecule, whereas the μ_αβ are the transition and permanent dipoles (see Figure 1 of ref (38)). It should be noted that these MH diabatic states are not strict diabats since they are not completely independent of the nuclear coordinates. However, for a given nuclear configuration, they can be used as a decent approximation of diabats. Note that the nonadiabatic couplings that arise due to nuclear position dependence of these MH states are relevant for dynamics, but they do not contribute to the potential energy surfaces discussed here.

Figure 1.

Visualization of an atomic system’s wave functions in its energy eigenstates (|g⟩ and |e⟩) and its first two MH diabatic states (|μ₊⟩ and |μ_–⟩).

Using the MH diabatic states, the matter Hamiltonian in eq 4 can be expressed as

10

where we have used the MH diabatic basis and V_ii(R) represents the diabatic potentials, V_ij(R) represents the diabatic coupling. This truncation of the matter Hilbert space is done by projecting the matter Hamiltonian to the lowest few eigenstates of Ĥ_el such that 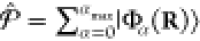. Then, the MH diabatic states are formed by diagonalizing 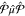. We want to emphasize that the extent to which a matter subspace can be truncated accurately strongly depends on the system under consideration.

The PF Hamiltonian in eq 2 under a finite set of the |μ_i⟩ basis is expressed as

11

where the diabatic state-specific shift q_i⁰(R) is

12

We notice that the photon field is described as a displaced Harmonic oscillator that is centered around −q_i⁰(R). This displacement can be viewed as a polarization of the photon field due to the presence of the molecule–cavity coupling, such that the photon field corresponds to a non-zero (hence polarized) vector potential, in contrast to the vacuum photon field.

We introduce the polarized Fock state (PFS) |n_i(R)⟩ ≡ |n_i⟩ as the Fock state of a displaced Harmonic oscillator, with the displacement specific to the diabatic state |μ_i⟩ such that

13

where n_i = 0, 1, 2···, ∞ is the quantum number for the PFS. Compared to the vacuum’s Fock state |n⟩, this PFS depends on the diabatic state (or, more generally, the eigenstate of μ^) of the molecule, and the position of the nuclei (through the R dependence in μ_i(R)). Due to the electronic state-dependent nature of the polarization, the PFS associated with different electronic diabatic states become nonorthogonal,³⁸ i.e., ⟨n_i|m_j⟩ ≠ δ_ijδ_nm.

To remove this shift of the photonic coordinate, a unitary transformation can be formed as

14

where eq 14 is a shift operator of the form such that it shifts an arbitrary operator Ô(q̂) by an amount q₀, .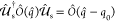

The polariton Hamiltonian under the polarized Fock state (PFS) representation can then be written as

15

The detailed expression of can be found in ref (38). In eq 15, one can clearly see that as the light–matter coupling strength χ increases, the overlap function between the displaced harmonic oscillators decreases for different diabatic states. This is because the state-specific displacement, q_i⁰, increases linearly with χ, causing ⟨m_j|n_i⟩ → δ_ijδ_nm.

In the very strong coupling limit (e.g., an infinite light–matter coupling), the overlap ⟨m_j|n_i⟩ approaches zero, effectively eliminating all diabatic electronic couplings V_ij(R). As such, the polariton Hamiltonian becomes 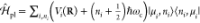, where the light and matter are effectively decoupled. This agrees with the recent theoretical analysis of atomic QED systems under the deep strong coupling limit.⁷⁸ It also indicates that, as the light–matter coupling goes large, the polariton state

16

meaning that the polariton state |Ψ_J⟩ becomes the tensor product of Mulliken–Hush diabatic states with the PFS state. Further, the polariton potential energy surface becomes

17

which means the polariton state will assume the same potential curvature as the MH diabatic states V_i(R) since the photonic energy is R-independent.

Equations 16 and 17 are considered the main theoretical results in this work. Below, we will use both the atomic cavity QED example and a model molecular cavity QED system to demonstrate its predictive power.

Special Case of the Atomic Cavity QED

To give an illustrative and familiar example, let us consider the case of an atom

18

where the transition dipole is μ_eg = ⟨e|μ^|g⟩. Note that the permanent dipoles are μ_ee = ⟨e|μ^|e⟩ = 0, μ_gg = ⟨g|μ^|g⟩ = 0. Thus, the dipole operator is expressed as

19

by defining the creation operator σ̂^† ≡ |e⟩⟨g| and annihilation operator σ̂ ≡ |g⟩⟨e| of the electronic excitation. The atom-cavity PF Hamiltonian becomes . Dropping the DSE (the last term) leads to the Rabi model⁷⁹

20

where further dropping the counter-rotating terms σ̂^†â^† and σ̂â leads to the well-known Jaynes–Cummings (JC) model,⁸⁰ with the details provided in the Appendix.

For atomic systems where μ_ee = μ_gg = 0,the eigenstates of μ^, i.e., the MH diabatic states are

21

which are commonly referred to as the qubit states⁸¹⁻⁸⁴ in the atomic, molecular, and optical (AMO) physics community. Under this basis, the dipole operator becomes

22

with the eigenvalue μ_± = ±μ_eg. Figure 1 provides a visualization of the wave functions for an atomic system in both its energy eigenstates and its MH diabatic states.

Using these diabatic states, the atomic Hamiltonian is expressed as

23

where Δ = E_e – E_g and 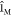is the identity operator for this matter model.

The PFS representation of this model then becomes

24

since V_±= 0, V_±,∓ = Δ/2, and there are no nuclear DOFs. As discussed in ref (81), by approximating that ⟨m_±|n_∓⟩ ≈ 0 for m ≠ n (valid for large couplings), the Hamiltonian in eq 24 becomes block diagonal and the eigenenergies and eigenstates can be analytically obtained as follows^81,82

25a

25b

It should be noted that this expression uses the notation from ref (81). These eigenstates should not be confused with the Jaynes–Cummings (JC) eigenstates (see eqs 50a and 50b) that are the exact eigenvectors of the JC Hamiltonian (see eq 49).

In the deep strong coupling limit, the overlap between the PFS ⟨n_–|n₊⟩ → 0. In this case, one can clearly see that the eigenstates |Ψ_±,n⟩ become doubly degenerate with E_+,n = E_–,n and the MH diabatic states |μ_±,n⟩ are the eigenstates of the light–matter Hamiltonian where the corresponding eigenenergies simplify to the energies of these MH states added to the energy of n photons.

Models and Computational Details

In this paper, we use this Shin–Metiu three-level system⁵² to demonstrate two different regimes of ground-state modifications. To demonstrate the ground-state potential modification when coupling a molecule to the cavity, we use the Shin–Metiu⁵² single-electron proton-transfer model truncated to three matter levels for the matter Hamiltonian. This model consists of fixed donor and acceptor ions with a proton being transferred between them, yielding one nuclear coordinate. The matter truncation is done in the MH basis, creating a model three-level system with donor (D), acceptor (A), and covalent (C) diabatic states, such that {|μ_i⟩}∈ {|D⟩, |A⟩, |C⟩}.

Shin–Metiu Model

The Shin–Metiu model⁵² is a one-dimensional molecular system that describes a proton-coupled electron transfer reaction between a donor and an acceptor ion. The model consists of a transferring proton, an electron, and two fixed ions (a donor ion and an acceptor ion). The total Hamiltonian of the molecular system is Ĥ_M = T̂_R + Ĥ_el, where T̂_R = P̂_R²/2m_p is the kinetic energy of the transferring proton, with proton mass m_p. In addition, Ĥ_el is the electronic Hamiltonian

26

where T̂_r = p̂_r²/2m_e represents the kinetic energy operator of the electron with mass m_e, V̂_eN describes the interaction between the electron and the three ions through the form of a modified Coulomb potential as follows

27

where r is the position and e = 1 au is the fundamental charge, R is the position of the proton, while R_D and R_A are the positions of the static donor and acceptor ion, respectively. Further, z_p, z_D, and z_A represent the charge of the proton, donor ion, and acceptor ion, respectively. Additionally, R_c characterizes the strength of the modified coulomb interaction between the electron and the ions.

The nuclear–nuclear interaction potential V_NN describes the coulomb repulsion between the proton and the static ions as follows

28

Computational Details

In this work, we use the Fourier grid Hamiltonian (FGH) approach^85,86 to solve the eigenvalue problem of all matter and polariton Hamiltonians. In particular, we use a total of N = 2000 grid basis {|r_i⟩} to describe the electronic degrees of freedom r in the range [R_D – 10, R_A + 10] (with Δr = 0.01 au), which allows us to solve the adiabatic states of the matter. The matrix elements of the electronic Hamiltonian Ĥ_el in this grid basis {|r_i⟩} are given by

29

where the ⟨r_i |T̂_r |r_j⟩ is given analytically^85,86 as follows

30

Directly diagonalizing the matrix of Ĥ_el at a given nuclear position R in this grid basis gives the accurate adiabatic electronic states, and in this work, we only focus on the lowest three adiabatic states

31

where a ∈ {0,1,2}. Further, the matrix elements for dipole moment operator μ̂ = R̂ + r̂, can be computed as

32

After solving for the lowest three adiabatic PESs, we project this dipole operator to the truncated Hilbert space of these adiabatic states, such that , where . By defining in this subspace, we can then find the matrix elements V_i(R) and V_ij(R) by transforming 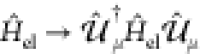, where V_i(R) and V_ij(R) are the diagonal and off-diagonal matrix elements, respectively, in this basis.

Additionally, the overlaps of the shifted Fock states, ⟨m_j|n_i⟩ are found using the relation⁸¹

33

for m < n, where L_m^n–m is an associated Laguerre polynomial.

Using all of the above components, we can solve for the polariton potential energy surface 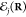of the Hamiltonian 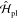(eq 15).

34

The polaritonic PESs 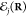can then be calculated by using the values of V_i(R) and V_ij(R) calculated from the pure matter system (through the above discrete variable representation method) and the PFS overlaps (eq 33), ⟨m_j|n_i⟩, and directly diagonalizing the matrix of 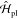. Note that identical results are obtained by solving eq 8 using the adiabatic-Fock basis |Φ_α(R)⟩⊗|n⟩, where |Φ_α(R)⟩ is the adiabatic states (see eq 6) and |n⟩ is the Fock state for the nonshifted field .

As expected from our theoretical analysis in eq 16, the polariton state approaches the tensor product of the Mulliken–Hush (MH) diabatic states and the PFS states as the light–matter coupling increases. The curvature of the polariton potential energy surface will also approach the MH diabatic states, as indicated in eq 17. In particular, for the Shin–Metiu three-level model system studied here, we consider three MH diabatic states, a donor state |D⟩ where the electron is localized on the donor atom, an acceptor state |A⟩ where the electron is localized on the acceptor atom, and an atomic state |C⟩ where the electron is localized on the transferring charged ion (proton). With a strong light–matter coupling strength, at a particular nuclear configuration R, the ground state of the light–matter hybrid will approach one of these diabatic states depending on which of the diabatic energies V_ii(R) = ⟨i|Ĥ_el|i⟩ with i ∈ {|D⟩, |A⟩, |C⟩} is the lowest.

Results and Discussion

In this work, we consider two particular sets of parameters, which we refer to as model I and model II. The parameters in the molecular Hamiltonian Ĥ_M are tabulated in Table 1. In model I, when strongly coupled to the cavity, the ground polariton potential will approach the diabatic state |C⟩; for model II, the ground polariton potential approaches the acceptor and donor diabatic states |A⟩ and |D⟩, depending on the nuclear configuration. This will modify the reaction barrier on the ground state. In both cases, the molecular model is coupled to a highly off-resonant cavity with ω_c = 3 eV (thus operating outside the vibrational strong coupling regime^42,53,87), and the number of Fock states was treated as a convergence parameter (converged with at most 50 Fock states for model I and 20 Fock states for model II).

Table 1. Parameters Used in the Molecular Hamiltonian Ĥ_M for Both Model I (Figure 2) and Model II (Figure 3).

parameter	model I	model II
zp, zD, zA	1 (unitless)	1 (unitless)
RD	–5.0 (Å)	–4.0 (Å)
RA	5.0 (Å)	4.0 (Å)
Rc	1.0 (Å)	1.5 (Å)
Rn	1.0 (Å)	1.0 (Å)
mp	1836 (au)	1836 (au)
me	1 (au)	1 (au)

Additionally, it should be noted that for both models, this paper considers a single molecule strongly coupled to a cavity. Experimentally this has not been achieved with Fabry–Pérot (FP) cavities. However, recent exciting progress both experimentally⁸⁸ and theoretically⁷⁶ in plasmonic cavities demonstrating strong coupling at the few emitter levels provides hope for realizing these effects in the future. The effects described in this work can also be observed when the light–matter coupling is weaker by simply having a steady-state photon population, say n ≈ 10¹–10² (not enough photons to reach the Floquet limit⁸⁹ where n → ∞). This is because the “diabatic” coupling terms are normalized by ⟨n_j|m_i⟩ terms which decay faster when n_j and m_j are large. Thus it may be possible to drastically modify the diabatic couplings at weaker light–matter couplings by compensating via many photons. Analogous results have also been derived for Floquet engineering of materials,^89,90 where the coupling between Floquet blocks decays as the light intensity increases. For molecular systems, strong fields also induce many problems that do not exist in the single-photon limit since the molecule can then absorb many photons from the field and be excited, ionized, dissociated, etc.

We emphasize that for plasmonic cavities, in addition to the transverse fields, there are direct Coulomb interactions between the atoms of the plasmonic nanoparticles (or surface) and the molecule in question. The degree to which the electrostatic interactions or the coupling to the transverse field is important will depend on the distance between the molecules and the metal surface (or nanoparticle) surface and how fast the evanescent field decays.

Figure 2 presents the results of coupling model I to the cavity. The diabatic states |D⟩, |C⟩, and |A⟩ in this model are depicted in the top panel of Figure 2a, whereas the ground adiabatic electronic states |Φ₀(R)⟩ at three nuclear configurations are depicted below the diabatic states. In this model, the covalent diabatic state is lower in energy than the donor and acceptor diabatic states, as shown in Figure 2b (dashed lines). As a result, the character of the ground adiabatic state is dominated by the covalent diabatic state |C⟩, especially near the top of the potential barrier (where R ≈ 0). In this case, the proton and the electron are transferred simultaneously from the donor ion to the acceptor ion, making this process an adiabatic hydrogen atom transfer reaction. This is schematically illustrated in Figure 2a, where the adiabatic (bottom panels) and diabatic (top panels) ground-state electron distributions are illustrated at the donor (R = −5.5), barrier (R = 0), and acceptor (R = 5.5) nuclear configurations. This shows how the electron follows the proton along the proton-transfer coordinate. In Figure 2b, the adiabatic and diabatic potential energy surfaces are plotted. It can be seen that the two wells in the adiabatic ground-state potential energy surface come from the coupling between the donor/acceptor diabats |D⟩ and |A⟩ with the covalent diabatic state |C⟩ through the diabatic couplings V_DC(R) and V_AC(R).

Figure 2.

Model I: Shin–Metiu model for the hydrogen atom transfer reaction. (a) Visualization of electron charge density for the lowest energy diabatic states at three different nuclear positions and the ground-state adiabatic states at the same positions. (b) Plot of the PESs for the adiabatic states ({|Φ⟩}) and the diabatic states ({|D⟩, |A⟩, |C⟩}). (c) Dipole eigenvalues for each diabatic state as a function of R. (d) Polaritonic ground-state PES, |Ψ₀⟩(R), displayed for various coupling strengths.

Figure 2c depicts the permanent dipole moments of the three MH diabats as a function of R. Note that the transition dipoles among the MH diabats are zero by definition (see eq 9). As expected, the permanent dipole of the covalent state |C⟩ is flat as the electron density sticks to the transferring proton. On the other hand, the permanent dipoles of the |D⟩ and |A⟩ states are linear with respect to the position of the transferring proton as in these states the electron density is localized on the donor/acceptor atom such that the permanent dipole is approximately μ_D/A(R) ≈ R – R_D/A.

Figure 2d depicts the potential energy surface for the photon-dressed adiabatic states |Φ_α,n⟩, as well as the polariton potential associated with the ground state |Ψ₀⟩. Near the barrier region (R ≈ 0), the ground adiabatic state coincides with the covalent diabatic state |C⟩, where the ground-state potential is nearly identical to MH diabatic potential V_C(R) for R ≈ 0. Thus, for this Shin–Metiu three-level system, even in the infinite light–matter coupling limit, the ground-state potential near the barrier region will not be modified as it is already very close to the MH diabatic state. In contrast, the ground-state potential can be expected to get significantly modified near the donor and acceptor wells as the ground state is formed by hybridizing the |D⟩ or |A⟩ with the |C⟩ states through a diabatic coupling. Increasing light–matter coupling effectively decreases the diabatic coupling ⟨0_C|0_D⟩·V_DC due to the decreasing ⟨0_C|0_D⟩ (with a similar effect for ⟨0_C|0_A⟩ ·V_AC). Thus, it will bring the ground-state potential closer to the MH diabats’ potential energy surface, as suggested in eq 17. This means that near ground-state potential minima (for R ≈ −5.5 and 5.5), the ground-state polariton potential will be pushed upward as it approaches the MH diabats lying above, thus effectively reducing the ground-state barrier height.

Another interesting feature of this ground-state modification shown here is that it is not sensitive to the cavity frequency ω_c as long as the photon frequency is not much smaller than the electronic energy gaps. This can be seen by analyzing eq 33, where the ⟨0_i |0_j⟩ overlap is a function of χ/ω_c (note that χ ∝ ω_c such that χ/ω_c is ω_c-independent), which is photon-frequency-independent for Fabry–Pérot (FP) cavities. This is because χ explicitly scales as 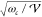, where is the cavity quantization volume. For a fixed mirror size in an FP cavity, , making χ ∝ω_c. As such, the overlap ⟨0_i |0_j⟩ is photon-frequency-independent, and the ground-state modification also remains independent of photon frequency as long as the photon frequency is not much smaller than the electronic energy gaps. For plasmonic cavities, the quantization volume is not as trivial to calculate, as such A₀ is no longer frequency-independent.

However, when ℏω_c ≪ (E_e – E_g), in addition to considering the light–matter coupling in terms of ⟨0_i|0_j⟩·V_ij, the couplings ⟨0_i|n_j⟩ ·V_ij also become relevant because E_e – E_g ≈ E_e – E_g + n_jℏω_c. Under this circumstance, the ground-state modification would become frequency dependent as smaller cavity frequencies bring more Fock states becoming energetically relevant. On the other hand, when photon frequency is comparable to or larger than electronic transition, the ground-state modification can be mainly understood by considering the ⟨0_i|0_j⟩V_ij term, and then the cavity modification becomes photon frequency-independent.

Model I, presented in Figure 2, is particularly salient in the context of recent computational work that investigates molecular hydrogen atom transfer reaction landscapes when coupling a molecule strongly to a cavity.⁹¹ In ref (91), Pavošević et al. model the proton-transfer reaction of a malonaldehyde molecule in the strong coupling regime. They found that when using self-consistent QED electronic structure methods (such as QED Hartree–Fock and QED coupled cluster level of theory), one observes a decrease in the barrier height of the proton-transfer reaction with strong electronic coupling. Our model through the PFS theory (eq 17) provides an intuitive explanation for this effect.

Figure 3 presents a different kind of modification of the ground-state polariton potential. The parameters for model II are picked such that the covalent state |C⟩ lies energetically higher than the |D⟩ and |A⟩ states. Thus, the ground adiabatic state is largely composed of |D⟩ and |A⟩ states hybridized through the diabatic coupling V_DA. As shown in Figure 3a, the electron density no longer follows along with the proton, especially in the middle panels of Figure 3a for R ≈ 0, in contrast to those in Figure 2. Instead, the charge density tunnels from the donor to the acceptor ion as the ground adiabatic state sharply changes its character from |D⟩ to the |A⟩ state near R ≈ 0. This model can be regarded as an example of a nonadiabatic proton-coupled electron transfer (PCET) reaction. Note that the permanent dipoles presented in Figure 3c are visually similar to the permanent dipoles shown in Figure 2c for model I, as the underlying nature of the MH diabats |D⟩, |A⟩, and |C⟩ is the same in both models.

Figure 3.

Model II: Shin–Metiu three-level proton-transfer model. (a) Visualization of electron charge density for the energy diabats at three different positions and the ground-state adiabat at the same positions. (b) Plot of the PESs for the adiabatic states ({|Φ⟩}) and the diabatic states ({|D⟩, |A⟩, |C⟩}). (c) Dipole eigenvalues for each diabatic state as a function of R. (d) Polaritonic ground-state PES, |Ψ⟩, and first excited state, |Ψ⟩, displayed for many coupling strengths.

The nonadiabatic transition from the donor to the acceptor state can be modulated by coupling to a cavity, following the same principles using PFS discussed above. As discussed before, the diabatic coupling V_DA·⟨0_D|0_A⟩ will be reduced, which modulates the nonadiabatic transition near the barrier at R = 0. In particular, the splitting at the avoided crossing decreases with an increase in the light–matter coupling strength.³⁸ This is illustrated in the inset in Figure 3d, which shows that the splitting gradually decreases with an increase in χ. Near the barrier, the lowest two polariton states approach the acceptor and donor diabatic states. In the limit of infinite light–matter coupling, the avoided crossing between the lowest two PESs becomes a conical intersection as the donor and acceptor states become decoupled.

These two models demonstrate different forms of ground-state modifications, but all are due to the same origin of the light–matter interactions that effectively scale down the diabatic couplings. In model I, the effective barrier height reduces significantly as the coupling increases. In model II, the avoided crossing between the first two adiabats decreases, approaching a conical intersection. In both cases, the fundamental mechanism is the same: the diabatic couplings between MH diabats decrease due to the decreasing overlap integral of two PFS, and the polariton potential energy surfaces approach the MH diabatic potential (eq 16) with increasing light–matter coupling. Under the infinite light–matter coupling limit, the polariton states reduce to the MH diabats tensor produced with PFSs (eq 17). The scaling of the diabatic couplings provides a new strategy for changing the ground-state chemical reactivity through electron–photon coupling in contrast to the operating principle of VSC, where cavity radiation can modify chemical reactivity through kinetics and dynamical effects.^42,53,92 That said, this strategy is limited, especially in the case of degenerate eigenvalues of the dipole operator (in a suitable truncated electronic subspace) such that the photon field associated with these two electronic states are displaced to the same extent, and the overlaps ⟨m_i|n_j⟩ = δ_mn regardless of the light–matter coupling strength (where i and j label the degenerated MH diabatic states). As a result, the diabatic couplings between such dipole-degenerate states remain unmodified under such circumstances.

Conclusions

Using the polarized Fock state (PFS) representation, we provide a simple theory to explain how strong electronic coupling can modify the ground-state polariton potential. We show that when coupled to the cavity, the diabatic couplings between Mulliken–Hush diabat states (which are the eigenstates of the electronic dipole operator) are modified. Using this theoretical framework, an increasing light–matter coupling will lead to a decrease of the diabatic coupling. In the infinite coupling limit, as the diabatic couplings go to zero, the MH diabats tensor product with the polarized Fock states become the eigenstates of the light–matter Hamiltonian (see eq 16). Consequently, as the coupling strength increases, the ground-state polariton PES approaches the lowest energy matter Mulliken–Hush diabatic state (see eq 17). This simple but intuitive theory explains several recently observed ground-state modifications due to strong light–matter interactions.⁹¹

In this paper, we demonstrate with three-level Shin–Metiu model systems that this modification of the ground-state either leads to a decrease of the relative barrier height (for model I in Figure 2) or a decrease of the avoided crossing between ground and excited states (for model II in Figure 3). This novel change in the ground-state chemical reactivity is achieved through strong electronic coupling as opposed to the more common use of vibrational strong coupling for modifying the ground-state chemical reactivity. This work provides a simple but powerful theoretical framework to understand how strong coupling between molecule and cavity can modify ground-state reactivities.

Appendix: Derivation of the Pauli–Fierz QED Hamiltonians

We provide a brief derivation of the Pauli–Fierz QED Hamiltonian. The cavity photon field Hamiltonian under the single-mode assumption is expressed as

35

where ω_c is the frequency of the mode in the cavity, â^† and â are the photonic creation and annihilation operators, and and are the photonic coordinate and momentum operators, respectively. Choosing the Coulomb gauge, ∇·Â = 0, the vector potential becomes purely transverse such that  = Â_⊥. Under the long-wavelength approximation,

36

where 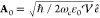, with as the quantization volume inside the cavity, ε₀ as the permittivity, and ê as the unit vector of the field polarization.

The minimal-coupling QED Hamiltonian in the Coulomb gauge (the p·A form) is expressed as

37

where p̂_j = −iℏ∇_j is the canonical momentum operator. We further introduce the Power–Zienau–Woolley (PZW) gauge transformation operator^74,75 as

38

The PZW transformation operator can also be expressed as . Recall that a momentum boost operator 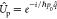boosts p̂ by the amount of p₀, such that Û_p Ô(p̂) Û_p^† = Ô(p̂ + p₀). Hence, Û simultaneously boosts the photonic momentum p̂_c by and the matter momentum P̂_j by z_jÂ. Using Û^† to boost the matter momentum, one can show that

39

hence, Ĥ_C can be mathematically obtained⁹³ by a momentum boost with the amount of −z_j for P̂_j and then adding Ĥ_ph.

The QED Hamiltonian under the dipole gauge (the d·E form^74,94) can be obtained by performing the PZW transformation on Ĥ_C as follows

40

where we have used eq 39 to express Ĥ_C, and the last three terms of the above equation are the results of ÛĤ_phÛ^†. Using q̂_c and p̂_c, one can instead show that

41

because the PZW operator boosts the photonic momentum p̂_c by . Term 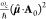is commonly referred to as the dipole self-energy (DSE).

The Pauli–Fierz (PF) QED Hamiltonian^9,70,71 can be obtained by using a unitary transformation on Ĥ_D. This is effectively a π/2 rotation in the phase space of the photonic DOF. To evaluate this, we use the following Baker–Campbell–Hausdorff (BCH) identity

42

Using the fundamental commutator [â^†, â] = −1, we have [â^†â, â] = â^†[â, â] + [â^†, â] â = −â. Denoting Û_ϕ = exp[iϕâ^†â] = e^– (with ),  = −iϕâ^†â. From the BCH identity, we have

43

Similarly, we have e^{–iϕâ†â}â^†e^iϕâ†â = e^–iϕâ^†. Choosing results in Û_ϕ^†âÛ_ϕ → iâ and Û_ϕ^†â^†Û_ϕ → −iâ^†. Using these results and applying Û_ϕ on Ĥ_D, we have the PF Hamiltonian as follows

44

where the coupling constant is 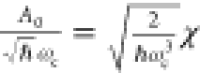as we used in eq 2. Note that we have used the fact that Û_ϕĤ_MÛ_ϕ^† = Ĥ_M, i.e., Û_ϕ, is an identity for the matter DOFs. Hence, the role of Û_ϕ is to switch p̂_c and q̂_c since, for a photon field, they are interchangeable due to the pure harmonic nature of the quantized field. The PF Hamiltonian has the advantage of a pure real Hamiltonian, and the photonic DOF can be viewed^9,71 and computationally treated^95,96 as “nuclear coordinates”.

In quantum optics, a two-level atom coupled to a single model in an optical cavity is a well-studied subject. This leads to well-known model Hamiltonians, such as the Rabi model and the Jaynes–Cummings model. Since these two models are also widely used in recent investigations of polariton chemistry, here, we briefly derive them from the PF Hamiltonian.

We consider a molecule with two electronic states

45

and the transition dipole is μ_eg = ⟨e|μ^|g⟩. Note that the permanent dipoles in a molecule μ_ee = ⟨e|μ^|e⟩, μ_gg = ⟨g|μ^|g⟩ are not necessarily zero, as opposed to the atomic case where they are always zero. Hence, it is not always a good approximation to drop them.

The Rabi model assumes that one can drop the permanent dipoles, and leads to the dipole operator expression in the subspace 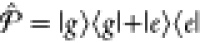as follows

46

where we have defined the creation operator σ̂^† ≡ |e⟩⟨g| and annihilation operator σ̂ ≡ |g⟩⟨e| of the electronic excitation. The PF Hamiltonian (eq 44) in the subspace thus becomes

47

Dropping the DSE (the last term) from eq 47 leads to the Rabi model

48

Dropping both the DSE and the counter-rotating terms σ̂^†â^† and σ̂â leads to the well-known Jaynes–Cummings model⁸⁰ as follows

49

The eigenstates of the JC model are analytically available, expressed as follows

50a

50b

where 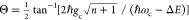is the mixing angle, and ΔE = E_e – E_g is the energy gap.

The limitations of these two models are thoroughly discussed in our recent work on Polariton-mediated charge transfer⁷³ and polariton-mediated photodissociation dynamics of diatomic molecules.³⁸

Author Contributions

^∥ A.M. and M.A.D.T. contributed equally to this work.

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Early-Career and Emerging Researchers in Physical Chemistry Volume 2”.