Statistical aspects of modeling the labor curve

Abstract

In a recent review by Cohen and Friedman, several statistical questions on modeling labor curves were raised. This article illustrates that asking data to fit a preconceived model or letting a sufficiently flexible model fit observed data is the main difference in principles of statistical modeling between the original Friedman curve and our average labor curve. An evidence-based approach to construct a labor curve and establish normal values should allow the statistical model to fit observed data. In addition, the presence of the deceleration phase in the active phase of an average labor curve was questioned. Forcing a deceleration phase to be part of the labor curve may have artificially raised the speed of progression in the active phase with a particularly large impact on earlier labor between 4 and 6 cm. Finally, any labor curve is illustrative and may not be instructive in managing labor because of variations in individual labor pattern and large errors in measuring cervical dilation. With the tools commonly available, it may be more productive to establish a new partogram that takes the physiology of labor and contemporary obstetric population into account.

We read the review by Cohen and Friedman¹ with great interest. Dr Friedman’s work profoundly changed obstetric practice and greatly advanced this field. His monumental contribution to obstetrics is undeniable. However, we believe that it is important to provide clarification of the modern statistical analysis of labor progression on 3 aspects.

1. Differences in philosophy and approach to construct a labor curve

The original Friedman curve published in 1954 was based on Dr Friedman’s personal observation of 500 women, from which he drew a sigmoid-shaped labor curve by hand.² No modern statistics or mathematical model were used. This curve became the central piece that guided his works for many years thereafter.

In 1969, Drs Friedman and Kroll³ used data from the Collaborative Perinatal Project⁴ and a prespecified model to fit a sigmoid-shaped curve and calculated duration of labor in various stages and phases and in a follow-up publication established normal standards for labor duration.⁵ The authors first defined stages and phases as follows: the latent phase from 0 to 2.5 cm of cervical dilation; the active phase from 2.5 to 10 cm; the deceleration phase from 9 to 10 cm; and the second stage from full dilation to delivery of the fetus.³

Subsequently, the authors searched the data points in the database and fit the corresponding points into the preconceived framework to estimate the duration of labor for each stage and phase. Thus, the estimates of duration for the stages and phases were influenced by their definitions. Although advanced for the time, this older approach may be limited because it forces the data points to fit into the established sigmoid curve.

In contrast, our modeling approach did not have any preconception about the pattern of the labor curve or a mathematical formula. We chose a generic, flexible statistical model (polynomial model) to fit the data and let the data tell us how the labor curve should look like. The order of the polynomial function was determined by the data (ie, a higher-order term continued to be added into the equation until it was no longer statistically significant).⁶

We also hoped that a high-order polynomial model might be flexible enough to depict the deceleration phase as described by the authors. It is worthwhile to point out that a low-order polynomial function (first order is a straight line; second order is a quadratic curve) is rigid and cannot identify subtle patterns in the labor curve. Using such a model to fit the data as advocated by the authors would be contradictory to our principle of model fitting.

Another advantage of our statistical approach is that it is transparent and reproducible. We used 2 statistical methods to study the labor progression: a traditional labor curve based on a polynomial function with repeated measures and a duration of labor centimeter by centimeter of cervical dilation based on an interval-censored regression adjusting for covariates. The exponential shape of the average labor curve and the accelerating pace of cervical dilation in active labor have been confirmed in other recent study populations with the same statistical methods.^7,8

2. Idealized vs average labor curves

The Friedman curve appears to be an idealized labor curve, although it was frequently called and used as a mean labor curve.^9,10 The original curve depicted labor starting at 0 cm.² But in reality, few women would have a totally closed cervix, spontaneous onset of labor, and a normal vaginal delivery within 12 hours (on average), although the starting point was changed from 0 to about 2 cm in 1978.¹¹

The more controversial issue lies in the deceleration phase in an active labor. The authors offered an attractive theory on why the deceleration phase may exist. But it may be questioned how likely it can be observed in routine clinical practice and plotted on an average labor curve. According to the Friedman curve, the deceleration phase in a normal labor starts at 9 cm and lasts for half an hour.²

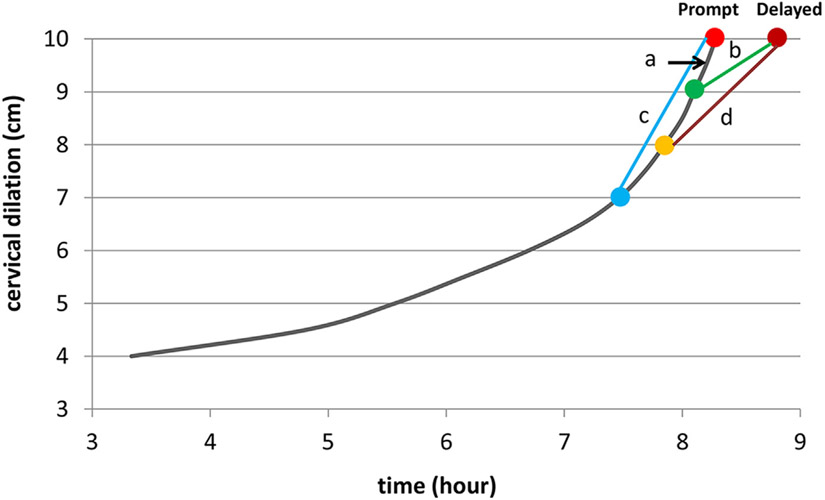
Figure 1 illustrates various scenarios on how one might observe the deceleration phase. To see this phenomenon, one must observe 9 cm of cervical dilation. If the cervical examination at 10 cm is not performed promptly, the duration of labor between 9 and 10 cm may be artificially lengthened, which could make the curve look like a deceleration (Figure 1, B). If the frequency of vaginal examinations is once every 2 hours, and the median duration of labor between 9 and 10 cm is 0.5 hour, what is the likelihood that a woman is observed at both 9 cm and promptly at 10 cm? The likelihood is very small. Thus, the deceleration phase may theoretically exist, but under the current practice, it is likely to be missed in the vast majority of women. Therefore, the average labor curve cannot depict the deceleration phase.

FIGURE 1.

Different scenarios of observation in labor progression

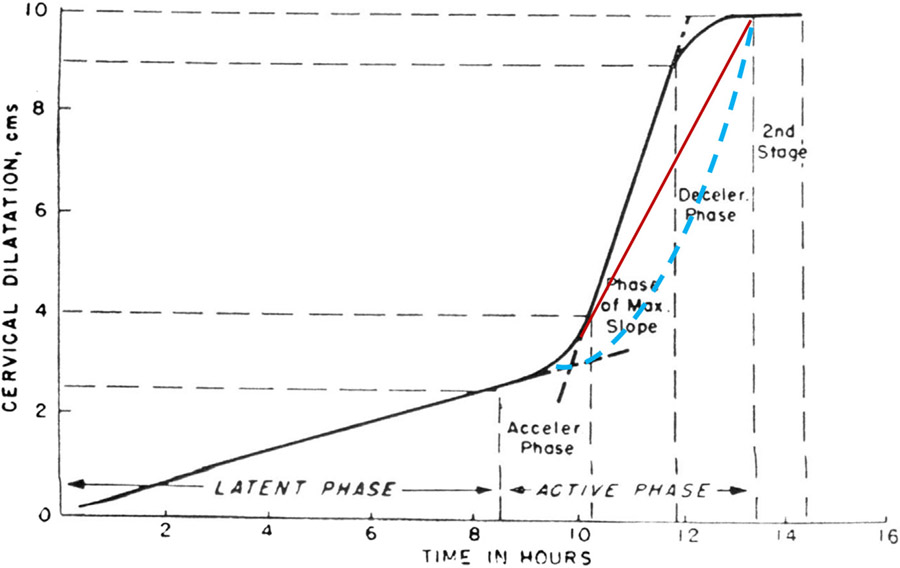
Keeping a deceleration phase in the average labor curve does have consequences. When the total duration of labor is fixed, the maximum slope of cervical dilation becomes steeper (ie, the speed of dilation is artificially increased). Figure 2 depicts 2 hypothetical labor curves without the deceleration phase. The exponential curve indicates that the impact may be particularly significant on earlier labor (between 4 and 6 cm).

FIGURE 2. Hypothetical Friedman curves without the deceleration phase.

Red line indicates a straight line; blue line indicates an exponential curve.

Adapted from Friedman.²

Using an idealized model to determine normal and abnormal labor in common practice is problematic. It may create a high percentage of false-positive cases of arrest of labor in the first stage. Our average labor curve was based on data from a large population: the Consortium on Safe Labor.¹² The values may be used as a reference for a contemporary obstetric population.

3. Effects of cesarean deliveries in the first stage of labor on the labor curve

Cohen and Friedman questioned the validity of our labor curve because we excluded women who had an intrapartum cesarean delivery in the first stage of labor.¹ Indeed, such exclusions may bias the results toward a faster labor curve (ie, in reality, labor progresses even more slowly currently than our labor curve shows). However, only 14.8% of nulliparous and 3.1% of multiparous women who presented in spontaneous labor had an intrapartum cesarean delivery.¹³

Exclusion of a small proportion of subjects should not substantially affect the pattern as well as the estimates of the curve. Nonetheless, to address this concern, we used the same Collaborative Perinatal Project data as used by Dr Friedman, in which the intrapartum cesarean rate was 2.6% in that era. The pattern of our labor curve remained the same,^6,12,14 confirming our findings. Furthermore, our interval censored regression, which utilizes the information from women who were still in labor prior to cesarean delivery, produced consistent results in both datasets: labor accelerates in the entire active phase, and no deceleration phase was observed in an average labor curve.^6,12,14

In summary, we believe that an evidence-based approach to construct a labor curve and establish normal values should allow the statistical model to fit observed data rather than selecting data to fit the preconceived model. It is also important to point out that any labor curve is illustrative and may not be instructive in managing labor because of the great variations in an individual labor pattern and large errors in measuring cervical dilation (because of timing and measurement errors). With the tools commonly available, it may be more productive to establish a new partogram¹⁵ that takes the physiology of labor and contemporary obstetric population into account.