Methods for automated delineation and assessment of EMG responses evoked by peripheral nerve stimulation in diagnostic and closed-loop therapeutic applications

Abstract

Objective:

Surface EMG measurements of the Hoffmann (H-) reflex are essential in a wide range of neuroscientific and clinical applications. One promising emerging therapeutic application is H-reflex operant conditioning, whereby a person is trained to modulate the H-reflex, with generalized beneficial effects on sensorimotor function in chronic neuromuscular disorders. Both traditional diagnostic and novel realtime therapeutic applications rely on accurate definitions of the H-reflex and M-wave temporal bounds, which currently depend on expert case-by-case judgment. The current study automates such judgments.

Approach:

Our novel wavelet-based algorithm automatically determines temporal extent and amplitude of the human soleus H-reflex and M-wave. In each of 20 participants, the algorithm was trained on data from a preliminary 3- or 4-minute recruitment-curve measurement. Output was evaluated on parametric fits to subsequent sessions’ recruitment curves (92 curves across all participants) and on the conditioning protocol’s subsequent baseline trials (~1200 per participant) performed near $H_{\max }$. Results were compared against the original temporal bounds estimated at the time, and against retrospective estimates made by an expert 6 years later.

Main results:

Automatic bounds agreed well with manual estimates: 95% lay within ±2.5 ms. The resulting H-reflex magnitude estimates showed excellent agreement (97.5% average across participants) between automatic and retrospective bounds regarding which trials would be considered successful for operant conditioning. Recruitment-curve parameters also agreed well between automatic and manual methods: 95% of the automatic estimates of the current required to elicit $H_{\max }$ fell within ±1.4% of the retrospective estimate; for the “threshold” current that produced an M-wave 10% of maximum, this value was ±3.5%.

Significance:

Such dependable automation of M-wave and H-reflex definition should make both established and emerging H-reflex protocols considerably less vulnerable to inter-personnel variability and human error, increasing translational potential.

1. Introduction

Event-related muscle responses, measured via surface electromyography (EMG), are valuable markers of neuromuscular function. In particular, the M-wave and the Hoffmann or (H-) reflex components, elicited by electrical stimulation of a peripheral nerve, provide valuable information for the diagnosis, treatment, and management of a wide range of conditions. These include spinal-cord and peripheral-nerve injury, mono- and polyneuropathies, stroke, traumatic brain injury, amyotrophic lateral sclerosis, multiple sclerosis, and Guillan-Barre’ syndrome [1, 2, 3, 4, 5, 6, 7, 8, 9]. Accurate assessment of the H-reflex and M-wave of skeletal muscle is critical for quantifying the excitability of spinal reflex pathways, as well as probing the plasticity that affects this excitability [10, 11, 12]. For a review of neurophysiological uses of the H-reflex, see Misiaszek [3].

An emerging therapeutic application of these markers is H-reflex operant conditioning, in which a person is given real-time visual feedback of the magnitude of each H-reflex response and trained to modulate the response size, leading to lasting changes in reflex magnitude and excitability [13, 14, 15]. This approach has been shown to have therapeutic benefits for people in whom spasticity impairs walking following spinal-cord injury [16, 17], and promising results are emerging in a variety of other neuromuscular conditions both for the H-reflex protocol [18] and for closely-related protocols that condition other evoked responses [19, 20].

The H-reflex and M-wave are quantified principally by their latency and magnitude, and by the associated recruitment curves that describe the relationship between stimulation intensity and response magnitude [21]. Accurate fitting of the M-wave and H-reflex recruitment curves provides valuable diagnostic information in and of itself, and also provides a way to titrate stimulus current for subsequent measurement of each individual participant. Recruitment curves rely on accurate assessment of the magnitude of both M- and H-responses. Estimation of magnitude, and hence of recruitment curve parameters, proceeds from an accurate estimate of latency and duration: typically, magnitude is estimated by the mean-rectified-value method, i.e. by taking the mean of the absolute value of the band-pass-filtered EMG signal between specific bounds $[t_{\text{start}},t_{\text{end}}]$ defined along the axis of time. These bounds are chosen manually, so the process is susceptible to inter-operator variability, and the time and expertise needed to make this judgment are impediments to clinical translation. Hence, there is a need for standardization and automation.

As an example of a reflex operant conditioning protocol, this study will examine operant down-conditioning of the soleus H-reflex. The protocol was described in detail by Hill et al. [15]. In short, following neurological injury spinal reflexes can become hyperactive. Reflex size is assessed by electrically evoking a motor responses. After assessing the baseline reflex amplitude, the participant is then tasked with keeping the reflex size below a target level, which is reinforced via trial-by-trial visual feedback of each individual reflex size as well as a cumulative success rate, on a computer screen. Over multiple sessions spanning several weeks, participants are typically able to reduce their reflex size, leading to reduction in spastic hyperreflexia and improvement in locomotion. A critical step in the therapy is the determination of the appropriate current intensity required to elicit an appropriately sized H-reflex. In order to determine the appropriate stimulating current level, a recruitment curve must first be collected. To plot the recruitment curve, the M-wave and H-reflex are manually identified, and then the optimal current is selected based on the H-reflex recruitment curve. As Hill et al. [15] point out, the protocol is sensitive to inaccuracies in the estimation of temporal bounds (see also the Discussion, below). Usually, the estimation of bounds is only finalized after several sessions, including repeated recruitment curve measurements and a large number (>1000) of repeated baseline trials.

As in any neural engineering application, translation to the clinic requires considerable automation both to reduce operational complexity and to mitigate the need for specialized expertise at the point of use. A standardized and automated way to estimate the onset and duration of the M-wave and H-reflex responses, as well as a way to automate the fitting of recruitment curves, will be critical for translating operant-conditioning therapy out of the laboratory and into clinics, with further collateral benefits to physiological basic research and clinical diagnostics. A successful algorithm would reproduce, based on a small amount of data, the decisions made by an expert human operator on a larger amount. The success of such an algorithm would facilitate clinical translation of reflex operant conditioning therapy into a commercial product, which is the subject of an ongoing collaboration between the authors and an upcoming clinical trial [22].

The present study describes a novel wavelet-based algorithm for automatically determining the bounds of the H-reflex and M-wave in the human soleus muscle, and quantifies the agreement between recruitment-curve parameters derived from bounds output by the algorithm and bounds chosen manually by a human expert. Wavelets are well-suited to H-reflex and M-wave modeling and have been applied for separation of muscle sources, evaluation of spectral properties, and prediction of motor output from EMG [23, 24, 25]. The present study reports a novel application of the Morlet wavelet for detecting the temporal limits of these evoked potentials. We demonstrate that the algorithm provides similar estimates of response bounds when compared to the expert, with consequent close agreement in estimating response magnitudes, in fitting recruitment-curve parameters, and in judging the success or failure of individual operant-conditioning trials.

2. Methods

2.1. Data Acquisition

This study is a post hoc analysis of previously recorded data. All human-subjects experiments were conducted in accordance with the principles embodied in the Declaration of Helsinki and in accordance with local statutory requirements. The research was approved by the Medical University of South Carolina Institutional Review Board (protocol numbers 42082, 46453, and 48307). All participants gave written informed consent to participate in the study. Recordings were acquired from 20 participants (13 male, 7 female). Participants were either survivors of stroke (N = 11, aged 40–76 years) or had no neurological injury (N = 9, aged 16–28 years). For each participant, evoked EMG responses were measured in the soleus muscle following electrical stimulation of the tibial nerve at the level of the popliteal fossa, following the protocol first described by Thompson et al. [13] and described in detail by Hill et al. [15]. Briefly, the protocol provides visual feedback to participants with the intention of reducing H-reflex amplitude over time. The full protocol consisted of 6 or more baseline sessions, followed by 30 training sessions conducted over a few months for each participant. In the current analysis, we used the data from just the baseline sessions, typically conducted over the course of about three weeks. Each baseline session consisted of a recruitment curve measurement (in which stimulation intensity was gradually increased, typically over the course of 25–50 trials, in a sequence tailored to each participant) followed by three sets of 75 baseline trials without visual feedback (all at the same effective stimulation intensity, designed to elicit an H-reflex response close to $H_{\max }$). After removing trials in which the signal or meta-data were corrupted or ambiguous, the complete data-set comprised 92 recruitment curves and 325 sets of baseline trials across all 20 participants, for an average of 170 recruitment-curve trials and 1192 baseline trials per participant.

2.2. Three Distinct Estimates of H-Reflex Bounds

The current analysis compares three different estimates of the H-reflex bounds, which will be referred to as the original, automatic, and retrospective estimates. These are defined as follows.

Original:

Bounds for the H-reflex were identified by author AKT and members of her laboratory at the time of recording (2016–2017) as part of the reflex operant conditioning protocol. Bounds were chosen separately for each participant by pooling all baseline trials from that participant’s baseline sessions and manually selecting the start and end of the H-reflex response prior to commencement of training sessions.

Automatic:

Bounds were also estimated by the automated algorithm described below in Section 2.3, using just the waveforms measured during each participant’s first full recruitment-curve measurement in the initial baseline session. The algorithm was designed, and a universal set of parameters $z$, $f$, ${\theta }_{\text{start}}$, ${\theta }_{\text{end}}$ (see Section 2.3) was chosen, such that the algorithm generally provided a good approximation to the original bounds across the various participants.

Retrospective:

Finally, after the automatic bounds were finalized for all 20 participants, the bounds were blindly re-estimated in a single session by author AKT in 2022. To do this, EMG signals from all baseline trials performed by each given participant were overlaid on a de-identified Microsoft PowerPoint slide, thereby summarizing the information that had been used to choose bounds for that participant at the time of recording (see Figure 1). One such slide was created for each of the 20 participants. Then the expert was asked to work through the slides, manually dragging the dotted lines from their initial positions at the edges of the slide to the appropriate horizontal positions to indicate the start and end of each participant’s H-reflex.

Figure 1:

Example of a PowerPoint slide used to obtain retrospective manual bounds from the expert. Green and red vertical lines could be dragged to indicate where the H-reflex should be considered to start and end, against the millisecond scale at the bottom. The same signals are shown both full-wave rectified (upper traces) and unrectified (lower traces), after high-pass filtering and removal of the stimulation artifact in both cases. Individual trials are overlaid in multiple colors from a single participant’s ~1192 trials, performed across six sessions at the same effective stimulus intensity; the thicker black trace shows the mean across trials. Participants were identified only by numbers that were randomly assigned for the purposes of this procedure, and unknown to the expert.

2.3. Automated Estimation of H-Reflex Bounds

For each participant, a single recruitment curve measurement was used as the input for automated estimation of H-reflex bounds—specifically, the first full recruitment curve measurement on the participant’s first session. Let $N$ be the number of stimulus intensities used to acquire the recruitment curve, typically with $R=4$ repetitions at each intensity. Also let $y_{n,r}(t)$ be the discretely-sampled waveform resulting from the $r^{\text{th}}$ repetition at the $n^{\text{th}}$ intensity. The stimulus artifact was removed prior to further processing by blanking the period during stimulation and fitting an exponential function of the form $A{\mathrm{e}}^{-t∕\tau }$ to the subsequent decay. Each waveform was then convolved with a complex Morlet wavelet of the form

$$\Psi (t)={\mathrm{e}}^{-2\pi ift-z{t}^2},$$

(where $z=40,000$ and $f=100$ were found to be broadly suitable for human soleus H-reflex data when $t$ is expressed in seconds) and the magnitude of the result of the convolution was taken:

$$g_{n,r}(t)=\mid y_{n,r}(t)\ast \Psi (t)\mid .$$

The resultant waveforms were grouped by stimulus intensity and each group average was computed:

$${\overline{g}}_n(t)=\frac{1}{R}\sum _{r=1}^R{g}_{n,r}(t).$$

To allow the M-wave and H-reflex time segments to be distinguished, a “hull” waveform $L(t)$ was then computed as the maximum value at each time-point across all stimulus intensities:

$$L(t)=\underset{n=1,\dots ,N}{\max }{\overline{g}}_n(t).$$

The waveform $L(t)$ has two or more peaks, the last of which (at time $t_H$) corresponds to the H-reflex while the penultimate peak (at time $t_M$) corresponds to the end of the M-wave. The valley between these two hull peaks, at

$$t_v=\underset{t_M<t<t_H}{\text{argmin}}L(t),$$

was used to segment the two response components. Let the height of the average H-reflex-corresponding peak at each stimulus intensity $n$, be denoted by

$$p_n=\underset{t>t_v}{\max }\overline{g}(t).$$

To find the bounds of the H-reflex, we then find the stimulation intensity that generates the largest such peak, $n^{\ast }={\text{argmax}}_n(p_n)$. Let the corresponding waveform be denoted as

$$h^{\ast }(t)={\overline{g}}_{n^{\ast }}(t):t>t_v$$

and further let

$$t_{\text{peak}}=\underset{t}{\text{argmax}}{h}^{\ast }(t)$$

and

$$\widehat{h}(t)=h^{\ast }(t)∕h^{\ast }(t_{\text{peak}}).$$

Thus $\widehat{h}(t)$ is the stimulation-locked waveform, averaged across repetitions at the single stimulation intensity that produced the highest H-reflex response, normalized such that the height of that response, at its peak at time $t_{\text{peak}}$, is 1.

The start of the H-reflex component is estimated as the point where $\widehat{h}(t)$ drops to ${\theta }_{\text{start}}=0.5$, working backwards from $t_{\text{peak}}$:

$$t_{\text{start}}=\underset{t<t_{\text{peak}}}{\text{argmin}}\mid \widehat{h}(t)-{\theta }_{\text{start}}\mid ,$$

and the end of the H-reflex component is estimated as the point where $\widehat{h}(t)$ drops to ${\theta }_{\text{end}}=0.7$, working forwards:

$$t_{\text{end}}=\underset{t>t_{\text{peak}}}{\text{argmin}}\mid \widehat{h}(t)-{\theta }_{\text{end}}\mid .$$

The convolution and final estimation steps are summarized graphically in Figure 2.

Figure 2:

A graphical representation of the key steps in the H-reflex bounds estimation algorithm. A: The averaged waveform to be analyzed. B: The real and imaginary components of the complex Morlet wavelet. C: The result of the convolution of the waveform in panel A and the wavelet in panel B. Blue, real component; red, imaginary component; gray, the magnitude of the complex waveform. D: The start and end bounds are taken as the times at which normalized magnitude of the convolution drops to 50% of the peak value before the peak and 70% of the peak value after the peak. Duration of waveforms is 30ms in each panel. (Vertical scaling differs between panels, and the two waveforms in panel D are not on the same vertical scale as each other.)

The parameters $f=100$, $z=40,000$, ${\theta }_{\text{start}}=0.5$ and ${\theta }_{\text{end}}=0.7$ were all chosen by hand such that they provided a good fit to the original manual bounds, with stable behavior across the whole participant group. The $f$ parameter controls the frequency of the wavelet, and the $z$ parameter determines the width. Several potential values of $f$ were tried, and 100 was settled on as this is close to the carrier frequency of the signal of interest observed in most human soleus reflex data. The $z$ parameter was adjusted similarly. Small values of $z$ led to very low, broad peaks in the convolution output which decreased the temporal precision of the onset and offset estimates. As $z$ was increased, the resulting peak became taller and narrower. However, if made too narrow, the result devolved into multiple peaks due to the polyphasic nature of the H-reflex. Since our goal was to identify precisely the onset of a single event, we chose a value of $z$ low enough that a single peak was consistently returned, but high enough to make that single peak as narrow as possible. The value of $z=40,000$ was chosen as this met all required criteria with a reasonable safety margin. Of course, the use of one-size-fits-all parameter values does not take into account individual differences in latency between the depolarization and repolarization of the muscle fibers (loosely, the “speed” of the H-reflex response). Empirically, a retrospective analysis found no systematic relationship between individual participants’ peak-to-peak latency and the discrepancy in their ultimate bound estimates relative to the manual bounds. Therefore, we concluded that our parameter settings yielded a wavelet basis function of sufficiently high bandwidth that the small mismatches between its carrier wavelength and the individual participants’ wavelengths produced negligible effects.

2.4. Determination of M-Wave Bounds

In the original operant-conditioning experiment, H-reflex amplitude was evaluated using the mean-rectified-value method. By contrast, the operant conditioning protocol demanded different trial-by-trial processing of the M-wave, which was instead evaluated according to its peak-to-peak amplitude. Since the peak-to-peak measure was much less sensitive to variations in the bounds, the original manual M-wave bound estimates tended to be much wider and more variable than the H-reflex bounds. This made the H-reflex and M-wave measures incommensurate, even when applying the mean-rectified measure to both, and hence demanded an alternative approach.

For the purposes of the current study, original, automatic and retrospective M-wave bounds were obtained deterministically based on the respective original, automatic and retrospective H-reflex bounds. The procedure leveraged the observation that, for all participants, the shapes of the two waveform components were highly correlated (provided the stimulation artifact had been removed as described earlier).

First, H-reflex amplitude was determined for each trial of the recruitment curve measurement, using the mean-rectified measure. Then, the two trials with the largest H-reflex were discarded (to reduce the influence of outliers) and the filtered, artifact-removed EMG signals for the next-largest 8 trials were averaged to form an H-reflex template, defined only between the bounds $[t_{\text{start}},t_{\text{end}}]$. Separately, the 8 trials with the largest stimulation intensities were averaged to obtain a template in which the M-wave was prominent. The correlation function between the two templates was evaluated, and the M-wave bounds were determined as $[t_{\text{start}}-\Delta t,t_{\text{end}}-\Delta t]$, where $\Delta t$ was the shift that maximized the correlation between the two templates.

2.5. Fitting Recruitment Curves

Previous approaches have used sigmoid functions to model both the M-wave recruitment curve [26] and the ascending part of the H-reflex recruitment curve [27]. The latter approach leaves open the question of how to judge when the curve is no longer ascending, which itself requires a fit. Such circularity is avoided in the approach of Brinkworth et al. [28], whose equation can be adapted to combine a nonlinearity with a Gaussian function. While this can provide fits to the full H-reflex recruitment curve, we found that it failed to capture certain features of many of our participants’ curves (such as the fact that it may level off at a non-zero value for high stimulating current values) with detrimental consequences for the accuracy in finding other key parameters or derived measures (such as the current $x_{\text{HMAX}}$ that produce maximal H-reflex responses).

In common with previous approaches, we model the M-wave recruitment curve as a logistic function of stimulus intensity $x$, scaled in the range $({\gamma }_m{\lambda }_m,{\lambda }_m)$:

$$M(x)={\lambda }_m\left(\frac{1-{\gamma }_m}{1+\text{exp}(-4{\mathrm{e}}^{{\beta }_m}(x-{\alpha }_m))}+{\gamma }_m\right).$$ (1)

To address the shortcomings of the previous approaches, we take the novel approach of modeling the H-reflex recruitment curve as a “hill curve” or product of two sigmoids:

$$H(x)=u(x)v(x)\text{where}$$ (2)

$$u(x)=\frac{{\lambda }_u}{1+\text{exp}(-4{\mathrm{e}}^{{\beta }_u}(x-{\alpha }_u))},\text{and}$$ (3)

$$v(x)=\frac{1-{\gamma }_v}{1+\text{exp}(-4{\mathrm{e}}^{{\beta }_u+\delta }({\alpha }_v-x))}+{\gamma }_v.$$ (4)

Thus, the ascending side of the hill, $u(x)$, is a logistic function scaled to the range $(0,{\lambda }_u)$, with its inflection point located at $x={\alpha }_u$ and its gradient at the inflection point equal to ${\lambda }_u{\mathrm{e}}^{{\beta }_u}$. The descending side, $v(x)$, is a logistic function scaled to the $({\gamma }_v,1)$, with its inflection point at $x={\alpha }_u$ and its gradient equal to $({\gamma }_v-1){\mathrm{e}}^{{\beta }_u+\delta }$ at that point—the asymmetry parameter $\delta$ is hence the log of the ratio between the normalized absolute slopes of the two sigmoids. The parameter ${\gamma }_v$, representing the proportional lower-asymptote value at high stimulation intensities, is constrained in the range [0, 1]—hence $v(x)$ has a maximum range of (0, 1) and can be interpreted as a probabilistic weighting that reflects the proportion of muscle fibers that are no longer available to contribute to the H-reflex (e.g., due to their recruitment into the earlier M-wave response).

Thus $M(x)$ has four parameters, $\{{\lambda }_m,{\alpha }_m,{\beta }_m,{\gamma }_m\}$, and $H(x)$ has six parameters: $\{{\lambda }_u,{\alpha }_u,{\beta }_u,{\gamma }_u,{\alpha }_u,\delta \}$. The location parameters ${\alpha }_m$, ${\alpha }_u$ and ${\alpha }_v$ were all constrained to be in the range $[\frac{x_1+x_2}{2},\frac{x_{N-1}+x_N}{2}]$. The log-normalized-gradient parameters ${\beta }_m$ and ${\beta }_u$ were constrained to be $\le \log {\max }_{n\in \{1,\dots ,N-1\}}1∕(x_{n+1}-x_n)$. Parameter fitting was performed using our custom Python software, which made use of the Trust Region Reflective optimizer [29] as implemented in version 1.7.3 of scipy [30]. The software includes automated heuristics that initialize the optimization with reasonably well-fitting values (a fairly easy task given the one-dimensional nature of the inputs) and did not require manual intervention in any of the data sets studied here. The software is available for use under an open-source license at https://pypi.org/project/RecruitmentCurveFitting

For a given set of optimized parameters, there is unfortunately no closed-form solution for the horizontal location of the peak, $x_{\text{HMAX}}$. However, given that there is only one maximum and we only need to search a one-dimensional space to find it, this is easy to solve to arbitrary precision using primitive iterative methods—we simply perform a few iterations of grid search, narrowing the range by a fixed factor each time.

3. Results

Analyses are based on the widely-used Bland-Altman approach [31, 32, 33] in which a new measure P is compared against a previous standard Q that quantifies the same phenomenon. Trends in the numeric discrepancy $P-Q$ are examined as a function of Q. The degree of agreement between the two measures is quantified by characterizing the distribution of $P-Q$ values—by their standard deviation, and/or by computing limits of agreement (LOA) which are percentiles of the distribution. For example, the 95% LOA are an estimate the range of values within which the discrepancy is expected to lie 95% of the time (note that both the upper and lower limits of agreement are themselves estimates, with an associated statistical uncertainty).

The ground truth is not available as such in any of the analyses. Therefore, we quantify the agreement between all pairs of methods of estimating bounds: automatic vs. original, automatic vs. retrospective, and retrospective vs. original. The distribution of discrepancies between the two manual estimates (retrospective vs. original) provides a rough benchmark for judging the performance of the automatic algorithm.

Figure 3 shows the agreement of the estimated H-reflex bounds themselves, in milliseconds. The discrepancies are roughly equal between all pairings, with a standard deviation between 1.0 and 1.3 ms and 95% LOA being around ±2.5 ms.

Figure 3:

Comparison of automatic and manual bounds estimates. Bland-Altman plots compare values of the original, retrospective, and automatic soleus H-reflex bounds in milliseconds relative to stimulation. A: Automatic vs. original bounds; B: Automatic vs. retrospective bounds; C: Original vs. retrospective bounds. In each panel, red left-pointing arrowheads denote the start of the H-reflex interval and blue right-pointing arrowheads denote the end of the H-reflex interval. Each participant is represented by one red and one blue arrowhead. Horizontal dashed lines denote 95% LOA. Error bars denote the standard error of the agreement limits, computed according to the method of Carkeet [33].

Figures 4 and 5 show the consequent discrepancies in estimation of the magnitude of the H-reflex response. The data are drawn from the baseline trials (repeated stimulation at the same effective intensity). H-reflex magnitudes are expressed as a percentage of each participant’s initial $H_{\max }$ measurement, as obtained from their first full recruitment curve. Panels A–C of Figure 4 show that overall (taking all participants together), the standard deviation of discrepancies is between 5 and 9 percentage points. They also show that, despite the consistent stimulation intensity, the responses are quite variable for some participants. This variability reveals that the arithmetic differences between magnitudes obtained via different estimation methods are proportional to the magnitudes themselves—an effect that is most clearly seen in the participants plotted in pink and gray. These linear relationships indicate that perturbing a bound causes a certain extra proportion of the energy of the H-reflex waveform to be captured, or omitted, rather than a fixed amount. The gradients noticeable for pink and gray participants, then, are simply indicators that these two participants have the largest mismatches of the group. Since these effects are largest in panels A and C, and smaller in B, it follows that a likely major source of these mismatches is error in the original bounds, which were subsequently corrected by the expert’s retrospective re-scoring. A proper Bland-Altman analysis should use log coordinates to present data that demonstrate such linear trends—accordingly, in panels D–F, we see that the trends no longer hold when we look at arithmetic differences in the logged magnitudes. The resulting units of discrepancy (log10 of percentage points of initial $H_{\max }$) are somewhat harder to interpret intuitively, however.

Figure 4:

Comparison of H-reflex magnitude estimates resulting from the three different bounds estimation methods. Bland-Altman plots compare the amplitude of the soleus H-reflex as estimated by original, retrospective, and automatic bounds, and normalized by $H_{\max }$ from each participant’s first full recruitment curve. On average, 1192 trials were collected from each participant with a current that elicited a reflex response close to $H_{\max }$. Different colors and marker shapes denote different participants. Horizontal dashed lines indicate the 95% LOA of the data pooled across all participants. Panels A–C show arithmetic differences between response magnitudes: A shows automatic vs. original bounds; B shows automatic vs. retrospective bounds; C shows retrospective vs. original bounds. Panels D–F show the same data as A–C, respectively, except that arithmetic differences are calculated between log₁₀ (magnitude) estimates. Steps of +0.05 or −0.5 in log₁₀ space correspond to a proportional 12.2% increase or 10.9% decrease, respectively.

Figure 5:

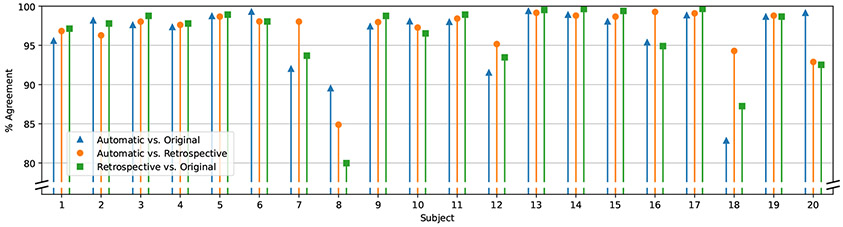
Agreement between automatic and manual bounds when classifying each response magnitude as a successful or unsuccessful operant-conditioning trial according to the protocol described in [15]. The height of each stem denotes how often different bounds led to the same classification of H-reflex magnitude. Blue triangles denote automatic vs. original manual bounds; orange circles denote automatic vs. retrospective manual bounds; green squares denote original manual vs. retrospective manual bounds. Each group of three stems shows results from a different participant.

Note that the participant denoted by gray circles still exhibits larger discrepancies than the rest of the group. This was Participant #8, who, uniquely among the participant group, displayed a different H-reflex latency in some sessions than others. This was likely due to a documented change in medication. Therefore, in this participant’s case, a single set of bounds did not serve to capture the H-reflex commensurately in all sessions and would be expected to lead to poor agreement.

For the specific application of H-reflex operant conditioning, it is important to know how big a difference the new automated method makes to the contingency of the conditioning protocol: to what extent would the classification of trials as successful or unsuccessful differ, depending on the bounds? To examine this, we applied the procedure described by Hill et al. [15] to the available sessions, as if they had been conditioning sessions: the 66.7^th percentile of the distribution of magnitudes was computed for each set of 75 trials, and used as a cutoff criterion for the subsequent set; magnitudes above the cutoff were considered failed trials, and magnitudes below the cutoff were considered successes. Figure 5 shows the proportion of trials on which the different bounds led to identical judgment of success or failure. Agreement was at least 80% for all participants, and at least 95% for most. When comparing automatic against retrospective bounds, only one participant exhibited an agreement of less than 90%, and again that was Participant #8 (discussed above) whose non-stationary H-reflex latency would be expected to lead to poor agreement in this test. Excluding that participant, the average agreement was 97.5% across the rest of the participants.

In Figure 6, the 95% LOA are shown relative to “standard” recruitment curves. The standard curves were obtained by calculating the median parameter value, across the whole data-set, for each of the parameters $\{{\lambda }_m,{\alpha }_m,{\beta }_m,{\gamma }_m,{\lambda }_u,{\alpha }_u,{\beta }_u,{\gamma }_v,{\alpha }_v,\delta \}$. Certain parameters and derived measures of interest are highlighted by the dashed lines: the inflection points, ${\alpha }_u$ and ${\alpha }_v$, of the rising and falling parts of the H-reflex recruitment curve, respectively; the stimulation current value $x_{\text{HMAX}}$ that lies between the two inflection points and which gives rise to the largest $H(x)$ value (i.e. the interpolated $H_{\max }$); the stimulation current value $x_{\mathrm{M}10}$ that gives rise to the interpolated M-wave size 10% of the way between minimum and maximum (M-wave threshold); and finally the interpolated $H_{\max }$ and $M_{\max }$ response sizes themselves ($H(x_{\text{HMAX}})$ and ${\lambda }_m$). For each of these, the distribution of discrepancies between one set of bounds and another was computed via a standardization procedure: when comparing parameters or derived measures $P$ from one bounds-estimation method against corresponding values $Q$ from another method across $d=1\dots D$ recruitment curves, the shorthand “P vs. Q”, as used in the legend of Figure 6, means “multiply each $P_d$ and $Q_d$ value by the scale factor $s_d$ that maps $Q_d$ to the corresponding fixed value from the ‘standard’ curve, then compute LOA from the resulting distribution of $s_d{P}_d-s_d{Q}_d$ discrepancies.” For $x_{\text{HMAX}}$, the standard deviation of standardized discrepancies $s_d{P}_d-s_d{Q}_d$ of automatic bounds $P$ relative to retrospective bounds $Q$ is 0.015 mA, which is 1.5% of the width ${\alpha }_v-{\alpha }_u$ of the standard H-reflex recruitment curve, or 0.6% of the standard $x_{\text{HMAX}}$ value. For the M-wave threshold $x_{\mathrm{M}10}$, the standard deviation of standardized automatic-vs-retrospective discrepancies is 0.037 mA, which is 1.5% of the standard $x_{\mathrm{M}10}$ value. The corresponding 95% LOA were [−1.1%, +1.4%] of typical $x_{\text{HMAX}}$ and [−1.7%, +3.5%] of typical $x_{\mathrm{M}10}$. Both measures reflect the location of the recruitment curves along the horizontal axis, and as such are relatively insensitive to changes in bounds because they are governed by the relative sizes, at different stimulus intensities, of the EMG responses. A change in bounds tends to have roughly the same proportional effect on response size at all stimulus intensities. By contrast, the aspects of Figure 6 that are measured in mV are dependent on absolute magnitudes of the same integrals, making them more sensitive to changes in bounds: the standard deviation of standardized $H_{\max }$ discrepancies is 0.085 mV, i.e. 6.5% of $H_{\max }$ itself, and the standard deviation for $M_{\max }$ is 0.14 mV, i.e. 6.3% of $M_{\max }$. Furthermore, unlike the current values, there was an appreciable bias: automatic bounds systematically estimated $H_{\max }$ and $M_{\max }$ as higher than the retrospective bounds, making the corresponding 95% LOA distinctly asymmetric: [−7.3%, +19%] for $H_{\max }$ and [−7.2%, +18%] for $M_{\max }$.

Figure 6:

Discrepancies between the recruitment curves derived from the automatic and the two manual methods of estimating bounds. A “standard” M-wave recruitment curve (blue) and H-reflex recruitment curve (orange) are plotted as solid lines. Dashed lines indicate various parameters of, and measures of interest derived from, the standard curves: the vertical orange lines show ${\alpha }_u$, $x_{\text{HMAX}}$ and ${\alpha }_v$, and the horizontal orange line shows $H_{\max }$; the vertical blue line shows $x$ at the 10% M-wave threshold and the horizontal blue line shows ${\lambda }_m$ (i.e. $M_{\max }$). Bars between symbols show 95% LOA around each of these parameters and derived measures, after standardization to the standard curves (see text for details).

4. Discussion

The preceding results show that estimation of the start and end of human soleus M-wave and H-reflex components can be automated using a small fraction of the data that is routinely used in H-reflex operant conditioning protocols for this purpose, while producing results that are close to those of a human expert. Specifically, the millisecond bound values from the automatic method agree well with the manual estimates (Figure 3). There is also a high degree of agreement between automatic and manual methods when we consider the resulting classification of each response magnitude as a successful or unsuccessful operant-conditioning trial (Figure 5). Automated determination of bounds also makes minimal difference to recruitment-curve parameters, and the recruitment curves from the automated method agree as well with the ones from manual methods as the curves from the two manual methods agree with each other (Figure 6).

Note that there is no objective ground truth against which we can compare the automated results. Rather, we rely on assessing the agreement between the automated bounds and those judged by experts. Some variation is to be expected between our “original” and “retrospective” expert bounds. Whereas the original bounds were the product of a team effort among laboratory members, the retrospective bounds were performed by a single expert, blind to the participants’ identity, anatomy, pathology and their bounds from other methods, but with the added benefit of 6 more years’ experience regarding the influence of H-reflex definition on the effectiveness of operant conditioning protocols. As such, the comparison between retrospective and original bounds does not provide a rigorous indication of any human expert’s reliability, but rather simply a rough benchmark for the variation that can occur in real-world usage. The most informative comparison is between the automatic and retrospective bounds (middle panels of Figures 3 and 4, and circles in Figures 5 and 6)—the retrospective bounds are the closest we have to a ground truth, and since they were estimated after the automatic bounds were finalized, the automatic algorithm would not have been unduly influenced by them. It is encouraging to note that, of the three comparisons, the automatic vs. retrospective comparison generally exhibited the tightest limits of agreement (LOA) between the millisecond values of the bounds themselves, the tightest LOA between resulting estimates of H-reflex size, the highest level of agreement on what constituted a successful or unsuccessful operant-conditioning trial, and the smallest perturbation of the fitted recruitment curves. This reduction in variability suggests that both established and emerging H-reflex protocols stand to benefit from adopting the automated approach, thereby becoming far less susceptible to inter-personnel variability and human error.

The focus on precision in determining H-reflex bounds is new relative to previous analytic approaches. H-reflex amplitude can be measured as either the peak-to-peak difference or the mean absolute (rectified) amplitude over a specified time window. For cases in which H-reflex morphology is simple (e.g., a biphasic response), peak-to-peak amplitude is well correlated with the mean rectified amplitude—cf. results of Tucker and Türker [34] on M-waves. Thus, due to its computational simplicity, peak-to-peak amplitude has been a commonly-used surrogate metric for H-reflex size. Indeed, most automated analyses to date have used this approach (for example, see Moukarzel et al. [35]). However, the peak-to-peak measurements may not reflect the totality of the underlying motoneuron discharge. EMG measurements of spinal reflex amplitude reflect the eficacy of sensory afferent excitation in generating action potentials in motoneurons [10, 1, 3]. Accordingly, the amplitude of the H-reflex component can be used to assess the effectiveness of muscle spindle afferent excitation (mostly via Ia fibers) in recruiting the studied muscle’s motoneuron pool—in short, the excitability of the H-reflex pathway. The imprecision of peak-to-peak measures is most clearly seen in other spinal reflexes that originate in less-synchronous (i.e., more temporally-dispersed) afferent excitation; in such cases, it is more common to see mean-rectified measures integrated over well-defined time windows, because these better reflect changes in motoneuron firing probability [36, 37, 38]. In reflex operant conditioning protocols it becomes important, even for the H-reflex, that we provide feedback on the mean rectified reflex amplitude over a tightly focused latency window. This is crucial for targeting a specific pathway, because it fixes the time window in which the subject is rewarded for increasing (in up-conditioning) or decreasing (in down-conditioning) the firing probability of the target muscle’s motoneurons in response to the corresponding afferent input [13]. In fact, EMG response immediately outside of the rewarded reflex time window does not necessarily change [13], betraying the fact that it may reflect sources of activation that are functionally distinct from the target pathway, which would dilute the measurement of the target if included. Accordingly, early reflex operant conditioning attempts that used wide reflex time windows failed to achieve conditioning (unpublished data observed by collaborators of author AKT). The windows used in these unsuccessful studies were 5–10ms wider than those subsequently used successfully by Thompson and colleagues [13, 16, 39, 18] and by Mrachacz-Kersting et al. [40]. Thus, quantifying the reflex size as mean rectified amplitude over a precisely-defined, tightly-focused latency window is highly recommended when the reflex measurement is used as a tool of neurobehavioral training such as reflex operant conditioning.

While the present algorithm is effective at identifying and quantifying the soleus H-reflex and M-wave, we benefit from the fact that the soleus lends itself easily to this analysis relative to other muscles. By virtue of the length of the nerve pathways to and from the spinal cord, the soleus produces M and H responses that are well separated in time. The present algorithm benefits from such clean separation of responses to accurately delineate the bounds of each response. However, H-reflex and M-wave measurements are equally clinically useful in the upper extremities, where the process of separating the responses is more challenging. In the flexor carpi radialis (FCR), for example, the M-wave and H-reflex often overlap [41, 42]. It would be necessary to modify the present algorithm for application to different muscle targets. In more proximal motor targets, M-wave and H-reflex can have significant temporal overlap. For this application, a similar wavelet-based approach could be used to transform the overlapping signals into overlapping Gaussian-like peaks. A different heuristic threshold to determine the approximate onset and offset of each response could then be developed by comparing experts' manual bounds with the transformed peaks. However, there is a limit to the degree to which overlapping responses can be separated post-hoc, and to the utility of the mean-rectified estimate when overlap is significant. In such cases, a more sophisticated source-separation algorithm could be used to isolate the responses of interest, using either a blind [43] or model-based [23] approach—in the latter case, perhaps taking advantage of the apparent similarity of the M- and H-responses. Such an algorithm is in development by the authors, but is beyond the scope of the present work.

The particular approach taken in section 2.4 assumes that the M-wave and H-reflex are isomorphic. Empirically, once the stimulation artifact had been removed, this was found to be the case in all the datasets we observed. However, the assumption of isomorphism needs to be investigated more thoroughly. A challenge here is the inadvertent recruitment of off-target muscles (e.g. gastrocnemii) at higher stimulus intensities, which can change the apparent shape of the M-wave and hence break the isomorphism. Multi-electrode recording, in combination with algorithmic source-separation techniques, may be of use in removing this confound. The algorithm might also benefit from application of deep-learning techniques that incorporate other sources of prior information to guide the fit, such as quantitative structural information about muscle density and identification of abnormalities [44, 45, 46].

The latency and duration of the M-wave and H-reflex can change based on disease progression, medication (as in the case of our Participant #8), time of day, or other factors. In the operant-conditioning application, maintaining consistent absolute bounds is critical, so such variation in response latency should simply be minimized by controlling its causes as far as possible. By contrast, in other applications it seems clear that the automated bounds-estimation algorithm could play an important role in longitudinal studies of the responses’ temporal characteristics, especially given that the algorithm requires only a few minutes of data to provide good estimates. Thus, the approach would be valuable in quantitative studies of H-reflex latency shifts in response to different perturbations, and in applications that use the H-reflex as a biomarker, such as detecting left-right asymmetries in H-reflex latency and amplitude as an early marker of radiculopathy [47, 48].

The methods used herein to fit H-reflex and M-wave recruitment curves could similarly be used to fit recruitment curves generated by non-electrical means, such as the mechanical stretch reflex of the soleus which can also be conditioned [40], or magnetically-induced motor evoked potentials.

In summary, we have shown that a relatively simple algorithm can effectively replicate an expert human’s ability to identify and characterize the H-reflex and M-wave during a motor control study. The proposed methods, while initially developed to automate a specific closed-loop application of H-reflex recruitment, could be widely applicable to a broad range of reflex and motor control applications. In all such applications, the algorithm could reduce the time, cost, complexity and variability associated with human expert judgments; thus it has great potential to enable effective translation of research protocols into clinical use.

The data that support the findings of this study are openly available at https://doi.org/10.17605/OSF.IO/SNA3F