Abstract
This paper proposes a deep learning framework to encode subject-specific transformations between facial and bony shapes for orthognathic surgical planning. Our framework involves a bidirectional point-to-point convolutional network (P2P-Conv) to predict the transformations between facial and bony shapes. P2P-Conv is an extension of the state-of-the-art P2P-Net and leverages dynamic point-wise convolution (i.e., PointConv) to capture local-to-global spatial information. Data augmentation is carried out in the training of P2P-Conv with multiple point subsets from the facial and bony shapes. During inference, network outputs generated for multiple point subsets are combined into a dense transformation. Finally, non-rigid registration using the coherent point drift (CPD) algorithm is applied to generate surface meshes based on the predicted point sets. Experimental results on real-subject data demonstrate that our method substantially improves the prediction of facial and bony shapes over state-of-the-art methods.
Keywords: Orthognathic surgical planning, Face-bone shape transformation, 3D point clouds, Point-displacement network
1. Introduction
Orthognathic surgery corrects craniomaxillofacial (CMF) deformities (Xia et al., 2015), primarily to improve facial appearances and secondarily to improve functions such as chewing, swallowing, and breathing (Shafi et al., 2013; Shahim et al., 2013). Due to the complexity of face and jaw anatomies, orthognathic surgery relies on precise surgical planning with the help of computer-aided surgical simulation (CASS) techniques (Xia et al., 2009, 2011; Yuan et al., 2017; Sonneveld et al., 2019). The techniques typically involve (1) reconstructing a 3D patient bony model from computed tomography (CT) or cone beam computed tomography (CBCT) scans; (2) simulating an osteotomy by virtually cutting the bony model into several bony segments; (3) moving the bony segments to desired positions to normalize jaw deformities (Wang et al., 2015). Surgeons can accurately and efficiently plan the bony movements using CASS (Wang et al., 2015; Xiao et al., 2021c,a). However, they cannot practically predict postoperative facial appearance from the normalized bony model during the surgical planning process, and just hope for the best that a postoperative face will “automatically” become normal following the surgery (Kim et al., 2019; Ma et al., 2021). However, this is often not true in practice because the relationship between bony and facial soft tissue movements is based on complex and non-trivial physical interactions (Bell and Ferraro, 1993). Therefore, there is an unmet need in predicting facial appearances given a normalized bony model to provide surgeons with visual updates needed for continuous optimization in surgical planning.
Current methods for the prediction of facial appearances mostly rely on biomechanical simulation methods, e.g., finite-element models (FEMs), mass–spring models (MSMs), and mass-tensor models (MTMs) (Nadjmi et al., 2014; Knoops et al., 2018; Kim et al., 2019). Biomechanical simulation requires labor-intensive and time-consuming data processing, preventing it from being applied in daily clinical scenarios. In recent years, face-bone transformation, which reconstructs a facial shape from a bony shape and vice versa, has been applied to multiple fields, such as forensic medicine (Paysan et al., 2009), CMF surgical planning (Xiao et al., 2019), archaeology (Duan et al., 2015), and animation (Nguyen et al., 2020). For example, in planning for the surgery of a patient with facial trauma, a patient-specific reference bony shape model is estimated from a facial surface reconstructed from the patient’s pre-traumatic portrait photos (Xiao et al., 2019). However, most methods for face-bone transformation are based on the unrealistic assumption that similar facial shapes have similar underlying bony shapes and vice versa, ignoring subject-specificity, thus resulting in limited performance.
Deep learning has been recently applied to surface parcellation (Gopinath et al., 2019; Zhao et al., 2019), dental surface labeling (Zanjani et al., 2019; Lian et al., 2020), and CMF shape prediction (Xiao et al., 2021a,b; Ma et al., 2022). State-of-the-art methods such as P2P-Net (Yin et al., 2018) perform end-to-end geometric learning on point clouds, the most straightforward and efficient representation of 3D models. High-level correspondences between different views (e.g., meso-skeletons and surfaces) can be captured for shape transformation.
Here, we propose a point-cloud deep neural network to learn subject-specific transformations between normal facial and bony shapes. Our method consists of three main steps. In the first step, we extract multiple point subsets from a high-resolution 3D model (i.e., facial surface or bony surface mesh) for efficient end-to-end network training. In the second step, we employ a bidirectional P2P-Conv to predict the transformations between the bony point clouds and the respective facial point clouds. Our P2P-Conv consists of two sub-networks: one to predict face-to-bone (F2B) transformation and the other to predict bone-to-face (B2F) transformation. P2P-Conv extends the state-of-the-art P2P-Net (Yin et al., 2018) by applying dynamic point-wise convolution (i.e., PointConv Wu et al., 2019) to comprehensively capture local-to-global spatial information of CMF shapes. In the third step, P2P-Conv predictions for multiple point subsets are combined to obtain a high-resolution point cloud output. A 3D surface mesh is finally reconstructed by non-rigid registration. Our method outperforms state-of-the-art methods in predicting facial and bony shapes on a dataset of 45 real subjects.
The contribution of our paper is three-fold:
We propose a deep learning framework to predict subject-specific transformations between facial and bony shapes. The core of the framework is a bidirectional P2P-Conv, comprehensively capturing the complex geometrical correspondences between bony and facial shapes.
We propose a strategy to augment the training set for P2P-Conv by extracting multiple pairs of non-overlapping facial and bony point subsets from each subject using a two-step point sampling strategy.
Our method improves the prediction accuracy of facial and bony shapes by 25.7% and 21.0%, respectively, compared with the sparse representation (SR) method described in Xiao et al. (2019).
The rest of the paper is organized as follows. Related work, including face-skull modeling and deep learning on 3D point clouds, is briefly reviewed in Section 2. The proposed framework is described in detail in Section 3. Experimental results are presented in Section 4. Finally, the paper is concluded in Section 5.
2. Related work
2.1. Face-skull modeling
Existing face-skull modeling methods are mainly proposed for forensic facial reconstruction from skull structure. For example, Paysan et al. (2009) proposed statistical shape models (SSMs) for faces and bones, optimized via ridge regression. Duan et al. (2014) constructed two tensor models for face and bony subspaces. Mapping from the bone subspace to the facial subspace is performed using partial least squares regression (PLSR). Other relevant methods can be found in Duan et al. (2015), De Buhan and Nardoni (2016), Shui et al. (2017) and Madsen et al. (2018). In a more recent work (Xiao et al., 2019), SR is employed to reconstruct reference bony models from pre-traumatic portrait photos. Specifically, two dictionaries are constructed for facial and bony models extracted from a set of normal subjects. Sparse coefficients are learned from a facial model reconstructed from the pre-traumatic portrait photos and are applied to the bony dictionary to generate in a bony model. However, these methods are based on the assumption that subjects with similar facial shapes have similar underlying bony shapes, unrealistically ignoring subject-specific relationships between facial and bony shapes.
2.2. Deep learning on 3D point clouds
2.2.1. Learning from point sets
There is a recent emergence of deep learning methods for point sets (Qi et al., 2017a; Li et al., 2018; Guo et al., 2019). A pioneering method, called PointNet, learns spatial features from unordered point sets (Qi et al., 2017a). PointNet++ (Qi et al., 2017b) extends PointNet by learning spatial features hierarchically. PointCNN (Li et al., 2018) utilizes -transformation for point permutation and employs -Conv, which is invariant to point ordering, to learn point shape information. SpiderCNN (Xu et al., 2018) extends convolutional operations from regular grids to irregular point sets by using parametrized convolutional filters. PointConv (Wu et al., 2019) defines density re-weighted convolution on point sets as a Monte Carlo estimate of a continuous 3D convolution.
2.2.2. Cross-domain shape transformation
Leveraging PointNet++ (Qi et al., 2017b), P2P-Net (Yin et al., 2018) learns geometric transformations between point-based shape representations from two domains. P2P-Net is a bidirectional point displacement network that transforms a source point set into a prediction of the target point set and vice versa. P2P-Net is a weakly-supervised network trained using paired point sets without strict P2P correspondence. However, PointNet++ does not explicitly consider the spatial distribution of points for point feature aggregation, and may fail to capture some helpful shape information. More recently, LOGAN (Yin et al., 2019) was proposed to perform cross-domain transformation based on a generative adversarial network (GAN) (Goodfellow et al., 2014) using shape information encoded in a shared latent space. LOGAN is an unsupervised network designed for learning transformation from unpaired shapes. Although easier to train due to its unsupervised nature, LOGAN does not perform P2P-Net on supervised tasks (Yin et al., 2019).
3. Materials and methods
3.1. Data and pre-processing
We randomly selected 45 CT head scans of normal subjects from our digital archive for method development and evaluation. Subjects with jaw deformities, previous jaw/facial cosmetic surgeries, or CMF trauma were excluded. These CT scans were deidentified and obtained from a digital library collection at the Department of Oral and CMF Surgery at Shanghai Ninth People Hospital, Shanghai Jiao Tong University School of Medicine (Yan et al., 2010). The images were acquired using a 64-slice GE scanner following a standard clinical protocol: 512 × 512 matrix, 25 cm field of view, and 1.25 mm slice thickness (Yan et al., 2010; Wang et al., 2015).
Facial and bony models were first automatically segmented from the CT scans using a deep-learning-based segmentation method proposed in Liu et al. (2021), followed by manual correction by an experienced oral surgeon. To align the segmented models to the same space for efficient training, we first rigidly registered each segmented bony model to a bony template. Then, the corresponding facial model was transformed using the transformation matrix obtained from the rigid registration. The bony template was predetermined as the bony model with landmarks closest to the average bony landmarks of the subjects in the dataset. The aligned facial and bony models were cropped to retain only the CMF region, which is pertinent to orthognathic surgery.
3.2. Overview of the proposed framework
The proposed bidirectional face-bone shape transformation framework consists of three main parts (Fig. 1). First, using a proposed two-step point sampling strategy, multiple non-overlapping point subsets are uniformly sub-sampled to represent the high-resolution bony or facial shape. Then, these bony (or facial) point subsets are fed to our P2P-Conv separately to predict the corresponding facial (or bony) point subsets. Our P2P-Conv consists of two sub-networks: F2B and B2F. Finally, the predicted point subsets in either the facial or bony domain are merged to generate a dense point set. A high-resolution surface mesh is generated by non-rigidly registering predetermined templates to the dense point set using the CPD algorithm (Myronenko and Song, 2010).
Fig. 1.
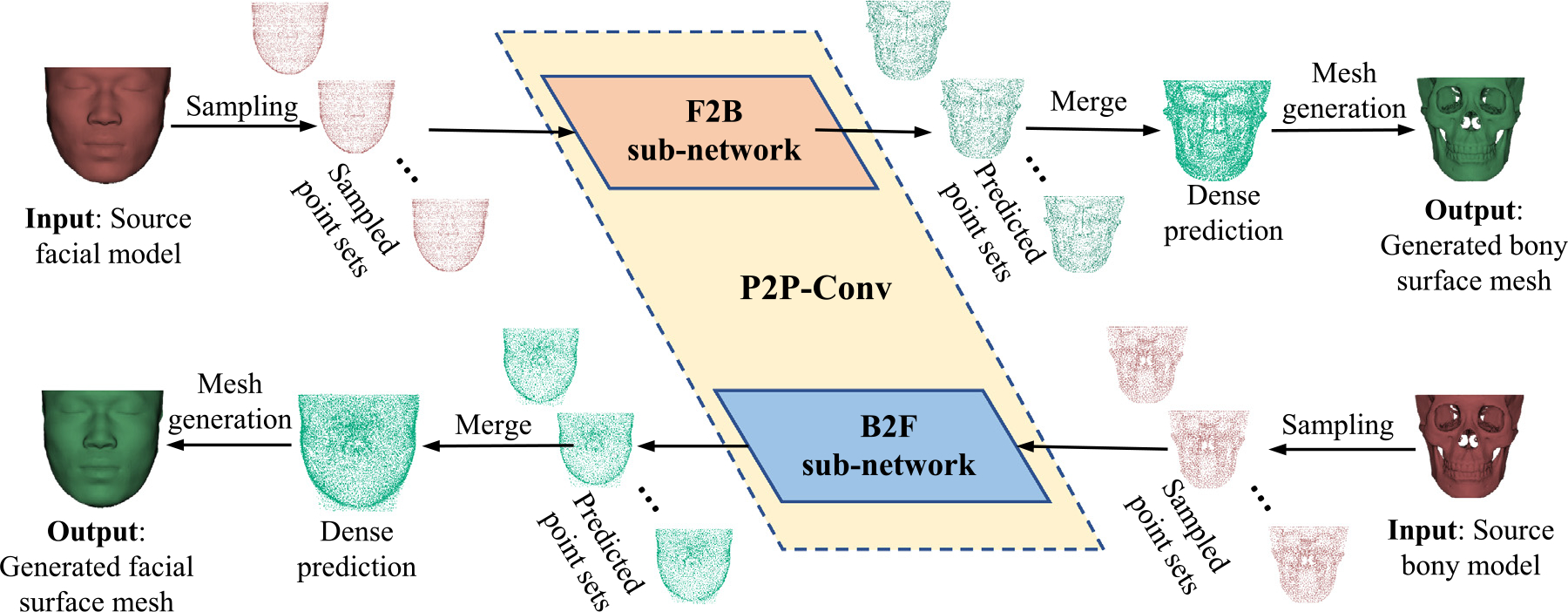
P2P-Conv for subject-specific nonlinear transformations between facial and bony shapes. P2P-Conv outputs generated from multiple point subsets are merged to generate dense surface meshes via non-rigid registration with a template.
3.3. Point sampling
Due to GPU memory limitations, we introduce a two-step point sampling strategy to sub-sample multiple non-overlapping point subsets from high-resolution facial and bony shapes. Specifically, given a high-resolution shape mesh non-overlapping -point subsets are first sub-sampled randomly from the mesh vertices. Then, Poisson-disk sampling (Yuksel, 2015) is employed to further uniformly sub-sample points from each point subset in , resulting in -point subsets . Poisson-disk sampling produces tightly-packed points, but are no closer to each other than a specified minimum distance. Compared to random sampling, Poisson-disk sampling provides a more uniform point distribution over the sampling domain.
3.4. P2P-Conv
We develop a bidirectional P2P-Conv to capture the nonlinear transformation (i.e., point displacement) between the facial and bony shapes. P2P-Conv is an extension of a state-of-the-art shape transformation network called P2P-Net (Yin et al., 2018). P2P-Net is a bidirectional shape transformation network-based on PointNet++. The training of the P2P-Net is weakly supervised by point sets of paired source and target shapes without relying on strict P2P correspondence. However, P2P-Net is inaccurate for complex shapes like the facial and bony shapes mainly because PointNet++ (Qi et al., 2017b) uses max-pooling to aggregate and propagate geometric features and is hence not effective in capturing localized spatial information. To improve accuracy, we employ PointConv (Wu et al., 2019) for dynamic point-wise convolution. PointConv is an extension of the Monte Carlo approximation of the 3D continuous convolution operator (Hermosilla et al., 2018). PointConv learns multi-layer perceptrons on local point coordinates to approximate continuous weight and density functions in convolutional filters. Compared with PointNet++, PointConv can capture more localized spatial information. Therefore, by leveraging PointConv, P2P-Conv can more comprehensively capture local-to-global spatial information to facilitate shape transformation.
3.4.1. Architecture
The architecture of P2P-Conv is shown in Fig. 2. Given a pair of CMF facial shape and bony shape , P2P-Conv learns the bidirectional transformation between point subsets from and , i.e., and .
Fig. 2.
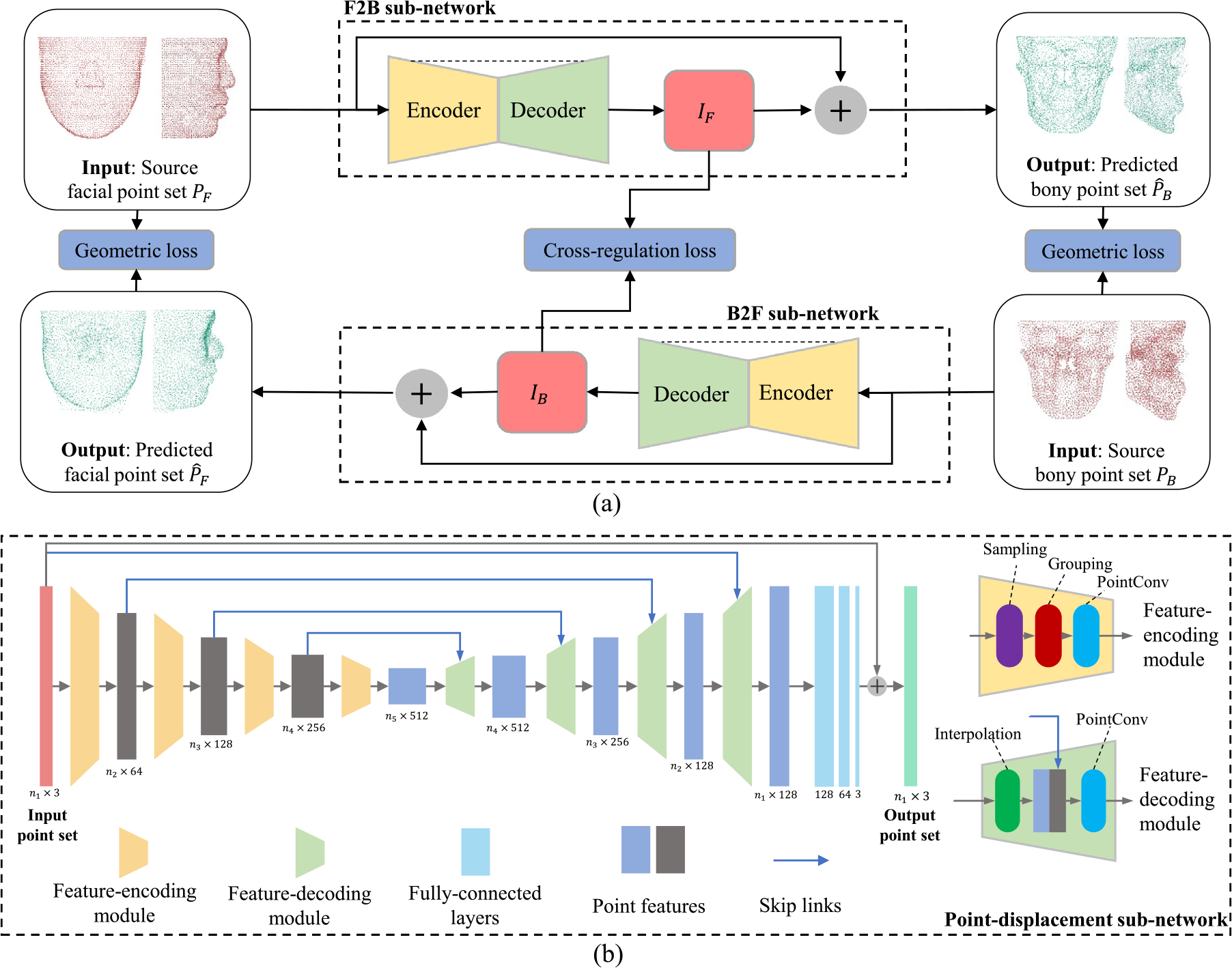
(a) The architecture of the bidirectional P2P-Conv displacement network for transformation between facial and bony shapes. Encoder and decoder blocks form the point feature abstraction and propagation modules based on the PointConv network (Wu et al., 2019). IF and IB denote the point displacement vectors associated with the facial and bony shapes, respectively. (b) PointConv-based point-displacement sub-network.
As shown in Fig. 2(a), P2P-Conv adopts a bidirectional architecture, similar to P2P-Net, and consists of two point-displacement sub-networks catering to transformations in opposite directions, i.e., F2B and B2F. The two point-displacement sub-networks share a common architecture as shown in Fig. 2(b). The F2B sub-network generates a set of displacement vectors that are applied to to predict the corresponding bony point set ,
| (1) |
B2F predicts the facial point set ,
| (2) |
Each sub-network in P2P-Conv learns a multi-scale feature embedding for each point using an encoder, consisting of sampling, grouping, and dynamic convolution layers (i.e., PointConv), as shown in Fig. 2(b). The sampling layer samples a subset of points from the given input point set using iterative farthest point sampling (Qi et al., 2017b). The grouping layer organizes the sampled point set from the sampling layer into point subsets using a ball query approach, which finds all points that are within a radius to the query point (Qi et al., 2017b). To abstract their point features, the PointConv layer performs convolutional operators on the grouped point subsets. The decoder consists of interpolation and PointConv layers. The interpolation layer propagates point features by interpolating feature values using inverse distance weighted average based on nearest neighbors (Qi et al., 2017b). Then, the interpolated features are concatenated with features from the encoder with the same resolution using skip links. Finally, PointConv is applied to the concatenated features. Point-wise outputs from the decoder are processed by a MLP to generate point-wise displacements (i.e., or ).
3.4.2. Loss functions
P2P-Conv is trained so that the predictions and are as close as possible to their targets and . In this work, we use the loss function of P2P-Net (Yin et al., 2018) to train P2P-Conv. Specifically, a geometric loss is used to measure the geometric differences between the predicted and target point sets. The loss consists of two terms: shape loss and point-density loss. The shape loss computes the sum of distance errors between the predicted point set and the target point set :
| (3) |
where denotes the Euclidean distance between points and represents the number of points in the predicted point set. Note that the shape loss is calculated without relying on P2P correspondence between the predicted point set and the target point set . The point-density loss measures the density similarity between and (Yin et al., 2018):
| (4) |
where denotes the ith point of the nearest points to from point set . Therefore, the geometric loss is defined as
| (5) |
where is a tuning parameter controlling the contribution of the density loss.
Complementary to the geometric loss, a cross-regularization loss is adopted to encourage the consistency between the displacement vectors and :
| (6) |
The total loss function of P2P-Conv is
| (7) |
where controls the contribution of the cross-regularization loss.
3.4.3. Data augmentation
We augment the training set to improve prediction accuracy and avoid overfitting. First, given a subject in the training set, non-overlapping facial point subsets , and non-overlapping bony point subsets , are sampled respectively from the facial and bony model of the subject using the two-step point sampling strategy described in Section 3.3. Each point subset contains 4096 points. Each sub-sampled facial point set can be paired with different bony point sets, generating a total of pairs of facial-bony point sets for training. These facial-bony point sets generated in data augmentation are paired since the facial and bony point sets are sub-sampled from the same subject. is set to 10 in our implementation.
3.5. Surface mesh reconstruction
According to Fig. 1, facial point subsets , sub-sampled from a high-resolution facial mesh surface are fed individually to the F2B sub-network, outputting predicted bony point subsets . The output point subsets are merged into a dense bony point set . The dense facial point set is obtained in the same manner. is set to five in our implementation. Mesh surfaces are then reconstructed for the predicted point sets with the help of multiple templates. One template is the facial/bony model averaged across all subjects. Three additional representatives facial/bony models are added as templates. We non-rigidly register the four bony templates to each predicted bony point set and select the registered template with the least error as the surface mesh of the predicted bony point set. The facial surface mesh is generated in the same manner.
3.6. Implementation details and parameter optimization
Due to GPU memory limitations, deep learning networks can only handle point sets of moderate size. For example, PointCov (Wu et al., 2019) can take no more than 5000 points. Therefore, we set the number of points in each point subset to . We separately feed point subsets to P2P-Conv to generate a dense point set prediction with points. The value of mainly affects the accuracy of the final reconstructed mesh surfaces and the mesh surface reconstruction time. We evaluated and measured the shape prediction error and surface reconstruction time for different ’s. Specifically, we randomly selected 36 subjects as the training set and one random subject from the training set for validation. We used the remaining nine subjects for testing. We used the square root of Chamfer Distances (CD) (Fan et al., 2017) to measure the shape error of the predicted facial surfaces:
| (8) |
where and represent a predicted point set and the ground truth, respectively. The results (Fig. 3) indicate that as increases, the shape error decreases but the time cost for mesh surface reconstruction increases. To balance between shape error and reconstruction time, we set to 5 and to 20,480 (5 × 4096). Sampling with 20,480 points using Poisson-disk sampling roughly covered the shape uniformly.
Fig. 3.

Shape error and reconstruction time as a function of the number of point subsets in point sampling.
The number of points associated with each layer in the point displacement sub-network was set to {4096,1024,256,64,32} following PointConv (Wu et al., 2019). The dimensions of the output point-feature vectors in the feature-encoding and feature-decoding modules were set to {64,128,256,512,512,256,128,128} following Qi et al. (2017b) and Wu et al. (2019). The MLP in P2P-Conv was designed with 128, 64, 3 channels following the point displacement networks proposed in Liu et al. (2019) and Ma et al. (2021). Using the Adam optimizer, P2P-Conv was trained by minimizing the loss function (7). The batch size was set to three due to GPU memory limitation. The training and validation logs of P2P-Conv, shown in Fig. 4 for one cross-validation, indicate that the model starts overfitting from 100 epochs. In our implementation, we trained our model with 200 epochs. The learning rate was set to 1e–3 and decayed to 1e–4 at discrete intervals during training following Yin et al. (2018). The value of in (4), in (5) and in (7) were empirically set to 16, 0.3 and 0.1, respectively. The aforementioned implementation parameters are summarized in Table 1. The models were trained on a machine with 32GB memory and an 11GB GeForce GTX 1080 Ti. It took roughly 25 mins to train one epoch using 3600 pairs of facial-bony point sets. The software libraries used in this implementation include Visualization Toolkit, Open3D and Tensorflow.
Fig. 4.

The training and validation logs of P2P-Conv.
Table 1.
Summary of hyperparameters.
4. Experiments
4.1. Competing methods
Our framework was first compared with two state-of-the-art methods, i.e., a principal component analysis (PCA)-based face-bone shape transformation framework (Shui et al., 2017) and a SR-based framework (Xiao et al., 2019). To verify the effectiveness of PointConv (Wu et al., 2019), we also compared our framework with PointNet++ and SpiderCNN. We used the same training and testing sets as the proposed method. The data was augmented to avoid overfitting. These methods are summarized as follows:
SR: The SR-based framework was implemented according to Xiao et al. (2019). Specifically, facial and bony dictionaries were constructed using the training subjects’ facial and bony point sets. Strict P2P correspondence was needed for point sets in the same domain. A facial template with 36 213 points and a bony template with 30 812 points were non-rigidly registered to the training subjects’ sampled facial and bony point sets using CPD, respectively. The warped facial and bony templates were used to construct the facial and bony dictionaries. The sparse coefficients of facial and bony point sets were used to construct the bony and facial shapes, respectively.
PCA: The PCA-based face-bone shape transformation framework was implemented according to the techniques in Shui et al. (2017). Specifically, SSMs of the skull and face were first constructed by PCA using the sub-sampled facial and bony point sets in SR. Then linear regression was employed to determine the relationship between facial and bony models. Given a skull, PC scores of the skull were estimated using the bony SSMs. To predict a face from the skull, a group of PC coefficients was calculated using the bony PC scores and the linear face-bone relationship. A 3D face was estimated by applying the PC coefficients to the facial statistical shape model.
PointNet++: P2P-Net using PointNet++ (Qi et al., 2017b) shape transformation framework was implemented according to Yin et al. (2018).
SpiderCNN: Like PointConv, SpiderCNN learns point features via convolution on irregular point sets. Convolution in SpiderCNN, called SpiderConv, is based on a family of parametrized filters (Xu et al., 2018). We implemented SpiderCNN-based P2P-Net using an architecture similar to P2P-Conv, but with PointConv encoder/decoder replaced with SpiderCNN encoder/decoder.
4.2. Experimental setup
We performed 5-fold cross-validation by randomly dividing the 45 normal subjects into 5 groups, each of which has 9 subjects. In each iteration, one group (9 subjects) was used for testing. In the remaining 4 groups (36 subjects), one subject was randomly reserved for validation, and the other 35 subjects were used for training. The results of the 5 cross-validations were averaged and reported.
Using our data augmentation method, we created 100 pairs of facial-bony point sets for each subject in the training set. For the testing set, pairs of facial-bony point sets were sub-sampled for each subject using our point sampling strategy. In the testing phase, the testing group’s facial and bony point sets were fed into the trained F2B and B2F sub-networks to predict the bony and facial point sets (20,480 points each), respectively. Then, the CPD registration was used to reconstruct the surface meshes.
Qualitative evaluation was done by comparing the predictions with the ground truths after rigid alignment. For quantitative evaluation, the shape error of the predicted point sets was first estimated using the square root CD. Then, landmark error (i.e., the Euclidean distances of 36 facial landmarks and 48 bony landmarks) and shape error were calculated for the generated facial and bony surface meshes. Among these landmarks, 16 facial and 31 bony landmarks were selected to evaluate the prediction accuracy in the jaw region more closely. The locations of these facial and bony landmarks are shown in Fig. 5. We performed the paired t-test between the shape errors achieved by our method and the competing methods.
Fig. 5.
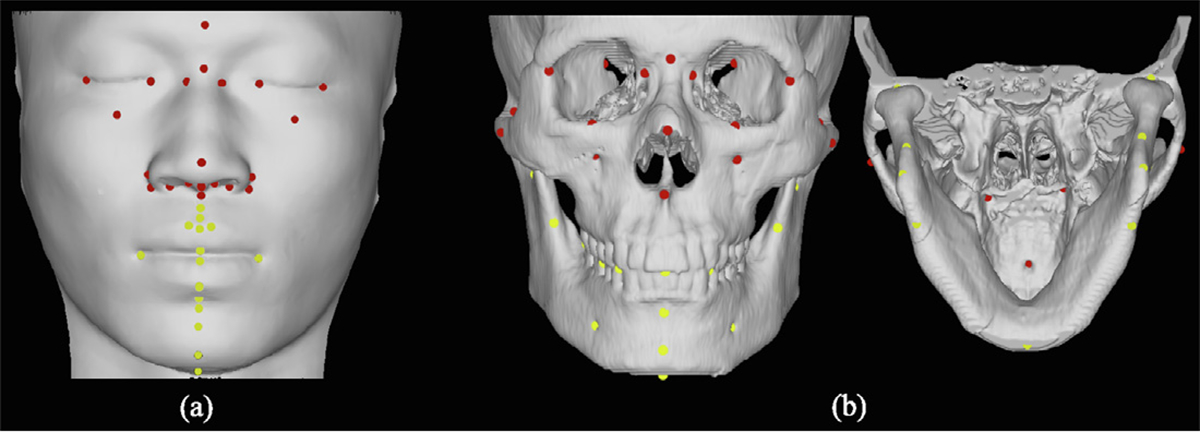
(a) Facial and (b) bony landmarks. Landmarks on the jaw are yellow.
4.3. Results
4.3.1. Qualitative evaluation
Figs. 6 and 7 show representative results of the facial and bony point sets predicted by P2P-Net, SpiderCNN-based P2P-Net and the proposed PointConv in comparison with the respective ground truths. For clarity, the results for only one point subset (4096 points) are shown. The results indicate that the facial and bony shapes predicted by P2P-Conv are in higher agreement with the ground truths than SR, PCA, and the other deep learning methods.
Fig. 6.
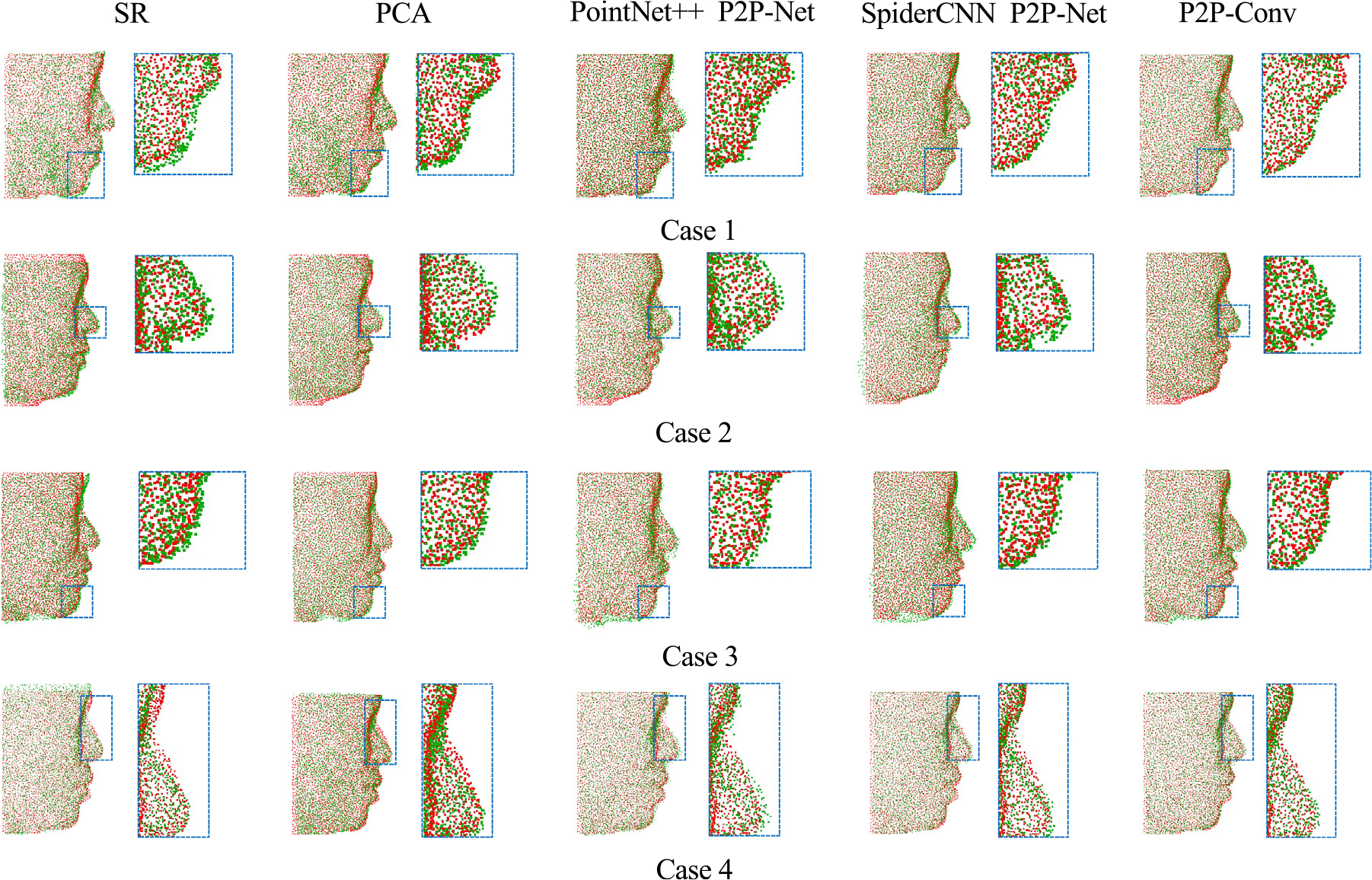
Predicted facial point sets (green) and the ground-truth point sets (red).
Fig. 7.

Predicted bony point sets (green) and the ground-truth point sets (red).
4.3.2. Quantitative evaluation
Table 2 summarizes the shape errors of the facial and bony point sets (4096 points) given by different methods before surface mesh generation. Table 3 shows the landmark-based error and shape error of the generated facial and bony surface meshes, which have around 30 000 and 50 000 vertices, respectively. The following observations can be made:
Table 2.
Shape error (mean ± standard deviation) between the predicted and ground-truth point sets of all subjects quantified via 5-fold cross-validation.
| SR | PCA | P2P-Net | SpiderCNN P2P-Net | P2P-Conv | |
|---|---|---|---|---|---|
|
| |||||
| Face shape error | 3.06 ± 0.57 mm* | 3.02 ± 0.53 mm* | 2.92 ± 0.51 mm* | 2.95 ± 0.57 mm* | 2.73 ± 0.40 mm |
| Facial 95% CI | (2.89, 3.23) | (2.86, 3.18) | (2.77, 3.07) | (2.78, 3.12) | (2.61, 2.85) |
| Bone shape error | 3.32 ± 0.24 mm* | 3.28 ± 0.23 mm* | 3.05 ± 0.20 mm* | 3.05 ± 0.21 mm* | 2.86 ± 0.17 mm |
| Bony 95% CI | (3.25, 3.39) | (3.32, 3.42) | (2.99, 3.10) | (2.99, 3.11) | (2.81, 2.91) |
Marks results where our method significantly outperforms a competing method with p < 0.05, paired t-test.
CI: Confidence interval of the mean.
Table 3.
Average landmark error (mean ± standard deviation) and shape error (mean ± standard deviation) between the predicted and ground-truth shapes of all subjects quantified via 5-fold cross-validation.
| SR | PCA | P2P-Net | SpiderCNN P2P-Net | P2P-Conv | ||
|---|---|---|---|---|---|---|
|
| ||||||
| Landmark error | Face | 4.86 ± 0.83 mm* | 4.70 ± 0.77 mm* | 4.32 ± 1.13 mm* | 3.95 ± 1.25 mm* | 3.61 ± 0.83 mm |
| Face (jaw) | 5.15 ± 0.96 mm* | 4.94 ± 0.93 mm* | 4.53 ± 1.23 mm* | 4.21 ± 1.36 mm* | 3.75 ± 1.08 mm | |
| Bone | 4.00 ± 0.50 mm* | 3.89 ± 0.48 mm* | 3.47 ± 0.60 mm* | 3.41 ± 0.51 mm* | 3.16 ± 0.56 mm | |
| Bone (jaw) | 4.28 ± 0.60 mm* | 4.12 ± 0.55 mm* | 3.75 ± 0.65 mm* | 3.80 ± 0.63 mm* | 3.47 ± 0.58 mm | |
|
| ||||||
| Shape error | Face | 2.90 ± 0.51 mm* | 2.88 ± 0.47 mm* | 2.67 ± 0.57 mm* | 2.45 ± 0.58 mm* | 2.16 ± 0.44 mm |
| Bone | 2.47 ± 0.20 mm* | 2.49 ± 0.21 mm* | 2.23 ± 0.29 mm* | 2.24 ± 0.25 mm* | 2.09 ± 0.19 mm | |
Marks results where our method significantly outperforms a competing method with p < 0.05, paired t-test.
Deep learning methods perform better than the PCA and SR methods. Note that, unlike SR and PCA, no P2P correspondence is needed to train the learning-based methods. Establishing point-wise correspondences of tens of thousands of points is time-consuming, limiting the practical application of the SR and PCA methods.
P2P-Conv outperforms PointNet++ and SpiderCNN-based P2P-Net, giving smaller landmark errors. This suggests that capturing local-to-global point features using PointConv leads to more accurate shape transformations.
P2P-Conv yields better prediction accuracy in the jaw region, the target area of orthognathic surgery.
Similar conclusions can be drawn from the surface deviation results shown in Fig. 8.
Fig. 8.

Color-coded surface deviation errors between the predicted surfaces and the ground-truth surfaces.
4.3.3. Effectiveness of data augmentation
We compared the performance of P2P-Net and P2P-Conv trained with and without data augmentation. Results summarized in Fig. 9 for a representative subject show that data augmentation results in shape prediction that is more accurate globally and locally with smoother edges and more uniform point sets. Using 5-fold cross-validation, the data augmentation strategy reduces the average facial/bony landmark errors from 4.94 mm/4.21 mm to 4.57 mm/3.96 mm for P2P-Net and from 4.16 mm/3.74 mm to 3.88 mm/3.41 mm for P2P-Conv.
Fig. 9.
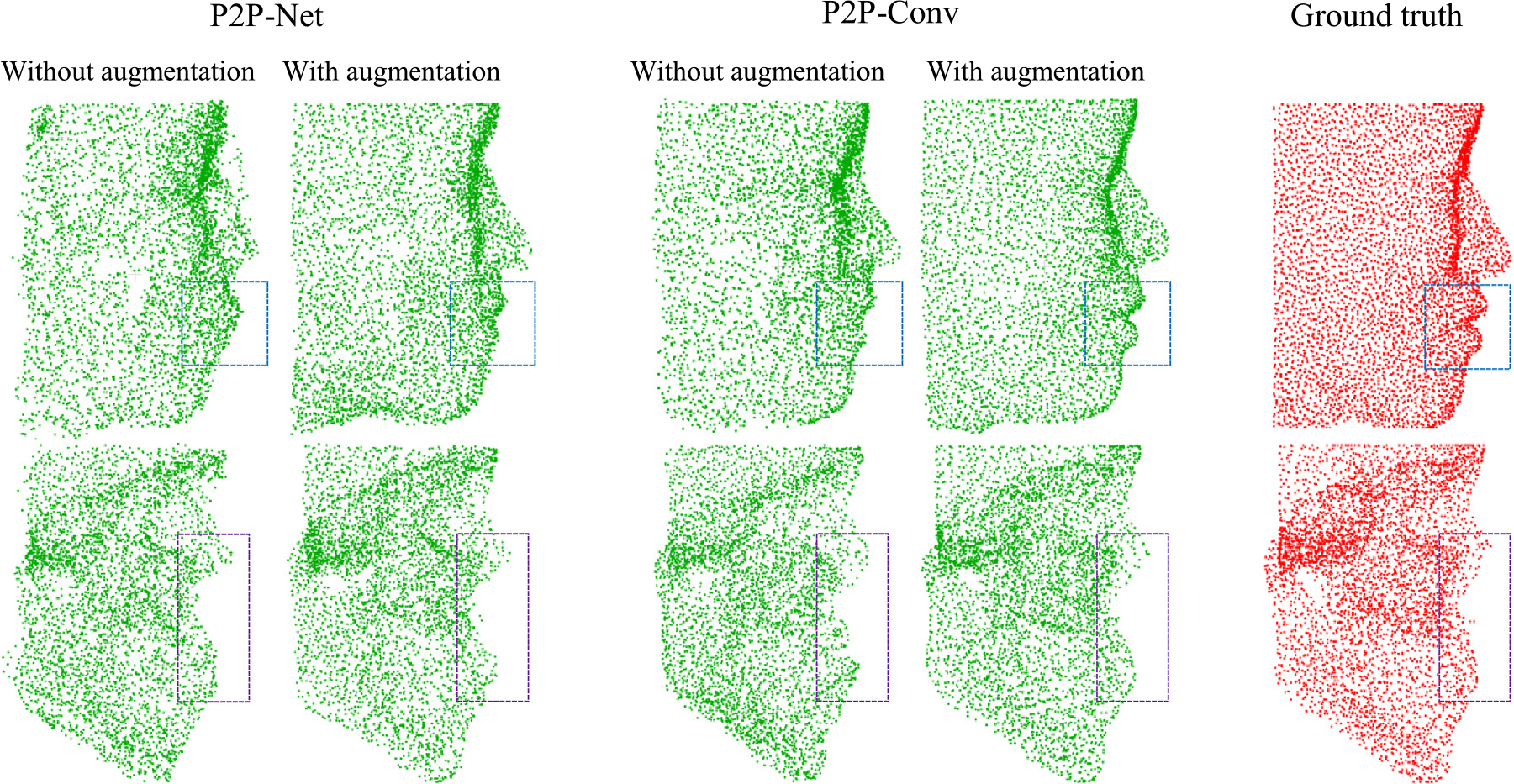
Facial and bony point sets predicted by P2P-Net and P2P-Conv with and without data augmentation.
4.3.4. Effectiveness of multi-template mesh generation
We compared the performance of mesh generation using multiple templates and an average template only. Multi-template mesh generation reduces the average facial/bony landmark errors from 3.88mm/3.41 mm to 3.61mm/3.16 mm.
4.3.5. Effectiveness of dense prediction
Dense prediction (20,480 points) captures local details better and reduces the average shape error of the facial mesh surfaces from 2.82 mm to 2.73 mm compared with sparse prediction (4096 points) (Fig. 10).
Fig. 10.

An example of sparse (4096) and dense (20,480) point predictions.
5. Conclusion and discussion
This paper presents a deep learning framework to learn the subject-specific nonlinear transformation between CMF facial and bony shapes for computer-aided orthognathic surgical planning. The core of the proposed framework is a bidirectional P2P-Conv network called P2P-Conv, which leverages PointConv to capture local correlations of 3D point sets for accurate shape transformation. To generate a dense prediction for complex shapes, we design a two-step point sampling strategy to uniformly sub-sample multiple non-overlapping point subsets as inputs to P2P-Conv. We augment the training set to improve the shape transformation accuracy. Qualitative and quantitative experimental results demonstrate that our framework more accurately estimates the transformation between CMF facial and bony shapes than state-of-the-art sparse-representation and deep-learning methods.
P2P-Conv outperforms the original P2P-Net (Yin et al., 2018) and the SpiderCNN-based (Xu et al., 2018) P2P-Net. Compared with P2P-Net, P2P-Conv yields smoother, more accurate, and uniform point sets. PointConv performs better than SpiderCNN, although both are convolution networks for point sets. PointConv is a full approximation of convolution and can perform point-set deconvolution similar to image deconvolution to propagate information in the coarse layers to finer layers (Wu et al., 2019). In contrast, SpiderCNN cannot perform point deconvolution due to its design (Xu et al., 2018), restricting its performance in our shape transformation task.
We use surface mesh templates to recover facial and bony surface meshes from predicted point sets. However, this approach can be limited in shape recovery. Fig. 11 shows an example where the reconstructed facial surface differs from its ground truth. Potential causes are as follows: (1) The employed non-rigid registration method might not be able to recover local shape information. (2) The templates could bias the generated surfaces. (3) The surface topology is fixed by the template. This limitation can be alleviated when applied to the postoperative facial appearance prediction task, where the patients’ pre-operative models are used to generate the final surface meshes.
Fig. 11.

An example of facial surface recovered using the proposed mesh generation method. (a), (b) and (c) are the selected facial surface mesh template, the recovered facial surface mesh, and the ground truth.
Our method achieves state-of-the-art performance by estimating the transformation between CMF facial and bony shapes. However, the performance is partially limited by the training sample size. This work used only 35 subjects to train P2P-Conv, causing unsatisfactory results compared with the SR-based method in some cases. There were three and two unsatisfactory cases for predicting facial and bony shapes, respectively. In the future, we will evaluate our method with more training samples collected from multiple sites. We will also pre-train the proposed network using abnormal subjects to improve performance.
In the future, we will augment the current framework with the ability to estimate prediction uncertainty. This can be achieved, for example, via deep ensembles, which have been shown to perform better than Monte Carlo dropout in uncertainty estimation for 3D point clouds (Hochgeschwender et al., 2020).
Code is available at https://github.com/Marvin0724/Face_bone_transform.
Acknowledgments
This study was supported in part by the National Institutes of Health (NIH), USA through grants R01DE022676, R01DE027251, and R01DE021863.
Footnotes
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Bell WH, Ferraro JW, 1993. Modern practice in orthognathic and reconstructive surgery. Plast. Reconstr. Surg. 92 (2), 362. [Google Scholar]
- De Buhan M, Nardoni C, 2016. A mesh deformation based approach for digital facial reconstruction. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan F, Huang D, Tian Y, Lu K, Wu Z, Zhou M, 2015. 3D face reconstruction from skull by regression modeling in shape parameter spaces. Neurocomputing 151, 674–682. [Google Scholar]
- Duan F, Yang S, Huang D, Hu Y, Wu Z, Zhou M, 2014. Craniofacial reconstruction based on multi-linear subspace analysis. Multimedia Tools Appl. 73 (2), 809–823. [Google Scholar]
- Fan H, Su H, Guibas LJ, 2017. A point set generation network for 3d object reconstruction from a single image. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. pp. 605–613. [Google Scholar]
- Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y, 2014. Generative adversarial nets. In: Advances in Neural Information Processing Systems. pp. 2672–2680. [Google Scholar]
- Gopinath K, Desrosiers C, Lombaert H, 2019. Graph convolutions on spectral embeddings for cortical surface parcellation. Med. Image Anal. 54, 297–305. [DOI] [PubMed] [Google Scholar]
- Guo Y, Wang H, Hu Q, Liu H, Liu L, Bennamoun M, 2019. Deep learning for 3D point clouds: A survey. arXiv preprint arXiv:1912.12033. [DOI] [PubMed] [Google Scholar]
- Hermosilla P, Ritschel T, Vázquez P-P, Vinacua À, Ropinski T, 2018. Monte carlo convolution for learning on non-uniformly sampled point clouds. ACM Trans. Graph. 37 (6), 1–12. [Google Scholar]
- Hochgeschwender N, Plöger P, Kirchner F, Valdenegro-Toro M, et al. , 2020. Evaluating uncertainty estimation methods on 3D semantic segmentation of point clouds. arXiv preprint arXiv:2007.01787. [Google Scholar]
- Kim D, Kuang T, Rodrigues YL, Gateno J, Shen SG, Wang X, Deng H, Yuan P, Alfi DM, Liebschner MA, et al. , 2019. A new approach of predicting facial changes following orthognathic surgery using realistic lip sliding effect. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 336–344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knoops PG, Borghi A, Ruggiero F, Badiali G, Bianchi A, Marchetti C, Rodriguez-Florez N, Breakey RW, Jeelani O, Dunaway DJ, et al. , 2018. A novel soft tissue prediction methodology for orthognathic surgery based on probabilistic finite element modelling. PLoS One 13 (5). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Bu R, Sun M, Wu W, Di X, Chen B, 2018. PointCNN: Convolution on x-transformed points. In: Advances in Neural Information Processing Systems (NeurIPs). pp. 820–830. [Google Scholar]
- Lian C, Wang L, Wu T-H, Wang F, Yap P-T, Ko C-C, Shen D, 2020. Deep multi-scale mesh feature learning for automated labeling of raw dental surfaces from 3D intraoral scanners. IEEE Trans. Med. Imaging 39 (7), 2440–2450. [DOI] [PubMed] [Google Scholar]
- Liu Q, Deng H, Lian C, Chen X, Xiao D, Ma L, Chen X, Kuang T, Gateno J, Yap P-T, et al. , 2021. Skullengine: A multi-stage CNN framework for collaborative CBCT image segmentation and landmark detection. In: International Workshop on Machine Learning in Medical Imaging. Springer, pp. 606–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Xia Q, Li S, Hao A, Qin H, 2019. Quantitative and flexible 3D shape dataset augmentation via latent space embedding and deformation learning. Comput. Aided Geom. Design 71, 63–76. [Google Scholar]
- Ma L, Kim D, Lian C, Xiao D, Kuang T, Liu Q, Lang Y, Deng HH, Gateno J, Wu Y, et al. , 2021. Deep simulation of facial appearance changes following craniomaxillofacial bony movements in orthognathic surgical planning. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 459–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma L, Xiao D, Kim D, Lian C, Kuang T, Liu Q, Deng H, Yang E, Liebschner MA, Gateno J, et al. , 2022. Simulation of postoperative facial appearances via geometric deep learning for efficient orthognathic surgical planning. IEEE Trans. Med. Imaging. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madsen D, Lüthi M, Schneider A, Vetter T, 2018. Probabilistic joint face-skull modelling for facial reconstruction. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. pp. 5295–5303. [Google Scholar]
- Myronenko A, Song X, 2010. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. Mach. Intell. 32 (12), 2262–2275. [DOI] [PubMed] [Google Scholar]
- Nadjmi N, Defrancq E, Mollemans W, Van Hemelen G, Bergé S, 2014. Quantitative validation of a computer-aided maxillofacial planning system, focusing on soft tissue deformations. Ann. Maxillofac. Surg. 4 (2), 171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen T-N, Tran V-D, Nguyen H-Q, Dao T-T, 2020. A statistical shape modeling approach for predicting subject-specific human skull from head surface. Med. Biol. Eng. Comput. 58 (10), 2355–2373. [DOI] [PubMed] [Google Scholar]
- Paysan P, Lüthi M, Albrecht T, Lerch A, Amberg B, Santini F, Vetter T, 2009. Face reconstruction from skull shapes and physical attributes. In: Joint Pattern Recognition Symposium. Springer, pp. 232–241. [Google Scholar]
- Qi CR, Su H, Mo K, Guibas LJ, 2017a. PointNet: Deep learning on point sets for 3D classification and segmentation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR). pp. 652–660. [Google Scholar]
- Qi CR, Yi L, Su H, Guibas LJ, 2017b. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In: Advances in Neural IInformation Processing Systems (NeurIPS). pp. 5099–5108. [Google Scholar]
- Shafi M, Ayoub A, Ju X, Khambay B, 2013. The accuracy of three-dimensional prediction planning for the surgical correction of facial deformities using maxilim. Int. J. Oral Maxillofac. Surg. 42 (7), 801–806. [DOI] [PubMed] [Google Scholar]
- Shahim K, Jürgens P, Cattin PC, Nolte L-P, Reyes M, 2013. Prediction of craniomaxillofacial surgical planning using an inverse soft tissue modelling approach. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 18–25. [DOI] [PubMed] [Google Scholar]
- Shui W, Zhou M, Maddock S, He T, Wang X, Deng Q, 2017. A PCA-based method for determining craniofacial relationship and sexual dimorphism of facial shapes. Comput. Biol. Med. 90, 33–49. [DOI] [PubMed] [Google Scholar]
- Sonneveld KA, Mai PT, Hardigan PC, Portnof JE, 2019. Theoretical basis for virtual skull orientation according to three-dimensional Frankfort horizontal plane for computer-aided surgical simulation. J. Craniofac. Surg. 30 (6), 1902–1905. [DOI] [PubMed] [Google Scholar]
- Wang L, Ren Y, Gao Y, Tang Z, Chen K-C, Li J, Shen SG, Yan J, Lee PK, Chow B, et al. , 2015. Estimating patient-specific and anatomically correct reference model for craniomaxillofacial deformity via sparse representation. Med. Phys. 42 (10), 5809–5816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu W, Qi Z, Fuxin L, 2019. Pointconv: Deep convolutional networks on 3d point clouds. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. pp. 9621–9630. [Google Scholar]
- Xia JJ, Gateno J, Teichgraeber JF, 2009. New clinical protocol to evaluate craniomaxillofacial deformity and plan surgical correction. J. Oral Maxillofac. Surg. 67 (10), 2093–2106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia J, Gateno J, Teichgraeber J, Yuan P, Chen K-C, Li J, Zhang X, Tang Z, Alfi D, 2015. Algorithm for planning a double-jaw orthognathic surgery using a computer-aided surgical simulation (CASS) protocol. Part 1: planning sequence. Int. J. Oral Maxillofac. Surg. 44 (12), 1431–1440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia JJ, Shevchenko L, Gateno J, Teichgraeber JF, Taylor TD, Lasky RE, English JD, Kau CH, McGrory KR, 2011. Outcome study of computer-aided surgical simulation in the treatment of patients with craniomaxillofacial deformities. J. Oral Maxillofac. Surg. 69 (7), 2014–2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao D, Deng HH, Kuang T, Ma L, Liu Q, Chen X, Lian C, Lang Y, Kim D, Gateno J, et al. , 2021b. A self-supervised deep framework for reference bony shape estimation in orthognathic surgical planning. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 469–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao D, Deng H, Lian C, Kuang T, Liu Q, Ma L, Lang Y, Chen X, Kim D, Gateno J, et al. , 2021a. Unsupervised learning of reference bony shapes for orthognathic surgical planning with a surface deformation network. Med. Phys. 48 (12), 7735–7746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao D, Lian C, Deng H, Kuang T, Liu Q, Ma L, Kim D, Lang Y, Chen X, Gateno J, et al. , 2021c. Estimating reference bony shape models for orthognathic surgical planning using 3D point-cloud deep learning. IEEE J. Biomed. Health Inf. 25 (8), 2958–2966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao D, Wang L, Deng H, Thung K-H, Zhu J, Yuan P, Rodrigues YL, Perez L, Crecelius CE, Gateno J, et al. , 2019. Estimating reference bony shape model for personalized surgical reconstruction of posttraumatic facial defects. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 327–335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y, Fan T, Xu M, Zeng L, Qiao Y, 2018. Spidercnn: Deep learning on point sets with parameterized convolutional filters. In: Proceedings of the European Conference on Computer Vision (ECCV). pp. 87–102. [Google Scholar]
- Yan J, Shen G, Fang B, Shi H, Wu Y, Shao Z, Xia B, Yu D, 2010. Three-dimensional CT measurement for the craniomaxillofacial structure of normal occlusion adults in Jiangsu, Zhejiang and Shanghai Area. China J. Oral Maxillofac. Surg. 8 (1), 2–9. [Google Scholar]
- Yin K, Chen Z, Huang H, Cohen-Or D, Zhang H, 2019. LOGAN: unpaired shape transform in latent overcomplete space. ACM Trans. Graph. 38 (6), 1–13. [Google Scholar]
- Yin K, Huang H, Cohen-Or D, Zhang H, 2018. P2p-net: Bidirectional point displacement net for shape transform. ACM Trans. Graph. 37 (4), 1–13. [Google Scholar]
- Yuan P, Mai H, Li J, Ho DC-Y, Lai Y, Liu S, Kim D, Xiong Z, Alfi DM, Teichgraeber JF, et al. , 2017. Design, development and clinical validation of computer-aided surgical simulation system for streamlined orthognathic surgical planning. Int. J. Comput. Assist. Radiol. Surg. 12 (12), 2129–2143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuksel C, 2015. Sample elimination for generating Poisson disk sample sets. In: Computer Graphics Forum, Vol. 34. Wiley Online Library, pp. 25–32. [Google Scholar]
- Zanjani FG, Moin DA, Claessen F, Cherici T, Parinussa S, Pourtaherian A, Zinger S, et al. , 2019. Mask-MCNet: Instance segmentation in 3D point cloud of intra-oral scans. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 128–136. [Google Scholar]
- Zhao F, Xia S, Wu Z, Duan D, Wang L, Lin W, Gilmore JH, Shen D, Li G, 2019. Spherical U-net on cortical surfaces: methods and applications. In: International Conference on Information Processing in Medical Imaging. Springer, pp. 855–866. [DOI] [PMC free article] [PubMed] [Google Scholar]


