Longitudinal effects of lipid indices on incident cardiovascular diseases adjusting for time-varying confounding using marginal structural models: 25 years follow-up of two US cohort studies

Abstract

Background

This study assesses the effect of blood lipid indices and lipid ratios on cardiovascular diseases (CVDs) using inverse probability-of-exposure weighted estimation of marginal structural models (MSMs).

Methods

A pooled dataset of two US representative cohort studies, including 16736 participants aged 42–84 years with complete information at baseline, was used. The effect of each lipid index, including low-density lipoprotein cholesterol (LDL-C), high-density lipoprotein cholesterol (HDL-C), triglyceride (TG), ratios of TC/HDL-C, LDL-C/HDL-C, and TG/HDL-C on coronary heart disease (CHD) and stroke were estimated using weighted Cox regression.

Results

There were 1638 cases of CHD and 1017 cases of stroke during a median follow-up of 17.1 years (interquartile range: 8.5 to 25.7). Compared to optimal levels, the risk of CVD outcomes increased substantially in high levels of TC, LDL-C, TC/HDL-C, and LDL-C/HDL-C. If everyone had always had high levels of TC (≥240 mg/dL), risk of CHD would have been 2.15 times higher, and risk of stroke 1.35 times higher than if they had always had optimal levels (<200 mg/dL). Moreover, if all participants had been kept at very high (≥190 mg/dL) levels of LDL-C, risk of CHD would have been 2.62 times higher and risk of stroke would have been 1.92 times higher than if all participants had been kept at optimal levels, respectively. Our results suggest that high levels of HDL-C may be protective for CHD, but not for stroke. There was also no evidence of an adverse effect of high triglyceride levels on stroke.

Conclusions

Using MSM, this study highlights the effect of TC and LDL-C on CVD, with a stronger effect on CHD than on stroke. There was no evidence for a protective effect of high levels of HDL-C on stroke. Besides, triglyceride was not found to affect stroke.

Introduction

Cardiovascular diseases (CVDs), mainly coronary heart disease (CHD) and stroke, remain the leading cause of premature death and a major cause of disability globally [1]. Previous epidemiological studies have suggested that unfavorable lipid indices levels may play an essential role in the occurrence and progression of cardiovascular events [2]. Most observational studies have investigated the effects of lipid indices on CVD using the information at baseline only. However, it is essential to consider subsequent changes in lipid profile and other CVD risk factors (e.g., hypertension, diabetes, smoking, drinking, obesity, and lipid-lowering drugs) to estimate a more precise effect [3].

In longitudinal studies of the effect of a time-varying exposure, some time-varying confounders may be affected by the prior exposure, so that they have the dual role of confounder and mediator in the causal pathway. In the presence of these variables, standard statistical models such as the time-dependent Cox regression model, which adjusts for all baseline and time-varying confounders, may provide biased estimates of the effect of exposure [[4], [5], [6], [7]] due to introducing collider-stratification bias [[8], [9], [10]] and over-adjustment bias [[11], [12], [13]]. Time-varying confounding affected by prior exposure is possible in estimating the effects of lipid indices on CVD, e.g., hypertension and body mass index as independent risk factors for CVD may be affected by preceding lipid levels, and also predict the subsequent lipid levels.

Marginal structural models (MSMs), developed by Robins et al. [14,15], are an alternative approach to estimating a time-varying exposure's causal effect, appropriately adjusting for time-varying confounders affected by prior exposure. The parameters of MSMs can be calculated using inverse probability-of-exposure weighting [[16], [17], [18], [19], [20]]. To our knowledge, there has been no published paper on the effects of lipid indices using marginal structural models. Using pooled data from two large prospective cohort studies from the US population, we sought to estimate the effects of lipid indices on CVDs, including CHD and stroke, separately in the presence of time-varying confounders using a marginal structural Cox model.

Methods

Study population

The present study was based on pooled data from two large prospective cohort studies sponsored by the National Heart, Lung, and Blood Institute (NHLBI), the ARIC (Atherosclerosis Risk In Communities) study [21] and the MESA study (Multi-Ethnic Study of Atherosclerosis) [22]. The data harmonization methodology of Maelstrom Research was used for pooling data [23]. The design details of each study have been described elsewhere [21,22]. Briefly, the ARIC study [21] is an ongoing prospective cohort study of 15,792 individuals aged 45–64 years recruited from four US communities (Washington County, MD; Forsyth County, NC; Jackson, MS; and suburban Minneapolis, MN). After the baseline examination between 1987 and 1989, participants were re-examined three times at triennial intervals; after approximately eleven years, a subset of participants have completed further visits, the most recent in 2016–17. The MESA study [22] is an ongoing prospective cohort study that includes 6,814 White and Black adults recruited from six US communities (Baltimore City and Baltimore County, MD; Chicago, IL; Forsyth County, NC; Los Angeles County, CA; New York, NY; and St. Paul, MN). Participants were aged 45–84 years and free of clinical CVD at baseline in 2000–2002. After the baseline examination, there have been five additional follow-up visits at biennial intervals, the most recent ongoing in 2016–18. In both studies, all participants (or proxies) were contacted annually by telephone to identify new hospitalizations and medical diagnoses. The studies' websites contain details of all the available data through a fully searchable data dictionary [24,25].

The ARIC and MESA studies were performed following the ethical standards in the Declaration of Helsinki. The Institutional Review Boards approved the ARIC study for each ARIC study affiliated institution, and the MESA study protocol was approved by the Institutional Review Board at each site. All participants provided written informed consent, and all methods were carried out following relevant guidelines and regulations.

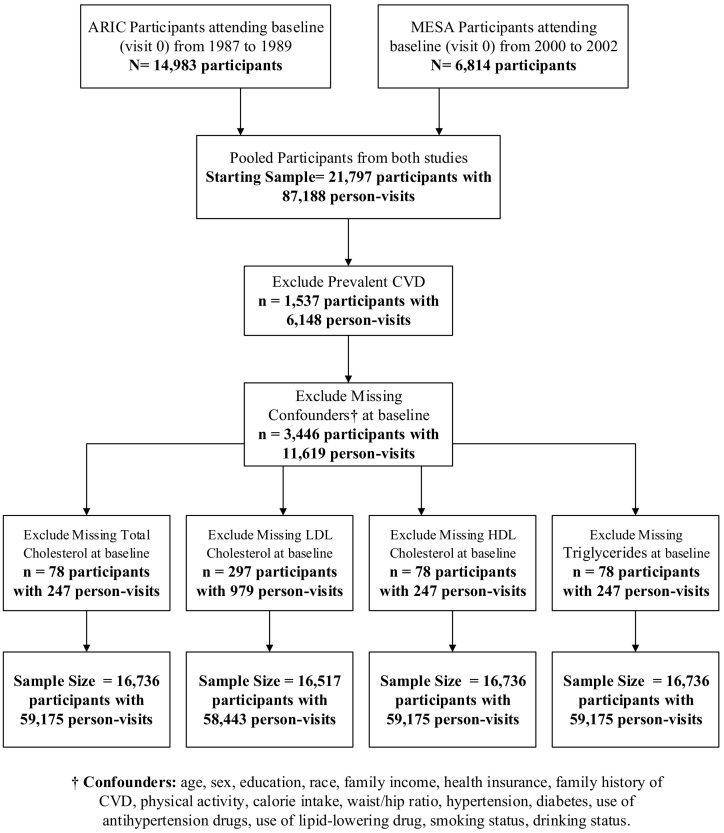
The present analyses were restricted to participants without known CVD and with complete data for each lipid component and confounders at baseline. Due to the large interval between the fourth and fifth visits in the ARIC study, data from the first four visits of both cohorts were used in the current study. The flowchart of the participant selection process and sample size for each lipid component is shown in Fig. 1.

Fig. 1.

Flow chart showing the derivation of final analysis samples from 21,797 participants in ARIC and MESA studies.

Exposures

The primary exposures of interest in the current analysis were serum lipid concentrations, including TC, LDL-C, HDL-C, TG, TC/HDL-C, LDL-C/HDL-C, and TG/HDL-C ratios. Clinical data collection for the ARIC and MESA studies has been reported on their websites (available at https://sites.cscc.unc.edu/aric/desc_pub and https://www.mesa-nhlbi.org/). Briefly, blood samples were collected after 12-h fasting using a standardized venipuncture procedure at each visit in both studies. EDTA plasma samples were aliquoted on ice and stored at −70°C until analysis. Total cholesterol and triglyceride were measured using standard enzymatic processes (Roche Diagnostics). The HDL-C level was measured using the cholesterol oxidase method after precipitation of non-HDL-C with magnesium/dextran. The LDL-C was calculated using the Friedewald formula from the total cholesterol, HDL-C, and triglyceride values <400 mg/dl.

The National Cholesterol Education Program (NCEP) guidelines were used to define categories of all lipid components at baseline and follow-up visits [26]. Each TC measurement was categorized into three groups: optimal (<200 mg/dL), borderline high (200–239 mg/dL), and high (≥240 mg/dL). LDL-C measurements were categorized into five groups: optimal (<100 mg/dL), near-optimal (100–129 mg/dL), borderline high (130–159 mg/dL), high (160–189 mg/dL), and very high (≥190 mg/dL). HDL-C measurements were categorized into four groups: low (<40 mg/dL), optimal (40–59 mg/ dL), high (60–79 mg/dL), and very high (≥80 mg/dL). Triglyceride values were categorized into three groups: optimal (<150 mg/dL), borderline high (150–199 mg/dL), and high (≥200–499 mg/dL). All lipid categories were determined by NCEP 2001 guidelines [27]; the very high category of HDL-C was determined based on previous studies suggesting a possible increased risk for CHD and total mortality events in participants with HDL-C >80 mg/dL [28,29]. Finally, quartiles of each lipid ratio were used to define their categories at each visit.

Outcomes

The primary outcomes of interest for our analysis were incident CHD, defined as myocardial infarction or CHD death, and stroke, defined as definite or probable hospitalized ischemic or hemorrhagic stroke events. Diagnosis of myocardial infarction generally required at least two of the following criteria: chest pain, electrocardiographic abnormalities consistent with myocardial infarction, and elevated cardiac biomarkers. Diagnosis of stroke generally required a persistent central neurologic deficit lasting >24 hours. Events were ascertained by following each participant at 9–12 months intervals using telephone calls. All events were adjudicated from medical records and death certificates for end-point classification and assignment of incidence dates by a review committee in both studies. In this study, outcome events confirmed by 31 December 2014 were included.

Confounders

Details of interview and data collection procedures for each study have been described on their websites. Briefly, both studies used standardized protocols and similar standard and validated methods to measure demographic characteristics and CVD risk factors at each study visit.

The potential confounders available only at baseline (visit 0) included age, sex, race (white, African American, Hispanic, and Asian), education (less than high school, high school, some college, and college +), family income (less than $16000, $16000–24999, $25000–34999, $35000–49999, more than $50000), family history of CVD, health insurance, calorie intake (Kcal), and physical activity (the metabolic equivalent of task (MET)-minute/week).

The time-varying confounders, measured at all visits including baseline, were lipid-lowering drugs use, hypertension (systolic blood pressure ≥90 or diastolic blood pressure ≥140 mmHg or taking any medication for high blood pressure) [30], antihypertensive drugs use, diabetes mellitus (fasting blood glucose ≥126 mg/dl or taking any medication for diabetes) [31], body mass index (categorized into three groups: <25, ≥25 to <30, ≥30 kg/m2) [32], waist-to-hip ratio (≥ 0.9 in men and ≥0.85 in women) [33], smoking status (defined as never, former, and current smoking cigarettes) and drinking status (defined as never, former, and current drinking alcoholic beverages). Baseline and time-varying confounders included HDL-C and triglyceride for the exposure TC and LDL-C; triglyceride and LDL-C for HDL-C; LDL-C and HDL-C for triglyceride; and LDL-C for triglyceride/HDL-c ratio as well. The confounders mentioned above were selected based on previous literature [5,[34], [35], [36], [37], [38], [39], [40], [41]].

Causal diagram

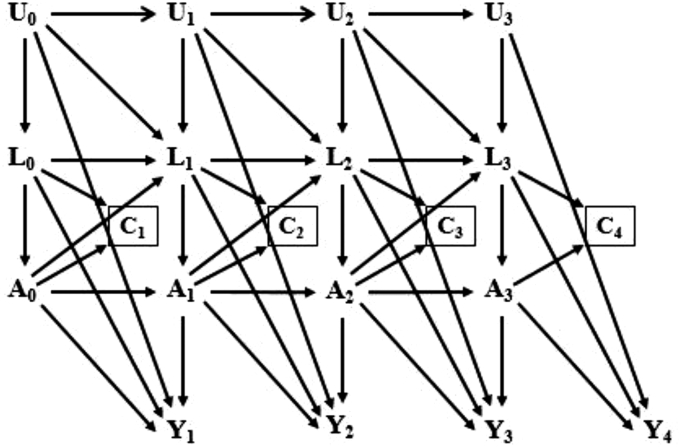
The causal directed acyclic graph [[42], [43], [44], [45], [46], [47], [48], [49], [50]] in Fig. 2 represents the assumed causal structure for the effects of each lipid index on CHD and stroke in the study population. Using the notation of Robins et al. [14], A(k) and Y(k+1) correspond to a lipid component at visit k (k= 0, 1, 2, 3) and CHD or stroke during the period (visit k, visit k+1), respectively. L(k) denotes a vector of measured time-varying confounders at visit k. L(0) includes the confounders available only at baseline as well. We use overbars to represent a covariate history, for example $\overline{\mathrm{A}}\left(k\right)$, $\overline{\mathrm{C}}\left(k\right)$, and $\overline{L}\left(k\right)$are a subject's observed histories of exposure, censoring, and measured confounders through visit k, respectively. U(k) denotes unmeasured causal risk factors at visit k for Y(k+1), and C(k+1) denotes censoring during the interval (visit k, visit k+1) (1 if censored and 0 otherwise). The square around C(k+1) indicates that our analyses are restricted to individuals who have not yet been censored. Fig. 2 represents the untestable assumption of no unmeasured confounders for exposure and censoring histories, given data on L(k), denoted by the absence of arrows from U(k) to A(k) and C(k+1). Note that for the simplicity of presentation, the arrows from L(0) to A(1), from A(0) to L(2), etc., were omitted.

Fig. 2.

Causal diagram representing the assumed causal structure for the effects of lipid indices (A(k)) on CHD or stroke (Y+1) in participants of ARIC and MESA studies across four visits (i.e., k = 0, 1, 2, 3). L(k) includes a vector of measured time-varying confounders at visit k, and L(0) consists of the baseline confounders and the baseline values of time-varying confounders. U(k) represents all unmeasured causal risk factors for Y(k+1) at visit k. C(k+1) denotes censoring during the period (visit k, visit k+1). The square around C(k+1) indicates that our analyses are limited to uncensored subjects.

Statistical methods

To estimate the effect of lipid indices on CHD and stroke, we fit separate marginal structural Cox models (Cox MSM) for each exposure and outcome (14 models). The parameters of these models were estimated using inverse probability-of-exposure-and-censoring weighting.

For our analyses, we specified the following Cox MSM:

$${\mathrm{\lambda }}_{{\mathrm{T}}_{\overline{\mathrm{a}}}}\left(\mathrm{t}|\mathrm{V}\right)={\mathrm{\lambda }}_{{\mathrm{T}}_{\overline{0}}}\left(\mathrm{t}\right){exp}^{\left(\sum _{\mathrm{i}=1}^{\mathrm{J}-1}{\mathrm{\beta }}_{\mathrm{i}}{\mathrm{a}}_{\mathrm{i}}\left(\mathrm{t}\right)+{\beta }_l^{\prime }\mathrm{V}\right)}$$

where ${\mathrm{\lambda }}_{{\mathrm{T}}_{\overline{\mathrm{a}}}}\left(\mathrm{t}|\mathrm{V}\right)$ denotes the counterfactual hazard of CHD or stroke at time t among subjects with the column vector of baseline covariates V (L(0)), if, possibly contrary to fact, they had followed the exposure history $\overline{a}$; a₁(t), a₂(t), …, a_J−1(t) are indicators for levels (J) of each lipid component at visit t, and β_l is a column vector of the parameters. Assuming the correct specification of our marginal structure model, the parameters β₁, …, β_J−1 have causal interpretations: they represent the causal log-hazard ratio for CHD or stroke, comparing always had an unfavorable level (levels 2, 3, ..., J) of a lipid component with their hazard of CHD or stroke if they always had an optimal (baseline) level.

In real longitudinal data analysis and the absence of censoring, each subject receives only one value of $\overline{\mathrm{a}}\left(k\right)$, the observed exposure history$\overline{\mathrm{A}}\left(k\right)$. Only the actual corresponding outcome Y(k+1) during the period (visit k, visit k+1) is observed. However, one can use inverse probability-of-exposure-and-censoring weighting to consistently estimate MSM parameters under the following four assumptions, most of which are untestable [44]: (1) conditional exchangeability assumes that no unmeasured confounders to adjust for both confounding and selection bias due to loss to follow-up; (2) positivity states that for any observed combination of values of the confounders, every level of exposure can and does occur; (3) consistency states that a subject’s counterfactual outcome at visit t under her/his observed value of exposure is equal to her/his observed outcome, which generally requires either a well-defined intervention or an assumption that any intervention used to achieve the exposure change has an equivalent effect; (4) correct specification of models used to estimate weights of exposure and censoring. They are discussed in more detail in the discussion. The stabilized inverse probability-of-exposure weights at visit t (SW_E(t)) are as follows:

$${\mathrm{SW}}_{E_i}\left(\mathrm{t}\right)=\prod _{\mathrm{k}=0}^{\mathrm{t}}\frac{Pr\left[\mathrm{A}\left(\mathrm{k}\right)={\mathrm{a}}_{\mathrm{i}}\left(\mathrm{k}\right)|\overline{\mathrm{A}}\left(\mathrm{k}-1\right)={\overline{\mathrm{a}}}_{\mathrm{i}}\left(\mathrm{k}-1\right),\mathrm{V}={\mathrm{v}}_{\mathrm{i}},\overline{\mathrm{C}}\left(\mathrm{k}\right)=\overline{0}\right]}{Pr\left[\mathrm{A}\left(\mathrm{k}\right)={\mathrm{a}}_{\mathrm{i}}\left(\mathrm{k}\right)│\overline{\mathrm{A}}\left(\mathrm{k}-1\right)={\overline{\mathrm{a}}}_{\mathrm{i}}\left(\mathrm{k}-1\right),\overline{\mathrm{L}}\left(\mathrm{k}\right)={\overline{\mathrm{l}}}_{\mathrm{i}}\left(\mathrm{k}\right),\overline{\mathrm{C}}\left(\mathrm{k}\right)=\overline{0}\right]}$$

Only the set of baseline confounders V was included in the numerator model, while both concurrent time-varying and baseline confounders were included in the denominator model. Note that V is included in the denominator because L(0) is part of $\overline{L}\left(k\right)$. We estimated the probabilities in the denominator through pooled multinomial logistic regression models for exposure that include exposure at the previous visit, concurrent time-varying and baseline confounders, and visit. The probabilities in the denominator were estimated using the same regression model but without the time-varying confounders.

The stabilized inverse probability-of-censoring weights at visit t (SW_C(t)) are as follows:

$${\mathrm{SW}}_{C_i}\left(\mathrm{t}\right)=\prod _{\mathrm{k}=0}^{\mathrm{t}}\frac{Pr\left[\mathrm{C}\left(\mathrm{k}+1\right)=0│\overline{\mathrm{C}}\left(\mathrm{k}\right)=\overline{0},\overline{\mathrm{A}}\left(\mathrm{k}\right)={\overline{\mathrm{a}}}_{\mathrm{i}}\left(\mathrm{k}\right),\mathrm{V}={\mathrm{v}}_{\mathrm{i}}\right]}{Pr\left[\mathrm{C}\left(\mathrm{k}+1\right)=0│\overline{\mathrm{C}}\left(\mathrm{k}\right)=\overline{0},\overline{\mathrm{A}}\left(\mathrm{k}\right)={\overline{\mathrm{a}}}_{\mathrm{i}}\left(\mathrm{k}\right),\overline{\mathrm{L}}\left(\mathrm{k}\right)={\overline{\mathrm{l}}}_{\mathrm{i}}\left(\mathrm{k}\right)\right]}$$

The probabilities in the numerator and denominator were calculated using pooled multinomial logistic regression models for censoring with the same predictors as exposure models.

To estimate the parameters of Cox MSM, we fit the following pooled logistic regression model with weights SW_Ti(t) = SW_Ei(t) × SW_Ci(t):

$$\text{Logit}Pr\left[\mathrm{D}\left(\mathrm{t}\right)=1│\mathrm{D}\left(\mathrm{t}-1\right)=0,\overline{\mathrm{A}}\left(\mathrm{t}-1\right),\mathrm{V}\right]={\mathrm{\alpha }}_0\left(\mathrm{t}\right)+\sum _{\mathrm{i}=1}^{\mathrm{J}-1}{\mathrm{\alpha }}_{\mathrm{i}}{\mathrm{A}}_{\mathrm{i}}\left(\mathrm{t}-1\right)+{\mathrm{\alpha }}_{\mathrm{l}}\mathrm{V}$$

Under the identifiability assumptions mentioned above and considering that the risk of an event is less than 10% per person-visit interval [51], the weighted estimates of α₁, α₂, …, α_J−1 would be approximately consistent for the causal parameters β₁, β₂, …, β_J−1of our Cox MSM.

As a sensitivity analysis, we also used lagged time-varying confounders (confounders measured in the previous visit) instead of concurrent confounders to estimate inverse probability-of-exposure weights [52]. Since using weights induces within-subject correlation, we applied cluster-robust standard errors to obtain 95% confidence intervals (CIs) [[53], [54], [55], [56]].

All analyses were performed using Stata Version 14.0 (Stata Corp; College Station, TX) [57] and R statistical software version 4.0.3 (R Foundation for Statistical Computing, Vienna, Austria).

Results

Sample characteristics

In total, 16,736 participants aged 42–84 years who had complete data at baseline (visit 0) and with no history of any cardiovascular diseases were included in the study. The main reasons for no inclusion were having a history of cardiovascular diseases and a lack of data on the confounders at baseline (Fig. 1). Baseline and time-varying characteristics of the participants have been summarized in Table 1. At baseline, the mean (SD) age was 56.7 (8.6) years, 54.5% were women, and 66.2% were white. Also, 61.3% had a family history of CVD, 75.4% were centrally obese, and 58.1% were current drinkers. The distribution of exposures and time-varying confounders changed over visits, e.g., the proportion of subjects with hypertension, diabetes, taking antihypertensive drugs, taking lipid-lowering medications, and obesity increased from baseline (visit 0) to visit 3, whereas the proportion of current smoking, current drinking, high levels of TC and LDL-C decreased.

Table 1.

Baseline and time-varying characteristics of participants across baseline and follow-up visits.

Characteristicsa	At baseline	During follow-up
	Visit 0 (n = 16,736)	Visit 1 (n = 15,837)	Visit 2 (n = 14,882)	Visit 3 (n = 13,876)
Sex, women (%)	9119 (54.5)	8667 (54.7)	8210 (55.2)	7705 (55.5)
Age, years	56.7 (8.4)	59.1 (8.1)	61.5 (7.8)	64.0 (7.7)
Race
White/Caucasian	11075 (66.2)	10595 (66.9)	10001 (67.2)	9360 (67.4)
African American/Black	3682 (22.0)	3382 (21.3)	3112 (20.9)	2826 (20.4)
Hispanic/Latino	1250 (7.5)	1168 (7.4)	1097 (7.4)	1048 (7.6)
Asian/Chinese	729 (4.5)	692 (4.4)	672 (4.5)	642 (4.6)
Education
Less than high school	3260 (19.5)	–	–	–
High school	4697 (28.1)	–	–	–
Some college	5543 (33.1)	–	–	–
College +	3236 (19.3)	–	–	–
Family income (per year)
Less than $16,000	3204 (19.1)	–	–	–
$16,000–24,999	2300 (13.7)	–	–	–
$25,000–34,999	2743 (16.4)	–	–	–
$35,000–49,999	3172 (19.0)	–	–	–
More than $50,000	5317 (31.8)	–	–	–
Health insurance	10657 (63.7)	–	–	–
Family history of CVD	10264 (61.3)	–	–	–
Physical activity (MET-minutes/week)	953.7 (1561.9)	–	–	–
Total energy intake (Kcal)	1601.7 (734.1)	–	–	–
Systolic blood pressure	122.3 (19.5)	121.9 (19.3)	123.5 (19.4)	125.5 (19.6)
Diastolic blood pressure	72.7 (10.7)	71.4 (10.2)	71.1 (10.3)	70.5 (10.2)
Hypertension	5817 (34.8)	5761 (36.4)	6096 (41.0)	6459 (46.6)
Antihypertensive drug	4794 (28.6)	5083 (32.1)	5483 (36.8)	5813 (46.6)
Lipid-lowering drug	3315 (19.8)	3834 (24.2)	4408 (29.6)	4774 (34.4)
Diabetes mellitus	1795 (10.7)	2109 (13.3)	2065 (13.9)	2106 (15.2)
Body mass index, kg/m2
Normal	5526 (33.0)	5000 (31.6)	4353 (29.3)	3861 (27.8)
Overweight	6677 (39.9)	6367 (40.2)	5909 (39.7)	5509 (39.7)
Obese	4530 (27.1)	4468 (28.2)	4620 (31.0)	4506 (32.5)
Waist/hip ratiob
Normal	4133 (24.7)	3878 (24.5)	2854 (19.2)	2338 (16.9)
Abdominal obesity, >0.90 for men and >0.85 for women	12603 (75.3)	11959 (75.5)	12028 (80.8)	11538 (83.2)
Smoking status
Never	7613 (45.5)	6803 (43.0)	6481 (43.5)	6075 (43.8)
Former	5604 (33.5)	6146 (38.8)	6125 (41.2)	5982 (43.1)
Current	3519 (21.0)	2888 (18.2)	2276 (15.3)	1819 (13.1)
Drinking status
Never	3781 (22.6)	3284 (20.7)	3267 (22.0)	2683 (19.3)
Former	3239 (19.4)	3621 (22.9)	3711 (24.9)	4268 (30.8)
Current	9716 (58.0)	8932 (56.4)	7904 (53.1)	6925 (49.9)
Total cholesterol, mg/dL
Optimal	7533 (45.0)	7705 (48.6)	7465 (50.2)	7555 (54.5)
Borderline high	5937 (35.5)	5587 (35.3)	5184 (34.8)	4610 (33.2)
High	3266 (19.5)	2545 (16.1)	2233 (15.0)	1711 (12.3)
LDL cholesterol, mg/dL
Optimal	3386 (20.5)	3610 (22.8)	3897 (26.2)	3980 (28.7)
Near optimal	5281 (32.0)	5301 (33.5)	5131 (34.5)	4962 (35.8)
Borderline high	4514 (27.3)	4239 (26.8)	3886 (26.1)	3374 (24.3)
High	2273 (13.8)	1890 (11.9)	1445 (9.7)	1176 (8.5)
Very high	1063 (6.4)	730 (4.6)	494 (3.3)	368 (2.7)
HDL cholesterol, mg/dL
Low	4106 (24.5)	4144 (26.2)	3450 (23.2)	3410 (24.6)
Optimal	8307 (49.6)	7794 (49.2)	7318 (49.2)	6832 (49.2)
High	3315 (19.8)	3026 (19.1)	3066 (20.6)	2840 (20.5)
Very High	1005 (6.1)	873 (5.5)	1048 (7.0)	794 (5.7)
Triglycerides, mg/dL
Optimal	12027 (71.9)	11157 (70.5)	10141 (68.2)	9529 (68.7)
Borderline high	2420 (14.4)	2363 (14.9)	2413 (16.2)	2171 (15.7)
High	2289 (13.7)	2317 (14.6)	2328 (15.6)	2176 (15.6)
Total cholesterol / HDL ratio
Quartile 1, (<3.27)	4177 (25.0)	4030 (25.5)	4278 (28.7)	3953 (28.5)
Quartile 2, (3.27–4.14)	4170 (24.9)	3869 (24.4)	3871 (26.0)	3690 (26.6)
Quartile 3, (4.15–5.24)	4169 (24.9)	3882 (24.5)	3613 (24.3)	3392 (24.5)
Quartile 4, (>5.24)	4217 (25.2)	4057 (25.6)	3120 (21.0)	2841 (20.4)
LDL cholesterol / HDL ratio
Quartile 1, (<1.91)	4138 (25.1)	4090 (25.8)	4457 (30.1)	4191 (30.2)
Quartile 2, (1.91–2.62)	4101 (24.8)	3936 (24.9)	3932 (26.4)	3723 (26.8)
Quartile 3, (2.62–3.47)	4111 (24.9)	3760 (23.7)	3513 (23.6)	3339 (24.2)
Quartile 4, (>3.47)	4167 (25.2)	3984 (25.2)	2951 (19.9)	2607 (18.8)
Triglycerides / HDL ratio
Quartile 1, (<1.39)	4184 (25.0)	3544 (22.3)	3450 (23.2)	3105 (22.4)
Quartile 2, (1.39–2.21)	4132 (24.7)	3795 (24.0)	3485 (23.4)	3208 (23.1)
Quartile 3, (2.21–3.67)	4205 (25.1)	4113 (26.0)	3911 (26.3)	3694 (26.6)
Quartile 4, (>3.67)	4212 (25.2)	4385 (27.7)	4036 (27.1)	3869 (27.9)

HDL indicates high-density lipoprotein; LDL, low-density lipoprotein; CVD, cardiovascular disease.

^aNumbers represent mean (SD) for continuous variables; numbers and percentages correspond to "Yes" for dichotomous variables.

^bDefined based on World Health Organization cut-off points.

Baseline characteristics of participants who remained in the study and those censored during follow-up are shown in Supplementary Table 1. In summary, for both events of CHD and stroke, the likelihood of being dropped out due to competing causes of death was more in men, blacks, people with an education of less than high school, family history of CVD, hypertension, diabetics, obese people, those taking lipid-lowering medication, people with a high waist-to-hip ratio, current smokers, former alcohol drinkers, and people with high levels of lipids, including HDL-C than others. Also, women, Hispanics, those with higher education, non-smokers, former alcohol drinkers, and people with normal total cholesterol and LDL-C levels were more likely to be censored due to loss of follow-up.

Marginal structural cox model

During a median (IQR) follow-up time of 17.1 (8.5 to 25.7) years, there were 1638 (9.8%) incident CHD and 5362 (32.0%) censored; 3616 (21.6%) subjects died from causes other than CHD (competing risk), and 1746 (10.4%) subjects were lost to follow-up. The incidence rate of CHD was 58.6 per 10,000 person-years (95% CI: 55.8–61.5). In addition, during a median (IQR) follow-up time of 18.1 (8.5 to 25.8) years, 1017 (6.1%) new cases of stroke occurred, and 5956 (35.6%) censored; 4038 (24.1%) subjects died from causes other than stroke (competing risk), and 1918 (11.5%) subjects were lost to follow-up. The incidence rate of stroke was 35.8 per 10,000 person-years (95% CI: 33.7–38.1). Among 16736 included subjects, 9736 (58.2%) and 9763 (58.3%), respectively, survived free of CHD and stroke to the end of follow-up.

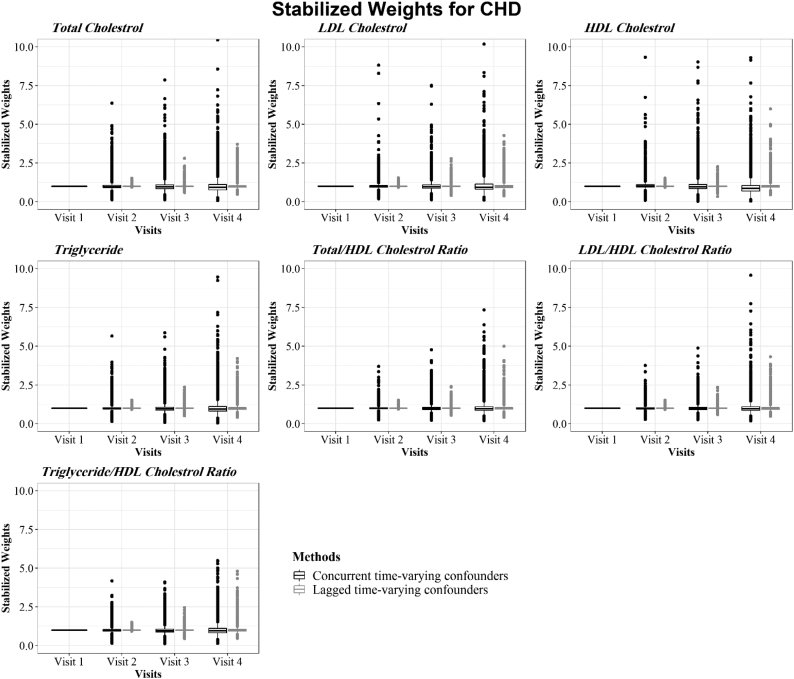
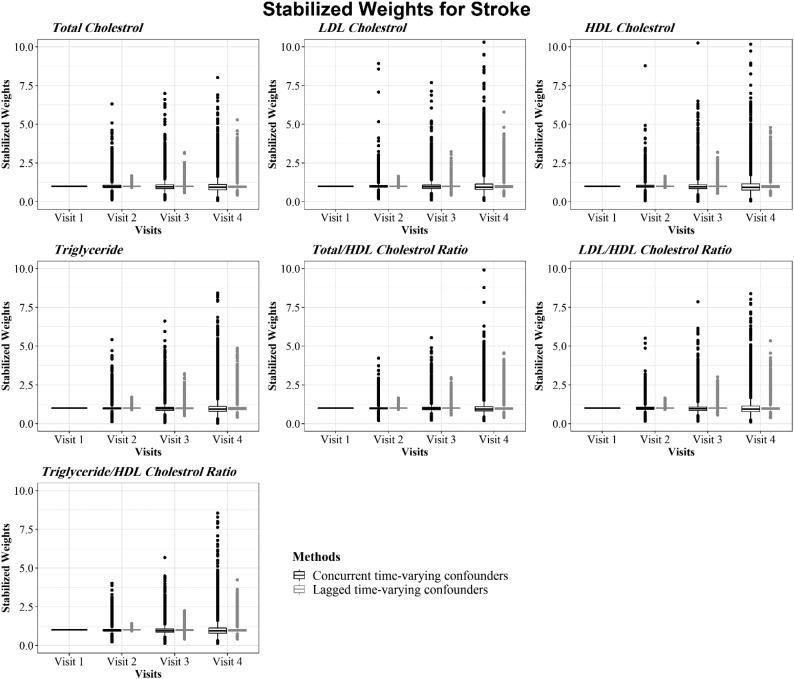
Model outputs for estimating the final stabilized weights of each lipid component at all visits for CHD and stroke are presented in Fig. 3, Fig. 4, respectively. The stabilized IPTWs used in the Cox MSMs had symmetric distributions centered around the ideal mean of 1 for all lipid indices at all visits, satisfying a necessary condition for correct model specification [53].

Fig. 3.

Distribution of stabilized weights used in the MSM models for CHD to adjust for concurrent and lagged time-varying confounders.

Fig. 4.

Distribution of stabilized weights used in the MSM models for stroke to adjust for concurrent and lagged time-varying confounders.

Fig. 5 presents MSM estimates of the hazard ratios (HRs) with 95% CIs for the effect of each lipid component on CHD and stroke risk. Based on the results of MSM adjusted for concurrent time-varying confounders, if all participants had been kept at a borderline high (200–239 mg/dL) and high (≥240 mg/dL) levels of TC, risk of CHD would have been 1.46 (95% CI, 1.28–1.66), or 2.15 times higher (95% CI, 1.82–2.55), and risk of stroke would have been 1.26 (95% CI, 1.08–1.48), or 1.35 (95% CI, 1.08–1.70) times higher than under a scenario in which all participants had been kept at the optimal levels, respectively. Also, if everyone had always had high (160–189 mg/dL) or very high (≥190 mg/dL) levels of LDL-C, risk of CHD would have been 1.85 times (95% CI, 1.51–2.28) and 2.62 times (95% CI, 1.94–3.52) higher, and risk of stroke would have been 1.39 times (95% CI, 1.03–1.85) and 1.92 times (95% CI, 1.21–3.04) higher than if they had always had the optimal levels (<100 mg/dL), respectively.

Fig. 5.

Hazard ratios and 95% confidence intervals for the effect of each lipid component on the risk of CHD (red) and stroke (blue). Estimates from two MSMs with joint IPTW and IPCW adjusted for concurrent and lagged time-varying confounders. HRs approximated from a pooled logistic regression.

Compared with a scenario in which all participants had been kept at the optimal levels of HDL-C (40–59 mg/ dL), the risk of CHD and stroke would have increased by 41% (HR, 1.41; 95% CI, 1.32–1.68), and 29% (HR, 1.29; 95% CI, 1.06–1.58) if all participants had been kept at a low HDL-C level (<40 mg/dL), respectively. If everyone had always had high (60–79 mg/dL) or very high (≥80 mg/dL) levels of HDL-C compared with if they had always had the the optimal levels (40–59 mg/dL), the risk of CHD would have decreased by 19% (HR, 0.81; 95% CI, 0.66–0.99) and 33% (HR, 0.67; 95% CI, 0.44–1.01), respectively, while the risk of stroke would have increased by 6% (HR, 1.06; 95% CI, 0.84–1.33) and 18% (HR, 1.18; 95% CI, 0.79–1.76). There was also little evidence of an effect of high levels of triglyceride on stroke (Fig. 5).

If all participants had been kept at the third (4.2–5.2) and fourth (≥5.2) quintiles of TC/HDL-C (≤3.3), risk of CHD would have been 1.52 (95% CI, 1.26–1.84), or 2.37 times higher (95% CI, 1.97–2.85), and risk of stroke would have been 1.45 (95% CI, 1.16–1.83), or 1.58 (95% CI, 1.25–1.99) times higher than under a scenario in which all participants had been kept at the first quintile, respectively. Besides, if everyone had been kept at the third (2.6–3.5) and fourth (≥3.5) quintiles of LDL-C/HDL-C, risk of CHD would have been 1.40 times (95% CI, 1.15–1.70) and 2.16 times (95% CI, 1.78–2.61) higher, and risk of stroke would have been 1.36 times (95% CI, 1.06–1.73) and 1.68 times (95% CI, 1.32–2.15) higher than if they had been kept at the first quintile (≤1.9), respectively. Moreover, if all participants had been kept at the third and fourth quartiles of triglyceride/HDL-C, the risk of CHD would have been higher than if all participants had been kept in the first quartile. At the same time, no association was found between triglyceride/HDL-C and stroke.

Results from sensitivity analyses adjusted for lagged time-varying confounders produced similar findings as our primary analyses, except for borderline high and high levels of triglyceride that demonstrated to be associated with incident CHD. The estimates for borderline high and high levels of triglyceride in the lagged analysis of CHD were slightly higher: hazard ratios were 1.21 (95% CI, 1.02–1.43) and 1.18 (95% CI, 1.00–1.39), respectively (Fig. 5).

Discussion

This large, pooled cohort study investigated the effect of lipid indices and lipid ratios on CHD and stroke using a Cox MSM. It was revealed that TC and LDL-C play roles in developing CHD and stroke with a weaker effect on stroke than CHD. We also observed no evidence for the protective effect of high levels of HDL-C on stroke. Besides, triglyceride was not found to affect stroke.

Although the association between lipids and CVD has been confirmed in numerous studies, most of them have used standard statistical methods, adjusting only for the baseline confounders [[58], [59], [60]]. We used the Cox marginal structural model, a causal inference model, because standard statistical methods may give biased effect estimates when time-varying confounders, such as lipid-lowering drugs and hypertension, are affected by previous exposure [4,14]. The inverse probability-of-exposure-and-censoring weighted estimators of MSMs can provide unbiased estimates of the causal effect of a time-varying exposure in this setting by appropriately adjusting for time-varying confounding and selection bias due to censoring [9,53]. To date, only one previous study has examined the effect of LDL-C and HDL-C on CVD and mortality using G-estimation [35]. Besides, since the underlying causes of CHD and stroke may be different, a better understanding of the association of lipids with subtype-specific CVD events rather than focusing on total CVD would be more enlightening for CVD prevention. Therefore, our study is the first that examined the effect of lipid indices and lipid ratios on the risk of CHD and stroke, separately using a method that adjusts for time-varying confounding.

Both MSMs adjusting for concurrent and lagged time-varying confounders suggested that risk of CHD and stroke would have been higher if everyone had had higher than optimal levels than if everyone had had optimal levels. The risk was higher for CHD than stroke. Our findings are consistent with the evidence obtained from some genetic studies and randomized trials suggesting the effect of LDL-C on both CHD and stroke [[61], [62], [63]]. In a Mendelian randomization study using genetic variants that confer lifelong LDL-C differences, the causal effect of LDL-C was more substantial for CHD than stroke: one mmol/L genetically higher LDL-C increased the risk of CHD by 50%, ischemic stroke by 12%, and cardioembolic stroke by 6% [61]. More potent effects of LDL-C on CHD than on stroke have also been shown in other observational studies [64].

In contrast, some randomized trials of LDL-C-lowering therapies, such as statin therapy, have shown the consistent effects of LDL-C-lowering treatments on CHD and stroke [62,65]. Tilling et al. also found a positive linear relationship for LDL-C with CHD using G-estimation [35]. Previous studies estimated the 18-years risks of stroke and MI under different scenarios of hypothetical interventions using the parametric g-formula showed that lowering total cholesterol to <6.22 mmol/l did not substantially alter the stroke risk [66], while it was associated with reduced MI risk, with a population risk ratio 0.87 [67]. Another study using the parametric g-formula found that long-term exposure to moderate levels of LDL-cholesterol has the same impact on CHD risk as shorter exposures to levels considered ‘high’ [68].

In line with Tilling et al. [35] showing a linear inverse relationship between HDL-C and CHD, using G-estimation, high levels of HDL-C in our study tended to have a protective effect on CHD using MSM adjusting for concurrent confounders. However, both MSMs found little evidence for the protective effect of HDL-C on stroke after adjusting for LDL-C and TG. Recent epidemiologic, genetic, and clinical trial studies have suggested that very high levels of HDL-C are associated with cardiovascular events and mortality [29,[69], [70], [71]]. Clinical studies have indicated that not only serum HDL-C concentration/quantity but also its qualities/properties can play a critical role in determining its overall effects on clinical outcomes [72,73]. The results obtained from Mendelian randomization studies have also shown that genetic mutations leading to very high HDL-C may play a role in this association and adversely affect CVD [[74], [75], [76]]. The discrepancy among different studies regarding the cardiovascular effects of high HDL-C may be explained by the very small sample size of individuals with very high HDL-C (i.e., >80 mg/dL) in most of the older studies, which limits the ability to conclude the risk of extremely high levels of HDL-C on CVD [77]. Furthermore, in many of these studies, the focus was on low concentrations of HDL-C, thereby failing to reveal associations at higher concentrations [78]. Our longitudinal study design considered not only variations in HDL-C itself over time but also changes in cardiovascular risk factors over time to estimate the risk of outcomes. In addition, a sufficient sample size of participants with > 80 mg/dl of HDL-C facilitated estimating differential effects of very high HDL-C levels on various CVD manifestations within a single population. Although some other recent studies had these strengths, our study can add evidence to the association.

Moreover, no strong evidence for the detrimental effect of TG on stroke was found in both MSMs after adjustment for LDL-C and HDL-C, even though the results suggest a possible minor effect on CHD. Although the exact role of TG in inducing CVD remains controversial, our results are consistent with those obtained from the largest Emerging Risk Factors Collaboration [79]. Genetic evidence linking TG levels and atherosclerosis risk revealed that almost all genetic variants associated with TG are linked with at least one other lipid trait, commonly reduced HDL-C [[80], [81], [82]]. A genetic study that applied inverse-variance-weighted Mendelian randomization to estimate lipid indices' causal effect on stroke demonstrated genetically elevated triglycerides are not associated with ischemic stroke or its subtypes [83]. On the other hand, randomized trials of agents lowering TG did not find any reduction in cardiovascular events [84,85]. In contrast, a recent systematic review and meta-regression analysis of randomized trials of TG-lowering therapies showed an association between TG-lowering and CVD risk reduction, even after adjusting for LDL-C lowering. It should be noted that the effect attenuated after excluding the Reduction of Cardiovascular Events with Icosapent Ethyl-Intervention Trial (REDUCE-IT) from the analysis [86].

Furthermore, both MSMs showed that a TC/HDL-C ratio higher than four and an LDL-C/HDL-C higher than 2.5 is associated with the greater risks of CHD and stroke. A TG/HDL-C higher than two was associated with CHD; however, there was little evidence for its association with stroke. Our findings are consistent with some previous observational studies [[87], [88], [89], [90]].

In cohort studies, since the exposure may change before current time-varying confounders, lagged time-varying confounders were adjusted for sensitivity analysis [52,54]. However, effect estimates in the MSM model with weights adjusted for concurrent confounders were weaker than those adjusting for lagged confounders. Generally, these two MSM models can produce different effect estimates, given that concurrent confounders are expected to have less measurement error than lagged confounders because of long measurement intervals. Also, the MSM model with weights adjusting for concurrent confounders may give biased estimates if they are affected by the exposure [52,54].

Our results should be interpreted in light of several limitations. First, measurement error in self-reported confounders such as smoking and drinking status may induce residual confounding [91,92]. Second, HR is not an ideal effect measure for causal inference as it is non-collapsible and has a built-in selection bias [[93], [94], [95]]. Third, using quartiles of lipid ratios instead of actual values in the analyses may reduce power and change non-differential to differential error [96,97]. Fourth, as discussed in more detail elsewhere [53], the validity of causal estimates using G-methods, including MSM, relies on four identifiability assumptions: well-defined exposure, exchangeability, positivity, and correct model specification [[98], [99], [100], [101]]. Our exposures were not well-defined as many interventions can be used to change them with different effects on CVD. Although lipid-lowering medications are potentially a more well-defined exposure to study than the lipid levels themselves, novel evidence supports a continuous and graded benefit of LDL-C reduction on cardiovascular risk across different types and doses of statin-based therapies [102,103]. Furthermore, many individuals cannot achieve sufficient LDLC reduction, do not tolerate effective doses, or are unwilling to take LDL-C-lowering medications [104]. Therefore, considering the different types, duration, and treatment doses administered are essential when evaluating lipid-lowering effects; unfortunately, these data were not available.

In addition, the issues of unmeasured confounding and model misspecification cannot be excluded. Although many time-varying and time-fixed confounders were used to justify the exchangeability assumption, there might still be some unmeasured confounders, such as diet quality, sodium intake, and household and ambient pollution. Furthermore, due to data availability, diet and physical activity, both potentially modifiable and affected by prior exposure, could not be treated as time-varying covariates. Another assumption for causal methods is positivity. We used V-stabilized weights with all baseline confounders in our analyses, which decreased the chance of random violations of the positivity assumption.

To determine the correct model, as described by Cole and Hernán [53], we informally explored the sensitivity of bias and precision of the effect estimate to different weight models specifications (e.g., considering non-linear vs. linear terms for continuous confounders using multivariate fractional polynomial models, adding lagged confounders and so on). The mean weights were also very close to one, suggested as a necessary condition for correct model specification [53].

Lastly, treating the competing risk of death as a right-censoring event can lead to a “cause-specific” interpretation including what would be observed in a counterfactual world where the competing event did not occur. Although it is unrealistic to imagine a scenario where we could entirely remove all other causes of death and produce such a population, this will not be the case for all research questions. On the other hand, the subdistribution method may help generate predicted probabilities that individuals will be in particular states. However, evidence stated that the subdistribution approach is more “predictive” while the cause-specific hazards are more fundamentally “causal.” In other words, the subdistribution risk is helpful for causal prediction, i.e., predicting counterfactual outcomes under a certain policy relative to a second policy [105,106].

Despite these limitations, this study had several strengths. First, we used a large harmonized data set from two US representative cohort studies with a large ethnically diverse population enrolled, a considerable follow-up time with multiple measurements on various covariates, and active follow-up for incident CVD and death. Second, to the best of our knowledge, this is the first study to evaluate the effects of lipid indices and lipid ratios on the CHD and stroke separately while appropriately adjusting for time-varying confounders affected by previous exposure.

In conclusion, using MSM appropriately adjusting for time-varying confounders, this study highlights the effect of TC and LDL-C on cardiovascular events, with a stronger effect on CHD than on stroke. Our results suggest that high levels of HDL-C may be protective for CHD, but not for stroke. There was also no evidence of an adverse effect of high triglyceride levels on stroke.

Ethics approval

The current study was performed following the ethical standards in the Declaration of Helsinki. The institutional review board approved the ARIC and MESA study protocols of each participating center. All methods were carried out following relevant guidelines and regulations. Approval for undertaking the current project was also obtained from the School of Public Health & Neuroscience Research center, Shahid Beheshti University of Medical Sciences, Tehran, Iran (IR.SBMU.PHNS.REC.1398.090).

Consent to participate

All ARIC and MESA participants provided written informed consent.

Consent for publication

Not applicable.

Availability of data and material

The datasets used during the current study are available from the corresponding author on reasonable request.

Funding

No funds, grants, or other support was received.

Authors' contributions

All authors contributed to the study's conception and design. FK, MA.M, DK, and HS raised the presented idea and designed the study. FK performed statistical analyses under the supervision of senior authors MA.M, DK, and HS. FK, DK, MA.M, MN, and HS interpreted the results. FK developed the first draft of the manuscript. MA.M, DK, MN, and HS critically reviewed the manuscript. All authors read and approved the final manuscript.

Declaration of Competing Interest

The authors have no relevant financial or non-financial interests to disclose.

Appendix A. Supplementary data

Supplementary material