A practical guide to handling competing events in etiologic time-to-event studies

Abstract

Competing events are events that preclude the occurrence of the primary outcome. Much has been written on mainly the statistics behind competing events analyses. However, many of these publications and tutorials have a strong statistical tone and might fall short in providing a practical guide to clinician researchers as to when to use a competing event analysis and more importantly which method to use and why.

Here we discuss the different target effects in the Fine-Gray and cause-specific methods using simple causal diagrams and provide strengths and limitations of both approaches for addressing etiologic questions. We argue why the Fine-Gray method might not be the best approach for handling competing events in etiological time-to-event studies.

Competing events (also referred to as competing risks) are events that compete with the primary event of interest such that they preclude the occurrence of the primary event [1,2]. Competing events often occur in cohort studies that require a very long period of follow-up, usually in diseases with long latency such as Alzheimer's disease, cancer and cardiovascular disease. For example, in a study that assesses the potential benefit of a certain drug on cancer, death of subjects due to stroke, before death due to cancer can occur, would be considered a competing event. Ignoring competing events in the analysis might lead to biased effect estimates of the exposure on the outcome [3].

A substantial body of literature has been written on the appropriate handling of competing events and interpretation of the result [1,2]. However, most use heavy statistical language that can be confusing to the average clinical researcher and do not dwell on the practical aspects (when to use them and why) of the available competing event methods [[2], [3], [4]]. Moreover, they do not elaborate on an important concept that is vital to understanding of competing events and the type of methodology needed to address them, mainly the target effect of interest.

Here we provide a practical guide to clinicians as to what competing events are and how to go about assessing the best method to use when considering the etiologic question of interest. We first start with a practical example:

Suppose you are interested to know if the direct oral anticoagulant (DOAC) dabigatran prevents stroke in patients with atrial fibrillation (AF). You design a large multicenter randomized trial and assign elderly patients with AF to either dabigatran or placebo. As death due to gastrointestinal bleeding (DGIB) is a competing event for stroke, your statistical consultant suggests using a competing-risk regression model, specifically the Fine-Gray method, and in this way, you obtain a hazard ratio of 0.80 with 95% confidence interval of (0.70, 0.91). Based on these results, can you conclude that dabigatran has a protective effect on stroke?

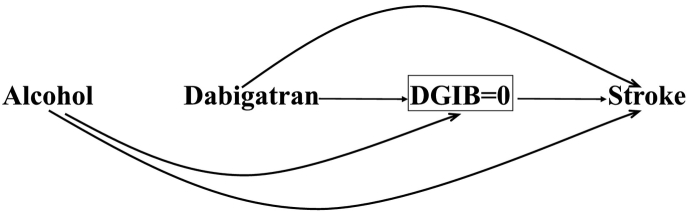
The causal diagram [[5], [6], [7], [8], [9], [10], [11], [12]] in Fig. 1 represents our study. The arrow from dabigatran to stroke depicts the direct (postulated) effect of dabigatran on stroke. The arrow from dabigatran to DGIB implies the effect of dabigatran on death secondary to a GI bleed, and the arrow from DGIB to stroke reflects that deaths preclude stroke occurrence. The causal path Dabigatran→DGIB→Stroke shows the indirect protective effect of dabigatran on stroke through DGIB.

Fig. 1.

A causal diagram demonstrating the total effect of dabigatran on stroke in patients with atrial fibrillation using the Fine-Gray approach in a randomized trial. The direct effect of dabigatran (pharmacological effect) is shown with an arrow from dabigatran to stroke head-to-tail. The arrow from dabigatran to DGIB implies the effect of dabigatran on death secondary to gastrointestinal bleeding (DGIB), and the arrow from DGIB to stroke reflects that the stroke occurrence is precluded by death due to GI bleeding. The causal path Dabigatran→DGIB→Stroke shows the indirect effect of dabigatran on stroke through DGIB.

In this study, participants are followed-up for the event of interest, stroke, but they may be removed from the observed population at risk due to losses to follow-up or competing events [13]. Study participants may be lost to follow-up because they are non-adherent to therapy or move to a new geographic location. For simplicity, we assume no loss to follow-up in the dabigatran and stroke example. Death due to gastrointestinal bleeding (DGIB) is considered a competing event for stroke.

It is important to note that the preceding reasons for removal of the subjects from the follow-up are distinct: while subjects who are lost to follow-up are still at risk of the event of interest (only the event time cannot be observed), those who experience the competing event are no longer at risk. More importantly, it is generally easier to prevent losses to follow-up (perhaps through allocation of resources) than it is to prevent deaths from different causes [3].

There are two common analytical approaches for the analysis of time-to-event data in the presence of competing events, both of which are based on modeling the hazard function (instantaneous failure rate): the cause-specific hazard method and the subdistribution hazard method (also known as the Fine-Gray method [1,2,4,14]). The aim of this paper is to describe these two methods and to illustrate which method is more appropriate for etiologic research questions and why.

1. Fine-Gray method

The Fine-Gray method is based on quantifying the unconditional risk of the event of interest in the presence of competing events, also known as the cumulative incidence function (CIF) [1,2,4,14]. This method models the subdistribution hazard function with the assumption that subjects who experience the competing event remain at risk, along with those who survive all events and are not censored [15]. For example, in the study of dabigatran and stroke, subjects who died of a GI bleed were deemed not to experience stroke. However, the Fine-Gray method does not censor these patients but keeps them in the risk set i.e., all subjects who are at risk of experiencing the primary event. This is because the Fine-Gray's objective is to answer the question “What is the total effect of dabigatran on stroke?” through both the direct (its potential anti-inflammatory effect on stroke) and indirect effects. The indirect effect includes reasons for which subjects on dabigatran do not live long enough to be diagnosed with stroke, e.g., death due to a GI bleed or even death due to bleeding from a car accident (as a result of dabigatran use).

The total effect can be unbiasedly estimated in an ideal randomized trial (i.e., with a large sample size, blinding and perfect adherence with treatment, and without losses to follow-up) using the Fine-Gray method as Fig. 1 shows both direct (Dabigatran→Stroke) and indirect (Dabigatran→DGIB→Stroke) paths are causal, traced out from dabigatran to stroke along arrows, head-to-tail [3]. Another advantage of the Fine-Gray method is that it relates well to public health as it informs policy makers about the marginal (total) impact of an intervention in the study population [14] e.g., the impact of dabigatran use by older adults on the total burden of stroke in the population. Two measures of the total effect can be obtained using the Fine-Gray approach: the (sub-distribution) hazard ratio (HR) and the cumulative incidence difference (CID). As the latter quantifies the difference in cumulative incidence of the exposed and unexposed groups, it is the preferred metric compared to the former (which is a ratio) from a public health perspective; moreover, the inverse of CID can be easily computed and is referred to as the number needed to treat (NNT), a familiar metric to clinicians that has a relatively simple interpretation [16] i.e., the number of patients needed to take dabigatran to prevent one stroke event.

However, when using the Fine-Gray approach, the total effect estimate might be difficult to generalize to other populations as the indirect effect depends on the risk of competing event(s), which varies over populations. More importantly, the indirect effect might not be generally of interest; the prevention of stroke through death due to a GI bleed is irrelevant as clinicians, policy makers and patients are more interested to know whether dabigatran lowers the risk of stroke through its direct pharmacologic effect. In fact, the Fine-Gray method cannot discriminate the proportion of the total effect mediated by the competing event, which can be even 100%: the preventive effect of dabigatran is essentially due to its indirect effect and not due to its pharmacological effect on stroke, as the hypothetical example in Fig. 2 illustrates.

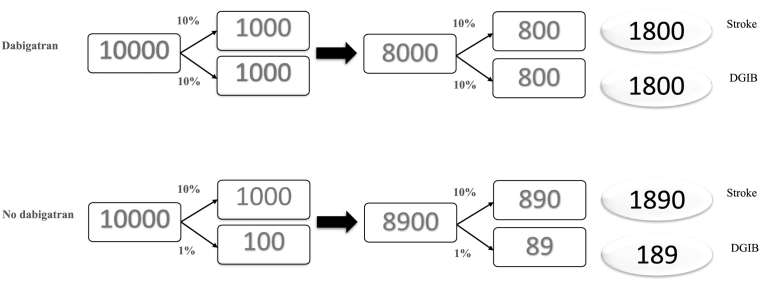
Fig. 2.

A hypothetical example of the protective total effect of dabigatran on stroke in patients with atrial fibrillation in the absence of a true pharmacological effect of dabigatran on stroke; the effect is only due to indirect effect of dabigatran on stroke through death secondary to gastrointestinal bleeding (DGIB).

Suppose the 5-year risk of stroke in both 10,000 dabigatran users and 10,000 nonusers is 10% and that dabigatran use has no effect on the risk of stroke; the risk of DGIB is 10% in those who received dabigatran and 1% in those who did not (Fig. 2). What is the 10-year CID between the two groups? Computing the cumulative incidence for dabigatran users, there will be 1000 stroke cases in 5 years (10% of 10,000) and 1800 in 10 years: as by the end of 5 years, 20% had either died or were diagnosed with stroke (leaving only 8000 at risk of stroke at the beginning of the second 5-year period), and subsequently 800 stroke cases were diagnosed during the second five year. Note that the cumulative incidence based on the Fine-Gray method does not remove deaths (the competing event) from the denominator, so it is 1800/10,000 for dabigatran users and using the same approach 1890/10,000 for nonusers, giving a CID of 0.009 and an NNT of 111.1 (1/0.009) in favor of dabigatran. However, the reason for this paradoxical beneficial effect of dabigatran is mainly because dabigatran users are more likely to die from a GI bleed during the first five years, subsequently there will be fewer people on dabigatran that survive long enough to be at risk of developing stroke at the beginning of the second five year: 8000 compared to 8900 in the no-dabigatran group.

This hypothetical example underscores that the protective effects for dabigatran on stroke obtained from Fine-Gray in our study can be explained, in part or in whole, by the indirect effect of dabigatran through DGIB. This method may inform us that dabigatran protects against stroke not through its anti-inflammatory effect (of potential interest) but through its indirect effect (not of much interest).

2. Cause-specific method

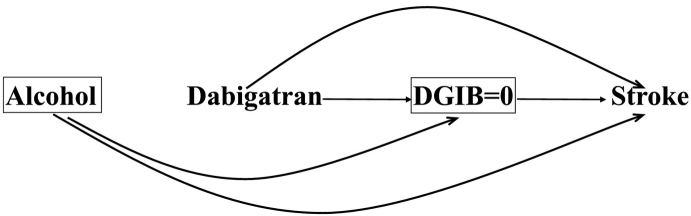
The cause-specific approach treats competing events as censored, and only considers the conditional risk of the event of interest had the competing event(s) not occurred [2,3,13]. Fig. 3 is a modified version of Fig. 1 in that it has a square around DGIB with a value equal to zero, indicating the restriction of the analysis to only those who have not been censored, i.e., those who did not die due to a GI bleed. Thus, according to Fig. 3, the indirect effect of dabigatran through DGIB has been blocked by conditioning on DGIB, highlighting the fact that the target effect in the cause-specific approach will be the direct effect [3].

Fig. 3.

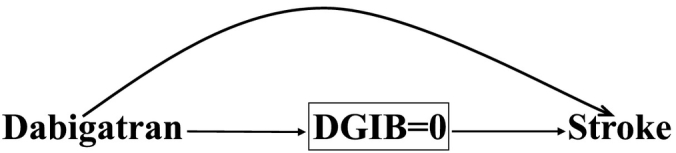
A causal diagram demonstrating the direct effect of dabigatran on stroke in patients with atrial fibrillation using the cause-specific approach in a randomized trial. The competing event death due to gastrointestinal bleeding (DGIB) is considered a censoring event represented by a square around DGIB = 0 signifying that only those who did not experience a DGIB are included in the analysis.

This method is based on modeling the cause-specific hazard which assumes that only subjects who survive all events and are not censored remain at risk [15]. However, censoring patients who might experience the competing event, where the competing event is also affected by the exposure, along with restricting the analysis to the uncensored, might lead to selection bias [[17], [18], [19]] if there is a common risk factor for the primary and competing events. For example, referring to our dabigatran and stroke example, DGIB is affected by dabigatran, and alcohol is a common risk factor for stroke and DGIB. The selection bias in this example can be explained by noting that subjects who are on dabigatran, but do not die due to a GI bleed, are less likely to be consuming alcohol (since dabigatran and alcohol are both causes of GI bleeds) and thus are less likely to be diagnosed with stroke. The selection bias that occurs through alcohol use may make one think that dabigatran is protective for stroke when in fact it has no pharmacological effect, under the assumption of no pharmacological effect of dabigatran on stroke; (for a detailed graphical explanation please see the Appendix).

In fact, the cause-specific method requires three assumptions. First, the intervention on the competing event has to be practical. In our example, death due to a GI bleed can be averted using specific interventions (e.g., use of proton pump inhibitors). But death due to any cause as a competing event is a less practical entity because interventions to avert such an event can be complex. Second, the censored and uncensored subjects should have shared the same distribution of risk factors; mainly the censoring (the competing event) has to be independent of the outcome. The presence of an unmeasured common risk factor (e.g., alcohol in our example) for the primary and competing events would violate this assumption. Third, there should be an adequate number of uncensored subjects in any level of the common risk factor and exposure. For example, one cannot have a situation where all those who use both dabigatran and alcohol die of a GI bleed.

Under the preceding assumptions, the cause-specific approach will provide a valid estimate of the direct effect of exposure on the outcome after adjustment for the common risk factors. This can be done using a Cox regression model with risk factors included in the model. Other more sophisticated methods, including inverse probability-of-censoring weighting (IPCW), can also be used. In this method, the inverse of the probability of no censoring (in subjects who were not censored), given the exposure of interest and common risk factors, are computed and assigned to each uncensored subject as the weight [[20], [21], [22], [23]]. Subsequently a weighted Cox model is performed, which includes only the exposure in model. IPCW effectively undoes the censoring process: it creates the ideal pseudo-population if no one had been censored and in which the exposure effect is the same as in the population. The Appendix graphically illustrates the traditional and weighting adjustments.

3. Discussion

Choosing the right approach to address competing events can often create a dilemma as to choosing the right analytical technique for a particular etiologic study question. The Fine-Gray method is popular for handling competing events. However, interpretability of its results for etiologic research questions is challenging as one cannot single out the biological effect of a particular exposure on the outcome, as it simply computes the total effect of the exposure on the outcome. In our example, where a protective effect of dabigatran on stroke is demonstrated using the Fine-Gray method, one cannot rule out that this protective effect, at least partially, reflects the indirect effect of dabigatran on stroke through death subsequent to a GI bleed.

In exceptional situations, the total effect of the exposure might be of interest, e.g., the effect of a drug on the prevention of nosocomial infection with discharge as the competing event, or effect of dabigatran on time to live birth with pregnancy loss as the competing event [3,14]. In most situations the indirect effect might not have any clinical or practical benefit to the researcher, clinician or policy makers (though the indirect effect may be of interest if the aim is to learn how to block such an effect) [24]. The Fine-Gray was mainly proposed for prediction modeling where the objective is to build the best model for predicting a particular outcome. However, many landmark epidemiologic studies that address an etiologic question still use this method to address competing events [25,26].

The cause-specific method is more intended to answer etiologic questions by estimating the direct effect of a particular exposure on an outcome. However, the validity of this method relies on some assumptions, including conceivable elimination of the competing event and no unmeasured risk factors for the primary and competing events, none of which are guaranteed even in a setting of an ideal randomized trial [3]. It is important to note that when the competing event is very rare or not affected by the exposure both Fine-Gray and cause-specific methods will generate similar results [4].

For simplicity of presentation, we illustrated the choice of competing risk model in the context of randomized clinical trials. However, perhaps the most prevalent study design where competing events might be consequential is probably in the case of observational cohort studies where the confounders for the effect of exposure on the primary event of interest should be appropriately adjusted for in the analysis (for both approaches). Moreover, for Fine-Gray method, the confounders of the effect of exposure on the competing event should also be adjusted for [27].

It is important to note that both Fine-Gray and cause-specific Cox regression models yield (subdistribution and cause-specific) hazard ratios which suffer from a built-in selection bias [28]. The reason for this bias is that the hazard function conditions on those who survives the primary event of interest, and survival can be affected by both exposure and an unmeasured cause of outcome (e.g., a protective haplotype), resulting in a selection bias. Given the bias inherent in hazard, it is preferred to perform risk (survival curve) comparisons [29] (please see Appendix for a graphical presentation of the built-in selection bias in the hazard ratio).

In sum, two main methodologies exist for addressing competing events for studies that address etiologic questions, the Fine-Gray method and the cause-specific method. We recommend using the cause-specific approach for the causal effect estimation in the presence of competing events with a careful consideration of the underlying assumptions, unless the indirect effect of the exposure on the outcome is of clinical significance in which case the Fine-Gray method can be used.

Contributions

MAM is the guarantor of this article. Dr. Mansournia is biostatistician and epidemiologist with a specialty in causal inference and is also the statistical deputy editor for the British Journal of Sports Medicine. Dr. Nazemipour is a biostatistician. Dr. Etminan is a pharmacoepidemiologist with experience in causal inference in drug safety studies. All authors have had extensive experience in the areas of causal inference and epidemiologic methodology.

Funding

We received no funding for this study.

Appendix A. Further graphical explanations in the analysis of time-to-event data with competing events

A.1. Selection bias in the cause-specific approach

The cause-specific approach assumes that censored and uncensored groups are conditionally exchangeable: i.e., within levels of some measured common risk factors for the outcome and censoring, the probability of outcome in the censored subjects would have been the same as that in the uncensored if they, contrary to fact, had not been censored. Conditional exchangeability will be met if censoring and outcome are independent given the common risk factors, known as independent-censoring assumption.

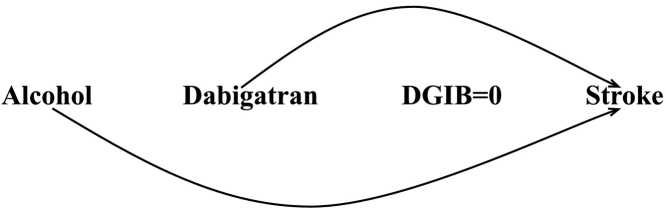
Conditional exchangeability is violated in the presence of unmeasured common risk factors, leading to selection bias. Suppose alcohol consumption (Appendix Fig. 1), a common risk factor for dabigatran and stroke, is unmeasured. The path Dabigatran→DGIB←Alcohol→Stroke is open, as the collider DGIB (death due to gastrointestinal bleeding is a common effect of dabigatran and alcohol) has been conditioned on, leading to selection bias. To see intuitively why the bias arises, suppose a subject who does not experience GI bleeding (and does not die) is on dabigatran. In such a situation it is also less likely that this subject is an alcohol (second cause of DGIB) user. As such dabigatran and alcohol become inversely associated with each other. Thus, taken together with alcohol being a risk factor for stroke, using the cause-specific approach, one might erroneously conclude that dabigatran is protective for stroke under the no direct effect.

A.2. Adjustment techniques for common risk factors in the cause-specific approach

Under the assumptions mentioned in the paper, the cause-specific approach will provide an unbiased estimate of the direct effect of exposure on the outcome after adjustment for the common risk factors. One potential analytical tool is the use of Cox regression, which includes the common risk factors in the model and yields the adjusted conditional hazard ratio. Appendix Fig. 2 represents this analysis for our study: the square around alcohol indicates adjustment (form of conditioning) for this variable by including it in the Cox model. Another approach is the use of inverse probability-of-censoring weighting (IPCW) in which the inverse of the probability of no censoring given exposure and common risk factors is assigned to each uncensored subject as the weight. Subsequently a weighted Cox model is performed, which includes only the exposure in model and produces the adjusted marginal hazard ratio. IPCW effectively undoes the censoring as it creates the ideal pseudo-population if no one had been censored and in which the exposure effect is the same as in the population. Appendix Fig. 3 displays the pseudo-population when the weights were estimated based on dabigatran and alcohol. There is no DGIB in this population (DGIB = 0), and so there are no arrows from alcohol and dabigatran to DGIB and from DGIB to stroke.

A.3. The inherent bias in the hazard ratio

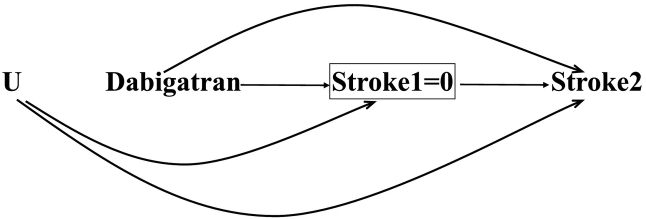
All hazard ratios derived from both the subdistribution and cause-specific hazards suffer from a built-in selection bias. The mechanism for this bias is that the hazard function conditions on those who survive the event of interest, and survival can be affected by both exposure and an unmeasured cause of the outcome. Appendix Fig. 4 illustrates the bias in the hazard ratio in our example. stroke1 and stroke2 denote the stroke at the first and second times, respectively. We assume that both dabigatran and the unmeasured haplotype (U) are protective factors for stroke as reflected by the arrows from dabigatran and U to both stroke1 and stroke2. The square around stroke1 shows that our interest also lies on the hazard at time 2, which is the probability of experiencing stroke at time 2 among (conditional on) those who have survived stroke at time 1. For simplicity, we did not include death due to gastrointestinal bleeding (DGIB) and alcohol use in this Figure. At baseline (time 0), dabigatran is independent of haplotype as the design was randomized, but among survivors of stroke at time 1 (stroke1 = 0), subjects who do not take dabigatran are more likely to have U than dabigatran users (because both dabigatran and haplotype are protective for stroke) and so are less likely to develop stroke. The corresponding biasing path is Dabigatran→Stroke1 ← U → Stroke2 in which the path is opened as a result of conditioning on stroke1. The built-in selection bias in the hazard ratio at time 2 weakens the protective effect of dabigatran; the bias increases with time so that the hazard ratio can even cross at the subsequent times, pretending dabigatran is a risk factor for stroke. Given the inherent bias in the hazard function, it is recommended that researchers perform risk (survival curve) comparisons irrespective of the presence of competing events.

Appendix Fig. 1.

Conditioning on death due to gastrointestinal bleeding (represented by a square around DGIB = 0) in the cause-specific approach introduces bias through the common risk factor alcohol.

Appendix Fig. 2.

Traditional adjustment for alcohol (represented by an square around) in the cause-specific approach.

Appendix Fig. 3.

Adjustment for alcohol through inverse probability-of-censoring weighting (represented by removing the arrows from alcohol and dabigatran through DGIB) in the cause-specific approach.

Appendix Fig. 4.

The built-in selection bias in hazard ratio. stroke1 and stroke2 are stroke in time 1 and 2, respectively, and U is a protective unmeasured haplotype. The hazard ratio at time 2 is biased as it conditions on those who have survived stroke1 (represented by an square around stroke1 = 0), making dabigatran and stroke2 to be associated through U.