Abstract
Introduced in 1983, Bland-Altman methods is now considered the standard approach for assessment of agreement between two methods of measurement. The method is widely used by researchers in various disciplines so that the Bland-Altman 1986 Lancet paper has been named as the 29th mostly highly cited paper ever, over all fields. However, two papers by Hopkins (2004) and Krouwer (2007) questioned the validity of the Bland-Altman analysis. We review the points of critical papers and provide responses to them. The discussions in the critical papers of the Bland-Altman method are scientifically delusive. Hopkins misused the Bland-Altman methodology for research question of model validation and also incorrectly used least-square regression when there is measurement error in the predictor. The problem with Krouwers' paper is making sweeping generalisation of a very narrow and somewhat unrealistic situation. The method proposed by Bland and Altman should be used when the research question is method comparison.
Keywords: Bland-Altman method, Agreement, Comparison methods, Criticisms of Bland-Altman method
Introduction
What is the purpose of a Bland-Altman plot? What research question is it designed to answer?
The first paper introducing the Bland-Altman plot appears in 1983 in The Statistician [1]. The paper introduces the topic of wanting ‘to compare two methods of measuring some quantity, such as blood pressure, gestational age, or cardiac stroke volume’. Immediately, before defining the research question, the authors state one situation which they do not intend to address: that of ‘calibration’, namely comparing a simple and approximate method of measurement with a very precise one giving the true values. Instead they focus on the situation where both methods have measurement error. The question they cite as not having been answered by current methods is this: ‘Do the two methods of measurement agree sufficiently closely?
What methods have been put forward for addressing this research question? What are their strengths and weaknesses?
Correlation is often erroneously used as part of an assessment as to whether two measures agree. The correlation coefficient measures the strength of linear association between two variables. If two methods of measurement are to be considered to be in agreement, it will be necessary for them to have a high degree of correlation (‘high’ being a matter of judgement as to what is acceptable). However this is not sufficient; Pearson's correlation, looking for a linear association, measures how well the linear form Y = a + bX between variables X and Y fits the data. It does not specify the values a and b must take; for the measures to agree, a would need to be 0 and b, 1. So if as in the example given by Bland and Altman [2] we analyzed measurements of subcutaneous fat using calipers and half-calipers, we would get a high agreement but a slope (b) near to 2. The values on the two measures would not be interchangeable, but our correlation coefficient would not tell us this. Similarly if we measured weights on two sets of scales and one were incorrectly zeroed, consistently adding 50 g to all measurements, the correlation coefficient may well show strong association between scales without picking up on this consistent disagreement. Whilst it is not wrong to report a correlation, and indeed can be helpful, it is not sufficient for describing how well two measures agree.
Regression is closely linked to correlation, and gives complementary information. In addition to strength of association (reported as r2, where r is Pearson's correlation coefficient), it also estimates the values of a and b which provide the best straight line approximation of the relationship between Y and X.
There are two problems with using linear regression for analysis of measurement agreement. The first is that least squares regression, the method most commonly used, assumes no measurement error in the independent variable of the equation (X). This may be fine if X were the absolute, known, true values but in the case where both Y and X are approximations to the true value this assumption does not hold. The knock-on effect of the independent measurement errors is that the slope of the line Y = a + bX is always lower than the true slope of the relationship would be if we could have measured both Y and X accurately:
The simple linear regression model is Yi = a + bXi + εi, but when there is a measurement error in X another term needs to be added to the model: Yi = a + b(Xi + δi) + εi, where δi is the random measurement error in X. Let the population variance of X be denoted by σX2 and the variance of measurement errors δi by σδ2. If we fit the model using ordinary least squares, the expected value of the slope whose true value (unknown) is b is.
| (1) |
[[1], p. 315]
One way to explain this is as follows. Measurement errors in X may result in two measured X values, X1 and X2 being recorded as near, further, or the same distance from, each other than the true values are. If they cross over so that X1 > X2 but the true value of X1 is smaller than that of X2, this reverses the direction of a line Y = a + bX since the direction of X1-X2 is changed. If the two are simply brought nearer together without crossing, the slope would be expected to increase; if they are brought further apart, the slope would decrease (the mean value of Y does not change because X has been incorrectly measured). If errors are centred around zero, the expectation is that half the time points are brought further apart, and half the time are either closer together or crossed over. This means that less than half the time points are closer without crossing; as this is the only situation in which the slope increases and it decreases in all others, on average the slope can be expected to decrease.
Another way to think of it is that the largest measured values observed are more likely to be overestimates than underestimates, since if they were underestimates the true values would be even further distanced from the main body of the data. Similarly the smallest values are more likely to be underestimates. On average, the Y values from underestimates will be larger than the true regression line would predict, because we should slide up the line to the true value, and smaller from overestimates. Hence we expect points at the extreme left of a graph to be above the true regression line and points at the extreme right to be below the line. This pulls the slope of the line closer to zero.
This problem of underestimation of the slope (and overestimation of the intercept) in the presence of X errors can be averted by using a form of regression which allows for errors in both Y and X (for example Deming regression [3]). However even then, regression has not fully answered the question of how well the measures agree which is the second problem. It is one thing to be able to report a slope and intercept close to 1 and 0 respectively, and a high r2 value. But in any real experiment the data will not lie perfectly along the regression line. How can we convert the r2, slope and intercept into useful information on how well the measures agree?
Bland-Altman analysis
The method proposed by Bland and Altman [2] provides an interpretation of measurement agreement which is easy to translate into clinical relevance, namely a reference range within which 95% of all differences between measurements using the two methods are likely to lie. It can be summarized in several steps:
-
1.
Is there an association between measurement error and the true value?
-
2.
If no to (1), calculate the mean and standard deviation of the difference between methods
-
3.
Use these figures to calculate
-
I.
The bias (=mean difference)
-
II.
A 95% reference range for difference between values for the two methods measuring the same true quantity (‘Limits of Agreement’): bias +/− 1.96 X standard deviation of differences [4].
-
4.
Bias and limits of agreement may be superimposed on a Bland-Altman plot for visual presentation of the data.
-
5.
Use the limits of agreement to assess whether differences are clinically acceptable
The Bland-Altman plot of difference vs. mean of the two methods is introduced in order to evaluate the question of agreement. It is worth noting that the plot itself is only a part of the method to answer this question; it is intended as a visual check on the data and as a helpful way to display the results. If we have two variable methods of measurement to compare, often the true value is unknown and so we use the mean of the two methods as our best estimator for the true value. Likewise without knowing the true value we do not know the measurement error itself, but the difference between methods is solely due to that error, and in fact difference, or how closely the methods agree, is the quantity we are interested in to answer the research question.
Note that if the Bland-Altman plot shows an association (if yes to step 1), steps 2 to 5 should not be applied. If the differences are correlated with the true value, bias and limits of agreement for the study sample will depend on the range of true values used in the study and hence are not generalizable to future use. Also assuming the variability in differences is positively correlated with the true values, superimposing the limits on the plot as in step 4 would instantly show that the limits are wider than they need to be for small true values and narrower than they need to be for large true values. One simple solution may be to log-transform the measurements and see if the differences and means of the log measurements are uncorrelated; if so, steps 1–5 can be carried out on the log scale and bias/limits of agreement translated back at the end (limits of agreement then being multiplicative rather than additive and should be interpreted as ratio). If translation to the log scale does not help matters, the standard Bland-Altman methods mentioned above may not be appropriate but a regression-based generalisation can be used [2]. There are also other solutions which have been described elsewhere [[5], [6], [7]].
We should note that as we are unable to measure the true value (step 1), we use the mean of the two measurements as our best guess [2]. Therefore, if we see a correlation in the Bland-Altman plot we should consider two things: first, whether this relationship is because the mean of the two measures is a poor surrogate for the true value, or second, whether there really is a relationship between difference and true value. The first is not always considered [8], but in fact if this is the only reason for the correlation, it may still be appropriate to apply the rest of the Bland-Altman method.
In what circumstances would we expect correlation in a Bland-Altman plot?
Let Y and X be the two measurements by two different methods. As noted in [8], the correlation between the difference and mean of the measurements is
| (2) |
where σX2 and σY2 are the variances of X and Y over the whole study population (not just the measurement error) (e.g. see P. 2338 [7]), and ρ is the correlation between X and Y. It is easy to see that this will be zero when the variances of X and Y are equal.
Using the formula above, if Var(X) = k Var(Y) and the correlation between X and Y isρ, correlation between (X-Y) and (X + Y)/2 is
| (3) |
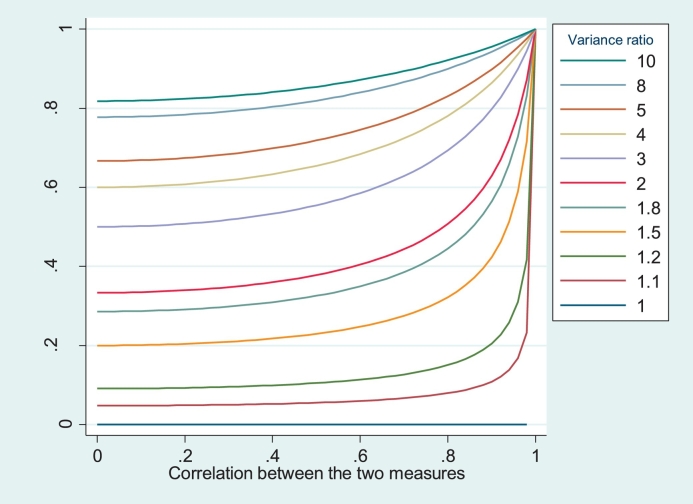
regardless of the variances. Table 1 gives values of this correlation for several variance ratios assuming a correlation between X and Y of 0.7; as shown in Fig. 1, the correlation in the Bland-Altman plot is larger as the magnitude of the correlation between X and Y increases.
Table 1.
Correlation between mean and difference, assuming a correlation between the two measures of 0.7.
| Variance ratio | 1 | 1.1 | 1.2 | 1.5 | 1.8 | 2 | 3 | 4 | 5 | 10 | 15 | 20 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Correlation | 0.00 | 0.07 | 0.13 | 0.27 | 0.39 | 0.44 | 0.63 | 0.72 | 0.78 | 0.89 | 0.93 | 0.95 | 0.98 |
Fig. 1.
Observed correlation between mean and difference of two methods, by correlation between the methods and ratio of variances of the two methods.
If the ratio of variances X and Y is far from 1 (e.g. 1.5 or more), a moderate-large correlation will be observed in the Bland-Altman plot regardless of any other factors. This correlation varies with the correlation between the two methods of measurement, but is ≥0.2 in magnitude in all cases where the ratio is greater than 1.5 (or less than 0.67), and ≥ 0.5 if the ratio is 3 or more.
Before deciding this is unacceptable and rejecting the Bland-Altman analysis, recall that the estimate of the ratio of interest is between the variance of X and variance of Y over all subjects in the sample. In most method comparison studies it is desirable to test the methods over a wide range of subjects, and hence there will be wide variability in true measurements between subjects. Therefore even if the within-subject variance due solely to measurement error is many times higher for X than for Y, it is rare for the variance of the measurement error to be large in comparison to the population variance, and hence the ratio k is rarely far from 1. For example in a study of gentamicin [9], measuring bacteria by two methods X and Y twice each, the ratio of X:Y within-subject (i.e. measurement error) variances is 4.24, but the ratio of total variances is no more than 1.30 (taking a single measurement by each method).
What does correlation in a Bland-Altman plot imply?
In the case of unequal variances, the Bland-Altman plot shows a relationship between the mean and the difference of single measures on the two methods, but it does not necessarily imply a relationship between the true value and the difference. Positive correlation suggests that the larger the mean of the two measurements, the larger the difference will be. Specifically, the difference is in a particular direction, with measure X likely to be larger than measure Y by a bigger difference, the larger the mean of the two measurements.
Suppose X is more variable than Y. Most of the big differences observed between X and Y will occur when X is at one of the extremes of its range, since it is far less likely for Y to take a nearby value. If there is a large (positive) difference between X and Y, it is likely to be because there is a value for X near the top of the range. In this instance, X will be much larger than Y and hence dominate the average. If, on the other hand, X takes a value near the bottom of the range, again the difference will be large (but negative) and the mean will also be low. If we plot the difference as X minus Y this leads to a predominance of extreme values in the top right and bottom left quartiles of the graph. Thus the mean and difference are indeed correlated if there is a big difference between variability of the two measures.
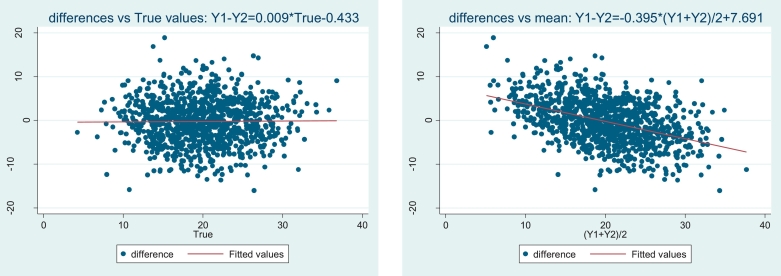
Note, however, that if the plot shows correlation but it is only with the mean and not necessarily with the true measurement value, the subsequent methods (calculating bias i.e. mean difference, and limits of agreement) are not invalid. It is merely that ordering the differences by average of the two methods is not as helpful as it would otherwise be. In a simulated data set it is possible to re-plot differences against true value instead of against mean; this shows that an association can appear of mean and difference whilst there is none between mean and true value (Fig. 2). In real experiments it is somewhat harder to tell the cause of the association in the Bland-Altman plot.
Fig. 2.
Bland-Altman plot and plot of differences against true values from simulation of two measurement methods, Y1 and Y2, with known true values. Data were constructed using the following Normal distributions N(mean, variance): True~N(20, 52),measurement error of Y1~N(0, 0.252)andmeasurement error of Y2~N(0, 52).
The alternative is, of course, that there is correlation in the Bland-Altman plot because there genuinely is a proportional bias in the data, with larger values subject to a larger measurement error. In this case calculating limits of agreement without first finding a suitable transformation of the data would not be appropriate.
What is an appropriate method when one measure is expected to be more variable than the other?
As noted above, the correlation in the plot does not necessarily invalidate the estimates of bias and limits of agreement, nor does it make it possible to assess whether proportional bias is present in either measure.
However to avoid false interpretation of the result, it may be preferable to determine the variance ratio of X:Y before using the Bland-Altman plot (and, if possible, before getting too far into the experiment). In this situation instead of taking unweighted mean and difference of single measures by each method, it would be necessary to take multiple readings on the more variable method and use the average of these in place of a single measure. Suppose now that var.(Y) = k Var(X), where k is an integer. Now the plot which we would expect to show no correlation is Ῡ-X vs. (Ῡ + X)/2, where Ῡ is averaged over k measurements. This can be extended to the situation where the variance ratio k is a fraction by taking different numbers of repeats on both X and Y and averaging these accordingly, e.g. for Var(X) = 3/2 Var(Y) take 3 measurements of Y and 2 of X, then plot Ῡ-Xbar vs. (Ῡ + Xbar)/2. This method would show a plot with little or no expected correlation; the interpretation then of a large correlation seen would really be that differences become larger as the true value becomes larger.
Whilst it is admittedly undesirable to have to find out the variance ratio a priori, the use of the weighted average at least has a sensible interpretation. When calculating limits of agreement, the limits stated are for the average of the more variable method in comparison to a single measurement by the less variable method (or another average, if both measures are repeated). If a new measure genuinely is more variable than the old, it is unlikely to be considered for common use unless it has big advantages in other areas (for example, if it is less invasive, or much cheaper). In these circumstances if it is possible to repeat the measure several times, it is clear that the estimate obtained will be much improved, and repeating the measure several times may be recommended in common usage. If a new measure is less variable than the old, repeats of the old are only required during the method comparison study itself.
The research problem: responses to the criticisms of the Bland-Altman methodology
Two recent papers have come to our attention, each citing specific areas within method comparison in which they believe a Bland-Altman analysis to be flawed in some way [10,11]. The objective of this paper is to review the points of the two papers and provide responses to them. In particular, we will address the following questions for each paper:
-
I.
What is the research question being addressed?
-
II.
What are the problems specific to this research situation?
-
III.
What are the methodological assumptions of the paper?
-
IV.
What are the limitations the paper attributes to the Bland-Altman plot in answering this question? What conclusions are drawn from this?
-
V.
What is the alternative method the authors propose to overcome these limitations?
-
VI.
What are the limitations in the alternative method? Have these been considered by the authors?
-
VII.
Are the claims and conclusions of the paper justified?
-
VIII.
What methods would be appropriate to answer the research question outlined?
Bias in Bland-Altman but not regression validity analyses [10]
The paper was published in Sportscience, which happens to have the author as its editor. A citation search (30 March 2020, Google Scholar) lists 114 citations.
What is the research question being addressed?
The research question of the article is not clearly stated. In the first paragraph of the main text he applies his results to the broad area of ‘comparing measures’. However the scenario illustrated and referred to throughout the text is limited to a single question. The research problem used is this: there are two measures to be compared, each related to a latent unmeasurable quantity. One of the measures is on a different scale to the other, and so both must be translated to the same scale before they can be compared. The research scenario envisaged appears to be that least-squares regression has already been used to find an equation to translate measure X onto the same scale as measure Y. Now the researchers are repeating the experiment to ‘validate’ or ‘re-calibrate’ the equation to a subsample of patients in a new study. Note that this is not the research question that the Bland-Altman analysis was originally intended to address.
The terminology used in the paper is hard to follow, so in the following commentary the values measured by instrument Y will be denoted by Yobs, and the values on the same scale calculated from X measurements and the regression equation, Ypred. The true value which the measurements aim to represent is denoted T. To the author's credit, a spreadsheet linked to the paper allows readers to re-create the calculations and analyses shown in the paper and to vary some assumptions. It is not explicit what data have been used for the simulations in the paper, but we assumed that the parameters stored in the spreadsheet are those used to generate data for the paper. The data specification is listed in Table 2.
Table 2.
Data specification for Hopkins' simulations (as used in spreadsheet).
| Sample size | 400 |
|---|---|
| Distribution of true values T | Normally distributed: Mean = 50; SD = 13 |
| Relationship between Yobs and T | Yobs = 0 + 1*T + eY |
| Distribution of eY (measurement errors in Yobs) |
Normally distributed: Mean = 0; SD = 3 |
| Relationship between X and T | X = 100 + 30*T+ eX |
| Distribution of eX (measurement errors in X) |
Normally distributed: Mean = 0; SD = 200 |
| Derivation of Ypred | Using equation from least-squares regression of Yobs on X |
| True equation relating Yobs and X | X = 100 + 30*Yobs + (eX - 30*eY) Yobs = −10/3 + 1/30*X+ (eY-1/30*eX) |
What are the problems specific to this research situation?
The problem specific to calibration is deriving the initial equation to translate X onto the same scale as Y. In some cases this will have been done already using a separate data set and in others, this will need to be done using the data to hand. As already discussed, using least squares regression to derive this equation carries the implicit assumption that there is no measurement error in the X variable. This is generally not the case and, as such, we suspect that this is not the method used in ‘proper‘calibration.
There is another problem in the specific example used by Hopkins, in that one instrument (X) has considerably larger measurement errors than the other, even after translating to the same scale. We are not aware that this is a typical of method comparison studies using different scales, at least not in a clinical context. However this problem does affect the results illustrated from the data set in this paper and, for that reason, generalisations to all calibration studies must be viewed with caution.
What are the methodological assumptions of this paper? Are they valid? How far are they generalizable?
There are several assumptions to address, which are not explicitly stated in the paper as assumptions, nor is their generalisability or validity discussed. In this paper it is assumed that Y is measured on the same scale as the underlying true quantity and X is not. Not unreasonable in Limits of Agreement method, though it is also possible in these problems that neither measure is on the same scale as the true values, depending on what it is that methods are being used to measure. The situation where both measures are on the same scale is not discussed in this paper, though this is the most common situation and is the one addressed by Bland and Altman. The paper needed to recognise this is the situation it is restricted to, in order not to extrapolate beyond the scope of the data.
The method used in this paper to translate X onto the same scale as Y is least squares regression of Y on X. An equation is fitted to the data, and this equation used to generate predicted values on the Y scale from X measurements (Ypred). The choice of this method is not discussed and there is a pivotal assumption in this paper that this has not introduced bias into the data. However, as discussed earlier, least squares regression underestimates the slope of the relationship between X and Y: in the example of Hopkins the slope estimate is 0.026 but the true value is 1/30 = 0.033 Hence (1) there is less variability in Ypred than Yobs and (2) there is proportional bias in Ypred. This means that for low values of T, Ypred is more likely to overestimate T, and for high values, underestimate.
The assumption that least squares regression is appropriate for translating X onto the same scale as Y is only valid in the situation where there is no measurement error in X. This is not true in the majority of such real-life problems; nor is it true for the simulation spreadsheet used to illustrate the paper. We could change the values in the simulation sheet to remove X errors, but this is not the data set generated and evaluated within the paper. However, the Bland-Altman plot will show positive correlation (r = 0.11) even though the correlation would be less than that when there is measurement error in X (r = 0.28). The reason for correlation in Bland-Altman plot even in the absence of measurement error in X is that Yobs = Ypred + eY and so var.(Yobs) > var.(Ypred).
The paper talks a lot about ‘error', however it is not always clear what value is being referred to. There are three components to the variation in measurements in this situation:
-
(1).
population variance of T
-
(2).
Variance of measurement errors in X
-
(3).
Variance of measurement errors in Y
Moving from the context of simulation to real-data studies, variance of measurement errors can be considered as within-subject variance, for data where the quantity T does not change between repeats. Population variance of T is the between-subject variance. The simulation spreadsheet uses a population variance for T of 169, measurement error variances of 9 for Y and 40,000 for X, with a true equation relating X to Y of Y = X/30–10/3 (plus measurement error terms of course). If the method for obtaining Ypred had not introduced bias, we would expect Ypred to have a measurement error variance of 40,000/900 = 400/9 (44.44); as it is, Ypred will have slightly smaller variance. So Ypred has nearly 5 times the measurement error variance of Yobs, and measurement error variance for Ypred is more than a quarter of the population variance in T. Whilst T has a population variance of 169, Yobs has a total variance (taking into account T's population variance and measurement error variance) of 178 and Ypred has an expected total variance of 134. This leads to a population variance of Yobs 1.3 times that of Ypred. The paper states that all the ‘constants and errors’ in the simulations used are arbitrary choices; and also that ‘the conclusions about bias that I am about to make are independent of these choices.’ In fact, the relationships between the three variance components listed above have a considerable effect on the correlation shown in a Bland-Altman plot.
What are the limitations ascribed to the Bland-Altman analysis? Are they correct? What conclusions are drawn from this?
The Bland-Altman plot is used by Hopkins for the comparison of Ypred to Yobs in the second (calibration) sample of the data, but the rest of the Bland-Altman analysis is not used. A trend line, presumably least-squares regression, is fitted to the Bland-Altman plot to show that there is a non-zero slope. This is interpreted as indicating proportional bias, and would lead researchers to conclude the instrument had not been calibrated correctly or that the sample was drawn from a different population to the original sample. There is indeed proportional bias in the data. However, Hopkins then asserts that there is nothing wrong with the instrument or subjects, but with the Bland-Altman plot. In fact the opposite is true; the Bland-Altman plot shows bias because there is bias. The problem is with the misuse of Bland-Altman analysis which should not be used for the assessment of model validity. Another problem is with the equation used to derive Ypred. Hopkins also extrapolates from this correlation in the plot that calculating limits of agreement is not a valid method in this situation. There is no justification given for this leap.
He does not focus explicitly on the problem as being related to different measurement error variances between his two measures. However, this is a problem in the simulated data he uses to illustrate the paper, and it is not necessarily typical of all calibration studies. The variances due to measurement error used in Hopkins' example simulations are very different for Ypred and Yobs; making them the same greatly reduces the correlation in the Bland-Altman plot. Correlation in a Bland-Altman plot can be caused by proportional bias and/or by differential total variances for the two methods of measurement; Hopkins has picked a scenario where both problems are present, which makes it harder to assess how much the correlation is due to each problem individually.
On P. 45, Hopkins asserts that the reader will not know how much ‘bias’ is artifactual and how much is real. This is incorrect, as shown in Fig. 1, if the expected variance ratio and expected correlation between measures are known then the expected correlation can also be calculated. This will at least give an idea of whether to worry about proportional bias in addition to the artifactual correlation.
What is the alternative method the authors propose to overcome these limitations?
The alternative method proposed in Hopkins' paper starts from the same initial calibration equation derived by least-squares regression, and hence the data contain the same proportional bias present in the previous analysis. However the author does not recognise this. The author proposes least-squares regression to ‘validate’ the initial calibration equation in a second sample. Ypred is calculated from the initial equation, and then Yobs is regressed on Ypred. The hope is that the data will show Yobs = 0 + 1* Ypred, and furthermore that if the slope and intercept differ from this, the equation can be used to fine-tune the initial equation to the second sample.
What are the limitations in this alternative method? Have these been recognised by the author?
The limitations of least-squares regression have been explained in an earlier section, namely that the method ignores any measurement error in Ypred (which is a consequence of measurement error in X), and hence the slope is underestimated and the intercept overestimated. This has been mentioned by the author, but dismissed because his simulations do produce data with an average slope of 1 and average intercept of 0. Why does this happen when our theory says the slope should be underestimated and the intercept overestimated? The reason is that least squares regression has been used twice. So in the initial sample, the regression equation derived had a shallower slope than it should have due to the measurement error in X. This shallower slope leads to a reduced variance of Ypred. Plotting Yobs against Ypred then, the slope should be greater than 1 because the equation for Ypred does not differentiate between the points sufficiently. But then due to measurement error carried through into Ypred, the slope (greater than 1) is underestimated and becomes approximately 1. The two errors cancel out.
Does this mean there is no problem with the method? No, it does not. All the second regression equation Yobs = 0 + 1*Ypred shows is that the sample is drawn from the same population as the first sample (which is forced in the simulations Hopkins runs), and the expected values of the equation would have been the same derived from either. This does not prove anything about bias; indeed, Hopkins' interpretation of the method is that it shows no bias, but the Bland-Altman does show bias and we know from the way Ypred has been derived that there should be bias. In this sense, the regression analysis leads to a false assurance that nothing is wrong.
One further issue with the method proposed by Hopkins is that he intends to adjust the initial equation so that it fits the second set of data perfectly.
Even if the expected values for the intercept and slope for the regressing Yobs on Ypred are 0 and 1 respectively, these values will vary considerably about the expected values for each given set of data. This second equation gives the same result as ignoring the initial equation and starting all over again regressing Y on X in the second sample.
Suppose that in our first sample the least-squares regression found that Y = 2 + 4*X.
Now using this equation to define Ypred = 2 + 4× in the second sample, observed Y in the second sample is related to Ypred by least-squares again: Yobs = 0.5 + 1.1Ypred. Adjusting to fit the second set of data then, we now have the equation for Yobs in terms of X: Yobs = 0.5 + 1.1*(2 + 4*X) or Yobs = 2.7 + 4.4*X. As Ypred is only a linear transformation of X, this is the very same result we would have got by simply regressing Y on X in the second sample and ignoring the equation derived in the first sample.
This equation should not be re-calculated on every sample on which the data is used; otherwise there is no fixed relationship to be utilised across studies for obtaining a measurement on the y scale from X. Therefore the quantity obtained and called ‘Ypred’ in different studies would not be the same quantity, and the only benefit of the first sample would be to have something to check against. Whether or not the equation is re-calculated, it is not clear what conclusion should be drawn if the slope and intercept are not precisely 1 and 0; there is no obvious way to decide how big a difference from these values would lead an investigator to decide the equation needs re-calibrating.
To what extent are the claims and conclusions of the paper justified?
The paper's conclusions are scattered throughout since the text is not organised into subsections. Conclusive remarks include:
-
1.
Artifactual bias arises in a Bland-Altman plot of any measures with substantial random error [abstract].
-
2.
‘The Bland-Altman analysis of validity should therefore be abandoned in favour of regression’ [abstract].
-
3.
‘Measurement error must be analyzed with regression’ [end].
-
4.
‘[Bland-Altman] plots can lead to an incorrect conclusion about the validity of a measure’ [P. 1].
-
5.
‘What's needed for a comparison of two or more measures is a generic approach more powerful even than regression to model the relationship and error structure of each measure with a latent variable representing the true value.’ [final paragraph].
We provide the following responses to the Hopkins conclusions:
-
1.
This is only partially true, though it has not been demonstrated by the paper and has never been denied by Bland and Altman. It is not true that for any measures with substantial random error an artifactual bias arises; this is only the case when the total (population & measurement error) variance for the one measure is several times larger than the other. It is not a problem if the variance of the measurement errors is similar for both measures, or if they are small in relation to the population variance of the true value. However if the ratio of total variances for the two measures is far from one, the plot will show a correlation between mean and difference. Even in this case, the term ‘bias’ is not particularly accurate; all it describes is that there is an association in the Bland-Altman plot.
-
2.
What this paper has shown conclusively, if not very clearly, is that validity studies as outlined by Hopkins should not be approached using regression since the results first introduce, and then conceal, bias. The Bland-Altman analysis is not designed to derive the equation in the first place but, once two measures on the same scale have been obtained, there is no reason why Bland-Altman analysis should not be used to assess agreement, subject of course to the pre-requisite check on association between differences and mean.
-
3.
While regression can be sometimes used for correcting the measurement error in X (e.g. regression calibration when a gold standard is available on the validation sub-study) [12], there is no justification for generalising this (false) conclusion about the inadequacy of Bland-Altman plots to all measurement agreement problems. As illustrated in this paper and many others by Bland and Altman, there are problems in regression analysis for assessment of agreement and the Bland-Altman analysis is intended to be an improvement on this. The incorrect claims on Hopkins' paper do not alter these facts.
-
4.
It has rather been shown that the Bland-Altman analysis leads to the correct conclusion, even if the conclusion is not what the researcher expects, and in fact it is the regression analysis that leads to incorrect conclusions.
-
5.
These methods are well-known in the SEM literature e.g. latent class analysis can be used for measurement error correction in one latent variable when there are several measured indicators for that variable. What is the best method depends on the context and the research question.
What is an appropriate method for comparing measures when the two measures are made on different scales (i.e. regression required to translate between them)?
Depending on the research objective, it may be necessary to translate the measures to the same scale in order to use them. Methods for this are beyond the remit of this paper, but lessons from paper [10] suggest least squares regression is not a suitable method. Other regression methods such as Deming regression which allow for error in both X and Y may produce a more accurate translation. As stated above, once two measures on the same scale have been obtained, there is no reason why Bland-Altman analysis should not be used to assess agreement, subject of course to the pre-requisite check on association between differences and mean.
An alternative method for analysing data on different scales would be to standardise both to a common scale, not by regression but by subtracting the mean of the measure and dividing by its standard deviation, to obtain values expressed in relation to the standard normal distribution with mean 0 and variance 1. These standardised X and Y measures can then be subjected to a Bland-Altman analysis. The resulting plot will, by design, not show any fixed bias (the mean of each variable is constrained to be zero); however, neither is it possible to show fixed bias when obtaining an initial equation to translate X and Y onto the same scale by regression. Instead, the analysis will show the extent to which an individual measurement, relative to the rest of the sample, is similarly located in that sample on both scales. For example, if a person has high blood glucose by one measure relative to the rest of the sample, is their blood glucose level also high by the other measure, compared to the rest of the sample? Any important reference standards, for example ‘upper limit of Normal’ for blood parameters, can be translated by ensuring that a value yielding the same centile of the Normal distribution is used in the alternative measure. Appropriate caution should be used in taking results or reference values into samples drawn from a different population to those in whom the measurement agreement study was derived.
Why Bland-Altman plots should use X, not (Y + X)/2 when X is a reference method [11]
This article was presented as a letter to the editor of Statistics in Medicine. A citation search (30 March 2020, Google Scholar) lists 277 citations.
What is the research question being addressed?
As with Hopkins' [10], the article is not split into sections or clearly structured; the research question being addressed is not explicitly stated. The intention appears to be to corroborate or refute the conclusion of Bland and Altman [8] that differences between two methods should be plotted against the mean of the two methods, specifically focusing on the situation when one method is a reference method. The work is heavily related to 2 formulae in the paper by Bland and Altman, although these are not reproduced by Krouwer. They are reproduced here for ease of reading; consider two methods of measurement Y (a field method) and X (a reference method), with population variances σY2 and σX2 respectively, and correlation ρbetween Y and X. Then the expected correlations of differences with the mean or with the reference method are:
| (4) |
and
| (5) |
What are the problems specific to this research situation?
Calibration studies may select samples for measurement systematically, picking samples with ‘known’ values spanning the range of plausible measurements, rather than taking a random sample from a population. This ensures that the accuracy of measurements throughout the range is explored. People may ascribe properties to the reference method such as high reproducibility, high precision, or lack of bias. However it is not necessarily always the case that a method held as a ‘gold standard’ or ‘reference’ method is of a high quality (nor reproducible); they may be used as the reference due to convention or because they are the simplest/cheapest method available. The reference result may be based on more replicates, although this is not always the case; even when it is, it is not a given that this will lead to lower measurement error than the test method.
What are the methodological assumptions of this paper? Are they valid? How far are they generalizable?
Although not explicit in the letter, the simulation shows that the sample selected for making measurements is not a random sample, but is systematic; 100 values evenly spaced throughout the range of the assay are selected as the known, true values (all integers from 101 to 200 in the case illustrated by Krouwer). This does not pose a problem for Bland-Altman analysis, which requires measurement errors to be normally distributed in order to calculate limits of agreement, but besides requiring that difference and mean are not correlated, there is no requirement for the sample of measurements to be from a particular distribution.
The situation addressed in the article makes the assumption that the reference method has considerably smaller ‘imprecision’, or measurement error, than the ‘commercial’ method. It also assumes that neither method contains bias; this may not always be the case, although it is a reasonable condition to impose for an initial exploration of the methodology.
Because there are three variables which can influence the correlation of Y, X or their average with their difference (σY2, σX2, andρ), Krouwer combines σY2 and σX2 into a single variable VarDiff = σY2−σX2 to simplify the problem. However the difference between two variances is not scale-invariant and [Eq. (4)] and [Eq. (5)] cannot be expressed solely in terms of VarDiff [‘V'] and ρ, but are also dependent on the value of one or other of the variances:
| (6) |
| (7) |
Hence the illustrative example presented in the letter is not widely generalizable, and the plots presented rely on a fixed value of one or other variance (which is not stated). A far better transformation to use would have been the ratio of the variances , since both [Eq. (4)] and [Eq. (5)] are independent of variances of Y and X given k and ρ:
| (8) |
| (9) |
Results are drawn from simulations using a single (fictitious) scenario assuming the range measurements of a sodium assay (100 to 200 mmol/L), no bias in measurements, and measurement errors with standard deviation ranging from 0.5 mmol/L to 10 mmol/L (which is acknowledged to be implausibly high for a sodium assay). Eight situations are explored, with varying combinations of X and Y measurement errors: in four situations X is held as the reference method (SD = 0.5 mmol/L) while Y has varying errors; in the other four, X and Y are constrained to have the same SD of measurement errors but that SD varies. The true values of measurements are uniformly, rather than Normally, distributed along the range of the assay and are not randomly sampled.
The other assumption made by the author is that his results are generalizable in the situation of comparing to a ‘gold standard’/reference method. These results are expressed in the plots, and show that (a) the correlation between test and reference methods is between 0.94 and 0.98, and (b) the difference between variances is between 0 and 100 when comparing a field to a reference method or between 0 and ~13 when comparing two field methods. These assumptions were arrived at by simulating data from a single situation, acknowledged not to be completely true to life, rather than from real-life data. The plausibility and generalisability of assumption (a) can be tested perhaps by looking at some real-life data sets; (b), while it can be tested, is not a helpful assumption due to lack of scale-invariance of VarDiff mentioned above. A difference in variances from 60cm2 to 80cm2 is between 0 and 100 when measured in cm, but not when measured in mm. Instead, it would be more appropriate to express the results in terms of the variance ratio, and examine plausible values for this quantity from real-life data.
What are the limitations ascribed to the Bland-Altman analysis? Are they correct? What conclusions are drawn from this?
Note that it is never disputed that Bland-Altman is the most appropriate analysis when measurement error variances are similar. The limitations are solely ascribed to the situation when one method is more variable than the other. The example used is a simulation, supposedly based on the range of a sodium assay although the measurement errors suggested are acknowledged as too large for a sodium assay. Inputs to simulation are stated as standard deviations for measurement error for X and Y; and a range for measurements (100 to 200) from which consecutive integer true values are used. Outputs were overall variances for X and Y and their correlation, together with correlations of difference with mean (‘BA’) and difference with X (‘No BA’). It is likely that simulated correlations, rather than expected values from [Eq. (4)] and [Eq. (5)], are presented in Table 1 and Fig. 1 of the paper.
The examples simulated use measurement errors of 0.5 mmol/L for a reference method and between 2 and 10 mmol/L for a test method. Whilst the paper is not clear, the spreadsheet gives more detail and these numbers appear to be standard deviations for the errors, which are taken to be normally distributed with zero mean (X and Y being unbiased). The method used for simulate is as follows.
-
1)
Generate 100 ‘true’ values (we will call this T), by non-random selection from a uniform distribution with range as defined by sodium assay (101 to 200)
-
2)
For each T generate a measurement of X and Y, which are unbiased for T but have measurement error with standard deviation listed as ‘error' in Table 1
-
3)
Repeat 40 times for each of the 8 parameter sets (varying combinations of standard deviations for X and Y)
-
4)
For each of the 8 × 40 = 320 samples:
-
a)
Correlate Y-X with X (‘No BA’)
-
b)
Correlate Y-X with (X + Y)/2 (‘BA’)
-
c)
Correlate Y with X (‘r')
-
d)
Find the variance of the X and Y measurements respectively, and calculate their difference Var(Y)-Var(X) (‘VarDiff’)
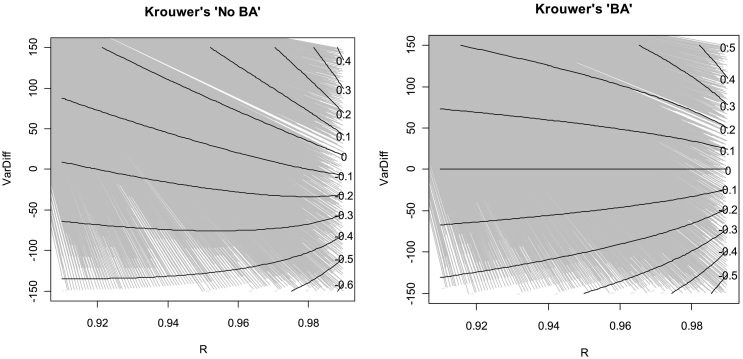
For each of the statistics mentioned in step 4, a single value is reported for each parameter set. Whilst it is not stated, this is most likely to be the mean over 40 repeats.
Krouwer then uses these results to select a ‘typical’ range for correlations of X and Y, and for VarDiff, then plots ‘BA’ and ‘No BA’ correlations against both these sets of parameters. It is not clear whether the values plotted are from the simulations or the ‘expected’ values from the equations although the irregularities in the lines, and the fact that a value for variance of X or Y is also required as input to the equations, suggest that simulations were used. Again based on these simulations, he superimposes ellipses on the plots to indicate the typical range of correlations ‘R' and variances differences ‘VarDiff’ that can be expected. It is not clear how precise boundaries of the ellipses have been calculated.
Limitations in the methodology include the following:
-
1.
Standard deviations for measurement error are unrealistically large (10) for some of the parameter sets.
-
2.
Ellipses represent values from simulations of a single assay (i.e. with fixed range 100 to 200 and hence fairly constant variances). VarDiff is not scale invariant, and so the ‘typical’ VarDiffs that can be expected in a calibration experiment cannot be answered by this single scenario. For example, simply imagine that rather than measuring in mmol/L we divide all measurements by 10 (to measure incmol/L). Whilst the correlations are not much affected, the [mean] variance differences are all between −0.2 and +0.5, rather than being from 0 to 100. Not only is the ellipsed now in the wrong place on the graphs presented, the contour graphs against VarDiff prepared for the original situation could no longer be used as the relationship has changed (being reliant as it is on the variance of either X or Y in addition to VarDiff and R).
-
3.
Results reported appear to be means over 40 simulations, yet these are then regarded as the limits of a ‘typical’ range. In fact the range over 40 simulations is more relevant to individual calibration studies; this gives a much wider area of possible results than the means alone.
In order to further explore Krouwer's results, the simulations have been re-created in Stata, using a different seed but following the steps as outlined above. Variance ratio, as well as variance difference, is calculated. The results from these simulations (Table 3) show:
-
1)
Correlations ‘r' are very closely matched to Krouwer's results; the ranges are fairly narrow.
-
2)
Mean values for ‘BA’ and ‘no BA’ are close to Krouwer's results when the values are far from 0, with some variation around 0 (as expected by chance). The ranges are reasonably wide, as can be expected with a sample size of 100.
-
3)
VarDiff is quite variable. While differences are reasonably re-constructible by taking average across all simulations, there are wide ranges for single samples within each parameter set. For example, with SD of measurement errors 5 for X and 5 for Y, the mean difference in variances is −0.8 but the range is from −96.7 to 84.0. This is considerably wider than the range of VarDiff 0 to 100 which Krouwer asserts in his pictures as the ‘likely’ range for calibration studies (presumably, erroneously, based on the means over 40 samples).
-
4)
Even in the (implausible) case 4 when the ratio of measurement error variances is 100/0.25 = 400, the ratio of variances for X and Y as population values is still not far from 1 (mean 1.13, range 1.02 to 1.28).
Table 3.
Simulation results from Stata. Table mirrors Krouwer's, but includes range as well as mean values, and variance ratio.
| ‘Error’ |
No BA |
BA |
r |
VarDiff |
VarRatio |
|---|---|---|---|---|---|
| Measurement error SD | Correlation between difference and X | Correlation between difference and mean | Correlation between X and Y | Difference between Variances | Ratio of variance Y to variance X |
| X = 0.5, Y = 2 | −0.0157 (−0.1995, 0.1500) | 0.0196 (−0.1658, 0.1848) | 0.9975 (0.9965, 0.9982) | 2.3 (−19.3, 22.4) | 1.00 (0.98, 1.03) |
| X = 0.5, Y = 5 | 0.0180 (−0.1278, 0.2020) | 0.1030 (−0.0386, 0.2780) | 0.9856 (0.9812, 0.9896) | 30.0 (−11.6, 82.0) | 1.04 (0.99, 1.10) |
| X = 0.5, Y = 7 | −0.0123 (−0.2392, 0.1491) | 0.1028 (−0.1026, 0.2614) | 0.9705 (0.9598, 0.9769) | 43.1 (−47.2, 113.1) | 1.05 (0.94, 1.13) |
| X = 0.5, Y = 10 | 0.0114 (−0.1425, 0.1674) | 0.1789 (0.0316, 0.3431) | 0.9465 (0.9314, 0.9620) | 105.7 (15.7, 232.4) | 1.13 (1.02, 1.28) |
| X = 2, Y = 2 | −0.0577 (−0.1911, 0.1115) | −0.0101 (−0.1505, 0.1541) | 0.9954 (0.9942, 0.9967) | −1.7 (−21.8, 22.4) | 1.00 (0.97, 1.03) |
| X = 5, Y = 5 | −0.1212 (−0.3300, 0.1166) | −0.0008 (−0.2045, 0.2219) | 0.9706 (0.9571, 0.9792) | −0.8 (−96.7, 84.0) | 1.00 (0.90, 1.10) |
| X = 7, Y = 7 | −0.1506 (−0.3326, 0.0507) | 0.0142 (−0.1788, 0.2261) | 0.9451 (0.9214, 0.9596) | 9.3 (−104.0, 137.6) | 1.01 (0.89, 1.17) |
| X = 10, Y = 10 | −0.2389 (−0.3986, −0.1013) | −0.0038 (−0.1858, 0.1345) | 0.8896 (0.8647, 0.9217) | −4.2 (−162.6, 119.9) | 1.00 (0.85, 1.15) |
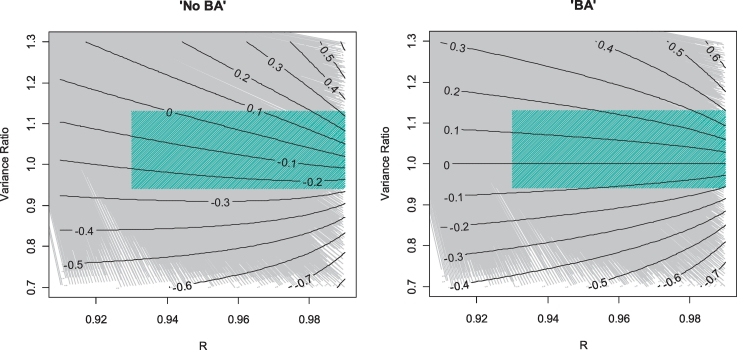
We have re-created the graphs of Krouwer using expected values from the formulae rather than simulation results (Fig. 3). In order to do this an assumption regarding the variance of X in the population has been made: this is assumed to be 842, which is approximately what the simulations show with a SD of measurement errors of 0.5 mmol/L. The lines have fewer irregularities, but the contours are in the same place, indicating the general method is the same.
Fig. 3.
Contour plots of expected correlations ‘No BA’ and ‘BA’ respectively, with varying variance difference and correlation of X and Y.
Repeating these plots using the ratio of the variances rather than their difference (Fig. 4), which requires no assumptions about variance of X, may be more useful in generalising results from the single sodium example to a wider range of calibration studies. From (Table 3), the variance ratios in the scenarios with one measurement more precise than the other range from 0.94 to 1.28 (means from 1.00 to 1.13), with correlations between 0.93 and 0.998 (means 0.95 to 0.998). Lower correlations tended to occur with higher variance ratios. This would suggest likely correlations in a Bland-Altman plot as shown in the blue shaded areas of (Fig. 4) [we have ignored values generated using an error SD of 10 since this is acknowledged by Krouwer to be implausible]; while neither plot shows zero going through the centre of this area, the Bland-Altman plot shows likelihood of a correlation with magnitude greater than 0.2 (particularly since variance ratios further from 1 are less plausible with high correlations R).
Fig. 4.
Contour plots of expected correlations ‘No BA’ and ‘BA’ respectively, with varying variance ratio and correlation of X and Y.
What is the alternative method the authors propose to overcome these limitations?
Plotting difference against the reference method, X, rather than against the mean of X and Y, as demonstrated in graphics above. No indication is given as to how to proceed once the plot has been drawn; should limits of agreement be drawn up? If so, would this be different in any way to the method of Bland and Altman?
What are the limitations in this alternative method? Have these been recognised by the author?
The plot is only a method for displaying the data and not a method for analysis. This point is not discussed.
From the graphs using variance ratio above, it seems that the method against X is not in fact any less likely than the Bland-Altman plot to show correlation, and indeed that the Bland-Altman plot correlation is always within acceptable bounds. Hence the new method selected is not superior to the Bland-Altman method and should not be used.
To what extent are the claims and conclusions of the paper justified?
The conclusions of the Krouwers' paper can be summarized as follow:
-
1.
‘These results support the use of plotting differences against X when X is a reference method’
-
2.
’and plotting differences against (X + Y)/2 when both methods are fields methods'
-
3.
‘These [calibration problem] method comparison studies conducted by manufacturers make up a significant portion of published method comparison studies.’
Here are the responses to the papers' statements mentioned above.
-
1.
This has been demonstrated in a single example, with assumptions acknowledged to be implausible, and artificial data, using a plot which does not have the most appropriate axes. The method is demonstrated to be slightly better using average values, but not over the range. This example does not support the conclusion.
-
2.
This conclusion is in concordance with the Bland and Altman papers [e.g. [1]], and justified by them. The justification by Krouwer is that because these methods are expected to have similar variances, with a difference of approximately zero. It would be more accurate to attribute this reason to the variance ratio being approximately one, which will happen when the difference is zero (but how ‘close’ to zero it needs to be is not scale invariant, whereas how ‘close’ to one the ratio need be, is).
-
3.
This may well be true, but is neither supported by data within the letter, nor by any citation e.g. a review of published method comparison studies. Instead it simply follows from the assertion that manufacturers do perform ‘calibration’ studies.
What is an appropriate method for the problem addressed?
Bland-Altman analysis. In the case of correlation in Bland-Altman plot one needs to consider transformation or the generalized form of Bland-Altman analysis using the regression-based approach [13].This letter gives no convincing argument as to why this should not be used.
Conclusions
The discussions in the critical papers of the Bland-Altman method are scientifically unjustified. Hopkins misused the Bland-Altman methodology for research question of model validation and also incorrectly used least-square regression when there is measurement error in the predictor. The problem with Krouwers' paper is making sweeping generalisation of a very narrow and somewhat unrealistic situation. The Bland-Altman analysis is the method of choice when the research question of interest is method comparison.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Altman D.G., Bland J.M. Measurement in medicine: the analysis of method comparison studies. J R Stat Soc Ser D (The Stat) 1983;32:307–317. [Google Scholar]
- 2.Bland J.M., Altman D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;8476:307–310. [PubMed] [Google Scholar]
- 3.Cornbleet P.J., Gochman N. Incorrect least-squares regression coefficients in method-comparison analysis. Clin Chem. 1979;25:432–438. [PubMed] [Google Scholar]
- 4.Bland J.M., Altman D.G. Statistics notes: measurement error. Bmj. 1996;312:1654. doi: 10.1136/bmj.312.7047.1654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ludbrook J. Confidence in Altman-Bland plots: a critical review of the method of differences. Clin Exp Pharmacol Physiol. 2010;37:143–149. doi: 10.1111/j.1440-1681.2009.05288.x. [DOI] [PubMed] [Google Scholar]
- 6.Carstensen B. Comparing methods of measurement: extending the LoA by regression. Stat Med. 2010;29:401–410. doi: 10.1002/sim.3769. [DOI] [PubMed] [Google Scholar]
- 7.Francq B.G., Govaerts B. How to regress and predict in a Bland-Altman plot? Review and contribution based on tolerance intervals and correlated-errors-in-variables models. Stat Med. 2016;35:2328–2358. doi: 10.1002/sim.6872. [DOI] [PubMed] [Google Scholar]
- 8.Bland J.M., Altman D.G. Comparing methods of measurement: why plotting difference against standard method is misleading. Lancet. 1995;8982:1085–1087. doi: 10.1016/s0140-6736(95)91748-9. [DOI] [PubMed] [Google Scholar]
- 9.Strike P.W. Butterworth-Heinemann; 2014. Statistical methods in laboratory medicine. [Google Scholar]
- 10.Hopkins W.G. Bias in Bland-Altman but not regression validity analyses. Sportscience. 2004;8:42–46. [Google Scholar]
- 11.Krouwer J.S. Why Bland-Altman plots should use X, not (Y+X)/2 when X is a reference method. Stat Med. 2008;27:778–780. doi: 10.1002/sim.3086. [DOI] [PubMed] [Google Scholar]
- 12.Rosner B., Spiegelman D., Willett W.C. Correction of logistic regression relative risk estimates and confidence intervals for measurement error: the case of multiple covariates measured with error. Am J Epidemiol. 1990;132:734–745. doi: 10.1093/oxfordjournals.aje.a115715. [DOI] [PubMed] [Google Scholar]
- 13.Bland J.M., Altman D.G. Measuring agreement in method comparison studies. Stat Methods Med Res. 1999;8:135–160. doi: 10.1177/096228029900800204. [DOI] [PubMed] [Google Scholar]