ABSTRACT
Antibodies are one of the predominant treatment modalities for various diseases. To improve the characteristics of a lead antibody, such as antigen-binding affinity and stability, we conducted comprehensive substitutions and exhaustively explored their sequence space. However, it is practically unfeasible to evaluate all possible combinations of mutations owing to combinatorial explosion when multiple amino acid residues are incorporated. It was recently reported that a machine-learning guided protein engineering approach such as Thompson sampling (TS) has been used to efficiently explore sequence space in the framework of Bayesian optimization. For TS, over-exploration occurs when the initial data are biasedly distributed in the vicinity of the lead antibody. We handle a large-scale virtual library that includes numerous mutations. When the number of experiments is limited, this over-exploration causes a serious issue. Thus, we conducted Monte Carlo Thompson sampling (MTS) to balance the exploration-exploitation trade-off by defining the posterior distribution via the Monte Carlo method and compared its performance with TS in antibody engineering. Our results demonstrated that MTS largely outperforms TS in discovering desirable candidates at an earlier round when over-exploration occurs on TS. Thus, the MTS method is a powerful technique for efficiently discovering antibodies with desired characteristics when the number of rounds is limited.
KEYWORDS: Antibody engineering, Bayesian optimization, machine learning, Monte Carlo method, protein engineering, Thompson sampling
Introduction
Antibody engineering is a modification technology applied to therapeutic antibodies to improve their efficacy, safety, and convenience for patients and caregivers. Recently, antibodies with higher functionality, such as pH-dependent antigen-binding antibodies, have been actively developed.1–4 To acquire the desired activity and pharmaceutical characteristics, a comprehensive mutagenesis approach was implemented, followed by extensive combinations of effective amino acid substitutions.3,4 However, because the number of possible combinations is usually large, it is unfeasible to experimentally evaluate all mutation combinations. Therefore, it would be extremely valuable if more efficient antibody engineering could be achieved using computational methods such as machine learning (ML). In this study, we investigated the optimization of pH-dependent antigen binding of an antibody using Bayesian optimization (BO) as an example of engineering highly functional antibodies.
pH-dependent antigen-binding antibodies have been demonstrated to extend the plasma half-life of antibodies, which were engineered to bind strongly to their antigens under neutral pH (blood circulation) and rapidly release them under acidic pH (acidic endosomes).2 A simple method to generate a pH-dependent antigen-binding antibody is to conduct histidine scanning on the antigen-binding region of the antibody to identify effective histidine substitutions that confer pH dependency.2,5 In addition, many pioneering studies using three-dimensional structures in antibody design have been reported.6–8 However, if the affinity of the lead antibody is insufficient, complex engineering is sometimes required to enhance binding under neutral conditions while maintaining or increasing pH dependency. In this case, it is preferable to efficiently explore the sequence space using ML, such as BO.
Thus far, several pioneering studies on the ML-based optimization of protein have been reported.9–11 As we usually evaluate multiple samples in each round, Thompson sampling (TS) can be a good choice, as reported earlier.10,11 However, TS requires initial data evenly covers search space to work well and this does not generally hold, because initial data biasedly distributes in the vicinity of the template sequence. Therefore, when exploring a vast sequence space that includes many mutations, TS does not necessarily work well due to over-exploration.12 Especially in protein experiments, where the round of experiments is limited, this over-exploration causes loss of efficiency in exploring.
To manage this practically important problem, we proposed Monte Carlo Thompson sampling (MTS) that controls an exploration-exploitation trade-off by defining the posterior distribution using the Monte Carlo method. In MTS, we can balance exploration-exploitation via the Monte Carlo approximation of the acquisition function instead of using the posterior distribution as is. Thus, MTS is a natural extension of TS. We evaluated our method for engineering pH-dependent antigen binding of a lead antibody for the neutralization of antigen X as a model case. Our results showed that MTS outperforms TS on discovering the desirable candidates overall. Especially, MTS works much better at earlier round that an over-exploration occurs on TS. Thus, our proposed method can be a useful technique to design a protein when the number of rounds is limited.
Results
Overall workflow
The workflow of this study is shown in Figure 1. It aims to improve the antigen-binding properties of an antibody over several rounds. We started with a lead antibody that required improvement of its antigen X-binding property as a template. We prepared an initial dataset consisting of the sequences of the lead antibody and its variants with a single amino acid substitution. Thereafter, we generated a virtual library for screening by combining single amino acid substitutions. We trained the predictive model using an initial training dataset. Gaussian process (GP) regression was used as a regression model for BO.13 Thereafter, candidates were selected to be evaluated in the next round through the BO from the virtual library. Following surface plasmon resonance (SPR) analysis, the antigen-binding properties of the candidates were added to the training data. This process was repeated until an antibody with desirable properties was discovered. In this study, we propose MTS instead of TS as a BO method, considering TS as the baseline model for this method.
Figure 1.
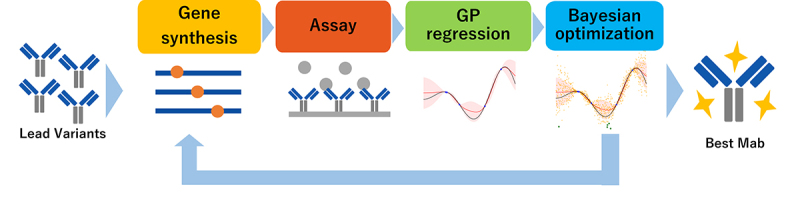
Overall workflow of the machine learning-guided antibody optimization.
Binding ability of lead antibody and its variants with single mutations
The affinity of the lead antibody (template) to antigen X was measured with SPR at pH 7.4 and pH 6.0. The calculated affinities at pH 7.4 and pH 6.0 were KD = (2.1 ± 0.015) × 10−8 and KD = (8.8 ± 1.5) × 10−6, respectively. The template antibody had a pH-dependent antigen-binding property, as the KD ratio at pH 6.0/pH 7.4 was 421. However, considering that the plasma concentration of antigen X was high (>300 nM), the antigen-binding affinity of the lead antibody was insufficient to completely neutralize the antigen at a realistic dose. Therefore, to create a recycling antibody that binds more strongly under neutral conditions and rapidly dissociates under acidic conditions, we performed comprehensive substitution (COSMO).3 In this process, all amino acid residues in the complementarity-determining regions (CDRs) and some key residues in the framework regions (FRs) were substituted with a different natural amino acid, except cysteine. Thus, 702 heavy-chain variants (substituted at 39 positions of the VH) and 596 light-chain variants (substituted at 33 positions of the VL) were generated. The pH-dependent antigen binding of these antibodies was analyzed using SPR. In general, the antigen-binding activity of neutralizing antibodies is evaluated by the association rate constant (ka [M−1 min−1]), dissociation rate constant (kd [min−1]), and equilibrium dissociation constant (KD [M]) values at neutral pH, while that of recycling antibodies should be evaluated by two factors: strong binding under neutral pH and rapid dissociation under acidic pH. Therefore, we introduced a single score (pH-dependent binding score) calculated from SPR analysis as an indicator of antigen binding to easily rank antibody variants and identify those with desired antigen-binding characteristics. The distribution of the pH-dependent binding scores for all variants is shown in Figure S1. The single mutation with the highest score was VL_S26F (COSMO-1), with a pH-dependent binding score of 0.852, which was improved from the template score of 0.451. However, the affinity of COSMO-1 was KD = (5.5 ± 0.023) × 10−9 at pH 7.4, and KD = (1.4 ± 0.035) × 10−7 at pH 6.0. Given that these kinetic parameters could be insufficient to completely neutralize antigen X and work as an efficient recycling antibody, further improvement of antigen binding at neutral pH and pH dependency is required.
Monte Carlo Thompson sampling
MTS balances the exploration-exploitation trade-off by defining a posterior distribution through the Monte Carlo method to relax the over-exploration issue in TS. We illustrate how MTS and TS explore the feature space in Figure 2. As shown in Figure 2, MTS attempts to explore the neighborhood of the training data and immediately discover a local optimum with limited rounds. Alternatively, TS explores distant locations from the training data and the neighborhood. Therefore, an over-exploration issue automatically arises in TS. The derivation of the MTS is described in the Methods section. To demonstrate the effectiveness of our proposed method, we evaluated the performance of MTS on synthetic data for simple and cumulative regret (Methods). Simple regret measures how fast a method finds the global optimum, and cumulative regret measures how well the samples are obtained on average. It is desirable to achieve good performance on both performance metrics in our problem setting. For MTS, we set the number of samples T to 100. From the results on synthetic data, we confirmed that MTS works better than TS regarding cumulative regret and is competitive with TS for simple regret (Figure S2ABC).
Figure 2.
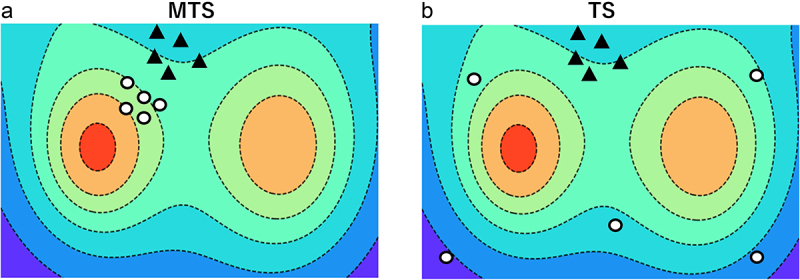
Illustration of how MTS and TS work. (A) MTS. (B) TS. Black triangles represent the initial training data. White circles represent candidate samples at next round.
Initial training data and generating the virtual library
We defined 703 sequences as initial training data with a single mutation from the template sequence. Twenty-four representative mutations that had better pH-dependent binding scores compared to template sequences were selected as seed sequences for generating virtual sequences (Table S1). These seed sequences contained 21 different mutated positions from the template sequence. First, 7,077,184 sequences were generated using all possible combinations from the seed sequences. To reduce the size of the virtual library, we limited 163,331 sequences to include two to six mutations. We defined them as virtual libraries for exploration in this study. Table 1 lists the sequence numbers generated for each mutation. As shown in Table 1, more sequences were generated as the number of mutations increased. This means that most generated sequences consisted of five or six mutated sequences.
Table 1.
The number of generated sequences at each mutation.
| mutation number | sequence number |
|---|---|
| 2 | 273 |
| 3 | 1958 |
| 4 | 9936 |
| 5 | 37944 |
| 6 | 113220 |
Learning a predictive model for pH-dependent binding score
As we aimed to find an antibody that strongly binds to an antigen under neutral conditions and dissociates under acidic conditions, we defined the pH-dependent binding score to quantitatively capture this characteristic from the Biacore sensorgram (Methods). GP regression was used to train a predictive model using the initial training data (Methods). To incorporate amino acid properties from a large-scale protein sequence, doc2vec was used to embed antibody sequences in a vector space of 512 dimensions (Methods).
Sequential optimization with MTS
We explored the sequence space thrice using Bayesian optimization. Subsequently, in the fourth round, the most promising candidates were selected according to predicted values from a learned GP regression model. The number of sampling for MTS was set to 100,000. To evaluate the difference in performance between MTS and TS, the pH-dependent binding scores of 47 sequences were evaluated for each round and method. Figure 3A shows the pH-dependent binding scores evaluated using SPR. To quantitatively evaluate the difference in the distribution of the pH-dependent binding score between MTS and TS, we show the maximum pH-dependent binding score, the median value, and the minimum value in Table 2. Figure 3A and Table 2 show that MTS outperformed TS. In particular, in rounds 1 and 2, MTS performs better than TS by a large margin. For MTS, the distribution of the pH-dependent binding scores steadily increased. Alternatively, for TS, the pH-binding scores were low in rounds 1 and 2, and increased substantially in round 3.
Figure 3.
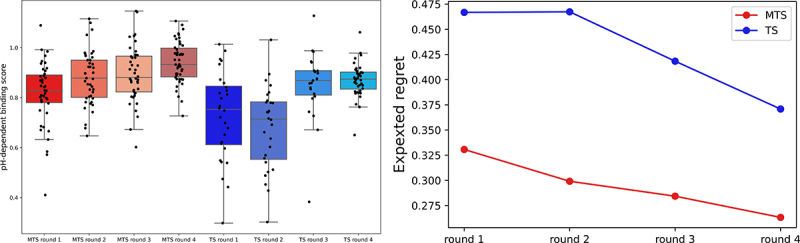
Performance comparison between MTS and TS. (A) Ph-binding score distributions proposed by MTS and TS. Redish boxplots indicate the Ph-dependent binding scores of MTS from round 1 to round 4, respectively. Bluish ones indicate the results of TS. The distributions of TS and MTS were evaluated by the Mann-Whitney U test. The P-values were 0.0347 for round 1, 4.91e-7 for round 2, 0.239 for round 3 and 4.98e-5 for round 4, respectively. (B) Expected cumulated regret for MTS and TS from round 1 to round 4.
Table 2.
Maximum, minimum and median values of Ph-dependent binding scores at each round for MTS and TS.
| method | round | max | min | median |
|---|---|---|---|---|
| MTS | 1 | 1.089 | 0.410 | 0.828 |
| 2 | 1.116 | 0.647 | 0.878 | |
| 3 | 1.147 | 0.602 | 0.881 | |
| 4 | 1.107 | 0.727 | 0.933 | |
| TS | 1 | 1.014 | 0.298 | 0.753 |
| 2 | 1.032 | 0.302 | 0.714 | |
| 3 | 1.128 | 0.383 | 0.869 | |
| 4 | 1.062 | 0.651 | 0.874 |
In addition to the exploration ability described above; it is also important to obtain better sequences during each round in our problem setting because the number of antibodies evaluated experimentally is usually limited. To evaluate the performance from the perspective of exploitation capability, we also showed the expected regret for MTS and TS (Figure 3B). Expected regret is defined as follows:
where is the global optimum, is the value obtained at round t, and is the number of sequences in round t.
As shown in Figure 3B, MTS works better than TS. Therefore, MTS can pick better sequences during exploration of the sequence space. In summary, these results indicated that MTS works better than TS regarding both exploration and exploitation abilities.
In addition to the binding properties, the number of expressed antibodies was also evaluated (Table S2 and Figure 4ABCD). Table S2 shows that MTS proposed more expressed antibodies compared to TS in all rounds. In particular, MTS markedly outperforms TS from round 1 to round 3 in the exploration phase. However, MTS and TS are comparable in round 4, which is an exploitation phase. To investigate the proposed sequences in more detail, we show the mutation numbers that were selected at each round for MTS and TS (Figure 4AB). From Figure 4AB, we can see that MTS picks fewer mutated sequences compared to TS. This indicated that TS explores far from the training sequences and MTS explores around the training sequence space. Figure 4CD represents the mutation numbers expressed in each round for MTS and TS. From Figure 4AC, we can see that the distributions of mutation numbers did not change between the proposed and expressed sequences. In contrast, Figure 4BD shows that the distributions of mutation numbers are different between the proposed and expressed sequences in TS. Therefore, antibodies with numerous mutations tend not to be expressed in TS.
Figure 4.
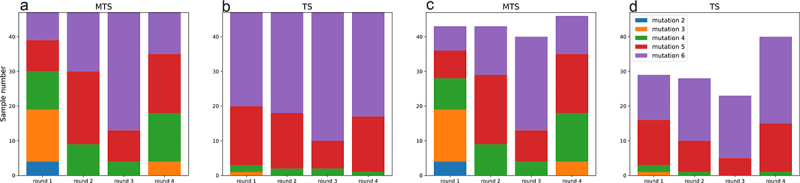
Stacked bar graph representation of mutation number included in candidate sequences at each round. (A) all sequences in MTS. (B) all sequences in TS. (C) expressed sequences in MTS. (D) expressed sequences in TS.
Discussion
Trajectory in sequence space explored during Bayesian optimization
To discuss the difference in sequence spaces between MTS and TS, we projected doc2vec embedded vectors for training sequences and proposed sequences into two dimensions using PCA (Figure 5A). We show the maximum Euclidean distance from the nearest sequence, median and minimum value in Table 3. From Figure 5A, we can see that MTS gradually explores from around the training sequences to a place far from them. TS explores a more diverse sequence space. This result showed that MTS works as intended, as shown in Figure 2A. To investigate sequence spaces quantitatively, distributions of the Euclidean distance from the nearest training sequences on the doc2vec embedded space were also shown (Figure 5B). Figure 5B clearly shows that MTS selects candidates in the vicinity of the training sequences and TS picks them far from the training sequences.
Figure 5.

Characteristics of sequence space explored during Bayesian optimization. (A) Visualization of embedding sequence space via PCA. Green points represent initial training data. Redish points are the sequences of MTS. Bluish points are the sequences of TS. (B) Comparison of Euclid distance in embedding space from the nearest sequence in the training data at each round. Redish boxplot represent the distribution of Euclid distance at each round on MTS. Bluish boxplot represent the distribution of Euclid distance at each round on TS.
Table 3.
Maximum, minimum and median values of Euclid distance in embedding space from the nearest sequence in the training data at each round for MTS and TS.
| method | round | max | min | median |
|---|---|---|---|---|
| MTS | 1 | 0.352 | 0.150 | 0.249 |
| 2 | 0.317 | 0.178 | 0.248 | |
| 3 | 0.317 | 0.156 | 0.240 | |
| 4 | 0.220 | 0.148 | 0.172 | |
| TS | 1 | 0.389 | 0.234 | 0.340 |
| 2 | 0.366 | 0.223 | 0.319 | |
| 3 | 0.362 | 0.239 | 0.303 | |
| 4 | 0.318 | 0.165 | 0.269 |
These results explain the characteristics of MTS that explore training sequences. Alternatively, TS tends to over-explore because it requires the search space to be homogeneously distributed to work well. However, in our problem setting, this assumption does not hold and most search spaces consist of more mutated sequences, as shown in Table 1. Thus, when exploring samples far from the training data and the number of trials is limited, it is crucial to balance exploration and exploitation. As MTS can control exploration and exploitation balance through the number of sampling to approximate the posterior distribution function, it can be an effective technique in our setting that needs to weigh exploitation.
Combinatorial mutation effects navigated with MTS
To discuss the effect of amino acids at each position in more detail, amino acid residues were identified in descending order of the pH-dependent binding score (Table 4A) and the best single amino acids (Table 4B). From Table 4AB, we can see that the pH-binding scores of these top 10 scored sequences were higher than those of the single best amino acids. Therefore, we successfully identified desirable combinations of mutations that were not found in a single mutation. Notably, the top 10 scored sequences did not necessarily include all single best mutations. For example, MTS-1 does not include the best single mutations at VH30, VH55, or VL26. Thus, the best combination of amino acids did not result from the best single mutations. Therefore, a Bayesian optimization method, such as MTS, is indispensable for exploring the combinatorial mutation space.
Table 4.
Summary of combinatorial mutation effects. (A) Ph-dependent binding scores and amino acid residues of the template sequence and top 10 sequences proposed by MTS. (B) Ph-dependent binding score and amino acid residue for best single mutations at each position included in the initial training data.
| sequence name | amino acid residues |
pH-dependent binding score | ||||||
|---|---|---|---|---|---|---|---|---|
| VH30 | VH54 | VH55 | VL26 | VL52 | VL54 | VL95 | ||
| template | S | S | G | S | S | L | S | 0.451 |
| MTS-1 | S | K | G | S | K | R | I | 1.147 |
| MTS-2 | S | K | K | F | K | R | I | 1.143 |
| MTS-3 | S | K | K | F | K | L | I | 1.116 |
| MTS-4 | R | S | G | S | K | R | I | 1.107 |
| MTS-5 | S | S | K | S | K | R | I | 1.100 |
| MTS-6 | S | K | K | F | S | R | I | 1.091 |
| MTS-7 | S | K | G | S | K | L | I | 1.089 |
| MTS-8 | S | K | K | F | K | R | S | 1.075 |
| MTS-9 | R | K | G | S | K | R | I | 1.073 |
| MTS-10 |
S |
K |
K |
F |
S |
L |
I |
1.057 |
| amino acid residue | ||||||||
| |
VH30 |
VH54 |
VH55 |
VL26 |
VL52 |
VL54 |
VL95 |
|
| Single best AA | R | K | K | F | K | R | I | |
| pH-dependent binding score | 0.706 | 0.628 | 0.770 | 0.852 | 0.516 | 0.597 | 0.651 | |
Detailed evaluation of the ML-guided antibodies
In this study, a newly defined pH-dependent binding score was used to measure the complex antigen-binding activity that requires both strong affinity under neutral pH and prompt dissociation under acidic pH. To confirm whether the increased pH-dependent binding score has improved the desired binding properties as a recycling antibody, the kinetics of the three antibodies, the template antibody, COSMO-1, and MTS-1, whose pH-dependent binding score was the best among single-substitution variants, were analyzed with SPR (Table 5). Each sensorgram is shown in Figure 6. The KD value of MTS-1 at pH 7.4 was 1.8 ± 0.038 nM, an approximately three-fold higher affinity than that of COSMO-1. The KD ratio (pH 6.0/pH7.4) of MTS-1, an index of pH-dependent binding, was 37, whereas that of COSMO-1 was 26, indicating that the pH dependency of MTS-1 was also enhanced. Whether MTS-1 has sufficient neutralizing activity and a prolonged half-life should be verified separately. Igawa et al. reported that a pH-dependent anti-IL-6 R antibody with a KD value of 1.8 nM at pH 7.4 and a KD ratio pH 6.0/pH 7.4 of 22.1-fold achieved a significant half-life extension in cynomolgus monkeys.2 Although the optimal affinity and degree of pH dependency vary depending on the antigen and mechanism of action, the MTS-1 antibody with a similar level of antigen-binding properties is expected to exhibit an improved pharmacokinetic profile. The protonation of histidine residues at approximately pH 6 is considered to play an important role in the pH-dependent interaction between the antigen and the antibody. According to the previous reports, while histidine is commonly used to confer pH dependency, basic residues (lysine, arginine) are involved in pH dependency on different kinds of antigens such as C5, Her2 and human FC.3,14,15 Notably, the sequence proposed by ML contained several basic lysine and arginine residues, which resulted in an increase in pH dependency. Although this study demonstrated an example of application to the optimization of pH-dependent antibodies, it is expected that similar learning methods will be used for other complex biologics optimization by proposing optimal sequences that have not previously been (or are difficult to be) identified by humans, thereby contributing to the acceleration of therapeutic development.
Table 5.
The results of Biacore sensorgram among the sequence with top Ph-binding score on MTS, the best with single mutation, and the template sequence.
| sequence name | pH 7.4 |
pH 6.0 |
KD ratio (pH 6.0/pH 7.4) | ||||
|---|---|---|---|---|---|---|---|
| ka (M − 1s − 1) | kd (s − 1) | KD (M) | ka (M − 1s − 1) | kd (s − 1) | KD (M) | ||
| template | (1.0 ± 0.015) ×105 | (2.2 ± 0.015) ×10−3 | (2.1 ± 0.015) ×10−8 | (7.4 ± 4.3) ×103 | (6.1 ± 2.3) ×10−2 | (8.8 ± 1.5) ×10−6 | 421 |
| COSMO-1 | (1.1 ± 0.0058) ×105 | (6.2 ± 0.025) ×10−4 | (5.5 ± 0.023) ×10−9 | (8.9 ± 0.10) ×104 | (1.3 ± 0.015) ×10−2 | (1.4 ± 0.035) ×10−7 | 26 |
| MTS-1 | (1.6 ± 0.029) ×105 | (2.9 ± 0.017) ×10−4 | (1.8 ± 0.038) ×10−9 | (1.0 ± 0.046) ×105 | (6.5 ± 0.067) ×10−3 | (6.5 ± 0.22) ×10−8 | 37 |
Figure 6.
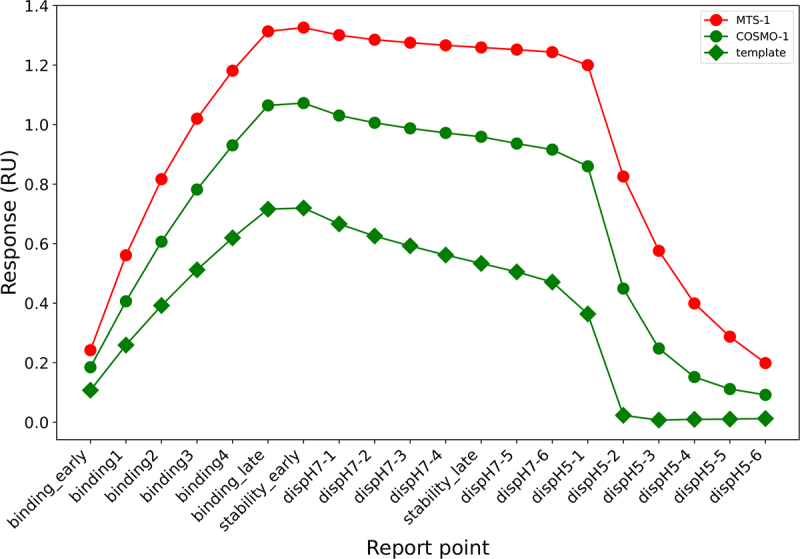
Comparison of Biacore sensorgrams among the sequence with top Ph-binding score on MTS, the best sequence with single mutation and the template sequence.
Related works
From the perspective of applying Bayesian optimization to protein design, there are two pioneering studies. Romero et al.9 applied GP-UCB to identify mutations that improve the thermostability of cytochrome P450. They successfully improved the thermostability of P450, but the GP-UCB algorithm was not used for batch Bayesian optimization, which we have addressed in this study. In the second method, Saito et al. applied TS to find mutations in green fluorescent protein (GFP) so that it fluoresced green to yellow.10,11 They showed that TS was effective in exploring desirable mutations. Our study is closely related to their work in that both studies used batch Bayesian optimization. However, they selected the positions to be mutated based on previous studies on GFP and yellow fluorescence protein. Therefore, they handled a relatively limited virtual sequence library with a maximum of four mutations. In contrast, we focused on exploring a much more diverse sequence library that includes numerous mutations compared to their study. As TS requires that the initial training data evenly cover the search space, it does not work well in our problem setting because of the over-exploration of TS. Instead, this was the motivation for our study. Consequently, the focus of our study is completely different from that of the previous studies. Several studies concerning batch Bayesian optimization have been conducted and these are based on a deterministic approach, not on stochastic approaches, such as TS. Nevertheless, there are related studies from the perspective of acquisition function. In particular, the Monte Carlo acquisition functions for Bayesian optimization are related to our study.13,16 They optimized the Monte Carlo acquisition function for batch Bayesian optimization through a reparameterization trick that can optimize the expectation of the objective function using auto-differentiation to compute the gradient. They approximated an acquisition function using posterior samples as follows:
where is the i-th realization from the posterior distribution and is the number of samplings. As described in the Methods section, the MTS also approximates a posterior distribution using the Monte Carlo method. Therefore, MTS and Monte Carlo acquisition functions are common, in that both methods utilize the Monte Carlo method. However, because MTS is based on TS, MTS approximates a posterior distribution instead of an acquisition function. This is different from the Monte Carlo Bayesian optimization. This difference is derived from the fact that TS requires a probability distribution for the posterior distribution to be approximated. For example, the beta distribution is usually used in the Bernoulli bandit problem. In this study, we formulated the problem to probabilistically select samples if they are top-ranked sampled from GP in the context of the Bernoulli bandit. Therefore, we used the beta distribution as a posterior distribution to be approximated.
Key study conclusions
In this study, to manage the issue of over-exploration of TS in exploring the antibody sequence space, we proposed an MTS that balances exploration and exploitation through the Monte Carlo approximation of the posterior distribution. We prepared an antibody library that consisted of single mutations as the initial data and evaluated the performance of MTS and TS in the process of identifying an antibody that strongly binds under neutral conditions and rapidly dissociates under acidic conditions. Our results showed that MTS can efficiently discover more desirable antibodies than TS can. When applying Bayesian optimization to protein design, over-exploration problems often occur because of the vast sequence space that includes numerous mutations. Although we applied MTS to antibody optimization in this study, our method can be applicable and useful for optimizing various types of protein functions.
Although we focused on a single property in this study, we generally need to optimize a template antibody in terms of multiple properties in the process of lead optimization. Therefore, we will consider expanding our method to multi-objective optimization in future work.
Materials and methods
Antibody preparation
To generate a dataset of antibodies with comprehensive single mutations, the COSMO approach was performed.3 Briefly, all residues in the CDRs and some FRs were substituted with different natural amino acids, except cysteine, which produced 18 variants from each of the residues (19 variants if the original amino acid was cysteine). For the heavy chain, 702 variants derived from 39 original positions were expressed. For the light chain, 596 variants derived from 33 original positions (two residues where the original residues were cysteine) were transiently expressed. To prepare the antibody with multiple mutations proposed by the ML model, we produced polymerase chain reaction (PCR) products, each containing an antibody-expression cassette with the proposed mutations, by PCR assembly of multiple DNA fragments. To express antibody variants with a single or multiple mutations, Expi293F cells (Thermo Fisher Scientific) were transfected with the PCR products for heavy or light chain variants and plasmids for the chain with no mutation. Antibody variants expressed by transfected cells were purified using MonoSpin ProA(GL Science) in a 96-well plate format, if necessary.
Surface plasmon resonance
The pH-dependent binding of the prepared antibodies to antigen X was assessed at pH 7.4 and pH 5.8 or pH 6.0 at 37°C using a Biacore 4000 or Biacore T200 instrument (Cytiva). Each antibody was captured onto Protein L (Cytiva) that was immobilized on a CM4 sensor chip (Cytiva), after which the antigen was injected into flow cells. Antibodies and analytes were diluted into their respective running buffers (ACES pH 7.4 and pH 5.8 or pH 6.0 (20 mM ACES, 150 mM NaCl, 1.2 mM CaCl2, 1 mg/mL bovine serum albumin, 1 mg/mL carboxymethyldextran, 0.05% Tween 20, 0.005% NaN3 [if necessary]). The analyte (antigen X) was diluted to 100 nM for screening and prepared by two-fold serial dilution starting from 200 nM at pH 7.4, and from 800 nM at pH 6.0, for kinetic analysis. The surface of the sensor chip was regenerated using 3 M MgCl2. Kinetic parameters were determined by fitting the sensorgrams with a 1:1 binding model using BIACORE 4000 Evaluation software or Biacore T200 Evaluation software (Cytiva). In the screening process, the pH-dependent binding property of each antibody was evaluated using a modified Biacore assay, in which an additional dissociation phase at pH 5.8 was integrated immediately after the dissociation phase at pH 7.4. In this evaluation, a pH of 5.8 was used for the additional dissociation phase instead of pH 6.0, to rank the dissociation rate of antibodies more clearly from the antibody and antigen complex under acidic conditions. To rank the antibody variants with a single score that considers both aspects of binding under neutral pH and rapid dissociation under acidic pH, the pH-dependent binding score (details are described in the following method), calculated from the report point of the SPR sensorgram, was defined and used as an index of evaluation. To obtain the report points of the sensorgram for calculation, custom report points were defined at equal intervals of seconds, in which 4 points for 120 s association at pH7.4, 6 points for 180 s dissociation at pH7.4, and 6 points for 180 s dissociation at pH5.8 were defined. In addition to predefined report points, each custom report point was named as binding 1–4, dispH7–1–6, and dispH5–1–6, respectively. In the evaluation of SPR, if the capture amount of antibody (Target 200 RU) was < 50 RU or > 500 RU at an antigen concentration of 0 nM, the data were excluded to omit samples with too low antibody expression or samples for which data were not correctly obtained because of analytical noise. As a result, 703 binding data of antibodies with a single substitution were used for the initial input data.
Ph-dependent binding score
To consider both binding ability under neutral conditions and dissociation under acidic conditions, we introduced a pH-dependent binding score that quantifies how strongly an antibody binds to an antigen under neutral pH and how quickly it dissociates under acidic conditions. The pH-dependent binding score is defined as follows:
where , and represent the binding ability under neutral conditions, binding stability under neutral conditions, and dissociation under acidic conditions, respectively. , , , , and are binding captures normalized by one of the lead antibodies under each condition (Figure S4) and were obtained from the Biacore sensorgram. From these definitions, is large when the antibody strongly binds to an antigen under neutral conditions; is small when the antibody stably binds under neutral conditions; and is small when the antibody immediately dissociates under acidic conditions. To balance binding ability under neutral conditions and dissociation under acidic conditions, α ranged from 0.7 to 2 and β ranged from 0.7 to 1.7 with 0.1 increments. Lastly, we set αto 1.3 and βto 0.9, such that the pH-dependent binding score fulfills our purpose. The significance of the pH-dependent binding score is that it also provides accurate data on antibody variants that bind too weakly or strongly under a single SPR assay condition. When evaluating a large number of antibody variants, it is not practical to set the antigen concentration for each antibody affinity, thus a certain screening condition is applied. However, it is often observed that general kinetic parameters such as ka, kd, and KD are inaccurate due to poor fitting, especially for antibodies that bind too weakly or strongly. We set the score to allow a realistic comparison of all antibody variants on the same scale.
Monte Carlo Thompson sampling
TS is a popular algorithm for the multi-armed bandit problem and Bayesian optimization, to balance exploration and exploitation.7 Particularly, in protein engineering through ML-based evolution, multiple samples have to be explored in each round.9,10 Thus, TS is suitable because it can naturally handle batch selection. The main idea of TS is to randomly draw samples according to its optimal posterior distribution. TS requires initial data to be evenly distributed in the search space to work well. However, this does not hold true in real-world applications. Specifically, when we handle a large-scale virtual protein sequence library, it is common for the search space to be differently distributed with training data because of the bias of available training data. In such cases, TS tends to be over-explored in a vast sequence space, and it is difficult to identify promising sequences within limited trials.
To address this issue, we proposed MTS to balance the exploration-exploitation trade-offs by redefining a posterior distribution using the Monte Carlo method.
We began with the original TS to derive the MTS algorithm. Suppose that , where and . First, TS randomly samples according to the posterior distribution .
Thereafter, the optimal candidate was selected based on the randomly sampled realization, where is the candidate set.
We can interpret the sampled realization as an acquisition function for TS. In other words, TS selects the optimal sample for a randomly sampled objective function.
To control the exploration-exploitation trade-off, we consider a method to control the uncertainty of the posterior distribution through the Monte Carlo method. If we write the sampled t-th realization from the posterior distribution as , we can write the redefined posterior distribution as follows:
where T is the number of random samplings, and g is the function to define the posterior distribution. Thereafter, we randomly sampled according to the redefined posterior distribution .
Finally, we select the optimal candidate based on a randomly sampled realization based on the acquisition function for the MTS.
In the batch Bayesian optimization setting, we selected samples with top-ranked values for the acquisition function. Note that is the same as when T is equal to 1, and the function of the redefined posterior distribution is . This means that is a special case of and MTS is a natural expansion of TS. From this definition, when T is small, has large uncertainty. Alternatively, when T is large, becomes more stable. Thus, we control the over-exploration for TS through the number of samplings T in the MTS. Figure S3 shows the generic pseudocode of MTS.
In this study, because we aimed to choose multiple candidates in each round, we set the redefined posterior distribution as the beta distribution. When we set as the success counter, i.e., the top-ranked number sampled from GP, and as the failure counter, i.e., in the beta distribution, the approximate posterior distribution is as follows:
where and are prior parameters, and we set the non-informative prior as in this study. This formulation intuitively means that we probabilistically select samples in terms of being top-ranked sampled from GP based on the Bernoulli bandit.17
Gaussian processes and feature vectors for antibody sequence
GP regression16 was used to train a predictive model for the pH-dependent binding score because an acquisition function was sampled for TS from a learned GP model. GP is an extension of the multivariate Gaussian distribution to an infinite dimension distribution, in which any distribution combination of dimensions is a Gaussian distribution. Suppose that , where and , a GP is a distribution over functions specified by its mean function and covariance function, that is, kernel function .
Note that this function is used as the posterior distribution when sampling the TS. To train a GP regression model, we used the Matern kernel with ν = 2.5 as a kernel function in this study.
The doc2vec18 was used to take advantage of large-scale protein sequences to embed antibody sequences in a learned embedding vector space. The doc2vec model was pre-trained using the UniProt database19 with lengths between 50 and 999 amino acids, according to a previous study.20 We obtained embedded representations from both VH and VL sequences, and concatenated these two vectors. Hyperparameters were set for doc2vec, i.e., k-mer , window size and dimension for embedding , and determined k = 3, w = 2, and d = 256 through five-fold cross-validation to minimize the mean squared error in the initial training data set. We used the Gensim library to train and infer doc2vec.21
Experimental setup on synthetic data
We used the five-well potential function, which has a two-dimensional potential with five local minima,22 to compare the performance. The landscape of the five-well potential function (Figure S2A). To mimic an over-exploration scenario that we focus on in this study, we sampled the initial data for training from a specific region, that is, (Rectangle region in Figure S2A). We set the number of initial data to three and the number of batch-sampled data to three at each round and compared the performance of MTS, TS, exploration only, and random sampling in terms of simple regret and cumulative regret until 15 rounds. We set the number of sampling to 1000 for the MTS. Simple and cumulative regret are defined as follows:
where is the global optimum and is the value obtained in round. We averaged them more than 10 times in each round (Figure S2BC).
Supplementary Material
Acknowledgments
We thank all research assistants in Chugai Pharmaceutical Co., Ltd. and Chugai Research Institute for Medical Science, Inc. for excellent experiment assistance.
Funding Statement
The author(s) reported there is no funding associated with the work featured in this article.
Disclosure statement
No potential conflict of interest was reported by the author(s).
Abbreviations
BO, Bayesian optimization; CDRs, complementarity-determining regions; COSMO, comprehensive substitution; FRs, framework regions; GFP, green fluorescent protein; GP, Gaussian process; ML, machine learning; MTS, Monte Carlo Thompson sampling; PCR, polymerase chain reaction; SPR, surface plasmon resonance; TS, Thompson sampling;mAb, monoclonal antibody
Author contributions
T.K and S.T analyzed the data by Bayes optimization. H.K performed the in vitro kinetic analysis. T.K, H.K, S.T, and R.T discussed the data and wrote the manuscript. S.M, H.S, Z.S, K.Y and H.T provided supervisory support and contributed to the critical discussion of this study. All authors reviewed the manuscript.
Supplementary material
Supplemental data for this article can be accessed online at https://doi.org/10.1080/19420862.2023.2244214
References
- 1.Haraya K, Tachibana T, Igawa T.. Improvement of pharmacokinetic properties of therapeutic antibodies by antibody engineering. Drug Metab Pharmacokinet. 2019;34:25–10. doi: 10.1016/j.dmpk.2018.10.003. [DOI] [PubMed] [Google Scholar]
- 2.Igawa T, Ishii S, Tachibana T, Maeda A, Higuchi Y, Shimaoka S, Moriyama C, Watanabe T, Takubo R, Doi Y, et al. Antibody recycling by engineered Ph-dependent antigen binding improves the duration of antigen neutralization. Nat Biotechnol. 2010;28(11):1203–07. doi: 10.1038/nbt.1691. [DOI] [PubMed] [Google Scholar]
- 3.Sampei Z, Haraya K, Tachibana T, Fukuzawa T, Shida-Kawazoe M, Gan SW, Shimizu Y, Ruike Y, Feng S, Kuramochi T, et al. Antibody engineering to generate SKY59, a long-acting anti-C5 recycling antibody. PLoS One. 2018;13(12):e0209509. doi: 10.1371/journal.pone.0209509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Muramatsu H, Kuramochi T, Katada H, Ueyama A, Ruike Y, Ohmine K, Shida-Kawazoe M, Miyano-Nishizawa R, Shimizu Y, Okuda M, et al. Novel myostatin-specific antibody enhances muscle strength in muscle disease models. Sci Rep. 2021;11(1):2160. doi: 10.1038/s41598-021-81669-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sulea T, Rohani N, Baardsnes J, Corbeil CR, Deprez C, Cepero-Donates Y, Robert A, Schrag JD, Parat M, Duchesne M, et al. Structure-based engineering of Ph-dependent antibody binding for selective targeting of solid-tumor microenvironment. MAbs. 2020;12(1):1682866. doi: 10.1080/19420862.2019.1682866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ruffolo JA, Guerra C, Mahajan SP, Sulam J, Gray JJ.. Geometric potentials from deep learning improve prediction of CDR H3 loop structures. Bioinformatics. 2020;36(Supplement_1):i268–i75. doi: 10.1093/bioinformatics/btaa457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Abanades B, Georges G, Bujotzek A, Deane CM, Xu J. Ablooper: fast accurate antibody CDR loop structure prediction with accuracy estimation. Bioinformatics. 2022;38(7):1877–80. doi: 10.1093/bioinformatics/btac016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Khan A, Cowen-Rivers AI, Grosnit A, Deik DG, Robert PA, Greiff V, Smorodina E, Rawat P, Akbar R, Dreczkowski K, et al. Toward real-world automated antibody design with combinatorial Bayesian optimization. Cell Rep Methods. 2023;3(1):100374. doi: 10.1016/j.crmeth.2022.100374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Romero PA, Krause A, Arnold FH. Navigating the protein fitness landscape with gaussian processes. Proc Natl Acad Sci U S A. 2013;110(3):E193–201. doi: 10.1073/pnas.1215251110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Saito Y, Oikawa M, Nakazawa H, Niide T, Kameda T, Tsuda K, Umetsu M. Machine-learning-guided mutagenesis for directed evolution of fluorescent Proteins. ACS Synth Biol. 2018;7(9):2014–22. doi: 10.1021/acssynbio.8b00155. [DOI] [PubMed] [Google Scholar]
- 11.Saito Y, Oikawa M, Sato T, Nakazawa H, Ito T, Kameda, T., Tsuda, K., Umetsu, M.. Machine-learning-guided library design cycle for directed evolution of enzymes: the effects of training data composition on sequence space exploration. ACS Catal. 2021;11(23):14615–24. doi: 10.1021/acscatal.1c03753. [DOI] [Google Scholar]
- 12.Phan M, Abbasi-Yadkori Y, Domke J. Thompson sampling and approximate inference. arXiv 2019;abs/1908.04970. 10.48550/arXiv.1908.04970. [DOI] [Google Scholar]
- 13.Balandat M, Karrer B, Jiang DR, Daulton S, Letham B, AG Wilson, Bakshy E. BoTorch: A framework for efficient Monte-Carlo Bayesian optimization. arXiv. 2019;abs/1910.06403. 10.48550/arXiv.1910.06403 [DOI] [Google Scholar]
- 14.Traxlmayr MW, Lobner E, Hasenhindl C, Stadlmayr G, Oostenbrink C, Rüker F, Obinger C. Construction of Ph-sensitive Her2-binding IgG1-Fc by directed evolution. Biotechnol J. 2014;9(8):1013–22. doi: 10.1002/biot.201300483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gera N, Hill AB, White DP, Carbonell RG, Rao BM, Karnik S. Design of pH sensitive binding Proteins from the hyperthermophilic Sso7d scaffold. PLoS One. 2012;7(11):e48928. doi: 10.1371/journal.pone.0048928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rasmussen CE, Williams CKI. Gaussian processes for machine learning. MIT Press; 2006. doi: 10.7551/mitpress/3206.001.0001. [DOI] [Google Scholar]
- 17.Chapelle O, Li L. An empirical evaluation of Thompson sampling. Adv Neural Inf Process Syst. 2011;24:2249–57. [Google Scholar]
- 18.Le Q, Mikolov T. Distributed representations of sentences and documents. In, International conference on machine learning. arXiv2014;32:1188-1196. doi: 10.48550/arXiv.1405.4053. [DOI] [Google Scholar]
- 19.The UniProt Consortium . UniProt: the Universal Protein knowledgebase. Nucleic Acids Res. 2017;45(D1):D158–D69. doi: 10.1093/nar/gkw1099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yang KK, Wu Z, Bedbrook CN, Arnold FH, Wren J. Learned protein embeddings for machine learning. Bioinformatics. 2018;34(15):2642–48. doi: 10.1093/bioinformatics/bty178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Řehůřek R, Sojka P. Software framework for topic modelling with large corpora. ELRA. 2010;45–50. doi: 10.13140/2.1.2393.1847. [DOI] [Google Scholar]
- 22.Lévy Flights PI. Lévy flights, non-local search and simulated annealing. Journal Of Computational Physics. 2007;226(2):1830–44. doi: 10.1016/j.jcp.2007.06.008. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


