Memory-friendly fixed-point iteration method for nonlinear surface mode oscillations of acoustically driven bubbles: from the perspective of high-performance GPU programming

Highlights

• •Nonlinear spherical stability analysis of acoustic bubbles.
• •Fixed-point iteration technique to handle implicit nature.
• •Theoretical comparison with Gauss elimination.
• •The role of GPU programming.
• •Analysis of arithmetic operation counts.
• •Analysis of memory bandwidth limitations.

Abstract

A fixed-point iteration technique is presented to handle the implicit nature of the governing equations of nonlinear surface mode oscillations of acoustically excited microbubbles. The model is adopted from the theoretical work of Shaw [1], where the dynamics of the mean bubble radius and the surface modes are bi-directionally coupled via nonlinear terms. The model comprises a set of second-order ordinary differential equations. It extends the classic Keller–Miksis equation and the linearized dynamical equations for each surface mode. Only the implicit parts (containing the second derivatives) are reevaluated during the iteration process. The performance of the technique is tested at various parameter combinations. The majority of the test cases needs only a single reevaluation to achieve ${10}^{-9}$ error. Although the arithmetic operation count is higher than the Gauss elimination, due to its memory-friendly matrix-free nature, it is a viable alternative for high-performance GPU computations of massive parameter studies.

1. Introduction

Irradiating a liquid domain with high-intensity and high-frequency ultrasound, bubble clusters are formed composed of micron-sized bubbles [2], [3]. The phenomenon is also called acoustic cavitation [4], [5]. During the radial pulsation of the bubbles, the compression phase can be so violent that thousands of degrees of Kelvin and hundreds of bars can be built-up inside the bubble inducing chemical reactions [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [12]. Such extreme conditions are the keen interest of sonochemistry [20], [21], [22] that regards the bubbles as micron-sized chemical reactors. It has various industrial applications: wastewater treatment [23], [24], [25], [26], synthesis of organic [27], [28], [29] chemical species or the production of metal nanoparticles [30], [31], [32], to name a few.

Sonochemistry faces major challenges in terms of energy efficiency and scale-up to magnitudes feasible for commercial applications [33], [34], [35]. One of the main reasons is that a large number of parameters needs to be optimised, which renders the experimental studies a trial-and-error approach. To highlight the magnitude of the problem, the reader is referred to a recent numerical study involving nearly 2 billion parameter combinations [36]. Therefore, numerical simulations of bubble clusters are viable approaches to produce optimal, large-scale and energy-efficient operation strategies.

A suitable bubble cluster simulator also struggles with many challenges. First, the nucleation of bubbles appears in seemingly random positions. The source of such bubbles still generates debate in the sonochemical society [37]. Second, due to primary and secondary Bjerknes forces, bubbles are moving in space producing various forms of cluster structure [38], [2], [3]. Third, as bubbles translate in space and time, they can merge to form larger bubbles [39], [40]. Fourth, the radial dynamics of the individual bubbles is highly nonlinear and chaotic [41], [42], [43], [44], [45], [46], [47], [48], which need to be appropriately resolved to capture the energy-focusing process of the contraction phase [49], [50], [51]. If feasible, the solution of the chemical kinetics is advisable to estimate the temporal composition of a bubble [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19]. Last but not least, large bubbles tend to be spherically unstable, and they can disintegrate into many smaller daughter bubbles [52]. Interaction of closely spaced bubbles can also disrupt the spherical stability [53].

This study focuses on the issue of shape instability since this is a primary source of losing the energy focusing during a bubble collapse. The task is highly parallelisable for bubble cluster dynamics simulations or large-scale parameter scans as the governing equations describing the shape stability of the individual bubbles are identical. This makes the employment of graphics processing units (GPUs) attractive, especially if one considers the tendency in high-performance computing: more than $97.8\%$ of the peak processing power of the Frontier supercomputer (put into service in 2022) comes from GPUs [54]. Therefore, high-performance GPU programming is the best approach today in simulating large-scale parameter studies (in the order of millions or even billions). However, an efficient GPU code needs careful thread and explicit memory management by the user; otherwise, the exploitation of the peak processing power can be as low as merely $5\%$, see one of our recent publications for details [55]. The identification of the possible bottlenecks and their solutions are highly model dependent. Thus, we proceed with a brief summary of the widely employed modelling techniques and with the justification of our choice.

Various approaches can be found in the literature with a variety of complexity to describe the shape deformation of a bubble. They are based on linear or non-linear perturbation theories; boundary integral method; boundary-fitted finite-volume (finite-element) method; or full 3D or 2D (axisymmetric) hydrodynamical simulations.

Linearised perturbation theories provide the simplest way of studying spherical stability [56], [57], [58], [59], [60]. Each shape mode consists of a decoupled second-order ordinary differential equation. The coupling with the radial dynamics is unidirectional. That is, the radial dynamics of the bubble is incorporated as a parametric excitation into the governing equations of the shape modes; however, the shape modes themselves do not influence the radial dynamics. Due to the simplicity of the model, GPU implementation is straightforward, and it is already done in our earlier publications [61], [62], [63]. The most severe limitation of the above-described approach is its linearity: the magnitudes of the shape modes tend to zero or grow to infinity. Finite amplitude surface mode oscillations cannot be analysed, which are the dominant dynamics in many situations. In addition, if the transient behaviour is essential; for instance, when the keen interest is the number of acoustic cycles the bubble survives (without a break up), the nonlinear coupling between the surface modes becomes essential to obtain realistic results (as the dynamics is far from the linear regime).

Including higher-order terms in a perturbation theory is the simplest way to extend a linearised model with non-linear terms that can prevent the infinite growth of the surface modes and produce finite amplitude, steady oscillations [64], [65], [1], [66], [67], [68], [69], [70], [71], [72], [73], [53], [74], [75]. There is a bi-directional coupling between the mean radial oscillation and the surface mode amplitude dynamics. In addition, the shape modes themselves are also mutually coupled; thus, this approach can capture the energy transition between the surface modes and the mean radial pulsation. The model is composed of globally coupled second-order ordinary differential equations (albeit the model complexity is significantly increased compared to the linearised approach), for which the use of GPUs is already widespread [76], [77], [78], [79], [80], [81], [82]. However, due to the implicit nature of the coupling, a linear system of algebraic equations has to be solved at every function evaluation for the second time-derivatives of the radial dynamics and the surface mode amplitudes. This can severely impact the performance since basic linear algebraic tasks are typically memory bandwidth limited applications [83], [84] (the computing units cannot be fed with enough data to keep them busy). The severity of the problem is demonstrated in Sec.5.2.

Perturbation theory assumes that the amplitudes of the surface mode oscillations are small. Although taking into account higher-order terms in the series expansion can increase the validity limit, and in practice, the non-linear type of models can agree well with experimental results having relatively large amplitudes, the correctness of the results cannot be guaranteed far from the linear behaviour. Boundary Integral Method (BIM) is a viable option to eliminate restrictions for the magnitude of the deformation [85], [86], [87], [88], [89]. Also, it is a computationally efficient technique: only the surface of the bubble needs to be discretised. Therefore, the spatial dimension of the problem is reduced by one. In an axisymmetric case, this means the discretisation only along a one-dimensional curve.

The perturbation theory and the BIM approach; referred to as Reduced Order Models (ROM); fundamentally deal with potential, inviscid and incompressible flows. Although with additional terms, the effect of viscosity and compressibility can be taken into account as approximations, the most accurate treatment of the non-spherical bubble oscillation is the solution of the complete set of conservation equations of the multi-phase hydrodynamics [90], [91], [92], [93] (e.g. employing a well-tested CFD software like OpenFOAM [94], [95], [96] or ALPACA [97]). However, the computation demand of the simplest 2D simulations is already orders of magnitude higher than the ROM approaches. Therefore, they are unfeasible for large-scale parameter scans of bubble clusters, regardless of the available computing power (e.g. via GPUs).

The boundary-fitted discretisation schemes are good candidates to solve the Navier–Stokes equations without simplification while keeping the bubble interface sharp and well-resolved [98], [99]. During the simulation, an orthogonal and time-dependent coordinate transformation ensures the automatic deformation of the mesh fitted to the boundary of the bubble [100], [101]. To the best knowledge of the authors, the technique is suitable only for 2D axisymmetric problems. Although this technique efficiently handles the bubble interface, the solution of the underlying conservation equations is still resource-intensive.

Considering the previous discussion, the trade-off between the model complexity (its validity limit) and runtime is a severe issue for large-scale parameter studies. As a compromise, nonlinear perturbation theory and the BIM method are good candidates for moderately viscous liquids with weak compressibility. Both approaches are computationally efficient (compared to the CFD techniques) and can be applied to 3D cases; thus, both are widely employed in the literature, see the aforementioned references. Although the BIM has a larger validity range regarding bubble-shape deformation, the present study focuses on models based on the nonlinear perturbation theory (adopted from [1]). The reason is that the governing equations are composed of Ordinary Differential Equations (ODEs), which fit well into the existing GPU library of our research group [102], [103]. In addition, the validity range is large enough to detect the inception of losing the energy focus of bubble collapses. Even though a bubble is fragmented in the long term, such a model is also capable of approximating the number of acoustic cycles (or collapses) the bubble can survive.

As it is already stated above, the primary numerical difficulty is related to the implicit nature of the coupled ODEs; that is, a linear system of equations has to be solved for every function evaluation, see Sec. 2 for more details. It is not an issue employing conventional Central Processing Units (CPUs) as many commercial software packages (e.g. Maple or Mathematica) can handle implicit ODE systems automatically. In addition, they can even generate highly optimised Fortran code making the application efficient for CPU clusters.

It is well-known that linear algebraic applications are usually limited by memory bandwidth, i.e., the system memory is not fast enough to feed the computing units with data [83], [84]. Assuming that one CPU core solves one ODE system and that the number of the employed surface modes is moderate (only a few tens maximum), the complete problem fits into the fast L1 cache of the CPU core. Such an extensive data reuse via the L1 cache eases the pressure on the slow system memory. Thus, for CPUs, system memory bandwidth is not a limiting factor.

For large-scale parameter studies, utilising the massive computing power of GPUs is a viable alternative (compared to CPUs). The millions or even billions of parameter combinations (independent tasks) can easily be distributed among a large number of GPU threads. The most straightforward parallelisation strategy is assigning one ODE system to a GPU thread, each with a different parameter set and/or initial conditions. However, while a large amount of fast cache memory is available for a single CPU thread, in the case of GPUs, hundreds or thousands of threads share a similar amount of fast on-chip cache memory. Therefore, direct or iterative solvers, where operations on moderately large or small matrices are involved, are memory bandwidth-bound approaches for the GPU [104]. The reason is simple: only a single matrix must be stored on a single CPU core, while hundreds or thousands of matrices must be stored somewhere in the GPU for a single streaming multiprocessor. The massive number of matrices is most probably stored in the slowest global memory of the GPU due to the fast on-chip memory capacity limitations (registers, shared memory or L1 cache), see Sec. 5.2 for details.

A memory-friendly, low storage (matrix-free) approach is a fixed point iteration method since only successive function evaluations are necessary, where the required state variables must already be available. Unfortunately, the convergence of a fixed-point iteration is not guaranteed; it might have a low convergence rate or even divergence. The main aim of the present study is to develop a fixed-point iteration technique with a fast convergence rate, which is specialised for the ODE systems originating from nonlinear perturbation theories. Altogether, four variants are tested on various parameter combinations of an acoustically excited microbubble. The best version requires only 1 to 3 function reevaluations to achieve ${10}^{-9}$ error.

The performance of the fixed-point iteration technique is compared with Gauss elimination. It is demonstrated that in terms of the raw arithmetic operation count, Gauss elimination is superior. However, via simple elementary calculations, it is shown that the performance of the Gauss elimination is limited by memory bandwidth. Depending on the GPU architecture, this bottleneck can be so severe that the Gauss elimination becomes slower by $40\%$ to $200\%$ compared to the best fixed-point iteration variant. The pressure on the global memory can be eased by extensive data reuse in the user-programmable shared memory, e.g., by decomposing the coefficient matrix into smaller chunks. However, such a task is far from trivial, architecture-dependent, and still, the memory bottleneck can only be eliminated partially while the complexity of the code increases significantly. Keep in mind that a fixed-point iteration needs only the reevaluation of some parts of the ODE function. Therefore, detailed runtime comparisons with specific implementations with other software packages or algorithms are out of the scope of the paper. Instead, this study provides best and worst-case scenarios for selecting the proper algorithm depending on the available hardware and the scale of the problem.

2. Governing equations

This section focuses on the description of the governing equation, which describes the volume oscillation and the shape deformation of a single bubble subjected to acoustic forcing. The model is based on the work of Shaw [64], [65], [1]. Assuming axisymmetric shape deformation, the bubble surface is described by the infinite series

$$r_b(\theta ,t)=R(t)+{\displaystyle \sum _{n=2}^{\infty }}{a}_n(t)P_n(\theta ),$$ (1)

where $R(t)$ is the bubble radius as a function of time t (i.e. the volume oscillation also referred to as the zeroth mode), $P_n(\theta )$ are the Legendre polynomials of order n (shape modes) and $a_n(t)$ are the corresponding shape mode amplitudes. In accordance with Eq. (1), the translational motion is neglected (first mode). The axisymmetric assumption is valid if the disturbance of the deformation has a definite direction; for instance, the direction of the acoustic wave or the direction of a neighbouring bubble. The system consists of coupled, second-order nonlinear ODEs, which describe the temporal evolution of the mean bubble radius (volume oscillation, spherical part) and the surface mode amplitudes (non-spherical part). The nonlinear coupling terms in the ODEs describe the interaction between the surface modes and the volume oscillation.

The equation describing the volume oscillation reads as

$$\left(1-\frac{\dot{R}}{c_L}\right)R\ddot{R}+\left(1-\frac{\dot{R}}{3c_L}\right)\frac{3}{2}{\dot{R}}^2=G+\frac{1}{c_L}\left(\dot{R}G+R\dot{G}\right)+{∊}^2\left(g_0+g_{0v}\right)$$ (2)

where $c_L$ is the sound speed of the surrounding liquid and the function

$$G(t)=\frac{p_{B_0}}{{\rho }_L}{\left(\frac{R_0}{R}\right)}^{3\gamma }+\frac{p_v}{{\rho }_L}-\frac{1}{{\rho }_L}\left(p_0+p_A\sin (\omega t)\right)-\frac{4{\mu }_L\dot{R}}{{\rho }_{L}R}-\frac{2\sigma }{{\rho }_{L}R},$$ (3)

describes the dynamic mechanical equilibrium at the bubble interface. Here, ${\rho }_L$ is the liquid density, $R_0$ refers to the equilibrium bubble radius, $\gamma$ is the polytropic exponent (adiabatic behaviour) and $p_v$ is the vapour pressure. The pressure far away from the bubble is composed of a static ambient pressure $p_0$ and a periodic component $p_A\sin (\omega t)$ with pressure amplitude $p_A$ and angular frequency $\omega$. The dynamic viscosity and the surface tension are represented by ${\mu }_L$ and $\sigma$, respectively. The equilibrium gas pressure inside the bubble can be expressed as

$$p_{B_0}=p_0-p_v+\frac{2\sigma }{R_0}\text{.}$$ (4)

The notation $∊$ in Eq. (2) indicates the order of the series expansion of the perturbation method. Note that only second-order terms are presented, which describes the influence of the surface modes on the volume pulsation of the bubble. Without these terms, Eq. (2) reduces to the Keller–Miksis equation [105], which describes the radial pulsation of a spherically symmetric bubble and considers the compressibility of the liquid to the first order. It is important to note that the original work of Shaw includes third-order terms. These terms significantly increase the complexity of the model and the computational demand; therefore, they are neglected throughout the present paper. It is demonstrated in Sec. 4 that keeping only the second-order terms, and neglecting the translational motion already provide good agreement with experimental data.

The second-order coupling terms can be divided into two parts. The inviscid part is defined as

$$g_0(t)={\displaystyle \sum _{n=2}^{\infty }}\frac{1}{(2n+1)(n+1)}\left[\left(n+\frac{3}{2}\right){\dot{a}}_n^2+(n+3)a_n{\ddot{a}}_n\right)\left(-(n-3)\left(\frac{\ddot{R}{a}_n^2}{R}+\frac{{\dot{R}}^2{a}_n^2}{2R^2}+\frac{2\dot{R}{a}_n{\dot{a}}_n}{R}\right)\right]+\left[\frac{p_{\infty }}{{\rho }_L}-\frac{p_{B_0}}{{\rho }_L}(1-3\gamma ){\left(\frac{R_0}{R}\right)}^{3\gamma }\right]{\displaystyle \sum _{n=2}^{\infty }}\frac{a_n^2}{(2n+1)R^2},$$ (5)

while the damping part (effect of liquid viscosity) is written as

$$g_{0v}(t)=\frac{{\mu }_L}{{\rho }_L}{\displaystyle \sum _{n=2}^{\infty }}\frac{2}{(2n+1)(n+1)}\left[\left(n^2+5n+2\right)\frac{a_n{\dot{a}}_n}{{\dot{R}}^2}-\frac{4n^2\dot{R}}{R^3}{a}_n^2\right]\text{.}$$ (6)

During the numerical simulations, the infinite series in Eqs. (5), (6) are truncated at a finite number $n=N$. In the scientific literature, the truncation varies between $N=8$ to 16 [66]. In this study, the authors increased it to $N=33$ to be able to examine the behaviour of the higher modes as well.

The dynamics of each surface mode are governed by a second-order ODE:

$$\epsilon \left\{R{\ddot{a}}_n+3\dot{R}{\dot{a}}_n\right)+\left[\left(n^2-1\right)(n+2)\frac{\sigma }{{\rho }_L{R}^2}-(n-1)\ddot{R}\right]a_n\left(+\frac{2{\mu }_L}{{\rho }_L}\left[(n-1)(n+2)\frac{\dot{R}}{R^2}{a}_n+(n+2)(2n+1)\frac{{\dot{a}}_n}{R}\right]\right\}={\epsilon }^2\left(g_n+g_{\mathit{nv}}\right)\text{.}$$ (7)

Here, the left-hand side of the equation corresponds to the system used for the linear stability examination by Plesset [106] (linear in terms of $a_n$). The second-order terms realise the non-linear feedback between the modes and the spherical oscillation (non-linear in terms of $a_n$). Similarly, as in the case of Eq. (2), the second-order terms can be divided into an inviscid part

$$g_n(t)={\displaystyle \sum _{i=2}^{\infty }}{\displaystyle \sum _{j=2}^{\infty }}\frac{(2n+1)(n+1)}{4}\left[\frac{\ddot{R}}{R}{a}_i{a}_j{G}_{d_{\mathit{nij}}}+\frac{{\dot{R}}^2}{R^2}{a}_i{a}_j{M}_{a_{\mathit{nij}}}+\frac{\dot{R}}{R}{\dot{a}}_j{a}_i{M}_{b_{\mathit{nij}}}\right)\left(+a_i{\ddot{a}}_j{M}_{c_{\mathit{nij}}}+{\dot{a}}_i{\dot{a}}_j{M}_{d_{\mathit{nij}}}\right]+{\displaystyle \sum _{i=2}^{\infty }}{\displaystyle \sum _{j=2}^{\infty }}{a}_i{a}_j{I}_{a_{\mathit{nij}}}\frac{(2n+1)(n+1)}{2R^2}\left[\frac{p_{\infty }}{{\rho }_L}-\frac{p_{B_0}}{{\rho }_L}{\left(\frac{R_0}{R}\right)}^{3\gamma }\right]\text{.}$$ (8)

and a damping part

$$g_{\mathit{nv}}(t)=\frac{{\mu }_L}{{\rho }_L}{\displaystyle \sum _{i=2}^{\infty }}{\displaystyle \sum _{j=2}^{\infty }}\frac{1}{4}(2n+1)(n+1)\left[\frac{{\dot{a}}_j{a}_i}{R^2}\left(Q_{b_{\mathit{nij}}}+Q_{b_{\mathit{jin}}}\right)+\frac{\dot{R}}{R^3}{a}_i{a}_j{Q}_{c_{\mathit{jin}}}\right],$$ (9)

where $I_a,G_d,M_a,M_b,M_c,M_d,Q_b$ are order-3 hypermatrices composed of integrals of Legendre polynomials or evaluations of Legendre polynomials; for the definitions, the reader is referred to papers [64], [65].

2.1. Rearrangement of the ODE system suitable for fixed-point iteration

Rewriting the governing equations to a first-order system by introducing additional variables leads to

$${\dot{x}}_1=\dot{R}=x_2,$$ (10)

$${\dot{\alpha }}_{1,n}={\dot{a}}_n={\alpha }_{2,n},$$ (11)

$${\dot{x}}_2=\ddot{R},$$ (12)

$${\dot{\alpha }}_{2,n}={\ddot{a}}_n\text{.}$$ (13)

For an efficient fixed-point iteration technique to compute the second derivatives, Eqs. (2), (7) are reorganised to separate explicit parts (need a single evaluation) and implicit parts (need re-evaluations):

$$h_1\ddot{R}=f_{\mathit{KM}}+f_{\mathit{KM}}^{\mathit{exp}}+f_{\mathit{KM}}^{\mathit{imp}}\left(\ddot{\mathit{R}},{\ddot{\mathit{a}}}_{\mathit{j}}\right),$$ (14)

$$h_2{\ddot{a}}_n=f_L^{\mathit{exp}}+f_L^{\mathit{imp}}\left(\ddot{\mathit{R}}\right)+f_{\mathit{NL}}^{\mathit{exp}}+f_{\mathit{NL}}^{\mathit{imp}}\left(\ddot{\mathit{R}},{\ddot{\mathit{a}}}_{\mathit{j}}\right)\text{.}$$ (15)

Observe that the order notation $∊$ is omitted for clarity. Also, in the implicit parts, the dependence on the second derivatives are also highlighted, where $j=2,\dots ,N$. According to Eqs. (2), (7), the leading coefficients in Eqs. (14), (15) are

$$h_1=\left(1-\frac{\dot{R}}{c_L}\right)R,$$ (16)

$$h_2=R\text{.}$$ (17)

In Eq. (14), the function

$$f_{\mathit{KM}}=G+\frac{1}{c_L}\left(\dot{R}G+R\dot{G}\right)-\left(1-\frac{\dot{R}}{3c_L}\right)\frac{3}{2}{\dot{R}}^2$$ (18)

is the well-known Keller–Miksis equation [105]. Although it is an explicit part, it is separated from $f_{\mathit{KM}}^{\mathit{exp}}$ to clearly highlight the subcase having spherical symmetry. The two other functions in Eq. (14) can be obtained by reorganising Eqs. (5), (6). The explicit part is

$$\begin{array}{c}{f}_{\mathit{KM}}^{\mathit{exp}}={\displaystyle \sum _{n=2}^N}\frac{1}{(2n+1)(n+1)}\left[\left(n+\frac{3}{2}\right){\dot{a}}_n^2-(n-3)\left(\frac{{\dot{R}}^2{a}_n^2}{2R^2}+\frac{2\dot{R}{a}_n{\dot{a}}_n}{R}\right)\right]\hfill \\ +\left[\frac{p_{\infty }}{{\rho }_L}-\frac{p_{B_0}}{{\rho }_L}(1-3\gamma ){\left(\frac{R_0}{R}\right)}^{3\gamma }\right]{\displaystyle \sum _{n=2}^{\infty }}\frac{a_n^2}{(2n+1)R^2}+\hfill \\ \frac{{\mu }_L}{{\rho }_L}{\displaystyle \sum _{n=2}^N}\frac{2}{(2n+1)(n+1)}\left[\left(n^2+5n+2\right)\frac{a_n{\dot{a}}_n}{{\dot{R}}^2}-\frac{4n^2\dot{R}}{R^3}{a}_n^2\right],\hfill \end{array}$$ (19)

while the implicit part is defined as

$$f_{\mathit{KM}}^{\mathit{imp}}={\displaystyle \sum _{n=2}^N}\frac{1}{(2n+1)(n+1)}\left[(n+3)a_n{\ddot{a}}_n-(n-3)\frac{\ddot{R}{a}_n^2}{R}\right]\text{.}$$ (20)

By rearranging Eqs. (7), (8), (9), the components of Eq. (15) are

$$\begin{array}{c}{f}_L^{\mathit{exp}}=-3\dot{R}{\dot{a}}_n-\left[\left(n^2-1\right)(n+2)\frac{\sigma }{{\rho }_L{R}^2}\right]a_n-\hfill \\ \frac{2{\mu }_L}{{\rho }_L}\left[(n-1)(n+2)\frac{\dot{R}}{R^2}{a}_n+(n+2)(2n+1)\frac{{\dot{a}}_n}{R}\right],\hfill \end{array}$$ (21)

$$f_L^{\mathit{imp}}=(n-1)\ddot{R}{a}_n,$$ (22)

$$f_{\mathit{NL}}^{\mathit{exp}}={\displaystyle \sum _{i=2}^N}{\displaystyle \sum _{j=2}^N}\frac{(2n+1)(n+1)}{4}\left[\frac{{\dot{R}}^2}{R^2}{a}_i{a}_j{M}_{a_{\mathit{nij}}}+\frac{\dot{R}}{R}{\dot{a}}_j{a}_i{M}_{b_{\mathit{nij}}}+{\dot{a}}_i{\dot{a}}_j{M}_{d_{\mathit{nij}}}\right]+{\displaystyle \sum _{i=2}^N}{\displaystyle \sum _{j=2}^N}{a}_i{a}_j{I}_{a_{\mathit{nij}}}\frac{(2n+1)(n+1)}{2R^2}\left[\frac{p_{\infty }}{{\rho }_L}-\frac{p_{B_0}}{{\rho }_L}{\left(\frac{R_0}{R}\right)}^{3\gamma }\right]+\frac{{\mu }_L}{{\rho }_L}{\displaystyle \sum _{i=2}^N}{\displaystyle \sum _{j=2}^N}\frac{1}{4}(2n+1)(n+1)\left[\frac{{\dot{a}}_j{a}_i}{R^2}\left(Q_{b_{\mathit{nij}}}+Q_{b_{\mathit{jin}}}\right)+\frac{\dot{R}}{R^3}{a}_i{a}_j{Q}_{c_{\mathit{jin}}}\right],$$ (23)

and

$$f_{\mathit{NL}}^{\mathit{imp}}={\displaystyle \sum _{i=2}^N}{\displaystyle \sum _{j=2}^N}\frac{(2n+1)(n+1)}{4}\left[\frac{\ddot{R}}{R}{a}_i{a}_j{G}_{d_{\mathit{nij}}}+a_i{\ddot{a}}_j{M}_{c_{\mathit{nij}}}\right]\text{.}$$ (24)

It is to be stressed that during the fixed-point iteration, only Eqs. (20), (22), (24) are re-evaluated. That is, the cost of one iteration is much less than a complete function evaluation.

3. Variants of fixed-point iteration techniques

In this section, only the definition of the iterations can be found with short notes of their advantages and disadvantages. Detailed convergence characteristics are given in Sec. 4, and a parameter study is shown in Sec. 4.1. The number of the required iterations $N_i$ to achieve a prescribed precision depends on the initial guess (how close it is to the solution) and the convergence rate of the iteration (divergence is also possible).

It is practical to investigate the classical fixed-point iteration first, examine its behaviour and improve it if necessary. Based on Eqs. (14), (15), this baseline iteration referred to as ${\mathit{FP}}_1$ throughout the paper, and reads as

$${\ddot{R}}^{(0)}=\frac{1}{h_1}\left[f_{\mathit{KM}}\right],$$ (25)

$${\ddot{a}}_n^{(0)}=\frac{1}{h_2}\left[f_L^{\mathit{exp}}+f_L^{\mathit{imp}}\left({\ddot{R}}^{(0)}\right)\right],$$ (26)

$${\ddot{R}}^{(n+1)}=\frac{1}{h_1}\left[f_{\mathit{KM}}+f_{\mathit{KM}}^{\mathit{exp}}+f_{\mathit{KM}}^{\mathit{imp}}\left({\ddot{R}}^{(n)},{\ddot{a}}_n^{(n)}\right)\right],$$ (27)

$${\ddot{a}}_n^{(n+1)}=\frac{1}{h_2}\left[f_L^{\mathit{exp}}+f_L^{\mathit{imp}}\left({\ddot{R}}^{(n)}\right)+f_{\mathit{NL}}^{\mathit{exp}}+f_{\mathit{NL}}^{\mathit{imp}}\left({\ddot{R}}^{(n)},{\ddot{a}}_n^{(n)}\right)\right],$$ (28)

where the upper index in the parenthesis indicates the actual iteration number. Observe that the initial guess (zeroth index) is estimated from the explicit parts of the system. The initial bubble wall acceleration is computed from the Keller–Miksis equation with spherical symmetry. Next, the initial acceleration of the shape mode amplitudes can be obtained from the linear part of their governing equations (initial bubble wall acceleration is also necessary). Initialising the fixed-point iteration via Eqs. (25), (26) is better than simply taking the initial values, e.g., from the previous time step. It is shown in Sec. 4 that this algorithm needs a relatively large iteration number to reach a given precision.

Due to the reasons mentioned above, improved versions are needed. The ${\mathit{FP}}_2$ variant is defined as follows

$${\ddot{R}}^{(0)}=\frac{1}{h_1}\left[f_{\mathit{KM}}\right],$$ (29)

$${\ddot{a}}_n^{(0)}=\frac{1}{h_2}\left[f_L^{\mathit{exp}}+f_L^{\mathit{imp}}\left({\ddot{R}}^{(0)}\right)\right],$$ (30)

$${\ddot{R}}^{(n+1)}=\frac{1}{h_1}\left[f_{\mathit{KM}}+f_{\mathit{KM}}^{\mathit{exp}}+f_{\mathit{KM}}^{\mathit{imp}}\left({\ddot{R}}^{(n)},{\ddot{a}}_n^{(n)}\right)\right],$$ (31)

$${\ddot{a}}_n^{(n+1)}=\frac{1}{h_2}\left[f_L^{\mathit{exp}}+f_L^{\mathit{imp}}\left({\ddot{R}}^{(n+1)}\right)+f_{\mathit{NL}}^{\mathit{exp}}+f_{\mathit{NL}}^{\mathit{imp}}\left({\ddot{R}}^{(n+1)},{\ddot{a}}_n^{(n)}\right)\right],$$ (32)

where the initial guess and the calculation of the bubble wall acceleration via Eq. (31) remain the same. However, this method uses Eq. (31) to calculate the second derivative of the mode amplitudes at the next iteration. Contrary to the previous case, with this substitution, the bubble wall acceleration in the current iteration stage ${\ddot{R}}^{(n+1)}$ is used to update ${\ddot{a}}_n^{(n+1)}$ to achieve faster convergence. Unfortunately, this special substituting does not significantly affect the iteration number or convergence.

Therefore, further modifications leads to the iteration technique ${\mathit{FP}}_3$:

$${\ddot{R}}^{(0)}=\frac{1}{h_1}\left[f_{\mathit{KM}}\right],$$ (33)

$${\ddot{a}}_n^{(0)}=\frac{1}{h_2}\left[f_L^{\mathit{exp}}+f_L^{\mathit{imp}}\left({\ddot{R}}^{(0)}\right)\right],$$ (34)

$${\ddot{R}}^{(n+1)}=\frac{1}{h_1}\left[f_{\mathit{KM}}+f_{\mathit{KM}}^{\mathit{exp}}+f_{\mathit{KM}}^{\mathit{imp}}\left({\ddot{R}}^{(n)},{\ddot{a}}_n^{(n)}\right)\right],$$ (35)

$${\ddot{a}}_n^{(n+\frac{1}{2})}=\frac{1}{h_2}\left[f_L^{\mathit{exp}}+f_L^{\mathit{imp}}\left({\ddot{R}}^{(n+1)}\right)\right],$$ (36)

$${\ddot{a}}_n^{(n+1)}=\frac{1}{h_2}\left[f_L^{\mathit{exp}}+f_L^{\mathit{imp}}\left({\ddot{R}}^{(n+1)}\right)+f_{\mathit{NL}}^{\mathit{exp}}+f_{\mathit{NL}}^{\mathit{imp}}\left({\ddot{R}}^{(n+1)},{\ddot{a}}_n^{(n+\frac{1}{2})}\right)\right],$$ (37)

where the initial guess and the calculation of the bubble wall acceleration remain the same as in the previous two cases. As an improvement, an intermediate or half step is added via Eq. (36) in order to pre-approximate ${\ddot{a}}_n$ from the linear parts of the ODE system employing the current bubble wall acceleration. In Eq. (37), this linear approximation is used. This slight modification improves the convergence rate significantly. Note that the term $f_L^{\mathit{imp}}$ appears both in Eqs. (36) and (37); thus, its has to be reevaluated twice. This behaviour can be taken into account via the factor $\lambda$ in Eq. (53) during the computation of the arithmetic operation count in Sec. 5.1.

The final version called ${\mathit{FP}}_4$ tries to further improve the iteration by introducing an additional intermediate approximation:

$${\ddot{R}}^{(0)}=\frac{1}{h_1}\left[f_{\mathit{KM}}\right],$$ (38)

$${\ddot{a}}_n^{(0)}=\frac{1}{h_2}\left[f_L^{\mathit{exp}}+f_L^{\mathit{imp}}\left({\ddot{R}}^{(0)}\right)\right],$$ (39)

$${\ddot{a}}_n^{(n+\frac{1}{2})}=\frac{1}{h_2}\left[f_L^{\mathit{exp}}+f_L^{\mathit{imp}}\left({\ddot{R}}^{(n)}\right)\right],$$ (40)

$${\ddot{R}}^{(n+1)}=\frac{1}{h_1}\left[f_{\mathit{KM}}+f_{\mathit{KM}}^{\mathit{exp}}+f_{\mathit{KM}}^{\mathit{imp}}\left({\ddot{R}}^{(n)},{\ddot{a}}_n^{(n+\frac{1}{2})}\right)\right],$$ (41)

$${\ddot{a}}_n^{(n+\frac{1}{2})}=\frac{1}{h_2}\left[f_L^{\mathit{exp}}+f_L^{\mathit{imp}}\left({\ddot{R}}^{(n+1)}\right)\right],$$ (42)

$${\ddot{a}}_n^{(n+1)}=\frac{1}{h_2}\left[f_L^{\mathit{exp}}+f_L^{\mathit{imp}}\left({\ddot{R}}^{(n+1)}\right)+f_{\mathit{NL}}^{\mathit{exp}}+f_{\mathit{NL}}^{\mathit{imp}}\left({\ddot{R}}^{(n+1)},{\ddot{a}}_n^{(n+\frac{1}{2})}\right)\right],$$ (43)

That is, the acceleration of the surface mode amplitudes are updated twice via the linear approximation. This increase the factor of the operation count to $\lambda =3$; however, the extra intermediate step makes convergence even faster.

4. Convergence rate of the fixed-point iterations

The biggest impact on the computational performance of a fixed-point iteration technique is its convergence rate. Simply put, fewer iteration means fewer reevaluation and less arithmetic operation count. This section is devoted to a detailed analysis of the convergence rates of the fixed-point iteration variants introduced in Sec. 3. First, only two test cases are examined having different parameter combinations, where experimental data are available to validate the numerical results. Next, the convergence rate is presented for a broader range of parameters.

The selected cases for a preliminary study are taken from the experimental work of Cleve et al. [67], see Figs. 5 and 6 therein. One has a dominant mode-2 oscillation with an equilibrium bubble radius of $R_0=46.9\mu \mathrm{m}$ and a pressure amplitude of $p_A=20.6\mathrm{kPa}$ (Case A). The other has dominant mode-3 dynamics at $R_0=70.5\mu \mathrm{m}$ and $p_A=12.8\mathrm{kPa}$ (Case B). For both cases, the driving frequency is $31.25\mathrm{kHz}$. The rest of the parameters defined in Sec. 2 are as follows: $c_L=1481\mathrm{m}/\mathrm{s}$, ${\rho }_L=998.19{\mathrm{m}}^3/\mathrm{kg}$, $\gamma =1.4$, $p_v=2353\mathrm{Pa}$, ${\mu }_L=0.0010005\mathrm{Pas}$, $\sigma =0.07275\mathrm{N}/\mathrm{m}$. Paper [67] presents the decomposition of the measured perimeter of the bubble into a sum of spherical part and surface modes with the help of Legendre polynomials. Therefore, directly comparing the measured and calculated times series curves is possible.

The ODE system (10), (24) is solved by the adaptive fifth-order Runge–Kutta–Cash–Karp (RKCK) method with fourth-order embedded error estimation. The absolute and relative tolerances are set to ${10}^{-8}$. A single time step has six stages that require six function evaluations. The fixed-point iteration technique is embedded into the function evaluation to obtain the second derivatives $\ddot{R}$ and ${\ddot{a}}_n$ with a prescribed precision. Its error is defined as

$$E^{(n)}=\left|f^{(n)}-f^{(n-1)}\right|,$$ (44)

where the vector f is composed of $\ddot{R}$ and ${\ddot{a}}_n$. If the error is smaller than the tolerance written as

$$T^{(n)}=\max \left(T_A,T_R·\min \left(\left|f^{(n)}\right|,\left|f^{(n-1)}\right|\right)\right),$$ (45)

the fixed-point iteration is considered converged (and terminated). The comparison is element-wise; that is, all the elements of $E^{(n)}$ must be smaller than the corresponding elements of $T^{(n)}$. The absolute $T_A$ and the relative $T_R$ tolerances are prescribed to ${10}^{-9}$, which are an order of magnitude smaller than that of the RKCK method to minimise the effect of the fixed-point iteration on the time step size selection. The convergence check starts from $n=1$ that compares the initial guess with the first complete evaluation of the ODE function. Thus, zero reevaluation is also possible if the initial guess based on the linear approximation is already precise enough.

The numerical simulations are summarised in Fig. 1. The left and right-hand sides are related to Cases A and B, respectively. The first row shows the mean bubble radius as a function of time. The second row depicts the time series curves of the first two most significant mode amplitudes normalised by the actual mean bubble radius. Due to the normalisation, the deviation from the small perturbation regime can be visualised explicitly. In the third row, the mode amplitudes are also given in microns to directly compare the numerics with measurements. The dimensionless time $\tau$ is defined via the period of the acoustic driving: $\mathrm{\Delta }\tau =1$ means one acoustic cycle. Altogether, 300 cycles are simulated in both cases. In Fig. 1, only the transition from the near equilibrium (in the absence of acoustic driving) to the steady oscillation is presented. The initial conditions were:

$$R(0)=R_0,$$ (46)

$$\dot{R}(0)=0,$$ (47)

$$a_n(0)={10}^{-12}\mathrm{m},\mathrm{if}n=2,3$$ (48)

$$a_n(0)=0,\mathrm{if}n>3$$ (49)

$${\dot{a}}_n(0)=0\text{.}$$ (50)

Fig. 1.

Time series curves for the preliminary test cases. Left-hand side: Case A at $R_0=46.9\mu \mathrm{m}$ and $p_A=20.6\mathrm{kPa}$. Right-hand side: Case B at $R_0=70.5\mu \mathrm{m}$ and $p_A=12.8\mathrm{kPa}$. For both cases, the driving frequency is $31.25\mathrm{kHz}$. From top to bottom, the first, second and third rows represent the mean bubble radius $R(t)$, the normalised shape mode amplitudes $a_n(t)/R(t)$ and the shape mode amplitudes $a_n(t)$ in micron, respectively.

The amplitudes of modes $a_2$, $a_4$, $a_3$ and $a_6$ shows an excellent agreement with the measured data presented in [67] via Figs. 5 and 6; although, the values of $a_n/R$ are as high as approximately $20\%$. Therefore, the model is not only valid for small perturbations but for relatively large amplitude oscillations as well. In addition, despite the neglection of the translational motion of the bubble in our governing equations, which has a comparable amplitude to the equilibrium radius $R_0$, the shape mode amplitudes still agree well with the measurements. From a numerical point of view, the preliminary tests of the convergence rate of our fixed-point iteration variants are carried out in validated situations.

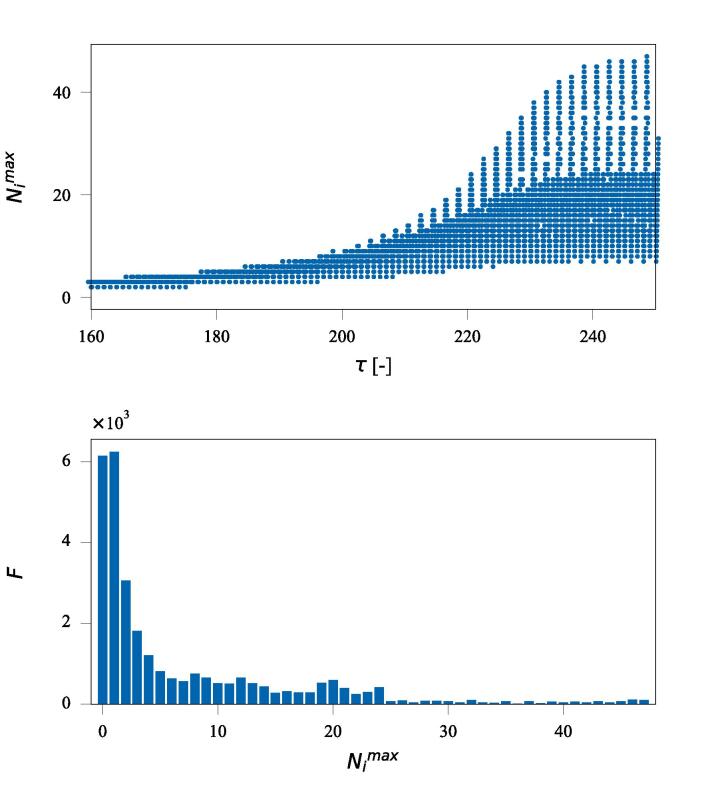
The required number of iterations varies from time step to time step and from function evaluation to function evaluation. This is demonstrated in the top panel of Fig. 2, where the maximum required iterations are shown as a function of time $\tau$ (Case A, fixed-point iteration variant ${\mathit{FP}}_1$). Observe how the iteration numbers increase with the magnitude of the shape mode amplitudes; compare the bottom-left panel of Fig. 1 with the top panel of Fig. 2. The RKCK method has six stages (six function evaluations), translating to six fixed-point iterations in a single time step. Generally, the number of iterations can differ at each stage. For simplicity, only the maximum value (worst case scenario) is recorded per time step denoted by $N_i^{\mathit{max}}$. Due to the high variability of $N_i^{\mathit{max}}$, only statistical comparison is possible for the convergence rates between the fixed-point iteration variants. For such purpose, a histogram is created for each simulation where the occurrences F of the values of $N_i^{\mathit{max}}$ are presented, see the bottom panel of Fig. 2 as an example. The average iteration number defined as

$$N_i^{\mathit{av}}=\frac{1}{N_{d\tau }}{\displaystyle \sum _{{\tau }_i}}{N}_i^{\mathit{max}}$$ (51)

can characterise a complete simulation ($0⩽\tau ⩽300$). The notation $N_{d\tau }$ stands for the number of the time steps.

Fig. 2.

Iteration number for Case A applying the fixed-point iteration variant ${\mathit{FP}}_1$. Top: maximum iteration number $N_i^{\mathit{max}}$ at each time step as a function of time $\tau$. Bottom: occurrences F of the values of $N_i^{\mathit{max}}$ for the complete simulation ($0⩽\tau ⩽300$).

Figure 3 summarises the histograms obtained for the two preliminary cases tested with the four fixed-iteration variants; see the figure caption for the layout details. The convergence rate of variants ${\mathit{FP}}_1$ (first row) and ${\mathit{FP}}_2$ (second row) is poor. The required number of function reevaluations can be as high as nearly 70. According to the detailed performance analysis carried out in Sec. 5, such high reevaluation numbers make these fixed-point iteration techniques inferior to the Gauss elimination; even though the fixed-point iteration is free of memory bandwidth limitations. A significant difference occurs between variants ${\mathit{FP}}_2$ and ${\mathit{FP}}_3$; compare rows three and four in Fig. 3. That is, an additional intermediate approximation for the acceleration of the shape mode amplitudes ${\ddot{a}}_n$ increases the convergence rate considerably. The maximum number of reevaluations for both test cases is five. Finally, introducing a second intermediate approximation (${\mathit{FP}}_4$, fourth row) further improves the convergence rate. In Case A (left-hand side), during the complete integration process of the ODE system, fixed-point iteration ${\mathit{FP}}_4$ always converged within a single reevaluation. For Case B, this number is increased to $N_i^{\mathit{max}}=3$; however, this is still a computationally efficient situation.

Fig. 3.

Summary of the histograms for Cases A (left side) and B (right side). The first, second, third and fourth rows correspond to fixed-point iteration variants ${\mathit{FP}}_1,{\mathit{FP}}_2,{\mathit{FP}}_3$ and ${\mathit{FP}}_4$, respectively.

Table 1 extracts the main statistical quantities from the eight histograms presented in Fig. 3. The average iteration numbers $N_i^{\mathit{av}}$ and the maximum value of $N_i^{\mathit{max}}$ in the histograms confirm the above conclusions. While being memory friendly, the fourth variant of the fixed-point iteration (${\mathit{FP}}_4$) has a fast convergence rate making the technique low-cost also in terms of arithmetic operation count.

Table 1.

Summary of the statistical properties of the fixed-point iteration variants (${\mathit{FP}}_1$-${\mathit{FP}}_4$) tested on Cases A and B.

	Case A		Case B
	$N_i^{\mathit{av}}$	$\max (N_i^{\mathit{max}})$	$N_i^{\mathit{av}}$	$\max (N_i^{\mathit{max}})$
${\mathit{FP}}_1$	6.9	46	28.1	69
${\mathit{FP}}_2$	6.8	46	27.9	69
${\mathit{FP}}_3$	1.9	5	3.8	5
${\mathit{FP}}_4$	1.0	1	2.4	3

4.1. Convergence rate for a wide range of parameters

Additional simulations are performed to test the convergence rate of the best fixed-point iteration variant ${\mathit{FP}}_4$ on a broader range of parameters. The driving frequency and the pressure amplitude are modified to $25\mathrm{kHz}$ and $1.1\mathrm{bar}$, respectively. Due to the much larger pressure amplitude, the bubble dynamics has much larger oscillation amplitudes. Consequently, stable oscillations of the surface modes occur at smaller bubble sizes (without a break-up). For this reason, the equilibrium radius $R_0$ as the control parameter is varied between $2\mu \mathrm{m}$ and $10\mu \mathrm{m}$ with a resolution of 8192. The simulation was run on an Nvidia RTX A5000 GPU (Ampere architecture) having $867.8$ GFLOPS double precision peak performance. The runtime was $108.5$ hours.

The first 268 acoustic cycles are regarded as transients, and the minima and maxima of the relative surface mode amplitudes $a_n/R$ are recorded at each of the subsequent 32 cycles. As a function of the control parameter $R_0$, these values are shown in the top panel of Fig. 4 up to mode number six. In the case of bubble break up ($a_n/R>1$), the complete simulation is discarded; see the missing parts at the regions of high $R_0$. Although the relative amplitude $a_n/R$ can be larger than $50\%$, where the governing equations might not be valid, the corresponding data is kept if stable oscillations are observed. The reason is to test the fixed-point iteration even under extreme conditions. In the bottom panel, the maximum value of $N_i^{\mathit{max}}$ of the complete integration procedure is plotted as a function of the control parameter $R_0$. It is clear that the required number of function reevaluations never exceeds one.

Fig. 4.

Parameter study to test the convergence rate of the fixed-point iteration variant ${\mathit{FP}}_4$ on a wider range of parameters. The driving frequency and pressure amplitude are $25\mathrm{kHz}$ and $1.1\mathrm{bar}$, respectively. The bubble size $R_0$ is varied between $4.5\mu \mathrm{m}$ and $6.5\mu \mathrm{m}$ with a resolution of 8192. Top panel: surface mode amplitudes. Bottom panel: maximum required function reevaluation.

5. Performance analysis in terms of GPU architecture

This section discusses the theoretical performance comparison of our best fixed-point iteration technique (${\mathit{FP}}_4$) with the Gauss elimination. As the Gauss elimination minimises the number of arithmetic operation count for solving a linear system of equations, this algorithm serves as a good baseline for comparison. It is shown that the arithmetic operation requirement and the hardware features of a GPU (theoretical peak performance of the compute units and the theoretical peak bandwidth of the memory subsystems) are enough to calculate best and worst-case scenarios for runtime estimations. It is also demonstrated that limitations by memory bandwidth can severely impact the overall runtime of an ODE function evaluation.

5.1. Analysis of the arithmetic operation count

The raw number of operation counts of a numerical technique is a fundamental metric. To reevaluate Eq. (20), one needs

$$N_{\mathit{KM}}^{\mathit{imp}}=8(N-1)$$ (52)

number of additions and multiplications. Here we assumed that the coefficients involving n are precomputed (possibly at compile time) and that the division by R is already available, e.g., during the evaluation of Eq. (19). Similarly, the arithmetic operation counts of Eqs. (22) and (24) are

$$N_L^{\mathit{imp}}=\lambda 2(N-1)$$ (53)

and

$$N_{\mathit{NL}}^{\mathit{imp}}=8{(N-1)}^3,$$ (54)

respectively. It was shown in Sec. 3 that Eqs. (22) needs to be reevaluated three times during a single iteration in the case of ${\mathit{FP}}_4$. This effect is taken into account by the factor $\lambda$. Its value depends on the fixed-iteration variant. In the current version, it is $\lambda =3$. The fact that division operation is not involved during the reevaluations is an important aspect of the proposed technique: an addition (subtraction) or multiplication is processed in one clock cycle; however, a division needs approximately 50–70 clock cycles. That is, a division is an extremely expensive operation, and its number must be kept minimal. The overall operation count (additions and multiplications) of the fixed-point iteration is

$$N_{\mathit{FP}}^{a/m}=N_i\left[N_{\mathit{KM}}^{\mathit{imp}}+N_L^{\mathit{imp}}+N_{\mathit{NL}}^{\mathit{imp}}\right]=N_i\left[8{(N-1)}^3+(8+2\lambda )(N-1)\right],$$ (55)

where $N_i$ is the number of the required iterations to achieve a given tolerance. The superscript $a/m$ emphasises the involvement only of additions and multiplications.

Gauss elimination minimises the number of arithmetic operation count for solving a linear system of equations. Therefore, this algorithm serves as a baseline for comparison. There is also a cubic dependence for the additions and multiplications:

$$N_G^{a/m}=\frac{1}{3}\left(2N^3+3N^2-5N\right)\text{.}$$ (56)

Gauss elimination, however, involves a relatively large number of division operations:

$$N_G^{\mathit{div}}=\frac{1}{2}\left[N(N+1)\right]\text{.}$$ (57)

Note that the divisions here cannot be eliminated or pre-computed at compile time. In addition, as the coefficient matrices differ from system to system, there are no common divisions between the GPU threads that can ease the arithmetic operation pressure. In the case of the Gauss elimination, the size of the linear equation system is $N$: one for the bubble wall acceleration and $N-1$ for the mode amplitude accelerations. Observe that the summations in Eqs. (20) and (24) are goes from 2 to $N$; therefore, their reevaluations depends only on $N-1$ (instead of $N$).

Table 2 summarises the required operation counts for three values of the system size $N$. As the number of the necessary function evaluations $N_i$ is not known in advance for the fixed-point iteration technique, only the operation count for a single reevaluation is highlighted (implicit part, second row). For the Gauss elimination, an equivalent operation count is also calculated by multiplying the division operation count with a factor of 50 (the minimum cost of a division in clock cycles) and adding to the operation count of the additions/multiplications (need a single clock cycle). Although in the majority of the examined cases the fixed-point iteration number is around $N_i=1$, the ratio of the implicit and the Gauss elimination reveals that the fixed-point iteration needs more operation by a factor of $1.3$ to $4.9$.

Table 2.

Summary of the arithmetic operation counts for different values of $N$.

$N$	8	15	33
${\mathit{FP}}_4$ ($N_i=1$, implicit part)	2842	22148	262592
Gauss (add/mul)	392	2002	24992
Gauss (div)	36	120	561
Gauss (equivalent)	2192	8450	53042
${\mathit{FP}}_4$/Gauss	1.3	2.6	4.9
explicit	10563	82866	984288
total (single function eval.)	13405	105014	1246880
implicit/total	0.21	0.21	0.21

Note that the operation counts of the fixed-point iteration is calculated only from Eqs. (20), (22) and (24), and the operation counts of the complete function evaluation is omitted. Comparing these numbers with the Gauss elimination is correct since determining the elements of the coefficient matrix also needs the evaluation of the complete function. Nevertheless, the arithmetic operations necessary to evaluate the explicit part of the ODE function are also an essential aspect of the comparison. That is, what is the share of the fixed-point iteration or Gauss elimination in the total computational requirements?.

The arithmetic operation count of the explicit parts defined by Eqs. (19), (21) and (23) is

$$N^{\mathit{exp}}=30{(N-1)}^3+(25+14)(N-1),$$ (58)

assuming again that the coefficients of n are precomputed and that the division by R is done only once per function evaluation (i.e. neglected). The explicit part must be evaluated only once for both the fixed-point iteration and the Gauss elimination algorithms. The total number of operation counts of the complete function evaluation is the sum of the implicit and explicit values. It is nearly five times larger than the implicit parts (a single reevaluation for the fixed-point iteration). Therefore, the overall effect of the superiority of the Gauss elimination (in terms of operation count) is much less than the factors $1.3$-$4.9$ presented in Tab. 2. In addition, in order to obtain a realistic picture, the memory hierarchy must also be taken into account.

5.2. Possible performance issues in terms of GPU memory subsystem

The structure of the governing equations presented previously allows the identification of possible performance bottlenecks in terms of the memory subsystem (registers, shared memory and L2 cache) of the GPU. Employing Gauss elimination requires the storage of a corresponding augmented coefficient matrix A with a size of $N(N+1)$ for each replication of the governing equations (i.e. for each GPU thread). If the memory subsystem of the GPU cannot be effectively utilised to store and use these coefficient matrices, the global memory bandwidth will limit the application performance.

Let us highlight the magnitude of the problem via some reference numbers. First, Tab. 3 summarises the available fast, on-chip memory types of the latest Nvidia GPU architectures (as of Q2, 2023). The last level L2 cache of a GPU is shared among all the threads, and its size is in the order of megabytes. Although not user programmable, a large portion of this memory type can be configured for persistent data (frequently reused by the threads). Which data goes into the persistent portion of the L2 cache is decided at runtime via the hit rate. Therefore, if data is frequently used (like the coefficient matrices), it is likely that it remains in the L2 cache. This feature of Nvidia GPUs is available from CUDA 11.0, and compute capability 8.0 and above (Ampere architecture). The compute units of a GPU are partitioned into Streaming Multiprocessors (SMs). Each SM has a dedicated user-programmable L1 cache called Shared Memory. Its size is in the order of tens of kilobytes. Due to the user-programmable feature, one can directly allocate memory for the coefficient matrices (if enough memory is available). The register file is the fastest memory type (practically has no latency). Each GPU thread has a dedicated number of registers. They are precious and scarce resources: the maximum available double precision registers are 127 for all GPU architectures.

Table 3.

Hardware features of different Nvidia GPU architectures (full implementation). The notation DP stands for double precision.

	Volta	Ampere	Hopper
	V100	A100	H100
compute capability	7.0	8.0	9.0
clock rate (MHz)	1530	1410	1755
SM count	84	128	144
DP units per SM	32	32	64
DP units per GPU	2688	4096	9216
peak DP computing power (TFLOPS)	8.2	11.6	32.3
max registers per thread (DP)	127	127	127
max shared memory per SM (kB)	96	164	228
max L2 cache per GPU (MB)	6	40	50
global memory bandwidth (GB/s)	900	1555	3352
global memory latency (clock cycles)	$\approx$400	$\approx$400	$\approx$400
shared memory bandwidth (GB/s)	16451	23101	32348
shared memory latency (clock cycles)	$\approx$20	$\approx$20	$\approx$20
L2 cache bandwidth (GB/s)	3133	7219	$\approx$8986
L2 cache latency (clock cycles)	$\approx$200	$\approx$200	$\approx$200
arithmetic operation latency (cl. cyc.)	$\approx$4	$\approx$4	$\approx$4
required memory bandwidth (GB/s)	67381	94623	264996
bandwidth ratio (required/global)	75	61	79
bandwidth ratio (required/L2 cache)	22	13	29
bandwidth ratio (required/shared)	4	4	8

In a simplified viewpoint, every piece of data that does not fit into the aforementioned memory types resides in the slowest global memory of the GPU. Its latency is high, in the order of several hundreds of clock cycles. This number of cycles must pass before a piece of data becomes available for computations after initiating a load operation. The strategy of the GPU to hide latency is to reside a large number of threads in an SM (the maximum is 2048). That is, while some threads wait for data (either from memory or previous computations), others might be ready to perform an arithmetic operation. On the other hand, a large number of residing threads per SM means fewer available registers, less shared memory and L2 cache per thread. Thus, a compromise must be found between latency hiding capability and on-chip memory overuse, which is usually not trivial. Optimally, all the data can reside in the registers, and the code can run practically without memory latency. In such cases, a high number of residing threads in an SM is not necessary. Unfortunately, our governing equation does not fit this category; therefore, efficient memory and thread management are mandatory. The present study focuses only on memory bandwidth limitation, and performance issues caused by latency are neglected. Thus, it is a best-case scenario for the Gauss elimination, where the number of threads residing simultaneously in an SM is reduced to allocate more registers and shared memory to a GPU thread. For this purpose, the number of threads per SM is set only to 256. Considering that the maximum is 2048, this number is quite small ($12.5\%$). Table 3 summarises the estimated latency of the different memory types. Arithmetic operation latency is also included for completeness. Although the number of threads per SM is considered to be the same for all architectures, due to the different number of SMs, the total number of threads launched per GPU is different, compare Tabs. 3 and 4.

Table 4.

Best and worst case scenarios of global memory pressure for different coefficient matrix sizes $N$.

$N$	8	15	33
matrix size	64	225	1089
registers per threads (DP)	127	127	127
threads per SM	256	256	256
threads per GPU (V100)	21504	21504	21504
threads per GPU (A100)	32768	32768	32768
threads per GPU (H100)	36864	36864	36864
registers req. (DP)	64	225	1089
shared memory req. (kB)	128	450	2178
L2 cache req. (MB, V100)	10.5	36.9	178.7
L2 cache req. (MB, A100)	16.0	56.3	272.3
L2 cache req. (MB, H100)	18.0	63.3	306.3
Gauss (equivalent arithm. op.)	2192	8450	53042
Gauss load/store best	144	480	2244
Gauss load/store worst	406	2478	25056
Gauss arith./mem. best	15.2	17.6	23.6
Gauss arith./mem. worst	5.4	3.4	2.1
Gauss slow factor (H100) best	1.9	4.5	3.3
Gauss slow factor (H100) worst	5.5	23.2	37.3

Assuming that all the data in a series of arithmetic operations need to be loaded from memory without data reuse and that the operands are double precision floating point numbers (8 bytes), the required memory bandwidth in GB/s is

$${\mathit{BW}}_r=8·1024·P_{\mathit{DP}},$$ (59)

where $P_{\mathit{DP}}$ is the peak double-precision performance of the hardware in TFLOPS (Tera FLoating Point operation per Second). The ratio of the required ${\mathit{BW}}_r$ and the available ${\mathit{BW}}_a$ memory bandwidth is a valuable hardware metric that defines the required number of arithmetic operations per memory transaction to eliminate bandwidth limitations. Table 3 summarises these hardware features for the different memory types and architectures. Observe that in the case of global memory, 60 to 80 arithmetic operations need to be performed for a single memory transaction. It is to be stressed that the number of the arithmetic and load/store operations are usually equal in linear algebraic tasks. For instance, a vector-vector multiplication of size n needs $2n$ memory loads (for the two vectors), whereas it only needs n additions and n multiplications. In other words, without extensive data reuse via registers, shared memory or L2 cache, the runtime might increase by a factor of 60 to 80; and the arithmetic operation count requirements, like the ones presented in Sec. 5.1, becomes meaningless.

The memory requirement to store the coefficient matrices for $N=8,15$ and 32 is summarised in Tab. 4. The corresponding matrix sizes are $64,225$ and 1089, respectively. If one intends to store the coefficient matrices in the fastest memory type (registers), the required number of double precision (DP) registers equals the coefficient matrix size. This can be satisfied only for small values of $N$. However, other data, e.g., vectors of the state variable, stages of the numerical integration or intermediate results, usually need to be stored in registers as well. Therefore, consuming half of the registers for the coefficient matrix alone is possible but can still produce suboptimal performance. Variables with no room in the register file are automatically spilt back to the slow global memory.

Putting the coefficient matrices into the shared memory needs the storage of as many matrices as the number of the residing threads in the SM. Considering double precision floating points (8 bytes) means $128,450$ and 2178 kilobyte storage requirement for $N=8,15$ and 33, respectively. Only the Ampere and the Hopper GPU architectures can store the coefficient matrices for small values of $N$.

The L2 cache requirement must be considered on a GPU basis. Due to the variable number of SMs, the total number of threads per GPU depends on the architecture; see Tab. 4. Accordingly, the required L2 cache capacity is a function of the matrix size $N$ and the GPU architecture. The corresponding three rows of Tab. 4 present the storage requirements in megabytes. Again, only the newest Ampere and Hopper architectures have enough capacity, and again only for small matrix sizes.

The motivation to develop a matrix-free solver is clearly demonstrated in this section. Storing coefficient matrices in fast on-chip GPU memories is feasible only for small problem sizes, see the bold numbers in Tab. 4. Otherwise, extensive global memory operations are expected that can degrade the performance of the code significantly. With fixed-point iteration techniques, the entire matrix storage problem can be eliminated.

How this knowledge translates to the Gauss elimination? First, the required number of load/store memory transactions must be calculated. In the best-case scenario, the memory transactions are two times the size of the augmented coefficient matrix (store when it is computed, and load for the elimination):

$$N_{G,b}^{l/s}=2N(N+1)\text{.}$$ (60)

Equation (60) assumes that all matrix elements are loaded only once. This means that the entire matrix fits into one of the fast memory types (e.g., shared memory). If there is insufficient fast memory capacity, the same elements must be loaded multiple times during the elimination process. Simply put, when an element is needed again, it is usually already evicted from the fast memory type by other data. Consequently, in the worst-case scenario, data is always loaded from the global memory during an arithmetic operation. In this situation, the load and store operations are calculated as

$$N_{G,w}^l={\displaystyle \sum _n}=2^N=\frac{1}{3}(N^3+3N^2+2N-6)$$ (61)

and

$$N_{G,w}^s={\displaystyle \sum _n}=2^{N-1}=\frac{1}{3}(N^3-N),$$ (62)

respectively. The best- and worst-case scenarios are shown in Tab. 4. The available ratio of the arithmetic operations and memory transactions is based on the equivalent operation count. Comparing this ratio with the required one presented in the last three rows in Tab. 3, it is clear that the Gauss elimination is limited by memory bandwidth (even for the best-case scenario). Dividing the available and the required ratios, slow-down factors are defined in the last two rows of Tab. 4 (H100 architecture only). Here we assume that for $N=8$, the augmented coefficient matrix fits into the L2 cache.

If there is not enough fast (e.g., shared) memory capacity, dividing the coefficient matrix into smaller slices and performing as many operations as possible on such a smaller portion of data before replacing it with others from the global memory is possible. Although these techniques can significantly reduce global memory transactions, they cannot eliminate memory bandwidth bottlenecks completely, as the same data still needs to be loaded multiple times from the global memory [107]. In addition, these techniques significantly increase the complexity of the control flow of the program. Although the discussion of such clever algorithms is out of the scope of the present study, they must lie between the best- and worst-case scenarios.

5.3. Overall performance comparison

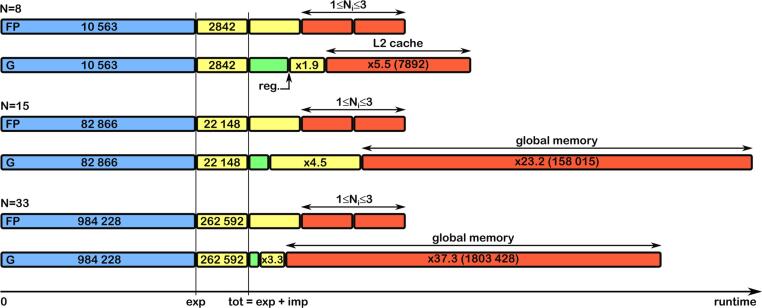
Based on the theoretical considerations discussed in Secs. 5.1 and 5.2, the estimated runtime comparisons (measured in clock cycles) between the fixed-point iteration (FP) and Gauss elimination (G) are shown in Fig. 5 at three values of $N$. For both techniques, the complete ODE function has to be evaluated once, which includes the explicit parts (blue rectangle) and an implicit part (one yellow rectangle). The numbers are the arithmetic operation counts also given in Tab. 2. Note that the total operation count of the complete function evaluation normalises the horizontal axis.

Fig. 5.

Best and worst case performance comparisons between the fixed-point iteration ${\mathit{FP}}_4$ and the Gauss elimination.

The best variant of the fixed-point iteration technique ${\mathit{FP}}_4$ needs $N_i=1$ to $3$ additional reevaluations of the implicit parts represented by the next three rectangles having an equal length. The red parts define the best- and worst-case scenarios that occurred during the employed parameter combinations in the present paper. In general, the fixed-point iteration technique provides a well-predictable performance.

If the augmented coefficient matrix fits into the GPU registers, the Gauss elimination is free of memory bandwidth limitations. The green rectangles in Fig. 5 presents such an optimal situation based only on the arithmetic operation counts. Although the Gauss elimination is superior regarding raw arithmetic operation counts, the actual runtimes can be significantly higher due to the bottleneck of memory bandwidth limitations. Applying the factors presented in the last two rows in Tab. 4 (H100 architecture), best- and worst-case scenarios can also be presented for the Gauss elimination; see the corresponding red rectangles. According to [107], the achieved performance of the Gauss–Jordan elimination is approximately between $9\%$ and $13\%$. Therefore, it is very likely that the performance of the Gauss elimination for our bubble dynamical problem is close to the presented worst-case scenario, which makes the fixed-point iteration a better alternative.

It is important to note again that additional storage capacity is necessary for the state variables, RKCK integrator stages, and other intermediate variables. However, these requirements are identical for the fixed-point iteration and the Gauss elimination. Furthermore, the performance of the Gauss elimination might further be degraded by the lack of latency hiding capabilities; see Sec. 5.2 for the related discussion. Finally, the increased complexity of the code is the cost of a clever algorithm that exploits the shared memory capacity by decomposing the Gauss elimination procedure into smaller subtasks. This has an overhead, e.g., because of the additional arithmetic operations. These issues mentioned above are omitted during the performance analysis.

6. Summary

Shape instability of acoustically driven microbubbles is a crucial aspect of sonochemistry. A shape-unstable bubble loses its energy-focusing potential leading to a reduced chemical yield. The investigation of the disintegration of bubbles and the acoustic cycles they can survive is a cumbersome task due to the large number of involved parameters. The complexity of the model and the peak processing power of the selected hardware determines the possible scale of a parameter study.

This paper focused on developing an efficient algorithm suitable for massive parameter scans of nonlinear spherical stability analysis on graphics processing units (GPUs). The main challenge is the solution of the emerging linear algebraic equation systems at every function evaluation during the numerical integration process of the governing equations (a set of second-order ordinary differential equations).

It is shown that the performance of the Gauss elimination is limited by memory bandwidth, although it is superior in terms of raw arithmetic operation counts. In the examined test cases, the runtime might increase by a factor as high as 37. Other direct or iterative solvers involving a coefficient matrix shall suffer from the same limitations.

Due to its matrix-free nature, a fixed-point iteration is free of the aforementioned memory issues (only successive function reevaluations are necessary). However, its performance heavily relies on the required number of iterations (reevaluations) to achieve a prescribed tolerance. Moreover, fixed-point iterations can even be divergent. This paper presents a specialised fixed-point iteration with a high convergence rate that needs only 1 to 3 reevaluations to retrieve ${10}^{-9}$ accuracy. Therefore, the proposed technique is superior to the Gauss elimination due to its memory friendliness despite its slightly higher arithmetic operation count.

CRediT authorship contribution statement

Péter Kalmár: Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualization. Ferenc Hegedűs: Funding acquisition, Project administration, Writing – original draft, Writing – review & editing. Dániel Nagy: Software, Resources. Levente Sándor: Supervision, Project administration, Writing – original draft.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.