Abstract
Accurate streamflow prediction is essential for efficient water resources management. Machine learning (ML) models are the tools to meet this need. This paper presents a comparative research study focusing on hybridizing ML models with bioinspired optimization algorithms (BOA) for short-term multistep streamflow forecasting. Specifically, we focus on applying XGB, MARS, ELM, EN, and SVR models and various BOA, including PSO, GA, and DE, for selecting model parameters. The performances of the resulting hybrid models are compared using performance statistics, graphical analysis, and hypothesis testing. The results show that the hybridization of BOA with ML models demonstrates significant potential as a data-driven approach for short-term multistep streamflow forecasting. The PSO algorithm proved superior to the DE and GA algorithms in determining the optimal hyperparameters of ML models for each step of the considered time horizon. When applied with all BOA, the XGB model outperformed the others (SVR, MARS, ELM, and EN), best predicting the different steps ahead. XGB integrated with PSO emerged as the superior model, according to the considered performance measures and the results of the statistical tests. The proposed XGB hybrid model is a superior alternative to the current daily flow forecast, crucial for water resources planning and management.
Subject terms: Environmental sciences, Hydrology
Introduction
Given the scarcity of water and the concerns about its future availability, it is essential to undertake studies that can aid in comprehending its dynamics for effective management. However, the variability of this water resource, attributed to climate change phenomena such as severe droughts, floods, storms, cyclones, and even human actions1 exhibits chaotic, non-linear characteristics and high stochasticity2, making prediction complex and still a significant challenge.
Machine learning models are currently used as alternatives to deal with this complexity; however, they often underperform due to their dependence on the chosen parameters. Various evolutionary search algorithms, such as genetic algorithms (GA), firefly algorithm (FFA), particle swarm optimization (PSO), salp swarm algorithm (SSA), gray wolf optimization (GWO), spotted hyena optimizer (SHO), differential evolution (DE), cuckoo search algorithm (CSA), Ant colony optimization (ACO), and even multi-objective optimization design (MOOD), have been proposed. These algorithms have demonstrated excellent global optimum search capabilities compared to classic optimization methods, leading to the development of hybrid models3–15. The application of these hybrid approaches for predicting hydrological variables is a relatively new technique that has shown significant improvement in forecasting16–24. Recent studies along these lines have been conducted for predicting river flows25–31.
The multivariate adaptive regression spline (MARS) model, combined with the differential evolution (MARS-DE) algorithm, was developed by32 to simulate water flow in a semi-arid environment, using antecedent values as inputs. According to the authors, the MARS-DE model demonstrated strong hybrid predictive modeling capabilities for water flow on a monthly timescale compared to LSSVR and the standard MARS model.
Multi-objective optimization design (MOOD) was employed by33 to select and fine-tune the weights of the models extreme learning machine (ELM) and echo state network (ESN), resulting in the hybrid models ELM-MOB and ESN-MOB. These hybrid models were developed for influent flow forecasting using past values as input variables. The results of these models were compared with the SARIMA model, demonstrating their superior performance. Specifically, the ESN-MOB model outperformed the others.
The prediction accuracy of the ANFIS-FFA hybrid model, which combines adaptive neuro-fuzzy inference systems (ANFIS) and the firefly algorithm (FFA), was evaluated by34 in predicting throughput using their antecedent values as inputs. The proposed hybrid model was compared with the classical version (ANFIS). The outcomes revealed that the FFA could enhance the prediction precision of the ANFIS hybrid model.
A study conducted by35 obtained results similar to those of34 when combining ANFIS and PSO (ANFIS-PSO). The proposed hybrid approach demonstrated the ability to generate accurate estimates for modeling upstream and downstream daily flows, in comparison to other approaches such as MARS and M5tree. Precipitation and discharge were used as input data for the model. In another study, Yaseen et al.36 developed a hybrid model named the extreme learning machine model (ELM) with the salp swarm algorithm (SSA-ELM). The developed model was compared with the classic ELM and other artificial intelligence (AI) models in monthly flow forecasting, utilizing antecedent values as inputs. The flow prediction precision of SSA-ELM exceeded that of the classic ELM and other AI models.
A recent algorithm called gray wolf optimization (GWO) was applied to enhance the effectiveness of artificial intelligence (AI) models by37. The findings indicated that AI models with integrated GWO (ANN-GWO, SVR-GWO, and MLR-GWO) outperformed standard AI methods such as ANN and SVR. Additionally, SVR-GWO exhibited better performance in predicting monthly flow compared to ANN-GWO and MLR-GWO. In another study, Tikhamarine et al.38, applied GWO in combination with Wavelet SVR (GWO-WSVR). The results showed that the GWO algorithm outperformed other optimization approaches like Particle swarm optimization (PSO-WSVR), shuffled complex evolution (SCE-WSVR), and multi-verse optimization (MVO-WSVR). These methods were also employed in tuning WSVR parameters, revealing the superiority of GWO in optimizing standard SVR parameters to improve flow prediction accuracy. Both studies used only past flow values as input variables.
The prediction capability of support vector regression (SVR) was optimized using various algorithms, namely spotted Hyena optimizer (SVR-SHO), ant lion optimization (SVR-ALO), Bayesian optimization (SVR-BO), multi-verse optimizer (SVR-MVO), Harris Hawks optimization (SVR-HHO), and particle swarm optimization (SVR-PSO). These algorithms were used to select the SVR parameters and were tested by39. The comparison results showed that SVR-HHO outperformed the SVR-SHO, SVR-ALO, SVR-BO, SVR-MVO, and SVR-PSO models in daily flow forecasting in the study basin, utilizing past flow values as input variables. In comparison with the competition, the new HHO algorithm demonstrated superior performance in making predictions.
The performance of extreme learning machine (ELM) models optimized by bioinspired algorithms, namely ELM with ant colony optimization (ELM-ACO), ELM with genetic algorithm (ELM-GA), ELM with flower pollination algorithm (ELM-FPA), and ELM with Cuckoo search algorithm (ELM-CSA), was compared in a study by40, for the prediction of evapotranspiration (ETo). The proposed models were evaluated and contrasted with the standard ELM model. The results indicated a greater ability of the bioinspired optimization algorithms to enhance the performance of the traditional ELM model in daily ETo prediction, particularly the FPA and CSA algorithms.
A new hybrid model for monthly flow forecasting, named ELM-PSOGWO (integrating PSO and GWO with ELM), was proposed by41. This approach was compared with the standard ELM, ELM-PSO, and ELM-PSOGSA methods (hybrid ELM with integrated PSO and binary gravitational search algorithm). The models were tested for accuracy using monthly precipitation and discharge data as inputs. The results indicated that the ELM-PSOGWO model outperformed the competition, demonstrating the ability to provide more reliable predictions of peak flows with the lowest mean absolute relative error compared to other techniques.
The deep learning hybrid model, known as the gray wolf algorithm (GWO)-based recurrent gated unit (GRU) (GWO-GRU), was developed by42 for forecasting daily flow rates, utilizing its antecedents as input variables. The proposed model was compared with a linear model. According to the findings, GWO-GRU outperforms the linear model.
The performance of the support vector machine hybrid model with particle swarm optimization (PSO-SVM) was evaluated by43 for short-term daily flow forecasting in rivers. The model used river flow, precipitation, evaporation, average relative humidity, flow velocity, average wind speed, and maximum and minimum temperature as input variables. The outcomes demonstrated that the hybrid model outperformed the standard SVM in predicting flow 1–7 days ahead. Furthermore, they found that the inclusion of meteorological variables improved flow prediction.
A hybrid model based on the integration of hybrid particle swarm optimization and gravitational search algorithms (PSOGSA) into a feed-forward neural network (FNN) (PSOGSA-FNN) was developed by44 for forecasting monthly flow, using its antecedent values as predictors. The outcomes indicated that the proposed model achieved better forecast accuracy and is a viable method for predicting river flow.
Various evolutionary algorithms, such as genetic algorithm (GA), fire-fly algorithm (FFA), gray wolf optimization (GWO), differential evolution (DE), and particle swarm optimization (PSO), were coupled with ANFIS and trained and tested for forecasting daily, weekly, monthly, and annual runoff using runoff antecedents as inputs by45. The findings showed that the hybrid algorithms significantly outperformed the conventional ANFIS model for all forecast horizons. Furthermore, ANFIS-GWO was identified as the superior hybrid model. In another study by46, a hybrid ANFIS model with integrated gradient-based optimization (GBO) was proposed for flow forecasting, using temperature data and antecedent flow values as predictors. The outcomes revealed that the proposed model is superior to the standard ANFIS.
In the same perspective, Haznedar and Kilinc29 developed a hybrid ANFIS model with an integrated genetic algorithm (GA) (ANFIS-GA) for streamflow prediction, using its past values as input. The outcomes demonstrated that the suggested model performs better than the standard ANFIS, LSTM, and ANN. Dehghani et al.47 applied the GWO-optimized ANFIS model for the recursive multi-step forecast of flow between 5 min and 10 days ahead, using antecedent values as inputs, and observed that the proposed model outperformed the standard in all forecast horizons.
Hybrid machine learning models were tested for flood prediction by19. In their study, the authors applied GWO-optimized MLP and SVR models (MLP-GWO and SVR-GWO) and observed that SVR-GWO achieved superior results compared to MLP-GWO. The results also demonstrate that using GWO as an optimizer results in a potential improvement in the performance of MLP and SVM models for flood forecasting.
Other recent hybrid approaches aimed at enhancing the performance of machine learning (ML) models for streamflow forecasting also deserve special mention. These include the linear and stratified selection in deep learning algorithms by48; forest-based algorithms applied to neural network models as investigated by49; the use of meta-heuristic algorithms (MHA) in artificial neural networks (ANN) as explored by50; PSO integration for parameter selection in ANN51; and novel hybrid approaches based on conceptual and data-driven techniques52. Table 1 presents the summary of some hybrid models resulting from the optimization of the parameters.
Table 1.
Summary of hybrid artificial intelligence methods by parameter optimization for flow forecasting.
| Reference | Case study | Hybrid model |
|---|---|---|
| 32 | Iraq | Differential evolution integrated into multivariate adaptive regression spline (MARS-DE) |
| 33 | Brazil | Echo state network and multi-objective optimization design (ESN-MOB) |
| 34 | Malaysia | Firefly optimization algorithm and adaptive neuro-fuzzy inference systems (ANFIS-FFA) |
| 35 | Pakistan | Particle swarm optimization algorithm and neuro-fuzzy inference systems (ANFIS-PSO) |
| 37 | Egypt | support vector regression with grey wolf optimization (GWO-SVR) |
| 38 | Algeria | Wavelet support vector regression with grey wolf optimization (GWO-WSVR) |
| 39 | India | Harris Hawks optimization and support vector regression (SVR-HHO) |
| 40 | China | Extreme learning machine with flower pollination algorithm (ELM-FPA) |
| 41 | Pakistan | Particle swarm optimization and gray wolf optimization with extreme learning machine (ELM-PSOGWO) |
| 53 | Iran | Support vector regression optimized by grasshopper optimization algorithm (GOA) with LASSO input selection |
| 36 | Iraq | Extreme learning machine model with salp swarm algorithm (SSA-ELM) |
| 42 | Turkey | Gated recurrent unit with grey wolf algorithm (GWO-GRU) |
| 43 | Malaysia | Particle swarm optimization and support vector machine (PSO-SVM) |
| 44 | Tukey | Hybrid particle swarm optimization and gravitational search algorithms with feed-forward neural network (FFN-PSOGSA) |
| 45 | Iran | Adaptive neuro-fuzzy inference systems with grey wolf optimization algorithm (GWO-ANFIS) |
| 46 | Pakistan | ANFIS with gradient-based optimization (GBO) (GBO-ANFIS) |
| 47 | Iran | ANFIS with GWO |
As noted earlier, many studies compare hybrid models with their corresponding standard models or compare the same ML model using different algorithms to select their parameters, often applied for one-step-ahead streamflow forecasting. In this work, various ML models are combined with different optimization algorithms for parameter selection, allowing us to identify not only the best ML model and the optimal parameter optimization algorithm but also the best hybrid model among those developed. It’s also important to highlight its application to multi-step-ahead forecasting, an area that is still relatively unexplored in the literature. From another perspective, there are very few studies on the combination of ML and hydrology in Africa, particularly in Mozambique. This work aims to address this gap, which represents a novel contribution to the field.
This study compares the performance of machine learning models combined with the genetic algorithm (GA), differential evolution (DE), and particle swarm optimization (PSO) algorithms for modeling and forecasting the flow of the Zambezi River, which is a tributary to the Cahora-Bassa hydroelectric dam in Mozambique. The forecasts are conducted within a short-term time horizon, specifically considering forecast horizons of 1, 3, 5, and 7 days ahead (a multistep-ahead forecasting strategy).
The paper is organized as follows: “Materials and methods” covers the study area, data, machine learning models, bioinspired optimization algorithms applied, and the proposed methodology. “Result and discussion” presents the results of the computational experiments, along with comparative analysis and discussion. Finally, “Conclusion” provides the conclusion.
Materials and methods
This section outlines the materials and methods employed in this study. It encompasses the study area and data, the machine learning (ML) models, and bioinspired algorithms utilized, and concludes with an overview of the proposed methodology.
Study area and data
The research area is situated in a sub-basin of the Zambezi River, specifically, the Medium Zambezi terminal, located upstream of the Cahora Bassa dam in Tete province, Mozambique. Figure 1 depicts the automatic monitoring stations used in this study.
Figure 1.
Location of the study area. The EMAs points indicate the automatic monitoring stations where the data under analysis in this work are collected54.
The Cahora-Bassa dam plays a critical role in Mozambique as it supplies the majority of the country’s electricity and that of neighboring regions. Additionally, it supports downstream economic activities in the Zambezi River delta, such as farming, pastoralist work, fishing, and the construction of access roads. The dam also contributes to mitigating natural disasters like droughts and floods.
Daily flow forecasts are indispensable for the operation of hydroelectric plants, including tasks such as optimizing the dam’s storage capacity, operational procedures, energy generation management, maintenance of ecological flows in the reservoir, and obtaining continuous flow records in non-calibrated catchments where direct measurements are unavailable.
The historical data analyzed in this research was provided by the Department of Water Resources and Environment of Hidroeléctrica de Cahora-Bassa (HCB), the largest electricity producer in Mozambique and the entity managing the Cahora-Bassa dam.
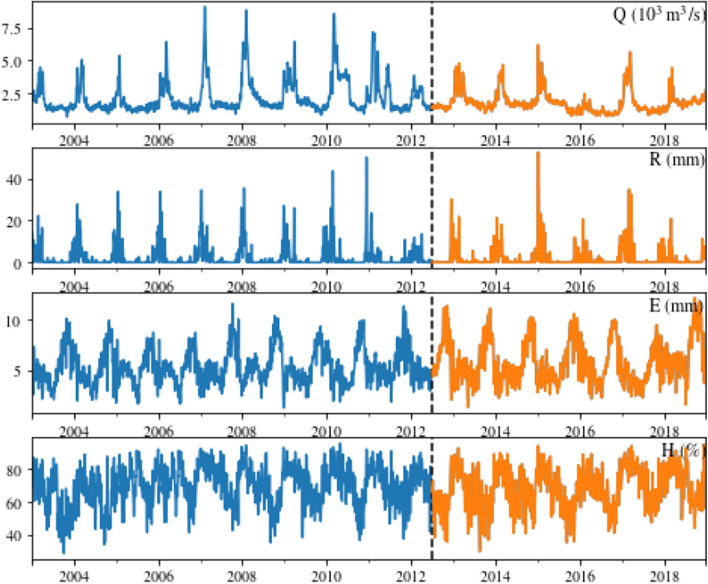
The dataset comprises daily time series for variables, including affluent flows (Q), precipitation (R), evaporation (E), and relative humidity (H). The dataset consists of 5844 observations, spanning from 2003 to 2018, divided into two subsets: the training and testing sets. It’s important to emphasize the seasonal characteristics of these variables. Figure 2 illustrates the training set in blue, ranging from 01/01/2003 to 06/30/2012, and the test set in orange, covering the period from 07/01/2012 to 12/31/2018.
Figure 2.
Daily data, total: 5844, between 2003 and 2018 (15 years). From 01/01/2003 to 06/30/2012 training (blue) and 07/01/2012 to 12/31/2018 test (orange)54.
It’s worth noting that the data analyzed in this study has been used in previous research conducted by the same authors26,54–57.
Machine learning models
This section provides a brief description of the machine learning (ML) models utilized in this study, which include extreme gradient boosting, elastic net, multivariate adaptive regression spline, extreme learning machine, and support vector regression.
Extreme gradient boosting (XGB)
XGB58–61 is an ensemble method that combines weak predictors to generate a strong predictor. XGB prediction for an i instance is
where .
Support vector regression (SVR)
SVR17,62–64 is a classic regression method that estimation function is:
where is a kernel function in a feature space, is the weight vector, b is a bias, and N is the number of samples.
Elastic net (EN)
EN65–68 is the generalized linear model expressed as:
| 1 |
where , and are respectively the norm and the norm of the parameter array, and is the the parameter’s rate .
Multivariate adaptive regression spline (MARS)
MARS69–71 is the method consist of sequential piecewise linear regression splines of the form:
| 2 |
where is a constant quantity, the m-th basis function, and is the unknown coefficient.
Extreme learning machine
ELM72–74 is an artificial neural network described by Eq. (3), i.e there are , and such that:
| 3 |
where is the i-th neuron in the hidden layer, is the connection weight of the ith neuron of the hidden layer and the neuron of the output layer, is the bias of the ith neuron of the hidden layer, and denotes an activation function.
Bioinspired optimization algorithms
Reservoir operation optimization is a complex nonlinear problem, involving a large number of decision variables and multiple constraints. In the field of water resources, various metaheuristic algorithms have been employed to address this issue. These methods often involve modifying existing algorithms or creating hybrid algorithms, ultimately contributing to the reduction of water deficits in reservoirs75. In this study, we employ and integrate three algorithms, which are described below. These algorithms play a crucial role in our machine learning (ML) models, aiding in the selection of optimal parameters.
Genetic algorithm (GA)
GA is a subclass of evolutionary algorithms used for the objective of optimization via natural genetics and selection76. The genetic operations are crossover, reproduction, and mutation77.
In the GA, a set of potential solutions to a problem are generated randomly. Each solution is evaluated using the adequacy function, which is intended to be optimized. New solutions is generated probabilistically from the best ones of the previous step, and some of these are inserted directly into the new population, while others are used as a basis to generate new individuals, using genetic operators76,78.
Diferential evolution (DE)
DE32,79,80 is a nature-inspired algorithm that adapts the individuals through mutation genetic operators, recombination, and selection81. DE consists of the following82 steps:
Initialization of parameters
- Population initialization.
4 Population evaluation: Compute and note each individual’s fitness scores.
- Mutation operation:
5 - Crossover operation, according to the equation:
6 - Selection operation, according to the equation:
7
Particle swarm optimization (PSO)
PSO83 is an algorithm based on the natural movements of biological swarms (flocks of birds) considering their position and speed41.
The PSO formula for the initial iteration is:
| 8 |
where and are, respectively, the particle’s position and speed, best position in the swarm and best personal value
Proposed methodology
A set of real data comprising four time series was used in the analysis: the river’s flow into the reservoir for electricity generation (Q), precipitation (R), evaporation (E), and humidity (H). The affluent flow serves as the output variable, while the rest are employed as input or predictor variables.
The task of forecasting several steps ahead in the inflow was initially approached by constructing a framework that includes input variables and their corresponding lags or delays, to accommodate the proposed machine learning models.
The determination of the number of lags/antecedents or delays for making predictions of the river’s affluent flow in the time horizon () was accomplished using partial autocorrelation functions (PACF), autocorrelation functions (ACF), and cross-correlation function (CCF). These methods serve as a straightforward means to suggest the number of antecedents, aiding in identifying the factors influencing the output variable.
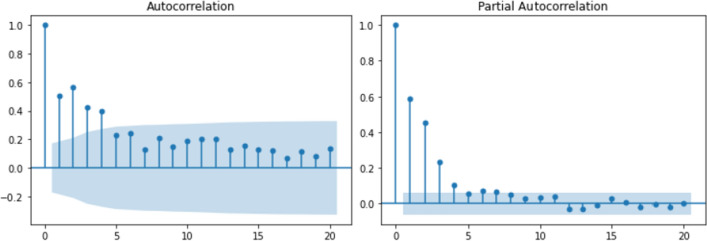
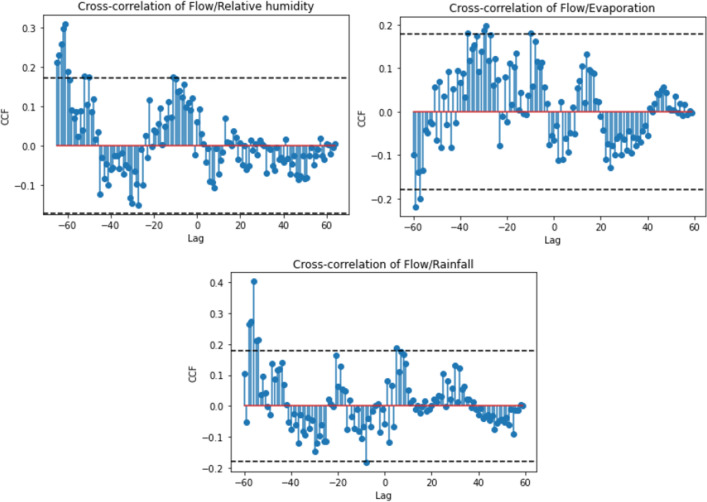
Autoregression analysis using ACF/PACF and CCF for the analyzed variables is depicted in Figs. 3 and 4, respectively. Figure 3 suggests that early lags may be predictive, while Fig. 4 indicates that none or all lags could potentially be used as a CCF selection criterion. Furthermore, in Fig. 4, a cyclical pattern (seasonality) is noticeable, identified by the decline of correlation in certain time intervals (days).
Figure 3.
Autocorrelation and partial autocorrelation functions. Lags within the shaded part are considered statistically non-significant54.
Figure 4.
Cross correlation functions between flow and precipitation, evaporation or relative humidity. The lags between the dashed lines are considered statistically non-significant54.
In this study, seven lags, corresponding to twenty-eight (28) input variables (4 original variables 7 lags), i.e., a matrix, were considered as input data for machine learning models using ACF/PACF as the selection criterion, since CCF was uninformative, given that the majority of lags fall within the dashed-line confidence interval, as shown in Fig. 4.
The non-significant autocorrelation observed between the response variable and the predictor variables in Fig. 4 may be attributed to the use of ACF/PACF or CCF, which are linear models. As a result, they may not detect hidden non-linear relationships or the frequent spatial variation in hydrological variables, as data from only one region were considered. Additionally, these models do not incorporate equations or physical relationships between flow and other variables. The presence of noise and hydrometeorological differences between training and test periods, known as non-stationarity, can also weaken this relationship84,85.
The machine learning models used in this study were elastic net (EN), extreme learning machine (ELM), extreme gradient boosting (XGB), support vector regression (SVR), and multivariate adaptive regression spline (MARS). The primary objective was to evaluate their predictive capabilities for flow across different time horizons.
These models had their parameters intelligently determined using bioinspired algorithms: differential evolution (DE), genetic algorithms (GA), and particle swarm optimization (PSO). The optimization problem’s objective function was the minimization of root mean square error (RMSE) calculated on the training set through a 5-fold walk-forward approach86. The experiments were conducted a total of 30 times, employing different random seeds. Table 2 illustrates the encoding of candidate solutions for each machine learning model to be used in each bioinspired algorithm.
Table 2.
Candidate solutions’ coding.
| Estimator | IP | Description | Settings/range |
|---|---|---|---|
| EN | Penalty term, | [] | |
| -ratio parameter, | [0,1] | ||
| ELM | No. neurons in the hidden layer, L | [1, 500] | |
| Regularization parameter C | [0.0001, 10000] | ||
| Activation function G | 1: Identity; 2: Sigmoid; 3: Hyperbolic Tangent; 4: Gaussian; 5: Swish; 6: ReLU; | ||
| SVR | Loss parameter, | [10, 100] | |
| Regularization parameter, C | [1, 10000] | ||
| Bandwidth parameter, | [0.001, 10] | ||
| MARS | Degree of piecewise polynomials, q | [0,3] | |
| Penalty factor, | [1, 9] | ||
| Maximum number of terms, M | [1, 500] | ||
| XGB | Learning rate, | [10, 1] | |
| No. weak estimators, | [10, 500] | ||
| Maximum depth, | [1, 20] | ||
| Regularization parameter, | [0, 100] |
The IP column denotes the internal parameter used in the bioinspired algorithms’ encoding.
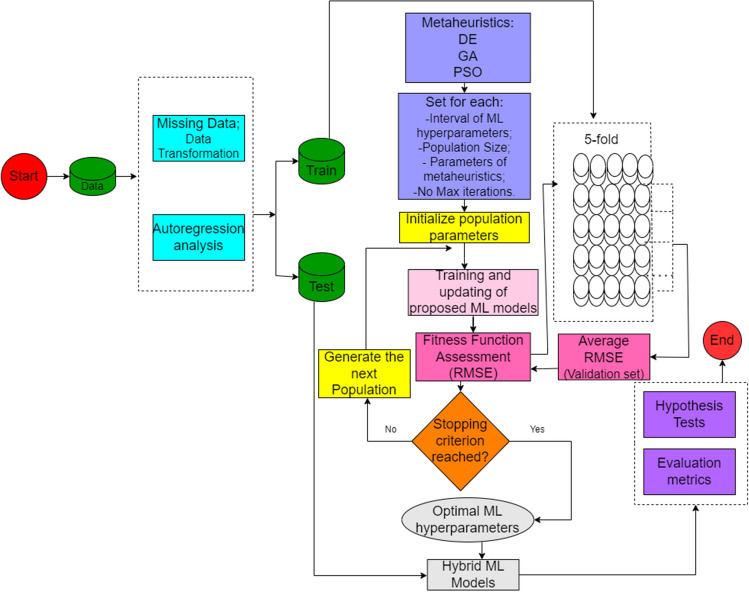
The bioinspired algorithms, in turn, had their parameters detailed according to Table 3 (representing the classic versions of optimization algorithms). Each algorithm employed a population size of 16, consisting of randomly distributed individuals, with uniform distribution applied within the search space. Each individual is represented as a vector, comprising the hyperparameters specific to the machine learning model under analysis, and the length of this vector is determined by the number of hyperparameters relevant to each particular machine learning model. Figure 5 illustrates the flow diagram summarizing all the steps involved in the development of this work.
Table 3.
Description of the specific parameters of the optimization algorithms.
Figure 5.
Flowchart summarizes the proposed methodology of the work.
To assess the performance of these models, eight different performance measures, which are commonly employed in hydrology to gauge the agreement between simulated and observed data89,90, were calculated to determine their robustness in terms of error and precision (refer to Table 4). Furthermore, statistical hypothesis tests, specifically ANOVA and Tukey tests91, were employed to evaluate the efficiency of the models. The distribution of performance measures, each based on 30 independent runs, was compared using the one-way ANOVA test. Subsequently, Tukey’s test was used for multiple comparisons of the performance means of the estimators (models) to identify the superior estimator among those analyzed in terms of performance, as well as for multiple comparisons of the performance means of the metaheuristics.
Table 4.
Performance metrics used in the test set.
| Metric acronym | Expression |
|---|---|
| WI | |
| RMSE | |
| MAE | |
| MAPE | |
| NSE | |
| KGE | |
| R |
WI is the Willmott indices92. RMSE, MAPE, and MAE are the root mean squared error, mean absolute percentage error, and mean absolute errors, respectively. KGE is Kling–Gupta efficiency93. NSE (Nash–Sutcliffe efficiency)94. and is the real and simulated values, respectively. is the mean of real streamflows. r are the Pearson’s coefficient and is the proportion between simulated and real values standard deviations, and is the proportion between the averages of the simulated and observed values.
Result and discussion
The flow predictions for the Cahora-Bassa reservoir were conducted with forecast horizons of 1, 3, 5, 7 days ahead, utilizing the following machine learning models: elastic net (EN), extreme learning machine (ELM), support vector regression (SVR), multivariate adaptive regression spline (MARS), and extreme gradient boosting (XGB). The parameters of these models were estimated through the use of differential evolution (DE), genetic algorithms (GA), and particle swarm optimization (PSO). This led to the development of a total of sixty (60) models, derived from the combinations of the five ML models, three metaheuristics, and four forecast horizons.
A successful execution is defined as one where the solution is both known and identified using a predetermined stopping criterion based on a maximum allowable number of evaluations. The best results among these models are denoted by being highlighted in bold.
Performance analysis of models optimized by DE
Table 5 presents a quantitative study of the models’ performance, displaying averages and corresponding standard deviations of the performance measures for models optimized by DE across different time horizons.
Table 5.
Descriptive statistics (means and standard deviations) of the performance measures of models optimized with DE in the test set.
| DA | Estimator | R | WI | RMSE | MAE | MAPE | NSE | KGE |
|---|---|---|---|---|---|---|---|---|
| 1 | ELM | 0.961 (0.006) | 0.979 (0.003) | 0.182 (0.013) | 0.118 (0.003) | 6.91 (0.210) | 0.915 (0.013) | 0.946 (0.008) |
| EN | 0.966 (0.00) | 0.982 (0.00) | 0.168 (0.00) | 0.112 (0.00) | 6.51 (0.006) | 0.929 (0.00) | 0.956 (0.00) | |
| MARS | 0.975 (0.00) | 0.987 (0.00) | 0.144 (0.00) | 0.099 (0.00) | 5.84 (0.037) | 0.948 (0.00) | 0.961 (0.002) | |
| SVR | 0.981 (0.00) | 0.990 (0.00) | 0.128 (0.002) | 0.096 (0.003) | 5.80 (0.182) | 0.958 (0.002) | 0.963 (0.008) | |
| XGB | 0.979 (0.00) | 0.989 (0.00) | 0.130 (0.003) | 0.094 (0.003) | 5.61 (0.167) | 0.957 (0.002) | 0.976 (0.001) | |
| 3 | ELM | 0.961 (0.003) | 0.979 (0.002) | 0.185 (0.007) | 0.121 (0.003) | 7.01 (0.185) | 0.913 (0.007) | 0.936 (0.005) |
| EN | 0.965 (0.00) | 0.981 (0.00) | 0.175 (0.00) | 0.115 (0.00) | 6.63 (0.006) | 0.923 (0.00) | 0.945 (0.00) | |
| MARS | 0.971 (0.003) | 0.985 (0.001) | 0.155 (0.008) | 0.096 (0.00) | 5.66 (0.034) | 0.939 (0.006) | 0.956 (0.003) | |
| SVR | 0.977 (0.00) | 0.988 (0.00) | 0.141 (0.004) | 0.100 (0.003) | 5.98 (0.154) | 0.949 (0.003) | 0.954 (0.008) | |
| XGB | 0.981 (0.00) | 0.990 (0.00) | 0.125 (0.002) | 0.096 (0.002) | 5.77 (0.082) | 0.960 (0.001) | 0.974 (0.002) | |
| 5 | ELM | 0.943 (0.003) | 0.969 (0.002) | 0.227 (0.007) | 0.150 (0.003) | 8.62 (0.187) | 0.870 (0.008) | 0.910 (0.005) |
| EN | 0.945 (0.00) | 0.970 (0.00) | 0.221 (0.00) | 0.147 (0.00) | 8.36 (0.005) | 0.877 (0.00) | 0.917 (0.00) | |
| MARS | 0.955 (0.002) | 0.976 (0.001) | 0.196 (0.005) | 0.135 (0.002) | 7.86 (0.122) | 0.903 (0.005) | 0.934 (0.005) | |
| SVR | 0.957 (0.001) | 0.976 (0.00) | 0.203 (0.004) | 0.138 (0.002) | 8.20 (0.161) | 0.895 (0.004) | 0.901 (0.006) | |
| XGB | 0.960 (0.00) | 0.979 (0.00) | 0.183 (0.002) | 0.137 (0.002) | 8.14 (0.107) | 0.916 (0.002) | 0.947 (0.003) | |
| 7 | ELM | 0.896 (0.006) | 0.943 (0.003) | 0.305 (0.010) | 0.196 (0.004) | 11.30 (0.288) | 0.764 (0.016) | 0.867 (0.009) |
| EN | 0.902 (0.00) | 0.947 (0.00) | 0.291 (0.00) | 0.188 (0.00) | 10.72 (0.006) | 0.785 (0.00) | 0.882 (0.00) | |
| MARS | 0.902 (0.023) | 0.946 (0.014) | 0.297 (0.035) | 0.190 (0.003) | 10.99 (0.132) | 0.773 (0.068) | 0.867 (0.029) | |
| SVR | 0.918 (0.005) | 0.953 (0.003) | 0.284 (0.010) | 0.184 (0.003) | 10.65 (0.196) | 0.795 (0.015) | 0.856 (0.009) | |
| XGB | 0.923 (0.004) | 0.958 (0.003) | 0.261 (0.009) | 0.187 (0.004) | 10.97 (0.196) | 0.828 (0.011) | 0.898 (0.008) |
The results, in general, indicate that the models achieved good performance. However, the SVR model outperformed the others in all performance measures, except for MAE and KGE, where the XGB model exhibited better results for the forecast horizon . Conversely, for the remaining horizons (, , and ), XGB demonstrated superior results in almost all measures, except for MAE for and , where the MARS model presented the lowest mean absolute error. It is noteworthy that while XGB did not always outperform the others, it consistently presented results very close to the best, ensuring its superiority and competitiveness in relation to the other models.
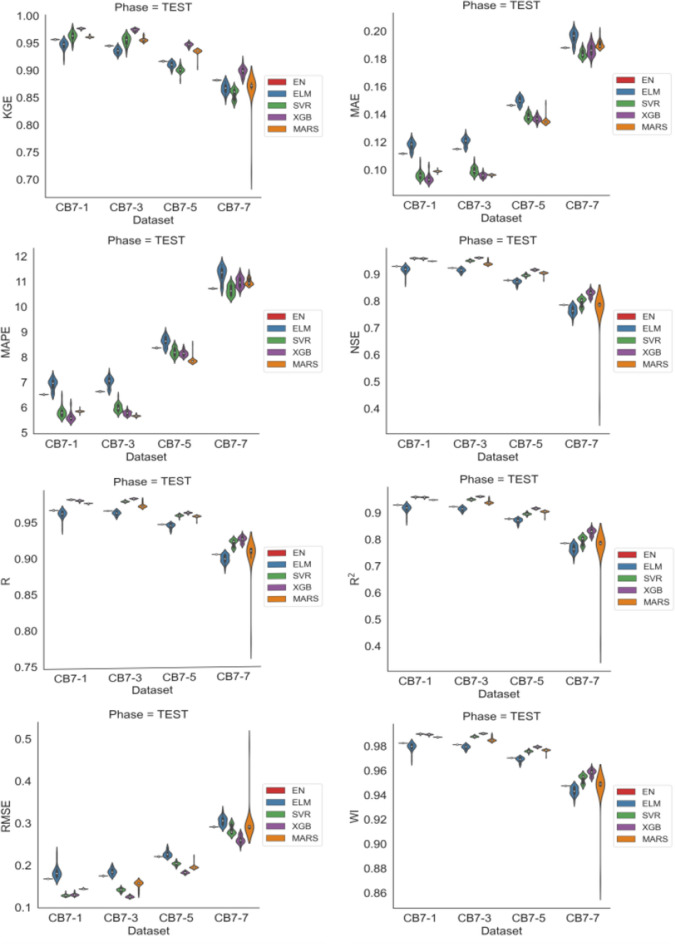
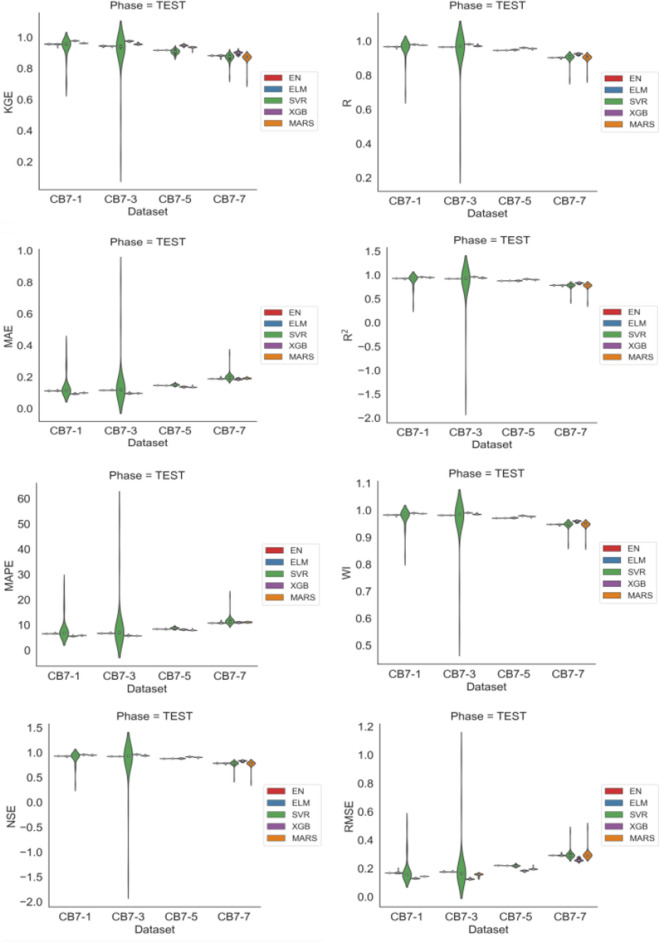
Figure 6 displays violin plots representing the distributions of performance measures across different time horizons. It’s evident that these distributions exhibit positive or negative asymmetries with some influence of outliers, and MARS was the model most affected by these outliers. Furthermore, in this figure, a pattern of declining performance of the models can be observed as the time horizon increases.
Figure 6.
Violin to DE charts showing the distributions of the 30 runs of each metric for each model across the different forecast horizons.
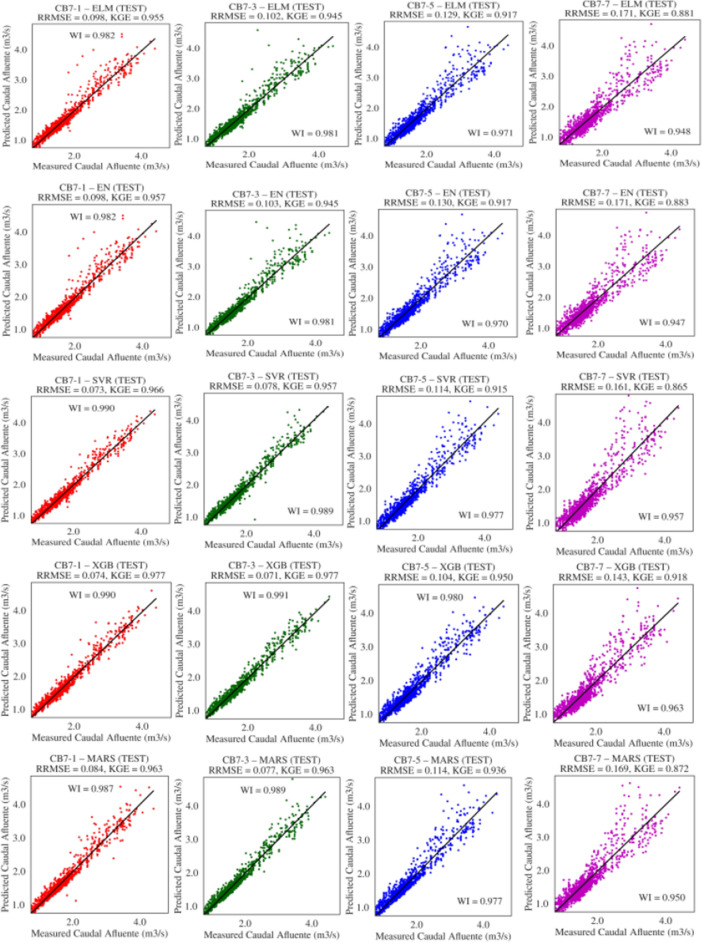
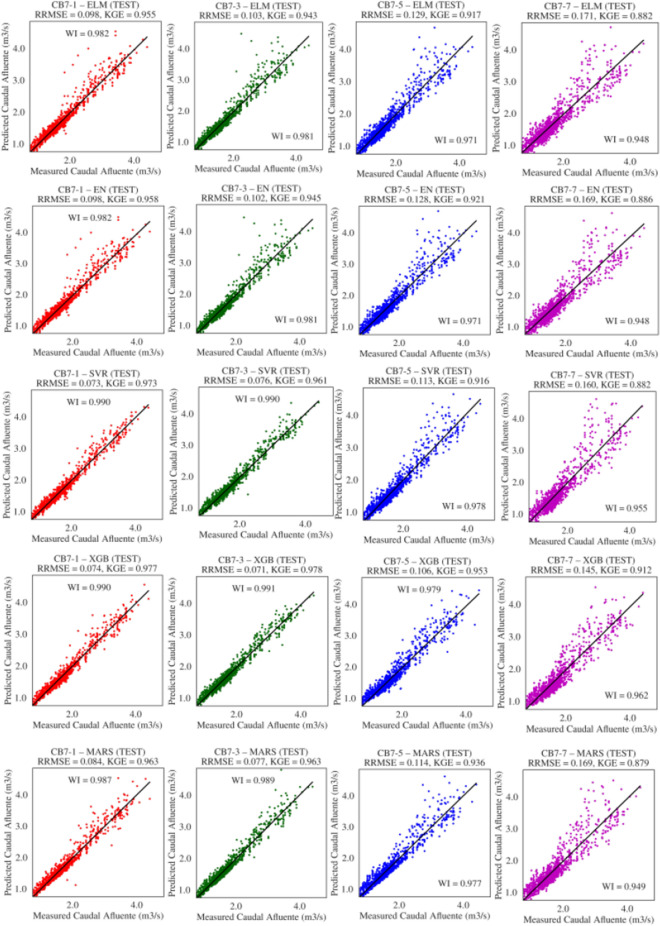
Figure 7 illustrates the graphs of the best solutions for each model according to RMSE; it is generally observed that the models achieved RMSE values very close to zero, ranging between 0.071 and 0.171. Specifically, XGB had the lowest RMSE of 0.071 m/s for , followed by SVR with 0.073 m/s for , MARS with 0.077 for forecast , and finally, ELM and EN both with 0.098 m/s for forecast . Other measures of agreement between observed and predicted data, such as KGE and WI, can also be observed. The SVR model obtained values of 0.966 and 0.990 for KGE and WI, XGB achieved 0.977 and 0.991, MARS scored 0.963 and 0.989, EN obtained 0.957 and 0.982, and ELM achieved 0.955 and 0.982, respectively. Furthermore, a good approximation between observed and predicted data can be seen in these graphs, with the closest approximation achieved by the XGB model for the forecast horizon .
Figure 7.
Best solution according to RMSE for flows of 1, 3, 5, 7 days ahead to DE showing levels of agreement between observed and predicted data.
Performance analysis of models optimized by GA
Table 6 presents the descriptive statistics, average performance, and standard deviation measures produced by the forecast models whose parameters were optimized by GA.
Table 6.
Descriptive statistics (means and standard deviations) of the performance measures of models optimized with GA in the test set.
| DA | Estimator | R | WI | RMSE | MAE | MAPE | NSE | KGE |
|---|---|---|---|---|---|---|---|---|
| 1 | ELM | 0.960 (0.005) | 0.979 (0.003) | 0.184 (0.012) | 0.118 (0.002) | 6.91 (0.140) | 0.914 (0.012) | 0.944 (0.008) |
| EN | 0.966 (0.00) | 0.982 (0.00) | 0.168 (0.00) | 0.112 (0.00) | 6.51 (0.008) | 0.929 (0.00) | 0.957 (0.00) | |
| MARS | 0.975 (0.00) | 0.987 (0.00) | 0.144 (0.00) | 0.099 (0.00) | 5.84 (0.038) | 0.948 (0.00) | 0.961 (0.002) | |
| SVR | 0.978 (0.003) | 0.987 (0.002) | 0.143 (0.012) | 0.113 (0.012) | 6.88 (0.790) | 0.947 (0.009) | 0.952 (0.010) | |
| XGB | 0.979 (0.00) | 0.989 (0.00) | 0.131 (0.003) | 0.094 (0.003) | 5.64 (0.160) | 0.956 (0.002) | 0.976 (0.002) | |
| 3 | ELM | 0.961 (0.003) | 0.979 (0.002) | 0.186 (0.007) | 0.121 (0.002) | 7.06 (0.138) | 0.912 (0.007) | 0.935 (0.005) |
| EN | 0.965 (0.00) | 0.981 (0.00) | 0.175 (0.00) | 0.115 (0.00) | 6.63 (0.011) | 0.923 (0.00) | 0.945 (0.00) | |
| MARS | 0.971 (0.003) | 0.985 (0.002) | 0.154 (0.009) | 0.096 (0.00) | 5.66 (0.039) | 0.939 (0.007) | 0.956 (0.004) | |
| SVR | 0.977 (0.002) | 0.987 (0.002) | 0.147 (0.011) | 0.114 (0.011) | 6.89 (0.711) | 0.945 (0.008) | 0.947 (0.012) | |
| XGB | 0.981 (0.00) | 0.990 (0.00) | 0.126 (0.003) | 0.096 (0.002) | 5.78 (0.085) | 0.960 (0.002) | 0.974 (0.002) | |
| 5 | ELM | 0.941 (0.005) | 0.968 (0.003) | 0.231 (0.010) | 0.151 (0.002) | 8.72 (0.161) | 0.865 (0.013) | 0.907 (0.008) |
| EN | 0.945 (0.00) | 0.970 (0.00) | 0.220 (0.00) | 0.146 (0.00) | 8.33 (0.026) | 0.877 (0.00) | 0.918 (0.001) | |
| MARS | 0.955 (0.002) | 0.976 (0.001) | 0.195 (0.005) | 0.135 (0.002) | 7.85 (0.122) | 0.903 (0.005) | 0.934 (0.005) | |
| SVR | 0.955 (0.002) | 0.974 (0.002) | 0.210 (0.008) | 0.150 (0.009) | 8.85 (0.532) | 0.888 (0.009) | 0.899 (0.010) | |
| XGB | 0.960 (0.00) | 0.979 (0.00) | 0.184 (0.002) | 0.138 (0.002) | 8.22 (0.124) | 0.914 (0.002) | 0.945 (0.005) | |
| 7 | ELM | 0.896 (0.004) | 0.943 (0.003) | 0.306 (0.007) | 0.196 (0.003) | 11.32 (0.236) | 0.763 (0.011) | 0.867 (0.007) |
| EN | 0.903 (0.00) | 0.948 (0.00) | 0.290 (0.00) | 0.188 (0.00) | 10.69 (0.032) | 0.786 (0.001) | 0.883 (0.001) | |
| MARS | 0.901 (0.022) | 0.946 (0.014) | 0.299 (0.034) | 0.191 (0.003) | 10.99 (0.161) | 0.771 (0.066) | 0.866 (0.028) | |
| SVR | 0.915 (0.004) | 0.951 (0.003) | 0.289 (0.009) | 0.185 (0.003) | 10.71 (0.226) | 0.787 (0.013) | 0.853 (0.009) | |
| XGB | 0.922 (0.004) | 0.958 (0.003) | 0.262 (0.010) | 0.187 (0.004) | 10.98 (0.193) | 0.826 (0.013) | 0.897 (0.009) |
The results indicate competitive performance among the models across all horizons: , , , and . The extreme gradient boosting (XGB) hybrid model outperforms other models for all measures and horizons, except for and , where MARS resulted in the lowest MAE, and for , where the SVR and EN models obtained the lowest MAE and MAPE, respectively. It is also worth noting that the MARS and SVR models achieved good results compared to ELM and EN.
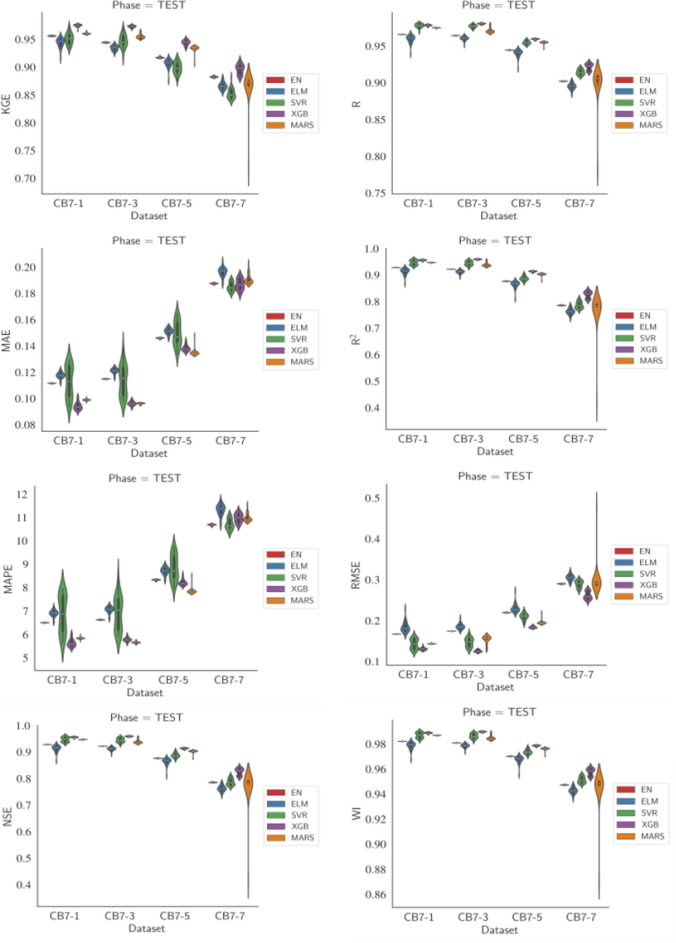
Figure 8 displays the distributions of the performance measures for each model across different time horizons. This figure reveals a decline in the models’ performance as the forecast horizon increases. Qualitatively, the XGB model consistently exhibits superior performance compared to the other models. Additionally, greater asymmetries are observed in the distributions of performance measures, with the presence of outliers. SVR and MARS had distributions more susceptible to extreme observations, leading to higher variability in their results.
Figure 8.
Violin plots for GA showing the distributions over 30 runs of the analyzed models on performance metrics across forecast horizons.
Figure 9 illustrates the graphs of the best solutions for each model according to the RMSE metric. Overall, the models achieved low RMSE values. However, XGB achieved the lowest RMSE of 0.071 m/s for , followed by SVR with 0.073 m/s for , MARS with 0.077 for forecast , and both ELM and EN with 0.098 m/s for forecast . Other goodness-of-fit measures can also be observed, such as KGE and WI, where the XGB model achieved values of 0.978 and 0.991, MARS scored 0.963 and 0.989, SVR obtained 0.973 and 0.990, EN achieved 0.958 and 0.982, and ELM attained 0.955 and 0.982, respectively.
Figure 9.
Best solution for each model according to RMSE for flows of 1, 3, 5, 7 days ahead with GA showing levels of agreement between observed and predicted data.
Furthermore, when comparing the observed data with data predicted by the models, it can be observed that they closely align with the ideal line, indicating a good approximation between the observed and predicted data. Specifically, the XGB model with a forecast horizon of exhibited the best approximation.
Performance analysis of models optimized by PSO
Table 7 presents the descriptive statistics, average performance, and standard deviation measures produced by the forecasting models with their parameters optimized by PSO.
Table 7.
Descriptive statistics (means and standard deviations) of the performance measures of models optimized with PSO in the test set.
| DA | Estimator | R | WI | RMSE | MAE | MAPE | NSE | KGE |
|---|---|---|---|---|---|---|---|---|
| 1 | ELM | 0.966 (0.002) | 0.982 (0.001) | 0.169 (0.006) | 0.112 (0.002) | 6.56 (0.116) | 0.928 (0.005) | 0.954 (0.004) |
| EN | 0.966 (0.00) | 0.982 (0.00) | 0.168 (0.00) | 0.112 (0.00) | 6.52 (0.013) | 0.929 (0.00) | 0.956 (0.00) | |
| MARS | 0.975 (0.00) | 0.987 (0.00) | 0.144 (0.00) | 0.099 (0.00) | 5.83 (0.029) | 0.948 (0.00) | 0.961 (0.002) | |
| SVR | 0.955 (0.055) | 0.975 (0.032) | 0.184 (0.081) | 0.139 (0.068) | 8.43 (4.52) | 0.897 (0.122) | 0.934 (0.066) | |
| XGB | 0.979 (0.00) | 0.989 (0.00) | 0.129 (0.002) | 0.093 (0.002) | 5.57 (0.127) | 0.958 (0.001) | 0.976 (0.001) | |
| 3 | ELM | 0.965 (0.00) | 0.981 (0.00) | 0.175 (0.002) | 0.116 (0.002) | 6.70 (0.112) | 0.922 (0.002) | 0.942 (0.002) |
| EN | 0.965 (0.00) | 0.981 (0.00) | 0.175 (0.002) | 0.115 (0.00) | 6.65 (0.026) | 0.922 (0.002) | 0.943 (0.002) | |
| MARS | 0.971 (0.003) | 0.985 (0.002) | 0.155 (0.009) | 0.096 (0.00) | 5.66 (0.035) | 0.939 (0.007) | 0.956 (0.004) | |
| SVR | 0.932 (0.142) | 0.960 (0.090) | 0.208 (0.169) | 0.156 (0.143) | 9.43 (9.50) | 0.818 (0.460) | 0.901 (0.148) | |
| XGB | 0.981 (0.00) | 0.990 (0.00) | 0.125 (0.003) | 0.096 (0.002) | 5.75 (0.125) | 0.960 (0.002) | 0.974 (0.003) | |
| 5 | ELM | 0.946 (0.00) | 0.971 (0.00) | 0.219 (0.00) | 0.146 (0.00) | 8.32 (0.007) | 0.878 (0.00) | 0.917 (0.00) |
| EN | 0.945 (0.00) | 0.970 (0.00) | 0.221 (0.00) | 0.147 (0.00) | 8.36 (0.002) | 0.876 (0.00) | 0.916 (0.00) | |
| MARS | 0.955 (0.002) | 0.976 (0.001) | 0.195 (0.005) | 0.135 (0.002) | 7.85 (0.123) | 0.903 (0.005) | 0.934 (0.005) | |
| SVR | 0.948 (0.002) | 0.971 (0.001) | 0.218 (0.006) | 0.150 (0.005) | 8.73 (0.316) | 0.879 (0.006) | 0.906 (0.014) | |
| XGB | 0.960 (0.001) | 0.979 (0.00) | 0.182 (0.003) | 0.137 (0.003) | 8.15 (0.126) | 0.916 (0.003) | 0.947 (0.005) | |
| 7 | ELM | 0.902 (0.003) | 0.947 (0.002) | 0.292 (0.005) | 0.189 (0.003) | 10.81 (0.255) | 0.783 (0.008) | 0.880 (0.006) |
| EN | 0.902 (0.00) | 0.947 (0.00) | 0.291 (0.00) | 0.188 (0.00) | 10.73 (0.011) | 0.785 (0.00) | 0.881 (0.00) | |
| MARS | 0.901 (0.023) | 0.945 (0.014) | 0.299 (0.035) | 0.192 (0.003) | 11.05 (0.145) | 0.770 (0.068) | 0.867 (0.029) | |
| SVR | 0.902 (0.025) | 0.946 (0.014) | 0.297 (0.031) | 0.202 (0.027) | 11.74 (1.85) | 0.773 (0.059) | 0.867 (0.028) | |
| XGB | 0.923 (0.004) | 0.958 (0.003) | 0.261 (0.009) | 0.186 (0.004) | 10.95 (0.173) | 0.828 (0.012) | 0.898 (0.009) |
The results demonstrated good performance of the models in all time horizons under analysis. The extreme gradient boosting (XGB) hybrid model outperformed the others in all performance measures for the horizon . For the remaining , , and , the XGB model also outperformed the other models in almost all measures, except for and , where MARS presented lower MAPE and MAE results, and for , where EN had the lowest MAPE.
Figure 10 displays the distributions of each performance measure for each model across different time horizons. The figure shows a relative balance in the performance measures of the models as the forecast horizon increases, with a downward trend. Asymmetries can also be observed in the distributions of performance measures, along with the presence of outliers. SVR exhibited the most extreme observations in its distributions, followed by MARS.
Figure 10.
Violin plots for PSO showing the distributions over 30 runs of the analyzed models on performance metrics across forecast horizons.
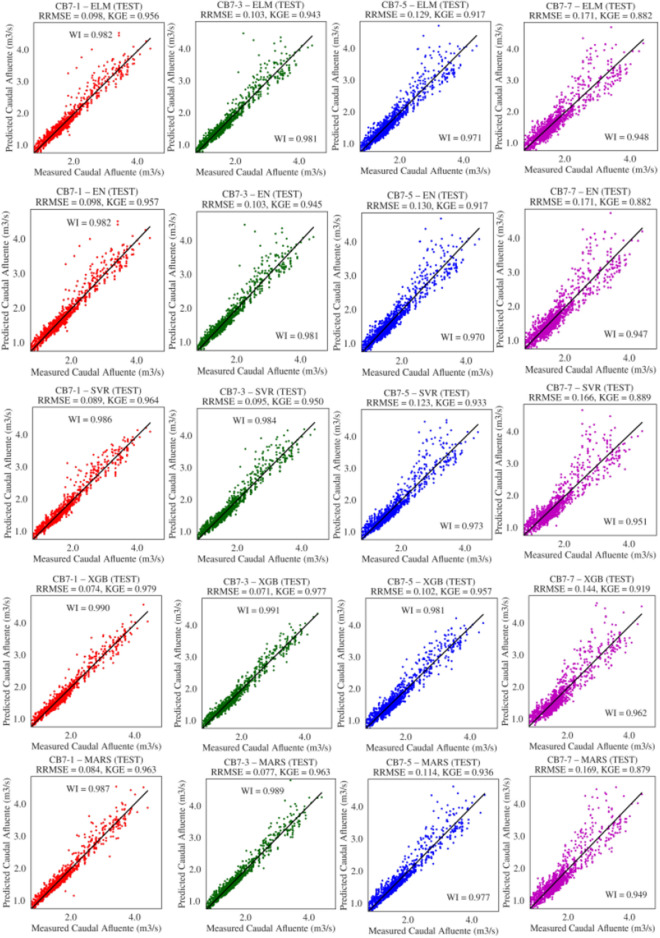
Figure 11 presents the graphs of the best solutions for each model according to the RMSE metric. It is evident that the models obtained small RMSE values ranging from 0.071 to 0.171, and the XGB model achieved the smallest RMSE of 0.071 m/s. Notably, the other models also achieved relatively low RMSE values: MARS with 0.077 m/s for both , SVR with 0.089 for forecast , and ELM and EN both with 0.098 m/s for forecast . Other goodness-of-fit measures can also be observed, such as KGE and WI, with the XGB model obtaining values of 0.977 and 0.991, MARS scoring 0.963 and 0.989, SVR achieving 0.964 and 0.986, EN reaching 0.957 and 0.982, and ELM attaining 0.956 and 0.982, respectively. Therefore, it can be observed that the horizons and have better fit qualities than and .
Figure 11.
Best solution for each model according to RMSE for flows 1, 3, 5, 7 days ahead with PSO, showing levels of agreement between observed and predicted data.
Furthermore, it can be noted in this figure that there is a good approximation between observed values and those predicted by the models. When comparing the observed data and the data predicted by the models to the ideal line, it is evident that they align closely along the same line. The XGB model with forecast horizon demonstrated the highest level of adherence.
Comparative analysis of the results and discussion
An analysis of the results obtained with different metaheuristics used in this work allowed us to quantitatively verify that, in general, all the models performed well across all the statistics used to evaluate their performance, even in relatively distant forecasting horizons. Therefore, the integration of evolutionary and/or bioinspired algorithms in the optimization of machine learning model parameters led to these positive results in multistep forecasting of daily flow.
Evolutionary/bioinspired algorithms have demonstrated their ability to find good approximations to complex problems and have achieved favorable results in determining high-quality solutions for these problems95, thus enabling the attainment of state-of-the-art results59.
Table 8 presents the results of the one-way ANOVA statistical test. The null hypothesis of the ANOVA test posits that the average on every measurement criterion is the same for all metaheuristics or estimators. As is evident, the null hypothesis is rejected for all metrics, as the p-values for each of them are less than the 0.05 significance level. This implies that all metrics are useful criteria for assessing different metaheuristics or prediction models.
Table 8.
p values ANOVA test for each performance measure.
| Metric | R | RMSE | MAPE | MAE | WI | NSE | KGE | |
|---|---|---|---|---|---|---|---|---|
| p value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
Table 9, on the other hand, presents the results of the Tukey test, which involves multiple comparisons of pairs of means from the metaheuristics. In the first column of this table, you will find the pairs of metaheuristics, followed by the mean difference in the second column, the corresponding p value in the third column, and the minimum and maximum limits of the confidence intervals associated with the differences in means for each metaheuristic pair, in the fourth and fifth columns, respectively. Lastly, the decision taken based on these comparisons is provided. The null hypothesis posits that the means of each pair of metaheuristics are equal. As observed, the null hypothesis is not rejected since all p values are greater than the significance level of 0.05. However, it’s worth noting that, despite the differences not being statistically significant, PSO exhibits relatively higher values compared to DE and GA, respectively, based on the magnitude of the p values.
Table 9.
Test of multiple comparisons of metaheuristic means-Tukey HSD, significance = 0.05.
| Pair | Meandiff | P-adj | Lower | Upper | Reject |
|---|---|---|---|---|---|
| DE-PSO | 0.004 | 0.268 | − 0.002 | 0.011 | False |
| DE-SGA | − 0.001 | 0.900 | − 0.007 | 0.005 | False |
| PSO-SGA | − 0.005 | 0.130 | − 0.012 | 0.001 | False |
PSO is a modern algorithm that has been successfully applied in engineering, demonstrating high performance compared to other metaheuristics83,96. It has been proven to be superior in several studies focusing on flow forecasting, with notable emphasis on the following references26,30,35,43,44,97, among others.
It’s important to highlight that DE and GA exhibited strongly non-significant differences. This observation aligns with the findings of Nguyen et al.98, who compared the performances of the extreme gradient boosting model relative to two evolutionary algorithms: genetic algorithms and differential evolution, i.e., GA-XGB and DE-XGB. Their study revealed that these models also displayed similar results.
The comparison between the machine learning models analyzed in this work is presented in Table 10, showing the results of the Tukey test () for multiple comparisons of means between pairs of models. The null hypothesis assumes that the means of each pair of models are equal. The results of this test reveal the rejection of the null hypothesis, as evident from the p values of some pairs being lower than the significance level of 0.05. This indicates that the averages of certain models differ from the averages of the other models. Specifically, the extreme gradient boosting (XGB) model outperformed the other models across all metaheuristics and forecast horizons, while the elastic net model exhibited lower results.
Table 10.
Test of multiple comparisons of means of the models-Tukey HSD, significance = 0.05.
| Pair | Meandiff | p-adj | Lower | Upper | Reject |
|---|---|---|---|---|---|
| ELM-EN | 0.004 | 0.753 | − 0.005 | 0.012 | False |
| ELM-MARS | 0.013 | 0.001 | 0.004 | 0.021 | True |
| ELM-SVR | 0.008 | 0.068 | − 0.000 | 0.017 | False |
| ELM-XGB | 0.030 | 0.001 | 0.021 | 0.038 | True |
| EN-MARS | 0.009 | 0.046 | 0.000 | 0.018 | True |
| EN-SVR | 0.005 | 0.572 | − 0.004 | 0.013 | False |
| EN-XGB | 0.026 | 0.001 | 0.017 | 0.035 | True |
| MARS-SVR | − 0.004 | 0.670 | − 0.013 | 0.005 | False |
| MARS-XGB | 0.017 | 0.001 | 0.008 | 0.026 | True |
| SVR-XGB | 0.021 | 0.001 | 0.013 | 0.030 | True |
Table 11 illustrates all the hybrid models generated by the combination of metaheuristics and analyzed models. A total of fifteen hybrid models are obtained and compared to determine the superior model.
Table 11.
Comparisons of hybrid models generated by combinations of models and metaheuristics under analysis.
| ELM | (DE-ELM) | (PSO-ELM) | (SGA-ELM) |
| EN | (DE-EN) | (PSO-EN) | (SGA-EN) |
| MARS | (DE-MARS) | (PSO-MARS) | (SGA-MARS) |
| SVR | (DE-SVR) | (PSO-SVR) | (SGA-SVR) |
| XGB | (DE-XGB) | (PSO-XGB) | (SGA-XGB) |
| DE | PSO | SGA |
By combining the results analyzed separately in Tables 9 and 10, which present the Tukey tests for comparisons between metaheuristics and between models, respectively, it is evident that the extreme gradient boosting model assisted by particle swarm optimization (PSO-XGB) stands out as the superior model among all the developed models in terms of performance.
The XGB model has already demonstrated its superiority in comparison to other models when tackling machine learning challenges on various platforms such as KDD Cup and Kaggle. It has also been employed in cutting-edge applications in the industry59 and has been utilized for classification and regression tasks, yielding validated results in various scenarios, including customer behavior prediction, sales forecasting, hazard prediction, ad click prediction, malware rating, and web text prediction61.
In the context of hydrology, this model has proven to be superior to random forest (RF)98,99, support vector machine (SVM)100,101, classification and regression trees (CART)98, artificial neural networks102, and recurrent neural networks103 in both simple and multistep flow prediction problems. Its exceptional performance has led to its application as an alternative for flood forecasting104.
Models based on decision trees (or ensembles) often outperform other models, including neural networks, in regression problems.
It is interesting to note that SVR and MARS achieved competitive average results considering the evaluated metrics. However, the presence of outliers for both models had a negative impact on their performance. Despite SVR and MARS having modeling features that did not match the performance of XGB, the evolutionary search played a crucial role in finding the appropriate internal parameters that led to effective flow modeling.
The models also exhibited good qualitative adherence or approximation between the observed and estimated data, indicating that the models were capable of reproducing the characteristics of the observed data series, such as level shifts during critical periods of lower and higher flows, trends, seasonality, and other hidden characteristics with excellent quality. Therefore, these models can provide valuable support for decision-making in reservoir operations planning.
However, this performance deteriorates as the forecast horizon increases, meaning that results from shorter horizons are superior to those from relatively more distant ones. The forecast horizon introduces greater complexity to the input–output relationship involving environmental variables and flow. Additionally, longer forecast horizons amplify the uncertainty in predicting the flow’s future value. In this scenario, making accurate predictions with machine learning models becomes increasingly challenging due to the rising nonlinearity and uncertainty reflected in performance metrics.
Another observed factor that adversely affects the models’ performance is the presence of outliers, which characterize the chaotic behavior and high stochasticity of the flow105. As a result, there is variability in the modeled time series data, with the variation being particularly pronounced during peak flows. Model estimation of extreme events or extreme flows is challenging. However, the significance of accurately identifying extreme flows in decision-making related to dam operations is emphasized, as incorrect forecasts of these events can lead to severe consequences in water resource management.
Many models developed in the literature primarily focus on one-step or simple forecasting. Nevertheless, the results demonstrate that for one-step-ahead forecasts, it is challenging to unequivocally favor one model over the others, as the models have achieved satisfactory results. In the case of the multi-step-ahead forecasting task, the influence of the stochastic components of time series becomes more prominent with increasing forecasting time, making it difficult to identify the number of significant lags of the variable(s) that impact the prediction process106.
Conclusion
In the context of sustainable and optimized water resource management and planning, the accurate prediction of flows is essential. Precise flow prediction remains a scientific challenge and has garnered significant attention due to the non-linear, non-stationary, and stochastic nature of these series.
The future of hydrological research is likely to involve maximizing information and extracting complex observations and data collected across all environmental systems to enhance the predictability of complex environmental variables. Often, predicting these variables requires extensive datasets and substantial computational resources.
This study aims to overcome these challenges by developing and evaluating five machine learning models: elastic net (EN), extreme learning machine (ELM), support vector regression (SVR), multivariate adaptive regression spline (MARS), and extreme gradient boosting (XGB). Additionally, three nature-inspired evolutionary algorithms—genetic algorithms (GA), differential evolution (DE), and particle swarm optimization (PSO)—are employed to select the internal parameters of these models. The performance of the five models is compared based on predictions at several steps (multi-steps)—1, 3, 5, and 7 days ahead of the inflow to the Cahora-Bassa dam in the Zambezi river basin, Mozambique. The data for this study were provided by the Department of Water Resources and Environment of Cahora-Bassa Hydroelectric (HCB) and cover the period from 2003 to 2018. A 5-fold walk-forward method is utilized for data partitioning into testing and training datasets.
Experiments were conducted to evaluate the forecasting capabilities of these models by applying performance measures and statistical hypothesis testing (ANOVA and Tukey). The obtained results indicate the following:
The nature-inspired evolutionary algorithms applied to assist in the model parameter selection of machine learning models can enhance their prediction capabilities.
PSO outperforms DE and GA as the superior algorithm for determining the optimal hyperparameters of ML models for forecasting, based on values obtained in each step of the considered time horizon.
The XGB model outperforms the others (SVR, MARS, ELM, and EN) in all evolutionary search algorithms for different forward steps, according to the performance measures and the results of the statistical tests, with the XGB model integrated with PSO being the superior model. Furthermore, SVR and MARS achieve competitive results with XGB.
There is good adherence or approximation of the data predicted by the models with the observed ones, even in distant horizons, indicating that the models can reproduce the characteristics of the observed data series with excellent quality. However, extreme values are predicted with some uncertainty.
Performance deteriorates as the forecast horizon increases, meaning that shorter horizons perform better than relatively more distant ones.
The proposed XGB hybrid model can be considered a superior alternative to the currently used models for daily flow forecasting, which is crucial for the operations of hydroelectric plants, including the allocation of the dam’s storage capacity and the optimization of operational procedures. It also plays a key role in the management of electric energy generation, the maintenance of ecological flows in the reservoir, and the continuous obtaining of flow records in non-calibrated catchments where measured flow data is unavailable.
However, it was observed that the forecasting accuracy diminishes with an increase in the forecast time. Therefore, as part of future studies, we intend to explore hybrid deep learning models, hybrid machine learning models with a multi-objective parameter selection, and variable selection techniques to analyze the reduction in the number of model inputs.
Author contributions
The development and analysis of the proposed framework were performed by H.H. and L.G. The source code was developed by A.M. and L.G. A.M. performed the data collection. A.M. wrote the first draft of the manuscript, and all authors commented on previous versions. All authors read and approved the final manuscript.
Funding
The authors acknowledge the support of the Brazilian funding agencies CNPq-Conselho Nacional de Desenvolvimento Científico e Tecnológico (Grants 429639/2016 and 401796/2021-3), and CAPES-Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (finance code 001).
Data availability
Data and materials can be obtained upon request from the corresponding author (alfeudiasm@gmail.com) or Contributing author (goliatt@gmail.com).
Code availability
Code can be obtained upon the corresponding author’s request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Henrique S. Hippert and Leonardo Goliatt.
References
- 1.Brito, L. D., et al.: Cidadania e governação em moçambique (2008).
- 2.Wegayehu EB, Muluneh FB. Multivariate streamflow simulation using hybrid deep learning models. Comput. Intell. Neurosci. 2021;20:21. doi: 10.1155/2021/5172658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv. Eng. Softw. 2014;69:46–61. [Google Scholar]
- 4.Goliatt L, Sulaiman SO, Khedher KM, Farooque AA, Yaseen ZM. Estimation of natural streams longitudinal dispersion coefficient using hybrid evolutionary machine learning model. Eng. App. Comput. Fluid Mech. 2021;15(1):1298–1320. [Google Scholar]
- 5.Saporetti CM, Fonseca DL, Oliveira LC, Pereira E, Goliatt L. Hybrid machine learning models for estimating total organic carbon from mineral constituents in core samples of shale gas fields. Mar. Pet. Geol. 2022 doi: 10.1016/j.marpetgeo.2022.105783. [DOI] [Google Scholar]
- 6.Halder B, Ahmadianfar I, Heddam S, Mussa ZH, Goliatt L, Tan ML, Sa’adi Z, Al-Khafaji Z, Al-Ansari N, Jawad AH, et al. Machine learning-based country-level annual air pollutants exploration using sentinel-5p and google earth engine. Sci. Rep. 2023;13(1):7968. doi: 10.1038/s41598-023-34774-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Goliatt L, Mohammad RS, Abba SI, Yaseen ZM. Development of hybrid computational data-intelligence model for flowing bottom-hole pressure of oil wells: New strategy for oil reservoir management and monitoring. Fuel. 2023;350:128623. doi: 10.1016/j.fuel.2023.128623. [DOI] [Google Scholar]
- 8.Ahmadianfar I, Halder B, Heddam S, Goliatt L, Tan ML, Sa’adi Z, Al-Khafaji Z, Homod RZ, Rashid TA, Yaseen ZM. An enhanced multioperator Runge-Kutta algorithm for optimizing complex water engineering problems. Sustainability. 2023;15:3. doi: 10.3390/su15031825. [DOI] [Google Scholar]
- 9.Basílio, S. D. C. A., Putti, F. F., Cunha, A. C., & Goliatt, L. An evolutionary-assisted machine learning model for global solar radiation prediction in minas Gerais region, southeastern Brazil. Earth Sci. Inform.10.1007/s12145-023-00990-0 (2023).
- 10.Heddam S, et al. Cyanobacteria blue-green algae prediction enhancement using hybrid machine learning-based gamma test variable selection and empirical wavelet transform. Environ. Sci. Pollut. Res. 2022 doi: 10.1007/s11356-022-21201-1. [DOI] [PubMed] [Google Scholar]
- 11.Ikram RMA, Goliatt L, Kisi O, Trajkovic S, Shahid S. Covariance matrix adaptation evolution strategy for improving machine learning approaches in streamflow prediction. Mathematics. 2022;10:16. doi: 10.3390/math10162971. [DOI] [Google Scholar]
- 12.Franco VR, Hott MC, Andrade RG, Goliatt L. Hybrid machine learning methods combined with computer vision approaches to estimate biophysical parameters of pastures. Evolut. Intell. 2022;20:1–14. [Google Scholar]
- 13.Saporetti CM, da Fonseca LG, Pereira E. A lithology identification approach based on machine learning with evolutionary parameter tuning. IEEE Geosci. Remote Sens. Lett. 2019;16(12):1819–1823. doi: 10.1109/LGRS.2019.2911473. [DOI] [Google Scholar]
- 14.Goliatt L, Yaseen ZM. Development of a hybrid computational intelligent model for daily global solar radiation prediction. Expert Syst. Appl. 2023;212:118295. doi: 10.1016/j.eswa.2022.118295. [DOI] [Google Scholar]
- 15.Basilio SDCA, Saporetti CM, Goliatt L. An interdependent evolutionary machine learning model applied to global horizontal irradiance modeling. Neural Comput. Appl. 2023 doi: 10.1007/s00521-023-08342-1. [DOI] [Google Scholar]
- 16.Adnan RM, Chen Z, Yuan X, Kisi O, El-Shafie A, Kuriqi A, Ikram M. Reference evapotranspiration modeling using new heuristic methods. Entropy. 2020;22:5. doi: 10.3390/e22050547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Radhika Y, Shashi M. Atmospheric temperature prediction using support vector machines. Int. J. Comput. Theory Eng. 2009;1(1):55. [Google Scholar]
- 18.Goliatt L, Sulaiman SO, Khedher KM, Farooque AA, Yaseen ZM. Estimation of natural streams longitudinal dispersion coefficient using hybrid evolutionary machine learning model. Eng. Appl. Comput. Fluid Mech. 2021;15(1):1298–1320. [Google Scholar]
- 19.Sahoo A, Samantaray S, Ghose DK. Multilayer perceptron and support vector machine trained with grey wolf optimiser for predicting floods in Barak river, India. J. Earth Syst. Sci. 2022;131(2):1–23. [Google Scholar]
- 20.Nguyen HD. Daily streamflow forecasting by machine learning in Tra Khuc River in Vietnam. Sci. Earth. 2022;20:20. [Google Scholar]
- 21.Ibrahim KSMH, Huang YF, Ahmed AN, Koo CH, El-Shafie A. A review of the hybrid artificial intelligence and optimization modelling of hydrological streamflow forecasting. Alex. Eng. J. 2022;61(1):279–303. [Google Scholar]
- 22.Mohammadi B. A review on the applications of machine learning for runoff modeling. Sustain. Water Resour. Manage. 2021;7(6):98. [Google Scholar]
- 23.Ehteram M, Sharafati A, Asadollah SBHS, Neshat A. Estimating the transient storage parameters for pollution modeling in small streams: A comparison of newly developed hybrid optimization algorithms. Environ. Monit. Assess. 2021;193(8):475. doi: 10.1007/s10661-021-09269-7. [DOI] [PubMed] [Google Scholar]
- 24.Goliatt L, Saporetti CM, Oliveira LC, Pereira E. Performance of evolutionary optimized machine learning for modeling total organic carbon in core samples of shale gas fields. Petroleum. 2023 doi: 10.1016/j.petlm.2023.05.005. [DOI] [Google Scholar]
- 25.Martinho AD, Saporetti CM, Goliatt L. Approaches for the short-term prediction of natural daily streamflows using hybrid machine learning enhanced with grey wolf optimization. Hydrol. Sci. J. 2022;0(0):1–18. doi: 10.1080/02626667.2022.2141121. [DOI] [Google Scholar]
- 26.Souza DP, Martinho AD, Rocha CC, Christo EDS, Goliatt L. Group method of data handling to forecast the daily water flow at the Cahora Bassa dam. Acta Geophys. 2022;20:1–13. [Google Scholar]
- 27.Difi, S., Elmeddahi, Y., Hebal, A., Singh, V. P., Heddam, S., Kim, S. & Kisi, O. Monthly streamflow prediction using hybrid extreme learning machine optimized by bat algorithm: A case study of Cheliff watershed, Algeria. Hydrol. Sci. J. (just-accepted) (2022).
- 28.Ikram RMA, Goliatt L, Kisi O, Trajkovic S, Shahid S. Covariance matrix adaptation evolution strategy for improving machine learning approaches in streamflow prediction. Mathematics. 2022;10(16):2971. [Google Scholar]
- 29.Haznedar B, Kilinc HC. A hybrid ANFIS-GA approach for estimation of hydrological time series. Water Resour. Manage. 2022;36(12):4819–4842. [Google Scholar]
- 30.Kilinc HC. Daily streamflow forecasting based on the hybrid particle swarm optimization and long short-term memory model in the orontes basin. Water. 2022;14(3):490. [Google Scholar]
- 31.Khosravi K, Golkarian A, Tiefenbacher JP. Using optimized deep learning to predict daily streamflow: A comparison to common machine learning algorithms. Water Resour. Manage. 2022;36(2):699–716. [Google Scholar]
- 32.Al-Sudani ZA, Salih SQ, Yaseen ZM, et al. Development of multivariate adaptive regression spline integrated with differential evolution model for streamflow simulation. J. Hydrol. 2019;573:1–12. [Google Scholar]
- 33.Ribeiro VHA, Reynoso-Meza G, Siqueira HV. Multi-objective ensembles of echo state networks and extreme learning machines for streamflow series forecasting. Eng. Appl. Artif. Intell. 2020;95:103910. [Google Scholar]
- 34.Yaseen ZM, Ebtehaj I, Bonakdari H, Deo RC, Mehr AD, Mohtar WHMW, Diop L, El-Shafie A, Singh VP. Novel approach for streamflow forecasting using a hybrid ANFIS-FFA model. J. Hydrol. 2017;554:263–276. [Google Scholar]
- 35.Adnan RM, Liang Z, Trajkovic S, Zounemat-Kermani M, Li B, Kisi O. Daily streamflow prediction using optimally pruned extreme learning machine. J. Hydrol. 2019;577:123981. [Google Scholar]
- 36.Yaseen ZM, Faris H, Al-Ansari N. Hybridized extreme learning machine model with salp swarm algorithm: A novel predictive model for hydrological application. Complexity. 2020;20:20. [Google Scholar]
- 37.Tikhamarine Y, Souag-Gamane D, Ahmed AN, Kisi O, El-Shafie A. Improving artificial intelligence models accuracy for monthly streamflow forecasting using grey wolf optimization (GWO) algorithm. J. Hydrol. 2020;582:124435. [Google Scholar]
- 38.Tikhamarine Y, Souag-Gamane D, Kisi O. A new intelligent method for monthly streamflow prediction: Hybrid wavelet support vector regression based on grey wolf optimizer (wsvr-gwo) Arab. J. Geosci. 2019;12(17):1–20. [Google Scholar]
- 39.Malik A, Tikhamarine Y, Souag-Gamane D, Kisi O, Pham QB. Support vector regression optimized by meta-heuristic algorithms for daily streamflow prediction. Stoch. Env. Res. Risk Assess. 2020;34(11):1755–1773. [Google Scholar]
- 40.Wu L, Zhou H, Ma X, Fan J, Zhang F. Daily reference evapotranspiration prediction based on hybridized extreme learning machine model with bio-inspired optimization algorithms: Application in contrasting climates of china. J. Hydrol. 2019;577:123960. [Google Scholar]
- 41.Adnan RM, Mostafa RR, Kisi O, Yaseen ZM, Shahid S, Zounemat-Kermani M. Improving streamflow prediction using a new hybrid elm model combined with hybrid particle swarm optimization and grey wolf optimization. Knowl.-Based Syst. 2021;230:107379. [Google Scholar]
- 42.Kilinc HC, Yurtsever A. Short-term streamflow forecasting using hybrid deep learning model based on grey wolf algorithm for hydrological time series. Sustainability. 2022;14(6):3352. [Google Scholar]
- 43.Zaini, N., Malek, M., Yusoff, M., Mardi, N. & Norhisham, S. Daily river flow forecasting with hybrid support vector machine–particle swarm optimization. In IOP Conference Series: Earth and Environmental Science, Vol 140, 012035 (IOP Publishing, 2018).
- 44.Meshram SG, Ghorbani MA, Shamshirband S, Karimi V, Meshram C. River flow prediction using hybrid psogsa algorithm based on feed-forward neural network. Soft. Comput. 2019;23:10429–10438. [Google Scholar]
- 45.Riahi-Madvar H, Dehghani M, Memarzadeh R, Gharabaghi B. Short to long-term forecasting of river flows by heuristic optimization algorithms hybridized with ANFIS. Water Resour. Manage. 2021;35:1149–1166. [Google Scholar]
- 46.Adnan RM, Mostafa RR, Elbeltagi A, Yaseen ZM, Shahid S, Kisi O. Development of new machine learning model for streamflow prediction: Case studies in Pakistan. Stoch. Environ. Res. Risk Assess. 2022;20:1–35. [Google Scholar]
- 47.Dehghani M, Seifi A, Riahi-Madvar H. Novel forecasting models for immediate-short-term to long-term influent flow prediction by combining ANFIS and grey wolf optimization. J. Hydrol. 2019;576:698–725. [Google Scholar]
- 48.Afan HA, Yafouz A, Birima AH, Ahmed AN, Kisi O, Chaplot B, El-Shafie A. Linear and stratified sampling-based deep learning models for improving the river streamflow forecasting to mitigate flooding disaster. Nat. Hazards. 2022;112(2):1527–1545. [Google Scholar]
- 49.Chong K, Huang Y, Koo C, Sherif M, Ahmed AN, El-Shafie A. Investigation of cross-entropy-based streamflow forecasting through an efficient interpretable automated search process. Appl. Water Sci. 2023;13(1):6. [Google Scholar]
- 50.Wei Y, Hashim H, Chong K, Huang Y, Ahmed AN, El-Shafie A. Investigation of meta-heuristics algorithms in ANN streamflow forecasting. KSCE J. Civ. Eng. 2023;27(5):2297–2312. [Google Scholar]
- 51.Vidyarthi, V. K. & Chourasiya, S. Particle swarm optimization for training artificial neural network-based rainfall–runoff model, case study: Jardine river basin. In Micro-Electronics and Telecommunication Engineering: Proceedings of 3rd ICMETE 2019, 641–647 (Springer, 2020).
- 52.Vidyarthi VK, Jain A. Incorporating non-uniformity and non-linearity of hydrologic and catchment characteristics in rainfall–runoff modeling using conceptual, data-driven, and hybrid techniques. J. Hydroinf. 2022;24(2):350–366. [Google Scholar]
- 53.Alizadeh Z, Shourian M, Yaseen ZM. Simulating monthly streamflow using a hybrid feature selection approach integrated with an intelligence model. Hydrol. Sci. J. 2020;65(8):1374–1384. [Google Scholar]
- 54.Martinho AD, Saporetti CM, Goliatt L. Approaches for the short-term prediction of natural daily streamflows using hybrid machine learning enhanced with grey wolf optimization. Hydrol. Sci. J. 2023;68(1):16–33. [Google Scholar]
- 55.Souza DP, Martinho AD, Rocha CC, da S. Christo E, Goliatt L. Hybrid particle swarm optimization and group method of data handling for short-term prediction of natural daily streamflows. Model. Earth Syst. Environ. 2022;8(4):5743–5759. [Google Scholar]
- 56.Martinho, A. D., Ribeiro, C. B., Gorodetskaya, Y., Fonseca, T. L. & Goliatt, L. Extreme learning machine with evolutionary parameter tuning applied to forecast the daily natural flow at Cahora Bassa dam, Mozambique. In Bioinspired Optimization Methods and Their Applications: 9th International Conference, BIOMA 2020, Brussels, Belgium, November 19–20, 2020, Proceedings 9, 255–267 (Springer, 2020).
- 57.Martinho, A. D., Fonseca, T. L. & Goliatt, L. Automated extreme learning machine to forecast the monthly flows: A case study at zambezi river. In Intelligent Systems Design and Applications: 20th International Conference on Intelligent Systems Design and Applications (ISDA 2020) Held December 12–15, 2020, 1314–1324 (Springer, 2021).
- 58.Chen, T. & Guestrin, C. Xgboost: A scalable tree boosting system. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 785–794 (2016).
- 59.Nguyen H, Nguyen N-M, Cao M-T, Hoang N-D, Tran X-L. Prediction of long-term deflections of reinforced-concrete members using a novel swarm optimized extreme gradient boosting machine. Eng. Comput. 2022;38(2):1255–1267. [Google Scholar]
- 60.Wang W, Shi Y, Lyu G, Deng W. Electricity consumption prediction using xgboost based on discrete wavelet transform. DEStech Trans. Comput. Sci. Eng. 2017;20:10. [Google Scholar]
- 61.Islam S, Sholahuddin A, Abdullah A. Extreme gradient boosting (xgboost) method in making forecasting application and analysis of USD exchange rates against rupiah. J. Phys. Conf. Ser. 2021;1722:012016. [Google Scholar]
- 62.Chang C-C, Lin C-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011;2:3. [Google Scholar]
- 63.Karthikeyan M, Vyas R. Practical Chemoinformatics. Springer; 2014. Machine learning methods in chemoinformatics for drug discovery; pp. 133–194. [Google Scholar]
- 64.Vapnik V, Golowich SE, Smola A, et al. Support vector method for function approximation, regression estimation, and signal processing. Adv. Neural Inf. Process. Syst. 1997;20:281–287. [Google Scholar]
- 65.Zou H, Hastie T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005;67(2):301–320. [Google Scholar]
- 66.Masini RP, Medeiros MC, Mendes EF. Machine learning advances for time series forecasting. J. Econ. Surv. 2021;20:20. [Google Scholar]
- 67.Al-Jawarneh AS, Ismail MT, Awajan AM. Elastic net regression and empirical mode decomposition for enhancing the accuracy of the model selection. Int. J. Math. Eng. Manage. Sci. 2021;6(2):564. [Google Scholar]
- 68.Liu W, Dou Z, Wang W, Liu Y, Zou H, Zhang B, Hou S. Short-term load forecasting based on elastic net improved GMDH and difference degree weighting optimization. Appl. Sci. 2018;8(9):1603. [Google Scholar]
- 69.Friedman JH. Multivariate adaptive regression splines. Ann. Stat. 1991;19(1):1–67. doi: 10.1177/096228029500400303. [DOI] [PubMed] [Google Scholar]
- 70.Zhang W, Goh ATC. Multivariate adaptive regression splines for analysis of geotechnical engineering systems. Comput. Geotech. 2013;48:82–95. [Google Scholar]
- 71.Alkhammash EH, Kamel AF, Al-Fattah SM, Elshewey AM. Optimized multivariate adaptive regression splines for predicting crude oil demand in Saudi Arabia. Discret. Dyn. Nat. Soc. 2022;20:22. [Google Scholar]
- 72.Huang G-B, Zhou H, Ding X, Zhang R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2012;42(2):513–529. doi: 10.1109/TSMCB.2011.2168604. [DOI] [PubMed] [Google Scholar]
- 73.Huang, G.-B., Zhu, Q.-Y. & Siew, C.-K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Neural Networks, 2004. Proceedings. 2004 IEEE International Joint Conference On, Vol. 2, 985–990 (IEEE, 2004).
- 74.Martinho AD, Saporetti CM, Goliatt L. Hybrid machine learning approaches enhanced with grey wolf optimization to the short-term prediction of natural daily streamflows. Hydrol. Sci. J. 2022;20:20. [Google Scholar]
- 75.Almubaidin MAA, Ahmed AN, Sidek LBM, Elshafie A. Using metaheuristics algorithms (MHAS) to optimize water supply operation in reservoirs: A review. Arch. Comput. Methods Eng. 2022;29(6):3677–3711. [Google Scholar]
- 76.Ramson SJ, Raju KL, Vishnu S, Anagnostopoulos T. Nature inspired optimization techniques for image processing—a short review. Nat. Inspired Optim. Tech. Image Process. Appl. 2019;20:113–145. [Google Scholar]
- 77.Akhter MN, Mekhilef S, Mokhlis H, Shah NM. Review on forecasting of photovoltaic power generation based on machine learning and metaheuristic techniques. IET Renew. Power Gener. 2019;13(7):1009–1023. [Google Scholar]
- 78.Whitley D. A genetic algorithm tutorial. Stat. Comput. 1994;4(2):65–85. [Google Scholar]
- 79.Zafar, A., Shah, S., Khalid, R., Hussain, S. M., Rahim, H. & Javaid, N. A meta-heuristic home energy management system. In 2017 31st International Conference on Advanced Information Networking and Applications Workshops (WAINA), 244–250 (IEEE, 2017).
- 80.Zhang Y, Song X-F, Gong D-W. A return-cost-based binary firefly algorithm for feature selection. Inf. Sci. 2017;418–419:561–574. [Google Scholar]
- 81.Mandal, A., Das, S. & Abraham, A. A differential evolution based memetic algorithm for workload optimization in power generation plants. In 2011 11th International Conference on Hybrid Intelligent Systems (HIS), 271–276 (IEEE, 2011).
- 82.Wang J, Li L, Niu D, Tan Z. An annual load forecasting model based on support vector regression with differential evolution algorithm. Appl. Energy. 2012;94:65–70. [Google Scholar]
- 83.Beniand G, Wang J. Swarm Intelligence in Cellular Robotic Systems. Springer; 1993. [Google Scholar]
- 84.Klemeš V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986;31(1):13–24. [Google Scholar]
- 85.Tongal H, Booij MJ. Simulation and forecasting of streamflows using machine learning models coupled with base flow separation. J. Hydrol. 2018;564:266–282. [Google Scholar]
- 86.Parmezan ARS, Souza VM, Batista GE. Evaluation of statistical and machine learning models for time series prediction: Identifying the state-of-the-art and the best conditions for the use of each model. Inf. Sci. 2019;484:302–337. [Google Scholar]
- 87.Carvalho, W. L. D. O.: Estudo de parâmetros ótimos em algoritmos genéticos elitistas. Master’s thesis, Brasil (2017).
- 88.Araujo RD, Barbosa H, Bernardino H. Evolução diferencial para problemas de otimização com restrições lineares. Univ. Federal Juiz Fora. 2016;46:25. [Google Scholar]
- 89.Costa, S. D. Estratégias de previsão multipassos à frente para vazão afluente em bacias hidrográficas de diferentes dinâmicas (2014).
- 90.Guilhon LGF, Rocha VF, Moreira JC. Comparação de métodos de previsão de vazões naturais afluentes a aproveitamentos hidroelétricos. Rev. Bras. Recur.Hídricos. 2007;12(3):13–20. [Google Scholar]
- 91.Tukey JW. Comparing individual means in the analysis of variance. Biometrics. 1949;20:99–114. [PubMed] [Google Scholar]
- 92.Pereira HR, Meschiatti MC, Pires RCDM, Blain GC. On the performance of three indices of agreement: An easy-to-use r-code for calculating the Willmott indices. Bragantia. 2018;77(2):394–403. [Google Scholar]
- 93.Gupta HV, Kling H, Yilmaz KK, Martinez GF. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009;377(1):80–91. [Google Scholar]
- 94.Nash JE, Sutcliffe JV. River flow forecasting through conceptual models part I—a discussion of principles. J. Hydrol. 1970;10(3):282–290. [Google Scholar]
- 95.Santos, C. E. D. S. Seleção de parâmetros de máquinas de vetores de suporte usando otimização multiobjetivo baseada em meta-heurísticas (2019).
- 96.Nguyen H, Nguyen N-M, Cao M-T, Hoang N-D, Tran X-L. Prediction of long-term deflections of reinforced-concrete members using a novel swarm optimized extreme gradient boosting machine. Eng. Comput. 2021;20:1–13. [Google Scholar]
- 97.Samanataray S, Sahoo A. A comparative study on prediction of monthly streamflow using hybrid ANFIS-PSO approaches. KSCE J. Civ. Eng. 2021;25(10):4032–4043. [Google Scholar]
- 98.Nguyen DH, Le XH, Heo J-Y, Bae D-H. Development of an extreme gradient boosting model integrated with evolutionary algorithms for hourly water level prediction. IEEE Access. 2021;9:125853–125867. [Google Scholar]
- 99.Sahour H, Gholami V, Torkaman J, Vazifedan M, Saeedi S. Random forest and extreme gradient boosting algorithms for streamflow modeling using vessel features and tree-rings. Environ. Earth Sci. 2021;80(22):1–14. [Google Scholar]
- 100.Ni L, Wang D, Wu J, Wang Y, Tao Y, Zhang J, Liu J. Streamflow forecasting using extreme gradient boosting model coupled with gaussian mixture model. J. Hydrol. 2020;586:124901. [Google Scholar]
- 101.Yu X, Wang Y, Wu L, Chen G, Wang L, Qin H. Comparison of support vector regression and extreme gradient boosting for decomposition-based data-driven 10-day streamflow forecasting. J. Hydrol. 2020;582:124293. [Google Scholar]
- 102.Osman AIA, Ahmed AN, Chow MF, Huang YF, El-Shafie A. Extreme gradient boosting (xgboost) model to predict the groundwater levels in Selangor Malaysia. Ain Shams Eng. J. 2021;12(2):1545–1556. [Google Scholar]
- 103.Heinen, E. D. Redes neurais recorrentes e xgboost aplicados à previsão de radiação solar no horizonte de curto prazo (2018).
- 104.Venkatesan E, Mahindrakar AB. Forecasting floods using extreme gradient boosting—a new approach. Int. J. Civil Eng. Technol. 2019;10(2):1336–1346. [Google Scholar]
- 105.Jiang Y, Bao X, Hao S, Zhao H, Li X, Wu X. Monthly streamflow forecasting using elm-ipso based on phase space reconstruction. Water Resour. Manage. 2020;34(11):3515–3531. [Google Scholar]
- 106.Rezaie-Balf M, Naganna SR, Kisi O, El-Shafie A. Enhancing streamflow forecasting using the augmenting ensemble procedure coupled machine learning models: Case study of aswan high dam. Hydrol. Sci. J. 2019;64(13):1629–1646. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data and materials can be obtained upon request from the corresponding author (alfeudiasm@gmail.com) or Contributing author (goliatt@gmail.com).
Code can be obtained upon the corresponding author’s request.