Probabilistic tensor decomposition extracts better latent embeddings from single-cell multiomic data

Abstract

Single-cell sequencing technology enables the simultaneous capture of multiomic data from multiple cells. The captured data can be represented by tensors, i.e. the higher-rank matrices. However, the existing analysis tools often take the data as a collection of two-order matrices, renouncing the correspondences among the features. Consequently, we propose a probabilistic tensor decomposition framework, SCOIT, to extract embeddings from single-cell multiomic data. SCOIT incorporates various distributions, including Gaussian, Poisson, and negative binomial distributions, to deal with sparse, noisy, and heterogeneous single-cell data. Our framework can decompose a multiomic tensor into a cell embedding matrix, a gene embedding matrix, and an omic embedding matrix, allowing for various downstream analyses. We applied SCOIT to eight single-cell multiomic datasets from different sequencing protocols. With cell embeddings, SCOIT achieves superior performance for cell clustering compared to nine state-of-the-art tools under various metrics, demonstrating its ability to dissect cellular heterogeneity. With the gene embeddings, SCOIT enables cross-omics gene expression analysis and integrative gene regulatory network study. Furthermore, the embeddings allow cross-omics imputation simultaneously, outperforming current imputation methods with the Pearson correlation coefficient increased by 3.38–39.26%; moreover, SCOIT accommodates the scenario that subsets of the cells are with merely one omic profile available.

Graphical Abstract

Graphical Abstract.

INTRODUCTION

Single-cell technologies enable cellular heterogeneity dissection at high resolution. Starting with single-cell RNA sequencing (scRNA-seq) (1), the technologies have been extended to DNA methylation, proteomics and chromatin accessibility, providing unprecedented opportunities to study biological systems from various perspectives (2). More recently, technological advances have allowed the capture of different types of molecules and epigenetic data from the same cell (3,4). Multiomic data capture information from multiple sources at a single cell resolution, allowing more comprehensive studies of cellular heterogeneity and biological systems (5,6). Cao et al. simultaneously measured the expression of RNA and chromatin accessibility of mouse kidney cells. They inferred the target genes for distal cis-regulatory elements from the covariance of the two arrays (7). Yan et al. showed that the joint profile of DNA methylation, RNA expression, and chromatin accessibility of human and mouse oocytes revealed the evolution of gene body methylation (8). Luo et al. discovered the relations between DNA methylation and gene expression for neuronal cells with multiomic measurement (9).

Despite advances in sequencing technology (7–14), the integrated analysis of single-cell multiomic data is statistically challenging. The challenges come from two aspects. First, single-cell data are inherently sparse. Zero-count occurrences can be due to either actual absence or technical errors, i.e., dropout events, in the scRNA-seq data (15). The problem is more severe for the chromatin accessibility data (16,17). Second, single-cell sequencing data exhibit high noise, and the high noise is due to low capture efficiency and shallow sequencing depth (18,19), leading to a deviated representation of the actual distribution.

The heterogeneity of multiomics poses another challenge for consensus inferences (4). First, sequencing data from different omics arise from distinct biological variations and technical bias (20). Second, the data to be integrated have various types. RNA expression and proteomic data can be discrete or continuous, whereas epigenomic data are binary. The distinct features of the omic data impede statistical modeling.

Methods developed for single-cell multiomic data integration are emerging. MOFA (21) and the updated version MOFA+ (22) perform joint matrix factorization to infer the cell representation in a latent space. scAI (17) extends the matrix factorization formulation by aggregating neighbors’ signals to rectify the sparsity of the data. totalVI (20) leverages variational autoencoder to learn the representations of cells in omics. The latest version of Seurat (23) applies the weighted nearest neighbor to build a joint cell–cell graph for downstream analysis. MultiVI (24) integrates RNA expression data and chromatin accessibility data with a deep generative model. Cobolt (25) provides a framework to integrate data from single and multiple modality platforms. Multigrate (26) applies a generative neural network to build multiomic reference collections for data integration.

The aforementioned methods are built on jointly projecting the cells into a latent space or graph while ignoring the integration at the gene level. The main reason is that most of these methods represent the multiomic data as a feature-wise concatenated matrix. In this context, cells are embedded in a shared space, whereas genes are embedded in separated spaces for multiple omics. Arranging the multiomic data in a 2D matrix fails to utilize the integrated information fully. Tensor, a higher-rank generalization of a matrix, offers a natural representation of data with multiple facets. A tensor can order the variables along different tensor dimensions, including cell, feature, and omic. Then, we can derive the integrated information for the variables by decomposing and embedding the tensor.

In this work, we propose a probabilistic tensor decomposition framework to extract embeddings from paired single-cell multiomic data. To deal with sparse, noisy, and heterogeneous single-cell data, we applied various distributions, including the Gaussian distribution, Poisson distribution, and negative binomial distribution, to model different data types. The framework can decompose a multiomic tensor into a cell embedding matrix, a gene embedding matrix, and an omic embedding matrix, allowing for various downstream analyses. We implemented the framework in an open source package named SCOIT (Single Cell multi-Omics data Integration with Tensor decomposition).

We applied SCOIT to eight single-cell multiomic datasets from various sequencing protocols, covering DNA methylation data, RNA expression data, proteomics data, and chromatin accessibility data. First, with integrated cell embeddings, SCOIT achieved better clustering accuracy than the nine state-of-the-art methods on heterogeneous datasets. Furthermore, the integrated gene embeddings allowed us to study gene expressions at different levels and investigate the post-transcriptional gene regulatory network, which single-omic data cannot offer. Moreover, we demonstrate that the embeddings from SCOIT allow multiomic imputation, outperforming the conventional imputation methods and current single-cell data imputation tools, measured by Pearson correlation coefficients and root mean square error. SCOIT provides a versatile framework flexible to new downstream analyses and applications.

MATERIALS AND METHODS

Multiomic datasets

We collected eight public single-cell multiomic datasets generated by various sequencing protocols, including sc-GEM (10), sci-CAR (7), SNARE-seq (11), PEA/STA (12), CITE-seq (13), SCoPE2 (14) and scNMT-seq (27). sc-GEM provided a dataset (SRA accession SRP077853) sequenced from human fibroblast cells that undergo reprogramming, which contains RNA expression and DNA methylation data. sci-CAR generated a dataset (GEO accession GSE117089) sequenced from an adult mouse kidney, jointly profiling RNA expression and chromatin accessibility data. SNARE-seq provided two datasets (GEO accession GSE126074) sequenced from neonatal and adult mouse cerebral cortices, respectively, including the RNA expression and chromatin accessibility data. PEA/STA offered a dataset sequenced from human glioblastoma cells containing RNA expression and proteomic data. CITE-seq provides a dataset (GEO accession GSE100866) with cellular indexing of RNA expression and epitopes from cord blood mononuclear cells. SCoPE2 quantified proteomics in innate immune cells (MassIVE ID MSV000083945 and MSV000084660) and provided parallel measurements of RNA expression by 10X Genomics (GEO accession GSE142392). scNMT-seq jointly measures transcriptome, DNA methylation, and chromatin accessibility in mouse embryonic stem cells (GEO accession GSE109262). We downloaded the processed data and the cell types identified with typical marker genes from the studies. CITE-seq did not provide the cell type information, so we labeled the cells with marker proteins (see Supplementary Table S1) as suggested (13). We summarize the statistics of the datasets in Supplementary Table S2.

Omic data processing

We applied various data normalization strategies according to data types. We performed min-max normalization for the sc-GEM data to scale the RNA expression data. For the data from sci-CAR and SNARE-seq, following the practice introduced in Seurat (23), we applied scTransform (28) to the RNA expression data and Signac (29) to the chromatin accessibility data for data normalization and dimension reduction. For the data from PEA/STA and SCoPE2, we performed a min-max normalization for the RNA expression and proteomic data since they are given as continuous values. For the RNA expression data from the CITE-seq, we kept the gene detected in at least 10% of the cells and applied log normalization as suggested (13), then applied min-max normalization to the RNA expression and proteomics data. For the RNA expression, DNA methylation, and chromatin accessibility data from scNMT-seq, we applied UMAP to reduce the data dimension to 300 as suggested (30).

SCOIT overview

This study proposes and implements SCOIT, a probabilistic tensor decomposition framework for integrating paired single-cell multiomic data. SCOIT accepts datasets from multiple omics, with missing values allowed, and it processes the data in two steps (Figure 1 A). First, it constructs a multiomic tensor with a union set of features (genes, loci, proteins, etc.). Second, it performs the probabilistic tensor decomposition with a user-specified distribution. SCOIT generates embedding matrices for omics, cells, and features; each omic type, each cell and each feature will be assigned an embedding vector. The embedding vector incorporates global and local embeddings to capture global and local variability. The embedding vectors form matrices and enable downstream analyses, including cell clustering, cell–cell graph construction, gene expression and regulation study, data imputation, etc. (Figure 1 B). SCOIT is available at https://github.com/deepomicslab/SCOIT.

Figure 1.

SCOIT provides a probabilistic tensor decomposition framework for the integration of single-cell multiomic data. (A) Overview: SCOIT constructs a multiomic tensor with the input of single-cell sequencing data from multiple omics. Then following a user-defined distribution, SCOIT decomposes the tensor into an omic embedding matrix, a global cell embedding matrix, a global gene (location, protein) embedding matrix, an omic-specific cell embedding matrix and an omic-specific gene (location, protein) embedding matrix. (B) Downstream analysis: the cell embedding matrices can be applied to cell clustering analysis and cell nearest neighbor (NN) graph construction; the gene embedding matrices can be applied to study the gene regulatory interactions and the expression across multiomics; the inferred tensor, computed from the embedding matrices, can be used for imputation.

Probabilisitc tensor decomposition framework

Notation and definition

We denote the number of omic profiles, the number of cells, and the number of genes as l, n and m, respectively. Denote the observed multiomic tensor as 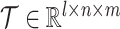, which is constructed with multiple cell × gene data matrices from single omics. Denote the inferred tensor as 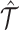, which can be decomposed into the omic embedding matrix , the global cell embedding matrix 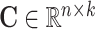, the global gene embedding matrix 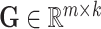, the omic-specific cell embedding matrix 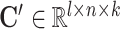, and the omic-specific gene embedding matrix 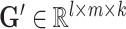, where k denotes the rank of decomposition of the tensor.

Multiomic tensor construction

Each single-omic data is a two-dimensional matrix (cell × gene (loc, protein, etc.)). We can construct a three-order multiomic tensor with the matrices. The data from different omics may contain different genes. We construct the multiomic tensor based on the union set of genes. The features of different omics do not have one-to-one correspondence for some sequencing protocols. For instance, CITE-seq measures RNA expression and epitope data, while one epitope expression is affected by multiple genes. In addition, sci-CAR and SNARE-seq simultaneously profile RNA expression and chromatin accessibility, while the latter gives measurements at different chromatin loci. In these instances, we construct multiple-feature tensors with the union set of features. The decomposition processing for a multiple-feature tensor is analogous to that for the tensor with the feature correspondence information (see Supplementary methods S1.1 and Supplementary Figure S1). In the following sections, we present the details on decomposing single feature (i.e. gene) tensors.

Omic-specific tensor decomposition

For an inferred tensor 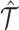, the omic-specific tensor decomposition is expressed element-wisely as

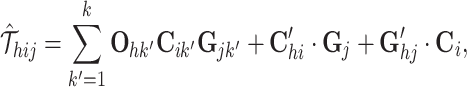(1)

where 1 ≤ h ≤ l, 1 ≤ i ≤ n, 1 ≤ j ≤ m, and O_h, C_i, G_j, , .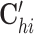

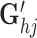
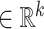Specifically, the first term is the sum of the element-wise products for three vectors O_h, C_i and G_j, capturing the global variability for cells and genes across the omics. We adopt a local element-wise product to maintain the variations in each vector (see Supplementary methods S1.2). The second term is the inner product of two vectors 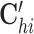and G_j, capturing the omic-specific variability for cells. The third term is the inner product of two vectors 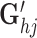and C_i, capturing the omic-specific variability of the genes. We give the geometrical interpretation for the formulation of the tensor decomposition in Supplementary Methods S1.3 and Supplementary Figure S2.

Distribution and likelihood objective function

Next, SCOIT derives the distributions with the mean 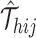to fit the observed multiomic tensor 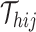. The variances of the distributions model the uncertainty from single-cell measurements (15). Then SCOIT maximizes the likelihood objective function to derive the embeddings. Compared with minimizing the sum-squared distance between 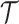and 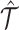, using suitable distributions yields a better fit to the single-cell datasets with inherent sparsity and high noise. SCOIT incorporates various likelihood models to cope with different data types, The models are chosen according to the data types, including a Gaussian distribution model for continuous data (21,22), a Poisson distribution model for discrete data, and a negative binomial distribution model for discrete data with high variances (15).

Then, we specify the details of the models with Gaussian distribution. The likelihood objective function is as

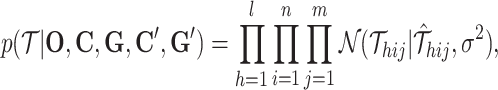(2)

where 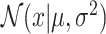is the Gaussian distribution density function with mean μ and variance σ². σ is a hyperparameter in SCOIT.

We recommend the likelihood model with Poisson distribution and negative binomial distribution for the discrete data, i.e. the count data. The likelihood function for the Poisson distribution is as

(3)

where 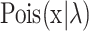is the probability density function of the Poisson distribution with mean and variance as λ. Since the mean and variance of the Poisson distribution are the same, it is inappropriate for overdispersed data. The negative binomial distribution gives an alternative by placing a gamma prior on λ as , where μ is the mean and υ is the variance of Gamma distribution. SCOIT applies the constant Fano factor assumption introduced by SAVER (15), which assumes that the variance scales linearly with the mean under a coefficient. Then the likelihood objective is as

(4)

where 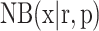is the probability density function of the negative binomial distribution with mean 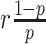and variance 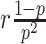(see Supplementary Methods S1.4 for the reparameterization procedure). β_hj denotes the Fano factor for gene j in omics h, which is a trainable parameter.

Model regularization

SCOIT applies L2 regularization to avoid overfitting, increase model interpretability and control the variability introduced. First, the penalty term shrinks the magnitude of embedding matrix elements and avoids unnecessary model complexity. Second, regularization addresses the sparsity of the embedding matrices, thus encouraging the learning of distinct features for some subsets of genes and samples. Third, the variability of the multiomic data comes from the five embedding matrices, O, C, G, C′ and G′. We introduce the individually tunable coefficient for the penalty term of each embedding matrix. By tuning the coefficients, we can integrate the data from the global and omic-specific sources. SCOIT also allows for an individual coefficient for each omic to facilitate downstream analyses.

Model optimization

The loss function combines the negative log-likelihood function and the regularization terms, which is as

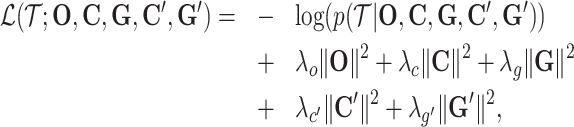(5)

where λ_o, λ_c, λ_g, 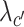, 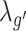are the coefficients for the penalty term of each embedding matrix.

SCOIT performs a gradient descent to minimize the loss function. To be specific, SCOIT initializes O, C, G, C′ and G′ with a Gaussian distribution (μ = 0, σ = 0.1) to give an unbiased prior. Then, SCOIT updates simultaneously O, C, G, C′ and G′ via Adam optimization algorithm (31) (see Supplementary Methods S1.5). Adam adopts momentum and an adaptive learning rate, which makes it suitable for sparse and noisy data. We implemented the optimization process with the Pytorch package and performed the computation on the GPU (Nvidia Tesla T4 16G) for acceleration.

Hyperparameter settings

SCOIT automatically adjusts the coefficients for the penalty terms according to the correlations between the multiomic datasets. To determine the multiomic correlations, SCOIT computes Pearson’s correlation coefficients between the datasets for the shared features, which are subsequently compared to the coefficients from the datasets with a permuted cell order to ensure statistical significance. To manifest an apparent correlation between the multiomic datasets, SCOIT requires a strong correlation strength (32,33) with statistical significance (P-value < 0.05) from the permutation test (34). In this case, SCOIT sets λ_o, λ_c, and λ_g to 0.01 and sets 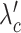, and 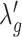to 1, to integrate the information from the global source. 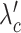Otherwise, SCOIT set λ_c and to 0.01 and set λ_o,  and λ_g to 1, to integrate the information from omic-specific sources. The detailed correlation analyses for the datasets used in the manuscript are shown in Supplementary Figure S3. The distributions used in the objective function are chosen according to the data types (see Distribution and likelihood objective function subsection). Supplementary Table S3 summarizes the distribution models, learning rates, and the number of epochs for all experiments. All other hyperparameters are set as defaults. We also investigate how hyperparameters affect performance, and the results show that SCOIT is robust to the choice of embedding dimensions and penalty term coefficients within a range of values, and the default parameter settings maintain stable performance across the datasets (Supplementary Figure S4).

Cell clustering and graph construction

In our experiment, we applied the n × k global cell embedding matrix as low-dimensional embeddings for the n cells. We then performed the downstream analysis with the embeddings, including cell clustering and NN graph construction.

For all the eight datasets, we conducted k-means clustering and constructed KNN graphs with the cell embeddings. For k-means clustering, we set k to the number of cell types and other parameters to the default. For the KNN graph, we connected each cell with the k-nearest (k was set to 20) cells, measured by Euclidean distance. Then we applied Leiden (35) to perform community detection for the graphs and labeled the cells. The graph construction and community detection functions are included in the SCOIT package.

Multiomic data imputation

A key benefit of SCOIT is its ability to facilitate the imputation across multiomic data. For imputation, SCOIT first pre-imputes the multiomic data with KNNImputer, which imputes the missing value with the mean value from k-nearest neighbors (k = 5). Then SCOIT performs probabilistic tensor decomposition for the pre-imputed data. After computing the embeddings O, C, G, C′ and G′, SCOIT can reconstruct the multiomic tensor 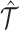with Equation 1, which recovers the values not measured in the observed multiomic tensor . It is worth noting that SCOIT can also accommodate the scenario that subsets of cells are merely observed in one omic dataset.

Benchmark methods

We applied PCA, TSNE (36), Seurat (23), totalVI (20), scAI (17), MOFA+ (22), MultiVI (24), Multigrate (26) and Cobolt (25) to embed cells in a common latent space as benchmark methods. For all the methods, we adhered to the tutorial provided on their websites and used the suggested data preprocessing steps and parameter configurations. Then, we applied the above clustering and community detection methods for the cell embeddings generated by the benchmark methods.

Specifically, for PCA and TSNE, we concatenated the multiple data matrices and performed the dimensional reduction along the gene dimension to generate low-dimensional embeddings. We applied the functions implemented in the sci-kit-learn package with the default parameters. For Seurat, following the suggested workflow, we performed normalization, feature selection, data scaling, and dimension reduction for RNA expression data; we applied TF-IDF feature selection and dimension reduction to epigenomic data; we used CLR normalization, data scaling, and dimension reduction for protein data. All of the preprocessing steps were performed with the built-in functions of Seurat. Then we applied UMAP (37) to the constructed weighted nearest neighbor graphs to obtain cell embeddings. totalVI is designed for CITE-seq data analysis. After normalizing each cell by total counts and applying log-transformation, we applied totalVI to the data with default settings. scAI is designed to combine transcriptomic and epigenomic data, so we excluded it from analyzing the datasets by PEA/STA2, CITE-seq and SCoPE2. We used the built-in preprocessing function for feature selection and log-normalization. We set the rank of the inferred factor as the number of cell types and other parameters as default. For MOFA+, we applied data transformation (see Omics data processing subsection) and Gaussian likelihood models as suggested. MultiVI is designed for integrating transcriptional and chromatin accessibility data. We filtered the genes detected in <1% of the cells and applied it to sci-CAR dataset and SNARE-seq dataset. For Multigrate, we applied the preprocessing steps introduced in Omics data processing subsection. For Cobolt, we used the count matrices as the inputs.

Concerning imputation, we applied KNNImputer and SimpleImputer in the sci-kit-learn package as benchmark methods. KNNImputer replaces the missing value with the mean value from k-nearest neighbors. We used the default settings (k = 5). SimpleImputer imputes the missing value with the mean value of the column. Also, we included two single-cell imputation tools, scImpute (38) and DeepImpute (39), for comparison. We concatenated the multiomic data as the inputs and applied the default settings.

Evaluation metrics

All clustering and community detection results are measured using the adjusted Rand index (ARI) (40), normalized mutual information (NMI) (41), and Fowlkes-Mallows index (FMI) (42). Given two sets of clusterings (or communities) U (true labels) and V (predicted labels) on n samples, U contains r clusters {U₁, U₂, …, U_r}, and V contains s clusters {V₁, V₂, …, V_s}. n_ij denotes the number of samples belonging to U_i and V_j.

ARI, which is the adjusted version of the Rand index, is defined as

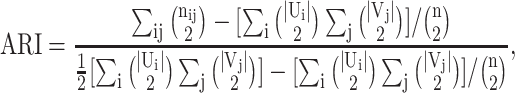(6)

where |U_i| and |V_j| denote the number of samples in U_i and V_j, respectively. ARI gives a similarity score between -1 and 1.

NMI is defined as the mutual information between U and V divided by the average entropy of U and V, which can be computed as

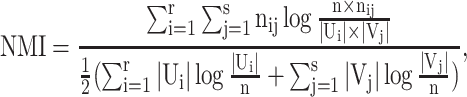(7)

giving a similarity score ranging from 0 to 1.

FMI is defined as the geometric mean between pairwise precision and recall, which is written as

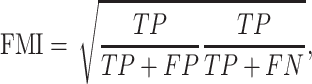(8)

where TP is the number of pairs of samples in the same cluster for both U and V; FP is the number of pairs of samples in the same cluster for V, but not for U; FN is the number of pair of samples in the same cluster for U, but not for V. FMI gives a score between 0 and 1.

RESULTS

SCOIT integrates RNA expression and DNA methylation data from sc-GEM

Sc-GEM jointly profiles RNA expression and DNA methylation at single-cell level (10). We applied SCOIT to analyze 224 human fibroblast cells in various stages of the reprogramming process sequenced with sc-GEM. Cells are labeled by their reprogramming stages. The RNA expression data contain 34 genes, and the DNA methylation data includes 27 genes. We construct the multiomic tensor with the union set of the genes.

SCOIT produces a global cell embedding matrix, i.e. one vector per cell, that gives each cell an integrated representation. According to the k-means clustering and the Leiden community detection (35) (see Cell clustering and graph construction subsection) with the cell embeddings generated by SCOIT and the benchmark methods, the SCOIT embeddings achieve the best performance according to various metrics (Figure 2A), with scAI ranked the second. We visualize the cell embeddings with uniform manifold approximation and projection (UMAP). As shown in Figure 2B, the projection of the SCOIT cell embeddings presents a linear structure that shares the same order as the trajectory of the reprogramming process. We also provide the projection of the embeddings learned by the benchmark methods in Supplementary Figure S5 for comparison.

Figure 2.

SCOIT reveals cellular heterogeneity and gene expression or methylation patterns from integrating gene expression and DNA methylation data of human fibroblast cells. (A) Comparison of k-means clustering performance (upper) and Leiden community detection performance (lower) with the input of cell embeddings generated by different methods, measured by ARI, NMI, and FMI. The higher bar corresponds to more concordance between the predicted and true labels. (B) The UMAP projections of the cell embeddings generated by SCOIT. Each point represents a cell color-coded by the true label. The arrow shows the time-ordered reprogramming process. (C) The projection values of SCOIT-generated pluripotency gene embeddings and somatic gene embeddings on cells from different programming time points. (D and E) The heatmap of correlations between the gene embeddings. Darker color indicates a higher Pearson correlation coefficient. The genes are grouped in red rectangles according to the gene expression pattern (D) and DNA methylation pattern (E).

Furthermore, we analyze the RNA expression and DNA methylation patterns using the global gene embedding matrix, i.e. one vector per gene. In the previous study (10), the genes in the RNA expression dataset are classified into pluripotent, intermediate, and somatic groups according to their transcriptional changes during the reprogramming process. Genes in the DNA methylation dataset are grouped into de novo methylation and demethylation according to their dynamic methylation patterns. Projecting the global embeddings for pluripotent and somatic genes onto cells (by an inner product) to study the dynamic gene distributions, We observe the increased expression of pluripotent genes and decreased expression of somatic genes across the programming process (Figure 2C). We compute the Pearson correlation coefficients between the genes using the global gene embedding matrix. Figure 2D and E shows higher correlations for genes in the same group, indicating that global gene embeddings capture shared patterns of RNA expression and DNA methylation.

SCOIT integrates RNA expression and chromatin accessibility data

We consider three datasets to evaluate the ability of SCOIT to integrate RNA expression and chromatin accessibility data. They are 8837 adult mouse kidney cells sequenced with sci-CAR (7), 5081 neonatal mouse cerebral cortex cells sequenced with SNARE-seq (11), and 10 309 adult mouse cerebral cortex cells sequenced with SNARE-seq (11). We independently perform dimensional reduction (see Omics data processing subsection) on the RNA expression and chromatin accessibility data to reduce the data size. SCOIT constructs the tensor with the processed matrices.

With the global cell embedding matrix generated by SCOIT, we perform k-mean clustering and community detection to label the cells. We also use the cell embeddings of the benchmark methods for comparison. SCOIT, TSNE, and Seurat achieve the best performance in k-means clustering, and SCOIT outperforms other methods in community detection for the three datasets (Figure 3A and C, Supplementary Figure S6A). The UMAP visualizations of the global cell embedding matrix (Figure 3B and D, Supplementary Figure S6B) show that cells with the same types cluster together and cells with different types are separated. Supplementary Figures S7–S9 show the UMAP visualization of the embeddings provided by the benchmark methods for comparison. The results suggest that the global cell embeddings learned by SCOIT give good representations of the cells.

Figure 3.

SCOIT reveals cellular heterogeneity from integrating RNA expression and chromatin accessibility data. (A and C) For data from adult mouse kidney cells sequenced by sci-CAR (A) and data from neonatal mouse cerebral cortices cells sequenced by SNARE-seq (C), we compare k-means clustering performance (upper) and Leiden community detection performance (lower) with the input of cell embeddings generated by different methods. ARI, NMI, and FMI measure the performance. (B and D) For data from adult mouse kidney cells sequenced by sci-CAR (B) and data from neonatal mouse cerebral cortices cells sequenced by SNARE-seq (D), we show the UMAP projections of the cell embeddings generated by SCOIT. Each point represents a cell color-coded by the true label. The cell types are shown on the top-right of the scatter plot.

SCOIT integrates RNA expression and proteomics data from PEA/STA

PEA/STA (12) provides a dataset containing RNA expression and proteomic data sequenced from 210 human glioblastoma cells to investigate the treatment effect of BMP4. Eighty-eight genes are measured in the RNA expression dataset, and 78 genes are measured in the proteomic dataset. A previous study (12) shows a low correlation between RNA expression and protein expression at the single-cell level in this dataset. SCOIT increases the coefficient of the penalty term for global gene embeddings, forcing the model to learn omic-specific gene embeddings (see Model regularization subsection).

We apply k-means clustering and community detection to global cell embeddings to distinguish cells with and without BMP4 treatment. SCOIT embeddings achieve the best clustering performance among all benchmark methods (Figure 4A). The UMAP visualization for cell embeddings from SCOIT also shows an apparent separation between control and BMP4-treated cells (Figure 4B and Supplementary Figure S10).

Figure 4.

SCOIT reveals cellular heterogeneity and the correlation between RNA and protein expression levels from integrating RNA expression and proteomics data of human breast adenocarcinoma cells. (A) Comparison of k-means clustering performance (upper) and Leiden community detection performance (lower) with the input of cell embeddings generated by different methods, measured by ARI, NMI, and FMI. (B) The UMAP projections of the cell embeddings generated by SCOIT. Each point represents a cell color-coded by the true label. The circles separate the untreated and treated cells. (C) The left bar plot shows the correlation between gene embeddings from RNA expression and proteomics generated by SCOIT. The higher bar corresponds to a higher Pearson correlation coefficient. The right scatter plots show the RNA and protein expression levels of CAV1, SOD1, ERBB2 and EPHA2, for all cells. The points are color-coded by the true label, sharing the legend in B. (D) The projections of SCOIT-generated gene embeddings on cells. Darker color indicates a higher value.

Next, we examine the correlations between RNA and protein expression levels. We compute the Pearson correlation coefficients between the RNA-specific and protein-specific gene embeddings. The distribution graph shows a lower correlation between the expression levels of RNA and proteins for most genes (Supplementary Figure S11), consistent with the previous report (12). We present the Pearson correlation coefficients for the genes measured in both omics in the bar plot in Figure 4C. We show the expression levels of RNA and proteins for the two genes, CAV1 and SOD1, with the highest correlations, and the two genes, ERBB2 and EPHA2, with the least correlations. CAV1 and SOD1 demonstrate strong correlations, while ERBB2 and EPHA2 demonstrate weak correlations, consistent with the Pearson correlation coefficients calculated from gene embeddings. The previous works show that several genes are activated after BMP4 treatment. We project the embeddings of these genes on all the cells, and the distributions present a significant enrichment on BMP4-treated cells (Figure 4D).

SCOIT integrates RNA expression and epitope data from CITE-seq

CITE-seq (13) simultaneously measures single-cell RNA expression and epitope data. We apply SCOIT to a CITE-seq dataset with 8617 cord blood mononuclear cells. The RNA expression dataset contains 36 280 genes, and the epitope dataset contains 13 surface proteins. SCOIT constructs a multiple-feature tensor (Supplementary methods S1.1) with the two datasets.

We conduct k-means clustering and community detection on the cell embeddings generated by SCOIT and the benchmark methods.We label the cells with the surface proteins, which are typically employed as markers to classify immune cells (13). With the identified labels, SCOIT and Seurat achieve superior performance according to various metrics (Figure 5A). Seurat automatically determines the importance of each omic and weights accordingly during integration, making it focus on more informative features. PCA, TSNE and MOFA+ have the poorest performance as they treat the features of each omics evenly. UMAP visualizations for cell embeddings are shown in Supplementary Figure S12.

Figure 5.

SCOIT reveals cellular heterogeneity and identifies distinct antigens from integrating RNA expression and epitopes data of cord blood mononuclear cells. (A) Comparison of k-means clustering performance (upper) and Leiden community detection performance (lower) with the input of cell embeddings generated by different methods, measured by ARI, NMI, and FMI. (B) The left scatter plot shows the UMAP projections of the ADT signals. Each point represents a cell color-coded by the true label. The right scatter plots show the projections of the SCOIT-generated epitope embeddings on cells. Darker color indicates a higher value.

We then investigate the correlations between the RNA and protein expression levels for the CITE-seq data. We identify six genes that encode the corresponding epitope and calculate the Pearson correlation coefficients between the gene embeddings and the 13 epitope embeddings generated by SCOIT. As shown in Supplementary Figure S13, gene embeddings have the highest coefficients with their encoded epitope embeddings, indicating a strong correlation between RNA and protein expression levels. We also show the projections of gene embeddings and their encoded epitope embeddings share similar distributions on cells.

Moreover, we apply epitope embeddings to study epitope distributions of different cell types. We identify eight cell-type-specific epitopes and project their embeddings onto the global cell embeddings. As shown in Figure 5B, embedding projection results in a higher value for cells with epitope expression. The result indicates that the embeddings capture the heterogeneity of epitopes.

SCOIT integrates SCoPE2 proteomic data and 10X RNA expression data

SCoPE2 (14) provides a proteomic dataset with 3042 proteins in 1490 single monocytes and macrophages and parallel measurement of RNA expression by 10X Genomics. Cells in the two datasets have been paired with the first shared principal components (14). Based on the set of genes from the two datasets that are combined, we construct a multiomic tensor as the input of SCOIT.

Applying the k-means clustering and community detection to the cell embeddings generated by SCOIT and the benchmark methods suggests that the SCOIT embedding outperforms all other embeddings (Figure 6A). The UMAP projections of the global cell embeddings given by SCOIT, Seurat, and Cobolt present a better collection of cell types (Figure 6B and Supplementary Figure S14). The results suggest that SCOIT generates informative representations for cells. Also, for the previously identified 30 most differential genes of macrophage and monocyte (14), we project the embeddings on the cells and observe a significant enrichment on the corresponding cell types (Figure 6B).

Figure 6.

SCOIT reveals cellular heterogeneity and dissects regulatory interactions by integrating RNA expression and proteomics data of innate immune cells. (A) Comparison of k-means clustering performance (upper) and Leiden community detection performance (lower) with the input of cell embeddings generated by different methods, measured by ARI, NMI and FMI. (B) The upper scatter plot shows the UMAP projections of cell embeddings generated by SCOIT. Each point represents a cell color-coded by the true label. The lower scatter plots show the projections of macrophage gene embeddings (left) and monocyte gene embeddings (right) on cells. (C) For transcription factors BRCA1, E2F1, HDAC1 and TP53, the violin plots show the correlation distributions between the gene embedding and its target gene embeddings (left for activated genes and right for repressed genes), generated by SCOIT. The dots inside the boxes show the Pearson correlation coefficients.

In addition, we apply global gene embeddings to study post-transcriptional gene regulation. We use TRRUST (43), a reference database for the human gene regulatory network, to identify target genes (including activated genes and repressed genes) for transcription factors (TF) in the SCoPE2 dataset. TFs with more than five activated genes and repressed genes in the SCoPE2 dataset are used for analysis to ensure statistical significance, resulting in four TFs, BRCA1, E2F1, HDAC1 and TP53 (Supplementary Table S4). Then we compute the Pearson correlation coefficients between the TF embeddings and their target gene embeddings to infer the correlations. As expected, TF embeddings correlate positively with activated gene embeddings and negatively with repressed gene embeddings (Figure 6C). The results also agree with previous findings (14).

SCOIT integrates scNMT-seq datasets across RNA expression, DNA methylation and chromatin accessibility

scNMT-seq (27) jointly profiles RNA expression, DNA methylation, and chromatin accessibility data from mouse embryonic stem cells in different embryogenesis stages. Among the 1940 cells in the RNA expression dataset, 1231 cells are absent in the DNA methylation dataset, while 1328 cells are absent in the chromatin accessibility dataset. SCOIT constructs a three-omics tensor for the datasets.

Applying the k-means clustering on the cell embeddings produced by SCOIT and the benchmark methods, we show the SCOIT-generated embedding exhibits superior clustering performance to all other embeddings (Figure 7A). Moreover, the UMAP projections of the cell embeddings obtained from SCOIT manifest a time-ordered embryogenesis trajectory, whereas other embeddings fail to capture the structure (Figure 7B and Supplementary Figure S15).

Figure 7.

SCOIT reveals cellular heterogeneity and imputes the DNA methylation and chromatin accessibility data for mouse embryonic stem cells. (A) Comparison of k-means clustering performance (upper) and Leiden community detection performance (lower) with the input of cell embeddings generated by different methods, measured by ARI, NMI and FMI. (B) The UMAP projections of the cell embeddings generated by SCOIT. Each point represents a cell color-coded by the embryogenesis timepoint. The arrow shows the time-ordered embryogenesis process. (C) The UMAP projections of the recovered DNA methylation and chromatin accessibility data from SCOIT. The upper scatter plots present the missing data as grey points, while the lower scatter plots annotate the missing data with RNA expression data, sharing the legend in B.

More than half of the cells measured in the RNA expression dataset are completely missing in the DNA methylation and chromatin accessibility data due to the limited sequencing resolution. In Figure 7C, we show the UMAP projections of the DNA methylation and chromatin accessibility data imputed with SCOIT. The recovered data display clear time-ordering structures, demonstrating that SCOIT can preserve the cellular heterogeneity from the datasets with frequent dropout events and effectively imputes the multiomic data.

SCOIT persists its performance with highly sparse and noisy data

To further assess the performance of SCOIT on highly sparse and noisy datasets, we add missing values and Gaussian noises to the sc-GEM dataset. We simulate the in silico sparse and noisy datasets under four settings: (i) setting 1–30% of the observations in the RNA expression dataset to the missing values; (ii) introducing Gaussian noise (mean: 5, variance: 1) to 1–30% of the observations in the RNA expression dataset; (iii) setting 1–30% of the observations in the DNA methylation dataset to the missing values and (iv) adding Gaussian noise (mean: 1, variance: 0.5) to 1–30% of the observations in the DNA methylation dataset.

We applied SCOIT to the simulated datasets and performed k-means clustering on the cell embeddings. The results are shown in Supplementary Figure S16. The performance remains stable for the datasets of various missing value distributions and noise amplitudes, with ARI ranging from 0.4857 to 0.5367, NMI ranging from 0.5912 to 0.6294, and FMI ranging from 0.5759 to 0.6095. The results indicate that SCOIT is robust to sparse and noisy datasets, which makes it suitable for single-cell sequencing data.

SCOIT effectively imputes multiomic data

To evaluate the imputation capability of SCOIT, we conduct the masking analysis for sc-GEM, PEA/STA, CITE-seq and SCoPE2 datasets under five simulation settings. In Simulation 1 and 2, we set 20% and 40% of the observations as missing values, respectively. In Simulation 3, 4 and 5, we set the observations from 10%, 20%, and 30% of the cells as missing values in one omic dataset, which is a common scenario in measurements of multiomic data. For each simulation, we repeat the experiment ten times. Then we quantify the performance with the Pearson correlation coefficients and the root mean square error.

As shown in Figure 8 and Supplementary Figure S17, SCOIT achieves the best recovery capacity across the simulated settings, with a 3.38–39.26% increase on the Pearson correlation coefficients and a 1.36–32.01% decrease on the root mean square error for sc-GEM dataset, a 0.57–9.29% increase on the Pearson correlation coefficients and a 3.55–18.47% decrease on the root mean square error for PEA/STA dataset, a 0.08–21.83% increase on the Pearson correlation coefficients and a 1.14–46.86% decrease on the root mean square error for CITE-seq dataset, and a 13.67–55.60% increase on the Pearson correlation coefficients and a 2.82–15.98% decrease on the root mean square error for SCoPE2 dataset.

Figure 8.

SCOIT achieves the best imputation performance on the sc-GEM dataset compared with SimpleImputer, KNNImputer, scImpute and DeepImpute. For sc-GEM dataset, we conduct the masking analysis under five simulation settings and compare the imputation performance concerning the Pearson correlation coefficient (upper) and root mean square error (lower). Higher Pearson correlation coefficients and lower root mean square error correspond to more concordance between the normalized imputed values and normalized original values. scImpute fails to generate results for the highly sparse data in Simulation 3, 4 and 5.

Notably, the advantage of SCOIT over the benchmark methods is more significant for Simulations 3, 4 and 5. Highly sparse datasets with one omic profile totally absent from subsets of the cells challenge the benchmark methods to model the distributions. However, SCOIT robustly imputes the data due to its ability to transfer and integrate information from various omics and cells.

DISCUSSION

Various single-cell multiomics sequencing protocols are emerging. Consequently, there is a growing need for a flexible and scalable method to pool the information from each molecular layer and deliver more comprehensive profiles for complex biological systems. Most existing methods treat each omics data as an independent matrix and conduct joint operations, such as dimension reduction or matrix factorization, on multiple matrices (4). Such inputs lead to a compromise on information loss. For instance, sc-GEM jointly profiles RNA expression and DNA methylation, with genes as the features. The matrix operation loses the corresponding gene information. Representing the multiomic data as a tensor can fully utilize the data, since each variable (omics, cell and gene) can be modeled as one dimension of the tensor.

We propose a probabilistic tensor decomposition framework to extract information from the multiomic tensor. Compared to the conventional tensor decomposition algorithm, such as canonical polyadic (CP) and Tucker, our framework generates global and local matrices to interpret multilayered biological information. With the adoptive penalty coefficients, users can obtain multiple sources of variation for various downstream analyses. In our case studies, we applied the local gene embeddings to analyze gene expression correlation among omics and the global gene embeddings to study post-transcriptional gene regulations.

SCOIT adjusts the coefficients automatically for the penalty terms according to the correlation between the multiple omics. For multiomic data with strong correlation, such as the sc-GEM dataset (Median Pearson correlation=0.7357), SCOIT employs a higher weight for the global gene embeddings; for multiomic data with low correlation, such as the PEA/STA dataset (median Pearson correlation = 0.1012), SCOIT gives a higher weight for the local gene embeddings. The settings of coefficients greatly affect the performance of SCOIT. For example, if we apply a high weight to the global gene embeddings for PEA/STA dataset, the k-means clustering performance tends to decrease from 0.7964 to 0.5781 for ARI, from 0.7909 to 0.5942 for NMI, from 0.8653 to 0.7183 for FMI.

A key feature of SCOIT is that it fully leverages the correspondence information, of both cells and genes, across omics, thus comprehensively linking the multiple molecular layers. In the experiments, we demonstrate that SCOIT generates more representative cell embeddings, quantified by cell clustering and community detection performance. Notably, SCOIT achieves a comparable performance with Seurat for the CITE-seq dataset, whereas it outperforms Seurat for the SCoPE2 dataset. This could be due to using 2,272 corresponding gene information across the RNA expression and proteomics datasets from SCoPE2. Also, the integration of gene information across omics facilitates a comprehensive gene analysis. In the case studies, we apply gene embeddings to explore gene enrichment, gene regulation, cross-omics gene expression, etc.

Another distinct characteristic of our tensor decomposition framework is the application of various distributions. High noise and sparsity have hindered single-cell sequencing data analysis. A probabilistic model with a suitable distribution can alleviate noise by modeling variations (44). SCOIT provides various distributions to deal with heterogeneous multiomic datasets. In our experiment, we apply the Gaussian distribution for the continuous data type and the negative binomial distribution for the count data with high variance (see Distribution and likelihood objective function subsection).

We expect the probabilistic tensor decomposition framework to be helpful beyond multiomic data integration. The framework applies to data with multiple variations. Each underlying source of variation is set as one dimension of the tensor, and the framework provides the embedding for each variable. For instance, our framework corrects the batch effect. Batch-specific systematic variations can be modeled as one dimension in the tensor. Using the tensor decomposition framework to the multi-batch tensor (batch× cell× gene), we obtain the embeddings for the three variables. The terms that include batch embeddings in the decomposition formulation can be removed for batch correction.

Data Availability

All the data in this paper are retrieved from public databases. SCOIT source code is deposited at Github https://github.com/deepomicslab/SCOIT and Zenodo https://doi.org/10.5281/zenodo.7886413.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

CityU Strategic Interdisciplinary Research Grant [7020005]. Funding for open access charge: CityU Strategic Interdisciplinary Research Grant [7020005].

Conflict of interest statement. None declared.