Abstract
Past swarm intelligence algorithms for solving UAV path planning problems have suffered from slow convergence, lack of complex constraints and guidance for local optimisation. It no longer meets the requirements of the Multi-UAV Cooperative Reconnaissance Mission Planning (MUCRMP) problem in the context of multi-radar detection. In this paper, a global optimisation model with the objective of a shorter distance within radar detection range of the UAV is proposed at first, including the planning of reconnaissance sequence between and within target groups, relative position to targets. More importantly, the imaging characteristics of the UAV and its minimum turning radius have been considered in depth in this study. Then an improved synthetic heuristic algorithm is proposed to solve the model, which obtains valuable reconnaissance mission plan. Finally, an example solution for a problem with 68 target point sizes is carried out, and the validity and feasibility of the model and algorithm are illustrated through the analysis given. Compared with the existing algorithms, the improved synthetic heuristic algorithm can give better anti-radar attributes to the UAV and efficiently improved the convergence speed in the specific reconnaissance mission.
Keywords: Multi-UAV, mission planning, hierarchical model, improved synthetic heuristic algorithm
Introduction
UAV can play the role of reconnaissance, intelligence, and surveillance in air combat, and has also begun to be applied in the fields of communication relay, electronic warfare, and anti-submarine warfare in recent years.1-4 Therefore, because of the strategic position of UAVs in modern area search and strike forces, they receive a lot of attention. The main task of UAV operations is to plan their path. The main objective of this task is to design a flight path to the target at the lowest combined cost, including the lowest probability of damage, the least amount of reconnaissance time and other factors, while meeting the performance requirements of the UAV. Because the mission execution environment of UAVs is relatively harsh, a single UAV can easily be countered by radio radar and other anti-reconnaissance equipment, interfered with, or even destroyed during the execution of the mission.5,6 Therefore, the cooperative reconnaissance of multi-UAV is particularly important.
Multi-UAV path planning is a prerequisite for multi-UAV cooperative reconnaissance. To efficiently complete the established combat missions, multiple UAVs must be researched and assigned.7–9 The process of mission planning usually involves professional knowledge in the field of control, operations research, decision theory, synergetics, information theory, artificial intelligence, communication theory and so on in academic areas.10–13
Taking mission requirements and environmental factors under multiple constraints into account, multi-UAV cooperative reconnaissance mission planning (MUCRMP) is an extremely complicated and challenging task.14–18 Furthermore, since MUCRMP is a traveling salesman problem essentially,19–21 it is an NP-hard problem in terms of complexity,22–26 and there is no method to find the optimal solution in the polynomial algorithm time, which increases a certain degree of difficulty for MUCRMP.
In recent years, many scholars have been engaged in the research of MUCRMP. Most of the research work focuses on the use of intelligent random search algorithms for optimization, such as ant colony optimization (ACO), 27 particle swarm optimization (PSO), 28 simulated annealing (SA) 29 and genetic algorithm (GA).30–32 In addition, part of the researchers pay attention to mission planning based on game theory33–35 and opportunity learning methods. 36 Chen et al. 27 propose a cooperative task assignment model and use ACO to solve it considering various targets under multiple constraints. Gao et al. 28 combine an improved two-stage resampling method with PSO and apply it to the UAV task assignment. Turker et al. 29 establish a reasonable task clustering optimization index and use SA combined with it to match the reconnaissance order. Ruan et al. 33 compare several existing metaheuristic optimization algorithms and propose a new method based on GT to analyze and design alliance formation games to determine the coverage deployment plan of UAVs. Yang et al. 36 propose a novel searching algorithm with the opportunity learning method to carry out the path planning mission and conduct a certain mathematical analysis of the search strategy for the UAVs maneuvering assignment. Although the content of these studies is related to the mission planning in the reconnaissance process of UAVs, they only pay attention to the situation where all UAVs take off from the same base. Some research shifted to the area of multi-base multi-UAV cooperative reconnaissance mission planning (M-MUCRMP),37–39 and solve the model using combined searching algorithms. Despite this improvement in MUCRMP, the problem of how to effectively evade the enemy's radio counter-reconnaissance methods has not been paid attention to in the current research process. There is also a lack of consideration in maneuvering turn for UAVs.
According to the requirements of the battlefield environment, starting from different bases is often more conducive to the successful execution of the mission for multi-UAV, in the process of the mission. Meanwhile, considering the maneuvering characteristic of UAVs and effectively evading detection devices, such as radar, are also issues that need to be resolved urgently. Based on the development of existing UAV mission planning, this paper proposes a multi-radar multi-target multi-base multi-UAV cooperative reconnaissance mission planning method that has not been studied before, which is more adapted to the battlefield environment and can achieve greater mission effectiveness. At the same time, an improved synthetic heuristic algorithm (ISHA) is proposed as a corresponding solution for an optimization.
The remainder of this paper is organized as follows. The hierarchical solution model based on the global optimization goal is presented in detail in Section 2. The design process of the proposed ISHA and the assignment of are given in Section 3. Section 4 describes an example of mission planning under the background of multi-radar detection interference and verifies the superiority of the proposed method through comparison. Finally, Section 5 delivers the conclusions and gives further research directions.
Proposed model
Problem description
For the detection range of radar, the distance generally refers to the linear distance between the radar station coordinates and the UAVs’ center coordinates in three-dimensional space. However, due to the low cruise altitude of the UAV, the radar detection distance can be approximated as the projection distance on the horizontal plane, for large-scale radar detection. The calculation of the shortest trajectory is also based on the proposed projection distance in a two-dimensional plane.
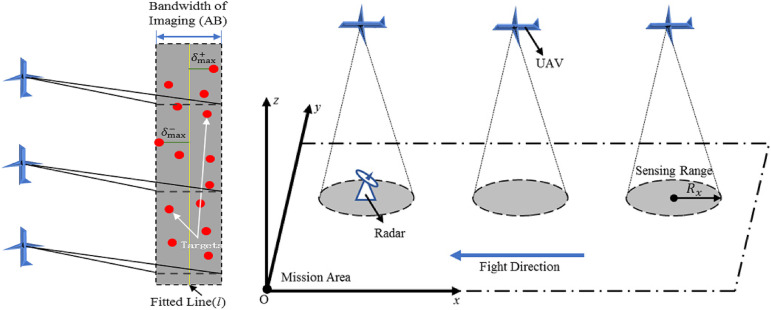
In terms of sensors mounted on UAVs, the most widely used applications are the unilateral side-view imaging sensor (indicated by S-1) and the downward circle-scanning imaging sensor (indicated by S-2) at present. S-1 has higher imaging resolution and better imaging effect, but it can only be imaged on one side, the imaging range is limited and the flight attitude of UAV is highly required. Compared with S-1, S-2 can detect a larger circular area, but the corresponding imaging resolution is lower. In response to the modern battlefield's requirements for high timeliness and reliability of intelligence information, UAVs carrying different sensors usually conduct reconnaissance missions at the same time or separately.
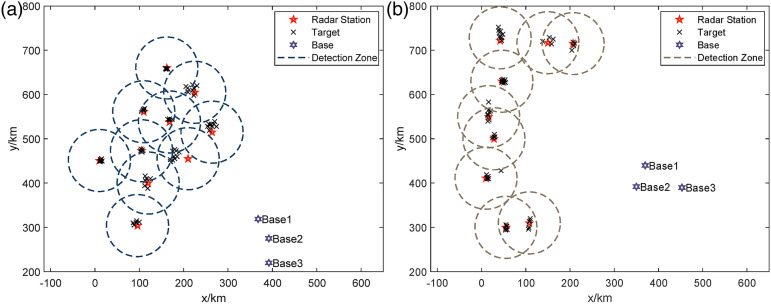
In a target group where radars are deployed, the projections of the radar detection range on the two-dimensional plane are usually adjacent to each other, and some of the projection areas even overlap. This type of cluster deployment can play a great counter-productive effect on the execution of UAV reconnaissance missions and cause great difficulties for There are currently two common deployment modes of radar cluster. Figure 1(a) shows a type of radar cluster with lumpy distribution on the two-dimensional plane while Figure 1(b) shows another type of radar cluster with a striped distribution. To serve the complex and difficult reconnaissance environment of the modern battlefield, the problem in this paper is launched with the interference background of the radar cluster.
Figure 1.
Deployment modes of radar cluster: (a) Radar cluster with lumpy distribution; (b) Radar cluster with a striped distribution.
Given the characteristics of UAVs, the problem of can be described as: planning UAVs’ reconnaissance strategy and trajectories to achieve optimal trajectory based on evading radar and other anti-reconnaissance equipment for UAV groups deployed in multiple strategic points in advance, with the mission of given reconnaissance area and targets. During the flight of UAVs, their maneuverable turning ability and detection sensors should be considered for optimization.
Model establishment
In the research process of this paper, the following assumptions are made for further simplification:
The various parameters in UAVs of the same model, such as speed and longest cruise time, are the same, ignoring the performance differences caused by the manufacturing process;
The speed of UAVs during the execution of the mission is always equal to the cruise speed, and the duration of take-off and landing is ignored; One of the bases is that within a certain turning radius in which the turning angle is not large, the speed change brought about by a change in direction is not significant. The drones are exceptionally fast and unaffected by power, environment, etc. throughout the process.
The impact of maneuvers on the flight speed and fuel consumption can be ignored during the flight of UAVs, such as climb, dive, and turn.
is a global optimisation problem with the objective of a shorter distance within radar detection range of the UAV. Under certain cruise speed conditions, an optimisation model with hierarchical characteristics is constructed with the flight trajectory of the UAV within radar detection range as the optimisation objective 40 . This model adds the consideration of UAV imaging characteristics and minimum turning radius. The mathematical model is described as follows.
| (1) |
| (2) |
Where (1) is the total path distance within the effective detection range of the defending radar, is a UAV reconnaissance mission, is the base of UAVs, is the imaging sensor of a UAV, is the takeoff time of a UAV, and is the reconnaissance path for the mission.
The objective in (1) is to minimise the path distance of the UAV within the radar detection range. This can be equated to the detection time of the radar under the assumption that the speed of the UAV remains constant. Furthermore, the optimisation of the mathematical model subjects to the following constraints 40 .
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
Model Solving Based on ISHA
is essentially a derivative form of the traveling salesman problem (TSP) 40 . It belongs to the category of NP-hard problems, and there is no algorithm that can solve this kind of problem in polynomial time. Therefore, heuristic algorithms are used to approximate the optimal solution 20 .
In this paper, due to the multiple constraints and complex maneuvering process analysis in it is necessary to use a hierarchical optimization model to solve the problem. The planning context of this paper is more complex and requires more elements to be considered, so it cannot be treated as an ordinary path planning program. Single heuristic algorithms, such as ACO and GA, consider only the final optimization objective during execution. In dealing with multi-constrained multi-objective problems, the current mainstream adoption of penalty functions and feasibility laws still suffers from the disadvantages of complex parameters and difficult operations. It is difficult to deal with how to treat feasible and infeasible solutions separately, and the imbalance problem between constraints and optimization objectives. Thus it cannot comprehensively analyze factors involving multi-base deployment optimization and UAV maneuvering characteristic. As a result, the final mission planning results are far from satisfactory. So this paper constructs the improved synthetic heuristic algorithm (ISHA) that combines the nearest neighbor insertion, 2-optimization (2-OPT) method and coverage search. Given the specific problems in the radar detection interference environment, we select the initial reconnaissance point, then establish the initial path between and within the target groups according to this point. Based on the output path, the order of reconnaissance between target points is changed in complex path intervals, to achieve iterative optimization. Finally, we perform coverage search optimization according to the UAV reconnaissance imaging mode, to determine the UAV reconnaissance points as the result.
Reconnaissance sequence between target groups
In the light of the complexity of all target positions of each group can be considered as being all gathered at the location of corresponding radar stations firstly, according to the idea of hierarchical optimization. In this case, the objective of searching optimal path can be expressed as:
| (13) |
where represents the path to traverse each target group, is a collection of radar station targets.
To lay the foundation for further optimization, we apply a two-stage synthetic heuristic algorithm which is a part of ISHA and combines the nearest neighbor insertion and 2-OPT method, to construct the single optimal route at first The solution process is summarized as follows:
Select the initial target point. In all target points of the mission planning, an appropriate target should be selected as the starting point according to the arrangement of radar cluster and location of the UAV bases, which is recorded as . The closest point to among the remaining targets, which is recorded as , should also be found to form the first path .
Insert neighbor points. One of the remaining target points , which is closest to each other, is found. In this case, a sub-path in the existing path sequence can be found to insert the point , making the difference between the newly created path and the original sub-path minimized. So that, the original path is expanded into .
Form a complete initial path. The searching process in Step2 is repeated until the obtained path contained all target points that need to be reconnoitered. At this time, the path is the required initial path constructed by ISHA.
Set initial conditions for secondary optimization. According to the magnitude of target points, the maximum number of iterations in secondary optimization is set. The counter in ISHA initializes parameter that records the number of iterations. Then the initial path constructed in Step3 is added to the optimizer.
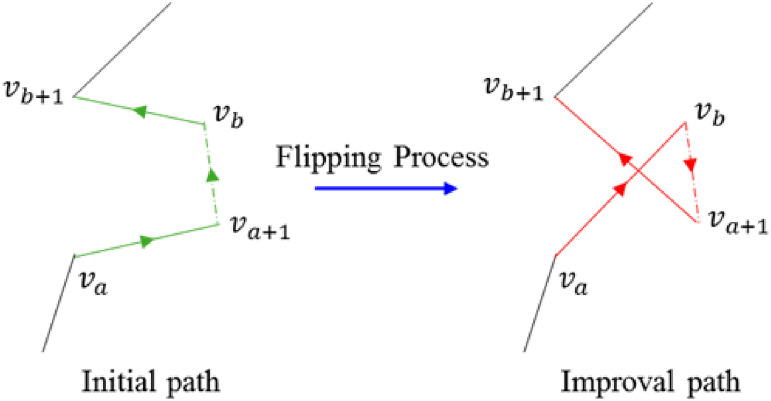
Flip the reconnaissance order to get a new path. In the path sections with dense target points, a sub-path is randomly selected. The order of point and in this path is reversed and add the path before to the new path is unchanged. Flip the path between and by its number and add it to the new path. As is shown in Figure 2, the original path becomes .
Optimize the reconnaissance sequence by iteration searching. For the new path obtained in Step5, if the length of the new path is not less than that of the original one, which means , the counter plus one. Otherwise, the original path is replaced with a shorter new one and is reset to zero. The process returns to Step5 after judgment.
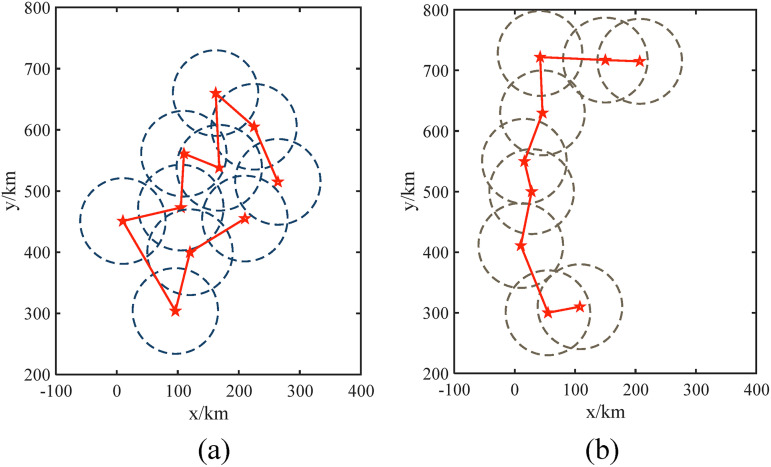
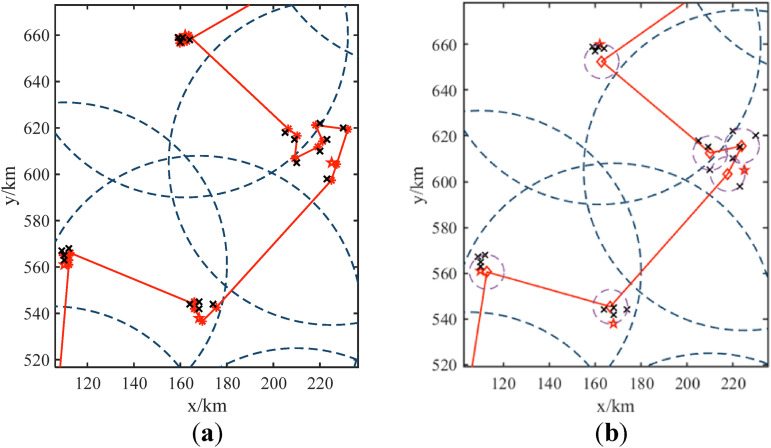
Output the result. The searching is stopped when , in Step6. At this time, the output path is the global optimal one. The mission planning results between target groups with lumpy and striped distribution are shown in Figure 3(a) and Figure 3(b) respectively.
Figure 2.
Flipping process of reconnaissance sequence.40
Figure 3.
Optimal reconnaissance sequence between target groups: (a) Sequence between target groups with lumpy distribution; (b) Sequence between target groups with stthe riped distribution.
It can be seen from the path planning results that there is no repeated crossing path in the optimized reconnaissance plan. Meanwhile, the extra cruise time can be avoided with all target groups covered, and the reconnaissance sequence between target groups in the radar cluster is effectively planned.
Detailed sequence within target groups
After determining the sequence of reconnaissance paths between target groups, it is necessary to plan specific reconnaissance paths for multiple targets in each target group. In the model-solving process at this stage, the impact of sensors carried by UAVs and their corresponding detection imaging modes on the detection position of UAVs is not considered for the time being. To find the shortest path that can traverse all target points in each target group, the objective in this stage is as follows:
| (14) |
where represents the reconnaissance sequence of the path in the target group i, involving . is the target set in the target group i.
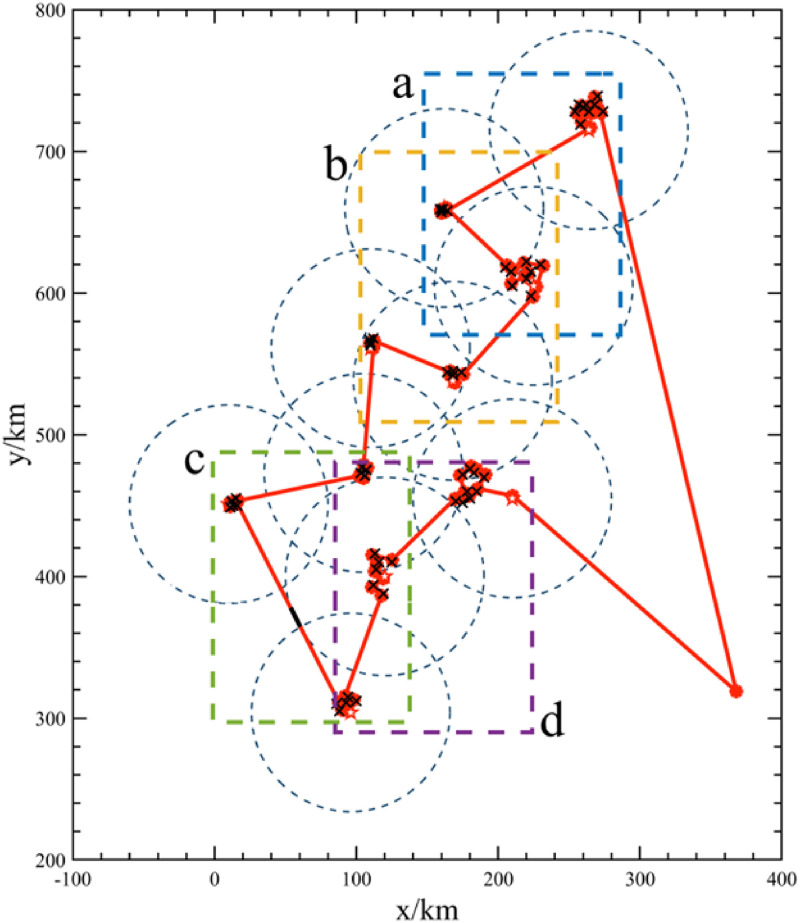
Because the detection imaging mode of the UAV is not considered for path optimization within the target group, it is still only necessary to use the two-stage synthetic heuristic algorithm for the time being. The sequence of the reconnaissance path in the constructed target groups is shown in Figure 4.
Figure 4.
Optimal reconnaissance sequence within target groups. A-d represents magnified path sequence in different sections respectively.
It is obvious from the magnified target reconnaissance sequence that the path connection between the small targets is mainly based on the shortcut connection form, and the coordinate positions of targets belonging to the adjacent group are also taken into account. The result shows that ISHA can not only play a great role in the optimization of the path reconnaissance sequence between large-scale target groups but is also effective when applied to the path planning of small targets within specific target groups.
Location optimization considering imaging sensor
Two imaging sensors are considered for UAVs in this paper. S-1 represents the unilateral side-view imaging sensor, while S-2 represents the downward circle-scanning imaging sensor. The imaging modes of two sensors are shown in Figure 5.
Figure 5.
The detection principle of the S-1 imaging sensor (top), Detection principle of the S-2 imaging sensor (bottom).
The UAV's imaging mechanism constraint is considered on the basis of determining the reconnaissance order of each target point to reconnoitre more targets with fewer reconnaissance times. This study focuses on the greedy algorithm of coverage search to form a complete ISHA scheme. The basic idea of coverage search is to include as many points as possible around a selected target point, thus reducing the number of searches.40
For UAVs carrying the S-1 imaging sensors, if the reconnaissance mission is to be completed, the target points need to be within the imaging bandwidth of UAVs in uniform linear motion, according to the distribution characteristics of the radar cluster. The reconnaissance sequence obtained after the first two-stage optimization in ISHA is used as the new optimization objective. The target in the sequence is added into a reconnaissance set in turn starting from the first one until the range of this reconnaissance set exceeds the imaging bandwidth. Then the second reconnaissance set is established till the completion of the whole reconnaissance mission.
Since it is necessary to judge whether the target is within the imaging bandwidth of a reconnaissance set in real-time, target points in the same set need to be fitted with the first-order linear least squares method. As is shown in the top half of Figure 5, the distance between each point and the fitted line l is calculated. In a target set, if the distance between the farthest two points on both sides of l is less than the imaging bandwidth , it can be considered that these targets belong to the same reconnaissance set. The UAV carrying the S-1 imaging sensor needs to move at a constant speed in a straight line, and the distance from one side of it to the reconnaissance set should be within a certain range. It maneuvers to the next imaging zone for target reconnaissance after completing the current mission. The path planning result of the UAV carrying the S-1 imaging sensor is shown in Figure 7(a).
Figure 7.
Path planning results of UAVs carrying different imaging sensors: (a) Path planning result of the UAV carrying the S-1 imaging sensor; (b) Path planning result of the UAV carrying the S-2 imaging sensor.40
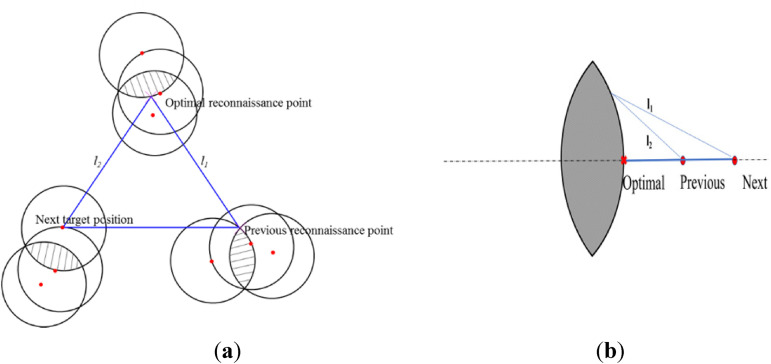
For UAVs carrying the S-2 imaging sensors, the distance between the reconnaissance position and targets needs to be not greater than the maximum imaging distance. Based on the obtained sequence, the reconnaissance position points which can detect multiple targets at the same time are looked for. The ultimate goal is to reach the requirement that the detection range of UAVs can cover all target points with as little cruise distance as possible.
Because of the characteristics of the S-2 imaging sensor, all target points are taken as the center of each circle, and the maximum imaging distance of the sensor is made to be the radius. Therefore the effective detection range for each target and areas where the detection range overlaps are obtained. According to the previous reconnaissance point and the next target point, the optimal reconnaissance point is chosen in the current area. The specific process is to use a straight line to connect the next target point with the previous reconnaissance point, and then find an optimal point that has the smallest sum of the distance from the two ends of the line to it, as the current reconnaissance point. The coverage searching process is shown in Figure 6, and the path planning result of the UAV carrying the S-2 imaging sensor is shown in Figure 7(b).
Figure 6.
The process of determining the reconnaissance point based on the coverage search: (a) General conditions;(b) Special case.
The path planning results with two different types of imaging sensors show that: The three-stage ISHA fused with the coverage search mechanism can accurately optimize the specific reconnaissance position according to the imaging characteristics of sensors on UAVs.40 It offers a viable technical solution for a more tailored model in complex detection environments.
Maneuvering turn
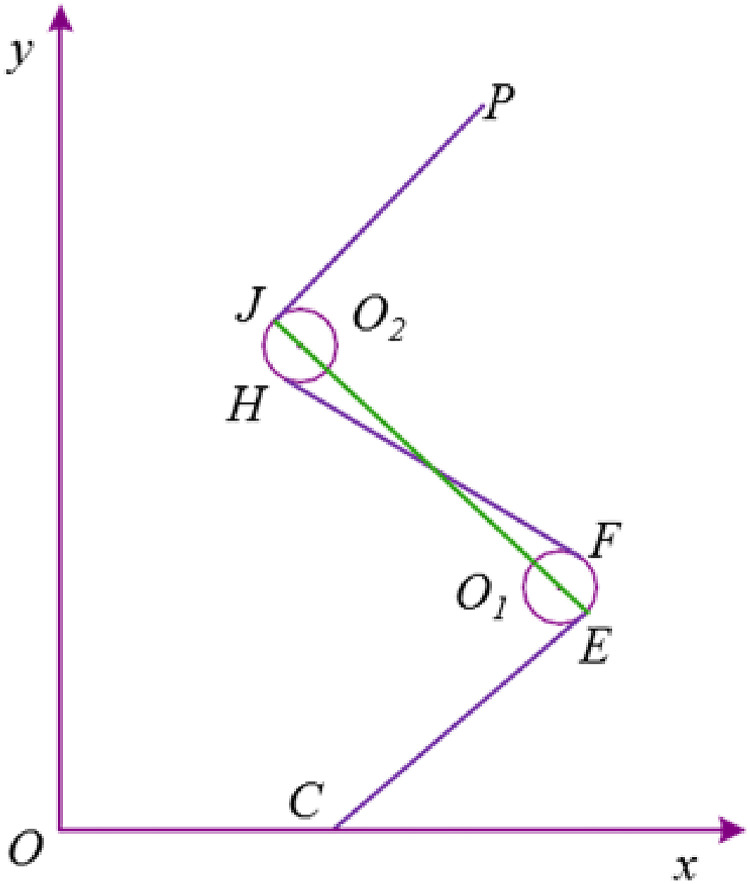
In the process of determining the sequence and location of the reconnaissance, the movement of the UAV at the turn needs to be optimized according to its maneuvering characteristic. In Figure 8, we determine the coordinates of the reconnaissance point C , point E , point J , and point P , then construct the UAV turning radius variable r, which is also the radius of circle and . The above variables are used to serve for the optimization of the broken line at the turning point. To get a smooth turning trajectory, the coordinates of point F and point H need to be solved. In the beginning, we need to make sure that the four points, involving the centers of circle and , point E and point J, are on the same straight line. The straight line is expressed as:
| (15) |
and the distance formulas from the centers of the circle and to the straight line CE and JP are constructed respectively:
| (16) |
then the center coordinates of and are gotten as and , and a system of equations based on them is as follows:
| (17) |
Figure 8.
The optimization mechanism of maneuvering turn.
So far, the two coordinates, and are solved, which means that all coordinate parameters in maneuvering turn are obtained. The corresponding optimization effect is also shown in Figure 8.
Final plan
In the above analysis, by fusing the characteristics of the nearest neighbor insertion, 2-OPT method and coverage search, a new ISHA is designed to plan the reconnaissance path. After optimizing the reconnaissance sequence of multiple UAVs, the obtained path is divided and assigned again in view of the current deployment of UAV bases (Constraint 12), and the specific requirement (Constraint 10). Therefore, UAVs departing from different bases perform segmented reconnaissance missions, and the plan of is established finally.
Example simulation
In this simulation experiment, to make the experimental data and analysis results have certain representation, we choose target groups fusing the characteristics of lumpy and striped distribution. 58 ordinary targets and 10 radar stations are set up, and the effective detection range of the attached radar to the UAV is 70 km. Target points of the radar station are named from A01 to J01 in turn, the other common target points are named according to the cluster division, and the specific division is shown in Table 1. There are also three UAV bases named , and , one UAV is deployed at each base.
Table 1.
Cluster division of target points.
| Cluster code | Target code | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | A01 | A02 | A03 | A04 | A05 | A06 | A07 | A08 | A09 | A10 |
| B | B01 | B02 | B03 | B04 | B05 | ---- | ---- | ---- | ---- | ---- |
| C | C01 | C02 | C03 | C04 | C05 | C06 | C07 | C08 | C09 | ---- |
| D | D01 | D02 | D03 | D04 | D05 | ---- | ---- | ---- | ---- | ---- |
| E | E01 | E02 | E03 | E04 | E05 | ---- | ---- | ---- | ---- | ---- |
| F | F01 | F02 | F03 | F04 | F05 | ---- | ---- | ---- | ---- | ---- |
| G | G01 | G02 | G03 | G04 | G05 | G06 | ---- | ---- | ---- | ---- |
| H | H01 | H02 | H03 | H04 | H05 | H06 | ---- | ---- | ---- | ---- |
| I | I01 | I02 | I03 | I04 | I05 | I06 | I07 | ---- | ---- | ---- |
| J | J01 | J02 | J03 | J04 | J05 | J06 | J07 | J08 | J09 | J10 |
Table 2.
Cruise time in the detection range of radar stations.
| Time(h) | ||||
|---|---|---|---|---|
| 30 | 50 | 70 | 90 | |
| Type of Algorithm | ||||
| ACO | 5.82 | 7.8 | 8.02 | 8.34 |
| PSO | 5.28 | 6.95 | 7.16 | 7.53 |
| AGA | 4.7 | 6.2 | 6.8 | 7 |
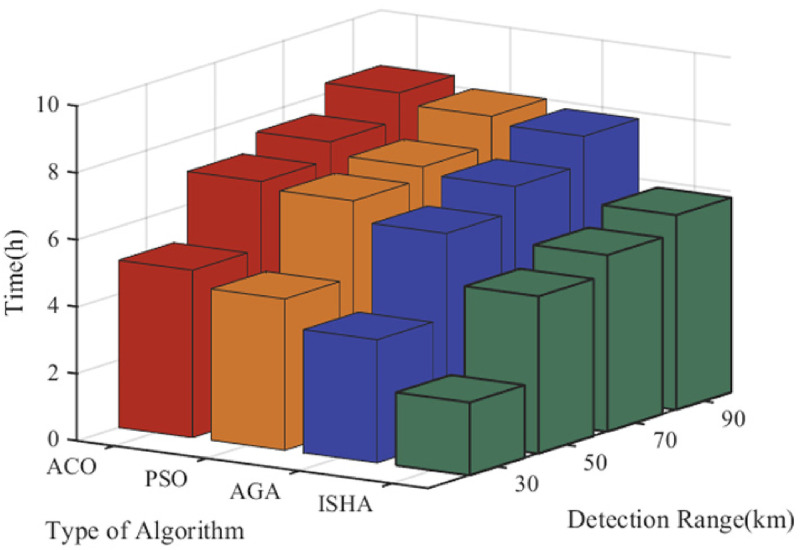
| ISHA | 2.18 | 3.68 | 4.52 | 5 |
Table 3.
Algorithm parameters.
| Algorithm | ACO | PSO | AGA | ISHA |
|---|---|---|---|---|
| Parameters | α = 3;β = 3 | C1=1.49445 | K1 = 1.0 | Max_count = 5000 |
| m = 50 | C2=1.49445 | K2 = 0.5 | ||
| Q = 100 | ω = 0.8 | K3 = 1.0 | ||
| Ρ = 0.5 | N = 200 | K4 = 0.5 |
UAVs in this simulation environment are all equipped with the S-1 imaging sensors whose detection bandwidth is 2 km. The cruise speed is 200 km/h, as the longest cruise time and altitude are 10 h and 1500 m respectively. Besides, the minimum turning radius is 70 m and the effective detection range of the radars attached to each target group to the UAV is 70 km. If multiple UAVs are used to perform reconnaissance missions at the same time, the distance between the two UAVs must be less than 200 m. After completing the reconnaissance mission, each UAV needs to return to the original base.
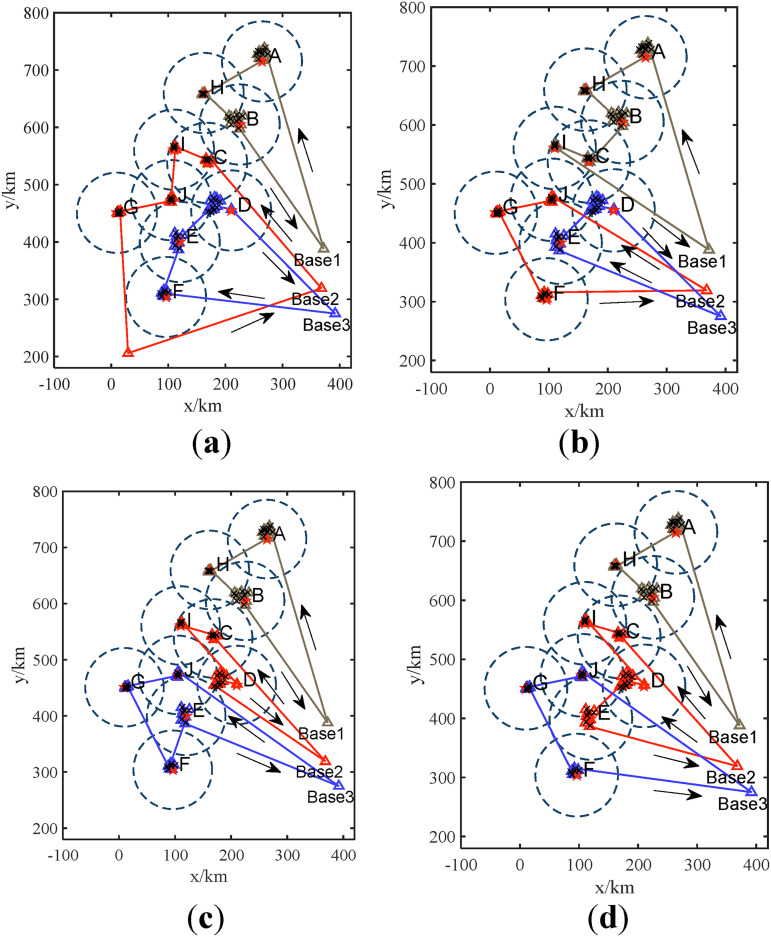
According to the characteristics of the mission example, the hierarchical optimization model and ISHA constructed in this paper can be applied to the above example, for analyzing the optimization problem in the mission instance layer by layer. For the realization of ISHA, the coordinates of bases and target groups, as well as the characteristic data of sensors and maneuvering turn need to be brought into the algorithm process. Firstly, the initial path built on the principle of nearest neighbor insertion is given to traverse all target points. Then the sequence of reconnaissance is flipped to determine a more reasonable path. Lastly, coverage search is applied to get the optimal reconnaissance position based on the obtained sequence and imaging characteristic of the sensor. The result of the final using ISHA is shown in Figure 9(a).40 For comparison, we apply the adaptive genetic algorithm (AGA), particle swarm optimization (PSO), and ant colony optimization (ACO) to solve the same path planning mission, the results are shown in Figure 9(b), Figure 9(c) and Figure 9(d) respectively.
Figure 9.
Final path planning results using different optimization algorithms: (a) Final path planning result using ISHA;40 (b) Final path planning result using AGA; (c) Final path planning result using PSO; (d) Final path planning result using ACO.
It can be seen from the above results that the reconnaissance sequence obtained by ISHA can make UAVs choose paths with the sparser radar coverage. To quantitatively show the comparison of the results obtained by different algorithms, the detection range of each radar station is set to the distance from 30 km to 90 km with the 20 km interval. In this case, the total cruise time of UAVs in different detection ranges can be displayed visually, under the premise of a certain speed. The comparison result is shown in Figure 10, in the form of a three-dimensional histogram. It is proved that ISHA can effectively reduce the cruise time under detection, compared with the other three optimization algorithms, and gives better anti-radar attributes to each UAV.
Figure 10.
The comparison of UAVs’ cruise time in the detection range of radar stations.
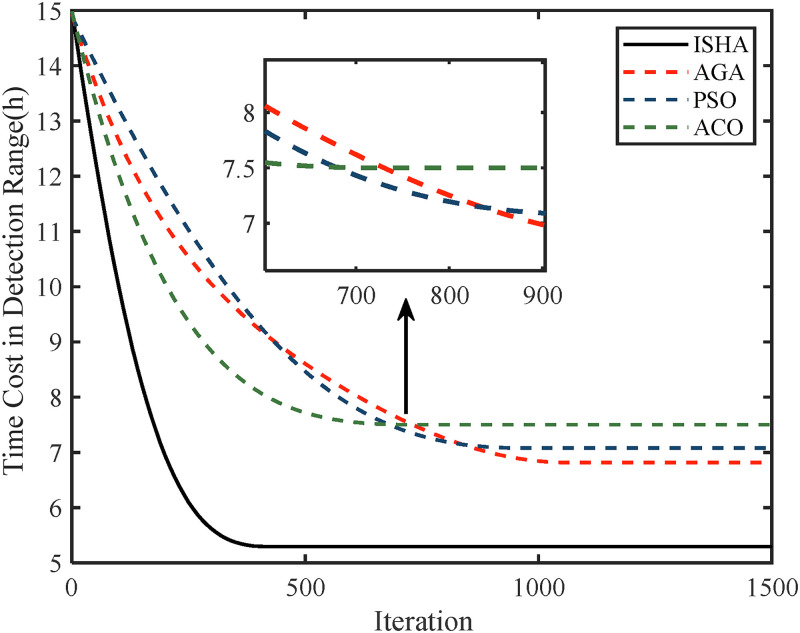
Furthermore, the optimization process of four algorithms with the number of iterations needs to be displayed to test the convergence speed of each optimization algorithm. We set the detection range of each radar station as 70 km. In this case, the convergence process for the algorithms is shown in Figure 11. The simulation results prove that ISHA not only demonstrates outstanding performance in making UAVs avoid radar detection, but also has advantages in convergence speed compared with the other three optimization algorithms.
Figure 11.
The optimization process of four different algorithms.
Conclusions
In this paper, we propose a hierarchical mathematical model for , and a novel optimization algorithm which is ISHA. The improved algorithm is applied to solve the model.
In , a hierarchical mathematical model, the optimization goal of the least time within the detection range, and the prerequisite of multiple UAVs on different bases are both taken into consideration. Under these circumstances, an optimization model that is more in line with a military background is established and implemented hierarchically. Various constraints including the imaging characteristics of UAVs equipped with sensors and maneuvering characteristics are also analyzed based on the position and attitude requirements of UAVs during the execution of the mission. To reduce the complexity of the required model, the optimization goal can be converted from the least time in detection range to the shortest path under the premise of maintaining the cruise speed.
To solve the model, we constructed the ISHA according to the characteristics of many existing optimization algorithms. The sequence between and within the target groups is solved first, then the specific reconnaissance positions to target points are found for optimization. Finally, the hierarchical model and proposed algorithm are applied to a mission planning example, with the reliability of the obtained result analyzed. The experimental results show that this novel method can give full play to the combat performance of UAVs, and solve the problem of optimal reconnaissance path planning not only in MUCRMP but also in .
But there are also certain flaws in this paper. In the process of building the model, since the flight process of the UAV is a dynamic process, the performance parameters of its various systems may also change continuously with the complex environment and cruise time, which is also a problem that we need to consider further. Moreover, the drone motion is divided into two different ways: constant speed and variable speed. A variable speed will be more in line with the reality of the situation.
In future work, we need to consider the comprehensive impact of more specific environmental factors on multi-UAV coordinated reconnaissance. The UAV's track is no longer just set as a cruise flight maintained at a stable altitude, but changes with terrain or climatic conditions. In addition, the structural differences of UAVs need to be taken into account for further research work.
Footnotes
Author contributions: Conceptualization, Y.S. and Y.L.; methodology, Y.S.; software, Y.S. and B.J.; validation, Y.S, Z.W. and Y.S.; formal analysis, Y.S.; investigation, Y.S.; resources, Y.S.; data curation, Y.S.; writing—original draft preparation, Y.S.; writing—review and editing, Y.S., Y.L., B.J., Z.W. and X.D.; visualization, Y.S.; supervision, Y.S.; project administration, Y.L.; funding acquisition, Z.W. All authors have read and agreed to the published version of the manuscript.
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
ORCID iD: Yanfei Liu https://orcid.org/0000-0002-8372-0307
References
- 1.Nex F, Remondino F. UAV For 3D mapping applications: a review. Appl Geomat 2014; 6: 1–15. [Google Scholar]
- 2.Chen Y-B, Luo G-C, Mei Y-S, et al. UAV Path planning using artificial potential field method updated by optimal control theory. Int J Syst Sci 2016; 47: 1407–1420. [Google Scholar]
- 3.Zhao Y, Yan L, Chen Y, et al. Robust and efficient trajectory replanning based on guiding path for quadrotor fast autonomous flight. Remote Sens 2021; 13: 972. [Google Scholar]
- 4.Liu Y, Qi N, Yao W, et al. Cooperative path planning for aerial recovery of a UAV swarm using genetic algorithm and homotopic approach. Appl Sci 2020; 10: 4154. [Google Scholar]
- 5.Kothari M, Postlethwaite I. A probabilistically robust path planning algorithm for UAVs using rapidly-exploring random trees. J Intell Robot Syst Theory Appl 2013; 71: 231–253. [Google Scholar]
- 6.Hutchison M, editorA method for estimating range requirements of tactical reconnaissance UAVs. Proceedings of AIAA’s 1st technical conference and workshop on unmanned aerospace vehicles; 2002 20–23 May; Portsmouth, Virginia: American Institute of Aeronautics and Astronautics. [Google Scholar]
- 7.Khoroshiltseva M, Slanzi D, Poli I. A pareto-based multi-objective optimization algorithm to design energy-efficient shading devices. Appl Energy 2016; 184: 1400–1410. [Google Scholar]
- 8.Wang Y, Wan W, Gou S, et al. Vision-based decision support for rover path planning in the chang’e-4 mission. Remote Sens 2020; 12: 624. [Google Scholar]
- 9.Tang A-D, Han T, Zhou H, et al. An improved equilibrium optimizer with application in unmanned aerial vehicle path planning. Sensors 2021; 21: 1814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mathew N, Smith SL, Waslander SL. Multirobot rendezvous planning for recharging in persistent tasks. IEEE Trans Robot 2015; 31: 128–142. [Google Scholar]
- 11.Deng Q, Yu J, Wang N. Cooperative task assignment of multiple heterogeneous unmanned aerial vehicles using a modified genetic algorithm with multi-type genes. Chin J Aeronaut 2013; 26: 1238–1250. [Google Scholar]
- 12.Marzoughi A, Savkin AV. Autonomous navigation of a team of unmanned surface vehicles for intercepting intruders on a region boundary. Sensors 2021; 21: 297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jo Y-i, Lee S, KH K. Overlap avoidance of mobility models for multi-UAVs reconnaissance. Appl Sci 2020; 10: 4051. [Google Scholar]
- 14.Tahar DN, Yalaoui F, Chu C, et al. A linear programming approach for identical parallel machine scheduling with job splitting and sequence-dependent setup times. Int J Prod Econ 2006; 99: 63–73. [Google Scholar]
- 15.Battulwar R, Winkelmaier G, Valencia J, et al. A practical methodology for generating high-resolution 3D models of open-pit slopes using UAVs: flight path planning and optimization. Remote Sens 2020; 12: 2283. [Google Scholar]
- 16.Bruggemann TS, Ford JJ, Walker RA. Control of aircraft for inspection of linear infrastructure. IEEE Trans Control Syst Technol 2010; 19: 1397–1409. [Google Scholar]
- 17.Ali M, Siarry P, Pant M. An efficient differential evolution based algorithm for solving multi-objective optimization problems. Eur J Oper Res 2012; 217: 404–416. [Google Scholar]
- 18.Santin R, Assis L, Vivas A, et al. Matheuristics for multi-UAV routing and recharge station location for complete area coverage. Sensors 2021; 21: 1705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Keller J, Thakur D, Likhachev M, et al. Coordinated path planning for fixed-wing UAS conducting persistent surveillance missions. IEEE Trans Autom Sci Eng 2016; 14: 17–24. [Google Scholar]
- 20.Li T, Bolic M, Djuric PM. Resampling methods for particle filtering: classification, implementation, and strategies. IEEE Signal Proc Mag 2015; 32: 70–86. [Google Scholar]
- 21.Hu X, Ma H, Ye Q, et al. Hierarchical method of task assignment for multiple cooperating UAV teams. J Syst Eng Electron 2015; 26: 1000–1009. [Google Scholar]
- 22.Wu H, Li H, Xiao R, et al. Modeling and simulation of dynamic ant colony’s labor division for task allocation of UAV swarm. Phys A 2018; 491: 127–141. [Google Scholar]
- 23.Kara I, editorArc based integer programming formulations for the distance constrained vehicle routing problem. 3rd IEEE international symposium on logistics and industrial informatics; 2011 25–27 Aug. 2011, pp. 33–38. Budapest, Hungary: IEEE. [Google Scholar]
- 24.Karaman S, Rasmussen S, Kingston D, et al., editors. Specification and planning of UAV missions: a process algebra approach. 2009 American control conference; 2009 10–12 June 2009, pp. 1442–1447. St Louis, MO, USA: IEEE. [Google Scholar]
- 25.Zhang X, Chen J, Xin B, et al. A memetic algorithm for path planning of curvature-constrained UAVs performing surveillance of multiple ground targets. Chin J Aeronaut 2014; 27: 622–633. [Google Scholar]
- 26.Meng W, He Z, Su R, et al. Decentralized multi-UAV flight autonomy for moving convoys search and track. IEEE Trans Control Syst Technol 2016; 25: 1480–1487. [Google Scholar]
- 27.Chen J, Ye F, Li Y, editors. Travelling salesman problem for UAV path planning with two parallel optimization algorithms. 2017 Progress in electromagnetics research symposium-fall (PIERS - FALL); 2017 19–22 Nov. 2017, pp. 832–837. Singapore: IEEE. [Google Scholar]
- 28.Gao Y, Zhang Y, Zhu S, et al., editors. Multi-UAV task allocation based on improved algorithm of multi-objective particle swarm optimization. 2018 International conference on cyber-enabled distributed computing and knowledge discovery (CyberC); 2018 18–20 Oct. 2018; Zhengzhou, pp. 443–450. China: IEEE. [Google Scholar]
- 29.Turker T, Yilmaz G, Sahingoz OK, editors. GPU-accelerated flight route planning for multi-UAV systems using simulated annealing. Proceedings of international conference on artificial intelligence: methodology, systems, and applications; 2016 7–10 September; Varna, pp. 279–288. Bulgaria: Springer. [Google Scholar]
- 30.Ye F, Chen J, Tian Y, et al. Cooperative task assignment of a heterogeneous multi-UAV system using an adaptive genetic algorithm. Electronics (Basel) 2020; 9: 687. [Google Scholar]
- 31.Huang H, Savkin AV. A method of optimized deployment of charging stations for drone delivery. IEEE Trans Transp Electrif 2020; 6: 510–518. [Google Scholar]
- 32.Cao Y, Wei W, Bai Y, et al. Multi-base multi-UAV cooperative reconnaissance path planning with genetic algorithm. Cluster Comput 2019; 22: 5175–5184. [Google Scholar]
- 33.Ruan L, Chen J, Guo Q, et al. A coalition formation game approach for efficient cooperative multi-UAV deployment. Appl Sci 2018; 8: 2427. [Google Scholar]
- 34.Kieffer E, Danoy G, Bouvry P, et al., editors. Hybrid mobility model with pheromones for UAV detection task. 2016 IEEE symposium series on computational intelligence (SSCI); 2016 6–9 Dec. 2016; Athens, Greece: IEEE. [Google Scholar]
- 35.Ni J, Tang G, Mo Z, et al. An improved potential game theory based method for multi-UAV cooperative search. IEEE Access 2020; 8: 47787–47796. [Google Scholar]
- 36.Yang Y, Minai A, Polycarpou M, editors. Decentralized cooperative search in UAV’s using opportunistic learning 2002 5–8 August; Monterey, p. 4590. California: American Institute of Aeronautics and Astronautics. [Google Scholar]
- 37.Mejias L, Diguet J-P, Dezan C, et al. Embedded computation architectures for autonomy in unmanned aircraft systems (UAS). Sensors 2021; 21: 1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nowakowski M, Sibilski K, Sibilska-Mroziewicz A, et al. Bifurcation flight dynamic analysis of a strake-wing micro aerial vehicle. Appl Sci 2021; 11: 1524. [Google Scholar]
- 39.Qu C, Gai W, Zhang J, et al. A novel hybrid grey wolf optimizer algorithm for unmanned aerial vehicle (UAV) path planning. Knowl Based Syst 2020; 194: 105530. [Google Scholar]
- 40.Liu J, Liu Y, Cong M, et al. A novel method for multi-uav cooperative reconnaissance mission planning in denied environment. 2021 International Symposium on Computer Science and Intelligent Controls (ISCSIC) 2021: 1–5. [Google Scholar]