Abstract
A growing consensus worldwide has indicated the need to protect the ecological environment and achieve sustainable development. Ensuring ecological protection and high-quality development of the Yellow River basin have become China's major national strategy. We reviewed extant literature, summarised government reports and guidance documents on the Yellow River basin, and proposed introducing a strong sustainable development theory into the study of total factor productivity (TFP). The spatial–temporal evolution and influencing factors of urban ecological TFP in the Yellow River basin are of great practical significance. We proposed a new ecological TFP indicator: the modified input-oriented Luenberger productivity indicator (MIL). Using panel data from 78 cities in the Yellow River basin during 2003–2019, we measured the urban ecological TFP. We adopted the geographic information system tool and kernel density estimation to analyse the temporal and spatial evolution of the indicator, as well as its spatial effects and influencing factors, using the global Moran's I index and dynamic spatial Durbin model (SDM). Our results show that, during the sample period, our indicator increased in cities in the region with an average annual growth rate of 0.627%, driven by technological progress. The average annual growth rate in urban areas showed a decreasing distribution of ‘downstream-midstream-upstream’. Fiscal decentralisation (FD), industrial structure (IND), financial development (FIN), urbanisation level (URB) and research and development (RD) investment improved growth rates in this and the adjacent regions through direct and indirect effects. However, environmental regulation (ER), opening level (OPEN) of cities and population density (POP) were obstacles to TFP growth.
Keywords: Strong sustainable development, Yellow River basin, ecological total factor productivity, spatial panel model, influencing factors
Introduction
The Yellow River was formed approximately 1.5 million years ago, after a long geological period of development and erosion; approximately 100,000 years ago, it became a marine water system flowing eastward into the sea. As the fifth largest river worldwide, it is 5464 km long. The average annual natural runoff is 53.5 billion m3 (1/17 times more than that of the Yangtze River). Its average annual sediment discharge and sediment concentration are 1.6 billion tons and 35 kg/m3, respectively, which are the highest worldwide. (Data source: http://www.yrcc.gov.cn/hhyl/hhgk/, Zhengzhou, China).
The Yellow River is essential to China's ecological construction. Grasslands, lakes and swamps dominate its upper reaches to form the primary runoff and water source conservation area, directly affecting the river's changing water resource trends. In the middle reaches, the Loess Plateau's ecological community characteristics are the root causes of soil erosion and riverbed siltation. The downstream estuary delta ecosystem, where over 1500 kinds of animals thrive, is among the most important wetland ecosystems located in China's warm temperate zone. Furthermore, the Yellow River is an important ecological corridor that not only provides water resources for arid basin areas, but also forms a belt ecosystem with the river course, ecological forests along the river, wetland parks and vast beach areas; this positively affects biodiversity maintenance and local climate regulation. 1 Environmental ‘ecology’ plays a critical role in the Yellow River basin's sustainable development and ‘ecosystem’ quality and stability determine the sustainable development ability and potential of cities located in the region.
The sustainable development theory is widely used to study economic development, 2 climate change,3–5 carbon emissions,6–8 carbon neutralisation,9–11 renewable energy12,13 and water environment.14,15 The weak sustainable development theory claims that natural and human-made capital can be substituted without considering ecological limits, which can cause serious ecological degradation. 16 The strong sustainable development theory posits that natural and human-made capital are not interchangeable, especially in the ecological environment. 17 In 2003, based on the strong sustainable development theory, the European Commission constructed a theoretical framework to identify key sources of natural capital, aiming to create a strong sustainability standard to protect key natural capital stock. At the United Nations’ 2012 ‘Rio + 20’ Global Sustainable Development Conference, the strong sustainability theory was officially identified as a new green development paradigm, requiring human social and economic development to respect the earth's boundaries and ecological constraints. 18
The traditional total factor productivity (TFP) index does not consider energy and environmental factors in the measurement process, which creates biased results. 19 Accordingly, scholars are gradually incorporating energy and environmental factors into the TFP research framework and promoting the evolution of traditional TFP to green TFP.20,21 Data envelopment analysis (DEA) is widely used to measure TFP. Energy is typically regarded as an input variable; pollution is regarded as a negative output variable. 22 The radial method requires reducing or expanding all inputs or outputs in equal proportion, 23 while, the non-radial method (slacks-based measure (SBM)) puts the relaxation variable directly into the objective function. While this eliminates the assumption that factor input is reduced and expanded in the same proportion, 24 it loses the proportion information between the input or output target value and actual value. In view of this, Tone and Tsutsui proposed a hybrid distance model epsilon-based measure compatible with radial and non-radial characteristics. 25 However, their method ignored the abnormal phenomenon that may occur in large-scale technological retrogression.20,26
Recently, with the development of spatial econometrics, some scholars have used Moran's I index to research on the spatial correlation. 27 Other scholars have referenced an SBM-DEA model and quantitatively evaluated environmental governance from various perspectives. Using an SBM-DEA model, Vlontzos et al. 28 evaluated EU member states’ environmental governance efficiency. However, the setting of the SBM model's direction vector is subjective and cannot overcome the deviation from using the same decision-making unit under different direction vector settings. 29 Mancini et al. 30 used a three-dimensional ecological footprint model to evaluate the dynamic evolution of natural capital while Wu et al. 31 applied Moran's I to calculate the spatial correlation effect of the Yellow River basin's total nitrogen pollution.
The Yellow River basin's environment is fragile and its economic development lags behind. These two factors restrict and influence each other. Some scholars posit that the environment will experience greater damage when economic development is low, 3 and some argue further that, with a certain extent of economic development, the damage will decrease. 32 Some scholars have found that improving the environment can promote regional economic growth. 33 In China, the ecological protection of the Yellow River basin is regulated by the government, which comprehensively supervises the region through relevant laws, system documents and policies. Table 1 shows that central local authorities have issued several government reports and policy documents on the Yellow River basin. In our review of earlier literature, government reports and guidance documents on the Yellow River basin, we identified ecology as the central factor for the region's sustainable development. We also found that the basin faces economic problems, including the issue of governance and people's livelihoods.
Table 1.
Government reports and policy documents related to the Yellow River basin.
| Time | Source | Document | Related content |
|---|---|---|---|
| 8 September 2021 | The CPC Central Committee and the State Council | Outline of ecological protection and high-quality development plan for the Yellow River Basin | This planning outline is a programmatic document to guide the ecological protection and high-quality development of the Yellow River basin at present and in the future. It proposes to firmly take the road of green and sustainable high-quality development. |
| 5 June 2020 | Supreme People ‘s Court | Opinions of the Supreme People's Court on Providing Judicial Services and guarantees for the ecological protection and high-quality development of the Yellow River Basin | Courts at all levels are required to firmly establish the concept of ‘green water and green mountains are golden mountains and silver mountains’, and promote high-level protection of the ecological environment and high-quality economic development in the Yellow River basin. |
| 28 May 2020 | Ministry of Water Resources | Action plan for water resources supervision in the Yellow River Basin | It is proposed to organise and deploy the supervision of water resources in the Yellow River basin and to standardise the behaviour of water abstraction. |
| 15 February 2022 | Shandong Provincial Party Committee and Government | Ecological protection and high-quality development planning of the Yellow River Basin in Shandong Province | Shandong will innovate the mode of ecological environment protection and comprehensively improve the ecological environment. |
| 24 February 2022 | Inner Mongolia Autonomous Region Committee and Government | Ecological protection and high-quality development planning of the Yellow River Basin in Inner Mongolia Autonomous Region | Inner Mongolia will unswervingly follow a new path of high-quality development oriented by ecological priority and green development, and strive to achieve high-level protection in high-quality development and promote high-quality development in high-level protection. |
| 6 May 2022 | Shaanxi Provincial Party Committee and Government | Ecological protection and high-quality development planning of the Yellow River Basin in Shaanxi Province | Shaanxi will accelerate the green transformation and development of the river basin, and make the Wei he River a ‘benchmark river’ for ecological protection in the Yellow River basin. |
Note: The ‘CPC Central Committee’ refers to the Central Committee of the Communist Party of China.
Materials and methods
Study motivation
We first reviewed previous literature and summarised government reports and guiding documents related to the Yellow River basin. Next, we determined our research method, constructed an econometric model and analysed the variables and data required for the study before, conducting statistical analysis. Finally, we developed specific policy recommendations based on our results. Our research framework is shown in Figure 1.
Figure 1.
Research framework.
The possible contribution of our article to existing theory is mainly twofold.
On one hand, we combine the strong sustainability theory and TFP theory in order to advance green TFP towards ecological TFP in consideration of the following concepts. First, when neoclassical economists introduced technological progress into the production function, they found that the key element of economic growth is the rate of technological progress (TFP). Second, weak sustainable development paradigm, argues that natural and man-made capital are interchangeable and that the limits of economic growth can be overcome through technological progress and innovation. The strong sustainable development view emphasises the hard constraint and irreplaceability of natural capital and argues that economic growth cannot exceed the carrying capacity of the ecological environment. Finally, existing research incorporates energy and environment as input or output variables into the research framework of TFP, promoting a shift from traditional to green TFP. We construct more comprehensive ecological and environmental indicators based on strong sustainable development theory, highlighting the non-decreasing development of environmental welfare and the irreplaceability of key natural capital, in a move towards ecological TFP.
On the other hand, we seek solutions to the current problems facing the development of the Yellow River basin. The Yellow River basin has entered late-stage industrialisation. With rapid economic growth and continuous city expansion, the area faces tighter resource constraints, serious environmental pollution and ecosystem damage. The ecological environment of the Yellow River basin is fragile and the economic development is relatively behind. We put forward an ecological TFP model in consideration of both factors to discuss how to carry out sustainable development in the Yellow River basin.
Methodology
Ecological environment evaluation method
Taking 2003 as the base period, we first standardised the original data using the fixed base efficiency coefficient method, then applied vertical and horizontal grading to determine basic indicator weights, 34 and finally used linear weighting to calculate the index of urban ecological environment quality in the Yellow River basin.
We used formula (1) to process the original data:
| (1) |
where xij(tk) and sij(tk) represent the original and standardised values of the jth index of the ith city in the tk year, respectively, and max[xj(t0)] and min[xj(t0)] represent the maximum and minimum values of the jth index of all cities in the base period, respectively.
Second, we estimated the objective weight coefficient ω. If the set of objects to be evaluated is s = { s1,s2,…sn }, the evaluation function of year tk is
| (2) |
where is the weight coefficient vector. The specific formula to describe the difference between evaluation objects by the sum of the squares of the total deviations of yi(tk) is
| (3) |
where Hk is m × n-order symmetric matrix, k = 1,2,…N.
We prove three conclusions. First, if limited, ωTω = 1 when ω is taken as the maximum eigenvalue for matrix H. When λmax(H) corresponds to the characteristic vector, δ2 takes the maximum and has ωTHω = λmax(H). Second, when Hk>0, tk(k = 1,2,…N), at the time tk, the order of Si of the evaluated object obtained by applying the transverse scattered grade method is the same.
Third, the comprehensive assessment index of ecological environment quality can be calculated as follows:
| (4) |
where Qi(tk) is the assessment index of ecological and environmental quality in the tk year of the ith city.
Theoretical derivation of ecological TFP
The strong sustainability theory emphasises the irreplaceable nature of key natural capital, such as resources and environment. It requires that the self-purification ability of the environment be constantly improved while damaging the ecological environment to ensure the non-reducibility of total environmental welfare. This article evaluates the overall environmental quality of the Yellow River basin from the two dimensions of ecological construction and ecological damage, and introduces environmental quality into the research framework of TFP. We use environmental construction as the input item and environmental damage as the undesirable output for the research framework of ecological TFP under a strong sustainable perspective.
Using the Cobb–Douglas production function for reference, we define a production function that includes capital (K), labour (L), energy (E) and ecological environment construction (EC):
| (5) |
wherein A refers to TFP, and ∂ K , ∂ L , ∂ E and ∂ EC, respectively, represent the output elasticity of capital, labour, energy and ecological EC. Logarithmic transformation produces
| (6) |
Through further differential derivation, capital productivity, labour productivity, energy productivity and ecological EC productivity can be represented by the following equations:
| (7) |
| (8) |
| (9) |
| (10) |
Factor productivity growth can be decomposed into changes in factor density and output elasticity. After summing up equations (7) to (10), we obtain
| (11) |
Further simplifying the dynamic changes of ecological TFP growth and subfactor productivity growth produces
| (12) |
In equation (12), the left-hand side represents the growth of ecological TFP, the first item on the right represents the sum of the growth of subfactor productivity, the second item on the right represents the mismatch value between subfactor productivity under the framework of ecological TFP and the third item on the right represents the output elasticity heterogeneity of subfactor productivity. When the output elasticity of subfactor productivity in the second mismatch value on the right is equal, the composition relationship between ecological TFP and subfactor productivity can be depicted, identifying the growth of ecological TFP in a strong sustainable perspective. From this simplification, we obtain
| (13) |
Equation (13) shows that the growth of ecological TFP can be decomposed into the items on the right-hand side of the equation. The first part on the right of the equation signifies the growth of subitem factor productivity and the second part reflects the degree of heterogeneity of ecological TFP in the period. The subelements cannot be completely replaced by other elements. Only when the output elasticity of the subelements is consistent do the ecological TFP and the subelement productivity reach a balanced configuration state.
Ecological TFP measurement model
Based on strong sustainability theory, we evaluated the ecology and integrated the comprehensive evaluation index of ecological and environmental quality from a strong sustainability perspective into an analysis framework to build the ecological TFP index.
Supposing N decision-making units, and each decision-making unit is put into m types of factors to generate s types of outputs in period T, then one decision-making unit j uses the ith input and obtains r outputs in period t, which can be expressed as and . If the production frontier is constructed, the production decision-making planning of unit o in period t is
| (14) |
| (15) |
According to Chambers (1996), the intertemporal MIL is defined as
| (16) |
wherein , , respectively, indicate the redundancy degree of the investment in phases T and T + 1 under the current production boundary; and denote the redundancy degree of phase T + 1 and phase T inputs under the production boundary of phases T and T + 1, respectively.
With reference to the decomposition concept of Chambers et al., 35 we build the modified input-oriented Luenberger productivity index (MIL), and allow the MIL productivity index to decompose into ecological efficiency change (MILEC) and technological progress change (MILTC):
| (17) |
| (18) |
The input factors include physical capital, human capital, energy input and eco-environmental construction. The input-oriented directional distance functions of K, L, E and EC can be constructed separately. can measure the productivity of each single factor according to the type of input factors, as shown in equations (19), (20), (21) and (22):
| (19) |
| (20) |
| (21) |
| (22) |
is the arithmetic mean of all input factor distance functions ; thus, ecological TFP index has the following ‘ total-separate’ logical relationship with , , and :
| (23) |
Spatial panel model
We investigated the influencing factors and spatial effects of ecological TFP in the Yellow River basin. The spatial econometric model is very sensitive to spatial weight matrix selection; therefore, based on theoretical analysis, we primarily selected the spatial weight matrices of urban geographical adjacency (W1) and economic distance (W2) to examine the robustness of the spatial model's empirical results. W1 is the binary adjacency spatial weight matrix. W1 = 1 when two cities are geographically adjacent, and 0 otherwise. W2 is weighted by the reciprocal of annual absolute difference between the per capita gross domestic product (GDP) of city i and of city j.
We used the spatial Durbin model (SDM) to capture the spatial correlation of ecological TFP in the Yellow River basin caused by regional interaction. Following Lesage and Pace, 36 we set the static SDM as follows:
| (24) |
We set the dynamic SDM as follows:
| (25) |
where subscripts i and t represent city and year, respectively; W is the selected spatial weight matrix. α1, α2, α3 and θ1, θ2, θ3 are the estimation coefficients of static SDM and dynamic SDM, respectively; and β1, β2, β3 and σ1, σ2, σ3 are the spatial interaction term coefficient of the corresponding variable. is the explained variable, which represents the ecological TFP ( ) and its decomposition terms ( , ). Fiscal decentralisation (FD) is the core explanatory variable. represents the first-order lag term of the ecological TFP ( ) and its decomposition terms ( , ) for each city and serves as the core explanatory variable of the dynamic SDM. Xit refers to relevant control variables used to control other exogenous factors that affect ecological TFP and its decomposition. εit is a random error term. λit and μit refer to individual and time fixed effects, respectively, which we used to capture the impact of unobservable factors and macro policy shocks on ecological TFP and its decomposition.
Research data
Input and output variables
Regarding physical capital (K), the capital stock was estimated using the perpetual inventory method with 2003 as the base period. 37 The calculation formula is as follows:
| (26) |
where is the current investment of the ith city in the tth year, and the actual fixed asset investment in the current year is used as the annual data of investment, is the price index of fixed asset investment in the tth year, and the depreciation rate is 9.6%.
To characterise human capital (L), we used employed persons in urban units. For energy input (E), energy consumption is expressed by the total amount of urban electricity consumption. For the eco-environmental construction index (EC), we adopted 13 indicators to measure the level of eco-environmental construction from the self-purification ability of the ecosystem and eco-environmental governance. For the desired output (GDP), we took 2003 as the base period, used cities’ real GDP. For the undesirable output (ED), we measured the degree of ecological environment damage from water resource consumption and air, water and solid pollution, including 11 indices. EC and ED were calculated using the vertical and horizontal scatter grade method.
We built a comprehensive evaluation system of the ecological environment of the Yellow River basin. Table 2 shows the specific evaluation indicators and weights.
Table 2.
Evaluation index system of ecological environment quality in the Yellow River basin.
| Dimension | Criterion | Specific index | Unit | Type | Weight |
|---|---|---|---|---|---|
| Ecological environment construction index | Self-purification of ecological environment | Total water resources | 100 million m3 | + | 0.004 |
| Annual rainfall 38 | ml | + | 0.032 | ||
| Annual average temperature | °C | + | 0.049 | ||
| Annual sunshine hours | hour | + | 0.035 | ||
| Per capita green area 39 | m2/person | + | 0.013 | ||
| Ecological environment governance | Industrial sulfur dioxide removal | 10,000 tons | + | 0.015 | |
| Industrial dust removal | 10,000 tons | + | 0.007 | ||
| Industrial wastewater discharge reaches scalar | 10,000 tons | + | 0.015 | ||
| Comprehensive utilisation rate of industrial solid waste | % | + | 0.050 | ||
| Urban domestic sewage treatment rate | % | + | 0.053 | ||
| Harmless treatment rate of domestic waste | % | + | 0.061 | ||
| Proportion of environmental protection and water conservancy management personnel | % | + | 0.016 | ||
| Output value of products of comprehensive utilisation of three waste types | 10,000 yuan | + | 0.010 | ||
| Ecological environment damage index | Water resource consume | Ecological water consumption | 100 million m3 | - | 0.062 |
| Domestic water consumption | 100 million m3 | - | 0.066 | ||
| Production water consumption 40 | 100 million m3 | - | 0.050 | ||
| Air pollution | PM2.5 concentration | micrograms / m3 | - | 0.041 | |
| Industrial NOx emissions | 10,000 tons | - | 0.061 | ||
| Industrial sulphur dioxide emissions | 10,000 tons | - | 0.058 | ||
| Industrial smoke emission | 10,000 tons | - | 0.063 | ||
| Water pollution | Industrial wastewater discharge | 10,000 tons | - | 0.061 | |
| Domestic wastewater discharge | 10,000 tons | - | 0.060 | ||
| Solid pollution | Production of industrial solid waste | 10,000 tons | - | 0.060 | |
| Domestic waste removal volume | 10,000 tons | - | 0.058 |
Dependent variable
MIL, MILEC and MILTC were the explained variables, representing the ecological TFP growth rate of cities in the Yellow River basin.
Independent variable
FD was the independent variable. In the Yellow River basin, FD is reflected in the biased investment of different local governments, which has a significant impact on the construction of ecological civilisation and improvement of ecological TFP.
Control variables
We controlled for several variables. (ER) reflected the strength of local government restrictions on polluting industries and environmental management. 41 For industrial structure (IND), if the development of the tertiary industry-added value is at its peak, and the pollution-added value is smaller than that of industry, it can promote MIL. We found that financial development (FIN) resulted in an expanded enterprise scale, which in turn stimulated large energy consumption demand. However, FIN can also promote a service-oriented and clean IND, thereby improving MIL. 42 Regarding urbanisation level (URB), from the perspective of unexpected output, the urbanisation process creates domestic pollutant emissions, leading to the deterioration of the environment. However, increased environmental demand, infrastructure improvement and urban development mode transformation can promote MIL. For opening level (OPEN), the ‘pollution refuge’ hypothesis posits that foreign capital causes environmental quality deterioration due to highly polluting enterprises. Conversely, the ‘pollutant paradise’ hypothesis argues that attracting foreign investment will bring environmentally friendly products and technological progress, thereby improving MIL in the inflow area. 43 The higher the level of research and development investment (RD), the faster the technological progress and the higher the MIL growth rate. The greater the population density (POP), the fewer per capita resources in the region, the weaker the environmental carrying capacity and the easier the formation of pollution accumulation; thus, higher POP may negatively impact MIL.
Table 3 provides the specific calculation methods and data sources of the regression variables.
Table 3.
Definitions of variables and data sources.
| Variable | Definition | Source |
|---|---|---|
| GDP | Economic growth: cities’ real GDP | CUSY |
| ED | Ecological environment damage: cities’ eco-environment damage index | Calculation |
| K | Physical capital: estimated using ‘perpetual inventory method’ | Calculation |
| L | Human capital: employed persons in urban units | CUSY |
| E | Energy input: annual total urban electricity consumption | USY |
| EC | Ecological environment construction: cities’ eco-environment construction index | Calculation |
| MIL | Modified Input-oriented Luenberger productivity indicator: ecological total factor productivity of cities in the Yellow River Basin | Calculation |
| FD | Fiscal decentralisation: urban annual per capita fiscal expenditure / (urban annual per capita fiscal expenditure + national annual per capita fiscal expenditure) | Wind Database |
| ER | Environmental regulation: urban pollution treatment cost / cities’ added value of secondary industry | Wind Database |
| IND | Industrial structure: cities’ tertiary sector value added/ cities’ GDP | CUSY |
| FIN | Financial development: balance of deposits and loans of financial institutions / cities’ GDP | USY |
| URB | Urbanisation level: size of cities’ urban population / total population | CUSY |
| OPEN | Opening level of cities: total foreign direct investment / cities’ GDP | USY |
| RD | Research and development investment: cities’ R&D investment / cities’ GDP | CUSY |
| POP | Population density: total cities’ annual average / total urban area | USY |
Notes: Calculation: Calculated by vertical and horizontal scatter grade method, CUSY: China Urban Statistical Yearbook, USY: Urban Statistical Yearbooks of cities in the Yellow River basin. For the data used in this study, the timeframe was from 2003 to 2019.
Data description
We selected panel data from 78 cities in the Yellow River basin between 2003 and 2019. The data for each indicator was collected from the Urban Statistical Yearbooks of cities in the Yellow River basin (2004–2020) and China Urban Statistical Yearbook (2004–2020). Some missing data was supplemented by the Wind Database and the yearbooks and Statistical Bulletins of various cities. Table 4 shows descriptive statistics for each variable.
Table 4.
Descriptive statistics of variables.
| Variable | Obs | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| GDP | 1326 | 972.037 | 1109.166 | 33.182 | 7738.417 |
| ED | 1326 | 0.654 | 0.069 | 0.546 | 0.889 |
| K | 1326 | 3510.166 | 4350.057 | 156.757 | 33430.68 |
| L | 1326 | 38.446 | 41.815 | 4.841 | 207.555 |
| E | 1326 | 962.448 | 919.089 | 1.806 | 7550.552 |
| EC | 1326 | 0.340 | 0.042 | 0.181 | 0.428 |
| MIL | 1326 | 0.101 | 0.029 | −0.035 | 0.226 |
| L1_MIL | 1248 | 0.100 | 0.029 | −0.035 | 0.226 |
| MILEC | 1326 | 0.021 | 0.009 | −0.068 | 0.108 |
| L1_MILEC | 1248 | 0.021 | 0.009 | −0.068 | 0.108 |
| MILTC | 1326 | 0.081 | 0.021 | −0.008 | 0.162 |
| L1_MILTC | 1248 | 0.080 | 0.021 | −0.008 | 0.162 |
| FD | 1326 | 0.458 | 0.139 | 0.004 | 0.855 |
| ER | 1326 | 0.044 | 0.050 | 0.005 | 0.401 |
| IND | 1326 | 0.372 | 0.101 | 0.114 | 0.687 |
| FIN | 1326 | 2.219 | 1.201 | 0.508 | 11.173 |
| URB | 1326 | 0.345 | 0.172 | 0.096 | 0.831 |
| OPEN | 1326 | 0.124 | 0.156 | 0.0001 | 0.209 |
| RD | 1326 | 0.147 | 0.205 | 0.008 | 0.631 |
| POP | 1326 | 3.690 | 3.054 | 0.500 | 14.400 |
EC: environment construction; ER: environmental regulation; FD: fiscal decentralisation; GDP: gross domestic product; IND: industrial structure; FIN: financial development; MIL: modified input-oriented Luenberger productivity index; MILEC: MIL productivity index to decompose into ecological efficiency change; MILTC: MIL productivity index to decompose into ecological efficiency change and technological progress change; OPEN: opening level; POP: population density; RD: research and development; URB: urbanisation level.
Spatial–temporal evolution of ecological TFP in the Yellow River basin
According to the authoritative programmatic document ‘Outline of ecological protection and high-quality development planning of the Yellow River Basin’, our study objects were 78 prefecture-level cities in 9 provinces and the regions of Qinghai, Sichuan, Gansu, Ningxia, Inner Mongolia, Shanxi, Shaanxi, Henan and Shandong through which flow the trunk and tributaries of the Yellow River. Among them, Xining, Haidong, Haibei, Hainan, Huangnan, Haixi, Yushu, Guoluo, Aba, Ganzi, Lanzhou, Jinchang, Baiyin, Tianshui, Wuwei, Zhangye, Pingliang, Jiuquan, Qingyang, Dingxi, Longnan, Yinchuan, Shizuishan, Wuzhong, Guyuan and Zhongwei are in the upstream region. Xi’an, Tongchuan, Baoji, Xianyang, Weinan, Yan’an, Yulin, Ankang, Shangluo, Taiyuan, Datong, Yangquan, Changzhi, Jincheng, Shuozhou, Jinzhong, Yuncheng, Xinzhou, Linfen, Luliang, Hohhot, Baotou, Wuhai, Ordos, Bayannaoer and Wulanchabu are in the midstream region. Jinan, Qingdao, Zibo, Zaozhuang, Dongying, Yantai, Weifang, Jining, Tai’an, Linyi, Dezhou, Liaocheng, Binzhou, Heze, Zhengzhou, Kaifeng, Luoyang, Pingdingshan, Anyang, Hebi, Xinxiang, Jiaozuo, Puyang, Xuchang, Luohe and Sanmenxia are in the downstream region.
Ecological TFP and decomposition items
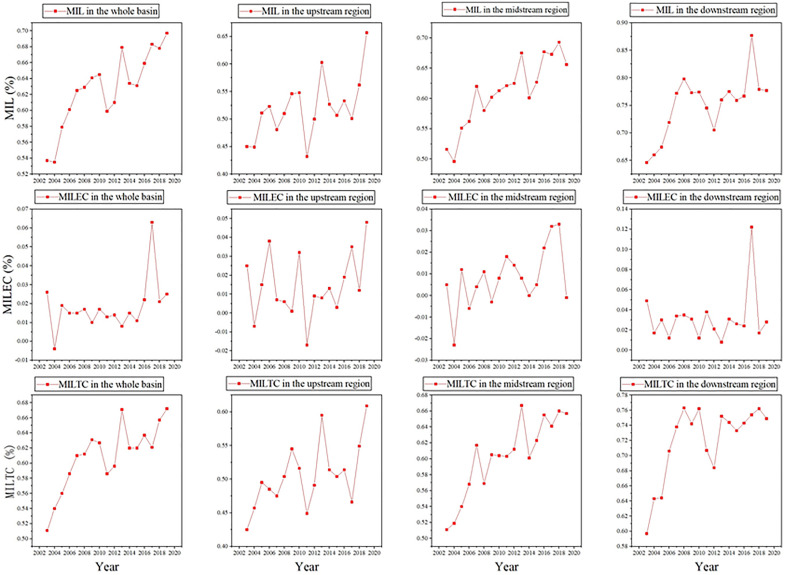
We used MAXDEA 8 Ultra® to measure MIL, MILEC and MILTC for cities in the Yellow River basin between 2003 and 2019. Then, we totalled the data for the cities in the upper, middle and lower reaches (Table 5).
Table 5.
Urban ecological TFP and its decomposition items in the upper, middle and lower reaches of the Yellow River basin (%).
| Year | MIL | MILEC | MILTC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Whole Basin |
Up stream |
Mid stream |
Down stream |
Whole basin | Up stream |
Mid stream |
Down stream |
Whole basin |
Up stream |
Mid stream |
Down stream |
|
| 2003 | 0.537 | 0.450 | 0.516 | 0.646 | 0.026 | 0.025 | 0.005 | 0.049 | 0.511 | 0.425 | 0.511 | 0.597 |
| 2004 | 0.535 | 0.449 | 0.496 | 0.660 | −0.004 | −0.007 | −0.023 | 0.017 | 0.540 | 0.457 | 0.519 | 0.643 |
| 2005 | 0.579 | 0.511 | 0.551 | 0.674 | 0.019 | 0.015 | 0.012 | 0.030 | 0.560 | 0.495 | 0.540 | 0.644 |
| 2006 | 0.601 | 0.523 | 0.562 | 0.719 | 0.015 | 0.038 | −0.006 | 0.012 | 0.586 | 0.485 | 0.568 | 0.706 |
| 2007 | 0.625 | 0.481 | 0.620 | 0.772 | 0.015 | 0.007 | 0.004 | 0.034 | 0.610 | 0.475 | 0.617 | 0.738 |
| 2008 | 0.629 | 0.510 | 0.580 | 0.798 | 0.017 | 0.006 | 0.011 | 0.035 | 0.612 | 0.504 | 0.569 | 0.763 |
| 2009 | 0.641 | 0.546 | 0.602 | 0.773 | 0.010 | 0.001 | −0.003 | 0.031 | 0.631 | 0.545 | 0.605 | 0.742 |
| 2010 | 0.645 | 0.548 | 0.613 | 0.774 | 0.017 | 0.032 | 0.008 | 0.012 | 0.627 | 0.516 | 0.604 | 0.762 |
| 2011 | 0.599 | 0.432 | 0.621 | 0.745 | 0.013 | −0.017 | 0.018 | 0.038 | 0.586 | 0.449 | 0.603 | 0.707 |
| 2012 | 0.610 | 0.500 | 0.625 | 0.705 | 0.014 | 0.009 | 0.014 | 0.021 | 0.596 | 0.491 | 0.612 | 0.684 |
| 2013 | 0.679 | 0.603 | 0.675 | 0.760 | 0.008 | 0.008 | 0.008 | 0.008 | 0.671 | 0.595 | 0.667 | 0.752 |
| 2014 | 0.634 | 0.527 | 0.601 | 0.775 | 0.015 | 0.013 | 0.000 | 0.031 | 0.620 | 0.514 | 0.601 | 0.744 |
| 2015 | 0.631 | 0.507 | 0.627 | 0.759 | 0.011 | 0.003 | 0.005 | 0.026 | 0.620 | 0.504 | 0.623 | 0.733 |
| 2016 | 0.659 | 0.533 | 0.677 | 0.767 | 0.022 | 0.019 | 0.022 | 0.024 | 0.637 | 0.514 | 0.655 | 0.743 |
| 2017 | 0.683 | 0.501 | 0.673 | 0.877 | 0.063 | 0.035 | 0.032 | 0.122 | 0.621 | 0.466 | 0.641 | 0.754 |
| 2018 | 0.678 | 0.562 | 0.693 | 0.779 | 0.021 | 0.012 | 0.033 | 0.017 | 0.657 | 0.549 | 0.660 | 0.762 |
| 2019 | 0.697 | 0.657 | 0.656 | 0.777 | 0.025 | 0.048 | −0.001 | 0.028 | 0.672 | 0.609 | 0.657 | 0.749 |
| Mean value | 0.627 | 0.520 | 0.611 | 0.751 | 0.018 | 0.014 | 0.008 | 0.032 | 0.609 | 0.505 | 0.603 | 0.719 |
MIL: modified input-oriented Luenberger productivity index; MILEC: MIL productivity index to decompose into ecological efficiency change; MILTC: MIL productivity index to decompose into ecological efficiency change and technological progress change; TFP: total factor productivity.
From 2003 to 2019, the ecological TFP of cities in the Yellow River basin showed an overall positive growth trend, with an average annual growth of 0.627%, cumulative growth of 10.032%, average annual growth of 0.018% for changes in ecological efficiency, cumulative growth of 0.306%, average annual growth of 0.609% for technological progress and overall cumulative growth of 10.353%. For ecological TFP (MIL), the distribution characteristics indicated that downstream cities (0.751) were larger than midstream (0.611) and upstream cities (0.520). From the perspective of ecological efficiency (MILEC), downstream cities (0.032) were larger than upstream (0.014) and midstream cities (0.008). Finally, from the perspective of scientific and technological progress (MILTC), we observed an evolutionary pattern in which downstream cities (0.719) were greater than midstream (0.603) and upstream (0.505) cities.
As shown in Figure 2, the urban ecological TFP in the Yellow River basin displayed a continuous growth trend, in which technological progress was the main driving force. The change and improvement trend for ecological efficiency was obvious, which further promoted ecological TFP growth. From 2003 to 2010, MIL grew rapidly. After 2010, the ecological TFP growth rate in the entire basin showed a W-type cyclical fluctuation upward trend. The periodic improvement of technological progress was the main driving force, reflecting that policy adjustments in sustainable development strategy could have significant effects. The open economic development of cities in the Yellow River basin has released the dividends of policy and system reform, and technology transfer and diffusion have promoted rapid industrial expansion. Technological progress showed a fluctuating growth rate, while ecological efficiency improved relatively slowly.
Figure 2.
Evolution of urban ecological total factor productivity (TFP) and its decomposition terms in the upper, middle and lower reaches of the Yellow River basin.
Time evolution
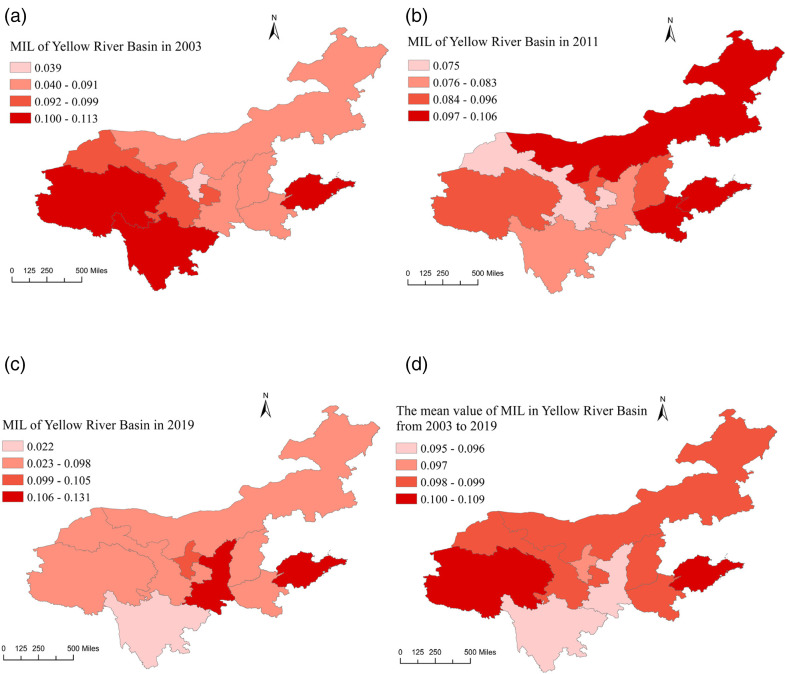
We used ArcGIS 10® to draw a MIL distribution map. Figure 3 (a) to (d) shows the changing trend of MIL in the Yellow River basin in 2003, 2011 and 2019 and the mean value. The MIL of the Yellow River basin was divided into four categories from low to high. The darker the red shading, the higher the year's MIL. The MIL data is based on the manual calculations.
Figure 3.
Temporal evolution maps of modified input-oriented Luenberger productivity index (MIL) in the Yellow River basin: (a) MIL distribution map 2003, (b) MIL distribution map 2011, (c) MIL distribution map 2019 and (d) MIL mean value map 2003–2019.
Figure 3 shows temporal evolution maps of the MIL in Yellow River basin. In 2003, the MIL index of urban agglomeration in the upstream and downstream regions were the highest These regions benefited from high ecological endowment in the upper reaches and strong economic foundation in the lower reaches. In 2011, the MIL index in the midstream region of Inner Mongolia began to improve because its energy endowment brought large benefits to promote ecological TFP improvement. In 2019, the MIL indices of cities in the midstream region of Shaanxi and downstream region of Shandong were the highest, owing to the absolute advantage of scientific and technological innovation strength in those cities.
Combined with the results in Table 5, we can conclude from the average MIL value between 2003 and 2019 that the average MIL values for cities in Shandong and Qinghai were the highest, reaching 0.109 and 0.103, respectively. Average MILEC was highest in cities in Shandong and Qinghai, with both at 0.0531. Average MILTC was highest for cities in Shandong. These findings reflect that the MIL index was the most sensitive to ecological effects and technological progress.
Spatial evolution
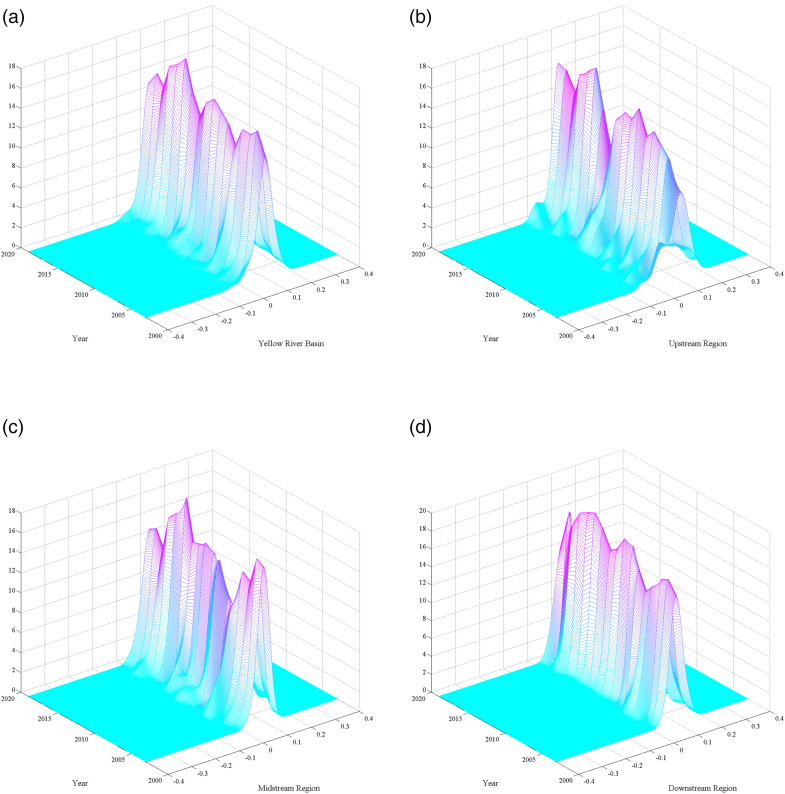
We used MATLAB R 2021® to create a kernel density distribution map of MIL in the entire basin and upstream, midstream and downstream regions between 2003 and 2019. Figure 4 (a) illustrates the main peak of the MIL index in cities across all regions was skewed left in the distribution. The bandwidth distribution was left-tailed and slightly expanded. The MIL index for cities in the Yellow River basin generally showed a fluctuating growth trend between 2003 and 2019, with an apparent extreme value effect. These results reflect that central and provincial capital cities occupy an absolutely dominant position in the investment of resources, such as the economy, science and technology, human resources and ecological EC. The siphon effect was evident; their ecological TFP continuously maintained a leading trend.
Figure 4.
Spatial evolution maps of modified input-oriented Luenberger productivity index (MIL) in Yellow River basin: (a) Whole basin, (b) upstream region, (c) midstream region and (d) downstream region.
Figure 4 (b), (c) and (d) shows the main peak of MIL in the upstream region had a small, rapid increasing trend and fluctuated in stages. An evident upward trend was observed for 2003–2019; the gap between high- and low-MIL cities gradually narrowed. The main peak of MIL in the midstream region ended with a shift to the left after a small range. This primarily manifested in a slight decline between 2003 and 2006, and an increase between 2006 and 2017 as the bandwidth continued shrinking from a left-tailing trend and ductility decreased. The downstream region exhibited a right-tailing phenomenon and ductility increased. MIL in the region was relatively stable; cities with high MIL expanded their regional differences, but cities with low MIL experienced a ‘catch-up effect’, and the interregional differences narrowed.
Empirical results and discussion
Global spatial autocorrelation measure
The analysis results shown in Table 6 indicate that the global Moran's I index of ecological TFP in the Yellow River basin from 2003 to 2019 was all positive. All years were significant at the 1% level, indicating a strong spatial correlation effect of ecological TFP in cities in the Yellow River basin, with a significant degree of agglomeration. Further analysis showed that the agglomeration degree fluctuated over time.
Table 6.
Moran's I test of ecological total factor productivity in the Yellow River basin (2003–2019).
| Year | Moran's I | P-value | Year | Moran's I | P-value |
|---|---|---|---|---|---|
| 2003 | 0.581*** | 0.000 | 2012 | 0.205** | 0.016 |
| 2004 | 0.585*** | 0.000 | 2013 | 0.318*** | 0.003 |
| 2005 | 0.425*** | 0.000 | 2014 | 0.325*** | 0.001 |
| 2006 | 0.539*** | 0.000 | 2015 | 0.319*** | 0.003 |
| 2007 | 0.538*** | 0.000 | 2016 | 0.318*** | 0.003 |
| 2008 | 0.358*** | 0.000 | 2017 | 0.354*** | 0.000 |
| 2009 | 0.327*** | 0.003 | 2018 | 0.293*** | 0.007 |
| 2010 | 0.202** | 0.016 | 2019 | 0.315*** | 0.003 |
| 2011 | 0.289*** | 0.008 |
Note: *, * * and * * * are significant at the 10%, 5% and 1% levels, respectively.
Dynamic spatial panel regression analysis
Regression analysis of ecological TFP
To determine whether spatial interaction effects occur in a model, Burridge 44 and Anselin et al. 45 proposed the Lagrange multiplier (LM) test method to examine spatial lag-explained variables and error correlation. We then used the LM test method. The LM spatial lag, robust LM spatial lag, LM spatial error and robust LM spatial error of both the and dynamic SDM all rejected the original assumption of a spatial correlation between the model lag term and the error term. Therefore, it was reasonable to adopt the dynamic SDM.
Before the regression analysis, we conducted a Hausmann's test of the panel data. The test resulted in a p-value of 0.000, which strongly rejected the null hypothesis and indicated the use of fixed effects. Accordingly, cities and years were fixed in the regression. We used a dynamic SDM for regression analysis. To ensure the robustness of the estimation results, we also used a static SDM to quantitatively identify the influencing factors of ecological TFP in the Yellow River basin. Table 7 shows the relevant estimation results.
Table 7.
Regression results of influencing factors for ecological total factor productivity in the Yellow River basin.
| Variable | Dynamic SDM(W1) | Dynamic SDM(W2) | Static SDM(W1) | Static SDM(W2) |
|---|---|---|---|---|
| L1_MIL | 0.347*** (0.077) |
0.479*** (0.067) |
/ | / |
| FD | 0.172*** (0.049) |
0.254*** (0.055) |
0.505*** (0.145) |
0.397** (0.172) |
| ER | −0.191** (0.086) |
−0.143** (0.056) |
−0.127* (0.070) |
−0.080 (0.114) |
| IND | 0.017*** (0.005) |
0.020** (0.008) |
0.029*** (0.005) |
0.030*** (0.011) |
| FIN | 0.038*** (0.007) |
0.042*** (0.016) |
0.052*** (0.018) |
0.069* (0.036) |
| URB | 0.033** (0.015) |
0.024** (0.011) |
0.063*** (0.011) |
0.055*** (0.017) |
| OPEN | −0.012 (0.013) |
−0.016 (0.012) |
−0.021 (0.013) |
−0.019* (0.010) |
| RD | 0.270*** (0.056) |
0.295** (0.124) |
0.360*** (0.081) |
0.427** (0.184) |
| POP | −0.438 (0.439) |
−0.446 (0.377) |
−0.669* (0.371) |
−0.622 (0.653) |
| W × L1_MIL | 0.069** (0.027) |
0.125* (0.065) |
/ | / |
| W × FD | −0.102*** (0.030) |
−0.022 (0.015) |
−0.156 (0.169) |
−0.191* (0.102) |
| W × ER | 0.121* (0.062) |
0.067*** (0.018) |
0.095*** (0.033) |
0.118** (0.046) |
| W × IND | 0.012** (0.005) |
0.007* (0.004) |
0.245* (0.123) |
0.010*** (0.002) |
| W × FIN | 0.016 (0.012) |
0.026 (0.029) |
0.015 (0.025) |
0.012 (0.014) |
| W × URB | 0.015** (0.007) |
0.011** (0.005) |
0.148** (0.075) |
0.157* (0.083) |
| W × OPEN | −0.027*** (0.004) |
−0.069*** (0.024) |
−0.211*** (0.035) |
−0.278* (0.146) |
| W × RD | 0.137* (0.071) |
0.211*** (0.049) |
0.194* (0.108) |
0.213** (0.101) |
| W × POP | −0.237 (0.162) |
−0.064 (0.081) |
−0.446 (0.458) |
−0.401 (0.408) |
| ρ | 0.197** (0.081) |
0.610*** (0.156) |
0.175** (0.074) |
0.438*** (0.168) |
| Adj.R2 | 0.542 | 0.505 | 0.451 | 0.460 |
| Sigma2_e | 6.370*** (1.622) |
6.965*** (1.831) |
6.119*** (1.447) |
6.505*** (1.601) |
| Obs | 1248 | 1248 | 1248 | 1248 |
| Diagnostic test | Value | |||
| Hausman test | 43.245*** | |||
| AR (1) | −3.211*** | |||
| AR (2) | −1.181 | |||
| Sargan | 23.916 | |||
Notes: *, * * and * * * are significant at 10%, 5% and 1% levels, respectively. Standard errors are shown in parentheses.
ER: environmental regulation; FD: fiscal decentralisation; FIN: financial development; IND: industrial structure; FIN: financial development; MIL: modified input-oriented Luenberger productivity index; OPEN: opening level; POP: population density; SDM: spatial Durbin model; RD: research and development; URB: urbanisation level.
Table 7 shows that the first-order autocorrelation, AR (1), of the residuals was significant at the 1% level. However, neither the second-order autocorrelation, AR (2), nor the Sargan statistic were significant. This supports our original assumption of no excessive identification of instrumental variables.
From the estimation results, L1_MIL was significant at the 1% level, indicating path dependence in ecological TFP improvement; it was reasonable to include in the estimation model. Additionally, the estimation results using the geographical adjacency spatial weight matrix (W1) and the economic distance spatial weight matrix (W2) were not significantly different from the estimation results of the dynamic SDM. The coefficients of the first-order and spatial lag terms of ecological TFP and the main explanatory variables were significant at least at the 5% level, and the symbols had not changed, indicating that the regression results were robust.
According to the estimation results of the dynamic SDM, the spatial autocorrelation coefficients (ρ) of the geographical adjacency spatial weight matrix (W1) and economic distance spatial weight matrix (W2) were 0.197 and 0.610, respectively, and significantly positive at least at the 5% level; this indicated a spatial spillover feature of ecological TFP in the Yellow River basin. Specifically, the MIL in this city was closely related to the ecological TFP level in cities with close geographical or economic distance. Under the geographical spatial weight and the economic distance spatial weight, the coefficients of L1_MIL were 0.069 and 0.125, respectively, and significantly positive at least at the 10% level, which indicates that the ecological TFP also has time lag. The improvement of the ecological TFP of the adjacent cities in a prior period can promote the improvement of the ecological efficiency of the city in question in the current period.
In the regression results for the dynamic SDM (W1) and dynamic SDM (W2), or for every 1% increase in the independent variable FD, MIL in the current period increases by 0.172% and 0.254%, respectively, which was significant at the 1% level. However, for every 1% increase in FD in cities with close geographical proximity and economic distance, MIL in this region decreased by 0.102% and 0.022%, respectively. This is due to the siphon effect of adjacent cities. The control variables IND, FIN, URB and RD all significantly promoted MIL. In contrast, ER had an inhibitory effect on MIL. All the variables were significant at the 5% levels, except for OPEN and POP, which also inhibited the MIL, but not significantly.
Analysis of direct and indirect effects
To further explore the direct and indirect impact of various factors on ecological TFP, we used the method of Lesage and Pace 36 to decompose the impact of various factors (Table 8).
Table 8.
Effect decomposition results of various factors.
| Varia ble | Geographical adjacency spatial weight matrix (W1) | Economic distance spatial weight matrix (W2) | ||||
|---|---|---|---|---|---|---|
| Direct effects | Indirect effects | Total effects | Direct effects | Indirect effects | Total effects | |
| FD | 0.174*** (0.061) |
−0.060*** (0.018) |
0.113*** (0.032) |
0.261*** (0.070) |
−0.017 (0.013) |
0.243 (0.174) |
| ER | −0.172* (0.102) |
−0.035** (0.017) |
−0.206*** (0.069) |
−0.151** (0.066) |
−0.071*** (0.018) |
−0.224*** (0.080) |
| IND | 0.017*** (0.004) |
0.011** (0.005) |
0.028*** (0.006) |
0.022** (0.009) |
0.012* (0.007) |
0.035** (0.014) |
| FIN | 0.047*** (0.009) |
0.008 (0.015) |
0.060 (0.050) |
0.047*** (0.016) |
0.021 (0.017) |
0.068* (0.037) |
| URB | 0.040** (0.017) |
0.023*** (0.007) |
0.066*** (0.015) |
0.028* (0.015) |
0.002** (0.001) |
0.031** (0.013) |
| OPEN | −0.014 (0.016) |
−0.025*** (0.007) |
−0.039* (0.023) |
−0.018 (0.014) |
−0.087** (0.037) |
−0.106** (0.045) |
| RD | 0.280*** (0.042) |
0.090* (0.051) |
0.375*** (0.073) |
0.302** (0.114) |
0.154*** (0.043) |
0.457** (0.196) |
| POP | −0.448 (0.391) |
−0.271 (0.221) |
−0.719 (0.778) |
−0.456 (0.297) |
−0.167 (0.157) |
−0.624 (0.440) |
Notes: *, * * and * * * are significant at 10%, 5% and 1% levels, respectively. Standard errors are shown in parentheses.
ER: environmental regulation; FD: fiscal decentralisation; FIN: financial development; IND: industrial structure; FIN: financial development; OPEN: opening level; POP: population density; RD: research and development; URB: urbanisation level.
Under both the geographical adjacency spatial weight matrix (W1) and economic distance spatial weight matrix (W2), the direct effect of the core independent variable FD on the ecological TFP of the Yellow River basin was significantly positive while, the indirect effect was significantly negative. Furthermore, the negative effect was more significant in geographically adjacent cities. This indicates that local FD has a negative spillover effect on the ecological TFP level of surrounding areas. Specifically, with increased FD, the siphon effect of ecological TFP in geographically adjacent cities increased, resulting in the decline of ecological TFP in local cities. 46
IND, FIN, URB and RD had significant roles in promoting the improvement of ecological TFP in the region and its geographical and economic adjacent areas. The effects of ER, OPEN and POP on local and surrounding areas was negative, but this was not statistically significant for POP.
Regression analysis of decomposition terms of ecological TFP
We introduced the MIL index to decompose into MILEC MILTC. We further analysed the decomposition terms of ecological TFP and judged their influencing factors.
Before we applied the SDM to MILEC and MILTC, we first performed the Hausman test on the two panel data sets. The tests resulted in a p-value of 0.000, which strongly rejected the null hypothesis and indicted the use of fixed effects. We then used the LM test method. The LM spatial lag, robust LM spatial lag, LM spatial error and robust LM spatial error of both the and dynamic SDM all rejected the original assumption of a spatial correlation between the model lag term and the error term. Therefore, it was reasonable to adopt the dynamic SDM. Finally, as shown in Tables 9 and 10, the first-order autocorrelation AR (1) of the residuals of these two panel models are significant at the 1% level; second-order autocorrelation AR (2) and Sargan statistics are not significant. This supports our original approach of not over identifying tool variables. We proceeded to analyse the regression results of MILEC and MILTC.
Table 9.
Regression results of influencing factors for ecological efficiency change in the Yellow River basin.
| Variable | Dynamic SDM(W1) | Dynamic SDM(W2) | Static SDM(W1) | Static SDM(W2) | |
|---|---|---|---|---|---|
| L1_MILEC | 0.135*** (0.034) |
0.218** (0.102) |
/ | / | |
| FD | 0.052* (0.029) |
0.104* (0.057) |
0.055 (0.035) |
0.118** (0.055) |
|
| ER | 0.225** (0.102) |
0.163* (0.086) |
0.184 (0.123) |
0.142** (0.063) |
|
| IND | 0.014* (0.008) |
0.032 (0.020) |
0.008* (0.005) |
0.029 (0.021) |
|
| FIN | 0068** (0.032) |
0.102** (0.046) |
0.044* (0.024) |
0.079 (0.056) |
|
| URB | 0.033 (0.031) |
0.054 (0.043) |
0.103 (0.142) |
0.115* (0.150) |
|
| OPEN | −0.069 (0.053) |
−0.106 (0.076) |
−0.118 (0.113) |
−0.096 (0.081) |
|
| RD | 0.011 (0.009) |
0.025** (0.012) |
0.030 (0.022) |
0.057** (0.027) |
|
| POP | −0.221 (0.148) |
−0.136 (0.088) |
−0.146* (0.081) |
−0.089* (0.050) |
|
| W × L1_MILEC | 0.032* (0.059) |
0.063* (0.077) |
/ | / | |
| W × FD | −0.039** (0.018) |
−0.018* (0.010) |
−0.055* (0.032) |
−0.102* (0.057) |
|
| W × ER | 0.023 (0.016) |
0.012* (0.006) |
−0.044 (0.036) |
0.086* (0.048) |
|
| W × IND | 0.025** (0.012) |
0.011* (0.006) |
0.058* (0.033) |
0.029 (0.019) |
|
| W × FIN | 0.044 (0.039) |
0.019 (0.017) |
0.011 (0.008) |
0.006** (0.003) |
|
| W × URB | 0.047 (0.035) |
0.032 (0.029) |
0.086* (0.046) |
0.053 (0.036) |
|
| W × OPEN | −0.264 (0.171) |
−0.170** (0.075) |
−0.282 (0.194) |
−0.355 (0.240) |
|
| W × RD | 0.068* (0.037) |
0.154 (0.103) |
0.148* (0.086) |
0.210 (0.173) |
|
| W × POP | −0.125 (0.094) |
−0.078 (0.062) |
−0.113* (0.066) |
−0.086 (0.069) |
|
| ρ | 0.101* (0.055) |
0.210** (0.098) |
0.137** (0.062) |
0.279** (0.130) |
|
| Adj.R2 | 0.497 | 0.455 | 0.423 | 0.474 | |
| Sigma2_e | 5.786*** (1.272) |
5.962*** (1.366) |
5.248*** (1.254) |
5.611*** (1.368) |
|
| Obs | 1248 | 1248 | 1248 | 1248 | |
| Diagnostic test | Value | ||||
| Hausman test | 23.271*** | ||||
| AR (1) | −5.806*** | ||||
| AR (2) | −1.251 | ||||
| Sargan | 21.916 | ||||
Notes: *, * * and * * * are significant at 10%, 5% and 1% levels, respectively. Standard errors are shown in parentheses.
ER: environmental regulation; FD: fiscal decentralisation; FIN: financial development; IND: industrial structure; FIN: financial development; MILEC: MIL productivity index to decompose into ecological efficiency change; OPEN: opening level; POP: population density; SDM: spatial Durbin model; RD: research and development; URB: urbanisation level.
Table 10.
Regression results of influencing factors for technological progress change in the Yellow River basin.
| Variable | Dynamic SDM(W1) | Dynamic SDM(W2) | Static SDM(W1) | Static SDM(W2) |
|---|---|---|---|---|
| L1_MILTC | 0.376*** (0.095) |
0.491*** (0.106) |
/ | / |
| FD | 0.167*** (0.051) |
0.263** (0.121) |
0.543** (0.257) |
0.365** (0.181) |
| ER | −0.115 (0.142) |
−0.074* (0.040) |
−0.155** (0.073) |
−0.083 (0.114) |
| IND | 0.026* (0.014) |
0.031** (0.013) |
0.035 (0.105) |
0.048* (0.025) |
| FIN | 0.147*** (0.032) |
0.162** (0.074) |
0.155** (0.071) |
0.176* (0.094) |
| URB | 0.023 (0.015) |
0.034* (0.018) |
0.033 (0.021) |
0.045** (0.022) |
| OPEN | 0.040 (0.035) |
0.057. (0.044) |
0.051 (0.040) |
0.069* (0.038) |
| RD | 0.349*** (0.073) |
0.310* (0.171) |
0.405** (0.193) |
0.486** (0.232) |
| POP | −0.017 (0.105) |
−0.052 (0.194) |
−0.028* (0.114) |
−0.076 (0.205) |
| W × L1_MILTC | 0.134*** (0.037) |
0.175** (0.080) |
/ | / |
| W × FD | −0.093*** (0.027) |
−0.064** (0.029) |
−0.104 (0.070) |
−0.128* (0.075) |
| W × ER | 0.098* (0.054) |
0.076* (0.043) |
0.101 (0.068) |
0.122* (0.068) |
| W × IND | 0.010** (0.005) |
0.003* (0.002) |
0.107 (0.091) |
0.042* (0.026) |
| W × FIN | 0.011 (0.010) |
0.017 (0.015) |
0.008 (0.011) |
0.010 (0.016) |
| W × URB | 0.127 (0.101) |
0.144* (0.081) |
0.155** (0.074) |
0.169* (0.095) |
| W × OPEN | 0.019 (0.013) |
0.036** (0.017) |
0.104 (0.115) |
0.128* (0.072) |
| W × RD | 0.102* (0.059) |
0.178** (0.080) |
0.155* (0.088) |
0.211** (0.095) |
| W × POP | −0.223 (0.201) |
−0.164 (0.107) |
−0.304* (0.172) |
−0.254 (0.170) |
| ρ | 0.203** (0.088) |
0.312** (0.140) |
0.198** (0.087) |
0.326*** (0.079) |
| Adj.R2 | 0.558 | 0.512 | 0.476 | 0.440 |
| Sigma2_e | 6.245*** (1.821) |
6.703*** (1.833) |
6.224*** (1.669) |
6.530*** (1.732) |
| Obs | 1248 | 1248 | 1248 | 1248 |
| Diagnostic test | Value | |||
| Hausman test | 28.177*** | |||
| AR (1) | −4.554*** | |||
| AR (2) | −1.008 | |||
| Sargan | 17.503 | |||
Notes: *, * * and * * * are significant at 10%, 5% and 1% levels, respectively. Standard errors are shown in parentheses.
ER: environmental regulation; FD: fiscal decentralisation; FIN: financial development; IND: industrial structure; FIN: financial development; MILTC: MIL productivity index to decompose into ecological efficiency change and technological progress change; POP: population density; SDM: spatial Durbin model; RD: research and development; URB: urbanisation level.
Regression analysis of ecological efficiency change
As shown in Table 9, L1_MILEC was significant at the 5% level; it was reasonable to include it in the estimation model. According to the estimation results of the dynamic SDM, the estimation results using the geographical adjacency spatial weight matrix (W1) and the economic distance spatial weight matrix (W2) were not significantly different. The coefficients of the first-order and spatial lag terms of ecological efficiency change and the main explanatory variables were significant at least at the 10% level, and the symbols had not changed, indicating that the regression results were robust.
According to MILEC regression estimation results, the spatial autocorrelation coefficients (ρ) of the geographical adjacency spatial weight matrix (W1) and economic distance spatial weight matrix (W2) were 0.101 and 0.210, respectively; these were significantly positive at the 10% and 5% levels, respectively, indicating that the changes in ecological efficiency in the Yellow River basin have significant spatial spillover effects. Specifically, the MILEC of the city is closely related to the ecological efficiency level of neighbouring cities geographically or economically. In addition, under the geographical spatial weight and the economic distance spatial weight, the coefficients of L1_MILEC were 0.032 and 0.063, respectively; both passed the 10% significance test, which indicates that MILEC also has time lag. The improvement of the ecological efficiency of geographically and economically adjacent cities in the prior period promotes the improvement of the ecological efficiency of the local city in the current period.
In the regression results for the dynamic SDM (W1) and dynamic SDM (W2), the coefficients of the independent variable FD were 0.052 and 0.104, respectively, which was significant at the 10% level. However, the increase of FD in the cities adjacent to the geographical distance and economic distance will lead to the decline of the city's ecological efficiency, which reflects the economic competition among the cities. The winner of the urban competition absorbs the adjacent superior resources, leading to the weakening of the ecological governance capacity of adjacent cities. Regarding control variables, ER, IND and FIN significantly promoted MILEC. Contrastingly, OPEN and POP inhibited MILEC, but not significantly.
Regression analysis of technological progress change
As shown in Table 10, L1_MILTC was significant at the 1% level, and it was reasonable to include it in the estimation model. From the estimation results of the dynamic SDM, we concluded that the estimation results using the geographical adjacency spatial weight matrix (W1) and the economic distance spatial weight matrix (W2) were not significantly different. The coefficients of the first-order and spatial lag terms of technological progress and the main explanatory variables were significant at least at the 5% level, and the symbols had not changed, indicating that the regression results were robust
According to the MILTC regression estimation results, the spatial autocorrelation coefficients (ρ) of the geographical adjacency spatial weight matrix (W1) and economic distance spatial weight matrix (W2) were 0.203 and 0.312, respectively. They were both significant at the 5% level, showing that technological progress has a significant diffusion effect among cities in the Yellow River basin. In addition, under the geographical and economic distance spatial weight, the coefficients of L1_MILTC were 0.134 and 0.175, respectively; they passed the 5% significance test, which indicates that MILTC also has time lag. The improvement of the technological progress of geographically and economically adjacent cities in the prior period promotes the improvement of the ecological efficiency of the specific city in the current period.
In the regression results for the dynamic SDM (W1) and dynamic SDM (W2), the coefficients of the independent variable FD were 0.203 and 0.312, respectively; they were significant at least at the 5% level. Under the geographical spatial weight (W1) and the economic distance spatial weight (W2), the coefficients of FD were −0.093 and −0.064, respectively, and they were significant at least at the 5% level. That means the increase of FD in adjacent cities will lead to the decline of the city's technological progress. Regarding control variables, IND, FIN and RD significantly promoted MILTC. On the contrary, ER and POP inhibited MILTC.
Discussion
From the estimation results of the static and dynamic SDMs, we concluded that financial decentralisation has significantly increased the growth rate of ecological TFP. Good governance of the Yellow River supported by fiscal policy will greatly impact the lives of river basin residents, who hope to not only live in a good ecological environment but also to experience a richer life and improved social welfare. To achieve this, the government must increase financial investment, implement urban flood control planning, 47 create employment opportunities and provide diversified public products.
IND, FIN, URB and RD investment improved growth rates indicating that the government should strengthen these factors. For example, increases in local environmental protection and scientific and technological investment, strengthened the spillover effect of environmental protection technology. This was in turn conducive to a mutual exchange and learning of environmental protection and emission reduction technologies among cross-regional enterprises, thereby effectively promoting ecological TFP. In contrast, ER, OPEN of cities, and POP suppressed the rise of ecological TFP. The government should address these negative effects. For instance, when introducing foreign capital for development, local governments should prevent its adverse impact on the local ecological environment.
Conclusions, policy recommendations and limitations
Conclusions
Based on strong sustainable development theory, we constructed the urban ecological environment evaluation system of the Yellow River basin from the dimensions of ecological damage and construction and incorporated it into the ecological TFP framework. We created a new ecological TFP indicator – MIL – to dynamically measure ecological TFP and used the kernel density estimation and dynamic SDM to analyse the spatial and temporal evolution of urban ecological TFP in the Yellow River basin along with its influencing factors. We additionally conducted further analysis on the direct and indirect effects of various influencing factors.
From 2003 to 2019, MIL in cities along the Yellow River basin showed an increasing trend, with average annual growth rates of 0.627%. The findings indicate that urban ecological TFP in the Yellow River basin showed a gradient increase of ‘upstream (0.520)-midstream (0.611)-downstream (0.751)’, and that technological progress (MILTC) was the main driving force.
In terms of time evolution, between 2003 and 2010, MIL in the Yellow River basin increased rapidly. After 2010, the ecological TFP growth rate in the entire basin showed a W-type cyclical fluctuation upward trend. From a spatial evolution perspective, the main peak of the MIL index in cities in all regions of the Yellow River basin showed a left-skewed distribution, and the bandwidth was distributed in a left-tailed manner and slightly expanded, with a fluctuating peak value.
By analysing the global Moran's I index and dynamic SDM, we found that urban ecological TFP in the Yellow River basin had a spatial agglomeration effect. Under the geographical adjacency (W1) and economic distance (W2) spatial weight matrices, different cities had strong spatial correlation effects. FD, IND, FIN, URB and RD investment promoted the improvement of MIL in specific and adjacent regions through direct and indirect effects. Contrastingly, ER, OPEN of cities, and POP were obstacles to MIL.
Policy recommendations
This study provides the following relevant policy recommendations. Owing to sporadic domestic epidemics and their unexpected impact on China's economy, many cities in the Yellow River basin have encountered financial deficits and sluggish economic development in recent years. Major water conservancy projects attract large investments, have a long industrial chain and create many employment opportunities. It is estimated that every 100 billion yuan invested in major water conservancy projects can drive GDP growth by 0.15% and create 490,000 new jobs, playing an important role in promoting stable economic growth. Given this, the state should strengthen macro-control, and promote the construction of Gu Xian, Hei Shan Gorge and Qi Kou, and other major water conservancy projects on the Yellow River. 48
However, the discharge of a large number of pollutants, deforestation and destruction of wetlands driven by economic interests along the Yellow River has weakened the connectivity of the river's aquatic habitat and the self-healing ability of the water environment, further damaging the overall ecosystem and ecological balance. All localities should strengthen oversight on ecological environment damage in the Yellow River basin, comprehensively improve water ecological protection and governance, increase the speed of constructing digital twin basins and digital twin projects, implement total factor and whole process governance and management, and further promote ecological TFP improvement through innovation. Meanwhile, in the basin, management behaviour (or lack thereof), in the upstream region could have an impact on the downstream region. Thus, it is necessary to promote coordinated governance of the regional ecological environment and to collaborate across regions to protect the environment and ensure that the environment and ecological TFP of the Yellow River basin improve qualitatively.
Further consideration is needed to improve the interregional ecological compensation mechanism; formulate objectives, approaches, methods and standards related to ecological compensation 49 ; increase financial support and ecological environment regulation and promote coordinated and sustainable development of the Yellow River basin's urban ecological environment and economy by improving the ecological TFP. For example, in 2021, Shandong (downstream) and Henan (upstream) provinces signed a ‘gambling agreement’. If the water quality averages the class III standard throughout the year, the two provinces do not compensate each other. If the water quality improves from class III to class II, Shandong will give Henan 60 million yuan in compensation. However, if the water quality deteriorates to category III, Henan will pay Shandong 60 million yuan in compensation. When Shandong paid Henan 126 million yuan from the Yellow River Ecological Compensation Fund the two provinces realised it was a win-win situation. We believe that it is important to realise ecological compensation goals in the form of an agreement. Moreover, it may be necessary to form an effective ecological protection coordination mechanism that fully considers all relevant regions’ actual situations.
Limitations
Several limitations of this study deserve discussion. We were not able to analyse regional differences in urban ecological TFP in the Yellow River basin, given length constraints. In the future, we can use the Dagum Gini coefficient method to reveal how the inter- and intra-regional differences in ecological TFP evolve in the Yellow River basin. Furthermore, we used SDM to identify influencing factors. In the future, we will use a spatial convergence model to further examine the spatial convergence effect and the convergence speed of urban ecological TFP. Finally, it is necessary for us to conduct in-depth research on ecological compensation in the region, not only through governmental policies, such as FD, but also from market-oriented ecological compensation methods, such as the value of ecological products.
Author biographies
Wan-Ping Yang is professor of Economics, School of Economics and Finance, Xi'an Jiaotong University.
Zhen-Ya Zhang is a doctoral student of Economics, School of Economics and Finance, Xi'an Jiaotong University.
Ping-Ping Luo is professor of Water and Environment, School of Water and Environment, Chang'an University.
Ya-Juan Wang is postdoctor of Management, School of management, FuDan University.
Footnotes
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the General Soft Science Projects of Shaanxi Province, Xi’an Jiao Tong University Basic Scientific Research Business Expenses Special Scientific Research Project, National Key Project of Statistical Science Research Project, Shaanxi Province Social Science Fund. Financial support came from the Fundamental Research Funds for Key Research Project of Philosophy and Social Science Research of the Ministry of Education (grant numbers 2023-CX-RKX-018, SK2022001, 2022LZ33, 2022D001 and 20JZD012).
ORCID iD: Zhen-Ya Zhang https://orcid.org/0000-0001-5018-4969
References
- 1.Guo S, Wu C, Wang Y, et al. Threshold effect of ecosystem services in response to climate change, human activity and landscape pattern in the upper and middle Yellow River of China. Ecol Indic 2022; 136: 108603. [Google Scholar]
- 2.Liu Y, Du J, Wang Y, et al. Evenness is important in assessing progress towards sustainable development goals. Natl Sci Rev 2021; 8: 38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Duan H, Yuan D, Cai Z, et al. Valuing the impact of climate change on China’s economic growth. Econ Anal Policy 2022; 74: 155–174. [Google Scholar]
- 4.Wang S, Cao Z, Luo P, et al. Spatiotemporal variations and climatological trends in precipitation indices in Shaanxi province, China. Atmosphere (Basel) 2022; 13: 44. [Google Scholar]
- 5.Duan H, Zhou S, Jiang K, et al. Assessing China’s efforts to pursue the 1.5°C warming limit. Science 2021; 372: 378–385. [DOI] [PubMed] [Google Scholar]
- 6.Zheng J, Mi Z, Coffman D, et al. The slowdown in China’s carbon emissions growth in the new phase of economic development. One Earth 2019; 1: 240–253. [Google Scholar]
- 7.Zhao B, Yang W. Does financial development influence CO2 emissions? A Chinese province-level study. Energy 2020; 200: 117523. [Google Scholar]
- 8.Zheng J, Mi Z, Coffman D, et al. Regional development and carbon emissions in China. Energy Economics 2019; 81: 25–36. [Google Scholar]
- 9.Zhao B,, Yang W. Allocation of carbon emission allowance based on DLA-GA model: a case study in China. Environmental Science and Pollution Research 2022; 29: 15743–15762. [DOI] [PubMed] [Google Scholar]
- 10.Zheng J, Duan H, Yuan Y. Perspective for China's carbon capture and storage under the Paris agreement climate pledges. Int J Greenhouse Gas Control 2022; 119: 103738. [Google Scholar]
- 11.Mo J, Cui L, Duan H. Quantifying the implied risk for newly-built coal plant to become stranded asset by carbon pricing. Energy Economics 2021; 99: 105286. [Google Scholar]
- 12.Sun S, Wang S, Zhang G, et al. A decomposition-clustering-ensemble learning approach for solar radiation forecasting. Sol Energy 2018; 163: 189–199. [Google Scholar]
- 13.Mi Z, Zheng J, Meng J, et al. Carbon emissions of cities from a consumption-based perspective. Appl Energy 2019; 235: 509–518. [Google Scholar]
- 14.Luo P, Mu Y, Wang S, et al. Exploring sustainable solutions for the water environment in Chinese and southeast Asian cities. Ambio 2022; 51: 1199–1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cao Z, Wang S, Luo P, et al. Watershed ecohydrological processes in a changing environment: opportunities and challenges. Water (Basel) 2022; 14: 1502. [Google Scholar]
- 16.Li Z, Li D, Yang W, et al. The spatial-temporal evolution and spatial convergence of ecological total factor productivity in China. Energy Environ 2020; 14: 1141. [Google Scholar]
- 17.Pearce DW, Atkinson GD. Capital theory and the measurement of sustainable development: an indicator of “weak” sustainability. Ecol Econ 1993; 8: 103–108. [Google Scholar]
- 18.Yang W, Zhao J. Study on China’s economic development from the perspective of strong sustainability. Singap. Econ. Rev 2020; 65: 161–192. [Google Scholar]
- 19.Yang J, Tang L, Mi Z, et al. Carbon emissions performance in logistics at the city level. J Cleaner Prod 2019; 231: 1258–1266. [Google Scholar]
- 20.Feng C, Huang J, Wang M. Analysis of green total-factor productivity in China's regional metal industry: a meta-frontier approach. Resources Policy 2018; 58: 219–229. [Google Scholar]
- 21.Bampatsou C, Halkos GE. Dynamics of productivity taking into consideration the impact of energy consumption and environmental degradation. Energy Policy 2018; 120: 276–283. [Google Scholar]
- 22.Ang F, Kerstens PJ. Decomposing the Luenberger–Hicks–Moorsteen total factor productivity indicator: an application to U. S. agriculture . Eur. J. Oper. Res 2017; 260: 359–375. [Google Scholar]
- 23.Phương VH. Total factor productivity growth, technical progress & efficiency change in Vietnam coal industry – Nonparametric approach. E3S Web Conf 2018; 35: 01009. 10.1051/e3sconf/20183501009 [DOI] [Google Scholar]
- 24.Herzer D, Donaubauer J. The long-run effect of foreign direct investment on total factor productivity in developing countries: a panel cointegration analysis. Empir Econ 2015; 54: 309–342. [Google Scholar]
- 25.Tone K, Tstusui M. An epsilon-based measure of efficiency in DEA: an alternative method for the affinity index. Eur J Oper Res 2010; 207: 1554–1563. [Google Scholar]
- 26.Otsuka A. Regional determinants of total factor productivity in Japan: stochastic frontier analysis. Ann Reg Sci 2017; 58: 579–596. [Google Scholar]
- 27.Färe R, Grosskopf S, Norris ME, et al. Productivity growth, technical progress, and efficiency change in industrialized countries. Am Econ Rev 1994; 84: 66–83. [Google Scholar]
- 28.Vlontzos G, Niavis S, Manos B. A DEA approach for estimating the agricultural energy and environmental efficiency of EU countries. Renewable Sustainable Energy Rev 2014; 40: 91–96. [Google Scholar]
- 29.Sueyoshi T, Goto M. DEA Approach for unified efficiency measurement: assessment of Japanese fossil fuel power generation. Energy Economics 2011; 22: 292–303. [Google Scholar]
- 30.Mancini MS, Galli A, Niccolucci V, et al. Stocks and flows of natural capital: implications for ecological footprint. Ecol Indic 2017; 77: 123–128. [Google Scholar]
- 31.Wu Z, Jiang M, Wang H, et al. Management implications of spatial–temporal variations of net anthropogenic nitrogen inputs (NANI) in the Yellow River basin. Environ Sci Pollut Res 2022; 29: 1–19. [DOI] [PubMed] [Google Scholar]
- 32.Dinda S. Environmental Kuznets curve hypothesis: a survey. Ecol Econ 2004; 49: 431–455. [Google Scholar]
- 33.Shi H, Chai J, Lu Q, et al. The impact of China's low-carbon transition on economy, society and energy in 2030 based on CO2 emissions drivers. Energy 2021; 239: 122336. [Google Scholar]
- 34.Yang W, Li D. Spatio-temporal evolution of ecological environment quality in China from a concept of strong sustainability. Environmental Science and Pollution Research 2022; 29: 28769–28787. [DOI] [PubMed] [Google Scholar]
- 35.Chambers RG, Chung Y, Färe R. Profit, directional distance functions, and nerlovian efficiency. J Optim Theory Appl 1998; 98: 351–364. [Google Scholar]
- 36.LeSage JP, Pace RK. Spatial econometric modeling of origin-destination flows. J Reg Sci 2008; 48: 941–967. [Google Scholar]
- 37.Yang W, Ban L. The green sustainable economic development model under sustainable use of energy and pollution control. Theor. Econ. Lett 2013; 3: 19–27. [Google Scholar]
- 38.Zhu W, Wang S, Luo P, et al. A quantitative analysis of the influence of temperature change on the extreme precipitation. Atmosphere (Basel) 2022; 13: 12. [Google Scholar]
- 39.Wei X, Yang J, Luo P, et al. Assessment of the variation and influencing factors of vegetation NPP and carbon sink capacity under different natural conditions. Ecol. Indic 2022; 112: 108834. [Google Scholar]
- 40.Luo P, Xu C, Kang S, et al. Heavy metals in water and surface sediments of the Fenghe river basin, China: assessment and source analysis. Water Sci Technol 2021; 84: 3072–3090. [DOI] [PubMed] [Google Scholar]
- 41.Tang D, Tang J, Xiao Z, et al. Environmental regulation efficiency and total factor productivity—effect analysis based on Chinese data from 2003 to 2013. Ecol Indic 2017; 73: 312–318. [Google Scholar]
- 42.Zhao B, Yang W, Wen J, et al. The financial market in China under the COVID-19. Emerging Markets Finance and Trade 2022; 58: 3726–3738. 10.1080/1540496X.2022.2070472 [DOI] [Google Scholar]
- 43.Huang Z, Zhang H, Duan H. How will globalization contribute to reduce energy consumption? Energy 2020; 213: 118825. [Google Scholar]
- 44.Burridge PR. On the Clifford test for spatial correlation. Journal of the Royal Statistical Society 1988; 42: 107–108. [Google Scholar]
- 45.Anselin L, Bera AK, Florax RJ, et al. Simple diagnostic tests for spatial dependence. Reg Sci Urban Econ 1996; 26: 77–104. [Google Scholar]
- 46.Zhang G, Liu W, Duan H. Environmental regulation policies, local government enforcement and pollution-intensive industry transfer in China. Comput. Ind. Eng 2020; 148: 106748. [Google Scholar]
- 47.Luo P, Luo M, Li F, et al. Urban flood numerical simulation: research, methods and future perspectives. Environ Model Softw 2022; 156: 105478. [Google Scholar]
- 48.Wang H, Zhao Y. Preliminary study on harnessing strategies for Yellow River in the new period. Journal of Hydraulic Engineering 2019; 50: 1291–1298. https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2019&filename=SLXB201911001&uniplatform=NZKPT&v=v4fUVjHrAoDHZYncF9cFNAuGY98956SZnWDf_GZgC7-mNJIv01G-rsHyne0Fy81 [Google Scholar]
- 49.Cui L, Duan H, Mo J, et al. Ecological compensation in air pollution governance: China's efforts, challenges, and potential solutions. International Review of Financial Analysis 2021; 74: 101701. [Google Scholar]