Abstract
In this paper, a new apodized fiber Bragg grating (FBG) structure, the Chebyshev apodization, is proposed. The Chebyshev polynomial distribution has been widely used for the optimal design of antennas and filters, but it has not been used for designing FBGs. Unlike the function of traditional Gaussian-apodized FBGs, the Chebyshev polynomial is a discrete function. We demonstrate a new methodology for designing Chebyshev-apodized FBGs: the grating region is divided by discrete n sections with uniform gratings, while the index change is used to express the Chebyshev polynomial. We analyze the Chebyshev-apodized FBGs by using coupled mode theory and the piecewise-uniform approach. The reflection spectrum and the dispersion of Chebyshev-apodized FBGs are calculated and compared with those of Gaussian FBGs. Moreover, a sidelobe suppression level (SSL), a parameter of the Chebyshev polynomial, along with the maximum ac-index change of FBGs are analyzed. Assume that the grating length is 20mm, SSL is 100 dB, the section number is 40, and the maximum ac-index change is 2 × 10−4. The reflection spectrum of Chebyshev apodized FBGs shows flattened sidelobes with an absolute SSL of −95.9 dB (corresponding to SSL=100 dB). The simulation results reveal that at the same full width at half maximum, the Chebyshev FBGs have lower sidelobe suppression than the Gaussian FBGs, but their dispersion is similar. We demonstrate the potential of using Chebyshev-apodized FBGs in optical filters, dispersion compensators, and sensors; Chebyshev apodization can be applied in the design of periodic dielectric waveguides.
Keywords: Fiber bragg gratings, Chebyshev polynomial, optical fiber filters, bragg reflectors, optical fiber devices
Introduction
Because of their narrow bandwidth, low insertion loss, high selectivity, immunity to electromagnetic interference, and lack of polarization sensitivity, fiber Bragg gratings (FBGs) have been widely applied as reflectors in fiber lasers, dispersion compensators, and filters in wavelength-division multiplexing (WDM) systems in optical communication. 1 FBGs are also used as photonic sensors due to their high environmental sensitivity, long-term stability, compact size, and low cost. They can be applied for measuring temperature, refractive index, pressure, strain, vibration, and bending,2,3 etc.. Recently, the applications of FBGs in fiber sensing have been developed by many technologies, such as weakly tilted FBGs integrated with black phosphorus, 4 and FBGs inscribed in a thin film deposited on a D-shaped fiber for refractive index sensors. 5 The grating profile can be either a uniform or arbitrary apodization functions (e.g. Gaussian, cosine, raised-cosine, cos2,6 Hamming, Blackman, Tanh, Sinc, Cauchy, 7 or Kaiser windowing functions 8 ). Apodization FBGs have many important applications, such as for dispersion compensation,7,9,10 for delay lines, 11 and as optical filters for WDM systems.6,12–14
Ouellette et al. first proposed a Gaussian apodization function as a dispersion compensator 15 and demonstrated the properties of the device. 16 Thibault et al. numerically simulated chirped FBGs with uniform and Gaussian profiles for efficient compensation. 9 A comparison of the characteristics of various apodization functions in linearly chirped fiber gratings for chromatic dispersion compensators has been presented by Pastor et al.. 7 Ennser et al. revealed that apodized FBGs functioned on the reflection and dispersion characteristics with different apodization profiles. 10
There are many applications of fibers in telecommunications. Marek Życzkowski et al. used optical vortices in fiber optic networks to increase the information flow and the data transmission security. 17 Rui Min et al. presented chirped FBGs inscribed in a microstructured polymer optical fiber for increasing the tunable dispersion. 18 Optical devices for dense WDM systems 19 require optical filters with narrow channel spacing and low insertion loss. Apodized FBGs can achieve high channel isolation with low sidelobes and a well-defined bandwidth. Lima et al. compared and optimized the reflection characteristics of various apodization profiles for FBGs. 6 They showed that FBGs with a Gaussian profile were suitable for an optical filter in a dense WDM system. Lima et al. also demonstrated that Gaussian apodization FBGs with a negative index change mean value can operate as group velocity dispersion compensators. 13 Feced et al. conducted the performance optimization of FBGs with a Gaussian apodization profile in a WDM system. 14
As previously stated, various apodization profiles have been studied and compared to determine their utility in filters of corrugated dielectric waveguides, 8 apodized FBGs for dispersion compensators,7,10 and apodized FBGs for filters in WDM systems. 6 These apodization profiles are continuous functions which mostly are based on sinusoidal or exponential functions. In this paper, we propose, to the best of our knowledge, a new apodized profile for FBGs based on the design of a grating structure with refractive index variation exhibiting the Chebyshev polynomial. We term this as Chebyshev-apodized structure.20,21 The Chebyshev polynomial distribution has been widely used for the optimal design of antennas and filters. 22 For example, the Chebyshev phased array antenna can provide a radiation pattern with equal side lobe levels. 23 It can also be applied in the design of surface acoustic wave (SAW) filters. 24
The Chebyshev polynomial includes the parameters of the number of antennae (n) and the sidelobe suppression level (SSL). The Chebyshev polynomial is not a continuous function. Therefore, the approach for applying Chebyshev apodization to designing FBGs should be different from that of traditional Gaussian apodization. In this paper, we present a methodology for designing Chebyshev-apodized FBGs: First, we divide gratings into n-discrete uniform sections to fit the parameters pertaining to the number of antennas, and second, we use index modulation to express the Chebyshev polynomial. Although several numerical methods have been developed to analyze FBGs such as inverse scattering algorithms 25 and the Genetic Algorithms (GAs), 26 the most common methods for the theoretical analyses of FBGs are based on coupled mode theory, which is a simple and intuitive numerical method that can provide accurate simulated results for FBGs.1,7,12,14,15,27 To analyze n-section FBGs, coupled mode theory with the piecewise-uniform approach (PUA) is applied to designing Chebyshev grating structures in this paper. 27 The SSL and maximum ac-index change of FBGs are analyzed. The calculated reflection spectrum of the Gaussian and Chebyshev-apodized FBGs are illustrated and are compared. Moreover, we simulate the dispersions of the Chebyshev and Gaussian-apodized FBGs with various FWHMs.
The phase mask method is a mature technique to make FBGs, where FBGs can be fabricated in a single mode fiber by combining a KrF 248-nm excimer laser and phase mask writing technique. We can order the phase mask with Chebyshev profiles to make Chebyshev-apodized FBGs; however, it is too costly to make a customized phase mask. By utilizing the translation stage, shifting the narrow laser beam, and controlling the exposure time in the fiber, a Chebyshev grating profile could be fabricated.
A key aspect of the Chebyshev-apodized FBGs is to produce a flattened sidelobe and to design the sidelobe suppression level. These properties can provide significant advantages in optical communication system and improve sensing accuracy in FBG sensors. Our goal is to achieve more efficient FBG design for applications as filters, dispersion compensators, reflectors, and sensors. Moreover, the methodology can be applied for designing periodic dielectric waveguides for filters, distributed Bragg reflector lasers, and dispersion compensators.
This paper is organized as follows. In Section 2, a brief introduction of the couple mode theory is presented. In Section 3, the reflection spectrum of Chebyshev-apodized FBGs with parameters of Chebyshev polynomial are analyzed and discussed. Moreover, the reflectivity and dispersion of Chebyshev-apodized FBGs also make comparisons with those of Gaussian-apodized FBGs in Section 3. Finally, conclusions are given in Section 4.
Mathmetical formulation
In this paper, we use coupled mode theory with the piecewise-uniform approach 27 to analyze Chebyshev-apodized FBGs. Assume that a time-harmonic wave propagates in the z-direction as exp(iβz-iωt), where β is a propagation constant, and ω is the angular frequency. An apodized FBG was applied to reduce the high sidelobes on the high-frequency side. Therefore, the refractive index of the fiber Bragg grating can be expressed as follows:
| (1) |
where n1, n2, and n3 are refractive indices of the core, cladding and surrounding region, respectively, Λ is the grating period, is the induced-dc index change over the grating region, and n 1 σ ac (z) represents the grating ac-index change.
The coupled equations can be written as follows:
| (2) |
| (3) |
where Aco(z) is the amplitude for the transverse core mode field traveling in the + z direction, Bco(z) is the amplitude for the transverse core mode field traveling in the − z direction. We define the small-detuning parameter and coupling coefficient as follows 1 :
| (4) |
| (5) |
where Er and Eϕ denote the electric fields transverse components of a vector function. The analytical solutions of Eq. (2) and Eq. (3) are written as:
| (6) |
| (7) |
| (8) |
By matching the boundary condition at each interface of sections, the transmission and reflection efficiencies can be obtained. The group delay Vg and dispersion D can be expressed as follows 28 :
| (9) |
| (10) |
where β is the propagation constant, ω is the angular frequency, λ is the wavelength, and c is the velocity of light in vacuum. The shape factor is defined as follows:
| (11) |
where BW20dB is a bandwidth of − 20 dB, and BW3db is a bandwidth of − 3 dB. Figure 1 shows the Block diagram of calculating the transmission and reflection efficiencies, group delay, and dispersion of Chebyshev-apodized FBGs. The detailed description of coupled mode theory with the piecewise-uniform approach can be referenced from the paper presented by Sun et al. 27
Figure 1.

Block diagram for calculating the transmission and reflection efficiencies, group delay, and dispersion of Chebyshev-apodized FBGs.
After the Chebyshev polynomial is used to design a phased array antenna, the number of antennas (n) and SSL can be determined. As previously stated, the Chebyshev polynomial is not a continuous function. Assume that the number of antennas represents the number of uniform gratings. Using Chebyshev apodization, we divide gratings into n-discrete uniform sections. Moreover, for the design of SAW devices, the duty cycle is selected to be a Chebyshev modulation term. 24 For FBGs, we use an “ac” index change to express Chebyshev apodization. Therefore, to design Chebyshev-apodized Bragg gratings, we need to determine the section number (SN) and the SSL. To analyze n-section FBGs, the piecewise-uniform technique is applied in the design of Chebyshev grating structures. 2
Results
A step-index fiber is used in our design. For the fiber structure, the radiuses of the core (r1) and cladding (r2) are 2.5 μm and 62.5 μm, respectively. 29 The refractive indices of the core (n1), cladding (n2), and surrounding region (n3) are 1.458, 1.45, and 1, respectively. Figure 2 shows the envelope profile of a Chebyshev apodization with an SN of 40 (SN = 40) and an SSL of 100 dB. Assume that the total length of the FBG is 20mm, 30 and that the length of each section is 0.5 mm. Figure 2 presents the envelope profile of a Chebyshev apodization with a non-zero dc-index change, where is equal to , and the maximum ac-index change of , labeled as , is 2 × 10−4. Each section in Figure 2 presents a uniform grating structure with a grating period Λ of 0.53μm.
Figure 2.
dc-index change of a chebyshev profile with 40 section uniform gratings, where is a chebyshev function and equals to , the gratings length is 20 mm, the length of each section is 0.5 mm, the maximum ac-index change of is 2 × 10−4, and the SSL is 100 dB. The grating period of each section is 0.53μm.
We use the PUA to calculate the spectrum of apodized FBGs. Figure 3 shows the transmission and reflection spectra of Chebyshev-apodized FBGs. The reflection spectrum of apodized FBGs is not symmetric in the resonant region due to the non-uniform index change in (1). The long-wavelength side has no sidelobes, and the short-wavelength side has several sidelobes. As shown in Figure 3, the − 3-dB resonant region ranges from 1539.16 to 1539.298 nm, where the corresponding bandwidth is 0.138 nm. The maximum reflectivity at 1539.218 nm is dB, while the transmissivity is − 8.35 dB. Sidelobe suppression is substantial on the long-wavelength side. For example, the sidelobe of reflectivity at a wavelength of 1539.68 nm is dB. The first sidelobe on the short-wavelength side is at 1539.08 nm with the reflection efficiency of dB. When the wavelength is less than 1538.81 nm, the sidelobe is at approximately dB. Minimum transmissivity is −8.349 dB in the band gap region. Outside the band gap region, the sidelobes of reflectivities are at almost − 100 dB. Surprisingly, reflectivity corresponds to a sidelobe suppression level of 100 dB.
Figure 3.
Transmission and reflection spectra of the chebyshev-apodized structure (parameters presented in Figure 1).
The symmetric transmission and reflection spectra are determined through two approaches. Firstly, the apodized structures with a zero dc-index change are used. Figure 4 shows that the constant dc-index change ( ) is 2 × 10−4, the maximum ac-index change is 2 × 10−4, the SN is 40, and the SSL is 100 dB. Secondly, we design a set of grating periods to obtain a symmetric spectrum. The grating period design rule depends on the relationship between propagation constants and coupling coefficients. 12 For the Chebyshev-apodized structure with grating period variations (also termed chirped gratings), the grating period of each section can be designed as follows:
| (9) |
where i is the section number, n is the total section number, Λi is the grating period at section i, and Λ0 is the original grating period. Assume that the total section number (n) is 40. κi and βi are the coupling coefficient and propagation constant at section i, respectively. Note that each section in Figure 2 has different grating periods. κn/2 is the coupling coefficient at section 20 (κ20). The grating period at the center section n/2 is the original one (Λ0). Figure 5 shows the grating period of each section of a Chebyshev-apodized structure as those presented in Figure 2. The grating period at the 20-th and 21-st sections in Figure 5 is 0.53μm. The grating period of each section is symmetric to the center section.
Figure 4.
Index change of a chebyshev profile with 40section uniform gratings and constant dc-index change, where is a constant of 2 × 10−4, is 2 × 10−4, and the SSL is 100 dB.
Figure 5.
The grating period of each section of chebyshev-apodized structure with grating period variation. The parameters correspond to those in Figure 1, which are calculated using Eq. (9). The total number of sections is 40. The grating period at the 20th and 21st sections is 0.53μm.
The transmission and reflection spectra of Chebyshev apodization with a zero-dc index change and with grating period variation are shown in Figure 6. The grating structure in Figure 6 is the same as the structures in Figure 4 and Figure 5. We find that the transmissivity and reflectivity of the two grating structures are overlapping and symmetric. The − 3-dB resonant region is from 1539.1845 to 1539.3175 nm, where the − 3-dB bandwidth of the reflection spectrum is 0.133 nm, and the − 20-dB bandwidth is 0.239 nm. The central wavelength at resonance is 1539.251 nm. The sidelobe suppressions show nearly equal sidelobe levels on the two sides of resonance, and are approximately 100 dB corresponding to wavelengths of 1539.94 and 1539.58 nm.
Figure 6.
Transmission and reflection spectra of a chebyshev-apodized FBGs with zero dc-index change and grating period variation under the same parameters as shown in Figure 3 and Figure 4. Note that spectra of zero dc-index change and grating period variation are the same.
Next, we vary the parameters of Chebyshev-apodized FBGs. For simplicity, the structure in Figure 4 is used for simulations. Figure 7 shows the reflection spectrum of Chebyshev-apodized FBGs where the SSLs are 60, 80 and 100 dB, the SN is 40, and is 2 × 10−4. For an SSL of 100 dB, the − 3-dB resonant region is from 1539.1845 nm to 1539.3175 nm. The − 3-dB bandwidth of the reflection spectrum is 0.133 nm, while the − 20-dB bandwidth is 0.239 nm. The central wavelength at resonance is 1539.251 nm with the maximum reflectivity of − 0.572 dB. The sidelobe suppressions on the two sides of resonance are − 97.28 and − 98.35 dB, corresponding to wavelengths of 1539.94 and 1539.58 nm, respectively. We define the absolute SSL of a reflection spectrum as the peak reflectivity minus the second peak of sidelobes. A comparison of the reflection spectrum of SSLs of 100, 80, and 60 dB shows sidelobe suppressions of − 95.9 dB, − 74.56 dB, and − 52.13 dB, respectively. This indicates that the SSL parameter of Chebyshev apodization can be used to design the sidelobe suppression of FBGs without changing the central resonant wavelengths. As presented in Figure 7, the central wavelengths of three SSLs and the − 3-dB bandwidths remain the same, while the − 20-dB bandwidths at SSLs of 100, 80, and 60 dB are 0.239, 0.217, and 0.207 nm, respectively. The − 20-dB bandwidth is reduced by 0.032 nm from an SSL of 100 to 60 dB.
Figure 7.
The reflection spectrum of chebyshev-apodized structure with SSL = 60 dB (red line), SSL = 80 dB (green line) and SSL = 100 dB (blue line), where SN = 40, and = 2 × 10−4. The grating period is 0.53 μm.
Figure 8 shows the reflection spectrum of Chebyshev-apodized FBGs with 2 × 10−5, 2 × 10−4 and 7 × 10−4, where the other parameters in Figure 8 are the same as those in Figure 7. When is increasing, the resonant wavelengths shift to the long-wavelength side, while the maximum reflection efficiencies, the resonant bandwidth, and sidelobe suppression also increase. Detailed results are presented in Table 1. The absolute sidelobe suppression level is close to − 74.56 dB (corresponding to SSL = 80 dB) when is less than 2 × 10−4. For example, at , the maximum reflectivity at resonance is − 14.53 dB at a sidelobe of − 93.2 dB. The sidelobe suppression is − 78.67 dB (approximately − 80 dB).
Figure 8.
Reflection spectrum of a chebyshev-apodized structure with = 2 × 10−5 (red line), 2 × 10−4 (blue line), and 7 × 10−4 (green line). The SSL is 80 dB, and SN is 40.
Table 1.
Resonant wavelength, − 20-dB bandwidth, and absolute sidelobe suppression level of a chebyshev-apodized structure with = 2 × 10−5, 2 × 10−4, and 7 × 10−4, where the SSL is 80 dB, and SN is 40.
| Resonant wavelength (nm) | 1539.142 | 1539.250 | 1539.548 |
| −20-dB bandwidth (nm) | 0.094 (1539.096∼1539.190) | 0.226 (1539.138∼1539.364) | 0.530 (1539.286∼1539.816) |
| Absolute Sidelobe suppression (dB) | −78.67 dB | −74.56 dB | −64.33 dB |
The spectrum of Chebyshev-apodized FBGs with different gratings lengths are analyzed. Figure 9 shows the reflection spectrum of Chebyshev-apodized FBGs with the grating lengths of 5 mm, 10 mm, and 20 mm, where the SSL is 100 dB, the SN is 40, and is 2 × 10−4. The central wavelengths at resonance are 1539.251 nm with three grating lengths. On the other hand, long grating lengths produce strong coupling effects, such as increasing maximum reflectivity and narrowing the resonant bandwidth. The maximum reflectivity are − 0.572 dB, − 3.81 dB, and − 7.90 dB, while the − 20-dB bandwidths are 0.61 nm, 0.38 nm, and 0.24 nm, corresponding to the grating lengths of 5 mm, 10 mm, and 20 mm, respectively.
Figure 9.
Reflection spectrum of a chebyshev-apodized structure with the gratings length of 20 mm, 10 mm, and 5 mm. The = 2 × 10−4, SSL is 100 dB, and SN is 40.
We compared the reflectivity and dispersion of the Chebyshev-apodized profile (SSL = 100) with that of the Gaussian-apodized profile of FBGs, where the section number is 40, and is 2 × 10−4. Gaussian apodization for a full width at half maximum (FWHM) of L/2 (10 mm) is calculated because an FWHM of L/2 is usually applied in the Gaussian apodization.1,25 We also simulate the Gaussian apodization for FWHM = 7 mm (≈ L/3) because the FWHM for Chebyshev apodization with an SSL of 100 dB is approximately L/3. Gaussian apodization for FWHM = L = 20 mm is also evaluated.
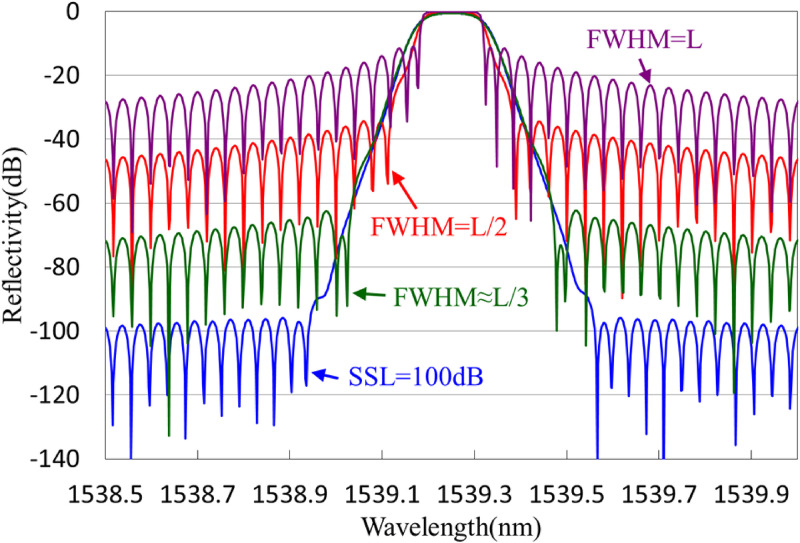
Figure 10 shows the reflectivities of Chebyshev (blue line for SSL = 100 dB), Gaussian grating structures with FWHM = 7mm≈L/3 (green line), Gaussian grating structures with FWHM = 10mm = L/2 (red line), and Gaussian grating structures with FWHM = 20mm = L (purple line). The absolute sidelobe suppression level on the two sides of resonance at an SSL of 100 dB for Chebyshev apodization are − 95.9 B (approximate to − 100 dB), whereas the sidelobe suppressions are approximately − 62.5 dB, − 34.4 dB, and − 11.6 dB for Gaussian apodization at FWHM≈L/3, FWHM = L/2, and FWHM = L, respectively. The results show that at a similar FWHM, the Chebyshev-apodized FBGs could provide higher sidelobe suppressions level than Gaussian-apodized FBGs could. Moreover, the sidelobe spectrum of Chebyshev apodization is approximately − 96 dB ranging from a wavelength of 1538.85 to 1538.55 nm. For the Gaussian-apodized FBGs, the sidelobe spectrum is from − 62.5 dB to − 72 dB with FWHM = 7 mm, from − 34.4 dB to − 46 dB with FWHM = 10 mm, and from − 11.6 dB to − 27.5 dB with FWHM = 20 mm. The sidelobe level of Chebyshev apodization is flatter than that of Gaussian apodization.
Figure 10.
Reflection spectra of chebyshev-apodized (blue line for an SSL of 100 dB) and Gaussian-apodized FBGs (green line for FWHM = 7 mm ≈ L/3, red line for FWHM = 10 mm = L/2, and purple line for FWHM = 20 mm = L).
The dispersion spectra of the Chebyshev and Gaussian grating structures are shown in Figure 11, where the blue line denotes Chebyshev apodization (SSL = 100 dB), the green line denotes Gaussian apodization with FWHM≈L/3, the red line denotes Gaussian apodization with FWHM = L/2, and the purple line is for FWHM = L. The insect of Figure 11 is the dispersion spectrum of FWHM = L. The dispersion of Chebyshev grating structures with SSL = 100 dB is similar to that of Gaussian structures with FWHM≈L/3. The maximum magnitude of dispersion for Chebyshev and Gaussian FBGs with FWHM≈L/3 are approximately 0.631 ps/nm·km. Note that the maximum magnitude of dispersion of Gaussian FBGs with FWHM = L/2 (dispersion = 1.872 ps/nm·km) is three times larger than those of Chebyshev and Gaussian FBGs with FWHM≈L/3 (dispersion = 0.631 ps/nm·km).
Figure 11.
Dispersion spectra of the chebyshev-apodized (blue line) and Gaussian-apodized FBGs. The green line represents FWHM = 7 mm, the red line denotes FWHM = 10 mm, and the purple line denotes FWHM = 20 mm. The insect is the dispersion spectrum of FWHM = 10 mm.
Table 2 shows the − 3-dB bandwidth, the − 20-dB bandwidth, the shape factor (defined as the 20-dB bandwidth divided by the 3-dB bandwidth) of four grating structures, and the maximum magnitude of dispersion. The − 3-dB bandwidths of the Chebyshev-apodized FBGs (∼0.133 nm) are wider than those of the Gaussian-apodized FBGs (∼0.128 nm). The shape factor of 1.797 for the Chebyshev apodization is worse than that for Gaussian apodization at FHWM = 10 mm (1.656) and better than that for Gaussian apodization at FWHM = 7 mm (1.906), while Gaussian apodization at FHWM = 10 mm has the smallest shape factor of 1.125 in Table 2. Moreover, as shown in Table 2 and the inset of Figure 11, Gaussian FBGs with FWHM = L has the largest maximum magnitude of dispersion (dispersion = 11.06 ps/nm·km).
Table 2.
Simulated results for the bandwidths, the shape factor, and the maximum magnitude of dispersion of chebyshev-apodized FBGs and Gaussian-apodized FBGs.
| Chebyshev apdoized-FBGs SSL = 100 dB | Gaussian apodized-FBGs FWHM = 7mm | Gaussian apodized-FBGs FWHM = 10mm | Gaussian apodized-FBGs FWHM = 20mm | |
|---|---|---|---|---|
| −3-dB bandwidth (nm) | 0.133 | 0.128 | 0.128 | 0.128 |
| −20-dB bandwidth (nm) | 0.239 | 0.244 | 0.212 | 0.144 |
| The shape factor | 1.797 | 1.906 | 1.656 | 1.125 |
| Maximum magnitude of dispersion (ps/nm·km) | 0.631 | 0.631 | 1.872 | 11.06 |
Conclusions
In this paper, Chebyshev index modulation is applied to design FBGs. The reflection spectrum and the dispersion of a Chebyshev apodization profile with 40 grating sections are calculated. We vary the SSL and maximum ac-index change ( ) to analyze the properties of Chebyshev-apodized FBGs. In Chebyshev apodization, the SSL can be used to determine the sidelobe suppression of FBGs. The analysis results demonstrate that the sidelobe suppressions are consistent with the parameter SSL of Chebyshev polynomial, and Chebyshev-apodized FBGs have the property of flattened sidelobes. When the grating lengths is 20 mm, SSL is 100 dB, the section number is 40, and the maximum ac-index change is 2 × 10−4, the reflection spectrum of Chebyshev apodized FBGs shows flattened sidelobe with absolute SSL of − 95.9 dB, where the sidelobe suppression level is close to 100 dB. We also compare Chebyshev- and Gaussian-apodized FBG structures in terms of reflection and dispersion spectra. The simulation results demonstrate that SSL related to Chebyshev apodization can be applied to design the sidelobe suppression of FBGs. The sidelobe suppression of the Chebyshev-apodized FBGs is more flattened than that of Gaussian-apodized FBGs. At a similar FWHM, the sidelobe suppression of Chebyshev apodization is lower than that of Gaussian apodization, and the dispersions of the two apodized profiles are similar. We show the potential of Chebyshev-apodized FBGs as filters, dispersion compensators, and sensors, etc., in optical telecommunications and optoelectronics. Moreover, the proposed apodization function can be applied in the design of periodic dielectric waveguides.
Acknowledgments
The authors thank Prof. Ruyen Ro, Prof. Chung-Long Pan (I-Shou University), and Wen-Fung Liu (Feng Chia University) for taking part in the discussions on Chebyshev apodization. This work was partially supported by the Ministry of Science and Technology of the Republic of China under grants MOST 108-2221-E-214-029-MY2, MOST 110-2221-E-214-018, and MOST 108-2221-E-214-030, and by I-Shou University under grants ISU100-08, and ISU-108-01-01A.
Footnotes
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
ORCID iDs: Nai-Hsiang Sun https://orcid.org/0000-0003-1560-1979
Jung-Sheng Chiang https://orcid.org/0000-0002-5801-2595
References
- 1.Erdogan T. Fiber grating Spectra. J Lightwave Technol 1997; 15: 1277–1294. [Google Scholar]
- 2.Guan BO, Ran Y, Feng FRet al. et al. Formation and applications of the secondary fiber Bragg grating. Sensors 2017; 17: 398-412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chiang JS, Chang HY, Sun NH, et al. High sensitive two-dimension tilted-meter based on chirped fiber Bragg gratings. IEEE Sensors J 2016; 16: 8477–8482. [Google Scholar]
- 4.Zhang Z, Liu K, Jiang JF, et al. Refractometric sensitivity enhancement of weakly tilted fiber Bragg grating integrated with black phosphorus. Nanomaterials 2020; 10: 1423-1433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Imas JJ, Zamarreño CR, Villar I, et al. Optimization of fiber Bragg gratings inscribed in thin films deposited on D-shaped optical fibers. Sensors 2021; 21: 4056-4070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lima MJN, Teixeira ALJ, da Rocha JRF. Optimization of apodized fiber grating filters for WDM systems. In: IEEE Lasers and electro-optics society, annual meeting conference, 1999 paper no. ThZ2, pp.876-877. [Google Scholar]
- 7.Pastor D, Capmany J, Ortega D, et al. Design of apodized linearly chirped fiber gratings for dispersion compensation. J Lightwave Technol 1996; 14: 2581–2588. [Google Scholar]
- 8.Cross PS, Kogelnik H. Sidelobe suppression in corrugated-waveguide filters. Opt Lett 1977; 1: 43–45. [DOI] [PubMed] [Google Scholar]
- 9.Thibault S, Lauzon J, Cliché JF, et al. Numerical analysis of the optimal length and profile of a linearly chirped fiber Bragg grating for dispersion compensation. Opt Lett 1995; 20: 647–649. [DOI] [PubMed] [Google Scholar]
- 10.Ennser K, Zervas MN, Laming RI. Optimization of apodized linearly chirped fiber gratings for optical communications. IEEE J Quantum Electron 1998; 34: 770–778. [Google Scholar]
- 11.Italia V, Pisco M, Campopiano S, et al. Chirped fiber Bragg gratings for electrically tunable time delay lines. IEEE J Sel Topics Quantum Electron 2005; 11: 408–416. [Google Scholar]
- 12.Carballar A, Muriel MA, Azana J. Fiber grating filter for WDM systems an improved design. IEEE Photonics Technol Lett 1999; 11: 694–696. [Google Scholar]
- 13.Lima MJN, Teixeira ALJ, da Rocha JRF. Simultaneous filtering and dispersion compensation in WDM systems using apodised fibre gratings. Ele Lett 3rd 2000; 36: 1412–1414. [Google Scholar]
- 14.Feced R, Zervas MN, Muriel MA. An efficient inverse scattering algorithm for the design of nonuniform fiber Bragg gratings. IEEE J Quantum Electron 1999; 35: 1105–1115. [Google Scholar]
- 15.Ouellette F. All-fiber filter for efficient dispersion compensation. Opt Lett 1991; 16: 303–305. [DOI] [PubMed] [Google Scholar]
- 16.Ouellette F, Cliche JF, Gagnon S. All-fiber devices for chromatic dispersion compensation based on chirped distributed resonant coupling. J Lightwave Technol 1994; 12: 1728–1738. [Google Scholar]
- 17.Życzkowski M, Brewczyński KD, Karol M. Innovative security technology for optical fiber data transmission using optical vortex. Proc Eng Technol Innov 2017; 5: 01–06. [Google Scholar]
- 18.Min R, Korganbayev S, Molardi C, et al. Largely tunable dispersion chirped polymer FBG. Opt Lett 2018; 43: 5106–5109. [DOI] [PubMed] [Google Scholar]
- 19.Chang YT, Cheng HC, Lin YC, et al. The design and implementation of scrambling wavelength hopping with AWG router and optical switch over secure WDM network. Proc Eng Technol Innov 2017; 5: 07–12. [Google Scholar]
- 20.Liau JJ, Chou CC, Chou CE, et al. The design of fiber Bragg gratings using a chebyshev index modulation. In: Optoelectronics and communications conference (OECC), paper No.7P-066, 2005. [Google Scholar]
- 21.Sun NH, Tsai MY, Hsueh YC, et al. Chebyshev apodization in fiber gratings. In: Progress in electromagnetics research symposium (PIERS), paper No. 1A5-7, 2019
- 22.Kraus JD. Antennas. 2nd ed.New York, NY, USA: McGraw-Hill College, 1988. [Google Scholar]
- 23.Alexopoulos A. Phased array analysis using a modified chebyshev approach. Edinburgh, South Australia, Australia: Defence Science and Technology Organisation, 2005. [Google Scholar]
- 24.Ro RY, Tung HY, Wu SJ. Design of two-track surface acoustic wave filters with width-controlled reflectors. Japanese J App Physics 2004; 43: 688–694. [Google Scholar]
- 25.Rebola JL, Cartaxo AVT. Performance optimization of Gaussian apodized fiber Bragg grating filter in WDM systems. J Lightwave Technol 2002; 20: 1537–1544. [Google Scholar]
- 26.Rostami A, Yazdanpanah-Goharrizi A. A new method for classification and identification of Complex fiber Bragg grating using the genetic algorithm. Prog Electromagn Res 2007; 75: 329–356. [Google Scholar]
- 27.Sun NH, Liau JJ, Kiang YW, et al. Numerical analysis of apodized fiber Bragg gratings using coupled mode theory. Prog Electromagn Res 2009; 99: 289–306. [Google Scholar]
- 28.Yariv A. Optical electronics in modern communications. 5th ed.New York, NY, USA: Oxford – Oxford University Press, 1996. [Google Scholar]
- 29.Erdogan T. Cladding-mode resonances in short- and long-period fiber grating filters. J Opt Soc Am A 1997; 14: 1760–1773. [DOI] [PubMed] [Google Scholar]
- 30.Sun NH, Hu CM, Chiang JS, et al. Grating-Outcoupled radiation in second-order fiber Bragg gratings. Fiber Integrated Opt 2014; 33: 47–55. [Google Scholar]