Design and manufacture of the novel drum worm pair

Abstract

Although a significant amount of research on robot joint reducer was conducted, there are few systematic investigations on a novel joint reducer adopting inner worm-gear plane enveloping drum worm drive. To satisfy the development of modular robot joint, the primary objective of this paper was to systematically investigate the drum worm drive adopted in the novel joint reducer with integrated structure of drive, transmission, and support in the following aspects: meshing theory, design, analysis, and manufacture. According to the gear meshing theory, mechanical design method, classical mechanics, finite element method, and machining principle of virtual center distance, the systematic investigations around the drum worm pair applied in the novel joint reducer were conducted including the macro and micro meshing theory, structure design, mechanical and contact properties analyses, and manufacturing method. The novel joint reducer’s integrated structure was designed, and the drum worm pair’s mechanical and contact properties analyses were conducted, which showed: (1) the worm’s bending stress and deflection, worm-gear teeth’s shear stress and bending stress as well as the maximum contact stresses were all below their corresponding allowable values; (2) the maximum contact stresses appeared at the engage-in position of the worm pair opposing to the engaging-out position where the largest contact areas appeared. Then the manufacturing of drum worm’s spiral tooth was conducted via the modified 4-axis linkage CNC grinder according to the conjugate motion. Finally the novel joint reducer’s industrial prototype was assembled. The novel joint reducer with integrated structure of drive, transmission and support was designed and manufactured for the first time. The flowchart of design and manufacture of the reducer’s drum worm pair in this process was formulated, which provides a new insight on the research of joint reducers as well as other fields.

Introduction

The joint is one of important modules of the robot, which has shown a development trend of modularization nowadays, and the integration degree of motor and reducer determines the modularity of robot joint. Harmonic transmission^1,2 and RV transmission ³ are most widely used in robot reducers, but they are hard to manufacture due to their complicated structures. Compared with above transmissions, in addition to advantages of large transmission ratio, compact structure, small volume, and high accuracy transmission, worm drive is also characteristic with self-locking function and simple structure, therefore researchers studied the application of it in robot joints. Otani et al. ⁴ and Choi et al. ⁵ proposed to equip the worm drive in the knee joint of a bipedal humanoid robot and the pitch joint of the shoulder and elbow of a military rescue robot, respectively. As well as, Jackson et al. ⁶ published the patent which described a kind of robot arm whose joint adopting worm-gears. However, the worm drive is used as one component cooperating with other transmissions in the above joints all driven by outside motors, yet there are few applications of built-in motors presently.

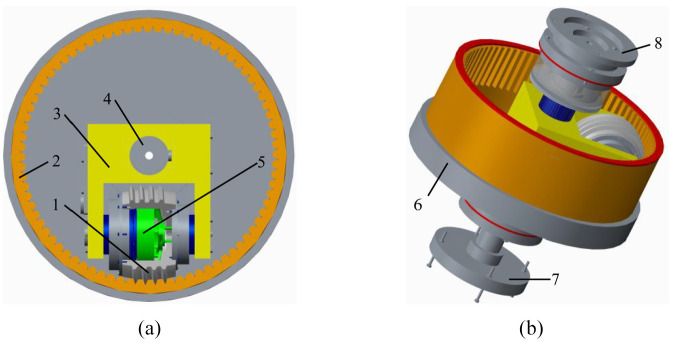
With the development of the modularization of robot joints,^7–10 recently we have proposed a novel precision joint reducer with a built-in motor, named as inner worm-gear plane enveloping drum worm drive reducer, which is characterized with the integrated structure of drive, transmission and support. As show in Figure 1, the reducer adopts the orthogonal internal meshing worm pair to realize the transmission, it is driven by an external rotor motor built into the hollow worm, and main components such as motor and worm are located within the worm-gear ring. In addition, worm-gear seats, brackets, bearings, etc. are utilized to support the reducer, without the need for the gearbox with complicated structure.

Figure 1.

Inner worm-gear plane enveloping drum worm drive reducer. 1. Worm; 2. Worm-gear; 3. Bracket; 4. Pillar; 5. Motor; 6. Worm-gear seat; 7. Fixed flange; 8. Output flange: (a) internal structure, and (b) whole structure.

In the area of the internal meshing worm drive, Chen et al.^11,12 proposed one kind of internal meshing worm pair adopting non-orthogonal worm drive with complicated gearbox, yet utilizing an external motor realizes its driving. It is necessary to have the function of backlash adjustment for backlash and friction compensation^13–16 in the field of high-precision reducer to realize small even zero clearance in order to guarantee high-precision transmission for precision devices such as robot joints. Qiu et al. ¹⁷ and Chen et al. ¹⁸ investigated the gradual-change tooth thickness planar worm gear drive and the variable tooth thickness involute gear enveloping hourglass worm drive, respectively. Both of above types adopt the variable tooth thickness worm-gear to realize backlash adjustment by adjusting relative position between the worm and worm-gear in axial direction of the worm-gear. The novel reducer realizes backlash adjustment by above method and it is characteristic with smaller volume, more compact structure, high-precision transmission, etc. due to the integrated structure.

Finite element method and numerical analysis are widely utilized to perform the contact and mechanics analyses of the worm drive. By this way, Rao ¹⁹ and Zheng et al. ²⁰ realized the failure and contact analysis of worm drive, respectively. In the field of manufacture, using the modified CNC grinder based on the machining principle of virtual center distance was to conduct the processing of the plane enveloping worm effectively.^11,21 Base on that, this paper focuses on the investigation of the drum worm pair of the novel reducer in such areas including design, analysis and manufacture.

Meshing theory

The meshing theory of the inner worm-gear plane enveloping drum worm pair is divided into two parts: macro and micro. The former is the basis for constructing the worm pair and the necessary condition for the design of the worm pair. The latter is the theoretical reference for evaluating the meshing properties of the worm pair, which is mainly used to analyze the meshing properties of the worm pair for optimization. In this study, the macro meshing theory of the worm pair is established for the process of design-analysis.

The tooth-surfaces on both sides of a worm-gear tooth are defined as generating plane A (abbreviated as plane A) and generating plane B (abbreviated as plane B), respectively. The conjugate surface is the plane A yet the non-conjugate surface is the plane B during the worm pair rotates forward (Figure 2), and the opposite is true with the reverse rotation. The planes A and B are tangent to the same base-cone, here the corresponding inclination angles meet ${\beta }_1={\beta }_2$ . In the case of ${\beta }_1={\beta }_2=0$ , the worm pair with the spur gear teeth on the worm-gear is the internal meshing form of the Wildhaber worm pair. ²² In the other case of ${\beta }_1={\beta }_2\ne 0$ , the worm pair with the symmetrical wedge-shaped teeth on the worm-gear is the internal meshing form of gradual-change tooth thickness planar worm pair, ¹⁷ it is characterized with the function of backlash adjustment and the distributions of its contact-lines on the plane A is different from that on the plane B. ²³ Let ${\beta }_1={\beta }_2\ne 0$ , the frame systems of the forward and reverse rotations of the worm pair are established separately to found the corresponding meshing theories.

Figure 2.

Inner worm-gear plane enveloping drum worm pair. 1. Worm-gear; 2. Drum worm; 3. Generating plane A; 4. Generating plane B.

The tooth-surface of the drum worm with a right-handed thread is formed by a series of worm-gear planar tooth-surfaces according to conjugate meshing motion. The coordinate frame systems of the forward and reverse rotations are shown in Figure 3(a) and (b), respectively. In Figure 3, the distance between origin points of fixed coordinate frames ${\sigma }_{\mathrm{b}}$ and ${\sigma }_{\mathrm{w}}$ which are founded in the initial positions of the worm-gear and worm respectively is the center distance A. The movable coordinate frame ${\sigma }_1$ is rigidly connected to the worm for recording its forward and reverse rotations angles through ${\phi }_1$ and ${\phi }_1\prime$ , respectively. The movable coordinate frames ${\sigma }_2$ , ${\sigma }_3$ , ${\sigma }_{\mathrm{p}}$ , and ${\sigma }_{\mathrm{q}}$ are all rigidly connected to the worm-gear, where ${\sigma }_3$ and ${\sigma }_{\mathrm{p}}$ are adopted to mark the meshing point P on the plane A, as well as ${\sigma }_2$ and ${\sigma }_{\mathrm{q}}$ mark the meshing point Q on the plane B. The rotation angle of the worm gear is recorded by ${\phi }_2$ and the position of the plane A is recorded by ${\phi }_3$ in the condition that the worm pair rotates forward. However, the rotation angle of the worm-gear is recorded by ${\phi }_3$ and the position of the plane B is recorded by ${\phi }_2$ during reverse rotation. The rotation angles ${\phi }_2$ and ${\phi }_3$ meet ${\phi }_2+{\phi }_3+\theta =180°$ , where $\theta$ ( $\begin{array}{c}°\hfill \end{array}$ ) is the relative angle between the planes A and B, and $\theta =2\arccos (d_{\mathrm{b}}/d_2)-1.1i\prime \pi$ .

Figure 3.

Coordinate frame systems: (a) forward rotation, and (b) reverse rotation.

According to the gear meshing theory, ²⁴ meshing functions of the forward and reverse rotations of the inner worm-gear plane enveloping drum worm drive are established in equations (1) and (2), respectively. The meshing point P appears on the plane A, the functions of meshing ${\mathrm{\Phi }}^{(3)}$ , second-type boundary ${\mathrm{\Phi }}_t^{(3)}$ and first-type boundary ${\mathrm{\Psi }}^{(3)}$ on the plane A are shown in equation (1) during rotating forward. And the meshing point Q appears on the plane B, the functions of meshing ${\mathrm{\Phi }}^{(2)}$ , second-type boundary ${\mathrm{\Phi }}_t^{(2)}$ and first-type boundary ${\mathrm{\Psi }}^{(2)}$ on the plane B are shown in equation (2) while rotating reverse. Let $i=2,3$ , the equations of contact-lines ${\mathrm{L}}^{(i)}$ , second boundary curves ${\mathrm{\Gamma }}_2^{(i)}$ and first boundary curves ${\mathrm{\Gamma }}_1^{(i)}$ on the planes A and B are obtained from ${\mathrm{\Phi }}^{(i)}=0$ , ${\mathrm{\Phi }}^{(i)}=0$ and ${\mathrm{\Phi }}_t^{(i)}$  = 0, ${\mathrm{\Phi }}^{(i)}=0$ and ${\mathrm{\Psi }}^{(i)}$  = 0, respectively.

$$\{\begin{array}{c}\frac{{\mathrm{\Phi }}^{(3)}}{{\omega }_1}=-v_3\sin {\phi }_3+i\prime u_3\cos \beta -A\sin \beta +u_3\cos {\phi }_3\sin \beta +r_b\sin {\phi }_3\sin \beta {\omega }_1\ne 0\hfill \\ \multicolumn{1}{c}{\frac{{{\mathrm{\Phi }}_t}^{(3)}}{-i\prime {{\omega }_1}^2}=-v_3\cos {\phi }_3+r_b\cos {\phi }_3\sin \beta -u_3\sin {\phi }_3\sin \beta }\\ \multicolumn{1}{c}{\frac{{\mathrm{\Psi }}^{(3)}}{{{\omega }_1}^2\cos \beta }=r_b-A\sin {\phi }_3+i{\prime }^2{r}_b-r_b{\cos }^2{\phi }_3+u_3\sin {\phi }_3\cos {\phi }_3+v_3{\cos }^2{\phi }_3\sin \beta }\\ \multicolumn{1}{c}{-i{\prime }^2{v}_3\sin \beta +2i\prime v_3\cos {\phi }_3\cos \beta }\end{array}$$ (1)

$$\{\begin{array}{c}\frac{{\mathrm{\Phi }}^{(2)}}{{\omega }_1}=-v_2\sin {\phi }_2-i\prime u_2\cos \beta -A\sin \beta +u_2\cos {\phi }_2\sin \beta +r_b\sin {\phi }_2\sin \beta {\omega }_1\ne 0\hfill \\ \multicolumn{1}{c}{\frac{{{\mathrm{\Phi }}_t}^{(2)}}{-i\prime {{\omega }_1}^2}=-v_2\cos {\phi }_2+r_b\cos {\phi }_2\sin \beta -u_2\sin {\phi }_2\sin \beta }\\ \multicolumn{1}{c}{\frac{{\mathrm{\Psi }}^{(2)}}{{{\omega }_1}^2\cos \beta }=-r_b+A\sin {\phi }_2-i{\prime }^2{r}_b+r_b{\cos }^2{\phi }_2-u_2\sin {\phi }_2\cos {\phi }_2-v_2{\cos }^2{\phi }_2\sin \beta }\\ \multicolumn{1}{c}{+i{\prime }^2{v}_2\sin \beta +2i\prime v_2\cos {\phi }_2\cos \beta }\end{array}$$ (2)

Design and manufacture process

The systematic design and manufacture process of the inner worm-gear plane enveloping drum worm pair is proposed in this part. Referring to design method of the plane enveloping hourglass worm pair, the drum worm pair is designed because they both belong to the planar worm-gear pair. According to meshing theory, classical mechanics, finite element method and machining principle of virtual center distance, etc., the flowchart of design and manufacture of the drum worm pair is proposed as shown in Figure 4.

Figure 4.

Flowchart of design and manufacture.

Design parameters

Design conditions

The inner worm-gear plane enveloping drum worm drive reducer is designed from inside to outside due to that it is driven by the known external rotor motor installed in the hollow worm. In the progress of design, the following conditions should be considered.

Motor parameters

U10PLUS KV32 motor manufactured by T-MOTOR is selected, whose parameters are shown in Table 1, here D and L represent the diameter and length, as well as ${\mathrm{P}}_{\mathrm{m}}$ and $n_{\mathrm{M}}$ express the maximum power and rotation speed, respectively.

Table 1.

Motor parameters.

D×L(m)	$P_m(\mathrm{kW})$	$n_{\mathrm{M}}(r/\min )$
$\varphi 0.0886\times 0.04$	2	1000–1600

Worm rotation speed n₁ (r/min), input power P₁(kW), transmission ratio i₁

The transmission ratio of the worm pair is designed as $i_1$  = 80. Because the worm with a right-handed single thread is directly driven by the motor, the worm rotation speed $n_1$ and input power $P_1$ meet $n_1=$ $n_{\mathrm{jm}}$ , $P_1=$ $P_m$ , here $n_{1\min }$ is defined as the minimum rotation speed of the worm, which is $n_{1\min }=1000(\mathrm{r}/\min )$ .

Work conditions

It is assumed that work time is no more than 8 h a day with starting no more than two times per hour, the work load is 100% with stable load, and the start load does not exceed 125% of the work load.

Machining accuracy and tooth-surface roughness of the worm pair

The machining accuracy of the worm pair needs to reach grade 6 in order to guarantee the tooth-surface roughness below $R_{a}0.63$ .

Material and heat treatment of the worm pair

In order to make the hardness reach HRC43∼55, the tooth-surface of the worm made from 40Cr steel is processed by grinding and then subjected to nitriding. The worm-gear made from ZQSn10-1 (tin bronze) is manufactured by sand casting and the hardness of its tooth-surface reaches HB80∼100. Based on above materials, the recommended range of the relative sliding speed $V_h$ between the worm and the worm-gear is $V_h\le 10\mathrm{m}/\mathrm{s}$ , ²⁵ which is calculated by $V_{\mathrm{h}}=\pi d_1{n}_1/\pi d_1{n}_1(60\cos \gamma (60\cos \gamma )$ .

Design parameters of the worm pair

As shown in Figure 5, compared with the hourglass worm pair on the same scale, the drum worm pair is characterized with smaller size and more compact structure due to the internal meshing transmission. The “crown” of the drum worm corresponds to the “throat” of the hourglass worm, and the distance $l_1$ from the crown of the worm to worm-gear axis is $l_1=0.5d_2-d_1$ .

Figure 5.

2 types plane enveloping worm pair. 1. Mid-plane of the worm; 2. Mid-plane of the worm-gear: (a) drum worm pair, and (b) hourglass worm pair.

Referring to the design method and parameters of the plane enveloping hourglass worm pair ²⁵ and combining with the function fitting method, the relevant design parameters of the right-handed inner worm-gear plane enveloping drum worm pair are determined as shown in Table 2. $h_{\mathrm{a}}$ , $h_{\mathrm{f}}$ , h, and c are the height of addendum, dedendum, full tooth and clearance, respectively, here $h_{\mathrm{a}}=0.7m_{\mathrm{t}}$ , $h_{\mathrm{f}}=0.9m_{\mathrm{t}}$ , $h=h_{\mathrm{a}}+h_{\mathrm{f}}$ , and $c=0.2m_{\mathrm{t}}$ . $d_{f1}$ is the root diameter of the drum worm at its crown, here $d_{f1}=d_1-2h_{\mathrm{f}}$ . $p_2$ and $s_2$ are the tooth pitch and tooth thickness of the worm-gear at the reference circle on its mid-plane, respectively, here $p_2=\pi m_{\mathrm{t}}$ , $s_2=0.55p_2$ . $z_2\text{'}$ signifies the number of worm-gear teeth contained in the worm tooth-slot, here the recommended range meets $z_2\text{'}\le 0.1z_2$ . $\tau$ represents the central angle of tooth pitch of the worm-gear, here $\tau =2\pi /z_2$ . ${\phi }_{2w}$ , $\phi \prime$ , and ${\phi }_0$ mean the angle range, end angle and start angle of the meshing, respectively, here ${\phi }_{2w}=z_2\prime \tau$ , $\phi \prime =\alpha -0.5(z\prime +0.45)\tau$ , ${\phi }_0=\phi \prime +{\phi }_{2w}$ . ${\theta }_z$ denotes the angle of the worm-gear tooth profile, here ${\theta }_z=180°-\theta$ . $\rho$ , $\eta$ , and K express the friction angle, efficiency and calculating coefficient respectively and they are determined referring to Worm Drive Design. ²⁵ $P_1\prime$ means the equivalent input power, here $P_1\prime =P_1/K$ . $u_{\mathrm{u}}$ and $u_d$ mark the upper and lower limit of $u_i$ ( $i=2,3$ ) respectively, here $u_{\mathrm{u}}=\sqrt{{(0.5d_2+h_a)}^2-{(0.5d_b)}^2}$ and $u_{\mathrm{d}}=\sqrt{{(0.5d_2-h_a)}^2-{(0.5d_b)}^2}$ . $T{\prime }_{2m}$ and $T{\prime }_{1m}$ indicate the maximum equivalent output and input torque respectively, here $T{\prime }_{2\mathrm{m}}=9550P_1\prime i_1\eta /n_{1min}$ and $T{\prime }_{1m}=T{\prime }_{2\max }/i_1\eta$ .

Table 2.

Parameters of the drum worm pair.

Parameter	$A(m)$	$m_{\mathrm{t}}(m)$	$d_{\mathrm{b}}(m)$	$z_2$	$z_2\text{'}$	$z_1$	$\beta (°)$	$B(m)$	$i_1$
Value	0.1	0.004	0.125	80	4	1	1	0.11	80
Parameter	$d_1(m)$	$d_2(m)$	$h_{\mathrm{a}}(\mathrm{m})$	$h_f(m)$	$h(m)$	$c(m)$	$d_{f1}(m)$	$p_2(m)$	$s_2(m)$
Value	0.12	0.32	0.0028	0.0036	0.0064	0.0008	0.1128	0.0126	0.0069
Parameter	$\theta (°)$	$\alpha (°)$	$\gamma (°)$	$\tau (°)$	${\phi }_{2w}(°)$	${\phi }_0(°)$	$\phi \prime (°)$	${\theta }_z(°)$	$\rho (°)$
Value	131.54	22.993	1.909	4.5	18	30.98	12.98	48.46	1.333
Parameter	$n_{1\min }(\mathrm{r}/min)$	K	$P_1\prime (\mathrm{kW})$	$\eta$ (%)	$u_{\mathrm{u}}(m)$	$u_d(m)$	$T{\prime }_{2m}(\mathrm{Nm})$	$T{\prime }_{1m}(\mathrm{Nm})$
Value	1000	0.9	2.22	71	0.1503	0.1434	1204	21.20

Mechanical properties analysis

Bending stress and deflection of the worm

Force analysis of the worm

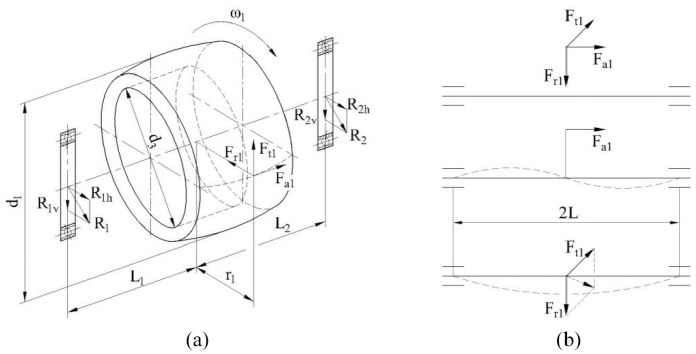
The force analysis of the worm in the case of forward rotation is shown in Figure 6(a) because the forces are same no matter whether the worm pair rotates forward or reverse. $L_1$ and $L_2$ represent the distances between the center of each bearing and the mid-plane of the worm, respectively. $d_3$ and $r_1$ express the diameter of the hole of the worm and the reference radius of the drum worm respectively, here $r_1=0.5d_1$ . ${\mathit{F}}_{t1}$ , ${\mathit{F}}_{\mathrm{a}1}$ , and ${\mathit{F}}_{\mathrm{r}1}$ signify the tangential force, axial force, radial force of the worm respectively, as well as ${\mathit{R}}_1$ and ${\mathit{R}}_2$ indicate the bearing reaction forces. Let $i=1,2$ , ${\mathit{R}}_{i\mathrm{h}}$ and ${\mathit{R}}_{i\mathrm{v}}$ mean the horizontal and vertical components of ${\mathit{R}}_i$ , respectively. According to Tables 1 and 2, parameters are obtained as follows: $r_1=$ 0.06 m, $d_3=$ 0.092 m, $L_1=L_2=L=$ 0.0395 m. And then those forces are calculated by equation (3) including ${\mathit{F}}_{t1}$ , ${\mathit{F}}_{\mathrm{a}1}$ , ${\mathit{F}}_{\mathrm{r}1}$ , ${\mathit{R}}_{1\mathrm{h}}$ , ${\mathit{R}}_{1\mathrm{v}}$ , ${\mathit{R}}_{2\mathrm{h}}$ , ${\mathit{R}}_{2\mathrm{v}}$ , ${\mathit{R}}_1$ , ${\mathit{R}}_2$ .

Figure 6.

Force analysis and deflection of the worm: (a) force analysis, and (b) schematic diagram of deflection deformation.

$$\{\begin{array}{c}{\mathit{F}}_{t1}=-{\mathit{F}}_{a2}=\frac{2T{\prime }_{1\max }}{d_1}{\mathit{F}}_{a1}=-{\mathit{F}}_{t2}=\frac{2T{\prime }_{2\max }}{d_2}{\mathit{F}}_{r1}=-{\mathit{F}}_{r2}=F_{t2}\tan \alpha \hfill \\ \multicolumn{1}{c}{{\mathit{R}}_{1v}={\mathit{R}}_{2v}=\frac{F_{t1}}{2}{\mathit{R}}_{1h}=\frac{F_{r1}L-F_{a1}{r}_1}{2L}{\mathit{R}}_{2h}=\frac{F_{r1}L+F_{a1}{r}_1}{2L}}\\ \multicolumn{1}{c}{R_i=\sqrt{{{\mathit{R}}_{\mathrm{ih}}}^2+{{\mathit{R}}_{\mathrm{iv}}}^2}i=1,2}\end{array}$$ (3)

Bending stress of the worm

According to the work conditions, the bending stress ${\sigma }_{\mathrm{F}1}$ is calculated by equation (4), where $K_s$ means the coefficient of concentrated load here $K_s=$ 2.6. ²⁵ W( $m^3$ ) and $M_{1b}$ (Nm) are the bending modulus and total bending moment of the worm on its mid-plane respectively, here $K_1$ and $K_2$ represent the bending moment coefficients.

$$\{\begin{array}{c}{\sigma }_{\mathrm{F}1}=M_{1b}{K}_s/W{K}_s=2.6\hfill \\ \multicolumn{1}{c}{W=0.1{d_{f1}}^3(1-(d_3/d_{f1}{)}^4)M_{1b}=9550\sqrt{{(0.5K_1{K}_2)}^2+{(P_1\prime /n_{1\min })}^2}}\\ \multicolumn{1}{c}{K_1=P_1\prime \eta i_1/n_{1\min }{K}_2=\sqrt{{(2L\tan \alpha +d_1)}^2+{(2L\tan {\gamma }_m)}^2}/d_2}\end{array}$$ (4)

$[{\sigma }_{\mathrm{F}1}]$ is the allowable value of ${\sigma }_{\mathrm{F}1}$ and is calculated by $[{\sigma }_{\mathrm{F}1}]$  =  $0.125({\sigma }_{b1}+{\sigma }_{s1})+24.50$ , where ${\sigma }_{b1}$ and ${\sigma }_{s1}$ represent the tensile strength and yield strength of 40Cr steel respectively, here ${\sigma }_{b1}$  = 833 MPa and ${\sigma }_{s1}$  = 637 MPa. ²⁵ Through calculation, values of ${\sigma }_{\mathrm{F}1}$ and $[{\sigma }_{\mathrm{F}1}]$ are ${\sigma }_{\mathrm{F}1}=$ 9.413 MPa and $[{\sigma }_{\mathrm{F}1}]=$ 208.25 MPa, respectively. The results meet ${\sigma }_{\mathrm{F}1}<$ $[{\sigma }_{b1}]$ which indicates that the bending stress of the worm satisfies the work requirements.

Deflection of the worm

Considering that the deflection deformation of the worm on its mid-plane is mainly affected by the tangential force ${\mathit{F}}_{t1}$ and radial force ${\mathit{F}}_{r1}$ as shown in Figure 6(b), the deflection y is calculated by equation (5), where J( $m^4$ ) and E(MPa) represent the equivalent inertia moment of the hollow worm on its mid-plane and the elastic modulus of 40Cr steel respectively, here E = 2.11 $\times {10}^5$  MPa. ²⁵

$$y=\frac{{(2L)}^3\sqrt{{F_{t1}}^2+{F_{r1}}^2}}{48\mathrm{EJ}}J=0.05({d_{f1}}^4-{d_3}^4)(0.375+0.625\frac{d_{f1}}{d_{a1}})$$ (5)

$[y]$ is the allowable value of y and is calculated by $[y]=0.001d_{f1}$ . The results are shown as y = 3.701× ${10}^{-8}$  m and $[y]$  = 1.128× ${10}^{-4}$ $m^4$ according to the parameters of Table 2, which meet y< $[y]$ . Therefore, the deflection of the worm satisfies the work requirements.

Shear stress and bending stress of the worm-gear teeth

Shear stress of the worm-gear teeth

As shown in Figure 7(a), $S(m^2)$ expresses the area of the worm-gear tooth root cross section (A-A), which is calculated by equation (6) where $s_{f2}(m)$ , $s_{f2\mathrm{u}}(m)$ , and $s_{f2\mathrm{d}}(m)$ represent the reference, maximum and minimum worm-gear tooth thickness on the section (A-A) respectively, as well as the processing width $B_1$ meet $B_1\approx 0.75B$ according to the distribution of the contact areas. ²³ $F_{\tau 2}(N)$ and $F_{t2m}(N)$ both acting on the horizontal plane perpendicular to the cross section (B-B) indicate the root shear force and the maximum circumferential force of a single worm-gear tooth respectively, and the angle between them is $(\gamma +\rho )$ . Considering that the worm pair meshes with multiple teeth during conjugation, $F_{t2m}$ is reduced by 2.5 times.

Figure 7.

Shear stress and bending stress of worm-gear teeth: (a) shear stress of worm-gear teeth, and (b) bending stress of worm-gear teeth.

Meanwhile $T{\prime }_{2\max }$ is amplified by 125% as the maximum output torque $T_{2m}$ for calculation.

$$\{\begin{array}{c}{\tau }_2=F_{\tau 2}/S\hfill \\ \multicolumn{1}{c}{F_{\tau 2}=\sqrt{F_{t2m}^2+{(F_{t2m}\tan ({\gamma }_m+\rho ))}^2}{F}_{t2m}=(2T_{2m})/(2.5d_2)T_{2m}=1.25T{\prime }_{2\max }}\\ \multicolumn{1}{c}{S=\frac{3}{8}B(s_{f2u}+s_{f2d})}\\ \multicolumn{1}{c}{s_{f2u}=s_{f2}+B\tan \beta s_{f2d}=s_{f2}-0.5B\tan \beta s_{f2}=s_2+2h_{\mathrm{f}}\tan (0.5{\theta }_z)}\end{array}$$ (6)

Substituting parameters of Table 2 into equation (6), the shear stress ${\tau }_2$ is obtained, here ${\tau }_2$  = 4.301 MPa. $[{\tau }_2]$ is the allowable value of ${\tau }_2$ and is calculated by $[{\tau }_2]=0.5{\sigma }_{b2}$ where ${\sigma }_{b2}$ represents the tensile strength of bronze (ZQSn10-1), here ${\sigma }_{b2}$  = 225.4 MPa. ²⁵ The allowable value $[{\tau }_2]$ is obtained by calculation, here $[{\tau }_2]$  = 112.7 MPa. The result shows ${\tau }_2$ < $[{\tau }_2]$ which indicates that the shear stress of the worm-gear teeth satisfies the work requirements.

Bending stress of worm-gear teeth

As shown in Figure 7(b), ${\mathit{M}}_{b2}(\mathrm{Nm})$ represents the moment acting on the root of a single worm-gear tooth under force $F_{t2m}$ . Point $o_{\mathrm{A}}$ is the centroid of the worm-gear tooth root cross section (A-A) whose coordinates in frame ${\sigma }_{\mathrm{oA}}(O_{\mathrm{A}};\mathrm{x},\mathrm{y})$ are ${\sigma }_{\mathrm{oA}}(3.939\times 10^{-2},0.603\times 10^{-2})$ calculated by equation (7). The frame ${\sigma }_{\mathrm{oA}}(O_{\mathrm{A}};x_{\mathrm{A}},y_{\mathrm{A}})$ is built at the centroid $o_{\mathrm{A}}$ , and then the inertia moment $I_{\mathrm{xA}}(m^4)$ and bending modulus $W_{\mathrm{xA}}$ ( $m^3$ ) of the trapezoidal section (A-A) to the axis $x_{\mathrm{A}}$ are calculated by equation (8).

Let $a=$ $0.5s_{f2u}$ and $b=$ $0.5s_{f2\mathrm{d}}$ , the bending stress ${\sigma }_{b2}$ under the moment ${\mathit{M}}_{b2}$ is calculated by equation (8) and the result is ${\sigma }_{b2}$  = 9.74 MPa. The allowable value of ${\sigma }_{b2}$ is represented as $[{\sigma }_{b2}]$ calculated by $[{\sigma }_{b2}]$  = 0.2 ${\sigma }_{b2}$ considering that the worm pair conducts forward and reverse rotations, and the result is $[{\sigma }_{b2}]$  = 45.08 MPa. Compared with $[{\sigma }_{b2}]$ , ${\sigma }_{b2}$ meets ${\sigma }_{b2}$ < $[{\sigma }_{b2}]$ which indicates that the bending stress of the worm-gear teeth satisfies the work requirements.

$$\overline{x}=\frac{{\int }_0^{0.75B}2x(\mathrm{a}-x\tan \beta )\mathrm{dx}}{S}\overline{y}=a$$ (7)

$$\{\begin{array}{c}{\sigma }_{b2}=\frac{M_{b2}}{W_{\mathrm{xA}}}{M}_{b2}=F_{t2m}{h}_{\mathrm{f}}{W}_{\mathrm{xA}}=\frac{I_{\mathrm{xA}}}{a}\hfill \\ \multicolumn{1}{c}{I_{\mathrm{xA}}={\int }_{-b}^{b}0.75B{y}^2\mathrm{dy}+{\int }_b^a{y}^2(a-y)\cot \beta \mathrm{dy}+{\int }_{-a}^{-b}{y}^2(a+y)\cot \beta \mathrm{dy}}\end{array}$$ (8)

Contact properties analysis

Finite element setting

The worm tooth-surfaces are obtained by ${\mathrm{\Phi }}^{(i)}(u_i,{\phi }_i)=0$ , $i=2,3$ (equations (1)–(2)) utilizing the movable coordinate method, here $u_i\in (u_d,u_u)$ , ${\phi }_i\in (\phi \prime ,{\phi }_0)$ . According to Table 2, the 3D models of the worm pair are established through software MATLAB and CREO combined with the size driving technology.

The contact stress of the 3D models of the worm pair is analyzed by the function, static structure analysis, in software WORKBENCH. The material library of the worm pair is established according to the material parameters as shown in Table 3, here E, $\nu$ and $\rho$ represent the elastic modulus, Poisson’s ratio, and density of materials, respectively.

Table 3.

Material parameters of the worm pair.

Component	Material	E(MPa)	$\nu$	$\rho$ ( $\mathrm{Kg}/{\mathrm{m}}^3$ )
Worm	40 Cr	$2.11\times 10^5$	0.277	7870
Worm-gear	ZQSn10-1	$1.05\times 10^5$	0.25	8930

According to Tables 1 and 2, the maximum torque $\mathit{T}(\mathrm{Nm})$ of the worm under working state is calculated by $\mathit{T}$  = 9550 $P_m/n_{1\min }$ and the result is shown as $\mathit{T}$  = 19.1Nm. Considering the installation position of the motor in the hollow worm as shown in Figure 1, the moments ${\mathit{M}}_p$ (forward rotation) and ${\mathit{M}}_q$ (reverse rotation) both acting on the right side of the worm are shown in Figure 8, here $M_p=M_q=T=19.1\mathrm{Nm}$ .

Figure 8.

Finite-element setting of the worm pair: (a) forward rotation, and (b) reverse rotation.

The spiral teeth of the worm could simultaneously mesh with four planar teeth of the worm-gear during the conjugation because of $z_2\prime$  = 4. The non-friction constraints of the forward and reverse rotations between conjugate tooth-surfaces are established consisting of the target surface and the contact surfaces (CS 1 to CS 4), which satisfy the “adjust to contact” in the simulation process as shown in Figure 8, respectively.

Finite element analysis

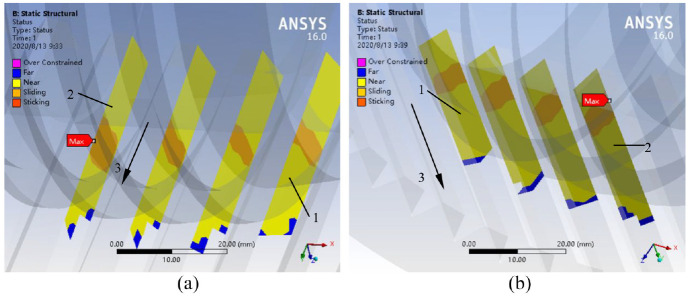
As shown in Figure 9, the contact areas of the forward and reverse rotations of the worm pair are analyzed by the contact tool of WORKBENCH, respectively. The contact areas diffuse in the direction of the increasing and decreasing tooth thickness of the worm-gear corresponding to the forward and reverse rotations, respectively. Regardless of forward or reverse rotation, the largest contact areas both appear at engaging-out position.

Figure 9.

Contact areas of the worm pair. 1. Engaging-in position; 2. Engaging-out position; 3. Direction of increasing tooth thickness: (a) forward rotation, and (b) reverse rotation.

The contact stress of the worm-gear tooth-surfaces needs to be analyzed due to lower hardness of the material adopted by the worm-gear. The contact stresses are mainly distributed on the planes A and B respectively corresponding to the forward (Figure 10(a)) and reverse (Figure 10(b)) rotations of the worm pair. The maximum contact stresses of the forward and reverse rotation are marked as ${\sigma }_{H2}^{\mathrm{A}}=98.85\mathrm{Mpa}$ and ${\sigma }_{H2}^{\mathrm{B}}=80.04\mathrm{Mpa}$ , respectively, and they appear at the engage-in position of the worm pair opposing to the engaging-out position (Figure 9) where the largest contact areas appear.

Figure 10.

Contact stress analysis of the worm-gear tooth-surface: (a) forward rotation, and (b) reverse rotation.

The allowable value of the contact stress of the worm-gear tooth-surfaces is represented as $[{\sigma }_{H2}]$ which is determined as $[{\sigma }_{H2}]$  = 180 MPa according to the design conditions. Compared with the maximum contact stresses ( ${\sigma }_{H2}^{\mathrm{A}}$ , ${\sigma }_{H2}^{\mathrm{B}}$ ), $[{\sigma }_{H2}]$ meets $[{\sigma }_{H2}]>{\sigma }_{H2}^i$ , $i=A,B$ , which indicates that the contact stresses of the worm-gear tooth-surfaces satisfy the work requirements.

Prototype manufacturing

Processing parameters

Base on that, the mechanical and contact properties of the drum worm pair satisfy the work requirements through above analyses, the prototype of the novel reducer with the drum worm pair is manufactured. According to the design parameters (Table 2), the processing parameters of the right-handed worm pair are shown in Table 4, where ${\phi }_{\mathrm{j}}(°)$ and ${\phi }_{\mathrm{j}}\text{'}(°)$ represent the start and end angles of the processing of the worm, respectively.

Table 4.

Processing parameters.

Parameter	$A(m)$	$m_{\mathrm{t}}(m)$	$d_{\mathrm{b}}(m)$	$z_2$	$z_2\text{'}$	$z_1$	$\beta (°)$	$B_1(m)$	${\phi }_{\mathrm{j}}/°$	${\phi }_{\mathrm{j}}\text{'}/°$
Value	0.1	0.004	0.125	80	4	1	0	0.08	40	0

Processing of the worm tooth-surface

The worm tooth-surface is processed according to the processing parameters in Table 4, here $\beta =0°$ in order to simplify the processing program. Because the tooth-surfaces on both sides of a worm-gear tooth are symmetrical with respect to a plane through the axis of the worm-gear, the worm can be engaged with the same worm-gear after being turned 180° in the radial direction of the worm. On this basis, the plane grinding wheel which is consistent with the trajectory of the worm-gear tooth-surface is adopted to process the worm tooth-surface. After the one side of the worm tooth-surface is processed, the other side is processed by the same grinding wheel after turning the worm 180° in the radial direction of the worm.

According to Table 4 and Figure 11, the worm tooth-surfaces are ground by the modified 4-axis linkage CNC grinder based on the machining principle of virtual center distance. The processing is completed by the 4-axis linkage of X-axis, Y-axis, Z-axis, and A-axis, where the origin ${\mathrm{O}}_2$ and ${\mathrm{O}}_{\mathrm{M}}$ represent the revolution center and rotation center of the grinding wheel respectively, the X-axis and Z-axis indicate translation axes of the rotation center (origin ${\mathrm{O}}_{\mathrm{M}}$ ), as well as the Y-axis and the A-axis express rotation axes of the rotation center (origin ${\mathrm{O}}_{\mathrm{M}}$ ) and the worm blank, respectively. The distance between the revolution center (origin ${\mathrm{O}}_2$ ) and the worm blank rotation axis (A-axis) is the center distance ( $\mathrm{A}=0.1\mathrm{m}$ ). During the machining, the processed surface of the worm blank is conjugated with the working face of the plane grinding wheel which is tangent to the base circle. The rotation center (origin ${\mathrm{O}}_{\mathrm{M}}$ ) of the grinding wheel moves from the start point (corresponding to ${\phi }_{\mathrm{j}}=40°$ ) to the end point (corresponding to ${\phi }_{\mathrm{j}}\prime =0°$ ) through a circular motion with the transmission ratio $i_1={\omega }_1/{\omega }_2=z_2/z_1=80$ , here ${\omega }_1$ and ${\omega }_2$ are the rotation speed of the worm blank and the revolution rotation of the plane grinding wheel, respectively.

Figure 11.

Processing of worm tooth-surface. 1. Worm blank; 2. Plane grinding wheel: (a) processing principle, and (b) modified 4-axis linkage CNC grinder.

Prototype assembly

The processed worm tooth-surface is shown in Figure 12(a), and the worm-gear is processed by the wire cutting. Then according to Figure 1, the industrial prototype of the inner worm-gear plane enveloping drum worm drive reducer is assembled and its internal structure is shown in Figure 12(b).

Figure 12.

Manufacture of prototype: (a) tooth-surface of drum worm, (b) internal components, (c) worm-gear seats (gearboxes), and (d) novel joint reducer. 1. Output flange; 2. Worm-gear seat; 3. Fixed flange.

In Figure 12(d), the outward appearance of the novel joint reducer is presented with overall size including length 436 mm and diameter 370 mm. In the reducer, the gearbox is simplified as the worm-gear seat for the support of the worm-gear and outputs rotation by the output flange fixed to it, as well as the fixed flange rigidly connected to the pillar is used to fix the reducer. The worm-gear seats with outer diameter 370 mm are displayed in Figure 12(c), they are made from 6061 aluminum in order to decrease their weights. However, the size of the reducer is large which is mainly affected by the motor’s size due to adoption of the design method from inside to outside. Therefore, the follow-up investigation of a special motor with smaller volume and larger power could help reduce the size of the reducer to make it more compact.

Conclusion

The design and manufacture of the novel worm pair were investigated in this paper and conclusions are shown as follows:

1. The novel joint reducer with integrated structure of drive, transmission and support was designed and manufactured for the first time. The reducer adopts a new type internal meshing plane enveloping worm pair consisting of a planar internal worm-gear and an orthogonal right-handed single-thread drum worm, and is driven by a built-in external rotor motor installed in the hollow worm. In addition, the structures of support components are simple and easy to process without the need of complicated gearboxes. Therefore the novel reducer is characteristic with compact structure, high transmission and manufacture accuracy, easy processing, backlash adjustment, and easy sealing, etc.

2. The systematic design and manufacture process of the novel worm pair was proposed, including meshing theory, structure design, properties analysis and prototype manufacturing.

3. The meshing theory of the novel worm pair was established according to the gear meshing theory and the design method of plane enveloping hourglass worm pair, as well as the design parameters of the worm pair were determined combined with the function fitting method.

4. In the terms of the mechanical and contact properties analysis, the bending stress and deflection of the worm, the shear and bending stress of the worm-gear teeth were analyzed by classical mechanics, as well as the contact stress of the worm-gear and the contact area of the worm pair were analyzed by WORKBENCH according to the finite element method. Through above analyses, the mechanical and contact properties of the worm pair were guaranteed to satisfy the work requirements.

5. The processing method of the drum worm was proposed where the drum worm was processed by the modified 4-axis linkage CNC grinder based on the machining principle of the virtual center distance, and the industrial prototype of the novel joint reducer was manufactured.

Author biographies

Jingzi Zhang is currently a Doctor Candidate at Sichuan University, China. His research interests include worm drive and mechanical design.

Jin’ge Wang is currently a Professor at Sichuan University, China. He received his PHD degree from Chongqing University, China, in 1992. His research interests include robot technology and mechanical transmission.

Kai Wang is currently an Associate Professor at Chengdu Vocational & Technical College of Industry. She received her PHD degree from Sichuan University, China, in 2017. Her research interest is worm drive.

Appendix

Notation

$m_{\mathrm{t}}$  transverse module, (m)

A, $A\prime$  center distance of the drum and hourglass worm pair, respectively, (m)

$d_b$  diameter of the basic circle on the mid-plane of the worm-gear, (m)

${\beta }_1$ , ${\beta }_2$  inclination angle of the plane A and B, respectively, ( $\begin{array}{c}°\hfill \end{array}$ ), here ${\beta }_1={\beta }_2=\beta$

$z_1$ , $z_2$  number of the worm threads and worm-gear teeth, respectively

$i_1$  transmission ratio of the worm pair, here $i_1=z_2/z_1$ , let $i\prime =1/i_1$

$d_2$  reference diameter of the worm-gear on its mid-plane, (m), here $d_2=z_2{m}_t$

$d_1$  reference diameter of the drum worm at its crown, (m), here $d_1=(d_2-2A)$

$\alpha$  transverse pressure angle, ( $\begin{array}{c}°\hfill \end{array}$ ), here $\alpha =\arcsin (d_b/d_2)$

$\gamma$  spiral angle of the drum worm at its crown reference circle, ( $\begin{array}{c}°\hfill \end{array}$ ), here $\gamma =\arctan (d_2/(i_1{d}_1))$

${\sigma }_b(o_b;{\mathit{i}}_b,{\mathit{j}}_b,{\mathit{k}}_b)$ , ${\sigma }_{\mathrm{w}}(o_{\mathrm{w}};{\mathit{i}}_{\mathrm{w}},{\mathit{j}}_{\mathrm{w}},{\mathit{k}}_{\mathrm{w}})$  fixed coordinate frames

${\sigma }_i(o_i;{\mathit{i}}_i,{\mathit{j}}_i,{\mathit{k}}_i)$  movable coordinate frames, here $i=1,2,3,p,q$

${\mathrm{Q}}^{(i)}(x_i,y_i,z_i)$ , ${\mathrm{P}}^{(i)}(x_i,y_i,z_i)$  coordinates of the meshing points P and Q in each corresponding coordinate frame, here $i=1,2,3,p,q,b,w$

${\phi }_1$ , ${\phi }_1\prime$  forward and reverse rotation angles of the worm, respectively, ( $\begin{array}{c}°\hfill \end{array}$ )

${\phi }_2$ , ${\phi }_3$  rotation angles of the movable coordinate frames ${\sigma }_2$ and ${\sigma }_3$ , respectively, ( $\begin{array}{c}°\hfill \end{array}$ )

$u_i$ , $v_i$  parameters of the plane A ( $i=3$ ) and B ( $i=2$ ), respectively, (m)

${\mathrm{\Phi }}^{(i)}$ , ${\mathrm{\Phi }}_t^{(i)}$ , ${\mathrm{\Psi }}^{(i)}$  function of meshing, second-type boundary and first-type boundary on the plane A ( $i=3$ ) and B ( $i=2$ ), respectively, here $i=3,2$

B, $B_1$  design width and processing width of the worm-gear, respectively, (m)

${\sigma }_{\mathrm{F}1}$  bending stress of the worm on its mid-plane, (MPa)

y deflection of the worm on its mid-plane, (m)

${\tau }_2$  shear stress of the worm-gear teeth, (MPa)

${\sigma }_{b2}$  bending stress of the worm-gear teeth (MPa)