Abstract
Purpose:
To develop a high-fidelity diffusion MRI acquisition and reconstruction framework with reduced echo-train-length for less T2* image blurring compared to typical highly accelerated echo-planar imaging (EPI) acquisitions at sub-millimeter isotropic resolution.
Methods:
We first proposed a circular-EPI trajectory with partial Fourier sampling on both the readout and phase-encoding directions to minimize the echo-train-length and echo time. We then utilized this trajectory in an interleaved two-shot EPI acquisition with reversed phase-encoding polarity, to aid in the correction of off-resonance-induced image distortions and provide complementary k-space coverage in the missing partial Fourier regions. Using model-based reconstruction with structured low-rank constraint and smooth phase prior, we corrected the shot-to-shot phase variations across the two shots and recover the missing k-space data. Finally, we combined the proposed acquisition/reconstruction framework with an SNR-efficient RF-encoded simultaneous multi-slab technique, termed gSlider, to achieve high-fidelity 720 μm and 500 μm isotropic resolution in-vivo diffusion MRI.
Results:
Both simulation and in-vivo results demonstrate the effectiveness of the proposed acquisition and reconstruction framework to provide distortion-corrected diffusion imaging at the mesoscale with markedly reduced T2*-blurring. The in-vivo results of 720 μm and 500 μm datasets show high-fidelity diffusion images with reduced image blurring and echo time using the proposed approaches.
Conclusions:
The proposed method provides high-quality distortion-corrected diffusion-weighted images with ~40% reduction in the echo-train-length and T2* blurring at 500μm-isotropic-resolution compared to standard multi-shot EPI.
Keywords: Echo-planar imaging, Distortion correction, Diffusion MRI
1. Introduction
Submillimeter-isotropic-resolution in-vivo diffusion MRI (dMRI) with echo-planar imaging (EPI) acquisition has shown great potential for reducing partial volume effects of laminar fiber analysis in superficial gray-matter (Assaf, 2019; Gulban et al., 2018; McNab et al., 2013; Wang et al., 2021), improving brain parcellation in gray-matter regions (Johansen-Berg et al., 2005; Leuze et al., 2014) and detecting small microinfarcts in cerebral small vessel Disease (Misquitta et al., 2022). The key challenges of submillimeter in-vivo dMRI acquisition include: i) the physiological noise and bulk motion-induced phase variations, ii) image distortions from magnetic susceptibility and eddy-current, iii) T2* blurring due to the long echo spacing (ESP) and echo-train-length (ETL), and iv) decreased SNR.
To address these issues, numerous acquisition, reconstruction, and post-processing techniques have been developed. During the lengthy ETL, the local B0 inhomogeneity from magnetic susceptibility and eddy-current can lead to voxel pile-ups, T2* blurring, and signal loss. Multi-shot EPI acquires the entire k-space in multiple excitations, which enables shorter ETL to mitigate distortion and blurring. However, due to the shot-to-shot phase variations, combining shots is difficult. To correct the shot-to-shot phase variations, both navigator-based (Dai et al., 2017; Holdsworth et al., 2008; Jeong et al., 2013; Porter and Heide-mann, 2009) and self-navigated methods (Chen et al., 2013; Chu et al., 2015; Moeller et al., 2020) with advanced reconstruction methods (Hu et al., 2019; Liao et al., 2017; Mani et al., 2017) are proposed to remove background phase of each shot.
To further eliminate the image distortions, additional acquisitions with reversed phase-encoding polarity were necessitated to account for the distortion in post-processing (e.g. FSL TOPUP (Andersson et al., 2003)). Furthermore, interleaved multi-shot EPI with reverse polarities and joint parallel imaging reconstruction method that incorporate field maps and shot-to-shot phase-difference maps into the forward model of the reconstruction were proposed (Zahneisen et al., 2017; Zhu et al., 2016), which allows for reduced g-factor penalty and higher in-plane acceleration factor compared to the conventional post-processing methods. Recently, a multi-shot EPI with spatial-temporal Controlled Aliasing in Parallel Imaging (CAIPI) sampling trajectory along ky-t dimension technique termed echo planar “time-resolved” imaging (EPTI) (Wang et al., 2019) was also proposed to achieve an efficient distortion-corrected high-resolution dMRI with relaxometry capability (Dai et al., 2022; Dong et al., 2022; Fair et al., 2021).
To boost the SNR of submillimeter dMRI acquisition, 3D volumetric encoding techniques have been developed (Engström and Skare, 2013). Compared to the 2D and simultaneous multi-slice (SMS) acquisitions (Feinberg et al., 2010; Larkman et al., 2001; Setsompop et al., 2012), the 3D multi-slab acquisition has higher SNR efficiency with short TR (Engström et al., 2015; Moeller et al., 2020). However, the 3D volumetric acquisition is also sensitive to the shot-to-shot phase variations from three dimensions and the reconstructed image is sensitive to slab-boundary artifacts due to the imperfect slab profile and spin-history issue. To solve these issues, 3D multi-slab acquisition uses a dual-SE-EPI sequence to acquire both image- and navigator-echoes (Chang et al., 2018; Dai et al., 2021). With robust slab-boundary correction methods (Van et al., 2015; Wu et al., 2016), the slab-boundary artifacts are much mitigated. gSlider-SMS (generalized SLIce Dithered Enhanced Resolution Simultaneous multi-slab) is another self-navigated 3D volumetric encoding technique (Setsompop et al., 2018), which performs consecutive RF-encoding rather than gradient encoding along slice direction for robust self-estimation and removal shot-to-shot phase corruption and a linear model-based reconstruction to resolve sub-slices within each acquired slab.
Our recent work proposed a multi-shot interleaved EPI with Blip-Up and -Down phase-encodings Acquisition (BUDA-EPI) and reconstruction framework (Cao et al., 2021; Liao et al., 2019a; Zhang et al., 2022) that incorporates B0 forward-modeling and structured-low-rank constraint to enable distortion-corrected and navigator-free dMRI. Combined with the SNR-efficient gSlider technique, it enables high-fidelity diffusion imaging across the whole-brain in vivo at 600 μm isotropic resolution (Liao et al., 2021). However, at higher resolutions at the mesoscopic scale such as 500 μm, the original BUDA with standard EPI trajectory can result in lengthy ETL and undesirable T2*-induced image blurring.
Building on our previous work, we further develop approaches to improve the quality and fidelity of mesoscale diffusion MRI, where: i) We developed a circular-EPI trajectory with a new approach for complementary readout (RO) and phase-encoding (PE) partial Fourier (pF) sampling across the blipped-up and blipped-down shots to reduce the ETL and TE, which enables reduced image blurring and improved SNR. Compared to a previously published work on circular 3D-EPI for fMRI by (Rettenmeier et al., 2019), the proposed circular-EPI trajectory with two-dimensional pF acquisition specifically targets submillimeter isotropic resolution diffusion imaging with reduced ETL, TE and point-spread-function. ii) We combined the circular trajectory with BUDA-EPI, where the variable ESP of the circular EPI trajectory was incorporated into the model-based joint parallel imaging reconstruction to correct image distortions induced by B0 inhomogeneity. To allow accurate estimation of B0 inhomogeneity and eddy-currents, we used constant echo-spacing sampling in the central k-space of both blip-up and -down shots. iii) We implemented a structured low-rank constraint with smooth phase prior (S-LORAKS) reconstruction (Haldar, 2014; Kim et al., 2017) across the two reverse-polarity shots to compensate shot-to-shot phase variations as well as offer a “smart readout and phase-encoding partial Fourier” approach, which could help prevent loss of resolution. Compared to our previous structured low-rank reconstruction (Liao et al, 2021), the use of implicit phase-constrained S-LORAKS reconstruction could account for both shot-to-shot phase variations and smooth background phase to enable high-fidelity partial Fourier filling in both phase and readout directions, which we thoroughly validated in Results section.
With the proposed gSlider-BUDA-circular-EPI acquisition with S-LORAKS reconstruction, we demonstrate high-fidelity 720 μm- and 500 μm-isotropic-resolution dMRI with ~40% reduction of ETL and T2* blurring compared to two-shot EPI sequence. This work is an extension of our earlier work, which was reported in a conference abstract form and presented as an oral presentation at the International Society of Magnetic Resonance in Medicine (ISMRM) 2022 (Liao et al., 2022).”
2. Methods
2.1. Trajectory and pulse sequence design
Circular EPI was first proposed for real-time cardiac imaging (Kerr et al., 1997) and a recent study (Rettenmeier et al., 2019) shows that the circular EPI with reduced readout length could also be beneficial in improving fast volumetric functional MRI. In our work, we combine circular-EPI with the two-shot blip-up and -down acquisition and augment it with both RO- and PE-pF sampling for high-resolution dMRI. Fig. 1(A) shows the sequence diagram and the sampling trajectories of gSlider-BUDA-circular-EPI, where the two circular-EPI shots are sampled with reversed PE polarity to obtain opposite distortion. As shown in Fig. 1(A), in each shot, the circular-EPI only covers ~30% of the total k-space area, using both RO- and PE-pF 5/8 sampling and full ramp-sampling, which significantly reduces ETL and TE. The missing k-space is filled using BUDA-S-LORAKS reconstruction, which leverages the two-shot complementary subsets of k-space data and the smooth background phase prior. More details of the BUDA-S-LORAKS reconstruction will be described in the next section.
Fig. 1.
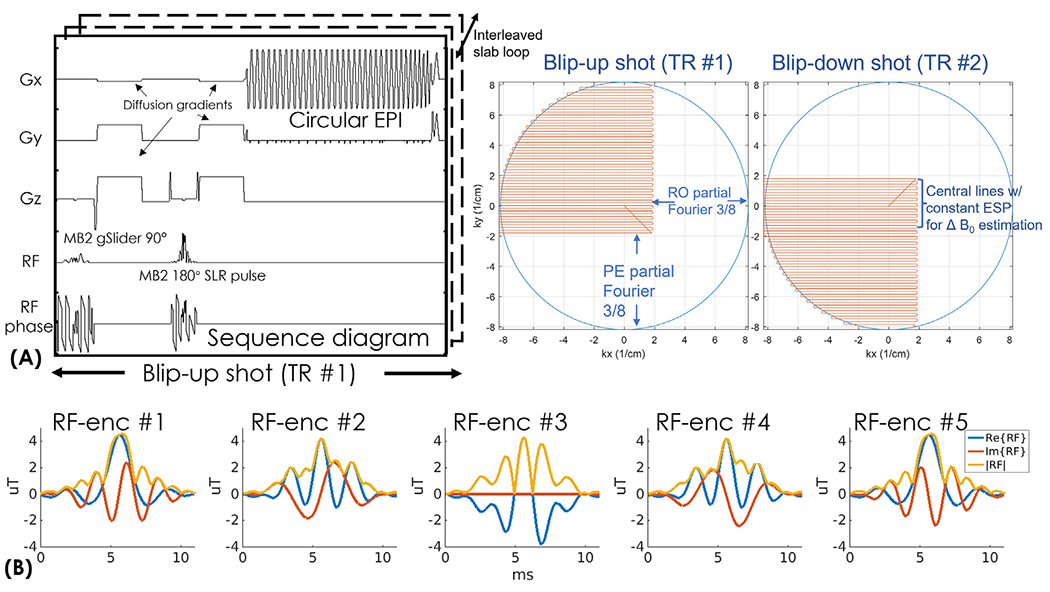
(A) The sequence diagram of the gSlider-BUDA-circular-EPI sequence and the trajectory of the proposed circular EPI with readout and phase-encoding partial Fourier acquisition. Central k-space are acquired with constant ESP for ΔB0 estimation. (B) The RF waveforms of the five gSlider RF-encodings pulses.
To estimate B0 inhomogeneity and eddy-current fields, the blip-up and -down low-resolution images are individually reconstructed using the central k-space lines which were acquired at a constant echospacing. The resolution of central part of k-space with full-Fourier coverage is kept at ~2mm, which could cover the low-frequency area well and be robust to potential k-space shift of the diffusion encoding that we kept to b=1000 s/mm2 at submillimeter resolution so that we have sufficient SNR.
Five gSlider RF slab-encodings (Fig. 1(C)) are used for a total of 10 circular-EPI shots per volume across blip-up and -down encodings, where both shots are acquired in an interleaved fashion. Both the gSlider RF slab-encodings and refocusing pulses are designed using the toolbox (https://github.com/wgrissom/gSliderRF) (Ma et al., 2017). Simultaneous multi-slab at MB = 2 is combined with gSlider RF pulses in the sequence to acquire data from 10 imaging slices simultaneously per shot. To reduce peak power of the RF pulses, VERSE method (Conolly et al., 1988) is performed on both gSlider-SMSb and the multi-band 180° refocusing RF pulses.
3. BUDA-S-LORAKS reconstruction
The flowchart of the proposed reconstruction pipeline is shown in Fig. 2. The reconstruction of each gSlider-encoding volume includes the following steps: i) Nyquist ghost correction with a constant gradient-delay and linear phase-error estimated from a calibration scan with Gy turned off (Rettenmeier et al., 2019). Due to the variable ESP and ramp-sampling in circular-EPI, 1D non-uniform FFT (NUFFT) is performed. ii) The central k-space of each shot is reconstructed using SENSE (Pruessmann et al., 1999) with l1 wavelet regularization. The reconstructed low-resolution images of a BUDA pair are used to estimate field map via FSL TOPUP (Andersson et al., 2003). iii) This field map is multiplied by the variable ESP of each ky-line to create the off-resonance operator Et in tth shot. Note that the operator of circular-EPI shot is reversed for the reversed phase-encoding polarity. iv) The operator Et is then incorporated into a model-based joint parallel imaging reconstruction with structured-low-rank constraint, with smooth phase prior (S-LORAKS operator) across the two shots to take advantage of the smooth background phase for pF-filling and account for shot-to-shot phase variations. This reconstruction can be expressed as:
| (1) |
where Ft is the undersampled Fourier operator in the tth shot, C are the coil sensitivities estimated from a FOV-matched gradient-echo prescan data using ESPIRiT (Uecker et al., 2015, 2014), xt is the distortion-corrected image in the tth shot and dt are the k-space data for shot t. The constraint Rr(H(·))is a non-convex regularization imposing rank-r approximation of the corresponding Hankel structured low-rank matrix H(S(x)), where S(x) is the S-LORAKS operator that constructs the Hankel matrix in the concatenated k-space of the two shots by leveraging the conjugate symmetry property of k-space (smooth phase prior in image domain). The S-LORAKS operator S(x) can be expressed as:
| (2) |
where S is a circular kernel (e.g., radius = 3) in the local k-space of each shot and S* is the kernel in the conjugate position of k-space, shown in Fig. 2. The subscripts “real” and “imag” represent the real and imaginary parts of the complex k-space data. Once the S and S* kernels are formed for both the blip-up and blip-down shots, we then slide them around the data to build the Hankel matrix H(S(x)), and apply the low rank constraint on this matrix. With multiple iterations, the missing k-space data are filled using S-LORAKS reconstruction. The BUDA-S-LORAKS reconstruction can also be extended to multiband (MB) dataset by concatenating the slice-group along the readout dimension (Moeller et al., 2010). In this work, we selected the rank-r = 80 and λ=0.0008 for the Rr(·) low-rank regularization. The maximum number of S-LORAKS iterations (inner loop) of 8 and the maximum number of data-consistency iterations (outer loop) of 20 is used for the diffusion datasets at submillimeter resolution. The demonstration reconstruction scripts are available online at: https://github.com/CongyuLiao/BUDA_SLORAKS. After this image reconstruction process, the reconstructed two-shot distortion-less images are then combined to produce a single image, where the background phase in each shot is estimated by real-valued post-processing and removed before the shot combination (Eichner et al., 2015; Holdsworth et al., 2012).
Fig. 2.
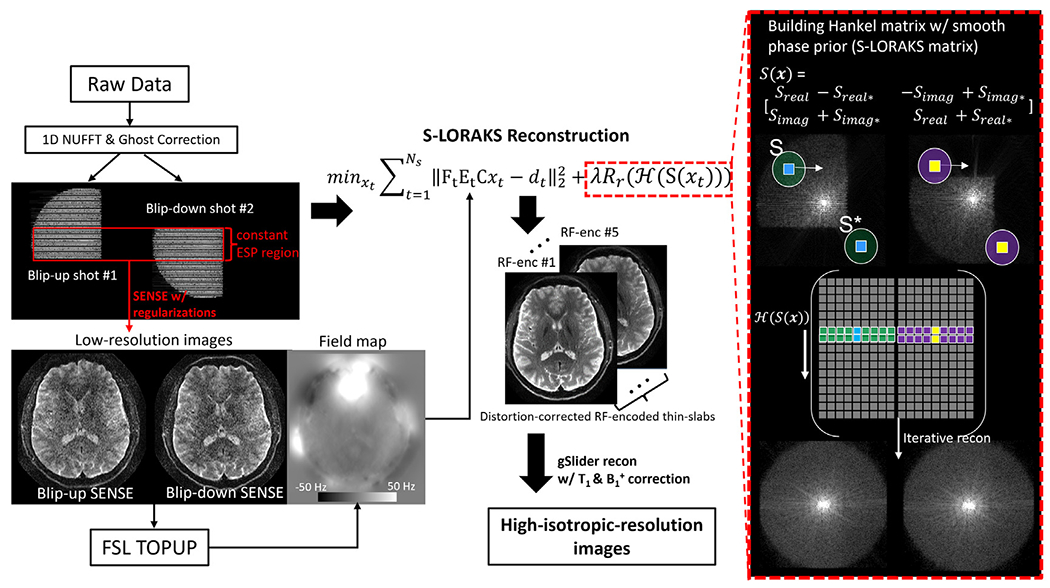
Flow chart of the gSlider-BUDA circular-EPI reconstruction.
The proposed reconstruction is performed for each gSlider RF-encoding volume, and subsequently, the reconstructed images of all RF slab-encoded volumes are combined in a forward-model-based reconstruction with T1 and B1+ corrections to create a high slice-resolution volume as per (Liao et al., 2020).
After reconstruction of each diffusion volumes, we utilized FSL “eddy” function (Andersson and Sotiropoulos, 2016) to model and correct head motions across diffusion volumes which should minimize head motion issues between these different diffusion directions.
4. Simulations
To characterize the advantages of circular-EPI over standard-EPI, we simulated both circular- and standard-EPI trajectories at 500 μm resolution with an in-plane acceleration factor of 4 per shot. Partial Fourier acquisition was also employed in these trajectories with 5/8 PE-pf on standard-EPI, and 5/8 RO- & PE-pF on circular-EPI (resulting in the central symmetrically sampled k-space region of 2.2 mm, which is deemed sufficient in capturing the smooth shot-to-shot phase variations). The gradient waveforms of the standard- and circular-EPI are shown in Fig. 3(A). For circular-EPTI, the maximum gradient amplitude is set to 50mT/m to avoid aliasing along the readout direction for a 23.4 cm readout FOV considering the maximum sampling bandwidth of 500kHz on our MR system. The maximum slew-rate is set to 200T/m/s to keep within the limits of the peripheral nerve stimulation and hardware limit. On the other hand, the standard-EPI trajectory is directly extracted from a product EPI sequence which reached the maximum gradient and slew rate of 37 mT/m and 188 T/m/s, respectively, while utilizing 30% ramp-sampling. To characterize the blurring effect from T2 and T2* relaxations, point-spread-function (PSF) was calculated for both circular- and standard-EPI assuming T2 and T2* values of 70 & 36 ms. To compare the PSFs between circular-EPI and conventional EPI in diffusion MRI, we also acquired new in vivo data to evaluate image quality. For BUDA-circular-EPI acquisition, we applied in-plane acceleration factor of 4 per shot with both readout and phase-encoding partial Fourier 5/8, while for BUDA-standard-EPI, we used in-plane acceleration factor of 4 per shot with only phase-encoding partial Fourier 6/8 acquisition that was used before with our previous reconstruction approach (Liao et al, 2021). This resulted in TE = 55ms for BUDA-circular EPI acquisition and TE = 70ms for BUDA-standard EPI acquisition.
Fig. 3.
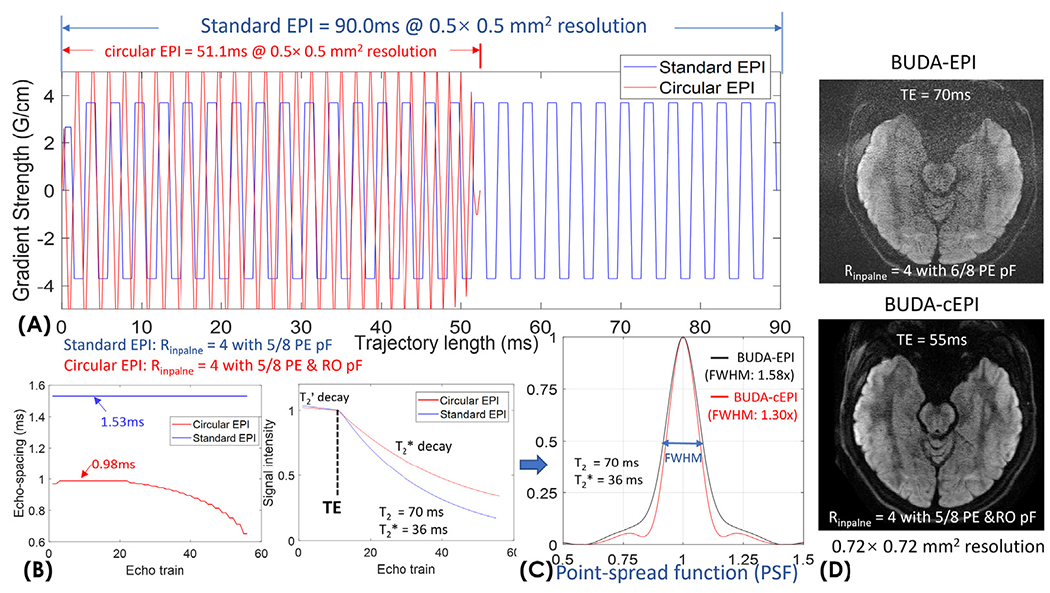
(A) Comparison of gradient waveforms for the circular-EPI and standard-EPI. (B) Echo-spacing and the signal curves of circular- and standard-EPI acquisitions. (C) The point-spread-functions were calculated for both circular- and standard-EPI to characterize T2’ and T2* blurring effect. (D) In-vivo comparison between BUDA-standard-EPI and BUDA-circular-EPI acquisitions at 0.72mm resolution.
To characterize the performance of S-LORAKS in reconstructing missing pF data of BUDA-circular-EPI, BUDA-circular-EPI with 6/8 RO- & PE-pF was simulated by applying a circular sampling mask to a fully-sampled data synthesized from reconstructing BUDA-standard-EPI with 6/8 PE-pF dataset (Fig. 4(A)). The in-vivo simulation data contained motion-induced shot-to-shot phase variations. The protocol of the acquired BUDA-standard-EPI data for this simulation is: FOV: 220 × 220mm, matrix size: 176 × 176, in-plane resolution: 1.25 mm × 1.25 mm, slice thickness: 2 mm, number of slices: 57, TR/TE = 2800/77 ms, multi-band factor: 3 with CAIPI-shift FOV/2 per shot (Setsompop et al., 2012), in-plane acceleration factor: 2 per shot, resulting in an effective echo-spacing of 0.37 ms, partial Fourier factor: 6/8, two interleaved BUDA shots with anterior to posterior (AP) and posterior to anterior (PA) phase-encodings. b value= 1000 s/mm2 with 32 diffusion directions acquired.
Fig. 4.
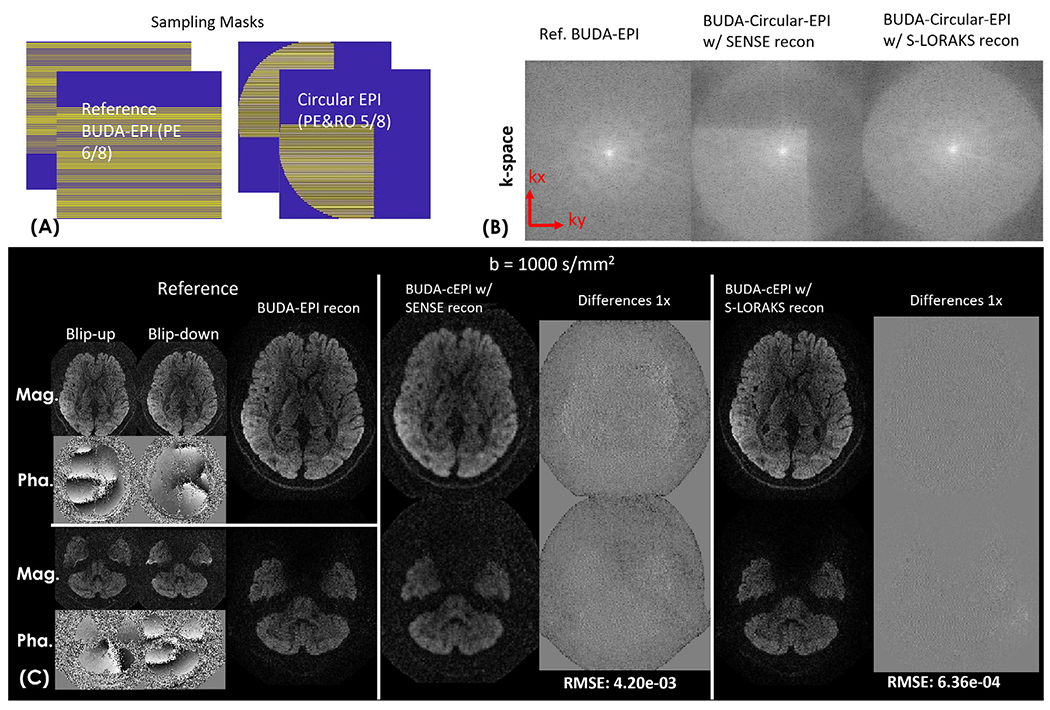
(A) Sampling masks of the standard-EPI with 5/8 phase-encoding partial Fourier and circular-EPI with both readout and phase-encoding partial Fourier. (B) Reconstruction performance comparison of BUDA-EPI vs. synthesized BUDA-circular-EPI with additional RO-pF generated from the same dataset. BUDA-circular-EPI reconstructed using SENSE without S-LORAKS resulted in missing high k-space data (reconstructed k-space of one of the two blip-up&down EPI-shots is shown), while incorporating S-LORAKS into the reconstruction can help effectively recover the missing k-space data. (C) reconstructed results and the difference maps of reference BUDA-standard-EPI (both magnitude and phase images of blip-up &down EPI-shots are shown), BUDA-circular-EPI with SENSE and S-LORAKS for b= 1000 s/mm2 images.
5. In-vivo acquisitions
To validate our proposed method, 10 healthy volunteers were scanned with the approval of the institutional review board (IRB) with informed consent obtained. To compare the reconstruction performance with and without S-LORAKS constraint on the prospectively undersampled dataset, we first acquired the in-vivo brain BUDA-circular-EPI dataset without gSlider encoding: FOV: 220 × 220 × 80 mm3 (16 slices, 5 mm slab thickness), image matrix size: 300 × 300, TR/TE = 5000/55 ms, Rinplane = 4 per shot with both RO- & PE-pF =5/8 (symmetric acquired k-space region of 2.2mm resolution). Fifty diffusion-directions with b =1000 s/mm2 and ten b=0 volumes were acquired. The total acquisition time is 10 min.
To achieve high slice resolution, 5 gSlider encodings were employed on top of the BUDA-circular-EPI sequence to provide high slice resolution with good SNR. In-vivo brain datasets were acquired with gSlider-BUDA-circular-EPI at 720 μm-isotropic resolution. The 720 μm data were acquired with: FOV: 220 × 220 × 57.6 mm3 (16 slabs, 3.6mm slab thickness, 5 gSlider encodings), image matrix size: 300 × 300, TR/TE = 5000/55 ms, Rinplane = 4 per shot with both RO- & PE-pF = 5/8. Ten diffusion-directions with b =1000 s/mm2 were acquired. The total acquisition time is 9 min.
To further push the image resolution and obtain mesoscale in vivo diffusion tensor results, we acquired 500 μm-resolution dataset with: FOV: 220 × 220 × 80 mm3 (32 slabs, 2.5mm slab thickness, 5 gSlider encodings), image matrix size: 440 × 440, TR/TE = 3500/65 ms, MB × Rinplane =2 × 4 per shot with both RO- & PE-pF = 5/8. Sixty diffusion-directions with b =1000 s/mm2 and interspersed ten b=0 volumes were acquired, which was repeated three times to achieve sufficient SNR for such high resolution. The total acquisition time was 105 min. Diffusion analysis and colored fractional anisotropy (FA) maps were generated using the FSL software (Jenkinson et al., 2012).
A FOV-matched low-resolution B1 + map was obtained to correct the B1 + inhomogeneity-induced slab-profile imperfection in gSlider reconstruction using a 1-minute Bloch-Siegert sequence (Sacolick et al., 2010) at 3.4 × 3.4 × 5 mm3 resolution.
To evaluate the reconstructed diffusion datasets of multiple healthy volunteers at various spatial resolutions, we repeated the same diffusion-direction 20 times and evaluated temporal SNR (tSNR) maps for both 720 μm and 500 μm diffusion images.
In this study, the sequence was developed based on KSFoundation platform (https://ksfoundationepic.org/). All the in-vivo data were acquired on a 3T GE Ultra High Performance (UHP) scanner (GE Healthcare, Waukesha, WI) with a NOVA 32-channel head-coil, and all the image reconstructions were performed in MATLAB (MathWorks, Natick, MA).
6. Results
Fig. 3 shows the comparison of ETL, T2* decay, and PSF between circular- and standard-EPI at 500 μm resolution. The trajectory lengths of circular- vs standard-EPI are 51.1 ms vs 90.0 ms, as shown in Fig. 3(A), which demonstrates a ~40% reduction in ETL (Fig. 3(B)). The minimum achievable TE for circular- vs standard-EPI are 65ms vs 79ms. The signal curves with T2’- and T2* decay during the echo-trains were simulated in Fig. 3(B) (signal intensity at TE was normalized to 1 to aid comparisons of T2’- and T2* decay of the two acquisitions). The corresponding PSFs were calculated as shown in Fig. 3(C), where the full-width-half-max (FWHM) of the PSF of BUDA-standard-EPI is 1.58 × that of the actual resolution, while the FWHM’s of the PSF of BUDA-circular-EPI is 1.30 ×; resulting in a 40% reduction in image-blurring for 500 μm acquisition. Fig. 3(D) presents an invivo slice of BUDA-EPI and BUDA-circular-EPI at 720 μm resolution. As seen in Fig. 3(D), the SNR of BUDA-circular-EPI is significantly higher than that of BUDA-EPI. Regarding image sharpness, BUDA-circular-EPI exhibits less blurring than standard-EPI and reveals more cortical information in the in vivo data.
Fig. 4 shows reconstruction performance with and without S-LORAKS constraint for the simulated BUDA-circular-EPI data with additional RO-pF (reconstructions termed “BUDA-SENSE” for reconstructing blip-up and down simultaneously only using the forward-model of the Eq.(1) without S-LORAKS constraint, and “BUDA-S-LORAKS” for reconstructing the BUDA-circular-EPI data with S-LORAKS constraint, respectively). Fig. 4(B) demonstrates that BUDA-circular-EPI reconstructed using SENSE without S-LORAKS resulted in missing high k-space data while incorporating S-LORAKS into the reconstruction enables effectively recovering this missing k-space. Fig. 4(C) indicates that incorporating S-LORAKS into the reconstruction resulted in a lower root-mean-square-error (RMSE) when compared to using SENSE alone, while also providing similar image quality when compared to the reference images (reconstructed from the BUDA-standard-EPI data) for b=1000 s/mm2.
Supporting movie S1(A) shows comparisons between reconstructed data from single-shot EPI (blip-up only) and BUDA-circular EPI with BUDA-SENSE and with BUDA-S-LORAKS reconstructions across 50 diffusion directions. The single-shot EPI results contain distortion artifacts that cause the brain to move/distort in the anterior-posterior differently across the diffusion directions. On the other hand, BUDA-circular-EPI results with BUDA-SENSE and with BUDA-S-LORAKS both are distortion-corrected with good geometric fidelity. Compared to the BUDA-SENSE reconstruction that loses resolution in the missing k-space regions, the proposed BUDA-S-LORAKS reconstruction fills out the missing k-space data and achieves improved resolution as shown in S1(A). S1(B) shows the colored FA maps of the same BUDA-circular-EPI data with BUDA-SENSE and BUDA-S-LORAKS reconstructions. The blue arrow in the zoomed-in view indicates the dark-band gap between adjacent sulci (i.e. it should go green-black-green instead of green-green) in the BUDA-S-LOARKS results, which is blurred out in the BUDA-SENSE reconstruction.
Fig. 5 shows representative single diffusion-weighted images and 10 diffusion-directions averaged images reconstructed by the proposed BUDA-S-LORAKS method at 720 μm-isotropic-resolution, where good SNR was achieved.
Fig. 5.
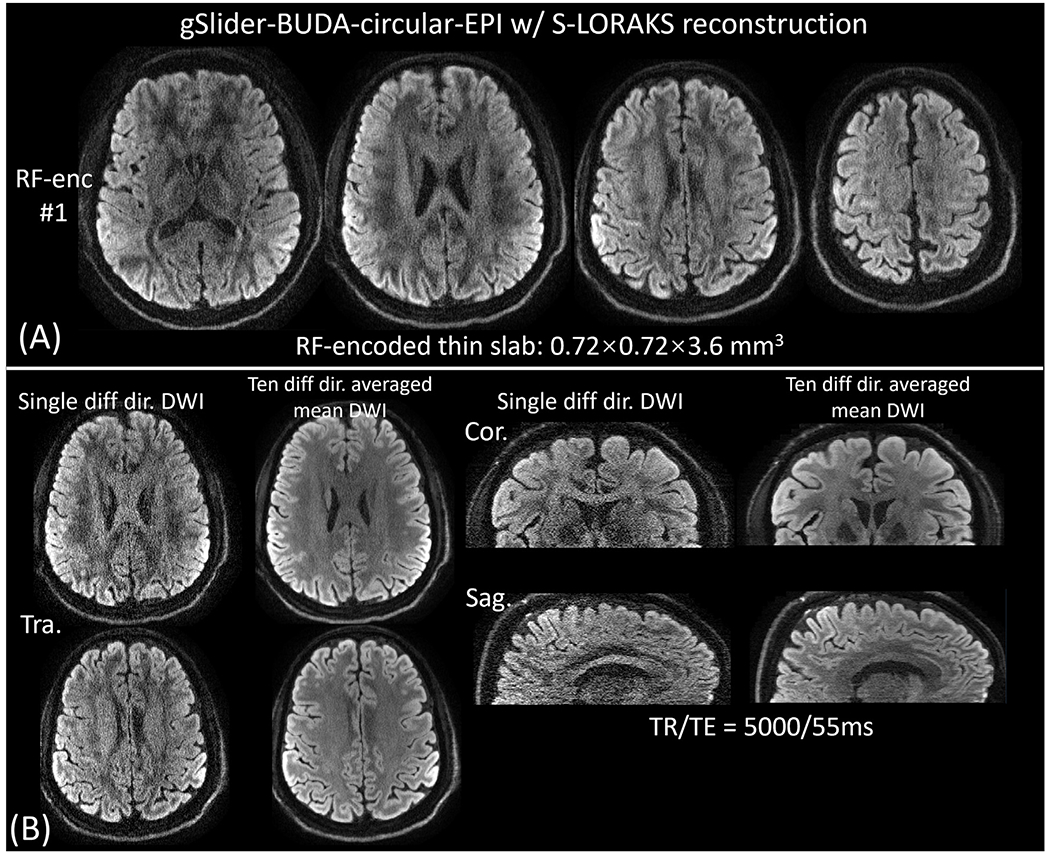
S-LORAKS reconstructed results for gSlider-BUDA-circular-EPI acquisition at 720 μM isotropic resolution. (A) Reconstructed gSlider encoded thin-slabs at 0.72 × 0.72 × 3.6 mm3 (1 out of 5 shown), and (B) diffusion-weighted and 10 diffusion-directions averaged 720 μM isotropic resolution reconstruction for two representative slices. Sagittal and coronal views are also shown in (B).
Fig. 6(A) shows the DWIs of the 500 μm diffusion data across 3 averages of 60 diffusion direction acquisition. Fig. 6(B) shows the FA map of a representative axial slice, and the zoom-in figure shows the high-resolution capability of the 500μm data. Since at this mesoscopic scale resolution the FA map from our scan is still noisy, we applied a spatially adaptive nonlocal means denoising method (Manjón et al., 2010) to increase SNR and enable a better depiction of the detailed high-resolution in-plane information. The denoised FA maps show high-quality mesoscale cortical diffusion images and the expected dark-band at the white-matter and gray-matter boundaries as the diffusion fibers turn sharply at these locations. The denoised colored-FA maps in three orthogonal views are shown in Fig. 6(C).
Fig. 6.
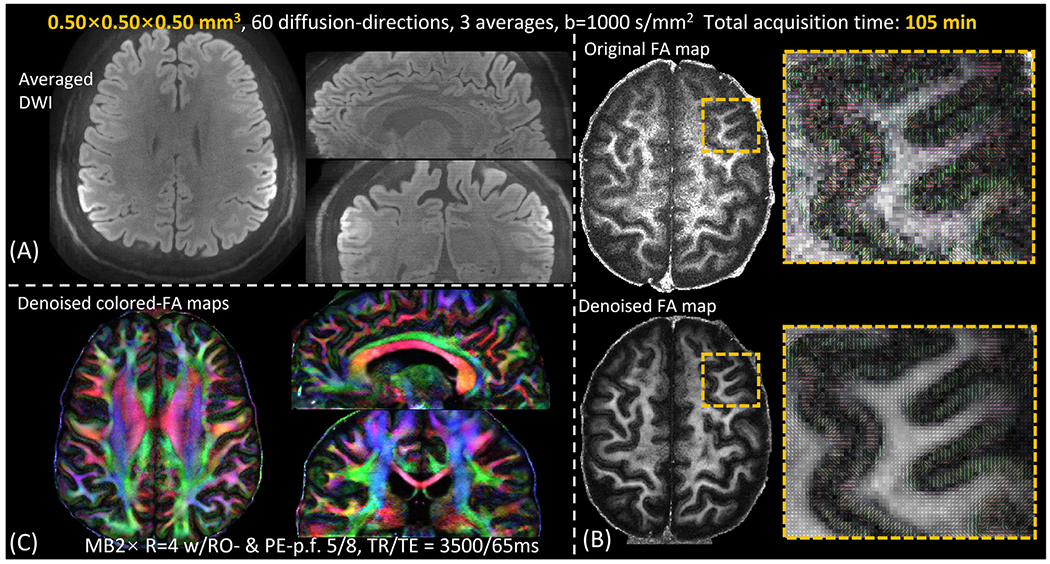
(A) averaged DWIs of the 500 μM diffusion data. (B) a representative slice of the FA maps and the zoom-in figures of the 500 μm data. To boost SNR, a spatially adaptive nonlocal means denoised results are also shown in (B). (C) Denoised colored-FA maps in three orthogonal views.
The calculated temporal SNR (tSNR) maps of 720 μm and 500 μm diffusion images are shown in Supporting figure S2. While the 720 μm images have sufficient tSNR (averaged SNR = 10.85) with our proposed reconstruction, the 500 μm data are noisy (averaged SNR = 3.02) and need to utilize the proposed acquisition technique together with denoising approaches that are emerging in the field (Haldar et al., 2013; Moeller et al., 2021; Muckley et al., 2021; Ramos-Llordén et al., 2021, 2020; Tian et al., 2020). With such a low SNR level at 500 μm resolution, it is also important to use real-valued diffusion in signal averaging and FA calculation, rather than taking the absolute value which would cause signal bias in low-SNR data (Jones and Basser, 2004; Eichner et al., 2015). In this work, we utilize real-valued diffusion post-processing in the BUDA-shot combination, which helps enable true signal averaging and mitigate the noise bias issue, resulting in better estimation of microstructure at high spatial resolution.
7. Discussion
In this work, for high-quality mesoscale diffusion imaging, we combine circular EPI acquisition with RO- and PE-pF sampling, to achieve a reduction in the ETL of ~ 40% and TE of 14 ms when compared to conventional EPI at 500 μm isotropic resolution. With interleaved blip-up and -down acquisition, the field maps (representing the combined effect of eddy current and field inhomogeneity) are estimated using the central k-space regions of the circular-EPI acquisition which is acquired using a constant ESP. The filed maps are then incorporated into the forward model of joint parallel imaging reconstruction using both the constant-ESP and the varying-ESP k-space lines to correct image distortions. Compared to reconstructing the blip-up and -down EPIs separately and then correcting for the image distortion via e.g. FSL TOPUP, joint multi-shot EPI reconstruction with build-in model-based distortion correction achieves improved reconstruction conditioning and reduced g-factor noise penalty (Liao et al., 2021). In addition, by using the S-LORAKS reconstruction across the acquired two-shot data, which takes advantage of the smooth background phase for partial Fourier filling and accounts for shot-to-shot phase variations, high-fidelity diffusion-weighted images could be obtained without the need for navigators. To improve SNR efficiency, we further combine the BUDA circular-EPI with gSlider-SMSb for submillimeter-isotropic-resolution dMRI. Using the proposed gSlider-BUDA-circular-EPI with S-LORAKS reconstruction, we achieve high-fidelity 500 μm-isotropic-resolution in-vivo dMRI.
Compared to the standard EPI trajectory, circular EPI trajectory is essentially an interleaved EPI trajectory that is clipped to a circle in k-space providing isotropic resolution. By acquiring data during the ramp and clipping the trajectory to a circle in k-space, a significant reduction in ETL over conventional square EPI is achieved. Combining the circular-EPI with both RO- and PE-pF sampling, the decreased readout duration, and ESP would further reduce TE and ETL (e.g., for the 500 μm case, 11ms circular EPI readout before the center k-space with dual 5/8 pF vs 18ms standard EPI readout before center k-space with 5/8 PE-pF, which results in (18-11) × 2 = 14ms TE reduction). Spiral imaging is another promising technique for high-resolution diffusion acquisition, which provides a shorter TE to increase SNR when compared to EPI with partial Fourier (Lee et al., 2021). Compared to the spiral and standard-EPI trajectory, the advantage of circular-EPI in high-resolution dMRI is its reduced sensitivity to off-resonance and blurring at the high-frequency k-space. The off-resonance-induced image distortions of the circular-EPI can be corrected using BUDA and the model-based parallel imaging reconstruction. The blurring of circular-EPI at high-frequency k-space is also less pronounced than spiral and standard-EPI trajectories. This is because spiral needs to cover π·(1/resolution) for each ky out in k-space at high frequencies (e.g. from ky to ky +Δ ky), while EPI needs to cover (1/resolution) from −kxmax to +kxmax, and circular-EPI can cover less by curving the standard-EPI trajectory with a smaller effective ESP at high k-space.
In this work, we corrected the Nyquist ghost by characterizing gradient delays and estimating the linear-phase term between EPI odd and even lines from the calibration scan with Gy gradient turned off. However, the imperfect gradient waveform at high gradient strength and slew rate could potentially cause residual Nyquist ghost and artifacts. In the future study, we plan to add “field camera” hardware (Gross et al., 2016) to the scanner and measure the multi-shot circular-EPI trajectories in real time, which could further improve the image quality. In addition, because the encoding speed of circular-EPI trajectory is primarily limited by the maximum usable gradient strength and slew rate, novel high-performance gradient systems (Feinberg et al., 2021; Foo et al., 2020) with higher maximum gradient strength, slew rate, and peripheral nerve stimulation threshold, as well as higher receiver bandwidth should help further reduce ETL and TE. For example, if the maximum usable gradient strength is increased to 200 mT/m, the slew rate is increased to 900 T/m/s and the maximum sampling bandwidth is increased to 2MHz, our 500 μm BUDA-circular-EPI’s ETL would be reduced from 51ms to 20 ms and TE would shorten by another 40% of 65ms to 39ms, which would offer an exciting possibility in high quality mesoscale in-vivo dMRI.
Intravoxel dephasing will lead to rapid signal decay over the readout period, causing much lower overall amplitude at the reconstructed voxel as well as blurring. This issue cannot be corrected via BUDA-estimated field map. However, we note that the ability to go to smaller voxel with our technique should help reduce the level of intravoxel dephasing. Moreover, with our shorter readout from circular EPI and “double” partial Fourier, the amount of signal attenuation across k-space will also reduce, which will help mitigate this issue.
In this work, S-LORAKS was implemented to correct shot-to-shot phase variations and recover missing k-space regions for BUDA-circular-EPI reconstruction. With the S-LORAKS reconstruction, the two-shot images with smoothly varying phases can be mapped into structured low-rank matrices because of consistent linear dependencies within local k-space neighborhoods. Compared to other phase-constrained image reconstruction methods such as virtual conjugate coil reconstruction (Blaimer et al., 2009; Liao et al., 2019b), the S-LORAKS reconstruction imposes phase constraint implicitly through low-rank matrix modeling and was demonstrated to have a good reconstruction performance of conventional partial Fourier scheme in previous studies (Bilgic et al., 2018; Kim et al., 2017). However, one of the challenges associated with implementing the S-LORAKS reconstruction is the slow reconstruction speed. In each iteration of the S-LORAKS reconstruction, building the structured Hankel matrix can be slow and computationally intensive, which limits the application of the proposed method. For the 0.72mm isotropic datasets, the reconstruction time of each diffusion direction is approximately 320 min per whole-brain volume (160 slices) without parallel computing. Using the MATLAB parallel computing toolbox, the reconstruction time can be reduced to 50 min per volume. For the whole-brain 0.50 mm isotropic datasets, with 60 diffusion directions and 3 averages, the total reconstruction time amounts to about 225 h. By dividing the dataset among 8 different computers, we were able to obtain the final reconstruction data in 30 h. Research to overcome this issue is being undertaken, in particular, employing deep learning methods to speed up low-rank-based reconstructions, which can provide more than 100x gain in reconstruction speed (Aggarwal et al., 2020; Hu et al., 2021; Yarach et al., 2022).
A 105-minute scan for diffusion imaging is challenging. However, the 105-minute protocol refers to scanning 60 diffusion-directions × 3 averages = 180 diffusion-directions for 0.5mm isotropic diffusion MRI at a low SNR level. For each diffusion direction, it takes approximately 35 seconds to acquire the whole-brain volume. To achieve a clinically feasible duration, a ten-diffusion-direction scan necessitates just 9 min and can provide high-quality 0.72mm isotropic mean diffusivity and apparent diffusion coefficient maps. Acquisition at such high isotropic resolution has started to be proven valuable for clinical applications now that approaches for acquiring such data are starting to become available. For instance, our recent study using standard gSlider-EPI acquisition at 0.86 mm isotropic (Misquitta et al., 2022) indicates that submillimeter isotropic DWI can help detect silent acute microinfarcts in patients with cerebral small vessel disease. With the improved acquisition and reconstruction strategies proposed in this work, there will be the feasibility of acquiring even higher resolution data at improved SNR, enabling detection and visualization of even smaller infarcts which in ex-vivo studies have shown to be hall mark of aging and dementia (Smith et al., 2012)
The motion sensitivity timeframe of each of our reconstructed diffusion volumes is 35s, which is 10 TRs from 5 gslider-encodings across blip-up and -down directions. This timeframe is shorter than that of other competing 3D multi-slab diffusion acquisitions. For example, 3D simultaneous multi-slab diffusion approaches require 86 seconds per volume at 1mm isotropic resolution (Dai et al., 2021). Various methods have been proposed to mitigate motion artifacts across gSlider encoding and blip up and down acquisitions per diffusion direction (Wang et al., 2018; Cao et al., 2020). These methods can significantly reduce the motion sensitivity, bringing the timeframe down to 3.5-7.0 seconds. Future work will include the incorporation of these techniques into this work. It is also worth noting that motion corruption artifacts in gSlider appear to be less severe compared to 3D k-space encoding approaches, given that each gSlider encoding can provide a thick-slab image. The resulting motion artifacts seem to be localized to blurring in the final reconstructed image (Wang et al., 2018) rather than extensive aliasing/blurring artifacts and spin-history induced slab-boundary artifacts found in 3D multi-slab approaches.
As we push forward with our encoding capability to achieve higher isotropic resolution dMRI, a significant decrease in voxel size will lead to a proportionate decrease in SNR. To achieve high SNR efficiency, gSlider simultaneous multi-slab acquisition was employed in this work, but SNR remains a challenge for 500 μm dMRI. To boost SNR, future work will explore the incorporation of recent promising diffusion denoising methods (Haldar et al., 2013; Moeller et al., 2021; Muckley et al., 2021; Ramos-Llordén et al., 2021, 2020; Tian et al., 2020) into our mesoscale dMRI framework.
8. Conclusion
In this work, we developed a gSlider-BUDA-circular-EPI with readout and phase-encoding partial Fourier acquisition, together with model-based S-LORAKS reconstruction to achieve high-fidelity in vivo diffusion MRI at the mesoscale. In comparison to standard EPI, the proposed method provides improved SNR and reduced blurring.
Supplementary Material
Acknowledgment
The authors thank Dr. Stefan Skare for his support with sequence programming based on the KS Foundation platform (https://ksfoundationepic.org/). This work was supported by: National Institutes of Health (NIH) research grants: R01MH116173, R01EB019437, U01EB025162, P41EB030006, R01EB016695. GE Healthcare grant: A-122.
Footnotes
Declaration of Competing Interest
The authors report no competing interests.
Credit authorship contribution statement
Congyu Liao: Conceptualization, Methodology, Software, Investigation, Validation, Visualization, Writing – original draft, Writing – review & editing. Uten Yarach: Conceptualization, Software, Validation, Visualization, Writing – review & editing. Xiaozhi Cao: Conceptualization, Methodology, Investigation, Writing – review & editing. Siddharth Srinivasan Iyer: Software, Investigation, Writing – review & editing. Nan Wang: Software, Investigation, Writing – review & editing. Tae Hyung Kim: Software, Investigation, Writing – review & editing. Qiyuan Tian: Software, Validation, Writing – review & editing. Berkin Bilgic: Software, Methodology, Validation, Writing – review & editing. Adam B. Kerr: Conceptualization, Methodology, Software, Validation, Writing – review & editing. Kawin Setsompop: Conceptualization, Methodology, Writing – review & editing, Supervision, Resources, Funding acquisition.
Supplementary materials
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.neuroimage.2023.120168.
Data and code availability statement
The demonstration BUDA-SLORAKS reconstruction scripts and the BUDA-circular-EPI raw k-space data are available online at: https://github.com/CongyuLiao/BUDA_SLORAKS.
References
- Aggarwal HK, Mani MP, Jacob M, 2020. Modl-mussels: model-based deep learning for multishot sensitivity-encoded diffusion mri. IEEE Trans. Med. Imaging 39, 1268–1277. doi: 10.1109/TMI.2019.2946501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson JLR, Skare S, Ashburner J, 2003. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage 20, 870–888. doi: 10.1016/S1053-8119(03)00336-7. [DOI] [PubMed] [Google Scholar]
- Andersson JLR, Sotiropoulos SN, 2016. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 125, 1063–1078. doi: 10.1016/j.neuroimage.2015.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assaf Y, 2019. Imaging laminar structures in the gray matter with diffusion MRI. Neuroimage doi: 10.1016/j.neuroimage.2017.12.096. [DOI] [PubMed] [Google Scholar]
- Bilgic B, Kim TH, Liao C, Manhard MK, Wald LL, Haldar JP, Setsompop K, 2018. Improving parallel imaging by jointly reconstructing multi-contrast data. Magn. Reson. Med 80, 619–632. doi: 10.1002/mrm.27076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blaimer M, Gutberlet M, Kellman P, Breuer FA, Köstler H, Griswold MA, 2009. Virtual coil concept for improved parallel MRI employing conjugate symmetric signals. Magn. Reson. Med 61, 93–102. doi: 10.1002/mrm.21652. [DOI] [PubMed] [Google Scholar]
- Cao X, Wang K, Liao C, Zhang Z, Srinivasan Iyer S, Chen Z, Lo WC, Liu H, He H, Setsompop K, Zhong J, Bilgic B, 2021. Efficient T2 mapping with blip-up/down EPI and gSlider-SMS (T2-BUDA-gSlider). Magn. Reson. Med 86, 2064–2075. doi: 10.1002/MRM.28872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao X, Liao C, Zhang Z, Manhard MK, He H, Zhong J, Bilgic B, Setsompop K, 2020. MOCO-BUDA: motion-corrected blip-up/down acquisition with joint reconstruction for motion-robust and distortion-free diffusion MRI of brain. In: ISMRM 28th Annual Meeting, Sydney, Australia, p. 0465. [Google Scholar]
- Chang HC, Hui ES, Chiu PW, Liu X, Chen NK, 2018. Phase correction for three-dimensional (3D) diffusion-weighted interleaved EPI using 3D multiplexed sensitivity encoding and reconstruction (3D-MUSER). Magn. Reson. Med 79, 2702–2712. doi: 10.1002/mrm.26944. [DOI] [PubMed] [Google Scholar]
- Chen N.kuei, Guidon A, Chang HC, Song AW, 2013. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). Neuroimage 72, 41–47. doi: 10.1016/j.neuroimage.2013.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chu ML, Chang HC, Chung HW, Truong TK, Bashir MR, Chen NK, 2015. POCS-based reconstruction of multiplexed sensitivity encoded MRI (POCSMUSE): a general algorithm for reducing motion-related artifacts. Magn. Reson. Med 74, 1336–1348. doi: 10.1002/mrm.25527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conolly S, Nishimura D, Macovski A, Glover G, 1988. Variable-rate selective excitation. J. Magn. Reson 78, 440–458. doi: 10.1016/0022-2364(88)90131-X. [DOI] [Google Scholar]
- Dai E, Lee PK, Dong Z, Fu F, Setsompop K, McNab JA, 2022. Distortion-free diffusion imaging using self-navigated cartesian echo-planar time resolved acquisition and joint magnitude and phase constrained reconstruction. IEEE Trans. Med. Imaging 41, 63–74. doi: 10.1109/TMI.2021.3104291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai E, Liu S, Guo H, 2021. High-resolution whole-brain diffusion MRI at 3T using simultaneous multi-slab (SMSlab) acquisition. Neuroimage 237, 118099. doi: 10.1016/J.NEUROIMAGE.2021.118099. [DOI] [PubMed] [Google Scholar]
- Dai E, Ma X, Zhang Z, Yuan C, Guo H, 2017. Simultaneous multislice accelerated interleaved EPI DWI using generalized blipped-CAIPI acquisition and 3D K-space reconstruction. Magn. Reson. Med 77, 1593–1605. doi: 10.1002/mrm.26249. [DOI] [PubMed] [Google Scholar]
- Dong Z, Wang F, Wald L, Setsompop K, 2022. SNR-efficient distortion-free diffusion relaxometry imaging using accelerated echo-train shifted echo-planar time-resolving imaging (ACE-EPTI). Magn. Reson. Med 88, 164–179. doi: 10.1002/MRM.29198. [DOI] [PubMed] [Google Scholar]
- Eichner C, Cauley SF, Cohen-Adad J, Möller HE, Turner R, Setsompop K, Wald LL, 2015. Real diffusion-weighted MRI enabling true signal averaging and increased diffusion contrast. Neuroimage 122, 373–384. doi: 10.1016/j.neuroimage.2015.07.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engström M, Mårtensson M, Avventi E, Skare S, 2015. On the signal-to-noise ratio efficiency and slab-banding artifacts in three-dimensional multislab diffusion-weighted echo-planar imaging. Magn. Reson. Med 73, 718–725. doi: 10.1002/mrm.25182. [DOI] [PubMed] [Google Scholar]
- Engström M, Skare S, 2013. Diffusion-weighted 3D multislab echo planar imaging for high signal-to-noise ratio efficiency and isotropic image resolution. Magn. Reson. Med 70, 1507–1514. doi: 10.1002/mrm.24594. [DOI] [PubMed] [Google Scholar]
- Fair MJ, Liao C, Manhard MK, Setsompop K, 2021. Diffusion-PEPTIDE: distortion- and blurring-free diffusion imaging with self-navigated motion-correction and relaxometry capabilities. Magn. Reson. Med 85, 2417–2433. doi: 10.1002/MRM.28579. [DOI] [PubMed] [Google Scholar]
- Feinberg DA, Dietz P, Liu C, Setsompop K, Mukherjee P, Wald LL, Vu AT, Beckett AJ, Insua IG, Schröder M, Stocker S, Rummert E, Mathias Dvids, 2021. Design and development of a next-generation 7T human brain scanner with high-performance gradient coil and dense RF arrays. In: ISMRM, p. 0562. [Google Scholar]
- Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Glasser MF, Miller KL, Ugurbil K, Yacoub E, 2010. Multiplexed echo planar imaging for sub-second whole brain FMRI and fast diffusion imaging. PLoS One 5, e15710. doi: 10.1371/journal.pone.0015710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foo TKF, Tan ET, Vermilyea ME, Hua Y, Fiveland EW, Piel JE, Park K, Ricci J, Thompson PS, Graziani D, Conte G, Kagan A, Bai Y, Vasil C, Tarasek M, Yeo DTB, Snell F, Lee D, Dean A, DeMarco JK, Shih RY, Hood MN, Chae H, Ho VB, 2020. Highly efficient head-only magnetic field insert gradient coil for achieving simultaneous high gradient amplitude and slew rate at 3.0T (MAGNUS) for brain microstructure imaging. Magn. Reson. Med 83, 2356–2369. doi: 10.1002/MRM.28087. [DOI] [PubMed] [Google Scholar]
- Gross S, Barmet C, Dietrich BE, Brunner DO, Schmid T, Pruessmann KP, 2016. Dynamic nuclear magnetic resonance field sensing with part-per-trillion resolution. Nat. Commun 7, 1–7. doi: 10.1038/ncomms13702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gulban OF, De Martino F, Vu AT, Yacoub E, Uğurbil K, Lenglet C, 2018. Cortical fibers orientation mapping using in-vivo whole brain 7 T diffusion MRI. Neuroimage 178, 104–118. 10.1016/j.neuroimage.2018.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haldar JP, 2014. Low-rank modeling of local k-space neighborhoods (LORA type=‘Periodical”KS) for constrained MRI. IEEE Trans. Med. Imaging 33, 668–681. doi: 10.1109/TMI.2013.2293974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haldar JP, Wedeen VJ, Nezamzadeh M, Dai G, Weiner MW, Schuff N, Liang ZP, 2013. Improved diffusion imaging through SNR-enhancing joint reconstruction. Magn. Reson. Med 69, 277–289. doi: 10.1002/mrm.24229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holdsworth SJ, Aksoy M, Newbould RD, Yeom K, Van AT, Ooi MB, Barnes PD, Bammer R, Skare S, 2012. Diffusion tensor imaging (DTI) with retrospective motion correction for large-scale pediatric imaging. J. Magn. Reson. Imaging 36, 961–971. doi: 10.1002/jmri.23710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holdsworth SJ, Skare S, Newbould RD, Guzmann R, Blevins NH, Bammer R, 2008. Readout-segmented EPI for rapid high resolution diffusion imaging at 3T. Eur. J. Radiol 65, 36–46. doi: 10.1016/j.ejrad.2007.09.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu Y, Levine EG, Tian Q, Moran CJ, Wang X, Taviani V, Vasanawala SS, McNab JA, Daniel BA, Hargreaves BL, 2019. Motion-robust reconstruction of multishot diffusion-weighted images without phase estimation through locally low-rank regularization. Magn. Reson. Med 81, 1181–1190. doi: 10.1002/mrm.27488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu Y, Xu Y, Tian Q, Chen F, Shi X, Moran CJ, Daniel BL, Hargreaves BA, 2021. RUN-UP: accelerated multishot diffusion-weighted MRI reconstruction using an unrolled network with U-Net as priors. Magn. Reson. Med 85, 709–720. doi: 10.1002/mrm.28446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM, 2012. Fsl. Neuroimage. 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- Jeong HK, Gore JC, Anderson AW, 2013. High-resolution human diffusion tensor imaging using 2-D navigated multishot SENSE EPI at 7 T. Magn. Reson. Med 69, 793–802. doi: 10.1002/mrm.24320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansen-Berg H, Behrens TEJ, Sillery E, Ciccarelli O, Thompson AJ, Smith SM, Matthews PM, 2005. Functional–anatomical validation and individual variation of diffusion tractography-based segmentation of the human thalamus. Cereb. Cortex 15, 31–39. doi: 10.1093/CERCOR/BHH105. [DOI] [PubMed] [Google Scholar]
- Jones DK, Basser PJ, 2004. Squashing peanuts and smashing pumpkins”: how noise distorts diffusion-weighted MR data. Magn. Reson. Med 52, 979–993. doi: 10.1002/mrm.20283. [DOI] [PubMed] [Google Scholar]
- Kerr AB, Pauly JM, Hu BS, Li KC, Hardy CJ, Meyer CH, Macovski A, Nishimura DG, 1997. Real-time interactive MRI on a conventional scanner. Magn. Reson. Med 38, 355–367. doi: 10.1002/mrm.1910380303. [DOI] [PubMed] [Google Scholar]
- Kim TH, Setsompop K, Haldar JP, 2017. LORAKS makes better SENSE: phase-constrained partial Fourier SENSE reconstruction without phase calibration. Magn. Reson. Med 77, 1021–1035. doi: 10.1002/mrm.26182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkman DJ, Hajnal JV, Herlihy AH, Coutts GA, Young IR, Ehnholm G, 2001. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J. Magn. Reson. Imaging 13, 313–317. doi:. [DOI] [PubMed] [Google Scholar]
- Lee Y, Wilm BJ, Brunner DO, Gross S, Schmid T, Nagy Z, Pruessmann KP, 2021. On the signal-to-noise ratio benefit of spiral acquisition in diffusion MRI. Magn. Reson. Med 85, 1924–1937. doi: 10.1002/mrm.28554. [DOI] [PubMed] [Google Scholar]
- Leuze CWU, Anwander A, Bazin PL, Dhital B, Stüber C, Reimann K, Geyer S, Turner R, 2014. Layer-specific intracortical connectivity revealed with diffusion MRI. Cereb. Cortex 24, 328–339. doi: 10.1093/cercor/bhs311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao C, Bilgic B, Tian Q, Stockmann JP, Cao X, Fan Q, Iyer SS, Wang F, Ngamsombat C, Lo WC, Manhard MK, Huang SY, Wald LL, Setsompop K, 2021. Distortion-free, high-isotropic-resolution diffusion MRI with gSlider BUDA-EPI and multicoil dynamic B0 shimming. Magn. Reson. Med 86, 791–803. doi: 10.1002/mrm.28748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao C, Cao X, Cho J, Zhang Z, Setsompop K, Bilgic B, 2019a. Highly efficient MRI through multi-shot echo planar imaging. Proc. SPIE, Wavelets and Sparsity XVIII, 11138, pp. 353–365. doi: 10.1117/12.2527183. [DOI] [Google Scholar]
- Liao C, Chen Y, Cao X, Chen S, He H, Mani M, Jacob M, Magnotta V, Zhong J, 2017. Efficient parallel reconstruction for high resolution multishot spiral diffusion data with low rank constraint. Magn. Reson. Med 77, 1359–1366. doi: 10.1002/mrm.26199. [DOI] [PubMed] [Google Scholar]
- Liao C, Manhard MK, Bilgic B, Tian Q, Fan Q, Han S, Wang F, Park DJ, Witzel T, Zhong J, Wang H, Wald LL, Setsompop K, 2019b. Phase-matched virtual coil reconstruction for highly accelerated diffusion echo-planar imaging. Neuroimage 194, 291–302. doi: 10.1016/j.neuroimage.2019.04.002. [DOI] [PubMed] [Google Scholar]
- Liao C, Stockmann J, Tian Q, Bilgic B, Arango NS, Manhard MK, Huang SY, Grissom WA, Wald LL, Setsompop K, 2020. High-fidelity, high-isotropic-resolution diffusion imaging through gSlider acquisition with B1+ and T1 corrections and integrated ΔB0/Rx shim array. Magn. Reson. Med 83, 56–67. doi: 10.1002/mrm.27899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao C, Yarach U, Cao X, Iyer SS, Wang N, Kim TH, Bilgic B, Kerr AB, Setsompop K, 2022. High-fidelity submillimeter-isotropic-resolution diffusion MRI through gSlider-BUDA and circular EPI with S-LORAKS reconstruction. In: ISMRM, London, p. 0042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J, Witzel T, Grissom WA, Setsompop K, 2017. Minimum peak power root-flipped gSlider-SMS RF pulses for high-resolution in vivo diffusion imaging. In: ISMRM, Honolulu, p. 0523. [Google Scholar]
- Mani M, Jacob M, Kelley D, Magnotta V, 2017. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn. Reson. Med 78, 494–507. doi: 10.1002/mrm.26382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manjón JV, Coupé P, Martí-Bonmatí L, Collins DL, Robles M, 2010. Adaptive nonlocal means denoising of MR images with spatially varying noise levels. J. Magn. Reson. Imaging 31, 192–203. doi: 10.1002/jmri.22003. [DOI] [PubMed] [Google Scholar]
- McNab JA, Polimeni JR, Wang R, Augustinack JC, Fujimoto K, Stevens A, Janssens T, Farivar R, Folkerth RD, Vanduffel W, Wald LL, 2013. Surface based analysis of diffusion orientation for identifying architectonic domains in the in vivo human cortex. Neuroimage 69, 87–100. doi: 10.1016/j.neuroimage.2012.11.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misquitta K, Daou M, Conklin J, Liao C, Setsompop K, Poublanc J, Shirzadi Z, Macintosh BJ, Tomlinson G, Cohn M, Aviv RI, Silver FL, Mandell DM, 2022. Detecting silent acute microinfarcts in cerebral small vessel disease using submillimeter diffusion-weighted magnetic resonance imaging: preliminary results. Stroke 53, E251–E252. doi: 10.1161/STROKEAHA.122.039723. [DOI] [PubMed] [Google Scholar]
- Moeller S, Pisharady PK, Ramanna S, Lenglet C, Wu X, Dowdle L, Yacoub E, Uğurbil K, Akçakaya M, 2021. NOise reduction with distribution corrected (NORDIC) PCA in dMRI with complex-valued parameter-free locally low-rank processing. Neuroimage 226, 117539. doi: 10.1016/J.NEUROIMAGE.2020.117539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moeller S, Ramanna S, Lenglet C, Pisharady PK, Auerbach EJ, Delabarre L, Wu X, Akcakaya M, Ugurbil K, 2020. Self-navigation for 3D multishot EPI with data-reference. Magn. Reson. Med 84, 1747–1762. doi: 10.1002/mrm.28231, mrm. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Uğurbil K, 2010. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain FMRI. Magn. Reson. Med 63, 1144–1153. doi: 10.1002/mrm.22361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muckley MJ, Ades-Aron B, Papaioannou A, Lemberskiy G, Solomon E, Lui YW, Sodickson DK, Fieremans E, Novikov DS, Knoll F, 2021. Training a neural network for Gibbs and noise removal in diffusion MRI. Magn. Reson. Med 85, 413–428. doi: 10.1002/MRM.28395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porter DA, Heidemann RM, 2009. High resolution diffusion-weighted imaging using readout-segmented echo-planar imaging, parallel imaging and a two-dimensional navigator-based reacquisition. Magn. Reson. Med 62, 468–475. doi: 10.1002/mrm.22024. [DOI] [PubMed] [Google Scholar]
- Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P, 1999. SENSE: sensitivity encoding for fast MRI. Magn. Reson. Med 42, 952–962. doi:. [DOI] [PubMed] [Google Scholar]
- Ramos-Llordén G, Ning L, Liao C, Mukhometzianov R, Michailovich O, Setsompop K, Rathi Y, 2020. High-fidelity, accelerated whole-brain submillimeter in vivo diffusion MRI using gSlider-spherical ridgelets (gSlider-SR). Magn. Reson. Med 84, 1781–1795. doi: 10.1002/mrm.28232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramos-Llordén G, Vegas-Sánchez-Ferrero G, Liao C, Westin CF, Setsompop K, Rathi Y, 2021. SNR-enhanced diffusion MRI with structure-preserving low-rank denoising in reproducing kernel Hilbert spaces. Magn. Reson. Med 86, 1614–1632. doi: 10.1002/mrm.28752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rettenmeier C, Maziero D, Qian Y, Stenger VA, 2019. A circular echo planar sequence for fast volumetric fMRI. Magn. Reson. Med 81, 1685–1698. doi: 10.1002/mrm.27522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sacolick LI, Wiesinger F, Hancu I, Vogel MW, 2010. B1 mapping by Bloch-Siegert shift. Magn. Reson. Med 63, 1315–1322. doi: 10.1002/MRM.22357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setsompop K, Fan Q, Stockmann J, Bilgic B, Huang S, Cauley SF, Nummenmaa A, Wang F, Rathi Y, Witzel T, Wald LL, 2018. High-resolution in vivo diffusion imaging of the human brain with generalized slice dithered enhanced resolution: simultaneous multislice (gSlider-SMS). Magn. Reson. Med 79, 141–151. doi: 10.1002/mrm.26653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL, 2012. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn. Reson. Med 67, 1210–1224. doi: 10.1002/mrm.23097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith EE, Schneider JA, Wardlaw JM, Greenberg SM, 2012. Cerebral microinfarcts: the invisible lesions. Lancet Neurol. 11, 272–282. doi: 10.1016/S1474-4422(11)70307-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian Q, Bilgic B, Fan Q, Liao C, Ngamsombat C, Hu Y, Witzel T, Setsompop K, Polimeni JR, Huang SY, 2020. DeepDTI: high-fidelity six-direction diffusion tensor imaging using deep learning. Neuroimage 219, 117017. doi: 10.1016/j.neuroimage.2020.117017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M, 2014. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn. Reson. Med 71, 990–1001. doi: 10.1002/mrm.24751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uecker M, Ong F, Tamir JI, Bahri D, Virtue P, Cheng JY, Zhang T, Lustig M, 2015. Berkeley advanced reconstruction toolbox. In: Proc. Intl. Soc. Mag. Reson. Med, p. 2486. [Google Scholar]
- Van AT, Aksoy M, Holdsworth SJ, Kopeinigg D, Vos SB, Bammer R, 2015. Slab profile encoding (PEN) for minimizing slab boundary artifact in three-dimensional diffusion-weighted multislab acquisition. Magn. Reson. Med 73, 605–613. doi: 10.1002/mrm.25169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang F, Dong Z, Tian Q, Liao C, Fan Q, Hoge WS, Keil B, Polimeni JR, Wald LL, Huang SY, Setsompop K, 2021. In vivo human whole-brain Connectom diffusion MRI dataset at 760 μm isotropic resolution. Sci. Data 8, 1–12. doi: 10.1038/s41597-021-00904-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang F, Dong Z, Reese TG, Bilgic B, Katherine Manhard M, Chen J, Polimeni JR, Wald LL, Setsompop K, 2019. Echo planar time-resolved imaging (EPTI). Magn. Reson. Med 81, 3599–3615. doi: 10.1002/MRM.27673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang F, Bilgic B, Dong Z, Manhard MK, Ohringer N, Zhao B, Haskell M, Cauley SF, Fan Q, Witzel T, Adalsteinsson E, Wald LL, Setsompop K, 2018. Motion-robust sub-millimeter isotropic diffusion imaging through motion corrected generalized slice dithered enhanced resolution (MC-gSlider) acquisition. Magn. Reson. Med 80, 1891–1906. doi: 10.1002/mrm.27196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu W, Koopmans PJ, Frost R, Miller KL, 2016. Reducing slab boundary artifacts in three-dimensional multislab diffusion MRI using nonlinear inversion for slab profile encoding (NPEN). Magn. Reson. Med 76, 1183–1195. doi: 10.1002/mrm.26027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarach U, Chatnuntawech I, Liao C, Teerapittayanon S, Iyer SS, Kim TH, Cho J, Bilgic B, Hu Y, Hargreaves B, Setsompop K, 2022. Rapid reconstruction of blip up-down circular EPI (BUDA-cEPI) for distortion-free dMRI using an Unrolled Network with U-Net as priors. In: ISMRM, London, p. 4348. [Google Scholar]
- Zahneisen B, Aksoy M, Maclaren J, Wuerslin C, Bammer R, 2017. Extended hybrid-space SENSE for EPI: off-resonance and eddy current corrected joint interleaved blip-up/down reconstruction. Neuroimage 153, 97–108. doi: 10.1016/J.NEUROIMAGE.2017.03.052. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Cho J, Wang L, Liao C, Shin H-G, Cao X, Lee J, Xu J, Zhang T, Ye H, Setsompop K, Liu H, Bilgic B, 2022. Blip up-down acquisition for spin- and gradient-echo imaging (BUDA-SAGE) with self-supervised denoising enables efficient T2, T2* , para- and dia-magnetic susceptibility mapping. Magn. Reson. Med 88, 633–650. doi: 10.1002/MRM.29219. [DOI] [PubMed] [Google Scholar]
- Zhu K, Dougherty RF, Wu H, Middione MJ, Takahashi AM, Zhang T, Pauly JM, Kerr AB, 2016. Hybrid-Space SENSE Reconstruction for Simultaneous Multi-Slice MRI. IEEE Trans. Med. Imaging 35, 1824–1836. doi: 10.1109/TMI.2016.2531635. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The demonstration BUDA-SLORAKS reconstruction scripts and the BUDA-circular-EPI raw k-space data are available online at: https://github.com/CongyuLiao/BUDA_SLORAKS.


