Abstract
Using deicing fluids is the main way of aircraft ground deicing, which plays an important role in ensuring flights’ safety. However, most of the airports use deicing fluids excessively to ensure the quality and efficiency of aircraft ground deicing, which will not only cause a large amount of deicing fluids wasted but also pollute water resources and the environment. Finding the optimal solution between deicing efficiency and deicing fluids consumption through effective methods is necessary. This article analyzes the energy conversion process of aircraft ground deicing, establishes multi-parameter optimization model for deicing, and optimizes the consumption of deicing fluids. The physical quantity, including the flow rate and the temperature of deicing fluids, is found as the main influence of the deicing time, which is the most concerned problem in the actual operation. Under the precondition of ensuring the deicing efficiency, the optimized parameters such as different ambient temperature, wing area, and icing thickness are obtained by genetic algorithm. The trend between the parameters with the change of environment has also been analyzed. Finally, the actual using condition in the capital airport and the optimized results are compared, and the results show that the usage of deicing fluids reduced 13% to 24%.
Keywords: Aircraft ground deicing, deicing model, genetic algorithm, parameter optimization, retention time
Introduction
The flight safety and punctuality rate exist serious risks because of the aircraft ground icing in bad weather. Aircraft ground deicing can avoid flying accidents and easing flight extensive delays caused by the aircraft icing on the ground, and it is widely used at home and abroad. As people travel efficiently, the efficiency of aircraft deicing on the ground and the safety of flight in ice and snow weather have become one of the hottest attention areas in the field of civil aviation. Aircraft deicing efficiency and safety are largely depending on the deicing equipment performance and parameters. Stable performance of deicing equipment can ensure the safety and quality of deicing. Scientifically optimized deicing parameters will improve the deicing efficiency and reduce the cost for deicing.1,2 At present, the deicing operation mode of most airports is the use of deicing fluids. The excessive use of deicing fluids will bring many problems, such as the waste of resources and increasing costs. Groundwater may also be polluted by the wasted deicing liquid generated after the deicing operation. So it is necessary to do research on the temperature and flow rate of deicing fluids which determine the efficiency of deicing operations. The environmental and economic problems caused by deicing operations in the airports will be mitigated through optimized parameters of aircraft deicing equipment.
Currently, hazards of aircraft icing are gradually recognized during flight practice, and the researches in the field of aviation aircraft deicing as well as anti-icing system also have been further improved. The deicing technology improves with the development of modern science and technology. Aircraft deicing can be divided into three types in accordance with deicing mechanism: freezing inhibitors, heat melting ice, and surface deformation. 3 It has already emerged a variety of new technologies, and some technology has been successfully tested and applied in aircraft ground deicing. Typical of these technologies include infrared deicing technology, microwave deicing technology, and steam deicing technology.
Aircraft deicing systems with the use of infrared rays are promoting systems such as the InfraTek™ system and the Ice Cat™ system. 4 InfraTek™ system can adjust the infrared wavelengths and infrared heat automatically according to the type and severity of the ice. This method can save 70% of ethylene glycol compared with the method of conventional chemical deicing. However, the deicing system of infrared deicing costs high for hangar construction, and there is controversy whether the infrared ray will damage the airframe of the aircraft. Ice Cat™ system underwent the relevant tests in the US Federal Aviation Administration, the US Air Force, and some other agencies. But both of them were not capable of a large area application. In addition, new material technology in aircraft deicing and anti-icing begin to emerge around the world. Innovative Dynamics company in America researched on the principle of shape memory alloy for aircraft deicing. 5 By preliminary estimates, the use of shape memory alloy can save a lot of energy, and it is the hotspot of deicing and anti-icing in the surface of aircraft as well as other surface structure, but there is still no mature technology systems or product applications.
Nowadays, aircraft ground deicing security still relies on the use of deicing fluids achieving deicing and anti-icing operation. Deicing and anti-icing take advantage of deicing equipment or system injecting the deicing fluids on the aircraft surface within required time to melt the ice. It will suppress the formation of ice in a certain time and make sure flights take off safely. Factors which affect the quality and speed of deicing mainly involve the deicing mechanism, deicing fluids parameters, deicing speed, and deicing equipment parameters.
Scott E Ornitz 6 studied the dependency relationships about deicing fluids retention time, deicing fluids concentration, temperature, and wind speed. He established the optimization model about deicing fluids concentration change with the external environment and used mixed-integer nonlinear programming to optimize deicing fluids volume by online intelligent optimization. This method overcame the uncertainties for the type of aircrafts, temperature of the environment, and parameters of equipment. Simultaneously, it established the theoretical basis of the amount of deicing fluids of aircraft deicing operation on the ground by this way. Funded by the Federal Aviation Administration, the researchers John D’Avirro and Michael Chaput 7 in APS Aviation, Inc., studied the using procedure and technology about deicing and anti-icing fluids, optimized the deicing parameters, and reduced the environmental pollution caused by deicing fluids. But this method was at the cost of reducing the efficiency of deicing, ignoring the most important time in the actual operation of the airport. Alexandre Zouzou et al. 8 took the deicing fluids retention time into account, established the model of deicing fluids retention time when temperature changes, obtained the relationship between deicing fluids retention time and temperature changes by numerical simulation, and compared this result with the condition of constant temperature. Bin and Liwen analyzed the heat transfer relationship during the deicing process, established the thermal equilibrium model of the process, and verified the energy model experimentally. But it did not analyze the specific parameters affecting the efficiency of deicing.
As seen from the above, it is necessary to establish a mathematical model of the deicing efficiency parameters and find the optimal solution between deicing efficiency and deicing fluids consumption through effective methods. However, there is no relevant research about the study of relationship among deicing effectiveness, deicing parameters, deicing efficiency, and deicing equipment parameters. This article aims at
Establishing the multi-parameter optimization model based on the heat balance equation in deicing process.
Solving the parameters optimization question by the genetic algorithm (GA) intelligent method, obtaining the optimization results of deicing fluids temperature and flow rate under different conditions.
Comparing and analyzing the optimized results with practical application of the capital airport.
Analyzing the results quantitatively and evaluating the validity of the model.
The outline of this article is as follows. In the “Energy analysis of aircraft ground deicing” section, we analyze the energy involved in the deicing process and build a model which can calculate deicing time and the deicing efficiency. In the “Parameters optimization based on GA” section, we introduce the process of solving multi-objective parameters optimization problem using MATLAB. Try to solve the parameters optimization in different ambient temperatures, surface area of the wing, and in different snow levels. In the “Result analysis” section, we calculate the amount of deicing fluids used on the basis of the “Parameters optimization based on GA” section and compare it with the actual data in the airport. Meanwhile, the feasibility of the method is demonstrated by comparing the deicing time with the retention time of the deicing fluids.
Energy analysis of aircraft ground deicing
Aircraft ground deicing is to spray the heated deicing fluids on the ice area of the aircraft surface mainly including the wings and empennage, and melt the ice on surface through heat transfer. We studied the deicing process on the wings and established the energy balance equation about deicing process based on energy balance principle with ignoring the effects of jet impingement in this article. The energy analysis diagram of aircraft deicing on the ground is shown in Figure 1. In the deicing process of the aircraft wings, the energy includes the following six aspects: 9
Figure 1.
Energy analysis in aircraft ground deicing.
The heat of high temperature deicing fluids Q,
Convection heat transfer between the wing surface and the surrounding ,
Thermal radiation between the wing surface and the air ,
The heat required to melt ice ,
The heat required to heat wing surface ,
Solar radiation .
Heat transfer is a very complex process and the following assumptions are made to simplify the analysis and calculation:
In winter snow, weather solar radiation is set to zero because the sun is usually covered and it can be neglected.
Does not consider heat exchanging between deicing fluids and the cryogenic air, and ignore the heat losses.
Ignore the effect of the wind speed to heat transfer process.
The energy balance equation can be obtained in aircraft ground deicing process by the assumptions above
| (1) |
Specific analysis of energy consumed in the deicing process is as follows.
The heat of deicing fluids with high temperature
The basic formula of heat flow convection in heat transfer process is shown in formula (2). 10 It becomes formula (3) when bring quality calculation formula into.
| (2) |
| (3) |
Convection heat transfer between the wing surface and the surroundings
The basic formula of heat flow convection in heat transfer is
| (4) |
Obtain the heat of convective heat transfer in this article
| (5) |
where is the coefficient of convective heat transfer in the formula above
| (6) |
Thermal radiation between the wing surface and the air
The following formula is the radiation heat flow according to the Law of Boltzmann, and the heat radiating equation is obtained
| (7) |
| (8) |
The heat to melt the ice on the aircraft surface
The following equation shows the heat to melt the ice including latent heat of melting and sensible heat of melting11,12
| (9) |
Sensible heat of melting
The formula of sensible heat of melting and the formula that after we have brought quality calculation show
| (10) |
| (11) |
Latent heat of melting
The basic formula of latent heat of melting and the formula after we have brought quality calculation show
| (12) |
| (13) |
The energy required to heat the wing surface
The formula of heat required for increasing wing surface temperature13,14 and consider the calculation of material aluminum alloy’s quality
| (14) |
| (15) |
Deicing process model
The parameters’ selection of aircraft deicing process is a multi-objective optimization problem. On one hand, the higher temperature and larger flow rate of the deicing fluids mean the higher deicing efficiency and the shorter deicing time. On the other hand, the rise of the concentration, temperature, and flow of deicing fluids will bring higher cost of airport and the waste of more resource. A multi-objective parameter optimization model of deicing process is established based on the law of energy conservation, and the optimal deicing parameters have been obtained through GA in this study.
Substituting equations (2) to (15) into equation (1), we can calculate the differential to the ice thickness and obtain the dynamic thickness equation of the changing ice on the aircraft wing surface
| (16) |
where
| (17) |
| (18) |
via finishing
| (19) |
Equation (19) is the dynamic equation of the changing ice thickness on the wing surface. Integrating equation (19), we can get the formula of the deicing time under certain conditions
| (20) |
Parameters’ optimization based on GA
GA is an important optimization algorithm in modern academic research, which constitutes the basis for a variety of evolutionary computation methods. 15 The operation of GA is actually the process of finding the optimal solution. We find that it is easier to get a global optimal solution by using GAs with appropriate crossover and mutation probabilities under certain constraints in this study. However, it is easier to get local optimal solutions using particle swarm optimization and other evolutionary algorithms. 16
GA consists of three basic operations: selection, crossover, and mutation. GA flowchart is shown in Figure 2.
Figure 2.

Pseudocode of genetic algorithm.
GA application
GA toolbox provides users with friendly GUI (Graphical User Interface) and a command-line invocation statement which is very convenient to apply. 17 In this article, we use GA Toolbox to optimize the temperature and flow rate of deicing fluids in the aircraft ground deicing process. The application kit can be divided into the following steps:
Step 1. Write the M file
We need to write the objective function equation (20) into the M file format before using GA optimization toolbox. The number of variables is set as two, which includes deicing fluids temperature and flow rate.
Step 2. Set the population parameters
We can control the diversity of population by setting the initial population range. To set the initial population range, we just need to define “Initial range” text box. The larger the initial population size, the easier it is to find the global optimal solution, but the running time also increases. In order to get the optimal solution and have a faster calculation speed at the same time, we take the population size as 2000 and the initial range from 0 to 60 with considering the existing constraints and the generations for stopping criteria experiment.
Step 3. Set the fitness scaling
We set the scaling function as Rank; it rules by defining every individual’s measurement by his or her order. The order of every individual is its position after sorting, which means the best adapted individual’s number is 1, followed by 2, and so on.
Step 4. Set the operating parameters
(i) Select the function
This article considers stochastic uniform as an alternative function, which can choose the ideal father generation for the next generation.
(ii) Reproduction parameters
Reproduction parameters include two aspects: elite count and crossover fraction. We set the elite count as 10 and crossover fraction value as 0.8 after repeated tests in the article.
(iii) Mutation function
This article selects the adaptive feasible function as a mutation function to carry on the mutation operation because Gaussian function is suitable for the situation that there are no constraints. Adaptive feasible randomly generates directions that are adaptive with respect to the last successful or unsuccessful generation. A step length is chosen along each direction so that linear constraints and bounds are satisfied. Due to the existence of constraints, the mutation function is implemented in this study using the adaptive feasible function.
(iv) Stopping criteria
The selection of the maximal generations is related to the initial population range; when the maximum generations exceed this number in a certain initial population range, the fitness function value will no longer change significantly.18,19 We finally set 150 generations as the stopping criteria after repeated tests. This can ensure that the deicing efficiency is not much different after parameters’ optimization and less deicing fluids wasted.
The results of optimized parameters
The fitness function is equation (20) which be written as the M file and the fitness value is the deicing time of the process with different deicing parameters. We solve the parameters’ optimization problem of deicing fluids, including its temperature and flow rate in aircraft ground deicing. At the same time, the results also need to meet the constraints of deicing equipment’s parameters in the optimization process. 20 The value of the maximum temperature, the range of concentration of deicing fluids, and maximum flow rate of deicing fluids are displayed
| (21) |
| (22) |
The basic value of parameters in the deicing model is shown in Table 1.
Table 1.
The basic parameters of the deicing model.
| Parameters | Value | Unit |
|---|---|---|
| 5 | ||
| ε | 0.057 | |
| σ | ||
| 0.002 | m | |
Through the MATLAB GA toolbox, we obtained the optimized parameters when it is in different ambient temperatures, concentration of deicing fluids, and in different snow levels.21,22 When the simulation is in different ambient temperatures and concentration of deicing fluids, the value of ice thickness is defaulted to 0.01 m. Since the individual value of the initial population is randomly generated within the initial range, the optimized solutions we get will be different even if we run the model under a fixed parameter condition. In the following experiments, we run 30 times under each condition and analyze the results. After excluding the outliers and averaging the results, we select the result that is close to the mean value as the final result.
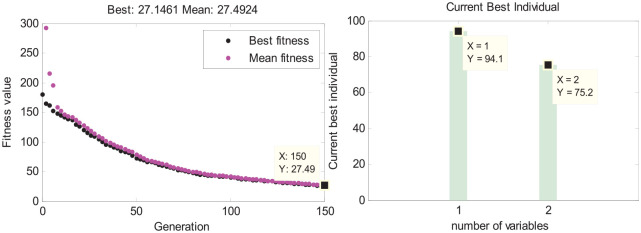
In the optimization process shown in Figures 3–5, only the ambient temperature among all the influencing factors is regularly changed. We run the model multiple times using the GA under each fixed environmental condition to obtain the final optimized results by averaging the values. Summarize the operating parameters and the final results in Table 2. It means when concentration of deicing fluids, surface area of the wing, and the ice thickness remain unchanged, the flow and the temperature of deicing fluids should increase with the ambient temperature decrease to ensure the efficiency of deicing operation. The deicing parameters are inversely related to the ambient temperature, and the proportional coefficient is related to environmental parameters of the experiment.
Figure 3.
Optimal curve when ambient temperature is −10°C.
Figure 4.
Optimal curve when ambient temperature is −20°C.
Figure 5.
Optimal curve when ambient temperature is −30°C.
Table 2.
The optimized parameters in different ambient temperatures.
| (°C) | (m2) | (m) | (L/min) | (°C) | |
|---|---|---|---|---|---|
| –10 | 50% | 122.6 | 0.01 | 80.5 | 71 |
| –20 | 50% | 122.6 | 0.01 | 94.1 | 75.2 |
| –30 | 50% | 122.6 | 0.01 | 103 | 81 |
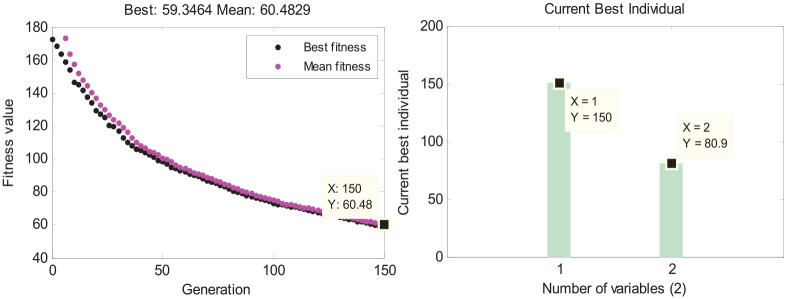
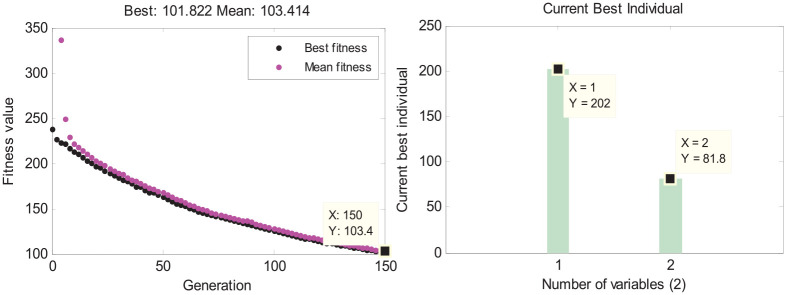
In the optimization process shown in Figures 6–8, only the area of the wing surface among all the influencing factors is regularly changed. The final optimized results and the operating parameters are summarized in Table 3. It means when the ambient temperature, concentration of deicing fluids, and the ice thickness remain unchanged, the flow and the temperature of deicing fluids should increase with the area of the wing surface to ensure the efficiency of deicing operation. The deicing parameters are inversely related to the area of the wing surface, and the proportional coefficient is related to the environmental parameters of the experiment.
Figure 6.
The optimal curve when the wing surface area is 122.6 m2.
Figure 7.
The optimal curve when the wing surface area is 361.6 m2.
Figure 8.
The optimal curve when the wing surface area is 845 m2.
Table 3.
The optimized parameters in different wing surface areas.
| (m2) | (°C) | (m) | (L/min) | (°C) | |
|---|---|---|---|---|---|
| 122.6 | –10 | 50% | 0.01 | 90.9 | 79.9 |
| 361.6 | –20 | 50% | 0.01 | 150 | 80.9 |
| 845 | –30 | 50% | 0.01 | 202 | 81.8 |
The snowfall and snow thickness can be converted in accordance with the ratio of 1:10. 23 It can be considered that the icing thickness is 0.01 m when the snow level is flurry snow, 0.02 m when the snow level is moderate snow, and 0.04 m when the snow level is heavy snow.
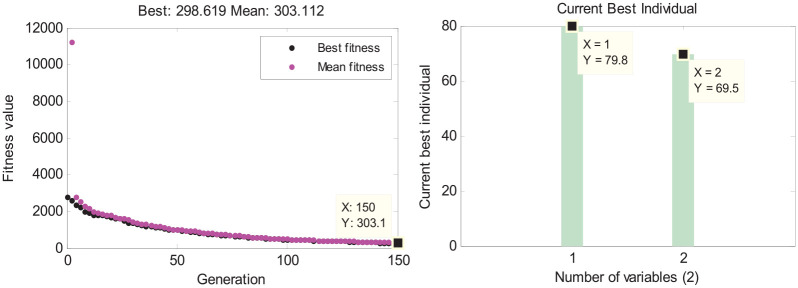
In the optimization process shown in Figures 9–11, only the thickness of ice among all the influencing factors is regularly changed. The final optimized results and the operating parameters are summarized in Table 4. It means that when the ambient temperature, surface area of the wing, and the concentration of deicing fluids remain unchanged, the flow and the temperature of deicing fluids should increase with the thickness of ice to ensure the efficiency of deicing operation. The deicing parameters are positive correlation with the icing thickness and the proportional coefficient is related to the environmental parameters of the experiment.
Figure 9.
The optimal curve when the snow level is flurry snow.
Figure 10.
The optimal curve when the snow level is moderate snow.
Figure 11.
The optimal curve when the snow level is heavy snow.
Table 4.
The optimized parameters in different snow levels.
| Snow level | (m) | (°C) | (m2) | (L/min) | (°C) | |
|---|---|---|---|---|---|---|
| Flurry snow | 0.01 | –10 | 50% | 122.6 | 79.8 | 69.5 |
| Moderate snow | 0.02 | –10 | 50% | 122.6 | 120 | 75.2 |
| Heavy snow | 0.04 | –10 | 50% | 122.6 | 179 | 80.9 |
Combined with the results above, we can use GA to optimize the model and get the parameters of deicing equipment under current condition if the measurable ambient temperature, aircraft surface area, concentration of deicing fluids, and ice thickness are known in the process of deicing operation. The optimization results can be used as the control standard of multi-parameter deicing equipment.
Result analysis
In the process of aircraft ground deicing, the deicing efficiency is ensured while the deicing fluids resource is saved as much as possible. According to equation (20) and the parameters’ optimization results above, the amount of deicing fluids to be used in different conditions can be calculated according to equation (23)
| (23) |
Meanwhile, the deicing fluids retention time is a very important index that should be considered in deicing operations. The operation of aircraft deicing needs to be completed and the aircraft should take off normally within the deicing fluids retention time, or the aircraft will need a second deicing and cause a series of flights delay.
The usage amount of deicing fluids
In this article, the amount of deicing fluids of capital airport for deicing in different conditions is taken as a reference and compared with the usage amount of deicing fluids, which is calculated from equation (23). The specific values of deicing fluids used in capital airport are shown in Table 5.
Table 5.
The deicing fluids consumption of the Beijing capital airport.
| The snowfall level | The consumption of the deicing fluids | The ratio of deicing fluids | Flights |
|---|---|---|---|
| Moderate snow | 80–100 t | 1:1 | 60–80 |
| Heavy snow | 180–200 t | 1:1 | 60–80 |
According to the investigation, the amount of deicing fluids used in the airport is basically linear with the thickness of ice. The second column in Table 5 shows the amount of 100% concentration of deicing fluids—the actual used amount is twice of this since the ratio of deicing fluids is 50%. The deicing fluids that every aircraft actual used under moderate snow and heavy snow weather can be calculated, and the range of deicing fluids used can be obtained by simple calculation. The minimum deicing fluids usage and the maximum number of aircrafts can be used to calculate the starting point for the linear relationship curve and the result is (10, 2000), which corresponds to the minimum snow thickness for moderate snow weather. The end point of the linear relationship curve is (30, 3300), which corresponds to the amount of deicing fluids consumed by each aircraft deicing in the maximum snow thickness of moderate snow weather. Similar results can be obtained in the case of heavy snow, and the amount of deicing fluids used corresponding to different snow thicknesses in the moderate snow and heavy snow can be obtained by this way.
The deicing fluids losses about 5% in practical application are considered. The consumption range of deicing fluids that every aircraft needs in the moderate snow weather is 1900–3100 L and in the heavy snow weather is 4100–5100 L. The deicing fluids consumption under different snow thickness weather is calculated by experimental simulation with the interval of every 5 mm ice thickness. Optimized results of deicing fluids in these different ice thicknesses are shown by a fitted curve.
Figures 12 and 13 show the optimized and actual consumption of deicing fluids in the case of moderate snow and heavy snow changing with the snow thickness.
Figure 12.

Moderate snow weather deicing fluids’ usage.
Figure 13.

Heavy snow weather deicing fluids’ usage.
From the experimental results, it is obvious that the optimized consumption of deicing fluids is increasing with the snow thickness more and more deep. Through the comparison, the optimized consumption results of the deicing fluids are lower than deicing fluids usage amount of the capital airport in the same situation. However, when the snow thickness is near heavy snow level, the airport’s consumption is less than the consumption results after optimization. The reason for this phenomenon is that when the snow thickness is increasing and approaching to the heavy snow level, the optimized result should be compared with the consumption of deicing fluids in heavy snow level of capital airport. We can conclude that compared with the airport actual deicing fluids usage, using the optimized parameters can save an average of 400 L deicing fluids in moderate snow and 1000 L in heavy snow. That is, the consumption of deicing fluids reduced 13% to 21% under moderate snow weather, and 19% to 24% under heavy snow weather.
In most cases, the optimized consumption of deicing fluids is lower than the actual usage amount of deicing fluids in the airport. Therefore, the optimized parameters including temperature and flow rate of deicing fluids have a certain value for reference when deicing operation is carried out.
Deicing time
The retention time of the deicing fluids is a fixed value while the deicing time is a variable one which is closely related to the thickness of the snow and the deicing parameters. The retention time of deicing fluids is 15 min when the deicing fluids concentration is 50% under snowy weather condition. According to this study, the deicing time under different ice thicknesses and the corresponding deicing parameters can be obtained by GA. To prevent a secondary deicing operation, there will be one to four deicing vehicles for deicing operation to ensure the deicing time within the retention time. The number of deicing vehicles for deicing operation depends on the snow conditions and the type of the aircraft in practice.
By choosing the appropriate ice thickness, we can get the required deicing time, but this is the operation time needed for one deicing vehicle. The actual deicing time is the simulated time divided by the number of deicing vehicles. In the process of aircraft ground deicing, there are usually two deicing cars used at the same time in the airport, and the type of aircraft is medium-sized. Through this calculation method, we can simulate the operation time of deicing and compare it with the retention time. Figures 14 and 15 show the deicing time of each deicing car under the conditions of moderate snow and heavy snow, with the increase in snow thickness.
Figure 14.
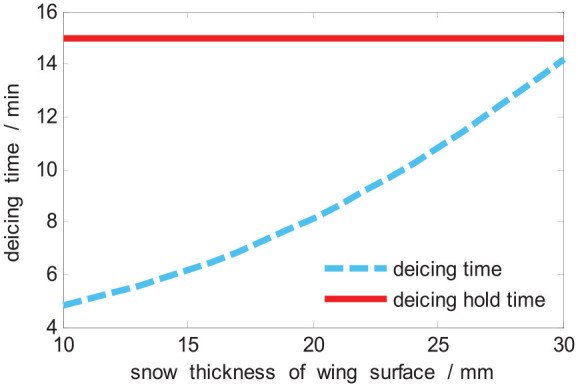
Deicing time in moderate snow weather.
Figure 15.

Deicing time in heavy snow weather.
From the above two figures, we can conclude that with the increase in the thickness of the snow, the deicing time will also increase if the parameters are constant. If the deicing operation takes longer than the deicing time, the aircraft needs to be deicing twice the time to prevent the area after deicing from freezing again. But it will waste a lot of time and affect the normal operation of a series of operations and flights. Overall, in moderate snow and heavy snow conditions, the time for deicing operation is 35% less than the retention time on average. According to the analysis of results, when we use the optimized parameters to perform deicing operation, the thinner ice means the larger interval time compared the deicing time with retention time and the thicker ice means the smaller interval time. The analysis of the results shows that in the thicker ice condition, the deicing parameters need to be appropriately changed to ensure the difference between the deicing time and the retention time, so there is no need to deice again.
The compared results show that the deicing time is always less than the retention time of deicing fluids; it means the parameters meet the time provisions of deicing. This section illustrates the reasons of the optimized results, and it shows that the method of this article could reduce the consumption of deicing fluids and control the deicing time within the retention time of deicing fluids.
Conclusion
In this article, the multi-parameter optimization model is established based on the heat balance equation of deicing process, and the parameters’ optimization question is solved by the GA to find the optimal solution in a certain situation. The deicing fluids temperature and flow rate of deicing fluids are the main parameters influencing the deicing efficiency in actual operation, and they are the key parameters to control the deicing equipment. We can get the parameters through intelligent evolutionary algorithm, which simulate the multi-parameter deicing model under different external environment.
Furthermore, the optimized results are compared and analyzed with practical deicing fluids usage amount of the capital airport. The results show that the usage of optimized parameters can save about 13% to 21% deicing fluids under moderate snow weather and 19% to 24% when it is heavy snow weather. The method achieved resource and cost saving while reduced environmental pollution. According to the algorithm simulation results, the time for the deicing operation meets the requirement when we use the optimal parameters of the deicing equipment. Therefore, it can be concluded that the multi-parameter deicing model is reliable, and the optimized parameters are used as the control index for deicing equipment.
Author biographies
Bin Chen received the B.S. degree from the Xi’an University of Science and Technology in 1998, the M.S. degree from Guangxi University in 2005, and the Ph.D. degree from Tianjin University, Tianjin, China, in 2018. His research is focused on airport ground support technology and control.
Yalei Yang received the B.S. degree from the Taiyuan University of Science and Technology in 2017, studying in Civil Aviation University of China for the M.S. degree.
Jianhua Liu received the B.S. degree from the Anyang Normal University in 2017, studying in Civil Aviation University of China for the M.S. degree.
Appendix 1
Notation
specific heat capacity of deicing fluids (J/kg.°C)
specific heat capacity of wing skin material (J/kg.°C)
concentration of deicing fluids
specific heat capacity of ice (J/kg.°C)
convective heat transfer coefficient (W/(m2.K))
melting latent heat (J/kg)
t time of deicing fluid spraying (min)
A wing surface area (m2)
F fitness function
flow of deicing fluid (L/min)
wing skin height (m)
ice thickness on the wing surface area (m)
characteristic length (m)
M weight of deicing fluids (kg)
Nusselt number
resource consumption of deicing (J)
latent heat required to melt ice (J)
sensible heat required to melt ice (J)
temperature of deicing fluid (°C)
surrounding temperature (K)
surface temperature of the wings (°C)
ε emissivity
η heat exchange efficiency
λ air thermal conductivity (W/(m.K))
density of deicing fluid (kg/m3)
wing skin material density (kg/m3)
density of ice (kg/m3)
σ Stefan–Boltzmann’s constant (W/(m2.K4))
Footnotes
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the Fundamental Research Funds for the Central Universities (grant no. 3122016B004) and the National Key Technology Research and Development Program of China (grant no. 2012BAG04B02).
ORCID iDs: Bin Chen  https://orcid.org/0000-0001-9216-6814
https://orcid.org/0000-0001-9216-6814
Yalei Yang  https://orcid.org/0000-0002-7297-9452
https://orcid.org/0000-0002-7297-9452
References
- 1.Bin C, Liwen W. Model simulation and experiment of aircraft deicing process using deicing fluids on ground. J Syst simul 2012; 24(3): 556–560. [Google Scholar]
- 2.Vigeant-Langlois L, Hansman R, Jr. The influence of icing information on pilot strategies for operating in icing conditions. In: 38th aerospace sciences meeting and exhibit, Reno, NV, 13January2000. [Google Scholar]
- 3.Hill EG. Overview of federal aviation administration aviation safety research for aircraft icing. In: 44th AIAA aerospace sciences meeting and exhibit, Reno, NV, 9–12 January 2006. Reston, VA: AIAA. [Google Scholar]
- 4.Xin L, Bai J, Jun H, et al. A spongy icing model for aircraft icing. Chinese J Aeronaut 2014; 27(1): 40–51. [Google Scholar]
- 5.Gerardi J, Ingram R, Catarella R. A shape memory alloy based de-icing system for aircraft. Aerospace Sciences Meeting & Exhibit 2013; 1–8. doi:10.2514/6.1995-454. [Google Scholar]
- 6.Ornitz SE. A mixed integer nonlinear programming model to optimize the use of aircraft deicing and anti-icing fluids. MSc Thesis, Florida Atlantic University, Boca Raton, FL, 2009. [Google Scholar]
- 7.D’Avirro J, Chaput M. Optimizing the use of aircraft deicing and anti-icing fluids, 2011, http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.260.1071&rep=rep1&type=pdf
- 8.Zouzou A, Louchez P, Bernardin S. Modeling of the draining and freezing of aircraft de-icing and anti-icing fluids. Aerosp Sci Meet Exhib 1998: 15–25. doi:10.2514/6.1998-576 [Google Scholar]
- 9.Chen B, Wang L, Gong R, et al. Numerical simulation and experimental validation of aircraft ground deicing model. Adv Mech Eng 2016; 8(5): 1–15. [Google Scholar]
- 10.Chang S, Ai S, Chen Y. A simulation method of aircraft wing surface icing process. J Syst Simul 2008; 10: 2538–2541. [Google Scholar]
- 11.Huang Y. Study on surface melting snow and heat absorption of solar radiation. PhD Thesis, Jilin University, Jilin, China, 2010. [Google Scholar]
- 12.Wang Q, Zheng M. Thesis of heat transfer. Xi’an, China: Xi’an Jiao Tong University Press, 2006, p. 150. [Google Scholar]
- 13.Hu X, Wu H, Chang C. Analysis of heat and mass transfer. Changsha, China: National Defense Science and Technology University Press, 2011, p. 156. [Google Scholar]
- 14.Giloy EW. An electric deicing system for aircraft. Electr Eng 2013; 69(2): 150–151. [Google Scholar]
- 15.Ge J, Qiu Y, Wu C. A review of genetic algorithms. Computer Appl Res 2008; 25(10): 2911–2916. [Google Scholar]
- 16.Gai K, Qiu M, Zhao H. Cost-aware multimedia data allocation for heterogeneous memory using genetic algorithm in cloud computing. IEEE T Cloud Comput 2016; 1, https://pdfs.semanticscholar.org/8e99/9d58b26d608ffbf8cd09e329084f8f12fa85.pdf?_ga=2.18991664.962852314.1567504491-2131551259.1566452231 [Google Scholar]
- 17.Lei Y, Zhang S. MATLAB genetic algorithm toolbox and its application. 2nd ed.Xi’an, China: Xi’ an University of Electronic Science and Technology Press, 2014, pp. 177–186. [Google Scholar]
- 18.Xu L. Research and application of multi-objective optimization problem based on genetic algorithm. Master’s Thesis, Central South University, China, 2007. [Google Scholar]
- 19.Shi F, Wang H, Yu L. 30 case analysis of MATLAB intelligent algorithm. Beijing, China: Beijing University of Aeronautics and Astronautics Press, 2011, pp. 57–68. [Google Scholar]
- 20.Zhao T, Wang R, Wang P. The application of genetic algorithm in energy-saving optimization control of VAV system. Control Eng 2009; 16(Suppl.): 110–113. [Google Scholar]
- 21.Tohsato Y, Ikuta K, Shionoya A, et al. Parameter optimization and sensitivity analysis for large kinetic models using a real-coded genetic algorithm. Gene 2013; 518: 84–90. [DOI] [PubMed] [Google Scholar]
- 22.Montazeri A, West C, Monk SD, et al. Dynamic modelling and parameter estimation of a hydraulic robot manipulator using a multi-objective genetic algorithm. Int J Control 2017; 90: 661–683. [Google Scholar]
- 23.Liu Y, Ren G, Yu H M. Climatology of snow in China. Geogr Sci 2012; 132(10): 1176–1185. [Google Scholar]