Statistical techniques for predicting rupture risk in abdominal aortic aneurysms: A contribution based on bootstrap

Abstract

The morphometry of abdominal aortic aneurysms (AAA) has been recognized as one of the main factors that may predispose them to rupture. The need to quantify the morphometry of AAA on a patient-specific basis constitutes a valuable tool for assisting in rupture risk prediction. Previous results of this research group have determined the correlations between hemodynamic stresses and aneurysm morphometry by means of the Pearson coefficient. The present work aims to find how the AAA morphology correlates with the hemodynamic stresses acting on the arterial wall. To do so, the potential of the bootstrap technique has been explored. Bootstrap works appropriately in applications where few data are available (13 patient-specific AAA models were simulated). The methodology developed can be considered a contribution to predicting the hemodynamic stresses from the size and shape indices. The present work explores the use of a specific statistical technique (the bootstrap technique) to predict, based on morphological correlations, the patient-specific aneurysm rupture risk, provide greater understanding of this complex phenomenon that can bring about improvements in the clinical management of aneurysmatic patients. The results obtained using the bootstrap technique have greater reliability and robustness than those obtained by regression analysis using the Pearson coefficient, thus allowing to obtain more reliable results from the characteristics of the samples used, such as their small size and high variability. Additionally, it could be an indicator that other indices, such as AAA length, deformation rate, saccular index, and asymmetry, are important.

Introduction

Abdominal Aortic Aneurysm (AAA) consists of a permanent dilation located in the abdominal aorta which is the result of a multifactorial process.

The clinical management of AAA rupture risk is currently based on geometrical indices: the transversal maximum diameter and the diameter growth rate.^1,2 However, using these parameters as a guide for decision-making to define the treatment of aneurismatic patients has not yielded the desired result, which is to accurately predict rupture for all AAAs.^3–5

Other mechanics-based indices have been proposed as better predictors of AAA rupture; namely, mechanical stress, wall stiffness and thickness, the saccular index, the effect of intraluminal thrombus, and aneurysm asymmetry.^6–8 Nevertheless, these indices do not consider the biological factors, so they are not fully correlated with the pathogenesis of AAA, causing implementation difficulties for daily clinical management.

Aneurysm rupture is a manifestation of the balance between the forces exerted by the blood (the hemodynamic stresses) on the arterial wall and the wall’s ability to withstand these forces. So recent studies have shown that mechanical stresses, via peak wall stress, could be a more reliable predictor than the maximum transverse diameter in the prediction of AAA rupture.^8,9 Furthermore, peak wall stress is known to be associated with aneurysm morphology. ¹⁰ Therefore, the spatial-temporal distribution of hemodynamic stress over the arterial wall is directly correlated to AAA morphometry. This link reveals the importance of the morphological and morphometric characterization of AAA for a better understanding of rupture risk. ¹¹ Our previous works^12–15 have shown this evidence. Soudah et al. ¹² and Vilalta-Alonso et al. ¹³ , the hemodynamic stresses were determined using Computational Fluid Dynamics (CFD) and the geometric characterization of the aneurysm was computed by a user-defined algorithm based on the lumen center line. For the geometric characterization, 12 size, and shape indices were defined. Following that, the correlations between AAA morphological characterization and hemodynamic stresses were determined through regression analysis by means of the Pearson coefficient. The statistical analysis confirmed that length, saccular index, and asymmetry significantly influenced the hemodynamic stresses and, consequently, the rupture risk. Superficially, this result seems to be surprising since the diameter of the aneurysm is not within the indices that influence rupture risk. According to the authors, this is coherent with the strategy adopted in the study, which consisted of choosing AAAs in the first stage of development. Seventy percent of the assessed aneurysms had D < 40 mm, so they can be considered small aneurysms and, consequently, there is no rupture risk in the near future. Soudah et al.,^14,15 the importance of the hemodynamic loads on rupture risk prediction were explored using computational intelligence.

Nevertheless, the statistical technique used in these works^12,13 has a limitation when applied to AAA rupture risk prediction. It is characteristic to cardiovascular diseases in general, and AAAs in particular, that the sample size is usually small and correlation analysis works better in applications where the sample is large. The small sample in aneurysmatic patients is due to the fact that the aneurysm is usually detected in advanced stages of development; also, it is well known that the aneurysm growth rate varies due to its initial diameter, with a more rapid growth seen in large aneurysms (50 mm or more). ¹⁶ Thus, taking into account the physical principle governing the aneurysm rupture phenomenon, “aneurysm morphometry is a potential rupture predictor,” as well as our previous results; in this paper, a new approach is explored that consists of applying a bootstrap-statistical technique to determine the relation between aneurysm morphology and hemodynamic stresses (wall shear stress and intraluminal pressure) to assess the rupture risk in AAAs.

Materials and methods

The present work follows the approach of AAA rupture risk prediction by means of statistical techniques. Previous results of the research group^12,13 determined the correlations between hemodynamic stresses and aneurysm morphometry using regression analysis with the Pearson coefficient. In the present study, the main objective is to explore the capability of the Bootstrap technique to appropriately predict AAA rupture risk. The same database, values for hemodynamic stresses and morphological indices, as defined and determined in previous studies, are used to make comparisons easier.

In arterial blood flow, the wall shear stress (WSS) expresses the force per unit area exerted by the wall on the fluid in a direction on the local tangent plane. Circumferential stresses due to blood pressure are transferred to all vessel wall layers (intima, media, and adventitia). On the other hand, shear stress is applied mainly to the inner layer of the arterial wall in contact with the blood, the vascular endothelium. Injury to the endothelium is presumed to be one of the initiating factors in aneurysm formation. Endothelial cells, directly in contact with blood flow under normal conditions, are sensitive to WSS. Abnormalities of the WSS may cause the dysfunction and/or loss of the endothelial layer.

The sample size has been selected trying to have the largest number of cases among those available in the hospital that has participated in the study over 2 years (precisely because the sample size is small, the bootstrap technique has been used). All aneurysms that have undergone a CT scan once they have been detected have been included. Ruptured aneurysms that have undergone a CT scan in the emergency room are excluded.

Details of the methodology used here have been reported previously and are summarized below.

AAA geometry

Lumen segmentation of the AAA surface and geometric reconstruction

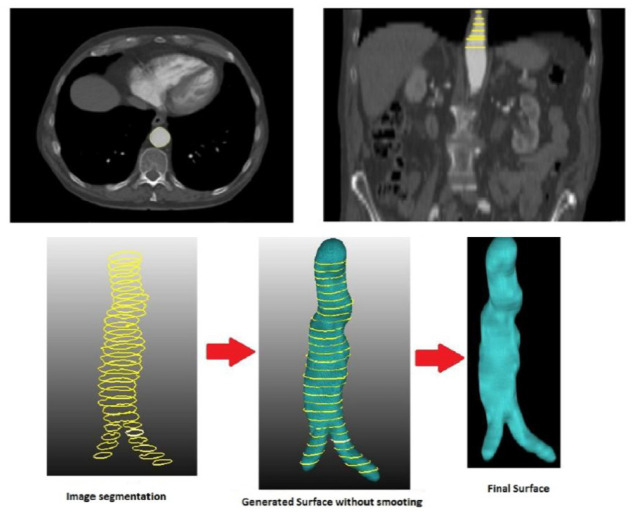
The procedure for AAA reconstruction involves the segmentation of the AAA’s lumen that generates the outside surface of the lumen. Two methods were used to do so: a semi-automatic method based on a level set algorithm executed with VMTK software; and a manual method using MeVisLab software. The first is fairly user friendly, as the user only has to select two internal points within the lumen belonging to extreme slices; whereas the manual method requires a highly experienced user to be able to precisely define the edge of the lumen. This latter method is only considered when it is not possible to use a contrast medium to perform a CT in the patient, or if high deviations are detected between the original CT image and the geometry generated by the semiautomatic segmentation method. Manual segmentation is carried out layer by layer and, once the process has been finalized, the MeVisLab automatically generates the volume in STL format. The smoothing process is the final step, applied through specific algorithms of the VMTK and MeVisLab software, while the generated geometry is stored in STL format. Figure 1 shows the workflow used in this work for AAA segmentation.

Figure 1.

Workflow representing the 3D AAA segmentation of the lumen and the AAA surface using the manual method.

Morphological characterization

In this study, we analyzed thirteen patients, at the Clinical Hospital of Valladolid (Spain), who were in the first phase of development of infrarenal aneurysm. All patients who participated gave their written consent since they were volunteers. In order to characterize the AAA shape and size, the main geometrical parameters were determined by means of a user-defined algorithm based on the lumen center line. For the thirteen AAA patient-specific segmented and reconstructed models, twelve shape and size indices were defined and computed. Figure 2 shows quite a few of these parameters.

Figure 2.

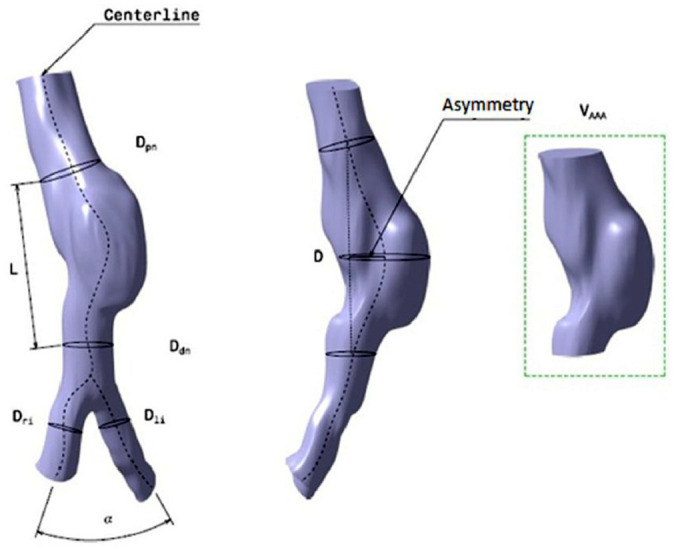
Schematic representation of the mean AAA geometric parameters, based on the lumen center line.

As stated in previous work, ¹³ seven size indices have been defined, as shown in Table 1. They are sorted in two kinds: 1D indices (in mm) and 3D index (in mm³).

Table 1.

Definition of size indices.

Size indices	Index	Definition
Indices 1D (mm)	D	Maximum transverse diameter
	Dpn	Neck proximal diameter (smallest diameter of the infrarenalartery, just before the AAA)
	Ddn	Neck distal diameter (smallest diameter of the aorta,just after the AAA)
	L	Aneurismal length (length between proximal anddistal necks)
	Dli	Left iliac diameter
	Dri	Right iliac diameter
Indices 3D (mm3)	VAAA	Volume of the AAA sac

The shape indices characterize the morphology of AAA. Five shape indices have been defined, and sorted into 2D and 0D indices, as shown in Table 2.

Table 2.

Definition of shape indices.

Shape indices	Index	Definition
Indices 0D	α	Bifurcation angle (the angle between the right and left iliac arteries)
Indices 2D	χ	Deformation rate D/Dpn (characterizes the actual deformation of the aorta, thus constituting a relationship between the maximum diameter of the aneurysm, D, and the proximal neck diameter, Dpn).
	γ	Saccular index D/L (assesses the length of the AAA region, which is the region affected by the formation and further development of the aneurysm, determined by the relationship between D and L).
	T	Tortuosity (the arc-chord ratio; the ratio of the length of the curve to the distance between its ends).
	e	Asymmetry (the result of the non-symmetry expansion of the aneurysm sac as a result of the expansion constraints introduced by the proximity to the spinal column). e = (D-La)/La, where D is the maximum diameter of the aneurysm and La is anterior length measured in the plane of maximum diameter.

Asymmetry, as defined in Table 2, clarify that the value of e decreases (typical values are between 0 and 1), the AAA tends to be more asymmetric. Therefore, e = 1 indicates the complete symmetry of the aneurysm, as shown in Figure 3.

Figure 3.

Asymmetry. e = (D-La)/La, where D is the maximum diameter of the aneurysm and La is anterior length measured in the plane of maximum diameter.

Tables 3 and 4 show the values of the size and shape indices used in this study.

Table 3.

Patient identification and AAA geometrical characteristics.

Patient	1D						3D
	D (mm)	Dpn (mm)	Ddn (mm)	L (mm)	Dli (mm)	Dri (mm)	VAAA (mm3)
A	30.34	19.77	23.36	80.42	14.74	12.50	49,223
B	33.07	26.91	29.70	82.71	15.73	17.62	43,623
C	42.96	20.90	17.82	102.19	12.22	11.85	51,862
D	41.39	24.53	33.56	94.23	18.27	12.32	55,935
E	34.80	20.88	30.35	109.71	20.23	15.16	44,386
F	33.51	20.53	23.92	114.88	15.50	13.01	32,740
G	40.05	32.18	34.86	104.16	23.43	15.67	40,608
H	50.99	24.23	39.33	105.47	14.81	21.45	83,186
I	37.28	23.45	24.28	89.19	11.44	11.45	46,676
J	40.88	25.60	25.90	80.38	9.90	11.18	45,780
K	42.23	22.02	30.15	85.50	21.63	19.94	43,130
L	29.81	20.71	19.00	92.39	15.70	11.88	30,538
M	37.52	33.39	21.66	99.12	12.20	14.80	51,388

Size indices: 1D ande 3D indices.

Table 4.

Patient identification and AAA geometrical characteristics.

Patient	0D	2D
	α (−)	γ (D/L)	χ (D/Dpn)	T (−)	e (−)
A	56.70	0.3773	1.535	0.0389	0.460
B	57.20	0.3998	1.229	0.0222	0.600
C	50.62	0.4204	2.056	0.0140	0.769
D	66.27	0.4392	1.687	0.0308	0.529
E	61.87	0.3172	1.667	0.0660	0.490
F	64.33	0.2917	1.632	0.0147	0.380
G	54.67	0.3845	1.245	0.0383	0.430
H	43.01	0.4835	2.104	0.0445	0.748
I	38.67	0.4180	1.590	0.0645	0.573
J	27.56	0.5086	1.597	0.0817	0.642
K	48.96	0.4939	1.918	0.0409	0.709
L	43.77	0.3227	1.439	0.0655	0.505
M	40.58	0.3785	1.124	0.0343	0.755

Shape indices: 0D and 2D indices.

The quantification of the shape and size of patient-specific AAAs has several benefits. Based on these indices and the wide clinical empirical evidence, there are several criteria for ranking AAAs. However, at present, there is no clinical consensus concerning their use.

Blood flow model and boundary conditions

After AAA segmentation, the 3D computational models were created to simulate and analyze the behavior of the AAA blood flow. The mesh generation software employed was GID. All the meshes in this study were made of tetrahedrons elements with a boundary layer. A mesh sensitivity analysis was carried out (to ensure the accuracy of the simulations) which had an error of less than 3% in the velocity profile for four random cases. For each case, we generated a computational mesh using random element sizes and a boundary layer with a thickness factor of 20% of the arterial radius, three sublayers and a 0.8 sublayer ratio. Depending on the case, the final mesh obtained in each case was between 2,000,000 and 2,500,000 tetrahedral elements. For the 13 acquisitions, the same medical image protocol, image processing and volume mesh technique were used.

In order to compare all cases, we use the same velocity profile and pressure value and profile for all patients (standard case of velocity and pressure in the descending aorta). The blood was considered to be homogeneous and incompressible with a constant-density of 1040 kg/m³; a Newtonian fluid with constant viscosity of 0.004 Pa.s. A transient blood flow was set up in the abdominal aorta (approximately above the infra renal arteries). To properly perform the statistical analysis, the velocity was calculated for each patient in order to get the same total volumetric flow rate of 350 ml for an entire cardiac cycle (inlet boundaries). ¹⁷ A pulsatile waveform pressure was imposed on the common iliac arteries (outlet boundaries). It is important to highlight that these profiles are not patient-specific data (the mapping of Magnetic Resonance velocity was not performed in these subjects), which may be a limitation of this study. In subsequent studies, a specific pressure and velocity profile of the patient will be used as boundary conditions.

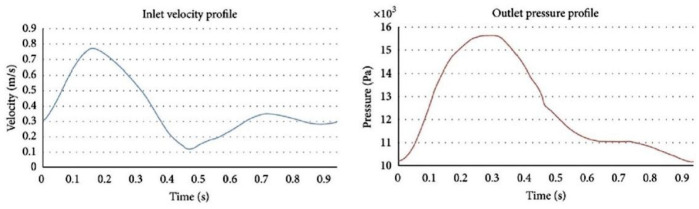
Therefore, to simulate blood flow, we used pulsatile waveforms defined by a UDF (User Define Function) that takes into account the velocity at the inlet boundaries and the pressure at the outlet boundaries, as shown in Figure 4.

Figure 4.

Pulsatile waveforms defined by a UDF (User Define Function) used. Inlet velocity profile and outlet pressure profile.

A user-friendly interface based on the commercial software Tdyn was used to perform the CFD analysis. ¹⁸ Tdyn is a fluid dynamics and multi-physics simulation environment based on the stabilized Finite Element Method that was solved by the Navier–Stokes equations. For each AAA model, the post-processed results were wall shear stress (Peak wall shear stress (PWSS) and the peak intraluminal pressure (PIP) on the aneurysmatic sac) and velocity. As stated above, the hemodynamic stresses are defined by the sum of the PWSS and the PIP, for each point on the aneurysmatic sac and for each simulation time. Three cardiac cycles were simulated and the analyses from the third cycle were extracted.

Statistical analyses: Bootstrap technique

In situations with a small sample size and a high variability among the observations, the assumptions of the theoretical distribution interrelated with the population under study are unknown, so it is desirable to make inferences concerning some of the parameters, as in the situation shown in this investigation. One of the most reliable alternatives for doing this is the Bootstrap technique.

The referential idea presented in Efron ¹⁹ is to build a probability model for determined statisticians based on the information provided by the sample, obviating the assumptions on the theoretical distribution, which are the basis for making inferences concerning the population. In this sense, we suppose that X is a random variable and there is a random sample of size n (x₁, x₂, …, x_n), with a probability distribution function given by $\mathrm{F}$ (x) $=\mathrm{P}({\mathrm{X}}_{\mathrm{i}}\le \mathrm{x}),$ which is written $(x_1,x_2,\dots ,x_n)~\mathrm{F}$ (x), or $\mathrm{x}~\mathrm{F}$ (x) for the sake of simplicity.

When the value of the parameter $\theta$ of a population is unknown and, consequently, it is desirable to use the estimator $\hat{\theta }$  =  $\mathrm{f}$ ( $\mathrm{x}$ ₁, $\mathrm{x}$ ₂, … $\mathrm{x}$ _n, $\theta$ ), the distribution of $\hat{\theta }$ is approximated, generating a set of independent results, $\hat{\theta }$ *b for $\mathrm{b}=1,2,\dots ,\mathrm{B}$ (where B constitutes the number of accomplished re-samples), and forging the empirical distribution function ${\hat{\mathrm{F}}}_{(\mathrm{x})}={\mathrm{F}}_{\mathrm{n}(\mathrm{x})}=\frac{1}{\mathrm{B}}\sum _{\mathrm{i}=1}^{\mathrm{B}}\mathrm{P}({\mathrm{X}}_{\mathrm{i}}\le \mathrm{x}),$ where $\mathrm{P}({\mathrm{X}}_{\mathrm{i}}\le \mathrm{x})=1$ if ${\mathrm{X}}_{\mathrm{i}}\le \mathrm{x}$ and 0 otherwise.

As a result of applying the Bootstrap method, each re-sample will somehow probably be different from the original sample, whereupon a statistician $\hat{\theta }$ *, calculated from one of those re-samples, will take a different value from that produced by another re-sample and from the observed $\hat{\theta }$ . Therefore, according to Mooney and Duval ²⁰ the frequency distribution of those $\hat{\theta }$ *, calculated from the re-samples, is an estimate of the $\hat{\theta }$ sample distribution.

The previous affirmation, which could be considered Bootstrap’s fundamental idea, assumes the use of the sample, considering that, by itself, it contains the basic information of the population; therefore, adjusting this method the more information about the population the sample contributes to will be so much better. A direct consequence is that the estimate obtained on the sample distribution of a statistician will improve as the size of the sample increases. Nevertheless, even with small samples, between 10 and 20 cases, the Bootstrap method can offer correct results, ²¹ though it is unsuitable for samples with a size lower than 5. ²²

There are authors ²³ who use two-step Bayesian inference models for the prediction of AAA growth, and complement them with the estimates of the distributions through resampling using Markov Chains Monte Carlo (MCMC). Although the work with the models is different from that proposed in this paper, as it is based on obtaining probabilities by the Bayesian method, there are no major differences in the fact of resampled data used to obviate the theoretical consideration of their original distribution.

Patient images are routinely used for teaching, training, and clinical research. General Medical Council (GMC) guidance is clear that confidentiality is a central tenet in patient care, that appropriate information sharing is also important and that a means to share such information without consent is through anonymization. So, explicit consent is only required if the patient is, or may be, identifiable.

Anonymous CT images were used for the study, so it is not necessary Ethics statement and Consent Statement.

Results

Correlation analysis methodology: Correlation between PWSS and D

A total of 13 patient-specific AAA models were simulated in this study. The correlation study and the results presented here are based on the application of the bootstrap techniques.

From the computational results, the PWSS values ranged between 0.414 and 17.60 Pa, also, since there is a slight asymmetry in the data obtained the median value, which is 4.51 Pa, is used. The PIP values ranged between 15,815 and 16,565 Pa, and as there is no asymmetry in the data obtained, the mean value, which is 16,185 Pa, is used.

Next, the correlation analysis performed using this method is shown. This method, more than an isolated application, lends itself to being combined with other statistical techniques to complement other applications to estimate problems, adjust regression models, contrast hypotheses, and analyses principal components, among others. ²⁴ In addition, to cite only a few instances, applications have dealt with correlation coefficients,^25,26 factorial analysis ²⁷ or structural equation models.^28–30

In this study, the Bootstrap methodology is applied to correlation analysis, which was carried out for each of the hemodynamic parameters and the defined geometric indexes. Due to the high number of variable pairs to study, and the fact that the Bootstrap methodology is analogous for all the analyses; we decided to explain the procedure and exemplify for the pair of variables PWSS and D. The remaining results with their interpretation are summarized later. The study was carried out in the following stages.

• (1) From the original sample, a new sample of equal size is extracted by means of random sampling with replacement. In this way, each individual observation has a probability of 1/n of being selected each time.

In Table 5, the first obtained subsample is shown; while, for each value of a re-sampled PWSS, its original value of D is matched, keeping the integrity of each observation.

Table 5.

Values of the original samples and first bootstrap resamples.

Models	Original sample		First resample
	PWSS (Pa)	D (mm)	PWSS (Pa)	D (mm)
A	3.190	30.34	6.471	37.28
B	0.414	33.07	4.420	42.96
C	4.420	42.96	11.020	40.05
D	6.100	41.39	6.290	40.88
E	13.200	34.80	0.414	33.07
F	17.600	33.51	4.507	37.52
G	11.020	40.05	3.380	50.99
H	3.380	50.99	4.215	29.81
I	6.470	37.28	3.380	50.99
J	6.290	40.88	13.200	34.80
K	2.169	42.23	17.600	33.51
L	4.215	29.81	3.380	50.99
M	4.507	37.52	2.169	42.23

• (2) For the obtained sample, the value of the Pearson’s coefficient correlation (r) is calculated. The value for the original sample is −0.17 and that of the first subsample is −0.36.

• (3) The two previous steps are repeated until a high number of estimates are obtained.

Theoretically, the magnitude of B in practice depends on the tests to be applied to the data. In Efron and Tibshirani ²⁴ it is affirmed that B should be between 50 and 200 in order to estimate the typical error of $\theta$ and at least 1000 to estimate confidence intervals around $\hat{\theta }$ by the percentile method. In general, with B = 1000, good results are usually obtained and values over 5000 do not add any advantage. ³¹

• (4) The function of the statistician’s empirical distribution is then built, which represents a good approximation to the real probability distribution for that statistician.

Then the estimator’s mean and its confidence interval are calculated.

The mean of all values of r was calculated as follows:

$$\hat{\mathrm{r}}=\frac{1}{1000}\sum _{\mathrm{b}=1}^{1000}{\hat{\mathrm{r}}}_{\mathrm{b}}^{*}=-0.143$$ (1)

The percentile method was used to conform the confidence interval, since it is used as a non-parametric variant when the variable parameters at population level are unknown, as in this case. The limits of the interval were calculated as follows, using a 90% level of confidence:

$$\hat{\mathrm{r}}*\left(\mathrm{inferior}\right)<r<\hat{\mathrm{r}}*\left(\mathrm{superior}\right)$$ (2)

With the inferior limit being B(α/2) and the superior limit B(1–α/2): 

$${{\hat{\mathrm{r}}}^{*}}_{50}<r<{{\hat{\mathrm{r}}}^{*}}_{950}$$ (3)

The values corresponding to the inferior and superior limits of the interval were obtained by ordering the values of r in increasing order and selecting those corresponding to observations 50 and 950, as follows:

$$-0.672<r<0.404$$ (4)

In this case, the calculated confidence interval contains the value zero, and it can be inferred that there is no significant correlation between PWSS and D for the 10% significance. This result, although unexpected, is in agreement with those obtained in Vilalta-Alonso et al. ¹³ and it is also consistent with the initial strategy of simulating AAAs which can be considered small (D < 40 mm) and, thus, with no rupture risk. Although cases of aneurysm rupture with maximum diameter values below 50–55 mm are known, the result is in accordance with the criteria currently used in the medical field, since 70% of aneurysm cases that have been studied are significantly below those values. Therefore, small aneurysms can be considered and, consequently, there is no risk of rupture in the coming months.

Correlation analysis of the peak wall shear stress (PWSS) versus size andshape indices

The analysis of the mean values of r of the Bootstrap re-samples (see Table 6) for each of the size and shape indices shows that the indices that significantly correlate to the 10% with the PWSS are Length (L), asymmetry (e), and saccular index (γ). The obtained results are similar to those previously reported, ¹³ but with greater reliability due to the use of the proposed method, among the advantages of which is precisely its utilization in situations as those shown here.

Table 6.

Correlations of PWSS versus different AAA morphological indices 1D, 3D, 2D, and 0D.

		PWSS
		Mean values of r	Lower limit	Upper limit
Indices 1D	D	−0.142	−0.671	0.404
	Dpn	−0.076	−0.566	0.645
	Ddn	0.059	−0.374	0.545
	L	0.686	0.211	0.923
	Dli	0.248	−0.469	0.719
	Dri	−0.266	−0.369	0.266
Indices 3D	VAAA	−0.359	−0.758	0.125
Indices 2D	χ (D/Dpn)	−0.058	−0.555	0.448
	γ (D/L)	−0.539	−0.870	0.083
	T	0.032	−0.607	0.734
	e	−0.617	−0.885	−0.146
Indices 0D	α	0.369	−0.329	0.763

Correlation analysis of the peak intraluminal pressure (PIP) versus indices 1D, 3D, 2D, and 0D

The analysis of the mean values of r of the Bootstrap re-samples (see Table 7) for each of the geometric indices show that the indices that significantly correlate to the 10% with PIP are Length (L), asymmetry (e), and the right iliac diameter (Dri). The obtained results are similar to those previously studied, ¹³ but with greater reliability due to the use of the proposed method.

Table 7.

Correlations of PIP versus indices 1D, 3D, 2D, and 0D.

		PIP
		Mean values of r	Lower limit	Upper limit
Indices 1D	D	−0.073	−0.511	0.460
	Dpn	0.138	−0.544	0.648
	Ddn	−0.244	−0–646	0.222
	L	0.526	0–097	0.828
	Dli	−0.161	−0.858	0.489
	Dri	−0.488	−0.803	−0.103
Indices 3D	VAAA	−0.234	−0.669	0.232
Indices 2D	D/Dpn (χ)	−0.178	−0.687	0.430
	D/L (γ)	−0.405	−0.788	0.145
	T	−0.032	−0.618	0.628
	e	−0.407	−0.744	−0.042
Indices 0D	α	0.019	−0.521	0.523

One of the main problems related to the definition of a numerical indicator for AAA rupture risk prediction is associated to the information available for studying the evolution, and possible rupture, of aneurysms.

As is well known, the size of the data for aneurysmatic patients is really small for various reasons. This pathology is usually detected in an advanced stage of development; therefore, its maximum transverse diameter will usually be larger than 50 mm. In this case, the aneurysm is considered to be large with a high rupture risk. In cases where the aneurysm is detected in an early stage, clinical management establishes a follow-up treatment consisting of one check-up per year. As the aneurysm’s growth rate can be fast, mainly when the maximum diameter is higher, no more than 2–3 CT scans are expected for these patients.

Discussion

The present work explores the use of a specific statistical technique (the bootstrap technique) to predict, based on morphological correlations, the patient-specific aneurysm rupture risk, provide greater understanding of this complex phenomenon that can bring about improvements in the clinical management of aneurysmatic patients.

It is well known that the bootstrap-statistical technique works well in applications with few available data, as in our case. Our hypothesis is that the results obtained from using this statistical technique will, in future steps and with more theoretical basics, allow us to achieve the accurate prediction of rupture risk, thus improving the clinical management of aneurismatic patients.

The results obtained have greater reliability and robustness than those obtained by means of the classic correlation analysis.

The hemodynamic stress (PWSS + PIP) is correlated with the asymmetry and aneurysm length.

In different studies, the aneurysm asymmetry has been suggested as one of the most relevant indices in rupture risk prediction. There are basically two kinds of AAA: saccular (aneurysms with asymmetry value tending to 0) and fusiform (aneurysms with asymmetry value close to 1). Most aneurysms are saccular and, in the present study, almost 77% are of this kind. The behavior of the blood flow within the aneurysmatic sac and, consequently, the temporal and spatial distribution of hemodynamic stresses, are characterized by the morphology of the AAAs, that is, by their shape. As the aneurysm loses asymmetry, the posterior wall becomes flatter due to the restriction imposed by the column, which induces significant changes in the flow field. Because of this, regions of recirculation arise near the proximal neck that pushes the central blood jet toward the posterior wall, provoking a high stress concentration on the said wall that is the most probable site of rupture.

According to our results, the correlations between the asymmetry and the hemodynamic stresses are negative; this means that those AAA with lower values of asymmetry (quantitative indicator tending to zero, according to Kleinstreur and Li ³² and Vilalta et al. ³³ ) have higher hemodynamic stresses and, consequently, a higher rupture risk.

The aneurism length is associated to rupture risk by two parameters: by itself and by the saccular index. The correlation between hemodynamic stress and L is positive, that is, as the aneurysm length is higher, the aneurysm rupture risk increases concomitantly. On the other hand, the saccular index reflects the relation between two simple but important geometric parameters of the aneurysm: the maximum diameter D and the length L. If we consider the individual relationships between D and L with the hemodynamic stresses discussed above, a significant weight of the saccular index on the hemodynamic stress prediction is to be expected.

The correlation between the saccular index and the hemodynamic stresses is negative, i.e., when a patient-specific aneurysm has small saccular index values, according to, Kleinstreur and Li ³² and Vilalta et al. ³³ the rupture risk is higher. In the present study, all models have small values for the saccular index (see Table 4) and, therefore, high mechanical loads on the arterial wall are to be expected.

Finally, the results found in this study showed the correlation between Dri and PIP. The existing data about this index as a rupture risk indicator is scarce, and are mostly based on case reports and small retrospective series without any relevant conclusion. The fact that Dri is one of the indices that influences the AAA rupture risk can be attributed to two factors. The first is associated to the greater frequency of aneurysms in the right iliac as opposed to the left iliac.^34,35 However, the direct relation between the existence of AAA and iliac artery aneurysm, the well known second aneurysm, has been verified.

One of the most important aspects when it comes to predicting and/or prognostic the AAAs rupture risk through correlations obtained by statistical and computational techniques is the validation of these results, that is if these correlations are capable of correctly predicting the rupture. In the study presented here, there is no model indicating ruptured aneurysm in the database used, and the main morphological and hemodynamic indicators that are associated with the rupture risk are the AAA diameter and the PWSS. By using different strategies to consider and classify patient groups with (low or high) risk of rupture and different statistical and computational techniques, recent studies have confirmed our results.

Leemans et al. ³⁶ some biomechanical metric, among which are aneurysm diameter, PWSS and wall stiffness, were compared for asymptomatic and symptomatic/ruptured AAA group and a random effects model was used to calculate the standard mean differences (SMDs) with 95% confidence interval. The results showed that PWSS is high in the symptomatic/ruptured group, with SMD of 1.11 (95% CI, p < 0.001) and, by means of controlled studies for D, it was demonstrated the correlation between D and PWSS for the same group. Logistic regression model to compute the probability of aneurysm progressing incorporating the lumen volume and WSS was used to study the enlargement of AAA in a sample of 81 patients. ³⁷ 50 patients were used as a derivation group for predicting the probability of growth at 1 year and they were divided into stable (<10-mL increase in aneurysm volume) and unstable (>10-mL increase in aneurysm volume) groups. For all patients, AAA characteristics were analyzed. The results were validated by a cohort with 31 patients. The main finding of this work is that the combined analysis proposed is better than AAA maximum diameter in isolation for predicting the growth of aneurysm with D < 50 mm.

Approaching the studying about markers for characterizing the AAA growth, a model for anticipate the aneurysm evolution toward rupture by using local correlations between hemodynamics indices and AAA growth it was built. ³⁸ In this work, the population was divided into three groups: control cases without AAAs (one is a woman and eight are men), cases with AAA but considered at low-risk, and cases with AAA at high-risk. Of the aneurysmatic patients population participating in the study, 5 are women and 27 are men. The authors computed the potential correlation between the different groups by a Welch’s t-test. From a clinical point of view, the results show that morphological metrics (D, lumen volume among others) can improve risk prediction greatly, but risk prediction works best by combining all metrics (variables hemodynamics, morphological, and clinical). According the authors, the information obtained by means of the developed risk predictors allows anticipating if the patient will evolve to a high-risk state or stay at low-risk in the foreseeable future, from the information at a given time. Similar results have been obtained by using computational techniques as machine learning, ³⁹ artificial intelligence. ⁴⁰

In the present study, some of the AAA models have a second aneurysm in the aortic iliac, so it can be assumed that this index is in some way relevant.

Also, most of the models studied have iliac diameter values higher than the threshold (20–25 mm), so it can be affirmed that aneurysms exist.

We hypothesize that, among the indices defined in this work that are correlated with the risk of rupture, the right iliac diameter is the one with the smallest weight. This index is not correlated with PWSS, which is recognized as an important indicator of the risk of rupture.

Vilalta-Alonso et al. ¹³ it is stressed that the results are, in general, consistent with other published results and have a strong theoretical basis. As pointed out in Martufi et al. ⁴¹ , it is unlikely that only one of the proposed geometric indices, in isolation, would be a reliable index for rupture risk prediction and future studies can be directed toward this end.

The theoretical foundations of the Bootstraps technique are clear with regard to its application in problems with a small number of samples, as in the pathology studied here, and that is demonstrated by the results obtained in this work. However, the work has some limitations mainly associated with the research strategy used. The main limitations are:

1. In the sample used, there is no include any case with ruptured aneurysm.

2. Database did not include some patient-specific information like age, gender, blood pressure, flow profile, medication information, and patient history. From a statistical point of view, the effectiveness of the use of a bootstrap methodology would not be affected by expanding the study. Bootstrap is not a specific technique, it is a general technique or methodology that allows using the information available in the data, dispensing with the external help of models or theoretical assumptions, avoiding the limitations of the classical statistical approach. It involves using the sample considering that it itself contains the basic information about the population and non-compliance with this aspect could be its only limitation. For that reason a sample size/power analysis was not performed in this study.

Conclusions

With the objective of improving our understanding of the AAA rupture risk phenomenon and its accurate prediction, a bootstrap-based correlation technique was applied. The use of the bootstrap-based correlation technique allows more reliable results to be obtained from the characteristics of the samples used, such as their small size and high variability, as well as the lack of information on the theoretical distribution of the population. The results obtained have greater reliability and robustness than those obtained by regression analysis using the Pearson coefficient and could be an indicator that other indices such as AAA length, deformation rate, saccular index, and asymmetry could also readily be incorporated into a surgeon’s decision-making. The bootstrap-based correlation technique used in this work can be considered a new methodology to predict the hemodynamic stresses from size and shape indices.

Author biographies

Félix Nieto-Palomo PhD in Mechanical Engineering. Received the MEng in 1999 and the Ph.D in 2016 in the Mechanical Engineering program from the University of Valladolid (Spain), where he is an Associate Professor at the Department of Mechanical Engineering. Working in CARTIF for over 10 years, he was a Project Manager and R&D engineer with expertise leading and participating in several National and European R&D projects. Currently he is the manager of IDECAL and the head of R & D department. Research on FEA (Finite Element Analysis), biomechanical systems and design of special machines. He has several papers in JCR-indexed journals, Conference papers and 6 patents.

María-Ángeles Pérez-Rueda received the MS and PhD degrees, both in Mechanical Engineering, from the University of Valladolid (Spain), in 1993 and 2000, respectively. She is Associate Professor. Since 1996, she is member of research Institute ITAP (Advanced Production Technologies Institute of the University of Valladolid). Scientific Advisor of the Mechanical Engineering Division of technological center CARTIF Foundation since July 2010. Her research interest are biomechanical systems, binary hyper-redundant manipulator (BHRM) for biomedical applications and dual quaternions.

Laurentiu-Mihai Lipsa is a Mechanical Engineer by the Faculty of Machine Manufacturing and Industrial Management, Gheorghe Asachi - Technical University of Iasi, Romania, 1998-2003. He obtained the Advanced Studies Diploma at the University of Valladolid in 2007. Full-time researcher in Manufacturing Processes Area of the Mechanical Engineering Division of CARTIF. The main area of activity is related to prototypes and industrial machines mechanical design and dynamic simulation. He is using design, simulation and calculation software as Catia, Inventor, MSC Adams, SolidWorks. He is participating as an inventor in several patents and is co-author in publications related to biomechanics like the influence of the geometry of abdominal aortic aneurysms in blood flow dynamics and the possibilities of rupture.

Carlos Vaquero-Puerta is a Full Professor of the University of Valladolid. Spain. Head of Service of Angiology and Vascular Surgery of the University Hospital of Valladolid. Spain. Author and director of 35 investigation projects financed by national and foreign public and private institutions. Publications of 19 Books, 129 Book Chapters, 493 Papers in International and Spanish Journals, 417 lectures in national and international institutions. Director of 92 Doctoral Theses (Doctorate Program, PhD University of Valladolid).

José-Alberto Vilalta -Alonso is an Industrial Engineer, Doctor in Technical Sciences and professor at the Technological University of Havana “José Antonio Echeverria”, Cujae. His academic and scientific areas of action are statistical analysis of data for decision-making and quality management.

Guillermo Vilalta-Alonso received his PhD in Mechanical Engineering in 2000 from University of São Paulo/Brazil. Since 2012 he serves as Associate Professor in the Thermal Sciences and Fluids Department/Federal University of São João del-Rei/Brazil. His research interests focus on computational modelling of fluids with different rheological behavior and on theory and applications in turbomachinery.

Eduardo Soudah-Prieto is a PhD in Biomedical Engineering from Universidad Politécnica de Cataluña (Spain). Dr. Soudah leads the Biomedical Group at the International Center for Numerical Methods in Engineering (CIMNE). My main research area is linking computational medical image and finite elements methods to create virtual medical models. My major challenge is to integrate my knowledge gained on computational medical image and computational methods into robust and fully reliable computer models and “in silico” environments that will help the development and testing of new therapies and better disease prediction and prevention tools, in healthcare.