Leaf-individual calibration for a double stack multileaf collimator in photon radiotherapy

Highlights

• •Leaf-individual multi-leaf collimator calibration increased treatment accuracy of double-stack multi-leaf-collimator.
• •Positional accuracy depended on gantry angle, leaf travel direction and single multi-leaf-collimator stack.
• •The presented method resulted in sub-millimeter multi-leaf-collimator positioning accuracy.

Abstract

Background and Purpose

In online adaptive stereotactic body radiotherapy treatments, linear accelerator delivery accuracy is essential. Recently introduced double stack multileaf collimators (MLCs) have new facets in their calibration. We established a radiation-based leaf-individual calibration (LIMCA) method for double stack MLCs.

Materials and Methods

MLC leaf positions were evaluated from four cardinal angles with test patterns at measurement positions throughout the radiation field on EBT3 radiochromic film for each single stack. The accuracy of the method and repeatability of the results were assessed. The effect of MLC positioning errors was characterized for a measured output factor curve and a clinical patient plan.

Results

All positions in the motor step – position calibration file were optimized in the established LIMCA method. The resulting double stack mean accuracy for all angles was 0.2 ± 0.1 mm for X1 (left bank) and 0.2 ± 0.2 mm for X2 (right bank). The accuracy of the leaf position evaluation was 0.2 mm (95% confidence level). The MLC calibration remained stable over four months. Small MLC leaf position errors (e.g. 1.2 mm field size reduction) resulted in important dose errors (−5.8 %) for small quadratic fields of 0.83 × 0.83 cm². Single stack position accuracy was essential for highly modulated treatment plans.

Conclusions

LIMCA is a new double stack MLC calibration method that increases treatment accuracy from four angles and for all moving leaves.

1. Introduction

Several photon radiotherapy treatment delivery machines comprise of recently introduced double stack multileaf collimators (MLCs) [1], [2]. Literature on the specific properties of this essential beam limiting device is still sparse [3]. The magnetic resonance (MR)-Linac is a new treatment delivery device that is capable of acquiring magnetic resonance images during treatment and performing treatment adaption while the patient is on the table [4], [5]. The MR-Linac is often utilized for high-dose, high-precision treatments in close proximity to organs at risk [6], [7], [8], [9].

The emergence of this technology poses a number of risks associated with the new process that lacks the possibility for traditional quality assurance measures such as pre-irradiation measurements [10], and further risks are associated with new mechanical parts, such as the double stack MLC. Several measures such as failure mode and effects analysis [11], patient-specific recalculations with independent secondary dose calculation algorithms [12], [13] and software tools to check important plan parameters of each patient treatment plan have been implemented for the adaptive process [14], [15].

However, these tools are unsuitable to detect any effects of machine uncertainties and plan deliverability issues related to the MLC. Several possible problems with MLC leaf position accuracy, reproducibility and dependence on leaf travel direction have been described [16]. Consequently, Linac delivery accuracy assessment and the related MLC characterization, calibration and quality assurance is of paramount importance.

In this study, we described the development and implementation of a leaf-individual MLC calibration (LIMCA) method and the resulting accuracy of the double stack MLC. The accuracy of the method and repeatability of the results were assessed. Further, we characterized the effect of MLC positioning errors for a measured output factor curve and a clinical patient plan in intensity modulated treatment planning.

2. Materials and Method

The technical design of the 0.35 T MR-Linac double stack MLC has been described in detail [2], [3]. The upper stack (MLC1) has in total 34 leaf pairs, with 30 being movable on left (X1) and right (X2) banks, whereas the lower stack (MLC2) has in total 35 leaf pairs with 29 being movable on each bank. The MLC stacks are mounted on a ring gantry and deliver intensity modulated radiotherapy (IMRT) treatments from all angles except 30° to 33° [17]. Additional information on the MLC and the vendor calibration procedure can be found in supplementary materials.

2.1. LIMCA procedure

The experimental design was similar to previously reported MLC quality assurance measurements [16]. All measurements were conducted with Gafchromic EBT3 radiochromic film of 30 × 30 cm² size in an RW3 slab phantom at source-to-surface distance 85 cm and in 5 cm depth. The MLC position was determined by irradiating stripes that were limited by all leaves of X1 and X2 bank (Y-length 24.1 cm) either of a single MLC stack or of both MLC stacks. Since there may be dependence of leaf position on direction of travel (hysteresis), all stripes were either limited by closing leaves (out-in) or by opening leaves (in-out) depending on the plan. To define leaf travel direction, a larger (out-in) or smaller (in-out) field was irradiated with 1 to 2 monitor units (MU) before irradiating the stripes of intended field size with 400 to 700 MU, compensating the flattening filter free Linac output. The possible number of film irradiations with different parameters was large: at least three (upper, lower and double stack) times multiplied by (cardinal angles) multiplied by two (in-out and out-in) films before and after LIMCA resulting in 48 films. Therefore, LIMCA took steps to make informed decisions about the reduction of film exposure. It was part of the procedure to guide the operator to an optimal MLC calibration with efficient use of resources.

Films were scanned with a Vidar Dosimetry Pro Advantage (RED) Scanner (Vidar Systems Corporation, Herndon, VA, USA) with a resolution of 0.09 mm in landscape direction [18] and calibrated by a red channel calibration using eight dose values and PTW (PTW-Freiburg, Freiburg, Germany) Mephysto software.

The evaluation was performed by an in-house written Matlab R2021a (The MathWorks, Inc., Natick, MA, USA) script. The script imported the calibrated digitized film image and performed a noise reduction (5x5 median filter). It determined the center position of the central stripe by finding the maximum values in X and Y to start analysis of profiles along the leaf travel direction (X). Central axis (CAX) deviation was defined as the difference between the center of the two full width half maximum (FWHM) (X1, X2) of the stripe and the reference position. Planned MLC leaf positions of the irradiated plan in the treatment planning system (TPS) served as reference positions. The center positions in Y-direction of each leaf for upper, lower or double stack measurements were stored within the code as well as the reference leaf travel X-positions for the selected plan.

Considering film rotation correction, average CAX deviations of five leaves from the top and five leaves from the bottom end of the two outer stripes on the film were found. The rotational angle between top and bottom ends was determined, averaged for the two stripes and applied to the film as rotational correction.

The double stack MLC has no absolute zero position that can be determined by collimator or jaws, laser markers on the film are not sufficiently precise and there is no way to place a radio-opaque marker on the Linac head. Therefore, the zero position of the film was determined by averaging CAX deviations of the central and the two outer fields. Translation as well as rotation could be corrected afterwards by the user. In this way, rotations as small as 0.02° and translations smaller than 0.1 mm were corrected.

Once the zero position of the film was determined, X-profiles were placed through the center of each leaf and MLC leaf positions were evaluated at each stripe’s position. The resulting CAX deviations, field sizes and left and right positioning differences of each leaf at each position were displayed.

2.2. Step 1: Hysteresis

We irradiated four films from gantry angle 0° (G0) which comprised of nine 1 × 24.1 cm² stripes: Upper stack in-out and out-in and lower stack in-out and out-in. In case of small hysteresis, the calibration procedure was described for in-out mode, thereby saving eight films. If hysteresis were larger, all sixteen in-out and out-in film measurements (four angles, upper and lower stack) could be performed in step 2 and considered in the position corrections.

2.3. Step 2: Angle-dependent position corrections for upper stack and lower stack

At this stage, small fields close to the reference positions in the motor step – position calibration file were irradiated for upper and lower stack for four cardinal gantry angles (G0, G90, G180, G270). Each of the eight films comprised of nine 1 cm wide fields, bounded by all movable leaves of the respective MLC stack at positions −13, −9.9, −6.6, −3.3, 0, 3.3, 6.6, 9.9, 13 cm (Fig. 1a). 1 cm small fields were chosen in order to be able to track all calibration file positions on one film.

Fig. 1.

a) and c) Film measurements during LIMCA. b) Motor step – position calibration depicted for one leaf in the X1 bank. The points mark the calibration positions in the file.

The differences between reference position and measured position were averaged across all angles for all leaves at all positions and added (same sign) to the position in the calibration file (Fig. 1b). The central (X = 0) calibration positions for all leaves were left unchanged.

2.4. Step 3: Field size & Double stack

The 1 cm wide fields have no lateral electron equilibrium on the central ray for 6 MV photons and are therefore considered small fields. This implies that the nominal field size is not equal to the measured field size. To ensure that field size requirements were met, three films were irradiated from G0: double stack, upper MLC and lower MLC. Each film comprised of five fields that were 2 cm wide and bounded by all movable leaves of the respective stack at positions X = −12, −6, 0, +6 and +12 cm (Fig. 1c). If upper and lower stack MLC field sizes were too small, fields could be opened in X1 and X2 direction. If only double stack field sizes were too small, MLC offset, that is positional agreement between upper stack and lower stack, should be verified. Provided this was optimal, X1 and X2 for both stacks could be adjusted.

2.5. Model of MLC calibration errors

To gain a better understanding of the importance of MLC calibration, a measured output factor curve was modeled with a hyperbolic fit function and dose delivery uncertainties were determined in dependence of field size respective MLC error [19].

In order to model a worst-case scenario, a highly modulated patient plan with a relatively small target volume (51 cm³) was recalculated with the clinical TPS using a 0.3 cm dose grid, 0.5 % statistical uncertainty and incorporating the magnetic field. Retrospective data analysis was approved by the ethics committee of the University Hospital (S-543/2018). The calculation settings comprised of a 0.3 cm dose grid and 0.5 % uncertainty in the planning target volume (PTV), considering the magnetic field. The plan featured 13 MLC segments smaller than 1 cm² delivering 27.8 % of the monitor units. Each leaf of the upper MLC was intentionally mispositioned by 0.6 mm (decreasing field sizes by 1.2 mm). PTV dose volume histogram parameter differences of D_95%, D_mean, D_1% and V_110% between original and recalculated plan were compared.

2.6. Accuracy and repeatability

After LIMCA, positioning accuracy was verified for all angles with double stack MLC measurements. These measurements were repeated bi-weekly from one angle for longitudinal quality assurance.

To assess the accuracy of the method, a plan was irradiated twice and the two films were evaluated independently. Detection accuracy was tested by intentional mispositioning of a four-leaf pattern in the motor step calibration file and evaluation.

All of the resulting mean positional differences were stated as mean of the absolute values ± one standard deviation.

3. Results

3.1. Step 1: Hysteresis

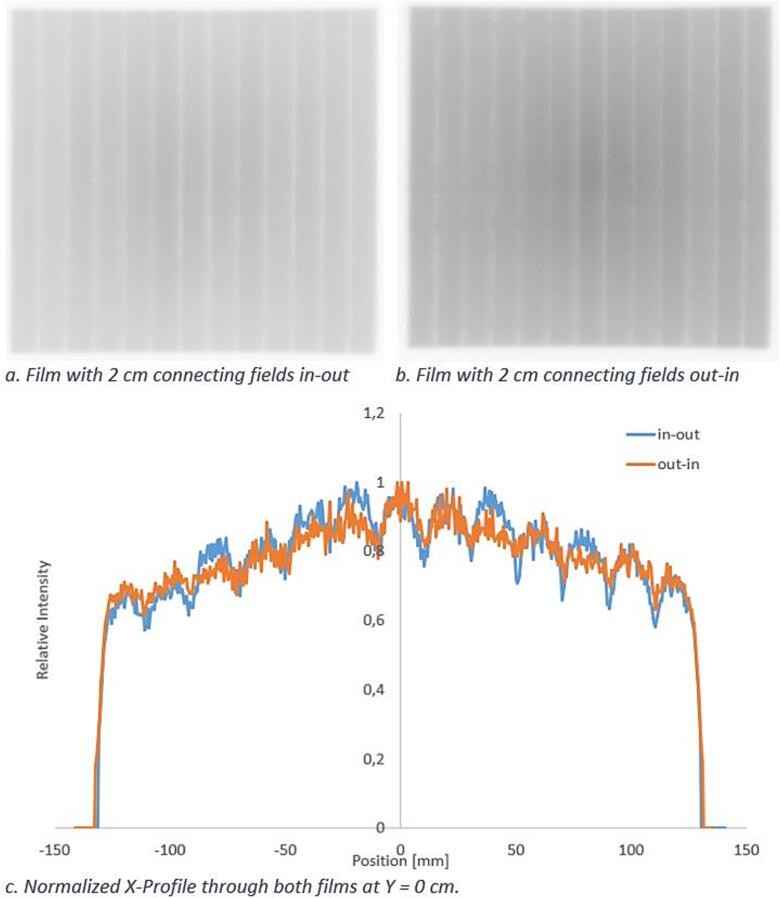
Average hysteresis was smaller than 0.3 mm for each of the leaf banks. For the inner positions between [-6.6, 6.6] cm the hysteresis was smaller than 0.5 mm (95% quantile). Fig. 2 shows a qualitative evaluation of hysteresis after LIMCA.

Fig. 2.

Qualitative evaluation of hysteresis from G0. Visual inspection of the connecting fields revealed only small differences between in-out and out-in film measurements. The fields measured from G0 were smaller because fields from G90, G270 and G180 tended to open for the studied double stack MLC. Comparing Fig. 2a with Fig. 2b, it was visible that the stripe width did not change substantially with leaf travel direction.

3.2. Steps 2 & 3: Angle-dependent and field size position corrections for upper stack and lower stack

For upper stack and lower stack from G0, Fig. 3 shows the suboptimal situation of leaf calibration before LIMCA was performed. The deviations were smaller for G0 than for G180.

Fig. 3.

Vendor calibration upper stack (a) and lower stack (b) average positioning differences [mm] from all angles. Of the nine measurement positions, five are shown (step 2). Green: absolute position difference smaller than 0.5 mm, Yellow: absolute position difference smaller than 1 mm, Red: absolute position difference larger than 1 mm. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

As a result of step two, the leaves were changed in position by up to 0.9 mm, on average by 0.2 mm. In step three, X1 was opened by 0.3 mm and X2 was opened by 0.4 mm for both stacks.

The resulting accuracy after LIMCA is shown in Fig. 4. The lowest leaf of X2 (leaf 4) showed irregular behavior and was therefore excluded from average analysis. The resulting double stack mean accuracy for all angles was 0.17 mm for X1 and 0.20 mm for X2. The average double stack field size for 20 mm fields was 19.6 mm for G0, 20.0 mm from G90, 20.2 mm from G180 and 19.9 mm from G270.

Fig. 4.

Post calibration double stack average positioning differences [mm] from all angles (step 3). Green: absolute position difference smaller than 0.5 mm, Yellow: absolute position difference smaller than 1 mm, Red: absolute position difference larger than 1 mm. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.3. Model of MLC calibration errors

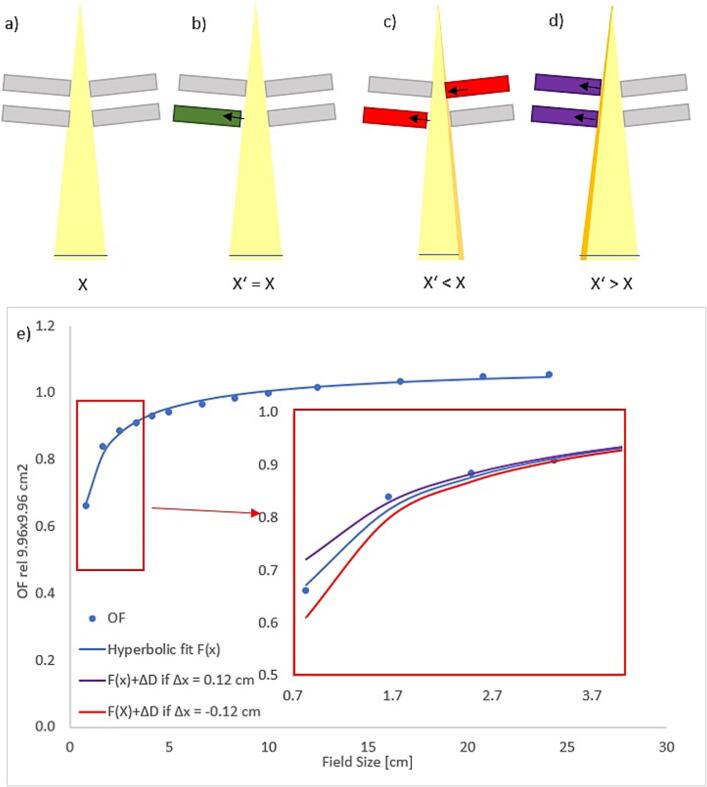
Fig. 5e shows the relationship between field size accuracy and dose accuracy extracted from output factor measurements fitted with a hyperbolic fit function. Considering our measured output factor curve, a 1.2 mm field size error lead to a dose deviation of −5.8 % for 0.83 × 0.83 cm² fields, which equaled a misposition of only 0.6 mm on each MLC bank.

Fig. 5.

a) Schematic representation of the MLC with upper stack and lower stack in perfect position (not to scale). X = isocenter plane field size. b) One side of the lower MLC stack opens but isocenter plane field size remains stable. c) One side of the upper stack closes and isocenter plane field size decreases. d) Both upper stack and lower stack X1 banks open and isocenter plane field size increases. e) Output factor changes caused by 0.12 cm field size changes for quadratic fields.

For the patient plan with mis-calibrated upper stack MLC leaves, PTV D_95% decreased by −6.0 %. PTV D_mean decreased by −3.5 %, PTV D_1% decreased by −3.1 % and PTV V_110% decreased by −13.7%. The dose distributions and dose volume histogram are shown in Fig. 6.

Fig. 6.

Patient plan comparison for upper stack de-calibrated leaves. a) Dose distribution of the clinical treatment plan. b) Dose distribution with upper stack de-calibrated leaves. c) Segment of the clinical treatment plan. d) Segment with upper stack field sizes decreased by 1.2 mm. Green: lower stack. Grey: upper stack. Blue: double stack. e) Comparison of the dose volume histograms of the plans. Dotted: Clinical plan. Line: de-calibrated plan. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.4. Accuracy and repeatability

The accuracy of the method as defined by repeated measurement and evaluation was 0.2 mm (95% confidence level). An intentional mispositioning of 2 mm of two leaves lead to a measured deviation of 1.7 mm.

Repeatability of the calibrated MLC positions was assessed over a time frame of four months, showing stable and repeatable behavior with deviations of smaller than 0.2 mm for 95 % of leaf positions (max 0.36 mm) when double stack measurements were performed.

4. Discussion

For radiotherapy treatment delivery machines with a double stack MLC, LIMCA was able to reduce overall positioning errors from four gantry angles and for all individual leaves throughout the radiation field. Through optimizing all MLC calibration positions, LIMCA reduced dose delivery uncertainties and errors.

Instead of only relying on the evaluation of combined double stack fields at seven positions from three angles (as described in supplementary materials), we performed a detailed analysis of a large number of MLC positions. Due to the staggered MLC stack design, round IMRT fields are often limited by only one MLC stack (see Fig. 6c), thus emphasizing the need for optimal single stack calibration precision.

The employed method (picket fence) is not new nor specific for double stack MLCs but was presented before [16] and can be considered a standard MLC quality assurance procedure. In contrast to the treatment delivery machines in previous works [1], [20], [21], the MR-Linac does neither include a flat panel detector nor visible light fields, therefore, all MLC calibration procedures after installation had to be performed with external detectors. It has been shown that it is feasible to perform double stack MLC quality assurance with a 2D ion chamber array [22], but for calibration measurements we selected film as the detector of choice because of its superior spatial resolution [23].

Guidelines for stereotactic IMRT treatments recommend MLC errors smaller than 1 mm for position accuracy and repeatability [24]. Nevertheless, many radiotherapy groups aim at a much higher spatial accuracy of the MLC of up to 0.3 mm [20], [21]. Several groups have presented MLC calibration techniques performed with film, arrays or water tank scans that resulted in sub-millimeter accuracy as LIMCA did [20], [21], [25]. Bayouth et al [16] and Zwan et al [26] have assessed MLC position accuracy dependence on leaf direction of travel and gantry angle, respectively. Cai et al [3] and Lim et al [1] have characterized the two commercially available double stack MLCs. A recent publication described Y-bank alignment of the double stack MLC in detail [27]. However, this is, to our knowledge, the first work to present a double stack calibration including gantry angle and hysteresis assessment.

A specific property of the MR-Linac MLC is that the zero position cannot be determined through collimator rotations [16], [20], [25]. The LIMCA procedure is therefore somewhat circular since CAX deviations of the fields were used to apply positional corrections and certain issues, such as rotation or an erroneous zero position of both stacks, cannot be detected through LIMCA but have to be excluded through different measures. This presupposed, LIMCAs rotation and translation positioning procedure intentionally at most underestimates necessary positioning corrections.

LIMCA’s accuracy is limited by film scan and evaluation uncertainties. Depending on the required accuracy, films can be saved for example by ignoring hysteresis effects as we described. Hysteresis has not yet been considered for positional corrections.

LIMCA relies on the assumption that all errors visible from the four cardinal angles are equally relevant. We assumed the measurements of cardinal angles were relevant for a 90-degree range and that leaf behavior was linear and that no interpolation between calibration positions in the motor step – position MLC calibration file and measured positions was necessary.

During MLC offset adjustment, it is impossible to align MLC2 perfectly from G180. Accordingly, resulting double stack fields tend to be smaller than single stack fields, especially at G ≠ 0. This can be included in LIMCA’s position corrections. Unavoidable misalignment (tenths of millimeters) between upper stack and lower stack tends to lead to smaller fields because the inner leaf defines the field edge. Increasing MLC offset accuracy remains to be investigated outside of the scope of this work.

If a single MLC stack limits the treatment field, the relationship from Fig. 5d can be directly applied. When both stacks limit the field, it has to be considered that the smaller stack will define the field size (see Fig. 5a–c). Therefore, there is a four times increased possibility that the field size error Δx is smaller than zero assuming that the error sign is equally distributed for both stacks.

Treatment plans at our institution use up to 30 % of monitor units delivered through segments that are smaller than 1 cm² [14]. Vendor protocols define that field size accuracy should be better than 2 mm for both X1 and X2 bank (1 mm tolerance for each bank). Calculated dose changes within the patient that result from mis-calibrated leaves emphasize the importance of an accurate single stack calibration.

Single stack and hysteresis measurements will be repeated quarterly to ensure stability. As next steps, the hanging leaf position differences may be corrected and hysteresis effects can be minimized for the leaves that show larger differences using the presented LIMCA method. Using the presented methods on other treatment delivery machines comprising of a double stack MLC can be explored, as several manufacturers now employ a double stack MLC on their treatment delivery machines.

This work is the first to assess a double stack MLC not simplified as one stack, but to differentiate the effects of the combination of two single stacks, such as smaller field size for offsets between the two stacks and the effects of single stack positioning errors. It was shown that the former approach is not sufficient, but that depending on the resulting MLC openings after beam sequencing, single stack positioning errors can have relevant effects.

In conclusion, LIMCA resulted in increased MLC position accuracy on the 0.35T MR-Linac. The resulting double stack mean accuracy for all cardinal angles was 0.2 ± 0.1 mm for X1 and 0.2 ± 0.2 mm for X2. It marks an important step towards MR-guided high precision stereotactic body radiotherapy and stereotactic radiosurgery treatments.

Funding information

The MR-Linac was kindly funded by the German Research Foundation DFG, Grant/Award Number: DE 614/16-1. For the publication fee we acknowledge financial support by Deutsche Forschungsgemeinschaft within the funding programme ‘Open Access Publikationskosten’ as well as by Heidelberg University.

CRediT authorship contribution statement

Carolin Rippke: Conceptualization, Methodology, Software, Validation, Formal analysis, Data curation, Writing – original draft, Writing – review & editing, Visualization, Project administration. C. Katharina Renkamp: Conceptualization, Methodology, Resources, Formal analysis, Investigation, Writing – review & editing, Supervision, Project administration. Charbel Attieh: Investigation, Writing – review & editing. Fabian Schlüter: Investigation, Conceptualization, Methodology, Resources. Carolin Buchele: Investigation, Conceptualization, Methodology, Resources. Jürgen Debus: Resources, Supervision, Funding acquisition. Markus Alber: Conceptualization, Methodology, Writing – review & editing, Supervision, Funding acquisition. Sebastian Klüter: Conceptualization, Methodology, Resources, Writing – review & editing, Supervision, Project administration, Funding acquisition.

Declaration of Competing Interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: The authors declare the following financial interests / personal relationships that may be considered as potential competing interests: JD received grants from CRI – The Clinical Research Institute GmbH, ViewRay Inc., Accuray International, Accuray Incorporated, RaySearch Laboratories AB, Vision RT limited, Astellas Pharma GmbH, Merck Serono GmbH, Astra Zeneca GmbH, Solution Akademie GmbH, Ergomed PLC Surrey Research Park, Siemens Healthcare GmbH, Quintiles GmbH, Pharmaceutical Research Associates GmbH, Boehringer Ingelheim Pharma GmbH Co, PTW-Freiburg Dr. Pychlau GmbH, Nanobiotix A.A. as well as IntraOP Medical, all outside the submitted work. MA receives royalties from Elekta AB and is owner of Scientific RT GmbH, all outside the submitted work. SK has received speaker fees and travel reimbursement from ViewRay Inc. outside the submitted work.

Appendix A. Supplementary data

The following are the Supplementary data to this article: