Abstract
Small extracellular vesicles (EVs) have emerged as a focal point of EV research due to their significant role in a wide range of physiological and pathological processes within living systems. However, uncertainties about the nature of these vesicles have added considerable complexity to the already difficult task of developing EV‐based diagnostics and therapeutics. Whereas small EVs have been shown to be negatively charged, their surface charge has not yet been properly quantified. This gap in knowledge has made it challenging to fully understand the nature of these particles and the way they interact with one another, and with other biological structures like cells. Most published studies have evaluated EV charge by focusing on zeta potential calculated using classical theoretical approaches. However, these approaches tend to underestimate zeta potential at the nanoscale. Moreover, zeta potential alone cannot provide a complete picture of the electrical properties of small EVs since it ignores the effect of ions that bind tightly to the surface of these particles. The absence of validated methods to accurately estimate the actual surface charge (electrical valence) and determine the zeta potential of EVs is a significant knowledge gap, as it limits the development of effective label‐free methods for EV isolation and detection. In this study, for the first time, we show how the electrical charge of small EVs can be more accurately determined by accounting for the impact of tightly bound ions. This was accomplished by measuring the electrophoretic mobility of EVs, and then analytically correlating the measured values to their charge in the form of zeta potential and electrical valence. In contrast to the currently used theoretical expressions, the employed analytical method in this study enabled a more accurate estimation of EV surface charge, which will facilitate the development of EV‐based diagnostic and therapeutic applications.
Keywords: charged nanoparticle, electrical properties, electrical valence, exosomes, extracellular vesicle isolation, small extracellular vesicles, surface characterization, surface charge, zeta potential
1. INTRODUCTION
Recent years have witnessed the rapid development of technologies for the characterization, manipulation, separation, and detection of heterogeneous populations of small extracellular vesicles (EVs) (Liang et al., 2021; Guo et al., 2018; Betzer et al., 2020; Lin et al., 2021). Small EVs are nanosized (<200 nm in diameter), spherical, membrane‐enclosed structures generated by cells, and can be found in almost all bodily fluids (e.g., blood, urine, and saliva) (Kalluri & LeBleu, 2020; Zhao et al., 2018; Doyle & Wang, 2019). For clarity and simplicity, this study uses the term 'small EVs' to refer to the vesicles isolated from the cell culture supernatant in alignment with the Minimal Information for Studies of Extracellular Vesicles 2018 (MISEV2018) guidelines (Théry et al., 2018).
Small EVs contain a substantial number of bioactive molecules (e.g., nucleic acids, proteins, and lipids) that they transfer among cells, thereby forming the basis of an intricate intercellular communication network that contributes to almost all physiological events and pathological processes (Ailuno et al., 2020; Matsumura et al., 2019; Yates et al.,2022a,2022b). The ability of EVs to travel/home to different parts of the body and cross biological barriers, including cell membranes, illustrates the enormous potential these particles may have for use in therapeutic applications, such as vaccine and drug/gene delivery (Bunggulawa et al., 2018; Kim et al., 2017; Y. Yang et al., 2018). Small EVs engineered to contain specific bioactive molecules have been reported to successfully transport their cargo to recipient cells (G. Liang et al., 2020; Y. Liang, Duan, et al., 2021). These vesicles can also exhibit characteristics which support their use for early diagnosis of diseases (Correll et al., 2022; Zhou et al., 2020). For instance, it has been extensively reported that small EVs derived from cancer cells exhibit surface markers and content characteristic of their cell of origin, thereby serving as diagnostic and prognostic indicators for different types of cancer (J.Zhang et al., 2020; Min et al., 2019). Although the potential of small EVs as diagnostic and therapeutic tools is being extensively studied, the true nature of these vesicles, and the exact ways in which they interact with each other and target substrates (e.g., recipient cells), have yet to be fully elucidated, posing a challenge to the development of EV‐based applications.
The development of clinically acceptable EV‐based applications requires a full understanding of their physical and biochemical properties. A very important, yet often overlooked, physical characteristic of EVs is their electrical charge, which dictates electrostatic interactions of these vesicles within colloidal systems like bodily fluids. The electrostatic properties of small EVs can affect their stability within bodily fluids, which is an important consideration when developing EV‐based therapeutics (Cha et al., 2009; S. Kumar & Sharma, 2020; Y. Wang et al., 2017). Indeed, the electrostatic properties of EVs can influence the outcome of EV‐protein and EV‐EV interactions (e.g., aggregation) while in transit, and ultimately, the ability of EVs to reach and successfully interact with target cells. In addition, pre‐screening and mapping of surface charge distribution on small EVs isolated from patient bodily fluids may serve as potential indicators for disease diagnosis (Akagi et al., 2015; Feng et al., 2021; Matsumura et al., 2019). For instance, in a study by Akagi et al. (2014), it was reported that the surface charge of small EVs secreted from cancer cells was significantly larger than that measured for small EVs secreted from normal cells. Whereas EV‐related electrostatic influences within biological systems are well‐appreciated, investigation of these electrostatic interactions in a dispersed system (e.g., bodily fluids) is quite complex due in large part to a lack of comprehensive understanding regarding the electrical charge of small EVs.
Investigation of the electrical characteristics of small EVs, including their surface charge distribution, may also lead to the development of much‐needed new technologies in the rapidly burgeoning field of EV research (Diaz‐Armas et al., 2022; Hassanpour Tamrin et al., 2021). The key challenges impeding the clinical utility of small EVs are the inability to efficiently isolate pure population of small EVs from other unwanted components in bodily fluids, and limitations associated with quantitative analysis of vesicles with high accuracy and reproducibility (Diaz‐Armas et al., 2022; Y. Kang et al., 2019). For example, the majority of advances in isolation, detection, and characterization of small EVs are label‐based approaches that require capture molecules (e.g., antibodies and aptamers) to target these vesicles. These capture molecules potentially contaminate EVs and alter their properties, thereby negatively impacting downstream analyses and their reliability for clinical applications (Gonzalez et al., 2021; Y. T. Kang et al., 2017). In contrast, focusing on the physical properties of small EVs (e.g., electrical surface charge) for the development of label‐free isolation techniques supports the maintenance of native characteristics of isolated EVs along with advantages in terms of cost, time, process simplicity and reproducibility (Hassanpour Tamrin et al., 2021; Shi et al., 2019; Y. Zhang et al., 2022). However, the majority of label‐free isolation techniques are still plagued by limitations resulting from the lack of validated methods to define the driving forces of processes in which the electrostatic contribution of small EVs is determinative, such as electrical‐based isolation methods (Hassanpour Tamrin et al., 2021; Diaz‐Armas et al., 2022). Knowledge about the surface charge of small EVs will better facilitate the development of novel, and more efficient isolation methods that advance efforts related to EV‐based applications.
Although a number of investigations have been undertaken to determine the electrical charges carried by nanosized biological particles (bionanoparticles) (Duran‐Meza et al., 2021 ; Leung et al., 2009; Michen & Graule, 2010), the actual surface potential of small EVs and a proper theoretical derivation enabling quantitative analysis of their surface charge have not yet been reported. Given the increasing importance of small EVs in clinical applications, there is a pressing need to establish an appropriate theoretical and experimental framework that enables the comprehensive characterization of the electrical properties of these vesicles. Figure 1 shows the structure of an ionic cloud around small EVs as a negatively charged structure and schematically describes the distribution of electric potential in an electrolyte solution. When small EVs are exposed to an electrolyte, a specific interfacial region is formed on the surface of these vesicles owing to the electrostatic interaction between their charged surface and the surrounding ions (Gokarn et al., 2011; Grimez & Liapis, 2001). This specific interfacial region, referred to as an electric double layer (EDL) (Ohshima et al., 1982; H. Wang & Pilon, 2011), is composed of two parallel layers of ions that surround a charged object; the Stern layer and the diffuse layer, wherein oppositely charged ions attract each other to form each layer (Henderson & Boda, 2009; H. Wang & Pilon, 2011). Ions in the Stern layer are tightly associated with the surface of small EVs, whereas ions in the diffuse layer move freely in the surrounding fluid and form a hydrodynamic boundary around the vesicles. To the best of our knowledge, most EV charge‐related studies available in the literature have reported a parameter known as zeta potential (ζ‐potential) (Kaddour et al., 2020; Mendivil‐alvarado et al., 2023; Gitlin et al., 2006). As shown in Figure 1, ζ‐potential is defined as the electric potential at the slip plane, and describes colloidal particle stability (Fuller & Koper, 2018; Lazzari et al., 2012). Whereas the ζ‐potential may be sufficient to give an idea of the stability and dispersion of small EVs, this parameter alone cannot provide a complete picture of actual surface charge (represented in terms of electrical valence or surface charge density). The reason is that the ζ‐potential does not consider the ions tightly associated with the particle surface, and therefore, the measured magnitude is smaller than the actual surface potential of the particle. In addition, interpreting the surface charge of nanosized particles including bionanoparticles presents a challenge due to the considerable shielding effect of the ionic cloud at the nanoscale. Given the small size of small EVs (<200 nm), the shielding effect of the ionic cloud around these vesicles is significant, but not considered within classical theoretical expressions that describe electrical valence or electric potential at the nanoscale.
FIGURE 1.
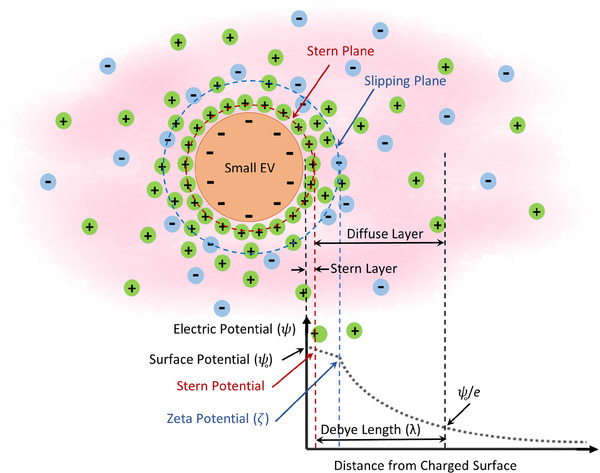
Distribution of electric potential in an electrolyte surrounding a charged particle including small EVs. The electric potential (ψ) decays away from the charged surface as a function of distance due to the formation of the electric double layer (EDL) which is composed of two parallel layers of ions surrounding a charged object: Stern layer and diffuse layer (Dukhin & Goetz, 2010). The thickness of the EDL is usually given at a distance termed as Debye length (λ), where the electric potential decreases in magnitude by e−1 of its maximum value (ψ0) (Ohshima, 2014; Dukhin & Goetz, 2010). The Stern plane is the interface separating the ions tightly associated with the particle surface (ions within the Stern layer) from the ions within the diffuse layer. The slip plane is the interface between the mobile phase of the surrounding electrolyte and the static phase of the electrolyte remaining attached to the particle, where the relative velocity of electrolyte to the particle is zero.
To quantify the surface charge of a particle in the form of either electrical valence or electric potential, the charged structure of the particle and the associated electrostatic forces should be experimentally explored when the particle is immersed in an electrolyte solution. Electrophoretic mobility (EM) measurements have been extensively reported as a powerful method to investigate the electrostatic properties of charged colloidal particles. EM defines the velocity of a charged particle under the effect of a uniform electric field. Indeed, EM is an experimental quantity measurable through different electrophoretic methods including capillary electrophoresis (Woken & Arriaga, 2014; Milanova et al., 2011), electrophoretic light scattering (Carvalho et al., 2018; Strand et al., 2001) and membrane‐confined electrophoresis (Filoti et al., 2015; Moody & Shepard, 2004). Regardless of the strengths and limitations of each measurement technique, a proper theoretical expression is required to correlate the obtained EM to a quantitative estimate of the particle surface charge (electrical valence or electric potential). To obtain an accurate representation of the surface charge, all possible limitations of each theoretical expression (relating EM and surface charge) should be carefully considered in their use for bionanoparticles (e.g., small EVs, proteins, and other bioactive molecules). Indeed, the critical question should be whether the currently used theoretical approximations are accurately applicable for all sorts of particles, even for bionanoparticles, or if extra considerations are needed to contemplate the shielding effect of the ionic cloud, a phenomenon called Debye shielding. There is no doubt that the main concern when investigating the surface charge of small EVs, and one which demands immediate attention, is to establish an appropriate theoretical expression for charge determination while taking into account the Debye shielding effect around these vesicles. Nevertheless, most published studies evaluating the charge of EVs have predominantly focused on ζ‐potential (Midekessa et al., 2020; Mendivil‐Alvarado et al., 2023). Importantly, ζ‐potential values continue to be determined primarily using classical theoretical approaches that tend to underestimate the ζ‐potential at the nanoscale. Additionally, relying solely on ζ‐potential cannot provide a comprehensive understanding of the electrical properties of small EVs, as it overlooks the influence of ions that tightly bind to the surface of these vesicles, thereby undermining the ability to accurately estimate their surface charge (electrical valence). This knowledge gap represents a substantial obstacle to fully understanding EV behavior, and has impeded the development of new, more effective techniques for the isolation, detection, and characterization of these vesicles.
In this study, two classical theoretical expressions (Smoluchowski's approximation and Hückel's approximation) (Ohshima, 1994; Bazant et al., 2009; Kilic et al., 2007), which are commonly used approximations for estimating the electrical properties of spherical particles, along with the contemporary analytical method developed by Ohshima and co‐workers (Kilic et al., 2007; Makino & Ohshima, 2010; Ohshima, 2001) were examined to appropriately determine surface charge of small EVs. Ohshima's analytical solution is the most predictive model for very small particles, and enables approximation of ζ‐potential and surface charge density while accommodating the important term of Debye shielding at the nanoscale (see detailed theoretical framework in Appendices) (Makino & Ohshima, 2010; Ohshima et al.,1982). The accuracy of this model has been validated based on published data for different colloidal particles including cells (Kinraide & Wang, 2010; Kinraide et al., 1998), gold nanoparticles (Makino & Ohshima, 2010; Agnihotri et al., 2009), and lipid bilayer structures like liposomes (Chibowski & Szczes, 2016), as well as bovine serum albumin (BSA) and human serum albumin (HSA) proteins (Jachimska et al., 2008; Tanford et al., 1955; Russell et al., 2016). Given the published data available for the protein charge estimates, this study used HSA protein as a candidate reference particle to investigate the accuracy of the three mentioned theoretical expressions (Smoluchowski's, Hückel's, and Ohshima's approximations) for determining the surface charge of bionanoparticles. Here, we (i) introduce a conceptual model to simulate the structure of ion distribution around a charged particle and to understand the EV‐electrolyte interface in a more systematic way; (ii) discuss parameters influencing EM of small EVs to provide sufficient working knowledge for EM measurement in a meaningful way; (iii) discuss different analytical methods and their precision to correlate the obtained EM to a quantitative estimate of EV charge in the form of electrical valence (or surface charge density) and ζ‐potential; (iv) introduce the most predictive analytics model for EV charge determination that maximizes interpretability and scientific value for electrical valence and ζ‐potential while overcoming common problems associated with classical analytical methods; (v) accurately determine ζ‐potential, surface charge density, and electrical valence of small EVs based on their EM values measured using dynamic light scattering (DLS). This study provides the most complete characterization to date of the electrical properties of bionanoparticles, including small EVs.
2. MATERIALS AND METHODS
2.1. Reagents and chemicals
Sodium chloride (NaCl; FW 58.44, ACS reagent, ≥ 99%), hydrochloric acid (HCl; ACS reagent, 37%), sodium hydroxide (NaOH, 10.0 N), protease inhibitors cocktail (Set III, EDTA‐Free), and radioimmunoprecipitation assay (RIPA) lysis buffer were purchased from Sigma‐Aldrich (Millipore Sigma, Canada). Human serum albumin (HSA, 100 μg.μL−1) and Dulbecco's phosphate‐buffered saline (10X PBS) were purchased from Invitrocare (Invitrocare Inc.) and Thermo Fisher (Thermo Fisher Scientific, Canada), respectively.
2.2. Cell culture
Adipose‐derived mesenchymal stem cells (AMSCs) were cultured to isolate small EV fractions from the culture supernatant. AMSCs were ethically obtained according to protocols approved by the Conjoint Health Research Ethics Board at the University of Calgary, and cultured using established cell culture methods developed at the Pharmaceutical Production Research Facility (PPRF) (Jung et al., 2010). AMSCs were statically cultured in PPRF‐msc6 medium while incubated at 37°C and in a humidified atmosphere containing 5% carbon dioxide. Tissue culture flasks with cell growth areas of 75 cm2 (T‐75) were coated with 0.1% gelatin and utilized to expand AMSCs in static culture (flasks were inoculated at 5000 cells.cm−2). Culture supernatant was collected every 72 h while the cells were passaged into a fresh medium. As determined using trypan blue exclusion, the number of viable cells during EV harvesting was 2.1 × 105 cells per mL of culture supernatant, with a cell viability rate of 98%. The morphology of cells was assessed using light microscopy (supplementary information, Figure S1). It should be noted that the fresh PPRF‐msc6 medium was examined for the size distribution of particles present, as well as the fraction of particles expressing tetraspanin proteins CD9, CD81, and CD63 (supplementary information, Figure S2 and Figure S3). This examination was conducted to ensure that fresh medium does not contain any EVs, or small EV‐sized particles, and thus could be used as a negative control. The DLS results confirmed that while the characterization of suspensions of nanoparticles with a narrow size distribution (tested in an experimental group of silica nanoparticles, Figure S2) could be easily performed, it remains challenging to characterize the size distribution of polydisperse solutions such as fresh PPRF‐msc6 medium and culture supernatant, which contain various particles and aggregated proteins.
2.3. Small EV isolation
Culture supernatant was collected after the cells were cultured for 72 h, and then processed by differential centrifugation, followed by ultracentrifugation to obtain EV‐enriched fractions (Livshts et al., 2015; Yu et al., 2018). Given that ultracentrifugation does not provide a completely pure population of small EVs, this study uses the term EV‐enriched fraction (containing small EVs along with varying amounts of impurities such as protein aggregates and lipids) to refer to the isolated small EVs. Figure 2 represents the procedure for obtaining EV‐enriched fractions in this study. The collected culture supernatant was centrifuged at 2,000 g and 4°C for 10 min (Thermo Scientific Sorvall Legend XT Centrifuge, TX‐750 rotor), and then at 10,000 g and 4°C for 30 min (Thermo Scientific Sorvall RC‐5C Plus Centrifuge, HS‐4 rotor) to remove residual cellular components and large particles like apoptotic bodies and larger microvesicles. The resulting supernatant was transferred into the ultracentrifuge tubes and diluted with cold PBS (1X) in a 1:1 ratio, and then ultracentrifuged at 100,000 g and 4°C for 2 h (Beckman Coulter Optima L‐100K Ultracentrifuge, 70 Ti rotor, k factor = 148) to obtain EV pellets. Since the ultracentrifuge tubes may collapse if not filled adequately, which limits EV recovery, all tubes were filled to a sufficient volume of 24 mL. The supernatant was discarded while the isolated EV pellet was re‐suspended in PBS (1X) and then stored at −80°C for later analysis. It should be noted that all relevant data of our experiments have been submitted to the EV‐TRACK knowledgebase (EV‐TRACK ID: EV230958) with the corresponding EV‐METRIC score of 67%.
FIGURE 2.
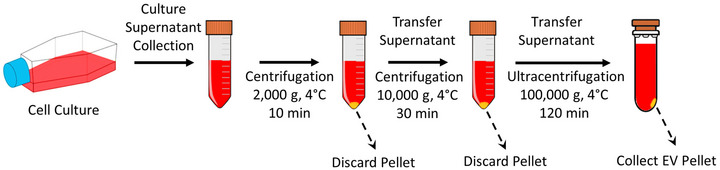
Flow chart of the procedure used to obtain EV‐enriched fractions using differential centrifugation and ultracentrifugation. Following cell culture preparation, the culture supernatant was collected and underwent a set of centrifugation steps at progressively higher spin speeds. First, large particles including dead cells, cell debris, and apoptotic bodies were removed using two differential centrifugation steps (2,000 g and 10,000 g). Then, EV‐enriched fractions were separated from smaller contaminants such as proteins, using ultracentrifugation (100,000 g).
2.4. Protein quantification
The protein content of all samples was measured using a bicinchoninic acid (BCA) protein assay (Pierce BCA Protein Assay kit, Thermo Fisher Scientific, Canada) according to the standard manufacturer protocols. Briefly, each sample (25 μL) was mixed with a working reagent (200 μL, 50:1 ratio of assay reagents A to B) and transferred to a 96‐well plate, which was then incubated for 30 min at 37°C. After cooling to room temperature, sample absorbance was measured using a spectrophotometer (BioTek Synergy HTX Multi‐Mode Microplate Reader) at 562 nm and converted to protein concentration (μg.mL−1) via a standard curve. To quantify EV‐enclosed proteins, isolated EV‐enriched fractions were lysed by adding RIPA buffer (containing 25 mM Tris‐HCl pH 7.6, 150 mM NaCl, 1% NP‐40, 1% sodium deoxycholate, and 0.1% SDS), followed by incubation at 4°C for 1 h and vortexing for 45 s, to release the protein content of isolated small EVs which was then measured by BCA assay. To prevent the proteolysis of proteins and maintain the phosphorylation status of the enclosed proteins, 10 μL protease inhibitor cocktail solution was mixed with 1 mL of RIPA lysis buffer prior to use. All reagents and instruments were pre‐cooled to minimize protein degradation. Pure PBS (1X) and RIPA buffer samples were used as the controls to confirm the absence of proteins for the background measurements. To examine the purity of the isolated EV‐enriched fractions, the concentration of free proteins (impurities) within the samples was measured before and after the isolation. At least three sets of measurements were performed for each sample.
2.5. Single particle interferometric reflectance imaging sensor (SP‐IRIS) analysis
Samples containing isolated EV‐enriched fractions were characterized based on the expression level of EV markers on a single vesicle basis using SP‐IRIS technology. SP‐IRIS is a multiplexed assay for the immuno‐capture of EVs on a microarray chip followed by digital detection of the captured vesicles by an interferometric imaging technique. Isolated EV‐enriched fractions were diluted with PBS (1X) and an ExoView R100 (NanoView Biosciences, Boston, MA) was utilized for particle counts of EV markers CD81, CD63, and CD9 using standard manufacturer protocols. Additional cargo analyses were carried out to determine the portion of particles expressing internal EV marker syntenin‐1 and negative marker GRP94. Briefly, samples were diluted with incubation buffer (supplied by NanoView Biosciences) and incubated on antibody‐coated chips overnight (18 h) at room temperature. After incubation, the chips were washed and stained with corresponding antibodies, and then placed into the automated reader to count the individual small EVs immune‐captured on each chip. For cargo analyses, the samples were first permeabilized prior to staining. All antibodies, washing and staining reagents were supplied by NanoView Biosciences. The SP‐IRIS examination of fresh PPRF‐msc6 medium, as a control group, confirmed there were no EVs in the fresh culture medium. The colocalization pie charts, as shown in Figure S3, indicate the absence of particles expressing two or more EV‐specific markers. It is important to note that the charts also demonstrate some non‐specific binding associated with ExoView chips, due to the presence of free proteins and their aggregates in the fresh medium.
2.6. Transmission electron microscopy (TEM) analysis
Isolated EV pellets, obtained after ultracentrifugation, were resuspended in PBS (EV‐enriched fractions obtained from 15 mL of culture supernatant were resuspended in 50 μL of PBS), and a 10–20 μL drop of the resulting EV dispersion was loaded onto parafilm. A formvar copper mesh grid was placed on top of each sample drop and incubated at room temperature for 30 min. Next, EV samples were fixed with 2.5% glutaraldehyde for 15 min, and then washed with distilled water for 5 min. Samples were then negatively stained using 2.6% uranyl acetate for about 30 seconds, washed with distilled water for 5 min, and dried at room temperature for 45 min. Finally, samples were imaged with a Hitachi transmission electron microscope (Hitachi H‐7650: 120 kV TEM, Hitachi High‐Tech, Tokyo, JP) at an accelerating voltage of 80 kV.
2.7. Dynamic light scattering (DLS) analysis
A Zetasizer Nano ZS (Malvern Instruments Ltd., Cambridge, UK) was utilized to measure EM and size distribution of particles using an established DLS technique. Under the effect of a uniform electric field applied across a pair of electrodes located at both sides of a capillary containing sample solution, DLS automatically determines EM of a charged particle as the ratio of particle velocity to the applied electric field strength. All measurements were conducted under similar experimental conditions of applied voltage (148 volts employed across a pair of electrodes within the Zetasizer cell), electrolyte viscosity (0.887 cP) and ionic strength (≤20 mM). To maintain the electrodes of the Zetasizer cell in an unsaturated state during the measurements and to minimize measurement errors, all particle samples (proteins and small EVs) were dispersed in diluted PBS (γ < 4.5 mS.cm−1). Considering that an electrolyte solution with low ionic strength is the main assumption in Ohshima's analytical method for determination of surface charge, the ionic strength of the sample solutions was kept as low as 20 mM during EM measurement (Virtanen et al., 2014; Palberg et al., 2004; Reiber et al., 2007). The mobility values were measured at different pH conditions (acidic pH of 3.5 and 4.5, neutral pH of 7.5, and basic pH of 10.5). The temperature was set to 25.0 ± 0.1°C. At least three sets of measurements were performed for each sample. The recorded data were analyzed using Zetasizer Software 7.12 (Malvern Instruments Ltd). Buffer solutions of hydrochloric acid (1N HCl) and sodium hydroxide (1N NaOH) were used to adjust pH, and a benchtop pH meter (Fisherbrand™ accumet™ AB150 pH Benchtop Meters) was used to measure the pH values for each electrolyte solution. Prior to conducting DLS examination of EV samples, ζ‐potential and size measurements were conducted in control groups (PBS with and without silica nanoparticles), as shown in Figure S2 (supplementary information).
2.8. ζ‐potential and electrical valence calculations
From the measured EM values, ζ‐potential of the isolated EV‐enriched fractions were calculated using three different theoretical approaches: (i) Hückel's approximation (Equation B6, Appendix B), (ii) Smoluchowski's approximation (Equation B7, Appendix B), and (iii) Ohshima's approximation (Equation B8, Appendix B). The measured EM values for the isolated small EVs were also converted into corresponding electrical valence values using three different estimations: (i) effective valence (Zeff , Equation B9, Appendix B), (ii) Debye‐Hückel‐Henry valence (ZDHH , Equation B10, Appendix B), and (iii) electrical valence derived from Ohshima's approximation (). To estimate electrical valence of particles based on Ohshima's expression, total amount of surface charge (q) per unit area (A) was first calculated and defined as the surface charge density ( = q/A) derived from Equation B11 (Appendix B). The obtained value of the surface charge density was then converted into the electrical valence (= A /e). To validate the analytical method discussed for surface charge determination in small EVs, HSA protein was chosen for use in proof‐of‐concept studies to explore its charge (under experimental conditions similar to the previous studies) and the results were compared to published data for the protein charge estimates. The following values were used for all calculations; η = 0.887 cP (solution viscosity), ρ = 997 kg.m−3 (solution density), T = 298.15 K (solution temperature), ɛ0 = 8.85×10−12 F.m−1 (vacuum permittivity), ɛr = 78.53 (relative permittivity), (radius of small EVs; isolated small EVs were depicted in the DLS analysis with an average diameter of ∼170 nm, PDI = 0.24), (radius of HSA protein based on the literature data) (Armstrong et al., 2004; Leggio et al., 2008; Jachimska et al., 2008).
2.9. Computational simulation
Simulating the structure of ion distribution around small EVs can facilitate a better understanding of the EV‐electrolyte interface while accounting for various parameters governing the behavior of the ionic cloud around small EVs. The Gouy‐Chapman‐Stern (GCS) model was employed in this study to describe the EV‐electrolyte interface representing a dual‐element concept containing both Stern (inner element) and diffuse (outer element) layers. According to GCS theory, ion concentration can be expressed by the Nernst–Planck equation, whereas electrostatic potential within the EDL, adjacent to a charged surface, can be defined by the Poisson equation. In this model, the bulk solution of electrolyte was considered to be an electroneutral solution (zero potential), where one‐half of the ions were anions and the other half cations (equal concentrations of cations and anions). Both cations and anions were treated as rigid spheres of the same size and as univalent ions. All equations used in this model have been summarized in Appendix A. The equations describing the structure of ion distribution and electric potential around small EVs were solved using the commercial finite element solver COMSOL Multiphysics (version 5.5, www.comsol.com) in one‐dimension along the EV radius. The simulated model was validated against published data for ζ‐potential and surface charge of (i) liposomes dispersed in 1 mM NaCl buffer solution (Chibowski & Szcześ, 2016), and (ii) plant cells in NaCl and KCl buffer solutions over the concentration range of 0.5‐65 mM (Kinraide & Wang, 2010; Kinraide et al., 1998), assuming a constant permittivity (ɛr = 78.53).
2.10. Statistical analysis
Statistical analyses were carried out using one‐way analysis of variance to investigate the differences between analytical methods. Where applicable, two‐tailed unpaired t‐tests were used to compare two experimental groups. Values were presented as the mean ± standard deviation. A probability value (p‐value) <0.05 indicated that a difference was statistically significant.
3. RESULTS
3.1. Characterization of the isolated small EVs
According to the described isolation protocol, EV‐enriched fractions were obtained from culture supernatant of AMSCs, and subsequently examined by TEM, DLS, and SP‐IRIS to investigate morphological characteristics and size distribution of the isolated vesicles. TEM imaging of the isolated EV‐enriched fraction displayed nanostructures with a cup‐shaped morphology in the size range that describes small EVs (Figure 3a) (Rickert et al., 2019; Gardiner et al., 2013; Szatanek et al., 2017; Théry et al., 2018). It should be noted that the cup‐shape is a characteristic morphology for EVs when they are visualized using TEM, and is a consequence of the drying process used prior to imaging (Jung & Mun, 2018). As depicted in the DLS analysis (Figure 3b), the isolated particle fractions displayed an average diameter of 169.6 ± 5.14 nm and an average polydispersity index (PDI) of 0.24 ± 0.02. Given that PDI values less than 0.4 have been considered an acceptable range for a homogenous population of lipid‐based carriers, like liposomes (Ribeiro et al., 2018; Jakubec et al., 2020; Mattera et al., 2020; Chen et al., 2011; Danaei et al., 2018), DLS analysis confirmed a relatively homogeneous size distribution for the isolated particle fractions, in which most of the isolated particles fall in the standard range defined for small EVs (Cocucci & Meldolesi, 2015; Zhang et al., 2019; Théry et al., 2018). Since DLS can measure particles ranging from 1 nm to 1 μm in size (Kaszuba et al., 2008), impurities co‐isolated with isolated EV‐enriched fractions after ultracentrifugation unavoidably impact the DLS analysis (supplementary information, Figure S4). According to the data collected (supplementary information, Figure S5a), about 1.5% of the free proteins existing in the culture supernatant co‐isolated with isolated EV‐enriched fractions after ultracentrifugation. To discriminate between small EVs and the co‐isolated impurities, SP‐IRIS (ExoView) was used to analyze size distribution of isolated particles expressing EV surface markers (CD9, CD63, CD81). Figure 3c shows a scatter plot of fluorescence intensity against diameter of particles bound to CD63 antibodies on ExoView chips, and the results indicated an average diameter of 56 ± 8 nm for the captured particles. Representative plots for the particles bound to CD81 and CD9 antibodies on ExoView chips have been reported in the supplementary information (Figure S6).
FIGURE 3.
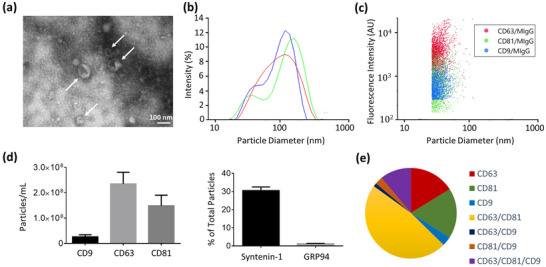
Characterization of isolated EV‐enriched fractions. (a) Transmission electron microscopy of AMSC‐derived EV‐enriched fraction. Arrows indicate EVs with a cup‐shape morphology (magnification of 30000×; scale bar = 100 nm). (b) Dynamic light scattering of isolated EV‐enriched fraction (a representative sample with three consecutive runs), indicating a homogeneous size distribution with an average diameter of 169.6 ± 5.14 nm (average PDI of 0.24 ± 0.02). (c) A scatter plot of fluorescence intensity against diameter of particles bound to CD63 antibodies on ExoView chips, normalized to non‐specific binding of proteins bound to mouse IgG (MIgG). (d) ExoView analysis of EV surface markers (CD9, CD63, CD81), internal EV marker of Syntenin‐1 and negative marker of GRP94. (e) Colocalization pie chart for the isolated particle fractions bound to CD63 antibodies on ExoView chips, showing a significant portion of colocalized particles expressing two or more EV‐specific markers (2.3 × 108 total particles bound to CD63).
In addition to vesicle morphology and size, the isolated particle fractions were analyzed using ExoView analysis for EV‐related surface markers (CD81, CD63 and CD9), internal EV marker Syntenin‐1, and endoplasmic reticulum marker GRP94 which tracks non‐exosomal cell debris co‐isolated with small EVs (Kowal et al., 2016; Théry et al., 2018). The results confirmed the presence of tetraspanin proteins CD9, CD81, and CD63 which are major constituents of small EVs (Figure 3d). ExoView analysis revealed significant expression of internal EV marker of Syntenin‐1, while the expression level of endoplasmic reticulum marker GRP94 (negative marker for small EVs) was quite infinitesimal (Figure 3d). Together, the results provided evidence that the isolated particle fractions contained small EVs. As depicted in the colocalization pie chart, the isolated particle fractions showed a large degree of colocalized particles expressing two or more EV‐specific markers with about 2.3 × 108 total particles bound to CD63 antibodies on ExoView chips (Figure 3e). The colocalization charts for the culture supernatant and isolated particle fractions bound to CD63, CD81, and CD9 antibodies are presented in the supplementary information (Figure S7). The presence of small EVs was further confirmed by examining the total protein concentration enclosed within the isolated particle fraction using a BCA assay. To quantify particle‐enclosed proteins, the isolated particle fractions were first exposed to RIPA lysis buffer to extract their protein content. Although there are different lysis buffers available for lysing membrane‐bound structures (e.g., small EVs), it was reported that the highest number of proteins and peptides were identified when RIPA buffer was used for lysis (Subedi et al., 2019). Analysis of total protein concentration simply indicated the protein content recovered from the isolated particle fractions was indicative of levels found in small EVs, thereby providing additional evidence suggesting that small EVs were the nanoparticles collected using the described isolation method (supplementary information, Figure S5b).
3.2. Computational investigation of EDL around small EVs
To better estimate the surface charge of small EVs, understanding the structure of ion distribution around these vesicles is of great importance. Currently, mathematical theories or computational modeling are the most predictive approaches to gain insights into ion distribution and electric potential around a charged particle given that there is no standard experimental method to directly study EDL structure (Vatamanu et al., 2011; Everts & Ravnik, 2018; Wu, 2022; Burt et al., 2014). Interaction between an electrolyte solution and a charged surface results in a double layer structure of ions (called EDL) around the charged surface, which was originally modeled by Helmholtz (Ohshima et al.,1982; H. Wang & Pilon, 2011). Whereas this model describes ion distribution around a charged particle as two sheets of charge (equal in magnitude but opposite in polarity), it inherently neglects ion diffusion and does not account for the mobile ions within the diffuse layer around the particle (Bard et al., 2022; Conway et al., 1951). Later, Gouy and Chapman modified the Helmholtz model to involve a diffuse layer of charge in the solution surrounding the charged surface (Chapman, 1913; Gouy, 1910). The Gouy‐Chapman model considers ions to be loosely attached to the surface, thereby describing ion distribution around a charged surface as an electric potential that drops off exponentially according to the coupled influences of diffusion and electrostatic forces. However, an immediate weakness apparent in this model is that it does not account for the finite size of ions and adsorption, thereby neglecting the ions tightly associated with the charged surface (Bard et al., 2022; Dukhin & Goetz, 2010). Owing to the inherent limitations of both the Helmholtz and Gouy‐Chapman models, a more sophisticated model is required to account for all ions around a charged particle; mobile ions within the diffuse layer and immobile ions strongly associated with the charged surface. Among different theoretical models (e.g., Helmholtz, Gouy, Stern, Chapman, Muller and Grahame) developed to describe the structure of ion distribution at the interface between a charged surface and electrolyte solution, the GCS model, combining the Helmholtz compact layer and the Gouy‐Chapman diffuse layer, is well‐established to investigate the EDL around a charged surface (Dukhin & Goetz, 2010; Brown et al., 2016; Oldham, 2008; Grahame, 1947). Indeed, the GCS model accounted for the ions tightly associated with the particle surface within the Stern layer while considering mobile ions within the diffuse layer. It should be considered that the GCS model breaks down for an electrolyte solution with high ion concentration (high ionic strength) and/or a charged surface representing high electric potential where the ions in the electrolyte solution can no longer be considered as point charges in the outer element (diffuse layer) of this model. In this study, we used the GCS model to investigate ion distribution and electric potential around small EVs.
For a typical planar EDL, the GCS model provides an appropriate quantitative prediction of ion distribution when the surface potential is low (< max , Equation A4, Appendix A) and electrolyte concentration is not too high (< cmax , Equation A3, Appendix A) (Kilic et al., 2007; Bazant et al., 2009). In the case of spherical structures, it has been reported that GCS theory provides an appropriate electrostatic model for a given charged particle with a surface potential lower than 40 mV as long as the ionic concentration of the electrolyte solution does not exceed 1 M (Wang and Pilon 2013; Huang et al., 2008a, 2008b; Huang, Sumpter, et al., 2010; Huang, Qiao, et al., 2010; J. Yang et al., 2021). Indeed, the point‐charge assumption associated with the diffuse layer in this model is only valid under the condition of low ionic strength and low electric potential at the surface of charged particles (Kilic et al., 2007; Bazant et al., 2009). Given the experimental condition (electrical conductivity < 2 mS.cm−1) for EM measurement in this study and the calculated ζ‐potential of small EVs (summarized in Table 1), it is confirmed that the charge estimation in this study follows the assumptions of low surface potential (ζ < 40 mV) and low ionic strength (≤ 20 mM electrolyte solution) (Palberg et al., 2004; Virtanen et al., 2014; Reiber et al., 2007).
TABLE 1.
Comparison of different theoretical approximations to estimate the electrical properties of small EVs and HSA proteins according to their measured EM.
| Mean zeta potential (mV) | Mean electrical valence | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Particle sample | pH | Κa Value (nm−1) | Mean measured EM (μm.cm.V−1.s−1) | Smoluchowski | Hückel | Ohshima | Surface charge density (C.nm−2) ✗10−21 | Zeff | ZDHH | ZOhshima |
| HSA protein | ∼3.5 | 1.36 | +0.10 | +1.3 | +0.9 | +1.9 | 0.9 | +0.4 | +1.3 | +0.8 |
| ∼4.5 | 1.36 | ‐0.20 | ‐2.6 | ‐1.7 | ‐3.7 | 1.7 | ‐0.7 | ‐2.5 | ‐1.6 | |
| ∼7.5 | 1.36 | ‐1.26 | ‐13.8 | ‐9.2 | ‐19.8 | 9.3 | ‐3.95 | ‐13.4 | ‐8.9 | |
| ∼10.5 | 1.36 | ‐1.34 | ‐15.9 | ‐10.6 | ‐22.7 | 10.7 | ‐4.5 | ‐15.4 | ‐10.3 | |
| Isolated small EVs | ∼4.5 | 33.02 | +0.32 | +4.1 | +2.7 | +4.3 | 1.2 | +28.1 | +1023.5 | +675.6 |
| ∼7.5 | 33.02 | ‐1.49 | ‐18.9 | ‐12.6 | ‐20.3 | 5.7 | ‐132 | ‐4808.1 | ‐3246.3 | |
| ∼10.5 | 33.02 | ‐2.30 | ‐29.3 | ‐19.5 | ‐31.4 | 9.2 | ‐204 | ‐7427.7 | ‐5183.8 | |
Note: The parameter κa was calculated according to the ionic strength of the buffer solution (14 mM) and hydrodynamic radius (a) of dispersed particles. In this study, HSA protein was considered to have an average hydrodynamic radius of 3.5 nm according to the literature values reported for the size of HSA protein. (Jachimska et al., 2008, Leggio et al., 2008, Armstrong et al., 2004) Hydrodynamic radius of small EVs was considered about 85 nm according to the size distribution depicted from DLS analysis in this study.
Using a single domain in one dimension (Figure 4a), representing the electrolyte phase from the charged surface of small EVs toward the bulk solution, the ion distribution and electric potential around small EVs were computed using COMSOL Multiphysics. In this study, the EDL model was solved for constant dielectric permittivity of ɛr = 78.5. Although most numerical investigations for the electric potential profile near a charged surface (either planar or spherical) have assumed a constant electrolyte dielectric permittivity, it should be highlighted that the relative dielectric permittivity is dependent on the field strength when the local electric field is sufficiently large (electric field strength > 107 V.m−1) (Booth, 1955; Booth, 1951; Yang et al., 2010). Indeed, electrolyte molecules become highly oriented around a charged surface with a large electric field, thereby causing the relative permittivity to significantly decrease as the electric field increases (Buckingham, 1956; Fulton, 2009; Yeh & Berkowitz, 1999). Dependency of electrolyte dielectric permittivity on electric field strength may lead to a significant change in the capacitance and electric potential profiles. Numerical studies have previously verified that compared to using constant permittivity, the predicted specific capacitance of spherical electrodes significantly decreases when a field‐dependent electrolyte permittivity is considered in simulating EDLs (Wang & Pilon, 2011; Wang et al., 2011). However, small EVs have low surface potential (ζ < 40 mV), and since their local electric field is not strong enough to cause a significant change in the dielectric permittivity, EDL models for small EVs do not need to account for a field‐dependent electrolyte permittivity. Thus, using a constant electrolyte dielectric permittivity (ɛr = 78.5) was a reasonable choice to simulate the EDL formed around small EVs.
FIGURE 4.
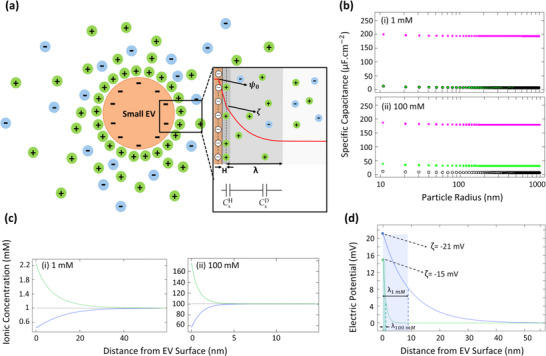
Simulated electrokinetic model for EDL around small EVs, obtained using COMSOL Multiphysics. (a) Schematic of the simulated domain according to the Gouy‐Chapman‐Stern Model; double layer structure of ions consisting of the Helmholtz layer (H) and the diffuse layer (λ). Surface potential, zeta potential, and bulk potential are denoted by ψ0, ζ, and , respectively. To describe the total EDL capacitance, the interfacial model was considered as two capacitances (diffuse and Helmholtz layers) combined in series; total capacitance of EDL is the sum of the individual capacitances of diffuse layer () and Helmholtz layer (). (b) The predicted specific capacitance for the Helmholtz layer (pink square), diffuse layer (green square), and total EDL (black circle) of small EVs dispersed in (i) 1 mM and (ii) 100 mM electrolyte solutions based on the Gouy‐Chapman‐Stern model assuming constant permittivity (ɛr = 78.5) for the electrolyte solution and constant surface charge density for small EVs (identical to a ζ‐potential of −35 mV). (c) Molar concentration profile for cations and anions around small EVs dispersed in (i) 1 mM and (ii) 100 mM electrolyte solutions, representing cation accumulation (green line) and anion depletion (blue line). (d) Electric potential profile around small EVs (diameter of 100 nm, constant surface charge density, surface potential of −22 mV) dispersed in an electrolyte solution with ionic strength of 1 mM (blue line) and 100 mM (green line). Debye length (λ) is a function of electrolyte ionic strength: the higher the ionic strength, the shorter the Debye length and the smaller the magnitude of the ζ‐potential.
For small EVs dispersed in an electrolyte solution, the surface‐electrolyte interface was treated as two capacitances (one for each of the diffuse layer and the Helmholtz layer) combined in series to describe the total EDL capacitance (Figure 4a). In this interfacial model, the diffuse layer was considered with a thickness corresponding to the Debye length, whereas the thickness of the Helmholtz compact layer (compact layer of ions in Stern layer) was approximated as the hydrated radius of a Na+ ion (0.36 nm) (Israelachvili, 2011) within the electrolyte solution to account for the finite size of ions (Bard et al., 2022; Masliyah & Bhattacharjee, 2006). Figure 4b shows the numerically predicted specific capacitance of the Helmholtz and diffuse layers, as well as the total specific capacitance as a function of particle radius while assuming vesicles with constant surface charge density (corresponding to the ζ‐potential of −35 mV, stable colloidal solution of small EVs). As shown in Figure 4b, all predicted specific capacitances slightly decreased with increasing particle radius and reached a plateau for particles with a radius larger than 20 nm, indicating that specific capacitance remained constant for small EVs (and even larger EVs) regardless of their size. As shown in Figure 4b, the compact layer of ions in the Stern layer (Helmholtz capacitance) had minimal impact on the total capacitance of the EDL around small EVs when the ionic strength was very low (1 mM, Figure 4b‐i), whereas neglecting the Helmholtz layer capacitance had a significant impact on the estimated total capacitance of EDL when ionic strength increased (100 mM, Figure 4b‐ii). The results indicate that only considering the ions within the diffuse layer (capacitance of diffuse layer) does not provide a comprehensive model for the total capacitance of EDL around a particle, specifically when ionic strength increases. This supports the fact that reporting ζ‐potential alone, an approach commonly found in the literature, does not lay out a complete picture of the electrical properties for bionanoparticles including small EVs since it ignores the effects of the Stern layer.
To theoretically investigate the impact of the ionic cloud (normally a few nanometers around small EVs) on the surface charge of small EVs, the structure of the EDL around these vesicles was simulated under the effect of ionic strength. With respect to the results shown in Figure 4b, and given the fact that specific capacitance represents a ratio of the total charge density divided by electric potential in a double layer structure (Equation 7A, Appendix A), it was supported that the predicted pattern for ion distribution and electric potential for EVs would be independent of their size. Figures 4c and 4d, respectively, represent ion distribution and electric potential profiles for small EVs dispersed in an electrolyte solution (1 and 100 mM, neutral pH condition), obtained using computational simulation. Since small EVs are negatively charged relative to the bulk solution (which is electroneutral), they attract cations while repelling anions. The simulation results showed that cations, but not anions, in the electrolyte solution accumulated at the surface of small EVs (Figure 4c). It also showed that the concentration of cations at the surface of a charged particle increased with increasing electrolyte ionic strength (green line, Figure 4c), thereby a thinner counterion layer is expected in a solution with higher ionic strength. Given the definition of Debye length (Equation 3B, Appendix B), it is obvious that the thickness of the counterion layer around a charged particle is mainly influenced by the ionic strength (i.e., salt concentration) of the electrolyte (Figure 4d). It was also confirmed that the ion concentration at the surface of small EVs is higher than in the surrounding bulk solution and decreases exponentially with distance away from the particle surface. As shown in Figure 4d, compression of the ionic cloud around the particles at higher ionic strength resulted in a considerable shift toward less negative values of ζ‐potential. The results were in qualitative agreement with what is experimentally reported for similar monovalent solutions such as KCl (Palberg et al., 2004; Semenov et al., 2010) and NaCl (Delgado et al., 1987; Reiber et al., 2007) solutions: the lower the salt concentration in an electrolyte solution, the greater the surface charge for the particles dispersed in that solution.
3.3. Electrolyte consideration for EM measurements
It is evident that charged particles subjected to a uniform electric field experience different electrophoretic forces (and accordingly, EM) depending on their surface charges, the strength of the applied field, and the surrounding medium characteristics (viscosity, pH, and ionic strength) (Masliyah & Bhattacharjee, 2006). In this study, all EM measurements were conducted under the same applied voltage and using the same electrolyte solution. The important consideration when using DLS is that the electrical conductivity of the processing sample should be sufficiently low (γ < 4.5 mS.cm−1) to retain the electrodes unsaturated during the measurements. Since PBS (1X) is enriched with plenty of ions (supplementary information, Table S1), it possesses high electrical conductivity ( ∼16 mS.cm−1, measured using DLS), which can interfere with EM measurements due to excessive heat and bubble generation, but can also damage sample and electrodes. Given that the DLS technique requires low electrical conductivity to operate properly, undiluted PBS or any biological fluid (e.g., culture medium and bodily fluids) that possesses high electrical conductivity (γ > 16 mS.cm−1) is not an appropriate dispersant for EM measurement. Therefore, PBS was first diluted with distilled water to an ionic strength of 20 mM to (i) ensure that the electrical conductivity is sufficiently low to remain less than 4.5 mS.cm−1 after adding bionanoparticles, and (ii) fulfill the main assumption (low ionic strength) specified in Ohshima's analytical method for surface charge determination (Palberg et al., 2004; Virtanen et al., 2014; Reiber et al., 2007).
Although PBS as an electrolyte solution can be diluted to obtain a desired ionic strength, the ionic strength of the solution changes once particles (proteins or small EVs) are added to the solution and varies with particle concentration (see the results in section 3.4.2). Therefore, ionic strength needs to be defined in terms of both salt and particle concentrations. Taking into account all the charged components present in the solution (either salt residues or particles), electrical conductivity can provide a more accurate determination of the solution ionic strength. Electrical conductivity of PBS solutions was investigated at various molar concentrations with an accuracy of up to 0.001 mS.cm−1 using DLS. To validate the accuracy of electrical conductivity measurements, electrical conductivity of NaCl solutions was first investigated at various molar concentrations ranging from 0.5 to 500 mM (supplementary information, Table S2). The measured values agreed with reported data for conductivity of salt water with different salinity (Culkin, 1986; Schmidt et al., 2018; Gadani et al., 2012; Peyman et al., 2007 ; Lewis, 1980). Distilled water with a measured electrical conductivity of 0.01 mS.cm−1, in agreement with literature values (<0.02 mS.cm−1, 25°C) (Ageev & Rybin, 2020; Golnabi et al., 2009), was also considered as a control solution. The results indicated a linear relationship between electrical conductivity and concentration of PBS solution; the higher the concentration of electrolyte solution, the greater electrical conductivity value (supplementary information, Figure S8). Given the collected data, it was concluded that electrical conductivity of sample solutions (PBS solution including particles) should be less than 2 mS.cm−1 to ensure all measurements were consistently conducted at low ionic strength in alignment with Ohshima's analytical method. This adjustment was made by using the same electrolyte solution (PBS diluted with distilled water) for all samples, and by making a proper concentration of the particles (either proteins or small EVs) so that final ionic strength remained identical with electrical conductivity of 2 mS.cm−1 for particle‐electrolyte mixture solution.
3.4. Factors influencing EM
The surface charge of bionanoparticles is a system property that is significantly affected by the temperature, dielectric constant, electrolyte composition and pH of the solution in which the charged particles are dispersed. For instance, it has been extensively reported that the charge of amphiphilic molecules like proteins is dependent on the pH and ion concentration (ionic strength) of the electrolyte solution (Luo et al., 2010; Jachimska et al., 2008; Lombardo et al., 2015; Zhulina & Leermakers, 2007; Sriprablom et al., 2019). To evaluate the influence of electrolyte solutions on the ζ‐potential and electrical valence of small EVs (and HSA proteins as candidate reference bionanoparticles), EM was utilized as a parameter that reflects surface charge properties under various experimental conditions of pH and ionic strength (Figure 5). The measured EM values for HSA proteins have been reported in the supplementary information (Figure S9)
FIGURE 5.
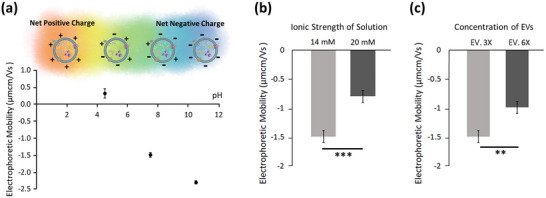
The effect of pH and buffer content on the EM of AMSC‐derived small EVs. (a) Measured EM of the isolated EV‐enriched fraction at various pH conditions (ionic strength of 14 mM). Small EVs are negatively charged structures under basic conditions (corresponding to a negative EM), while transforming toward a more positive structure as electrolyte acidity is increased. (b) Measured EM of small EVs (collected from 3 mL culture supernatant) in diluted PBS with ionic strength of ∼20 mM and ∼14 mM (pH∼7.5). In an electrolyte with lower ionic strength (14 mM), small EVs exhibited a larger magnitude of EM, accounting for a greater surface charge. (c) Measured EM for small EVs dispersed in diluted PBS with ionic strength of 14 mM (pH∼7.5). Two EV groups were experimentally tested; the first contained small EVs collected from 3 mL of culture supernatant (EV. 3X) and the second from 6 mL of culture supernatant (EV. 6X). Particle dispersions with lower particle concentration represented a greater magnitude of EM and accordingly a greater surface charge. **p‐value < 0.01, ***p‐value < 0.001.
3.4.1. EM as a function of pH
The pH of a solution can influence the total electrical charge of small EVs by affecting the net charge of polar groups such as phosphates and amino acids (Righetti, 2004; Sillero & Maldonado, 2006; Guckeisen et al., 2019). To experimentally investigate the effect of pH on EV surface charge, EM of small EVs (isolated from 3 mL of culture supernatant and dispersed in 1 mL of diluted PBS with an ionic strength of 14 mM) was measured under different pH conditions (acidic, neutral, and basic pH) while keeping ionic strength constant. The results reconciled previous experimental findings made on the EM of small EVs over different pH conditions (Midekessa et al., 2020). Small EVs were found to be negatively charged under basic conditions (pH∼10.5, ionic strength of 14 mM) with a mean EM value of −2.3 μm.cm.V−1.s−1, and unsurprisingly, transitioned to being more positively charged as electrolyte acidity increased (Figure 5a). Small EVs dispersed in a neutral pH electrolyte (pH∼7.5) generally exhibited a lower magnitude of EM (and accordingly, lower surface charge) compared to those dispersed in a basic electrolyte. This effect can be attributed to the presence of proteins and phosphate groups on the surface of small EVs that harbor ample anionic sites under physiological pH values (pH∼7.5). Our finding showed that EVs became a positively charged structure with a mean value of +0.32 μm.cm.V−1.s−1 for EM at pH∼4.5 (ionic strength of 14 mM).
3.4.2. EM as a function of buffer content and ionic strength
Any change in buffer (electrolyte solution) content impacts the electrical conductivity of the solution and accordingly EM of particles dispersed in that solution. It has been reported that EM of a charged particle varies with either particle or residual salt concentration existing in an electrolyte solution (Austin et al., 2020; Botin et al., 2020; Medrano et al., 2009).
To experimentally examine the effect of ionic strength on EV surface charge, EV‐enriched fractions obtained from 3 mL of culture supernatant were dispersed in 1 mL of diluted PBS with a molar concentration of either 20 mM or 14 mM, and the EM was measured for each sample under physiological pH conditions (pH∼7.5). As expected from the simulated electrokinetic model (Figure 4), the EM of small EVs decreased with increasing ionic strength of the electrolyte (Figure 5b). The measured EM of small EVs showed a considerable shift toward more negative values in the lower molar concentration of PBS, supporting a greater surface charge in an electrolyte solution with lower ionic strength. These results were in a good agreement with previous studies investigating the effect of buffer content and dilution effects on EM of small EVs (Petersen et al., 2018; Midekessa et al., 2020). This effect may be attributed to the electrical conductivity of the solution (supplementary information, Figure S8), where a significant shift toward higher conductivity was noticed at a higher molar concentration of PBS (170 mM PBS with γ ∼16 mS.cm−1, 20 mM PBS with γ ∼1.95 mS.cm−1, 14 mM PBS with γ ∼1.35 mS.cm−1). It also confirmed that EM values were impacted by changing concentrations of EVs. Figure 5c shows the measured EM values for two experimental groups containing EV‐enriched fractions collected from either 3 mL culture supernatant (EV. 3X) or 6 mL culture supernatant (EV. 6X) and then dispersed in 1 mL of diluted PBS (ionic strength of 14 mM and pH∼7.5). Small EVs in a sample solution with a higher particle concentration (EV. 6X) represented a negative structure with a mean EM value of −0.99 μm.cm.V−1.s−1, but become increasingly negative as EV concentration was decreased. The mean EM value of −1.49 μm.cm.V−1.s−1 was recorded for small EVs in a sample solution with a lower particle concentration (EV. 3X). These findings support the fact that electrolyte content (either particle or residual salt concentration) has a significant impact on the EM of small EVs.
3.5. Interpretation of EM data
Bionanoparticles including proteins and small EVs are charged spherical nanostructures that can translocate in an electrolyte when exposed to a steady and uniform electric field. Under such conditions, the EM of these particles can be described as the ratio of particle velocity (U) to the strength of the applied electric field (E), given by Equation B1 (Appendix B) (Oddy & Santiago, 2004). Considering that particle velocity is a function of physical properties (e.g., size and surface charge), EM coupled with particle size can be used to determine the electrical charge on the surface of a particle. In this study, the surface charge on small EVs and HSA proteins was expressed in the form of electrical valence and ζ‐potential using different theoretical approximations.
After evaluating commonly used, classical theoretical approaches for estimating the electrical properties of bionanoparticles, a simple analytical method contemporarily derived by Ohshima and co‐workers was used to calculate ζ‐potential and electrical valence of small EVs and HSA proteins based on their measured EM. The accuracy of Ohshima's expression for the charge determination of other colloidal particles (e.g., proteins, cells, liposomes and gold nanoparticles) has been confirmed (Russell et al., 2016; Agnihotri et al., 2009; Zhou et al., 2020; Correll et al., 2022; You et al., 2022; Jiang et al.,2019 ; Yin et al., 2021; Kanninen et al., 2016; Chand et al., 2021). This analytical method enabled an accurate charge predication for bionanoparticles as it corrects for the Debye shielding effect, which is a phenomenon not considered within classical theoretical approximations (Agnihotri et al., 2009; Ohshima et al., 1982; Ohshima, 1994; Makino & Ohshima, 2010; Ohshima, 2001; ). Table 1 shows a summary of the measured EM values, ζ‐potential and electrical valence calculated for HSA proteins and isolated small EVs dispersed in diluted PBS as an electrolyte solution.
3.5.1. Estimated ζ‐potential
ζ‐potential values were estimated via Henry's equation (Equation B8; Appendix B) where EM was defined as a function of particle size (a) and Debye‐Hückel parameter (κ). Depending on the magnitude of κa, Henry's equation can be approximated to Hückel's formula (Equation B6; Appendix B) or Smoluchowski's formula (Equation B7, Appendix B), which are two commonly used classical theoretical approximations for estimating ζ‐potential. It should be noted that Hückel's equation is applicable where κa ≪ 1, whereas Smoluchowski's equation is used where κa ≫ 1. Figure 6a shows a contour plot of the parameter κa, plotted as a function of particle size and ionic strength of the electrolyte (using MATLAB R2021b, MathWorks, Inc.), identifying the acceptable domains for Smoluchowski's and Hückel's approximations. For bionanoparticles, including small EVs, representing low surface potential under physiological conditions (moderate ionic strength, κ∼1), it is apparent that κa values remain out of the acceptable range of Smoluchowski's and Hückel's approximations. In this case, Ohshima's approximation (Equation B8, Appendix B), which considers arbitrary values of κa (Ohshima, 2001; Ohshima et al., 1983), can serve as a general approximation for Henry's function (Equation B4, Appendix B) to estimate ζ‐potential. As shown in Figure 6b, ζ‐potential determined using Ohshima's approximation results in statistically different values of ζ‐potential compared to Smoluchowski's and Hückel's methods, specially under basic condition.
FIGURE 6.
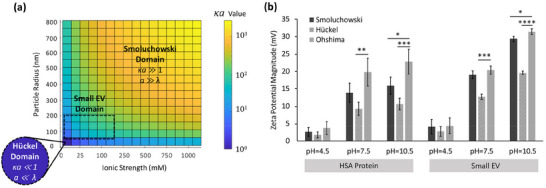
Comparing different theoretical approximations for surface charge of small EVs. (a) A contour plot of the parameter κa as a function of particle size and ionic strength of the electrolyte, obtained using MATLAB. The parameter κa values are colored according to their acceptable range for (i) very large particles (a ≫ λ) fitted with Smoluchowski's approximation (κa ≫1, ideally for κa > 1000), (ii) very small particles (a ≪ λ) fitted with Hückel approximation (κa ≪1), and (iii) small EVs, representing a considerable Debye length even under high ionic strength of normal physiological conditions (λ > 0.7 nm). (b) ζ‐potential determined using Smoluchowski's, Hückel's, and Ohshima's approximations under different pH conditions for two experimental groups of HSA protein and small EVs. *p‐value < 0.05, **p‐value < 0.01, ***p‐value < 0.001, ****p‐value < 0.0001.
Compared to HSA proteins, small EVs exhibited a significantly greater magnitude of ζ‐potential (Table 1), in agreement with published values indicating greater negative charge of EVs, including small EVs (Gitlin et al., 2006; Midekessa et al., 2020; Molnar et al., 2016; Melzer et al., 2019; Salarpour et al., 2019; Kaddour et al., 2020). The existence of negatively charged phospholipids on EV membranes significantly contribute to the total negative charge of small EVs, thereby being a likely reason for the greater surface charge values in small EVs compared to proteins. It has been demonstrated that the negatively charged membrane of EVs is mostly composed of phosphatidylserine (Figure S10) (Hosseini‐Beheshti et al., 2012; Skotland et al., 2017; Matsumoto et al., 2017; Llorente et al.,2013; Charoenviriyakul et al., 2018) which is the major anionic phospholipid class in mammalian cells (Naumowicz & Figaszewski, 2014; Vance, 2018). In addition, it has been reported that the outer leaflet of the plasma membranes are relatively rich in phosphatidylcholine (Figure S10) (Tuck, 2011 ; A. Kumar et al., 2021; Skotland et al., 2019; W. Wang et al., 2020). Notably, phosphatidylcholine lipids are characterized by a strongly negative charge; ζ‐potential value for phosphatidylcholine liposomes have been reported to be approximately −62 mV under identical conditions (Bondar et al., 2012).
3.5.2. Estimated electrical valence
Given the fact that ζ‐potential defines the electric potential at the slip plane, and does not correct for the effect of ions tightly associated with the Stern layer, surface charge density (quantity of charge per unit area, C.m−2) or electrical valence (a derivative form of surface charge density) may represent a more appropriate descriptor for the electrical properties of a charged particle. The electrical valence (Z) is a quantized value of the electric charge (q), equal to the ratio of electric charge (in coulombs, C) to the elementary‐charge constant (e = 1.602176634×10−19 C). Effective valence (Zeff ) and Debye‐Hückel‐Henry valence (ZDHH ) are two quantities extensively used to describe surface charge in the form of an electrical valence (Filoti et al., 2015; Chibowski and Szczes, 2016; Rasmussen et al., 2020; Ren et al., 2019; Sotomayor‐Perez et al., 2012). However, the main concern when reporting Zeff and ZDHH as an estimation for the electrical valence of bionanoparticles is whether these terms correctly contemplate the shielding effect of the ionic cloud associated with the Stern layer at the nanoscale. To investigate the accuracy of Zeff (Equation B9, Appendix B) and ZDHH (Equation B10, Appendix B) for determining the net charge (electrical valence) of bionanoparticles, BSA protein was chosen as the candidate reference. This choice was based on the availability of published experimental and computational data regarding the net charge of BSA protein under conditions that could be replicated in this study. In addition to Zeff and ZDHH , the estimation of electrical valence in bionanoparticles was investigated through Ohshima's expression, and a novel term was introduced here (ZOhshima ) to define the electrical valence. Considering Ohshima's expression (Equation B11, Appendix B), which represents the relation between ζ‐potential and surface charge density, the estimated value of ζ‐potential (already derived from EM using Equation B8, Appendix B) was simply converted into ZOhshima .
The term Zeff represents the apparent charge at the hydrodynamic boundary around the particle, where the ions move freely and diffuse in the fluid surrounding the particle due to Coulombic interactions. The relationship between Zeff and EM has been defined based on Stokes' law for friction forces acting on a particle in a viscous fluid (Edward, 1970; Sotomayor‐Perez et al., 2012; Filoti et al., 2015). However, Stokes’ formula is only applicable to macroscopic particles dispersed within an electrolyte solution with high ionic strength, where the electrophoretic motion of the charged particles can be defined as a purely hydrodynamic motion by Stokes’ Drag force (Edward, 1970; Sotomayor‐Perez et al., 2012; Filoti et al., 2015). In contrast, ZDHH adjusts Zeff by taking into account the Debye shielding effect through Debye‐Hückel's approximation, thereby providing a more accurate estimation for the net surface charge of a particle (Filoti et al., 2015; Gokarn et al., 2011; Moody et al., 2005). As listed in Table 2, the results showed that Zeff for BSA protein was six times smaller than ZDHH . Indeed, Zeff does not consider the effect of the ions tightly associated with the Stern layer, thereby underestimating the actual electrical valence. Although, ZDHH takes into account the effect of Debye shielding, when investigating the net charge of BSA proteins, a significant difference was noted between ZDHH and the recorded value for the electrical valence of BSA protein using hydrogen ion titration (Table 2) (Tanford et al., 1955). Such a significant difference, given that hydrogen ion titration is one of the reference techniques for confirmation of charge interpretation using analytical methods (Cannan et al., 1941; Winzor, 2004; Gorin & Mover, 1942), indicates that ZDHH may not be accurate in estimating the net surface charge of bionanoparticles. Likewise, comparison with computational methods such as PROPKa3 and Sednterp (www.rasmb.org) (Olsson et al., 2011; Filoti et al., 2015), predicting protein charge from amino acid compositions (Olsson et al., 2011; Filoti et al., 2015), questioned the validity of ZDHH in explaining the actual surface charge of bionanoparticles. Compared to ZDHH, our results confirmed that ZOhshima represented a significantly more accurate estimation for the electrical valence of bionanoparticles; ZOhshima was statistically equivalent to charge estimations derived both from computational methods (PROPKa3 and Sednterp) and the titration technique (Table 2). Indeed, Ohshima's expression accurately defines surface charge density as a function of κa while correcting for the Debye shielding effect and taking into account the ions tightly associated with the Stern layer (Makino & Ohshima, 2010; Ohshima et al., 1982, 2011). Using Ohshima's expression, the maximum relative error in surface charge estimation of a spherical particle was reduced to less than 1% for κa > 1 (Ohshima, 1994), thereby supporting the use of this approach for small EVs and proteins.
TABLE 2.
Comparison of different (experimental and theoretical) methods to determine electrical valence of BSA protein (pH of 8.1, 25°C).
| Electrical valence from theoretical/experimental technique | Determined value | Ref. |
|---|---|---|
| Effective valence (Zeff ) | ‐4.08 | This study |
| Debye‐Hückel‐Henry valence (ZDHH ) | ‐25.86 | This study |
| Calculated electrical valence using Ohshima's expression (ZOhshima ) | ‐17.99 | This study |
| Computed electrical valence from amino acid composition using PROPKa3 | ‐16.00 | Olsson et al., 2011; Filoti et al., 2015 |
| Computed electrical valence from amino acid composition using Sednterp | ‐18.30 | Filoti et al., 2015 |
| Electrical valence using hydrogen ion titration | ‐17.00 | Tanford et al., 1955 |
Note: The measured EM of BSA was −1.12 (μm.cm.V−1.s−1) assuming a radius of 3.48 nm. (Filoti et al., 2015).
4. DISCUSSION
Accurate knowledge about the electrical nature of small EVs, a fundamental, but often overlooked parameter, can serve to underpin new electrical‐based processes for isolation, manipulation and characterization of these vesicles, thereby facilitating research aimed at better understanding small EVs and promoting the translation of these vesicles to clinical settings. Current approaches for measuring electrical properties are not necessarily accurate, and classical theoretical approaches for determination of surface charge at the nanoscale has significant limitations. Thus, there exists a significant knowledge gap in accurately determining EV surface charge, whether in the form of ζ‐potential or electrical valence.
Based on the simulation and experimental data presented in this study, it was clearly shown that pH and electrolyte content (either particle or residual salt concentration) had a significant impact on EM, and accordingly surface charge of small EVs. To ensure that free protein contaminants co‐isolated with the EV‐enriched fractions did not interfere with surface charge measurements, both ζ‐potential and electrical conductivity were examined in a control group consisting of HSA protein solution containing an equivalent protein concentration to that co‐isolated with the EV‐enriched fractions (0.07 mg/mL). The results indicated that the protein concentration of 0.07 mg/mL was not sufficient to yield any significant ζ‐potential measurements using DLS techniques. This finding suggests that there was no interference with surface charge measurements caused by free protein contaminants co‐isolated with the EV‐enriched fractions. The result was also supported by electrical conductivity measurements as electrical conductivity of sample solutions (PBS solution including particles) can reflect the influence of the electrolyte solution on the surface charge of EVs. To assess whether protein impurities had any significant impact on the measured electrical conductivity of the diluted PBS (electrolyte solution) used for resuspending the EV‐enriched fractions during surface charge examination, the electrical conductivity of the HSA protein solution (0.07 mg/mL) was examined. The results revealed no significant difference in the electrical conductivity of the diluted PBS with and without a protein concentration of 0.07 mg/mL, indicating that protein fraction co‐isolated with EVs did not contribute significantly to the overall electrical conductivity of sample, and consequently, does not affect surface charge measurements. Other parameters, including detergent additives, buffer viscosity, temperature, and ionic valency of ions (monovalent, divalent, or trivalent ions) present in the solution also influence EM of charged particles and therefore, their surface charge (Petersen et al., 2018; Midekessa et al., 2020). Although the effect of these parameters was outside the scope of this study, interactions of particles at the solid‐solid and solid‐liquid interfaces under the effect of all these parameters should be assessed to accurately define the relationship between buffer content and EM of any charged particles. Notably, the relationship between EM and buffer content is complex with no general guideline to individually define the effects of every mentioned parameter.
Variation in the electrolyte composition changes the ionic strength of the electrolyte solution and results in the divergence of the Debye length at different ionic strength levels (Masliyah & Bhattacharjee, 2006; Sotomayor‐Perez et al., 2012), as confirmed by computational data in this study (Figure 4d). Ohshima and co‐workers (Ohshima et al., 1983), demonstrated that the effect of ionic strength could be reflected in the surface charge of particles when the expression term of EM was defined as a function of Debye length (Equation B8, Appendix B) to account for the Debye shielding effect. Given that Debye length is a defining parameter for the particle translocation under the effect of an electric field (Ali & Qian, 2011), it is important to have control on the parameters impacting electrolyte content and its ionic strength during EM measurement. Knowing that the impact of electrolyte content can be reflected in the electrical conductivity of a sample (supplementary information, Figure S8), this study suggests monitoring electrical conductivity which is practically feasible during EM measurement using DLS.
Experimentally collected electrophoretic data (measured EM value) can be used to calculate the electrical valence and ζ‐potential of a charged particle using a theoretical expression. However, several such expressions exist, and there are no reports to determine which one most accurately calculates these important electrical properties for small EVs. In this study, the accuracy of different theoretical approximations was assessed with respect to the parameter κa, which represents the Debye shielding effect, an important term ignored in classical theoretical expressions (Smoluchowski's and Hückel's approximations). As shown in Figure 6a, Hückel's formula is only applicable for very small particles when parameter κa is sufficiently small (κa ≪1 or a ≪ λ). Extremely low ionic strength (I ≪ 1 mM) is required to make this approximation valid for small particles with diameters less than 10 nm. For small EVs, which have κa values out of the acceptable range of Hückel's approximation, this approximation does not reliably describe the relationship between EM and ζ‐potential, even within a highly diluted electrolyte solution (I ≪ 1 mM). In contrast, as depicted in Figure 6a, Smoluchowski's formula is applicable only for sufficiently large particles (micron sized) representing a large value of the parameter κa (κa ≫1 or a ≫ λ) where the Debye shielding effect can be neglected, ideally for the κa values greater than 1000. The ionic cloud around a charged particle reduces the EM of that particle due to the distortion of the EDL by an externally applied electric field (Stellwagen & Stellwagen, 2003). This can lead to an underestimation of the ζ‐potential values if a correction factor is not included in the calculation. Therefore, Smoluchowski's approximation, neglecting the required correction factor, is only recommended for very large particles suspended in a solution with high ionic strength (I > 150 mM, γ ≫ 4.5 mS.cm−1), where the ionic cloud around the particle is highly compact (small Debye length compared to the particle size). However, such high ionic strength is practically out of the range of the electrical conductivity acceptable for EM measurements using the techniques like DLS (needing low electrical conductivity, γ < 4.5 mS.cm−1).
As particle size decreases, specifically in the nanoscale region (represents considerable Debye length), the deviation from Smoluchowski's formula becomes more significant. For small particles including proteins and small EVs, the Debye shielding effect is significant and consequently, a ζ‐potential value calculated using Smoluchowski's expression will have considerable error. It should also be highlighted that the κa value significantly decreases for small EVs when they are dispersed in a solution with ionic strength acceptable for EM measurements using the DLS technique (I < 50 mM, corresponding to γ < 4.5 mS.cm−1). In the case of small EVs with diameters less than 200 nm, representing small κa values and considerable size of Debye length, it is obvious that the parameter κa is out of the applicable range of Smoluchowski's formula (Figure 6a), even within an electrolyte solution with high ionic strength (e.g., undiluted PBS, culture medium, and bodily fluids representing ionic strength > 170 mM).
Importantly, both Smoluchowski's and Hückel's equations are inapplicable to particles with ζ‐potential in excess of the thermal voltage at room temperature () (Ohshima, 1994; Bazant et al., 2009; Kilic et al., 2007), where the absolute value of ζ‐potential is greater than 25 mV (), even though the κa values remain in an acceptable range for these two approximations. According to published values for the ζ‐potential of small EVs (Melzer et al., 2019; Kaddour et al., 2020), along with our experimental data (Table 1), it is evident that ζ‐potential in small EVs could be greater than the limited value for Smoluchowski's and Hückel's approximations depending on the electrolyte solution surrounding these vesicles. For instance, EM measurements in this study indicated that small EVs had a mean EM value of −2.3 μm.cm.V−1.s−1 at pH∼10.5 (ionic strength of 14 mM), corresponding to a ζ‐potential of about −31 mV, where and κa values were out of the acceptable range of both Smoluchowski's and Hückel's approximations. Therefore, a general approximation for Henry's function is still needed to interpret EM of small EVs with no limit on the magnitude of ζ‐potential while correcting for arbitrary values of κa.
As opposed to Smoluchowski's and Hückel's equations, which are two widely used approximations for Henry's formula, Ohshima's expression supports a broad range of κa for any value of the ζ‐potential. Ohshima's expression represented a more accurate approximation for Henry's function with the relative errors less than 1% (Ohshima, 1994). This suggests that surface charge values estimated based on Ohshima's analytical method are considerably more reliable at the nanoscale. It should be noted that compatibility of Ohshima's expressions with the published data for electrical characteristics of five different‐sized spherical gold nanoparticles (5‐154 mM buffer solutions) (Makino & Ohshima, 2010; Agnihotri et al., 2009), albumin proteins (5‐150 mM buffer solutions) (Filoti et al., 2015; Jachimska et al., 2008; Tanford et al., 1955; Russell et al., 2016), liposomes (1 mM buffer solution) (Chibowski & Szczes, 1955), and plant cell membranes (0.5‐65 mM buffer solutions) (Kinraide & Wang, 2010; Kinraide et al., 1998) strongly supports the validity of Ohshima's method for estimation of surface charge for bionanoparticles. Comparing different theoretical approximations, depicted in Figure 6b, it was confirmed that there was a meaningful difference between the ζ‐potential values calculated from Ohshima's expression and two other expressions (Smoluchowski's and Hückel's formula), indicating that ζ‐potential values were underestimated if not calculated based on the Ohshima's expression.
Although ζ‐potential serves as a key parameter to characterize the electrostatic interaction between particles in a colloidal system, it should be noted that ζ‐potential does not take into account the ions associated with the Stern layer, and thereby it cannot be synonymous with the concept of surface charge in bionanoparticles. As confirmed by our computational simulation for EDL capacitance, the ions within the diffuse layer (corresponds to the diffuse layer capacitance in Figure 4b) by themselves cannot present the total capacitance of EDL around small EVs unless the Debye shielding effect is considered. The results showed that neglecting the ions tightly associated with a charged surface (Helmholtz capacitance, Figure 4b) would have a significant impact on the estimated overall charge of small EVs since the ionic cloud associated with the Stern layer produces a shielding effect. Consequently, ζ‐potential is insufficient to infer the electrical characteristics of bionanoparticles. In contrast, surface charge density or electrical valence (which is directly derived from surface charge density) corrects for the ions tightly associated with the Stern layer, making it an appropriate descriptor for the electrical properties of charged particles. In the case of small EVs, where the thickness of ionic cloud is considerable compared to the particle size, Zeff cannot provide an accurate estimation for the electrical valence of the particle. Indeed, Zeff ignores the ions tightly associated with the Stern layer, thereby leading to significant underestimations of charge. On the other hand, while ZDHH has been widely used as a more intuitive description for the net surface charge of a particle (Gokarn et al., 2011; Sotomayor‐Perez et al., 2012 ; Filoti et al., 2015; Moody et al., 2005), it fails to adequately explain the electrophoretic motion of bionanoparticles, particularly under low ionic strength, which is a critical requirement for techniques such as DLS to measure EM (γ < 4.5 mS.cm−1). Our results also showed that ZDHH for bionanoparticles was not as accurate as ZOhshima , the electrical valence derived from the surface charge density estimated using Ohshima's expression (Table 2). Indeed, an accurate estimation for the electrical valence of bionanoparticles including small EVs requires accounting for not only the Stern layer, but also the dependency of EM on the ionic strength of electrolyte solution, which are not truly contemplated in classical theoretical expressions, but are in Ohshima's expression.
Given that electrical valence and ζ‐potential are modeled values and strongly depend on the theoretical approximation used, it is very important to (i) utilize a proper theoretical approximation to correlate EM to a quantitative estimate of the charge, and (ii) measure EM under experimental conditions that are aligned with the assumptions associated with the utilized theoretical approximation. Since Ohshima's expressions are associated with arbitrary values of κa, and takes into account the Debye shielding effect, this approach for measuring the surface charge of bionanoparticles is preferable compared to other theoretical approaches. Therefore, substituting currently used classical theoretical methods with Ohshima's expressions would enable more accurate quantitative estimations of charge while addressing the difference between theoretical and experimental approaches reported in the literature for electrical charge determination of bionanoparticles. Considering that the electrical conductivity of the sample being analyzed is a deterministic factor for proper EM measurement using DLS, and that Ohshima's expression is associated with low ionic strength assumptions (<20 mM), this study recommends maintaining the electrical conductivity of the prepared sample (electrolyte solution including particles) lower than 2 mS.cm−1 for a valid subsequent interpretation of measured EM. Indeed, it is required to control experimental conditions (e.g., electrical conductivity) impacting the ionic strength of the sample solutions during EM measurement. Variation in electrolyte characteristics such as pH and ionic strength drastically affects EM values, and particle charge status cannot be truly deduced from ζ‐potential or electrical valence in the absence of the reported values for pH and ionic strength of the electrolyte in which EM measurements were taken. Therefore, it is highly recommended to report the measurement condition (e.g., pH and ionic strength) and corresponding data (e.g., measured EM), along with the calculated values of ζ‐potential and electrical valence. Contemplating all the required considerations discussed in this study for a reliable surface charge investigation, this study suggests the protocol provided in Figure 7 for surface charge determination in small EVs. As the default equation in the DLS instrument is Smoluchowski's approximation, it is crucial to substitute the appropriate equations (Ohshima's approximation, as discussed in this study and summarized in Figure 7) before conducting EM measurements and reporting ζ‐potential values.
FIGURE 7.

A step‐by‐step guide for surface charge determination in small EVs.
5. CONCLUSION
With the burgeoning demand to take advantage of the rich information provided by small EVs along with plentiful attempts implemented for development of reliable technologies to facilitate fundamental research on small EVs and their clinical applications, adequate and proper characterization of these vesicles is of paramount importance. The technical challenges associated with the unknown surface characteristics of small EVs and their electrostatic interactions within a biological system have been a major hurdle to advancing EV‐based applications. Although electrical properties of EVs have been the subject of intense studies in characterization, detection, isolation and manipulation of small EVs, the surface charge of these vesicles has not yet been accurately determined. This study investigated the challenges inherently associated with the theoretical approximations for surface charge estimation in small EV. It found that classical theories failed to consider the impact of ions within the Stern layer surrounding EVs, leading to an underestimation of the surface charge of small EVs. It also demonstrated that a contemporary analytical method proposed by Ohshima and co‐workers could be used to accurately estimate ζ‐potential and electrical valence of small EVs. The results of this study also confirmed that variation in electrolyte characteristics (e.g., pH and ionic strength) had a significant impact on the electrophoretic behavior of small EVs, suggesting that presenting the value of ζ‐potential or electrical valence, without reporting the precise experimental conditions, is insufficient to infer EV surface charge. Bridging this knowledge gap is crucial as it will not only deepen our understanding of EV behavior and function in biological systems, but will enable the development of novel electrical‐field based manipulation techniques for isolation, detection, characterization, and application of small EVs.
AUTHOR CONTRIBUTIONS
Sara Hassanpour Tamrin: Conceptualization; data curation; formal analysis; investigation; methodology; validation; visualization; writing—original draft; writing‐review and editing. Jolene Phelps: Data curation; writing—review and editing. Amir Sanati Nezhad: Writing—review and editing. Arindom Sen: Conceptualization; funding acquisition; resources; supervision; writing—original draft; writing—review and editing.
CONFLICT OF INTEREST STATEMENT
The authors declare no conflicts of interest.
Supporting information
Supporting Information
ACKNOWLEDGEMENT
This research was supported by the Natural Sciences and Engineering Research Council of Canada (RGPIN‐2019‐07196).
APPENDIX A.
Equations Describing Ion Distribution Around Charged Nanoparticles:
For a relatively low electric potential and low ion concentration, ion distribution in EDL structures can be mathematically expressed by Poisson‐Boltzmann (PB) equations. In the PB theory, ions are treated as point charges and their concentration is expressed according to the Boltzmann distribution (Equation A1), whereas electrostatic potential within the EDL, adjacent to a charged surface, is defined by the Poisson equation (Equation A2) (Kilic et al., 2007):
| (A1) |
| (A2) |
where ci is equilibrium concentration of the ith ionic species, is bulk molar concentration of the ith ionic species, zi is the valence of the ith ionic species, e is the elementary electric charge, kB is Boltzmann's constant, T is the absolute temperature, ɛr and ɛo are, respectively, the relative permittivity and the permittivity of a vacuum. The electric potential arising from the charged surface is denoted by, and ρ is the charge density (measured in coulomb.m−3). Owing to the point‐charge assumption associated with the PB theory, the ion concentration should not exceed a maximum concentration of cmax (Equation A3) while corresponding to a maximum surface potential of ψmax (Equation A4) (Kilic et al., 2007; Bazant et al., 2009). Effective diameter of ions is denoted by D where a maximum ion concentration corresponds to the cubic packing of ions (NA is Avogadro's number).
| (A3) |
| (A4) |
To describe the EV‐electrolyte interface, the GCS model was employed, and the EDL was modeled using a dual‐element concept including both Stern (inner element) and diffuse (outer element) layers (Figure 4). For a binary symmetric electrolyte (z1 = z2 = z), the GCS model can be mathematically expressed as:
| (A5) |
Using the GCS theory, EV‐electrolyte interfacial region was considered as two capacitances combined in series to describe the total EDL capacitance. According to the equation used for the capacitance of a parallel plate capacitor (Equation A6), the capacitance per unit area (specific capacitance, expressed in F.m−2) equals surface charge density (σ) stored in the capacitor (measured in coulomb.m−2) divided by potential difference in double layer (measured in volt), given by Equation A7:
| (A6) |
| (A7) |
where C and are, respectively, capacitance and specific capacitance, Q is the stored electric charge in a capacitor (measured in coulombs), A is total surface area of a charged surface corresponding to the conductive plates making up the capacitor, is voltage across the capacitor, is potential difference in a double layer around the charged surface, d is distance between the two conductive plates making up the capacitor. Given the definition of the specific capacitance (Equation A7), the individual capacitance of the diffuse layer () and the Helmholtz layer () can be expressed using Equation A8 and Equation A9, respectively. Total capacitance () of EDL which is less than any of individual capacitances can be defined using Equation A10:
| (A8) |
| (A9) |
| (A10) |
where ψ0 is electric potential at the charged surface,is electric potential of the bulk solution, is charge density within the Helmholtz compact layer, is charge density within the diffuse layer, a is radius of the charged nanoparticles (e.g., small EVs), H (corresponding to the radius of solvated ions) is thickness of the Helmholtz layer, and λ (corresponding to the Debye length) is thickness of the diffuse layer.
APPENDIX B.
Equations for Zeta (ζ)‐Potential Estimation of Charged Nanoparticles:
Considering colloidal particles, including proteins and small EVs, translocating in an electrolyte exposed to a steady and uniform electric field, EM (μ) of the particle can be described as the ratio of particle velocity (U) to strength of the applied electric field (E), given by Equation B1 (Oddy & Santiago, 2004). For diluted spherical particles with low surface charge, μ can be related to ζ‐potential using Henry's equation (Equation B2):
| (B1) |
| (B2) |
| (B3) |
| (B4) |
| (B5) |
where η is solution viscosity, ɛr is relative permittivity, ɛo is permittivity of the vacuum, a is hydrodynamic radius of the particle, κ is the Debye‐Hückel parameter, NA is Avogadro's number, e is elementary electric charge, I is ionic strength of the electrolyte, kB is Boltzmann's constant, T is the absolute temperature, f(κa) is Henry's function (Henry, 1931), and En(κa) is the exponential integral of order n. Henry's equation can be approximated to Hückel's (Equation B6) and Smoluchowski's (Equation B7) mobility expressions, where approximating Henry's function with a given value of 0.67 and 1, respectively. For the particles representing a κa value out of the acceptable range of Smoluchowski's and Hückel's approximations, Ohshima and co‐workers (Ohshima, 1994; Ohshima et al., 1983) showed that Henry's function can be approximated as a function of particle size and Debye length (λ) with negligible errors in a binary symmetrical electrolyte solution (equal valence of the cation and anion, ) with ionic mobile species of valence z (Equation B8).
| (B6) |
| (B7) |
| (B8) |
Equations for Electrical Valence (Z) Estimation of Charged Nanoparticles:
Effective valence (Zeff ), Debye‐Hückel‐Henry valence (ZDHH ), and Ohshima valence (introduced as ZOhshima in this study) are all quantized value of the electric charge (q), equal to the ratio of electric charge (in coulombs, C) to the elementary‐charge constant (e = 1.602176634×10−19 C).
| (B9) |
| (B10) |
Having the μ‐ζ relationship (Equation B8), EM could be simply converted into the surface charge density (σ) if there exists an appropriate ζ‐σ relationship for the spherical charged particles. Solving the PB equation for the electric potential around a spherical particle suspended in an electrolyte solution results in a ζ‐σ relationship. Compared to the numerical tables available to solve the spherical PB equation (Loeb et al., 1961; Hansen, 1962), Ohshima and co‐worker (Makino & Ohshima, 2010 ; Ohshima et al., 1982) derived the following analytical expression for the ζ‐σ relationship (Equation B11), which appeared simpler and more accurate for a spherical particle in a symmetrical electrolyte composed of ionic mobile species of valence z. Using Equation B11, the maximum relative error in surface charge estimation of a spherical particle was reduced to less than 1% for κa > 1, (Ohshima, 1994) supporting a good approximation for small EVs and proteins. ZOhshima can be directly derived from the surface charge density (ZOhshima = Aσ Ohshima /e), where A is total surface area of the charged particle (A = 2 ).
| (B11) |
Hassanpour Tamrin, S. , Phelps, J. , Nezhad, A. S. , & Sen, A. (2023). Critical Considerations in Determining the Surface Charge of Small Extracellular Vesicles. Journal of Extracellular Vesicles, 12, e12353. 10.1002/jev2.12353
REFERENCES
- Ageev, I. , & Rybin, Y. M. (2020). Features of measuring the electrical conductivity of distilled water in contact with air. Measurement Techniques, 62(10), 923–927. [Google Scholar]
- Agnihotri, S. M. , Ohshima, H. , Terada, H. , Tomoda, K. , & Makino, K. (2009). Electrophoretic mobility of colloidal gold particles in electrolyte solutions. Langmuir, 25(8), 4804–4807. [DOI] [PubMed] [Google Scholar]
- Ai, Y. , & Qian, S. (2011). Direct numerical simulation of electrokinetic translocation of a cylindrical particle through a nanopore using a Poisson–Boltzmann approach. Electrophoresis, 32(9), 996–1005. [DOI] [PubMed] [Google Scholar]
- Ailuno, G. , Baldassari, S. , Lai, F. , Florio, T. , & Caviglioli, G. (2020). Exosomes and extracellular vesicles as emerging theranostic platforms in cancer research. Cells, 9(12), 2569. 10.3390/cells9122569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akagi, T. , Kato, K. , Hanamura, N. , Kobayashi, M. , & Ichiki, T. (2014). Evaluation of desialylation effect on zeta potential of extracellular vesicles secreted from human prostate cancer cells by on‐chip microcapillary electrophoresis. Japanese Journal of Applied Physics, 53(6S), 06JL01. [Google Scholar]
- Akagi, T. , Kato, K. , Kobayashi, M. , Kosaka, N. , Ochiya, T. , & Ichiki, T. (2015). On‐chip immunoelectrophoresis of extracellular vesicles released from human breast cancer cells. PLoS One, 10(4), e0123603. 10.1371/journal.pone.0123603 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong, J. K. , Wenby, R. B. , Meiselman, H. J. , & Fisher, T. C. (2004). The hydrodynamic radii of macromolecules and their effect on red blood cell aggregation. Biophysical Journal, 87(6), 4259–4270. 10.1529/biophysj.104.047746 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Austin, J. , Fernandes, D. , Ruszala, M. J. , Hill, N. , & Corbett, J. (2020). Routine, ensemble characterisation of electrophoretic mobility in high and saturated ionic dispersions. Scientific reports, 10(1), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bard, A. J. , Faulkner, L. R. , & White, H. S. (2022) Electrochemical methods: Fundamentals and applications. John Wiley & Sons. [Google Scholar]
- Bazant, M. Z. , Kilic, M. S. , Storey, B. D. , & Ajdari, A. (2009). Towards an understanding of induced‐charge electrokinetics at large applied voltages in concentrated solutions. Advances in Colloid and Interface Science, 152(1–2), 48–88. 10.1016/j.cis.2009.10.001 [DOI] [PubMed] [Google Scholar]
- Betzer, O. , Barnoy, E. , Sadan, T. , Elbaz, I. , Braverman, C. , Liu, Z. , & Popovtzer, R. (2020). Advances in imaging strategies for in vivo tracking of exosomes. Wiley Interdisciplinary Reviews: Nanomedicine and Nanobiotechnology, 12(2), e1594. [DOI] [PubMed] [Google Scholar]
- Bondar, O. V. , Saifullina, D. , Shakhmaeva, I. , Mavlyutova, I. , & Abdullin, T. (2012). Monitoring of the zeta potential of human cells upon reduction in their viability and interaction with polymers. Acta Naturae (англоязычная версия), 41(12), 78–81. [PMC free article] [PubMed] [Google Scholar]
- Booth, F. (1951). The dielectric constant of water and the saturation effect. The Journal of Chemical Physics, 19(4), 391–394. [Google Scholar]
- Booth, F. (1955). Dielectric constant of polar liquids at high field strengths. The Journal of Chemical Physics, 23(3), 453–457. [Google Scholar]
- Botin, D. , Carrique, F. , Ruiz‐Reina, E. , & Palberg, T. (2020). Non‐monotonic concentration dependence of the electro‐phoretic mobility of charged spheres in realistic salt free suspensions. The Journal of Chemical Physics, 152(24), 244902. [DOI] [PubMed] [Google Scholar]
- Brown, M. A. , Abbas, Z. , Kleibert, A. , Green, R. G. , Goel, A. , May, S. , & Squires, T. M. (2016). Determination of surface potential and electrical double‐layer structure at the aqueous electrolyte‐nanoparticle interface. Physical Review X, 6(1), 011007. [Google Scholar]
- Buckingham, A. (1956). Theory of the dielectric constant at high field strengths. The Journal of Chemical Physics, 25(3), 428–434. [Google Scholar]
- Bunggulawa, E. J. , Wang, W. , Yin, T. , Wang, N. , Durkan, C. , Wang, Y. , & Wang, G. (2018). Recent advancements in the use of exosomes as drug delivery systems. Journal of Nanobiotechnology, 16(1), 81. 10.1186/s12951-018-0403-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burt, R. , Birkett, G. , & Zhao, X. (2014). A review of molecular modelling of electric double layer capacitors. Physical Chemistry Chemical Physics, 16(14), 6519–6538. [DOI] [PubMed] [Google Scholar]
- Cannan, R. K. , Kibrick, A. , & Palmer, A. (1941). The amphoteric properties of egg albumin. Annals of the New York Academy of Sciences, 41(4), 243–266. [Google Scholar]
- Carvalho, M. , Felício, M. R. , Santos, N. C. , Gonçalves, S. , & Domingues, M. M. (2018). Application of light scattering techniques to nanoparticle characterization and development. Frontiers in Chemistry, 6, 237. 10.3389/fchem.2018.00237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cha, E. J. , Kim, J. E. , & Ahn, C. H. (2009). Stabilized polymeric micelles by electrostatic interactions for drug delivery system. European Journal of Pharmaceutical Sciences, 38(4), 341–346. 10.1016/j.ejps.2009.08.006 [DOI] [PubMed] [Google Scholar]
- Chand, S. , Gowen, A. M. , Savine, M. , Moore, D. Y. , Clark, A. R. , Huynh, W. , Wu, N. , Odegaard, K. E. , Weyrich, L. , Bevins, R. A. , Fox, H. S. , Pendyala, G. , & Yelamanchili, S. V. (2021). A comprehensive study to delineate the role of an extracellular vesicle‐associated microRNA‐29a in chronic methamphetamine use disorder. Journal of Extracellular Vesicles, 10(14), e12177. 10.1002/jev2.12177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chapman, D. L. (1913). LI. A contribution to the theory of electrocapillarity. The London, Edinburgh, and Dublin philosophical magazine and journal of science, 25(148), 475–481. [Google Scholar]
- Charoenviriyakul, C. , Takahashi, Y. , Morishita, M. , Nishikawa, M. , & Takakura, Y. (2018). Role of extracellular vesicle surface proteins in the pharmacokinetics of extracellular vesicles. Molecular pharmaceutics, 15(3), 1073–1080. [DOI] [PubMed] [Google Scholar]
- Chen, M. , Liu, X. , & Fahr, A. (2011). Skin penetration and deposition of carboxyfluorescein and temoporfin from different lipid vesicular systems: In vitro study with finite and infinite dosage application. International journal of pharmaceutics, 408(1–2), 223–234. [DOI] [PubMed] [Google Scholar]
- Chibowski, E. , & Szcześ, A. (2016). Zeta potential and surface charge of DPPC and DOPC liposomes in the presence of PLC enzyme. Adsorption, 22(4), 755–765. [Google Scholar]
- Cocucci, E. , & Meldolesi, J. (2015). Ectosomes and exosomes: Shedding the confusion between extracellular vesicles. Trends in cell biology, 25(6), 364–372. [DOI] [PubMed] [Google Scholar]
- Conway, B. , Bockris, J. M. , & Ammar, I. (1951). The dielectric constant of the solution in the diffuse and Helmholtz double layers at a charged interface in aqueous solution. Transactions of the Faraday Society, 47, 756–766. [Google Scholar]
- Correll, V. L. , Otto, J. J. , Risi, C. M. , Main, B. P. , Boutros, C. , Kislinger, T. , Galkin, V. E. , Nyalwidhe, J. O. , Semmes, O. J. , & Yang, L. (2022). Optimization of small extracellular vesicle isolation from expressed prostatic secretions in urine for in‐depth proteomic analysis. Journal of Extracellular Vesicles, 11(2), e12184. 10.1002/jev2.12184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Culkin, F. (1986). Calibration of standard seawater in electrical conductivity. Science of the Total Environment, 49, 1–7. [Google Scholar]
- Danaei, M. , Dehghankhold, M. , Ataei, S. M. , Hasanzadeh Davarani, F. , Javanmard, R. , Dokhani, A. , Khorasani, S. N. , & Mozafari, M. R. (2018). Impact of particle size and polydispersity index on the clinical applications of lipidic nanocarrier systems. Pharmaceutics, 10(2), 57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delgado, A. , Gonzälez‐Caballero, F. , Cabrerizo, M. , & Alados, I. (1987). The primary electroviscous effect in monodisperse polystyrene suspensions. Acta polymerica, 38(1), 66–70. [Google Scholar]
- Diaz‐Armas, G. G. , Cervantes‐Gonzalez, A. P. , Martinez‐Duarte, R. , & Perez‐Gonzalez, V. H. (2022). Electrically driven microfluidic platforms for exosome manipulation and characterization. Electrophoresis, 43(1–2), 327–339. [DOI] [PubMed] [Google Scholar]
- Doyle, L. M. , & Wang, M. Z. (2019). Overview of extracellular vesicles, their origin, composition, purpose, and methods for exosome isolation and analysis. Cells, 8(7), 727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dukhin, A. S. , & Goetz, J. (2010). Fundamentals of interface and colloid science. In Studies in Interface Science (vol. 24, 21–89). Elsevier. [Google Scholar]
- Duran‐Meza, A. , Villagrana‐Escareño, M. , Ruiz‐García, J. , Knobler, C. , & Gelbart, W. (2021). Controlling the surface charge of simple viruses. Plos one, 16(9), e0255820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edward, J. T. (1970). Molecular volumes and the Stokes‐Einstein equation. Journal of chemical education, 47(4), 261. [Google Scholar]
- Everts, J. C. , & Ravnik, M. (2018). Complex electric double layers in charged topological colloids. Scientific reports, 8(1), 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng, K. , Xie, X. , Yuan, J. , Gong, L. , Zhu, Z. , Zhang, J. , Li, H. , Yang, Y. , & Wang, Y. (2021). Reversing the surface charge of MSC‐derived small extracellular vesicles by εPL‐PEG‐DSPE for enhanced osteoarthritis treatment. Journal of Extracellular Vesicles, 10(13), e12160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filoti, D. I. , Shire, S. J. , Yadav, S. , & Laue, T. M. (2015). Comparative study of analytical techniques for determining protein charge. Journal of Pharmaceutical Sciences, 104(7), 2123–2131. 10.1002/jps.24454 [DOI] [PubMed] [Google Scholar]
- Forsyth, B. , Liu, B. Y. , & Romay, F. J. (1998). Particle charge distribution measurement for commonly generated laboratory aerosols. Aerosol Science and Technology, 28(6), 489–501. [Google Scholar]
- Fuller, M. , & Köper, I. (2018). Polyelectrolyte‐coated gold nanoparticles: The effect of salt and polyelectrolyte concentration on colloidal stability. Polymers (Basel), 10(12), 1336. 10.3390/polym10121336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fulton, R. L. (2009). The nonlinear dielectric behavior of water: Comparisons of various approaches to the nonlinear dielectric increment. The Journal of chemical physics, 130(20), 204503. [DOI] [PubMed] [Google Scholar]
- Gadani, D. , Rana, V. , Bhatnagar, S. , Prajapati, A. , & Vyas, A. (2012). Effect of salinity on the dielectric properties of water.
- Gardiner, C. , Ferreira, Y. J. , Dragovic, R. A. , Redman, C. W. , & Sargent, I. L. (2013). Extracellular vesicle sizing and enumeration by nanoparticle tracking analysis. Journal of Extracellular Vesicles, 2(1), 19671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gitlin, I. , Carbeck, J. D. , & Whitesides, G. M. (2006). Why are proteins charged? Networks of charge–charge interactions in proteins measured by charge ladders and capillary electrophoresis. Angewandte Chemie International Edition, 45(19), 3022–3060. [DOI] [PubMed] [Google Scholar]
- Gokarn, Y. R. , Fesinmeyer, R. M. , Saluja, A. , Razinkov, V. I. , Chase, S. F. , Laue, T. M. , & Brems, D. N. (2011). Effective charge measurements reveal selective and preferential accumulation of anions, but not cations, at the protein surface in dilute salt solutions. Protein Science, 20(3), 580–587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golnabi, H. , Matloob, M. , Bahar, M. , & Sharifian, M. (2009). Investigation of electrical conductivity of different water liquids and electrolyte solutions.
- Gonzalez, M. I. , González‐Arjona, M. , Santos‐Coquillat, A. , Vaquero, J. , Vázquez‐Ogando, E. , de Molina, A. , Peinado, H. , Desco, M. , & Salinas, B. (2021). Covalently labeled fluorescent exosomes for in vitro and in vivo applications. Biomedicines, 9(1), 81. 10.3390/biomedicines9010081 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorin, M. H. , & Mover, L. S. (1942). The valence of corpuscular proteins. The Journal of General Physiology, 25(6), 785–803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gouy, M. (1910). Sur la constitution de la charge électrique à la surface d'un électrolyte. Journal of Physics: Theories and Applications, 9(1), 457–468. [Google Scholar]
- Grahame, D. C. (1947). The electrical double layer and the theory of electrocapillarity. Chemical reviews, 41(3), 441–501. [DOI] [PubMed] [Google Scholar]
- Grimes, B. A. , & Liapis, A. I. (2001). Modeling and analysis of the electrokinetic mass transport and adsorption mechanisms of a charged adsorbate in capillary electrochromatography systems employing charged nonporous adsorbent particles. Journal of Colloid and Interface Science, 234(1), 223–243. 10.1006/jcis.2000.7269 [DOI] [PubMed] [Google Scholar]
- Guckeisen, T. , Hosseinpour, S. , & Peukert, W. (2019). Isoelectric points of proteins at the air/liquid interface and in solution. Langmuir, 35(14), 5004–5012. [DOI] [PubMed] [Google Scholar]
- Guo, S.‐C. , Tao, S.‐C. , & Dawn, H. (2018). Microfluidics‐based on‐a‐chip systems for isolating and analysing extracellular vesicles. Journal of Extracellular Vesicles, 7(1), 1508271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagey, D. W. , Kordes, M. , Görgens, A. , Mowoe, M. O. , Nordin, J. Z. , Moro, C. F. , Löhr, J. M. , & El Andaloussi, S. (2021). Extracellular vesicles are the primary source of blood‐borne tumour‐derived mutant KRAS DNA early in pancreatic cancer. Journal of Extracellular Vesicles, 10(12), e12142. 10.1002/jev2.12142 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen, R. S. (1962). The electrical double layer around a spherical colloid particle. computation of the potential, charge density, and free energy of the electrical double layer around a spherical colloid particle. Journal of the American Chemical Society, 84(7), 1325–1326. [Google Scholar]
- Hassanpour Tamrin, S. , Sanati Nezhad, A. , & Sen, A. (2021). Label‐free isolation of exosomes using microfluidic technologies. ACS Nano, 15(11), 17047–17079. 10.1021/acsnano.1c03469 [DOI] [PubMed] [Google Scholar]
- Henderson, D. , & Boda, D. (2009). Insights from theory and simulation on the electrical double layer. Physical Chemistry Chemical Physics, 11(20), 3822–3830. [DOI] [PubMed] [Google Scholar]
- Henry, D. (1931). The cataphoresis of suspended particles. Part I.—The equation of cataphoresis. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 133(821), 106–129. [Google Scholar]
- Hosseini‐Beheshti, E. , Pham, S. , Adomat, H. , Li, N. , & Guns, E. S. T. (2012). Exosomes as biomarker enriched microvesicles: Characterization of exosomal proteins derived from a panel of prostate cell lines with distinct AR phenotypes. Molecular & Cellular Proteomics, 11(10), 863–885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang, J. , Qiao, R. , Sumpter, B. G. , & Meunier, V. (2010). Effect of diffuse layer and pore shapes in mesoporous carbon supercapacitors. Journal of Materials Research, 25(8), 1469–1475. [Google Scholar]
- Huang, J. , Sumpter, B. G. , & Meunier, V. (2008a). Theoretical model for nanoporous carbon supercapacitors. Angewandte Chemie, 120(3), 530–534. [DOI] [PubMed] [Google Scholar]
- Huang, J. , Sumpter, B. G. , & Meunier, V. (2008b). A universal model for nanoporous carbon supercapacitors applicable to diverse pore regimes, carbon materials, and electrolytes. Chemistry–A European Journal, 14(22), 6614–6626. [DOI] [PubMed] [Google Scholar]
- Huang, J. , Sumpter, B. G. , Meunier, V. , Yushin, G. , Portet, C. , & Gogotsi, Y. (2010). Curvature effects in carbon nanomaterials: Exohedral versus endohedral supercapacitors. Journal of Materials Research, 25(8), 1525–1531. [Google Scholar]
- Israelachvili, J. N. (2011). Intermolecular and surface forces. Academic press. [Google Scholar]
- Jachimska, B. , Wasilewska, M. , & Adamczyk, Z. (2008). Characterization of globular protein solutions by dynamic light scattering, electrophoretic mobility, and viscosity measurements. Langmuir, 24(13), 6866–6872. 10.1021/la800548p [DOI] [PubMed] [Google Scholar]
- Jakubec, M. , Maple‐Grødem, J. , Akbari, S. , Nesse, S. , Halskau, Ø. , & Mork‐Jansson, A. E. (2020). Plasma‐derived exosome‐like vesicles are enriched in lyso‐phospholipids and pass the blood‐brain barrier. Plos one, 15(9), e0232442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang, L. , Dong, H. , Cao, H. , Ji, X. , Luan, S. , & Liu, J. (2019). Exosomes in pathogenesis, diagnosis, and treatment of Alzheimer's disease. Medical science monitor: International medical journal of experimental and clinical research, 25, 3329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordon, K. (2014). Real‐time elctrophoretic mobility in membrane confined electrophoresis. University of New Hampshire. [Google Scholar]
- Jouyban, A. , & Kenndler, E. (2006). Theoretical and empirical approaches to express the mobility of small ions in capillary electrophoresis. Electrophoresis, 27(5–6), 992–1005. 10.1002/elps.200500696 [DOI] [PubMed] [Google Scholar]
- Jung, M. K. , & Mun, J. Y. (2018). Sample preparation and imaging of exosomes by transmission electron microscopy. JoVE (Journal of Visualized Experiments), 131, e56482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung, S. , Sen, A. , Rosenberg, L. , & Behie, L. A. (2010). Identification of growth and attachment factors for the serum‐free isolation and expansion of human mesenchymal stromal cells. Cytotherapy, 12(5), 637–657. 10.3109/14653249.2010.495113 [DOI] [PubMed] [Google Scholar]
- Kaddour, H. , Panzner, T. D. , Welch, J. L. , Shouman, N. , Mohan, M. , Stapleton, J. T. , & Okeoma, C. M. (2020). Electrostatic surface properties of blood and semen extracellular vesicles: Implications of sialylation and HIV‐induced changes on EV internalization. Viruses, 12(10), 1117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalluri, R. , & LeBleu, V. S. (2020). The biology, function, and biomedical applications of exosomes. Science, 367(6478), eaau6977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang, Y. , Purcell, E. , Palacios‐Rolston, C. , Lo, T. , Ramnath, N. , Jolly, S. , & Nagrath, S. (2019). Isolation and profiling of circulating tumor‐associated exosomes using extracellular vesicular lipid‐protein binding affinity based microfluidic device. Small, 15(47), e1903600. 10.1002/smll.201903600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang, Y. T. , Kim, Y. J. , Bu, J. , Cho, Y. H. , Han, S. W. , & Moon, B. I. (2017). High‐purity capture and release of circulating exosomes using an exosome‐specific dual‐patterned immunofiltration (ExoDIF) device. Nanoscale, 9(36), 13495–13505. 10.1039/c7nr04557c [DOI] [PubMed] [Google Scholar]
- Kanninen, K. M. , Bister, N. , Koistinaho, J. , & Malm, T. (2016). Exosomes as new diagnostic tools in CNS diseases. Biochimica et Biophysica Acta (BBA)‐Molecular Basis of Disease, 1862(3), 403–410. [DOI] [PubMed] [Google Scholar]
- Kaszuba, M. , McKnight, D. , Connah, M. T. , McNeil‐Watson, F. K. , & Nobbmann, U. (2008). Measuring sub nanometre sizes using dynamic light scattering. Journal of nanoparticle research, 10(5), 823–829. [Google Scholar]
- Kilic, M. S. , Bazant, M. Z. , & Ajdari, A. (2007). Steric effects in the dynamics of electrolytes at large applied voltages. I. Double‐layer charging. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 75(2), Pt 1, 021502. 10.1103/PhysRevE.75.021502 [DOI] [PubMed] [Google Scholar]
- Kim, S. M. , Yang, Y. , Oh, S. J. , Hong, Y. , Seo, M. , & Jang, M. (2017). Cancer‐derived exosomes as a delivery platform of CRISPR/Cas9 confer cancer cell tropism‐dependent targeting. Journal of Controlled Release, 266, 8–16. [DOI] [PubMed] [Google Scholar]
- Kinraide, T. B. , & Wang, P. (2010). The surface charge density of plant cell membranes (σ): An attempt to resolve conflicting values for intrinsic σ. Journal of Experimental Botany, 61(9), 2507–2518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinraide, T. B. , Yermiyahu, U. , & Rytwo, G. (1998). Computation of surface electrical potentials of plant cell membranes: Correspondence to published zeta potentials from diverse plant sources. Plant Physiology, 118(2), 505–512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kowal, J. , Arras, G. , Colombo, M. , Jouve, M. , Morath, J. P. , Primdal‐Bengtson, B. , Dingli, F. , Loew, D. , Tkach, M. , & Théry, C. (2016). Proteomic comparison defines novel markers to characterize heterogeneous populations of extracellular vesicle subtypes. Proceedings of the National Academy of Sciences, 113, E968–E977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan, M. (2017). A simple model for electrical charge in globular macromolecules and linear polyelectrolytes in solution. The Journal of Chemical Physics, 146(20), 51011–510112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar, A. , Sundaram, K. , Mu, J. , Dryden, G. W. , Sriwastva, M. K. , Lei, C. , Zhang, L. , Qiu, X. , Xu, F. , Yan, J. , Zhang, X. , Park, J. W. , Merchant, M. L. , Bohler, H. C. , Wang, B. , Zhang, S. , Qin, C. , Xu, Z. , Han, X. , … Zhang, H. (2021). High‐fat diet‐induced upregulation of exosomal phosphatidylcholine contributes to insulin resistance. Nature Communications, 12(1), 1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar, S. , & Sharma, B. (2020). Leveraging electrostatic interactions for drug delivery to the joint. Bioelectricity, 2(2), 82–100. 10.1089/bioe.2020.0014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazzari, S. , Moscatelli, D. , Codari, F. , Salmona, M. , Morbidelli, M. , & Diomede, L. (2012). Colloidal stability of polymeric nanoparticles in biological fluids. Journal of Nanoparticle Research, 14(6), 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leggio, C. , Galantini, L. , & Pavel, N. V. (2008). About the albumin structure in solution: Cigar expanded form versus heart Normal shape. Physical Chemistry Chemical Physics, 10(45), 6741–6750. 10.1039/b808938h [DOI] [PubMed] [Google Scholar]
- Leung, C. , Kinns, H. , Hoogenboom, B. W. , Howorka, S. , & Mesquida, P. (2009). Imaging surface charges of individual biomolecules. Nano letters, 9(7), 2769–2773. [DOI] [PubMed] [Google Scholar]
- Lewis, E. (1980). The practical salinity scale 1978 and its antecedents. IEEE Journal of Oceanic Engineering, 5(1), 3–8. [Google Scholar]
- Liang, G. , Zhu, Y. , Ali, D. J. , Tian, T. , Xu, H. , Si, K. , Sun, B. , Chen, B. , & Xiao, Z. (2020). Engineered exosomes for targeted co‐delivery of miR‐21 inhibitor and chemotherapeutics to reverse drug resistance in colon cancer. Journal of Nanobiotechnology, 18(1), 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang, Y. , Duan, L. , Lu, J. , & Xia, J. (2021). Engineering exosomes for targeted drug delivery. Theranostics, 11(7), 3183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang, Y. , Lehrich, B. M. , Zheng, S. , & Lu, M. (2021). Emerging methods in biomarker identification for extracellular vesicle‐based liquid biopsy. Journal of Extracellular Vesicles, 10(7), e12090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin, B. , Lei, Y. , Wang, J. , Zhu, L. , Wu, Y. , Zhang, H. , Wu, L. , Zhang, P. , & Yang, C. (2021). Microfluidic‐based exosome analysis for liquid biopsy. Small Methods, 5(3), 2001131. [DOI] [PubMed] [Google Scholar]
- Livshts, M. A. , Khomyakova, E. , Evtushenko, E. G. , Lazarev, V. N. , Kulemin, N. A. , Semina, S. E. , Generozov, E. V. , & Govorun, V. M. (2015). Isolation of exosomes by differential centrifugation: Theoretical analysis of a commonly used protocol. Scientific Reports, 5, 17319. 10.1038/srep17319 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llorente, A. , Skotland, T. , Sylvänne, T. , Kauhanen, D. , Róg, T. , Orłowski, A. , Vattulainen, I. , Ekroos, K. , & Sandvig, K. (2013). Molecular lipidomics of exosomes released by PC‐3 prostate cancer cells. Biochimica et biophysica acta (BBA)‐Molecular and Cell Biology of Lipids, 1831(7), 1302–1309. [DOI] [PubMed] [Google Scholar]
- Loeb, A. L. , Overbeek, J. T. G. , Wiersema, H. , & King, C. (1961). The electrical double layer around a spherical colloid particle. Journal of The Electrochemical Society, 108(12), 269C. [Google Scholar]
- Lombardo, D. , Kiselev, M. A. , Magazù, S. , & Calandra, P. (2015). Amphiphiles self‐assembly: Basic concepts and future perspectives of supramolecular approaches. Advances in Condensed Matter Physics, 2015, 151683. [Google Scholar]
- Luo, Z. , Åkerman, B. , Zhang, S. , & Nordén, B. (2010). Structures of self‐assembled amphiphilic peptide‐heterodimers: Effects of concentration, pH, temperature and ionic strength. Soft Matter, 6(10), 2260–2270. [Google Scholar]
- Makino, K. , & Ohshima, H. (2010). Electrophoretic mobility of a colloidal particle with constant surface charge density. Langmuir, 26(23), 18016–18019. 10.1021/la1035745 [DOI] [PubMed] [Google Scholar]
- Masliyah, J. H. , & Bhattacharjee, S. (2006). Electrokinetic and colloid transport phenomena. John Wiley & Sons. [Google Scholar]
- Matsumoto, A. , Takahashi, Y. , Nishikawa, M. , Sano, K. , Morishita, M. , Charoenviriyakul, C. , Saji, H. , & Takakura, Y. (2017). Role of phosphatidylserine‐derived negative surface charges in the recognition and uptake of intravenously injected B16BL6‐derived exosomes by macrophages. Journal of Pharmaceutical Sciences, 106(1), 168–175. [DOI] [PubMed] [Google Scholar]
- Matsumura, S. , Minamisawa, T. , Suga, K. , Kishita, H. , Akagi, T. , Ichiki, T. , Ichikawa, Y. , & Shiba, K. (2019). Subtypes of tumour cell‐derived small extracellular vesicles having differently externalized phosphatidylserine. Journal of Extracellular Vesicles, 8(1), 1579541. 10.1080/20013078.2019.1579541 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattera, V. S. , Pereyra Gerber, P. , Glisoni, R. J. , Ostrowski, M. , Verstraeten, S. V. , Pasquini, J. M. , & Correale, J. (2020). Extracellular vesicles containing the transferrin receptor as nanocarriers of apotransferrin. Journal of Neurochemistry, 155, 327–338. [DOI] [PubMed] [Google Scholar]
- Medrano, M. , Perez, A. , Lobry, L. , & Peters, F. (2009). Electrophoretic mobility of silica particles in a mixture of toluene and ethanol at different particle concentrations. Langmuir, 25(20), 12034–12039. [DOI] [PubMed] [Google Scholar]
- Melzer, C. , Rehn, V. , Yang, Y. , Bähre, H. , von der Ohe, J. , & Hass, R. (2019). Taxol‐loaded MSC‐derived exosomes provide a therapeutic vehicle to target metastatic breast cancer and other carcinoma cells. Cancers, 11(6), 798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendivil‐Alvarado, H. , Limon‐Miro, A. T. , Carvajal‐Millan, E. , Lizardi‐Mendoza, J. , Mercado‐Lara, A. , Coronado‐Alvarado, C. D. , Rascón‐Durán, M. L. , Anduro‐Corona, I. , Talamás‐Lara, D. , Rascón‐Careaga, A. , & Astiazarán‐García, H. F. (2023). Extracellular vesicles and their zeta potential as future markers associated with nutrition and molecular biomarkers in breast cancer. International Journal of Molecular Sciences, 24(7), 6810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michen, B. , & Graule, T. (2010). Isoelectric points of viruses. Journal of Applied Microbiology, 109(2), 388–397. [DOI] [PubMed] [Google Scholar]
- Midekessa, G. , Godakumara, K. , Ord, J. , Viil, J. , Lättekivi, F. , Dissanayake, K. , Kopanchuk, S. , Rinken, A. , Andronowska, A. , Bhattacharjee, S. , Rinken, T. , & Fazeli, A. (2020). Zeta potential of extracellular vesicles: Toward understanding the attributes that determine colloidal stability. ACS Omega, 5, 16701–16710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milanova, D. , Chambers, R. D. , Bahga, S. S. , & Santiago, J. G. (2011). Electrophoretic mobility measurements of fluorescent dyes using on‐chip capillary electrophoresis. Electrophoresis, 32(22), 3286–3294. 10.1002/elps.201100210 [DOI] [PubMed] [Google Scholar]
- Min, L. , Zhu, S. , Chen, L. , Liu, X. , Wei, R. , Zhao, L. , Yang, Y. , Zhang, Z. , Kong, G. , Li, P. , & Zhang, S. (2019). Evaluation of circulating small extracellular vesicles derived miRNAs as biomarkers of early colon cancer: A comparison with plasma total miRNAs. Journal of Extracellular Vesicles, 8(1), 1643670. 10.1080/20013078.2019.1643670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molnár, G. , Fendrych, M. , & Friml, J. (2016). Plasma membrane: Negative attraction. Nature Plants, 2(7), 1–2. [DOI] [PubMed] [Google Scholar]
- Moody, T. P. , Kingsbury, J. S. , Durant, J. A. , Wilson, T. J. , Chase, S. F. , & Laue, T. M. (2005). Valence and anion binding of bovine ribonuclease A between pH 6 and 8. Analytical Biochemistry, 336(2), 243–252. [DOI] [PubMed] [Google Scholar]
- Moody, T. P. , & Shepard, H. K. (2004). Nonequilibrium thermodynamics of membrane‐confined electrophoresis. Biophysical Chemistry, 108(1–3), 51–76. [DOI] [PubMed] [Google Scholar]
- Naumowicz, M. , & Figaszewski, Z. A. (2014). The effect of pH on the electrical capacitance of phosphatidylcholine–phosphatidylserine system in bilayer lipid membrane. The Journal of membrane biology, 247(4), 361–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oddy, M. H. , & Santiago, J. G. (2004). A method for determining electrophoretic and electroosmotic mobilities using AC and DC electric field particle displacements. Journal of Colloid and Interface Science, 269(1), 192–204. 10.1016/s0021-9797(03)00601-5 [DOI] [PubMed] [Google Scholar]
- Ohshima, H. (1994). A simple expression for Henry's function for the retardation effect in electrophoresis of spherical colloidal particles. Journal of Colloid and Interface Science, 168(1), 269–271. [Google Scholar]
- Ohshima, H. (2001). Approximate analytic expression for the electrophoretic mobility of a spherical colloidal particle. Journal of Colloid and Interface Science, 239(2), 587–590. 10.1006/jcis.2001.7608 [DOI] [PubMed] [Google Scholar]
- Ohshima, H. (2014). Interaction of colloidal particles. In Colloid and interface science in pharmaceutical research and development, 1–28. Elsevier. [Google Scholar]
- Ohshima, H. , Healy, T. W. , & White, L. R. (1982). Accurate analytic expressions for the surface charge density/surface potential relationship and double‐layer potential distribution for a spherical colloidal particle. Journal of colloid and interface science, 90(1), 17–26. [Google Scholar]
- Ohshima, H. , Healy, T. W. , & White, L. R. (1983). Approximate analytic expressions for the electrophoretic mobility of spherical colloidal particles and the conductivity of their dilute suspensions. Journal of the Chemical Society, Faraday Transactions 2: Molecular and Chemical Physics, 79(11), 1613–1628. [Google Scholar]
- Oldham, K. B. (2008). A Gouy–Chapman–Stern model of the double layer at a (metal)/(ionic liquid) interface. Journal of Electroanalytical Chemistry, 613(2), 131–138. [Google Scholar]
- Olsson, M. H. , Søndergaard, C. R. , Rostkowski, M. , & Jensen, J. H. (2011). PROPKA3: Consistent treatment of internal and surface residues in empirical p K a predictions. Journal of chemical theory and computation, 7(2), 525–537. [DOI] [PubMed] [Google Scholar]
- Palberg, T. , Medebach, M. , Garbow, N. , Evers, M. , Fontecha, A. B. , Reiber, H. , & Bartsch, E. (2004). Electrophoresis of model colloidal spheres in low salt aqueous suspension. Journal of Physics: Condensed Matter, 16(38), S4039. [Google Scholar]
- Petersen, K. E. , Shiri, F. , White, T. , Bardi, G. T. , Sant, H. J. , Gale, B. K. , & Hood, J. L. (2018). Exosome isolation: Cyclical electrical field flow fractionation in low‐ionic‐strength fluids. Analytical chemistry, 90(21), 12783–12790. [DOI] [PubMed] [Google Scholar]
- Peyman, A. , Gabriel, C. , & Grant, E. (2007). Complex permittivity of sodium chloride solutions at microwave frequencies. Bioelectromagnetics: Journal of the Bioelectromagnetics Society, The Society for Physical Regulation in Biology and Medicine, The European Bioelectromagnetics Association, 28(4), 264–274. [DOI] [PubMed] [Google Scholar]
- Pochapski, D. J. , Carvalho dos Santos, C. , Leite, G. W. , Pulcinelli, S. H. , & Santilli, C. V. (2021). Zeta potential and colloidal stability predictions for inorganic nanoparticle dispersions: Effects of experimental conditions and electrokinetic models on the interpretation of results. Langmuir, 37(45), 13379–13389. [DOI] [PubMed] [Google Scholar]
- Popowski, K. , Lutz, H. , Hu, S. , George, A. , Dinh, U. , & Cheng, K. (2020). Exosome therapeutics for lung regenerative medicine. Journal of Extracellular Vesicles, 9(1), 1785161. 10.1080/20013078.2020.1785161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen, M. K. , Pedersen, J. N. , & Marie, R. (2020). Size and surface charge characterization of nanoparticles with a salt gradient. Nature Communications, 11(1), 2337. 10.1038/s41467-020-15889-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiber, H. , Köller, T. , Palberg, T. , Carrique, F. , Reina, E. R. , & Piazza, R. (2007). Salt concentration and particle density dependence of electrophoretic mobilities of spherical colloids in aqueous suspension. Journal of colloid and interface science, 309(2), 315–322. [DOI] [PubMed] [Google Scholar]
- Ren, H. , He, Y. , Liang, J. , Cheng, Z. , Zhang, M. , Zhu, Y. , Hong, C. , Qin, J. , Xu, X. , & Wang, J. (2019). Role of liposome size, surface charge, and PEGylation on rheumatoid arthritis targeting therapy. ACS applied materials & interfaces, 11(22), 20304–20315. 10.1021/acsami.8b22693 [DOI] [PubMed] [Google Scholar]
- Ribeiro, L. N. d. M. , Couto, V. M. , Fraceto, L. F. , & De Paula, E. (2018). Use of nanoparticle concentration as a tool to understand the structural properties of colloids. Scientific reports, 8(1), 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Righetti, G. (2004). Determination of the isoelectric point of proteins by capillary isoelectric focusing. Journal of chromatography A, 1037(1–2), 491–499. [DOI] [PubMed] [Google Scholar]
- Rikkert, L. G. , Nieuwland, R. , Terstappen, L. , & Coumans, F. (2019). Quality of extracellular vesicle images by transmission electron microscopy is operator and protocol dependent. Journal of extracellular vesicles, 8(1), 1555419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell, B. , Jachimska, B. , Kralka, I. , Mulheran, P. , & Chen, Y. (2016). Human serum albumin encapsulated gold nanoclusters: Effects of cluster synthesis on natural protein characteristics. Journal of Materials Chemistry B, 4(42), 6876–6882. [DOI] [PubMed] [Google Scholar]
- Saari, H. , Turunen, T. , Lõhmus, A. , Turunen, M. , Jalasvuori, M. , Butcher, S. J. , Ylä‐Herttuala, S. , Viitala, T. , Cerullo, V. , Siljander, R. , & Yliperttula, M. (2020). Extracellular vesicles provide a capsid‐free vector for oncolytic adenoviral DNA delivery. Journal of Extracellular Vesicles, 9(1), 1747206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salarpour, S. , Forootanfar, H. , Pournamdari, M. , Ahmadi‐Zeidabadi, M. , Esmaeeli, M. , & Pardakhty, A. (2019). Paclitaxel incorporated exosomes derived from glioblastoma cells: Comparative study of two loading techniques. DARU Journal of Pharmaceutical Sciences, 27(2), 533–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt, H. , Seitz, S. , Hassel, E. , & Wolf, H. (2018). The density–salinity relation of standard seawater. Ocean Science, 14(1), 15–40. [Google Scholar]
- Semenov, I. , Papadopoulos, P. , Stober, G. , & Kremer, F. (2010). Ionic concentration‐and pH‐dependent electrophoretic mobility as studied by single colloid electrophoresis. Journal of Physics: Condensed Matter, 22(49), 494109. [DOI] [PubMed] [Google Scholar]
- Shen, M. , & Chen, T. (2021). Mesenchymal stem cell‐derived exosomes and their potential agents in hematological diseases. Oxidative Medicine and Cellular Longevity, 2021, 4539453. 10.1155/2021/4539453 [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Shi, L. , Kuhnell, D. , Borra, V. J. , Langevin, S. M. , Nakamura, T. , & Esfandiari, L. (2019). Rapid and label‐free isolation of small extracellular vesicles from biofluids utilizing a novel insulator based dielectrophoretic device. Lab on a Chip, 19(21), 3726–3734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sillero, A. , & Maldonado, A. (2006). Isoelectric point determination of proteins and other macromolecules: Oscillating method. Computers in Biology and Medicine, 36(2), 157–166. [DOI] [PubMed] [Google Scholar]
- Sims, K. R. , He, B. , Koo, H. , & Benoit, D. S. W. (2020). Electrostatic interactions enable nanoparticle delivery of the flavonoid myricetin. ACS Omega, 5(22), 12649–12659. 10.1021/acsomega.9b04101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skotland, T. , Ekroos, K. , Kauhanen, D. , Simolin, H. , Seierstad, T. , Berge, V. , Sandvig, K. , & Llorente, A. (2017). Molecular lipid species in urinary exosomes as potential prostate cancer biomarkers. European journal of cancer, 70, 122–132. [DOI] [PubMed] [Google Scholar]
- Skotland, T. , Hessvik, N. P. , Sandvig, K. , & Llorente, A. (2019). Exosomal lipid composition and the role of ether lipids and phosphoinositides in exosome biology. Journal of Lipid Research, 60(1), 9–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sotomayor‐Pérez, A. C. , Karst, J. C. , Ladant, D. , & Chenal, A. (2012). Mean net charge of intrinsically disordered proteins: Experimental determination of protein valence by electrophoretic mobility measurements. In Intrinsically Disordered Protein Analysis, 331–349. Springer. [DOI] [PubMed] [Google Scholar]
- Sotres, J. , & Baró, A. (2010). AFM imaging and analysis of electrostatic double layer forces on single DNA molecules. Biophysical journal, 98(9), 1995–2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sriprablom, J. , Luangpituksa, P. , Wongkongkatep, J. , Pongtharangkul, T. , & Suphantharika, M. (2019). Influence of pH and ionic strength on the physical and rheological properties and stability of whey protein stabilized o/w emulsions containing xanthan gum. Journal of Food Engineering, 242, 141–152. [Google Scholar]
- Stellwagen, E. , & Stellwagen, N. C. (2003). Probing the electrostatic shielding of DNA with capillary electrophoresis. Biophysical journal, 84(3), 1855–1866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strand, S. P. , Tømmeraas, K. , Vårum, K. M. , & Østgaard, K. (2001). Electrophoretic light scattering studies of chitosans with different degrees of N‐acetylation. Biomacromolecules, 2(4), 1310–1314. 10.1021/bm015598x [DOI] [PubMed] [Google Scholar]
- Subedi, P. , Schneider, M. , Philipp, J. , Azimzadeh, O. , Metzger, F. , Moertl, S. , Atkinson, M. J. , & Tapio, S. (2019). Comparison of methods to isolate proteins from extracellular vesicles for mass spectrometry‐based proteomic analyses. Analytical biochemistry, 584, 113390. [DOI] [PubMed] [Google Scholar]
- Szatanek, R. , Baj‐Krzyworzeka, M. , Zimoch, J. , Lekka, M. , Siedlar, M. , & Baran, J. (2017). The methods of choice for extracellular vesicles (EVs) characterization. International journal of molecular sciences, 18(6), 1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanford, C. , Swanson, S. A. , & Shore, W. S. (1955). Hydrogen ion equilibria of bovine serum albumin1. Journal of the American Chemical Society, 77(24), 6414–6421. [Google Scholar]
- Théry, C. , Witwer, K. W. , Aikawa, E. , Alcaraz, M. J. , Anderson, J. D. , Andriantsitohaina, R. , Antoniou, A. , Arab, T. , Archer, F. , Atkin‐Smith, G. K. , Ayre, D. C. , Bach, M. , Bachurski, D. , Baharvand, H. , Balaj, L. , Baldacchino, S. , Bauer, N. N. , Baxter, A. A. , Bebawy, M. , … Zuba‐Surma, E. K. (2018). Minimal information for studies of extracellular vesicles 2018 (MISEV2018): A position statement of the International Society for Extracellular Vesicles and update of the MISEV2014 guidelines. Journal of Extracellular Vesicles, 7(1), 1535750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thind, A. , & Wilson, C. (2016). Exosomal miRNAs as cancer biomarkers and therapeutic targets. Journal of extracellular vesicles, 5(1), 31292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuck, S. (2011). Extracellular vesicles: Budding regulated by a phosphatidylethanolamine translocase. Current Biology, 21(24), R988–R990. [DOI] [PubMed] [Google Scholar]
- Vance, J. E. (2018). Historical perspective: Phosphatidylserine and phosphatidylethanolamine from the 1800s to the present. Journal of lipid research, 59(6), 923–944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vatamanu, J. , Cao, L. , Borodin, O. , Bedrov, D. , & Smith, G. D. (2011). On the influence of surface topography on the electric double layer structure and differential capacitance of graphite/ionic liquid interfaces. The Journal of Physical Chemistry Letters, 2(17), 2267–2272. [Google Scholar]
- Virtanen, J. , Sosnick, T. , & Freed, K. (2014). Ionic strength independence of charge distributions in solvation of biomolecules. The Journal of Chemical Physics, 141(22), 12B604_1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, H. , & Pilon, L. (2011). Accurate simulations of electric double layer capacitance of ultramicroelectrodes. The Journal of Physical Chemistry C, 115(33), 16711–16719. [Google Scholar]
- Wang, H. , & Pilon, L. (2013). Mesoscale modeling of electric double layer capacitors with three‐dimensional ordered structures. Journal of Power Sources, 221, 252–260. [Google Scholar]
- Wang, H. , Varghese, J. , & Pilon, L. (2011). Simulation of electric double layer capacitors with mesoporous electrodes: Effects of morphology and electrolyte permittivity. Electrochimica Acta, 56(17), 6189–6197. [Google Scholar]
- Wang, J. , Ma, P. , Kim, D. H. , Liu, B. F. , & Demirci, U. (2021). Towards microfluidic‐based exosome isolation and detection for tumor therapy. Nano Today, 37, 101066. 10.1016/j.nantod.2020.101066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, W. , Zhu, N. , Yan, T. , Shi, Y. , Chen, J. , Zhang, C. , Xie, X. , Liao, D. , & Qin, L. (2020). The crosstalk: Exosomes and lipid metabolism. Cell Communication and Signaling : CCS, 18(1), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, Y. , Huang, L. , Shen, Y. , Tang, L. , Sun, R. , Shi, D. , Webster, T. J. , Tu, J. , & Sun, C. (2017). Electrostatic interactions between polyglutamic acid and polylysine yields stable polyion complex micelles for deoxypodophyllotoxin delivery. International Journal of Nanomedicine, 12, 7963–7977. 10.2147/IJN.S140573 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winzor, D. J. (2004). Determination of the net charge (valence) of a protein: A fundamental but elusive parameter. Analytical biochemistry, 325(1), 1–20. [DOI] [PubMed] [Google Scholar]
- Wolken, G. G. , & Arriaga, E. A. (2014). Simultaneous measurement of individual mitochondrial membrane potential and electrophoretic mobility by capillary electrophoresis. Anal Chem, 86(9), 4217–4226. 10.1021/ac403849x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, J. (2022). Understanding the electric double‐layer structure, capacitance, and charging dynamics. Chemical Reviews, 122(12), 10821–10859. [DOI] [PubMed] [Google Scholar]
- Xu, R. (2015). Light scattering: A review of particle characterization applications. Particuology, 18, 11–21. [Google Scholar]
- Yang, J. , Gallegos, A. , Lian, C. , Deng, S. , Liu, H. , & Wu, J. (2021). Curvature effects on electric‐double‐layer capacitance. Chinese Journal of Chemical Engineering, 31, 145–152. [Google Scholar]
- Yang, L. , Fishbine, B. H. , Migliori, A. , & Pratt, L. R. (2010). Dielectric saturation of liquid propylene carbonate in electrical energy storage applications. The Journal of chemical physics, 132(4), 044701. [DOI] [PubMed] [Google Scholar]
- Yang, Y. , Hong, Y. , Cho, E. , Kim, G. B. , & Kim, I.‐S. (2018). Extracellular vesicles as a platform for membrane‐associated therapeutic protein delivery. Journal of extracellular vesicles, 7(1), 1440131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yates, A. G. , Pink, R. C. , Erdbrügger, U. , Siljander, M. , Dellar, E. R. , Pantazi, P. , Akbar, N. , Cooke, W. R. , Vatish, M. , Dias‐Neto, E. , Anthony, D. C. , & Couch, Y. (2022a). In sickness and in health: The functional role of extracellular vesicles in physiology and pathology in vivo: Part II: Pathology: Part II: Pathology. Journal of Extracellular Vesicles, 11(1), e12190. 10.1002/jev2.12190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yates, A. G. , Pink, R. C. , Erdbrügger, U. , Siljander, M. , Dellar, E. R. , Pantazi, P. , Akbar, N. , Cooke, W. R. , Vatish, M. , Dias‐Neto, E. , Anthony, D. C. , & Couch, Y. (2022b). In sickness and in health: The functional role of extracellular vesicles in physiology and pathology in vivo: Part I: Health and Normal Physiology: Part I: Health and Normal Physiology. Journal of Extracellular Vesicles, 11(1), e12151. 10.1002/jev2.12190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeh, I.‐C. , & Berkowitz, M. L. (1999). Dielectric constant of water at high electric fields: Molecular dynamics study. The Journal of chemical physics, 110(16), 7935–7942. [Google Scholar]
- Yin, Y. , Chen, H. , Wang, Y. , Zhang, L. , & Wang, X. (2021). Roles of extracellular vesicles in the aging microenvironment and age‐related diseases. Journal of Extracellular Vesicles, 10(12), e12154. 10.1002/jev2.12154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- You, Y. , Muraoka, S. , Jedrychowski, M. P. , Hu, J. , McQuade, A. , Young‐Pearse, T. L. , Aslebagh, R. , Shaffer, S. A. , Gygi, S. P. , Blurton‐Jones, M. , Poon, W. W. , & Ikezu, T. (2022). Human neural cell type‐specific extracellular vesicle proteome defines disease‐related molecules associated with activated astrocytes in Alzheimer's disease brain. Journal of Extracellular Vesicles, 11(1), e12183. 10.1002/jev2.12183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu, L. , Zhu, J. , Liu, J. , Jiang, F. , Ni, W. , Qu, L. , Ni, R. , Lu, C. , & Xiao, M. (2018). A comparison of traditional and novel methods for the separation of exosomes from human samples. BioMed Research International, 2018, 3634563. 10.1155/2018/3634563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, J. , Shi, J. , Zhang, H. , Zhu, Y. , Liu, W. , Zhang, K. , & Zhang, Z. (2020). Localized fluorescent imaging of multiple proteins on individual extracellular vesicles using rolling circle amplification for cancer diagnosis. Journal of Extracellular Vesicles, 10(1), e12025. 10.1002/jev2.12025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Y. , Liu, Y. , Liu, H. , & Tang, W. H. (2019). Exosomes: Biogenesis, biologic function and clinical potential. Cell & bioscience, 9(1), 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Y. , Murakami, K. , Borra, V. J. , Ozen, M. O. , Demirci, U. , Nakamura, T. , & Esfandiari, L. (2022). A label‐free electrical impedance spectroscopy for detection of clusters of extracellular vesicles based on their unique dielectric properties. Biosensors, 12(2), 104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao, M. , Yang, Y. , Guo, Z. , Shao, C. , Sun, H. , Zhang, Y. , Sun, Y. , Liu, Y. , Song, Y. , Zhang, L. , Li, Q. , Liu, J. , Li, M. , Gao, Y. , & Sun, W. (2018). A comparative proteomics analysis of five body fluids: Plasma, urine, cerebrospinal fluid, amniotic fluid, and saliva. PROTEOMICS – Clinical Applications, 12(6), 1800008. 10.1002/prca.201800008 [DOI] [PubMed] [Google Scholar]
- Zhou, B. , Xu, K. , Zheng, X. , Chen, T. , Wang, J. , Song, Y. , Shao, Y. , & Zheng, S. (2020). Application of exosomes as liquid biopsy in clinical diagnosis. Signal Transduction and Targeted Therapy, 5(1), 144. 10.1038/s41392-020-00258-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhulina, E. , & Leermakers, F. (2007). Effect of the ionic strength and pH on the equilibrium structure of a neurofilament brush. Biophysical journal, 93(5), 1452–1463. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information


