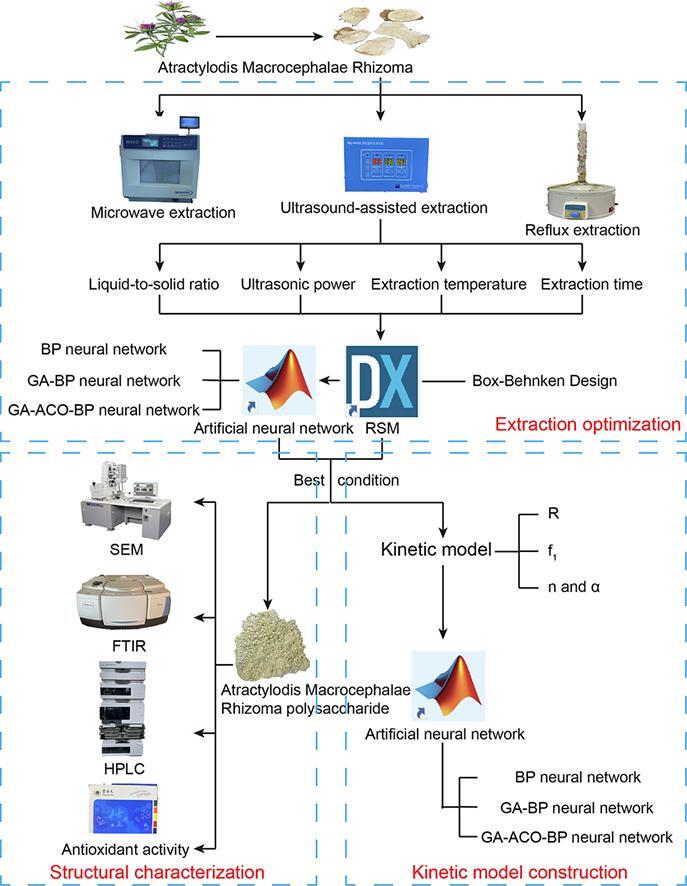
Graphical abstract
Keywords: Extraction, Kinetic modelling, Atractylodis Macrocephalae Rhizoma, Response surface methodology, Artificial neural network
Highlights
-
•
The extraction conditions were optimized by three artificial neural network models and response surface methodology model.
-
•
The predictive ability of the developed kinetic equation and three artificial neural networks was evaluated.
-
•
The structure of polysaccharide was characterized, and the monosaccharide types and contents were determined.
Abstract
Atractylodis Macrocephalae Rhizoma (AMR) is the dried rhizome of Atractylodes macrocephala Koidz, which is widely used in the development of health products. AMR contains a large number of polysaccharides, but at present there are fewer applications for these polysaccharides. In this study, the effects of different extraction methods on the Atractylodis Macrocephalae Rhizoma polysaccharide (AMRP) yield were investigated, and the conditions for ultrasound-assisted extraction were optimized by response surface methodology (RSM) and three neural network models (BP neural network, GA-BP neural network and ACO-GA-BP neural network). The best conditions were a liquid-to-solid ratio of 17 mL/g, ultrasonic power of 400 W, extraction temperature of 72 °C, and extraction time of 40 min, which yielded 31.31% AMRP. The kinetic equation of AMRP was determined and compared with the results predicted by three neural network models. It was finally determined that the extraction conditions, kinetic processes and kinetic equation predicted by the GA-ACO-BP neural network were optimal. In addition, AMRP was characterized using SEM, FTIR, HPLC, UV, XRD, and NMR, and the structural study revealed that AMRP has a rough exterior and a porous interior; moreover, it contains high levels of glucose (5.07%), arabinose (0.80%), and galactose (0.74%). AMRP has three crystal structures, consisting of two β-type monosaccharides and one α-type monosaccharide. Additionally, the effectiveness of AMRP as an antioxidant was demonstrated in an in vitro experiment.
1. Introduction
Atractylodis Macrocephalae Rhizoma is the dried rhizome of Atractylodes macrocephala Koidz., family Asteraceae. AMR is commonly utilized as an herb in traditional medicine to strengthen the spleen and benefit Qi [1]. Clinically, it is widely employed as an antitumour and anti-inflammatory medication, and it also enhances gastrointestinal system performance [2], [3]. In addition, AMR is regarded by the Chinese National Health Commission as a type of traditional Chinese medicine that can be used in healthy food and as one of the eight precious herbs of Zhejiang Province in China. AMR is broadly utilized in the development of foods and medicines.
AMR is rich in volatile oils, polysaccharides and lactones. It has been demonstrated that the volatile oil of AMR improves humoral dysregulation of the gastric mucosa [4], alleviating chronic atrophic gastritis. Three acidic AMRPs effectively stimulated the immune system by encouraging the release of cell NO, indicating that they are potential immunoregulatory agents [1]. Atractylenolide I can suppress glycolysis and induce apoptosis by blocking the JAK2/STAT3 signalling pathway in colorectal cancer cells [5]. The majority of researches to date have focused on the pharmacological effects of the AMR lactones, yet AMR has a higher percentage of polysaccharides; therefore, the function of AMRPs cannot be disregarded.
In the preliminary stage of this experiment, various extraction methods (microwave extraction, reflux extraction, and ultrasound-assisted extraction) were compared, and it was discovered that ultrasound-assisted extraction produced the maximum yield of AMRP under the same conditions. Ultrasound can produce a mechanical effect that can increase the penetration of solvent into the herb surface and accelerate the dissolution of the active ingredients. Moreover, the solubility of active ingredients are increased by the thermal effect that the ultrasonic process can produce. The heating temperatures are generally mild, which can effectively protect the biological activity of heat-sensitive ingredients during the extraction process [6], [7]. In conclusion, ultrasound-assisted extraction was chosen for this experiment.
The RSM is widely used for optimizing extraction conditions and essentially determines the coefficients of a linear polynomial through a design of experiments [8], [9]. However, the polynomial only reaches the second power, which restricts its ability to describe the relationship between some complex independent variables and response variables. Due to their superior predictive powers, artificial neural networks, representing a new science that mimics how the human brain processes information, are used in the environmental, energy, medicinal, and other fields [10], [11]. However, due to cases of poor fit or overfit caused by inaccurate weights and thresholds in back propagation (BP) neural networks, a genetic algorithm (GA) can be introduced to make improvements, simulate natural selection, find the best solution, optimize the weights and thresholds and improve accuracy [12]. The ant colony optimization (ACO) algorithm is a method that simulates the transmission of pheromones among ants to optimize the search for aim paths [13]. Subsequently, optimizing pheromones through the GA and then optimizing the weights and thresholds of the BP neural network through the ACO algorithm can further improve the prediction performance of the neural network.
The concentrations of active ingredients at various periods are difficult to calculate, because extraction is a complex process. In this experiment, we studied the effects of four key influencing factors on the yield of AMRP, predicted the best extraction conditions with RSM and three neural network models, and subsequently evaluated and compared them. Thereafter, we determined the extraction kinetic equation, which was once again predicted by three neural network models, and compared the predictive abilities of the kinetic equation and neural network models. The structures of the polysaccharides were immediately characterized by SEM, FTIR, HPLC, UV, XRD and NMR methods. Finally, the antioxidant activity of the polysaccharides was investigated.
2. Materials and methods
2.1. Materials and chemicals
AMR was purchased from Huadong Chinese Medicine Co., Ltd. (Zhejiang, China) and identified by Dr. Shuili Zhang of Zhejiang Chinese Medical University. Anthrone and ammonium acetate were purchased from Macklin Biochemical Technology Co., Ltd. (Shanghai, China). Glucose, arabinose and galactose were purchased from Chengdu DeSiTe Biological Technology Co., Ltd. (Sichuan, China). 2,2-Diphenyl-1-1-picrylhydrazyl radical and 2,2′-azino-bis-(3-ethylbenzothiazoline-6-sulfonic acid) were purchased from Chengdu Push Biotechnology Co., Ltd. Microporous membranes were purchased from SORFA Life Science Co., Ltd. (Beijing, China). The Ferric Reducing Antioxidant Power kit was purchased from Beyotime Institute of Biotechnology (Jiangsu, China). Chromatography grade acetonitrile was obtained from TEDIA (Fairfield, OH, USA). Deionized water was produced with a Millipore water purification system (Millipore Co., Ltd., Billerica, MA, USA).
2.2. Comparison of three extraction methods
Ultrasound-assisted extraction, microwave extraction and reflux extraction are common methods for active ingredient extraction [14], and the effects of these three methods on the yield of AMRP were compared in this experiment.
Ultrasonic-assisted extraction: The AMRP yield was calculated after accurately weighing 5 g of AMR powder, adding 50 mL of water, and placing the flask in a bath sonicator for 30 min. The condition parameters were set as follows: the power was 300 W, and the temperature was 60 °C.
Microwave extraction: For this experiment, 5 g of AMR powder was accurately weighed, placed in a 100 mL round-bottom flask with 50 mL of water, and then microwaved for 30 min at 60 °C at a power of 300 W.
Reflux Extraction: Five grams of AMR powder was precisely weighed, 50 mL of water was added, and the mixture was refluxed for 30 min in a 100 mL round-bottom flask.
The yields of AMRP from the different extraction methods were determined according to the AMRP determination method in 2.3.1, and the best extraction method was selected.
2.3. Optimization of the AMRP extraction conditions
2.3.1. Extraction and determination of AMRP
The polysaccharide from AMR was obtained using water extraction and alcohol precipitation methods. The dried powder of AMR (5 g) was mixed with distilled water, and the mixture was extracted with the help of a bath sonicator equipped with a digitally controlled low-frequency sonotrode. Afterwards, the resulting solution was filtered to remove insoluble residue, added to 5 times the volume of absolute ethanol and placed in the refrigerator at 4 °C for one hour. Then, the crude polysaccharide was obtained by centrifugation (4000 rpm, 20 min).
The concentration of AMRP was determined in accordance with the Chinese Pharmacopoeia (2020 edition) with minor modifications [15].
In brief, the crude polysaccharide was dissolved in hot water and mixed with 0.1 mol/L anthrone sulfuric acid, and the mixture was incubated in boiling water and ice water for 10 min each. The absorbance was then measured at 583 nm. The extraction yield was calculated as follows:
| (1) |
where c (g/mL) is the concentration of AMRP, v (mL) is the volume of the extract, and M (g) is the weight of the AMR.
2.3.2. Single-factor experimental design
The yield of AMRP was affected by various factors, such as solvent type, solid-to-liquid ratio, extraction temperature, ultrasonic power, and extraction time. The polysaccharides were soluble in water but insoluble in ethanol. As the main aim of this work was to maximize the yield of polysaccharides, water was selected as the solvent. The liquid-to-solid ratio (5:1, 10:1, 15:1, 20:1, 25:1 mL/g), ultrasonic power (250, 300, 350, 400 W), extraction temperature (20, 40, 60, 80 °C) and extraction time (30, 60, 90, 120, 150 min) were investigated to optimize the yield of AMRP. When estimating the effect of one variable on the yield, the remaining variables remained constant, as only one variable was changed at a time to determine the effective ranges for the optimization experiment.
2.3.3. Box-Behnken experimental design
Box-Behnken Design (BBD) of RSM has been widely used for extraction optimization because it makes finding the optimal process conditions possible with fewer experiments [16].
Based on the results of the single-factor experiments, the preliminary ranges of solid-to-liquid ratio, ultrasonic power, extraction temperature and extraction time were determined. To obtain the best combination of the four variables, 29 experiments were designed with the help of Design-Expert 12, with each variable having three levels. The coded and uncoded levels and the 29 runs are listed in Table 1. The yield of AMRP was taken as the response. The quadratic polynomial formula for AMRP yield as a function of these four variables is summarized as follows:
| (2) |
where Y is the yield of AMRP, (i or j = 1, 2, 3, 4) represents the four variables, represents a constant term, (i = 1, 2, 3, 4) indicates the coefficient of the linear portion, (i, j = 1, 2, 3) indicates the coefficients of the quadratic portion, and ε is the residual.
Table 1.
The actual and predicted data from the BBD design.
| Runs | liquid-to-solid ratio (mL/g) | ultrasonic power (W) | extraction temperature (℃) | processing time (min) | Yield (%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Actual | RSM Predicted | BP Predicted | GA-BP Predicted | GA-ACO-BP Predicted | |||||
| 1 | −1 (10) | −1 (3 0 0) | 0 (60) | 0 (30) | 25.13 | 25.18 | 25.67 | 23.73 | 24.32 |
| 2 | 1 (20) | −1 (3 0 0) | 0 (60) | 0 (30) | 8.34 | 10.81 | 21.06 | 9.22 | 8.97 |
| 3 | −1 (10) | 1 (4 0 0) | 0 (60) | 0 (30) | 18.76 | 18.76 | 19.04 | 19.66 | 18.47 |
| 4 | 1 (20) | 1 (4 0 0) | 0 (60) | 0 (30) | 23.88 | 26.29 | 24.26 | 25.02 | 26.53 |
| 5 | 0 (15) | 0 (3 5 0) | −1 (40) | −1 (10) | 18.46 | 21.7 | 20.28 | 18.74 | 21.19 |
| 6 | 0 (15) | 0 (3 5 0) | 1 (80) | −1 (10) | 18.71 | 18.74 | 18.42 | 17.77 | 19.95 |
| 7 | 0 (15) | 0 (3 5 0) | −1 (40) | 1 (50) | 18.51 | 20.95 | 17.36 | 18.29 | 19.15 |
| 8 | 0 (15) | 0 (3 5 0) | 1 (80) | 1 (50) | 23.11 | 22.34 | 24.75 | 22.57 | 22.95 |
| 9 | −1 (10) | 0 (3 5 0) | 0 (60) | −1 (10) | 19.23 | 20.07 | 23.50 | 19.23 | 19.01 |
| 10 | 1 (20) | 0 (3 5 0) | 0 (60) | −1 (10) | 21.21 | 21.19 | 21.53 | 21.06 | 21.88 |
| 11 | −1 (10) | 0 (3 5 0) | 0 (60) | 1 (50) | 24.55 | 26.04 | 24.17 | 20.53 | 24.37 |
| 12 | 1 (20) | 0 (3 5 0) | 0 (60) | 1 (50) | 17.44 | 18.07 | 17.40 | 17.78 | 16.96 |
| 13 | 0 (15) | −1 (3 0 0) | −1 (40) | 0 (30) | 19.31 | 21.17 | 21.69 | 19.58 | 18.82 |
| 14 | 0 (15) | 1 (4 0 0) | −1 (40) | 0 (30) | 23.56 | 19.33 | 17.83 | 22.95 | 21.29 |
| 15 | 0 (15) | −1 (3 0 0) | 1 (80) | 0 (30) | 8.32 | 14.01 | 13.60 | 19.49 | 9.26 |
| 16 | 0 (15) | 1 (4 0 0) | 1 (80) | 0 (30) | 25.30 | 24.91 | 25.58 | 25.86 | 24.63 |
| 17 | −1 (10) | 0 (3 5 0) | −1 (40) | 0 (30) | 25.20 | 24.33 | 26.95 | 24.92 | 24.09 |
| 18 | 1 (20) | 0 (3 5 0) | −1 (40) | 0 (30) | 22.41 | 19.98 | 21.78 | 17.27 | 22.62 |
| 19 | −1 (10) | 0 (3 5 0) | 1 (80) | 0 (30) | 24.11 | 22.61 | 23.09 | 22.57 | 21.05 |
| 20 | 1 (20) | 0 (3 5 0) | 1 (80) | 0 (30) | 23.18 | 20.12 | 22.20 | 25.86 | 21.70 |
| 21 | 0 (15) | −1 (3 0 0) | 0 (60) | −1 (10) | 23.21 | 18.09 | 20.27 | 22.87 | 23.47 |
| 22 | 0 (15) | 1 (4 0 0) | 0 (60) | −1 (10) | 18.33 | 19.36 | 19.80 | 22.94 | 17.61 |
| 23 | 0 (15) | −1 (3 0 0) | 0 (60) | 1 (50) | 21.21 | 16.25 | 16.90 | 22.50 | 22.02 |
| 24 | 0 (15) | 1 (4 0 0) | 0 (60) | 1 (50) | 22.87 | 24.05 | 20.42 | 23.35 | 25.82 |
| 25 | 0 (15) | 0 (3 5 0) | 0 (60) | 0 (30) | 29.45 | 27.32 | 15.34 | 27.67 | 27.98 |
| 26 | 0 (15) | 0 (3 5 0) | 0 (60) | 0 (30) | 26.53 | 27.32 | 15.34 | 27.67 | 27.98 |
| 27 | 0 (15) | 0 (3 5 0) | 0 (60) | 0 (30) | 26.96 | 27.32 | 15.34 | 27.67 | 27.98 |
| 28 | 0 (15) | 0 (3 5 0) | 0 (60) | 0 (30) | 25.06 | 27.32 | 15.34 | 27.67 | 27.98 |
| 29 | 0 (15) | 0 (3 5 0) | 0 (60) | 0 (30) | 28.60 | 27.32 | 15.34 | 27.67 | 27.98 |
2.3.4. Comparation of the three kinds of artificial neural networks
A neuron is the basic unit of biological information processing, and an artificial neural network is a mathematical model that simulates biological information processing. The BP neural network was proposed by Rumelhart and McCelland [17] in 1986 as a multilayer feedforward network trained by the error back propagation algorithm, and it is now one of the most widely used neural network models. BP neural networks, which are highly nonlinear with self-learning and adaptative abilities, have been applied in various fields. The BP neural network uses the steepest descent learning rule to continuously adjust the weights and thresholds of the network by back propagation to minimize the error of the network. The topology of the BP neural network consists of three layers: input layer, hidden layer and output layer, with full connectivity between layers [18]. The BP neural network calculates the weights and thresholds, which is a layer-by-layer state updating process. Its working principle can be understood as follows. The input layer neurons receive the signal and pass it to the hidden layer neurons. The hidden layer neurons process the signals through the “tansig” activation function and pass the results to the output layer neurons, which are processed with the “purelin” output function. Subsequently, the results are passed out of the output layer [19].
However, if the error between the output and the desired value is not satisfied, the error will be back-propagated along the pathway layer by layer and the weights and thresholds of each layer will be corrected. In brief, a BP neural network can be viewed as a highly nonlinear mapping from input to output. The structural model of neurons can be expressed as shown in Formula (3):
| (3) |
where xi (i = 1,2,…, R) is the input, wi (i = 1,2,…, R) represents the connection weights between neurons, b = w0 is the threshold, f is the activation function (output function), and y is the function output.
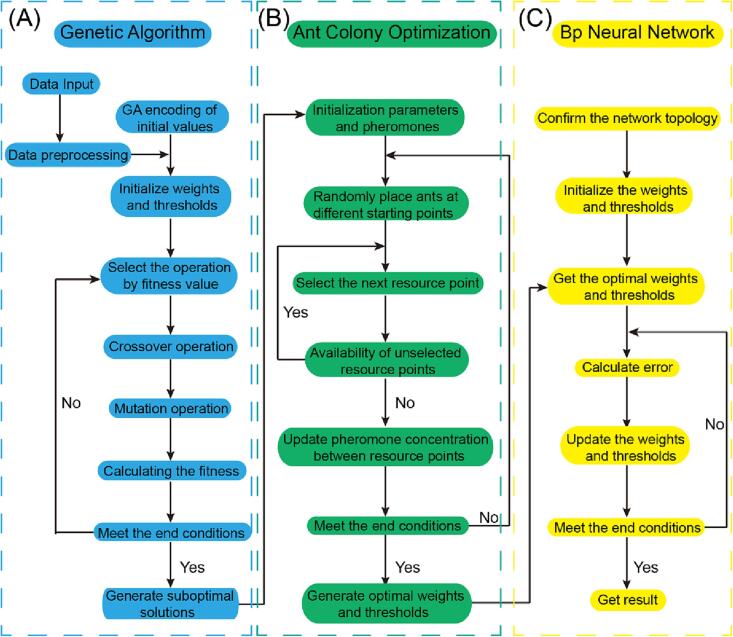
Unfortunately, in long-term practice, it has been found that the steepest descent method often causes the final result falling into the local minimum, and there are also problems such as low learning efficiency and parameter sensitivity. Thus, making the final result jump out of the local minimum is an area of improvement for the neural network. The genetic algorithm [20] is an optimization search algorithm based on natural selection and genetic principles, which introduces “survival of the fittest” into the process of parameter optimization (Fig. 3A). This algorithm tends to encode the chromosomes of the population, evolve generation by generation, produce the optimal individual, and finally decode the optimal individual to obtain the optimal solution [21].
Fig. 3.
Flowchart of GA-ACO-BP algorithm.
The algorithm starts with parallel computations from multiple points instead of being limited to one point, thus effectively preventing it from becoming trapped in a local optimal solution. Consequently, we can use the global search performance of the genetic algorithm to find the region of the optimal solution of the problem and then use the error back propagation method to find the optimal solution. In this experiment, the genetic algorithm was used to optimize the weights and thresholds of the BP neural network to construct the GA-BP neural network.
The ant colony optimization algorithm was first proposed by Dorigo M, Maniezzo V, and Colorni A in 1992 to solve the optimization problem by simulating ant colonies searching for food sources [22]. The behaviour of an ant is extremely simple, but ant colonies exhibit extremely complex behaviours. Moreover, the exchange of information and mutual assistance between individuals is achieved through pheromones, enabling the colonies to move towards the goal (Fig. 3B). The ant algorithm is also a stochastic search algorithm that consists of two phases: the adaptation phase and the collaboration phase. In the adaptation phase, each candidate solution adjusts its own structure by accumulating experience, and in the collaboration phase, the optimal solution is generated through information exchange between the candidate solutions [23], [24]. This experiment uses a genetic algorithm to optimize the ant colony pheromones and generate new populations to improve the prediction accuracy of the BP neural network and finally construct the GA-ACO-BP neural network.
Using MATLAB 2020a to construct a three-layer neural network, the input layer consisted of four neurons, including solid-to-liquid ratio, ultrasonic power, extraction temperature and extraction time, and one neuron in the output layer was the yield of AMRP. The experimental data were divided into a training set (21 datasets) and a test set (8 datasets). The number of hidden layer neurons was finally determined based on the mean square error (MSE) of the training set. The number of neurons in the hidden layer was estimated by the empirical Formula (4):
| (4) |
where m is the number of neurons in the input layer, n is the number of output layer neurons, and a = 1 to 10.
The BP neural network, GA-BP neural network, and GA-ACO-BP neural network were used to train, fit, and find the best process conditions. The performance of the model was evaluated by the coefficient of determination (R2), mean absolute error (MAE), and root mean square error (RMSE), which were calculated with the following formulas [25], [26]:
| (5) |
| (6) |
| (7) |
where is the predicted value of each model, is the actual value, and is the average of the dataset. RSS, ESS, and TSS denote the regression sum of squares, residual sum of squares, and total sum of squares, respectively. In addition, the optimal process was verified experimentally.
2.4. Kinetic modelling of extraction
In general, the extraction of active ingredients from Chinese medicines can be divided into three processes, penetration, dissolution and diffusion, where the determining factor for the decoction rate of drugs is diffusion. Based on Fick's first law and Higbie's penetration theory, Linxin Han [27] derived the kinetics equation for extraction from herbs:
| (8) |
where f1 is the parameter related to the concentration of the herb, M is the liquid-to-solid ratio, R is the solvent absorption rate of the herb, σ1 is the particle size of the herb, and is the parameter related to the diffusion coefficient and particle size of the herb.
Subsequently, Yang Chen simplified Eq. (8) by fusing σ1 into parameter , reducing the number of parameters that need to be measured directly and generating the new parameter :
| (9) |
Then, the logarithm can be taken of both sides of the equation:
| (10) |
2.4.1. Determination of R
Approximately 2, 4, 6, 8, and 10 g of AMRP powder were weighed in a conical flask, and extraction was performed according to the optimal conditions obtained in 2.3.4. Linear regression of the water absorption (Y) as a function of the weight of the dry AMRP (X) was performed. The slope of the equation was R.
2.4.2. Determination of
According to the derivation of Yang Chen, f1 can be expressed as:
| (11) |
Based on this experiment, C1b-C10 can be interpreted as the total content of polysaccharides in the AMR, which was measured following the protocols in the Chinese Pharmacopoeia [15], and then was calculated.
2.4.3. Determination of and
Twenty samples were weighed and extracted according to the optimal extraction conditions. The first extraction ended at 2 min, and the polysaccharide yield was measured, followed by the second ending at four minutes, and so on. The logarithms of the time and AMRP concentration were taken and examined following Eq. (10). The final calculation gave and .
2.5. Model building
Artificial neural networks can be used not only for fitting but also for prediction. Each AMRP yield starting from the eighth minute was used as the response variable, and the AMRP yield at the three time points before this was used as independent variables. A 4 × 17 time series matrix was obtained, of which 13 sets of data were used as the training set and the remaining were used as the test set. The BP, GA-BP, and ACO-GA-BP neural networks were constructed by MATLAB software, and the models were compared; refer to 2.3.4 for the specific method.
2.6. Characterization of AMRP
2.6.1. Scanning electron microscopy
The stereoscopic features of AMRP were determined by scanning electron microscopy (SEM). Cellophane tape was used to secure a small amount of dried AMRP powder to the metal, the stubs were sputtered with a thin layer of gold using a gold sputter and then the samples were observed by SEM [28].
2.6.2. FTIR spectroscopy analysis
Approximately 1 mg of AMRP powder was combined with 20 mg of KBr, and each sample was then ground into fine powder and formed into a thin tablet. Spectra were recorded for each sample in the range of 4000 to 400 nm. Prior to taking measurements, the clean sampling stage was taken as the background spectrum [29].
2.6.3. Monosaccharide composition
Preparation of internal standard solution: First, 70 mg of glucosamine hydrochloride was accurately weighed in a 10 mL volumetric flask, and the volume was fixed with distilled water.
Preparation of standard solution: First, 4 mg of glucose, 2 mg of galactose and 2 mg of arabinose were weighed in a 25 mL volumetric flask and dissolved in distilled water, and then 0.5 mL of internal standard solution was added. Subsequently, 400 μl of the mixture was aspirated into a tube, and before reacting in a 70 °C water bath for 100 min, a PMP methanol solution of 0.5 mol/L and sodium hydroxide solution of 0.3 mol/L were added at the same time. Then, the reaction solution was blended with 0.3 mol/L HCl (500 μl). To remove the excess PMP, the reaction products were extracted three times using 2 mL of chloroform. Finally, the standard solution was obtained after the supernatant was passed through a 0.22 μm microporous membrane.
Preparation of sample solution: After absorbing 400 μl of 0.5 mg/mL AMRP, according to the standard solution preparation method, the sample solution was finally obtained.
The determination of the monosaccharide composition of AMRP was carried out with Agilent 1200 high-performance liquid chromatography (HPLC) instrument at 30 °C and a flow rate of 1 mL/min. The mobile phase consisted of acetonitrile (A) and 0.02 mol/L ammonium acetate solution (B). The gradient elution program was set as follows: 0–15 min, 15%-15% A and 15–45 min, 15%-30% A; the optimal detection wavelength was 220 nm.
2.6.4. Measurement of the protein and uronic acid contents
The absorbance of AMRP from 200 to 600 nm was measured by a UV–visible spectrophotometer, and the protein content was determined by a BCA kit. The content of uronic acid was determined by the m-hydroxydiphenyl method, and a standard curve was drawn using galacturonic acid as the standard [30].
2.6.5. X-ray diffraction (XRD)
XRD technology is a crucial analytical technique that can reveal further details about AMRP, such as whether it is amorphous or crystalline. In a 2θ range of 5-80°, an angle speed of 1°/min and a step of 0.02°, XRD data were collected at room temperature.
2.6.6. Nuclear magnetic resonance (NMR)
AMRP was first dissolved in D2O, dried in a vacuum for 24 h, and then redissolved in D2O to conduct the deuterium exchange. The chemical composition of AMRP was then verified using an NMR spectrometer [31].
2.7. In vitro antioxidant activity
Exactly 25 mg of AMRP and vitamin C were weighed and then transferred to a 1 mL volumetric flask. A stock solution of each sample was prepared in distilled water to achieve a concentration of 25 mg/mL. Concentrations of 10 mg/mL, 5 mg/mL, 1 mg/mL, 0.5 mg/mL and 0.1 mg/mL were obtained through dilutions of the stock solution.
2.7.1. DPPH radical scavenging assay
The antioxidant activity of the extracts was measured using the DPPH radical scavenging assay in 96-well plates. One hundred microlitres of each prepared solution was mixed with 100 µl of a methanolic solution of DPPH (0.02 mM) and incubated at room temperature for 30 min, with vitamin C serving as a positive control. The absorbance was recorded at 517 nm [32]. Antioxidant activity was calculated based on the following formula:
| (12) |
where Ai is the absorbance of sample + DPPH; Aj is the absorbance of sample + absolute ethanol; and Ac is the absorbance of absolute ethanol + DPPH.
2.7.2. ABTS radical scavenging assay
Exactly 7.67 mg of ABTS powder and 1.32 mg of potassium persulfate were dissolved in absolute ethanol and transferred to two 2 mL volumetric flasks. The capacity was then filled with absolute ethanol, and the two freshly prepared solutions were combined for incubation at room temperature in the dark for 16 h. The ABTS radical cation (ABTS·+) is produced by the mixture. After incubation, the ABTS·+ solution was diluted with absolute ethanol to obtain an absorbance of 0.7 ± 0.05 at 734 nm.
The assay was carried out by mixing 40 µl of AMRP with diluted ABTS·+ solution (160 µl) and left at room temperature for 10 min, with vitamin C serving as a positive control. The absorbance of the solution was measured at 734 nm [33]. ABTS radical scavenging activity was calculated according to the following equation:
| (13) |
where Acontrol was determined by using absolute ethanol instead of diluted ABTS·+ solution.
2.7.3. FRAP assay
To prepare the FRAP reagent, acetate buffer (pH 3.6) with TPTZ (2,4,6-tri (2-pyridyl)-1,3,5-triazine) solution (10 mM) in 40 mM hydrochloric acid (HCl) and 20 mM ferrous sulfate heptahydrate at a ratio of 10:1:1 (v/v/v) were mixed. Six millilitres of AMRP extracts were combined with FRAP reagents (180 µl) and incubated at 37 °C for 4 min with vitamin C as a positive control. A wavelength of 593 nm was used to measure the absorbance. Ferrous sulfate heptahydrate solutions (0.15, 0.3, 0.6, 0.9, 1.5 mM) were used to generate the standard curve, and the ferric reducing antioxidant power of the samples are presented as ferrous sulfate equivalents.
3. Results and discussion
3.1. Selection of the best extraction method
In the end, reflux extraction yielded 17.63 ± 3.49% AMRP, whereas microwave extraction yielded 18.36 ± 2.66% AMRP. Ultrasonic-assisted extraction yielded 21.95 ± 1.71% AMRP.
Since AMRP is unstable at high temperature, the reflux extraction method yielded the least amount of AMRP due to its higher temperature, this method is unfavourable for the extraction of thermally unstable ingredients. The theoretical basis for microwave extraction is that microwave radiation boosts the temperature and pressure inside plant cells, rupturing the cell walls and liberating the active ingredients. The principle of ultrasound-assisted extraction is to use the cavitation effect of ultrasound to destroy the plant cell membrane and release the active ingredients. The extraction of thermally unstable compounds benefited from the moderate warming procedures used by microwave and ultrasonic-assisted extraction. From the comprehensive experimental results, the highest yield of AMRP was obtained by ultrasound-assisted extraction, and ultrasound-assisted extraction was chosen as the extraction method in this experiment.
3.2. Single-factor experiments for extraction
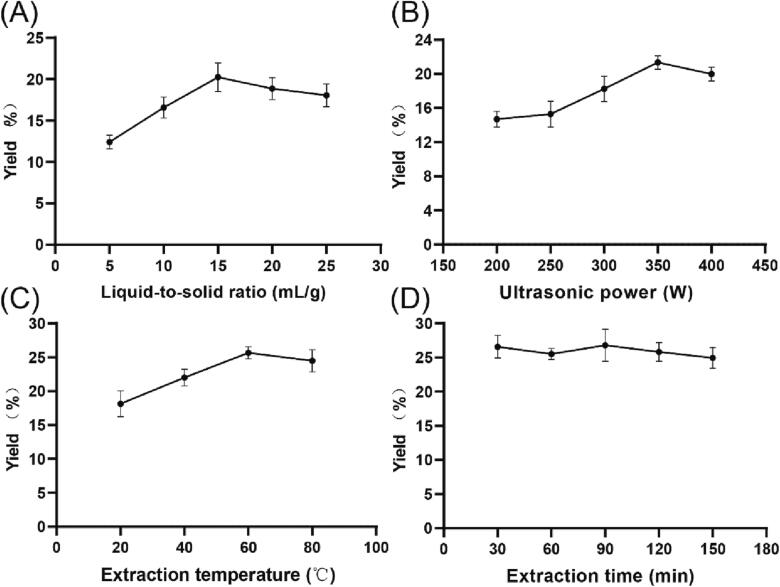
The effect of different variables on the yield of AMRP is displayed in Fig. 1, which basically show an increasing and then decreasing trend, with the exception of extraction time. The point with the highest response value and the two points near it were selected to be the three different levels of BBD, as follows: the liquid-to-solid ratio points were 10:1, 15:1 and 20:1 mL/g; the ultrasonic power points were 300, 350, 400 W; and the extraction temperature points were 40, 60, 80 °C. From 30 min onwards, the AMRP yield remained essentially constant, possibly because AMRP was fully extracted before 30 min, so 10, 30 and 50 min were chosen as the levels of BBD.
Fig. 1.
Effect of different variables on AMRP yield. A: liquid-to-solid ratio, B: ultrasonic power, C: extraction temperature, D: extraction time.
3.3. RSM model fitting and analysis
Optimization of the AMRP extraction process by the BBD method was carried out with 29 experiments. Table 1 shows the four variables and their levels, as well as the results of the experimental and predicted values of AMRP yield. The actual AMRP yields were in the range of 8.32–29.45%. Moreover, the data were fitted to a quadratic polynomial regression equation with the following general equation form:
y = 27.32–1.71A + 2.26B-0.3945C + 0.7125D + 5.48AB + 0.4632AC-2.27AD + 3.18BC + 1.63BD + 1.09CD-2.58A2-4.48B2-2.98C2-3.4D2.
where A is the liquid-to-solid ratio, B is the ultrasonic power, C is the extraction temperature, and D is the extraction time. The binomial coefficients showed that ultrasonic power and extraction time had positive correlations with the yield, while extraction temperature and extraction time had negative correlations. The most significant positive and negative interactions were found to be between the liquid-to-solid ratio and ultrasonic power and the liquid-to-solid ratio and extraction time, respectively. To assess the validity of the quadratic polynomial model, ANOVA was used (Table 2). The interaction between the liquid-to-solid ratio and ultrasonic power (0.0072) was significant, and the low p value (0.0409) shows that ultrasonic power can significantly alter the AMRP yield. The created model was excellent, as evidenced by the model's low p value (0.0252) and the lack of fit's high p value (0.0619). R2 (0.7483), adjusted R2 (0.4966), and predicted R2 (-0.376) were used to evaluate the fit of the model, but the low values reflected the poor fitting. The reproducibility of the model was demonstrated by the coefficient of variation (16.01).
Table 2.
ANOVE analysis of RSM model.
| Source | Sum of Square | DF | Mean Square | F value | p value |
|---|---|---|---|---|---|
| Model | 505.06 | 14 | 36.08 | 2.97 | 0.0252* |
| A-A | 35.11 | 1 | 35.11 | 2.89 | 0.111 |
| B-B | 61.55 | 1 | 61.55 | 5.07 | 0.0409* |
| C-C | 1.87 | 1 | 1.87 | 0.1539 | 0.7007 |
| D-D | 6.09 | 1 | 6.09 | 0.5021 | 0.4902 |
| AB | 119.94 | 1 | 119.94 | 9.89 | 0.0072** |
| AC | 0.8584 | 1 | 0.8584 | 0.0708 | 0.7941 |
| AD | 20.66 | 1 | 20.66 | 1.7 | 0.2129 |
| BC | 40.53 | 1 | 40.53 | 3.34 | 0.089 |
| BD | 10.67 | 1 | 10.67 | 0.8797 | 0.3642 |
| CD | 4.73 | 1 | 4.73 | 0.3899 | 0.5424 |
| A2 | 43.07 | 1 | 43.07 | 3.55 | 0.0805 |
| B2 | 130.23 | 1 | 130.23 | 10.73 | 0.0055** |
| C2 | 57.73 | 1 | 57.73 | 4.76 | 0.0467* |
| D2 | 75.05 | 1 | 75.05 | 6.19 | 0.0261* |
| Residual | 169.86 | 14 | 12.13 | ||
| Lack of Fit | 157.85 | 10 | 15.79 | 5.26 | 0.0619 |
| Pure Error | 12.01 | 4 | 3 | ||
| Cor Total | 674.92 | 28 | |||
| R2 | 0.7483 | ||||
| Adj R2 | 0.4966 | ||||
| Pred R2 | −0.375 | ||||
| C.V. % | 16.01 |
*p < 0.05, ** p < 0.01 represents statistical significance.
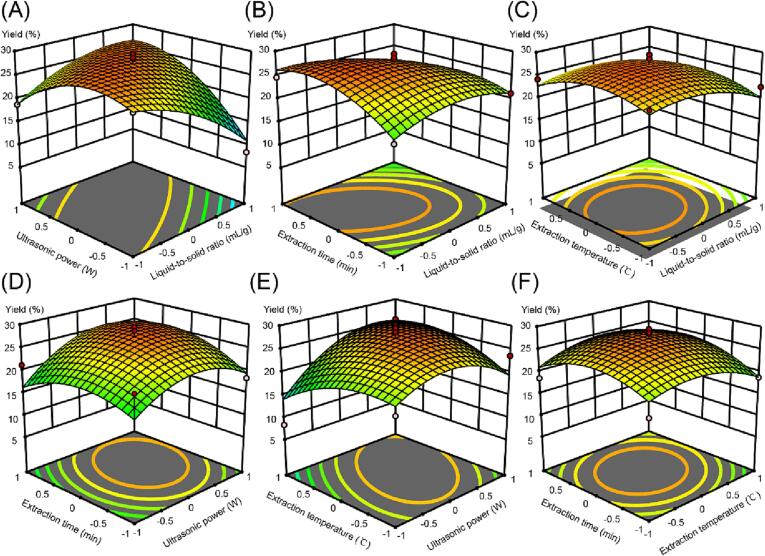
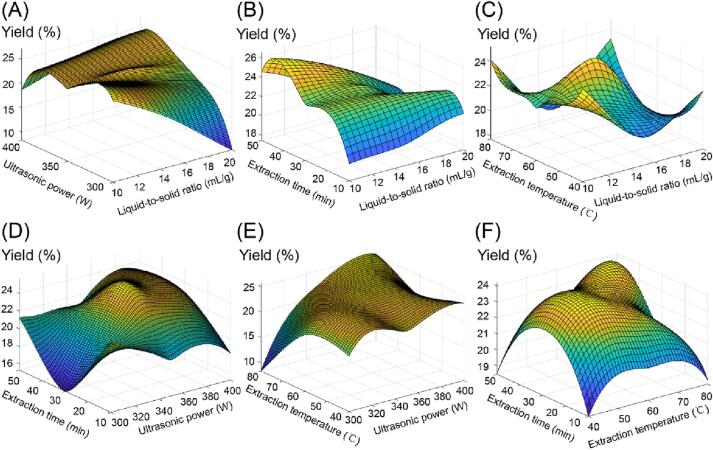
To clarify the correlations between the extracted AMRP value and the four variables, 3D surface plots were created (Fig. 2). With the increase in each variable, the AMRP yield showed a trend of increasing and then decreasing or increasing and then flattening. As the liquid-to-solid ratio increased from 10 to 15 mL/g, the yield increased. The main reasons for this phenomenon may be that the increase in solvent volume enhances the area of solvent–solute contact and allows more polysaccharides to be extracted. However, too much solvent did not increase the yield significantly but instead wasted resources (Fig. 2A, 2B, 2C). The increase in temperature accelerated the movement of AMRP molecules and improved solubility, thus increasing the yield. However, too high of a temperature can cause degradation and oxidation of AMRP, resulting in lower yields. In addition, too low of a temperature was not conducive to the dissolution of polysaccharides (Fig. 2C, 2E, 2F). In a certain range, a higher ultrasonic power (Fig. 2A, 2D, 2E) and a longer extraction time (Fig. 2B, 2D, 2F) can increase the AMRP yield, but excessive power and time were counterproductive due to the reduction of cavitation intensity.
Fig. 2.
Response 3D surface plot of the four variables to the interaction of AMRP yield. A: the interaction between liquid-to-solid ratio and ultrasonic power, B: the interaction between liquid-to-solid ratio and extraction time, C: the interaction between liquid-to-solid ratio and extraction temperature, D: the interaction between extraction time and ultrasonic power, E: the interaction between extraction temperature and ultrasonic power, F: the interaction between extraction time and extraction temperature.
The highest AMRP yield predicted by RSM was 27.8%, and the optimal extraction process required a 13 mL/g liquid-to-solid ratio, 350 W of ultrasonic power, 60 °C extraction temperature and 35 min of extraction time.
3.4. Comparation of the RSM model and three artificial neural network models
Three artificial neural network models were developed to describe the nonlinear relationship between four input variables and one output variable. Each model had three layers: an input layer, a hidden layer, and an output layer. The number of neurons in the hidden layer was determined by Eq. (4). The optimal number of neurons in the hidden layer was identified as 7 (Table 3) by comparison of the MSE of the training set when the number of neurons in the hidden layer varied. Next, the BP neural network was built, with a training number of 1000. Every time the model was trained, the weights and thresholds were updated, with a minimum error of the training target of 0.00001. When the model reached the training number or the error value between the output and the true value was less than 0.00001, the whole process stopped, and the final result was the output (Table 1). The optimal extraction conditions were as follows: liquid-to-solid ratio of 10 mL/g, ultrasonic power of 400 W, extraction temperature of 77 °C, and extraction time of 50 min, yielding 37.63% AMRP.
Table 3.
Effect of the number of hidden neurons of BP neural network, GA-BP neural network, GA-ACO-BP neural network.
| Hidden num | MSE of BP | MSE of GA-BP | MSE of GA-ACO-BP |
|---|---|---|---|
| 3 | 0.28 | 0.79 | 0.32 |
| 4 | 0.22 | 0.20 | 0.38 |
| 5 | 0.81 | 0.43 | 0.37 |
| 6 | 0.17 | 0.20 | 0.33 |
| 7 | 0.07 | 0.28 | 0.75 |
| 8 | 0.25 | 0.35 | 0.36 |
| 9 | 0.37 | 0.16 | 0.08 |
| 10 | 0.29 | 0.37 | 0.11 |
| 11 | 0.20 | 0.17 | 0.77 |
| 12 | 0.15 | 0.26 | 0.25 |
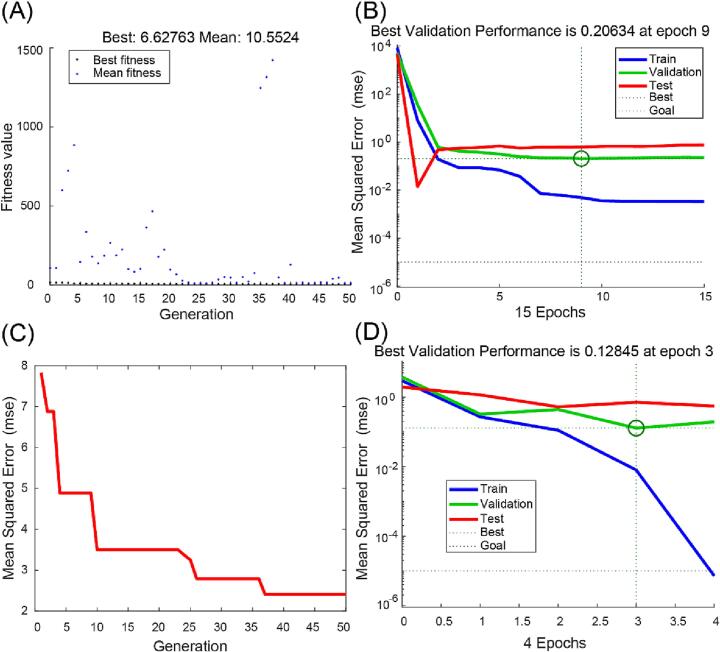
The GA-BP neural network was constructed by optimizing the thresholds and weights through a genetic algorithm. First, the parameters of the GA were initialized, the initial population size was set to 30, the maximum number of iterations was set to 50, the crossover probability was set to 0.8, and the variation probability was set to 0.2. The relationship between each generation and fitness value was calculated, as shown in Fig. 4A. The best fitness value was 6.63, and the mean fitness value was 10.55. Through population selection, crossover, and variation, the weights and thresholds were continuously updated, and finally, the weights and thresholds that met the convergence conditions were obtained. The optimal weights and thresholds were assigned to the BP neural network for prediction (Table 1) with a training number of 1000, and the minimum error of the training target was set to 0.00001. As the number of epochs increased, the number of updates of the neural network weights also increased, and the model went from underfitting to overfitting, so it was necessary to limit the number of epochs. Fig. 4B shows the performance of the training set and the test set at different numbers of epochs. The optimal extraction conditions were a liquid-to-solid ratio of 11 mL/g, ultrasonic power of 300 W, extraction temperature of 46 °C, and extraction time of 24 min, yielding 31.07% AMRP.
Fig. 4.
The performance of the GA-BP and GA-ACO-BP model. A: fitness function plot of GA-BP neural network. B: GA-BP neural network MSE for different data sets. C: MAE of the GA-ACO-BP model with different generation. D: GA-ACO-BP neural network MSE for different data sets.
The GA-ACO-BP neural network was constructed as shown in Fig. 3. The optimal weights and thresholds were found by improving the ant colony algorithm with a genetic algorithm. The initial population size, maximum number of iterations, crossover probability and variation probability were the same as those of the GA-BP neural network. The pheromone volatility coefficient was set to 0.9, the transfer probability constant was set to 0.2, and the total amount of information released was 1. Then, the best pheromone was confirmed by the genetic algorithm, the initial pheromone was confirmed by the updated ACO algorithm, and then the iteration started. The mean square error gradually decreased as the number of iterations increased. When the number of iterations was 37, the mean square error tended to be smooth (Fig. 4C). Finally, the optimal weights and thresholds were assigned to the BP neural network and the number of training iterations and the minimum error of the training target were set as those in the GA-BP neural network; the performance of the training and test sets are shown in Fig. 4D. The optimal extraction conditions were a liquid-to-solid ratio of 17 mL/g, ultrasonic power of 400 W, extraction temperature of 72 °C, and extraction time of 40 min, yielding 31.31% AMRP.
Although the p value of the RSM model was less than 0.05 and the lack of fit was greater than 0.05, the model was successfully established. However, the R2 was only 0.7483, indicating that the model had poor fit and inferior predictive ability to accurately determine the optimal extraction conditions.
According to Table 1, the data predicted by GA-ACO-BP were the closest to the true value. In addition, the four models were compared using R2, MAE, and RMSE, as shown in Table 4. The GA-ACO-BP model had the lowest MAE and RMSE, while the error between the data predicted by the RSM model and the true value was larger and only less than that of the BP model, which may be because the fit of the RSM model was low (R2 = 0.7483); the R2 of the GA-ACO-BP model was 0.8368, which represents the best fit among all of models and further indicated that the model had the best predictive power. In addition, the RSM model was limited to binomial regression, while the GA-ACO-BP model was able to respond to highly nonlinear relationships, which also led to a gap in the predictive power.
Table 4.
Extraction model performance comparison of RSM, BP neural network, GA-BP neural network and GA-ACO-BP neural network.
| RSM | BP | GA-BP | GA-ACO-BP | |
|---|---|---|---|---|
| R2 | 0.7483 | 0.6762 | 0.7776 | 0.8368 |
| RMSE | 2.42 | 5.95 | 2.76 | 1.46 |
| MAE | 1.85 | 3.90 | 1.62 | 1.14 |
The predictive ability of the four models was experimentally verified. Theoretically, the highest AMRP yield was predicted by the BP model (37.63%), but the experimental results showed the opposite (22.42 ± 4.67%), which may be due to the larger prediction error of the BP model. The highest AMRP yield (29.99 ± 4.13%) was obtained under the best conditions predicted by GA-ACO-BP, followed by GA-BP and then the RSM model. In summary, the GA-ACO-BP model was the best model, and the parameters obtained for the four variables were the best process.
Based on the modelling, corresponding 3D plots of the four factors and the AMRP yield were also constructed, and it can be seen that the relationships reflected in these figures were more complex than the corresponding 3D plots output by the RSM, which may also be because the RSM was limited to binomial regression. Fig. 5A-C shows a general trend of increasing and then decreasing AMRP yield as the liquid-to-solid ratio increased. The AMRP yield increased before decreasing when the power was 300–350 W. The same trend was observed in the power range of 350–400 W (Fig. 5A, D, E). The effect of extraction temperature on AMRP yield also basically showed a rising and then decreasing trend (Fig. 5C, E, F), and the same was true for extraction time. Many locally optimal solutions appear in these plots.
Fig. 5.
Neural network 3D surface plot of the four independent variables to the interaction of AMRP yield. A: the interaction between liquid-to-solid ratio and ultrasonic power, B: the interaction between liquid-to-solid ratio and extraction time, C: the interaction between liquid-to-solid ratio and extraction temperature, D: the interaction between extraction time and ultrasonic power, E: the interaction between extraction temperature and ultrasonic power, F: the interaction between extraction time and extraction temperature.
3.5. Kinetic models for UAE
Linear regression of the weight of dry AMR based on water absorption yielded equation y = 1.3481x-0.0809 with an R2 = 0.9992, demonstrating a relatively high degree of model fit with a dry AMR solvent absorption rate of 1.3481.
According to the content determination method established by the 2020 edition of the Chinese Pharmacopoeia, the mean value of the mass fraction of total AMRP for this experiment was measured to be 63.93 ± 1.13%, and was calculated to be 0.72 according to Eq. (11).
Based on the experimental data, linear regression of lnCb as a function of lnt was conducted to examine whether the experimental data adhered to Eq. (10). When the liquid-to-solid ratio was 17 mL/g, the linear regression equation was InCb = 0.2957 Int + 1.785, R2 = 0.9842. According to the equation, the corresponding values were combined to obtain n = -0.69 and = 443.82.
Substituting the above-derived R into Eq. (9), the kinetic equation for AMRP extraction established in this study was determined as follows:
| (14) |
According to the established kinetic equation, the AMRP yields were predicted from 8 to 40 min at two-minute intervals with a liquid-to-solid ratio of 17 mL/g. According to Table 6, the predicted and true values of AMRP yield were in good agreement, which suggested that the extraction kinetic model developed in this experiment can more accurately depict the dissolution pattern of AMRP.
Table 6.
The actual and predicted data of kinetic models.
| Time (min) | AMRP concentration (mg/mL) | ||||
|---|---|---|---|---|---|
| Actual | Equation predicted | BP predicted | GA-BP predicted | GA-ACO-BP predicted | |
| 8 | 10.77 | 11.02 | 11.71 | 11.09 | 10.76 |
| 10 | 11.41 | 11.77 | 12.45 | 11.11 | 11.39 |
| 12 | 13.09 | 12.43 | 12.90 | 12.70 | 13.06 |
| 14 | 13.33 | 13.01 | 13.74 | 13.24 | 13.25 |
| 16 | 13.39 | 13.53 | 14.71 | 13.48 | 13.43 |
| 18 | 13.83 | 14.01 | 15.46 | 14.04 | 14.15 |
| 20 | 14.57 | 14.45 | 15.58 | 14.27 | 14.43 |
| 22 | 14.21 | 14.87 | 15.68 | 14.70 | 15.08 |
| 24 | 15.28 | 15.25 | 15.77 | 15.49 | 15.83 |
| 26 | 15.85 | 15.62 | 15.84 | 15.90 | 15.93 |
| 28 | 16.77 | 15.96 | 15.87 | 16.48 | 16.15 |
| 30 | 16.27 | 16.29 | 15.89 | 17.03 | 16.49 |
| 32 | 16.36 | 16.61 | 15.89 | 17.17 | 16.74 |
| 34 | 16.86 | 16.91 | 15.89 | 17.18 | 17.01 |
| 36 | 17.03 | 17.20 | 15.89 | 17.17 | 16.93 |
| 38 | 17.73 | 17.47 | 15.89 | 17.20 | 17.16 |
| 40 | 17.85 | 17.74 | 15.89 | 17.22 | 17.76 |
3.6. Comparison of the kinetic model and three artificial neural network models
This experiment compared the established kinetic equation and the abilities of three artificial neural network models to predict the AMRP concentration at different times. The model building method was the same as described in 2.3.4 and 3.4. The MSEs of the training set of different neurons in the hidden layer are shown in Table 5. The optimal numbers of hidden layer neurons in the BP neural network, GA-ACO-BP neural network, and GA-ACO-BP neural network were 6, 7 and 4, respectively. According to Table 7, the BP neural network has the smallest R2 (0.9039) and the largest RMSE (1.01) and MAE (0.89), which implies the worst predictive ability. The GA-BP neural network had the highest R2 (0.9825), which indicated the best data fit, but the RMSE (0.41) and MAE (0.35) were larger. In a comprehensive analysis, the GA-ACO-BP neural network and the constructed kinetic equation fit well (R2 = 0.9651 and 0.9689), and the RMSE (0.36 and 0.35) and MAE (0.25 and 0.27) were small, which indicated its superior predictive ability.
Table 5.
Effect of the number of hidden neurons of BP neural network, GA-BP neural network, GA-ACO-BP neural network.
| Hidden num | MSE of BP | MSE of GA-BP | MSE of GA-ACO-BP |
|---|---|---|---|
| 3 | 0.22 | 0.07 | 0.03 |
| 4 | 0.09 | 0.02 | 0.01 |
| 5 | 0.08 | 0.12 | 0.06 |
| 6 | 0.02 | 0.03 | 0.08 |
| 7 | 0.17 | 0.01 | 0.07 |
| 8 | 0.05 | 0.39 | 0.04 |
| 9 | 0.04 | 0.06 | 0.09 |
| 10 | 0.02 | 0.11 | 0.06 |
| 11 | 0.07 | 0.08 | 0.06 |
| 12 | 0.64 | 0.04 | 0.04 |
Table 7.
Kinetic model performance comparison of RSM, BP neural network, GA-BP neural network and GA-ACO-BP neural network.
| Eq. (14) | BP | GA-BP | GA-ACO-BP | |
|---|---|---|---|---|
| R2 | 0.9689 | 0.9039 | 0.9825 | 0.9651 |
| RMSE | 0.35 | 1.01 | 0.41 | 0.36 |
| MAE | 0.27 | 0.89 | 0.35 | 0.25 |
3.7. SEM analysis
The surface and internal structures of AMRP were observed at various magnifications using SEM. Magnified at 250 × and 500× (Fig. 6A, B), AMRP exhibited irregular characteristics and an uneven surface. At 1000×, 3000×, 5000 × and 10000×, we can see the loose interior of AMRP with many voids, reflecting weak intermolecular forces, and the polysaccharide structures were tightly wound together with a large number of honeycomb-like cavities in the middle (Fig. 6C, D, E, F).
Fig. 6.
SEM images of AMRP. A: ×250, B: ×500, C: ×1000, D: ×3000, E: ×5000, F: ×10000.
3.8. FTIR spectroscopy of AMRP
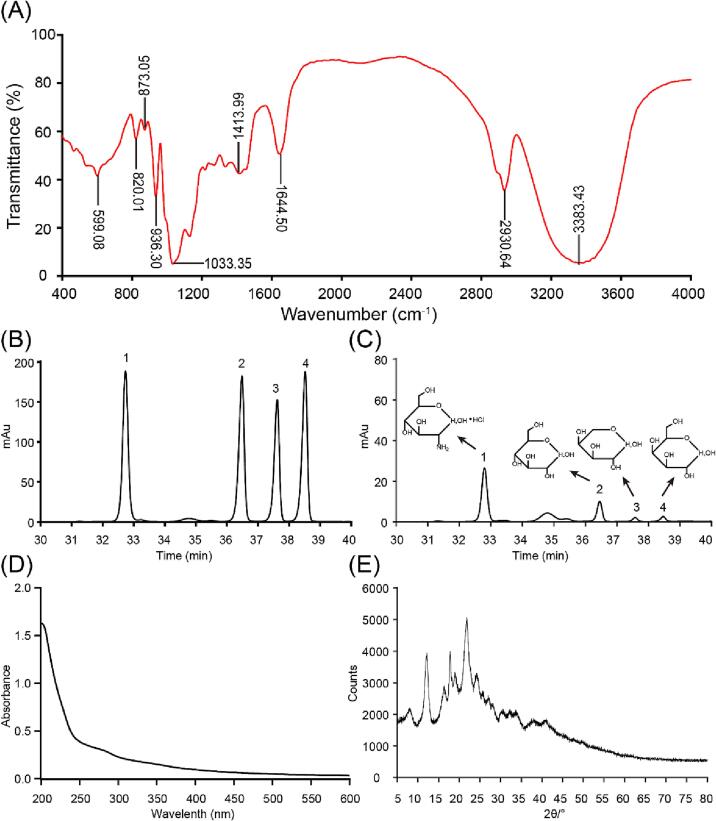
Fig. 7A shows the FTIR spectrum of AMRP in the range of 400 to 4000 cm−1. The sample had a strong and broad absorption at 3383.43 cm−1, which indicates the stretching vibration of O-H bonds. The bands at 2930.64 cm−1 could be attributed to the C-H stretching vibration and bending vibration. The absorption at 1644.50 cm−1 represented the C = O stretching vibration. The strong band at 1033.35 cm−1 was caused by the overlap of C-O-C and C-O-H stretching vibrations, implying that AMRP contained pyran rings. Moreover, due to the presence of α-pyranose and β-pyranose, there were absorption peaks at 820.01 and 873.05 cm−1.
Fig. 7.
A: FTIR spectroscopy analysis of AMRP. B: mixed standard solution, C: AMRP sample. (1: glucosamine hydrochloride, 2: glucose, 3: galactose, 4: arabinose). D: Ultraviolet spectroscopy. E: XRD analysis.
3.9. Monosaccharide composition analysis
The monosaccharide composition of AMRP was monitored by HPLC using glucosamine hydrochloride as an internal standard. In summary, the correction factor was determined by analysing the mixed standard solution and then calculating the content of each monosaccharide. Fig. 7B, C demonstrates the presence of several monosaccharides in AMRP, including glucose, galactose, and arabinose. The monosaccharide composition results showed that glucose was the major sugar in AMRP, accounting for 5.07%, followed by arabinose and galactose, accounting for 0.80% and 0.74%, respectively.
3.10. Protein and uronic acid content analysis
As shown in Fig. 7D, AMRP had no absorption peaks at 260 nm or 280 nm, indicating the absence of nucleic acids and proteins, and this result was consistent with the test results of the BCA assay, which revealed that the protein content in AMRP was 0.07 ± 0.02 mg/mg. The content of uronic acid measured by the m-hydroxydiphenyl assay was 0.04 ± 0.01 mg/mg. Thus, both of these materials were present in incredibly small amounts.
3.11. XRD analysis
X-ray diffraction techniques are widely used to identify the crystallinity of substances; crystalline components exhibit sharp, narrow peaks, whereas amorphous components exhibit broad peaks. Fig. 7E depicts the AMRP XRD pattern. The findings revealed significant absorption peaks at 12.10°, 17.78°, and 21.76°, indicating the presence of a distinct microcrystalline structure in AMRP, as well as minor absorptions at 7.90°, 16.36°, 18.98°, and 24.26°, revealing the existence of a subcrystalline structure and an amorphous structure elsewhere.
3.12. NMR analysis
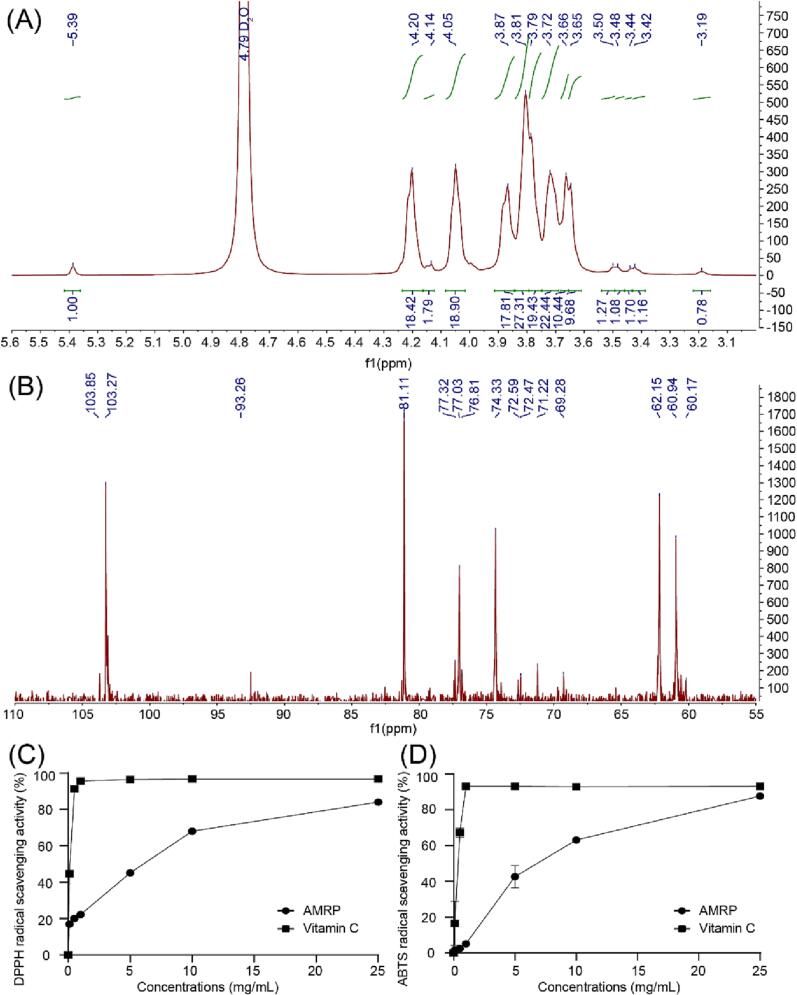
In general, the anomeric proton signal with δ less than 5.00 ppm are considered β-type, and those with δ greater than 5.00 ppm are considered α-type. Three anomeric protons were observed in the 1H NMR spectrum of AMRP (Fig. 8A), indicating that AMRP consists of one α-type monosaccharide (δ 5.39) and two β-type monosaccharides (δ 4.20, 4.14 ppm), which was consistent with the FTIR results. The proton signals of H2-H6 were concentrated in the δ 3.00–4.40 ppm range, which is typical of polysaccharide signal peaks. From the 13C NMR spectrum (Fig. 8B), we observed that the carbon signals of AMRP were mainly concentrated in the range of δ 60.00–105.00 ppm. In the anomeric carbon region, three main signal peaks appeared at δ 103.85 and 103.27 ppm (attributed to β-type) and δ 93.26 ppm (attributed to α-type) and the stronger signal peaks between δ 60.00–85.00 ppm could be attributed to C2-C6.
Fig. 8.
A: 1H NMR spectrum of AMRP. B: 13C NMR spectrum of AMRP. C: DPPH radical scavenging activity. D: ABTS radical scavenging activity.
3.13. Antioxidant activity analysis
Polysaccharides, polyphenols and flavones are physiologically active compounds with antioxidant, anti-inflammatory and antimicrobial properties. In this experiment, the antioxidant activity of AMRP was evaluated by DPPH, ABTS and FRAP assays.
The results from the DPPH and ABTS assays are shown in Fig. 8C, D. In general, the antioxidant activity data from the DPPH and ABTS assays for AMRP and vitamin C are expressed as the amount of antioxidant required to decrease the initial concentration by 50%. The IC50 values of AMRP and vitamin C were 6.60 µg/mL and 0.20 µg/mL, respectively. AMRP thus has a lower IC50 value than vitamin C in the DPPH experiment. Moreover, for the ABTS assay, the IC50 value of AMRP was 6.55 µg/mL, which was lower than that of vitamin C (IC50 = 0.48 µg/mL), indicating that AMRP is a good antioxidant.
The FRAP assay measures the ability of antioxidants present in the sample to reduce Fe3+ to Fe2+ in the presence of tripyridyl-s-triazine (TPTZ). The FRAP values of AMRP and vitamin C were determined to be 0.32 ± 0.02 mmol/g and 2.33 ± 0.02 mmol/g, respectively, in the FRAP assay.
4. Conclusion
In this experiment, the effects of different extraction methods on the yield of AMRP were investigated, and then RSM and three neural network models were used to optimize the ultrasound-assisted extraction conditions of AMRP. The extraction conditions explored by ACO-GA-BP were as follows: liquid-to-solid ratio of 17 mL/g, ultrasonic power of 400 W, extraction temperature of 72 °C, and extraction time of 40 min. Under these conditions, the yield of AMRP was 31.31%, which was higher than the optimized yields determined by the other models. Following the successful establishment of an equation that appropriately described the kinetics of AMRP, three artificial neural network models were evaluated, and the ACO-GA-BP model and the created equation produced the best kinetic model simulation. AMRP was characterized by SEM, FTIR, and HPLC, and the findings revealed that its surface was rough and its interior was hollow, and it contained glucose (5.07%), arabinose (0.80%), and galactose (0.74%). The results from the in vitro antioxidant tests showed that AMRP had strong antioxidant potential. These results provide a theoretical basis for further in-depth study of AMRP. By the UV method, AMRP was found to be a neutral sugar without protein or uronic acid. The XRD spectrum indicated that a microcrystalline structure, subcrystalline structure and amorphous structure were all present in AMRP. The NMR spectrum showed that AMRP contained two β-type monosaccharides and one α-type monosaccharide.
5. Discussion
Extraction is the process of removing the active ingredients from herbs, and the extraction yield of a given herb will vary depending on the extraction method used. Herbs whose active ingredients are easily destroyed by heat and herbs with hard cell walls that make the extraction of active ingredients challenging are suitable for ultrasonic-assisted extraction. Ultrasound-assisted extraction promotes the extraction of active ingredients through the mechanical effect of ultrasonic waves, thermal effect, bubble action, and other mechanisms. Microwave extraction through the high-frequency vibrations produced by the microwave cause friction and collision of the molecules, so that the active ingredients in the herb can be quickly released into the solvent. Microwave extraction is suitable for volatile components or when the herb contains ingredients that are susceptible to high temperature damage. Reflux extraction is the process of combining herbs and solvents and heating them in a water bath at a steady temperature or using a heating apparatus so that the herbs' active components gradually dissolve into the solvent. This method works well for herbs with easily soluble components [34], [35]. Compared with reflux extraction, the other two methods noted above are suitable for herbs that are unstable under heating conditions. In this experiment, three different extraction methods were compared, and ultrasound-assisted extraction was the best method in terms of polysaccharide extraction yield. Each extraction technique has its own benefits, drawbacks, and application ranges. In a practical setting, the optimum extraction technique must be chosen based on a number of variables, including time, energy consumption, and the characteristics of the active components.
Response surface methodology is an experimental design method based on mathematical models that describes the relationship between input and output variables by building mathematical models, depending on which type of experimental optimization is performed. However, when the number of input variables rises, the results of the response surface show a worse fit, leading to issues such as poor fit, significant lack of fit, and an insignificant model [36]. The introduction of artificial neural networks do well to solve these problems. An artificial neural network is a computational model that simulates a biological nervous system and consists of many simple neurons that can be used for various tasks, such as pattern recognition, classification, prediction, and optimization. Artificial neural networks can efficiently process a large amount of data, learn from a large amount of data, constantly change their own weights and thresholds, and gradually improve their ability to fit and predict the data, which is very helpful for the interpretation of some nonlinear problems; moreover, they can be better than RSM models. When the problem changes, the artificial neural network can adjust the structure and parameters according to the true conditions to adapt to different environments [37]. Three artificial neural networks were trained to fit the extraction process and the kinetics of AMRP in this experiment. The three neural networks' ability to fit and predict, as well as their performance with response surface models and kinetic equations, were all assessed using the metrics R2, RMSE, and MAE. When studying the extraction process, it was discovered that the GA-ACO-BP model performed better than other models in terms of fitting and prediction, and the highest yield of AMRP was obtained under the predicted ideal process conditions. The RSM model's overall performance was only slightly better than that of the BP model. The 3D graph presented by the RSM model showed a single trend of the relationship between output and input variables in a roof-form shape, while the 3D graph generated by the neural network showed a more complex relationship between the output and input variables. In the kinetic study, the kinetic equations established with the ACO-GA-BP model were more comprehensive than those from the other models. As previously demonstrated, artificial neural networks, particularly those that have been algorithmically optimized, exhibit exceptional fitting and prediction abilities. However, artificial neural networks can have several drawbacks, such as the need for a substantial amount of training data, and therefore, they cannot be employed effectively with a very small number of samples. When there are too many parameters in the model, it tends to be overfit, resulting in a decrease in the generalization ability of the model. Moreover, it is easy to find only a local optimal solution when the fitting is insufficient. Artificial neural networks have been optimized and improved since their inception, and this experiment provides a reference for solving these problems in the future.
As important bioinformatic molecules, plant polysaccharides exhibit biological activities, and their effect mechanisms that are inextricably linked to their complex structures. However, the existing techniques are unable to comprehensively resolve polysaccharide structures, and thus only certain properties can be determined. In this experiment, the surface and internal structures of AMRP were observed by SEM, the functional groups of AMRP were analysed by FTIR, and the types and contents of monosaccharides were determined using HPLC. In addition, the protein and glyoxylate contents of AMRP were determined. The crystalline form AMRP was also analysed using XRD, and NMR was used to determine the type of glycosidic bonds and the mode of connection [31]. Future research will concentrate on controlling a single variable to examine the polysaccharide structure, because the AMRP structure can be affected by the origin, growth environment, extraction process, and purification process, which is one of the major factors restricting the study of the biological activities of polysaccharides.
High contents of free radicals can cause oxidative damage to the body and ageing [38]. The ability of plant polysaccharides to neutralize free radicals has been extensively documented [28]. AMRP is a good scavenger of free radicals and this ability is positively correlated with concentration, which may be attributed to the hydrogen donating ability of the reducing hydroxyl groups in polysaccharides. However, the biological activities of polysaccharides are not only limited to antioxidant capacity, but these compounds also have antitumour, immune function improvement, and blood glucose and lipid regulating effects [3], [39], [40], so this experiment cannot be restricted to only antioxidant ability. AMRP will be further researched in depth to examine its other biological activities and provide more references for its development and application.
Data availability
Data will be made available on request.
CRediT authorship contribution statement
Junjie Qiu: Methodology, Investigation, Writing – original draft, Writing – review & editing. Menglin Shi: Methodology, Investigation, Writing – original draft, Writing – review & editing. Siqi Li: Data curation, Visualization. Qianyi Ying: Data curation, Visualization. Xinxin Zhang: Data curation. Xinxin Mao: Data curation. Senlin Shi: Writing – review & editing, Supervision, Project administration. Suxiang Wu: Writing – review & editing, Supervision, Project administration.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Contributor Information
Senlin Shi, Email: pjstone@163.com.
Suxiang Wu, Email: wsx173@126.com.
References
- 1.Cui Y.S., Li Y.X., Jiang S.L., et al. Isolation, purification, and structural characterization of polysaccharides from Atractylodis Macrocephalae Rhizoma and their immunostimulatory activity in RAW264.7 cells[J] Int. J. Biol. Macromol. 2020;163:270–278. doi: 10.1016/j.ijbiomac.2020.06.269. [DOI] [PubMed] [Google Scholar]
- 2.Yan H., Sun Y., Ma Y., et al. Determination of atractylon in rat plasma by a GC-MS method and its application to a pharmacokinetic study[J] J. Pharm. Anal. 2015;5(5):327–331. doi: 10.1016/j.jpha.2015.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wu Y., Yao J., Xie J., et al. The role of autophagy in colitis-associated colorectal cancer[J] Signal Transduct. Target. Ther. 2018;3:31. doi: 10.1038/s41392-018-0031-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wang L., Wang F., Zhang X., et al. Transdermal Administration of Volatile Oil from Citrus aurantium-Rhizoma Atractylodis Macrocephalae Alleviates Constipation in Rats by Altering Host Metabolome and Intestinal Microbiota Composition[J] Oxid. Med. Cell. Longev. 2022;2022:9965334. doi: 10.1155/2022/9965334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Li Y., Wang Y., Liu Z., et al. Atractylenolide I Induces Apoptosis and Suppresses Glycolysis by Blocking the JAK2/STAT3 Signaling Pathway in Colorectal Cancer Cells[J] Front. Pharmacol. 2020;11:273. doi: 10.3389/fphar.2020.00273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Liu Y., Zhe W., Zhang R., et al. Ultrasonic-assisted extraction of polyphenolic compounds from Paederia scandens (Lour.) Merr. Using deep eutectic solvent: optimization, identification, and comparison with traditional methods[J] Ultrason. Sonochem. 2022;86 doi: 10.1016/j.ultsonch.2022.106005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Guo L., Kong N., Zhang X., et al. Multimode ultrasonic extraction of polysaccharides from maca (Lepidium meyenii): Optimization, purification, and in vitro immunoregulatory activity[J] Ultrason. Sonochem. 2022;88 doi: 10.1016/j.ultsonch.2022.106062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang J.S., Mu T.H., Ma M.M. Optimization of ultrasound-microwave assisted acid extraction of pectin from potato pulp by response surface methodology and its characterization[J] Food Chem. 2019;289:351–359. doi: 10.1016/j.foodchem.2019.03.027. [DOI] [PubMed] [Google Scholar]
- 9.Mohammed A., Rivers A., Stuckey D.C., et al. Alginate extraction from Sargassum seaweed in the Caribbean region: Optimization using response surface methodology[J] Carbohydr. Polym. 2020;245 doi: 10.1016/j.carbpol.2020.116419. [DOI] [PubMed] [Google Scholar]
- 10.Mocanu D.C., Mocanu E., Stone P., et al. Scalable training of artificial neural networks with adaptive sparse connectivity inspired by network science[J] Nat. Commun. 2018;9(1):2383. doi: 10.1038/s41467-018-04316-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hasson U., Nastase S.A., Goldstein A. Direct Fit to Nature: An Evolutionary Perspective on Biological and Artificial Neural Networks[J] Neuron. 2020;105(3):416–434. doi: 10.1016/j.neuron.2019.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shi C.F., Yang H.T., Chen T.T., et al. Artificial neural network-genetic algorithm-based optimization of aerobic composting process parameters of Ganoderma lucidum residue[J] Bioresour. Technol. 2022;357 doi: 10.1016/j.biortech.2022.127248. [DOI] [PubMed] [Google Scholar]
- 13.Churkin A., Retwitzer M.D., Reinharz V., et al. Design of RNAs: comparing programs for inverse RNA folding[J] Brief. Bioinform. 2018;19(2):350–358. doi: 10.1093/bib/bbw120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sengar A.S., Rawson A., Muthiah M., et al. Comparison of different ultrasound assisted extraction techniques for pectin from tomato processing waste[J] Ultrason. Sonochem. 2020;61 doi: 10.1016/j.ultsonch.2019.104812. [DOI] [PubMed] [Google Scholar]
- 15.Commission C.P. Chinese Medical Science Press; Beijing, China: 2020. Pharmacopoeia of the People's Republic of China[M] p. 295. [Google Scholar]
- 16.Hung B.P., Harvestine J.N., Saiz A.M., et al. Defining hydrogel properties to instruct lineage- and cell-specific mesenchymal differentiation[J] Biomaterials. 2019;189:1–10. doi: 10.1016/j.biomaterials.2018.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hunt L.T., Hayden B.Y. A distributed, hierarchical and recurrent framework for reward-based choice[J] Nat. Rev. Neurosci. 2017;18(3):172–182. doi: 10.1038/nrn.2017.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang J., Ju R., Chen Y., et al. Automated retinopathy of prematurity screening using deep neural networks[J] EBioMedicine. 2018;35:361–368. doi: 10.1016/j.ebiom.2018.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shi Y., Li Y., Cai M., et al. A Lung Sound Category Recognition Method Based on Wavelet Decomposition and BP Neural Network[J] Int. J. Biol. Sci. 2019;15(1):195–207. doi: 10.7150/ijbs.29863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jin L., Jin W., Zhang Y., et al. Simultaneous optimization of the extraction process of Yangyin Yiqi Huoxue prescription with natural deep eutectic solvents for optimal extraction yield and antioxidant activity: A comparative study of two models[J] Phytomedicine. 2022;102 doi: 10.1016/j.phymed.2022.154156. [DOI] [PubMed] [Google Scholar]
- 21.Lee G.E., Kim R.H., Lim T., et al. Optimization of accelerated solvent extraction of ellagitannins in black raspberry seeds using artificial neural network coupled with genetic algorithm[J] Food Chem. 2022;396 doi: 10.1016/j.foodchem.2022.133712. [DOI] [PubMed] [Google Scholar]
- 22.Dorigo M., Maniezzo V., Colorni A. Ant system: optimization by a colony of cooperating agents[J] IEEE Trans. Syst. Man Cybern. B Cybern. 1996;26(1):29–41. doi: 10.1109/3477.484436. [DOI] [PubMed] [Google Scholar]
- 23.Yang K., Duan Q., Wang Y., et al. Transiently chaotic simulated annealing based on intrinsic nonlinearity of memristors for efficient solution of optimization problems[J] Sci. Adv. 2020;6(33):eaba9901. doi: 10.1126/sciadv.aba9901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Moses M.E., Cannon J.L., Gordon D.M., et al. Distributed Adaptive Search in T Cells: Lessons From Ants[J] Front. Immunol. 2019;10:1357. doi: 10.3389/fimmu.2019.01357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Xu S., Wan H., Zhao X., et al. Optimization of extraction and purification processes of six flavonoid components from Radix Astragali using BP neural network combined with particle swarm optimization and genetic algorithm[J] Ind. Crop. Prod. 2022;178 [Google Scholar]
- 26.Yu z-x, zhang y-y, zhao x-x,, et al. Simultaneous optimization of ultrasonic-assisted extraction of Danshen for maximal tanshinone IIA and salvianolic acid B yields and antioxidant activity: A comparative study of the response surface methodology and artificial neural network[J] Ind. Crop. Prod. 2021;161 [Google Scholar]
- 27.Han L., Ni J., Xuan L., et al. Modeling the kinetics of aqueous decoction extraction of Acanthopanax[J] Zhong Cheng Yao. 2011;33(02):240–245. [Google Scholar]
- 28.Wang K., Guo J., Cheng J., et al. Ultrasound-assisted extraction of polysaccharide from spent Lentinus edodes substrate: Process optimization, precipitation, structural characterization and antioxidant activity[J] Int. J. Biol. Macromol. 2021;191:1038–1045. doi: 10.1016/j.ijbiomac.2021.09.174. [DOI] [PubMed] [Google Scholar]
- 29.Wu H., Li M., Yang X., et al. Extraction optimization, physicochemical properties and antioxidant and hypoglycemic activities of polysaccharides from roxburgh rose (Rosa roxburghii Tratt.) leaves[J] Int. J. Biol. Macromol. 2020;165(Pt A):517–529. doi: 10.1016/j.ijbiomac.2020.09.198. [DOI] [PubMed] [Google Scholar]
- 30.Wu J., Xu Y., Liu X., et al. Isolation and structural characterization of a non-competitive alpha-glucosidase inhibitory polysaccharide from the seeds of Litchi chinensis Sonn[J] Int. J. Biol. Macromol. 2020;154:1105–1115. doi: 10.1016/j.ijbiomac.2019.11.170. [DOI] [PubMed] [Google Scholar]
- 31.Wu J., Ming Q., Zhai X., et al. Structure of a polysaccharide from Trichoderma atroviride and its promotion on tanshinones production in Salvia miltiorrhiza hairy roots[J] Carbohydr. Polym. 2019;223 doi: 10.1016/j.carbpol.2019.115125. [DOI] [PubMed] [Google Scholar]
- 32.Mostafa H., Airouyuwa J.O., Maqsood S. A novel strategy for producing nano-particles from date seeds and enhancing their phenolic content and antioxidant properties using ultrasound-assisted extraction: A multivariate based optimization study[J] Ultrason. Sonochem. 2022;87 doi: 10.1016/j.ultsonch.2022.106017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hadidi M., Amoli P.I., Jelyani A.Z., et al. Polysaccharides from pineapple core as a canning by-product: Extraction optimization, chemical structure, antioxidant and functional properties[J] Int. J. Biol. Macromol. 2020;163:2357–2364. doi: 10.1016/j.ijbiomac.2020.09.092. [DOI] [PubMed] [Google Scholar]
- 34.Yu z-x, zhang y-y, zhao x-x,, et al. Simultaneous optimization of ultrasonic-assisted extraction of Danshen for maximal tanshinone IIA and salvianolic acid B yields and antioxidant activity: A comparative study of the response surface methodology and artificial neural network[J] Ind. Crop. Prod. 2021:161. [Google Scholar]
- 35.Xu S., Wan H., Zhao X., et al. Optimization of extraction and purification processes of six flavonoid components from Radix Astragali using BP neural network combined with particle swarm optimization and genetic algorithm[J] Ind. Crop. Prod. 2022;178 [Google Scholar]
- 36.Dogan H., Aydin temel f, cagcag yolcu o,, et al. Modelling and optimization of sewage sludge composting using biomass ash via deep neural network and genetic algorithm[J] Bioresour. Technol. 2023;370 doi: 10.1016/j.biortech.2022.128541. [DOI] [PubMed] [Google Scholar]
- 37.Yilmaz E.C., Aydin temel f, cagcag yolcu o,, et al. Modeling and optimization of process parameters in co-composting of tea waste and food waste: Radial basis function neural networks and genetic algorithm[J] Bioresour. Technol. 2022;363 doi: 10.1016/j.biortech.2022.127910. [DOI] [PubMed] [Google Scholar]
- 38.Moore S., Berger N.D., Luijsterburg M.S., et al. The CHD6 chromatin remodeler is an oxidative DNA damage response factor[J] Nat. Commun. 2019;10(1):241. doi: 10.1038/s41467-018-08111-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Fu X., Wang Q., Wang Z., et al. Danggui-Shaoyao-San: New Hope for Alzheimer's Disease[J] Aging Dis. 2016;7(4):502–513. doi: 10.14336/AD.2015.1220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Li X.J., Xiao S.J., Chen J., et al. Inulin-type fructans obtained from Atractylodis Macrocephalae by water/alkali extraction and immunoregulatory evaluation[J] Int. J. Biol. Macromol. 2023;230 doi: 10.1016/j.ijbiomac.2023.123212. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.