Abstract
People tend to spend the majority of their time indoors. Indoor air properties can significantly affect humans’ comfort, health, and productivity. This study utilizes measurement data of indoor conditions in a kindergarten in Sofia, Bulgaria. Autoregressive integrated moving average (ARIMA) and long short-term memory (LSTM) recurrent neural network (RNN) models were developed to predict CO levels in the educational facility over the next hour based on 2.5 h of past data and allow for near real-time decision-making. The better-performing model, LSTM, is also used for temperature and relative humidity forecasting. Global comfort is then estimated based on threshold values for temperature, humidity, and CO. The predicted values ranged between 0.938 and 0.981 for the three parameters, while the prediction of global comfort conditions achieved a 91/100 accuracy.
Keywords: predictive modeling, machine learning, indoor environment, comfort conditions, air quality
1. Introduction
Most people nowadays tend to spend 90% of their time indoors—at home, at work, in school, or other enclosed environments [1,2]. Numerous studies have linked poor indoor conditions with symptoms such as eye, nose, and throat irritation; headaches; fatigue; skin dryness; and asthma-like symptoms [3,4,5,6]. These symptoms are most commonly observed in indoor spaces with a high number of occupants [7] and are connected to a condition named “sick building syndrome” (SDS) [8]. Even short-term exposure to inadequate indoor conditions could cause harm to more sensitive groups such as children or the elderly or people with other health conditions such as cardiovascular or respiratory diseases [9,10]. In fact, young children are at even higher risk due to their 2–3 times higher volume of inhaled air with respect to their body weight compared to adults [11].
The quality of the indoor environment in educational facilities is often determined by different factors such as air pollution, temperature, relative humidity, ventilation rate, concentration of volatile organic compounds, etc. Particulate matter (PM and PM), for instance, has generally been associated in several studies with increased mortality rate, and respiratory and cardiovascular conditions, especially among children [12,13]. The Indoor Air Hygiene Institute states that PM levels above 35 g/m during a 24 h period are considered unhealthy [14]. Carbon dioxide (CO) concentrations above 1000 ppm have been proven to contribute to headaches, decreased cognitive performance, dry cough, and respiratory problems in young children [15,16,17]. Low ventilation rates, high temperatures, and low relative humidity also have a negative influence on the children’s overall learning performance [18,19]. Therefore, the environmental conditions in kindergartens and schools play a vital role in the children’s learning efficiency, short- and long-term health, and well-being.
Monitoring different indoor parameters in real time is essential to ensuring a healthy environment. The availability and affordability of computational resources over the past few decades have enabled the utilization of various models, including artificial intelligence (AI) and machine learning (ML) models, for the prediction of future environmental conditions [20]. The most commonly used models in such forecasting studies are regression models, support vector machines, artificial neural networks (ANN), decision trees, random forests, and generalized boosting models [21].
The aim of this study is to comprehensively assess the indoor environmental conditions and present a short-term prediction of the comfort conditions inside a kindergarten room in Sofia, Bulgaria using a recurrent neural network (RNN). While certain parameters such as particulate matter, temperature, and relative humidity have received considerable attention in previous research [20], the inclusion of CO as a critical parameter is of significant importance. Monitoring, control, and prediction of CO alongside other parameters provides a holistic understanding of the indoor environment. The rest of this article is structured as follows: Section 2 describes the materials and methods of this study. Section 3 then demonstrates the results and discussions. Finally, Section 4 presents the conclusion and future works.
2. Materials and Methods
2.1. Site Description
The current study employs data from a kindergarten room located in a residential area in Sofia, Bulgaria. The selected indoor space is located on the ground level and is naturally ventilated. The room is occupied from Monday to Friday between 7:00 a.m. and 5:30 p.m. except holiday periods.
2.2. Data Collection and Instrumentation
The measuring equipment is placed on a wall opposite the windows. It consists of temperature and relative humidity sensor (https://www.bosch-sensortec.com/media/boschsensortec/downloads/datasheets/bst-bme280-ds002.pdf (accessed on 12 July 2023)), a fine particulate matter sensor (https://eu.mouser.com/datasheet/2/187/HWSC_S_A0012942921_1-3073234.pdf (accessed on 12 July 2023)), and a CO sensor (https://f.hubspotusercontent40.net/hubfs/9035299/Documents/AAS-920-634G-Telaire-T6713-Series-011321-web.pdf (accessed on 12 July 2023)). The measurement ranges are, respectively, [−40, 85] C, [0, 100]%, [0, 1000] g/m, and [0, 5000] ppm. The measurement ranges adequately cover the air property values expected to be observed in the current study. The fine particulate matter sensor measures PM and provides estimates for PM, PM, and PM based on the PM values. A sound alarm signals the teachers that the CO levels have crossed the acceptable threshold of 1000 ppm and urges them to open the windows.
The sampling campaign took place between August 2021 and October 2022 with measurements recorded at irregular intervals.
2.3. Data Preparation and Analysis
The whole data set consists of 97,637 records, which are resampled into 15 min interval measurements using weighted mean. The resulting data set consists of 43,872 observations. Around a quarter of those observations, however, have missing values. Forward filling is used in cases of up to two consecutive missing values while longer periods of missing data are removed. The more significant such intervals are (1) 14 September–6 October 2021, (2) 29 April–9 June 2022, (3) 16 June–27 July 2022, (4) 5 August–11 August 2022, and (5) 5 October–13 October 2022. Finally, this results in a data set with 31,524 observations whose descriptive statistics are presented in Table 1.
Table 1.
Descriptive statistics of the cleaned data set.
| T (C) | RH (%) | CO (ppm) | PM (g/m) | |
|---|---|---|---|---|
| mean | 21.14 | 41.96 | 753.8 | 7.96 |
| std | 3.14 | 7.25 | 436.4 | 4.59 |
| min | 12.93 | 19.47 | 374.0 | 0.00 |
| 25% | 18.48 | 36.87 | 439.0 | 4.00 |
| 50% | 20.55 | 41.73 | 568.3 | 7.00 |
| 75% | 23.60 | 46.70 | 904.8 | 10.67 |
| max | 31.04 | 66.70 | 3247.0 | 38.00 |
It can be seen that the maximum values of both the CO and PM levels exceed the recommended thresholds. Further investigation reveals that PM exceeds the limit of 35 g/m only five times during the recorded period of over a year, as observed in Figure 1.
Figure 1.
PM measurements over the whole recorded period. The horizontal line represents the threshold level of 35 g/m.
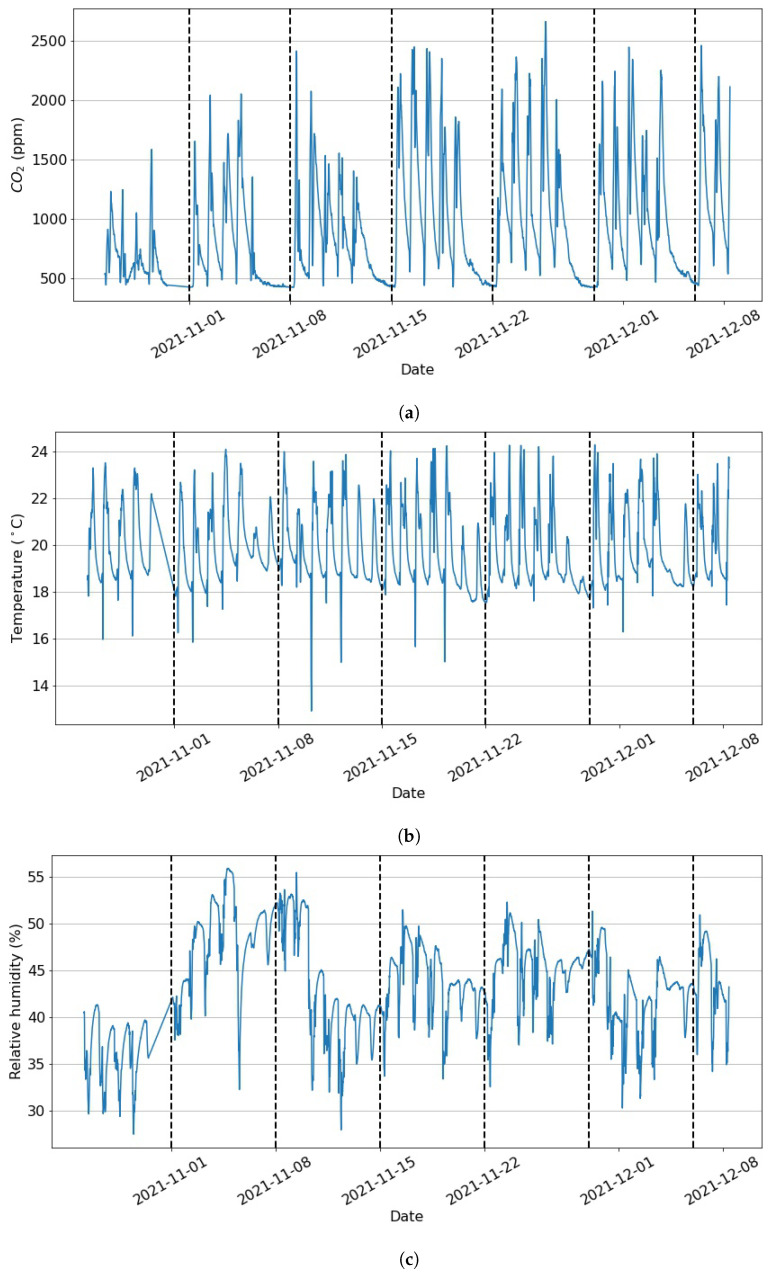
Potential reasons for this could be low levels of PM in the outdoor air in the vicinity of the kindergarten and regular cleaning routines in the facility. On the other hand, during the days when the kindergarten room is occupied (between 7:00 a.m. and 5:30 p.m.), the mean concentration of CO is greater than the allowed concentration of 1000 ppm. Thus, this study will focus on predicting CO levels and comfort conditions, which pose a much greater threat to the children in this kindergarten room. Figure 2 shows an excerpt of the data representing the CO, temperature, and relative humidity measurements over a period of around 40 days. It is observed that the CO levels exceed the threshold level of 1000 ppm on a daily basis. In fact, further analysis shows that unhealthy levels of CO are present more than 15% of the time and more than 23% of the time during the days between 7:00 a.m. and 5:30 p.m. As seen in Figure 2, a cyclical pattern is observed where the measured parameters exhibit peaks during the days and significantly lower values over the nights. In addition, the CO plot (Figure 2a) reveals a notable drop in concentrations during the weekends. Thus, the time of the day and the type of day (weekdays or weekends) are considered as additional features in the presented study.
Figure 2.
Example (a) CO, (b) temperature, and (c) relative humidity data. The vertical lines present the end of a week and the beginning of a new one.
In order to ensure that the models are trained on data from all the year round, the data set is randomly split into training, validation, and testing in an 80:10:10 ratio, which is a commonly reported split in literature [22,23,24]. Because the various features display different ranges and orders of magnitude, all data are re-scaled into the range between 0 and 1 using min–max normalization so that they can be easily interpreted on the same scale. Additional data from 16 May to 15 June 2023 were acquired at a later stage and are used only as a testing data set.
2.4. ARIMA
The autoregressive integrated moving average (ARIMA) model combines the differenced autoregressive model with the moving average model to perform time series forecasting [25]. The autoregressive (AR) model expresses the observation at the current time, , as a linear combination of observations at p previous times. Thus, the model has the form:
| (1) |
where are the observations, is a constant, are the regression coefficients, and e is an error term, usually a zero-mean Gaussian noise. The number p is selected with the help of a partial autocorrelation function (PACF) [26].
The differenced model (I) represents the change between consecutive data points in a series and is used to convert a non-stationary time series into a stationary one. The presence of non-stationarity in the time series, and thereby the need for differencing, can be determined through the augmented Dickey–Fuller (ADF) test [27]. First-order differencing can be expressed as:
| (2) |
In a moving average (MA) model the forecast error is linearly dependent on past respective errors. It can be expressed as:
| (3) |
where is the forecast error of data point i, are the regression coefficients, q is the order of the moving average, and I is a constant. The order of q is obtained based on the autocorrelation function (ACF) [26]. Combining all three components, the ARIMA model can be expressed as:
| (4) |
2.5. Long Short-Term Memory (LSTM) Recurrent Neural Network (RNN)
A long short-term memory (LSTM) network is a variation of a recurrent neural network (RNN) that handles the problem of storing long-term information [28]. In the conventional RNN, the backpropagated errors tend to either vanish or increase exponentially. An LSTM architecture consists of three gates—input gate, forget gate, and output gate—which control the flow of information. The input gate controls the input data that flows into the cell state, which stores the long-term memory of past events. The forget gate determines whether information from the previous time step is kept or forgotten. Finally, the output gate is used to decide the value of the next hidden state. The gates’ outputs can be described as follows [29]:
| (5) |
| (6) |
| (7) |
| (8) |
where , , and are, respectively, input, forget, and output gates; is the gate activation function; is a candidate to a cell memory; and are weight matrices; is the input data; is the output of previous cells; and are bias terms.
Then, a new memory state value, , and a cell output, , are calculated using the following equations:
| (9) |
| (10) |
2.6. Comfort Conditions
The comfort conditions refer to the measurements of temperature, relative humidity, and CO. The threshold levels, L, for each parameter are defined in accordance with national and international regulations, as summarized in Table 2. The optimal conditions for temperature and relative humidity are set to adhere to the guidelines provided by the Bulgarian regulation for kindergartens [30], where it is recommended to maintain the temperature between C and C and the relative humidity between and . As previously stated, CO levels above 1000 ppm are considered unhealthy. Levels between ppm and ppm are characterized as acceptable, while CO concentration below 600 ppm is most desirable and constitutes a healthy environment [31]. Using these threshold levels for the three parameters, 27 different indoor comfort conditions can be defined, as described in Table 3, with 1 signifying the greatest comfort and 27–the least comfort. It is important to note that unlike the other parameters under investigation, which exhibit well-defined threshold ranges, PM only has a single critical value. This led us to focus our detailed analysis on temperature, relative humidity, and CO levels. Moreover, the infrequent occurrence of elevated PM levels indicates a limited impact on the overall indoor environmental quality and occupant comfort conditions.
Table 2.
Threshold values for indoor comfort conditions.
| Parameter | L1 | L2 |
|---|---|---|
| Temperature (C) | 18 | 21 |
| Relative Humidity (%) | 30 | 60 |
| Carbon Dioxide (ppm) | 600 | 1000 |
Table 3.
Indoor comfort conditions categorization.
| N. | Temperature, T (C) | Relative Humidity, RH (%) | Carbon Dioxide, CO (ppm) |
|---|---|---|---|
| 27 | T above L2 | RH above L2 | CO above L2 |
| 26 | T above L2 | RH below L1 | CO above L2 |
| 25 | T below L1 | RH above L2 | CO above L2 |
| 24 | T above L2 | RH between L1 and L2 | CO above L2 |
| 23 | T below L1 | RH below L1 | CO above L2 |
| 22 | T below L1 | RH between L1 and L2 | CO above L2 |
| 21 | T between L1 and L2 | RH above L2 | CO above L2 |
| 20 | T between L1 and L2 | RH below L1 | CO above L2 |
| 19 | T between L1 and L2 | RH between L1 and L2 | CO above L2 |
| 18 | T above L2 | RH above L2 | CO between L1 and L2 |
| 17 | T above L2 | RH below L1 | CO between L1 and L2 |
| 16 | T above L2 | RH between L1 and L2 | CO between L1 and L2 |
| 15 | T below L1 | RH above L2 | CO between L1 and L2 |
| 14 | T between L1 and L2 | RH above L2 | CO between L1 and L2 |
| 13 | T above L2 | RH above L2 | CO below L1 |
| 12 | T above L2 | RH below L1 | CO below L1 |
| 11 | T above L2 | RH between L1 and L2 | CO below L1 |
| 10 | T below L1 | RH above L2 | CO below L1 |
| 9 | T below L1 | RH below L1 | CO between L1 and L2 |
| 8 | T between L1 and L2 | RH above L2 | CO below L1 |
| 7 | T below L1 | RH between L1 and L2 | CO between L1 and L2 |
| 6 | T between L1 and L2 | RH between L1 and L2 | CO between L1 and L2 |
| 5 | T below L1 | RH below L1 | CO below L1 |
| 4 | T between L1 and L2 | RH below L1 | CO between L1 and L2 |
| 3 | T below L1 | RH between L1 and L2 | CO below L1 |
| 2 | T between L1 and L2 | RH below L1 | CO below L1 |
| 1 | T between L1 and L2 | RH between L1 and L2 | CO below L1 |
3. Results and Discussion
3.1. CO Concentrations Prediction—ARIMA vs. LSTM
For the prediction of CO concentrations in the kindergarten room, ARIMA and LSTM models are used. The parameters for AR (p), the lag difference (d), and MA (q) are chosen based on ACF and PACF plots, shown in Figure 3, and the ADF test. The ADF test suggests that the time series is already stationary, which means that no differencing is needed. Despite the fact that all investigated lags up to are indicated as significant in the ACF plot in Figure 3a, the value of p is selected to be 10, which represents a trade-off between choosing a sufficient number of past measurements and computational cost. In addition, the behavior of the PACF (Figure 3b) indicates that the degree to which the current time point is directly influenced by events more than 10 lags apart is insignificant. Finally, based on the slow change of the ACF and the long autoregressive behavior, the value of q is chosen as zero. Thus the final predictor reduces to a pure AR model.
Figure 3.
(a) ACF and (b) PACF plots of the whole data set. Blue shading in (a) depicts the significance region.
The architecture of the RNN used throughout this study is the same for all three predicted variables. It consists of four layers, two LSTM and two fully connected hidden layers with respective outputs and parameters shown in Table 4. The RNN utilizes the Adam optimizer with , , and , as recommended in [32]. In addition, a learning rate schedule is defined using exponential decay with an initial learning rate of 0.05, 400 decay steps, and a decay rate of 0.95.
Table 4.
RNN architecture. Shape format reads (number of samples propagated through network, number of neurons in layer) or (number of samples propagated through network, number of time steps, number of neurons in layer). None denotes determination at runtime.
| Layer | Type | Shape | Parameters |
|---|---|---|---|
| 1 | LSTM | (None, 10, 64) | 17,408 |
| 2 | LSTM | (None, 64) | 33,024 |
| 3 | Dense | (None, 32) | 2080 |
| 4 | Dense | (None, 4) | 132 |
Both models use information about the 10 previous measurements to predict 4 steps (1 h) ahead utilizing the sliding window algorithm (see, e.g., [33]). This short-term prediction offers a balance between prediction accuracy and computational efficiency and allows for near real-time decision-making. Unlike ARIMA, which only allows the use of a single feature, the LSTM includes two additional features—the time and the type of day (weekday or weekend).
Both models were run on a Dell Latitude 7400 with 4-core Intel(R) Core(TM) i7-8665U CPU and 16 GB of RAM, and their computational time was 45 min and 8 h in favor of the LSTM model. The results of the training process for the two models are shown in Figure 4. It can be seen that the coefficient of determination, , in all cases is higher when LSTM is used. The results for temperature and relative humidity exhibit a qualitatively similar behavior to that of CO, and are thus omitted here for brevity. As a result, LSTM is used in the further prediction of temperature, relative humidity, and overall comfort of the indoor conditions.
Figure 4.
CO predictions vs. measurements plots (a) using ARIMA on the training set; (b) using LSTM on the training set; (c) using ARIMA on the validation set; (d) using LSTM on the validation set; (e) using ARIMA on the testing set; (f) using LSTM on the testing set.
3.2. Comfort Conditions Prediction
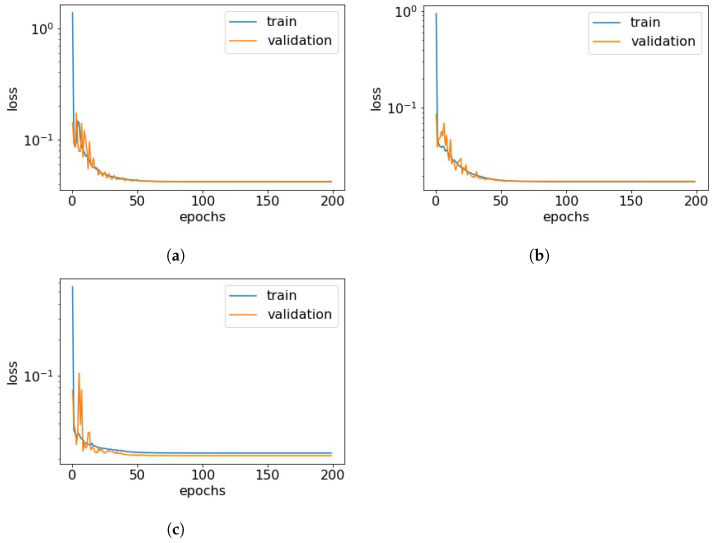
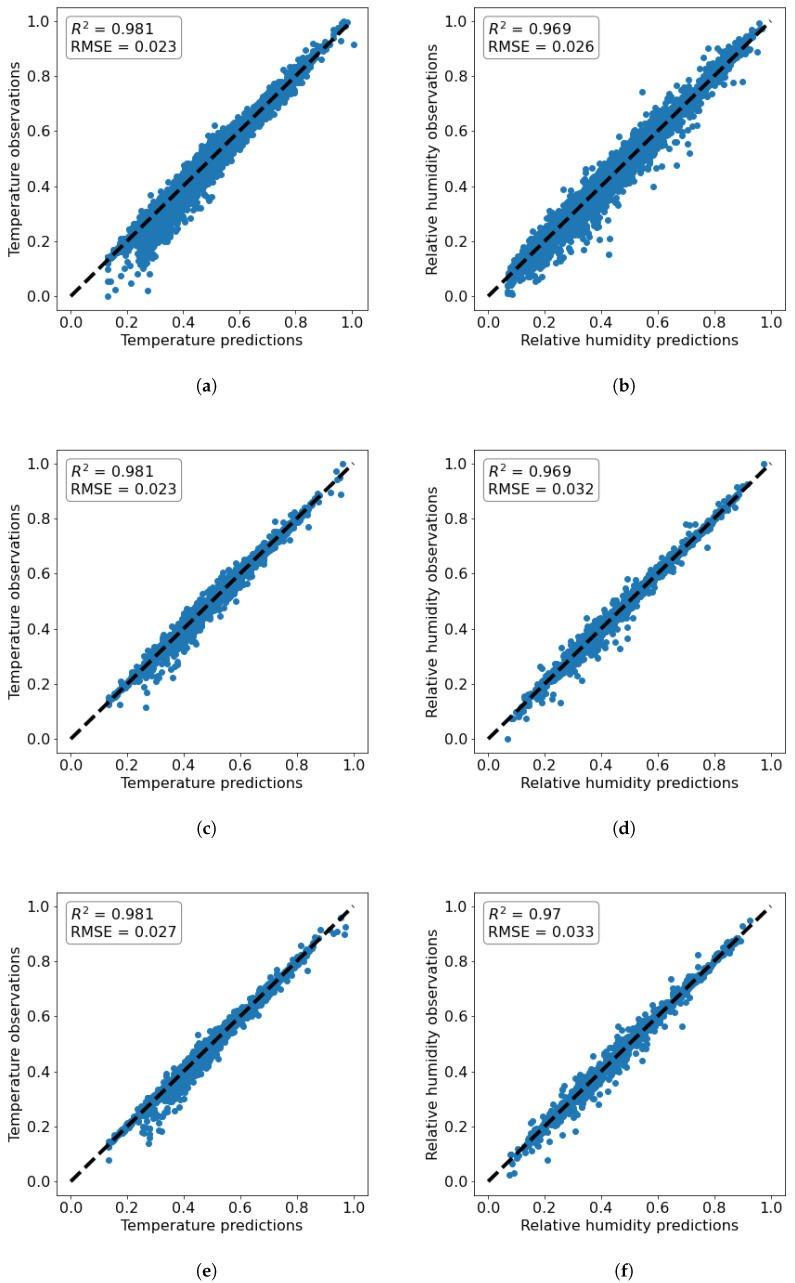
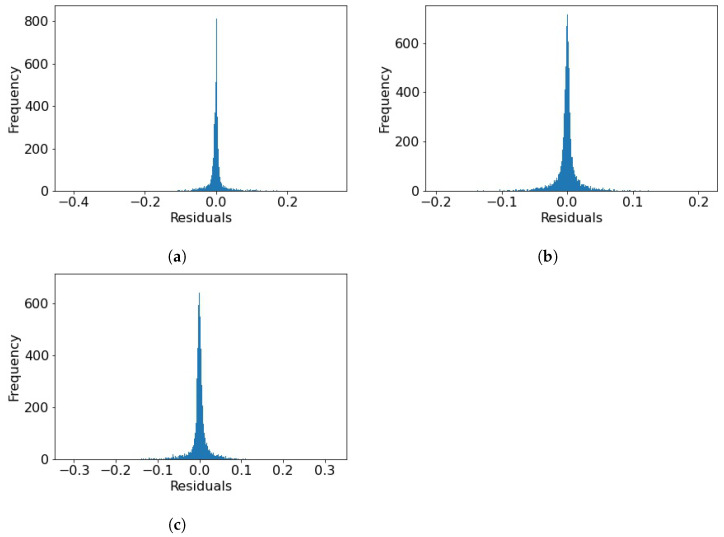
Initially, the comfort conditions in the kindergarten room are determined based on the measurements and Table 3 so that every recording is assigned a category between 1 and 27. CO concentrations, temperature, and relative humidity are then all predicted 1 hour ahead using three separate LSTM models utilizing the architecture described in Section 3.1 and the loss functions of the training processes can be seen in Figure 5. This approach allows for a detailed understanding of the predicted values for each parameter and the factors influencing the comfort conditions. The results are presented in Figure 6. The coefficients of determination for temperature and relative humidity show a very high prediction accuracy. In addition, Figure 7 presents residual plots for all three predicted variables. The distribution of residuals suggests that the models are performing well, and the cluster around zero implies that the predicted values are close to the actual values. However, in all cases outliers can also be observed, which signals that the models could still be improved, and further investigation to identify the factors that contribute to those deviations may be needed in future work. Based on the predictions for these three variables, a forecast for the comfort conditions is also formed. A report for a post-analysis classification is presented in Table 5, which demonstrates the high precision in discovering the correct comfort categories. It can be seen that the comfort conditions are forecast correctly with an average accuracy of 91%, which indicates a good ability of the model to correctly identify instances across all categories. The zero precision of the obvious outliers in Categories 14 and 15 can potentially be attributed to the lack of sufficient data (a single point for each) in those categories, despite the apparent lack of correlation between the size of the support and precision counts.
Figure 5.
Loss function plots for (a) CO, (b) temperature, and (c) relative humidity.
Figure 6.
LSTM predictions vs. measurements plots (a) of temperature on the training set; (b) of relative humidity on the training set; (c) of temperature on the validation set; (d) of relative humidity on the validation set; (e) of temperature on the testing set; (f) of relative humidity on the validation set.
Figure 7.
Residuals plots for the prediction of (a) CO, (b) temperature, and (c) relative humidity.
Table 5.
Comfort conditions classification report. ‘Precision’ is the ratio of correct positive predictions to all positive predictions; ‘recall’ is the ratio of correct positive predictions to all positive instances; ‘f1-score’ is the weighted harmonic mean between precision and recall; ‘support’ indicates the number of occurrences of each class in the data set.
| N. | Precision | Recall | f1-Score | Support |
|---|---|---|---|---|
| 1 | 0.92 | 0.94 | 0.93 | 5098 |
| 2 | 0.75 | 0.79 | 0.77 | 317 |
| 3 | 0.92 | 0.93 | 0.93 | 2406 |
| 4 | 0.63 | 0.64 | 0.63 | 233 |
| 5 | 0.89 | 0.54 | 0.67 | 78 |
| 6 | 0.90 | 0.87 | 0.89 | 3571 |
| 7 | 0.91 | 0.93 | 0.92 | 1896 |
| 8 | 0.67 | 0.50 | 0.57 | 4 |
| 9 | 0.31 | 0.19 | 0.24 | 21 |
| 11 | 0.98 | 0.96 | 0.97 | 8524 |
| 12 | 0.88 | 0.73 | 0.80 | 173 |
| 13 | 0.96 | 0.90 | 0.93 | 219 |
| 14 | 0.00 | 0.00 | 0.00 | 1 |
| 15 | 0.00 | 0.00 | 0.00 | 1 |
| 16 | 0.81 | 0.84 | 0.82 | 2090 |
| 17 | 0.70 | 0.74 | 0.72 | 245 |
| 18 | 0.61 | 0.45 | 0.52 | 31 |
| 19 | 0.91 | 0.89 | 0.90 | 2861 |
| 20 | 0.58 | 0.53 | 0.55 | 62 |
| 21 | 0.94 | 0.94 | 0.94 | 17 |
| 22 | 0.89 | 0.91 | 0.90 | 570 |
| 24 | 0.87 | 0.92 | 0.90 | 2865 |
| 26 | 0.75 | 0.82 | 0.78 | 211 |
| 27 | 0.96 | 0.80 | 0.87 | 30 |
| accuracy | 0.91 | 31,524 | ||
| average | 0.74 | 0.70 | 0.71 | 31,524 |
| weighted avg | 0.91 | 0.91 | 0.91 | 31,524 |
To put those figures in a more applied perspective, a time domain comparison is presented in Figure 8 showing the results on the additional data set covering a period of 30 days in 2023. Despite the good accuracy, a decrease in the coefficient of determination is notable for all three variables. The forecast of CO concentrations exhibits the largest deterioration, which can most clearly be seen in the prediction of the baseline and some of the peaks. This indicates the need for periodic retraining to ensure sustained accuracy in real-time predictions.
Figure 8.
(a) CO, (b) temperature, and (c) relative humidity predictions vs. measurements plots obtained using LSTM on the 30-day testing data set in 2023.
4. Conclusions
This study highlights the importance of monitoring and ensuring healthy indoor environments, particularly in educational facilities such as kindergartens. Poor indoor conditions can have significant implications for the well-being and learning efficiency of children. The research employed real-time monitoring and ML techniques to predict environmental conditions. The results demonstrate that the LSTM model outperforms a classical AR model in predicting CO concentrations, providing higher accuracy and shorter computational time. Furthermore, the study addresses the prediction of comfort conditions based on temperature, relative humidity, and CO levels. The forecast comfort conditions align closely with the actual conditions, achieving an average accuracy of 91%, when using the LSTM model.
These findings emphasize the significance of proactive measures to mitigate indoor air quality issues in educational settings. Implementing effective ventilation strategies, maintaining optimal temperature and humidity levels, and addressing CO buildup are essential for creating a healthy and conducive learning environment for children. The integration of ML techniques, as demonstrated in this study, can serve as valuable tools for continuous monitoring and prediction of indoor conditions, facilitating timely interventions and promoting the well-being of occupants.
Further research will focus on refining and expanding the predictive models to include additional factors that influence indoor air quality, examine different sliding window horizons, and study the effect of dependence between temperature, humidity, and CO, which were considered independent in this study. Moreover, investigation into PM variations, especially with additional threshold levels, could also be a subject of future research in contexts where its levels are more consistently elevated. Additionally, the results obtained in this study can be used as the foundation of a computational fluid dynamics (CFD) simulation, which would offer a better understanding of the airflow patterns. This would enable the evaluation of different ventilation strategies, such as natural ventilation, mechanical ventilation, or a combination of both, to determine their effectiveness in maintaining a healthy indoor environment.
Author Contributions
Conceptualization, R.M. and D.P.-A.; methodology, R.M.; software, R.M.; formal analysis, R.M.; investigation, R.M. and P.O.H.; resources, R.M.; data curation, R.M.; writing—original draft preparation, R.M.; writing—review and editing, D.P.-A. and P.O.H.; visualization, R.M.; supervision, D.P.-A. and P.O.H.; project administration, D.P.-A.; funding acquisition, D.P.-A. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The complete data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Funding Statement
This research is part of the GATE Project supported by the Horizon 2020 WIDESPREAD-2018-2020 TEAMING Phase 2 Programme under Grant Agreement No. 857155 and by the Operational Programme Science and Education for Smart Growth under Grant Agreement No. BG05M2OP001-1.003-0002-C0. P. O. Hristov is funded by the National Scientific Program “Petar Beron i NIE” under the AUDiT project no. KP06-DB/3. The authors gratefully acknowledge the support of the Scientific Fund of Sofia University, under Agreement No. 80-10-209/22.05.2023.
Footnotes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
References
- 1.Leech J.A., Nelson W.C., Burnett R.T., Aaron S., Raizenne M.E. It’s about time: A comparison of Canadian and American time-activity patterns. J. Expo. Sci. Envoron. Epidemiol. 2002;12:427–432. doi: 10.1038/sj.jea.7500244. [DOI] [PubMed] [Google Scholar]
- 2.The European Comission. [(accessed on 26 June 2023)]. Available online: https://ec.europa.eu/commission/presscorner/detail/en/IP_03_1278.
- 3.Seppänen O.A., Fisk W.J., Mendell M.J. Association of Ventilation Rates and CO2 Concentrations with Health and Other Responses in Commercial and Institutional Buildings. Indoor Air. 1999;9:226–252. doi: 10.1111/j.1600-0668.1999.00003.x. [DOI] [PubMed] [Google Scholar]
- 4.Jaakkola J.J.K., Heinonen O.P., Seppänen O. Sick building syndrome, sensation of dryness and thermal comfort in relation to room temperature in an office building: Need for individual control of temperature. Environ. Int. 1989;15:163–168. doi: 10.1016/0160-4120(89)90022-6. [DOI] [Google Scholar]
- 5.Sofuoglu S.C., Moschandreas D.J. The link between symptoms of office building occupants and in-office air pollution: The indoor air pollution index. Indoor Air. 2003;13:332–343. doi: 10.1111/j.1600-0668.2003.00192.x. [DOI] [PubMed] [Google Scholar]
- 6.Moschandreas D.J., Sofuoglu S.C. The indoor environmental index and its relationship with symptoms of office building occupants. J. Air Waste Manag. Assoc. 2004;54:1440–1451. doi: 10.1080/10473289.2004.10470999. [DOI] [PubMed] [Google Scholar]
- 7.Mäkeläinen I., Moisio S., Reisbacka H., Turtiainen T. Indoor occupancy and radon exposure in Finland. Radioact. Environ. 2005;7:687–693. [Google Scholar]
- 8.Joshi S.M. The sick building syndrome. Sick Build. Syndr. 2008;12:61–64. doi: 10.4103/0019-5278.43262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Weuve J. Exposure to Particulate Air Pollution and Cognitive Decline in Older Women. Arch. Intern. Med. 2012;172:219–227. doi: 10.1001/archinternmed.2011.683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kaiser J. How Dirty Air Hurts the Heart. Science. 2005;307:1858–1859. doi: 10.1126/science.307.5717.1858b. [DOI] [PubMed] [Google Scholar]
- 11.World Health Organization . Principles for Evaluating Health Risks in Children Associated with Exposure to Chemicals. WHO; Geneva, Switzerland: 2006. [Google Scholar]
- 12.Pope C.A., III, Dockery D.W. Health Effects of Fine Particulate Air Pollution: Lines that Connect. J. Air Waste Manag. Assoc. 2006;56:709–742. doi: 10.1080/10473289.2006.10464485. [DOI] [PubMed] [Google Scholar]
- 13.Pope C.A., III, Ezzati M., Dockery D.W. Fine-particulate air pollution and life expectancy in the United States. N. Engl. J. Med. 2009;360:376–386. doi: 10.1056/NEJMsa0805646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Indoor Air Hygiene Institute. [(accessed on 26 June 2023)]. Available online: https://www.indoorairhygiene.org/pm2-5-explained/
- 15.Coley D.A., Greeves R., Saxby B.K. The Effect of Low Ventilation Rates on the Cognitive Function of a Primary School Class. Int. J. Vent. 2007;6:107–112. doi: 10.1080/14733315.2007.11683770. [DOI] [Google Scholar]
- 16.Gaihre S., Semple S., Miller J., Fielding S., Turner S. Classroom Carbon Dioxide Concentration, School Attendance, and Educational Attainment. J. Sch. Health. 2014;84:569–574. doi: 10.1111/josh.12183. [DOI] [PubMed] [Google Scholar]
- 17.Simoni M., Annesi-Maesano I., Sigsgaard T., Norback D., Wieslander G., Nystad W., Canciani M., Sestini P., Viegi G. School air quality related to dry cough, rhinitis and nasal patency in children. Eur. Respir. J. 2010;35:742–749. doi: 10.1183/09031936.00016309. [DOI] [PubMed] [Google Scholar]
- 18.Simanic B., Nordquist B., Bagge H., Johansson D. Indoor air temperatures, CO2 concentrations and ventilation rates: Long-term measurements in newly built low-energy schools in Sweden. J. Build. Eng. 2019;25:100827. doi: 10.1016/j.jobe.2019.100827. [DOI] [Google Scholar]
- 19.Teli D., Bourikas L., James P.A.B., Bahaj A.S. Thermal Performance Evaluation of School Buildings using a Children-based Adaptive Comfort Model. Procedia Environ. Sci. 2017;38:844–851. doi: 10.1016/j.proenv.2017.03.170. [DOI] [Google Scholar]
- 20.Saini J., Dutta M., Marques G. Indoor air quality prediction systems for smart environments: A systematic review. J. Ambient Intell. Smart Environ. 2017;12:433–453. doi: 10.3233/AIS-200574. [DOI] [Google Scholar]
- 21.Bellinger C., Jabbar M.S.M., Zaïane O., Osornio-Vargas A. A systematic review of data mining and machine learning for air pollution epidemiology. BMC Public Health. 2017;17:907. doi: 10.1186/s12889-017-4914-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mustafa M.F., Talib A.M., Rashid R.Z.J.A., Ismail I., Awang A., Saad M.N.M., Zahari M.S. Development of Gas Flow Characteristic Prediction for Industrial Flow Meter using Long Short-Term Memory (LSTM); Proceedings of the 2022 International Conference on Future Trends in Smart Communities (ICFTSC); Kuching, Malaysia. 1–2 December 2022. [Google Scholar]
- 23.Shah D., Campbell W., Zulkernine F.H. A Comparative Study of LSTM and DNN for Stock Market Forecasting; Proceedings of the 2018 IEEE International Conference on Big Data (Big Data); Seattle, WA, USA. 10–13 December 2018. [Google Scholar]
- 24.Xu X., Zhang Y. Thermal coal price forecasting via the neural network. Intell. Syst. Appl. 2022;14:200084. doi: 10.1016/j.iswa.2022.200084. [DOI] [Google Scholar]
- 25.Kotu V. Data Science: Concepts and Practice. 2nd ed. Morgan Kaufmann Publishers; Burlington, MA, USA: 2019. Bala Deshpande. [Google Scholar]
- 26.Flores J.H.F., Engel P.M., Pinto R.C. Autocorrelation and partial autocorrelation functions to improve neural networks models on univariate time series forecasting; Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN); Brisbane, Australia. 10–15 June 2012. [Google Scholar]
- 27.Dickey D.A., Fuller W.A. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. J. Am. Stat. Assoc. 1979;74:427–431. [Google Scholar]
- 28.Hochreiter S., Schmidhuber J. Long short-term memory. Neural Comput. 1997;9:1735–1780. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- 29.Smagulova K., James A.P. Overview of Long Short-Term Memory Neural Networks. In: James A.P., editor. Deep Learning Classifiers with Memristive Networks: Theory and Applications. Springer International Publishing; Berlin/Heidelberg, Germany: 2020. pp. 139–153. [Google Scholar]
- 30.Ordinance № 3 from 05.02.2007 Regarding Health Requirements in Kindergartens. [(accessed on 26 June 2023)]; Available online: https://www.mh.government.bg/media/filer_public/2015/04/17/naredba3-ot-05-02-2007g-zdravni-iziskvania-detski-gradini.pdf.
- 31.Tagliabue L.C., Cecconi F.R., Rinaldi S., Ciribini A.L.C. Data driven indoor air quality prediction in educational facilities based on IoT network. Energy Build. 2021;236:110782. doi: 10.1016/j.enbuild.2021.110782. [DOI] [Google Scholar]
- 32.Kingma D.P., Ba J. Adam: A Method for Stochastic Optimization; Proceedings of the 3rd International Conference for Learning Representations; San Diego, CA, USA. 7–9 May 2015. [Google Scholar]
- 33.Palpanas T., Vlachos M., Keogh E., Gunopulos D., Truppel W. Online amnesic approximation of streaming time series; Proceedings of the 20th International Conference on Data Engineering; Boston, MA, USA. 2 April 2004; pp. 339–349. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The complete data presented in this study are available on request from the corresponding author.