Understanding locomotion in trilobites by means of three-dimensional models

Summary

Trilobites were one of the first animals on Earth to leave their imprints on the seafloor. Such imprints represent behavioral traces related to feeding or protection, in both cases implying different types of locomotion. Modeling how trilobites moved is essential to understand their evolutionary history and ecological impact on marine substrates. Herein, locomotion in trilobites is approached by means of three-dimensional models, which yielded two main gait types. These two gaits reflect basic behaviors: burrowing and walking. This model reveals that trilobites could change their gait and consequently increase rapidly their speed varying the amplitude of the metachronal wave, a change independent from their biological structure. Fast increases in speed enhanced the protection of trilobites against predators and sudden environmental crises. The trilobite body pattern constrained their gaits, controlled by the distance between the pair of legs and between legs in a same segment.

Graphical abstract

Highlights

• •Kinematic models reflect two behaviors: burrowing and walking
• •Longitudinal amplitude and wave number control the gaits
• •Specific number of segments improves stabilization of gaits
• •Relationship between gaits and caudalization trends in trilobites

Wildlife behavior; Paleontology; Computational bioinformatics

Introduction

Locomotion strategies reflect the relationship between an organism and its environment—how it feeds, reproduces, and protects itself from predators and how and where it lives.¹ However, although the fossil record provides a high number of behavioral evidences, to figure out the relationships between an organism and its environment is not an easy task. This is mainly because the integrated body structure of an organism and the morphology of its components determine the locomotion strategies (gaits) available to it. Thus, the same organism can produce an indeterminate number of traces according to different gaits. This is the case for instance in trilobites and five of their most common traces associated with locomotion: Rusophycus, Cruziana, Monomorphichnus, Dimorphichnus, and Diplichnites^2,3,4 (see Figure S1). These likely represent a continuum of locomotion from the resting position or very slow motion (Rusophycus), through burrowing locomotion (Cruziana) and finally walking and/or “striding” upon the substrate (Diplichnites).³ Although some attempts have been carried out to understand trilobite locomotion,^5,6,7 their gaits are not well understood, and this work attempts to address this. Therefore, the aim of this work is 2-fold. The first aim is to gain an understanding of how trilobite gaits are related to traces, using a mathematical model which allows visualizing the results in a 3D interface. The different gaits obtained by the model provide different virtual traces, which help us to argue the plausible behavior of trilobites using such gaits. The second aim of this work is to make a simulator in Blender suitable for all users with or without computer skills. This simulator will allow the user to create different virtual traces by changing different parameters such as the size and shape (i.e., body structure) of the trace maker, and also the parameters of the metachronal wave controlling the gait. The metachronal wave is a sequential action which produces a traveling movement in many multilegged animals. This will provide researchers with a new source of information to discuss the relationship between trilobites and their environment.

Results and discussion

3D model of Placoparia cambriensis to understand gaits in trilobites

The Video S1 shows the 3D model locomotion cycle of Placoparia (P.) cambriensis, an iconic Ordovician trilobite well known from the UK, Spain, and Morocco (Figures 1 and 2; see Data S1). Understanding gaits in a multisegmented animal like a trilobite requires finding a mathematical expression that generates coordinated cycles of rhythmic activity with displacement. Thus, adapting equations described by Hussong,⁸ we consider a single leg (i.e., endopodite and exopodite), which we will treat as a simple harmonic oscillator. For each cycle, the last segment of the endopodite goes through the positions to whose height depends on the time according to a sinusoidal function (Equation 1):

$$y\left(t\right)=Asen\left(\omega t\right)$$ (Equation 1)

where ω is the angular velocity in rad/s and t is the time (s) and legs only move up and down.

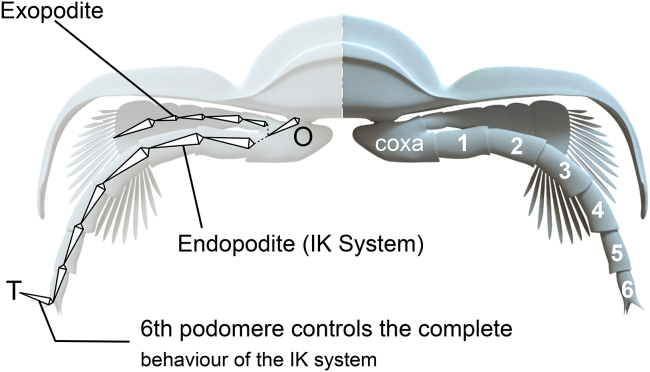
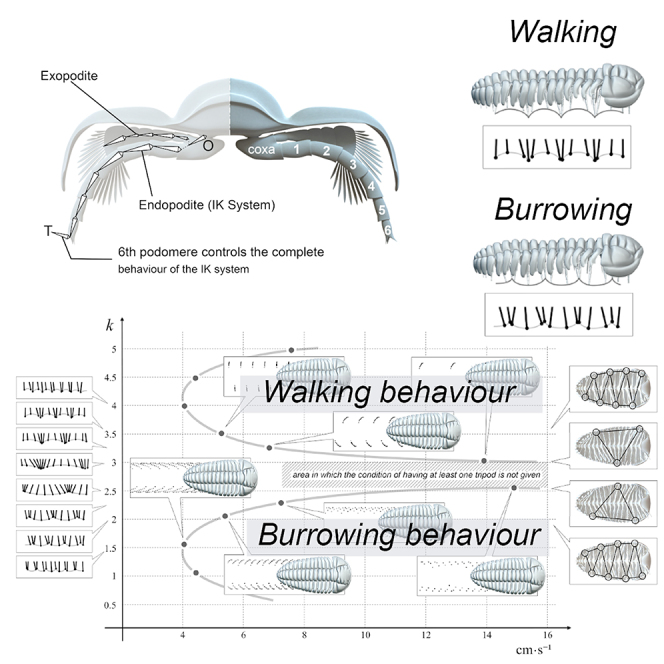
Figure 1.

Cross section showing the legs and IK systems in the endopodite from O to T

For the animation the exopodite copies the movement of the IK system.

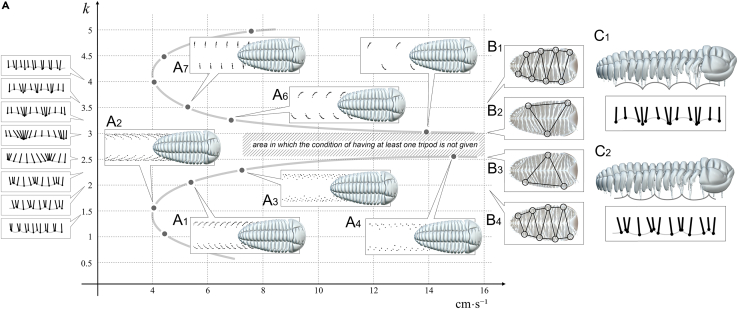
Figure 2.

Three-dimensional reconstruction of Placoparia cambriensis showing different gaits

(A) Locomotion modeling showing two symmetrical curves in Placoparia cambriensis, one curve with low wave numbers and its symmetrical with high wave numbers (k values) which correspond with two main gaits according to Manton's conditions.⁹

(B) Ventral view showing the tripods.

(C₁) Legs meeting close to the trilobite body (higher k values in the upper symmetrical curve).

(C₂) Legs meeting on the substrate (low k values in the lower symmetrical curve). See text for explanation.

If we wanted to set an initial height determined for the position of the last leg segment, we would add a phase shift δ (Equation 2)

$$y\left(t\right)=Asen\left(\omega t+\delta \right)\pi$$ (Equation 2)

Now we will apply that simple harmonic oscillatory movement to every trilobite leg. We will apply a phase shift to the oscillatory movements of each leg. That gait will be a function of how far away the extremity of origin is that we fix. The height of the distal end of each endopodite will no longer only depend on time but will also depend on the distance, that is, the relative position of that leg in the whole organism. We will therefore have a wave (Equation 3)

$$y\left(x,t\right)=Asen\left(kx\pm \omega t+\delta \right)$$ (Equation 3)

where kx is an expression of the gap between the successive legs and depends on the relative position of each leg inside the set. The factor k is the wave number. It is important to note that the value of phase shift δ is not the phase shift between successive legs but the value of the phase shift that fixes the initial position and that affects all legs equally (Supplemental information, Data S1, Video S1).

So far, we have determined that if we apply a simple harmonic movement to the ends of all legs with a lag according to their position in the set, we will obtain a wave movement for the set of those distal ends. The space that separates the legs that move in unison is called $\lambda$ or wavelength. In other words, to find a leg oscillating in an identical way to any given leg, we need to move a distance equal to $\lambda$, for which a complete cycle will have been completed $(2\pi rad$). The wave number (k) is precisely the expression of the necessary wavelength $\left(\lambda \right)$ to repeat a complete oscillation

$$\left(k=\frac{2\pi }{\lambda }\right)\text{.}$$ (Equation 4)

These equations describe the movement of the legs exclusively on the Y axis for an advance movement; it is also necessary to describe displacement on the X axis. Thus, the movement of equivalent positions associated with the wave defined by the oscillations of the set of the leg will allow an effective movement. For this we consider the superposition of two wave movements a longitudinal wave (i.e., the oscillation occurs in the direction of propagation) and a transverse wave (i.e., oscillation is perpendicular to the propagation). Both waves should be out of phase with each other radians. Therefore, the movement will be under the control of two equations (Equations 5 and 6):

$$y\left(x,t\right)=A1sen\left(kx\pm \omega t+\delta \right)$$ (Equation 5)

$$y\left(x,t\right)=A2\mathit{cos}\left(kx\pm \omega t+\delta \right)$$ (Equation 6)

A₁ is the amplitude of the transverse wave that determines the magnitude of the vertical displacement of each leg.A₂ is the amplitude of the longitudinal wave. It is the expression of the value of the "stride" used in the displacement cycle.k is the wave number that works as a form factor modulating the geometry of the resulting wave. According to the value of the number of waves, it will be possible for some or other amplitudes without the ends of the legs to collide with each other. Of the wave number the trilobite velocity will therefore depend on the variable that determines the greater or lesser amplitude of the "stride". The wave number of a sinusoidal waveform traveling at constant speed v is given by

$$k=v/T$$ (Equation 7)

where v is the speed and T is the number of cycles per unit of time.x is the distance between successive extremities. In the model, we make the approximation of considering a constant distance between legs, although this is not strictly enforced especially in the pygidium and nearby rings.ω is the angular speed. The number of cycles of displacement per unit of time of each leg depends on its value.δ is the offset that marks the initial position of each leg. It helps us to assign the gap between legs on the right side and the left side of the trilobites. The opposites corresponding to the same segment will be out of phase with each other.

Once we have obtained the mathematical expression that generates coordinated cycles of rhythmic activity, i.e., the gaits; we need to constrain the locomotion and give two conditions according to Manton⁹: i) at least one tripod (i.e., at least three points of contact—two on one side and one on the other) and ii) do not cross legs (Figure 2). To avoid that the legs did not interfere, we used collision detection.

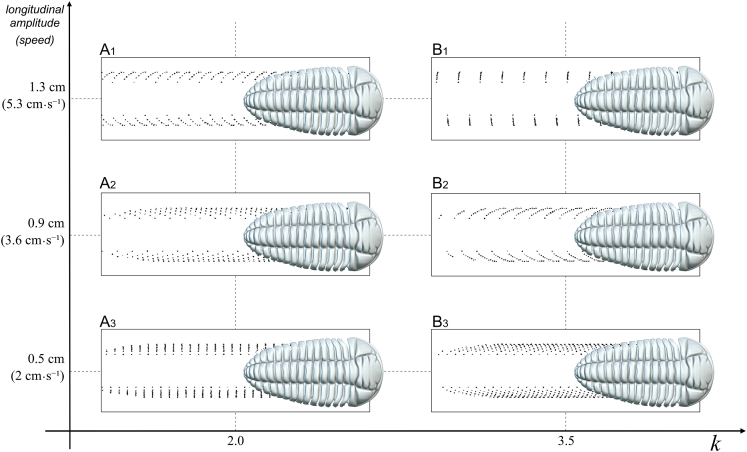
Modeling without any substrate results shows two symmetrical curves, one curve with low wave numbers and its symmetric curve with high wave number (k values) (Figure 2, Supplemental information, Video S2). Thus, for a range of increasing k values and constant A₂ values, Figure 2 initially shows a non-linear accelerated increase in the speed. This is a consequence of increasing the width of the stride, until the gait model reaches the area where the tripod condition is not given (Figure 2A₁–A₄, Supplemental information, Video S2). If the k values increase further, the gait model goes through the domain where tripods are generated again (see Figure 2A₅-A₇). Higher k values involve shorter strides and decreasing speed (Figure 2A₆–₇). Figure 2B shows ventral views of the trilobite model showing the tripod condition from higher k values with several tripods (Figure 2B₁) to lower k values decreasing the number of tripods (Figure 2B_2–3) and increasing again toward very low k values. An interesting point is the fact that the variation of the wave number (k) not only generates an expected change in the rhythm of advance but also causes a change in the way it occurs. With lower k values legs meet down in the substrate (Figure 2C₁), while with higher k values legs meet up in the distal area close to the trilobite body (Figure 2C₂). These two symmetrical curves produce a diverse range of trilobite tracks, where stride and speed increase proportionally. However, we can change the stride using the same k. Figure 3 shows variations in the stride and speed using the same k value (k=2 and k = 3.5). The k values are those obtained in Figure 2. The vertical axis shows the longitudinal amplitude values (the stride in biological terms), which increase until the distal ends of the legs meet, consequently increasing the velocity, since they are proportional to each other for a given fixed frequency. Consequently, if the stride decreases, the speed also decreases at the same k value. The Video S2 shows in real time how the traces change at the same velocity (0.05 m s⁻¹) using different wave number (k = 2.30 and k = 3.10). The Video S3 displays gaits and virtual traces in Placoparia using wave numbers (k) between 0.3 and 2.2. Our model agrees with Manton^6,9,10 in that higher speed locomotion does not depend on the length of legs itself, or even on the different lengths of fore, middle, and rear legs,¹¹ but on the pattern of the gait. The model produces gaits with many tripods at low velocities (k ≤ 2), while one or two large metachronal waves are obtained with high velocities (k ≥ 2). Thus, a change in the gait (from many tripods to a large metachronal wave) is inherent when increasing speed in multilegged animals.^12,13 In fact, velocity can be increased independently of the biological properties of the legs (e.g., elastic energy storage) simply by changing the gait.¹³ The gait with a large metachronal pattern at high running speeds can help arthropods to avoid overstraining involved muscles and may facilitate energy-efficient high-speed locomotion at the same time.^12,13 However, a single metachronal wave was likely avoided by trilobites due to biophysical constraints (see following discussion). The highest speed in the Placoparia model is 16 cm s⁻¹ with a large metachronal wave; above this velocity the tripod condition is not reached. This velocity is below the maximum speed of some terrestrial arthropods; for instance, the running speed of some cockroaches and spiders is around 60 cm·s^-1,^12,14 while some crabs reach up to 19 cm·s^-1.^15,16 Different external (i.e., buoyancy, fluid density) and internal factors (i.e., length of the legs, distance between pair of legs; see following discussion) constrain the velocity of multilegged arthropods and explain the differences between terrestrial and marine arthropods. Thus, the velocity obtained in the model may be realistic. This model suggests an optimization of locomotion at two different velocities, one slower and one faster. This mechanism may represent an escape strategy as protection against predators or other external factors.

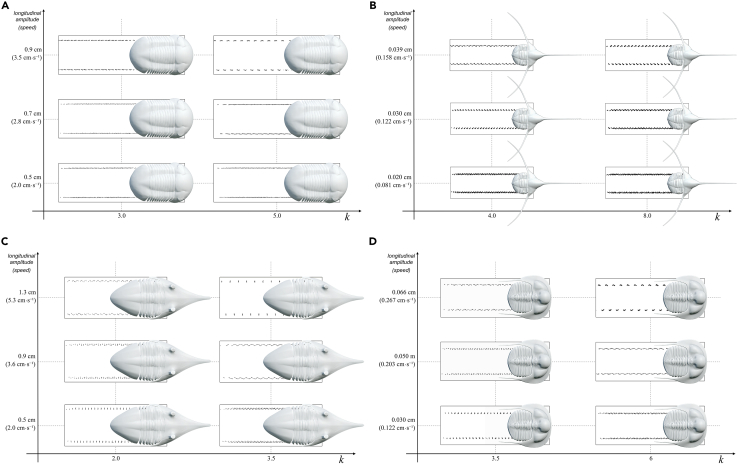
Figure 3.

Relationship between the longitudinal amplitude (stride) and wave number (k) in Placoparia cambriensis

(A1–A3) Traces made with k = 2.

(B1–B3) Traces made with k = 3.5.

See text for explanation.

The 3D models adding substrate show that V-set patterns generally open in the direction of the trilobite locomotion (Figures 2, 3, 4, and 5), as is widely accepted.^2,3,4,5 However, these 3D models also suggest that under certain circumstance, V-set patterns can close in the direction of the trilobite locomotion (Figures 2 and 3). The 3D models demonstrate that very low k values (1.5) and low velocities (4 cm/s) can produce traces with V-sets closing in the direction of the trilobite locomotion (Supplemental information, Videos S3 and S4). Note that the V-set pattern is not dependent on the velocity or stride; 3D models of trilobites with the same stride and velocity but different k values produce V-set patterns both opening and closing in the direction of the locomotion (e.g., see Figure 3 with a longitudinal amplitude of 0.9 and 3.6 cm/s, Supplemental information, Video S3). On the other hand, Crimes³ argued that the V angle was inversely proportional to the speed of the organism. Our locomotion models at very low velocities produce transversal V-set patterns or very wide V-angles, with more acute angles seemingly related to higher k values. In addition, the V-angles depend on the general body pattern rather than locomotion speed (see following discussion). Manton^9,17 demonstrated that stride is an important factor since longest strides accompany greatest speeds, and our models agree with her observations (Figure 3, Supplemental information, Videos S2 and S3). Trace morphologies change consistently with increasing stride length (including inversion of morphologies in some cases), and traces with intermediate morphologies are made by gaits with intermediate stride values. In addition, taphonomic bias can play an important role in the preservation of traces, and other features such as the position of furrows or general context can provide clues about the direction of locomotion.

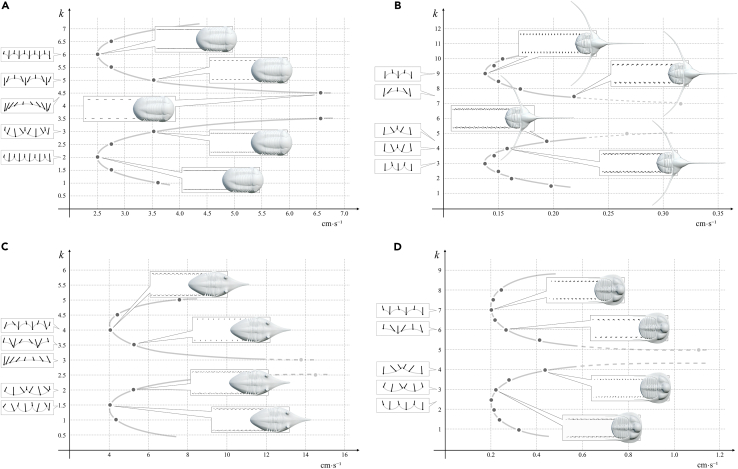
Figure 4.

Locomotion modeling showing two symmetrical curves, one curve with low wave numbers and its symmetrical with high wave number (k values) which correspond with two main gaits

(A) Illaenus

(B) Lonchodomas.

(C) Megistaspis and (D) Tetraspis.

See text for explanation.

Figure 5.

Relationship between the longitudinal amplitude (stride) and wave number (k)

(A) Illaenus

(B) Lonchodomas.

(C) Megistaspis and (D) Tetraspis.

See text for explanation.

Relationship between gaits employed and behavior

Our locomotion models predict similar gaits to those observed in extant myriapods or isopods.¹⁸ Thus, trilobite legs could meet either 1) close to the trilobite body (high k values, upper symmetrical curve in Figure 2B, Video S2) or 2) or close to the substrate (low k values lower symmetrical curve in Figure 2C, Video S2), with variation within these two general gaits dependent on the mathematical parameters described earlier. These two general gaits are also present in myriapods and isopods.⁶ According to Manton,¹⁷ those gaits where legs meet on the substrate correspond with lower velocities and those gaits where legs meet close to the body correspond with higher velocities. These two gait types could have advantages depending on the type of substrate or kind of behavior (benthic or semi-infaunal). The first locomotion type, with legs meeting close to the substrate (low k values and lower velocities, Figure 2C), puts the legs in contact with most of the substrate, and each footprint is very close to the following one. The obtained tracks with this locomotion type (k ∼ 2, strides∼ 0.005 and 0.0125 m, velocities 4 and 8 cm/s Figures 2A and 3, Video S3) in some ways resemble Cruziana, which has been interpreted as a feeding trace fossil of trilobites, with the central V-sets as a result of burrowing and displaying two clear areas, the endopodite V-marking divided by a central ridge and the external fine markings^2,19 (see Figures S1A–S1C). Note that these two plots (Figure 2A) must differ from true Cruziana because only the footprints of the legs are recorded and legs in our simulations do not sweep along the sediment. Thus, these plots represent only the central V-set seen in Cruziana; central ridge and fine lineation are not represented here. The second locomotion type with legs meeting close to the trilobite body (upper symmetrical curve in Figure 2B, higher k values) makes an increment in the space between every V-set. This produces a transversal V-set pattern with a k = 3.5, which may also correspond with a resting behavior producing a Rusophycus-like trace fossil. This agrees with the hypothesis of Kesidis²⁰ in the production of Cruziana tenella by means of successive Rusophycus eutendorfensis. Osgood⁴ also suggested that Rusophycus pudicum were produced by nektobenthic trilobites where the organism settled to the bottom, burrowed, and then swam out of the excavation. Hopping locomotion can also explain this sort of traces⁷; Esteve et al. suggested that Olenoides serratus could hop short distances and recently by means of computational fluid dynamic simulations argued that Placoparia was able to hop a short distance generating thrust by pushing the substrate with its anterior legs, followed by a gliding phase where its center of mass was not surrounded by a tripod of supporting legs, since legs were no longer in contact with the substrate.²¹ In fact, the metachronal wave produced in our 3D model with high values between k = 3 and 3.5, where legs meet close to the body, corresponds with metachronal waves suitable for swimming.^22,23 Therefore, although slow locomotion was possible even with transversal V-set patterns, this sort of metachronal wave could be more efficient in a hopping locomotion. Instead, the tracks obtained with k = 2 and 2.5 resemble Diplichnites, which has been interpreted as walking behavior upon the substrate²⁴ (Figure 2, Supplemental information, Videos S3 and S4). Manton^17,25 showed how footprints get farther apart as speed increases. In our model, the metachronal wave does not have any tripod in the area between k = 2.6 and k = 2.9; therefore locomotion could not be possible. In contrast to myriapods and other multisegmented arthropods, the gait was without twisting movement since it was unlikely that the trilobite body could move in that way, because of trilobites’ lack of articulations for twisting; thus lateral undulations of the body were not employed to increase velocity.^10,25 Manton²⁵ showed that each metachronal wave can be composed of the same number of legs or different number of legs and consequently the points of support of the body are almost evenly spaced in those with same number or spaced with unequal distances in those with different number. A smaller number of legs comprising a metachronal wave denotes not only a relatively shorter backstroke but also a shorter pace duration and results in a faster speed. Therefore, this supports the idea that Cruziana is produced by a slow locomotion, with a low number of legs in each metachronal wave employed during feeding or burrowing behaviors (Cruziana and Rusophycus), with Diplichnites representing a faster locomotion.

Assessment of locomotion mechanics in trilobites with different body pattern by means of a gaits simulator

The body structure of a trilobite, number of segments in the thorax (i.e., number of pairs of legs), separation between pairs of legs and between legs in the same tergites, length of every segment, or the length of legs are key parameters involved in trilobite gaits.⁶ These morphological parameters of known trilobites can be introduced in Blender (see Data S2–S6). Since the mathematical parameters also control the gait, in the simulator we can change the wave number (k) and the stride (for a given leg length). To demonstrate how the simulator can assess gait, we compare four trilobites with a homonomous condition in the trunk (i.e., all segments are of similar form) and both isopygous and micropygous conditions.

Here, we show the results of trilobites with different number of segments and different degree of caudalization (Placoparia, 12 segments and micropygous; Illaenus, 10 segments and isopygous; Megistaspis, 8 segments and isopygous; Lonchodomas, 5 segments and isopygous; and Tetraspis, 6 segments and micropygous). Simulations in all cases show gaits with the legs meeting close to the sediment (lower k) or close to the body (higher k). However, given differences in body structure, speed limits change and the virtual traces are slightly different. The results do not show a relationship between higher number of segments and high speed in Placoparia, Illaenus, and Megistaspis (Figures 2 and 4). Additional simulation using measurements of Eccaparadoxides pranoanus—a well-known Cambrian micropygous taxon with 14 segments—provides a maximum speed of 9 cm s⁻¹ (see Data S6). Therefore, these results suggest that the proper body structure constrains speed and consequently different lifestyles. The results also show that in trilobites with a smaller number of segments (i.e., fewer pairs of legs), accommodating fewer metachronal waves, the condition of getting at least one tripod is reached more easily (Lonchodomas and Tetraspis, Figure 4). According to Manton,¹⁷ instability of locomotion becomes a problem when there are fewer supporting points distributed along the two sides of the body. On the other hand, long metachronal waves result in the anterior and posterior part of the body being unsupported for short periods (Figures 2 and 4). This suggests that those gaits with large metachronal waves could create strains in the trilobite body. Accordingly, it is logical to think that those gaits with a long (single) metachronal wave along the trilobite body, for instance in Placoparia or Megistaspis gaits with k ∼ 3 or in Illaenus with k ∼ 4 (Figures 4 and 5), were avoided by these trilobites. Thus, this biophysical constraint suggests a trade-off between the number of segments in the trunk (caudalization degree) and stabilization during locomotion since trilobites with a higher number of segments represent more supporting points allowing faster speed. This trade-off explains why the caudalization trend in trilobites²⁶ suffered in some cases a regression and derived groups increased the number of segments in the thorax (e.g., Aulacopluera from the Silurian of the Czech Republic^27,28).

Limitations of the study

Locomotion results for different taxa depend on the accuracy of 2D or 3D reconstructions of morphology as the position of appendages can change the velocity of the model (and hence the virtual trace fossils obtained). In addition, the true length of the legs is unknown for many trilobites, and longer or shorter legs will modify the gaits. However, these limitations do not change the fact that in gaits with lower k values legs will meet down in the substrate, while in gaits with higher k values legs will meet up in the distal area close to the trilobite body. Furthermore, future research may also take into consideration a number of biomechanical variables (e.g., stress, strain, or hydrodynamics) to assess the relationship between gaits (ethology) and number of segments in trilobites and other arthropods.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Blender 3.0	Blender Foundation	https://www.blender.org/
Experimental Models: Organisms/Strains
Placoparia cambriensis	Museo Geominero, Madrid, Spain.	VPA-8
Illaenussarsi	Swedish Museum of Natural History.	AR62003
Megistaspisextenuata	Swedish Museum of Natural History.	AR61562
Lonchodomas sp.	National Museum of Natural History, Prague, Czech Republic.	NMP-L15165
Tetraspis sp.	National Museum of Natural History, Prague, Czech Republic.	NMP-L16621
Eccaparadoxides pradoanus	Museo de Ciencias Naturales de la Universidad de Zaragoza	MPZ2011⁄19

Resource availability

Lead contact

Further questions should be directed to the lead contact: Jorge Esteve (jorgeves@ucm.es).

Materials availability

The specimens are housed at the Museo Geominero, Madrid, Spain (MGM), at the Museo de Ciencias Naturales de la Universidad de Zaragoza (MPZ), at the National Museum of Natural History, Prague, Czech Republic (NM-L) and at the Swedish Museum of Natural History (AR).

Data and code availability

• •All data reported in this paper will be shared by the lead contact upon request.
• •No novel code was used in this study.
• •Any additional information required to reanalyze the data reported in this paper can be found in the Supplemental information or from the lead contact upon request.

Experimental model and study participant details

Trilobites

All specimens used here were studied with permission from the organizations listed in the key resources table.

Trace fossils

The Figure 1S shows examples of trace fossils comparable with the virtual traces obtained in our study.

Methods details

Fossil three-dimensional modeling

To assess locomotion in trilobites we used a 3D model of Placoparia cambriensis Hicks 1875 (MGM-VPA-81) from the Middle Ordovician of Spain preserved in 3D and previously used to study the kinematics of enrolment and the hydrodynamic properties of trilobites.^21,29 The specimens were scanned using a DAVID SLS 2 Structured Light 3-D Scanner (∼100 lm) in the Centro de Asistencia a la Investigación (CAI) de Arqueometría y Análisis Arqueológico of the Complutense University, Madrid, Spain (see Esteve et al.^29,30 for more details). In addition, we have used 3D reconstructions of four Ordovician trilobites preserved in 3D [Illaenus and Megistaspis from the Middle Ordovician of Sweden (AR) and Lonchodomas (NMP-L15165) and Tetraspis (NMP-L16621) from the Middle Ordovician of Czech Republic] with different body patterns in order to compare the results between different taxa (see Supplemental information). The specimens from Czech Republic were scanned at the National Museum in Prague by X-ray micro-tomography using a SkyScan 1172 at 141 μA and 70 kV with Al+Cu Filter. N-Recon Software (Bruker) was used for reconstruction. The locomotion model was developed using the open-source software Blender (https://www.blender.org/) with animation nodes for Blender (https://animation-nodes.com/). This animation node allows calculating the mathematical expressions that control the movement of the model and visualizing such movement in real time (Videos S1 and S2, Data S1, S2, S3, S4, S5, and S6). Raw data (i.e. Blender files, Data S1, S2, S3, S4, S5, and S6) and videos were deposited on Mendeley at https://data.mendeley.com/datasets/5sywh8knxd/draft?a=1281efd2-e6a2-40ad-922a-0059ba9956d7).

Locomotion modeling

Multilegged animals, with exception of insects and some arachnids, use metachronal waves of motion to move.³¹ The movement was modelled using two waves to simulate the metachronal wave: i) a longitudinal wave (i.e. the oscillation occurs in the direction of propagation) and ii) a transverse wave (i.e. oscillation is perpendicular to the propagation) (Video S1). The wavelength and the metachronal wave was defined using an analogous of the metachronal wave model between beating cilia.^8,32 This analogous allows to restrict the wave amplitude A of the metachronal wave by the endopodites length and the thickness of the metachronal wave. With this mathematical approach, we can simulate trilobite gaits. A locomotion model should be compatible with the biology of arthropods in general, and be capable of describing the displacement cycle observed in living organisms with functional morphology similar to Class Trilobita. We find physical-mathematical expressions that generate metachronal waves of motion comparable with those generated by the body's neural circuits (central pattern generators or CPG). Given the complexity of applying (articulation by articulation) a motor behavior capable of reproducing a coordinated movement for a whole leg, we will resort to the use of inverse kinematics (IK).³³ Through IK we can determine, at a given moment, the position of each one of the segments of the extremities knowing only the origin of a said chain (the point where it is inserted in its corresponding ring) and the position of the last segment. It will be that last segment where we will apply the physical-mathematical expressions that emulate the CPG generated by the neuronal circuits of the organism. The use of IK will extend the movements associated with these expressions to the rest of the segments, which will describe the cycle of locomotion. IK uses algorithms that, through iteration processes, determine the positions of the segments intermediate between the position of the origin and the final segment of the chain. Trilobites have a double chain of extremities (endopodite and exopodite, Figure 1). The relation of the elements of the IK chain is defined in Blender by a Jacobian matrix formed by the first order partial derivatives of a function. Their Jacobian solutions are a linear approximation that determine the positions of their elements (translation and rotation) for a given instant. The degrees of freedom of those positions are determined in part by the position and orientation starting point for those elements. This position can sometimes generate unwanted movements of the elements of the chain with turns incongruous with the actual behavior of the legs. Thus, we reject the use of IK to assess locomotion in trilobites. However, given that trilobite had composed legs (endopodite and exopodite), in our approach, it will be the last segment of the endopodite that controls the movement of the remaining segments, both of the endopodite and exopodite. The exopodite only copies, using IK, the angle values of homologous segments of the endopodite (Data S1, S2, S3, S4, S5, and S6).

Quantification and statistical analysis

No statistical analysis is included in this study.

Published: July 31, 2023