Abstract
Background Data protection policies might prohibit the transfer of existing study data to interested research groups. To overcome legal restrictions, simulated data can be transferred that mimic the structure but are different from the existing study data.
Objectives The aim of this work is to introduce the simple-to-use R package Mock Data Generation (modgo) that may be used for simulating data from existing study data for continuous, ordinal categorical, and dichotomous variables.
Methods The core is to combine rank inverse normal transformation with the calculation of a correlation matrix for all variables. Data can then be simulated from a multivariate normal and transferred back to the original scale of the variables. Unique features of modgo are that it allows to change the correlation between variables, to perform perturbation analysis, to handle multicenter data, and to change inclusion/exclusion criteria by selecting specific values of one or a set of variables. Simulation studies on real data demonstrate the validity and flexibility of modgo.
Results modgo mimicked the structure of the original study data. Results of modgo were similar with those from two other existing packages in standard simulation scenarios. modgo's flexibility was demonstrated on several expansions.
Conclusion The R package modgo is useful when existing study data may not be shared. Its perturbation expansion permits to simulate truly anonymized subjects. The expansion to multicenter studies can be used for validating prediction models. Additional expansions can support the unraveling of associations even in large study data and can be useful in power calculations.
Keywords: data privacy, perturbation analysis, statistical disclosure control, synthetic data, validation study
Introduction
Sharing original study data with other researchers may be prohibited due to data protection regulations. Alternatively, original study data may be transferred only once at the end of a study. It might, however, be important to test the data transfer pipeline and to establish the data analysis pipeline before the trial is ended. Simulated data that mimic the structure of the original data are a suitable alternative in these cases. Furthermore, synthetic data may be analyzed instead of real data to obtain valid inferences. 1 2 Using simulated data, researchers may run exploratory analyses and prepare scripts that can be later run on the original data; for examples, see refs. 3 4 Simulated datasets can be used to augment study data to ameliorate problems caused by small sample sizes. 5 6 Furthermore, simulated data combined with perturbation analyses can be used to test and compare statistical and machine learning techniques, and they may also be employed for power analyses and sample size estimation. 7 8 9 10 Finally, synthetic data can also be provided together with code that was used in a research publication to enhance reproducible research.
In this work, we introduce the R package modgo (MOck Data GeneratiOn) for generating synthetic data from available study data. The modgo (pronounced moʊdʒoʊ ) package supports input datasets having a mix of continuous and/or ordinal and/or dichotomous variables. The package allows for varying sample sizes, unbalanced outcome data, multicenter studies, changes of inclusion criteria, and perturbation of continuous variables. We use simulations on real-world data to demonstrate that the simulated datasets mimic the characteristics of the original data. We illustrate the package capabilities using data from the machine learning data repository of the University of California in Irvine (UCI), 11 and the Golub data from the OpenIntro data repository. 12
Methods
The key of the algorithm is that it is a two-step procedure. In the first step, the original data are transformed, and a correlation matrix is estimated. In the second step, data are simulated by utilizing the correlation matrix estimated in the first step. The simulated data are transferred back to the original scale. The next two subsections focus on the technical details of these two steps in the data simulation algorithm. The core algorithm is described in detail in Algorithm 1 . Expansions of the core algorithm are outlined next, which is followed by outlining the simulation study. This section closes with an introduction to the illustrative data.
Step 1: From the Original Data to the Correlation Matrix
The goal of step 1 is to compute a
p
×
p
covariance matrix
Σ
, where
p
is the number of variables in the original dataset. The underlying assumption is that after suitable transformations all
p
variables in the data follow a centered multivariate normal distribution, with
Σ
being an estimate of the covariance matrix.
Σ
is initialized as the
p
×
p
identity matrix. Then, the rank-based inverse normal transformation
13
is applied to each continuous variable, namely, for each continuous variable
X
taking values
x
1
,
x
2
, …,
x
n
and associated ranks
r
1
,
r
2
, …,
r
n
, the transformation
 is applied, where Φ is the cumulative distribution function of the standard normal random variable and Φ
−1
its inverse. Ordinal variables—including dichotomous as a special case—require a different approach. Ordinal variables are assumed to be categorized versions of latent standard normally distributed variables, and the corresponding entries in the matrix
Σ
are computed using the polychoric correlation.
14
Those entries of
Σ
corresponding to a rank-based inverse normal transformed continuous and an ordinal variable are computed using the polyserial correlation.
15
The resulting matrix
Σ
may not be positive definite. In such a case, the nearest positive definite matrix
16
is computed and assigned to
Σ
. Observe that
Σ
is a correlation matrix because all entries on the diagonal are fixed to 1.
is applied, where Φ is the cumulative distribution function of the standard normal random variable and Φ
−1
its inverse. Ordinal variables—including dichotomous as a special case—require a different approach. Ordinal variables are assumed to be categorized versions of latent standard normally distributed variables, and the corresponding entries in the matrix
Σ
are computed using the polychoric correlation.
14
Those entries of
Σ
corresponding to a rank-based inverse normal transformed continuous and an ordinal variable are computed using the polyserial correlation.
15
The resulting matrix
Σ
may not be positive definite. In such a case, the nearest positive definite matrix
16
is computed and assigned to
Σ
. Observe that
Σ
is a correlation matrix because all entries on the diagonal are fixed to 1.
Step 2: From the Correlation Matrix to Simulated Data on the Original Scale
To simulate data that mimic the characteristics of the original data, observations are drawn from the centered multivariate normal distribution with covariance
Σ
in step 2a. In step 2b, for each newly generated variable
Y
, associated with an original variable
X
, taking values
x
1
,
x
2
, …,
x
n
,
 is computed, where
is computed, where
 is the inverse empirical cumulative distribution function (percentile function) of
x
1
,
x
2
, …,
x
n
Observe that the range of
is the inverse empirical cumulative distribution function (percentile function) of
x
1
,
x
2
, …,
x
n
Observe that the range of
 is
x
1
,
x
2
, …,
x
n
, and therefore only values appearing in the original dataset can be generated with this approach.
is
x
1
,
x
2
, …,
x
n
, and therefore only values appearing in the original dataset can be generated with this approach.
Expansions
Expansion 1—Changing the strength of associations: To describe the idea we assume that the first variable for estimating the correlation matrix is denoted by y , all other variables are denoted by x = ( x 1 , x 2 , …, x p−1 ) ' . The correlation matrix Σ is partitioned into
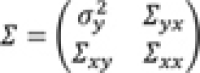 , where
, where
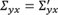 is the vector of correlations between
y
and
x
1
,
x
2
, …,
x
p−1
. To change the strength of association between
y
and components of
x
, only the corresponding correlations
Σ
xy
need to be changed.
is the vector of correlations between
y
and
x
1
,
x
2
, …,
x
p−1
. To change the strength of association between
y
and components of
x
, only the corresponding correlations
Σ
xy
need to be changed.
Expansion 2—Selection by thresholds of variables: If investigators want to select observations by specific values, such as age > 65 years in a study involving subjects with a wider age range, we suggest simulating the intended number of observations n sim in the first step. Next, the proportion of subjects p s fulfilling the conditions, here: age > 65 years, is determined. Third, 10% more subjects than expected are simulated for achieving the total number of required subjects fulfilling the conditions, i.e., an additional 1.1 ∙ 1/ p s of subjects is simulated. If < 10% of the simulated observations fulfill the condition, the procedure stops; a force option is available.
Expansion 3—Perturbation analysis: Starting point is a continuous variable with mean μ and variance σ 2 on the original scale. This continuous variable may be disturbed by adding an independent normally distributed noise with mean 0 and variance σ p 2 with the aim that the variance of the perturbated variable is identical to the variance of the original variable. If we assume that the perturbation variance σ p 2 is a proportion of σ 2 , say σ p 2 = p σ 2 , 0 < p < 1, then the original variable needs to be multiplied by
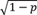 . With this, the perturbated variable has variance
σ
2
. In the program, the user may specify the continuous variables to be perturbed and the perturbation proportion (default: 1/10). Since the perturbation is performed on the original scale, i.e., after back transformation of the simulated data, values may be obtained that differ from values observed in the original dataset. A related additional option is that a normally distributed noise with mean 0 and variance
σ
p
2
=
p
σ
2
is added to the simulated data. With this perturbation, the variance of the perturbed variable is
p
times larger than the variance of the original variable.
. With this, the perturbated variable has variance
σ
2
. In the program, the user may specify the continuous variables to be perturbed and the perturbation proportion (default: 1/10). Since the perturbation is performed on the original scale, i.e., after back transformation of the simulated data, values may be obtained that differ from values observed in the original dataset. A related additional option is that a normally distributed noise with mean 0 and variance
σ
p
2
=
p
σ
2
is added to the simulated data. With this perturbation, the variance of the perturbed variable is
p
times larger than the variance of the original variable.
Expansion 4—Multicenter studies: Different centers in multicenter studies may differ in their structure. The user can therefore perform multiple modgo runs, one for each study, and then combine the different modgo results with an external function provided by modgo. The combined dataset can be used for analyses.
Expansion 5—Fixing proportions of cases and controls: Varying ratios of cases and controls may be simulated as follows. First, the correlation matrix is estimated separately for cases and controls. Second, cases and controls are simulated according to the pre-defined set of proportions for cases and controls.
Simulation Studies Using the Cleveland Clinic Data
To demonstrate the validity of the implementations in the modgo package, we selected the Cleveland Clinic Heart Disease Dataset from the UCI machine learning data repository. 11 The Cleveland Clinic dataset is well suited for demonstrating modgo's capabilities as it consists in continuous, binary, and ordinal categorical variables. The Cleveland Clinic Heart Disease project aimed at developing an automate for diagnosing coronary artery disease (CAD) using individual patient characteristics. The training data consisted in 303 consecutive patients referred for coronary angiography to the Cleveland Clinic between May 1981 and September 1984. 17 Data from three other centers with a total of 617 patients were used for external validation. 17 These were (i) 200 patients drawn from all consecutive subjects between 1984 and 1987 at the Veterans Administration Medical Center in Long Beach, California, USA, (ii) 294 patients drawn from the Hungarian Institute of Cardiology (Budapest) between 1983 and 1987, and (iii) 123 patients drawn from the University Hospitals Zurich and Basel, Switzerland, in 1985. A brief description of the Cleveland Clinic Dataset can be found in Supplementary Material (Quarto markdown in Supplement S1 , output in Supplement S1a [available in the online version]).
In Illustration 1, we show the correlation matrix of the original dataset, the mean correlation matrix of 500 simulated datasets from a modgo run with default settings, the mean correlation matrix of 500 simulated datasets from a modgo run that used as an intermediate covariance matrix the correlation matrix calculated by sbgcop R package, 18 and the mean correlation matrix of 500 simulated datasets produced by SimMultiCorrData package. 19 Furthermore, we present differences between the mean correlation matrices and the correlation matrix of the original dataset. We also show the distribution of several variables in the original data and the simulated data. All code and output are provided in Supplementary Material (Quarto markdown in Supplement S2 , output in Supplement S2a [available in the online version]).
In Illustration 2, we demonstrate modgo expansion 2 and generated simulated datasets that only included samples with age > 65 years. In Illustration 3, we present expansion 5 of modgo and generated datasets with pre-specified case–control proportions, here 90% of the patients with CAD. Finally, Illustration 4 uses the three validation datasets and shows how to deal with multicenter studies using modgo (expansion 4).
Simulation Studies Using the Golub Data
To demonstrate the performance of modgo on large datasets, we selected the Golub gene expression data from the OpenIntro data repository. 12 The Golub data consists in 72 subjects, 7129 gene probes and 6 additional variables. The data available on OpenIntro are the result of a merging of two versions of the original Golub data, 20 and it contains normalized expression values. We dropped the variable samples from the dataset because this variable is the sample number (person identifier). Furthermore, the variable tissue.mf was generated from the tissue type (bone marrow or peripheral blood) and the recruiting clinic. To avoid obvious linear dependency in the data, we dropped tissue.mf from the dataset. In fact, inclusion of tissue.mf in the dataset led to a matrix with negative eigenvalues. The main aim for this Illustration 5 is to demonstrate that such large datasets can be simulated by using modgo. All code and output are provided in Supplementary Material (Quarto markdown in Supplement S3 , output in Supplement S3a [available in the online version]).
Results
Illustration 1: Comparison of Correlation Matrices
Fig. 1 shows the correlation matrix of the original dataset ( Fig. 1A ) and the mean correlation matrices of 500 modgo simulated datasets ( Fig. 1B ), 500 modgo simulated datasets when the correlation matrix was estimated using sbgcop as intermediate covariance matrix ( Fig. 1C ), and correlation matrix simulated datasets produced by SimMultCorrData package ( Fig. 1D ). All simulation methods produced correlation matrices close to the original correlation matrix. Fig. 2 displays the difference of the original dataset correlation to the mean of the correlation of 500 datasets simulated by modgo ( Fig. 2A ), the combination of sbgcop and modgo ( Fig. 2B ), and the SimMultiCorrData package ( Fig. 2C ). modgo and SimMultiCorrData mean correlations showed almost no differences to the original correlation matrix, while the mean correlation of the combination of sbgcop with modgo deviated from the original correlation matrix.
Fig. 1.
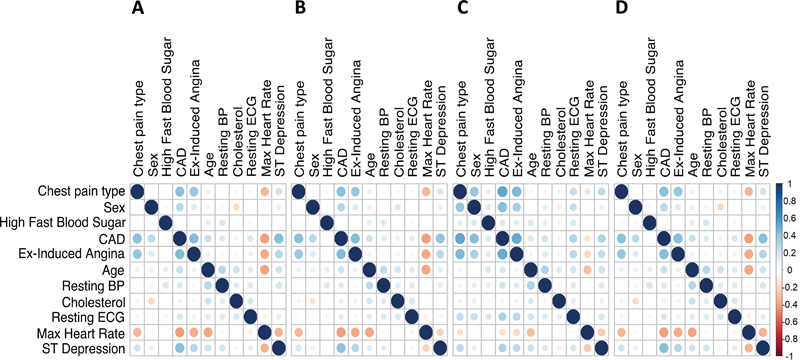
Correlation plots for the Cleveland Clinic data. ( A ) Correlation matrix for the original data; ( B ) mean correlation matrix of 500 datasets simulated by Mock Data Generation (modgo); ( C ) mean correlation matrix of 500 simulated dataset produced by modgo when it used the correlation matrix estimated by sbgcop as an intermediate covariance matrix; ( D ) mean correlation matrix of 500 simulated dataset by SimMultiCorrData. BP, blood pressure; CAD, coronary artery disease; ECG, electrocardiogram.
Fig. 2.
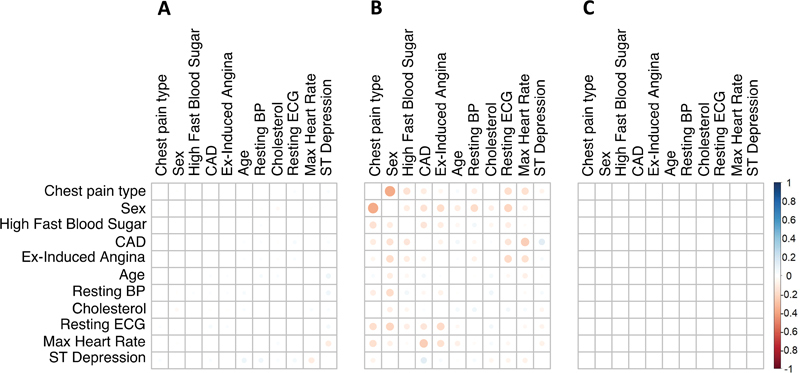
Difference between the correlation matrix estimated from the original data and the mean correlation matrix estimated by 500 runs of Mock Data Generation (modgo) ( A ), the combination of sbgcop for estimation of the correlation matrix used for simulations with modgo ( B ), and the mean correlation from 500 simulated dataset generated with SimMultiCorrData ( C ). BP, blood pressure; CAD, coronary artery disease; ECG, electrocardiogram.
The deviation between the original correlation matrix and the mean correlation matrix for the sbgcop–modgo combination has a large effect in the logistic regression coefficients estimated from the original and the simulated Cleveland Clinic Data ( Table 1 ). For logistic regression, we selected the three variables with the highest correlation with CAD, i.e., exercise-induced angina, age, max heart rate, and ST depression. In addition, we chose age, which is used for illustration in Illustration 2. Table 1 , column 2, displays odds ratios for the logistic regression model using the original Cleveland Clinic Data. Odds ratios and empirical 2.5 and 97.5% quantiles from the three simulation approaches are displayed in columns 3 to 5 for 500 simulated datasets per simulation approach. While estimated odds ratios were homogeneous and close to the original ones for modgo and SimMultiCorrData, they differed substantially for exercise-induced angina and ST depression when simulations were done with the combination of sbgcop and modgo.
Table 1. Logistic regression results for the Cleveland Clinic data.
| Variable | Original | modgo | sbgcop-modgo | SimMultiCorrData |
|---|---|---|---|---|
| Exercise-induced angina (yes) | 4.43 | 4.45 (2.38–8.17) | 10.16 (5.52–19.26) | 4.55 (2.78–8.04) |
| Age (years) | 1.02 | 1.02 (0.98–1.06) | 1.05 (1.01–1.08) | 1.02 (0.99–1.06) |
| Max heart rate (bpm) | 0.98 | 0.97 (0.95–0.99) | 1.00 (0.99–1.02) | 0.97 (0.96–0.98) |
| ST depression (mm) | 1.92 | 2.07 (1.52–2.86) | 1.60 (1.26–2.23) | 2.18 (1.69–2.86) |
Displayed are odds ratios for the original data (column 2). Three simulation methods were employed, and the medians of the odds ratios and empirical 2.5 and 97.5% quantiles of the odds ratios (in parenthesis) are displayed from 500 simulated datasets per simulation method. Column 3 shows results when simulations were done with modgo, column 4 when modgo was used with the correlation matrix estimated by sbgcop, and column 5 when simulations were done with SimMultiCorrData.
Fig. 3 shows the distribution for one continuous, one ordinal, and one dichotomous variable in the original Cleveland Clinic data and the first dataset simulated with modgo, sbgcop–modgo and SimMultiCorrData. All simulated datasets had similar distributions for the three variables for these single simulated datasets. Distribution plots for additional variables are provided in Supplementary Material ( Supplement 2 [available in the online version]).
Fig. 3.
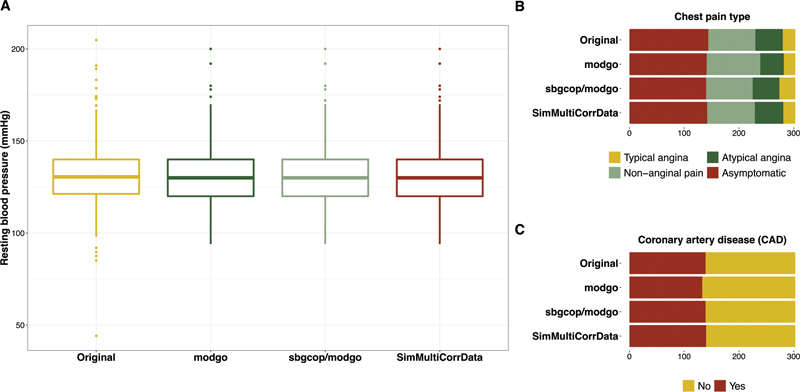
Distributions of one continuous, one ordinal and one dichotomous variable from the Cleveland Clinic data for the original data, and single simulated datasets obtained from Mock Data Generation (modgo), the combination of modgo and sbgcop, and SimMultiCorrData. ( A ) Box plot of the continuous variable resting blood pressure (mmHg); ( B ) bar plot for chest pain type, an ordinal variable with four categories; ( C ) bar plot for the dichotomous variable coronary artery disease (CAD).
Illustration 2: Cleveland Clinic Data with Selection by Age
In some applications, it is important to investigate the effect on subpopulations, e.g., patients with age > 65 years. Such a subgroup selection can be achieved in modgo by threshold definitions; illustrative code is provided in Supplementary Material ( Supplement 1 [available in the online version]). Fig. 4 shows the distribution of three variables for the original dataset and a single dataset simulated with modgo that contains subjects with age > 65 years. The distribution of all three variables in the entire population differs from the distribution when only subjects older than 65 years were included in the simulation model. Table 2 presents the medians of the odds ratio and 2.5 and 97.5% quantiles of the odds ratios from a logistic regression with CAD as the dependent variable, and exercise induced angina, age, and ST depression as independent variables. Odds ratio estimates for the simulated data with age > 65 years were similar to the original data.
Fig. 4.
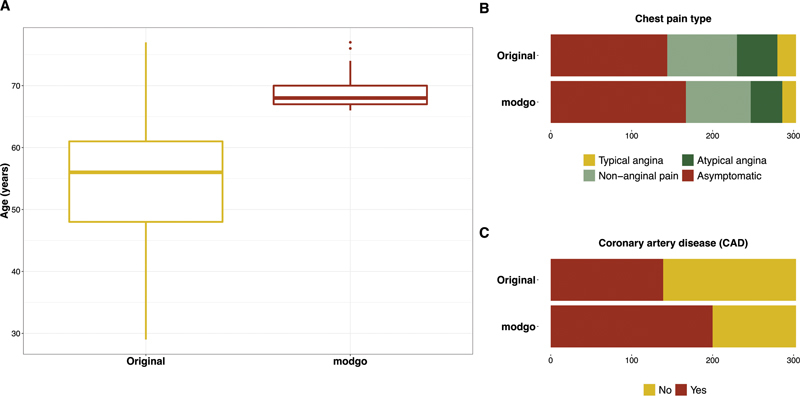
Distribution plots for the original Cleveland Clinic data and simulated data when all simulated subjects were forced to be more than or equal to 65 years. ( A ) Box plots for the continuous variable age; ( B ) bar plots for the categorical variable chest pain type; ( C ) bar plots for the dichotomous variable coronary artery disease (CAD).
Table 2. Logistic regression results for the Cleveland Clinic data. Displayed are odds ratios and 95% confidence intervals (in parenthesis) for the original data (column 2).
| Variable | Original | modgo | ||
|---|---|---|---|---|
| As original | Age > 65 years | 90% CAD | ||
| Exercise-inducedangina (yes) | 4.43 | 4.45 (2.38–8.17) | 4.65 (2.28–11.80) | 4.51 (1.67–29.31) |
| Age (years) | 1.02 | 1.02 (0.98–1.05) | 1.03 (0.92–1.16) | 1.02 (0.97–1.08) |
| Max heart rate (bpm) | 0.98 | 0.97 (0.95–0.99) | 0.97 (0.96–0.99) | 0.97 (0.94–0.99) |
| ST depression (mm) | 1.92 | 2.07 (1.52–2.86) | 2.07 (1.51–2.95) | 2.22 (1.40–4.79) |
Three simulation scenarios are displayed in this table, and the medians of the odds ratios and empirical 2.5 and 97.5% quantiles (in parenthesis) are shown for each simulation scenario. Column 3 shows results when simulations were done to mimic the original data. Column 4 displays results when age of subjects had to be > 65 years, and column 5 when the proportion of patients with coronary artery disease (CAD) had to be 90% (rounded from top). Results are based on 500 replicates per simulation model.
Illustration 3: Cleveland Clinic Data with Different Case–Control Proportions
An additional extension of modgo is the change of the proportion of cases and control in the simulated dataset compared with the original dataset. Illustrations on correlation matrices and variables distributions from modgo simulated datasets with CAD proportion equals to 90% percent are provided to Supplementary Material ( Supplement S1a , Figs. S13 and S14 [available in the online version]). Table 2 shows logistic regression estimates for simulated datasets with 90% CAD cases. Medians of odds ratio exhibited negligible changes from the modgo run that mimicked the original dataset. However, the variability of the odds ratio estimates was significantly larger, especially for the dichotomous variable exercise-induced angina.
Illustration 4: Cleveland Clinic Data with Multicenter Setting
To illustrate the application of modgo in multicenter studies, we used the data from all four centers of the Cleveland Clinic Project. Table 3 , column 2, provides the odds ratios estimated from logistic regression of the pooled original datasets. In one simulation approach using modgo, we ignored the multicenter nature of the data. Specifically, the correlation matrix was estimated from a single dataset across all centers, and data were simulated from this correlation matrix. In another simulation approach, the multicenter nature of the data was reflected. Correlation matrices were estimated by center, and data were simulated for each center separately. The simulated data for the four centers were then pooled, and a logistic regression model was estimated.
Table 3. Logistic regression results for the Cleveland Clinic data when all four datasets were used for estimation (Cleveland Clinic, Swiss, Hungarian and Veterans).
| Variable | Original | modgo | |
|---|---|---|---|
| Validation datasets | As single dataset | Multicenter approach | |
| Exercise-induced angina (Yes) | 3.80 | 4.37 (3.13–6.10) | 3.83 (2.66–5.73) |
| Age ( y ears) | 1.03 | 1.03 (1.02–1.05) | 1.03 (1.01–1.05) |
| Max heart rate (bpm) | 0.98 | 0.98 (0.97–0.98) | 0.98 (0.97–0.98) |
| ST depression (mm) | 1.70 | 1.52 (1.29–1.78) | 1.78 (1.52–2.12) |
Displayed are odds ratios for the original datasets (column 2). Two simulation approaches were used with modgo, and medians of odds ratios and empirical 2.5 and 97.5% quantiles (in parenthesis) are displayed in the last two columns. Column 3 the multicenter nature of the data was ignored, and data from all centers were pooled for simulating new data; column 4: the multicenter nature of the data was taken into account. Correlation matrices were estimated per center, data were simulated per center and pooled before running logistic regression.
Table 3 shows that odds ratio estimates were different from original estimates when the multicenter nature of the data was ignored during the simulation (column 3). Odds ratio estimates were, however, closer to the original estimates, when the multicenter nature of the data was adequately taken into account (column 4).
Illustration 5: Data simulation with the Golub data
For the Golub data, Fig. 5A displays the correlation plots for the data (panel A) and the mean correlation plots for 500 runs of modgo ( Fig. 5B –D) for the four categorical variables and the first 6 gene expression variables. The corresponding differences between the original correlation and the average of the modgo runs are shown in Fig. 5E to G . Specifically, respectively, Fig. 5B and E show the mean correlation and the difference to the original correlation estimated by modgo, when run in its default mode. The default mode means that the specific correlation coefficients for categorical variables are used, such as polychoric correlations, the nearest positive definite matrix to the correlation matrix is estimated and used for simulations, and normally distributed random variables are generated with mvrnorm from the MASS library with default tolerance of 10 −6 . Fig. 5C and F correspondingly show the results for 500 modgo, when all correlations were estimated with the Pearson correlation coefficient. Finally, Fig. 5D and G display the mean estimated correlation matrix from 500 modgo runs and the difference between the original correlation matrix and the mean estimated correlation matrix, respectively, when modgo was run with a high tolerance of 10 in mvrnorm, without estimation of the nearest positive definite correlation matrix, and when the correlations were estimated with the correlation coefficients estimated using the correlation coefficients for categorical variables. Fig. 5E to G show that the largest difference between original and simulated correlation coefficients can be observed for modgo runs, when correlations—even for categorical variables—were obtained from Pearson correlation coefficients.
Fig. 5.
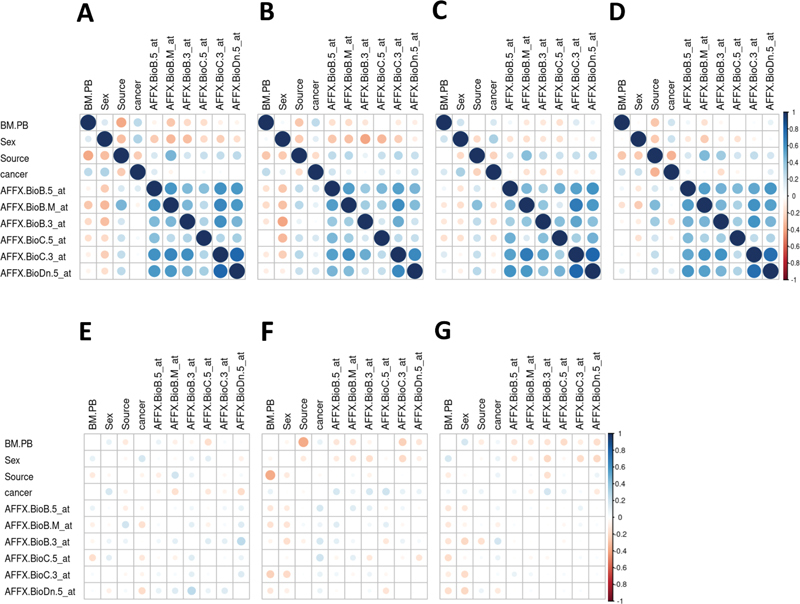
Correlation plots for the Golub data and difference between the correlation matrix estimated from the original data and the mean correlation matrix estimated by 500 runs of Mock Data Generation (modgo). ( A ) Correlation matrix for the original data; ( B ) mean correlation matrix of 500 datasets simulated by modgo; ( C ) mean correlation matrix of 500 datasets simulated by modgo, when all correlations were estimated with the Pearson correlation coefficient; ( D) mean correlation matrix of 500 datasets simulated by modgo, when a large tolerance of 10 is used for generating the normally distributed random variables was used; ( D ) mean correlation matrix of 500 datasets simulated by modgo; ( E ) difference between the correlation matrix estimated from the original data and the mean correlation matrix estimated by 500 runs of modgo; ( F ) difference between the correlation matrix estimated from the original data and the mean correlation matrix estimated by 500 runs of modgo, when correlations were estimated using Pearson correlation; ( G ) difference between the correlation matrix estimated from the original data and the mean correlation matrix estimated by 500 runs of modgo, when a large tolerance was used in generating the normally distributed random variables.
Fig. 6C reveals that the Pearson correlation-based approach was slower than the approach which used a large tolerance for simulating the normally distributed random variables. Note that the high tolerance approach is not available as standard in modgo. In Fig 6. A and C , run times are given, when 250 cores from two compute nodes were used on our high-performance computing (HPC) environment, where each node is equipped with 128 cores each (2 EPYC 7742, 2TB RAM, 11.2 TB NVMe). Fig. 6C shows that modgo can be run on the Golub data in its default mode, when many cores are available for calculations. Fig. 6A displays that run time increases exponentially with the number of variables, and Fig. 6B shows that it is always good to have many cores because run time decreases exponentially with the number of cores.
Fig. 6.
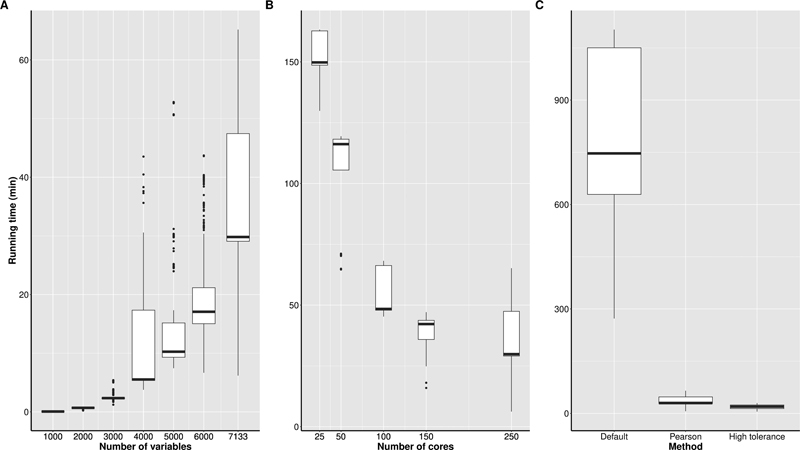
Run time using the Golub data for various configurations of the high-performance computer. ( A ) Variation of the number of variables included in the simulations for 500 Mock Data Generation (modgo) runs with 250 cores; ( B ) variation of the number of cores for generating 500 modgo datasets with all variables; ( C ) variation of the modgo method (default: estimation of correlation coefficients with polychoric, etc. correlations, calculation of the nearest positive definite matrix, standard tolerance for simulating normally distributed variables; Pearson: estimation of correlation coefficients with Pearson correlations and calculation of the nearest positive definite matrix; high tolerance: estimation of correlation coefficients with polychoric, etc. correlations, without transformation to the nearest positive definite matrix, and high tolerance for simulating normally distributed variables).
Discussion
In practice, there may be a difference between data protection and data privacy policies on the one hand and the willingness or the requirement to share data by researchers. We have shown that the R package modgo can efficiently simulate continuous, binary, and ordinal categorical variables that mimic original study data. Results from modgo and the SimMultiCorrData package were similar for simple simulation scenarios. However, thanks to the implemented expansions, more complex simulation scenarios could be considered in modgo compared with SimMultiCorrData. The simulations also showed that the calculation of the correlation matrix with sbgcop in combination with simulating data using modgo did not perform as well as modgo and SimMultiCorrData.
The main question is whether there truly was need for yet another R simulation package mimicking original study data. Indeed, other packages also generate mock datasets from an original one. For example, Demirtas and Gao 21 described a total of 16 packages which he and his colleagues, mentees, and students developed. Although Demirtas and Gao developed this large number of different packages, the expansions, which we need in our own research are not available. Additional R packages, such as GenOrd, which is partly based on, 22 SimMultiCorrData and SimCorrMix, 19 and GenData 23 also do not come with this flexibility. However, the basic concepts of many of the packages are identical to those that we have used in the development of modgo. Specifically, both the rank inverse normal transformation 13 and the calculation of polychoric and polyserial correlation coefficients 21 has been used by others, for example, see refs. 13 21 A main difference between the approaches generally taken by Demirtas and Gao 21 and modgo is that we suggest to combine rank inverse normal transformation with the specific correlation coefficients. Demirtas and Gao 21 generally used the Fleishman distributions to simulate non-normal distributions. 24 The main advantage of using Fleishman distributions is that simulated data are transformed to the original scale without using original observations. The approach taken in modgo is different. With the optional perturbation module, the simulated data may be alienated so that no observations on the original scale are present in the simulated data.
An important component for modgo's performance is the correlation matrix, which needs to be estimated before new data can be simulated and which needs to be positive definite. This is important because the correlation matrix may only be positive semidefinite in case of data with many features and few samples. Even more, the variable tissue.mf in the Golub data are completely confounded with the two variables tissue type and sex. The estimated correlation matrix which contains all three variables has negative eigenvalues.
The illustration with the Golub data has shown that runtime of modgo increases exponentially with the number of features. Large datasets thus require the availability of an HPC and parallelization. In this setting, we recommend using a 3-step approach, where in step 1 the correlation matrix is estimated. In step 2 the nearest positive definite matrix is calculated in case the correlation matrix obtained in step 1 is not positive definite. Finally, the new samples are simulated in step 3. Runtime of simulations can be reduced by using a higher tolerance when normally distributed samples are generated. Another important aspect to computational speed is the way correlations are estimated when categorical variables are involved. When Pearson correlations are used even for categorical variables, runtime is substantially lower, but at the cost of more pronounced differences between original and simulated samples. In contrast, when correlation coefficients are used that have been developed for categorical variables, such as polychoric and polyserial correlation coefficients, runtime is higher with the benefit of more precise simulated data.
Despite its flexibility, modgo has a couple of limitations. Specifically, the package cannot handle unordered categorical data as unordered. Our empirical evidence shows, however, that the simulation option for ordered categorical delivers a reasonably well matching of simulated and original distributions. Furthermore, right-censored data, specifically survival data cannot be simulated with modgo. In contrast, data from threshold models, such as the Tobit model, 25 can be simulated directly because of the rank inverse normal transformation. However, the correlation estimates may be slightly biased because they do not take into account the threshold(s). Estimates may be improved using the approaches described elsewhere. 26 27 28 Finally, we stress that our simulation approach is based on the availability of individual patient data and may not be applied to aggregated data. 29
The modgo package has several strengths when compared with other packages. First, all information is directly extracted from the individual patient data/study participant data, and the simulations are not based on aggregated data that only work with summary statistics. Second, modgo is simple to use. For example, other packages may require the estimates of means, variances, correlations, and other association parameters. However, modgo only asks the user to provide (a) a dataset and (b) indicate which variables of the dataset are continuous, categorical, and are dichotomous. Third, modgo offers several expansions, which are not available in other simulation tools. For example, the user can easily simulate data from multiple studies with the multicenter extension. Similarly, the correlation between variables may be changed to alter the relationship between dependent and independent variables in a regression setting. Furthermore, thresholds may be set for changing the inclusion criteria when generating a simulated study. Next, the proportion of cases and controls in a case–control study may be easily altered. Finally, and most importantly, the simulated data may be perturbed further to alienate structures present in the data. This approach can also be used for checking the robustness of an already developed statistical model. 30
The package may be used in several real data applications. Specifically, we have already used modgo for power calculations of a validation study. In detail, we developed a prediction model using one dataset. With the aim to validate the findings, we calculated the required sample size for a validation study by simulating mock data from the original available dataset. The flexibility to alter the correlations between variables allowed for a change in the effect of the independent on the dependent variables. In another application, we have used original data to generate machine learning models for prediction, similar to. 31 This approach may also be used for parameter tuning in machine learning. 32 Due to data privacy issues, the original data may not be transferred to other groups. However, the model development can be illustrated using simulated data that mimic the actual observed study data.
Conclusions
modgo is a simple-to-use R package that allows to mimic original study data if these may not be shared due to data privacy restrictions. The perturbation module guarantees the anonymization of real patient data so that only mock data are provided. modgo comes with several expansions, which allow to adapt the simulation process to specific needs of users, such as multicenter studies.
Funding Statement
Funding The authors received no specific funding for this study.
Conflict of Interest F.O. and A.Z. are listed as co-inventors of an international patent on the use of a computing device to estimate the probability of myocardial infarction (International Publication Number WO2022043229A1). F.O. and A.Z. are shareholders of the ART-EMIS Hamburg GmbH. A.Z. is scientific director and G.K. is bioinformatician of Cardio-CARE, which is shareholder of the ART-EMIS Hamburg GmbH.
Data Availability Statement
All relevant data are within the manuscript and its Supporting Information files.
Code Availability (Software Application or Custom Code)
All code including the R package is available as Supplementary Material (available in the online version).
Authors' Contribution
G.K. was involved in programming and writing, editing, and review of original draft. F.O. was involved in methodology, programming, and writing, editing, and review of the original draft. A.Z. was involved in methodology, supervision, and writing, editing, and review of the original draft.
Authors are listed alphabetically.
Algorithm 1.
The original data consists of n observations, p con continuous variables, and p ord ordinal variables, including binary variables as a particular case, with 0 < p = p_con + p_ord and p_con, p_ord >= 0. The simulated data will have n sim observations.
Step 0: Initialize a p × p matrix Σ with the p × p identity matrix. The entry ( i, j ) of Σ corresponds the i th and j th variables of the original data.
Step 1: If p con > 0, then for each continuous variable X taking values x 1 , x 2 , …, x n apply the associated rank-based inverse normal transformation
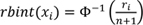 , where
r
1
,
r
2
, …,
r
n
are the ranks of the
x
1
,
x
2
, …,
x
n
and Φ
−1
is the inverse of the standard normal cumulative distribution function Φ.
, where
r
1
,
r
2
, …,
r
n
are the ranks of the
x
1
,
x
2
, …,
x
n
and Φ
−1
is the inverse of the standard normal cumulative distribution function Φ.
Step 2: If p con > 0, compute the covariances between all pairs of rank-based normal inverse transformed continuous variables Y i and Y j and store these covariance estimates in the corresponding entries of Σ .
Step 3: If p ord > 1, compute the polychoric correlations between all pairs of (original) ordinal variables X 1 and X 2 , with X 1 ≠ X 2 , and store these correlation estimates in the corresponding entry of the matrix Σ .
Step 4: If p con > 0 and p ord > 0 compute all polyserial correlations between all pairs of original ordinal variables X i and rank-based normal inverse transformed variables Y j and store these correlation estimates in the corresponding entries of Σ .
Step 5: If Σ is not positive definite, compute the nearest positive definite matrix to Σ according to reference 16 and assign the resulting matrix to Σ .
Step 6: Draw n sim p -dimensional vectors from the centered multivariate normal distribution with covariance matrix Σ .
Step 7:For each original variable X taking values x 1 , x 2 , …, x n , let Y be the variable simulated in the previous step corresponding to X , taking values y 1 , y 2 , …, y nsin . For each y i compute
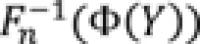 where
where
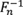 is the inverse of the empirical cumulative distribution of
x
1
,
x
2
, …,
x
n
. Do this for each variable
Y
in the data simulated in Step 6. The resulting
n
sim
×
p
data matrix is the output of the algorithm.
is the inverse of the empirical cumulative distribution of
x
1
,
x
2
, …,
x
n
. Do this for each variable
Y
in the data simulated in Step 6. The resulting
n
sim
×
p
data matrix is the output of the algorithm.
Supplementary Material
References
- 1.Rubin D B. Discussion: statistical disclosure limitation. J Off Stat. 1993;9:461–468. [Google Scholar]
- 2.Raghunathan T E, Reiter J P, Rubin D B. Multiple imputation for statistical disclosure limitation. J Off Stat. 2003;19:1–16. [Google Scholar]
- 3.Falcaro M, Castañon A, Ndlela Bet al. The effects of the national HPV vaccination programme in England, UK, on cervical cancer and grade 3 cervical intraepithelial neoplasia incidence: a register-based observational study Lancet 2021398(10316):2084–2092. [DOI] [PubMed] [Google Scholar]
- 4.Horvat P, Gray C M, Lambova A et al. Comparing findings from a friends of cancer research exploratory analysis of real-world end points with the cancer analysis system in England. JCO Clin Cancer Inform. 2021;5:1155–1168. doi: 10.1200/CCI.21.00013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Li D-C, Fang Y-H, Lai Y-Y, Hu S C. Utilization of virtual samples to facilitate cancer identification for DNA microarray data in the early stages of an investigation. Inf Sci. 2009;179:2740–2753. [Google Scholar]
- 6.Fowler E E, Berglund A, Schell M J, Sellers T A, Eschrich S, Heine J. Empirically-derived synthetic populations to mitigate small sample sizes. J Biomed Inform. 2020;105:103408. doi: 10.1016/j.jbi.2020.103408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pavlou M, Ambler G, Seaman S, De Iorio M, Omar R Z. Review and evaluation of penalised regression methods for risk prediction in low-dimensional data with few events. Stat Med. 2016;35(07):1159–1177. doi: 10.1002/sim.6782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.König I R, Weimar C, Diener H-C, Ziegler A. Vorhersage des Funktionsstatus 100 Tage nach einem ischämischen Schlaganfall: Design einer prospektiven Studie zur externen Validierung eines prognostischen Modells. Z Arztl Fortbild Qualitatssich. 2003;97(10):717–722. [PubMed] [Google Scholar]
- 9.Burgard J P, Kolb J-P, Merkle H, Münnich R. Synthetic data for open and reproducible methodological research in social sciences and official statistics. AStA Wirtsch Sozialstat Arch. 2017;11:233–244. [Google Scholar]
- 10.AbdelMalik P, Kamel Boulos M N. Multidimensional point transform for public health practice. Methods Inf Med. 2012;51(01):63–73. doi: 10.3414/ME11-01-0001. [DOI] [PubMed] [Google Scholar]
- 11.Dua D, Graff C. UCI machine learning repository. Irvine: University of California, School of Information and Computer Science; 2019 Accessed March 20, 2023 at:http://archive.ics.uci.edu/ml
- 12.Golub T R, Slonim D K, Tamayo Pet al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring Science 1999286(5439):531–537. [DOI] [PubMed] [Google Scholar]
- 13.Beasley T M, Erickson S, Allison D B. Rank-based inverse normal transformations are increasingly used, but are they merited? Behav Genet. 2009;39(05):580–595. doi: 10.1007/s10519-009-9281-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Olsson U. Maximum likelihood estimation of the polychoric correlation coefficient. Psychometrika. 1979;44:443–460. [Google Scholar]
- 15.Olsson U, Drasgow F, Dorans N J. The polyserial correlation coefficient. Psychometrika. 1982;47:337–347. [Google Scholar]
- 16.Higham N J. Computing the nearest correlation matrix—a problem from finance. IMA J Numer Anal. 2002;22:329–343. [Google Scholar]
- 17.Detrano R, Janosi A, Steinbrunn W et al. International application of a new probability algorithm for the diagnosis of coronary artery disease. Am J Cardiol. 1989;64(05):304–310. doi: 10.1016/0002-9149(89)90524-9. [DOI] [PubMed] [Google Scholar]
- 18.Hoff P D. Extending the rank likelihood for semiparametric copula estimation. Ann Appl Stat. 2007;1:265–283. [Google Scholar]
- 19.Fialkowski A, Tiwari H. SimCorrMix: simulation of correlated data with multiple variable types including continuous and count mixture distributions. R Journal. 2019;11:250–286. [Google Scholar]
- 20.OpenIntro Data Sets. OpenIntro; 2023. Accessed March 20, 2023 athttps://www.openintro.org/data
- 21.Demirtas H, Gao R. Mixed data generation packages and related computational tools in R. Commun Stat Simul Comput. 2022;51:4520–4563. [Google Scholar]
- 22.Ferrari P A, Barbiero A. Simulating ordinal data. Multivariate Behav Res. 2012;47(04):566–589. doi: 10.1080/00273171.2012.692630. [DOI] [PubMed] [Google Scholar]
- 23.Ruscio J, Kaczetow W. Simulating multivariate nonnormal data using an iterative algorithm. Multivariate Behav Res. 2008;43(03):355–381. doi: 10.1080/00273170802285693. [DOI] [PubMed] [Google Scholar]
- 24.Demirtas H, Hedeker D. Multiple imputation under power polynomials. Commun Stat Simul Comput. 2008;37:1682–1695. [Google Scholar]
- 25.Amemiya T. Tobit models—a survey. J Econom. 1984;24:3–61. [Google Scholar]
- 26.Aitkin M A, Hume M W. Correlation in a singly truncated bivariate normal distribution II. Rank correlation. Biometrika. 1966;52:639–643. [PubMed] [Google Scholar]
- 27.Gajjar A V, Subrahmaniam K. On the sample correlation coefficient in the truncated bivariate normal population. Commun Stat Simul Comput. 1978;7:455–477. [Google Scholar]
- 28.Aitkin M A. Correlation in a singly truncated bivariate normal distribution. Psychometrika. 1964;29:263–270. [PubMed] [Google Scholar]
- 29.Demirtas H, Doganay B. Simultaneous generation of binary and normal data with specified marginal and association structures. J Biopharm Stat. 2012;22(02):223–236. doi: 10.1080/10543406.2010.521874. [DOI] [PubMed] [Google Scholar]
- 30.Teo Y Y, Small K S, Clark T G, Kwiatkowski D P.Perturbation analysis: a simple method for filtering SNPs with erroneous genotyping in genome-wide association studies Ann Hum Genet 200872(Pt 3):368–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Malley J D, Kruppa J, Dasgupta A, Malley K G, Ziegler A. Probability machines: consistent probability estimation using nonparametric learning machines. Methods Inf Med. 2012;51(01):74–81. doi: 10.3414/ME00-01-0052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hepp T, Schmid M, Gefeller O, Waldmann E, Mayr A. Approaches to regularized regression—a comparison between gradient boosting and the lasso. Methods Inf Med. 2016;55(05):422–430. doi: 10.3414/ME16-01-0033. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All relevant data are within the manuscript and its Supporting Information files.


