Abstract
The usage of additive manufacturing techniques has increased dramatically in recent years. Fabricated parts are no longer simple prototypes, but rather structural components whose mechanical characteristics must be understood before printing. One of the weaknesses of 3D printing is the high variability of dimensional, geometric, and mechanical properties, which is due to the combination of various printing parameters, including the number of walls, roofs, and floors, filling patterns, and printing layer thickness.
This study aims to predict the mechanical properties of onyx printed parts as a function of the number of walls and a solid pattern through an analytical approach based on the rule of mixtures and numerical finite element simulation. The influence of the number of walls on the mechanical properties of onyx printed parts was characterised by uniaxial tensile tests. The results show that walls have a significant impact on the final mechanical properties of the parts. The study found that the higher the number of walls, the greater the mechanical properties of the parts. The rule of mixtures approach allowed us to predict the mechanical properties with good accuracy, with prediction errors observed ranging from 1% to 10% depending on the number of walls in the parts. The numerical simulation using finite elements was carried out using the properties of the walls and the solid pattern obtained from tensile testing, enabling a comparison between the experimental test and the rule of mixtures. The results show that the mechanical properties obtained by the rule of mixtures and numerical simulation are consistent with the physical tensile test.
Keywords: 3D printing, Walls effect, Mechanical properties, Tensile test, Rule of mixtures, Finite element simulation
1. Introduction
Additive manufacturing (AM), or 3D printing, offers several advantages, including acceptable accuracy, cost-effectiveness, and most importantly, the ability to fabricate complex shapes. R. Surya Teja et al. [1] demonstrated this ability by printing a reduced-size replica of the Eiffel Tower. The most common 3D printing technology is Fused Deposition Modelling (FDM), which is now used to fabricate industrial and functional parts for applications in various sectors, including medical, automotive, aerospace, defence, and consumer goods. FDM can be used to produce bone scaffolds for medical applications [2] and was even deployed during the COVID-19 pandemic to produce medical devices [3]. To be profitable in terms of production time and cost, this method of manufacturing must be able to produce small and medium series parts in compliance with industrial standards. Thanks to recent advances in the field, AM has strong potential to be a serial process [4,5]. For example, in 2017, a partnership between Adidas and Carbon (an American company) allowed them to manufacture 100,000 new-generation shoes with a lattice-structure sole made using 3D technology (Digital Light Synthesis DLS). Each sole was printed in just 19 min, and the process was qualified as cost-effective and reliable, despite the complexity of the sole shape according to Adidas and Carbon.
The FDM process is complex due to the many available parameters that affect the quality and mechanical properties of the manufactured products. These parameters include the orientation of parts on the building platform, layer thickness, density, printing pattern, number of walls, and the addition of reinforcing fibre. In a review article, D. Popescu et al. [6] showed that a small printing layer thickness, a small raster angle, and a small air gap improve the mechanical tensile properties of printed parts. In another study, M.T. Birosz [7] investigated the influence of FDM fill patterns on the mechanical properties of PLA printed parts and found that honeycomb and gyroid patterns have better mechanical strength. The work of Y. Zang et al. [8] indicated that the geometric shape and thickness of the samples also affect their mechanical properties. The mechanical performance of parts is highly dependent on their mechanical properties, making it important to characterise these properties by examining the influence of specific printing parameters. Many studies have reported on the characterisation of mechanical properties of parts manufactured using this technology, particularly fiber-reinforced parts, including those reinforced with short and long fibres [9,10].
Thus far, several studies have shown that the orientation and positioning of parts on the printing platform influence the parts' mechanical properties. According to the study carried out by R. Zou et al. [11], ABS parts obtained in FDM can be considered isotropic because the orientation does not significantly influence the mechanical properties of the parts. The work carried out by Chacón J. M et al. [12] shows that parts printed in PLA have different behaviours depending on the orientation of the parts. Vertical orientation provides lower mechanical properties than a flat and lateral orientation. The same results were found by M. Somiredy et al. [13].
As with any manufacturing process, FDM can be optimised, but this requires knowledge of the machine parameters. A recent study by S. Sahoo et al. [14] investigated layer thickness (0.1–0.2–0.3 mm), fill density (25–35–45%), and printing speed (40–50–60 mm/s). The optimal parameters for high strength were a layer thickness of 0.1 mm, a density of 35%, and a printing speed of 60 mm/s. S. Mangala et al. [15] studied infill density (25–50–75%), infill pattern (gyroid - triangle - grid), and layer thickness (0.1–0.15–0.2 mm). Their Design of Experiment (DOE) showed that the optimal Young's modulus was obtained with a triangle pattern, layer thickness of 0.15 mm, and density of 75%, while the optimum CO2 emission was obtained with a gyroid pattern, layer thickness of 0.1 mm, and density of 25%. There is little research that examines the influence of the number of walls or contours on the mechanical properties of printed parts. For example, A. Gebisa et al. in two different studies [16,17] included the number of walls in their parameter list to find optimal parameters via a DOE. They discovered that walls contribute less to the increase of mechanical properties in tension and bending than the other parameters.
Most of the studies on this topic concern office or research printers. Our study will focus on the Markforged X7 printer, an industrial printer using onyx material, which is widely used in the industrial sector. Onyx is the most widely used thermoplastic of the Markforged X7 printers. In the literature, authors have studied it on several occasions. For example, D. Krzikalla et al. [18] studied the flexural properties of long carbon fibre-reinforced onyx matrix. Recently, Y. Liu et al. [19] published their work on the influence of printing parameters (printing direction, filling patterns and number of walls) on the compressive strength and energy absorption of a negative stiffness honeycomb cell structure (NSH–C) printed with onyx material. They found that flat printing, triangular pattern, and two wall layers are the optimal parameters.
This study focuses specifically on examining the relationship between the number of walls and the mechanical properties of parts printed using onyx material with the Markforged X7 industrial printer. The main objective of this study is to develop an analytical expression that can predict the mechanical properties of printed parts based on the number of walls selected. This expression will be useful for designers and engineers to estimate and optimise mechanical properties before printing the parts. Following this, a numerical simulation was carried out to predict the overall behaviour of the parts. A comparison was made between the experimental tests, the analytical expression, and the simulation to determine the relative error between the three methods. To achieve this objective, the study was carried out in three main sections: the first section outlines the experimental approach; the second section presents the results and discussions; and the final section provides the study's conclusions and future prospects.
2. Material and method
2.1. Printing material, 3D printer and specimen dimensions
Onyx used is a black filament with a diameter of 1.75 mm, manufactured in roll form and marketed by the company Markforged. It is a nylon (Polyamide 6) filled with approximately 40% of short micro carbon fibres. Markforged does not provide further details about the onyx material. Onyx can be printed alone or reinforced with long fibres to enhance the mechanical properties of the printed parts [20]. The supplier has reported a Young's modulus of 2400 MPa and a yield strength of 40 MPa for parts printed solely with onyx material.
The test specimens were manufactured using the Markforged X7 industrial series 3D printer. This printer can print industrial parts in a volume of 330 mm × 270 mm x 200 mm, depending on the quality requirements of the part. The X7 printer uses a range of materials, including onyx, onyx FR, onyx FR-A, and white nylon, which can be reinforced with continuous carbon, glass, or Kevlar fibres. It has several printing variables accessible via its Eiger slicing software, such as layer thickness, number of walls, orientation and geometric positioning of the parts on the printing platform, number of fibre layers, fibre orientation (0°, 45°, 90°), fibre placement mode (concentric, isotropic), and type of printable patterns (triangular, rectangular, hexagonal, gyroid, or solid) [21,22].
The tensile specimen studied was modelled using Inventor software and then exported in STL format before being imported into Markforged's slicing software (Eiger). In this study, all specimens were printed with a density of 100% solid pattern, with successive layers printed at ± 45° (see Fig. 2). After printing, a tensile test was performed according to ASTM D638. Fig. 1 shows the geometry and dimensions of the specimen.
Fig. 2.
Illustrative image of walls and layers deposition.
Fig. 1.
Shape and dimensions of the test piece (units: mm for dimensions and ° for angles).
This shape is based on ASTM D3039, which is specifically designed for the tensile testing of fibre-reinforced components. This particular shape was chosen to prevent the jaws of the tensile testing machine from breaking. The printing parameters are outlined in Table 1. In this study, we investigate the impact of the number of walls (contours) on the mechanical properties of parts printed with onyx material using the Markforged X7 printer. The number of walls, or contours, was set at 5 to ensure that the specimens (pure wall specimens) had a sufficient cross-section after the cutting operation for tensile test characterisation.
Table 1.
Printing parameters.
| Parameters | specifications |
|---|---|
| Pattern and density | Solid - 100% |
| Layer thickness – wall width | 0,1 mm–0.4 mm |
| Part orientation | Flat |
| Walls (contours) count | 1–10 |
| Successive layer deposition | ±45° |
2.2. Cutting operation of the test parts
In order to conduct tests on pure wall and pure solid specimens, it was necessary to remove the walls from the printed parts using a cutting technique. However, onyx is an abrasive material, which makes conventional cutting methods such as wire cutting, machining, and saw cutting unsuitable. Cutting with water and ethanol lubrication of the cutting tool was attempted but was abandoned due to onyx's high sensitivity to moisture. Additionally, a cutting process that generates significant heat is not suitable as it can degrade the mechanical properties of onyx. Some researchers have used waterjet cutting in their studies without considering the material's sensitivity to water, as in the case of the studies conducted by K. Saeed et al. and Y. Zhang et al. [8,23].
To overcome these challenges, a manual cutting method using a very thin saw blade (0.2 mm thick) was employed. The printed specimens were placed on a flat surface to ensure straight and smooth cuts and avoid stress concentrations and premature crack initiation during the tensile test. A thin wooden board was also used to hold the cuts in position in a vice. The cutting tool, and specimens after cutting are shown in Fig. 3.
Fig. 3.
a-cutting operation, b-pure wall specimens, c-specimens without walls.
After the cutting operation, the dimensions of the parts were measured using a calliper. The mean dimensions of the pure wall specimens are 4 mm in width and 2.1 mm in thickness, while the pure infill (solid) specimens measure 11.5 mm in width and 4 mm in thickness. The variation in dimensions of the specimens is ± 0.2 mm. Given the small variation in the dimensions of the cut samples, the effect of dimensions on the mechanical properties is considered negligible.
2.3. Uniaxial tensile test
The experimental test conducted in this study was a uniaxial tensile test, which was carried out using an Instron 5569 tensile machine with a 50 KN force cell. The strain stress was measured with a 12.5 mm gauge length extensometer and 40% of maximum elongation. The test speed was determined based on several tests according to ASTM D638, and a displacement speed of 10 mm/min was chosen for the tests. The data acquisition was performed using Instron's Bluehill Universal software, and the data was processed in accordance with the recommendations of the standard used. Young's modulus was calculated by considering the linear part of the nominal stress-strain curve, as was also done by S. Hasanov et al. [24] in their work. In this study, a linear regression was used in Excel software with a regression coefficient R2 > 0.99 to determine Young's modulus along the linear part of the curves. To ensure accuracy, each test was carried out with 3 samples under the same test and printing conditions, considering the number of tests to be conducted. The elastic limit adopted is Re0.2%, which corresponds to the yield strength at 0.2% strain, similar to the approach taken by J. Narajo-Lozada et al. [25]. The tensile test was performed on pure wall specimens, solid specimens, and specimens with a varying number of walls.
2.4. Mechanical properties prediction by ROM approach
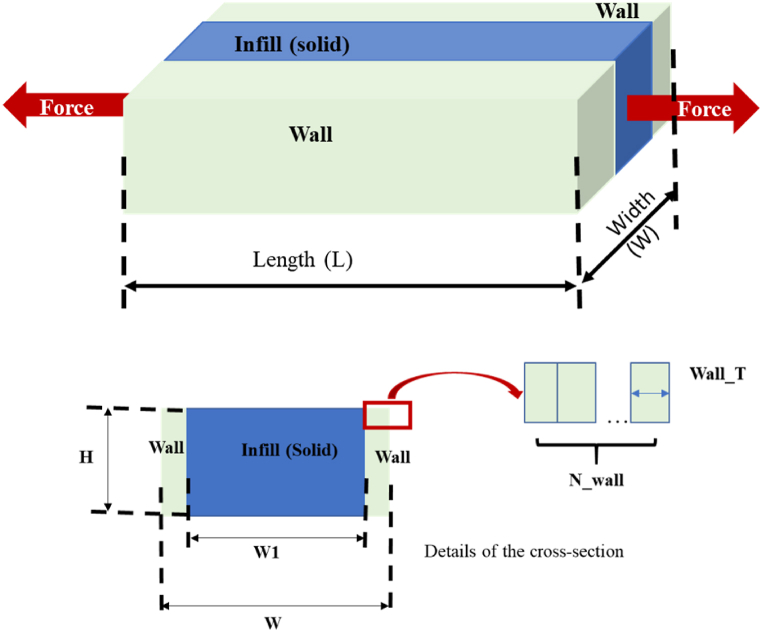
The aim of implementing the Rule of Mixtures (ROM) is to predict the mechanical properties of 3D printed parts based on the number of walls. This law of mixture is typically used to predict the mechanical properties of composite parts that have long or short fibres [26,27]. However, there are no analytical or predictive models in the literature for predicting the mechanical properties of 3D printed parts based on the number of walls. Fig. 4 shows the volume representation of the walls and solid parts.
Fig. 4.
Volume configuration of walls and infill pattern L: length of the specimen (useful length), H: height of the specimen, W: width of the specimen, W1: width of the solid, N_Wall: number of walls, Wall_T: wall thickness = 0.4 mm.
Consider V: the volume of the specimen; V1: the volume of infill (solid); V2: the volume of walls.
: the ratio volume of walls and : the fraction volume of the infill (solid).
The total volume of the specimen and the volume of walls were calculated by equations (Eq. 1), (Eq. 2)).
| (Eq. 1) |
| (Eq. 2) |
Width of infill (solid) was calculated by equation (3). Equation (4) calculates the volume of walls.
| (Eq. 3) |
| (Eq. 4) |
The fraction volume of infill (solid) () and the fraction volume of walls () were calculated by equation (5):
| (Eq. 5) |
The Young modulus was calculated by equation (6).
| (Eq. 6) |
Equation (6) can be simplified by combining relations 1,2,3,4,5 and the tensile Young's modulus of 3D printed parts with a different number of walls was expressed by equation (7).
| (Eq. 7) |
The yield strength (Re) was calculated by replacing Young's modulus of the walls and the solid with the yield strength of the walls (Re_walls) and the yield strength of the solid (Re_solid) respectively (Eq. (8)).
| (Eq. 8) |
2.5. Numerical simulation
Finite element simulation was used to perform a numerical simulation of a tensile test, using the commercial software Abaqus Standard, with the aim of predicting the mechanical properties of a part containing a variable number of walls. In this case study, the mechanical properties of a specimen containing four walls were predicted. The walls and the solid were assumed to be isotropic and homogeneous. In their study, D. Krzikalla et al. [18] considered identical properties for the walls and the solid parts, and assumed onyx as an isotropic material. When the specimen is reinforced with long fibres, a laminated shell or 3D homogeneous composite strategy can be used for the numerical simulation, as used in Refs. [18,28]. The elastic parameters used for the simulation are shown in Table 2, and Poisson's ratio (with a value of 0.3) was obtained from the literature [28].
Table 2.
Average mechanical properties of walls and infill pattern.
| test sample | E (MPa) | Re (MPa) |
|---|---|---|
| Walls | 5530 | 54 |
| Filling pattern | 1660 | 23 |
The plasticity curve used for the simulation was obtained by extracting the plastic domain from the experimental curve using a parameter identification with the Hollomon law. C3D8R finite elements were used.
3. Results and discussion
3.1. Tensile test results
The mechanical properties of the specimens were determined by means of a uniaxial tensile test. This section presents the results of the tensile test for the pure solid pattern, pure walls, and specimens with varying numbers of walls. The mechanical properties evaluated are mainly Young's modulus (E) and yield strength (Re). The specimens typically broke in the useful length, often in the center of the specimen between the gauge length of the extensometer, as illustrated in Fig. 5. This confirms that the dimensions and shape of the specimens were suitable for testing.
Fig. 5.
Tensile test and breaking zone of the specimens.
3.1.1. Mechanical properties of the walls and the solid
The results presented in Table 2 indicate that the walls have a 70% higher Young's modulus than the solid pattern. Regarding yield strength, the walls are 57% stronger than the solid pattern. This is partly due to the 3D printing process used by the X7 printer, which prints the walls and the interior of the parts (solid) differently. The walls are printed in the direction of the tensile load, while the solid is printed by successive layers at ± 45° to this load direction. Additionally, the onyx used in the printing process is pre-filled with 40% micro carbon fibres, resulting in a different mechanical response between the walls and the solid. The mechanical behaviour of the assembly (walls and solid) can be likened to a composite material, with the walls representing layers at 0° and the solid representing layers at ± 45°. Previous studies have shown that the mechanical properties of 0° oriented layers in composite materials are higher than those of differently oriented layers [29]. Short fibre reinforced plastics also exhibit different mechanical behaviours depending on the orientation angle of the layers [30]. The results also indicate that the walls elongate less than the solid, with up to 50% less elongation being observed. This is due to the more ductile nature of the solid compared to the walls. In comparison to classical composites, the layers oriented at ± 45° exhibit a more ductile behaviour than the layers oriented at 0°, which generally have a brittle behaviour.
The stress-strain curves of the walls and the solid obtained from the tensile test are shown in Fig. 6. The curves exhibit good repeatability of the tests. The values shown in Table 2 are the average values of Young's modulus (E) and yield strength (Re) of the curves.
Fig. 6.
Stress-strain curves for walls and solid pattern.
3.1.2. Influence of walls’ number on the mechanical properties
Specimens with varying numbers of walls (1, 2, 4, 8, 10 walls) were printed and analyzed to determine their influence on mechanical properties. Three tests were performed on each specimen, and the average properties were recorded. Table 3 presents the average Young's modulus and yield strength for each sample, while Fig. 7 shows the stress-strain curves of the tensile test.
Table 3.
Average mechanical properties according to the number of walls.
| Number of walls | E (MPa) | Re (MPa) |
|---|---|---|
| 0 | 1660 | 23 |
| 1 | 1816 | 22 |
| 2 | 2429 | 32 |
| 4 | 2661 | 31 |
| 8 | 3971 | 44 |
| 10 | 4515 | 48 |
Fig. 7.
Stress-strain curves of specimens (0–10 walls).
The results indicate that mechanical properties increase as the number of walls increases. For instance, the Young's modulus of the 10-wall specimen is 1.85 times greater than that of the 2-wall specimen. Similarly, the 10-wall specimen is 1.5 times stronger than the 2-wall specimen. Notably, the 10-wall specimen contains 67% walls and 33% solid by volume, while the 2-wall specimen contains 13% walls and 87% solid by volume. This confirms that mechanical properties increase with an increase in the volume of walls. However, a previous study by A. Gebisa et al. [16] on the tensile properties of ULTEM 9085 showed that the number of walls had low influence on the mechanical properties compared to other printing parameters, such as the raster angle, the raster width, and the air gap. The same parameters were studied in the bending test by the same authors, who also concluded that walls have less influence [17]. However, their work has shown that the mechanical properties of a 1-wall and a 5-wall specimen increase slightly. Recent work by Y. Liu [19] also confirmed that the wall layers positively influence the mechanical properties of onyx parts.
The increase in mechanical properties of the samples in this work can be compared to the increase in mechanical properties of a composite material. Typically, when the number of fibre layers or the volume of fibres increases, there is a corresponding increase in the mechanical properties of the composite. In our case, the walls represent the fibres and the solid pattern represents the matrix of the composite. Thus, an increase in the number of walls would lead to an increase in the mechanical properties.
Fig. 7 shows that the elongation of the specimens decreases as the number of walls increases. For example, the 10-wall specimen has less than 10% deformation, while the 2-wall specimen reaches 22% deformation. Due to the low ductility of the walls compared to the solid, the ductility of the specimens decreases as the number of walls increases. Comparing the mechanical properties of the onyx material provided by the manufacturer, our two-walled sample has the same Young's modulus values but a different yield strength (Re = 32 MPa in the present work versus Re = 40 MPa provided by Markforged).
3.2. Predicted results by ROM
The results obtained using equations (Eq. 7), (Eq. 8)) of the mixture rule (ROM) are reported in Table 4. The prediction errors produced by the ROM on the Young's modulus are shown in Fig. 8.
Table 4.
Comparison between experimental results and ROM results (*** are not tested).
| Number of walls | E ROM (MPa) | E Test (MPa) | Re ROM (MPa) | Re Test (MPa) |
|---|---|---|---|---|
| 0 | 1660 | 1660 | 23 | 23 |
| 1 | 1918 | 1816 | 25 | 22 |
| 2 | 2176 | 2429 | 27 | 32 |
| 3 | 2434 | *** | 29 | *** |
| 4 | 2692 | 2661 | 31 | 31 |
| 5 | 2950 | *** | 33 | *** |
| 6 | 3208 | *** | 35 | *** |
| 7 | 3466 | *** | 37 | *** |
| 8 | 3724 | 3971 | 39 | 44 |
| 9 | 3982 | *** | 42 | *** |
| 10 | 4240 | 4515 | 44 | 48 |
Fig. 8.
Prediction error between ROM and tensile test for Young's modulus.
The prediction error for the Young's modulus value ranges between 1% and 10%, while for the yield strength, the prediction error is between 1% and 15%. These prediction errors generated by ROM are considered acceptable compared to other studies where ROM was used to predict the mechanical properties of long fibre composites. For instance, A. Avanzini et al. [10] observed an error of 3% in their work on carbon fibre reinforced onyx. In contrast, J. Narajo-Lozada [25] reported a much higher prediction error of up to 60% when the volume fraction of fibres was higher than 11%.
In this study, the prediction errors do not exceed 15%, despite the high volume fraction of the walls. The observed prediction errors in ROM can be explained by the fact that the samples are not actual composite materials, and also by the fact that porosities were not considered. The orientation of samples on the printing bed and the type of pattern (triangular, hexagonal, or rectangular pattern) were not considered in this study; only the flat orientation of the samples and the solid pattern were studied.
3.3. Simulation results
In order to simulate the model, fixed boundary conditions and linear displacement speed (Fig. 9) were applied to the specimen. The post-processing was performed by recovering the reaction forces and the displacement of two nodes at an initial distance of 12.5 mm corresponding to the initial length of the extensometer. The calculation of nominal stresses and strains uses Eq. (9) and Eq. (10) expressions.
| (Eq. 9) |
| (Eq.10) |
with F: force (N), Ao: cross-sectional area of a specimen (mm2), L: instantaneous length of the extensometer and Lo: its initial length, which is 12.5 mm.
Fig. 9.
Modelling and simulation of a 4-wall specimen tensile test (velocity applied = 0.167 mm/s).
To validate the numerical model, three simulation steps are required:
-
•
First step: Simulating the behaviour of walls alone. This step involves simulating the behaviour of walls alone and verifying that there is a correlation between the numerical and experimental results. The numerical model comprises 5427 elements with an approximate size of 0.5 mm per element.
-
•
Second step: Simulating the infill pattern alone (solid infill). This step verifies the correlation between the simulation and the experimental test. The model comprises 32562 elements with a 0.5 mm size per element. Fig. 11 shows the simulation results for the first two steps.
-
•
Third step: Simulating a 4-wall part. A sample containing four walls (total thickness 1.6 mm x 2) is used. The approach is to divide the specimen into two parts, one representing the walls and the other representing the pattern. Each part is then associated with the corresponding material properties (Fig. 9). The connection between the walls and the filling pattern is considered perfect, which allows the generation of a continuous mesh between the walls and the pattern. A convergence study was conducted to obtain an optimal element size to eliminate the influence of element size on the numerical results.
Fig. 11.
Simulation results. a) Comparison of the experimental and numerical stress-strain curve of a 4-wall layer specimen, b) stress-strain field of the 4-wall layer specimen, c) strain fields of the infill and walls, and d) stress fields of the infill and walls.
The final model comprises 46800 elements with an approximate size of 0.5 mm per element. Fig. 10 shows the results of the simulation of walls and solid pattern (1st step and 2nd step), and Fig. 11 shows the results of the simulation of the 4-wall specimen.
Fig. 10.
Simulation results of the pattern and walls: Comparison of experimental and numerical behaviour curves of the walls and the solid pattern.
We observe a good correlation between the experimental curves and the numerical curves of walls and solid parts. This allows us to validate the numerical models of the walls and the solid. The third step (4-wall specimen simulation) of the simulation can now be performed. The results (shown in Fig. 11a) demonstrate good agreement between the experimental and numerical curves. The stress and strain fields of the specimen, the walls, and the solid are homogeneous (as seen in Fig. 11b and c), which confirms that the simulation was well-parameterised. The maximum observed Von Mises stress value of 92 MPa is located in the walls; in the infill pattern, the maximum stress is 42 MPa (Fig. 11d). The proper superposition of the two curves makes it possible to exploit the elastic domain of the numerical curve to determine the equivalent Young's modulus of the specimen. The numerical yield strength can also be calculated from this numerical curve. A comparison between the numerical, experimental, and ROM values is presented in Table 5.
Table 5.
Comparison of elastic properties.
| Experimental | R.O.M | Simulation | |
|---|---|---|---|
| Young modulus (MPa) | 2661 | 2692 | 2630 |
| Yield strength (MPa) | 31 | 31 | 32 |
The assumption of a perfect bond between the walls and the infill pattern may not be valid due to the gap observed between the experimental and numerical curves in the plastic range (from 4% strain). For large plastic deformations, there must be a phenomenon of non-adhesion between the walls and the infill, which causes the experimental stresses of the specimen to drop. A difference in the hardness of the walls and the infill can explain this gap.
The results demonstrate that the Young's modulus obtained using the three methods is very similar. This validates the method based on the rule of mixtures and the one based on a numerical simulation. These findings also confirm that the idea of defining a specimen numerically and separately with mechanical properties obtained by the tensile test on the walls and the infill pattern is fully justified. This approach provides a new tool to consider the effect of the number of walls on the mechanical elastic properties of 3D printed parts. This tool is valuable for designing printed parts because it enables engineers to determine how many walls are required to meet the mechanical requirements of the part before printing.
3.4. Application to a structural part
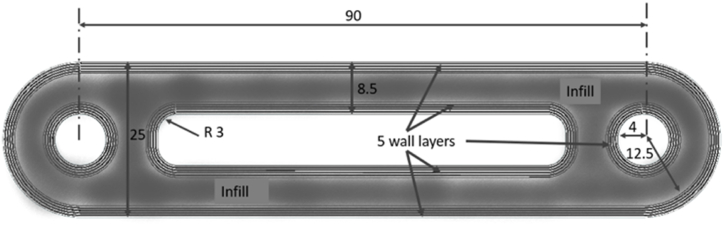
The developed method (ROM and simulation) was applied to a connecting rod subjected to mechanical tensile stress to predict its mechanical behaviour. The objective is to compare the mechanical properties, particularly Young's modulus and yield stress, obtained from an experimental tensile test with the results obtained from a numerical simulation and analytical calculation based on the ROM. The printing parameters for the rod are a layer thickness of 0.1 mm, a solid infill pattern, and five layers of walls, with the dimensions and printing parameters given in Fig. 12.
Fig. 12.
Connecting rod dimensions and printing parameters (dimension units: mm). The printing is done with a layer thickness of 0.1 mm, a solid filling pattern, 5 walls, and a total height of the printed connecting rod of 5 mm.
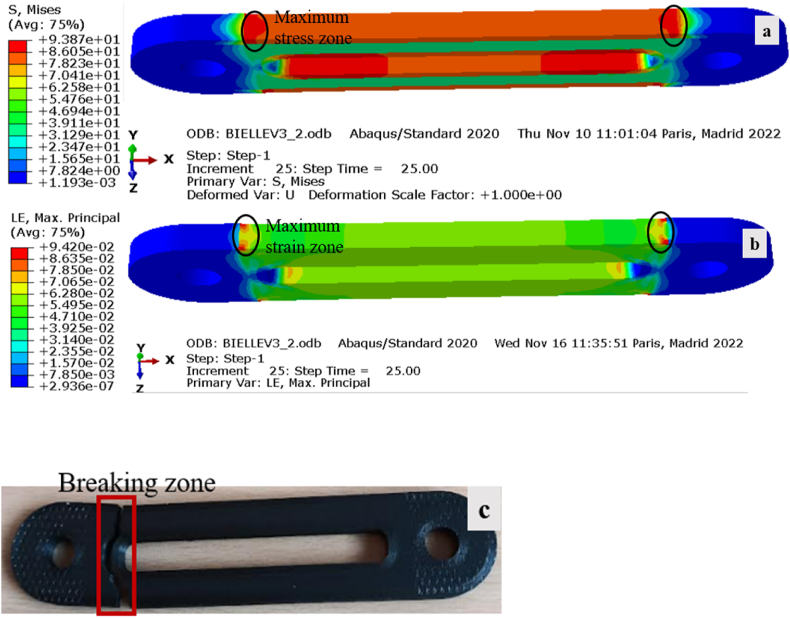
The simulation results (Fig. 13a and b) show that the walls' maximum stress level is 93 MPa. The experimental failure zone observed after the test corresponds to the level of maximum stress and maximum strain (Fig. 13c).
Fig. 13.
Results of the simulation and physical test of the connecting rod: a) Von Mises stress, b) strain, c) physical test of connecting rod with failure zone.
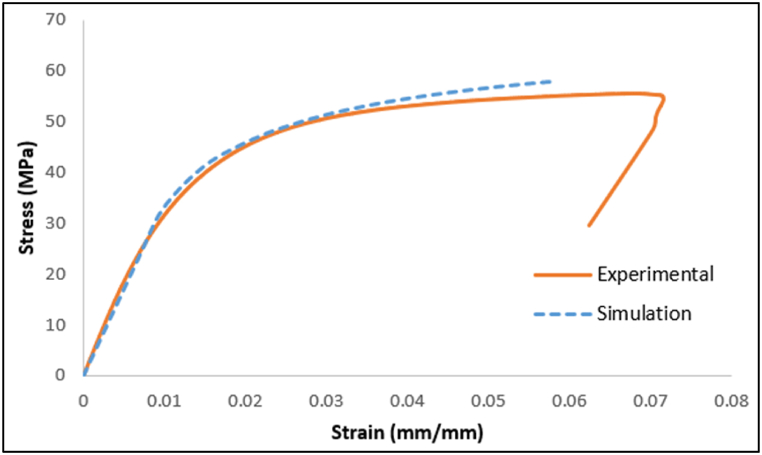
The stress-strain curve of the connecting rod obtained from the simulation and the experimental test is plotted in Fig. 14. Both curves show good correlation in the elastic part. However, a gap in the plastic domain is observed between the two curves after 3% deformation, as previously observed on the tensile test specimen. The elastic properties, namely Young's modulus and yield stress, were calculated by utilizing the elastic range of the numerical simulation curve. An analytical calculation based on the rule of mixtures of Young's modulus and yield strength was also performed. All the results are presented in Table 6. The error on Young's modulus between the test and the analytical calculation is around 10%, 12% with the numerical simulation, and there is a 2% error between the simulation and the analytical calculation.
Fig. 14.
Comparison of experimental and numerical behaviour of connecting rod.
Table 6.
Comparison of elastic properties.
| Experimental | R.O.M | Numerical | |
|---|---|---|---|
| Young's modulus (MPa) | 3865 | 3481 | 3402 |
| Yield strength (MPa) | 40 | 37 | 39 |
The results demonstrate the effectiveness of both the rule of mixtures and numerical simulation methods in predicting the mechanical behavior of 3D printed parts based on the number of walls. This allows for the optimization of the number of walls in the printing parameters when designing a structural part subjected to tensile stresses. The finite element method provides information on the overall stress distribution in the part, including identifying the potential failure zone. For a quick preliminary calculation, the rule of mixtures method is a useful tool for calculating the mechanical elastic properties.
4. Conclusion and perspectives
The aim of this study was to predict the mechanical properties of specimens under tension as a function of the number of walls and the infill pattern. An experimental approach was used to characterise the properties of the walls and the infill pattern separately. The method involved precisely cutting the walls and the infill pattern to characterise them individually. The study showed that the walls have a significant influence on the mechanical properties of the parts. Specimens with a higher number of walls were found to be the most rigid and mechanically strongest. Between a specimen with 1 wall and a specimen with 10 walls, there was up to a 60% increase in Young's modulus. However, the global strain of the specimens decreased as the number of walls increased, with a 70% reduction in deformation between a 1-wall layer specimen and a 10-wall layer specimen.
After characterising the individual walls and the infill pattern, a mixture law was implemented to predict the mechanical properties of the specimens as a function of the number of walls they contain. The results showed consistency between the predicted Young's modulus and that obtained by the experimental tensile test, with only small deviations observed in yield stress predicted by the rule of mixtures.
Finite element simulation was also used to determine the Young's modulus and equivalent yield strength of a 4-wall layer specimen, and the results were consistent with the experimental results. The methods were validated through the mechanical design of a structural part (a connecting rod), with coherence observed between the different results. This validated the possibility of designing parts with an optimum number of walls on the X7 printer in onyx material.
In the future, the porosity should be considered through tomographic analysis and scanning electron microscopy to improve the accuracy of the numerical model. The connection between walls and a filling pattern through experimental characterisation should also be considered to improve the numerical model's realism and efficiency, such as the use of cohesive elements in Abaqus in the plastic part. It should be noted that the numerical simulation overestimates a large part of the plastic domain compared to experimental tests.
Furthermore, integrating positioning parameters (such as lateral and vertical positioning of the parts on the printing bed), using other printing patterns, and adding fibres would be crucial for a more comprehensive and powerful prediction tool.
Funding
This study was not funded by any structure or organization.
Data availability statement
Data will be made available on request.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Author's contribution statement
Daouda Nikiema: Conceived and designed the experiments; performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Ndèye Awa Sène: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Pascale Balland, Alain Sergent: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Surya Teja R., Lokesh M., Deepak Kumar S., Ramana Rao P.S.V. 3D printing of complex structures: case study of Eiffel tower. Mater. Today Proc. 2022 doi: 10.1016/j.matpr.2022.12.037. [DOI] [Google Scholar]
- 2.Winarso R., Anggoro P.W., Ismail R., Jamari J., Bayuseno A.P. Application of fused deposition modeling (FDM) on bone scaffold manufacturing process: a review. Heliyon. 2022;8 doi: 10.1016/j.heliyon.2022.e11701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Siripongpreda T., Hoven V.P., Narupai B., Rodthongku N. Emerging 3D printing based on polymers and nanomaterial additives: enhancement of properties and potential applications. Eur. Polym. J. 2023;184 doi: 10.1016/j.eurpolymj.2022.111806. [DOI] [Google Scholar]
- 4.Seibold M. Additive manufacturing for serial production of high-performance metal parts. Mech. Eng. 2019;141:49–50. doi: 10.1115/1.2019-MAY5. [DOI] [Google Scholar]
- 5.Vaneker T., Bernard A., Moroni G., Gibson I., Zhang Y. Design for additive manufacturing: framework and methodology. CIRP Ann. 2020;69:578–599. doi: 10.1016/j.cirp.2020.05.006. [DOI] [Google Scholar]
- 6.Popescu D., Zapciu A., Amza C., Baciu F., Marinescu R. FDM process parameters influence over the mechanical properties of polymer specimens: a review. Polym. Test. 2018;69:157–166. doi: 10.1016/j.polymertesting.2018.05.020. [DOI] [Google Scholar]
- 7.Ramalingam P.S., Mayandi K., Balasubramanian V., Chandrasekar K., Stalany V.M., Munaf A.A. Effect of 3D printing process parameters on the impact strength of onyx – glass fiber reinforced composites. Mater. Today Proc. 2020;45:6154–6159. doi: 10.1016/j.matpr.2020.10.467. [DOI] [Google Scholar]
- 8.Zhang Y., Choi J.P., Moon S.K. Effect of geometry on the mechanical response of additively manufactured polymer. Polym. Test. 2021;100 doi: 10.1016/j.polymertesting.2021.107245. [DOI] [Google Scholar]
- 9.Polyzos E., Van Hemelrijck D., Pyl L. Numerical modelling of the elastic properties of 3D-printed specimens of thermoplastic matrix reinforced with continuous fibres. Compos. Part B Eng. 2021;211 doi: 10.1016/j.compositesb.2021.108671. [DOI] [Google Scholar]
- 10.Avanzini A., Battini D., Giorleo L. Finite element modelling of 3D printed continuous carbon fiber composites: embedded elements technique and experimental validation. Compos. Struct. 2022;292 doi: 10.1016/j.compstruct.2022.115631. [DOI] [Google Scholar]
- 11.Zou R., Xia Y., Liu S., Hu P., Hou W., Hu Q., Shan C. Isotropic and anisotropic elasticity and yielding of 3D printed material. Compos. Part B Eng. 2016;99:506–513. doi: 10.1016/j.compositesb.2016.06.009. [DOI] [Google Scholar]
- 12.Chacón J.M., Caminero M.A., García-Plaza E., Núñez P.J. Additive manufacturing of PLA structures using fused deposition modelling: effect of process parameters on mechanical properties and their optimal selection. Mater. Des. 2017;124:143–157. doi: 10.1016/j.matdes.2017.03.065. [DOI] [Google Scholar]
- 13.Somireddy M., Czekanski A. Anisotropic material behavior of 3D printed composite structures – material extrusion additive manufacturing. Mater. Des. 2020;195 doi: 10.1016/j.matdes.2020.108953. [DOI] [Google Scholar]
- 14.Sahoo S., Sutar H., Senapati P., Shankar Mohanto B., Ranjan Dhal P., Kumar Baral S. Experimental investigation and optimization of the FDM process using PLA. Mater. Today Proc. 2022;74:843–847. doi: 10.1016/j.matpr.2022.11.208. [DOI] [Google Scholar]
- 15.Mangla S.K., Kazancoglu Y., Sezer M.D., Top N., Sahin I. Optimizing fused deposition modelling parameters based on the design for additive manufacturing to enhance product sustainability. Comput. Ind. 2023;145 doi: 10.1016/j.compind.2022.103833. [DOI] [Google Scholar]
- 16.Zanin A. ScienceDirect ScienceDirect ScienceDirect influence of 3D printing FDM process parameters on tensile property of ULTEM influence of 3D printing FDM process 9085 parameters on tensile property of ULTEM costing models for capacity optimization in industry 4. Procedia Manuf. 2019;30:331–338. doi: 10.1016/j.promfg.2019.02.047. [DOI] [Google Scholar]
- 17.Gebisa A.W., Lemu H.G. 2018. Investigating Effects of Fused-Deposition Modeling (FDM) Processing Parameters on Flexural Properties of ULTEM 9085 Using Designed Experiment; pp. 1–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Krzikalla D., Měsíček J., Halama R., Hajnyš J., Pagáč M., Čegan T., Petrů J. On flexural properties of additive manufactured composites: experimental, and numerical study. Compos. Sci. Technol. 2022;218 doi: 10.1016/j.compscitech.2021.109182. [DOI] [Google Scholar]
- 19.Liu Y., Jiang W., Hu W., Ren L., Deng E., Wang Y., Song C., Feng Q. Compressive strength and energy absorption characteristics of the negative stiffness honeycomb cell structure. Mater. Today Commun. 2023;35 doi: 10.1016/j.mtcomm.2023.105498. [DOI] [Google Scholar]
- 20.Bárnik F., Vaško M., Handrik M., Dorčiak F., Majko J. Comparing mechanical properties of composites structures on Onyx base with different density and shape of fill. Transport. Res. Procedia. 2019;40:616–622. doi: 10.1016/j.trpro.2019.07.088. [DOI] [Google Scholar]
- 21.Fernandes R.R., Tamijani A.Y., Al-Haik M. Mechanical characterization of additively manufactured fiber-reinforced composites. Aero. Sci. Technol. 2021;113 doi: 10.1016/j.ast.2021.106653. [DOI] [Google Scholar]
- 22.Prajapati A.R., Dave H.K., Raval H.K. Effect of fiber reinforcement on the open hole tensile strength of 3D printed composites. Mater. Today Proc. 2021;46:8629–8633. doi: 10.1016/j.matpr.2021.03.597. [DOI] [Google Scholar]
- 23.Saeed K., McIlhagger A., Harkin-Jones E., McGarrigle C., Dixon D., Ali Shar M., McMillan A., Archer E. Characterization of continuous carbon fibre reinforced 3D printed polymer composites with varying fibre volume fractions. Compos. Struct. 2022;282 doi: 10.1016/j.compstruct.2021.115033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hasanov S., Gupta A., Nasirov A., Fidan I. Mechanical characterization of functionally graded materials produced by the fused filament fabrication process. J. Manuf. Process. 2020;58:923–935. doi: 10.1016/j.jmapro.2020.09.011. [DOI] [Google Scholar]
- 25.Naranjo-Lozada J., Ahuett-Garza H., Orta-Castañón P., Verbeeten W.M.H., Sáiz-González D. Tensile properties and failure behavior of chopped and continuous carbon fiber composites produced by additive manufacturing. Addit. Manuf. 2019;26:227–241. doi: 10.1016/j.addma.2018.12.020. [DOI] [Google Scholar]
- 26.Fu S.Y., Lauke B., Mäder E., Yue C.Y., Hu X. Tensile properties of short-glass-fiber- and short-carbon-fiber-reinforced polypropylene composites. Compos. Part A Appl. Sci. Manuf. 2000;31:1117–1125. doi: 10.1016/S1359-835X(00)00068-3. [DOI] [Google Scholar]
- 27.Heidari-Rarani M., Rafiee-Afarani M., Zahedi A.M. Mechanical characterization of FDM 3D printing of continuous carbon fiber reinforced PLA composites. Compos. Part B Eng. 2019;175 doi: 10.1016/j.compositesb.2019.107147. [DOI] [Google Scholar]
- 28.Galati M., Viccica M., Minetola P. A finite element approach for the prediction of the mechanical behaviour of layered composites produced by Continuous Filament Fabrication (CFF) Polym. Test. 2021;98 doi: 10.1016/j.polymertesting.2021.107181. [DOI] [Google Scholar]
- 29.Galati M., Viccica M., Minetola P. A finite element approach for the prediction of the mechanical behaviour of layered composites produced by Continuous Filament Fabrication (CFF) Polym. Test. 2021;98 doi: 10.1016/j.polymertesting.2021.107181. [DOI] [Google Scholar]
- 30.Bhandari S., Lopez-Anido R.A., Wang L., Gardner D.J. Elasto-plastic finite element modeling of short carbon fiber reinforced 3D printed acrylonitrile butadiene styrene composites. Jom. 2020;72:475–484. doi: 10.1007/s11837-019-03895-w. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.