Abstract
A problem in spatial transcriptomics is detecting differentially expressed (DE) genes within cell types across tissue context. Challenges to learning DE include changing cell type composition across space and measurement pixels detecting transcripts from multiple cell types. Here, we introduce a statistical method, Cell type-Specific Inference of Differential Expression (C-SIDE), that identifies cell type-specific DE in spatial transcriptomics, accounting for localization of other cell types. We model gene expression as an additive mixture across cell types of log-linear cell type-specific expression functions. C-SIDE’s framework applies to many contexts: DE due to pathology, anatomical regions, cell-to-cell interactions, and cellular microenvironment. Furthermore, C-SIDE enables statistical inference across multiple /replicates. Simulations and validation experiments on Slide-seq, MERFISH, and Visium datasets demonstrate that C-SIDE accurately identifies DE with valid uncertainty quantification. Lastly, we apply C-SIDE to identify plaque-dependent immune activity in Alzheimer’s disease and cellular interactions between tumor and immune cells. We distribute C-SIDE within the R package https://github.com/dmcable/spacexr.
Introduction
Spatial transcriptomics technologies profile gene expression in parallel across hundreds or thousands of genes across spatial measurement units, or pixels [1-7]. These technologies have the potential to associate gene expression with cellular contexts such as spatial position, proximity to pathology, or cell-to-cell interactions. Studying gene expression changes, termed differential expression (DE), within tissue context has the potential to provide insight into principles of organization of complex tissues and disorganization in disease and pathology [1,8,9].
Current methods for addressing DE in spatial transcriptomics fall into two categories: nonparametric and parametric methods. Nonparametric DE methods [10-12] do not use constrained hypotheses about gene expression patterns, but rather fit general smooth spatial patterns of gene expression. Some of these approaches do not take cell types into account [10], while others operate on individual cell types [12]. Discovering non-parametric differential gene expression can be advantageous to generate diverse exploratory hypotheses. However, if covariates are available, for example, predefined anatomical regions, parametric approaches increase statistical power substantially and provide directly interpretable parameter estimates. Specific DE problems have been addressed with ad-hoc solutions such as detecting gene expression dependent on cell-to-cell colocalization [13] or anatomical regions [14], but no general parametric framework is currently available. In contrast, general parametric frameworks have been widely applied across bulk and single-cell RNA-sequencing (scRNA-seq) to test for differences in gene expression across cell type, disease state, and developmental state, among other problems [15,16]. Furthermore, although multi-sample, multi-replicate differential expression methods exist for bulk and single-cell RNA-seq [15,16], no statistical framework accounting for technical and biological variation [17] across samples and replicates has been established for the spatial setting. We refer to samples as spatial transcriptomics experiments that differ in biological conditions (e.g. different biological individuals or conditions), whereas replicates are used to describe repeat experiments across identical conditions and biological samples.
An important challenge unaddressed by current spatial transcriptomics DE methods is accounting for observations generated from cell type mixtures. In particular, sequencing-based, RNA-capture spatial transcriptomics technologies, such as Visium [5], GeoMx [6], and Slide-seq [1,2], can capture multiple cell types on individual measurement pixels. The presence of cell type mixtures complicates the estimation of cell type-specific differential expression (i.e. DE within a cell type of interest) because different cell types have different gene expression profiles, independent of spatial location [18,19]. Although imaging-based spatial transcriptomics technologies, such as MERFISH [3], ExSeq [7], and STARmap [4], have the potential to achieve single cell resolution, these technologies may encounter mixing across cell types due to diffusion or imperfect cellular segmentation [20]. Several methods [18,21-23] have been developed to identify cell type proportions in spatial transcriptomics datasets. However, at present no method accounts for cell type proportions in DE analysis. Here, we demonstrate how not accounting for cell type proportions leads to biased estimates of differential gene expression due to cell type proportion changes or contamination from other cell types.
In this work we introduce Cell type-Specific Inference of Differential Expression (C-SIDE), a general parametric statistical method that estimates cell type-specific DE in the context of cell type mixtures. The first step is to estimate cell type proportions on each pixel using a cell type-annotated single-cell RNA-seq (scRNA-seq) reference [18]. Next, we fit a parametric model, using predefined covariates such as spatial location or cellular microenvironment, that accounts for cell type differences to obtain cell type-specific DE estimates and corresponding standard errors. The model accounts for sampling noise, gene-specific overdispersion, multiple hypothesis testing, and platform effects between the scRNA-seq reference and the spatial data. Furthermore, the C-SIDE model permits statistical inference across multiple experimental samples and/or replicates to achieve more stable estimates of population-level differential gene expression.
Using simulated and real spatial transcriptomics data, we show C-SIDE accurately estimates cell type-specific differential expression while controlling for changes in cell type proportions and contamination from other cell types. We also demonstrate how cell type mixture modelling increases power, especially when single cell type measurements are rare. Furthermore, on Slide-seq, MERFISH, and Visium datasets, we demonstrate how C-SIDE’s general parametric framework enables testing differential gene expression for diverse hypotheses including spatial position or anatomical regions [24], cell-to-cell interactions, cellular environment, or proximity to pathology. By associating gene expression changes with particular cell types, we use C-SIDE to systematically link gene expression changes to cellular context in pathological tissues such as Alzheimer’s disease and cancer.
Results
C-SIDE learns cell type-specific DE in spatial transcriptomics
Here, we develop Cell type-Specific Inference of Differential Expression (C-SIDE), a statistical method for determining differential expression (DE) in spatial transcriptomics datasets (Figure 1a). C-SIDE inputs one or more experimental samples of spatial transcriptomics data, consisting of as the observed RNA counts for pixel , gene , and experimental sample . We then assume Poisson sampling so that,
| (1) |
with the expected count and the total transcript count (e.g. total UMIs) for pixel on experimental sample . Accounting for platform effects and other sources of technical and natural variability, we assume is a mixture of cell type expression profiles, defined by,
| (2) |
with the cell type-specific expected gene expression rate for pixel , gene , experimental sample , and cell type ; the proportion of cell type contained in pixel for experimental sample ; a gene-specific random effect that accounts for platform variability; and a random effect to account for gene-specific overdispersion.
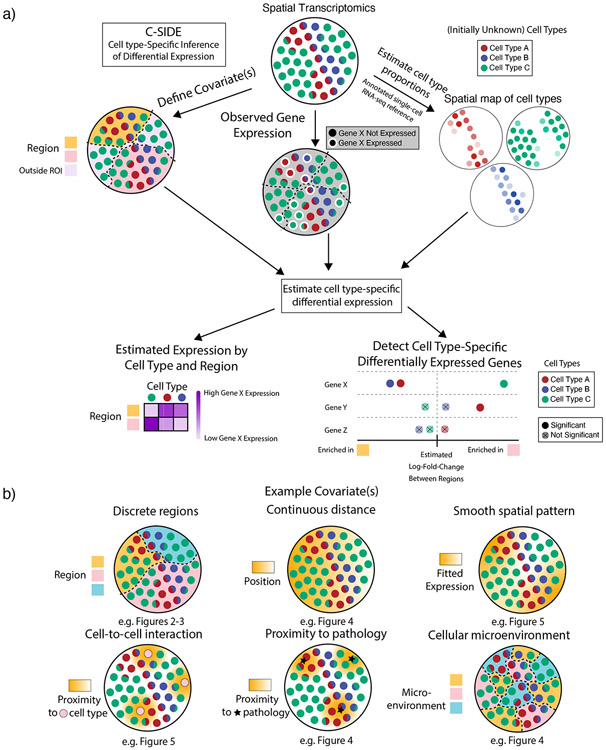
Figure 1:
Cell type-Specific Inference of Differential Expression learns cell type-specific differential expression from spatial transcriptomics data.
(a) Schematic of the C-SIDE Method. Top: C-SIDE inputs: a spatial transcriptomics dataset with observed gene expression (potentially containing cell type mixtures) and a covariate for differential expression. Middle: C-SIDE first assigns cell types to the spatial transcriptomics dataset, and covariates are defined. Bottom: C-SIDE estimates cell type-specific gene expression along the covariate axes.
(b) Example covariates for explaining differential expression with C-SIDE. Top: Segmentation into multiple regions, continuous distance from some feature, or general smooth patterns (nonparametric). Bottom: density of interaction with another cell type or pathological feature or a discrete covariate representing the cellular microenvironment.
To account for cell type-specific DE, we model across pixel locations the log of the cell type-specific profiles as a linear combination of covariates used to explain differential expression. Specifically, we assume that,
| (3) |
Here, represents the intercept term for gene and cell type in sample , and represents the ’th covariate, evaluated at pixel in sample . Similarly as in linear and generalized linear models [25], , also called the design matrix, represents predefined covariate(s) that explain DE, and the corresponding coefficient(s) each represent the DE effect size of covariate for gene in cell type for sample .
With this general framework we can describe any type of DE that can be parameterized with a log-linear model. Examples include (Figure 1b):
Differential expression between multiple regions. In this case, the tissue is manually segmented into multiple regions (e.g. nodular and anterior cerebellum, Figure 3). Design matrix contains discrete categorical indicator variables representing membership in 2 or greater regions.
Differential expression due to cellular environment or state (a special case of (1). Pixels are discretely classified into local environments based on the surrounding cells (e.g. stages in the testes Slide-seq dataset, Figure 4).
Differential expression as a function of distance to a specific anatomical feature. In this case, is defined as the spatial position or distance to some feature (e.g. distance to midline in the hypothalamus MERFISH dataset, Figure 4).
Cell-to-cell interactions. In this case, we define a cell-to-cell interaction as DE within one cell type due to co-localization with a second cell type (e.g. immune cell density in cancer, Figure 6). For this problem, is the continuous density of cell type .
Proximity to pathology. Similar to (4), except covariate represents density of a pathological feature (e.g. Alzheimer’s Αβ plaque, Figure 4), rather than cell type density.
General spatial patterns (termed nonparametric). In this case, we define design matrix to be smooth basis functions [26], where linear combinations of these basis functions represent the overall smooth gene expression function and can accommodate any smooth spatial pattern.
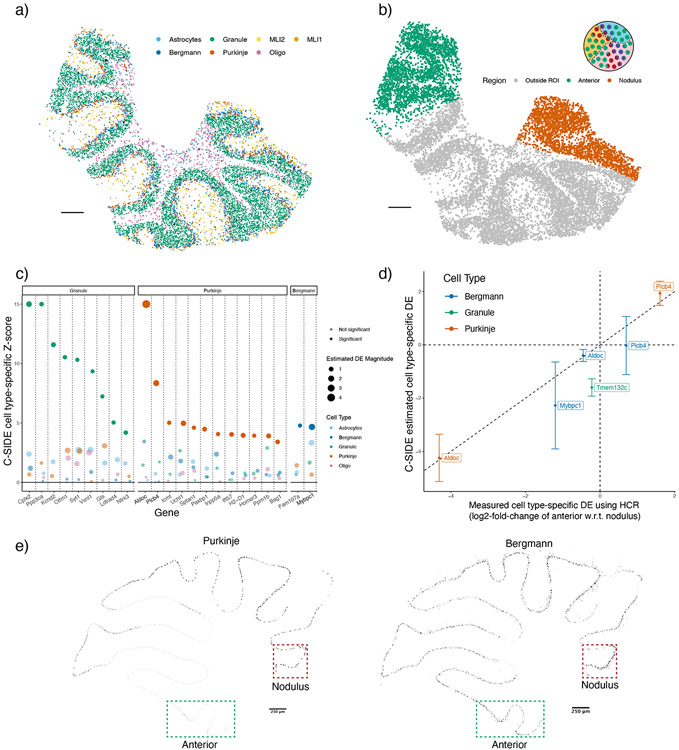
Figure 3:
C-SIDE’s estimated cell type-specific differential expression is validated by HCR-FISH. C-SIDE ran on (n = 3) replicates of cerebellum Slide-seq data.
(a) C-SIDE’s spatial map of cell type assignments. Out of 19 cell types, the seven most common appear in the legend. Reproduced from [18]. Three total replicates were used to fit C-SIDE.
(b) Covariate used for C-SIDE, representing the anterior lobule region (green) and nodulus (red). Schematic refers to the C-SIDE problem type outlined in Figure 1b.
(c) C-SIDE Z-score for testing for DE for each gene and for each cell type. Genes are grouped by cell type with maximum estimated DE, and estimated DE magnitude appears as size of the points. Bold genes appear below in HCR validation.
(d) Scatterplot of C-SIDE DE estimates vs. HCR measurements for cell type-specific log2 differential expression. Positive values indicate gene expression enrichment in the anterior region. Error bars represent C-SIDE confidence intervals for predicted DE on a new biological replicate. A dotted identity line is shown, and cell types are colored.
(e) HCR images of Aldoc continuous gene expression. Only pixels with high cell type marker measurements for Purkinje (left) and Bergmann (right) are shown. Regions of interest (ROIs) of nodulus and anterior regions are outlined in green and red, respectively.
All scale bars 250 microns.
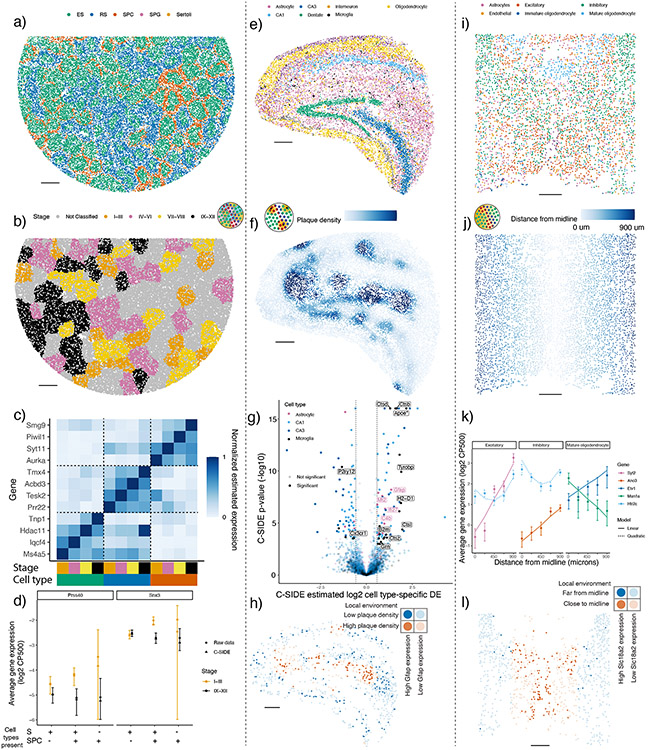
Figure 4:
C-SIDE discovers cell type-specific DE in a diverse set of problems on testes, Alzheimer’s hippocampus, and hypothalamus datasets.
All panels: results of C-SIDE on the Slide-seqV2 testes (left column), MERFISH hypothalamus (middle column), and Slide-seqV2 Alzheimer’s hippocampus (right column). Schematics in b,f,j reference C-SIDE problem types (Figure 1b).
(a) C-SIDE’s spatial map of cell type assignments in testes. All cell types are shown with most common in legend.
(b) Covariate used for C-SIDE in testes: four discrete tubule stages.
(c) Cell type and tubule stage-specific genes identified by C-SIDE. C-SIDE estimated expression is standardized between 0 and 1 for each gene. Columns represent C-SIDE estimates for each cell type and tubule stage.
(d) Log2 average expression (in counts per 500 (CP500)) of pixels grouped based on tubule stage and presence or absence of spermatid (S) cell types (defined as elongating spermatid (ES) or round spermatid (RS)) and/or spermatocyte (SPC) cell type. Circles represent raw data averages while triangles represent C-SIDE predictions, and error bars around circular points represent ± 1.96 s.d. (37 ≤ n ≤ 2236 pixels per group, Supplementary Notes). Genes Prss40 and Snx3 are shown on left and right, respectively.
(e) Same as (a) for Alzheimer’s hippocampus (n = 4 replicates).
(f) Covariate used for C-SIDE in Alzheimer’s hippocampus: continuous density of Aβ plaque.
(g) Volcano plot of C-SIDE DE results in log2-space, with positive values corresponding to plaque-upregulated genes. Color represents cell type, and a subset of significant genes are labeled. Dotted lines represents 1.5x fold-change cutoff used for C-SIDE.
(h) Spatial visualization of Gfap, identified by C-SIDE as DE in astrocytes. Red/blue represents high/low plaque density areas, respectively. Bold points represent astrocytes expressing Gfap at least 1 CP500.
(i) Same as (a) for hypothalamus.
(j) Covariate used for C-SIDE in hypothalamus: midline distance.
(k) Log2 average expression (CP500) of C-SIDE significant DE genes for excitatory, inhibitory, and mature oligodendrocyte cell types. Single cell type pixels are binned by midline distance, and points represent raw data averages while lines represents C-SIDE predictions and error bars around points represent ± 1.96 s.d. (34 ≤ n ≤ 411 pixels per group). (Supplementary Notes).
(l) Spatial visualization of Slc18a2, identified by C-SIDE as DE in inhibitory neurons. Red/blue represents close/far to midline, respectively. Bold points are inhibitory neurons expressing Slc18a2 at least 10 CP500.
All scale bars 250 microns.
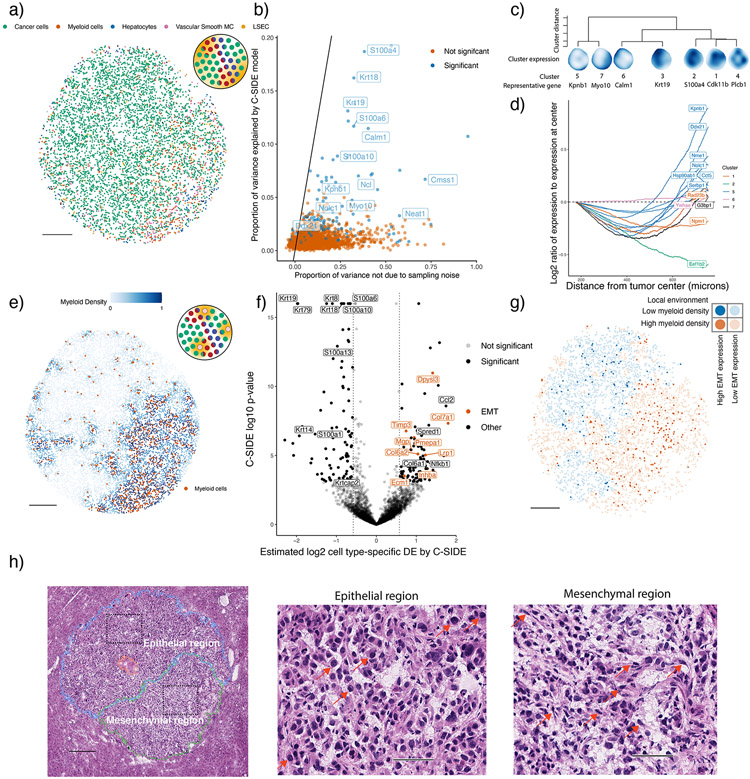
Figure 6:
C-SIDE enables the discovery of differentially expressed pathways in a KrasG12D/+ Trp53−/− (KP) mouse model.
All panels: C-SIDE ran on multiple cell types; plots show C-SIDE results on the tumor cell type. Nonparametric/parametric C-SIDE results are shown in b–d and e–h, respectively.
(a) C-SIDE’s spatial map of cell type assignments. Out of 14 cell types, the five most common appear in the legend.
(b) Scatter plot of C-SIDE R2 and overdispersion (defined as proportion of variance not due to sampling noise) for nonparametric C-SIDE results on the tumor cell type. Identity line is shown, representing the maximum possible variance explained.
(c) Dendrogram of hierarchical clustering of (n = 162 significant genes) C-SIDE’s fitted smooth spatial patterns at the resolution of 7 clusters. Each spatial plot represents the average fitted gene expression patterns over the genes in each cluster.
(d) Moving average plot of C-SIDE fitted gene expression (normalized to expression at center) as a function of distance from the center of the tumor for 12 genes in the Myc targets pathway identified to be significantly spatially DE by C-SIDE.
(e) Covariate used for parametric C-SIDE: continuous density of myeloid cell types in the tumor. Schematic refers to C-SIDE problem type (Figure 1b).
(f) Volcano plot of C-SIDE log2 DE results (n = 4201 pixels) on the tumor cell type with positive values representing upregulation near myeloid immune cells. A subset of significant genes are labeled, and dotted lines represent 1.5x fold-change cutoff.
(g) Spatial plot of total expression in tumor cells of the 9 DE epithelial-mesenchymal transition (EMT) genes identified by C-SIDE in (f). Red/blue represents myeloid-dense and myeloid-poor areas, respectively. Bold points represent tumor cells expressing these EMT genes at least 2.5 counts per 500.
(h) Hematoxylin and eosin (H&E) image of adjacent section of the tumor (n = 1 section). Left: mesenchymal (green), necrosis (red), and epithelial (blue) annotated tumor regions, with dotted boxes representing epithelial and mesenchymal areas of focus for the other two panels. Middle/right: enlarged images of epithelial (middle) or mesenchymal (right) regions. Red arrows point to example tumor cells with epithelial (middle) or mesenchymal (right) morphology.
50 micron scale bars (h) middle/right. All other scale bars 250 microns.
To estimate this complex model with a computationally tractable algorithm, in the first step, we assume does not vary with and and estimate using a previously published algorithm [18]. This assumption does not substantially affect cell type proportion estimates because the gene expression variability across cell types is large relative to the variability across space, for most genes. Some pixels are identified as single cell types while others as mixtures of multiple cell types. Fixing the estimates, we next use maximum likelihood estimation to estimate the cell type-specific DE coefficients a with corresponding standard errors, allowing for false discovery rate-controlled hypotheses testing (Methods). Lastly, C-SIDE performs statistical inference across multiple replicates and/or samples to estimate consensus population-level DE (Methods, Supplementary Figure 1).
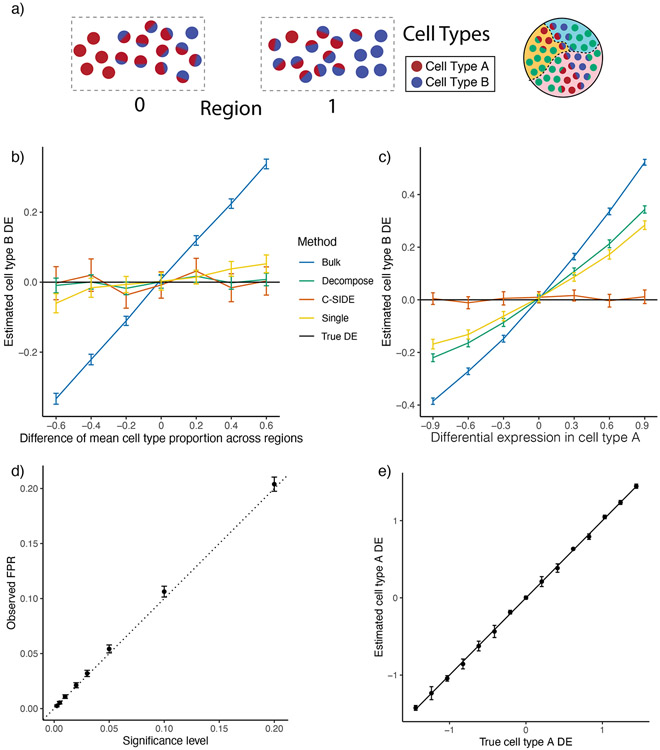
Because ground truth cell type-specific DE is unknown in spatial transcriptomics data, we first benchmarked C-SIDE’s performance on a simulated spatial transcriptomics dataset in which gene expression varied across two regions. Considering the challenging situation where two cell types, termed cell type A and cell type B, are colocalized on pixels within a tissue, we simulated, using a single-nucleus RNA-seq cerebellum dataset, spatial transcriptomics mixture pixels with known proportions of single cells from two cell types known to spatially colocalize [27] (Methods, Figure 2a). Across two spatially-defined regions, we varied both the true cell type-specific gene expression of cell types A and B as well as the average cell type proportions of cell types A and B (Figure 2a, Supplementary Figure 2). We compared C-SIDE against three alternative methods (Methods): Bulk, bulk DE (ignoring cell type); Single, single cell differential expression that approximates each cell type mixture as a single cell type; and Decompose [18], a method that decomposes mixtures into single cell types prior to computing DE. By varying cell type frequencies between the two regions without introducing DE, we observed that C-SIDE correctly attributes gene expression differences across regions to differences in cell type proportions rather than spatial differential expression (Figure 2b, Supplementary Figure 2); in contrast, the Bulk method incorrectly predicts spatial DE since it does not control for differences of cell type proportions across regions.
Figure 2:
C-SIDE provides unbiased estimates of cell type-specific differential expression in simulated data.
All: C-SIDE was tested on a dataset of simulated mixtures of single cells from a single-nucleus RNA-seq cerebellum dataset. Differential expression (DE) axes represent DE in log2-space of region 1 w.r.t. region 0.
(a) Pixels are grouped into two regions, and genes are simulated with ground truth DE across regions. Each region contains pixels containing mixtures of various proportions between cell type A and cell type B. The difference in average cell type proportion across regions is varied across simulation conditions.
(b) Mean estimated cell type B Astn2 DE (differential expression) across two regions as a function of the difference in mean cell type proportion across regions. Astn2 is simulated with ground truth 0 spatial DE, and an average of (n = 100) estimates is shown, along with standard errors. Black line represents ground truth 0 DE (cell type B). Four methods are shown: Bulk, Decompose, Single, and C-SIDE (Methods).
(c) Same as (b) for Nrxn3 cell type B differential gene expression as a function of DE in cell type A, where Nrxn3 is simulated to have DE within cell type A but no DE in cell type B.
(d) For each significance level, C-SIDE’s false positive rate (FPR), along with ground truth identity line (s.e. shown, n = 1500, 15 genes, 100 replicates per gene).
(e) C-SIDE mean estimated cell type A differential expression vs. true cell type A differential expression (average over n = 500 replicates, s.e. shown). Ground truth identity line is shown, and one gene is used for the simulation per DE condition (out of 15 total genes).
Next, we simulated cell type-specific differential expression (DE) by varying the DE in cell type A while keeping cell type B constant across regions. Background DE in cell type A contaminated estimates of differential expression in cell type B for all three alternatives models Bulk, Decompose, and Single (Figure 2c, Supplementary Figure 2). In particular, Decompose assigns gene expression to cell types for each pixel independently but does not have information to distinguish which cell type is responsible for DE in mixture pixels. In contrast, C-SIDE’s joint model of cell type mixtures and cell type-specific DE correctly identified differential expression in cell type A, but not cell type B. Next, we verified that, under the null hypothesis of zero DE, C-SIDE’s false positive rate was accurately controlled, standard errors were accurately estimated, and confidence intervals contained the ground truth DE (Figure 2d, Supplementary Figure 2). Finally, when nonzero differential expression was simulated, C-SIDE achieved unbiased estimation of cell type-specific DE (Figure 2e). We also found that the power, false positive rate, and true positive rate of C-SIDE depends on gene expression level, number of cells, and DE magnitude (Supplementary Figure 2). Lastly, on Slide-seq, MERFISH, and Visium spatial transcriptomics data, we verified that C-SIDE’s fitted Poisson-lognormal distribution accurately fits the empirical spatial transcriptomics gene expression distribution (Supplementary Figure 3-5). Thus, our simulations validate C-SIDE’s ability to accurately estimate and test for cell type-specific differential expression in the cases of asymmetric cell type proportions and contamination from other cell types.
To validate C-SIDE’s ability to discover cell type-specific differential expression on spatial transcriptomics data, we collected Slide-seqV2 data [2] (including one replicate sourced from a prior study [18]) for three cerebellum replicates. We identified a spatial map of cell types (Figure 3a), previously shown to correspond to known cerebellum spatial architecture [18]. We used discrete localization in the anterior lobule or nodulus regions (Figure 3b), a known axis of spatial gene expression variation within the cerebellum [27], as a covariate for estimating cell type-specific DE across regions using C-SIDE (Figure 3c, Supplementary Figure 6, Supplementary Table 1). As experimental validation, we performed hybridization chain reaction (HCR) on four genes identified by C-SIDE to be differentially expressed in specific cell types, and we observed high correspondence between C-SIDE’s estimates of cell type-specific DE and DE measurements from HCR data (Figure 3d, R2 = 0.89). For example, we examined Aldoc and Plcb4, two genes expressed in both Purkinje and Bergmann cell types, which are known to spatially colocalize in the cerebellum and appear as mixtures on Slide-seq pixels [18]. C-SIDE determined that both Aldoc (log2-fold-change = −4.24, p < 10−8) and Plcb4 (log2-fold-change = 1.93, p < 10−8) were differentially expressed in the Purkinje cell type, but not the Bergmann cell type. Similarly, HCR images of Aldoc and Plcb4 showed substantial differential expression within Purkinje cells across the nodulus and anterior lobule, whereas expression within Bergmann cells was relatively even across regions (Figure 3d-e). Next, we used C-SIDE to obtain cell subtype-specific DE estimates. Except for one gene, cell type-specific spatial DE did not differ significantly between a cell type and its subtypes. Furthermore, due to reduced sample size, C-SIDE had reduced statistical power to detect subtype-specific DE (Supplementary Figure 7). We conclude that C-SIDE can successfully identify cell type-specific spatial DE in spatial transcriptomics tissues, even when multiple cell types are spatially colocalized.
C-SIDE solves diverse DE problems in spatial transcriptomics
We next explored the effect of discrete cellular microenvironments on cell type-specific DE in the mouse testes Slide-seq dataset [9]. C-SIDE’s testes principal cell type assignments (Figure 4a) revealed tubular structures corresponding to cross-sectional sampling of seminiferous tubules. Individual tubules have distinct stages of spermatogonia development, grouped into four classes of stages I–III, IV–VI, VII–VIII, and IX–XII, which were determined from the prior testes Slide-seq study [9] (Figure 4b). We applied C-SIDE to identify genes that were differentially expressed, for each cell type, across tubule stages (Supplementary Table 2). C-SIDE identified genes expressed in a single tubule stage within a single cell type (Figure 4c) which are known drivers of cellular development across stages [9]. For instance, the gene Tnp1 was identified by C-SIDE as upregulated in the IX–XII stage within the elongating spermatid (ES) cell type, in agreement with the known biological role of Tnp1 in nuclear remodeling of elongating spermatids at the late tubule stage [28] (Supplementary Figure 8). Furthermore, a majority of C-SIDE-identified stage-specific genes followed cyclic patterns, consistent with previously-characterized seminiferous epithelial cycle [29] (Supplementary Figure 8).
Next, we evaluated C-SIDE’s ability to identify DE for cell types that primarily appear as mixtures with other cell types, particularly the spermatocyte (SPC) cell type. According to C-SIDE cell type assignments, SPC frequently co-mixes with the ES and round spermatid (RS) cell types, consistent with previous histological studies [30] (Supplementary Figure 8a). By utilizing cell type mixtures, C-SIDE obtained increased power for identifying differentially expressed genes compared to a method only using single cell type pixels (Supplementary Notes, Supplementary Figure 8b-c), especially for spermatocyte cell type (217 significant SPC DE genes discovered by C-SIDE vs. 1 DE gene for the single-cell method). For most SPC DE genes, including Prss40 (log2-fold-change = 1.72, p = 8 · 10−5) and Snx3 (log2-fold-change = 1.17, p < 10−8), pixels containing SPC but not spermatids were too rare to determine DE (Figure 4d). Instead, C-SIDE determined DE specifically in SPC cells by detecting significant spatial differences among pixels containing both SPC and spermatid cell types, but not within pure spermatid pixels. Therefore, C-SIDE’s cell type mixture modeling uniquely enables DE discovery in highly-mixed cell types.
Aβ plaque-dependent DE in Alzheimer’s disease
We next explored pathological staining, in particular Aβ plaques, as a continuous covariate for cell type-specific gene expression changes. We performed Slide-seqV2 on the hippocampal region of a genetic mouse model of amyloidosis in Alzheimer’s disease (AD) [31] (J20, n= 4 slices, Methods). C-SIDE’s cell type assignments (Figure 4e) which were consistent with past characterizations of hippocampus cellular localization [18]. We collected paired Aβ plaque staining images (Anti-Human Aβ Mouse IgG antibody, Methods) to quantify Aβ plaque density as a covariate for C-SIDE (Figure 4f, Supplementary Figure 10). We then used C-SIDE to identify genes whose expression depended in a cell type-specific manner on plaque density (Figure 4g, Supplementary Table 6). For instance, in astrocytes colocalizing with Aβ plaque, C-SIDE detected upregulation of Gfap (Figure 4h, Supplementary Figure 10, log2-fold-change = 1.35, p < 10−8), consistent with Gfap’s known role in Aβ plaque attenuation [32], and the C4b complement gene (log2-fold-change = .85, p = 1 · 10−4), which is involved in plaque-associated synaptic pruning in Alzheimer’s disease [33-35]. Moreover, several cathepsin proteases including Ctsb (log2-fold-change = 1.65, p < 10−8), Ctsd (log2-fold-change = 1.30, p < 10−8) Ctsl (log2-fold-change = 1.96, p = 4 · 10−6), and Ctsz (log2-fold-change = 1.11, p = 3 · 10−4) were determined to be differentially upregulated in microglia around plaque, consistent with the role of cathepsins in amyloid degradation [36] (Supplementary Figure 10). In microglia, we also identified known homeostatic microglia markers [37,38] including P2ry12 (log2-fold-change = −1.33, p < 10−8) and Cx3cr1 (log2-fold-change = −0.68, p = 3 · 10−4) as downregulated in the presence of plaque. Apoe, known to have Aβ plaque-dependent upregulation within microglia [39], was also detected (log2-fold-change = 1.58, p < 10−8). Finally, the anti-inflammatory gene Grn was upregulated in microglia near plaque (log2-fold-change = 0.79, p = 6 · 10−4), consistent with prior knowledge [40].
Spatial gene expression changes in imaging-based transcriptomics
We next applied C-SIDE across different spatial technology length scales, from near single-cell resolution imaging-based spatial transcriptomics (e.g. MERFISH) to lower-resolution technologies such as Visium. First, we applied C-SIDE to a MERFISH mouse hypothalamus dataset. During development, hypothalamic progenitors create radial projections out from the hypothalamic midline, which are used as scaffolds for the migration of differentiating daughter cells [41]. Thus, we investigated radial distance to the hypothalamus midline as a predictor of DE in hypothalamus cell types. C-SIDE’s assigned cell types were consistent with the prior MERFISH hypothalamus study [8] (Figure 4i). Although most pixels were single cell types, a non-negligible proportion (12.6% double cell type pixels out of n = 3790 total pixels) were mixtures of multiple cell types. Using midline distance as a covariate for C-SIDE (Figure 4j), we detected genes in hypothalamus excitatory, inhibitory, and mature oligodendrocyte cell types whose expression depended either linearly or quadratically on distance from the midline (Figure 4k, Supplementary Table 3-4). For instance, Slc18a2 (Figure 4l), identified as upregulated within inhibitory neurons near the midline (log2-fold-change = 6.14, p < 10−8), is required for dopaminergic function in certain inhibitory neuronal subtypes [42], which are known to localize near the hypothalamus midline [8]. Next, we used C-SIDE to address the known challenging problem of cellular segmentation in imaging transcriptomics [20]. Since C-SIDE can operate on both cell type mixtures and single cells, we hypothesized that cell segmentation could be skipped altogether and replaced by defining pixels as a fixed grid (Figure 5a). Indeed, skipping segmentation did not substantially change C-SIDE DE estimates (Figure 5b) and reduced C-SIDE uncertainty (Supplementary Figure 9) due to an inclusion of more counts that would be discarded during segmentation.
Figure 5:
C-SIDE enables differential expression discovery on diverse spatial transcriptomics technologies including Visium and MERFISH.
All panels: results of C-SIDE on the Visium lymph node (middle and bottom rows) and MERFISH hypothalamus (top row).
(a) C-SIDE’s spatial map of cell type assignments in the hypothalamus, where pixels were defined deterministically as squares without segmentation. All cell types are shown, and the most common cell types appear in the legend.
(b) Scatter plot of C-SIDE estimated inhibitory cell type differential expression with an without cell segmentation.
(c) Covariate used for C-SIDE: discrete region of B cell-rich areas in the lymph node. Overlayed with Visium histology image.
(d) Volcano plot of C-SIDE dendritic cell differential expression results in log2-space, with positive values corresponding to upregulated genes in the B cell regions. A subset of significant genes are labeled (two-sided Z-test with FDR control, Methods). Dotted lines represents 1.5x fold-change cutoff used for C-SIDE.
(e) Spatial plot of total expression of the CXCL13 gene, which was determined by C-SIDE to be differentially expressed in dendritic cells (DCs). Color represents counts per spot.
(f) Average expression (in counts per 500 (CP500)) of CXCL13 as a function of dendritic cell proportion and germinal center localization. Points represent raw data averages while lines represents C-SIDE predictions and error bars around points represent ± 1.96 s.d. (75 ≤ n ≤ 326 points per group).
All scale bars 250 microns.
DE discovery in lower resolution spatial transcriptomics
We next tested whether C-SIDE on a Visium human lymph node dataset, with spot size 55 microns [43], resulting in a higher degree of cell type mixtures. By using B cell proportion as the C-SIDE covariate, we tested for gene expression changes within the B cell-rich germinal centers (GCs), essential regions for B cell maturation. We note consistency between B cell-rich regions and GC morphology from histology (Figure 5c). C-SIDE identified germinal center-driven DE (Figure 5d, Supplementary Figure 9, Supplementary Table 5), such as correctly identifying GC B cell markers, including RGS13 (log2-fold-change = 1.26, p = 2 · 10−5) and STMN1 (log2-fold-change = 1.07, p < 10−8), as upregulated in GC B cells [44]. Moreover, C-SIDE detected GC-localized follicular dendritic cell (DC) markers CR2 (log2-fold-change = 2.40, p < 10−8) and FDCSP (log2-fold-change = 1.30, p < 10−8) as upregulated in DCs within germinal centers [45]. Importantly, despite 3-4 cell types mixing per spot, C-SIDE accurately determined which cell type(s) was responsible for differential gene expression. For instance, the chemokine CXCL13 was upregulated in B cell-rich regions (Figure 5e). Despite dendritic cells comprising no more than 3 – 15% of each spot (Supplementary Figure 9), C-SIDE was attributed the spatial pattern of CXCL13 to DCs (log2-fold-change = 1.84, p < 10−8), consistent with the role of DCs in secreting CXCL13 to attract B cells to GCs [46]. C-SIDE assigned CXCL13 DE to dendritic cells by utilizing that DE between the B cell-rich region and the B cell-poor region increased as a function of DC proportion (Figure 5f). Thus, C-SIDE can determine cell type-specific DE, even for rare cell types that are consistently mixed with other cells.
C-SIDE discovers tumor-immune signaling in a mouse tumor model
Finally, we applied C-SIDE to identify genes with cell type-specific spatial DE in a Slide-seq dataset of a KrasG12D/+ Trp53−/− (KP) mouse tumor model [47], where we analyzed a metastatic lung adenocarcinoma tumor deposit in the liver. First, C-SIDE found several cell types within the tumor, including both tumor cells and myeloid cells (Figure 6a). Next, we ran C-SIDE nonparametrically to discover arbitrary smooth gene expression patterns (Supplementary Notes, Supplementary Table 7). We found three categories of genes within tumor cells: genes with variation due to sampling noise, spatial variation (explained by the C-SIDE model), or non-spatial biological variation (Figure 6b, Supplementary Figure 11). We then hierarchically clustered the C-SIDE estimated spatial patterns of DE genes into seven clusters (Figure 6c, Supplementary Figure 11). Testing for gene set enrichment (Supplementary Notes), we identified the Myc targets gene set as enriched in cluster 5 (7 out of 12 genes, p = 2 · 10−4, two-sided binomial test, Supplementary Table 8), a cluster most highly expressed at the tumor boundary (Figure 6d). High expression of Myc target genes potentially indicates an increased rate of proliferation [48] at the boundary, a proposed correlate of tumor severity [49]. For example, the most DE Myc target gene, Kpnb1 (Supplementary Figure 11, p = 1 · 10−5), is an oncogene that drives cell proliferation and suppresses apoptosis [50].
We next used C-SIDE to detect cell-to-cell interactions between tumor cells and immune cells, which are known to influence tumor cell behavior [51]. Using myeloid cell type density as the C-SIDE covariate (Figure 6e), C-SIDE identified genes with immune cell density-dependent DE (Figure 6f, Supplementary Table 9), including several genes that were also discovered by nonparametric C-SIDE (Supplementary Figure 11). One of the genes with the largest effects, Ccl2 (log2-fold-change = 1.74, p < 10−8), is a chemotactic signaling molecule known to attract myeloid cells [52]. Furthermore, we tested C-SIDE’s DE gene estimates for aggregate effects across gene sets and found that the epithelial-mesenchymal transition (EMT) pathway was significantly upregulated near immune cells (Figure 6f, Supplementary Figure 11, p = 0.0011, permutation test (Methods), Supplementary Table 8). C-SIDE additionally identified EMT-regulator Nfkb1 as positively DE in tumor cells in immune-rich regions (log2-fold-change = 1.10, p = 1 · 10−5) [53]. As validation, we find most tumor cells expressing EMT genes localized to immune-rich regions (Figure 6g). Furthermore, a hematoxylin and eosin (H&E) tumor stain (Figure 6h) demonstrated a EMT morphological change in the immune-rich region (spindle-shaped tumor cells) relative to the immune-poor region (polygonal-shaped tumor cells). Thus, morphological and gene expression changes imply that the immune microenvironment influences EMT in this tumor model [54].
Discussion
Elucidating spatial sources of differential gene expression is a critical challenge for understanding biological mechanisms and disease with spatial transcriptomics. Here we introduced C-SIDE, a statistical method to detect cell type-specific DE in spatial transcriptomics datasets. C-SIDE takes as input one or more biologically-relevant covariates, such as spatial position or cell type colocalization, and identifies genes, for each cell type, that significantly change their expression as a function of these covariates. Tested on simulated spatial transcriptomics data, C-SIDE obtained unbiased estimation of cell type-specific differential gene expression with a calibrated false positive rate, while other methods were biased from changes in cell type proportion or contamination from other cell types. In the cerebellum, we additionally used HCR experiments to validate C-SIDE’s ability to identify cell type-specific DE across regions. We further applied C-SIDE to a detect DE depending on tubular microenvironment in the testes, midline distance in the MERFISH hypothalamus, germinal center localization in Visium lymph node, and Aβ plaque density in the Alzheimer’s model hippocampus. Finally, we applied both nonparametric and parametric C-SIDE procedures in a mouse tumor model to discover an increase in tumor cells undergoing EMT transition in immune-rich regions.
Several studies have established the importance of accounting for cell type mixtures in assigning cell types in spatial transcriptomics data [18,21-23]. However, it remains a challenge to incorporate cell type proportions into models of cell type-specific spatial differential gene expression. C-SIDE enables such cell type-specific DE discovery by creating a statistical model of gene expression in the presence of cell type mixtures. Other potential solutions, such as bulk DE, approximation as single cell types, and decomposition into single cell types can be confounded by cell type proportion changes and contamination from other cell types. C-SIDE solves these issues by controlling for cell type proportions and jointly considering differential expression within each cell type. Even in imaging-based spatial transcriptomics methods such as MERFISH, we detected some pixels with cell type mixtures, indicating potential diffusion or imperfect cell segmentation [20]. To control for cell type proportions in DE analysis, C-SIDE can estimate cell types directly or import cell type proportions from any cell type mixture identification method [18,21-23].
C-SIDE’s parametric mode provides a unified framework for detecting biologically-relevant differential expression in spatial transcriptomics tissues along diverse axes including spatial distance, proximity to pathology, cellular microenvironment, and cell-to-cell interactions. In settings without prior biological hypotheses, C-SIDE may be run nonparametrically to discover general cell type-specific spatial gene expression patterns. C-SIDE can also be used to test among multiple models of DE, such as the linear and quadratic models applied to the hypothalamus dataset. To help decide between multiple relationships between covariates and gene expression, C-SIDE generates plots to visualize predicted and observed gene expression as a function of a particular covariate. C-SIDE can also utilize multiple covariates in a joint model of gene expression, such as spatial position and cell type colocalization, although more complicated models require more data to fit accurately. Beyond individual samples, C-SIDE can also model biological and technical variability in complex multi-sample, multi-replicate experiments. Multi-replicate experiments, though more costly, produce more robust DE estimates by reducing spurious discoveries of DE on single replicates.
One challenge for C-SIDE is obtaining sufficient DE detection statistical power, which can be hindered by low gene expression counts, small pixel number, or rare cell types. C-SIDE increases its statistical power by including cell type mixture pixels in its model. Ongoing technical improvements in spatial transcriptomics technologies [2] such as increased gene expression counts, higher spatial resolution, and increased pixel number, will increase the discovery rate of C-SIDE. Another limitation of C-SIDE is the requirement of an annotated single-cell reference for reference-based identification of cell types. Although single-cell atlases are increasingly available, they may contain missing cell types or substantial platform effects [18], and certain spatial transcriptomics tissues may lack a corresponding single-cell reference. An ongoing challenge for spatial transcriptomics is to learn cell type proportions in the absence of an annotated single cell reference.
We envision C-SIDE to be particularly powerful in detecting cell type-specific gene expression changes in pathology. First, prior Alzheimer’s disease (AD) studies have discovered candidate genes for disease-relevance through GWAS, bulk RNA, proteomics, and single-cell RNA-seq [34,55]. Here, with C-SIDE using Aβ plaques as a covariate, we identify many genes previously identified by these methods including Gfap in astrocytes [32] and Apoe in microglia [39]; furthermore, we progress a step further towards mechanistic understanding by directly associating spatial plaque localization with cell type-specific differential expression. For example, prior studies have associated complement pathway activation in plaque-dense areas with synaptic pruning [33] and neuronal degeneration [34]. Using C-SIDE we specifically assign complement protein C4b plaque-localized activation to astrocytes [56], which could be caused by a plaque-triggered, cytokine-dependent signaling cascade [35]. Additionally, the downregulation of the homeostatic microglia marker P2ry12 in AD is associated with neuronal cell loss [37]. Using C-SIDE, we further localize this downregulation to plaque-associated microglia, suggesting that plaque-dense areas trigger microglia activation and downregulate homeostatic microglia genes [38]. Lastly, the anti-inflammatory gene granulin (Grn), discovered by C-SIDE as upregulated in microglia near plaques, attenuates microglia activation [40,57], potentially mitigating plaque deposition and cognitive pathological decline [58].
Second, C-SIDE has the potential to elucidate cellular interactions. For example, recent studies have characterized cell-to-cell interactions of immune cells influencing the behavior of tumor cells [51]. Likewise, on a Slide-seq dataset of a mouse tumor model, C-SIDE identified synergistic cell-to-cell signaling between tumor cells and myeloid immune cells. For example, Ccl2, upregulated in immune-adjacent tumor cells, chemotactically recruits myeloid cells and induces pro-tumorigenic behavior, including growth, angiogenesis, and metastasis, in myeloid cells [52]. Likewise, the epithelial-mesenchymal transition (EMT) pathway, upregulated near myeloid cells, promotes tumor development and metastasis [54]. Although C-SIDE can establish such associations, conclusive establishment of molecular mechanism requires future experimentation. Among other hypotheses, it is plausible that myeloid cells induce tumor cells to undergo the EMT transition, potentially through the NF-κB (also identified as upregulated by C-SIDE) signaling pathway [51,54]. Therefore, C-SIDE, combined with pathological measurements, can elucidate cell type-specific responses to disease. We envision C-SIDE as a powerful framework for studying the impacts of spatial and environmental context on cellular gene expression in spatial transcriptomics data.
Methods
Ethics statement
All procedures involving animals at the Broad Institute were conducted in accordance with the US National Institutes of Health Guide for the Care and Use of Laboratory Animals under protocol number 0120-09-16. No field samples were collected for this study.
C-SIDE model
Here, we describe Cell type-Specific Inference of Differential Expression (C-SIDE), a statistical method for identifying differential expression (DE) in spatial transcriptomics data. We define the C-SIDE model in equations (1), (2), and (3). Prior to fitting C-SIDE, the design matrix is predefined to contain covariates, variables on which gene expression is hypothesized to depend such as spatial position or cellular microenvironment. Recall that represents the ’th covariate, evaluated at pixel in experimental sample . For each covariate , there is a corresponding coefficient , representing a gene expression change across pixels per unit change of within cell type of experimental sample . Next, recall from (2) random effects and , which we assume both follow normal distributions with mean 0 and standard deviations and , respectively. The overdispersion magnitude, varies across gene (Supplementary Figure 12), and modeling gene-specific overdispersion is necessary for controlling the false-positive rate of C-SIDE.
Due to our finding that genes can exhibit DE in some but not all cell types (Figure 3c), C-SIDE generally does not assume that genes share DE patterns across cell types, allowing for the discovery of cell type-specific DE. We also developed an option where DE can be assumed to be shared across cell types (Supplementary Notes). C-SIDE can be thought of as a modification of the generalized linear model (GLM) [25] in which each cell type follows a cell type-specific log-linear model before an additive mixture of all cell types is observed. See Fitting the C-SIDE model and Hypothesis testing for C-SIDE model fitting and hypothesis testing, respectively.
Parameterization of the design matrix
For specific construction of design matrix for each dataset, see Cell type estimation and construction of covariates. Recall the specific examples of design matrix presented in Figure 1b. In general, can obtain the following forms:
Indicator variable. In this case, is always either 0 or 1, representing DE due to membership within a certain spatially-defined pixel set. The coefficient is interpreted as the log-ratio of gene expression between the two sets for cell type and gene in experimental sample .
Continuous variable. In this case, can take on continuous values representing, for example, distance from some feature or density of some element. The coefficient is interpreted as the log-fold-change of gene expression per unit change in for cell type and gene in sample .
Multiple categories. In this case, we use to encode membership in sets. For each , we define to be an indicator variable representing membership in set for sample . To achieve identifiability, the intercept is removed. The coefficient is interpreted as the average gene expression in set for cell type and gene . Cell type-specific DE is determined by detecting changes in across within cell type and sample .
Nonparametric. In this case, we use to represent smooth basis functions, where linear combinations of these basis functions represent the overall smooth gene expression function. By default, we use thin plate spline basis functions, calculated using the mgcv package [26].
In all cases, we normalize each to range between 0 and 1. The problem is equivalent under linear transformations of , but this normalization helps with computational performance. The intercept term, when used, is represented in as a column of 1’s.
Fitting the C-SIDE model
C-SIDE estimates the parameters of (1), (2), and (3) via maximum likelihood estimation. First, all parameters are independent across samples, so we fit the model independently for each sample. For population inference across multiple samples, see Statistical inference on multiple samples/replicates. Next, the parameters of and are estimated by the RCTD algorithm [18]. C-SIDE can also optionally import cell type proportions from external cell type proportion identification methods [21-23]. Here, some pixels are identified as single cell types while others as mixtures of multiple cell types. We can accurately estimate cell type proportions and platform effects without being aware of differential spatial gene expression because differential spatial gene expression (average 0.38 in e.g. cerebellum Slide-seq data) is smaller than gene expression differences across cell types (average s.d. 1.09 in e.g. cerebellum Slide-seq data). After determining cell type proportions, C-SIDE estimates gene-specific overdispersion magnitude for each gene by maximum likelihood estimation (Supplementary Notes). Finally, C-SIDE estimates the DE coefficients a by maximum likelihood estimation. For the final key step of estimating , we use plugin estimates (denoted by ) of , , and . After we substitute (3) into (1) and (2), we obtain:
| (4) |
| (5) |
We provide an algorithm for computing the maximum likelihood estimator of , presented in the Supplementary Notes. Our likelihood optimization algorithm is a second-order, trust-region [59] based optimization (Supplementary Notes). In brief, we iteratively solve quadratic approximations of the log-likelihood, adaptively constraining the maximum parameter change at each step. Critically, the likelihood is independent for each gene (and sample ), so separate genes are run in parallel in which case there are parameters per gene and sample.
Hypothesis testing
In addition to estimating the vector (dimensions by ) for gene and sample , we can compute standard errors around . By asymptotic normality [60] (Supplementary Notes), we have approximately that (setting to be the total number of pixels),
| (6) |
where is the Fisher information of model (4), which is computed in the Supplementary Notes. Given this result, we can compute standard errors, confidence intervals, and hypothesis tests. As a consequence of (6), the standard error of , denoted , is .
First, we consider the case where we are interested in a single parameter, , for and fixed and for each cell type and gene ; for example, could represent the log-fold-change between two discrete regions. In this case, for each gene , we compute the z-statistic, . Using a two-tailed z-test, we compute a p–value for the null hypothesis that as , where is the distribution function of the standard Normal distribution. Finally, -values are calculated across all genes within a cell type to control the false discovery rate (FDR) using the Benjamini-Hochberg procedure [61]. We used a FDR of .01 (0.1 for nonparametric case) and a fold-change cutoff of 1.5 (N/A for nonparametric case). Additionally, for each cell type, genes were pre-filtered so that the expression within the cell type of interest had a total expression of at least 15 unique molecular identifiers (UMIs) over all pixels and that the mean normalized expression is at least as large as expression within each other cell type. The parameter (default 50%, set to 25% on Alzheimer’s dataset) is used to filter out marker genes of other cell types that may contaminate the DE estimates of the cell type of interest. We recommend setting between 25% – 50%, trading off between increasing DE discoveries and risking false discoveries due to marker gene contamination.
For the multi-region case, we test for differences of pairs of parameters representing the average expression within each region, correcting for multiple hypothesis testing by scaling -values. We select genes which have significant differences between at least one pair of regions. For other cases in which we are interested in multiple parameters, for example the nonparametric case, we test each parameter individually and scale -values due to multiple hypothesis testing.
Statistical inference on multiple samples/replicates
When C-SIDE is run on multiple replicates, we recall and are the DE and standard error for replicate , where , and is the total number of replicates. We now consider testing for DE across all replicates for covariate , cell type , and gene . In this case, we assume that additional biological or technical variation across samples exists, such that each unknown is normally distributed around a population-level DE , with standard deviation :
| (7) |
Under this assumption, and using (6) for the distribution of the observed single-sample estimates , we derive the following feasible generalized least squares estimator of (Supplementary Notes),
| (8) |
Here, and are obtained from C-SIDE estimates on individual samples (see (6)), whereas represents the estimated variance across samples (Supplementary Figure 12). Please see the Supplementary Notes for additional details such as the method of moments procedure [62] for estimating and the standard errors of . Intuitively, our estimate of the population-level differential expression is a variance-weighted sum over the DE estimates of individual replicates, similar to meta-analysis methods [62]. We next use these estimates and standard errors to test the hypothesis that as described in Hypothesis testing. For the case of multiple biological samples and multiple replicates within each sample see Supplementary Notes. Multiple sample inference with nonparametric C-SIDE requires a common coordinate system, and we create a common spline basis and then test each coefficient across all samples.
Spatial transcriptomics, scRNA-seq, Aβ imaging, and HCR data
Using the Slide-seqV2 protocol [2] (Supplementary Notes), we collected four Alzheimer’s Slide-seq mouse hippocampus sections [31] on a female 8.8 month old J20 Alzheimer’s mouse model [31] and three Slide-seq mouse cerebellum sections (one from a previous study [18]). The Slide-seq mouse testes [9] and cancer [47], MERFISH hypothalamus [8], and Visium lymph node [43] datasets were obtained from prior studies. The tumor dataset represented a KrasG12D/+ Trp53−/− (KP) mouse metastatic lung adenocarcinoma tumor in the liver. We utilized cell type-annotated scRNA-seq datasets for the testes [63], hypothalamus [8], cerebellum [27], cancer [47], lymph node [23], and Alzheimer’s hippocampus datasets [64].
Slide-seq data was preprocessed using the Slide-seq tools pipeline [2]. Spatial transcriptomic spots were filtered to a minimum of 100 UMIs, and the region of interest (ROI) was cropped prior to running C-SIDE using overall anatomical features. For example, in Slide-seq Alzheimer’s hippocampus, the somatosensory cortex was cropped out prior to analysis.
For the Alzheimer’s dataset, to define an amyloid plaque C-SIDE covariate, we collected fluorescent images of DAPI and amyloid beta (Aβ), using IBL America Amyloid Beta (N) (82E1) Aβ Anti-Human Mouse IgG MoAb on sections adjacent to the Slide-seq data. We co-registered the DAPI image to the adjacent Slide-seq total UMI image using the ManualAlignImages function from the STutility R package [65]. To calculate plaque density, plaque images were convolved with an exponentially-decaying isotropic filter, using a threshold at the 0.9 quantile, normalized to be between 0 and 1, and averaged over two adjacent amyloid sections.
For in situ RNA hybridization validation of cerebellum DE results, we collected hybridization chain reaction (HCR) data on genes Aldoc, Kcnd2, Mybpc1, Plcb4, and Tmem132c (Supplementary Table 10) [66]. We simultaneously collected cell type marker genes [27] of Bergmann (Gdf10), granule (Gabra6), and Purkinje (Calb1) cell types. Data from Kcnd2 was removed due to measuring tissue autofluorescence rather than RNA. ROIs of nodular and anterior regions were cropped, and background, defined as median signal, was subtracted. For this data, DE was calculated as the log-fold-change, across ROIs, of average gene signal over the pixels within the ROI containing cell type markers of a particular cell type. Pixels containing marker genes of multiple cell types were removed. C-SIDE single-sample standard errors in Figure 3d were calculated by modeling single-sample variance as the sum of the variance across samples and variance representing uncertainty around the population mean.
Cell type proportion estimation and covariate construction
For each dataset, we constructed at least one covariate, an axis along which to test for DE. All covariates were scaled linearly to have minimum 0 and maximum 1. For the cerebellum dataset, the covariate was defined as an indicator variable representing membership within the nodular region (vs. the anterior region). For the testes dataset, a discrete covariate represented the cellular microenvironment of tubule stage, labels obtained from tubule-level gene expression clustering (four stages, I–III, IV–VI, VII–VIII, and IX–XII) from the previous Slide-seq testes study [9]. For the cancer dataset, the myeloid cell type density covariate was calculated by convolving the cell type locations, weighted by UMI number, with an exponential filter. For this dataset, we also ran C-SIDE nonparametrically. For the Alzheimer’s hippocampus dataset, see Collection and preprocessing. For the MERFISH hypothalamus dataset, the covariate was linear or quadratic midline distance. For the quadratic MERFISH C-SIDE model, we conducted hypothesis testing on the quadratic coefficient. To estimate platform effects and cell type proportions, RCTD ran with default parameters on full mode for the testes and lymph node datasets and doublet mode for other datasets [18].
Validation with simulated gene expression dataset
We created a ground truth DE simulation, from the cerebellum single-nucleus RNA-seq dataset, to test C-SIDE on mixtures between two cell type layers. We restricted to Purkinje and Bergmann cell types, which are known to spatially colocalize. To simulate a cell type mixture of cell types A (Purkinje) and B (Bergmann), we randomly chose a cell from each cell type, and sampled a predefined number of UMIs from each cell (total 1, 000). We defined two discrete spatial regions (Figure 1a), populated with A/B cell type mixtures. We varied the mean cell type proportion difference across the two regions and also simulated the case of cell type proportions evenly distributed across the two regions. Cell type-specific spatial differential gene expression also was simulated across the two regions. To simulate cell type-specific differential expression in the gene expression step of the simulation, we multiplicatively scaled the expected gene counts within each cell of each cell type. An indicator variable for the two spatial bins was used as the C-SIDE covariate.
Additional computational analysis
For confidence intervals on data points or groups of data points (Figure 4d, Figure 4k), we used the predicted variance of data points from C-SIDE (Supplementary Notes). Likewise, for such analysis we used predicted counts from C-SIDE at each pixel (Supplementary Notes). For the testes dataset, a cell type was considered to be present on a bead if the proportion of that cell type was at least 0.25 (Figure 4d). Additionally, cell type and stage-specific marker genes were defined as genes that had a fold-change of at least 1.5 within the cell type of interest compared to each other cell type. We also required significant cell type-specific DE between the stage of interest with all other stages (fold-change of at least 1.5, significance at the level of 0.001, Monte Carlo test on Z-scores). Cyclic genes were defined as genes whose minimum expression within a cell type occurred two tubule stages away from its maximum expression, up to log-space error of up to 0.25. For analyzing C-SIDE on cerebellum subtypes, we focused on five granule subtypes since granule was the most commonly occurring cell type, thus yielding the most statistical power (Supplementary Figure 7). We tested for significant differences in the estimated DE coefficients between the subtype model and the original model without subtypes.
For nonparametric C-SIDE on the tumor dataset, we used hierarchical Ward clustering to cluster quantile-normalized spatial gene expression patterns into 7 clusters. For gene set testing on the tumor dataset, we tested the 50 hallmark gene sets from the MSigDB database [67] for aggregate effects in C-SIDE differential expression estimates for the tumor cell type. For the nonparametric case, we used a binomial test with multiple hypothesis correction to test for enrichment of any of the 7 spatial clusters of C-SIDE-identified significant genes in any of the 50 gene sets. For the parametric case, we used a permutation test on the average value of C-SIDE scores for a gene set. That is, we modified an existing gene set enrichment procedure [68] by filtering for genes with a fold-change of at least 1.5 and using a two-sided permutation test rather than assuming normality. In both cases, we filtered to gene sets with at least 5 genes and we used Benjamini-Hochberg procedure across all gene sets to control the FDR at 0.05. The proportion of variance not due to sampling noise (Figure 6b) was calculated by considering the difference between observed variance on normalized counts and the expected variance due to Poisson sampling noise.
We considered and tested several simple alternative methods to C-SIDE, which represent general classes of approaches. First, we considered a two-sample Z-test on single cells (defined as pixels with cell type proportion at least 0.9). Additionally, we tested Bulk differential expression, which estimated DE as the log-ratio of average normalized gene expression across two regions. The Single method of differential expression rounded cell type mixtures to the nearest single cell type and computed the log-ratio of gene expression of cells in that cell type. Finally, the Decompose method of DE used a previously-developed method to compute expected gene expression counts for each cell type [18], followed by computing the ratio of cell type-specific gene expression in each region.
Implementation details
C-SIDE is publicly available as part of the R package https://github.com/dmcable/spacexr. The quadratic program that arises in the C-SIDE optimization algorithm is solved using the quadprog package in R [69]. Prior to conducting analysis on C-SIDE output, all ribosomal proteins and mitochondrial genes were filtered out. Additional parameters used for running C-SIDE are shown in Supplementary Table 11. C-SIDE was tested on a Macintosh laptop computer with a 2.4 GHz Intel Core i9 processor and 32GB of memory (we recommend at least 4GB of memory to run C-SIDE). For example, we timed C-SIDE with four cores on one of the Slide-seq cerebellum replicates, containing 2, 776 pixels across two regions, 5 cell types, and 4, 812 genes. Under these conditions, C-SIDE ran in 13 minutes and 47 seconds (excluding the cell type assignment step in which computational efficiency has been described previously [18]).
C-SIDE can be run using a general covariate matrix with the function run.CSIDE. In most cases, a more specific function exists for specific covariates including run.CSIDE.single (one covariate), run.CSIDE.regions (multiple regions), or run.CSIDE.nonparam (nonparametric). Moreover, to generate covariates for e.g. run.CSIDE.single, the functions exvar.celltocell.interactions and exvar.point.density can be used to calculate covariates for the density of cell types or additional features, respectively. For multiple replicates/samples, the function run.CSIDE.replicates can be used, while the function CSIDE.population.inference performs population inference across these replicates. Multi-replicate analysis requires covariates to be consistently defined; for example, in non-parametric mode the coordinates must exist in a common coordinate system, which can be obtained, for instance, by alignment. Please see https://github.com/dmcable/spacexr/tree/master/vignettes for Vignettes for running C-SIDE, https://github.com/dmcable/spacexr/tree/master/documentation for additional documentation, and Supplementary Software 1 for the manual for the spacexr R package.
Supplementary Material
Acknowledgements
We thank Robert Stickels for providing valuable input on the analysis. We thank Tongtong Zhao and Zachary Chiang for generously providing the cancer Slide-seq data. We thank Samuel Marsh (Harvard Medical School / Boston Children’s Hospital) for kindly providing mouse J20 Alzheimer’s model samples. We thank members of the Chen lab, Irizarry lab, and Macosko lab including Tushar Kamath for helpful discussions and feedback. D.C. was supported by a Fannie and John Hertz Foundation Fellowship and an NSF Graduate Research Fellowship. This work was supported by an NIH Early Independence Award (DP5, 1DP5OD024583 to F.C.), the NHGRI (R01, R01HG010647 to F.C. and E.Z.M), as well as the Burroughs Wellcome Fund, the Searle Scholars Award, and the Merkin Institute to F.C.. R.A.I. was supported by NIH grants R35GM131802 and R01HG005220.
Footnotes
Competing Interests Statement
E.Z.M. and F.C. are listed as inventors on a patent application related to Slide-seq. F.C. is a paid consultant for Celsius Therapeutics and Atlas Bio. The remaining authors declare no competing interests.
Data Availability Statement
Slide-seq V2 data generated for this study and additional data are available at the Broad Institute Single Cell Portal https://singlecell.broadinstitute.org/single_cell/study/SCP1663.
We also used the following publicly available datasets in our study. MERFISH hypothalamus dataset was accessed from Dryad https://doi.org/10.5061/dryad.8t8s248. Visium human lymph node is available at https://www.10xgenomics.com/resources/datasets/human-lymph-node-1-standard-1-1-0. Testes Slide-seq data can be accessed at https://www.dropbox.com/s/ygzpj0d0oh67br0/Testis_Slideseq_Data.zip?dl=0. Cancer Slide-seq data is available at https://singlecell.broadinstitute.org/single_cell/study/SCP1278. Hallmark gene sets were accessed from https://www.gsea-msigdb.org/.
Code Availability Statement
C-SIDE is implemented in the open-source R package spacexr, with source code freely available at https://github.com/dmcable/spacexr. Additional code used for analysis in this paper is available at https://github.com/dmcable/spacexr/tree/master/AnalysisCSIDE.
References
- [1].Rodriques SG et al. Slide-seq: A scalable technology for measuring genome-wide expression at high spatial resolution. Science 363, 1463–1467 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Stickels RR et al. Highly sensitive spatial transcriptomics at near-cellular resolution with Slide-seqV2. Nature biotechnology 39, 313–319 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Chen KH, Boettiger AN, Moffitt JR, Wang S & Zhuang X Spatially resolved, highly multiplexed RNA profiling in single cells. Science 348 ( 2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Wang X. et al. Three-dimensional intact-tissue sequencing of single-cell transcriptional states. Science 361 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].10x Genomics. 10x genomics: Visium spatial gene expression. https://www.10xgenomics.com/solutions/spatial-gene-expression/ (2020). [Google Scholar]
- [6].Zollinger DR, Lingle SE, Sorg K, Beechem JM & Merritt CR GeoMx RNA assay: High multiplex, digital, spatial analysis of RNA in FFPE tissue. In In Situ Hybridization Protocols, 331–345 (Springer, 2020). [DOI] [PubMed] [Google Scholar]
- [7].Alon S. et al. Expansion sequencing: Spatially precise in situ transcriptomics in intact biological systems. Science 371 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Moffitt JR et al. Molecular, spatial, and functional single-cell profiling of the hypothalamic preoptic region. Science 362 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Chen H. et al. Dissecting mammalian spermatogenesis using spatial transcriptomics. Cell Reports 37, 109915 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Svensson V, Teichmann SA & Stegle O SpatialDE: identification of spatially variable genes. Nature methods 15, 343–346 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Sun S, Zhu J & Zhou X Statistical analysis of spatial expression patterns for spatially resolved transcriptomic studies. Nature methods 17, 193–200 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Zhu J, Sun S & Zhou X SPARK-X: non-parametric modeling enables scalable and robust detection of spatial expression patterns for large spatial transcriptomic studies. Genome Biology 22, 1–25 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Dries R. et al. Giotto: a toolbox for integrative analysis and visualization of spatial expression data. Genome biology 22, 1–31 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Butler A, Hoffman P, Smibert P, Papalexi E & Satija R Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nature biotechnology 36, 411–420 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Love MI, Huber W & Anders S Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome biology 15, 1–21 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Robinson MD, McCarthy DJ & Smyth GK edgeR: a Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 26, 139–140 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Haghverdi L, Lun AT, Morgan MD & Marioni JC Batch effects in single-cell RNA-sequencing data are corrected by matching mutual nearest neighbors. Nature biotechnology 36, 421–427 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Cable DM et al. Robust decomposition of cell type mixtures in spatial transcriptomics. Nature Biotechnology 1–10 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Regev A. et al. Science forum: the human cell atlas. Elife 6, e27041 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Petukhov V. et al. Cell segmentation in imaging-based spatial transcriptomics. Nature Biotechnology 1–10 (2021). [DOI] [PubMed] [Google Scholar]
- [21].Andersson A. et al. Single-cell and spatial transcriptomics enables probabilistic inference of cell type topography. Communications biology 3, 1–8 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Dong R & Yuan GC SpatialDWLS: accurate deconvolution of spatial transcriptomic data. Genome biology 22, 1–10 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Kleshchevnikov V. et al. Cell2location maps fine-grained cell types in spatial transcriptomics. Nature biotechnology 1–11 (2022). [DOI] [PubMed] [Google Scholar]
- [24].Zhao E. et al. Spatial transcriptomics at subspot resolution with BayesSpace. Nature Biotechnology 1–10 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Hardin JW, Hardin JW, Hilbe JM & Hilbe J Generalized linear models and extensions (Stata press, 2007). [Google Scholar]
- [26].Wood S & Wood MS Package ‘mgcv’. R package version 1, 29 (2015). [Google Scholar]
- [27].Kozareva V. et al. A transcriptomic atlas of mouse cerebellar cortex comprehensively defines cell types. Nature 598, 214–219 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Zhao M, Shirley CR, Mounsey S & Meistrich ML Nucleoprotein transitions during spermiogenesis in mice with transition nuclear protein Tnp1 and Tnp2 mutations. Biology of reproduction 71, 1016–1025 (2004). [DOI] [PubMed] [Google Scholar]
- [29].Hasegawa K & Saga Y Retinoic acid signaling in Sertoli cells regulates organization of the blood-testis barrier through cyclical changes in gene expression. Development 139, 4347–4355 (2012). [DOI] [PubMed] [Google Scholar]
- [30].Xu J. et al. Computerized spermatogenesis staging (CSS) of mouse testis sections via quantitative histomorphological analysis. Medical image analysis 70, 101835 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Mucke L. et al. High-level neuronal expression of Aβ1–42 in wild-type human amyloid protein precursor transgenic mice: Synaptotoxicity without plaque formation. Journal of Neuroscience 20, 4050–4058 (2000). URL https://www.jneurosci.org/content/20/11/4050. https://www.jneurosci.org/content/20/11/4050.full.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Kraft AW et al. Attenuating astrocyte activation accelerates plaque pathogenesis in APP/PS1 mice. The FASEB Journal 27, 187–198 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Hong S. et al. Complement and microglia mediate early synapse loss in Alzheimer mouse models. Science 352, 712–716 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Zhou Y. et al. Human and mouse single-nucleus transcriptomics reveal TREM2-dependent and TREM2-independent cellular responses in Alzheimer’s disease. Nature medicine 26, 131–142 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Veerhuis R. et al. Cytokines associated with amyloid plaques in Alzheimer’s disease brain stimulate human glial and neuronal cell cultures to secrete early complement proteins, but not C1-inhibitor. Experimental neurology 160, 289–299 (1999). [DOI] [PubMed] [Google Scholar]
- [36].Bernstein HG & Keilhoff G Putative roles of cathepsin B in Alzheimer’s disease pathology: The good, the bad, and the ugly in one? Neural regeneration research 13, 2100 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Sobue A. et al. Microglial gene signature reveals loss of homeostatic microglia associated with neurodegeneration of Alzheimer’s disease. Acta neuropathologica communications 9, 1–17 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Keren-Shaul H. et al. A unique microglia type associated with restricting development of alzheimer’s disease. Cell 169, 1276–1290 (2017). [DOI] [PubMed] [Google Scholar]
- [39].Serrano-Pozo A, Das S & Hyman BT APOE and Alzheimer’s disease: advances in genetics, pathophysiology, and therapeutic approaches. The Lancet Neurology 20, 68–80 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Mendsaikhan A, Tooyama I & Walker DG Microglial progranulin: involvement in Alzheimer’s disease and neurodegenerative diseases. Cells 8, 230 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Zhou X. et al. Cellular and molecular properties of neural progenitors in the developing mammalian hypothalamus. Nature communications 11, 1–16 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Romanov RA et al. Molecular interrogation of hypothalamic organization reveals distinct dopamine neuronal subtypes. Nature neuroscience 20, 176–188 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].10x Genomics. V1_Human_Lymph_Node - Datasets - Spatial Gene Expression. https://support.10xgenomics.com/spatial-geneexpression/datasets/1.1.0/V1_Human_Lymph_Node (2020). [Google Scholar]
- [44].Milpied P. et al. Human germinal center transcriptional programs are de-synchronized in B cell lymphoma. Nature immunology 19, 1013–1024 (2018). [DOI] [PubMed] [Google Scholar]
- [45].Abe Y. et al. A single-cell atlas of non-haematopoietic cells in human lymph nodes and lymphoma reveals a landscape of stromal remodelling. Nature Cell Biology 1–14 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Weinstein AM & Storkus WJ Chapter six - therapeutic lymphoid organogenesis in the tumor microenvironment. In Wang X-Y & Fisher PB (eds.) Immunotherapy of Cancer, vol. 128 of Advances in Cancer Research, 197–233 (Academic Press, 2015). URL https://www.sciencedirect.com/science/article/pii/S0065230X15000317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Zhao T. et al. Spatial genomics enables multi-modal study of clonal heterogeneity in tissues. Nature 1–7 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Dang CV c-Myc target genes involved in cell growth, apoptosis, and metabolism. Molecular and cellular biology 19, 1–11 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Jiménez-Sánchez J. et al. Evolutionary dynamics at the tumor edge reveal metabolic imaging biomarkers. Proceedings of the National Academy of Sciences 118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Kodama M. et al. In vivo loss-of-function screens identify KPNB1 as a new druggable oncogene in epithelial ovarian cancer. Proceedings of the National Academy of Sciences 114, E7301–E7310 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Chen DP et al. Peritumoral monocytes induce cancer cell autophagy to facilitate the progression of human hepatocellular carcinoma. Autophagy 14, 1335–1346 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Lim SY, Yuzhalin AE, Gordon-Weeks AN & Muschel RJ Targeting the CCL2-CCR2 signaling axis in cancer metastasis. Oncotarget 7, 28697 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Pires BR et al. NF-kappaB is involved in the regulation of EMT genes in breast cancer cells. PloS one 12, e0169622 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Dongre A & Weinberg RA New insights into the mechanisms of epithelial-mesenchymal transition and implications for cancer. Nature reviews Molecular cell biology 20, 69–84 (2019). [DOI] [PubMed] [Google Scholar]
- [55].Satoh J.-i. et al. TMEM106B expression is reduced in Alzheimer’s disease brains. Alzheimer’s research & therapy 6, 1–14 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Walker DG, Kim SU & McGeer PL Expression of complement C4 and C9 genes by human astrocytes. Brain research 809, 31–38 (1998). [DOI] [PubMed] [Google Scholar]
- [57].Götzl JK et al. Opposite microglial activation stages upon loss of PGRN or TREM 2 result in reduced cerebral glucose metabolism. EMBO molecular medicine 11, e9711 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Minami SS et al. Progranulin protects against amyloid β deposition and toxicity in alzheimer’s disease mouse models. Nature medicine 20, 1157–1164 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
Methods References
- [59].Yuan YX A review of trust region algorithms for optimization. In Iciam, vol. 99, 271–282 (2000). [Google Scholar]
- [60].Van der Vaart AW Asymptotic statistics, vol. 3 (Cambridge university press, 2000). [Google Scholar]
- [61].Benjamini Y & Hochberg Y Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal statistical society: series B (Methodological) 57, 289–300 (1995). [Google Scholar]
- [62].DerSimonian R & Laird N Meta-analysis in clinical trials. Controlled clinical trials 7, 177–188 (1986). [DOI] [PubMed] [Google Scholar]
- [63].Green CD et al. A comprehensive roadmap of murine spermatogenesis defined by single-cell RNA-seq. Developmental cell 46, 651–667 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Saunders A. et al. Molecular diversity and specializations among the cells of the adult mouse brain. Cell 174, 1015–1030 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Bergenstråhle J, Larsson L & Lundeberg J Seamless integration of image and molecular analysis for spatial transcriptomics workflows. BMC genomics 21, 1–7 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Dirks RM & Pierce NA Triggered amplification by hybridization chain reaction. Proceedings of the National Academy of Sciences 101, 15275–15278 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Liberzon A. et al. Molecular signatures database (MSigDB) 3.0. Bioinformatics 27, 1739–1740 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Irizarry RA, Wang C, Zhou Y & Speed TP Gene set enrichment analysis made simple. Statistical methods in medical research 18, 565–575 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Turlach BA & Weingessel A quadprog: Functions to solve quadratic programming problems. R package version 1.5-5 (2013). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Slide-seq V2 data generated for this study and additional data are available at the Broad Institute Single Cell Portal https://singlecell.broadinstitute.org/single_cell/study/SCP1663.
We also used the following publicly available datasets in our study. MERFISH hypothalamus dataset was accessed from Dryad https://doi.org/10.5061/dryad.8t8s248. Visium human lymph node is available at https://www.10xgenomics.com/resources/datasets/human-lymph-node-1-standard-1-1-0. Testes Slide-seq data can be accessed at https://www.dropbox.com/s/ygzpj0d0oh67br0/Testis_Slideseq_Data.zip?dl=0. Cancer Slide-seq data is available at https://singlecell.broadinstitute.org/single_cell/study/SCP1278. Hallmark gene sets were accessed from https://www.gsea-msigdb.org/.
C-SIDE is implemented in the open-source R package spacexr, with source code freely available at https://github.com/dmcable/spacexr. Additional code used for analysis in this paper is available at https://github.com/dmcable/spacexr/tree/master/AnalysisCSIDE.