Development and validation of a machine learning-supported strategy of patient selection for osteoarthritis clinical trials: the IMI-APPROACH study

Abstract

Objectives

To efficiently assess the disease-modifying potential of new osteoarthritis treatments, clinical trials need progression-enriched patient populations. To assess whether the application of machine learning results in patient selection enrichment, we developed a machine learning recruitment strategy targeting progressive patients and validated it in the IMI-APPROACH knee osteoarthritis prospective study.

Design

We designed a two-stage recruitment process supported by machine learning models trained to rank candidates by the likelihood of progression. First stage models used data from pre-existing cohorts to select patients for a screening visit. The second stage model used screening data to inform the final inclusion. The effectiveness of this process was evaluated using the actual 24-month progression.

Results

From 3500 candidate patients, 433 with knee osteoarthritis were screened, 297 were enrolled, and 247 completed the 2-year follow-up visit. We observed progression related to pain (P, 30%), structure (S, 13%), and combined pain and structure (P ​+ ​S, 5%), and a proportion of non-progressors (N, 52%) ∼15% lower vs an unenriched population. Our model predicted these outcomes with AUC of 0.86 [95% CI, 0.81–0.90] for pain-related progression and AUC of 0.61 [95% CI, 0.52–0.70] for structure-related progression. Progressors were ranked higher than non-progressors for P ​+ ​S (median rank 65 vs 143, AUC = 0.75), P (median rank 77 vs 143, AUC = 0.71), and S patients (median rank 107 vs 143, AUC = 0.57).

Conclusions

The machine learning-supported recruitment resulted in enriched selection of progressive patients. Further research is needed to improve structural progression prediction and assess this strategy in an interventional trial.

1. Introduction

Although there are many challenges affecting clinical trials, a major bottleneck is the selection of the right patients for the right treatment. The aim is to include a well-defined population in which the intervention is likely to be effective. For example, when the goal of a treatment is to slow down the disease, the inclusion criteria need to identify patients at high risk of progression, so that the treatment effects can be better observed within the trial duration. Finding such criteria is difficult for slowly progressing diseases such as osteoarthritis, dementia, or chronic pain, as the understanding of their pathophysiology is still evolving. This leads to large and long-lasting, or unsuccessful clinical trials [1,2].

Osteoarthritis (OA) is the most common form of arthritis [3] with a high unmet medical need for disease-modifying treatments. It is characterised by structural damage to cartilage and periarticular bones, and is often accompanied by low-grade inflammation, resulting in pain and disability. Currently, no pharmacological treatment is available that could slow down or stop OA progression. The lack of therapeutic success other than physiotherapy [4] is attributed, at least in part, to the inability to enrich clinical trials with progressive patients [5].

The increasing amount of data from OA studies opens up the possibility of using machine learning (ML) algorithms to inform the patient selection process. Although these algorithms require extensive experimentation and parameter tuning, they can extract complex patterns present in the data overlooked by simpler methods routinely used in medical science [6]. Recent diagnostic applications of ML models to medical images resulted in expert-level performance [7]. However, that was only possible with large and consistently formatted datasets.

The IMI-APPROACH consortium brings together data from five OA cohorts, runs a new prospective clinical study focusing on knee OA [8], and uses it as a “clinical trial of ML”. That is, an ML-supported selection strategy is implemented in the cohort recruitment to prioritise progressive patients, and is validated after 24 months using the follow-up data. The objective of this work is to realistically estimate how well this selection strategy could work if used in a clinical trial. Therefore, in this article we (1) describe the design of the ML-supported selection strategy, (2) evaluate its performance in simulated recruitment scenarios, and finally (3) prospectively analyse the accuracy of the generated patients ranking. We specifically focus on the enrichment in progressors among the top patients and the stochastic differences between ranks of progressors and non-progressors.

2. Methods

2.1. Overview

Patients from existing cohorts across five European clinical centres were identified and enrolled into the IMI-APPROACH study using a two-stage recruitment process. In both stages, we used specialised machine learning models trained to categorise the patients into four groups, representing different level of observed disease progression. In the first stage, historical data were used to predict the probability that a given patient will progress within the two-year duration of the IMI-APPROACH study. Based on the likelihood of progression, patients in each cohort were ranked, and those with highest ranks were invited to the second stage.

Invited patients went through a supplemental screening visit, during which, up-to-date measurements of pain intensity and radiographic features of the index knee were collected. The probability of progression was predicted again, and the final ranking was constructed for enrolment. Based on the ranks, the top 75% of the screened patients were enrolled in the study.

After 24 months, the actual progression was measured, and the positioning of progressive patients in the screening ranking was evaluated.

2.2. Data

Table 1 describes the source cohorts used in the study. HOSTAS [9] and DIGICOD [10] cohorts included primarily hand OA patients, but as OA commonly affects more than one joint, these patients often develop knee OA as well. PROCOAC [11] and CHECK [12] are the largest long-running European cohorts focused on knee and hip OA. Finally, MUST [13] is a general OA cohort with no follow-up visits. All data were de-identified by the cohort owners before analysis.

Table 1.

Characteristics of the cohorts used in model training and recruitment.

cohort	location	patients	median age	sex (M/F)	visits	activity	focus
MUST	Oslo, NO	630	64	30%/70%	1	2010–2013	–
HOSTAS	Leiden, NL	538	62	16%/84%	3	2009–2017	hand
DIGICOD	Paris, FR	377	67	16%/84%	2	2013–2017	hand
PROCOAC	A Coruña, ES	983	68	26%/74%	7	2002–2016	knee/hip
CHECK	Utrecht, NL	1002	58	20%/80%	10	2006–2015	knee/hip

Because each of the source cohorts followed a different study protocol, syntactic and semantic incompatibilities between them were inherent and had to be resolved through data harmonisation. Typically, the harmonisation ends with a single dataset with a common subset of attributes (shared across all cohorts). In our case, the resulting common subset was too small to define OA progression. Therefore, instead of harmonising all data into a single dataset, we performed a custom made pairwise harmonisation to a reference cohort (CHECK). For all cohorts, the mapping to CHECK was possible only for 10–30% of the original attributes (see eTable 1 in the Supplement).

2.3. Patient categories

Patient categorisation [7] used in this work shares some similarities with the FNIH biomarker study [14] and includes one non-progressive category (N) and three progressive categories related to pain (P), structure (S), and combined pain and structure (P ​+ ​S). Structural progression was measured using radiographic readings of minimum joint space width (JSW), performed with Knee Images Digital Analysis (KIDA) [15]. Pain was measured using the pain subscale from the WOMAC questionnaire [16]. Progression was analysed for periods of observation no shorter than two years to match a typical length of a clinical trial (see eFig. 1 in the Supplement).

To decide the category, measurements at the beginning and at the end of a period were compared. A period was assigned the S category if the minimum JSW decreased by at least 0.3 ​mm per year. A period was assigned the P category if the pain increased at least by the minimal clinically important difference per year (5 points on a 0–100 scale) and was substantial at the end of a period (at least 40 points). For a rapid pain increase of at least 10 points per year, the end pain threshold was lower (at least 35 points). The P category was also assigned if substantial pain (at least 40 points) was sustained at both the start and the end of a period. A period was assigned the P ​+ ​S category if criteria for both P and S were satisfied, and the remaining N category if neither of them was satisfied.

2.4. Classification algorithm

The machine learning strategy was chosen based on previous experiments with CHECK and OAI cohorts [17]. We used a multi-model approach (duo classifier) built on top of the cost-sensitive variant of the random forest algorithm [18], where the probability of satisfying the progression criteria (pain or structure related) was independently estimated by two sub-models (see eFig. 2 in the Supplement).

2.5. Model scoring

To express the clinical preference for patients in P ​+ ​S category and to realistically estimate the effect of selection of top patients from the ranking, we designed a domain-specific recruitment score that represents an average quality of simulated selections of different size (see eEquation 2 in the Supplement). We used it to pick the best model parameter configuration.

2.6. Recruitment

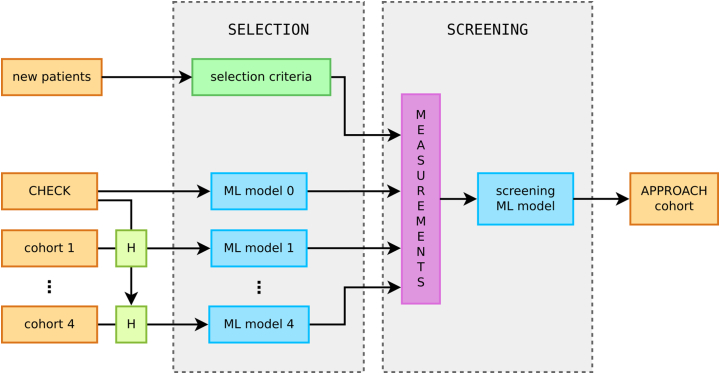
Initially, we expected the recruitment to be performed with two independent machine learning models. A selection-specific model, trained to identify patients from the harmonised cohort to invite for a screening visit, and a screening-specific model, trained to support the post-screening enrolment decisions. However, the pairwise harmonisation resulted in five different datasets (four harmonised and the original CHECK cohort) and required training of cohort-specific selection models. Fig. 1 shows the two stages of the recruitment and the ML models used in the process.

Fig. 1.

Two stages of the recruitment process. All historical data were pairwise harmonised to CHECK to train the cohort-specific models. These models were used to score each patient and construct a ranking of candidates for the screening visit. Up-to-date measurements taken at the screening visit were used by the screening model to generate the final ranking, from which ≈75% of patients were enrolled into the IMI-APPROACH cohort. Option to recruit new patients from outside of the existing cohorts was part of the contingency plan and rarely used (mainly in Oslo).

2.6.1. Selection stage

As all cohorts have been harmonised to a common subset of attributes with CHECK, we trained each selection model on the CHECK data (using it as a proxy for the real cohort) and then made predictions using the real cohort patients's data (specifically, the most recent visit). The data were used unfiltered and the distribution of the categories across periods was: 63% N, 12% P, 20% S and 5% P ​+ ​S.

Due to the variable timing of the historical visits (see eTable 3 in the Supplement), an additional complication occurred. The model training had to be adjusted, to ensure that when a patient's most recent visit has taken place several years prior, the model still predicts progression during the period of the IMI-APPROACH study, that is shifted forward in time (see Fig. 2 for illustration). As a result, multiple selection models were trained with different time shifts: 4 for HOSTAS, 3 for PROCOAC and DIGICOD, 2 for MUST, and 1 for CHECK patients.

Fig. 2.

Illustration of a shift in time between the most recent visit and the period in which the disease progression needs to be predicted.

To construct a balanced aggregated ranking for each cohort we applied three different ranking functions and a shift-dependent penalty (for details see eMethods 1.3.6 in the Supplement).

2.6.2. Screening stage

The screening model was trained on the CHECK data limited to a subset of attributes measured during the screening visit including: basic patient information (age, sex, BMI), pain intensity questionnaires (KOOS, NRS), and KIDA radiographic features (bone density, eminence height, joint space width, femoral-tibial angle, osteophyte area). These attributes had high impact on the decisions of the all-attribute model and were practical to measure during a short visit.

We assumed that all patients at this stage will fulfil the American College of Rheumatology (ACR) classification criteria for knee OA, and we filtered out from the training set all periods that did not satisfy them at baseline. The filtering reduced the number of training periods from 3001 to 1917 and the distribution of categories was altered to 61.1% N, 15.5% P, 17.5% S and 5.8% P ​+ ​S.

The screening process remained open to new patients, from outside of the existing cohorts. They were subject to the same inclusion/exclusion criteria (see NCT03883568) and were evaluated by the same screening model.

2.7. Enrolment

The enrolment objectives were: (1) to include approximately 300 patients in total, (2) to balance the proportion of enrolled to rejected patients at the 3:1 level (≈25% rejections) locally (for each recruitment centre) and globally (for the entire study), (3) to distribute the screening visits across the recruitment centres according to the inclusion targets: 150 in Utrecht, 30 in Oslo, 30 in A Coruña, 60 in Leiden, and 30 in Paris. Due to limitations in centres capacity and patient availability, the inclusion targets were modified to 50 in Leiden and 20 in Paris, and the other three centres included more patients to compensate.

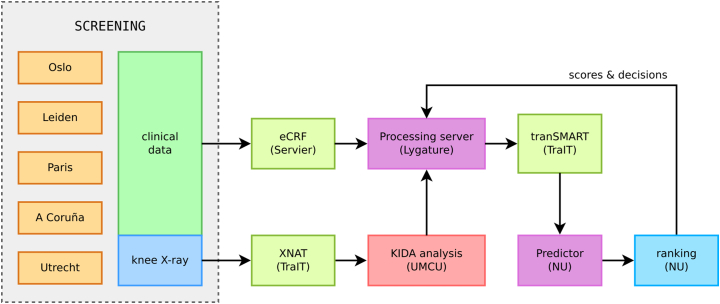
The enrolment decisions were made weekly, following the availability of new screening data. To closely monitor the enrolment progression and minimize delays, we developed a web application to support the decision making process. It automatically fetched new patient data, used the screening model to make predictions and generated the ranking, visualised the current progress, and allowed to preview the impact of an enrolment decision before it was made. Fig. 3 illustrates the exact flow of data after the screening visit.

Fig. 3.

Data flow between project partners during the decision-making process. The clinical data were entered into an electronic case report form (eCRF) and the index knee radiographs were uploaded to the XNAT database [16]. The images were analysed centrally at Utrecht (which took 1–2 weeks), and the resulting KIDA readings together with the eCRF data were imported to the tranSMART data warehouse [17]. After that, the screening model predictions were made and the patients were ranked. Based on that ranking, each centre capacity and inclusion numbers, enrolment was decided and the baseline visits were scheduled no later than 9 weeks after the screening visit.

2.8. Validation

The recruitment strategy was validated using the actual progression observed at the end of the study. The evaluation used 223 patients with complete pain data and KIDA radiographic features at 24-month follow-up. Each patient was assigned a progression category, using the same criteria as in the model training.

To verify the usefulness of the ranking, that is whether progressive patients were given higher rank than non-progressors, we compared the distribution of ranks between patients in different categories, and the proportion of progressors in the top and the bottom half of the ranking.

Additionally, the screening model prediction quality was assessed with the F₁ score and area under the ROC curve (AUC), using the separate P and S probabilities returned by the model. F₁ score is a measure of a binary classifier performance used in information retrieval and was designed for problems with rare positive examples. F₁ score is defined as a harmonic mean of positive predictive value (precision) and sensitivity (recall), and it attempts to balance conflicting goals of retrieving as little false positives as possible (high precision) while retrieving all relevant information (high recall). Compared to the AUC, the F₁ score represents a trade-off between true positives, false positives and false negatives, while AUC represents a trade-off between true positives and false positives alone.

2.9. Statistical analysis and performance comparison

In model selection and parameter tuning, the ML model performance was estimated on samples not used in training with repeated 10-fold stratified cross-validation, which resulted in 2500 models tested per parameter configuration. Throughout the article, the median score across all cross-validation repeats is reported (for details see eMethods 1.3.2 in the Supplement).

In comparison of ranks a one-sided non-parametric Mann-Whitney U test was used, with correction for ties and continuity, and significance level α ​= ​0.025. For each comparison, group medians, the U test value, the effect size (rank-biserial correlation [19]), and the p-value was reported.

Confidence intervals of the screening model classification performance were computed using the bootstrap percentile method (n ​= ​1000).

All ML experiments were performed using the scikit-learn library [20]. In data harmonisation, preprocessing, analysis and generation of statistics, we used pandas [21], NumPy [22], and SciPy [23]. For data visualisation we used seaborn [24] and Matplotlib [25].

3. Results

3.1. Selection of the best models

We performed a large number of simulated recruitment experiments to find best model parameters (maximising the recruitment score). Table 2 shows the results for all models (selection and screening) with the best of the three ranking functions. Often the recruitment score and other measures (F₁ score, AUC) disagreed on the choice of the best model configuration, as the latter do not model the clinical preference for enriched cohort, but only focus on the pure classification performance.

Table 2.

Results of the simulated recruitment for model configurations with the highest recruitment score. For each model the proportions of recruited patients in non-progressive category (N), and three progressive categories related to pain (P), structure (S), and combined pain and structure (P ​+ ​S) are shown. Additionally, the value and the corresponding rank amongst all configurations (in brackets) of the F₁ score and the area under the ROC curve is given, together with the recruitment score (RS) using progressive weights.

selection model	r.fun.	N	only P	only S	P ​+ ​S	F1 score	AUC(P)	AUC(S)	RS
MUST, 3y shift, top 60	sum	45%	37%	12%	7%	0.658 (32)	0.696 (50)	0.429 (70)	0.216
MUST, 5y shift, top 60	sum	50%	38%	7%	5%	0.669 (15)	0.803 (11)	0.514 (65)	0.164
HOSTAS, no shift, top 60	sum	23%	52%	7%	18%	0.458 (83)	0.628 (43)	0.570 (62)	0.428
HOSTAS, 2y shift, top 60	sum	42%	32%	15%	12%	0.478 (83)	0.642 (12)	0.482 (44)	0.336
HOSTAS, 3y shift, top 60	sum	47%	37%	10%	7%	0.597 (77)	0.718 (1)	0.449 (72)	0.196
HOSTAS, 5y shift, top 60	sum	67%	27%	5%	2%	0.584 (76)	0.696 (10)	0.548 (5)	0.068
DIGICOD, no shift, top 30	z-score	27%	40%	7%	27%	0.422 (71)	0.735 (28)	0.596 (8)	0.379
DIGICOD, 2y shift, top 30	z-score	43%	30%	10%	17%	0.468 (82)	0.643 (45)	0.597 (16)	0.292
DIGICOD, 3y shift, top 30	sum	50%	37%	10%	3%	0.596 (77)	0.680 (28)	0.353 (43)	0.113
PROCOAC, 2y shift, top 30	z-score	23%	30%	27%	20%	0.510 (79)	0.695 (12)	0.592 (11)	0.438
PROCOAC, 3y shift, top 30	sum	40%	47%	7%	7%	0.626 (75)	0.677 (72)	0.392 (35)	0.200
PROCOAC, 5y shift, top 30	sum	50%	40%	7%	3%	0.615 (77)	0.679 (35)	0.476 (19)	0.128
CHECK, 2y shift, top 150	z-score	35%	31%	21%	14%	0.507 (59)	0.697 (20)	0.621 (2)	0.449
screening model, top 150	z-score	29%	30%	18%	23%	0.544 (47)	0.667 (60)	0.617 (36)	0.537
uninformed selection		63%	12%	20%	5%	—	—	—	—

The exact differences in simulated recruitment between the model with a highest F₁ score and models with a highest recruitment score (for all ranking functions and weight schemes) are detailed in eTables 5–18, and the distribution of F₁ and AUC scores is shown in eFigs. 4–17 in the Supplement. The difference in favour of the recruitment score is visible for all models and is bigger for the models with a smaller time shift.

3.2. Harmonisation and model confidence

To ensure that models trained on harmonised data do not return vastly different predictions compared to those trained with all CHECK attributes, we compared the probability distributions returned by the models (see eFig. 18 in the Supplement). The differences were more prominent for pain but minor overall.

We performed a similar comparison for selection models using different time shifts. We found a decline in model confidence with the increased time shift (see eFig. 19 and further analysis of joint distributions in eFigs. 20–33 in the Supplement).

3.3. Screening model trustworthiness

To understand the decision-making mechanism of the screening model we analysed the relative importance of each attribute as estimated by the Random Forest algorithm. The output of the model with respect to pain was influenced the most by the WOMAC scores (total score and the three sub-scores) and NRS pain, and with respect to structure by minimum JSW. and to a lesser degree by femoral-tibial angle, mean JSW, the eminence height, and the osteophytes area in the medial tibia region. For a detailed ranking (also for other models) see eFigs. 34–39 in the Supplement.

3.4. Screened patients

Table 3 provides an insight into the characteristics of patients who went through the screening visit. The group is far from being uniform but with almost no differences between men and women (except the slightly higher reported pain).

Table 3.

Characteristics of patients who completed the screening visit. Median, 1st and 3rd quartile are reported (except the last column).

	Age	BMI	JSW Min	JSW Mean	WOMAC Pain	Pain Now	Count
Women	68 [62–72]	26.7 [24.0–30.3]	2.49 [1.63–3.16]	5.36 [4.71–6.02]	25 [10–45.0]	3 [1–5]	76.5%
Men	69 [62–72]	26.5 [24.2–30.2]	2.74 [1.65–3.43]	6.05 [5.37–6.67]	25 [10–37.5]	2 [1–5]	23.5%

3.5. Ranking and enrolment decisions

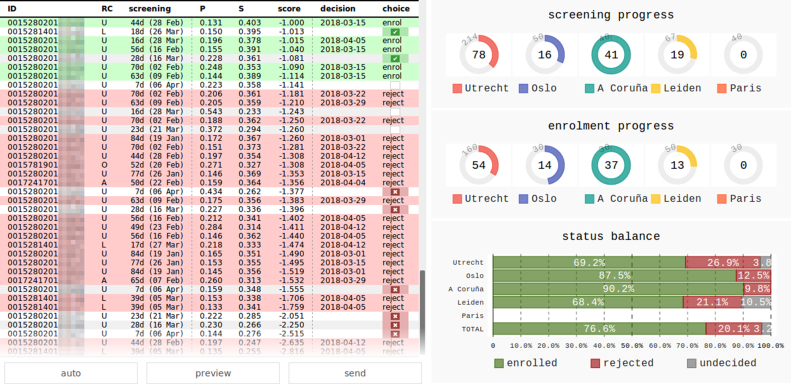
The flexible, threshold-free approach to enrolment decision, allowed us to balance the recruitment at each centre, and at the same time achieve the global target of ≈25% rejections (see eTable 4 in the Supplement for exact numbers). It was facilitated by the development of an online decision support tool (see Fig. 4), that allowed us to monitor the state of recruitment, and preview the impact of decisions before making them.

Fig. 4.

Screenshot of the web-based tool used to make the enrolment decisions. Patients screened so far in all recruitment centres (RC) are listed in the ranking score order. Patients without decision are in white rows, enrolled are in green, and rejected are in red rows. The choice column shows a decision being made with a tick or a cross. The plots on the right show number of screened and enrolled patients per RC, and the balance between enrolled and rejected patients (total and per RC).

Supplementary Video 1 shows a time lapse of the state of the ranking and the results of all the recruitment decisions. Each enrolment decision had to be made within a fixed 9-week window between the screening and the baseline visit. Typically, there was a 1–2 weeks wait to complete the image assessment before the screening model could rank a patient, and with 2–3 weeks needed for visit scheduling, this resulted in 4–6 weeks to decide who to enrol/reject. That decision window was useful in case of “borderline” patients, as it was possible to wait for more patient data (more context) and make better informed decisions.

The following is/are the supplementary data related to this article.

Video S1

Time lapse of the recruitment decisions and state of the ranking between February 2018 and March 2019.2

3.6. Recruitment validation

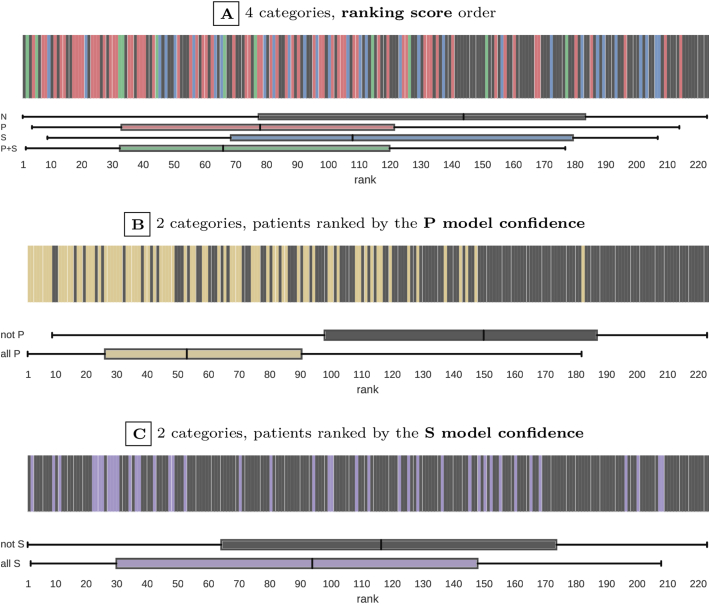
The actual progression observed at the 24-month follow-up visit was used to evaluate the quality of the screening model ranking. Fig. 5A shows the exact positions of progressive patients in the ranking. The P ​+ ​S patients, on whom we focused the recruitment, had over two times higher median rank than non-progressive patients. Specifically, the ranks of progressors were higher than non-progressors for P ​+ ​S patients (median rank 65 vs. 143, U ​= ​323, ES ​= ​0.489, P ​= ​0.004), P patients (median rank 77 vs. 143, U ​= ​2200, ES ​= ​0.429, P ​< ​0.001), and S patients (median rank 107 vs. 143, U ​= ​1483, ES ​= ​0.140, P ​= ​0.112). Overall, over 75% of P ​+ ​S and P patients were ranked higher than the median non-progressive patient.

Fig. 5.

Distribution of the actual progressors in the screening model ranking (based on 2-year follow-up). Patient categories are represented with colours. Subfigure A compares four categories: no progression (N), only pain-related progression (P), only structure-related progression (S), and combined progression (P ​+ ​S). Subfigures B and C compare two categories: all pain-related progression (P∪P ​+ ​S) vs. others (N∪S), and all structure-related progression (S∪P ​+ ​S) vs. others (N∪P). The top (highest) rank is 1. The distribution of ranks within each category is summarised with a box plot. The box edges mark lower and upper quartiles, with median shown in the middle, and whiskers indicate the minimum and maximum rank.

The differences in rank distribution become even more clear when four patient categories are reduced to a binary choice: all P (P∪P ​+ ​S) vs. not P (N∪S) shown in Fig. 5B (median rank 52 vs. 149, U ​= ​1618, ES ​= ​0.714, P ​< ​0.001), or all S (S∪P ​+ ​S) vs. not S (N∪P) shown in Fig. 5C (median rank 92 vs. 115, U ​= ​2890, ES ​= ​0.225, P ​= ​0.012).

The distribution of categories amongst the recruited patients was: 51.57% N, 30.4% P, 13.45% S, and 4.93% P ​+ ​S. In the top half of the ranking, the proportion of non-progressors decreases to 36.04% and all the progressive categories are enriched: 43.24% P, 14.41% S, and 6.31% P ​+ ​S. The opposite happens in the bottom half, the proportion of non-progressors increases to 66.96% and all the progressive categories get smaller: 16.96% P, 12.50% S, and 3.57% P ​+ ​S. Comparing the two halves, the top one had almost two times more P ​+ ​S patients, and over 2.5 times less non-progressors. We can estimate how an unenriched population would look like from the class distribution in the CHECK cohort (our training set) and observe that it would have ∼20% more non-progressors, 50% less P patients, but ∼30% more S patients and ∼20% more P ​+ ​S patients.

The actual classification performance of the screening model was at the same level or higher than what was estimated with cross-validation on CHECK data: F₁ score of 0.60 [95% CI, 0.53–0.67] (vs. 0.54), AUC(P) of 0.86 [95% CI, 0.81–0.90] (vs. 0.67), AUC(S) of 0.61 [95% CI, 0.52–0.70] (vs. 0.62). Further statistical analysis of the observed progression has been published elsewhere [26].

4. Discussion

Due to inherent diversity in underlying aetiology and disease progression among patients, enriching OA clinical trials for participants likely to benefit from a treatment is a complex problem with several practical constraints. A straightforward application of machine learning was not possible and several pragmatic adjustments to the recruitment process had to be made to address data limitations, lower accuracy of the models, and visit scheduling constraints.

The observed enrichment at 2-year follow-up was smaller than in the simulated recruitment, despite that (1) the screening model classification performance was better than estimated with cross-validation, and (2) a significant difference between the ranks of progressors and non-progressors was found. This is likely a result of conservative rejection rate (25% only). In a recent large OA clinical trial (NCT03595618), 3.5 times more patients were screened than enrolled (rejection rate >75%). That is equivalent to rejection of the bottom 50% of our ranking, which would result in only 36% of non-progressors (vs. estimated 29% for the screening model). However, a small number of enrolled P ​+ ​S patients (6% vs. estimated 23%) reveals scope for further improvement. With broader and more precise data now collected in a uniform manner for the IMI-APPROACH cohort (serum/urine markers, MRI/CT imaging, motion sensors, a broad range of questionnaires), further research is needed to develop the next iteration of the selection strategy, targeting more sensitive outcomes (e.g. loss of cartilage thickness) or focusing more on e.g. functional limitations rather than pain, and possibly directly estimating the outcomes future values (i.e. moving from classification to a regression problem).

4.1. Flexibility

The proposed recruitment process not only targets the clinically relevant patients more accurately, but also is more flexible than the conventional inclusion criteria. Namely, it can (1) predict the progression in a specific time-window, matching the duration of a trial, (2) use the predictions to rank patients in order of clinical preference, (3) use the ranking to balance the enrolment across multiple recruitment centres, and (4) achieve assumed inclusion targets without sacrificing the rejection ratio.

4.2. Effort

The implementation of the recruitment strategy required a lot of effort. Starting from data harmonisation, through training and evaluation of multiple machine learning models, to maintaining efficient data transfers for each round of the enrolment decisions. However, in a general case much less effort might be necessary. For example, time shifted models would not be needed, if the source cohorts had recent visits. Similarly, a single selection model would be enough if the cohort's protocols were more aligned (e.g., had the same primary joint) and harmonisation into a single dataset was possible. Furthermore, the screening stage could have been omitted with the screening model applied directly to the cohort data if these were complete and recently collected.

4.3. Limitations

The differences between the cohort protocols limited the harmonisation options, and forced a non-direct approach to model training, with the CHECK cohort as a proxy. This resulted in selection models trained on a different population than the one the predictions were made for. Although in simulated recruitment the proxy effect on model performance was smaller than the effect of the time shift, better results (a higher ranking score) for cohorts other than CHECK could be expected, if a direct training is possible.

Similarly, the screening model was trained on the CHECK cohort, but applied to patients from all five cohorts. That makes it by definition more tuned to correctly rank the CHECK-like patients. If it could have been trained on mixed-cohort data, it would have adjusted better to the inherent differences in patient demographics.

Given that for a large time shift the model performance was only slightly better than a random choice, the importance of the selection stage could be questioned. Better results could be obtained by screening more patients, as the prediction on up-to-date data was more confident.

Additionally, some of the selection stage models has focused on patients with higher age and BMI (see eFig. 39 in the Supplement), who might not be the ones responding well to new treatments. This could be avoided if the screening model was used alone.

The standard measures we based the progression on (WOMAC, JSW), are rather insensitive and require a long observation window [2,27]. To shorten the clinical trial time more precise and less error-prone measures of progression are needed.

4.4. Relation to previous research

Multiple aspects of patient recruitment have been studied before. From patient engagement and retention [28] (including the use of advertising to accelerate recruitment, or methods to predict whether a patient will accept an invitation to a trial), through modelling of the recruitment rates and timelines [29], prediction of the recruitment centre performances [30], prediction of treatment outcomes based on past clinical trials [31], to finally, the clinical trial matching platforms helping patients to find ongoing trials in which they could take part, and trial recruitment support systems (CTRSS) that allow searching for eligible patients in databases of medical records [32]. When such databases do not exist, natural language processing systems have been used to categorise clinical notes directly [33].

However, patient selection considering the disease progression and its pace has been understudied. This work represents the first attempt to design and implement in clinical practice a ML-supported strategy to select fast progressing OA patients, which could be applied in future interventional trials to increase their efficiency. Although the strategy was discussed in context of OA, it could generalise to trials in other diseases where retrospective data is available.

Author contributions

Conceptualisation: Bacardit, Bay-Jensen, Berenbaum, Blanco, Haugen, Kloppenburg, Ladel, Lafeber, Lalande, Larkin, Loughlin, Marijnissen, Mobasheri, Weinans, Welsing, Widera — Methodology: Bacardit, Welsing, Widera — Software: Danso, Widera — Formal analysis: Widera — Investigation: Danso, Berenbaum, Blanco, Haugen, van Helvoort, Kloppenburg, Loef, Magalhães, Marijnissen, Welsing, Widera — Resources: Bacardit, Bay-Jensen, Berenbaum, Blanco, Haugen, Kloppenburg, Ladel, Lafeber, Lalande, Larkin, Loughlin, Marijnissen, Mobasheri, Weinans — Data curation: Danso, Peelen — Writing – Original Draft: Widera — Writing - Review & Editing: all authors — Visualisation: Widera — Supervision: Bacardit, Ladel, Lafeber, Lalande, Loughlin — Project Administration: Bacardit, Ladel, Lafeber, Lalande, Larkin, Loughlin, Weinans — Funding Acquisition: Bacardit, Bay-Jensen, Ladel, Lafeber, Lalande, Larkin, Loughlin, Mobasheri, Weinans.

Role of funding

The research leading to these results has received support from the Innovative Medicines Initiative Joint Undertaking under Grant Agreement no.115770, resources of which are composed of financial contribution from the European Union's Seventh Framework Programme (FP7/2007-2013) and EFPIA companies' in kind contribution. See www.imi.europa.eu and www.approachproject.eu. This communication reflects the views of the authors and neither IMI nor the European Union and EFPIA are liable for any use that may be made of the information contained herein.

The funder of the study had no role in study design, data collection, data analysis, data interpretation, or writing of the article.

Data sharing

Data are available on reasonable request. Access to de-identified participant data and other documents (study protocol, consent form, statistical analysis plan) can be requested from the IMI-APPROACH Steering Committee.

Ethical approval information

The study is being conducted in compliance with the protocol, Good Clinical Practice (GCP), the Declaration of Helsinki, and applicable ethical and legal regulatory requirements (for all countries involved), and is registered under clinicaltrials. gov no. NCT03883568. All participants have received oral and written information, and provided written informed consent.

Declaration of competing interest

A. Bay-Jensen is a full-time employee and shareholder of Nordic Bioscience. C. Ladel was an employee of Merck KGaA at the project start. A. Lalande is employed by Institut de Recherches Internationales Servier. J. Larkin is employed by, and shareholder in GlaxoSmithKline. I.K. Haugen consults for Novartis and has received funding from Pfizer. M. Kloppenburg receives consulting fees from Abbvie, Pfizer, Levicept, GlaxoSmithKline, Merck-Serono, Kiniksa, Flexion, Galapagos, Jansen, CHDR, Novartis, and UCB. F. Berenbaum reports personal fees from AstraZeneca, Boehringer, Bone Therapeutics, CellProthera, Expanscience, Galapagos, Gilead, Grunenthal, GSK, Eli Lilly, Merck Sereno, MSD, Nordic, Nordic Bioscience, Novartis, Pfizer, Roche, Sandoz, Sanofi, Servier, UCB, Peptinov, 4 ​P Pharma, 4 Moving Biotech and grants from TRB Chemedica, outside the submitted work. F.J. Blanco has received consulting fees or other remuneration from AbbVie, Pfizer, UCB, Bristol-Myers Squibb, Roche, Servier, Bioiberica, Sanofi, Grünenthal, GlaxoSmithKline, Lilly, Janssen, Regeneron, Amgen, and TRB Chemedica, outside the submitted work. A. Mobasheri receives fees/funding from Merck KGaA, Kolon TissueGene, Pfizer, Galapagos-Servier, Image Analysis Group (IAG), Artialis, Aché Laboratórios Farmacêuticos, AbbVie, Guidepoint Global, Alphasights, Science Branding Communications, GSK, Flexion Therapeutics, Pacira Biosciences, Sterifarma, Bioiberica, SANOFI, Genacol, Kolon Life Science, BRASIT/BRASOS, GEOS, MCI Group, Alcimed, Abbot, Laboratoires Expansciences, SPRIM Communications, Frontiers Media, and University Health Network (UHN) Toronto. No other disclosures were reported.

Handling Editor: Professor H Madry

Appendix A. Supplementary data

The following are the Supplementary data to this article.